Appendix A
Characteristics of STRIDE Cocaine Data
This appendix provides supplementary information on characteristics of the System to Retrieve Information from Drug Evidence (STRIDE) cocaine data. STRIDE contains data on acquisitions of illegal drugs by the Drug Enforcement Administration (DEA) and the Metropolitan Police of the District of Columbia (MPDC). This discussion, which complements the description of the STRIDE data in Chapter 3, is oriented toward assessing the usefulness of STRIDE for constructing price indices for cocaine. The statistics reported in this appendix are obtained from the version of the STRIDE data that was supplied to the committee by the DEA. The DEA revises the contents of STRIDE from time to time, so the results reported here may not coincide precisely with results that are obtained from other versions of the data. The committee is confident, however, that the main qualitative conclusions reached using its version of STRIDE would also be reached using other versions.
SPARSENESS OF THE DATA
There are over 160 DEA field offices in the United States. Each is responsible for a geographical area surrounding the city in which it is located. In any given year, STRIDE contains few or no records of purchases by most field offices. This is especially true for small purchases. In 1996, for example, 35 percent of the field offices recorded no purchases of cocaine base. Another 34 percent recorded only 1–9 purchases. Moreover, 55 percent of the offices recorded no purchases of cocaine base in quanti-
ties of 5 gm or less, and 32 percent recorded only 1–9 such purchases. Only 6 percent of field offices recorded more than 50 purchases of cocaine base, and only 2 percent recorded more than 50 purchases of quantities of 5 gm or less. These statistics vary somewhat among years and forms of cocaine (powder cocaine and cocaine base), but the message they convey remains the same. It is that in any given year, STRIDE contains little or no information about the price of cocaine, especially the price of retail quantities, in most of the geographical areas covered by DEA field offices.
The sparseness of the STRIDE data limits their usefulness for constructing price indices. There are few cities in which there are enough records of purchases to make precise estimates of prices and price functions, especially for retail quantities. One way of dealing with this problem is to construct price indices only for the few cities for which STRIDE contains relatively large numbers of observations. Many policy studies, however, have used STRIDE to construct a price index for the nation as a whole by pooling all of the STRIDE price data for a given time period. Such a procedure would be acceptable if the price functions of interest were the same in all regions of the country and for all forms of cocaine. As discussed later, however, prices recorded in STRIDE differ greatly among cities and forms of cocaine.
Some studies have attempted to compensate for these differences by allowing the levels of the price functions of different cities to be different. That is, the price functions in different cities are assumed to be parallel lines or curves. Some studies also assume that the distances between the price functions of different cities remain constant over time. However, price functions estimated from STRIDE data have different shapes in different cities and for different forms of cocaine, and the distances between different price functions change over time. Compensating for different shapes as well as variations in levels over time requires estimating a different price function for each city and form of cocaine in each year, but this is not possible because of the small number of observations in STRIDE for most cities. Thus, the STRIDE data can be used to construct a national price index for cocaine only by assuming that price functions in different cities are similar in certain ways—but the STRIDE data can be used to show that the required assumptions are false.
VARIABILITY OF SAMPLE CHARACTERISTICS
The characteristics of the STRIDE data vary greatly among the cities in which the number of observations is relatively large. The characteristics also vary among years within these cities. The figures and table that follow illustrate this variation. Figure A.1 shows year-to-year variations in the numbers of recorded purchases of cocaine base in four cities. Until
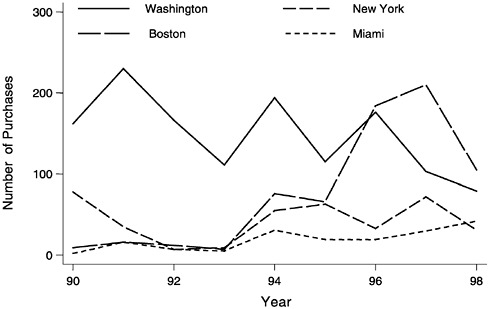
FIGURE A.1 Numbers of purchases of cocaine base in four cities.
1996, there were more purchases in Washington, D.C., than in the other cities.1 After 1996, there were more purchases in Boston than elsewhere. Throughout the period 1990–1998, there were more purchases in Washington, D.C., than in New York, although Washington, D.C., is a smaller city than New York. Boston is also smaller than New York, but in 1996– 1998 there were more purchases in Boston than in New York.
Figure A.2 shows year-to-year variations in the fraction of cocaine purchases of amounts of 5 gm or less in each of four cities. In New York, the fraction of such “small” purchases varies between 5 percent and 47 percent, depending on the year. The fraction of small purchases in Boston increased over the period 1990–1998, whereas there was no strong trend in the other cities. The fraction of small purchases tends to be lower in Detroit than in the other cities except in 1990–1991, when the fraction was lower in Boston.
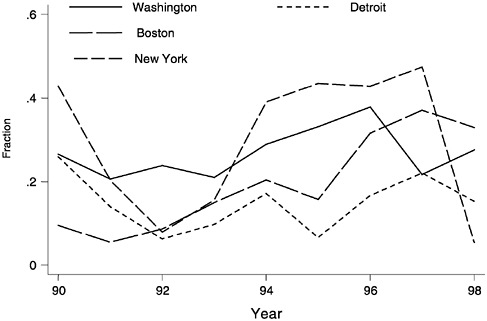
FIGURE A.2 Fractions of cocaine purchases of 5 grams or less in four cities.
Figure A.3 shows the ratio of cocaine seizures to purchases in four cities. Until 1997, the ratio was larger in Miami than in the other cities. The ratio in Chicago increased over the period and exceeded that in Miami in 1998. By contrast, the ratio in Boston decreased over time.
Table A.1 provides further evidence of the variation over time and among cities of the characteristics of the STRIDE data. This table shows year-to-year variations in the median quantities of cocaine base purchased in each of four cities during 1990–1998. The variations in the medians are large within cities over time and among cities. For example, the ratio of the highest to lowest median purchase is 13 in Boston and 20 in New York. In 1996, the median quantity purchased in Detroit was 20 times larger than the median quantity purchased in Boston.
STRIDE does not contain information that reveals the reasons for city-to-city and year-to-year variations in the characteristics of the data. It is likely, however, that much of the variation is due to differences in purchase strategies and law enforcement opportunities among cities and years. Miami, for example, is an important port of entry for cocaine, and this accounts for the large ratio of seizures to purchases there. Chicago has become increasingly important as a transshipment point, and this is likely to account for the increase in the ratio of seizures to purchases
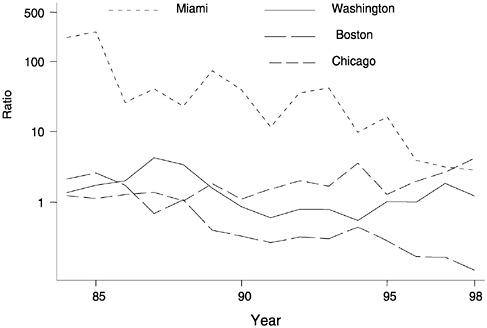
FIGURE A.3 Ratio of cocaine seizures to purchases in four cities.
TABLE A.1 Median Size (gm) of Purchases of Cocaine Base in Four Cities
|
Year |
Boston |
Detroit |
New York |
Washington |
|
1994 |
26 |
22 |
15 |
14 |
|
1995 |
14 |
48 |
7 |
7 |
|
1996 |
2 |
41 |
6 |
9 |
|
1997 |
3 |
23 |
3 |
26 |
|
1998 |
6 |
18 |
60 |
21 |
there. In addition, the relatively low proportions of purchases of below 5 gm shown in Figure A.2 and the larger-than-retail-size median purchase sizes shown in Table A.1 reflect the DEA’s focus on large cocaine dealing operations. Since nearly all cocaine is ultimately sold to consumers in small quantities (less than 5 gm), the total number of retail-size transactions almost certainly exceeds the total number of transactions involving
larger quantities.2 Thus, the distributions of purchase sizes in the STRIDE data for most of the cities and years shown in Table A.1 are unlikely to be representative of the distributions of purchase sizes in real markets. Similarly, it is likely that year-to-year variations in median purchase sizes of factors of 7 (Boston) to 20 (New York) reflect variations in law enforcement activity, rather than in market characteristics.
In summary, the STRIDE data display characteristics that are consistent with the conclusion that the DEA’s data acquisition criteria vary greatly among cities and over time within cities. The characteristics are also consistent with the conclusion that the STRIDE data are not representative of cocaine markets in the cities in which purchases are made. Rather, the data reflect the law enforcement strategies and opportunities of the DEA field offices that made the purchases. Further evidence supporting this conclusion is presented later in this appendix.
DIFFERENCES IN PRICES OF POWDER COCAINE AND COCAINE BASE
Cocaine is sold in several chemically distinct forms, the most important being cocaine powder and cocaine base (crack). Possibly because of the sparseness of the STRIDE data, most existing price indices are based on the assumption that the price of cocaine is independent of its form. Thus, for example, it is assumed that the price of (say) one gram of 65 percent pure cocaine base is the same as the price of one gram of 65 percent pure powder cocaine. This assumption makes it possible to combine the records of purchases of all forms of cocaine in a single dataset for purposes of constructing a price index. The combined dataset is larger than the ones that would be available if the different forms of cocaine were treated separately. However, the practice of combining data on purchases of different forms of cocaine yields misleading results if the different forms have different prices.
As is explained in Chapter 3, there are good reasons for believing that the prices of powder cocaine and cocaine base may be different. The prices of powder cocaine and cocaine base in STRIDE support this belief. The prices of the two forms of cocaine are very different in the STRIDE
data. Caulkins (1997) also found differences between the price functions of powder cocaine and cocaine base.
The prices of different forms of cocaine can be compared by estimating a price function for each form. This section reports the results of estimating price functions of the form
(A.1)
where P is the real price of a purchase (in dollars per gram), Q is the amount purchased (in grams), Π is the purity of the purchased cocaine (expressed as a percentage), and Z is a dummy variable that indicates whether the purchase was made in the central city. Z=1 if the purchase was made in the central city, and Z=0 otherwise. U is an unobserved random variable whose median is zero. Thus, (A.1) is a model for the median price conditional on Q, Π, and Z. Logarithmic models similar to (A.1) are widely used for the analysis of the STRIDE data. The median price is estimated here instead of the mean because (1) the median is less sensitive to outlier price observations than the mean is and (2) the use of the median simplifies the conversion of logarithms of prices to prices. However, estimation of mean instead of median prices does not change the conclusion that the prices of powder cocaine and cocaine base are different. The real price, P, is the nominal price (cost/quantity) divided by the consumer price index for the quarter in which the purchase took place.
Model (A.1) was estimated by using the method of least absolute deviations and STRIDE data for the following cities and years: Boston for 1994–1998, San Diego for 1987–1989, and Washington, D.C., for 1989–1992. STRIDE contains relatively large numbers of purchases of both powder cocaine and cocaine base for these city-year combinations. STRIDE contains few records of purchases of powder cocaine or cocaine base or both for other cities and years. The price of a given quantity, purity, and form of cocaine depends on the number of packages that are purchased. To avoid complications arising from this dependence, only single-package purchases were used to estimate (A.1). The model was estimated separately for powder cocaine and cocaine base in each city-year combination.
The estimation results are summarized in Figure A.4. The figure shows predicted median prices of 0.8 gm of 65 percent-pure powder cocaine and cocaine base that is purchased in the central city. The predicted values are obtained from the formula
(A.2)
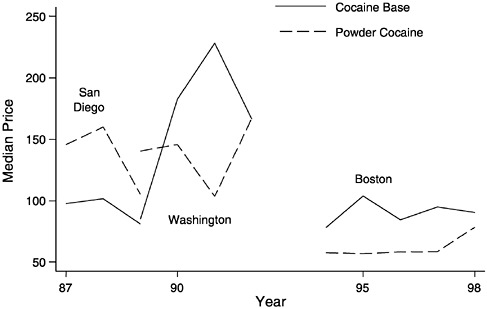
FIGURE A.4 Median prices of powder cocaine and cocaine base in three cities.
where ![]() is the predicted median price and
is the predicted median price and ![]() is the estimated value of βj. It can be seen from the figure that the median prices of powder cocaine and cocaine base are very different.3 There is no systematic relation between the prices of the two forms of cocaine. The price of powder cocaine was higher than that of cocaine base in San Diego during 1987–1989, but the price of cocaine base was higher in Boston during 1994–1998. In Wash
is the estimated value of βj. It can be seen from the figure that the median prices of powder cocaine and cocaine base are very different.3 There is no systematic relation between the prices of the two forms of cocaine. The price of powder cocaine was higher than that of cocaine base in San Diego during 1987–1989, but the price of cocaine base was higher in Boston during 1994–1998. In Wash
ington, D.C., the price of cocaine base was below the price of powder cocaine in 1989 but above it in 1990 and 1991. Some of the price differences are very large. For example, the price of cocaine base is 85 percent higher than the price of powder cocaine in Boston in 1995. In Washington in 1989, the price of powder cocaine was 70 percent above the price of cocaine base. In San Diego in 1988, the price of powder cocaine exceeded the price of cocaine base by 62 percent. In addition, the prices of the two forms of cocaine may move in different directions over time. For example, in Washington, D.C., the price of cocaine base increased from 1989–1991, but the price of powder cocaine decreased over this period. Between 1991– 1992, however, the price of cocaine base in Washington, D.C., decreased, whereas the price of powder cocaine increased.
In summary, the prices of powder cocaine and cocaine base estimated from STRIDE data can be very different. Price indices that are obtained by combining data on purchases of different forms of cocaine (thereby assuming that the prices of different forms are equal) are likely to be misleading.
DIFFERENT PRICE FUNCTIONS IN DIFFERENT CITIES
As is discussed in Chapter 3, there are good reasons for expecting the price functions of powder cocaine and cocaine base to be different in different cities. Consequently, a price index that is obtained by combining price data from different cities can produce misleading results (see the example in Chapter 3). This section uses STRIDE data for cocaine base to illustrate the differences among the price functions of different cities.
The price functions of different cities can be compared by estimating model (A.1) separately for each city. Earlier in this appendix, model (A.1) was estimated by using the method of least absolute deviations and STRIDE data. Estimates were obtained for Boston, Detroit, New York, and Washington, D.C., for 1994–1998. The use of these cities and years provides a relatively large number of observations for the comparison. Likewise, as earlier, only single-package purchases were used. The model was estimated separately for each city and year. Because the price functions of powder cocaine and cocaine base are different, separate price functions must be estimated for each form of cocaine. The price functions used for the illustrations in this section are for cocaine base.
The estimation results are summarized in Figure A.5. The figure shows predicted median prices of 0.8 gm of 65 percent-pure cocaine base that is purchased in the central city. The predicted values are obtained from equation (A.2). There are large differences among the prices in different cities. In 1995, for example, the price in Washington, D.C., was 2.57
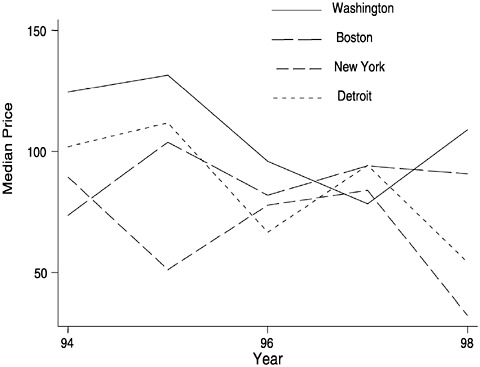
FIGURE A.5 Median prices of cocaine base in four cities.
times the price in New York. Moreover, the relations among the prices in different cities vary from year to year. For example, the price in Detroit was 40 percent above the price in Boston in 1994 and 40 percent below the price in Boston in 1998.4
Because of the sparseness of the STRIDE data, existing price indices are obtained by combining data from different cities. Some analysts have attempted to account for differences in prices among cities by including city-specific intercept terms in (A.1). These allow ß0 to be different in different cities. Intercept shifts allow the price in one city to be a constant multiple of the price in another. As shown in Figure A.5, however, the multipliers that relate prices among different cities vary over time and therefore cannot be accounted for by intercept shifts that are not time varying. Moreover, intercept shifts cannot account for differences among cities or over time in the slope coefficients ß1–ß3. The committee is
aware of only one study in which intercept shifts vary over time and none in which the slope coefficients vary over time and among cities. Thus, no existing studies based on STRIDE fully account for the variation in cocaine price functions among cities and over time. This is probably due to the sparseness of STRIDE data. Fully accounting for all of the variation requires estimating a separate price function for each city and year, but there are not enough observations in STRIDE to permit this for most years and cities. Thus, although combining data from different cities is unavoidable to obtain national-level price indices from STRIDE, such indices are likely to be misleading.
PRICES IN THE STRIDE DATA MAY NOT BE REPRESENTATIVE OF MARKET PRICES
The results presented in the previous sections show that the STRIDE data are sparse, that they reflect variations in law enforcement strategies among cities and over time, that different forms of cocaine have different prices, and that prices are different in different cities. It remains possible, however, that the STRIDE price data for a given city, year, and form of cocaine are representative of market prices for that city, year, and form of cocaine. This section presents evidence suggesting that STRIDE prices are not representative of market prices.
The analysis leading to this conclusion consists of comparing models of the price of cocaine base that are estimated from different subsets of the STRIDE data. The data for the Washington, D.C., area include records of purchases by agents of the DEA and by agents of the Metropolitan Police of the District of Columbia. Separate models of the price of cocaine base can be estimated using the DEA and MPDC purchases. If the DEA and MPDC data were representative of the relations among price, quantity, and purity in the Washington, D.C., area, then the models estimated from each data set would be identical up to the effects of random sampling errors. The evidence presented here, however, suggests that there are large, systematic differences among models estimated from the two datasets.
The estimated model is
(A.3)
In this equation, Pijt denotes the real price of purchase i by agency j(j= MPDC or DEA) in year t. Qijt and Πijt, respectively, are the quantity and purity of cocaine base in purchase i by agency j in year t. VAijt=1 if
purchase ijt took place in the Virginia suburbs of Washington, D.C., and 0 otherwise. MDijt=1 if purchase ijt took place in the Maryland suburbs and 0 otherwise. Only the DEA makes purchases in the Virginia and Maryland suburbs, so VAijt and MDijt are included only if j=DEA. Uijt is an unobserved random variable whose median is zero, and the ß’s are coefficients that are allowed to be different in different years and in the models for DEA and MPDC purchases.
In equation (A.3), the dependence of logP on logQ has the form of a linear spline with a knot at log Q=–1.25. This specification is used because plots of log P vs. log Q or the MPDC data have kinks in the vicinity of log Q=–1.25. Plots of logP vs. logQ for the DEA data do not show kinks, but the spline specification is used for the DEA model to facilitate comparisons with the MPDC model.
Table A.2 shows summary statistics for the DEA and MPDC cocaine base data. It is clear that the DEA is oriented toward larger purchases than is the MPDC. The distributions of the amounts purchased by the DEA and MPDC overlap, however. In particular, both datasets contain purchases of quantities that are below and quantities that are above one gram. Moreover, estimating (A.3) by using only observations for which Q =10 gm does not change the conclusion of this section, which is that that prices estimated from the MPDC and DEA data are systematically different from one another.
The results of estimating (A.3) are shown in Figure A.6. The figure shows the estimated median prices of 0.8 gm of 65 percent pure cocaine base that are obtained using the DEA and MPDC data. The two sets of estimates are very different. The prices estimated from the DEA data exceed those estimated from the MPDC data by 19 percent to 155 percent, depending on the year. Moreover, the DEA and MPDC data produce different estimates of price changes over time. Between 1991 and 1993, the
TABLE A.2 Summary Statistics for Cocaine Base Purchases
|
Agency |
Variable |
Median |
Mean |
|
Metropolitan Police of the District of Columbia |
Cost ($) |
20 |
126 |
|
Quantity (gm) |
0.16 |
2.5 |
|
|
% of purchases of 5 gm or less |
90 |
|
|
|
Purity (%) |
81 |
77 |
|
|
Drug Enforcement Agency |
Cost ($) |
1,000 |
1,369 |
|
Quantity (gm) |
21 |
36 |
|
|
% of purchases of 5 gm or less |
30 |
|
|
|
Purity (%) |
69 |
67 |
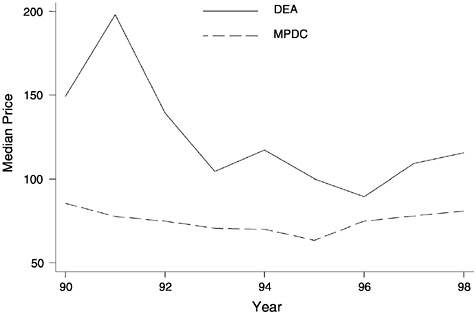
FIGURE A.6 Median prices of cocaine base in Washington, D.C., estimated from Drug Enforcement Agency and Metropolitan Police of the District of Columbia data.
DEA price estimate decreased by 47 percent, whereas the MPDC estimate decreased by only 9 percent.
Conversations with DEA officials have provided a possible explanation for the price differences displayed in Figure A.6. DEA officials believe that agents of the MPDC have better knowledge of local drug markets and greater personal familiarity with retail dealers than do agents of the DEA. Therefore, agents of the MPDC are thought to be able to bargain for lower retail prices than can agents of the DEA. In addition, DEA officials believe that the MPDC has a lower budget for drug purchases than does the DEA, thereby giving MPDC agents a stronger incentive to obtain a low price.
The finding that the DEA and MPDC data lead to different models for the price of cocaine base implies that the DEA and MPDC data on prices of cocaine base cannot both be representative of true market conditions. The data do not provide evidence on whether prices estimated from either data set accurately represent true market conditions. It is possible that one dataset gives a good approximation of true market conditions, whereas the other does not. It is also possible that neither dataset accurately represents true market conditions. Without evidence on this matter, the STRIDE data cannot be relied on to provide accurate estimates of cocaine prices and price changes.















