Teachers' Understanding of Fundamental Mathematics
Following the small-group discussions on the preworkshop assignment from Liping Ma's book Knowing and Teaching Elementary Mathematics (1999), a panel set the stage for thinking about the two overarching questions that were the focus of the workshop:
-
What is the mathematical knowledge teachers need to know to teach well?
-
How can teachers develop the mathematical knowledge they need to teach well?
PANELISTS
Knowledge of Fundamental Mathematics for Teaching
Liping Ma, Stanford University
Elementary Teachers and Essential Mathematical Knowledge
Mark Saul, Bronxville High School
What Is Fundamental Mathematics?
Genevieve Knight, Coppin State College
Knowledge of Fundamental Mathematics far Teaching1
Liping Ma, Cathy Kessel
What mathematical knowledge do elementary teachers use in teaching? About 10 years ago, Deborah Ball and her colleagues at Michigan State University carried out a research project to address this question (Ball, 1988; Kennedy, Ball, & McDiarmid, 1993). Teachers were asked how they would respond to classroom scenarios in which mathematical ideas played crucial roles. As a graduate student, the first author of this paper worked on this project and was struck by the teachers ' responses. Her memories of elementary teaching in China suggested that Chinese teachers would react quite differently.
She investigated this suspicion in her dissertation research, asking Chinese elementary teachers the same questions that had been asked of U.S. teachers. To analyze the responses of both groups of teachers, she developed the notion of profound understanding of fundamental mathematics (PUFM). Fundamental mathematics is a foundation for later learning. It is primary because it contains advanced mathematical topics in rudimentary form, and it is elementary because it is at the beginning of students' learning. Profound has three related meanings —deep, vast, and thorough—and profound understanding reflects all three. A deep understanding of fundamental mathematics is defined to be one that connects topics with ideas of greater conceptual power. A broad understanding connects topics of similar conceptual power. And thoroughness is the capacity to weave all parts of the subject into a coherent whole. Profound understanding of fundamental mathematics is an understanding of fundamental mathematics that is deep, broad, and thorough.
Teachers with PUFM are able to reveal and represent ideas and connections in terms of mathematics teaching and learning. Such teaching and learning tends to be connected, display multiple perspectives, demonstrate awareness of basic ideas of mathematics, and have longitudinal coherence. Like a taxi driver who knows a road system well, teachers with PUFM know many connections among past, present, and future under-
|
1 |
The essence of this paper was contained in the remarks of Liping Ma at the opening panel session of the Workshop. |
standing of mathematics. They know how to guide students from their current understandings to further learning and to prepare them for future travel. Such teaching and learning is possible because the road system of fundamental mathematics has depth, breadth, and thoroughness, allowing teachers to connect student understandings with topics to be learned.
This is not the case in the United States, where knowing elementary mathematics is sometimes, perhaps often, construed as knowing how to add, subtract, multiply, and divide whole numbers and fractions. 2 In terms of content, this characterization is insufficient—at the very least, elementary mathematics concerns geometry as well. But for Chinese teachers with PUFM, it is insufficient in another way. Those in Ma's study would say, “It is not enough to know how, one must also know why.” The attitude expressed by this saying may affect a teacher's own knowledge—if knowing how is insufficient, one must find a rationale for mathematical procedures. Moreover, it may affect a teacher's goals for students—if knowing how is insufficient, students must come to understand why. In contrast, a teacher without this attitude may still know how and why, but not think it important that students know both. Or a teacher without this attitude may know how, but not why—and may not be able to answer students' questions, nor see the importance of student questions. Thus a teacher's attitude may affect not only the mathematics the teacher knows but also the mathematics the teacher teaches.
Other mathematical attitudes displayed by Chinese teachers include the following: claims must be justified with mathematical arguments, it is desirable to approach the same topic in multiple ways, and it is desirable to preserve the consistency of an idea in different contexts. Such attitudes may affect a teacher's knowledge by contributing to its coherence and connectedness—and also affect a teacher's teaching.
These fall in the category of what Jerome Bruner (1977) calls basic attitudes and considers as one aspect of the structure of a discipline. Another aspect of disciplinary knowledge identified by Bruner is basic principles. In the case of elementary mathematics (and perhaps all disciplines), basic attitudes have a symbiotic relationship with basic principles. For example, justifications in elementary mathematics often draw on the distributive law. Solving a fraction problem in multiple ways might draw on relationships between a fraction and a division, division as the inverse of multiplication, or relationships between fractions and decimals. In the base-10 system, noting the consistency of the relationship between 10 and 1, 100 and 10, and so on leads to the idea of the rate of 10: Each unit of higher value is composed of 10 or powers of 10 lower value units. This leads to the more general principle of the rate of composing a higher valued unit—the rate is 10 in the base-10 system, but there are other possibilities. For instance, the binary system has a rate of 2.
Like basic attitudes, basic principles may play a role in teaching, as well as knowing, mathematics. They may appear as parts of what Chinese teachers call a “knowledge package” for a given topic—a network of conceptual and procedural topics that support and are supported by
|
2 |
This perception of what it means to know elementary mathematics has been challenged by many in the U.S., in particular by the writers of the various National Council of Teachers of Mathematics Standards. |
its learning. An experienced Chinese teacher said
You should see a knowledge “package” when you are teaching a piece of knowledge. And you should know the role of the present knowledge in that package. You have to know that the knowledge you are teaching is supported by which ideas or procedures, so your teaching is going to rely on, reinforce, and elaborate the learning of these ideas. (Ma, 1999, p. 18)
To see a topic to be taught as part of a package of knowledge, rather than in isolation, requires a way of thinking that may not be common in the United States. When U.S. elementary teachers were asked how they would respond to a student's mistake in calculating 123 × 645, they focused on the given problem. When Chinese teachers were asked the same question, about 20% made comments such as
This mistake should have happened when students learn multiplication by two-digit numbers. The mathematical concept and the computational skill of multidigit multiplication are both introduced in the learning of the operation with two-digit numbers. So the problem may happen and should be solved at that stage. (Ma, 1999, pp. 45-46)
This reflects a general principle in the organization of knowledge packages: Not all topics receive equal emphasis. Some are considered key pieces, and teachers take particular care that students understand them. Two-digit multiplication is a key piece for the three-digit multiplication package because the simplest form of the “moving over ” idea involved in multidigit multiplication occurs in the two-digit case. Such attention to an idea in its first and simplest form allows teachers to pay less attention to later and more complicated forms. One Chinese teacher in the study put it this way, “To tell you the truth, I don't teach my students multiplication by three-digit numbers. Rather, I let them learn it [on] their own.”
Figure 1 shows a model of the knowledge package for subtraction with regrouping derived from interviews with Chinese teachers. [Here “regrouping” includes more than “borrowing.” Instead, the intended meaning is that some digit in the base-10 representation needs to be decomposed to make the computation. For example, in computing 15 − 7, one can't simply work with the digits 1, 5, and 7. Instead, one needs to decompose the 1 as 10 ones and group some or all of the 10 ones with the 5 (e.g., 2 ones might be grouped with the 5).]
The topic under discussion appears in a rectangle surrounded by other topics that occur in the curriculum (in ovals), and basic principles (in rectangles with rounded edges). Key pieces of the package have thick borders.
The central sequence in the subtraction package goes from the topic of addition and subtraction within 10, to addition and subtraction within 20, to subtraction with regrouping of numbers between 20 and 100, then to subtraction of large numbers with regrouping. “Addition and subtraction within 10” is addition with sums of 10 or less and subtraction with minuends of 10 or less, which don't require carrying or regrouping. For example, 10 − 4 = ? has a minuend of 10, and requires no regrouping. A related addition problem 4 + 6 = ? has the sum of 10, and requires no carrying. “Addition and subtraction within 20 ” is addition with sums between 10 and 20 and subtraction with minuends between 10 and 20.
Three levels of subtraction with regrouping problems are related to this central sequence:
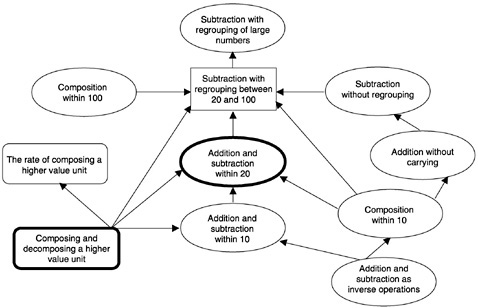
Figure 1. The Knowledge Package for Subtraction
From Ma (1999). Used by permission of Lawrence Erlbaum Associates.
-
minuends between 10 and 20, e.g., 15 − 7;
-
minuends between 19 and 100, e.g., 53 − 25;
-
minuends with three or more digits, e.g., 203 − 15.
Each of these levels concerns a new idea and a new skill:
-
decomposing a ten;
-
splitting a ten from several other tens, then decomposing it;
-
successive decomposition, e.g., decomposing 1 hundred as 10 tens, then 1 ten as 10 ones.
The different levels of regrouping problems correspond to pieces of the knowledge package shown in Figure 1. However, other necessary pieces of knowledge do not occur as separate topics in the curriculum. Instead, students' learning of curriculum topics supports and is supported by knowledge of basic principles: composing and decomposing a higher value unit, the rate for composing a higher value unit, and addition and subtraction as inverse operations.
How do teachers help students focus on these basic principles? Teacher Mao (a pseudonym), speaking from thirty years of experience, described how questions can play a role in student learning:
What is the rate for composing a higher value unit? The answer is simple: 10. Ask students how many ones there are in a 10, or ask them what the rate for composing a higher value unit is, their answers will be
the same: 10. However, the effect of the two questions on their learning is not the same. When you require them to think about the rate for composing a higher value unit, you lead them to a theory that explains the fact as well as the procedure. Such an understanding is more powerful than a specific fact. Once [students] realize that the rate of composing a higher value unit, 10, is the reason why we decompose a ten into 10 ones, they will apply it to other situations. (Ma, 1999, pp. 10-11)
Teacher Mao's description illustrates how attitude toward mathematics may affect a teacher's choice of questions. Both questions, “What is the rate for composing a higher value unit?” and “How many ones are there in a 10?” have the same answer. But a teacher with the attitude that one must know why as well as how chooses the question that leads toward an understanding of the basic principle. This choice reflects the kind of knowledge that the teacher wants students to learn. But, as Teacher Mao says, this knowledge can be applied in other situations, so this choice also affects students' future learning.
Teacher Mao's description suggests that answering the question “What mathematical knowledge do elementary teachers use in teaching? ” has two aspects: what to teach and how to teach it. The two aspects are often considered as separate—content and pedagogy—and taught to prospective teachers as separate subjects—mathematics and methods. But, just as a mathematical attitude toward elementary mathematics makes it more than a collection of disconnected procedures, the “knowledge package” way of thinking about teaching elementary mathematics makes knowledge for teaching more than content plus pedagogy. Instead, Teacher Mao and other Chinese teachers show us that content and pedagogy may be two sides of the same coin. Whether this coin will ever become common currency in the United States will depend not just on the individual efforts of teachers, but also on the way those teachers are prepared and supported—by their colleges and universities, their working conditions, and the depth, breadth, and thoroughness of the mathematics they teach.
ACKNOWLEDGMENTS
We thank Rudy Apffel, Gail Burrill, Sue Helme, and Cherisa Yarkin for their comments on this paper.
Ball, D. L. ( 1988). Knowledge and reasoning in mathematical pedagogy: Examining what prospective teachers bring to teacher education. Unpublished doctoral dissertation, Michigan State University, East Lansing.
Bruner, J. ( 1977). The process of education. Cambridge, MA: Harvard University Press.
Kennedy, M. M., Ball, D. L., & McDiarmid, G. W. ( 1993). A study package for examining and tracking changes in teachers' knowledge (NCRTL Technical Series 93-1). East Lansing, MI: The National Center for Research on Teacher Education.
Ma, L. ( 1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum.
National Council of Teachers of Mathematics. ( 1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
Mark Saul
One learns to dread certain moments in the classroom, moments which are as awkward as they are inevitable. Among those I dread the most is a question which eventually occurs to someone in the class: “ What's the last math we have to learn?” I don't have a good answer for this one. I've tried to tell students of the joy of mathematics, that I look forward to learning more math the same way I look forward to a good meal, and that there's always more math. But these last four words somehow never go over well. Instead, the news is perceived as a bombshell: your travails are never really finished. There's always more math.
It's these same four words that define the problem in talking about the mathematical background of elementary school teachers. Where does one stop? How much mathematics must an elementary school teacher know? The facile answer is: as much as possible, and the more, the better. Liping Ma's book gives a more sober view of the situation. She tells us, among other things, that even in elementary arithmetic, there is a depth to the knowledge necessary to teach, and that one could spend years simply acquiring this depth. So we are led to ask a more careful question: what is essential to an elementary teacher 's understanding of mathematics? Here is a quick and tentative list. It is not meant to be exhaustive but rather to stimulate inquiry. Which items are most central to the elementary teacher's life? Which are less important? Which are described too generally, or too specifically? What's left out?
A deep knowledge of arithmetic, of at least the rational numbers, is certainly essential to an elementary teacher's background. How this deep knowledge is acquired and exactly what it consists of are not simple questions and certainly do not belong in a list such as this one. However, it is not hard to see that a knowledge of arithmetic algorithms is close to the center of arithmetic. Whether these algorithms are carried out mentally, with paper and pencil, with manipulatives, or with a calculator, and in what proportion these and other methods should be combined, are again issues worthy of much more discussion.
The study of algorithms leads to the issue of algebra. How much algebra must elementary teachers know? We can make a distinction here. One view of algebra is as “generalized arithmetic” (the phrase is Newton's), and it seems to me important that elementary school teachers (indeed,
elementary school students) know about the use of variables to stand for numbers, and of algebraic expressions as a record of the results of binary operations on numbers.
There is a higher conception of algebra, which is still on an elementary level and which may or may not be appropriate to the education of elementary teachers. This is the conception of algebra as the study of the field of rational expressions (not just rational numbers), an insight which is the contribution of I. M. Gelfand (Gelfand & Shen, 1993). The notion that variables can stand for algebraic expressions, and not just rational numbers, is the beginning of another level of the learning of algebra, which may or may not be central to the work of the elementary school teacher.
It seems to me that elementary teachers must also know something about geometry. I am not referring to the usual taxonomies of geometric figures that one finds in elementary texts, nor to the various algebraic formulas that describe geometric figures. Rather, I am thinking of how figures are imbedded in (Euclidean) space, how they relate to each other, and how they move (that is, the study of geometric transformations). Again, I think of the words of I. M. Gelfand, who once commented to me that Descartes and Hilbert shaped the study of geometry in the schools: Descartes by introducing coordinates and algebraic methods, and Hilbert by modernizing and perfecting the axiomatic method of Euclid. Geometry can also be considered as a set of models of space, how objects are located in space, and how they move in space.
Another part of mathematics which I would offer as fundamental to the education of elementary school teachers is the language in which mathematics is expressed. This is largely the language of set theory: union, intersection, the null set, quantifiers, negation, but also functional notation and the idea of an isomorphism as a structure-preserving function.
Related to the language of mathematics is a set of concepts I call the nature of mathematics, that is, the notion that mathematics is logic-driven. Teachers (and indeed any educated person) ought to know what an axiomatic system is, what existence and uniqueness of an object mean, what it means to assert that something is possible or impossible (and not just very difficult), and what it means in mathematics to construct an object. Perhaps more important, teachers should understand the nature of mathematical truth. It is not dogmatic, as is theological truth. It is not conventional, as is political or moral truth. I am in danger of embracing here one particular philosophy of mathematics, or rather of rejecting certain others. This is not my point. What I mean to say is that the nature of mathematical truth, however conceived, ought to be discussed at some point in the training of elementary school teachers.
Any list such as the one I've just given raises more questions than it answers. One of the most important is: how does such a list for elementary school teachers differ from a similar list for the general public? Or does it? How should the body of knowledge outlined above be shaped to fit the needs of the elementary teacher? Liping Ma (1999) notes that much of the “deep knowledge” of the Chinese teachers she interviewed was acquired during their own elementary and middle school education. Our problem is that we need to start this cycle in motion.
A related question is: how should the elementary schoolteacher come to know about these ideas? Hyman Bass has commented in his conversation, for example, that a close study of arithmetic
would eventually lead to a consideration of the other essential topics of mathematics. It seems to me that it would take great art to make this happen. Nonetheless, it may be a fruitful approach.
There are certainly other fruitful approaches. The important thing to note is that this process of bringing mathematical knowledge to teachers must be thought about carefully. We must not stray, either to the left or to the right. There are two important and common errors. Vladimir Retakh, a colleague who teaches at the university level, once commented to me: “Some people think that if you have passed Calculus II then you are ready to teach Calculus I.” This is certainly erroneous. The message here is that people working with teachers must themselves know considerably more mathematics than they are teaching.
But can one have too much mathematics? Another common error in working with teachers is to provide too much mathematical information, too quickly, and in the wrong way. The situation is something like the bursting of a dam: a powerful and useful force is dissipated and rendered destructive. To continue the metaphor, we must have a sluice or spigot to regulate the amount and direction of mathematics begin dispensed. This regulator, of course, is knowledge of pedagogy, the pedagogy of teacher education.
It's a difficult process and requires a synergism that, I think, is evident in this group of people. And still it is difficult. Working with teachers involves a synthesis of mathematical and pedagogical knowledge that we are just beginning to achieve. We have a long road ahead, but also an exploration that can only get more exciting as it unfolds.
Gelfand, I. M., & Shen, A. ( 1993). Algebra. Boston, MA: Birkhäuser.
Ma, L. ( 1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum.
Genevieve Knight
Forty years ago, Allendoerfer & Oakley (1959) published a textbook titled Fundamentals of Freshman Mathematics. The purpose was to give a modern treatment of those topics in mathematics that were needed to fill the gap between intermediate algebra, analytic geometry, and calculus. The book was influenced by the recommendations of many who were working even then to implement a reform of the mathematics curriculum. In the “To the Student” messages, students were challenged to master the language and essential ideas of elementary mathematics. When the students finished the book, they should have been prepared to study more advanced ideas of calculus, differential equations, and modern algebra that are the keystones of modern scientific and engineering developments. Notice the use of the words “elementary mathematics ” and “fundamentals of freshman mathematics.”
The panelists were asked to address teachers' understanding of fundamental mathematics. But first, we need to consider some questions. What teacher groups are the focus? Are the teachers elementary generalists? Mathematics teacher education majors? K-4 teachers with an area of concentration in mathematics? Non-teacher focused majors? What is fundamental mathematics? Is it a collection of topics? Courses? Experiences? Has the mathematics community agreed what constitutes fundamental mathematics?
According to Ma (1999), fundamental mathematics is elementary, foundational, and primary. It is elementary because it is at the beginning of mathematics learning. It is primary because it contains the rudiments of more advanced mathematical concepts. It is foundational because it provides a foundation for students' further learning in mathematics.
In Liping Ma's work, she refers to the mathematics for elementary teachers that is really conceptual understanding, fundamental to shaping the foundation for young learners to mentally assemble discrete units of knowledge to form units of units that eventually generate complex structures in abstract mathematics. Teachers recall their own early experiences that gave meaning to mathematics for them. Hence, they engage their students in activities that generate conceptual understanding. Teachers take part in discourse with students to verify that valid conclusions are supported by correct understandings of the mathematics. Ma's
summaries also indicate that teachers who conceptually understand this fundamental mathematics produce students who themselves exhibit conceptual understanding, have the ability to learn and to reason, and are able to achieve.
It is crucial that we begin to give some reflective thought to what is meant by fundamental mathematics. If we are to promote teacher understanding of fundamental mathematics, we must have (a) an explicit set of defining properties of what is meant by fundamental mathematics and (b) a well-designed system that allows us to determine when a teacher or student “understands.”
As a community, we need to examine what is fundamental mathematics and collectively promote research that will enable us to prepare elementary teachers to teach for student understanding. As we engage in conversations over the next few days, let us attempt to share best thoughts and practices. All of the voices actually engaged in the educative process must be heard. The list of participants represents a wide range of people who value education and have many experiences to share. Our focus is what mathematics should teachers know and be able to do so that students can learn, understand, and achieve. Tonight, think about the words Liping Ma used to describe her research. Organize your operational definitions, come ready to communicate, and bring closure to the conversation on Sunday.
Allendoerfer, C. B., & Oakley, C. O. ( 1959). Fundamentals of freshman mathematics. New York: McGraw-Hill.
Ma, L. ( 1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum.












