Page 41
Digital Geometry Processing
PETER SCHRÖDER
Department of Computer Science California Institute of Technology Pasadena, California
WIM SWELDENS
Lucent Technologies Murray Hill, New Jersey
There have been three waves of multimedia so far: sound, images, and video. At present we are witnessing the arrival of the fourth wave of multimedia: three-dimensional geometry. Each of these waves was initiated by increases in acquisition capabilities, compute power, storage capacity, and transmission band-width for the respective type of data. As Moore's law moved along, we first saw digital sound in the 1970s, digital images in the 1980s, and digital video in the 1990s. An average PC will soon be able to handle digital geometry.
Each new digitization wave brings with it the need for new processing tools. Typical elements of a signal processing toolbox are denoising, compression, transmission, enhancement, detection, analysis, editing, and so forth. While analog circuitry can handle only the most basic processing tasks, as soon as the data are digitized, a whole new realm of algorithms becomes feasible. This has led to an explosion in digital signal processing research, aimed at the development of suitable mathematical representations, their manipulation, and associated computational paradigms. One example is the ubiquitous use of digital sound, from portable CD players to musical instruments and digital cellular phones. More recently, increasing network bandwidth and compute power have contributed to a revolution in the distribution of music over networks and on personal computers. Similar observations can be made about images and video.
In a sense, the cheap and plentiful availability of a data type has led to a spur in the development of methods to wring usefulness from these data, which, in turn, has stimulated progress in the underlying technology to support the respective type of data.
In a very similar way we are now witnessing the arrival of a new data type: three-dimensional geometry. To be sure, geometric modeling has been around for a long time, but geometry was created “by hand,” in a tedious custom pro-
Page 42
cess. Strides in the acquisition of three-dimensional geometry through low- and high-end three-dimensional scanners are now making digital proxies of geometry available for processing in a much broader way. Example sources of such geometry range from the sculptures of Michelangelo 1 to manufactured products 2 and the earth itself. 3
Once again, we need to build a toolbox of fundamental algorithms and mathematics to process this new class of digital geometry data. This time the task is significantly more challenging than before.
FOURIER OR NOT FOURIER
Multimedia data of the first three waves can be modeled easily as being defined on a section of Euclidean geometry. Sound is defined as a function of time—that is, on a one-dimensional line. Similarly, images are naturally defined as functions over a section of a two-dimensional plane. Finally, video is most naturally modeled as a function over a section of three-dimensional space—two dimensions in space and one in time. Another useful abstraction is that of sampling. A given datatype is digitized by sampling it at regular intervals (either space or time) and converting the measured values into binary numbers. The act of sampling and the regular spacing between samples make Fourier analysis and the Fourier transform the quintessential tools to understand and manipulate the content of such signals. If the underlying mathematical space were not Euclidean, the regular spacing of samples could not be achieved. For example, consider a sphere. There are no equispaced sampling patterns on the sphere beyond those given by the five Platonic solids. A digital image produced by one of today's cameras, however, is a regular matrix of picture elements, each representing a sample of the image irradience on the two-dimensional image plane.
This regular sampling allows the computation of the Fast Fourier Transform (FFT), one of the most popular algorithms in digital signal processing. Once in the Fourier domain, it is easy to remove noise, for example, or to enhance the image. 4 Recently, new multiresolution and time-frequency-based methods such as wavelets have proven to be a valuable alternative to the Fourier transform in many applications. These methods introduce the notion of scale into the analysis. For example, some phenomena being measured may occur at a broader scale while others appear at a finer scale. Adding this element allows us to zoom in and out of particular features in the data, yet even these methods still rely on the Fourier transform for their design and analysis.
1 Digital Michelangelo Project, Stanford University; models with more than 109 samples.
2 Reverse engineering and noninvasive inspection.
3 See the recent shuttle radar topography mission, for example.
4 In practice, algorithms often do not perform an actual Fourier transform to achieve these effects. Nevertheless, the Fourier transform is essential for understanding how to design and analyze such algorithms.
Page 43
Geometry, however, relies in an essential way on a non-Euclidean setting: curves, surfaces, and, more generally, manifolds. Unfortunately, curved geometry does not readily admit a Fourier transform, let alone a fast transform algorithm. Additional complications arise in software and hardware implementations. What used to be simple arrays or streams of regularly arranged data is now a complex topological data structure requiring much more sophisticated algorithms to handle. In general, there is no way around these difficulties when the underlying geometry is not flat. For example, consider data defined on a sphere, such as measurements that are a function of direction. One could map the sphere to a section of the plane and then use regular sampling and Fourier transforms. It is well known, however, that no such mapping can avoid singularities resulting in uncontrollable artifacts. Instead, one needs to take the essential nature of the sphere into account. These arguments apply even more so when the underlying surface is more complicated.
Luckily, some recent techniques inspired by wavelet constructions and commonly referred to as “multiresolution algorithms” offer a basis for the development of a digital geometry processing toolbox. These techniques, developed at the intersection of mathematics (wavelet analysis) and computer science (graphics), are based on subdivision (Zorin and Schröder, 2000), lifting (Sweldens, 1997), and second-generation wavelets (Daubechies et al., 1999) and carry over to the curved geometry setting.
THE POWER OF SEMIREGULAR MESHES
We have seen that it is impossible to keep the regularity—that is, the regular Cartesian arrangement of samples—of the Euclidean setting when going to surfaces. However, we can do almost as well using so-called semiregular meshes. These are constructed through a process of recursive quadrisection, an idea that originated in the area of subdivision. In a coarse mesh consisting of a generally small number of triangles, each triangle is recursively split into four subtriangles. In standard subdivision, where this approach is used to produce smooth surfaces, the new point positions are computed based on local averaging. A few of the steps in such a sequence are shown in Figure 1. Instead, we use point positions that are samples of the desired geometry, in effect adding displacements—or wavelet details—to a subdivision surface. This combination of sub-division and details, or wavelets, can be compared to the Euclidean geometry signal processing setting with its low- and high-pass filters. Although the results from that setting are not immediately applicable to the surface setting, they do provide guidance.
Because of the recursive quadrisection process by which these sampling patterns are built, we can build fast hierarchical transforms. These generalize the fast wavelet transform to the surface setting. While it is much harder to prove smoothness and approximation properties in this more general setting, first re-
Page 44
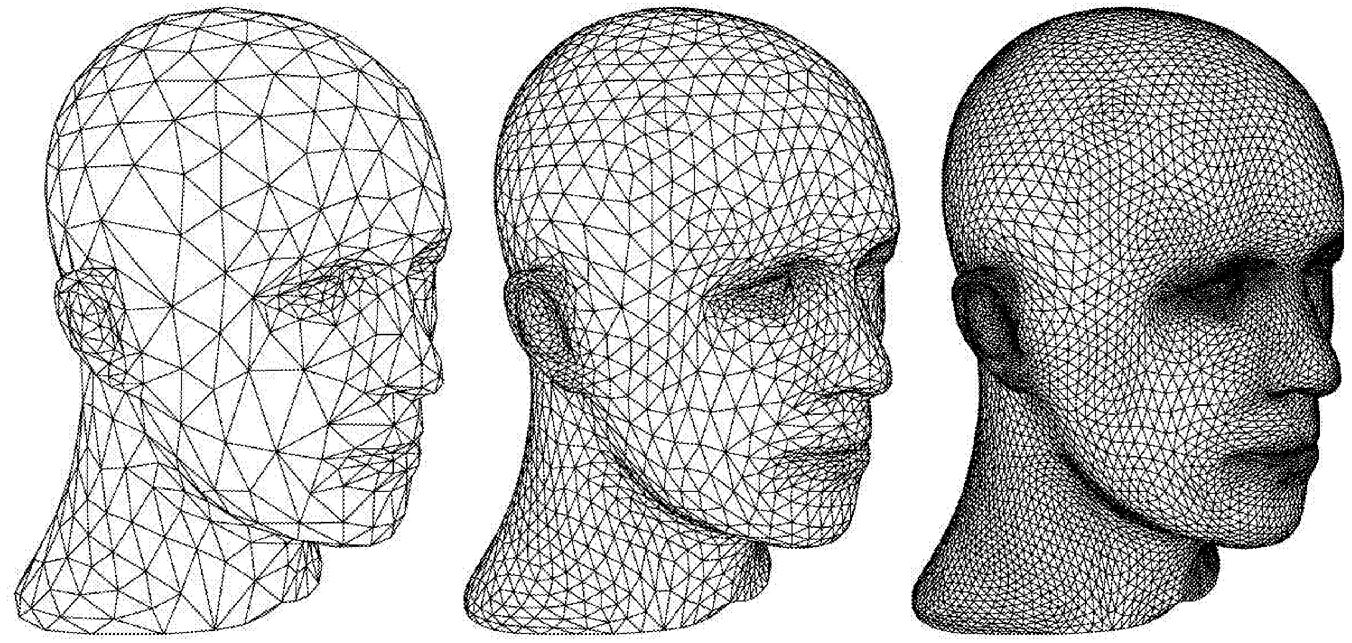
~ enlarge ~
FIGURE 1 Example of subdivision for a surface, showing three successive levels of refinement. On the left is an initial triangle mesh approximating the surface. Each triangle is split into four according to a particular subdivision rule (middle). On the right the mesh is subdivided in this fashion once again.
sults exist and are extremely encouraging. For example, these constructions can be used for very efficient progressive transmission algorithms. Imagine a file format for geometry that has the property that the first bits in the file provide a rough outline of the shape, and as more bits arrive, more and more details of the shape are revealed.
CONCLUSIONS
The fourth wave of multimedia—that of geometry—creates new mathematical and algorithmic challenges that cannot be answered with straightforward extensions of signal processing techniques from the Euclidean setting. However, ideas from multiresolution, subdivision, and second-generation wavelets provide the foundation of a new digital geometry processing apparatus based on semiregular meshes.
REFERENCES
, , , and . 1999. Wavelets on irregular point sets. Philosophical Transactions of the Royal Society of London A 357: 2397–2413.
1997. The lifting scheme: A construction of second generation wavelets. SIAM Journal on Mathematical Analysis 29(2): 511–546.
Zorin, D., and P. Schröder, eds. 2000. Subdivision for modeling and animation. Course notes from the 27th International Conference on Computer Graphics and Interactive Techniques (SIG-GRAPH), New Orleans, July 23–28, 2000.




