4
Evaluation of Conceptual and Quantitative Models of Fluid Flow and Chemical Transport in Fractured Media
Brian Berkowitz,1 Ronit Nativ,2 and Eilon Adar3
ABSTRACT
Patterns of fluid flow and chemical transport in heterogeneous porous and fractured media tend to be highly complex. Models of flow and transport processes in these systems must account for the inherent heterogeneity and scaling properties of porous rocks, as well as the typically sparse and uncertain field data that can be obtained to characterize a geological formation. Recent introduction of advanced theoretical and experimental techniques is providing new insight into our understanding of these highly non-uniform patterns. Statistical network models can be used to characterize the structure of pore and fracture systems, and to define power laws that quantify flow and transport processes within them. In a similar spirit, a random walk formalism can quantify anomalous (non-Gaussian) patterns of chemical transport that are frequently observed in laboratory and field experiments. Analyses of transport of reactive chemicals, including effects of precipitation and dissolution, as well as changes in fracture morphology, also demonstrate highly non-uniform behavior. In the context of these results, we discuss some conceptual and quantitative models of fluid flow and chemical transport in the fractured vadose zone, and the laboratory and field data that are required to evaluate them.
|
1 |
Department of Environmental Sciences and Energy Research, Weizmann Institute of Science, Rehovot, Israel |
|
2 |
Department of Soils and Water, The Hebrew University of Jerusalem, Rehovot, Israel |
|
3 |
Blaustein Institute for Desert Research, Ben Gurion University of the Negev, Israel |
INTRODUCTION
Major efforts have been devoted over the last two decades to the development of realistic theoretical models capable of simulating flow and transport processes in fractured and heterogeneous porous formations. These efforts have led to significant understanding of the dynamics of flow and transport processes in these systems. However, predictive capabilities related to real fractured and heterogeneous media remain limited. This is due, in part, to the very complex nature of fracture networks in the subsurface, and to the virtual impossibility of obtaining detailed structural, hydraulic, and geochemical characterizations of fractures in situ, in diverse geological and lithological settings. As a result, studies must often rely on extrapolation of exposed features and indirect measurements, together with subjective considerations, to generate a statistical characterization of fracture systems (e.g., Berkowitz and Adler, 1998).
These analyses are demanding because fractures exist in a broad range of geological formations and rock types, and are produced under a variety of geological and environmental processes. As a result of the variability in rock properties and structures, as well as the variety in fracturing mechanisms, fracture sizes range from microfissures of the order of microns to major faults of the order of kilometers, while fracture network patterns range from relatively regular polygonal arrangements to apparently random distributions. The hydraulic and transport properties of these formations vary considerably, being dependent largely on the degree of fracture interconnection, aperture variations in the fractures, and chemical characteristics of the fractures and host rock.
With regard to fluid flow and chemical transport processes in fractured vadose zones, our ability to predict actual flow and transport behavior —and even our understanding of the basic dynamics—is severely limited, and in some cases rudimentary. Several factors force development of specific conceptual pictures and models tailored to dealing with these processes: (1) fracture walls are rough; (2) fractures often contain filling material; (3) this filling material and the walls themselves are subject to processes of chemical reaction, dissolution, precipitation, mineralization, and/or particle detachment and trapping; (4) fluid migration in partially saturated conditions occurs in preferential paths and channels, with a complex interplay between the fractures and the porous host rock; and (5) fluid and chemical migration patterns are often temporally and spatially unstable. Quantitative models of fluid flow and chemical transport in the fractured vadose zone must therefore be predicated on conceptual pictures of fractured, heterogeneous, and otherwise “disordered” porous media, which account for a variety of non-uniform flow and transport behaviors.
In this chapter, we consider conceptual pictures and quantitative models of fluid flow and chemical transport in fractured and heterogeneous porous media relevant to the fractured vadose zone. To this end, we build on our more established understanding of these processes in saturated systems. Other models spe-
cific to fluid flow and chemical transport in unsaturated fractured media, such as film flow and fracture-matrix interactions, are discussed in other chapters in this volume. Given the wide variety of flow and transport processes, and the different perspectives that arise as a function of the actual problem of interest, the quantitative models that we examine are problem-specific. Clearly, there is no single generic model that is appropriate, and so as a consequence, a range of probabilistic and statistical approaches must be introduced.
In the next section, we discuss conceptual pictures and modeling approaches for fluid flow and chemical transport. We consider these processes at the scale of individual fractures and in fracture networks. Several experimental efforts are then examined, and in light of these results, we address the issue of how to evaluate conceptual and quantitative models at the laboratory and field scales.
CONCEPTUAL PICTURES AND MODELING APPROACHES FOR FLUID FLOW AND CHEMICAL TRANSPORT
Single Fractures
Fluid Flow in Saturated Fractures
Many laboratory experiments (e.g., Raven and Gale, 1985; Pyrak-Nolte et al., 1987; Durham and Bonner, 1994) and field studies (e.g., Novakowski et al., 1985, 1995; Rasmuson and Neretnieks, 1986; Raven et al., 1988) indicate that the classical view of a rock fracture as a pair of smooth, parallel plates is not adequate to fully quantify fluid flow. However, though more advanced conceptual models have been introduced in recent years, an alternative model for flow in fractures has yet to be generally accepted. Moreover, some very basic aspects of the theoretical problem remain largely unstudied.
A critical, intimately related issue is the validity of the local cubic law. To date, the majority of theoretical and simulation studies of single-fracture flow (Iwai, 1976; Brown, 1987; Moreno et al., 1988; Thompson and Brown, 1991; David, 1993; Unger and Mase, 1993; Amadei and Illangasekare, 1994) have postulated that local flow magnitudes are well described by the Reynolds equation. From this equation, local flow magnitudes are proportional to the cube of the local aperture; hence the name “local cubic law” (LCL). The LCL, a key feature in conceptual models, states that the volumetric flow through a fracture varies as the cube of the fracture aperture. Thus definition of fracture aperture, and application of the LCL, strongly influence quantitative analyses and interpretation of laboratory and field measurements on flow in fractures.
The Reynolds equation originates from lubrication theory, which was formulated for narrow void spaces between artificially smoothed surfaces. However, the roughness of rock fracture surfaces is usually more significant and irregular, and has been shown to possess self-affine fractal properties, with a roughness, or
Hurst exponent H ![]() 0.8 (Brown and Scholz, 1985; Poon et al., 1992; Schmittbuhl et al., 1995). A typical self-affine fracture surface with H = 0.8 is shown in Figure 4-1. Moreover, computer simulations (Mourzenko et al., 1995; Brown et al., 1995) have compared predictions from the Stokes and Reynolds equations, and suggest that the Reynolds equation is of limited validity for rough fractures. The adequacy of the LCL for rough geometries remains, essentially, an open question.
0.8 (Brown and Scholz, 1985; Poon et al., 1992; Schmittbuhl et al., 1995). A typical self-affine fracture surface with H = 0.8 is shown in Figure 4-1. Moreover, computer simulations (Mourzenko et al., 1995; Brown et al., 1995) have compared predictions from the Stokes and Reynolds equations, and suggest that the Reynolds equation is of limited validity for rough fractures. The adequacy of the LCL for rough geometries remains, essentially, an open question.
A detailed review of these studies is beyond the scope of this report. Here we focus on a new approach that we have proposed recently, which addresses the above issues. Oron and Berkowitz (1998) used a two-dimensional order-of-magnitude analysis of the Navier-Stokes equations for a general rough-wall geometry to examine the LCL assumption. This study hypothesized that LCL behavior should not be assumed to be correct or incorrect a priori for the entire fracture; rather, it should be studied on a local basis. As a result, three conditions can be defined for the applicability of LCL flow, as a leading-order approximation, in a local fracture segment with parallel or nonparallel walls. Consider a local cross section of some fracture segment of length L, with a typical halfaperture B. We define a geometric aspect ratio parameter, δ ≡ B/L, and a nondimensional local roughness parameter ε ≡ max(σu/B, σl/B) << 1, where σu and σl are the root-mean-square roughnesses (deviations from the means) of the upper and lower walls, respectively, averaged over the length L. Oron and Berkowitz (1998) demonstrated that the LCL is an adequate first-order approximation

FIGURE 4-1 A typical self-affine fracture surface, generated numerically on a 128 × 128 grid with H = 0.8. After Oron, A. P., and B. Berkowitz, 1998. Flow in rock fractures: The local cubic law assumption reexamined. Water Resources Research 34: 2811-2825. Copy-right by American Geophysical Union.
of the flow under three conditions: (1) the local segment must be long enough relative to its aperture, so that δ2 << 1; (2) over this segment length, ε << 1; and (3) inertial effects are limited via Re·max(δ,ε) << 1, where Re is the Reynolds number in the segment.
These conditions define dynamic-geometric conditions for LCL flow, which are a function of fluid velocity, relative to the fracture aperture and the (relative) wall roughness. From these conditions it follows that the cubic law aperture should be measured as an average over a distance L, normal to the mean trend of the walls, and not with point-by-point methods as suggested by, for example, Ge (1997) or Mourzenko et al. (1995). An illustration of various methods for defining the aperture is given in Figure 4-2. The orientation of measurement over L is set by the general orientation of the segment. Under the above conditions, the LCL, even though it is only a first-order approximation, provides second-order accuracy for estimates of local discharge and of mean fluid velocity. The LCL may also be adapted to pathways with nonparallel walls, as long as the mean path half-angle is moderate. Moreover, the aspect-ratio condition (1) sets a finite resolution in the x-y plane to all analyses based on the LCL. Also, these conditions suggest that even when Re is as low as ~1-10, transition to non-LCL (nonlaminar) flow may occur.
Extending to the third dimension, in addition to defining apertures over segment lengths, Oron and Berkowitz (1998) find that the geometry of the contact regions between fracture walls influences flow paths more significantly than might be expected from consideration of only the nominal area fraction of these contacts. Moreover, this effect is enhanced by the presence of non-LCL regions around these contacts. Accounting for the self-affine nature of fracture walls, typical (fractal) fracture wall contact areas generated numerically are illustrated in Figure 4-3. We find a wide variability among the hydraulic conductivity maps, in terms of the shape of the regions in which LCL flow exists, due to the varying distribution and morphology of contact and non-LCL regions in the fractures. While contact ratios of 0.1-0.2 are usually assumed to have a negligible effect, our calculations suggest that contact ratios as low as 0.03-0.05 can be significant. Analysis of computer-generated fractures with self-affine walls demonstrates a nonlinear increase in contact area, and a faster-than-cubic decrease in the overall hydraulic conductivity, with decreasing fracture aperture. These results are in accordance with existing experimental data on flow in fractures (Durham and Bonner, 1994; see also the summary in Figure 14 of Mourzenko et al., 1997).
We conclude this section by considering the fundamental ill-posedness of this problem. In view of the complexity of local flow behavior, a global cubic law need not exist for every fracture; the cubic law results from the parabolic velocity profile in perfect Poiseuille flow, and not from any dimensional considerations. Flow, or permeability, versus aperture curves are derived indirectly, on the basis of displacement measurements on the perimeter of laboratory fracture samples. At best, one can measure the mechanical aperture, that is, the apparent, average,

FIGURE 4-2 A demonstration of the various methods for measuring the LCL aperture, Shown are the vertical aperture (short dashes), the normal-to-local-centerline aperture of Ge (1997) (dots), and the ball aperture of Mourzenko et al, (1995). The approach of Oron and Berkowitz (1998) indicates that the cubic law aperture is not a point-by-point property but an average over a segment; the bold dashes on the pathway walls indicate a possible division into cubic law segments. The location marked with an arrow is inadequate for local cubic law because of a rapidly varying wall geometry. The rightmost, diagonal segment has a diverging angle that makes this region marginal for cubic law flow. After Oron, A. P., and B, Berkowitz, 1998. Flow in rock fractures: The local cubic law assumption reexamined. Water Resources Research 34: 2811-2825. Copyright by American Geophysical Union.
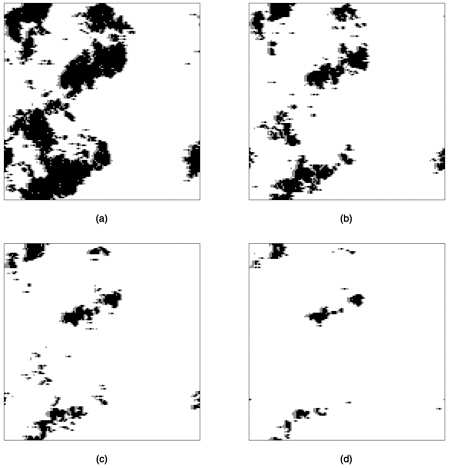
FIGURE 4-3 Maps of the estimated local hydraulic conductivity for a numerically generated fracture with self-affine walls, with H = 0.8 and a grid size of 128 × 128, for flow in the x-direction (left to right). The length of each side of the map is equivalent to 6.4 mm. Black indicates fracture wall contact, while grey indicates regions where LCL is not applicable; LCL flow exists only in the white regions. Average fracture apertures are (a) 100 µm, (b) 150 µm, (c) 175 µm, and (d) 200 µm. After Oron, A. P., and B. Berkowitz, 1998. Flow in rock fractures: The local cubic law assumption reexamined. Water Resources Research 34: 2811-2825. Copyright by American Geophysical Union.
separation between the fracture walls. In general, we do not have exact information on the (varying) void space within the sample itself, as it changes under different applied stresses, as well as following geochemical reactions (see the next section and the section on Field-Scale Analysis of Fluid Flow and Chemical Transport in the Fractured Vadose Zone), and we have only relative displacement
measurements rather than the actual aperture values. Any conversion of these measurements to local apertures, and definition of an effective aperture, is based on assumptions and convenience. As a consequence, although natural, the question of flow versus aperture, and validity of a cubic law, may be the wrong one to ask about rough fractures.
Chemical Transport Processes in Saturated Fractures
In addition to rough fracture walls, the presence of filling material further influences the hydraulic properties of a fracture. In general, fracture wall roughness and fracture infilling evolve over time, as a function of a variety of dynamic mechanical and geochemical processes (e.g., Steefel and Lichtner, 1994). There is evidence that these changes may also take place over very short time intervals. It is critical that we understand these processes, which can occur naturally or be induced artificially (e.g., by injection of grouting in efforts to seal underground repository walls).
The highly complex interactions between the mass transport mechanisms and the changing properties of a fractured porous medium make quantitative analysis of such systems very difficult. Precipitation and dissolution can significantly modify the physical and chemical properties of fractured media. Physical changes in fracture aperture, tortuosity, and thus effective mass diffusivities and permeabilities are coupled to the subsequent fluid flow and solute transport and the precipitation and dissolution reactions. As such, a variety of closure patterns can be observed in the field, which range from fully filled (mineralized) fractures to those with pockets or irregular layers on the walls. Chemical changes in the fractures, such as sorption and reaction capacities, also have a significant effect on chemical transport and fracture wall evolution.
As a first step to quantifying precipitation/dissolution processes in fractures, we first consider modeling of reactive transport. A considerable body of literature deals with the transport of conservative contaminants in individual fractures. In contrast, however, little attention has been devoted to the analysis of the transport of reactive contaminants in fractures. The existing literature has been reviewed by Berkowitz and Zhou (1996), who developed a model to quantify the transport of reactive contaminants in a simplified fracture. The model, which accounts for advection, molecular diffusion, and interphase mass transfer between the aqueous phase and the fracture walls, demonstrates that the solute transport is controlled by the interplay between the Damköhler number (characterizing the effect of reaction relative to that of molecular diffusion on solute transport) and the Peclet number (characterizing the effect of advection relative to that of molecular diffusion on solute transport).
Clearly, sorption reactions in groundwater systems involve many kinds of chemical constituents and different chemical and physical processes. Thus no single model can successfully describe all kinds of sorption reactions. Berkowitz
and Zhou (1996) considered several surface reaction models, including irreversible first-order kinetics, instantaneous reversible reactions, and reversible first-order kinetics. They determined criteria under which one can model reactive solutes as nonreactive, and reversible reactions as irreversible, in terms of time evolution of concentration distributions. They also gave a criterion for applicability of the local equilibrium assumption and subsequent use of a retardation coefficient.
Numerical models describing precipitation and dissolution in porous media and fractures were presented by Sallès et al. (1993) and Békri et al. (1995), who investigated a variety of idealized geometries that included parallel plate channels and channels with opposite protrusions on each wall. Similar numerical models for precipitation in deterministic and stochastic fractures were presented by Mourzenko et al. (1996) and Békri et al. (1997). Numerical models for precipitation and dissolution in a constant aperture fracture and the surrounding evolving porous matrix were given by Savage and Rochelle (1993) and Steefel and Lichtner (1994). Realistic parameters were used to simulate a fracture originating from a cement-bearing nuclear waste repository. These studies examined effects on the surrounding medium but did not study the evolution of the fracture geometry itself. A model for the evolution of fracture network maze patterns, for fractures with initially large apertures, was presented by Palmer (1975, 1991), while Dreybrodt (1996) analyzed the time needed for the development of mature karst channels. A numerical model to investigate the minimum hydrogeochemical conditions for fracture dissolution in limestone was given by Groves and Howard (1994a). Their results indicate that the selective enlargement of fracture flow passages may be strongly influenced by their initial sizes. Groves and Howard (1994b) and Howard and Groves (1995) then developed numerical models for fracture dissolution in limestone for laminar and turbulent flow. Their results show that for laminar flow, passage enlargement taking place early in the conduit network development is highly selective, while the transition to turbulent flow often results in more general passage enlargement.
Dijk and Berkowitz (1998) examined the evolution of fracture aperture over the entire length of the fracture, as a function of time, due to solute precipitation and dissolution. Irreversible first-order kinetic surface reactions were considered. The effect of the relevant transport mechanisms, the fracture geometries, and the initial and boundary conditions on the evolution of the fracture properties, fluid flow, and solute transport for geological systems and timescales were investigated. Calculations were based on a wide range of parameter values estimated from data available in the literature. Results showed the evolution of the solute transport and fracture geometry as a function of the Damköhler and Peclet numbers. Figure 4-4 illustrates typical simulated fracture mineralization patterns. Fracture closure times are found to be of the order of days to millions of years, for half-life reaction times (Langmuir and Mahoney, 1984) of the order of seconds to years, and for fluid residence times of the order of minutes to days. These closure times are compatible with typical hydrogeological time scales.
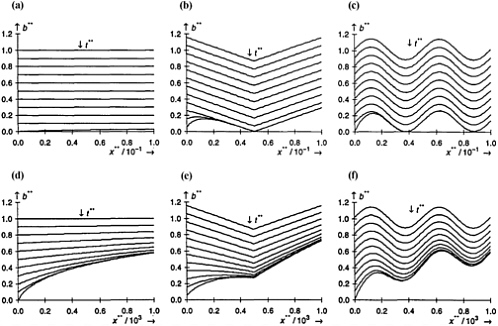
FIGURE 4-4 Simulated fracture mineralization patterns for three fractures and two rates of flow and chemical reaction. Predicted dimensionless half-aperture b** as a function of dimensionless location within the fracture, x**, and of dimensionless time t**. For initially flat (a), (d); linearly constricted (b), (e); and sinusoidal (c), (f) fracture walls. Line of symmetry (fracture center) in each fracture is given by the x-axis. Cases (a), (b), (c): large flow rate relative to rate of reaction; cases (d), (e), (f): low flow rate relative to rate of reaction. Modified from Dijk, P. E., and B. Berkowitz, 1998. Precipitation and dissolution of reactive solutes in fractures. Water Resources Research 34(3): 457-470. Copyright by American Geophysical Union.
Fluid Flow and Chemical Transport in Partially Saturated Fracture Systems
The conceptual pictures and quantitative models of fluid flow and chemical transport in the fully saturated fractures that we have discussed above are not directly applicable to fluid flow and chemical transport in the fractured vadose zone. However, our established understanding of these processes in saturated systems forms a valuable knowledge base from which we can work.
In the context of fluid flow and chemical transport in partially saturated fractured systems, we can consider flow in initially unsaturated (or partially saturated) single fractures, accounting only for the fracture itself, or accounting for the fracture together with the porous medium in which it is embedded. However, even at this stage, we must define what, precisely, we mean by infiltration, or fluid flow and chemical transport, in unsaturated (or partially saturated) fractures. Consider a fracture that is, initially, completely unsaturated. As shown by, for example, Di Pietro et al. (1994) and Di Pietro (1996), using numerical simulations with lattice gas automata, the pattern of infiltration and fluid distribution is largely a function of the rate of infiltration (relative to the dimensions of the fracture). In other words, for high rates of fluid entering the fracture, the fracture becomes fully saturated, and we need consider only the transient advance of the wetting front as partially saturated (e.g., Nicholl et al., 1992, 1993a, 1993b). For slower rates of fluid infiltration, film flows can develop along the fracture walls. The significant advance of fluid along such films, even with thicknesses of the order of 1 µm, has been demonstrated by Tokunaga and Wan (1997). Similar observations about saturation patterns can be made for mixed fracture/porous matrix systems (e.g., Glass and Norton, 1992). Models that account for film flow and fracture-matrix interactions are discussed in detail in other chapters in this volume, and we therefore do not dwell on them here.
A critical feature in these cases is that medium heterogeneity and irregular distributions of fluid lead to the development of preferential flow paths. Because fluid flow patterns may be highly ramified and sensitive to small-scale details, use of simulation models that yield only averaged, “effective” behavior may be of highly limited value, and will in many instances yield meaningless results. We can, however, conceptualize the fracture/porous matrix system as a heterogeneous porous medium, particularly if the fracture has very rough walls, and/or contains filling material. Several modeling approaches can then be considered, depending upon whether the emphasis is on (1) the steady-state fluid flow and transient chemical transport through a partially saturated domain, or (2) the transient evolution of either the advancing front of fluid or contaminant, or the actual flow paths.
In the former case, flow and transport models for heterogeneous, fully saturated domains can be applied simply by restricting the conducting, saturated portion of the domain to account for the air phase (e.g., Birkholzer and Tsang, 1997). Alternatively, in the latter case, we can introduce a variety of pore network
and other statistical models (such as percolation theory variants) in order to focus on an advancing wetting front or a transient infiltration pattern (Blunt and Scher, 1995), or use a “dripping faucet” analogy (Shaw, 1984) to characterize the often irregular (chaotic) patterns of inflow and outflow in such fractures. Simple growth models that mimic the essential physics of growth processes are known for specific instances, such as viscous fingering (Paterson, 1984; Lenormand et al., 1988), capillary fingering (Wilkinson and Willemsen, 1983; Wilkinson, 1986; Lenormand et al., 1988), and gravity fingering (Meakin et al., 1992; Glass and Yarrington, 1996). Other generalized growth models that attempt to mimic the full range of behavior are the subject of current investigations (Ewing and Berkowitz, 1998; Glass et al., 1998). Such models account for a wide range of viscous, gravity, and capillary forces, all in the presence of medium heterogeneities.
The literature devoted to description of these various models is vast, and is beyond the scope of this analysis. The interested reader can find detailed descriptions of these models, and extensive references to the relevant literature, in, for example, Blunt and Scher (1995), Berkowitz and Ewing (1998), Ewing and Berkowitz (1998), and Glass et al. (1998).
Fracture Networks
We consider now conceptual and quantitative models of fluid flow and chemical transport in fracture networks. These models are influenced directly by the flow and transport mechanisms and behaviors outlined above for single fractures.
Network Structure and Fluid Flow
The complex and usually non-Gaussian nature of distributions of fluid fluxes and migrating contaminants in fracture networks is well-known in the literature. In particular, field and laboratory experiments in natural fractures have demonstrated strong evidence of channeling and highly preferential flow paths in individual fractures and in fracture networks (e.g., Neretnieks et al., 1982; Neretnieks, 1993 and references therein). Field data, for example, from a large-scale investigation of fracture flow in a granite uranium mine at Fanay-Aug ères, France, show a difference of four orders of magnitude between the largest and smallest injection flow rates, despite very good fracture connectivity. Cacas et al. (1990a, 1990b) concluded that the high degree of heterogeneity and channeling is due to a broad distribution of fracture conductivities, and that it overwhelmingly governs fluid flow and transport behavior.
In order to study these phenomena, two-dimensional (2D) (e.g., Schwartz et al., 1983; Smith and Schwartz, 1984; Charlaix et al., 1987; David, 1993; Berkowitz and Scher, 1997, 1998) and three-dimensional (3D) (e.g., Andersson
and Dverstorp, 1987; Billaux et al., 1989; Cacas et al., 1990a, 1990b; Nordqvist et al., 1996) models have considered aspects of the influences of fracture connectivity and fracture conductivity distributions, both in fracture planes and at the scale of a full fracture network. Tsang and Tsang (1987), Tsang et al. (1988), Moreno and Neretnieks (1993), and others have used similar models and also replaced the heterogeneities by systems of statistically equivalent, variable aperture, one-dimensional channels. The major emphasis of these studies has been on analysis of contaminant breakthrough curves.
Another approach to modeling flow and transport in fracture networks, which is able to capture distinct preferential flow paths and channeling, is based on percolation theory (e.g., Englman et al., 1983; Robinson, 1983, 1984; Hestir and Long, 1990; Balberg et al., 1991; Berkowitz and Balberg, 1993; Berkowitz, 1995). In this framework, and near the percolation threshold—the point at which the fractures are “just connected” across the entire domain—network structures display channeling patterns and transport properties that are quantifiable by power law relationships. The proximity to the threshold often depends on the scale of measurement, and in some cases the backbone substructure is obscured due to the presence of many disconnected fractures. However, there is considerable evidence from field measurements and theoretical considerations that many fieldscale fracture networks are indeed near the percolation threshold (Chelidze, 1982; Guéguen et al., 1991; Crampin and Zatsepin, 1996; Renshaw, 1996).
The principal feature of disordered networks near the percolation threshold is the distribution of critical single bonds that connect large “blobs” of fractures. Flow through the percolating cluster occurs only along the backbone, that is, the hydraulically conducting portion of the percolating cluster. Many of the open fracture segments in a percolation-generated domain do not conduct fluid, since either they do not belong to the percolating cluster, or they form dangling branches on the backbone analogous to dead-end pores.
The analogy between real fracture networks and percolation systems is well known. Real fracture networks can, at least in some cases, be mapped to percolation lattices and random domains (e.g., Winterfeld et al., 1981; Jerauld et al., 1984a, 1984b; Hestir and Long, 1990) and, in general, the same percolation scaling properties hold for lattices and continuum systems. Numerical simulations of 3D fracture networks can map fractures to a regular orthogonal array of platelets (Englman and Jaeger, 1990). Alternatively, flow channels that exist within the planes of real fractures (Neretnieks, 1993) can be mapped to networks of tubes.
In general, models accounting for fracture-system complexity have thus been based on the incorporation of fracture planes containing aperture distributions, or idealized flow paths in 3D connecting the centers of intersecting disks, or geometrically sparse networks near the percolation threshold. Most recently, Margolin et al. (1998) developed a lattice model that includes all of these key elements in a single framework. This approach allows a simple characterization
of a range of geometrical structures with a range of aperture distributions, in both 2D and 3D fracture systems. The model uses anisotropic percolation to generate random interconnecting bonds (representing channels within fractures), and accounts for aperture variation within fracture planes and among fractures.
Margolin et al. (1998) examined the interplay and relative importance of the key factors that lead to formation of channeled flow paths in fracture networks. Specifically, they considered (1) structural effects, including network density and anisotropy, and (2) hydraulic effects, governed by aperture variability. The presence of rough-walled fractures and filling material can also be incorporated in the aperture variability. Analysis of flow in these lattice networks demonstrates that either of the elements—fracture geometry and aperture variability —can give rise to channeled flow, and that the interplay between them is especially important. Figure 4-5 illustrates typical preferential flow patterns in this system. The bonds represent channels within fracture planes. As the degree of aperture variability increases, the preferential paths become sparser and more sharply defined. Thus, in practical terms, it is clear that parameter values that are measured or inferred for use in discrete fracture network models may have only limited physical significance. A critical observation for our analysis is that the effect of large aperture variability renders even dense networks poor conductors, so that from the point of view of fluid flow, the networks behave as though near the percolation threshold. Margolin et al. (1998) developed a scaling relationship that quantities the dependence of effective hydraulic conductivity on aperture variability and on the network structure and fracture element density; this result is also used to derive an explanation for the field-length dependence of permeability frequently observed in fractured formations.
In light of the above, it seems reasonable to expect that in many field-scale situations, the portion of the fracture network that actively contributes to fluid flow and chemical transport is, functionally, near a percolation threshold, due either to structural characteristics and/or aperture variability. Analogously, in partially saturated systems, only a small fraction of fracture areas actually conduct fluid (as discussed earlier), and we therefore suggest that fluid flows in partially saturated fracture networks may also exhibit flow patterns similar to those shown in Figure 4-5. Moreover, the presence of film flow may permit preferential (or percolation-like) fluid flow and chemical transport even in fractured porous media with very low bulk saturation. In these contexts, dynamics of fluid flow and chemical transport in fracture networks can also be quantified using the modeling approaches outlined earlier.
Chemical Transport
The issue of how to quantify the migration of contaminants in fractured and fractured-porous geological formations has received overwhelming attention during the last three decades, and a vast literature dealing with the subject has
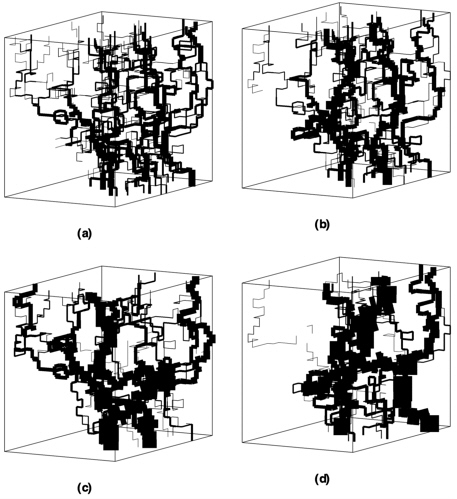
FIGURE 4-5 Illustration of channeled flow in fracture networks. Typical spatial distributions of (normalized) bond discharges in three-dimensional lattice networks, for a range of bond aperture variability (defined by b, the standard deviation of the log aperture). The lattice is relatively well connected and consists of 30 percent of the bonds (located randomly) in a full orthogonal lattice. (a) b = 0.0, (b) b = 0.5, (c) b = 1.0, (d) b = 2.0. The thickness of the bonds is proportional to the relative discharges they carry; only those bonds carrying at least 1 percent of the total volumetric flow through the network are shown. After Margolin, G., B. Berkowitz, and H. Scher, 1998. Structure, flow, and generalized conductivity scaling in fracture networks. Water Resources Research 34(9): 2103-2121. Copyright by American Geophysical Union.
developed. And yet, our ability to quantitatively predict contaminant migration in these systems remains severely limited, and questions remain about how best to model such transport. Discrete fracture models require detailed information on structural and hydraulic properties of fractures, and are hampered by heavy computational requirements. On the other hand, use of the advection-dispersion equation (ADE), and stochastic theories that generalize the ADE by substituting a more detailed stochastic process for the Fickian assumption, have not successfully quantified observed behavior (e.g., Dagan and Neuman, 1997).
It is beyond the scope of this report to review all of the relevant literature. Rather, we shall briefly discuss a new framework that we have recently proposed (Berkowitz and Scher, 1995, 1997, 1998; Berkowitz et al., 2000) in which frequently observed anomalous (non-Gaussian) chemical transport can be quantified: if the variation in the velocity field is sufficiently large, a highly discrete picture of the contaminant (particle) motion can be developed. The particle motion is approximated as a series of discrete steps, each having a different velocity. The particle's position is determined at the points of transition between these steps. A continuous time random walk (CTRW) can be introduced to naturally account for the cumulative effects of a sequence of transitions. The transitions are characterized by ψ(s, t), the probability rate for a displacement s with a difference of arrival times of t. In the CTRW approach, one can determine the evolution of the particle distribution (plume), P(s, t), for a general ψ(s, t), so there is no a priori need to consider the moments of P(s, t). The challenge is to map the important aspects of the particle motion in the medium onto a ψ(s, t). A mapping that results in a ψ(s, t) with an algebraic low velocity tail for large time leads to the description of anomalous transport (e.g., non-Gaussian plumes).
We have applied the CTRW to an explicit, discrete medium—a random fracture network. We analyzed a series of Monte Carlo transport simulations based on synthetic random fracture networks (Berkowitz and Scher, 1997, 1998). The spatial and temporal behavior of the contaminant advance, based on particle tracking simulations in these networks, is shown in Figure 4-6a, while theoretical concentration profiles based on CTRW are shown in Figure 4-6b. The CTRW curves are characterized by a peak that lies close to the origin, with a forward tail that spreads in response to the flow field. As time progresses, the distribution approaches a step function, increasingly uniform in space, with the residual position of the peak indicated by the sharp drop near the origin.
The shapes of the spreading pulse P(x, t) shown in Figure 4-6 are qualitatively similar to those found from the particle tracking simulations in these fracture networks. Despite the statistical noise in these results due to vertical averaging and a relatively small number of realizations, the CTRW theory reproduces the development of highly skewed particle plumes. Significantly, the CTRW solution also captures the variation of both the movement of the center of mass of the particles and the standard deviation of particle location around this center of mass.
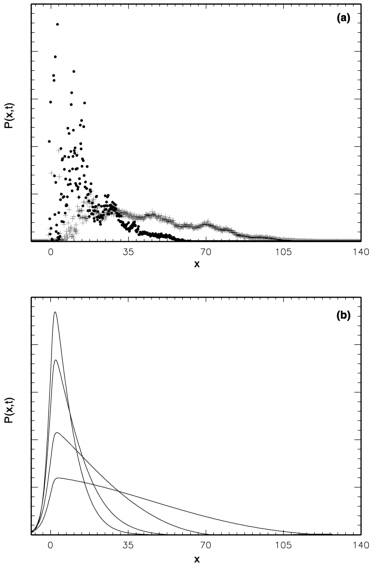
FIGURE 4-6 Profiles of the spatial distribution of a contaminant at two relative times (t = 1, points; t = 2.5, crosses), determined from numerical simulations of particle transport in a two-dimensional, random fracture network. The concentration profile, P(x, t) is the vertical average (along the y-axis) of P(s, t), in arbitrary units; particle injection point is at x= 0. (b) Profile of the spatial distribution of a contaminant, P(x, t), determined from the CTRW solution, at four relative times t = 1, 2.5, 10, and 37.5. The concentration profile, P(x, t), is the vertical average (along the y-axis) of P(s, t), in arbitrary units; particle injection point is at x = 0. After Berkowitz, B., and H. Scher, Phys. Rev. Lett. 79(20), 1997, pp. 4038-4041. Copyright by the American Physical Society.
As in the previous sections, we suggest that this framework, developed for fully saturated systems, may also be suitable for describing chemical transport in partially saturated fractured media. In partially saturated systems, only a small portion of the domain actually conducts fluid and chemicals, and as suggested in the section on Network Structure and Fluid Flow, fluid flows in partially saturated fracture networks may also exhibit flow patterns similar to those shown in Figure 4-6. Thus, it may be possible to modify the transition probability ψ(s, t) to capture the broad distribution of fluid velocities (from fast film flows to stagnant regions, as well as fracture-matrix interactions). Alternatively, and especially for slower flow regimes, statistical growth models such as outlined in the section on Fluid Flow and Chemical Transport in Partially Saturated Fracture Systems may be applicable.
EVALUATION OF CONCEPTUAL AND QUANTITATIVE MODELS: FIELD AND LABORATORY DATA
From the survey in the previous section, it is clear that a variety of theoretical models must be invoked in order to quantify the broad spectrum of fluid flow and chemical transport behaviors. Similarly, experiments at a variety of laboratory and field scales, under both fully and partially saturated conditions, are required in our efforts to understand and predict these behaviors. In this context, we discuss below several recent, representative experimental studies.
Laboratory-Scale Study of Single Fractures
As discussed in the section on Single Fractures, the roughness of fracture walls, and dynamic changes in the roughness (as well as filling material) can significantly influence the hydraulic properties of a fracture. Fluid flow in roughwalled rock fractures is complex even under laminar flow regimes, and measuring flow in such fractures is prohibitively difficult. As a result of the paucity of experimental data, existing models are based largely on unvalidated assumptions and simplifications. Dijk et al. (1999) use nuclear magnetic resonance imaging (NMRI) to directly measure flow patterns in natural rock fractures, and to examine the effects of fracture wall morphology. The investigation focuses on a qualitative and quantitative description of the fracture surface geometry, water flow velocities and flow rates, flow and stagnant regions, critical aperture and velocity paths, and flow pattern stability and reproducibility. In particular, the effects of a sharp step discontinuity of the fracture walls are studied.
Four sets of 2D slices through a 3D velocity image, including a pair of (zero fluid velocity) calibration tubes, are displayed in Plate 3. The 3D velocity images presented here show the velocity components in the principal (z) flow direction. A variety of flow features, including irregular distributions of high- and low-velocity zones, and the effect of the fracture discontinuity can be detected easily.
The significant backflow region in the vicinity of the fracture discontinuity is indicated by the arrow. It should be noted that in the vicinity of rough fracture walls, eddies and turbulent regions may develop, while at some distance from the walls, fully laminar flow is expected to occur.
From the velocity data and theoretical considerations, the applicability of the local cubic law (LCL) is examined. As a result of the complex 3D geometry, velocity profiles are generally parabolic, as assumed by the LCL, but often highly asymmetric with respect to the fracture walls. These asymmetric velocity profiles are clustered together, with significant correlations; they are not just local random phenomena. Analysis of the z-direction velocity component in a single cross-sectional plane (Dijk et al., 1999) suggests that the effects of the measured asymmetry on volumetric flow rates are insignificant. However, analysis of the complete 3D distribution of the z-direction velocity components (Dijk and Berkowitz, 1999) demonstrates that the actual flow rate is significantly less than that predicted by the LCL. It is expected, moreover, that the asymmetries will have a significant influence on chemical solute transport, dissolution, and precipitation. The features discussed in these studies emphasize the strong heterogeneity and the highly 3D nature of the flow patterns in natural rock fractures, even for relatively small Reynolds numbers, and the need for 3D flow analyses.
Fracture wall morphology may change over time as a result of geochemical and mechanical processes. The evolution of unsaturated fracture walls was investigated by Weisbrod et al. (1998, 1999), who used high-resolution laser scanning to measure topographical variations of fractured chalk surfaces. The chalk surfaces were either (1) immersed in tap water and then air-dried over two wetting cycles, for 10 min and for 14 h (Weisbrod et al., 1998), or (2) installed in customized flow cells and exposed to short flow events (8, 9, and 24 h) of synthetic rainwater, followed by long drying periods (Weisbrod et al., 1999). Both coated and uncoated fracture surfaces were investigated in the latter study. The surfaces were found to erode by up to 0.352 mm following the two cycles of immersion in tap water and by up to 0.313 mm following the three cycles of synthetic rainwater flow. Erosion was more pronounced in the coated surface than in the uncoated surface, reflecting its mechanical instability. Figure 4-7 shows the changes in one of the (uncoated) fracture walls after each of the wetting cycles, along with the changes in topography along a single crosssectional profile of a fracture wall. The changes in wall morphology can be related to a non-uniform release of particles from the fracture walls. The erosion thickness was found to be strongly correlated to the thickness of a layer calculated from the total accumulated mass of particles and soluble salts released from the surface. An important result is that processes of precipitation and dissolution, as well as particle deposition, weathering, and clay swelling, may be significant in relatively soft rock formations. Moreover, these processes may be enhanced in the fractured vadose zone because of the transient nature of water infiltration and water retention.
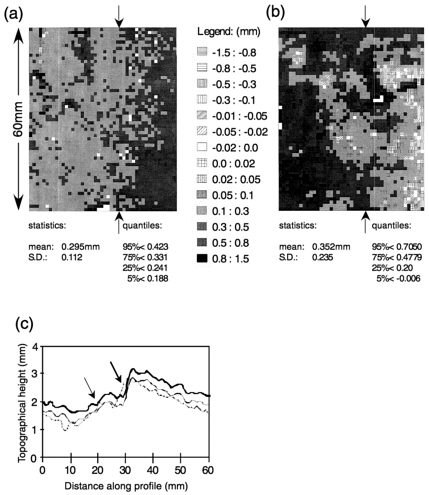
FIGURE 4-7 Map of the topographic height difference of a fracture wall following (a) a 10-min wetting cycle and (b) a 14-h wetting cycle. Note that some areas, particularly along the right edge, were uplifted after the 14-h wetting cycle. Basic statistics characterizing the differences are also shown. Each map contains ~2500 data points. Positive and negative values indicate decreases and increases in topographical height, respectively. Figure 4-7c shows the topographical height of three profiles along a cross section of the fracture wall sample, indicated by the arrows on (a) and (b). The bold line depicts the initial topographical height of the sample. The solid and dashed lines were obtained after submerging the core in tap water for 10-min and 14-h, respectively. After Weisbrod, N., R. Nativ, D. Ronen, and E. Adar, 1998. On the variability of fracture surfaces in unsaturated chalk. Water Resources Research 34: 1881-1887. Copyright by American Geophysical Union.
Chemical Transport
We introduced a CTRW framework (see above) to quantify anomalous (non-Gaussian) chemical transport in fractured and heterogeneous porous media. We have used these solutions (Berkowitz and Scher, 1998) to suggest the occurrence of anomalous transport in natural, heterogeneous porous media, by interpreting field data from a large-scale field study performed at the Columbus Air Force Base (Adams and Gelhar, 1992). At this site, a highly heterogeneous alluvial aquifer, bromide was injected as a pulse and traced over a 20-month period by sampling from an extensive 3D well network. The tracer plume that evolved was remarkably asymmetric and could not be described by classical Gaussian models (Adams and Gelhar, 1992). Significantly, the CTRW captured the variation of both the movement of the center of mass of the particles and the standard deviation of particle location around this center of mass in the direction of flow, determined from the field data. Here, in agreement with CTRW theory, interpretation of the moments suggested that both the mean and standard deviation of the plume position scale with time (t) as t0.6. Details of the CTRW solutions and full analyses of these data, including discussion of how the parameters for the CTRW model can be obtained from site data, are given in Berkowitz and Scher (1998) and Berkowitz et al. (2000).
We have also recently used the CTRW framework to evaluate the first passage time distributions, or breakthrough curves, and compared them to measurements from a tracer migration experiment in a heterogeneous sandbox model (Berkowitz et al., 2000). We find that the curves fit the range of measured data remarkably well, and in particular match both the early time behavior and the late time (long tail) concentration breakthroughs. In contrast, these data could not be adequately modeled using the (Gaussian) ADE.
Clearly, long tail or otherwise skewed concentration profiles can, in some cases, be reconciled with the ADE by, for example, imposing a trend in the mean velocity. However, such trends can only be considered if they are indicated by site-specific field measurements. On the other hand, the CTRW theory would appear to be a promising general framework that allows analysis of transport in formations containing complex heterogeneities, at large scale, which are not amenable to analysis using classical advection-dispersion theory. While much research remains to be done in this direction, the CTRW seems to represent a potentially valuable tool in the assessment of dispersive processes in heterogeneous porous media.
Our analysis of laboratory and field data indicates that the observed anomalous (non-Gaussian) behavior results from subtle features in the flow fields. These distributions are present in (steady-state) partially saturated porous media, and incorporate mixtures of fast and slow paths, over long and short distances. We suggest, therefore, that similar behaviors will be found in partially saturated systems, as a function of the degree of saturation and of the medium itself.
Field-Scale Analysis of Fluid Flow and Chemical Transport in the Fractured Vadose Zone
A small number of studies have attempted to directly measure fracture flow in laboratory set-ups (as discussed above), but extrapolation of such results to field conditions is not straightforward. The few studies in which fracture flow and transport were investigated on a field scale determined these parameters indirectly, that is, via the matrix surrounding the preferential pathways. Measurements of matrix chemical and isotopic compositions (Komor and Emerson, 1994; Nativ et al., 1995; Wood et al., 1997), or matrix water content and permeability (Scanlon, 1991, 1992) were used to infer preferential flow and transport in the embedded fractures. Dahan et al. (1998) presented a methodology designed to address the need for direct quantitative measurements of flow and transport in fractures. These measurements provide insight into field-scale heterogeneity that strongly affects the measured properties.
The methodology and the experimental set-up described here were developed and applied in a study located in the northern part of the Negev Desert, Israel. A large chemical industrial complex and the National Site for Treatment and Isolation of Hazardous Wastes have been operating there since 1975. The underlying geological infrastructure in the region consists of an Eocene chalk formation partly covered by thin layers of sand and loess. Because of the aridity of the area (180 mm/yr rainfall) and the low permeability of the chalk matrix (~2 millidarcy), the vadose zone was considered to be a natural barrier to potential groundwater contamination resulting from the industrial activities on the land surface. However, the high concentration of industrial pollutants found in the local groundwater (Nativ and Nissim, 1992), as well as other factors such as seasonal fluctuations in groundwater levels, water table responses to flood events, and the occurrence of tritium in the groundwater (Nativ and Nissim, 1992; Rophe et al., 1992), indicate that the groundwater is rapidly affected by on-surface activities. Evidently, infiltrating water and contaminants bypass the low-permeability chalk matrix via preferential flow paths, possibly through the numerous vertical to subvertical fractures intersecting the chalk matrix (characterized by Bahat, 1988). Indeed, preferential water flow and solute transport across the fractured chalk in the vadose zone was demonstrated using chemical and isotopic tracers (Nativ et al., 1995).
The experimental set-up described here (see Figure 4-8) was designed to measure directly and to assess the spatial distribution of flow and transport along fractures from water ponded at the land surface (Dahan et al., 1998). The experimental site was located in an ephemeral wash. Twenty-one percolation ponds were installed sequentially on top of a freshly cleaned rock ledge, along 5.3 m of a vertical fracture opening, dividing it into 21 equal sections. The area of each pond was 25 × 40 cm and its depth was 35 cm. One meter below the surface of the rock ledge, a 25-cm-diameter, 4.3-m-long horizontal borehole was cored along
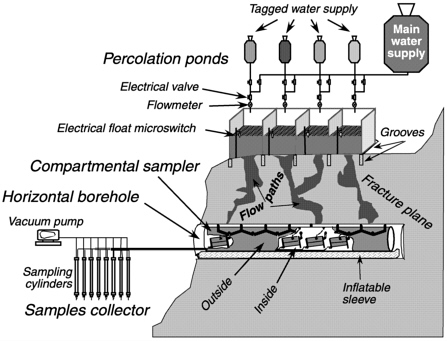
FIGURE 4-8 Schematic cross section of a measurement system designed to determine water fluxes and tracer migration rates in a field set-up through a single natural fracture in the vadose zone. The system components are a set of individually tagged percolation ponds, located above a rock ledge intersected by a vertical fracture; a horizontal borehole cored into the same fracture at a depth below the ledge and the percolation ponds; a compartmental sampler introduced into the borehole to collect the tagged water drained from the various ponds; and a sample collector to retrieve the fluids stored in the compartmental sampler. After Dahan et al. (1998). Reprinted by permission of Ground Water. Copyright 1998.
the fracture plane. A compartmental sampler composed of 21 cells (each 20 cm long) was introduced into the borehole. Thus packers attached to the top of the sampler divided the fracture opening at the borehole ceiling into 21 separate sections. The use of various tracers in the percolation ponds, and their detection in the drained effluents, enables delineation of flow trajectories connecting the ponds at the fracture inlet to the sampler cells in the horizontal borehole below.
A five-day (119-h) experiment was held in May 1997. The percolation ponds were filled to a constant water head, and the flow rate out of each pond was automatically measured and recorded as soon as water was introduced into the ponds. Simultaneously, the flow rate of the drained effluents collected by the sampler in the horizontal borehole was measured and the water was sampled for
tracer concentration. The active flow paths along the fracture plane were resolved by two tracer tests. In each test, water in the percolation ponds was tagged, for 6 h and 4.5 h during the first and second tests, respectively. The first tracer test (test A) began 43 h after the beginning of the experiment, and the second test (test B) started 29 h later. The flow trajectories were defined by relating the tracers found in the various sampler cells in the borehole to their source ponds on the surface where they were applied. Details of the entire experiment are given in Dahan et al. (1999).
Flow rates into the upper opening of the fracture from each of the percolation ponds and into the lower opening in each of the sampler cells are presented in Figure 4-9. The temporal flow rates reflect the variability in fluid flow from each of the ponds to each of the sampler cells. The high variability in maximum flow rates observed at the inlet and outlet sides of the fracture indicates that only about 50 percent of the length of the fracture opening allowed any appreciable flow, whereas less than about 20 percent of the fracture opening transmitted high flow rates. Significantly, the temporal variations in flow rates—with no clear pattern—persisted throughout the duration of the five-day experiment; a steady flow pattern was not reached in any of the ponds or sampler cells during this period. Both abrupt and gradual temporal variations were observed.
Turbidity measurements in the drained effluents reflect the transport of suspended material through the fracture. Abrupt changes in turbidity (with maximum values of about 1500 nephelometric turbidity units [NTU]) were observed in samples from most cells throughout the duration of the experiment. These fluctuations reflect the unstable structure of the fracture void and its filling material (as noted by Weisbrod et al., 1998, 1999), and are linked to flow rate changes and stability.
Flow trajectories through the fracture—between the percolation ponds and the sampler cells—were estimated on the basis of the tracer tests, as well as by correlating fluxes between ponds and cells. The connecting lines in Figure 4-10 represent the relative contribution from each pond to each sampler cell. This relative contribution was determined by the percentage of the maximum relative concentration of a tracer derived from a pond and observed in the sampler cell. Not surprisingly, the flow trajectories between the ponds and the sampler cells—separated by only 1 m—were often not vertical, but rather shifted horizontally along the fracture plane.
Two important—and perhaps unexpected—observations can be made. First, the paths of tagged water from different source ponds often crossed without any observed mixing. For example, tagged water from pond 8 moving to sampler cells 4 and 5 crossed the zone where tagged water from ponds 3, 5, and 7 drained downward (Figure 4-10), and yet no indication of tracer from these ponds was found in sampler cells 4 and 5. This finding suggests that flow paths consist of discrete and unconnected channels within the main fracture plane. These flow paths could arise through the complex structure of the consolidated and unconsolidated
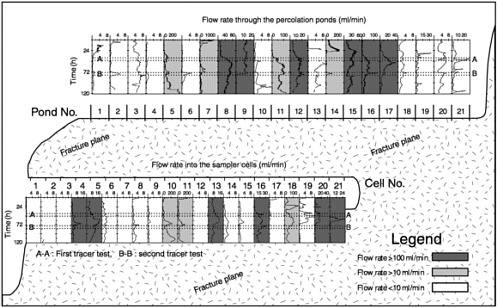
FIGURE 4-9 Temporal variations in the flow rate of each of the percolation ponds (above) and the sampler cells (below). The figure displays the exact position of the ponds with respect to the sampler cells. The flow-rate scale is variable according to the maximum measured flow rate in each individual pond/cell. The duration of the two tracer tests A and B is shown by dotted lines (A-A and B-B, respectively) on both graphs. After Dahan, O., R. Nativ, E, Adar, B, Berkowitz, and Z. Ronen, 1999. Field observation of flow in a fracture intersecting unsaturated chalk. Water Resources Research 35(11): 3315-3326. Copyright by American Geophysical Union.
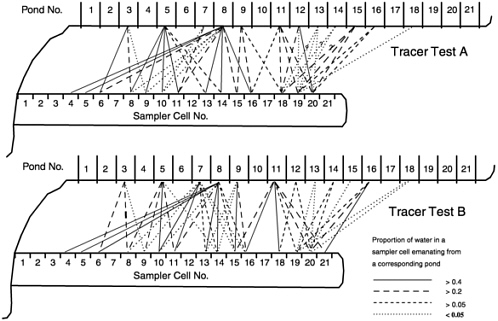
FIGURE 4-10 Flow trajectories connecting the source ponds on land surface to the sampler cells in the borehole, as defined by the two tracer tests. The line styles represent the relative water contribution of a certain pond to its corresponding sampler cell. After Dahan, O., R. Nativ, E. Adar, B. Berkowitz, and Z. Ronen, 1999. Field observation of flow in a fracture intersecting unsaturated chalk. Water Resources Research 35(11): 3315-3326. Copyright by American Geophysical Union.
filling material with the fracture void, micro-dissolution channels along the fracture walls, or intersecting small fractures.
Second, the relative contributions of fluid from each pond to each sampler cell changed significantly during the experiment. The temporal variations in flow paths during the two tracer tests (Figure 4-10) are remarkable—evidently due to dissolution of filling material and walls, as well as to particle mobilization, migration, and entrapment, as evidenced by the turbidity measurements. Analysis of the data also indicated that the instability of the flow regime observed on a small scale at each individual fracture segment did not decrease on larger scales, for several combined segments or for the entire flow domain.
The observations of Dahan et al. (1998) suggest that large portions of the fracture plane play only a minor role, with small sections controlling most of the flow activity, probably within a few major discrete flow paths. Close examination of the fracture opening along the bottom of the ponds and along the borehole ceiling indicated that the hydraulically active sections of the fracture are related to dissolution channels along its plane. These dissolution channels were found to be closely related to fracture plane crossings between the main fracture plane and secondary fracture planes.
CONCLUDING REMARKS
We have considered aspects of fluid flow and chemical transport in the fractured vadose zone by building on our more established (though by no means complete) understanding of these processes in saturated systems. Other relevant experiments and models specific to unsaturated fractured media, such as film flow and fracture-matrix interactions, are discussed in other chapters in this volume.
Fluid flow and chemical transport behavior in fractured porous formations is highly complex. Models of flow and transport in these systems must account for the inherent heterogeneity and scaling properties of porous rocks, as well as the typically sparse and uncertain field data that can be obtained to characterize a geological formation. In the fractured vadose zone, key physical parameters that must be considered include, over a range of scales, the geometrical and hydraulic characteristics of individual fractures, their interconnection within networks, and their interplay with the porous host rock. Analysis of chemical transport must also include parameters that describe chemical reaction, dissolution, and precipitation, and particle detachment and trapping, all of which lead to spatial and temporal variations in flow and transport patterns. These parameters are also fundamental to flow and transport models in saturated, highly heterogeneous formations, and similar conceptual frameworks and quantitative tools can often, though not always, be applied. For example, the finding that 3D flow paths within a fracture plane can consist of discrete and unconnected channels supports our
suggestion that fractures in the vadose zone may be treated as highly heterogeneous porous media.
From the modeling point of view, it is important to distinguish between predictions of large-scale (average) and small-scale flow and transport behavior. Here we stress the importance of capturing essential fluid flow and chemical transport behavior, such as highly ramified fluid flow patterns; such behavior is often extremely sensitive to small-scale medium details. Large-scale (average) models are clearly irrelevant for analysis of small-scale fluid velocity and chemical concentration distributions, or, for example, for prediction of first arrival times of a contaminant. But significantly, models that attempt to apply effective, or homogenized, parameters to describe even the average flow and transport behavior in heterogeneous media often fail. Careful measurement in the laboratory and the field has indeed demonstrated the dominant influence of small-scale heterogeneity. Thus, we consider alternative modeling approaches, depending on whether the emphasis is on steady-state fluid flow and transient chemical transport through a partially saturated domain, or on transient evolution of either the advancing front of fluid or contaminant, or of the actual flow paths.
It is essential that we obtain additional field and laboratory data in order to determine the applicability of these various models. To date, there exist only a very limited number of large-scale laboratory and field experiments in the fractured vadose zone. A major difficulty lies in actually measuring the parameters of interest, particularly under unsaturated conditions. The other key difficulty is that we must account for high degrees of uncertainty, and for the interplay of flow and transport dynamics over a range of spatial and temporal scales. For example, if fluid flow in the fractured vadose zone follows a path analogous to a percolation system near the threshold, then the likelihood of measuring and actually delineating this path is very small. On the other hand, theoretical investigations of fluid flow and chemical transport, predicated on available experimental evidence, have yielded tremendous insight into the dynamics of flow and transport in the fractured vadose zone. The use of probabilistic and statistical tools allows us to characterize these dynamics, and to place quantitative bounds on fluid flow and chemical transport processes. New experiments with measurements that are sensitive over a range of scales to the geometrical, hydraulic, and chemical heterogeneity of fractured vadose zones are required to further refine these models.
ACKNOWLEDGMENT
Brian Berkowitz thanks the European Commission Environment and Climate Program (Contract No. ENV4-CT97-0456) for partial support.
REFERENCES
Adams, E. E., and L. W. Gelhar, 1992. Field study of dispersion in a heterogeneous aquifer. 2. Spatial moment analysis. Water Resources Research 28(12): 3293-3308.
Amadei, B., and T. Illangasekare, 1994. A mathematical model for flow and solute transport in non-homogeneous and anisotropic rock fractures. Int. J. Rock Mech. Min. Sci. & Geomech. Abs. 31: 719-731.
Andersson, J., and B. Dverstorp, 1987. Conditional simulations of fluid flow in three-dimensional networks of discrete fractures. Water Resources Research 23(10): 1876-1886.
Bahat, D., 1988. Early single layer and late multi-layer joints in the lower Eocene chalk near Beer Sheva, Israel. Annales Tectonicae ii: 3-1.
Balberg I., B. Berkowitz, and G. E. Drachsler, 1991. Application of a percolation model to flow in fractured hard rocks . Journal of Geophysical Research 96(B6): 10015-10021.
Békri, S., J. F. Thovert, and P. M. Adler, 1995. Dissolution of porous media. Chem. Eng. Sci. 50(15): 2765-2791.
Békri, S., J. F. Thovert, and P. M. Adler, 1997. Dissolution and precipitation in fractures. Eng. Geol. 48: 283-308.
Berkowitz, B., 1995. Analysis of fracture network connectivity using percolation theory . Math. Geology 27(4): 467-483.
Berkowitz, B., and P. M. Adler, 1998. Stereological analysis of fracture network structure in geological formations. Journal of Geophysical Research 103(B7): 15,339-15,360.
Berkowitz, B., and I. Balberg, 1993. Percolation theory and its application to groundwater hydrology. Water Resources Research 29(4): 775-794.
Berkowitz, B., and H. Scher, 1995. On characterization of anomalous dispersion in porous and fractured media. Water Resources Research 31(6): 1461-1466.
Berkowitz, B., and J. Zhou, 1996. Reactive solute transport in a single fracture, Water Resources Research 32(4): 901-913.
Berkowitz, B., and H. Scher, 1997. Anomalous transport in random fracture networks, Phys. Rev. Lett. 79(20): 4038-4041.
Berkowitz, B., and R. P. Ewing, 1998. Percolation theory and network modeling applications in soil physics . Surveys in Geophysics 19(1): 23-72.
Berkowitz, B., and H. Scher, 1998. Theory of anomalous contaminant migration in random fracture networks . Phys. Rev. E 57(5): 5858-5869.
Berkowitz, B., H. Scher, and S. E. Silliman, 2000. Anomalous transport in laboratory-scale, heterogeneous porous media . Water Resources Research 36(1): 149-158(correction: 36(5): 1371).
Billaux, D., J. P. Chiles, K. Hestir, and J. Long, 1989. Three-dimensional statistical modelling of a fractured rock mass: An example from the Fanay-Augères mine. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr. 26(3/4): 281-299.
Birkholzer, J., and C.-F. Tsang, 1997. Solute channeling in unsaturated heterogeneous porous media. Water Resources Research 33(10): 2221-2238.
Blunt, M., and H. Scher, 1995. Pore-level modeling of wetting. Phys. Rev. E 52: 6387-6403.
Brown, S. R., 1987. Fluid flow through rock joints: The effect of surface roughness. Journal of Geophysical Research 92B: 1337-1347.
Brown, S. R., and C. H. Scholz, 1985. Broad bandwidth study of the topography of natural rock surfaces. Journal of Geophysical Research 90B: 12,575-12,582.
Brown, S. R., H. W. Stockman, and S. J. Reeves, 1995. Applicability of the Reynolds equation for modeling fluid flow between rough surfaces. Geophysical Research Letters 22: 2537-2540.
Cacas, M. C., E. Ledoux, G. de Marsily, B. Tillie, A. Barbreau, E. Durand, B. Feuga, and P. Peaudecerf, 1990a. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation. 1. The flow model. Water Resources Research 26(3): 479-489.
Cacas, M. C., E. Ledoux, G. de Marsily, A. Barbreau, P. Calmels, B. Gaillard and R. Margritta, 1990b. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation. 2. The transport model. Water Resources Research 26(3): 491-500.
Charlaix, E., E. Guyon, and S. Roux, 1987. Permeability of a random array of fracture of widely varying apertures . Transp. Porous Media 2: 31-43.
Chelidze, T. L., 1982. Percolation and fracture. Phys. Earth Planet. Int. 28: 93-101.
Crampin, S., and S. V. Zatsepin, 1996. Rock, dead or alive? Theory prompts new understanding of fluid-rock interaction and shear-wave splitting. EOS, Transactions, American Geophysical Union 77(30): 281.
Dagan, G. and S. P. Neuman (eds.), 1997. Subsurface Flow and Transport: A Stochastic Approach. Cambridge: Cambridge University Press.
Dahan, O., R. Nativ, E. Adar, and B. Berkowitz, 1998. A measurement system to determine water flux and solute transport through fractures in the unsaturated zone. Ground Water 36: 444-449.
Dahan, O., R. Nativ, E. Adar, B. Berkowitz, and Z. Ronen, 1999. Field observation of flow in a fracture intersecting unsaturated chalk. Water Resources Research 35(11): 3315-3326.
David, C., 1993. Geometry of flow paths for fluid transport in rocks. Journal of Geophysical Research 98(B7): 12,267-12,278.
Di Pietro, L. B., 1996. Application of a lattice-gas numerical algorithm to modelling water transport in fractured porous media. Transp. Porous Media 22: 307-325.
Di Pietro, L. B., A. Melayah, and S. Zaleski, 1994. Modeling water infiltration in unsaturated porous media by interacting lattice gas-cellular automata. Water Resources Research 30(10): 2785-2792.
Dijk, P. E., and B. Berkowitz, 1998. Precipitation and dissolution of reactive solutes in fractures. Water Resources Research 34(3): 457-470.
Dijk, P. E., and B. Berkowitz, 1999. Three-dimensional flow measurements in rock fractures. Water Resources Research 35(12): 3955-3960.
Dijk, P. E., B. Berkowitz, and P. Bendel, 1999. Investigation of flow in water-saturated rock fractures using nuclear magnetic resonance imaging (NMRI). Water Resources Research 35(2): 347-360.
Dreybrodt, W., 1996. Principles of early development of karst conduits under natural and man-made conditions revealed by mathematical analysis of numerical models. Water Resources Research 32(9): 2923-2935.
Durham, W. B., and B. P. Bonner, 1994. Self-propping and fluid flow in slightly offset joints at high effective pressures. Journal of Geophysical Research 99(B5): 9391-9399.
Englman, R., and Z. Jaeger, 1990. Fracture in concrete due to percolating cracks and pores. Physica A 168: 655-671.
Englman, R., Y. Gur, and Z. Jaeger, 1983. Fluid flow through a crack network in rocks. J. Appl. Mech. 50: 707-711.
Ewing, R. P., and B. Berkowitz, 1998. A generalized growth model for simulating initial migration of dense non-aqueous phase liquids. Water Resources Research 34(4): 611-622.
Ge, S., 1997. A governing equation for fluid flow in rough fractures. Water Resources Research 33(1): 53-61.
Glass, R. J., and D. L. Norton, 1992. Wetted-region structure in horizontal unsaturated fractures: Water entry through the surrounding porous matrix. In: Proceedings, International High Level Radioactive Waste Management Conference, Las Vegas, Nevada, April.
Glass, R. J., and L. Yarrington, 1996. Simulation of gravity fingering in porous media using a modified invasion percolation model. Geoderma 70: 231-252.
Glass, R. J., M. J. Nicholl, and L. Yarrington, 1998.A modified invasion percolation model for low-capillary-number immiscible displacements in horizontal rough-walled fractures: Influence of local in-plane curvature. Water Resources Research 34(12): 3215-3234.
Groves, C. G., and A. D. Howard, 1994a. Minimum hydrochemical conditions allowing limestone cave development . Water Resources Research 30(3): 607-615.
Groves, C. G., and A. D. Howard, 1994b. Early development of karst systems. 1. Preferential flow path enlargement under laminar flow. Water Resources Research 30(10): 2837-2846.
Guéguen, Y., C. David, and P. Gavrilenko, 1991. Percolation and fluid transport in the crust. Geophysical Research Letters 18(5): 931-934.
Hestir, K., and J. C. S. Long, 1990. Analytical expressions for the permeability of random two-dimensional Poisson fracture networks based on regular lattice percolation and equivalent media theories. Journal of Geophysical Research 95(B13): 21565-21581.
Howard, A. D., and C. G. Groves, 1995. Early development of karst systems. 2. Turbulent flow. Water Resources Research 31(1): 19-26.
Iwai, K., 1976. Fundamental Studies of Fluid Flow Through a Single Fracture. Ph.D. dissertation, University of California, Berkeley.
Jerauld, G. R., J. C. Hatfield, L. E. Scriven, and H. T. Davis, 1984a. Percolation and conduction on Voronoi and triangular networks: A case study in topological disorder. J. Phys. C17: 1519-1529.
Jerauld, G. R., L. E. Scriven, and H. T. Davis, 1984b. Percolation and conduction on the 3D Voronoi and regular networks: A second case study in topological disorder. J. Phys. C17: 3429-3439.
Komor, S. C., and D. G. Emerson, 1994. Movement of water, solute and stable isotopes in unsaturated zones of two sand plains in the upper Midwest. Water Resources Research 30: 253-267.
Langmuir, D., and J. Mahoney, 1984. Chemical equilibrium and kinetics of geochemical processes in groundwater studies. In: First Canadian/American Conference in Hydrogeology. B. Hitchon and E. I. Wallick, eds. Dublin, Ohio: National Water Well Association, pp. 69-75.
Lenormand, R., E. Touboul, and C. Zarcone, 1988. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 189: 165-187.
Margolin, G., B. Berkowitz, and H. Scher, 1998. Structure, flow, and generalized conductivity scaling in fracture networks. Water Resources Research 34(9): 2103-2121.
Meakin, P., J. Feder, V. Frette, and T. Jøssang, 1992. Invasion percolation in a destabilizing gradient. Phys. Rev. A 46: 3357-3368.
Moreno, L., and I. Neretnieks, 1993. Fluid flow and solute transport in a network of channels. Journal of Contaminant Hydrology 14: 163-192.
Moreno, L., Y. W. Tsang, C. F. Tsang, F. V. Hale, and I. Neretnieks, 1988. Flow and tracer transport in a single fracture: A stochastic model and its relation to some field observations. Water Resources Research 24: 2033-2048.
Mourzenko, V. V., J.-F. Thovert, and P. M. Adler, 1995. Permeability of a single fracture: Validity of the Reynolds equation . J. Phys II France 5: 465-482.
Mourzenko, V. V., S. Békri, J. F. Thovert, and P. M. Adler, 1996. Deposition in fractures. Chem. Eng. Comm. 148(15): 431-464.
Mourzenko, V. V., O. Galamay, J.-F. Thovert, and P. M. Adler, 1997. Fracture deformation and influence on permeability. Phys. Rev. E56(3): 3167-3184.
Nativ, R., and I. Nissim, 1992. Characterization of a desert aquitard: Hydrologic and hydrochemical consideration. Ground Water 30: 598-606.
Nativ, R., E. Adar, O. Dahan, and M. Geyh, 1995. Water recharge and solute transport through the vadose zone of fractured chalk under desert conditions. Water Resources Research 31: 253-261.
Neretnieks, I., 1993. Solute transport in fractured rock: Applications to radionuclide waste repositories. In: Flow and Contaminant Transport in Fractured Rock. J. Bear, C.-F. Tsang, and G. de Marsily, eds. New York: Academic Press, Inc., pp. 39-127.
Neretnieks, I., T. Eriksen, and P. Tähtinen, 1982. Tracer movement in a single fissure in granitic rock: Some experimental results and their interpretation. Water Resources Research 18(4): 849-858.
Nicholl, M. J., R. J. Glass, and H. A. Nguyen, 1992. Gravity-driven fingering in unsaturated fractures. In: Proceedings, International High Level Radioactive Waste Management Conference, Las Vegas, Nevada, April.
Nicholl, M. J., R. J. Glass, and H. A. Nguyen, 1993a. Small-scale behavior of single gravity-driven fingers in an initially dry fracture. In: Proceedings, International High Level Radioactive Waste Management Conference, Las Vegas, Nevada, April.
Nicholl, M. J., R. J. Glass, and H. A. Nguyen, 1993b. Wetting front instability in an initially wet unsaturated fracture . In: Proceedings, International High Level Radioactive Waste Management Conference, Las Vegas, Nevada, April.
Nordqvist, A. W., Y. W. Tsang, C.-F. Tsang, B. Dverstorp, and J. Andersson, 1996. Effects of high variance of fracture transmissivity on transport and sorption at different scales in a discrete model for fractured rocks. Journal of Contaminant Hydrology 22: 39-66.
Novakowski, K. S., G. V. Evans, D. A. Lever, and K. G. Raven, 1985. A field example of measuring hydrodynamic dispersion in a single fracture. Water Resources Research 21: 1165-1174.
Novakowski, K. S., P. A. Lapcevic, J. Voralek, and G. Bickerton, 1995. Preliminary interpretation of tracer experiments conducted in a discrete rock fracture under conditions of natural flow. Geophysical Research Letters 22: 1417-1420.
Oron, A. P., and B. Berkowitz, 1998. Flow in rock fractures: The local cubic law assumption reexamined . Water Resources Research 34: 2811-2825.
Palmer, A. N., 1975. The origin of maze caves. National Speleological Society 37: 56-76.
Palmer, A. N., 1991. The origin and morphology of limestone caves. Geological Society of America Bulletin 103: 1-21.
Paterson, L., 1984. Diffusion-limited aggregation and two-fluid displacements in porous media. Phys. Rev. Lett. 52: 1621-1624.
Poon, C.Y., R. S. Sayles, and T. A. Jones, 1992. Surface measurement and fractal characterization of naturally fractured rocks. J. Phys. D 25: 1269-1275.
Pyrak-Nolte, L. J., L. R. Meyer, N. G. W. Cook, and P. A. Witherspoon, 1987. Hydraulic and mechanical properties of natural fractures in low permeable rock. Proc. 6th Int. Cong. Rock Mech. 225-231.
Rasmuson, A., and I. Neretnieks, 1986. Radionuclide transport in fast channels in crystalline rock. Water Resources Research 22: 1247-1256.
Raven, K. G., K. S. Novakowski, and P. A. Lapcevic, 1988. Interpretation of field tracer tests of a single fracture using a transient solute storage model. Water Resources Research 24: 2019-2032.
Raven, K. G., and J. E. Gale, 1985. Water flow in a natural rock fracture as a function of stress and sample size. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr. 22(4): 251-261.
Renshaw, C. E., 1996. Influence of subcritical fracture growth on the connectivity of fracture networks. Water Resources Research 32(6): 1519-1530.
Robinson, P. C., 1983. Connectivity of fracture systems: A percolation theory approach. J. Phys. A 16(3): 605-614.
Robinson, P. C., 1984. Numerical calculations of critical densities for lines and planes . J. Phys. A 17(4): 2823-2830.
Rophe, B., B. Berkowitz, M. Magaritz, and D. Ronen, 1992. Analysis of subsurface flow and anisotropy in a fractured aquitard using transient water level data. Water Resources Research 28: 199-207.
Sallès, J., J. F. Thovert, and P. M. Adler, 1993. Deposition in porous media and clogging. Chem. Eng. Sci. 48: 2839-2858.
Savage, D., and C. A. Rochelle, 1993. Modeling reactions between cement pore fluids and rock: Implications for porosity change. Journal of Contaminant Hydrology 13: 365-378.
Scanlon, B. R., 1991. Evaluation of moisture flux from chloride data in desert soils. Journal of Hydrology 128: 137-156.
Scanlon, B. R., 1992. Evaluation of liquid vapor water flow in desert soils based on chlorine-36 and tritium tracers and nonisothermal flow simulations. Water Resources Research 28: 285-297.
Schmittbuhl, J., F. Schmitt, and C. H. Scholz, 1995. Scaling invariance of crack surfaces. Journal of Geophysical Research 100B: 593-597.
Schwartz, F. W., L. Smith, and A. S. Crowe, 1983. A stochastic analysis of macroscopic dispersion in fractured media . Water Resources Research 19(5): 1253-1265.
Smith, L., and F. W. Schwartz, 1984. An analysis of the influence of fracture geometry on mass transport in fractured media. Water Resources Research 20(9): 1241-1252.
Shaw, R., 1984. The Dripping Faucet as a Model Chaotic System. Santa Cruz, Calif.: Aerial Press.
Steefel, C. I., and P. C. Lichtner, 1994. Diffusion and reaction in rock matrix bordering a hyperalkaline fluid-filled fracture. Geochemica et Cosmochimica Acta 58: 3595-3612.
Thompson, M. E., and S. R. Brown, 1991. The effect of anisotropic surface roughness on flow and transport in fractures. Journal of Geophysical Research 96B: 21,923-21,932.
Tokunaga, T. K., and J. Wan, 1997. Water film flow along fracture surfaces of porous rock. Water Resources Research 33: 1287-1295.
Tsang, Y. W., and C. F. Tsang, 1987. Channel model of flow through fractured media. Water Resources Research 23(3): 467-479.
Tsang, Y. W., C. F. Tsang, I. Neretnieks, and L. Moreno, 1988. Flow and tracer transport in fractured media: A variable aperture channel model and its properties. Water Resources Research 24(12): 2049-2060.
Unger, A. J. A., and C. W. Mase, 1993. Numerical study of the hydromechanical behavior of two rough fracture surfaces in contact. Water Resources Research 29: 2101-2114.
Weisbrod, N., R. Nativ, D. Ronen, and E. Adar, 1998. On the variability of fracture surfaces in unsaturated chalk. Water Resources Research 34: 1881-1887.
Weisbrod, N., R. Nativ, E. Adar, and D. Ronen, 1999. The impact of intermittent rainwater and wastewater flow on coated and uncoated fractures in chalk. Water Resources Research 35(11): 3211-3222.
Wilkinson, D., 1986. Percolation effects in immiscible displacement. Phys. Rev. A 34: 1380-1391.
Wilkinson, D., and J. F. Willemsen, 1983. Invasion percolation: a new form of percolation theory. J. Phys. A: Math. Gen. 16: 3365-3376.
Winterfeld, P. H., L. E. Scriven, and H. T. Davis, 1981. Percolation and conductivity of random two-dimensional composites . J. Phys. C 14: 2361-2376.
Wood, W. W., K. A. Rainwater, and D. B. Thompson, 1997. Quantifying macropore recharge: Examples from a semi-arid area. Ground Water 35(6): 1097-1106.


































