8
What Do Drops Do? Surface Wetting and Network Geometry Effects on Vadose-Zone Fracture Flow
Thomas W. Doe1
ABSTRACT
Capillary conceptual models of vadose zone flow predict that large pores and open fractures should transmit water only when the rock as a whole approaches saturation. Observations, such as bomb-pulse radionuclides at Yucca Mountain, indicate more rapid transport in fractures at lower overall saturation values than capillary theory would suggest. These and other observations encourage a reexamination of vadose-zone conceptual models for fractures. In addition to film flow processes, this paper suggests that flow as discrete drops may also play a role in flow on fracture surfaces at lower saturation values. The study of drop flow versus film flow and capillary flow is strongly influenced by the wetting properties of the rock. Specifically, characteristics of a zero-contact angle versus a finite-contact angle may control whether flows occur as continuous films or discrete drops on fracture surfaces.
Drops in fractures may contact either one wall or both walls, in which case they may also be called capillary islands or blobs. Drops are static unless their mass exceeds a critical value to initiate sliding. The resistance to drop flow arises from wetting effects in addition to viscous effects, and in some circumstances wetting effects may dominate, especially in the initiation of flow. Drop flows appear in fracture-flow experiments described in the technical literature. The dependence of flow processes on contact angle emphasizes the importance of understanding wetting processes on natural fractures and on material used in laboratory simulations.
|
1 |
Golder Associates, Inc., Redmond, Washington |
Vadose flow in fracture networks is mainly in the direction of fracture dip. Strongly preferred nonvertical dip directions in fracture networks can divert flow from vertical directions toward the direction of fracture dip. Fracture network geometries can also lead to flow focussing into relatively small portions of the fracture network.
INTRODUCTION AND BACKGROUND
The movement of water and the transport of contaminants in the vadose zone have become matters of national importance. Vadose zone concerns are critical for radioactive waste disposal projects that involve thick unsaturated zones such as at Yucca Mountain or Ward Valley. Beyond these specific projects, the vadose zone has developed increased importance for problems of groundwater contamination, particularly in arid regions.
The dominant conceptual model for vadose zone flow can be called the capillary conceptual model. The capillary conceptual model of flow holds that water flows in pore spaces that contain continuous films held in place by capillary tension (Richards, 1931). The analytical backbone of the capillary model is Richards' equation (Richards, 1931).
According to the capillary model, capillary tension increases with decreasing pore size. Due to their higher capillary tension and lower matric potential, smaller pores will be the first to accept water on imbibition, and the last to yield water on drainage. As water preferentially resides in that portion of the rock having the lowest permeability (that is, the smaller pores), unsaturated rocks should be poor conductors of water except at saturation values of nearly one. As rocks become less saturated, the relative permeability of the rock to water also decreases. Because the capillary model conceptualizes flow in continuously connected pore water, flow ceases when the water in the pores becomes disconnected as the rock reaches its residual saturation value.
Wang and Narasimham (1985) and Peters and Klavetter (1988) extended the capillary conceptual model to fractured rock. As fractures tend to include the largest openings, particularly in fractured, consolidated rock, matrix pores should fill before fractures. The use of porous analogs and continuum models for flow in fractures has been justified by assuming that the roughness of fractures and the interactions of fracture asperities behave similarly to intergranular pores. Peters and Klavetter (1988) developed a continuum model for water movement in unsaturated fractures based on analogs of capillary tube bundles and derived equations of similar form to Richards' equation.
In Wang and Narasimhan's (1985) model, water is retained in fractures only at capillary bridges, which allow flow between the matrix blocks but not along the fracture (Figure 8-1a). According to Wang and Narasimhan (1985), “within a partially drained fracture, the presence of a relatively continuous air phase will produce practically infinite resistance to liquid flow in the direction parallel to the
fracture.” Within this conceptual model, fractures would contain continuous water only at saturation values that approach one. In arid regions, where infiltration rates are low and rocks may be expected to have low saturation values, these extensions of the capillary conceptual model to fractures predicted that fracture flow would be virtually nonexistent in thick vadose zones.
The capillary conceptual model has its roots in soil physics, a discipline that primarily supports agriculture and forestry concerns. For these applications, which are mainly in fine-grained soils, the capillary conceptual model has been successful and has stood the test of time. In rocks with larger voids and fractures, some questions have arisen.
The soil physics literature notes potential inconsistencies between capillary flow theory and natural behavior. Jury et al. (1991) have discussed the problems of flow in fractures and zones with large pores (macropores): “At the present time there is no complete theory describing water flow through structural voids (sometimes called macropore flow). There is uncertainty over how important subsurface voids can be in water flow, since if large they should only fill at matric potentials near saturation. Nonetheless, substantial indirect evidence of flow through structural voids has been obtained by tracer studies. These have shown that a fraction of a chemical application can migrate to substantial depths with only a small amount of water input” (Jury et al., 1991, p. 153). Hillel's (1980) soil physics textbook notes that a “ very challenging problem related to the infiltration into swelling soils is how to account for the role of cracks when a field of swelling soil is allowed to dry on top. In due time, a system of regularly spaced cracks appear. Infiltration into such cracked soil, in its initial stages at least, is obviously different from the orderly, one-dimensional process described by most existing theories. Much of the applied water bypasses the surface zone as it runs directly into the cracks.”
In recent years, several studies have produced evidence that vadose-zone flow in fractured rocks occurs at higher velocities than simple capillary-based models would predict. Pruess et al. (1999) summarize these observations, which include detection of bomb-pulse radionuclides in the Yucca Mountain underground test facility. Such radionuclides, which were produced by the atmospheric nuclear testing of the 1950s and early 1960s, suggest downward water movements of hundreds of meters in tens of years. These are considered “fast flows” relative to those expected from capillary theory. Pruess (1999) defines the fundamental paradox of unsaturated fracture flow: how can fast flow occur in the presence of the strong matrix imbibitions of partially saturated rock?
Laboratory testing on simulated fractures has turned up behavior that appears inconsistent with capillary flow theory. In particular, Su et al. (1999) note the formation of isolated drops on surfaces with connecting bridges that form, disconnect, and reform with time. Various spatial and temporal instabilities that are not predicted by Richards' equation have been reported in laboratory experiments. These include instabilities that lead to fingering (Glass et al., 1995), as
well as cyclic pressure and flow rate variations despite constant-input sources (Persoff and Pruess, 1995). Similar cycling behavior is also reported in experiments using coarse-grained soil analogs (Prázak et al., 1992). Prázak notes that this behavior is not consistent with the expectations of Richards' equation. A later section of this paper discusses laboratory observations in greater detail.
Several conceptual models have been proposed that may resolve the inconsistency issues. Pruess (1999) notes the apparent paradox of fracture flow in the presence of large matrix imbibition potentials. A solution to this paradox, he points out, is to limit the interactions of the matrix and the fractures. This can be accomplished by using a dual-permeability model (Figure 8-1b) that views the fractures and matrix as separate, but interacting flow systems (see chapter 11). This approach may be justified on several conceptual bases, such as (1) fracture coatings that restrict flow between the fractures and matrix, or (2) focusing mechanisms that restrict flow to a small portion of the fracture network. The fracture
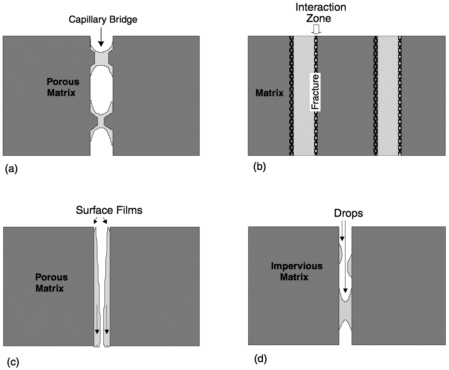
FIGURE 8-1 Conceptual models of vadose fracture flow processes: (a) model of Wang and Narasimhan (1985); (b) Dual-Permeability Model with fracture-matrix interaction zone; (c) Film-Flow Model of Tokunaga and Wan (1997); (d) Drop-Flow Model with one-walled and two-walled drops.
matrix interaction term is difficult to measure but it can be obtained by inverse modeling using an appropriate data set for calibration. The focusing mechanisms may derive from some combination of the fracture geometries and the flow processes.
One alternative model to capillary flow is the film flow model (Figure 8-1c; Tokunaga and Wan, 1997), which proposes the existence of films on fracture surfaces that form when the matrix approaches saturation and water is expelled to the fracture surfaces. Film flow requires a water source that is sufficient to maintain the film, which may be appreciable given the flow capacities of films. For situations where the water flow is not as great, we explore drop flows (Figure 8-1d) as yet another alternative conceptual model. Another difference between drop flows and film flows is the influence of wetting properties. Film flows presume a zero contact angle, while drop flows may apply when the contact angle is nonzero.
This paper places a major focus on drops. The paper was originally conceived as a review of fracture network models and the geometric considerations that might influence vadose-zone groundwater flow. In the course of preparing this paper, other questions of fundamental flow processes in fractures arose. These questions were inspired by many hours observing water flow on the glass windshield of an automobile caught in Seattle traffic. Observations of water on glass surfaces show discontinuous drops that stick to the surface and are immobile until they reach a critical size and begin to slide. At first glance this drop process does not conform to assumptions of the capillary conceptual model, which holds that flow happens in continuous films, and stops when the water becomes discontinuous, as in drops. Can one reconcile the flow of water in discontinuous drops with capillary theory? Or does drop flow constitute a fundamentally different flow process? How does flow in drops compare with other alternatives to capillary flow such as film flow (Tokunaga and Wan, 1997)?
Drop flow studies are extensive in the fluid mechanics and surface chemistry literature, but have received little attention in the soil physics or hydrogeology literature. This paper intends to develop awareness of the drop flow model as a potential alternative to capillary models for vadose zone fracture flow. The paper proposes drop flow as a means of moving water at saturation levels where water becomes discontinuous in the pore spaces and along fracture surfaces.
As such, this paper does not propose a specific practical approach to using drop flow mechanisms in analyses or numerical simulations. To become a practical tool, drop flow studies would need to deal with many of the same issues that conventional capillary flow models continue to wrestle with, such as how to deal with upscaling and heterogeneity of properties. Even if studies do not produce practical new methods, the periodic re-examination of conceptual models for their compatibility with natural observations and fundamental physical processes is desirable under any circumstances. Such a re-examination becomes necessary when the inferences of accepted conceptual models become inconsistent with observations of the natural world.
This paper defines “drop” as an isolated body of liquid that is not continuous with the rest of the liquid phase. For fractures, this definition includes drops that contact neither wall (this requires a large fracture aperture), a single wall, or both walls (Figure 8-1d). Some authors use terms other than “drop” for features that contact both walls. Kneafsey and Pruess (1998) use the term “capillary island,” while Su (personal communication, 2000) uses the term “blobs.” The reason for considering single-wall features and double-wall features together as “drops” lies in the similar physics of flow, as discussed below.
In the following sections, this paper reviews the fundamentals of surface-liquid interactions. This is an important starting point, as wetting properties and contact angles control, in part, whether liquids spread in films in zero contact angle systems, or isolate themselves into drops in systems with nonzero contact angles. Measurements of contact angles on quartz and on materials commonly used for laboratory simulation of fracture flow, such as glass or epoxy, are not zero. A nonzero contact angle suggests that water forms discontinuous drops and rivulets on surfaces rather than the continuous adsorbed films suggested by Richards (1931) or film flow theory (Tokunaga and Wan, 1997).
The next section reviews literature on the behavior of drops on surfaces. The movement of drops on surfaces or between surfaces for liquid-solid systems with nonzero contact angle differs significantly from conventional hydrogeologic thinking. Specifically, on single surfaces or fractures with large aperture, water forms a discontinuous network of drops or rivulets depending on the flow rate. The resistance to drop flow arises from the energy requirements for wetting the surface in advance of the drop, and viscosity enters only when the drop achieves some appreciable velocity. Drops that lack sufficient mass to allow gravity to overcome this wetting resistance are immobile. Following the discussion of the physics of drop flow, we review experiments on fracture flow in the laboratory.
Finally, we discuss how these concepts can be extended to fracture networks. This section looks at geometric factors that may lead to localization of flow in focused pathways.
SPREADING, WETTING, AND FLUID ADHESION ON SURFACES
An understanding of flow on surfaces requires an appreciation of the physics of wetting and wettability. This section briefly reviews the basics of this topic. For further discussion please refer to, for example, Berg (1993) or Hiemenz and Rajagopalan (1997); this discussion draws heavily from those references. According to Berg (1993), “wettability” refers to “the response evinced when a liquid is brought into contact with a solid surface initially in contact with a gas or another liquid. ” As Berg points out, several things can happen when a liquid contacts a solid surface, including:
-
the liquid may spread spontaneously, forming a film whose extent is limited only by the mass of liquid available; or
-
the liquid may spread on the surface until it achieves an equilibrium with the gas and the solid to form a three-phase interface with a contact angle; or
-
the liquid may have no interaction with the surface at all.
Which of these processes occurs depends on the wetting properties of the liquid and the surface. Depending on those properties, one may expect a range of processes that are important for vadose zone flow.
Wetting is classically viewed in terms of surface energies that are associated with interfaces between liquids, solids, and gases. These surface energies are related to the surface tensions σLG for the liquid-gas interface, σLS for the liquid-solid interface, and σSG for the solid-gas interface. If we assume as Berg (1993) does that practical differences between the free energies of the liquid and solid with the gas phase and with a vacuum are negligible, then σLG ≈ σL and σSG≈ σS.
First, let us consider the liquid itself. Liquids, particularly water, may have a strong cohesion, which reflect the water's attraction to itself. The work of cohesion, WC, is defined as the work required to create a unit surface area of liquid. Separating a single mass of water into two masses creates two surfaces where there had been one. If a unit area of liquid has a surface energy reflected by σL, then the divided bodies will have twice that energy; hence, WC= 2σL.
In contrast to cohesion, which describes interfaces in a single material, adhesion describes the interface between two different materials, such as a liquid and a solid. If we view the work of adhesion, WA, as the work required to disjoin or de-wet a unit area of solid-liquid interface, then the de-wetting process creates two new surfaces with the energies associated with the liquid and the solid, and it eliminates the interface between the liquid and solid; hence, WA= σS+σL− σLS.
The work of wetting, WW, refers to the work required to de-wet a unit area of solid surface. As this de-wetting creates a solid-gas surface at the expense of a liquid-solid surface, the work may be expressed as the difference of the surface energies of solid-gas surface and the liquid-solid interface, or, WW= σS− σSL. This wetting process occurs when liquid is imbibed or drained from a material such as pores or capillary tubes. A final useful wetting relationship is the work of spreading, WS. If a surface has been coated or covered with a liquid, this is the work required to create a unit area of solid-gas interface while eliminating unit areas of liquid-gas interface and liquid-solid interface; hence WS= σS− σL− σLS. The work of spreading can also be arrived at by taking the difference of the work of cohesion and the work of adhesion.
Thomas Young (1805) studied the contact angle at the junction of a solid, a liquid, and a gas phase. Young's law relates the contact angle to the surface tensions by:
(8.1)
Substituting Young's law (Equation 8.1) into the wetting relationships ties them to contact angle as:
WA= σLG(1+cosθ), (8.2)
WW = σLG cosθ, (8.3)
WS = σLG(cosθ−1). (8.4)
Berg (1993) points out that these values of work are the negative free energies associated with these processes, hence positive values for Equations 8.2 through 8.4 indicate that adhesion, wetting, or spreading occur spontaneously.
For each process, there is a critical contact angle that separates positive values from negative values for these expressions. The ranges of these critical angles and the associated processes are shown in Figure 8-2. Adhesion (Equation 8.2) occurs provided the contact angle is less than 180°. A practical implication of this relationship is that the liquid can produce drops that are capable of “sticking” to a surface when the contact angle is less than 180°. If the contact angle is 180°, there is no adhesion between the liquid and the solid.
With respect to wetting2 (Equation 8.3), the critical contact angle is 90°. This is the contact angle that differentiates capillary rise from capillary depression.
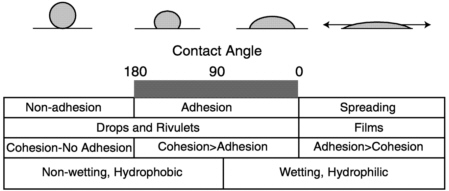
FIGURE 8-2 Relationship between adhesion, cohesion, wetting, spreading, and contact angle.
|
2 |
The definition of the term “wetting” can be confusing as it has many uses depending on the circumstances. Some authors use “wetting” to refer to any system where there is adhesion, that is, contact angles less than 180° (Padday, 1993), while others, including Richards (1931), use “wetting” nearly synonymously with spreading, or a contact angle of zero. Perhaps the most common usage is for contact angles less than 90°. |
This is an extremely important relationship for vadose zone flow as noted in the equations for capillary rise, H, in tubes and between parallel plates with separations of e, a fluid with density ρw, subject to gravitational acceleration, g, (Wang and Narasimhan, 1985):
(8.5)
If the contact angle is less than 90°, then liquids spontaneously imbibe into smaller pore spaces, such as pores and fracture asperities that are in contact. Such a condition is considered hydrophilic. At higher contact angles, liquids require work to be brought in contact, and thus are nonimbibing, or hydrophobic. The 90° contact angle and the surface-energy processes it represents are a fundamental separator of hydrophilic behavior and hydrophobic behavior.
As to spreading (Equation 8.4), the critical contact angle is zero, as any positive contact angle produces negative values of the spreading coefficient. When a liquid spreads, it spontaneously forms films on surfaces rather than drops. Thus the zero contact angle is critical for defining film flows. The zero contact angle thus provides a separator between regimes where film flows will dominate, from those where drops will be more prevalent at lower saturations.
Contact Angles for Geologic Materials and Surface Roughness Effects
The previous section reviewed the fundamentals of wetting, spreading, and adhesion. The properties of wettability are reflected in the contact angle. Specific values of contact angle separate regimes that exhibit differences of flow process, such as film flow versus drop flow, and hydrophilic versus hydrophobic behavior.
Literature reviews of contact angle data for geologic materials turned up relatively few references. There may be several reasons for this. Contact angles are commonly assumed to be zero as a matter of convenience due to the complexities that nonzero contact angles introduce to theoretical development (Letey et al., 1962). Furthermore, contact angles may change with time and the duration of contact with water (Carillo et al., 2000). Natural materials are heterogeneous, and may display different properties even at small scales. Finally, contact angles are notoriously irreproducible unless care is taken to keep the surface free of contamination (Berg, 1993). Such cleanliness is not a concern of nature. Despite the technical concerns with contact angle, its importance to questions of hydro-phobicity and preferential flow cannot be denied, even though contact angles are hard to measure.
In reviewing contact angles, one may start with laboratory measurements on mineral surface and laboratory modeling materials. Studies by Sklodowska et al. (1999) of liquid interaction in ore processing report contact angles of water on quartz and glass to be 32.79 ± 1.12° and 51.05 ± 0.84°, respectively. Sobolev et
al. (2000) determined dynamic contact angles on quartz capillaries and found that contact angles varied between approximately 30° and 70° depending on capillary radius and flow velocity. Su et al. (1999) report contact angles of 33° and 63° respectively for the glass and epoxy used in fracture visualization studies.
Contact angles have been measured in soils by a variety of methods, including times required for infiltration, time for penetration of water drop into a soil surface, and capillary rise methods (Yuan and Hammond, 1968). Pal and Varade (1971) report contact angle measurements of about 60° on untreated, sieved sands. Bachmann et al. (2000) applied sieved soils to surfaces using adhesives and measured the resulting contact angles from drop profiles. These measurements may approximate behaviors of rough, heterogeneous fractures. A portion of the sand grains were treated with hydrophobic coatings. Their measured contact angles varied from 0° to 120° depending on the percentage of hydrophobic grains in the soil.
It should be noted that the laboratory contact angles discussed above (except for the soil measurements) are given for smooth surfaces, and we will refer to these as intrinsic contact angles. The effective contact angle may be reduced by surface micro-roughness. This effect is well demonstrated in the application of paints or adhesives, where it is common to roughen a surface prior to application to assure better adhesion. Hazlett (1993) provides an overview of the literature on this effect. He concluded that the phenomenon was real, although there was not yet a consensus on its causes. Viewed thermodynamically, a rough topography has a greater effective surface area, and thus a greater surface energy, than a smooth surface with the same plan view area. Although various theories on the effects of roughness on contact angle remain open to discussion, the effect of roughness on contact angle has been verified experimentally. Bikerman (1950) demonstrated this phenomenon in experiments on the inclination angle for the sliding of drops on treated steel surfaces. The inclination angle at which drops slide is a function of the contact angle, and for the same steel material Bikerman showed a 21° decrease in the sliding angle through progressive stages of surface treatment to decrease the roughness.
The topic of roughness is very important for the design of laboratory experiments. If laboratory experiments are to reproduce realistic wetting behaviors, the simulated fracture surfaces will need to incorporate the full range of roughness effects that are present on natural fractures. Experimental approaches that use castings of natural fractures may recreate the larger scale asperities while missing the finer roughness scales that affect wetting properties.
The issue of contact angle and roughness is critical for using laboratory experiments as analogs for natural flow. Many analog experiments use smooth surfaces of glass or epoxy for which the intrinsic contact angles range between 20° and 65°. These contact angles indicate that spreading conditions do not exist and the flow will assume the form of rivulets or drops. However, roughness may contribute sufficient additional surface energy to reduce the effective contact
angles to zero. This possibility is suggested by qualitative observations of wetting on roughened glass used in film flow experiments where spreading on horizontal surfaces implied a zero contact angle (Wan et al., 2000; Tokunaga et al., 2000).
FLUID MOVEMENT ON SINGLE SURFACES WITH NONZERO CONTACT ANGLES
As discussed above, the energy relationships between the liquid and the surface influence the fundamental flow processes on that surface. Current flow theories assume continuous adsorbed water films and a contact angle of zero. Film flow theories (Tokunaga and Wan, 1997) also assume a zero contact angle. If the contact angle is not zero, water may tend to form drops or rivulets. This section describes the flow processes for such systems.
Drop and Rivulet Flows
If the liquid has a contact angle with a flat surface, the cohesion of the liquid exceeds its adhesion to the surface, and the liquid will form discontinuous drops unless the flux of liquid is sufficient to keep the surface flooded. Although there is little theoretical literature on the flow of drops between two surfaces, extensive work has been done on flow on single surfaces (Sadhal et al., 1997).
This section concentrates on drop flows; however, flows on surfaces where the water has a nonzero contact angle can take several forms depending on the flow rate. At high flow rates, the water can form a curtain that completely floods the surface. As the flow proceeds down an inclined surface, the curtains that begin as uniform fronts may break up into rivulets. The rivulets have a regular spacing (Huppert, 1982; Johnson et al., 1999), with a spacing, or wavelength, λmax, that is related to the thickness of the film and the ratio of viscous to capillary forces as expressed by the capillary number, Ca:
(8.6)
(8.7)
where K is an experimental constant, d0 is the thickness, d0m is a theoretical thickness, Q is the flow rate, ρ is fluid density, σ is the surface tension, n is an experimentally determined power (theoretically 1/3), and v is the kinematic viscosity.
The formation of rivulets on single surfaces is similar in form to the finger flows described by Glass et al. (1995), but it results from different processes. Glass and colleagues explain fingers as the result of a gravitational density instability that arises when a lower density fluid is trapped beneath a higher density fluid. The only upward path for the lower density fluid is through the overlying
fluids. Fingering also arises when such trapping does not exist, as noted by Lenormand and Zarcone (1989), in which case the origin of the fingering, like the rivulets on single surfaces, is a capillary instability rather than density instability.
Physics of Drop Sliding
Drops are familiar companions to our everyday lives. Drops are common on glass windows, mirrors, car windshields, ceramic tiles, and clear plastic disposable cups like those the airlines use for beverages. Aside from being a curiosity in day-to-day living, the understanding of drops has many practical applications. The encouragement of spreading and the avoidance of drops are essential for paints, adhesives, and coatings. Drop promotion is essential for waterproofing. Drops affect condenser design, as the energy transfer on the surfaces of condensers is more efficient for drops rather than for films, especially if the condenser surfaces are inclined and the drops can roll off to expose fresh surfaces for condensation (Dussan and Chow, 1983). Drops are important for spray retention on foliage, as chemical applications will work better if drops adhere rather than roll off the surfaces of foliage (Furmidge, 1962).
Sadhal et al. (1997) provide an extensive review of drop statics and dynamics. The basic form of drops on surfaces is that of a section of sphere distorted by gravitational effects. On a horizontal surface, the profile of the drop meets the surface at the contact angles for the vapor-solid-liquid system. On inclined surfaces, gravity distorts the drop so that it has a larger contact angle on the downdip side of the drop than on the updip side. The updip and downdip contact angles are called the advancing and retreating contact angles, or θa and θr, respectively (Figure 8-3), and the difference between these values is the contact angle hysteresis.
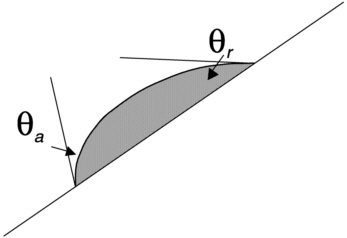
FIGURE 8-3 Advancing and receding contact angles for drops.
Furmidge (1962) experimented with drop retention of sprays on solid surfaces in the course of research to optimize the retention of agricultural applications on the surfaces of foliage. He noted that spraying spatters fluid on the surfaces with different sizes. As the spraying continues, drops coalesce and grow to a critical size at which they are no longer static and slide off the surface. Furmidge placed drops of various sizes and masses on smooth brass plates, which he tilted to induce sliding.
When a drop slides down an inclined surface, it wets an area equal to the width of the drop times the distance the drop has moved ( Figure 8-4). A similar area is dewatered behind the path of the drop. Based on the differences in the work performed by the advancing, wetting surface and the retreating, de-wetting surface, Furmidge gave the sliding criterion for drops in terms of a critical angle of inclination for the surface, φ, or
ρgVsinφ = wσ(cosθr − cosθa), (8.8)
where ρ is fluid density, σ is the surface tension, V is the volume of the drop, and w is the drop width. Note that width refers here to the length dimension of the drop perpendicular to the dip direction of the slope.
Furmidge (1962) proposed this relationship on empirical grounds; however, Dussan (1985) and Dussan and Chow (1983) showed that it could be proven by physical fundamentals. The insight afforded by this equation is that drops are held in place by various surface energies that include the fluid surface tension and the adhesive forces, which are lumped into the definition of the contact angle. Equation 8.8 shows that the resistance to sliding is based on the width of the drop and not on its total contact area with the surface. If two drops have the same
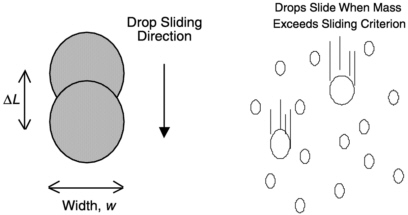
FIGURE 8-4 Sliding criteria for drops.
volume but different widths, the longer, narrower drop will resist sliding more than the wider, shorter one. Later experiments on drop sliding by Extrand and Kumagai (1995) showed that the contact angle hysteresis (the difference between the cosines of the advancing and receding contact angles) varies with drop shape, and the retentive forces could vary with the drop length. Dussan and Chow (1983) analyzed the dynamics of drop sliding theoretically and developed expressions for drop velocities. These analyses are quite complex and will not be repeated here. The approach does assume that contact angles are functions of drop velocity, and the resistance to movement changes with velocity. If the resistance increases, drops will achieve a stable velocity on surfaces rather than accelerate indefinitely.
Drop Sliding Between Parallel Plates Where the Drop Contacts Both Plates
The major portion of the work on drop flows comes from applications to single surfaces. These analyses are directly relevant to flow on fracture surfaces, provided the height of the drop is less than the fracture aperture, and the drop is in contact with only one fracture wall. Drops in contact with both walls of a fracture have been observed in experiments (Kneafsey and Pruess, 1998; Su et al., 1999).
The problem of a drop contacting both fracture walls has not been studied as rigorously as the case of a single surface. We might expect, however, that having a drop in contact with two surfaces changes the problem mainly by requiring two surfaces to be wetted rather than one. Hence a first approximation for drops in contact with both fracture walls is that the wetting resistance doubles by having to wet two surfaces instead of one.
If we assume the drop is circular with a radius, r, its approximate volume will be the area of the drop times the parallel plate aperture, e. The width of the drop will be 2r. We also introduce an additional factor of two for the two surfaces. For a drop in contact with both parallel plates, Furmidge's sliding criterion defines a critical radius for sliding, rc, which becomes:
(8.9)
Figure 8-5 shows the critical drop size for vertical parallel plates as a function of aperture and contact angle. This figure assumes the advancing and retreating contact angles are ±50 percent of the contact angle on a horizontal surface.
Drops may contact either one wall or both walls of the fracture depending on the height of the drop and aperture of the fracture. We can use Furmidge's relationships to assess whether the drop flow will be drops in contact with one wall or with both walls. If the heights of the critically-sized drops are smaller than the fracture aperture, then we should expect that flow is on one fracture wall only.
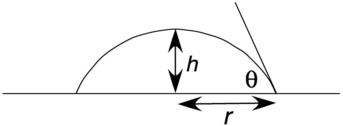
FIGURE 8-5 Spherical cap representation of a drop on a planar surface.
To make a calculation of a critically-sized drop on a single wall, we must make assumptions about the shape of the drop to calculate its height. The heights and shapes of drops are determined by a complicated interaction of surface properties and gravity; however, to get a rough approximation, we may assume that the drop has the form of a spherical cap (Figure 8-6). In this analysis we assume that the liquid-surface contact angle defines the portion of the sphere that forms that cap. For example, a contact angle of 30° would use a cap lying 30° about the top of a sphere. The volume of such a spherical cap is
(8.10)
where r is the radius of the drop on the surface.
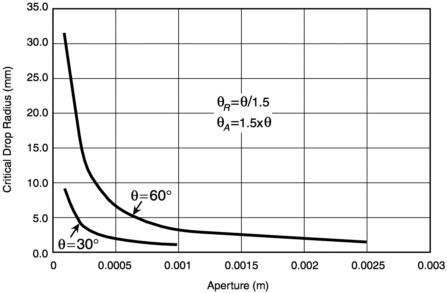
FIGURE 8-6 Critical drop radius for sliding between two parallel plates.
Inserting this volume expression into Furmidge's sliding criterion allows solution for the critical drop radius, rc, that will induce drop sliding, which is
(8.11)
The height, hc, of a drop that is critically sized for sliding can be derived by trigonometry from the geometry of the spherical cap as:
(8.12)
Assume that advancing and receding contact angles are a factor of 1.5 greater or less than the basic contact angle, θ, and the surfaces are vertical. Then rc will vary from about 2 mm to 1 mm for contact angles of 30° and 90°. The corresponding drop heights will be 0.5 mm and 0.9 mm, respectively. Due to the square root relationship in calculating r, the drop size has a reduced sensitivity to the contact angles. Again, this is a rough approximation subject to experimental testing due to the use of a spherical form for the volume calculation.
These analyses suggest that the heights of critical drops on single surfaces will be on the order of a millimeter or less. Hence, we may expect that single-walled drop flow will occur for fractures larger than 1 mm in aperture, and two-walled flow will occur in fractures with less than 0.5 mm aperture for contact angles consistent with air, water, and quartz or glass.
Larger aperture fractures will be more conducive to flow by drop sliding than smaller fractures for two reasons. If we consider drops in contact with both walls, the critical volume for drop sliding will be larger for smaller aperture fractures, and the radius of a critical fracture will be larger. Larger aperture fractures are also more conducive to flow because they are more likely to contain drops in contact with single walls, and these drops have less resistance to flow because they wet only one surface.
Asperities can be expected to play a role in sliding and drop retention. With asperities, the radius of the drop required for sliding will need to be larger for at least two reasons. Asperities reduce the volume of the drop for a given drop radius; and thus the drop requires a larger radius to slide. Second, the drop will leave behind a volume of water as capillary retention at the asperity's point of contact or the point of least wall separation, if contact is not made.
Once drops begin to move they should continue to slide unless they lose volume, the fracture aperture changes, surface properties of the fracture change, or the inclination angle of the fracture changes. Drops may gain volume by coalescence with small static drops in their path. They may also lose volume by evaporation or imbibition to the matrix along the fracture walls. Drops may also
lose volume to asperities, as they would leave behind some mass in capillary retention.
The movement of water in drops will differ in significant ways to the capillary conceptual model of water movement in the vadose zone and to film flow concepts. Specifically:
-
The initiation of flow is related to the wetting properties of the surfaces, and once water is moving, wetting resistance may play an equal or more significant role than viscous drag along the fracture walls.
-
Drops can be immobile; drops will remain in place until they accumulate sufficient volume to overcome wetting resistance, and they become immobile again if they lose mass or fracture conditions change. Once immobile, they will remain immobile until additional mass enters the drop.
-
Darcy's law may not apply if the flow resistance is not primarily viscous and the concept of a potential gradient does not apply to discontinuous drops.
-
Drop movement is not a diffusion process.
In terms of boundary conditions, drop flows are best described by flow rate or flux boundary conditions, as head boundary conditions do not apply. In this case, there are clear relationships based on conservation of mass for drop velocity, flux, and saturation. Subject to experimental verification, the application of a constant flux at the top of a fracture results in an accumulation, or storage, of drops or mass at the top of the fracture until a drop reaches a mass sufficient to initiate sliding. At higher fluxes, this flow might occur as a rivulet. At flow fluxes, the mass should emerge from the lower boundary as drops. The long-term average fluxes would balance the influx; however, the instantaneous outflow rate could be high or nothing depending on whether or not a drop was emerging at any particular moment.
EXPERIMENTAL EVIDENCE
Laboratory experiments of flow in simulated fractures are important for understanding flow processes. This section presents a brief review of experiments involving flow in simulated fractures.
Rasmussen (1991) performed experiments on a vertical fracture simulated by two glass panels. The test involved injecting water into a hole in the interior of the fracture under constant head conditions. The sustained injection of the constant-head condition created a region of local saturation primarily downward from the injection point, but also a slight distance upward. The main use of the experiment was to provide data to compare with numerical models of the air-water interface. The experimental results largely agreed with the analytical predictions of the position of the air-water interface, with some variability caused by air bubbles entrapped in the water-saturated zone. Because of the constant-head
injection conditions, the flow occurred in locally saturated rivulets rather than as drops or films.
Fourar et al. (1993) performed two-phase flow experiments on smooth and rough fractures and correlated the results to porous media and pipe models. The experiments used smooth glass plates and plates with 1 mm beads in the aperture of the fracture to simulate roughness. The fracture materials were glass, the liquid was water, and the gas was compressed air. The experimental conditions involved the pressure injection of air into initially water-filled fractures, which would appear to be a better analog for oil reservoir processes than for vadose zone flow. Of particular interest in these experiments is the structure of the phases. The structure of the two phases varied with the gas injection rate. At low gas injection rates, the gas bubbles disperse into the water. With increasing rate, the bubbles start to become unstable and begin to finger. At yet higher gas rates, the gas occupies the major portion of the fracture. At these higher gas flow rates, the flow geometry of the water varied with the water injection rate. At lower water injection rates, the water moved as liquid drops in the gas stream. At higher liquid rates, the water flowed as unstable films on the fracture walls. The expectation for a porous medium was that each phase would occupy its own continuous network of pores, the wetting phase in the smaller pores and the nonwetting phase in the larger. The experiments, on the other hand, showed that only one phase was continuous and the other phase traveled as either bubbles or drops. The occupancy locations of the phases were constantly changing.
Nicholl et al. (1994) prepared experiments using commercial glass plates with textured surfaces to represent the fractures and deionized water with small amounts of dye to represent the liquid. The test conditions involved slug injections of water at the top of the air-filled fracture. The basic hypothesis of the experiment was that the flow process was one of density inversion, that is, the entry of higher-density water at the top of the flow system would displace the lower-density air, and the geometry of the water distribution would reflect the gravitational instability. The primary observation of the experiment was the breakup of the water invasion front into fingers (Figure 8-7). Being a slug injection, the fingers were not replenished as they moved down the steeply dipping fracture, and they left drained regions behind them. Smaller fingers were observed to have lower velocities or to stop altogether. Ultimately the liquid would form disconnected clusters, or “drops,” though Nicholl et al. do not use this term. This paper also presents the results of dyed water injections in the top of a natural fracture, which showed clearly the development of fingers. One significant point of this work was to demonstrate that the fingering is primarily the result of instability in the wetting front independent of aperture heterogeneity.
Persoff and Pruess (1995) report fracture flow experiments using epoxy replicas of natural fractures. The epoxy is reported to have a contact angle of 20° on flat surfaces. Distilled water and nitrogen gas were used for the wetting and nonwetting phases, respectively. As with the experiments of Fourar et al. (1993),
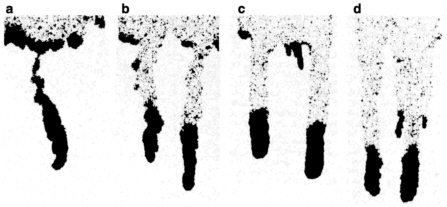
FIGURE 8-7 Fingers and drops from laboratory experiments. From Nicholl, M. J., R. J. Glass, and S. W. Wheatcraft, 1994. Gravity-driven infiltration instability in initially dry nonhorizontal fractures. Water Resources Research 30: 2533-2546. Copyright by American Geophysical Union.
these experiments involved gas injection into initially water-filled fractures. Despite the constant rate injections of gas and water, the pressure did not achieve steady values as pressures and flow oscillated with intermittent water blockage and clearing of critical pathway throats in the fracture.
Kneafsey and Pruess (1998) simulated thermally driven two-phase flow effects. Their experiments used natural fractures, epoxy casts of natural fractures, flat glass, and textured glass. The glass fractures were prepared both with and without sandblasting to enhance surface roughness. Pentane was used as the liquid phase. Although the major experimental aim was to demonstrate thermal effects, such as heat pipes, the work did record a variety of flow structures and regimes. The three types of flow were continuous rivulets, intermittent rivulets and drops, and films. Continuous rivulets occurred on the rapid introduction of the pentane or when there was sufficient liquid supply to support continuous flow. Intermittent flow occurred from quasi-stable, saturated islands. When mass was added to an island by flow or condensation, it produced an intermittent rivulet. Drops are described as extreme forms of rivulet, where liquid would accumulate at the top of a wider-aperture section of the fractures and release a drop when the mass became sufficient to overcome the capillary resistance. In some cases, drops fell freely without touching the fracture walls. Film flows occurred when the aperture of the fracture was larger than the film thickness and may have also transported fluid to the saturated islands.
Su et al. (1999) further document intermittent flow effects in rough-walled fractures using experimental conditions more closely related to vadose percolation
than those of Kneafsey and Pruess (1998). These experiments used epoxy casts of natural fractures and water with a dye to aid visualization. The contact angle of water on the epoxy was 63°, which was similar to values observed for drops on smooth granite surfaces. The experiments varied the angle of inclination of the fracture. The fractures were dry prior to the introduction of the water under constant rate conditions. The fracture replica tests produced fingers of liquid rather than a uniform wetting front. The fingers broke off to form capillary islands, which were connected to the water source and to one another by thin rivulets or threads (Figure 8-8). The seepage velocities of these systems were of the order of 0.02 cm/s. Su et al. (1999) note that current analytical and numerical models of flow in unsaturated porous media do not predict this type of intermittent flow.
Su et al. (1999) followed up their fracture-cast experiments with further tests on glass parallel plates. The plates were arranged to form multiple constant-
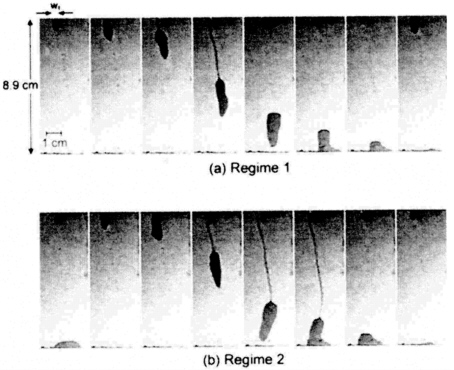
FIGURE 8-8 Drop or blob flow between parallel plates. From Su, G. W., J. T. Geller, K. Pruess, and F. Wen, 1999. Experimental studies of water seepage and intermittent flow in unsaturated, rough-walled fractures. Water Resources Research 35: 1019-1037. Copyright by American Geological Union.
aperture regions. These experiments defined three regimes under conditions of constant-rate flow:
-
lower flows where islands break off from the water source and move down the fracture;
-
intermediate flows where the islands remain connected to the source by threads until they reach the downstream end of the fracture, where they break off; and
-
higher flow rates where the source and the sink maintained a continuous thread.
In summary, experimental work on both fractures and coarse porous media indicate conditions of discontinuous flow in the form of drops or rivulets. This behavior is not surprising given the finite contact angles of the liquid-surface systems that are used for the experiments. Another manifestation of drop flow modes is oscillations in outlet flows that occur when drops are exiting the flow system.
The occurrence of drop and rivulet flows may be an artifact of using smooth surfaces for experiments. Where experiments used casts of natural fractures, it is not clear whether or not the process reproduces the micro-roughness in addition to the macro-roughness of the visible asperities. One observation in reviewing experiments is the importance of measuring and reporting the contact angles of the fluids and the surfaces that are used.
FRACTURE NETWORK GEOMETRY AND VADOSE FLOW
As mentioned in the introduction, the occurrence of fast flow in fractures in the presence of strong matrix imbibition is a major paradox in unsaturated fracture flow systems. Pruess (1999) attempted to reconcile these observations by limiting the surface area for fracture and matrix interactions. Pruess (1999) suggested ways to limit surface area: “(1) reduction of fracture wall area available for imbibition due to spatial localization of flow, (2) reduction of time available for imbibition due to the episodic nature of seepage, and (3) reduction of fracture matrix flow due to the presence of mineral coatings of low permeability on the fractures walls.” In our discussions below, we will look mainly at the localization of flow in fracture networks for reducing matrix-fracture contact.
Driving Forces and Fracture Dip
An understanding of fracture network effects in vadose flow begins with the effect of fracture dip on the driving forces. The driving force for vadose fracture flow is gravity, and gravity acts in the direction of the dip of conducting fractures. The influence of gravitational acceleration varies with the sine of the dip angle.
Within the interior of a fracture, the direction of flow should be coincident with the fracture dip angle. A key issue for flow direction involves how effectively asperities and variability of surface properties can affect flow direction. If asperities occur as random islands of contact, they may serve as locations of storage, but would not affect the flow direction in the fracture. However, an asperity pattern that creates linear ridges could act as a “wick” and divert flow off the fracture dip direction. Such linear asperity zones could arise from either mechanical processes, such as arrest lines formed during tensile propagation, or geochemical processes that preferentially deposit or dissolve material along channels or ridges. Variability of surface wettability can also affect flow direction. Variations in surface materials or roughness could create regions with lower wetting resistance, and thus create pathways that are not strictly in the direction of fracture dip.
The edges of fractures may have special properties and processes compared with the rest of the fracture. The edge of the fracture forms a boundary, which will have a lower dip inclination than the rest of the fracture. However, an edge of a fracture likely has a smaller aperture and higher capillary suction, hence a continuous water film may occupy the fracture edge and be a path for preferential flow.
If we assume that the driving forces for flow are dominantly gravitational, and flow is in the dip direction of fractures, we can develop several mechanisms for flow localization arising from the geometries of fracture networks. These include flow diversion, flow focusing, and flow connectivity.
Flow Diversion
A common assumption of vadose zone flow is the assumption of vertical hydraulic gradient. When flow is confined to fracture planes, this assumption is correct only if the fractures are vertical. If the fractures are not vertical the hydraulic gradient will be reduced by the sine of the fracture dip. Furthermore, if the fractures have a dominant dip direction, the dominant flow direction may be skewed away from vertical toward the direction of fracture dip.
Dominant dip directions may arise in bedded rocks such as sedimentary or volcanic rocks where there are fracture sets that follow the weakness along the bedding planes. Exfoliation joints or other topographically controlled fracture systems could serve a similar purpose. The overall effect of a preferred dip direction would be a diversion of the flow from vertical toward the dip direction. Figure 8-9 illustrates this effect.
Flow Focusing
Flow focusing is another potential consequence of fracture network geometry. Pruess (1999) presented an extensive discussion of focusing effects, where
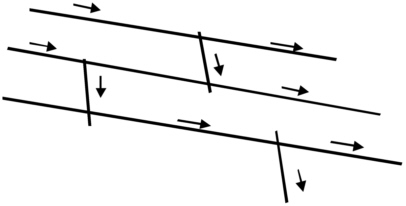
FIGURE 8-9 Flow diversion by fractures with strongly preferred orientations.
he divided focusing mechanisms into “external” and “internal.” External focusing is the localization of flow on the external boundaries of the flow system. This may involve localization at surface drainages or at the surface exposures of fractures.
Internal flow focusing is controlled by the fracture network geometry. Pruess (1999) showed how barriers to flow can focus the flow to small portions of the fracture system. When a flow encounters a barrier, the flow is diverted to the down-dip edge of the barrier. The flow stream from this point is considerably more focused than it was upstream of the barrier. Numerical simulations using a Richards' equation-based flow simulator show that these focused flows do not spread as gravitational forces overwhelm dispersive effects. The sorts of features that may serve as barriers include zones of fracture closure due to mineralization or stress. Fracture intersections in sparsely fractured rock also may serve as focusing agents (Figure 8-10).
Two other conceptual models involving focused flow in fracture networks deserve mention. The first is the “weeps” model (Gauthier et al., 1992), which assumes fracture flow in local regions of saturation. A form of weeps model, conditioned to the fracture-matrix interaction effects in numerical models, was developed by Ho and Wilson (1998). The second involves numerical methods to validate the active fracture area in dual-permeability models (Liu et al., 1998).
Gauthier et al. (1992) developed a simplified, “weeps” approach to vadose fracture flow for the Yucca Mountain project. They viewed fracture flow as occurring in locations of local fracture saturation, or weeps, distributing the flow based on the parallel plate approximations for fracture transmissivity. The basis of the method is not fundamental flow processes, but rather a mass balance approach. The model uses the assumed infiltration rate to the fractured rock, and determines the number of saturated fractures that will accommodate the assumed
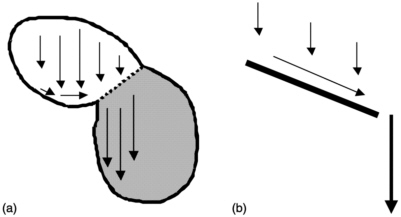
FIGURE 8-10 Flow focusing: (a) focussing at intersection; (b) diversion at barrier. After Pruess (1999).
rate. The model also assumes little or no matrix interaction based on the rationale that fracture coatings impede matrix-fracture interaction. Gauthier (1994) extended the model to allow weeps of different sizes. The weeps approach was specifically designed to assess the number and distribution of inflow points to a repository. As such, it attempts to be a bounding calculation. For systems with low infiltration rates, as in arid environments, the weeps model provides insights into how a few fractures may be sufficient to accommodate the entire flux. For example, an infiltration rate of 15 mm/year over a 1-km2 area could be accommodated theoretically by a single, 1-m-long fracture with an aperture of slightly less than a millimeter.
Ho and Wilson (1998) combined the “weeps” approach with the results of dual-permeability modeling to arrive at the wetted and active portions of a fracture network at Yucca Mountain. They started with the fracture-matrix reduction factor that comes out of a dual-permeability model that had been calibrated to matrix saturation and geochemical data. The fracture-matrix reduction factor is the portion or the percentage of the total fracture surface area that is available for fracture-matrix mass transfers. They then assumed that the product of the total fracture area and the fracture-matrix reduction factor was the active flowing area of the fractures. Using values of fracture spacing obtained by fracture mapping to obtain the total fracture area, they applied the fracture-matrix interaction term to get weep spacings. The flow rate per weep is the total percolation flux (L/T) multiplied by the area associated with each weep. The approach used several assumptions including homogeneous, vertical fractures with constant spacing.
Liu et al. (1998) developed another method for estimating the portion of the fracture system that is actively flowing water. Their conceptual model assumes that the active portion of the connected fracture space, fa, is a number between 0 and 1. This active portion is assumed to be related to the effective fracture saturation by a power of γ, which is a positive constant related to the network properties. The saturation is “effective” in that it is scaled to make the residual saturation zero:
(8.13)
Liu goes on to derive van Genuchten relationships for capillary pressures and relative permeability in terms of γ. The γ term cannot be measured directly. It becomes a parameter that comes out of an inverse modeling procedure. This procedure adjusts parameter values using forward models that successively iterate until it obtains optimized estimates of parameter values. In the case of Liu et al. (1998), the inversion of fracture properties primarily is conditioned to reproduce measured matrix saturation and water potential data. Using data from Yucca Mountain, Liu et al. (1998) constrained their inversion using fracture trace maps and fracture permeability data from pneumatic tests.
Connectivity Considerations
Perhaps the most significant distinction of fracture networks from porous continua is the question of connectivity. Fractures force fluids to flow on discrete pathways, which may be highly discontinuous in sparsely fractured rock masses. In order to have a fracture pathway from the surface to the water table, the fracture pathway must have continuity. Within sparse fracture networks, fracture pathways from the surface may dead end, and could potentially host local perched water bodies (Stephens, 1996). Conversely, paths that connect with the water table may not have connection to water sources at the surface, in which case, the fracture pathway will be preferentially drained. Variable connectivity of fracture networks, therefore, is a potential agent for focusing flow.
SUMMARY AND CONCLUSIONS
The observation of fast flow in vadose fracture networks encourages a re-examination of the capillary model of vadose-zone flow for fractures. One important aspect of capillary flow models is the assumption that flow ceases when the saturation drops to the point where the liquid no longer forms a continuous phase. This paper develops an alternative conceptual model involving the flow of drops and to a lesser extent rivulets. The existence of drops implies a nonzero contact
angle, which is counter to a common, though not universal, assumption in vadose flow studies.
Measurements of contact angles on rock materials suggest that contact angles with water are greater than zero. Such a wetting relationship encourages the formation of drops and rivulets, whose flow physics is fundamentally different from conventional hydrogeologic models. While gravity drives flow in both conventional and drop flows, for drops and rivulets on open fractures, the resistance arises from wetting phenomena in addition to viscosity. Drops are static unless their mass provides sufficient energy to overcome wetting resistances.
Drops may occur as either single-wall or two-wall drops, if both fracture walls are contacted. Single-wall drops are more likely in larger fractures, and they will be more likely to slide because contact with the second wall increases resistance to flow. Single-wall drops are more likely in fractures with apertures greater than 1 mm.
Laboratory experiments on simulated fractures show drop and rivulet effects. These effects may arise from the use of modeling materials that have nonzero contact angles with the water. A critical question in the use of laboratory results is whether or not these artificial surfaces simulate real fractures. Real fractures may have significant micro-roughness that can reduce the apparent contact angle to zero; thus changing the flow process from drops to films. The current understanding of wetting properties of fractures is incomplete, but essential if appropriate processes are to be identified and used in simulations and analyses.
Fracture network geometry affects vadose-zone fracture flow in several ways. First, gravity encourages flow in the dip direction of the fracture. Gravitational effects are dip-angle dependent varying by the sine of the dip angle. A directional consequence of this phenomenon is that preferred orientations of fractures can create diversion effects that direct flow in vertical directions.
Fracture network geometries serve to focus flow to a portion of the fracture network that is small. Barriers within fractures, fracture edges, and fracture intersections all confine flow to portions of networks. Fracture networks may be discontinuous. Discontinuous pathways that are preferentially connected to the surface will tend to pond or act as perched zones. Discontinuous paths that preferentially connect to the water table will drain. Fast-path flow will be enhanced by the presence of continuous, large-aperture pathways.
REFERENCES
Bachman, J., R. Horton, R. van der Pleog, and S. Woche, 2000. Modified sessile drop method for assessing initial soil-water contact angle of sandy loam. Soil Science Society of America Journal 64: 564-567.
Berg, J. C., 1993. Role of acid-base interactions in wetting and related phenomena. In J. Berg, ed. Wettability. New York: Decker, pp. 75-148.
Bikerman, J. J., 1950. Sliding of drops from surfaces of different roughnesses. Journal of Colloidal Science 5: 349-359.
Carillo, M. L. K., J. Letey, and S. Yates, 2000. Measurement of initial soil-water contact angle of water repellent soils. Soil Science Society of America Journal 63: 433-436.
Dussan V. E. B., 1985. On the ability of drops of bubbles to stick to non-horizontal surfaces of solids. Part 2. Small drops or bubbles having contact angles of arbitrary size. Journal of Fluid Mechanics 151: 1-20.
Dussan V. E. B., and R. T. Chow, 1983. On the ability of drops or bubbles to stick to non-horizontal surfaces of solids. Journal of Fluid Mechanics 137: 1-29.
Extrand, C. W., and Y. Kumagai, 1995. Liquid drops on an inclined plane: The relationship of contact angles, drop shape, and retentive force. Journal of Colloid and Interface Science 170: 515-521.
Fourar, M., S. Bories, R. Lenormand, and P. Persoff, 1993. Two-phase flow in smooth and rough fractures: Measurement and correlation by porous-medium and pipe flow models. Water Resources Research 29: 3699-3708.
Furmidge, C. G. L., 1962. Studies at phase interfaces. 1. The sliding of liquid drops on solid surfaces and a theory for spray retention. Journal of Colloidal Science 17: 309-324.
Gauthier, J. H., M. L. Wilson, and F. C. Lauffer, 1992. Estimating the consequences of significant fracture flow at Yucca Mountain. High Level Radioactive Waste Management, Proceedings of the Third Annual International Conference, American Nuclear Society, pp. 891-898.
Gauthier, J. H., 1994. An updated fracture flow model for total-system performance assessment of Yucca Mountain. High Level Radioactive Waste Management, Proceedings of the Fifth Annual International Conference, American Nuclear Society, pp. 1663-1670.
Glass, R., M. J. Nicholl, and V. C. Tidwell, 1995. Challenging models for flow in unsaturated rock through exploration of small-scale processes. Geophysical Research Letters 22: 1457-1460.
Hazlett, R. D., 1993. On surface roughness effects in wetting phenomena. In: K. L. Mittal, ed. Contact Angle, Wettability, and Cohesion. VSP Utrecht, Netherlands, pp. 173-181.
Hiemenz, P. C., and R. Rajagopalan, 1997. Principles of Colloid and Surface Chemistry. 3rd ed. Marcel Dekker, Inc., New York, 650 p.
Hillel, D., 1980. Fundamentals of Soil Physics. Academic Press, New York, 413 p.
Ho, C. K., and M. Wilson, 1998. Calculation of discrete fracture flow paths in dual continuum models . High Level Radioactive Waste Management, Proceedings of the Seventh International Conference, American Nuclear Society, pp. 375-377.
Huppert, H. E., 1982. Flow and instability of a viscous current down a slope. Nature 300: 427-429.
Johnson, M. F. G., R. A. Schluter, M. J. Miksis, and S. G. Bankoff, 1999. Experimental study of rivulet formation on an inclined plate by fluorescent imaging. Journal of Fluid Mechanics 394: 339-354.
Jury, W. A., W. R. Gardner, and W. H. Gardner, 1991. Soil Physics. 5th ed. Wiley, New York.
Kneafsey, T. J., and K. Pruess, 1998. Laboratory experiments on heat-driven two-phase flows in natural and artificial rock fractures. Water Resources Research 34: 3349-3367.
Lenormand, R., and C. Zarcone, 1989. Capillary fingering: Percolation and fractal dimension. Transport in Porous Media 4: 52-61.
Letey, J., J. Osvorn, and R. Pelishek, 1962. Measurement of liquid-solid contact angles in soil and sand. Soil Science 93: 149-153.
Liu, H. H., C. Doughty, and G. Bodvarsson, 1998. An active fracture model for unsaturated flow and transport in fractured rocks. Water Resources Research 34: 2633-2646.
Nicholl, M. J., R. J. Glass, and S. W. Wheatcraft, 1994. Gravity-driven infiltration instability in initially dry nonhorizontal fractures. Water Resources Research 30: 2533-2546.
Padday, J. F., 1993. Spreading, wetting, and contact angles. In K. L. Mittal, ed. Contact Angle, Wettability, and Cohesion. VSP Utrecht, Netherlands, pp. 97-108.
Pal, D., and S. B. Varade, 1971. Measurement of contact angle of water in soils and sand. Journal of Indian Society of Soil Science 19: 339-446.
Persoff, P., and K. Pruess, 1995. Two-phase flow visualization and relative permeability measurement in natural rough-walled rock fractures. Water Resources Research 31: 1175-1186.
Peters, R. R., and E. A. Klavetter, 1988. A continuum model for water movement in an unsaturated fractured rock mass. Water Resources Research 24: 416-430.
Prázak, J., M. Sír, F. Kubik, J. Tywoniak, and C. Zarcone, 1992. Oscillation phenomena in gravity-driven drainage in coarse porous media. Water Resources Research 28: 1849-1855.
Pruess, K, 1999. A mechanistic model for water seepage through thick unsaturated zones in fractured rocks of low matrix permeability. Water Resources Research 35: 1039-1051.
Pruess, K., B. Faybishenko, and G. Bodvarsson, 1999. Alternative concepts and approaches for modeling flow and transport in thick unsaturated zones of fractured rocks. Journal of Contaminant Hydrology 38: 281-322.
Rasmussen, T.C., 1991. Steady fluid flow and travel times in partially saturated fractures using a discrete air-water interface. Water Resources Research 27: 66-77.
Richards, L. A., 1931. Capillary conduction of liquids through porous mediums. Physics 1: 318-333.
Sadhal, S. S., P. S. Ayyaswamy, and J. N. Chung, 1997. Transport phenomena with drops and bubbles. Springer Verlag, Berlin.
Sklodowska, A., M. Wozniak, and R. Matlakowska, 1999. The method of contact angle measurements and estimation of work of adhesion in bioleaching of metals. Biological Procedures Online 1(3): (www.science.uwaterloo.ca/bpo/).
Sobolev, V., N. Churaev, M. Velarge, Z. Zorin. 2000. Surface tension and dynamic contact angle of water in quartz capillaries . Journal of Colloid and Interface Science 222: 51-54.
Stephens, D., 1996. Vadose Zone Hydrology. CRC Press, Boca Raton.
Su, G. W., J. T. Geller, K. Pruess, and F. Wen, 1999. Experimental studies of water seepage and intermittent flow in unsaturated, rough-walled fractures. Water Resources Research 35: 1019-1037.
Tokunaga, T. K., and J. Wan, 1997. Water film flow along fracture surfaces in porous rock. Water Resources Research 33: 1287-1295.
Tokunaga, T. K., J. Wan, and S. Sutton, 2000. Transient film flow on rough fracture surfaces. Water Resources Research 36: 1737-1746.
Wan, J., T. K. Tokunaga, T. Orr, J. O'Neill, and R. W. Conners, 2000. Glass casts of rock fracture surfaces: A new tool for studying flow in a partially saturated, fractured, porous medium. Water Resources Research 36: 355-360.
Wang, J. S., and T. N. Narasimhan, 1985. Hydrologic mechanisms governing fluid flow in saturated, fractured porous media. Water Resources Research 21: 1861-1874.
Young, T., 1805. On the cohesion of fluids. Philos. Transactions Royal Society of London A84.
Yuan, T. L., and L. Hammond, 1968. Evaluation of available methods for soil wettability measurement with particular reference to soil-water contact angle determination . Soil and Crop Science Society of Florida Proc. 28: 56-63.




























