7
Pipes, Tubes, and Beakers: New Approaches to Teaching the Rational-Number System
Joan Moss

PEANUTS reprinted by permission of United Feature Syndicate, Inc.
Poor Sally. Her anger and frustration with fractions are palpable. And they no doubt reflect the feelings and experiences of many students. As mathematics education researchers and teachers can attest, students are often vocal in their expression of dislike of fractions and other representations of rational numbers (percents and decimals). In fact, the rational-number system poses problems not only for youngsters, but for many adults as well.1 In a recent study, masters students enrolled in an elementary teacher-training program were interviewed to determine their knowledge and understanding of basic rational-number concepts. While some students were confident and produced correct answers and explanations, the majority had difficulty with the topic. On attempting to perform an operation involving fractions, one student, whose sentiments were echoed by many, remarked, “Oh fractions! I know there are lots of rules but I can’t remember any of them and I never understood them to start with.”2
We know from extensive research that many people—adults, students, even teachers—find the rational-number system to be very difficult.3 Introduced in early elementary school, this number system requires that students reformulate their concept of number in a major way. They must go beyond whole-number ideas, in which a number expresses a fixed quantity, to understand numbers that are expressed in relationship to other numbers. These new proportional relationships are grounded in multiplicative reasoning that is quite different from the additive reasoning that characterizes whole numbers (see Box 7-1).4 While some students make the transition smoothly, the majority, like Sally, become frustrated and disenchanted with mathematics.5 Why is this transition so problematic?
A cursory look at some typical student misunderstandings illuminates the kinds of problems students have with rational numbers. The culprit appears to be the continued use of whole-number reasoning in situations where it does not apply. When asked which number is larger, 0.059 or 0.2, a majority of middle school students assert that 0.059 is bigger, arguing that the number 59 is bigger than the number 2.6 Similarly, faulty whole-number reasoning causes students to maintain, for example, that the fraction 1/8 is larger than 1/6 because, as they say, “8 is a bigger number than 6.”7 Not surprisingly, students struggle with calculations as well. When asked to find the sum of 1/2 and 1/3, the majority of fourth and sixth graders give the answer 2/5. Even after a number of years working with fractions, some eighth graders make the same error, illustrating that they still mistakenly count the numerator and denominator as separate numbers to find a sum.8 Clearly whole-number reasoning is very resilient.
Decimal operations are also challenging.9 In a recent survey, researchers found that 68 percent of sixth graders and 51 percent of fifth and seventh graders asserted that the answer to the addition problem 4 + .3 was .7.10 This example also illustrates that students often treat decimal numbers as whole numbers and, as in this case, do not recognize that the sum they propose as a solution to the problem is smaller than one of the addends.
The introduction of rational numbers constitutes a major stumbling block in children’s mathematical development.11 It marks the time when many students face the new and disheartening realization that they no longer understand what is going on in their mathematics classes.12 This failure is a cause for concern. Rational-number concepts underpin many topics in advanced mathematics and carry significant academic consequences.13 Students cannot succeed in algebra if they do not understand rational numbers. But rational numbers also pervade our daily lives.14 We need to be able to understand them to follow recipes, calculate discounts and miles per gallon, exchange money, assess the most economical size of products, read maps, interpret scale drawings, prepare budgets, invest our savings, read financial statements, and examine campaign promises. Thus we need to be able to
|
BOX 7-1 Lamon,15 whose work on proportional reasoning and rational number has made a great contribution to our understanding of students’ learning, elucidates the distinction between relative and absolute reasoning. She asks the learner to consider the growth of two fictitious snakes: String Bean, who is 4 feet long when the story begins, and Slim, who is 5 feet long. She tells us that after 5 years, both snakes have grown. String Bean has grown from 4 to 7 feet, and Slim has grown from 5 to 8 feet (see the figure below). She asks us to compare the growth of these two snakes and to answer the question, “Who grew more?”  Lamon suggests that there are two answers. First, if we consider absolute growth, both snakes grew 3 feet, so both grew the same amount. The second answer deals with relative growth; from this perspective, String Bean grew the most because he grew 3/4 of his length, while Slim grew only 3/5 of his length. If we compare the two fractions, 3/4 is greater than 3/5, and so we conclude that String Bean has grown proportionally more than Slim. Lamon asks us to note that while the first answer, about the absolute difference, involves addition, the second answer, about the relative difference, is solved through multiplication. In this way she shows that absolute thinking is additive, while relative thinking is multiplicative. |
understand rational numbers not only for academic success, but also in our lives as family members, workers, and citizens.
Do the principles of learning highlighted in this book help illuminate the widespread problems observed as students grapple with rational number? Can they point to more effective approaches to teaching rational number? We believe the answer to both these questions is “yes.” In the first section below we consider each of the three principles of How Students Learn, beginning with principle 2—the organization of a knowledge network that emphasizes core concepts, procedural knowledge, and their connections. We then turn to principle 1—engaging student preconceptions and building on existing understandings. Finally we consider metacognitive instruction as emphasized in principle 3.
The second section focuses on instruction in rational number. It begins with a description of frequently used instructional approaches and the ways in which they diverge from the above three principles. We then describe an experimental approach to teaching rational number that has proven to be successful in helping students in fourth, fifth, and sixth grades understand the interconnections of the number system and become adept at moving among and operating with the various representations of rational number. Through a description of lessons in which the students engaged and protocols taken from the research classrooms, we set out the salient features of the instructional approach that played a role in shaping a learning-centered classroom environment. We illustrate how in this environment, a focus on the interconnections among decimals, fractions, and percents fosters students’ ability to make informed decisions on how to operate effectively with rational numbers. We also provide emerging evidence of the effectiveness of the instructional approach. The intent is not to promote our particular curriculum, but rather to illustrate the ways in which it incorporates the principles of How People Learn, and the observed changes in student understanding and competence with rational numbers that result.
RATIONAL-NUMBER LEARNING AND THE PRINCIPLES OF HOW PEOPLE LEARN
The Knowledge Network: New Concepts of Numbers and New Applications (Principle 2)
What are the core ideas that define the domain of rational numbers? What are the new understandings that students will have to construct? How does a beginning student come to understand rational numbers?
Let us look through the eyes of a young student who is just beginning to learn about rational number. Until this point, all of her formal instruction in
arithmetic has centered on learning the whole-number system. If her learning has gone well, she can solve arithmetic problems competently and easily makes connections between the mathematics she is learning and experiences of her daily life. But in this next phase of her learning, the introduction of rational number, there will be many new and intertwined concepts, new facts, new symbols that she will have to learn and understand—a new knowledge network, if you will. Because much of this new learning is based on multiplicative instead of whole-number relations, acquiring an understanding of this new knowledge network may be challenging, despite her success thus far in mathematics. As with whole-number arithmetic, this domain connects to everyday life. But unlike whole numbers, in which the operations for the most part appear straightforward, the operations involved in the learning of rational numbers may appear to be less intuitive, at odds with earlier understandings (e.g., that multiplication always makes things bigger), and hence more difficult to learn.
New Symbols, New Meanings, New Representations
One of the first challenges facing our young student is that a particular rational number can take many forms. Until now her experience with symbols and their referents has been much simpler. A number—for example, four—is represented exclusively by one numeral, 4. Now the student will need to learn that a rational number can be expressed in different ways—as a decimal, fraction, and percent. To further complicate matters, she will have to learn that a rational-number quantity can be represented by an infinite number of equivalent common and decimal fractions. Thus a rational number such as one-fourth can be written as 1/4, 2/8, 3/12, 4/16, 0.25, 0.250, and so on.
Not only does the learning of rational number entail the mastery of these forms and of the new symbol systems that are implied, but the learner is also required to move among these various forms flexibly and efficiently.16 Unfortunately, this flow between representations does not come easily.17 In fact, even mature students are often challenged when they try to understand the relations among the representations.18 To illustrate how difficult translating between fractions and decimals can be, I offer two examples taken from our research.
In a recent series of studies, we interviewed fourth, sixth, and eighth graders on a number of items that probed for rational-number understanding. One of the questions we asked was how the students would express the quantity 1/8 as a decimal. This question proved to be very challenging for many, and although the students’ ability increased with age and experience, more than half of the sixth and eighth graders we surveyed asserted that as a decimal, 1/8 would be 0.8 (rather than the correct answer, 0.125).
In the next example, an excerpt taken from an interview conducted as part of a pretest, Wyatt, a traditionally trained fifth-grade student, discussed ordering a series of rational numbers presented to him in mixed representations.
|
Interviewer |
Here are 3 numbers: 2/3, 0.5, and 3/4. Could you please put these numbers in order from smallest to largest? |
|
Wyatt |
Well, to start with, I think that the decimal 0.5 is bigger than the fractions because it’s a decimal, so it’s just bigger, because fractions are really small things. |
The response that 1/8 would equal 0.8 should be familiar to many who have taught decimals and fractions. As research points out, students have a difficult time understanding the quantities involved in rational number and thus do not appear to realize the unreasonableness of their assertion.19 As for Wyatt’s assertion in the excerpt above that decimals and fractions cannot be compared, this answer is representative of the reasoning of the majority of the students in this class before instruction. Moreover, it reflects more general research findings.20 Since most traditional instruction in rational number presents decimals, fractions, and percents separately and often as distinct topics, it is not surprising that students find this task confusing. Indeed, the notion that a single quantity can have many representations is a major departure from students’ previous experience with whole numbers; it is a difficult set of understandings for them to acquire and problem-laden for many.21
But this is not the only divergence from the familiar one-to-one correspondence of symbol to referent that our new learner will encounter. Another new and difficult idea that challenges the relatively simple referent-to-symbol relation is that in the domain of rational number, a single rational number can have several conceptually distinct meanings, referred to as “subconstructs.” Now our young student may well become completely confused.
The Subconstructs or the Many Personalities of Rational Number
What is meant by conceptually distinct meanings? As an illustration, consider the simple fraction 3/4. One meaning of this fraction is as a part–whole relation in which 3/4 describes 3 of 4 equal-size shares. A second interpretation of the fraction 3/4 is one that is referred to as the quotient interpretation. Here the fraction implies division, as in 4 children sharing 3
pies. As a ratio, 3/4 might mean there are, for example, 3 red cars for every 4 green cars (this is not to be confused with the part–whole interpretation that 3/7 of the cars are red). Rational numbers can also indicate a measure. Here rational number is a fixed quantity, most frequently accompanied by a number line, that identifies a situation in which the fraction 1/4 is used repeatedly to determine a distance (e.g., 3/4 of an inch = 1/4, 1/4, 1/4). Finally, there is the interpretation of rational number as a multiplicative operator, behaving as an operation that reduces or enlarges the size of another quantity (e.g., the page has been reduced to 3/4 its original size).
The necessity of coordinating these different interpretations requires a deep understanding of the concepts and interrelationships among them. On the one hand, a student must think of rational numbers as a division of two whole numbers (quotient interpretation); on the other, she must also come to know these two numbers as an entity, a single quantity (measure), often to be used in another operation. These different interpretations, generally referred to as the “subconstructs” of rational number, have been analyzed extensively22 and are a very important part of the knowledge network that the learner will construct for rational number.
Reconceptualizing the Unit and Operations
While acquiring a knowledge network for rational-number understanding means that new forms of representation must be learned (e.g., decimals, fractions) and different interpretations coordinated, the learner will encounter many other new ideas—ideas that also depart from whole numbers. She will have to come to understand that rational numbers are “dense”—meaning that between any two rationals we can find an infinity of other numbers. In the whole-number domain, number is discrete rather than continuous, and the main operation is counting. This is a very big change indeed.23
Another difficult new set of understandings concerns the fundamental change that students will encounter in the nature of the unit. In whole numbers, the unit is always explicit (6 refers to 6 units). In rational numbers, on the other hand, the unit is often implied. But it is the unstated unit that gives meaning to the represented quantities, operations, and the solutions. Consider the student trying to interpret what is meant by the task of multiplying, for example, 1/2 times 1/8. If the student recognizes that the “1/8” in the problem refers to 1/8 of one whole, she may reason correctly that half of the quantity 1/8 is 1/16. However since the 1 is not stated but implied, our young student may err and, thinking the unit is 8, consider the answer to be 1/4 (since 4 is one-half of 8)—a response given by 75 percent of traditionally instructed fourth and sixth graders students in our research projects.
New Conceptualizations: Understanding Numbers As Multiplicative Relations
Clearly the transition to learning rational numbers is challenging. Fundamentally, students must construct new meanings for numbers and operations. Development of the network of understandings for rational numbers requires a core conceptual shift: numbers must be understood in multiplicative relationship.
As a final illustration, I offer one more example of this basic shift. Again, consider the quantity 3/4 from our new learner’s perspective. All of our student’s prior learning will lead her to conclude that the 3 and 4 in 3/4 are two separate numbers that define separate quantities. Her knowledge of whole numbers will provide an additive understanding. Thus she will know that 3 and 4 are contiguous on the number line and have a difference of 1. But to interpret 3/4 as a rational number instead of considering these two numbers to be independent, as many students mistakenly continue to do,24 our student must come to understand this fraction as a new kind of quantity that is defined multiplicatively by the relative amount conveyed by the symbols. Suddenly numbers are no longer simple. When placed in the context of a fraction, 3 and 4 become a quantity between 0 and 1. Obvious to adults, this numerical metamorphosis can be confusing to children.
How can children learn to make the transition to the complex world of rational numbers in which the numbers 3 and 4 exist in a relationship and are less than 1? Clearly, instruction will need to support a major conceptual change. Looking at students’ prior conceptions and relevant understandings can provide footholds to support that conceptual change.25
Students’ Errors and Misconceptions Based on Previous Learning (Principle 1)
As the above examples suggest, students come to the classroom with conceptions of numbers grounded in their whole-number learning that lead them astray in the world of rational numbers. If instruction is to change those conceptions, it is important to understand thoroughly how students reason as they puzzle through rational-number problems. Below I present verbatim interviews that are representative of faulty understandings held by many students.
In the following excerpt, we return to our fifth grader, Wyatt. His task was to order a series of rational numbers in mixed representations. Recall his earlier comments that these representations could not be compared. Now as the interview continues, he is trying to compare the fractions 2/3 and 3/4. The interview proceeds:
|
Interviewer |
What about 2/3 and 3/4? Which of those is bigger? |
|
Wyatt |
Well, I guess that they are both the same size because they both have one piece missing. |
|
Interviewer |
I am not sure I understand what you mean when you say that there is one piece missing. |
|
Wyatt |
I’ll show you. [Wyatt draws two uneven circles, roughly partitions the first in four parts, and then proceeds to shade three parts. Next he divides the second circle into three parts and shades two of them (see Figure 7-1). O.K., here is 3/4 and 2/3. You see they both have one part missing. [He points to the unshaded sections in both circular regions.] You see one part is left out, so they are both the same. |
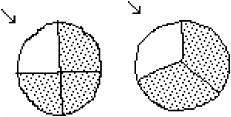
FIGURE 7-1
Wyatt’s response is typical in asserting that 2/3 and 3/4 must be the same size. Clearly he has not grasped the multiplicative relations involved in rational numbers, but makes his comparisons based on operations from his whole-number knowledge. When he asserts that 2/3 and 3/4 are the same size because there is “one piece missing,” Wyatt is considering the difference of 1 in additive terms rather than considering the multiplicative relations that underlie these numbers.
Additive reasoning is also at the basis of students’ incorrect answers on many other kinds of rational-number tasks. Mark, a sixth grader, is working on a scaling problem in which he is attempting to figure out how the length and width of an enlarged rectangle are related to the measurements of a smaller, original rectangle. His challenge is to come up with a proportional relation and, in effect, solve a “missing-term problem” with the following relations: 8 is to 6 as 12 is to what number?
|
Interviewer |
I have two pictures of rectangles here (see Figure 7-2). They are exactly the same shape, but one of them is bigger than the other. I |
|
|
made this second one bigger by taking a picture of the first one and then enlarging it just a bit. As you can see, the length of the first rectangle is 8 cm and the width is 6 cm. Unfortunately, we know only the length of the second one. That is 12 cm. Can you please tell me what you think the width is? |
|
Mark |
Well, if the first one (rectangle) is 8 cm and 6 cm, then the next one is 12 cm and 10 cm. Because in the 8 and 6 one (rectangle) you subtract 2 from the 8 (to get the difference of the width and the length). So in the bigger rectangle you have to subtract 2 from the 12. So that’s 10. So the width of the big rectangle is 10. |
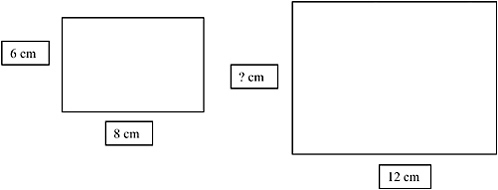
FIGURE 7-2
Mark’s error in choosing 10 instead of the correct answer of 9 is certainly representative of students in his age group—in fact, many adults use the same kind of faulty reasoning.26 Mark clearly attempts to assess the relations, but he uses an additive strategy to come up with a difference of 2. To answer this problem correctly, Mark must consider the multiplicative relations involved (the rectangle was enlarged so that the proportional relationship between the dimensions remains constant)—a challenge that eludes many.
It is this multiplicative perspective that is difficult for students to adopt in working with rational numbers. The misconception that Mark, the sixth grader, displays in asserting that the height of the newly sized rectangle is 10 cm instead of the correct answer of 9 cm shows this failure clearly. Wyatt
certainly was not able to look at the relative amount in trying to distinguish between the quantities 2/3 and 3/4. Rather, he reasoned in absolute terms about the circles, that “… both have one piece missing.”
Metacognition and Rational Number (Principle 3)
A metacognitive approach to instruction helps students monitor their understanding and take control of their own learning.27 The complexity of rational number—the different meanings and representations, the challenges of comparing quantities across the very different representations, the unstated unit—all mean that students must be actively engaged in sense making to solve problems competently.28 We know, however, that most middle school children do not create appropriate meanings for fractions, decimals, and percents; rather, they rely on memorized rules for symbol manipulation.
The student errors cited at the beginning of this chapter indicate not only the students’ lack of understanding of rational number, but also their failure to monitor their operations and judge the reasonableness of their responses.29 If classroom teaching does not support students in developing metacognitive skills—for example, by encouraging them to explain their reasoning to their classmates and to compare interpretations, strategies, and solutions—the consequences can be serious. Student can stop expecting math to make sense. Indeed for many students, rational number marks the point at which they draw this conclusion.
INSTRUCTION IN RATIONAL NUMBER
Why does instruction so often fail to change students’ whole-number conceptions? Analyses of commonly used textbooks suggest that the principles of How People Learn are routinely violated. First, it has been noted that—in contrast to units on whole-number learning—topics in rational number are typically covered quickly and superficially. Yet the major conceptual shift required will take time for students to master thoroughly. Within the allotted time, too little is devoted to teaching the conceptual meaning of rational number, while procedures for manipulating rational numbers receive greater emphasis.30 While procedural competence is certainly important, it must be anchored by conceptual understanding. For a great many students, it is not.
Other aspects of the knowledge network are shortchanged as well, including the presentation and teaching of the notation system for decimals, fractions, and percents. Textbooks typically treat the notation system as something that is obvious and transparent and can simply be given by definition at a lesson’s outset. Further, operations tend to be taught in isolation and
divorced from meaning. Virtually no time is spent in relating the various representations—decimals, fractions, percents—to each other.31
While these are all significant problems and oversights, however, there are more basic problems with traditional instruction. The central problem with most textbook instruction, many researchers agree,32 is the failure of textbooks to provide a grounding for the major conceptual shift to multiplicative reasoning that is essential to mastering rational number. To support this claim, let us look at how rational number is typically introduced in traditional practice.
Pie Charts and a Part–Whole Interpretation of Rational Numbers
Most of us learned fractions with the model of a pie chart, and for many people, fractions remain inextricably linked to a picture of a partly shaded shape. Instruction traditionally begins with the presentation of pictures of circles (pies) and rectangles (cakes) that are partitioned and partially shaded. First, students are asked to count the number of parts in the whole shape and then the number of parts shaded. They then use these counts as the basis for naming and symbolically representing fractions. They learn that the top number, the numerator, always indicates how many pieces are shaded and that the bottom number, the denominator, always tells how many pieces there are in all. Next, using these same sorts of pictures (see Figure 7-3), instruction continues with simple addition and subtraction operations: “Two shaded 1/4 pieces (the bottom half of the circle) + 1 shaded 1/4 piece (the top left piece of the circle) = 3 shaded 1/4 pieces or 3/4.”
From a psychological perspective, this introduction is sound because it is based on students’ present knowledge and aligned with their experiences both in and out of school. We know that students’ formal mathematics programs have been based on counting, and that from everyday experience, students know about cutting equal pieces of pies and cakes. Thus, the act of assessing partitioned regions is well within their experience.
From a mathematical point of view, the rationale for this introduction is
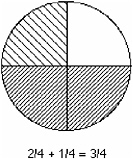
FIGURE 7-3
also clear. Mathematically, this approach promotes an understanding of one particular aspect of rational number—the way rational numbers indicate parts of a whole. This part–whole subconstruct is one of the basic interpretations of rational numbers.
However, this introduction is grounded in additive thinking. It reinforces the very concept that students must change to master rational number. Children tend to treat the individual parts that result from a partition as discrete objects. The four pieces into which a pie is cut are just four pieces. Although the representation does have the potential to bring out the multiplicative relations inherent in the numbers—considering the shaded parts in relation to the whole—this is not what students naturally extract from the situations presented given their strong preconceptions regarding additive relationships.33
Recall that Wyatt, the fifth grader, asserted that 2/3 and 3/4 were the “same sized” number, supporting his erroneous claim with reference to pie charts. He explained that the picture showed they were both missing one piece. His lack of focus on the different relations that are implied in these two fractions is evident from his interpretation.
Alternative Instructional Approaches: Ratio and Sharing
For some time now, researchers have wondered whether alternative instructional approaches can help students overcome this misunderstanding. As Kieren34 points out, “… rather than relying on children’s well developed additive instincts we must find the intuitions and schemes that go beyond those that support counting. Whole number understandings are carefully built over a number of years; now we must consider how rational number understanding develops and is fostered.”
But what would such instruction look like? Over the last several years, a number of innovative approaches have been developed that highlight the multiplicative relations involved, a few of which are highlighted here. Kieren35 has developed a program for teaching fractions that is based on the multiplicative operations of splitting. As part of his approach he used paper folding rather than pie charts as its primary problem situation. In this approach, both the operator and measure subconstructs are highlighted. Confrey’s36 3-year developmental curriculum uses a number of contexts for ratio, including cooking, shadows, gears, and ramps.37 Streefland’s38 approach to teaching fractions is also driven by an emphasis on ratio. His basic image is of equal shares and quotients. In his procedure for teaching fractions, children are presented with realistic situations in which they are asked to share a quantity of something, such as chocolate bars or pancakes (e.g., five children sharing two bars). To represent these situations, children use a notation system that they devise themselves, which emphasizes proportional rather
than additive relations. Mack’s39 approach is to engage the students in part–whole activities as a starting point, and to ground these concepts in realistic situations in which students are pressed to consider the multiplicative relations. Finally, Lamon40 has devised programs that address each of the subconstructs separately. All of these programs and others developed by the Rational Number Project have demonstrated a significant impact on the participating students.
Below I present a different approach to teaching rational number that I developed with my colleague Robbie Case. Our approach, shown through controlled experimental trials to be effective in helping students in the fourth, fifth, and sixth grades41 gain a strong initial grounding in the number system, also highlights multiplicative understanding, with an additional focus on the interrelations among fractions, decimals, and percents.42 While there is no one best method or best set of learning activities for rational number,43 our approach provides an opportunity to describe how instruction in rational number can be built around the principles of How People Learn that are the theme of this volume.
First, as will be elaborated, our curriculum is based on our analyses of students’ prior understandings (Principle 1). Our instructional strategy is to help students to further develop these informal understandings and then integrate them into a developmentally sequenced set of activities designed to help them develop a network of concepts and relations for rational numbers (Principle 2). Finally, as will be illustrated throughout our accounts of the lessons, a central feature of this program is the fostering of a metacognitive approach to rational number (Principle 3). By providing students with an understanding of the interconnections among decimals, fractions, and percents, our curriculum helps them develop the ability to make informed decisions on how best to operate with rational numbers.
Pipes, Tubes, and Beakers: A New Approach to Rational-Number Learning
Percents as a Starting Point
In our curriculum, rather than teaching fractions and decimals first, we introduce percents—which we believe to be a “privileged” proportion in that it only involves fractions of the base 100.44 We do this through students’ everyday understandings. We situate the initial learning of percent in linear measurement contexts, in which students are challenged to consider the relative lengths of different quantities. As will be shown below, our initial activities direct students’ attention to ideas of relative amount and proportion from the very beginning of their learning of rational number. For example, we use beakers of water: “If I fill this beaker 50 percent full, approxi-
mately where will the line be? Now fill this bigger beaker 50 percent full. Do you notice that although they are both 50 percent full, there is more water in this bigger one?” These ideas of percents and proportion serve as an anchoring concept for the subsequent learning of decimals and fractions, and then for an overall understanding of the number system as a whole.
Starting Point: Visual Proportional Estimation and Halving and Doubling
Our starting point in developing our curriculum was to consider students’ informal knowledge and the intuitions they have developed that could serve as a foundation. (As has been shown many times in this chapter, students have previous understandings and knowledge of mathematics that are not productive for rational-number understanding.) To this end, we highlighted two kinds of understandings that students have generally developed by this age. One is an ability to estimate proportions visually such as halves;45 the other is an ability to work with successive halving46 (see Box 7-2).
|
BOX 7-2 Proportional Understandings While we know that formal proportional reasoning is slow to develop47 it has nonetheless been shown that children from a very early age have a strong propensity for making proportional evaluations that are nonnumerical and based on perceptual cues. For example, young children have little difficulty perceiving narrow, upright containers in proportional terms. Although they can see which of two such containers has more liquid in it in absolute terms, they can also see which has more in proportional terms. That is to say, they can see which one is fuller.48 Halving and Doubling The ability to do repeated halving is evident is students’ reasoning at this age. As Confrey and Kieren49 point out, halving and doubling have their roots in a primitive scheme that they call splitting. Splitting, they assert, is based on actions that are purely multiplicative in nature and are separate from those of additive structures and counting. Whereas in counting the actions are joining, annexing, and removing, in splitting the primitive action is creating simultaneous multiple versions of an original by dividing symmetrically, growing, magnifying, and folding. |
Although one of these sets of understandings—proportional estimation—is primarily visual and nonnumerical, while the other, halving and doubling, is numeric, both have their grounding in multiplicative operations. It was our proposal that if we could help students merge these separate kinds of multiplicative understandings, we would allow them to construct a core conceptual grounding for rational numbers.50
Our strategy from the beginning was to develop what we called a “bridging context”51 to help students first access and then integrate their knowledge of visual proportions and their flexibility in working with halving numbers. The context we chose was to have students work with percents and linear measurement. As will be elaborated below, students were engaged from the start of the instructional sequence in estimating proportional relations based on length and in using their knowledge of halving to compute simple percent quantities. In our view, the percent and measurement context allowed students to access these initial kinds of understandings and then integrate them in a natural fashion. We regarded the integration of initial intuitions and knowledge as a foundation for rational-number learning.
Why Percent As a Starting Point?
While we found that starting with percent was useful for highlighting proportionally, we also recognized that it was a significant departure from traditional practice. Percent, known as the most difficult representation for students, is usually introduced only after fractions and decimals. Several considerations, however, led to this decision. First, with percents students are always working with the denominator of 100. We therefore postpone the problems that arise when students must compare or manipulate ratios with different denominators. This allows students to concentrate on developing their own procedures for comparison and calculation rather than requiring them to struggle to master a complex set of algorithms or procedures for working with different denominators.
Second, a further simplification at this beginning stage of learning is that all percentages have a corresponding decimal or fractional equivalent that can be relatively easy to determine (e.g., 40 percent = 0.40 or 0.4 = 40/100 or 4/10 or 2/5). By introducing percents first, we allow children to make their preliminary conversions among the different rational-number representations in a direct and intuitive fashion while developing a general understanding of how the three representations are related.
Finally, children know a good deal about percents from their everyday experiences.52 By beginning with percents rather than fractions or decimals, we are able to capitalize on children’s preexisting knowledge of the meanings of these numbers and the contexts in which they are important.53
Curriculum Overview
The curriculum is divided into roughly three parts. First the students are introduced to a single form of rational number—percent—using concrete props that highlight linear measurement. After students have spent time working with percents in many contexts, we present our next form of rational number, the two-place decimal. We do this in the context of percent, illustrating that a two-place decimal number is like the percent of the way between two whole numbers. Finally, our focus turns to activities that promote comparing and ordering rational numbers and moving among decimals and percents. Fractions are also taught at this stage in relation to percents and decimals.54 The sections that follow provide details of many of the activities we devised and include accounts of how fourth, fifth, and sixth graders from our research classrooms worked through these activities. These lessons are described in a fair amount of detail so that interested teachers can try some of these activities with their own students. I also include these details to illustrate the strategies that were used to foster students’ pride and investment in and willingness to monitor their work.
Lessons Part 1: Introduction to Percents
Percents in Everyday Life
Imagine a typical fourth-, fifth-, or sixth-grade class, in which the students have received no formal instruction in percent. Thus each time we implemented our curriculum, we began the lessons with discussions that probed the students’ everyday knowledge of this topic. These questions generated a great number of responses in each of our research classrooms. Not only were the students able to volunteer a number of different contexts in which percents appear (e.g., siblings’ school marks, price reductions in stores, and taxes on restaurant bills), but they also had a strong qualitative understanding of what different numerical values “mean.” For example, students commented that 100 percent means “everything,” 99 percent means “almost everything,” 50 percent means “exactly half,” and 1 percent means “almost nothing.” As one student remarked, “You know if you are on a diet you should drink 1 percent milk instead of 4 percent milk.”
Pipes and Tubes: A Representation for Fullness
To further explore students’ intuitions and informal understandings, we presented them with a set of props specifically designed for the lessons. The set included a series of black drainage pipes (of varying heights) with white venting tubes55 on the outside that could be raised or lowered, simulating
the action of water filling them to different levels (see Figures 7-4a and 7-4b). To discover more about the students’ understanding of percents and proportion, we asked them to consider how they would use these props to teach percent to a younger child. Again the students were full of ideas, many of which are central to the knowledge network for rational number.
First students demonstrated their understanding of the unit whole, as mentioned earlier, a concept that is often elusive in traditional instruction: “Each of these pipes is 100 percent.” They also demonstrated understanding of the part–whole construct: “If you raise the tube up here [pointing to three-quarters of the length of the pipe], then the part that is covered is 75 percent, and the part that is left over is 25 percent.” Students also naturally displayed their sense of rational number as operator: “This is 50 percent of the tube, and if we cut it in half again it is 25 percent.” In addition, students demonstrated insights for proportions: “50 percent on this bigger pipe is bigger than 50 percent on this little pipe, but they’re both still 50 percent.” The idea of rational number as a measure was also embedded in the students’ reasoning! “I know this is about 75 percent covered, because this first bit is 25 percent, and if you move the 25 percent piece along the tube three times, you get 75 percent.” Clearly, they had strong intuitions about the general properties and interpretations of rational numbers in their informal understandings of percent.
We also were interested to see whether the use of these props could generate ideas about another difficult concept—the elusive idea of percents greater than 100.56 Sam, an eager student, attempted to demonstrate this to his classmates. He first held up a tall pipe (80 cm): “We know that this whole pipe is 100 percent.” Next, he picked up a second, shorter pipe (20 cm) and stood it beside the taller one, estimating that it was about 25 percent of the taller pipe. To confirm this conjecture, he moved the smaller pipe along the taller one, noting that it fit exactly four times. “Okay,” he declared, “this is definitely 25 percent of the longer pipe. So, if you join the two [pipes] together like this [laying both pipes on the ground and placing the shorter one end to end with the larger], this new pipe is 125 percent of the first one.”
Percents on Number Lines: More Estimation
In addition to drainage pipes, we included activities with laminated, meter-long number lines calibrated in centimeters to provide students with another way of visualizing percent (see Figures 7-5a and 7-5b). For example, we incorporated exercises in which children went on “percent walks.” Here the number lines, which came to be known as “sidewalks,” were lined up end to end on the classroom floor with small gaps between them. Students challenged each other to walk a given distance (e.g., “Can you please walk 70 percent of the first sidewalk? Now, how about 3 whole sidewalks and 65
percent of the fourth?”). The number-line activities were used to consolidate percent understandings and to extend the linear measurement context.
Computing with Percent
Next we introduced beakers of water with varying degrees of fullness (see Figures 7-6a and 7-6b). In keeping with the previous lessons, the students used percent terminology to estimate the “fullness” of these containers: “Approximately what percent of this beaker do you think is full?” or “How high will the liquid rise when it is 25 percent full?” As it turned out, the children’s natural tendency when confronted with fullness problems was to use a repeated halving strategy. That is, they determined where a line representing 50 percent would go on the cylinder, then 25 percent, then 12 1/2 percent, and so on. These activities with fullness estimates led naturally to a focus on computation and measurement. For example, if it was discovered on measuring a beaker that it was 8 cm tall, then 4 cm from the bottom was the 50 percent point, and 2 cm was the 25 percent point. The halving strategies exemplified in these calculations became the basis for the computations the students tackled next.
Invented Procedures
Despite the move to calculating, the children were not given any standard rules to perform these operations, and so they naturally employed a series of strategies of their own invention using halves, quarters, and eighths as benchmarks to guide their calculations. For example, to calculate 75 percent of the length of a 60 cm desktop, the students typically considered this task in a series of steps: Step 1, find half, and then build up as necessary (50 percent of 60 = 30); Step 2, use a halving strategy to find 25 percent of 60, and if 50 percent of 60 = 30, then 25 percent of 60 = 15); and Step 3, sum the parts (30 + 15 = 45).
String Challenges: Guessing Mystery Objects
String measurement activities also proved to be an excellent way of considering percent quantities and calculating percentages using benchmarks. A string challenge that became a regular feature of classroom life was what we called “The Mystery Object Challenge.” In this activity, which often started the lessons, the teacher held up a piece of string that was cut to the percent of the length of a certain object in the room. The routine went something like this:
|
Teacher |
I have here a length of string that is 25 percent of the height of a mystery object in the classroom. Any ideas as to what the mystery object might be? |
|
Student |
I think that it is the desktop or maybe the poster on the wall. |
|
Teacher |
How did you figure that out? |
|
Student |
Well, I just imagined moving the string along the desk four times and I think it works. [The student, then, carefully moving the string along the desk, was able to confirm her assertion.] |
Since these kinds of challenges were so popular with the children, we went on to invite pairs of students to find their own mystery object to challenge their classmates. Students went around the room, measured their chosen object, and then cut a piece of string to a percent of the total. As a culminating activity, the students made what they called “percent families” of strings using the length of their mystery object as a base. Each pair of children was given a large piece of cardboard on which they pasted lengths of string to represent the benchmarks of 100 percent, 50 percent, 25 percent, 75 percent, and 12 1/2 percent of the height of the object. These activities provided opportunities for calculating percents (e.g., if the object was 70 cm long, students would have to calculate and then measure and cut strings of 50 percent lengths, or 35 cm; of 25 percent lengths, or 17.5 cm; of 75 percent lengths, or 52.5 cm; etc.). Furthermore, the visual displays thus produced proved helpful in reinforcing the idea of proportion for the students. As students often remarked, “Our string lengths are different even though all of our percents are the same.”
Summary of Lessons Part 1
The first phase of the lessons began with estimations and then calculations of percent quantities. These initial activities were all presented in the context of linear measurement of our specially designed pipes and tubes, beakers of water, string, and number lines. Students were not given formal instruction in specific calculating procedures; rather, they naturally employed procedures of their own that involved percent benchmarks and repeated halving. While percent was the only form of rational number that we officially introduced at this point, students often referred to fractions when working on these initial activities. At the beginning, all of the children naturally used the term “one-half” interchangeably with “fifty percent,” and most knew that 25 percent (the next split) could be expressed as “one-quarter.”
We also told them that the 12 1/2 percent split was called “one-eighth” and showed them the fraction symbol 1/8.
Although the props were enjoyable to the students, they also served an important function. The activities consistently helped students integrate their sense of visual proportion with their ability to do repeated halving. Our goal in all of these initial activities was to create situations in which these two kinds of informal understandings could become linked and serve as a foundation for the students’ further learning of this number system.
Lessons Part 2: Introduction of Decimals
While the first phase of the lessons was designed to extend and elaborate students’ knowledge of percent, the next phase moved the students to a new developmental level. At this point in our instructional program, we introduced students to a new form of rational number—the two-place decimal. The initial decimal lessons also had a strong focus on measurement and proportion.
Research has confirmed that a solid conceptual grounding in decimal numbers is difficult for students to achieve.57 The similarities between the symbol systems for decimals and whole numbers lead to a number of misconceptions and error types.58 Grasping the proportional nature of decimals is particularly challenging. In our program, we made a direct link from percents—which by now the students thought of in proportional terms—to decimals. In fact, we told the students that since they were now “percent experts,” they could become “decimal experts.” What we did with the students at this point was show that a two-place decimal number represents a percentage of the way between two adjacent whole numbers. In this way of thinking, a decimal represents an intermediate distance between two numbers (e.g., 5.25 is a distance that is 25 percent of the way between 5 and 6).
Decimals and Stopwatches
To begin the lessons in decimals, the students were given LCD stopwatches with screens that displayed seconds and hundredths of seconds (the latter indicated by two small digits to the right of the numbers; see Figure 7-7). The students were asked to consider what the two “small numbers” might mean and how these small numbers related to the bigger numbers to the left (seconds). After experimenting with the stopwatches, the children noted that there were 100 of these small time units in 1 second. With this observation, they made the connection to percents: “It’s like they are percents of a second.” After considerable discussion of what to name these small time intervals (e.g., some suggested that they were milliseconds), the students came to refer to these hundredths of seconds as

FIGURE 7-7
“centiseconds,” a quantity they understood to be the percentage of time that had passed between any 2 whole seconds. We continued our work with decimals and stopwatches, with a focus on ordering numbers.
Magnitude and Order in Decimal Numbers
To illuminate the difficult concepts of magnitude and order (recall Wyatt’s assertion that 2/3 = 3/4 and others’ comments that 0.2 is smaller than 0.059), we devised many activities to help the students work with ordering decimals. The first of these activities was the “Stop-Start Challenge.” In this exercise, students attempted to start and stop the watch as quickly as possible, several times in succession. After discussion, they learned to record their times as decimals. So, for example, 20 centiseconds was written as .20, 9 centiseconds as 0.09, and so on. Next, the students compared their personal quickest reaction time with that of their classmates, then ordered the times from quickest to slowest. In this exercise, the students could learn from their experience of trying to get the quickest time that, for example, 0.09 is a smaller number than .10 and eventually realize that .09 is smaller than .1. Another stopwatch game designed to actively engage students in issues of magnitude was “Stop the Watch Between”: “Can you stop the watch between 0.45 and 0.50?” We also explored decimals through the laminated
number lines, whereby students were asked to indicate parts of 100 using decimal representations: “Please put a mark where 0.09 is on this number line.”
Summary of Lessons Part 2
In this second level of the instructional program, the students were introduced to decimals for the first time. Students worked on many activities that helped them first understand how decimals and percents are related and then learn how to represent decimals symbolically. As the decimal lessons proceeded, we moved on to activities designed to help students to consider and reflect on magnitude. Thus the final activities included situations in which students engaged in comparing and ordering decimals. This level of the program was the first step in students’ learning to translate among the representations of rational number and gain fluency with different kinds of operations.
Lessons Part 3: Fractions and Mixed Representations of Rational Numbers
Fractions First: Equivalencies
As noted earlier, although the curriculum began with percents as the initial representation of rational numbers, we found that the students made many references to fractions. Now, at this final level of the program, our goal was to give students a chance to work with fractions more formally and then provide them with opportunities to translate flexibly among fractions, decimals, and percents. In a first series of activities, students worked on tasks in which they were asked to represent a fraction in as many ways as they could. Thus, for example, if their assignment was to show 3/4, students typically responded by presenting fraction equivalencies, such as 6/8 and 75/100. Students were also asked to compose “word problems” that incorporated fractions and were in turn given to their classmates to solve. Another activity that students enjoyed a great deal was challenging others to find the answers to equations of their own invention with questions such as “How much more to make one whole? (for example, 1/8 + 1/2 + 1/16 + 1/4 + ? = 1),” or “Is the following equation true or false? (1/4 + 1/8 + 5/10 + 1/8 = 1).” The reasoning of a fifth grader as he attempted to answer this question is typical of the reasoning of many of his classmates: “Well, 5/10 is 1/2. If you add 1/4 that makes three-quarters, so you need another quarter to make a whole and you have two-eighths, so it does equal one whole and so it is true!”
While students initially used fractions in these equations, they soon incorporated the other representations in challenges they composed. For example, one student posed the following question: “Here is my equation: 1/ 8 + 12.5 percent + 1/4 + .25 percent + ? = 1. How much more to make one whole?” To discover the missing quantity, the students’ reasoning (anchored in percents and decimals) sounded something like this: “Well 12 1/2 (1/8) and 12 1/2 is 25 percent and another 25 percent (1/4) makes 50 percent and another .25 makes 75 percent so you would need another 25 percent to make a whole.”
Crack the Code
The students carried out further work on conversions with the LCD stopwatches used earlier in the program. In a favorite game called “Crack the Code,” students moved between representations of rational numbers as they were challenged to stop the watch at the decimal equivalent of different fractions and percents. For example, given a relatively simple secret code, e.g., 2/5, students stopped the watch at close to 40 centiseconds or 0.40 seconds as possible. Similarly with slightly more complex secret codes, such as “1/4 + 10 percent,” students had to stop the watch at .35 seconds. This allowed them to increase their understanding of the possibility of fluid movement between representations.
Card Games
In one set of lessons, I gave the students a set of specially designed cards depicting various representations of fractions, decimals, and percents (e.g., there was a 3/8 card, a card with .375, and a card that read 37 1/2 percent). The students used the cards to design games that challenged their classmates to make comparisons among and between representations.
In the first game, the leader dealt the cards to the students, who in turn placed one card from their hand face up on the classroom floor. The challenge was to place the cards in order of increasing quantity. Students who disagreed with the placement of a particular card challenged the student who had gone before. This led to a great deal of debate. Sarah, for instance, had a card on which was written 5/9. This was a fraction that the students had not previously encountered in their lessons, and Sarah was not sure where to place it. Finally, she put the 5/9 card before a card on which was 50 percent, thus revealing that she thought that 5/9 was less than 50 percent. “That can’t be right,” asserted Jules. “In order to get 1/2 (50 percent) you would have to have 4 point 5 ninths and that is less than 5/9 so, 5/9 is larger than 1/2.” The game ended when the children reached consensus and the
teacher confirmed that all of the cards had been ordered correctly. The cards took up the entire length of the classroom by the time every student had placed his or her cards on the floor!
A second card game employing the same deck of cards, invented by a pair of students, had as its goal not only the comparison of decimals, fractions, and percents in mixed representations, but also the addition and subtraction of the differences between these numbers. This game again used the LCD stopwatches introduced earlier in the lessons. The two students who invented the game, Claire and Maggie, based it on the popular card game War. The students dealt the whole deck into two “hands,” then simultaneously turned over the top card. The winner’s score is increased by the difference in value of the two cards. In one turn, for example, Maggie’s card had .20 written on it and Clare’s had 1/8. What happened next is transcribed from the videotape of their play:
|
Claire |
OK, now we have to figure out who has more. |
|
Maggie |
I do. ‘Cause you only have 121/2 percent [one-eighth] but I have 20 percent. So mine is more. |
|
Claire |
Yeah, you’re right; Ok I have to write down your score…. Hum … So that’s 20 percent take away 121/2 percent so that’s 7 1/2 [percent]. [Claire then took a pencil, and finding Maggie’s place in the score column, wrote .075.] |
At this point in the lessons, most of the students were comfortable thinking about percents, decimals, and fractions together. In fact, they assumed a shorthand way of speaking about quantities as they translated from fraction to percent. To illustrate this, I present a short excerpt from a conversation held by a visiting teacher who had watched the game the two girls had started and asked them to explain their reasoning.
|
Teacher |
I was interested to know how you figured out which of the numbers is more, .20 or one-eighth. First of all, how did you know that one-eighth is equal to 12 1/2 percent? |
|
Maggie |
Ok, it is like this. One-eighth is half of one-fourth, and one-fourth is 25 percent. So, half of that is 12 1/2 percent. |
|
Teacher |
Well, you certainly know percents very well. But what about decimals? Do you know what 12 1/2 percent is as a decimal? |
|
Claire: |
You see, 12 1/2 percent is like point 12 and a half and that’s the same as point 12 point 5, because the point five is like half. |
|
Maggie: |
Yeah, but in decimals you have to say it’s really point 125. |
Summary of Lessons Part 3
In the third part of the curriculum, we focused primarily on students’ uses of mixed representations. We began with some formal activities with fractions and equivalencies, including tasks in which students had to work with and devise lengthy equations. We also had the students make up their own games and challenges to help them gain more practice in this kind of flexible movement from one operation to another. One of our primary goals here was to provide students with habits of mind regarding multiple representations that will be with them throughout their learning and lay the foundations for their ability to solve mathematical problems.
Results from Our Studies
To date, variations of our curriculum have been implemented and assessed in four experimental classrooms. From the very first lessons, students demonstrated and used their everyday knowledge of percents and worked successfully with percents in situations that called on their understanding of proportion. Our particular format also allowed students to express their informal knowledge of other concepts and meanings that are central to rational number understanding. Recall that when working with the pipes and tubes and the beakers of water, students successfully incorporated ideas of the rational-number subconstructs of measure, operator, and ratio. What was also evident was that they had a strong understanding of the unit whole and its transformations. Similarly, when decimals were introduced in the context of stopwatches, the students readily made sense of this new representation and were able to perform a variety of computations. Finally, by the end of the experimental sessions, the students had learned a flexible approach to translating among the representations of rational numbers using familiar benchmarks and halving and doubling as a vehicle of movement.
While the class as a whole appeared to be engaged and motivated by the lessons, we needed to look at the improvement made by individual students at the end of the experimental intervention. We were also interested to see how the performance of students in the experimental group compared with that of students who had traditional classroom instruction. To these ends, we assessed the experimental students on a variety of tasks before and after the course of instruction and administered these same tasks
to students from classrooms in which textbook instruction had been provided.59
Briefly, we found that students in the experimental group had improved significantly.60 Further, the scores that they obtained after instruction were often higher than those of children who had received instruction in conventional classrooms and who were many years older. Not only were students in the experimental classrooms able to answer more questions than did the “textbook” students, but the quality of their answers was better. Specifically, the experimental group made more frequent reference to proportional concepts in justifying their answers than did the students in the nonexperimental group. What follows are some examples of changes in students’ reasoning following participation in the experimental program, consisting of selections from interviews that were conducted following the conclusion of the experimental classes.
Children’s Thinking After Instruction
Let us return to the question posed to Wyatt at the start of the program (and excerpted at the beginning of this chapter) and look at the responses of two students, Julie and Andy, whose reasoning was typical of that of the other students at the end of the program.
|
Interviewer |
Here are three numbers: 2/3, 0.5, and 3/4. Could you please put these numbers in order from smallest to largest? |
|
Julie |
Well, let’s see. Point 5 is the smallest because 3/4 is 75 percent. I am not exactly sure what 2/3 is as a percent but it is definitely more than a half. Can I use this paper to try it out? [Julie took two pieces of paper. Holding them horizontally, she first folded one in four equal parts and then pointed to three sections, remarking that this was 3/4. Next she folded the second sheet in three pieces and then lined the two pages up together to compare the differences between the 2/3 and 3/4]. So 3/4 is the biggest. |
Andy responded to this same question differently.
|
Andy |
It’s easy: .5 is 50 percent and 2/3 is 66 percent, and so it goes first .5 then 2/3 and then 3/4 cause that’s 75 percent. |
As can be seen, both Andy and Julie correctly ordered the numbers using their knowledge of percent as a basis for their reasoning. Andy, a high-achieving student, simply converted these quantities to percents. Julie, identified as a lower achiever, used paper folding as a way of finding the bigger fraction. Both used multiplicative solutions, one concrete and one abstract.
Another example taken from posttest interviews illustrates not only the students’ understanding of order and magnitude, but also their understanding of the density property of rational numbers—that there is an infinite number of numbers between any two rational numbers.
|
Interviewer |
Can any fractions fit between one-fourth and two-fourths? And if so, can you name one? |
|
Maggie |
Well, I know that one-quarter is 25 percent and so two quarters is a half, so that’s 50 percent. So, there’s tons of numbers between them like 40 percent. So that would be 40/100. |
|
Jed |
One-quarter is the same as 2/8 and 2/4 is the same as 4/8, so the answer is three-eighths. |
The above answers are in sharp contrast to those of children before our instruction or those from traditional classrooms, the majority of whom claimed no numbers could come between 1/4 and 2/4.
In a final example, students were asked to compute a percent of a given quantity—65 percent of 160. Although this type of computation was performed regularly in our classrooms, 65 percent of 160 was a significantly more difficult calculation than those the students had typically encountered in their lessons. Furthermore, this item required that students work with 10 percent as well as with the familiar benchmarks (25 percent, 50 percent, 75 percent, and 12 1/2 percent) that served as a basis for most of their classroom work. Despite these differences, students found ways to solve this difficult problem.
|
Interviewer |
What is 65 percent of 160? |
|
Sascha |
Okay, 50 percent of 160 is 80. Half of 80 is 40, so that is 25 percent. So if you add 80 and 40 you get 120. But that (120) is too much because that’s 75 percent. So you need to minus 10 percent (of 160) and that’s 16. So, 120 take away 16 is 104. |
|
Neelam |
The answer is 104. First I did 50 percent, which was 80. |
|
|
Then I did 10 percent of 160, which is 16. Then I did 5 percent, which was 8. I added them [16 + 8] to get 24, and added that to 80 to get 104. |
For anyone who has seen a colleague pause when asked to compute a percentage, as one must, say, to calculate a tip, the ease with which these students worked through these problems is striking.
Knowledge Network
These are only a few examples from the posttest interviews that illustrate the kinds of new understandings and interconnections students had been able to develop through their participation in the curriculum. Overall, our analyses of the children’s thinking revealed that students had gained (1) an overall understanding of the number system, as illustrated by their ability to use the representations of decimals, fractions, and percents interchangeably; (2) an appreciation of the magnitude of rational numbers, as seen in their ability to compare and order numbers within this system; (3) an understanding of the proportional- and ratio-based constructs of this domain, which underpins their facility with equivalencies; (4) an understanding of percent as an operator, as is evident in their ability to invent a variety of solution strategies for calculating with these numbers; and (5) general confidence and fluency in their ability to think about the domain using the benchmark values they had learned, which is a hallmark of number sense.
Our research is still in an early stage. We will continue to pursue many questions, including the potential limitations of successive halving as a way of operating with rational numbers, downplaying of the important understandings associated with the quotient subconstruct, as well as a limited view of fractions. Furthermore, we need to learn more about how students who have been introduced to rational numbers in this way will proceed with their ongoing learning of mathematics.
While we acknowledge that these questions have not yet been answered, we believe certain elements of our program contributed to the students’ learning, elements that may have implications for other rational-number curricula. First, our program began with percents, thus permitting children to take advantage of their qualitative understanding of proportions and combine that understanding with their knowledge of the numbers from 1 to 100, while avoiding (or at least postponing) the problems presented by fractions. Second, we used linear measurement as a way of promoting the multiplicative ideas of relative quantities and fullness. Finally, our program emphasized benchmark values—of halves, quarters, eighths, etc.—for moving among equivalencies of percents, decimals, and fractions, which allowed students to be flexible and develop confidence in relying on their own procedures for problem solving.
CONCLUSION: HOW STUDENTS LEARN RATIONAL NUMBER
Principle #1: Prior Understandings
For years mathematics researchers have focused their attention on understanding the complexities of this number system and how to facilitate students’ learning of the system. One well-established insight is that rational-number teaching focused on pie charts and part–whole understandings reinforces the primary problem students confront in learning rational number: the dominance of whole-number reasoning. One response is to place the multiplicative ideas of relative quantity, ratio, and proportion at the center of instruction.
However, our curriculum also builds on our theory and research findings pointing to the knowledge students typically bring to the study of rational number that can serve as a foundation for conceptual change. Two separate kinds of understandings that 10-year-olds typically possess have a multiplicative orientation. One of these is visual proportional estimation; for children, this understanding usually functions independently of numbers, at least initially. The second important kind of understanding is the numerical procedure for repeated halving. By strengthening and merging these two understandings, students can build a solid foundation for working flexibly with rational numbers.
Our initial instructional activities are designed to elicit these informal understandings and to provide instructional contexts that bring them together. We believe this coordination produces a new interlinked structure that serves both as foundation for the initial learning of rational number and subsequently as the basis on which to build a networked understanding of this domain.
Principle #2: Network of Concepts
At the beginning of this chapter, I outlined the complex set of core concepts, representations, and operations students need to acquire to gain an initial grounding in the rational-number system. As indicated above, the central conceptual challenge for students is to master proportion, a concept grounded in multiplicative reasoning. Our instructional strategy was to design a learning sequence that allowed students to first work with percents and proportion in linear measurement and next work with decimals and fractions. Extensive practice is incorporated to assure that students become fluent in translating between different forms of rational number. Our intention was to create a percent measurement structure that would become a central network to which all subsequent mathematical learning could be
linked. This design is significantly different from traditional instruction in rational number, in which topics are taught separately.
Principle #3: Metacognition
In this chapter, I have not made detailed reference to students’ developing metacognition. Yet the fostering of metacognition is in fact central to our curriculum. First, as the reader may have noted, we regularly engaged the students in whole-group discussions in which they were asked to explain their reasoning and share invented procedures with their classmates. We also designed the lessons so that students worked in small groups to collaborate in solving problems and constructing materials; we thereby provided students with a forum to express and refine their developing understandings. There were also many opportunities for students to consider how they would teach rational number to others, either younger students or their own classmates, by designing their own games and producing teaching plans for how these new concepts could be taught. In all these ways, we allowed students to reflect on their own learning and to consider what it meant for them and others to develop an understanding of rational number. Finally, we fostered metacognition in our program through the overall design and goals of the experimental curriculum, with its focus on interconnections and multiple representations. This focus, I believe, provided students with an overview of the number system as a whole and thus allowed them to make informed decisions on how best to operate with rational numbers.
Final Words
I conclude this chapter with an interchange, recorded verbatim, between a fourth-grade student and a researcher. Zach, the fourth grader, was being interviewed by the researcher as part of a posttest assessment. The conversation began when Zach had completed two pages of the six-page posttest and remarked to the interviewer, “I have just done 1/3 of the test;…that is 33.3 percent.” When he finished the third page, he noted, “Now I have finished 1/2 or 50 percent of the test.” On completing the fourth page he remarked, “Okay, so I have now done 2/3 of the test, which is the same as 66 percent.” When he had completed the penultimate page, he wondered out loud what the equivalent percentage was for 5/6: “Okay, let’s see; it has got to be over 66.6 percent and it is also more than 75 percent. I’d say that it is about 80 percent….No, wait; it can’t be 80 percent because that is 4/5 and this [5/6] is more than 4/5. It is 1/2 plus 1/3…so it is 50 percent plus 33.3 percent, 83.3 percent. So I am 83.3 percent finished.”
This exchange illustrates the kind of metacognitive capability that our curriculum is intended to develop. First, Zach posed his own questions,
unprompted. Further, he did not expect that the question had to be answered by the teacher. Rather, he was confident that he had the tools, ideas, and concepts that would help him navigate his way to the answer. We also see that Zach rigorously assessed the reasonableness of his answers and that he used his knowledge of translating among the various representations to help him solve the problem. I conclude with this charming vignette as an illustration of the potential support our curriculum appears to offer to students beginning their learning of rational number.
Students then go on to learn algorithms that allow them to calculate a number like 83.3 percent from 5/6 efficiently. But the foundation in mathematical reasoning that students like Zach possess allow them to use those algorithms with understanding to solve problems when an algorithm has been forgotten and to double check their answers using multiple methods. The confidence created when a student’s mathematical reasoning is secure bodes well for future mathematics learning.
NOTES
|
59. |
Kalchman et al., 2000; Moss, 1997, 2000, 2001; Moss and Case, 1999. |
|
60. |
From pre- to posttest, achieving effect sizes between and 1 and 2 standard deviations. |
REFERENCES
Armstrong, B.E., and Bezuk, N. (1995). Multiplication and division of fractions: The search for meaning. In J.T. Sowder and B.P. Schappelle (Eds.), Providing a foundation for teaching mathematics in the middle grades (pp. 85-120). Albany, NY: State University of New York Press.
Ball, D.L. (1990). The mathematics understanding that prospective teachers bring to teacher education elementary school. Journal, 90, 449-466.
Ball, D.L. (1993). Halves, pieces and twoths: Constructing and using representational contexts in teaching fractions. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 157-196). Mahwah, NJ: Lawrence Erlbaum Associates.
Baroody, A.J. (1999). Fostering children’s mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Lawrence Erlbaum Associates.
Behr, M.J., Lesh, R., Post, T.R., and Silver, E.A. (1983). Rational-number concepts. In R. Lesh and M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 91-126). New York: Academic Press.
Behr, M.J., Wachsmuth, I., Post, T.R., and Lesh, T. (1984). Order and equivalence of rational numbers: A clinical teaching experiment. Journal for Research in Mathematics Education, 15(4), 323-341.
Behr, M.J., Harel, G., Post, T.R, and Lesh, R. (1992). Rational number, ratio, and proportion. In D.A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 296-333). New York: Macmillan.
Behr, M.J., Harel, G., Post, T.R, and Lesh, R. (1993). Rational numbers: Towards a semantic analysis: Emphasis on the operator construct. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 13-48). Mahwah, NJ: Lawrence Erlbaum Associates.
Carpenter, T.P., Kepner, H., Corbitt, M.K., Lindquist, M.M., and Reys, R.E. (1980). Results of the NAEP mathematics assessment: Elementary school. Arithmetic Teacher, 27, 10-12, 44-47.
Carpenter, T.P., Fennema, E., and Romberg, T.A. (1993). Toward a unified discipline of scientific inquiry. In T. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 1-12). Mahwah, NJ: Lawrence Erlbaum Associates.
Case, R. (1985). Intellectual development: Birth to adulthood. New York: Academic Press.
Case, R. (1998, April). A psychological model of number sense and its development. Paper presented at the annual meeting of the American Educational Research Association, San Diego, CA.
Case, R., and Okamoto, Y. (1996). The role of central conceptual structures in the development of children’s thought. Monographs of the Society for Research in Child Development, 246(61), 1-2. Chicago, IL: University of Chicago Press.
Confrey, J. (1994). Splitting, similarity, and the rate of change: A new approach to multiplication and exponential functions. In G. Harel and J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 293-332). Albany, NY: State University of New York Press.
Confrey, J. (1995). Student voice in examining “splitting” as an approach to ratio, proportions and fractions. In L. Meira and D. Carraher (Eds.), Proceedings of the 19th international conference for the Psychology of Mathematics Education (vol. 1, pp. 3-29). Recife, Brazil: Universidade Federal de Pernambuco.
Cramer, K., Post, T., and Behr, M. (1989). Cognitive restructuring ability, teacher guidance and perceptual distractor tasks: An aptitude treatment interaction study. Journal for Research in Mathematics Education, 20(1), 103-110.
Cramer, K., Post, T., and Currier, D. (1993). Learning and teaching ratio and proportion: Research implications. In D. Owens (Ed.), Research ideas for the classroom: Middle grade mathematics (pp. 159-179). New York: Macmillan.
Hart, K. (1988). Ratio and proportion. In J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 198-220). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J. (1992). Mathematical, cognitive, and instructional analyses of decimal fractions. In G. Leinhardt, R. Putnam, and R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 283-322). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J., and Behr, J.M. (1988). Capturing the major themes. In J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (vol. 2, pp. 1-18). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J., and Wearne, D. (1986). Procedures over concepts: The acquisition of decimal number knowledge. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 199-244). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J., Wearne, D., and Taber, S. (1991). Fourth graders’ gradual construction of decimal fractions during instruction using different physical representations. Elementary School Journal, 91, 321-341.
Kalchman, M., Moss, J., and Case, R. (2000). Psychological models for the development of mathematical understanding: Rational numbers and functions. In S. Carver and D. Klahr (Eds.), Cognition and Instruction: 25 years of progress. Mahwah, NJ: Lawrence Erlbaum Associates.
Karplus, R., and Peterson, R.W. (1970). Intellectual development beyond elementary school II: Ratio, a survey. School Science and Mathematics, 70(9), 813-820.
Karplus, R., Pulos, S., and Stage, E.K. (1981). Proportional reasoning of early adolescents. Berkeley, CA: University of California, Lawrence Hall of Science.
Karplus, R., Pulos, S., and Stage, E.K. (1983). Proportional reasoning of early adolescents. In R. Lesh and M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 45-90). Orlando, FL: Academic.
Kerslake, D. (1986). Fractions: Children’s strategies and errors. Windsor, UK: NFER Nelson.
Kieren, T.E. (1992). Rational and fractional numbers as mathematical and personal knowledge. In G. Leinhardt, R. Putnam, and R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 323-372). Mahwah, NJ: Lawrence Erlbaum Associates.
Kieren, T.E. (1993). Rational and fractional numbers: From quotient fields to recursive understanding. In T. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 49-84). Mahwah, NJ: Lawrence Erlbaum Associates.
Kieren, T.E. (1994). Multiple views of multiplicative structure. In G. Harel and J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 387-397). Albany, NY: State University of New York Press.
Kieren, T.E. (1995). Creating spaces for learning fractions. In J.T. Sowder and B.P. Schappelle (Eds.), Providing a foundation for teaching mathematics in the middle grades. Albany, NY: State University of New York Press.
Lachance, A., and Confrey, J. (1995). Introducing fifth graders to decimal notation through ratio and proportion. In D.T. Owens, M.K. Reed, and G.M. Millsaps (Eds.), Proceedings of the seventeenth annual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 395-400). Columbus, OH: ERIC Clearinghouse for Science, Mathematics and Environmental Education.
Lamon, S.J. (1993). Ratio and proportion: Children’s cognitive and metacognitive processes. In T.P. Carpenter, E. Fennema, and T.A. Romberg, (Eds.), Rational numbers: An integration of research (pp. 131-156). Mahwah, NJ: Lawrence Erlbaum Associates.
Lamon S.J. (1994). Ratio and proportion: Cognitive foundations in unitizing and norming. In G. Harel and J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 89-122). Albany, NY: State University of New York Press.
Lamon, S.J. (1995). Ratio and proportion: Elementary didactical phenomenology. In J.T. Sowder and B.P. Schappelle (Eds.), Providing a foundation for teaching mathematics in the middle grades. Albany, NY: State University of New York Press.
Lamon, S.J. (1999). Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. Mahwah, NJ: Lawrence Erlbaum Associates.
Lembke, L.O., and Reys, B.J. (1994). The development of, and interaction between, intuitive and school-taught ideas about percent. Journal for Research in Mathematics Education, 25(3), 237-259.
Lesh, R., Post, T., and Behr, M. (1988). Proportional reasoning. In M. Behr and J. Hiebert (Eds.), Number concepts and operations in the middle grades (pp. 93-118). Mahwah, NJ: Lawrence Erlbaum Associates.
Mack, N.K. (1990). Learning fractions with understanding: Building on informal knowledge. Journal for Research in Mathematics Education, 21, 16-32.
Mack, N.K. (1993). Learning rational numbers with understanding: The case of informal knowledge. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 85-105). Mahwah, NJ: Lawrence Erlbaum Associates.
Mack, N.K. (1995). Confounding whole-number and fraction concepts when building on informal knowledge. Journal for Research in Mathematics Education, 26(5), 422-441.
Markovits, Z., and Sowder, J.T. (1991). Students’ understanding of the relationship between fractions and decimals. Focus on Learning Problems in Mathematics, 13(1), 3-11.
Markovits, Z., and Sowder, J.T. (1994). Developing number sense: An intervention study in grade 7. Journal for Research in Mathematics Education, 25(1), 4-29, 113.
Moss, J. (1997). Developing children’s rational number sense: A new approach and an experimental program. Unpublished master’s thesis, University of Toronto, Toronto, Ontario, Canada.
Moss, J. (2000). Deepening children’s understanding of rational numbers. Dissertation Abstracts.
Moss, J. (2001). Percents and proportion at the center: Altering the teaching sequence for rational number. In B. Littweiller (Ed.), Making sense of fractions, ratios, and proportions. The NCTM 2002 Yearbook (pp. 109-120). Reston, VA: National Council of Teachers of Mathematics.
Moss, J. (2003). On the way to computational fluency: Beginning with percents as a way of developing understanding of the operations in rational numbers. In Teaching children mathematics (pp. 334-339). Reston, VA: National Council of Teachers of Mathematics.
Moss, J., and Case, R. (1999). Developing children’s understanding of rational numbers: A new model and experimental curriculum. Journal for Research in Mathematics Education, 30(2), 119, 122-147.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Curriculum and evaluation standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
National Research Council. (2001). Adding it up: Helping children learn mathematics. Mathematics Learning Study Committee, J. Kilpatrick, J., Swafford, J., and B. Findell (Eds.). Center for Education. Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Noelting, G. (1980a). The development of proportional reasoning and the ratio concept. Part I: Differentiation of stages. Educational Studies in Mathematics, 11, 217-253.
Noelting, G. (1980b). The development of proportional reasoning and the ratio concept. Part II: Problem-structure at successive stages: Problem-solving strategies and the mechanism of adaptive restructuring. Educational Studies in Mathematics, 11, 331-363.
Nunes, T., and Bryant, P. (1996). Children doing mathematics. Cambridge, MA: Blackwell.
Ohlsson, S. (1988). Mathematical meaning and applicational meaning in the semantics of fractions and related concepts. In J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (vol. 2, pp. 53-92). Mahwah, NJ: Lawrence Erlbaum Associates.
Parker, M., and Leinhardt, G. (1995). Percent: A privileged proportion. Review of Educational Research, 65(4), 421-481.
Post, T., Harel, G., Behr, M., and Lesh, R. (1991). Intermediate teachers’ knowledge of rational number concepts. In E. Fennema, T. Carpenter, and S. Lamon (Eds.), Integrating research on teaching and learning mathematics (pp. 177-198). Albany, NY: State University of New York Press.
Post, T.R., Cramer, K.A., Behr, M., Lesh, R., and Harel, G. (1993). Curriculum implications of research on the learning, teaching and assessing of rational number concepts. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 327-362). Mahwah, NJ: Lawrence Erlbaum Associates.
Resnick, L.B., and Singer, J.A. (1993). Protoquantitative origins of ratio reasoning. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 107-130). Mahwah, NJ: Lawrence Erlbaum Associates.
Resnick, L.B., Nesher, P., Leonard, F., Magone, M., Omanson, S., and Peled I. (1989). Conceptual bases of arithmetic errors: The case of decimal fractions. Journal for Research in Mathematics Education, 20(1), 8-27.
Sowder, J.T. (1988). Mental computation and number comparison: Their roles in the development of number sense and computational estimation. In J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (vol. 2, pp. 182-198). Mahwah, NJ: Lawrence Erlbaum Associates.
Sowder, J.T. (1992). Making sense of numbers in school mathematics. In G. Leinhardt, R. Putnam, and R. Hattrup, (Eds.), Analysis of arithmetic for mathematics (pp. 1-51). Mahwah, NJ: Lawrence Erlbaum Associates.
Sowder, J.T. (1995). Instructing for rational number sense. In J.T. Sowder and B.P. Schappelle (Eds.), Providing a foundation for teaching mathematics in the middle grades. Albany, NY: State University of New York Press.
Spinillo, A.G., and Bryant, P. (1991). Children’s proportional judgements: The importance of “half.” Child Development, 62, 427-440.
Streefland, L. (1991). Fractions: An integrated perspective. In L. Streefland (Ed.), Realistic mathematics education in primary school (pp. 93-118). Utrecht, The Netherlands: Freudenthal Institute.
Streefland, L. (1993). Fractions: A realistic approach. In T.P. Carpenter, E. Fennema, and T.A. Romberg (Eds.), Rational numbers: An integration of research (pp. 289-327). Mahwah, NJ: Lawrence Erlbaum Associates.
Wearne, D., and Hiebert, J. (1988). Constructing and using meaning for mathematical symbols: The case of decimal fractions. In J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (vol. 2, pp. 220-235). Mahwah, NJ: Lawrence Erlbaum Associates.






