6
Learning with Understanding: Seven Principles
During the last four decades, scientists have engaged in research that has increased our understanding of human cognition, providing greater insight into how knowledge is organized, how experience shapes understanding, how people monitor their own understanding, how learners differ from one another, and how people acquire expertise. From this emerging body of research, scientists and others have been able to synthesize a number of underlying principles of human learning. This growing understanding of how people learn has the potential to influence significantly the nature of education and its outcomes.
The committee’s appraisal of advanced study is organized around this research on how people learn (see, for example, Greeno, Collins, and Resnick, 1996; National Research Council [NRC], 2000b; 2001a; Shepard, 2000). Our appraisal also takes into account a growing understanding of how people develop expertise in a subject area (see, for example, Chi, Feltovich, and Glaser, 1981; NRC, 2000b). Understanding the nature of expertise can shed light on what successful learning might look like and help guide the development of curricula, pedagogy, and assessments that can move students toward more expert-like practices and understandings in a subject area. To make real differences in students’ skill, it is necessary both to understand the nature of expert practice and to devise methods that are appropriate to learning that practice.
The design of educational programs is always guided by beliefs about how students learn in an academic discipline. Whether explicit or implicit, these ideas affect what students in a program will be taught, how they will be taught, and how their learning will be assessed. Thus, educational program designers who believe students learn best through memorization and repeated practice will design their programs differently from those who hold that students learn best through active inquiry and investigation.
The model for advanced study proposed by the committee is supported by research on human learning and is organized around the goal of fostering
learning with deep conceptual understanding or, more simply, learning with understanding. Learning with understanding is strongly advocated by leading mathematics and science educators and researchers for all students, and also is reflected in the national goals and standards for mathematics and science curricula and teaching (American Association for Advancement of Science [AAAS], 1989, 1993; National Council of Teachers of Mathematics [NCTM], 1989, 1991, 2000; NRC, 1996). The committee sees as the goal for advanced study in mathematics and science an even deeper level of conceptual understanding and integration than would typically be expected in introductory courses.
Guidance on how to achieve learning with understanding is grounded in seven research-based principles of human learning that are presented below (see Box 6-1).1 In Chapter 7, these principles are used as the framework for the design of curricula, instruction, and assessments for advanced study—three facets of classroom activity that, when skillfully orchestrated by the teacher, jointly promote learning with understanding. These principles also serve as the foundation for the design of professional development, for it, too, is a form of advanced learning.
The design principles for curriculum, instruction, assessment, and professional development provide one of the organizing frameworks of the committee’s analysis of the AP and IB programs (see Chapters 8 and 9, this volume). While it could be argued that all components of the educational system (e.g., preservice training and leadership) should be included (and we believe they should), our analysis was limited to these four facets. Although this framework was developed to assess current programs of advanced study, it also can serve as a guide or framework for those involved in developing, implementing, or evaluating new educational programs.
SEVEN PRINCIPLES OF HUMAN LEARNING
Principle 1: Principled Conceptual Knowledge
Learning with understanding is facilitated when new and existing knowledge is structured around the major concepts and principles of the discipline.
Highly proficient performance in any subject domain requires knowledge that is both accessible and usable. A rich body of content knowledge about a subject area is a necessary component of the ability to think and
|
BOX 6-1 Seven Principles of Learning
|
solve problems in that domain, but knowing many disconnected facts is not enough. Research clearly demonstrates that experts’ content knowledge is structured around the major organizing principles and core concepts of the domain, the “big ideas” (e.g., Newton’s second law of motion in physics, the concept of evolution in biology, and the concept of limit in mathematics) (see, for example, Chi et al., 1981; Kozma and Russell, 1997). These big ideas lend coherence to experts’ vast knowledge base; help them discern the deep structure of problems; and, on that basis, recognize similarities with previously encountered problems. Research also shows that experts’ strategies for thinking and solving problems are closely linked to rich, well-organized bodies of knowledge about subject matter. Their knowledge is connected and organized, and it is “conditionalized” to specify the context in which it is applicable.
If one conceives of advanced study as moving students along a continuum toward greater expertise, then advanced study should have as its goal fostering students’ abilities to recognize and structure their growing body of content knowledge according to the most important principles of the discipline. Therefore, curriculum and instruction in advanced study should be designed to develop in learners the ability to see past the surface features of any problem to the deeper, more fundamental principles of the discipline.
Curricula that emphasize breadth of coverage and simple recall of facts may hinder students’ abilities to organize knowledge effectively because they do not learn anything in depth, and thus are not able to structure what they are learning around the major organizing principles and core concepts of the discipline. Even students who prefer to seek understanding are often forced into rote learning by the quantity of information they are asked to absorb.
Principle 2: Prior Knowledge
Learners use what they already know to construct new understandings.
When students come to advanced study, they already possess knowledge, skills, beliefs, concepts, conceptions, and misconceptions that can significantly influence how they think about the world, approach new learning, and go about solving unfamiliar problems (Wandersee, Mintzes, and Novak, 1994). People construct meaning for a new idea or process by relating it to ideas or processes they already understand. This prior knowledge can produce mistakes, but it can also produce correct insights. Some of this knowledge base is discipline specific, while some may be related to but not explicitly within a discipline. Research on cognition has shown that successful learning involves linking new knowledge to what is already known. These links can take different forms, such as adding to, modifying, or reorganizing knowledge or skills. How these links are made may vary in different subject areas and among students with varying talents, interests, and abilities (Paris and Ayers, 1994). Learning with understanding, however, involves more than appending new concepts and processes to existing knowledge; it also involves conceptual change and the creation of rich, integrated knowledge structures.
If students’ existing knowledge is not engaged, the understandings they develop through instruction can be very different from what their teacher may have intended; learners are more likely to construct interpretations that agree with their own prior knowledge even when those interpretations are in conflict with the teacher’s viewpoint. Thus, lecturing to students is often an ineffective tool for producing conceptual change. For example, Vosniadou and Brewer (1992) describe how learners who believed the world is flat perceived the earth as a three-dimensional pancake after being taught that the world is a sphere.
Moreover, when prior knowledge is not engaged, students are likely to fail to understand or even to separate knowledge learned in school from their beliefs and observations about the world outside the classroom. For
example, despite instruction to the contrary, students of all ages (including college graduates) often persist in their belief that seasons are caused by the earth’s distance from the sun, rather than the inclination of the earth’s axis relative to the plane of its orbit around the sun, which affects the amount of solar energy striking the northern and southern regions of the earth as it orbits the sun (Harvard-Smithsonian Center for Astrophysics, Science Education Department, 1987). Roth (1986) similarly found that students continued to believe plants obtain food from the soil, rather than making it in their leaves, even after they had been taught about photosynthesis; this belief persisted since many failed to recognize that the carbon dioxide extracted from the air has weight and makes up most of a plant’s mass.
Effective teaching involves gauging what learners already know about a subject and finding ways to build on that knowledge. When prior knowledge contains misconceptions, there is a need to reconstruct a whole relevant framework of concepts, not simply to correct the misconception or faulty idea. Effective instruction entails detecting those misconceptions and addressing them, sometimes by challenging them directly (Caravita and Hallden, 1994; Novak, 2002).
The central role played by prior knowledge in the ability to gain new knowledge and understanding has important implications for the preparation of students in the years preceding advanced study. To be successful in advanced study in science or mathematics, students must have acquired a sufficient knowledge base that includes concepts, factual content, and relevant procedures on which to build. This in turn implies that they must have had the opportunity to learn these things. Many students, however, particularly those who attend urban and rural schools, those who are members of certain ethnic or racial groups (African American, Hispanic, and Native American), and those who are poor, are significantly less likely to have equitable access to early opportunities for building this prerequisite knowledge base (Doran, Dugan, and Weffer, 1998; see also Chapter 2, this volume). Inequitable access to adequate preparation can take several forms, including (1) lack of appropriate courses (Ekstrom, Goertz, and Rock, 1988); (2) lack of qualified teachers and high-quality instruction (Gamoran, 1992; Oakes, 1990); (3) placement in low-level classes where the curriculum focuses on less rigorous topics and low-level skills (Burgess, 1983, 1984; Nystrand and Gamoran, 1988; Oakes, 1985); (4) lack of access to resources, such as high-quality science and mathematics facilities, equipment, and textbooks (Oakes, Gamoran, and Page, 1992); and (5) lack of guidance and encouragement to prepare for advanced study (Lee and Ekstrom, 1987).
Students who lack opportunities to gain important knowledge and skills in the early grades may never get to participate in advanced classes where higher-order skills are typically taught (Burnett, 1995). Consequently, these
students may be precluded very early in their school careers from later participation in advanced study—even when they are interested and motivated to enroll. In essence, they are “tracked away.” The end result is that many students are denied access to important experiences that would prepare them to pursue the study of mathematics and sciences beyond high school.
Principle 3: Metacognition
Learning is facilitated through the use of metacognitive strategies that identify, monitor, and regulate cognitive processes.
To be effective problem solvers and learners, students need to determine what they already know and what else they need to know in any given situation. They must consider both factual knowledge—about the task, their goals, and their abilities—and strategic knowledge about how and when to use a specific procedure to solve the problem at hand (Ferrari and Sternberg, 1998). In other words, to be effective problem solvers, students must be metacognitive. Empirical studies show that students who are metacognitively aware perform better than those who are not (Garner and Alexander, 1989; Schoenfeld, 1987).
Metacognition is an important aspect of students’ intellectual development that enables them to benefit from instruction (Carr, Kurtz, Schneider, Turner, and Borkowski, 1989; Flavell, 1979; Garner, 1987; Novak, 1985; Van Zile-Tamsen, 1996) and helps them know what to do when things are not going as expected (Schoenfeld, 1983; Skemp, 1978, 1979). For example, research demonstrates that students with better-developed metacognitive strategies will abandon an unproductive problem-solving strategy very quickly and substitute a more productive one, whereas students with less effective metacognitive skills will continue to use the same strategy long after it has failed to produce results (Gobert and Clement, 1999). The basic metacognitive strategies include (1) connecting new information to former knowledge; (2) selecting thinking strategies deliberately; and (3) planning, monitoring, and evaluating thinking processes (Dirkes, 1985).
Experts have highly developed metacognitive skills related to their specific area of expertise. If students in a subject area are to develop problem-solving strategies consistent with the ways in which experts in the discipline approach problems, one important goal of advanced study should be to help students become more metacognitive. Fortunately, research indicates that students’ metacognitive abilities can be developed through explicit instruction and through opportunities to observe teachers or other content experts as they solve problems and consider ideas while making their thinking visible to those observing (Collins and Smith, 1982; Lester et al., 1994;
Schoenfeld, 1983, 1985). Having students construct concept maps2 for a topic of study can also provide powerful metacognitive insights, especially when students work in teams of three or more (see Box 6-2 for a discussion of concept maps). It is important to note that the teaching of metacognitive skills is often best accomplished in specific content areas since the ability to monitor one’s understanding is closely tied to the activities and questions that are central to domain-specific knowledge and expertise (NRC, 2000b).
Principle 4: Differences Among Learners
Learners have different strategies, approaches, patterns of abilities, and learning styles that are a function of the interaction between their heredity and their prior experiences.
Individuals are born with potential that develops through their interaction with their environment to produce their current capabilities and talents. Thus among learners of the same age, there are important differences in cognitive abilities, such as linguistic and spatial aptitudes or the ability to work with symbolic quantities representing properties of the natural world, as well as in emotional, cultural, and motivational characteristics.
Additionally, by the time students reach high school, they have acquired their own preferences regarding how they like to learn and at what pace. Thus, some students will respond favorably to one kind of instruction, whereas others will benefit more from a different approach. Educators need to be sensitive to such differences so that instruction and curricular materials will be suitably matched to students’ developing abilities, knowledge base, preferences, and styles. (Annex 6-1 illustrates some of the ways in which curriculum and instruction might be modified to meet the learning needs of high-ability learners.)
Appreciation of differences among learners also has implications for the design of appropriate assessments and evaluations of student learning. Students with different learning styles need a range of opportunities to demonstrate their knowledge and skills. For example, some students work well
|
2 |
Concept maps are two-dimensional, hierarchical representations of concepts and relationships between concepts that model the structure of knowledge possessed by a learner or expert. The theory of learning that underlies concept mapping recognizes that all meaningful learning builds on the learner’s existing relevant knowledge and the quality of its organization. The constructivist epistemology underlying concept maps recognizes that all knowledge consists of concepts, defined as perceived regularities in events or objects or their representation, designated by a label, and propositions that are two or more concepts linked semantically to form a statement about some event or object. Free software that aids in the construction of concept maps is available at www.cmap.coginst.uwf.edu. |
|
BOX 6-2 Use of Concept Maps Figures 6-1 and 6-2 are examples of actual concept maps constructed by a high school student. Figure 6-1 was made at the beginning of the study of meiosis and shows that the student did not know how to organize and relate many of the relevant concepts. The student equated meiosis with sexual reproduction and was not clear on how meiosis relates to homologous chromosomes. These maps are presented without editing. 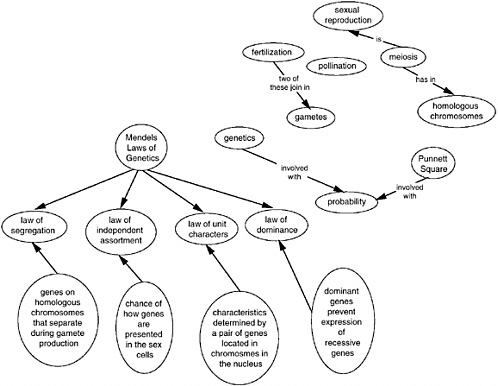 FIGURE 6-1 Concept map made by an advanced biology student early in the study of meiosis and genetics. Note that several concepts are not integrated into the student’s knowledge structure, and he has the misconception that meiosis is sexual reproduction. SOURCE: J. Novak (Jan. 2001) personal correspondence. Used with permission. |
|
Figure 6-2, a concept map made at the end of the study, reveals an elaborated, integrated understanding of the process. The student now has integrated the meanings of meiosis and sexual reproduction, homologous chromosomes, and other concepts. While some concept meanings still appear a bit fuzzy, the student has clearly made progress in the development of understanding, and his knowledge structure can serve as a good foundation for further study. 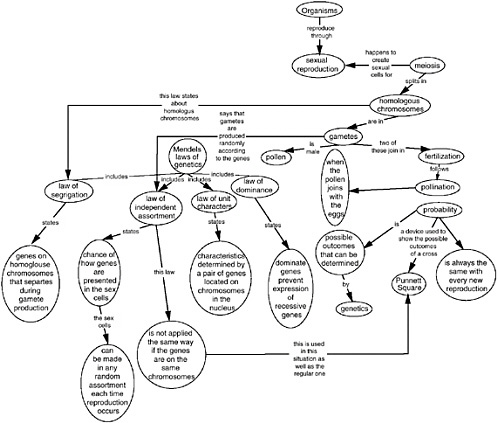 FIGURE 6-2 Concept map drawn by the same student at the end of the study unit on meiosis. Note that the original misconceptions about the nature of meiosis have been remediated, and more concepts have been integrated into the student’s knowledge structure. SOURCE: J. Novak (Jan. 2001) personal correspondence. Used with permission. |
under pressure, while the performance of others is significantly diminished by time constraints. Some excel at recalling information, while others are more adept at performance-based tasks. Some express themselves well in writing, while others do not. Thus using one form of assessment will work to the advantage of some students and to the disadvantage of others (Mintzes, Wandersee, and Novak, 2001; O’Neil and Brown, 1997; Shavelson, Baxter, and Pine, 1992; Sugrue, Valdes, Schlackman, and Webb, 1996).
Principle 5: Motivation
A learner’s motivation to learn and sense of self affects what is learned, how much is learned, and how much effort will be put into the learning process.
Humans are motivated to learn and to develop competence (Stipek, 1998; White, 1959). Motivation can be extrinsic (performance oriented), for example to get a good grade on a test or to be accepted by a good college, or intrinsic (learning oriented), for example to satisfy curiosity or to master challenging material. Regardless of the source, learners’ level of motivation strongly affects their willingness to persist in the face of difficulty. Intrinsic motivation is enhanced when learning tasks are perceived as being interesting and personally meaningful and are presented at the proper level of difficulty. A task that is too difficult can create frustration; one that is too easy can lead to boredom.
Research has revealed strong connections between learners’ beliefs about their own abilities in a subject area and their success in learning about that domain (Eccles, 1987, 1994; Garcia and Pintrich, 1994; Graham and Weiner, 1996; Markus and Wurf, 1987; Marsh, 1990; Weiner, 1985). Some beliefs about learning are quite general. For example, some students believe their ability to learn a particular subject or skill is predetermined, whereas others believe their ability to learn is substantially a function of effort (Dweck, 1989). Believing that abilities are developed through effort is most beneficial to the learner, and teachers and others should cultivate that belief (Graham and Weiner, 1996; Weiner, 1985). The use of instructional strategies that encourage conceptual understanding is an effective way to increase students’ interest and enhance their confidence about their abilities to learn a particular subject (Alaiyemola, Jegede, and Okebukola, 1990; Cavallo, 1996).
Cultivating the belief among a broad range of students that the ability to learn advanced science and mathematics is, for the most part, a function of effort rather than inherited talent, ability, and/or intelligence has other benefits as well. For example, the belief that successful learning in advanced study is a matter of effort fosters risk taking in course selection and promotes students’ motivation to succeed in challenging situations (Novak and
Gowin, 1984). A belief in the value of effort is especially important for students who are traditionally underrepresented in advanced study. For students to maintain their beliefs about the role of effort in successful performance, teachers and other school personnel must act in ways that do not contradict students’ sense that they are capable of understanding science and mathematics and that sustained effort will produce such understanding, even though there may be struggles along the way.
Several recent studies document the power of a high school culture that expects all students to spend time and effort on academic subjects and is driven by a belief that effort will pay off in high levels of academic achievement for everyone, regardless of prior academic status, family background, or future plans. When such norms and expectations are held in common for all students, they define the school’s culture. In such settings, remediation of skill deficits takes on a different character, teachers are able and willing to provide rigorous academic instruction to all students, and all students respond with effort and persistence (Bryk, Lee, and Holland, 1993; Lee, 2001; Lee, Bryk, and Smith, 1993; Lee and Smith, 1999; Marks, Doane, and Secada, 1996; Rutter, 1983).
Principle 6: Situated Learning
The practices and activities in which people engage while learning to shape what is learned.
Research on the situated nature of cognition indicates that the way people learn a particular domain of knowledge and skills and the context in which they learn it become a fundamental part of what is learned (Greeno, 1993; Lave, 1991). When students learn, they learn both information and a set of practices, and the two are inextricably related. McLellan (1996, p. 9) states that situated cognition “involves adapting knowledge and thinking skills to solve unique problems … and is based upon the concept that knowledge is contextually situated and is fundamentally influenced by the activity, context, and culture in which it is used.” Learning, like cognition, is shaped by the conventions, tools, and artifacts of the culture and the context in which it is situated.
Because the practices in which students engage as they acquire new concepts shape what and how the students learn, transfer is made possible to the extent that knowledge and learning are grounded in multiple contexts (Brown, Collins, and Duguid, 1989). Transfer is more difficult when a concept is taught in a limited set of contexts or through a limited set of activities. When concepts are taught only in one context, students are not exposed to the varied practices associated with those concepts. As a result, students often miss seeing the concepts’ applicability to solving novel problems en-
countered in real life, in other classes, or in other disciplines. It is only by encountering the same concept at work in multiple contexts that students can develop a deep understanding of the concept and how it can be used, as well as the ability to transfer what has been learned in one context to others (Anderson, Greeno, Reder, and Simon, 1997).
If the goal of education is to allow learners to apply what they learn in real situations, learning must involve applications and take place in the context of authentic activities (Brown et al., 1989). J. S. Brown and colleagues (1989, p. 34) define authentic activities as “ordinary practices of a culture”—activities that are similar to what actual practitioners do in real contexts. A. L. Brown and colleagues (1993) offer a somewhat different definition: given that the goal of education is to prepare students to be lifelong learners, activities are authentic if they foster the kinds of thinking that are important for learning in out-of-school settings, whether or not those activities mirror what practitioners do. Regardless of which definition is adopted, the importance of situating learning in authentic activities is clear. Collins (1988) notes the following four specific benefits: (1) students learn about the conditions for applying knowledge, (2) they are more likely to engage in invention and problem solving when learning in novel and diverse situations and settings, (3) they are able to see the implications of their knowledge, and (4) they are supported in structuring knowledge in ways that are appropriate for later use.
Teachers can engage learners in important practices that can be used in different situations by drawing upon real-world exercises, or exercises that foster problem-solving skills and strategies that are used in real-world situations. Such an approach provides language, activities, and procedures that can acculturate students into the community of scholars and lifelong learners. Problem-based and case-based learning are two instructional approaches that create opportunities for students to engage in practices similar to those of experts. Technology also can be used to bring real-world contexts into the classroom. The committee emphasizes that with all of these approaches, care must be taken to provide multiple opportunities for students to engage in activities in which the same concept is at work; otherwise learning could become overly contexualized.
Principle 7: Learning Communities
Learning is enhanced through socially supported interactions.
Learning can be enhanced when students have the opportunity to interact and collaborate with others on instructional tasks. In learning environments that encourage collaboration among peers, such as those in which most practicing scientists and mathematicians work, individuals build com-
munities of practice, have opportunities to test their own ideas, and learn by observing others. Research demonstrates that opportunities for students to articulate their ideas to peers and to hear and discuss others’ ideas in the context of the classroom is particularly effective in bringing about conceptual change (Alexopoulou and Driver, 1996; Carpenter and Lehrer, 1999; Cobb, Wood, and Yackel, 1993; Kobayashi, 1994; Towns and Grant, 1997; Wood, Cobb, and Yackel, 1991). Social interaction also is important for the development of expertise, metacognitive skills, and formation of the learner’s sense of self.
The social nature of learning has important implications for the consequences of the ways in which students are grouped for instruction. For example, students who are placed in low-track classes often have less time to collaborate and interact around instructional tasks. Research indicates that teachers in low-track science and mathematics classes spend more time than teachers in higher-track classes on routines, and more frequently provide seatwork and worksheet activities that are designed to be completed independently (Oakes, 1990). Additionally, teachers in higher-track classes often orchestrate more frequent and varied opportunities for students to participate in small-group problem-solving activities than are provided by teachers in lower-track classes, who tend to focus on behavior management and on maintaining control during learning activities. Some might contend that teachers in both types of classes are responding to the needs of their students. However, teachers must strike a balance between providing the structure that is often appropriate for low-ability students and the active engagement that allows these students to learn at deeper levels.
Newmann and Wehlage (1995) identify teaching strategies that promote intellectual quality and authenticity. One of the most powerful strategies is the “substantive conversation,” in which students engage in extended conversational exchanges with the teacher and/or peers about subject matter in a way that builds an improved or shared understanding of ideas or topics. The authors stress that such subject matter conversations go far beyond reporting facts, procedures, or definitions; they focus on making distinctions, applying ideas, forming generalizations, and raising questions. According to the results of research by Gamoran and Nystrand (1990), the opportunities for such substantive engagement are far fewer in low-track than in higher-track classes.
CONCLUSION
The seven principles of learning set forth in this chapter are not ends in themselves. Their usefulness lies in the guidance they provide for the design of curriculum, instruction, assessment, and professional development for
advanced study that fosters in students a deep conceptual understanding of a domain. The next chapter articulates design principles for advanced study that draw on these principles of learning.
ANNEX 6-1 CHARACTERISTICS OF HIGH-ABILITY LEARNERS AND IMPLICATIONS FOR CURRICULUM AND INSTRUCTION
Differences among learners have implications for how curriculum and instruction should be structured.3 Provided below is an example of how a better understanding of learning can assist teachers in structuring their curricula and instruction more appropriately to meet the needs of a particular group of students. Different strategies would most likely be used to meet the needs of other students, although there might be some overlap.
Characteristic: High-ability learners display an exceptionally rich knowledge base in their specific talent domain. Within that domain, they tend to achieve formal operational thought earlier than other students and to display advanced problem-solving strategies. High-ability learners are also able to work with abstract and complex ideas in their talent domain at an earlier age.
Implication: High-ability learners are ready to access the high school mathematics and science curriculum earlier than other students. Thus the high school mathematics and science sequence should be offered to them beginning in middle school.
Characteristic: High-ability students pick up informally much of the content knowledge taught in school, and as a result, that knowledge tends to be idiosyncratic and not necessarily organized around the central concepts of the discipline.
Implication: Assessment of what the learner has already mastered through diagnostic testing is critical. Instruction needs to build on what is already known and on previous experiences, filling in the gaps and correct-
ing misconceptions. It also must help the student organize his or her knowledge around the central ideas of the discipline. A full course in a content area often is not needed; either it could be skipped, with gaps being filled in as needed, or the curriculum compacted. “The proper psychology of talent is one that tries to be reasonably specific in defining competencies as manifested in the world, with instruction aimed at developing the very competencies so defined” (Wallach, 1978, p. 617).
Characteristic: High-ability learners learn at a more rapid rate than other students and can engage in simultaneous rather than only linear processing of ideas in their talent domain.
Implication: The pace at which the curriculum is offered must be adjusted for these learners. The curriculum also must be at a more complex level, making interdisciplinary connections whenever possible. That is, the curriculum should allow for faster pacing of well-organized, compressed, and appropriate learning experiences that are, in the end, enriching and accelerative.
Characteristic: Many high-ability students will have mastered the content of high school mathematics and science courses before formally taking the courses, either on their own, through special programs, or through Web-based courses.
Implication: Opportunities for testing out of prerequisites should be provided. Many high-ability students could be placed directly in an AP science course, skipping the typical high school–level prerequisite, or begin the IB program earlier than is typical.
Characteristic: High-ability students often can solve problems by alternative means and not know the underlying concept being tapped by a test item (e.g., can solve an algebra problem but not know algebra).
Implication: Assessments should not be solely in multiple-choice format; students must be able to show their work in arriving at a solution.
Characteristic: The motivation of high-ability students to achieve often becomes diminished because of boredom in school, resulting in underachievement.
Implication: Because one facet of effective teaching involves assessing the student’s status in the learning process and posing problems slightly exceeding the level already mastered (Hunt, 1961), it is important to provide curricula for high-ability students that are developmentally appropriate for them. Doing so will not only meet the intellectually talented student’s educational needs, but also facilitate his or her development of good study skills, more realistic self-concepts, and achievement motivation. Growth in
achievement motivation and self-efficacy arises out of challenge and satisfaction in mastering tasks that appropriately match capabilities.
Characteristic: The capacity for learning of high-ability students is underestimated and thus becomes underdeveloped, especially if learning criteria lack sufficient challenge, and curriculum is not adequately knowledge rich and rigorous.
Implication: Curriculum must be targeted at developing especially deep and well-organized knowledge structures that with time will begin to approximate those of experts. Doing so will foster cognitive development, higher-level thinking skills, and creativity. The depth of the curriculum should allow gifted learners to continue exploring an area of special interest to the expert level. Curricula for these students should enable them to explore constantly changing knowledge and information and develop the attitude that knowledge is worth pursuing in a global society.
Characteristic: High-ability children are advanced in their critical and creative thinking skills. They tend to spend much more time up front (i.e., metacognitively) than in the execution phase of problem solving.
Implication: The basic thinking skills to be developed in high-ability students are critical thinking, creative thinking, problem finding and solving, research, and decision making. Those skills should be mastered within each content domain.
Characteristic: High-ability students prefer unstructured problems in which the task is less well defined. They also like to structure their own learning experiences. They do not require careful scaffolding of material or step-by-step learning experiences to master new material or concepts; in fact, they become frustrated with such approaches.
Implication: Opportunities to identify and solve problems should be provided. Interdisciplinarity, greater in-depth exploration of areas of interest, and autonomous learning should be encouraged. Meaningful project work in content areas, in which real-world products are generated, is appropriate as it allows students the opportunity to create on their own and to apply and expand ideas learned in class. To facilitate such work, curricula should encourage exposure to, selection of, and use of specialized and appropriate resources.
Characteristic: High-ability students have the capacity to make connections easily among disparate bodies of knowledge and to deal effectively with abstractions and complexity of thought.
Implication: Curricula ought to emphasize providing students with a deep understanding of the important concepts of a discipline and how they
are organized, as well as identify important pathways between disciplines so that separate facets of knowledge are understood as being integrated. Curricula should allow for the development and application of productive thinking skills to instill in students the capacity to reconceptualize existing knowledge and generate new knowledge.
Characteristic: Eminent persons tend to have been profoundly influenced by a single individual, such as an educator. Students in the top mathematical/science graduate programs have reported research experiences during high school at unusually high levels. Those who are precocious in creative production tend to exhibit outstanding achievement in adult life.
Implication: Mentorships, internships, or long-term research opportunities should be provided for advanced students.
Characteristic: High-ability students who become productive adults in a domain have passed through that domain’s specific stages. Doing so took them much time and sustained effort, with the talent development process having begun well before secondary school.
Implication: Accelerated learning experiences are critical, given that the development of talent proceeds from practice and mastery of increasingly more difficult and complex skills at an individual rate, and mastery of a domain’s knowledge base and the concomitant reorganization of cognitive structures are both necessary for creativity.
Characteristic: High-ability students develop greater expectations, feel better about themselves, and engage in higher-level processing or discourse when working with other students of similar ability.
Implication: High-ability students need the challenge and stimulation of being together for at least part of every school day, with expectations set high enough to challenge their potential ability to meet them.

















