3
High Energy Density Laboratory Plasmas
INTRODUCTION
Imagine taking the output of the entire global power grid for a few billionths of a second and focusing it with a large laser onto the surface of a hollow capsule no bigger than the head of a pin. Next, imagine filling the capsule with isotopes of hydrogen (deuterium and tritium), then sitting back to “watch the action.” The capsule responds by imploding at velocities of up to 300 km/s, that is, at speeds approaching 0.1 percent of the speed of light! (See Figure 3.1.) At peak compression, the temperatures and densities at the center are of order 108 kelvin (10 keV) and 100 g/cm3, with pressures approaching 100 Gbar (~1016 P). These conditions mimic those found at the center of the Sun. Not surprisingly, the outcome is a “microsun,” for a very brief moment (0.1 ns) spewing forth a miniexplosion of neutrons and alpha particles from nuclear fusion. The pursuit of this “controlled astrophysics in the laboratory” is the routine business of the inertial confinement fusion (ICF) program in the United States, and it forms the focus of an enormous variety of high energy density (HED) physics research.
High energy density physics, as said earlier, is the study of the collective properties of matter under extreme conditions of temperature and density. Not surprisingly, this study of extreme science has considerable overlap with astrophysics and nuclear weapons physics, as well as inertial confinement fusion research. This chapter gives a broad survey of laboratory HED physics, starting in the next section with a list of important scientific questions that could potentially be addressed on
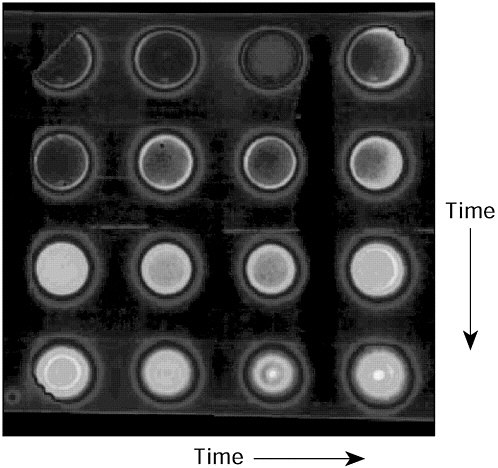
FIGURE 3.1 X-ray pinhole camera “movie” of a directly driven inertial confinement fusion implosion on the OMEGA laser system, from the laser irradiating the shell at early times, to the formation of a hot spot. Each image has ~50-ps temporal resolution, and the total duration of the “movie” is ~3.2 ns. The initial target diameter (upper left image) is ~1 mm, and the final compressed core diameter (third image, bottom row) is <100 µm. Courtesy of the Laboratory for Laser Energetics, University of Rochester.
HED facilities. Then various experimental facilities are described; the section on “Facilities” is devoted to a discussion of a wide range of HED physics phenomena, and areas of overlap with astrophysics and other branches of physics are pointed out. Some applications of HED physics are then described, and the final section of the chapter describes some of the opportunities for high energy density physics studies in the laboratory.
KEY QUESTIONS
It is now possible for experimental science to enter into a regime that has been, until now, largely the exclusive domain of theoretical and computational physics, namely, the collective behavior of matter under extreme conditions of density and temperature. Such conditions are commonplace in astrophysics, yet laboratory experimental mileposts are rare. Indeed, the report of the National Research Council’s Committee on the Physics of the Universe, Connecting Quarks with the Cosmos,1 has embraced the need for laboratory exploration of physics under extreme conditions on HED facilities. As a guiding framework for describing this experimental frontier, the Committee on High Energy Density Plasma Physics presents a list of fundamental questions that could potentially benefit from experiments on current or future HED facilities:
-
Can thermonuclear ignition be achieved in the laboratory? Can high-yield inertial confinement fusion implosion experiments contribute to our understanding of aspects of thermonuclear supernova explosions? Can nucleosynthesis of the heavy elements (Z>50) be studied using the intense burst of 1019 neutrons from high-yield capsule implosions? Can thermonuclear ignition lead to energy production (and possibly then to hydrogen production) through inertial fusion energy?
-
Can the transition to turbulence in compressible flows be understood? Can supersonic turbulent flows be generated?
-
Is there a fundamentally new, first-order phase transition unique to the plasma state, the so-called plasma phase transition (PPT)? Do mixtures (e.g., He-H, C-O, and so on) undergo phase separation at sufficiently high densities? Can metallic hydrogen ever exist in the solid state, or do quantum zero-point vibrations prevent this?
-
Can laboratory experiments help to discriminate among competing models of planetary interiors and planetary formation? Can experiments help establish whether the core of Jupiter is solid or liquid? Is convection not possible in Jupiter’s metallic hydrogen layer, and what are the consequences for Jupiter’s interior?
-
Can intense bursts of thermal electron-positron plasmas be created and studied in the laboratory? Can relativistic jets and shocks be generated from such an electron-positron fireball relevant to gamma-ray burst models? Are the dynamics of such relativistic jets and shocks fundamentally different from those of their nonrelativistic counterparts?
-
Can conditions of radiation-dominated matter be created in the laboratory? Can conditions relevant to radiation-dominated black-hole or neutron star accretion disks be generated and probed? At low densities, can an equilibrium photoionized plasma be created in the density-independent, radiation-dominated regime? At high densities, can conditions be created in which radiation pressure dominates particle pressure? Are there new dynamics for this case, such as a photon bubble instability?
-
Can macroscopic assemblies of fully degenerate matter (degenerate electrons and degenerate ions) be created, and their thermal and mechanical properties measured? Can plasma transport coefficients be determined under such conditions of extreme degeneracy, where continuum lowering dominates opacities and quantum effects dominate the plasma?
-
Can the equation of state of bulk nuclear matter be determined in the laboratory? Can the conditions of “core bounce” (i.e., the nuclear rebound) in core-collapse supernovae be experimentally reproduced? Can the structure of neutron star interiors be experimentally accessed?
-
Can a phase transition to the quark-gluon plasma be inferred? Can the properties of a quark-gluon plasma be determined?
-
Can sufficiently high densities be created in the laboratory to allow pycnonuclear fusion reactions (genuine cold fusion) to be observed? Can nuclear reactions under highly screened conditions in dense plasmas relevant to the cores of massive stars be studied in the laboratory? Can macroscopic assemblies of relativistically degenerate matter (Fermi temperature, ΘFermi>mec2) be created in the laboratory, and their equations of state be determined? Can the boundary between a stable white dwarf core and one that will unstably collapse to a neutron star be verified in the laboratory?
-
Can a radiatively collapsed shock be created in the laboratory? Would new thin-shell instabilities be created as a result? Can strong magnetohydrodynamic (MHD) shocks be created? Can a collisionless shock be created, or
-
its mechanism be inferred? Can shock-induced particle acceleration be demonstrated?
-
Can astrophysical jet formation and jet collimation mechanisms be elucidated with laboratory experiments?
-
Can ultrastrong magnetic fields, B>1 gigagauss, be experimentally created and their effect on the surrounding plasma be studied? Can magnetic fields relevant to the atmosphere of neutron stars be created, and aspects of the complex radiative MHD processes be experimentally reproduced? Can the so-called radiation-bubble instability be replicated?
FACILITIES
Experimental facilities available for high energy density research include high-energy (relatively long-pulse) lasers, high power (very short pulse) lasers, pulsed-power devices, high-current particle beam accelerators, and combinations of these. New facilities planned or under construction will extend still further the range of high energy density conditions achievable. Tables 3.1 through 3.5 list a variety of HED facilities currently in operation, under construction, or in the serious planning stages. Figure 3.2 is an illustration of the National Ignition Facility (NIF) currently under construction at Lawrence Livermore National Laboratory. When completed, it will produce ~2 MJ of laser energy and will be the flagship high energy density facility in the United States.
TABLE 3.1 Three Currently Operating High Energy Density Facilities That Provide the Highest Energy Densities to Experimental Targets
|
Existing |
OMEGA (University of Rochester— Laboratory of Laser Energetics) |
Z-machine (Sandia National Laboratories) |
Atlas (Los Alamos National Laboratory; To Be Moved to Nevada Test Site) |
|
|
Type |
Laser |
Pulsed power |
X-ray source |
Pulsed power |
|
Photon energy |
3.5 eV |
20 MA as Z-pinch driver |
50–250 eV (BB)a |
30 MA as Z-pinch driver |
|
Pulse length |
0.1–4 ns (longer with pulse stacking) |
~100-ns rise time |
5–15 ns |
4.5-µs rise time |
|
Spot size |
0.1–3 mm |
N/A |
~1-mm cylinder |
N/A |
|
E/pulse |
30 kJ |
16 MJ stored energy |
1.8 MJ |
24 MJ stored energy |
|
Repetition rate |
1 per hr |
A few per day |
1 per day |
<1 per day |
|
Peak intensity |
~1×1016 W/cm2 |
N/A |
X ray: 1×1014 W/cm2 |
N/A |
|
aBB indicates that the given photon energies refer to typical hohlraum temperatures that are achieved. |
||||
TABLE 3.2 High Energy Density Facilities, Including Those Typically Associated with Particle Physics
TABLE 3.3 High Energy Density Facilities Currently Under Construction or Contemplated in the Near Future
|
Facility |
PW-Class Lasers |
NIF |
Z-R (x ray) |
LHC |
|
Energy/particle |
1.5 eV |
3.6 eV; 600 eV BBa for ICF |
100–250 eV (BB)a |
7 TeV |
|
Pulse length |
0.5 ps |
0.2–20 ns (longer with pulse stacking) |
10 ns |
0.25 ns (1 bunch) |
|
Spot size |
5 µm |
0.2–5 mm |
1-mm cylinder |
16 µm |
|
E/pulse |
0.5~5 kJ |
1.8 MJ |
>3 MJ |
334 MJ in 2.8×103 bunches |
|
Repetition rate |
Up to 2 per hr |
2 per day |
1 per day |
4×107 Hz |
|
Peak intensity |
1×1021 W/cm2 |
2×1015 W/cm2 |
4×1014 W/cm2 |
1×1019 W/cm2 |
|
NOTE: Somewhat lower peak intensities than those listed, in the 1012 W/cm2 range with a ~1-mm target, are planned for the electron beam facility Dual Axis Radiographic Hydrodynamic Test (DARHT) (not listed); similar intensities are planned for future proton drivers as well. aBB means that the given photon energies refer to typical hohlraum temperatures that are expected for ICF experiments. |
||||
Table 3.1 shows characteristic parameters for three of the largest currently operating, high energy density facilities: the OMEGA laser; the fast, magnetic pinch Z-machine; and the relatively slow pulsed-power facility Atlas. All three of these facilities were built primarily for high energy density plasma studies relevant to nuclear weapons science, including inertial confinement fusion, but the National
TABLE 3.4 Possible Future High Energy Density Facilities
TABLE 3.5 Examples of Current and Future International High Energy Density Facilities
|
Facility |
Type of Facility |
Country |
||
|
GSI PW |
PW-class laser+ion storage ring |
Germany |
||
|
MAGPIE |
TW pulsed power |
Great Britain |
||
|
Vulcan+PW |
ICF-class+PW-class |
Great Britain |
||
|
LULI |
PW-class lasers |
France |
||
|
LIL |
First stage of ignition class |
France |
||
|
Laser Megajoule |
Ignition-class laser |
France |
||
|
Gekko+PW |
ICF-class+PW-class lasers |
Japan |
||
|
NOTE: The approximate parameters for the various types of facilities can be found in Tables 3.1 through 3.4. Several facilities will have a combination of longer-pulse lasers and ultrahigh-power (petawatt) lasers. |
||||
Nuclear Security Administration, which operates them, makes a portion of their time available for fundamental high energy density physics research.
Table 3.2 shows other existing HED facilities. These include ICF-class lasers not listed in Table 3.1, high-intensity (terawatt [TW]) laser and pulsed-power systems typically found in universities, and particle physics facilities that can achieve HED conditions (often in combination with other HED technologies). Many of these smaller laser systems can be operated at a significantly higher repetition rate than is possible with high-energy laser systems. These high-average-power systems can perform hundreds or thousands of experiments, allowing detailed data to be
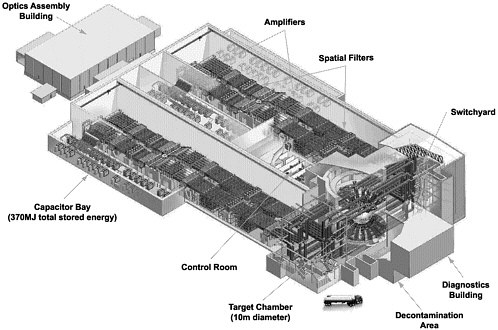
FIGURE 3.2 Rendering of the ~2-MJ National Ignition Facility (NIF) that is currently under construction at Lawrence Livermore National Laboratory, showing the location of various components and support facilities. When completed, the NIF will be the nation’s highest-power MJ-class high energy density physics facility, built primarily for weapons-relevant high energy density physics research, including inertial confinement fusion. Up to 15 percent of the laser time is planned to be available for basic science experiments. Courtesy of Lawrence Livermore National Laboratory.
obtained. High-average-power laser systems will also be required for laser-drive inertial fusion energy.
Tables 3.3 and 3.4 list future high energy density facilities, either under construction or being discussed, though significant technological advances may be required to build these advanced systems, which will extend the range of high energy density conditions available for experiments. The National Ignition Facility will be the flagship high energy density facility in the United States. Similar development of high energy density facilities is occurring outside the United States.
Table 3.5 lists some of these facilities. The LMJ laser facility, under construction in France, will have capabilities similar to those of the NIF.
Active foreign research efforts under way and the availability of an increasing suite of international facilities will continue to allow active international collaborations to be pursued. In fact, a number of the experimental results shown in the subsequent sections (particularly in Figures 3.7, 3.9, and 3.10) are the results of international efforts and collaborations involving U.S. researchers collaborating on international facilities or foreign researchers collaborating on U.S. facilities.
HIGH ENERGY DENSITY PHYSICS PHENOMENA
This section describes a number of physics phenomena of wide scientific interest that are unique to HED conditions. The density-temperature phase diagram for hydrogen, shown in Figure 3.3, provides a convenient roadmap through the most important HED regimes. The upper left-hand side of the figure corresponds to extremely high densities and low temperatures where quantum-mechanical degeneracy pressure dominates. The lower right-hand side corresponds to regimes of extremely high temperature and low densities, where radiation effects dominate. Intermediate between these two extremes, radiation, particle, and degeneracy pressures can all contribute to the plasma dynamics. A key distinguishing feature of the HED facilities is that macroscopic volumes of matter can be placed in these extreme conditions for laboratory study.
High Energy Density Materials Properties
When an object (solid, liquid, or gas) is subjected to an increase in external pressure, p, it tends to compress according to p=−β (ΔV/V), where β is its bulk modulus, and (ΔV/V) is the compression. Solids typically have β≈1 Mbar; hence, very high pressures are needed to compress a solid. When p/β≪1, the material compression is negligible, and its response is well described by elasticity theory. In the HED regime, however, p/β≥1 by definition. Here, the response of matter is no longer a gentle perturbation, but rather a significant, perhaps even violent, compression or deformation. At sufficiently high pressures and densities, molecules can dissociate and atoms can ionize, each of which affects the compressibility and deformation. Solids can undergo phase transitions to reach lower collective energy states and twinning transitions, in response to sufficient applied shear stresses. New techniques for studying the time-resolved response of materials to extreme pressures and applied stresses have been developed in recent years. An illustrative selection of examples is described below.
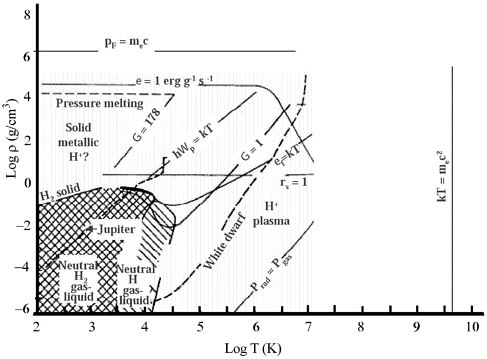
FIGURE 3.3 Phase diagram for hydrogen in temperature-density space showing the great complexity of even the simplest molecule. Courtesy of H.M.Van Horn, University of Rochester, now at National Science Foundation.
High-Pressure Equation of State
The equation of state (EOS) of a material can be experimentally determined by applying a known external pressure to a sample and measuring its volumetric response (compression). If the applied pressure is in the form of a shock, the material response is determined through the Rankine-Hugoniot relations. Modern HED drivers are also capable of delivering shaped pressure pulses that enable isentropic compression experiments, or other off-Hugoniot conditions. High energy density facilities are particularly well suited for EOS studies at high compression, because of the very high pressures possible. A high-energy laser can be used to launch a strong-shock wave by ablation pressure. Pulsed-power devices can launch “flyer plates” with which to shock a sample by impact, or they can produce isentropic compression by
applying a tailored magnetic pressure pulse directly to the surface of a conducting sample. Alternatively, by appropriate pulse shaping, compressions to higher density at a given peak pressure can also be achieved, thereby probing off-Hugoniot regimes. Gas guns, explosively driven flyer plates, and electromagnetic launchers can also be used to launch shock waves in materials for compression studies. In addition, static techniques such as diamond anvil cells can be used to generate moderately high pressures in materials.
Hydrogen is the simplest and most ubiquitous element in the universe, and its EOS is critical to planetary structure and planetary formation models, as well as to the performance of inertial confinement fusion capsule implosions and stockpile stewardship. Yet it has an impressively complicated phase diagram, as shown in Figure 3.3. The EOS measurements of hydrogen over the past decade have yielded several surprises. For example, the theoretically predicted plasma phase transition has yet to be experimentally observed. With the recent availability of large high energy density experimental systems (first the Nova laser, and now OMEGA, Z, and NIKE), multimegabar EOS measurements have become possible in liquid hydrogen. As high energy density systems continue to move to higher energies (e.g., the NIF), the parameter space accessible to experiments will be greatly expanded. As mentioned in Chapter 2, new results could significantly impact models of planetary structure and possibly planetary formation models, and they could also affect the modeling of inertial confinement fusion implosions. It should also be noted that in measurements relevant to planetary interiors, the experimental results should be directly applicable, without any scaling (see Figure 1.1 in Chapter 1), provided they are made at the correct density, temperature, and equilibrium states. Measurements of reflectivity and conductivity of shocked hydrogen allow observation of the dielectric-to-metallic transition. The temperature in the shock-compressed material can be determined by various spectroscopic techniques. Taken together, these measurements provide powerful tests of models of the properties of dense, degenerate plasmas. To have significant impact on models of planetary interiors, the accuracy of the experimental measurements needs to approach 1 percent in density, 20 percent in temperature, and factors of 2 in solubility and transport coefficients.
Theories and simulations of the EOS of dense, strongly coupled, Fermi-degenerate plasmas are a very active area of ongoing research. Semiempirical models, such as the “chemical picture,” typically use effective pair potentials fit to experimental data. Ab initio simulations using molecular dynamics or Monte Carlo models attempt to calculate the plasma conditions from first principles. Most of these models assume equilibrium conditions. Given that experiments on HED facilities can have rather brief time scales, a few nanoseconds, or sometimes even less, there may be a need for kinetic theories to explicitly calculate the evolution to
equilibrium. This remains an open question. Several of the models referred to above predict that pressure ionization of the plasma occurs through a first-order phase transition, called the plasma phase transition (PPT). The PPT has never been experimentally observed, though experimental searches continue. If the PPT were found to exist, it would have a profound impact on models of planetary interiors and planetary formation.
Dynamic Response of Materials
The time-resolved response of a solid-state lattice to an impulsive applied stress is a new area of research. Determining how a lattice responds to a shock requires a combination of quantum mechanics (via an interatomic potential), statistical physics of a large but finite number of discrete objects (lattice points), and continuum dynamics for following material deformation or flows. Knowing which approximations “work” in putting a theoretical treatment together requires comparisons with data. In particular, for an applied stress in a given direction, one would like to know the lattice response in all directions, including the direction of the applied stress. The experimental techniques to make such tensorial measurements are rapidly being developed. It seems very likely that within this decade the fundamental problem of lattice response to a shock will be solved.
The most promising experimental tool for probing the lattice response of a solid-state sample to an impulsive stress is time-resolved hard x-ray diffraction, a technique that measures the lattice spacing. A solid-state lattice has a multitude of options in its repertoire for responding to applied stresses, and which response occurs depends on the magnitude of the stress, the lattice temperature, the strain rate, and the ambient pressure, among other things. A large number of these deformation mechanisms (e.g., uniaxial elastic compression, hydrostatic plastic compression, twinning, solid-to-solid phase transitions, melting) can in principle be inferred from high signal-to-noise ratio, multi-lattice-plane diffraction measurements. An excellent example of such a measurement is shown in Figure 3.4. In this case, matter was impulsively heated at the surface with a ~70-fs laser pulse from a high-repetition-rate (1 kHz) Ti:sapphire laser, and probed with bursts of 10 keV x rays from the Advanced Photon Source. The diffraction signal, which integrates more than 6000 laser shots, shows both the lattice expanding due to the heating from the laser, and an oscillatory pattern due to coherent phonons being launched into the interior of the lattice. As the heat conducts away, the expansion of the lattice subsides over an interval of ~1/2 ns.
Several other techniques exist or are being developed for probing the lattice response to deformation. Among these are extended x-ray absorption fine structure, 2nd harmonic reflectivity, and coherent anti-Stokes Raman spectroscopy. Each
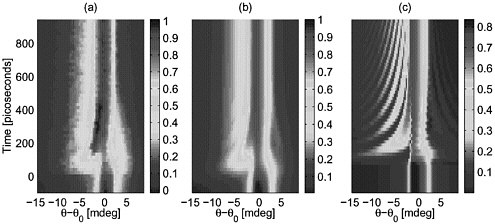
FIGURE 3.4 Time-resolved x-ray diffraction from an InSb crystal that is irradiated with a 70-fs laser pulse from a 1-kHz repetition rate Ti:sapphire laser, synchronized with a burst of collimated 10-keV x rays from the Advanced Photon Source (APS). The pump-probe derived experimental image is shown in (a), and the results from a simulation (with ideal resolution) are shown in (c). Image (b) shows the simulation with the experimental resolution convolved into it. The x-ray scattering angle θ0 corresponds to the Bragg condition for the 10-keV x rays under ambient conditions. When the laser turns on at t=0, both lattice expansion (θ−θ0<0) and lattice compression (θ−θ0>0) are observed in the diffracted x rays. The oscillations observed vertically, most clearly seen in the simulations, are due to the coherent phonons caused by the acoustic wave launched into the InSb, that is, the crystal is literally “ringing” due to the 70-fs laser-induced impulse. SOURCE: Reprinted, with permission, from D.A.Reis, M.F.DeCamp, P.H.Bucksbaum, R.Clarke, E.Dufresne, M.Hertlein, R.Merlin, R. Falcone, H.Kapteyn, M.M.Murnane, J.Larsson, T.Missalla, and J.S.Wark, 2001, “Probing Impulsive Strain Propagation with X-Ray Pulses,” Phys. Rev. Lett. 86:3072–3075, copyright 2001 by the American Physical Society.
technique examines different aspects to the lattice response as a function of time, position, and temperature. Taken collectively, these measurements of lattice response to deformation allow a new regime of material science at ultrahigh pressures and strain rates to take root and grow.
Radiation Flow and Material Opacities
The previous section dealt with extreme conditions in cool dense matter, mainly solids, where quantum mechanics dominates. Next let us “turn up the heat” several
notches, moving into the right-hand side of the phase diagram of Figure 3.3, where radiation effects dominate. The most interesting effects in this regime often involve gradients that allow thermal energy to flow. At high enough temperature the heat flow is dominated by radiation transport and opacity provides the resistance. The ionization state and opacity of “high-Z” plasma (any Z>about 20) under high-temperature conditions is enormously complex, and can have a dominant impact on the heat flow in ICF hohlraums, stellar interiors, and supernova explosions. The regimes break down into categories such as equilibrium versus nonequilibrium, optically thick versus optically thin, collisional versus radiation dominated, and static versus flowing plasma. Each regime has its own applications and “grand challenge” problems to solve. One of the best examples of laboratory measurements helping to understand an astrophysical object, beat-mode Cepheid variable stars, was a result of accurate calculations and measurements of the opacity of iron under conditions relevant to stellar envelopes.
Partially or Fully Degenerate Matter
Cool dense matter corresponds to conditions where kT/ΘF≪1, and Γ=e2/akT≫1, where ΘF is the Fermi temperature and Γ is the plasma coupling constant, that is, the ratio of the interparticle coulomb energy (for typical interparticle spacing, a) to the particle thermal energy, kT. Here, Fermi-Dirac statistics is the rule. Hot matter corresponds to regimes where degeneracy effects are negligible (kT/ΘF≫1), and kinetic energy dominates potential energy (Γ≪1), where a classical Maxwell-Boltzmann description of the plasma works well. In between lies a theoretical “no-man’s land,” where kT/ΘF≈1 and Γ≈1. The standard simplifying approximations no longer apply. Quantum effects neither dominate nor are negligible, making this terra incognita particularly troublesome theoretically. The scientific community has until now largely set this difficult regime aside for future generations to deal with. A new cadre of scientists, emboldened by a repertoire of new scientific tools—massively parallel computers and new experimental facilities—is now confronting this problem under the innocuous rubric of “warm dense matter.”
On the theoretical side, numerical simulation capabilities using massively parallel computing have progressed significantly. The theories, with their numerical implementation, can now begin to model experimental results in this warm dense matter regime, including EOS and opacity studies. On the experimental side, high-explosive techniques can achieve temperatures greater than 1 eV over large (compared to laser-driven systems) volumes of matter. Higher energy densities can be obtained with laser-driven techniques and dense Z-pinches. Development of new high-power, short-pulse sources in the XUV and x-ray regimes look extremely promising to create and diagnose these conditions. These sources, based at high-
energy accelerator facilities, include an XUV free-electron laser—the Teraelectronvolt Energy Superconducting Linear Accelerator Test Facility (TTF II) at the Deutsche Elektronen-Synchrotron (DESY) center in Germany—and X-ray FELs—the Linac Coherent Light Source (LCLS) being developed at the Stanford Linear Accelerator Center (SLAC), and the Teraelectronvolt Energy Superconducting Linear Accelerator (TESLA) under development at DESY. Other techniques based on using subpicosecond laser pulses may yield short-pulse x-ray sources as well. A significant advantage in the use of radiation above optical frequencies is that it allows for greatly enhanced diagnostic access, since warm dense matter systems are characteristically opaque to visible light.
One way to access warm dense matter states is through the use of ultrafast laser systems to heat matter on a time scale that is short compared to its hydrodynamic response time. This allows solid-state density materials to be heated to temperatures in the high energy density regime (e.g., densities, temperatures, and energy densities of 1024 cm−3, a few electronvolts, and ~1012 ergs/cm3=1011 J/m3, respectively). Thus, recent advances in ultrafast laser technology allow the creation of high energy density systems that were previously unattainable.
Dynamic Plasma Evolution
So far, this chapter has described matter solely in terms of static quantities—for example, p/B, kT/ΘF, Γ=e2/akT, and so on. Material flow, however, brings in a whole new dimension and can indeed have dramatic effects on the response of matter to extreme conditions. Under incompressible conditions (p/B≪1), the study of material flows constitutes the field of classical fluid dynamics. In HED conditions (p/B≥1), studies of material flows are new, and experimental mileposts are sparse to nonexistent. The following section discusses dynamic plasma evolution, that is, HED flow dynamics.
Classical Fluid Instabilities, Including Nonlinear Behavior
There are two relevant dimensionless parameters in classical fluid flow. These are the Reynolds number, Re≡ρuL/µ=Lu/v, and the Mach number, Ma≡u/a. Here, ρ is the fluid density, u the relative fluid velocity in the flow frame, L the flow spatial scale, µ the fluid (shear) viscosity, v=µ/ρ is the fluid kinematic viscosity, a=(γRuT/W)1/2 is the (local) speed of sound for a perfect gas, γ=cp/cv is the ratio of specific heats, Ru the universal gas constant, and W the molecular weight (molar mass).
The Reynolds number (Re) is a measure of the relative importance of viscous damping to inertial or convective forces and gauges hydrodynamic stability when
no other (e.g., MHD) forces are important. At low values, Re generally serves as a yardstick for the generation of instabilities. At higher values, it characterizes the turbulent state. Typically, values of Re<40 to 50 correspond to stable flow, Re>40 to 50 marks the onset of unbounded (free-shear) flow instabilities, Re>a few times 103 signals the onset of wall-bounded flow instabilities, and Re>a few times 104 triggers the transition to fully developed (bona fide) turbulence. The latter transition appears to occur in all high-Reynolds-number flows, and demarks a weaker sensitivity to further increases in Reynolds number. In a turbulent flow, the Reynolds number is also a measure of the range of spatial scales that participate in the dynamics. This can be estimated based on Kolmogorov-scaling arguments, yielding Lmin/Lmax≈CLRe−3/4, where CL≈16π≈50, as also supported by experiment. Post-transitional flows exhibit enhanced mixing relative to pretransitional flows. Figures 3.5 and 3.6 show examples of this transition in turbulent shear layers and jets, and its consequences on scalar (i.e., concentration) fields, as measured by laser-induced fluorescence. As these examples illustrate, there can be significant qualitative and quantitative differences between pre- and post-transitional flows. Inferences from experiments, or simulations, in the pre-transitional regime cannot be applied to fully developed (post-transitional) flows. In the context of future HED experiments

FIGURE 3.5 Shear-layer scalar field. Blue: pure high-speed fluid. Red: pure low-speed fluid. Color bars denote intermediate compositions. Left: Re=2.3×103; right: Re=2.0×104. Courtesy of P.Dimotakis, California Institute of Technology and M.M.Koochesfahani, Michigan State University.
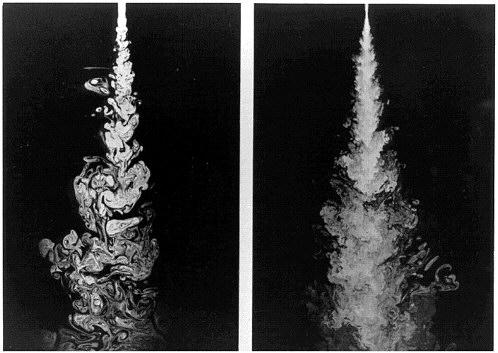
FIGURE 3.6 Jet-fluid concentration field in the plane of symmetry of turbulent jets. Left: Re=2.3×103; right: Re=10.0×103. Courtesy of P.Dimotakis, California Institute of Technology.
and simulations, especially as length scales and energy density increase in HED laboratory experiments and increases in computational power permit ever-increasing Reynolds numbers to be simulated, post-transitional flows will be encountered. This will mark a major step forward in the experimental and numerical capability to reproduce complex, high-Reynolds-number flows.
The Mach number (Ma) measures compressibility (density variations), the ratio of kinetic to thermal energy, and the ability of the flow to form and sustain shocks. This can be seen by expressing the local, specific thermal energy h (thermal energy per unit mass) in terms of the local sound speed, a, i.e., h≈cpT≈a2/(γ−1), an exact relation for a perfect gas. The Mach number then expresses the ratio of kinetic energy per unit mass, K=u2/2, to thermal energy per unit mass in the flow, h, since Ma=[2K/(γ−1)h]1/2, also exact for a perfect gas. In addition, the Mach number scales the flow density fluctuations, Δρ. In particular, for Ma not too large, one can
show, with only mild assumptions, that Δρ/ρ≈M2/2. As the Mach number becomes comparable to unity, the flow will generate shocks, that is, the flow can sustain fluid-property jumps across a few mean free paths.
These relations also indicate that if a significant fraction of the energy density manifests itself as a (specific) kinetic energy, K, the flow will be characterized by high Reynolds numbers and must be turbulent. Also, if K/h is large, the Mach number is also large, and the flow will be compressible. If both Reynolds number and Mach number are large, compressibility, shocks, and turbulence will coexist. Compressible turbulence and the coupling and interactions of shocks with turbulence are to a large extent unexplored territory, at present, both experimentally and computationally.
The fundamental instabilities that induce and sustain turbulence are sensitive to compressibility effects. For example, supersonic shear layers grow considerably more slowly than their incompressible counterparts. Further, shocks provide an additional dissipation mechanism, indicating that the Kolmogorov cornerstones of classical incompressible turbulence need to be modified or, at least, augmented. Compressible turbulence must be characterized as an important research area. Pursuits in this important HED regime are limited, as only scant information is available from theory, experiment, or simulations.
Interestingly, the Mach and Reynolds numbers also enter into determining the boundary between a continuum fluid description and a free-streaming, molecular (rarefied) description of the flow. This can be seen from the approximate gas-kinetic expression for the viscosity, µ≈2 ρaλf/3, where λf is the mean free path. From the relation for the Reynolds and Mach numbers, we see that they can also be expressed as Ma≈Re Kn, where Kn≡λf/L is the Knudsen number, that is, the ratio of the mean free path to the flow scale. Continuum hydrodynamics require Kn≪1, or, Re≫Ma.
This phenomenology is potentially much richer in plasmas where electron and ion velocities can differ, offering additional measures for compressibility and turbulence. As with shocks and turbulence, the corresponding magnetohydrodynamic regimes are not well understood, except in simple cases. Finally, in very energetic plasma flows such as very high Mach number jets or shocks, radiation can significantly alter the dynamics. At sufficiently high temperature and density, the photon “fluid” carries a significant fraction of the energy density. If the scale of the photon mean free path is long compared to characteristic spatial scales of the flow, then radiative cooling can remove thermal energy, lowering the temperature and pressure and increasing the compressibility and Mach number of the flow. High-Reynolds-number, high-Mach-number flows including radiative effects are common in astrophysics (see Figures 3.7(c) and 3.9(a)), but are largely unexplored in laboratory studies. Existing and future HED facilities should be able to make major inroads into this frontier territory.
High-Mach-Number Shocks
The experimental investigation of the dynamics of strong shocks, that is, high-Mach-number shocks, is a relatively new area. Experimental facilities have only recently accessed this hydrodynamic regime. HED facilities, in particular, excel in this respect because they can focus macroscopic energies into microscopic volumes in nanosecond time intervals. Fundamental issues abound, such as what the effect of strong shocks passing through a turbulent medium is, and how radiative emissions and magnetic fields couple to the dynamics. Though difficult to attain in the laboratory, strong shocks in astrophysics are the rule, not the exception. Examples include the enormously energetic shock unleashed by the “nuclear spring” at the core of a supernova (Ma~10), the shocks launched by the passage of high-Mach-number protostellar jets through the interstellar medium (Ma~10 to 20), and the shocks created by the stellar winds from newly formed young stars that sweep away the remaining molecular clouds out of which they were born (Ma~5), to name a few.
Aspects of strong-shock astronomical dynamics can be scaled down into the laboratory if conditions on certain key dimensionless parameters such as Mach number and also Reynolds number are met. For dynamics that are not dominated by turbulence and turbulent mixing, the equations suggest that such scaling is possible. Figure 3.7 illustrates this point by juxtaposing the results of a computer simulation of a supernova explosion and a Chandra x-ray image of a supernova remnant with images of strong-shock laboratory experiments that capture aspects of the same supernova dynamics.
Those aspects of the supernova dynamics in the explosion phase can be approximated by the inviscid/nondiffusive equations for compressible hydrodynamics, namely, the Euler equations. Two systems will exhibit similar evolution if the dimensionless Euler number, Eu=L/τ(ρ/p)1/2, with L and τ the characteristic length and time scale, and ρ and p the density and pressure, is the same in the two systems. For example, the simulated supernova illustrated in Figure 3.7(a) and the laser experiment illustrated in Figure 3.7(b) differ in spatial scale by 13 to 14 orders of magnitude and 11 orders of magnitude in time. If both are at sufficiently high Reynolds number, Peclet number, and Mach number and if they have similar Euler numbers, important aspects of these two disparate systems will dynamically evolve in a similar fashion.
Several types of HED facilities allow strong shocks to be created and studied. For example, there is a long history of using gas guns, essentially sophisticated, high-tech “gun barrels,” for studying strong-shock physics issues. Shock strengths of up to 4 to 5 Mbar (4–5×1011 Pa) are possible by this technique. An alternate way to generate strong shocks is to use magnetic-pinch facilities, of which the Z-machine is the largest, to accelerate flyer plates (without producing shock waves) to velocities

FIGURE 3.7 Results of a computer simulation of supernova explosion (a) and a Chandra x-ray image of a supernova remnant (b) with images of strong-shock laboratory experiments that reproduce aspects of the same supernova dynamics, (c) and (d). SOURCES: Images (a) courtesy of NASA, the Chandra X-Ray Observatory Center, Smithsonian Astrophysical Observatory; (b) K.Kifonidis, Max-Planck-Institut fuer Astrophysik; (c) K.Budil, Lawrence Livermore National Laboratory; and (d) reprinted, with permission, from J.Grun, J.Stamper, C.Manka, J.Resnick, R.Burris, J.Crawford, and B.H.Ripin, 1991, “Instability of Taylor-Sedov Blast Waves Propagating Through a Uniform Gas,” Phys. Rev. Lett. 66:2738–2741, copyright 1991 by the American Physical Society.
of 10 to 20 km/s. The flyer plate then impacts onto samples, triggering shocks of strengths that can exceed 10 Mbar. Planned Z-machine refurbishments and upgrades (turning Z into ZR) will enable both high peak current and tailored current pulse shape. Pressures up to 3 Mbar in liquid deuterium, 15 Mbar in Al, and over 40 Mbar in most high-Z materials will be possible using flyer plates. High-power laser facilities offer the means to reach the highest pressures, albeit over smaller sample sizes and shorter measurement durations. Planar shocks of 50 Mbar, or more, are possible on the OMEGA laser. At the NIF this number will extend into the hundreds of megabars, perhaps even as high as 1 Gbar.
Radiative Hydrodynamics
Very strong shocks and very high Mach number flows invariably enter the regime of coupled radiative hydrodynamics. Indeed, perhaps one of the defining features of HED facilities is their ability to create and probe a wide variety of radiative-hydrodynamic conditions. As discussed in Chapter 2, radiative hydrodynamics is very prevalent in astrophysics. Colliding galaxies, supernovae, and hypersonic jets of particles streaming out of accreting black holes all glow profusely due to radiative hydrodynamics. At extreme temperatures, the matter becomes radiation-dominated, meaning that the pressure from the radiation itself completely overwhelms all other sources of pressure. This is the situation thought to exist in the vicinity of accreting neutron stars and black holes. Theoretical models and computer simulations for radiative hydrodynamic systems abound, but they suffer from large uncertainties due to the complexity of the physics involved and the lack of experimental checkpoints. The field of high energy density physics and astrophysics would benefit greatly from testbed laboratory data in relevant regimes of coupled radiation hydrodynamics.
Over the past 15 years, examples of radiative shock experiments have been demonstrated on a number of HED facilities around the world, including both lasers and magnetic pinch facilities. Strong shocks have been driven into low-density targets of gas or foam, and the radiative characteristics of the shocks measured. An example of a strongly radiative, cylindrical shock from Z is shown in Figure 3.8 (right-hand image), juxtaposed with the glowing shocked circumstellar nebula of Supernova 1987A remnant (Figure 3.8, left-hand image). In dimensionless terms, these two radiative shocks—one in SNR1987A in the Large Magellanic Cloud, our second-nearest neighbor galaxy, and the other at Sandia National Laboratories in Albuquerque—occupy a very similar parameter space in radiative hydrodynamics. In both cases, the shocks are strong, Ma=vshock/csound≫1, and the radiative cooling time is short compared to a characteristic hydrodynamic time, χ=τrad/τhydro≪1.
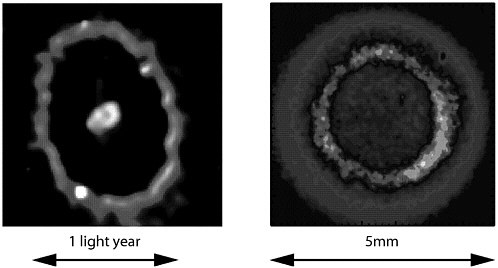
FIGURE 3.8 An example of a strongly radiative, cylindrical shock from Z is shown (right), juxtaposed with the glowing shocked circumstellar nebula of Supernova 1987A remnant (left). Courtesy of (left) P.Garnavich, Harvard-Smithsonian Center for Astrophysics and NASA; and (right) J.Bailey, Sandia National Laboratories.
It may also be possible to experimentally create conditions of radiation-dominated hydrodynamics and turbulence relevant to the vicinities of accreting neutron stars and black holes. This potential is only starting to be explored, but the extraordinary ability to focus macroscopic amounts of energy into microscopic volumes in nanosecond and even picosecond time intervals make this possibility fertile for consideration. It has already been shown on the ultraintense, ultra-short-pulse lasers that temperatures well into the relativistic regime (T>1 MeV) are achievable.
High-Mach-Number Jets
High-Mach-number jets arise in a number of research areas, such as combustion, aerodynamics, fusion research, climatology, and defense research. In astrophysics, high-Mach-number jets and even relativistic jets are at the center of several fundamental unsolved problems, such as how stars form and what drives active galactic nuclei (AGN). An example of a protostellar astrophysical jet is shown in Figure 3.9(a).
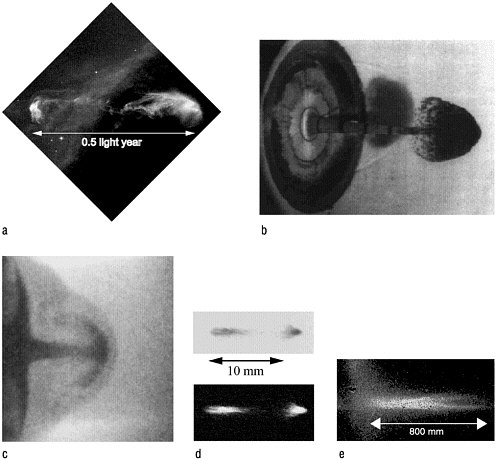
FIGURE 3.9 Examples of high-Mach-number jets: (a) Hubble Space Telescope image of a protostellar astrophysical jet (HH 47); (b) an Mjet~30 jet explosively driven from a conical liner of Cu; (c) laser light converted to an x-ray drive that “imploded” a solid cylindrical pin of Al; the free end of the Al pin was mounted flush against a reservoir of plastic; (d) radiatively cooled jets at Imperial College Z-pinch; and (e) radiatively cooled jets at the Nova laser. SOURCES: Images (a) courtesy of Space Telescope Science Institute and NASA; (b) reprinted, with permission, from L.L.Shaw, S.A.Muelder, D.W.Baum, and K.A.Winer, 1994, “Hypervelocity Explosive-Driven Metal Jet in Air,” Phys. Fluids 6(9):S10, copyright 1994 by the American Institute of Physics; (c) reprinted, with permission, from J.M.Foster, B.H. Wilde, P.A.Rosen, T.S.Perry, M.Fell, M.J.Edwards, B.F.Lasinski, R.E.Turner, and M.L.Gittings, 2002, “Supersonic Jet and Shock Interactions,” Phys. Plasmas 9:2251–2263, copyright 2002 by the American Institute of Physics; (d) courtesy of S.Lebedev, Imperial College London; (e) reprinted, with permission, from D.R.Farley, K.G.Estabrook, S.G.Glendinning, S.H.Glenzer, B.A.Remington, K.Shigemori, J.M.Stone, R.J.Wallace, G.B.Zimmerman, and J.A.Harte, 1999, “Radiative Jet Experiments of Astrophysical Interest Using Intense Lasers,” Phys. Rev. Lett. 83:1982–1985, copyright 1999 by the American Physical Society.
In the laboratory, high-Mach-number jets can be generated in a variety of ways, and under an even wider variety of extreme conditions, as illustrated in Figures 3.9(b) through 3.9(e). For example, the Majet~30 jet [where jet Mach number is defined as Majet=vjet/cs(jet), with cs(jet) being the speed of sound] shown in Figure 3.9(b) is explosively driven from a conical liner of copper (Cu). This jet of Cu is thought to be in the solid state, meaning that the temperature of the jet is below the melt temperature of Cu. Experiments on high-Mach-number, hydrodynamic jets and radiatively collapsing jets have also been demonstrated both on lasers and on pulsed-power facilities. In the case of the high-Mach-number hydrodynamic jets (Figure 3.9(c)), the laser light was converted to an x-ray drive, which “imploded” a solid cylindrical pin of aluminum (Al). The free end of the Al pin was mounted flush against a reservoir of plastic (CH). The high pressure imploded Al plasma jets out into the CH reservoir, forming an Majet≈3 hydrodynamic jet.
In the case of the radiative jets (Figure 3.9(e)), a conical surface of Au was directly illuminated for 100 ps with high-intensity (~3×1015 W/cm2) laser light. The hot, high-velocity ablated plasma “implodes” onto the cone axis and jets outward from the cone at ~700 km/s. Due to the high initial temperatures, kT~1 keV, the Au plasma very rapidly radiatively cools itself, triggering a radiative collapse over a ~1/2-ns interval. Due to the radiative cooling, the sound speed in the Au drops, raising the jet Mach number to 50 or more. An x-ray image in emission from this experiment is shown in Figure 3.9(e). An experiment done on a magnetic pinch machine generated a similar radiatively cooled jet, as shown in Figure 3.9(d). In this case, the spatial and temporal scales are over an order of magnitude larger.
Ablation Front Hydrodynamics
Another unique regime accessible on HED facilities is ablation front dynamics. In such a setting, intense radiation bathes a surface, causing ablation or photoevaporation. The absorbing layers become hot and vaporize, in response to which a strong-shock compression wave is launched into the sample. This is the fundamental dynamics of inertial confinement fusion, where millimeter-scale capsules are imploded by this ablation pressure at the capsule surface (see Figure 3.1). Such an ablation front is hydrodynamically unstable, and any surface imperfections grow, due to the Rayleigh-Taylor instability. An example of such a hydrodynamic instability experiment in planar geometry is shown in Figure 3.10(b), and a spherical version of this type of experiment is shown in Figure 3.10(c). A particularly impressive example of ablation front dynamics can be found in astrophysics in radiatively driven molecular clouds. The most notable example here is the Eagle Nebula in M16, otherwise referred to as the Pillars of Creation (Figure 3.10(a)). Here, radiation incident on the dense cloud surface from two nearby bright young UV stars triggers

FIGURE 3.10 Ablation front hydrodymanics: (a) the Eagle Nebula in M16, otherwise referred to as the Pillars of Creation; (b, c) x-ray radiography of hydrodynamic instability experiments in (b) planar and (c) spherical geometry. These images show a spherical capsule imploded with a thermal x-ray drive on the Nova laser. The capsules had preimposed ripples imposed on their outer surfaces, to study the hydrodynamic instabilities relevant to ICF capsule implosions in convergent geometry. SOURCES: Images (a) courtesy of NASA; (b) S.Obenshain, U.S. Naval Research Laboratory; (c) reprinted, with permission, from S.G.Glendinning, J.Colvin, S.Haan, D.H.Kalantar, O.L.Landen, M.M.Marinak, B.A.Remington, R.Wallace, C.Cherfils, N.Dague, L.Divol, D.Galmiche, and A.L.Richard, 2000, “Ablation Front Rayleigh-Taylor Growth Experiments in Spherically Convergent Geometry,” Phys. Plasmas, 7:2033–2039, copyright 2000 by the American Institute of Physics.
photoevaporation or ablation pressure on the cloud surface. This shock compresses the cloud and subsequently accelerates it away from the stars. Theoretical considerations show that several aspects of this radiative dynamic can be scaled to the laboratory for close-up scrutiny.
APPLICATIONS
Besides their fundamental interest and their relevance to astrophysics, laboratory HED plasmas have several important applications. Although not discussed in this report, much of laboratory HED progress to date has been spurred by the relevance of HED plasmas to the nation’s nuclear weapons stockpile. In this section, some of the many other applications of HED physics to science and society are described.
Inertial Confinement Fusion
The first goal of inertial confinement fusion (ICF) research is controlled laboratory implosion of fusionable material to a condition of ignition and propagating burn. A further goal of this research is the production of safe, reliable energy in quantities suitable for practical commercial application (inertial fusion energy) by igniting a succession of fusion fuel capsules.
Inertial confinement fusion relies on inertia to confine fusionable material, usually a mixture of deuterium and tritium (DT), for a time long enough for a significant number of fusion reactions to occur. Matter compressed by laser-, x-ray-, or ion-beam-driven ablation can be considered to be a high energy density plasma for essentially all phases of the process from earliest compression, through energy production from fusion reactions, through replete, extinguishing burn.
The canonical ICF implosion scenario is that of central hot spot ignition, in which a hollow DT sphere is symmetrically imploded to a density (ρ)×radius (R) (areal density) of 0.3 g/cm2 and a temperature (kT) of order 10 keV. In the limit of radial symmetry, success (propagating burn, i.e., spread of DT fusion reactions to the fuel surrounding the central hot spot) is predicted for a wide range of driver-capsule configurations.
The two most commonly envisioned central hot spot systems are direct and indirect drive ICF. In direct drive ICF, the driving beams, usually high-intensity (1015 W/cm2) lasers of short wavelength light (0.35 to 0.25 µm), directly irradiate a spherical capsule surface. As the surface is heated, matter blows off (ablates) and the capsule implodes, accelerating the compressed hollow sphere walls inward to high final velocities (3×107 cm/s). For indirect drive ICF, the process is similar, with laser light replaced by a spatially uniform bath of x rays (wavelength ~0.1 µm), character-
ized by an effective blackbody temperature of hundreds of electronvolts. The x rays are produced and contained in a spherical or cylindrical can, a hohlraum, that is fabricated of high-atomic-number (Z) metals. Drivers used to generate the hohlraum x rays include lasers, Z-pinches, and beams of heavy ions.
It is generally agreed that the following five criteria determine a successful ICF implosion, each with outstanding issues and active research:
-
A sufficient amount of driver energy must be transferred to the shell. Plasma instabilities in the shell corona can inhibit uniform, efficient coupling of driver energy into the target.
-
The imploded capsule must be sufficiently dense for fusion conditions to be achievable with laboratory-scale drivers. Considerable research in equation-of-state, opacity, and other processes is required to be able to quantify this criterion.
-
The implosion must be sufficiently symmetric at length scales long relative to the shell thicknesses for the generation of a well-formed hot spot that will create a DT fusion “spark” at the center.
-
The shell must be sufficiently stable to the short wavelength Rayleigh-Taylor instability to confine the core gas to full compression in order for ignition conditions to be achieved. This instability, which is seeded by all of the small-scale imperfections of the driving beams and shell surface and mass, is the subject of intense ongoing research.
-
The pellet must reach a condition of sufficient ρR and T for alpha-particle-driven ignition of the hot spot and the surrounding fuel (propagating burn) to occur.
As with many systems with well-defined postulates, the relaxation of one criterion can sometimes lead to most interesting alternate systems. In the case of ICF, completely relaxing the fourth criterion has led to the idea of fast ignition. In fast ignition, the ρR for ignition is first achieved with standard drivers and capsules that range from spherical shells to hemispheres of webbed foams. The ignition beam will then be generated from high-intensity, collimated electrons or ions that result from petawatt laser-matter interaction. Thus, the fast ignitor concept reduces the requirements on the compression phase of an inertial confinement target. Any ICF driver could, in principle, be used to assemble the compressed fuel. In addition, driver configurations that would not lead to ICF ignition because of stability or other limitations may produce viable drivers. While compression is relatively easy and has already been demonstrated to a significant level in the laboratory, being able to couple the ignitor “spark” to the compressed fuel is far from determined. The introduction of this concept in the early 1990s, along with the development of very high
intensity (~1018 W/cm2 or higher), high-energy (~1 kJ) laser drivers, has resulted in significant active research on very high intensity laser matter and laser plasma interactions.
The body of inertial fusion energy (IFE) research takes as its starting point a single successful ICF implosion with high gain (energy>100 times driving energy) and seeks to develop from this a system that is commercially viable. For laboratory systems that produce a few hundred megajoules or more of nuclear energy per shot, this means successful ICF implosions at ~1-Hz repetition rates for several years without substantial plant maintenance.
A number of requirements devolve from this highest-level specification: inexpensive mass production of well-characterized targets; high-repetition-rate drivers; a target chamber that will survive years of intense implosions/explosions and also produce reliable, useful heat from the ICF-generated neutrons; a sufficiently accurate target injection system; and some way to deal with radioactive by-products and waste.
Inertial fusion energy systems are postulated for every ICF driver. Ongoing IFE research is focused on the development of full systems that can simultaneously meet all of the requirements for success. The goal of the IFE effort is an end-to-end inertial fusion energy system in a demonstration test phase in the United States within the next few decades.
Spin-offs
The development of high-power lasers for high energy density applications has other applications as well. For example, the class of pump lasers under development for extreme ultraviolet applications would make a significant contribution to turbulence research. Diode-pumped Nd:YAG lasers with ~0.25 to 0.4 J/pulse at 532 nm, 0.5 to 1 kHz, with good beam quality, would permit three-dimensional measurements of fully developed turbulence. These measurements would use laser-induced fluorescence and other laser-diagnostic techniques, coupled with high-resolution, 1,0002 pixels or better, low-noise, digital-imaging detectors operating at framing rates that match the laser pulse repetition rate. These specifications are dictated by dynamic turbulence scaling at a minimum Reynolds number of 104, signal-to-noise considerations for candidate laser diagnostic techniques, and data-acquisition considerations. Such experiments provide significant exploration capabilities in the three-dimensional structure of turbulence, data for subgrid-scale modeling, as well as validation data for the next-generation turbulence numerical simulations.
Other relevant spin-offs for HED include laser machining (manufacture of precision holes for the automotive and airline industries, microelectromechanical systems (MEMS) manufacture, for example), directed-energy lasers for national
security (both the technology and lethality). There are also numerous technology spin-offs in the area of diagnostics, lasers, target fabrication, and pulse power.
Extreme Ultraviolet Lithography
Extreme ultraviolet lithography has been identified by International SEMATECH as the leading candidate technology for next-generation lithography. The light sources for these tools consist of a laser interacting with a cold xenon gas jet to produce a high energy density plasma that generates broadband line radiation. The conversion efficiency of the radiated power within the bandwidth of the multilayer optical components centered at 13.4 nm is on the order of 1 percent, and the source power requirement on the first collection optic is nominally 100 W. Typical parameters of the radiating plasma source are ne~1022 cm−3, Te~50 eV, I=1012 W cm−2 today, and up to an order-of-magnitude performance increment is planned. However, at ~0.1 Mbar with little evidence of collective effects, extreme ultraviolet lithography is very much at the low end of the high energy density plasma spectrum.
This technology has huge market potential and could prove to be the most significant potential commercial application of high energy density plasmas. The present SEMATECH roadmap calls for market insertion of extreme ultraviolet lithography around 2006, following the 157-nm fluorine dimer source systems, which are presently under active development, to expose chips with 50- to 70-nm critical dimension features. Because of excellent depth of focus, extreme ultraviolet lithography is a multigeneration technology that will carry lithography to the “end of silicon,” with respect to achievable minimum smaller feature size. The technology also benefits from ties to existing optical lithography infrastructure and techniques.
Applications to Medical Physics
Researchers are beginning to explore the application of ultrashort-pulse lasers to surgery. Typical operating parameters are 0.1 to 1 TW/pulse and intensities from 0.03 to 3×1016 W/cm2-pulse at millijoule energy levels. Under these conditions, small-volume, high-temperature, short-duration plasmas are created from flash heating of material via multiphoton absorption of the intense laser light. Plasma heating times are so short that photo ablation dominates over thermal ablation. Tissue removal appears insensitive to tissue color and exhibits very little if any collateral damage owing to plasma durations shorter than thermal conduction times. Typical ablation rates are 1 micron/pulse, thus placing a premium on operating lasers at high average power (1 to 10 W) in order to achieve removal rates in the millimeter per second range. In combination with plasma luminescence spectroscopy, this technology can be used to selectively ablate tissue of different mineral content—for
example, ablating bone away from sensitive nerves. Medical applications include delicate spinal surgery, tumor resection from brain tissue, corneal sculpting, bone debulking, and hard plaque removal in totally occluded arteries. The development of low-cost, high average power lasers will be required in order to fully exploit the technology for medical applications.
Medical applications of short-pulse lasers include the following:
-
Femtosecond surgery. This surgery is based on the absence of collateral damage when femtosecond lasers ablate tissues. Currently more than 10,000 patients a year in the United States are having photorefractive surgery. A spin-off company from the Center for Ultrafast Optical Science at the University of Michigan has developed the tool to perform this surgery.
-
Precision radiography. Because the light can be focused on an extremely small spot, a micrometer x-ray source can be created. The small spot size acts as a point source and facilitates radiography with magnification. This could be important for mammography and small animal studies.
-
Hadron therapy. High-energy protons that can be created with high-intensity lasers can be used as an inexpensive alternative to the cyclotron for hadron therapy.
OPPORTUNITIES FOR GENERATING AND UTILIZING HIGH ENERGY DENSITY CONDITIONS IN THE LABORATORY
As described in previous sections, many existing and near-term facilities are or soon will be available to produce high energy density conditions in the laboratory. This section describes some of the technologies and capabilities associated with these systems and notes some of the research opportunities afforded by them
Existing and future National Nuclear Security Administration high energy density facilities, such as high-power lasers and magnetic pinch generators, are uniquely capable of probing the behavior of macroscopic collections of matter under extreme conditions. The distinguishing feature of these facilities is their ability to probe macroscopic collections of matter under extreme conditions of compression, deformation, and flow. Conditions relevant to nuclear weapons research, inertial confinement fusion, the center of Earth, the core of Jupiter, the interior of stars, and possibly even the vicinity of black holes can be recreated in the laboratory. The time intervals over which such extreme conditions can be maintained are necessarily brief, typically being measured in billionths of seconds (10−9 s). With high temporal-and spatial-resolution detectors and diagnostics designed to operate in this short-pulse mode, high-fidelity measurements of the states and properties of matter under these conditions can be made. The following subsections list a few high-impact
physics opportunities that present themselves for pursuit on existing or future HED facilities, briefly pointing out their significance.
High Energy Density Physics Opportunities in the Laboratory
Transition to Turbulence
Turbulence conjures up images of chaotic, unpredictable flows where disorder is the rule, not the exception. Yet, in steady-state flows, phenomenological rules and descriptions for turbulent flows have been developed. A key unsolved question, however, is the transition to turbulence. How do flows “decide” whether they should be turbulent, and over what time span does this transition occur. The high energy density facilities are quite unique in their ability to create high-Reynolds-number flows, over a time span covering their transition to turbulence.
Radiation-Dominated Hydrodynamics
It seems plausible that dynamically evolving flows, and even turbulent flows, could be created on HED facilities such as ZR (the proposed refurbished version of the Z-machine at Sandia National Laboratories) or NIF, in which the pressure is dominated by radiation pressure, Pr. To achieve such conditions requires high temperatures, so that Pr=4σTr4/3c≫neTe+niTi, where σ is the Stefan-Boltzmann constant and c is the speed of light in vacuum. Such a flow extended into the turbulent regime would access the conditions that might be found in accretion disks surrounding massive black holes. Another radiation-dominated flow of broad scientific interest is an ablation front. Referred to as a photoevaporation front in astrophysics, the necessary conditions are thought to prevail in the star-forming regions of dense molecular clouds.
There is a potential to combine a megajoule-class laser or magnetic pinch facility with laser heating by a petawatt-class laser to produce matter in a condition of radiation-dominated hydrodynamics. In this regime, the radiation pressure greatly exceeds the thermal particle pressure. Qualitatively unique dynamics can evolve in this regime, depending on the density, temperature, and optical depth of the plasma. Such radiation-dominated hydrodynamics may have relevance to black hole and neutron star accretion dynamics, supernova shocks, and possibly even the dynamics of the early universe in the radiation-dominated epochs.
Dense, Degenerate Plasmas
The properties of dense, Fermi degenerate matter is of broad scientific interest, especially in geophysics and planetary physics, as well as from a fundamental
materials perspective. The interiors of planets are at high pressure and are often Fermi degenerate. Understanding the behavior of iron and iron-like alloys at pressures as high as 3 Mbar or more (T~7000 to 8000 K) is relevant to the structure of Earth’s interior and the formation of Earth’s magnetic field. In the giant gaseous planets and extrasolar planets, the equation of state of H and that of He are the most important quantities. The challenge is to develop the techniques to be able to make equation-of-state measurements to 1 percent accuracy if laboratory experiments are to be able to affect the models of planetary interiors and planetary formation. For example, in the 1- to 10-Mbar pressure regime (T=103 to 104 K), the structure of planetary interiors depends rather sensitively on the details of how H transitions to the metallic state. This in turn affects whether the cores of gas giant planets such as Jupiter are thought to be a rocky solid or gaseous, a distinction that differentiates two standard planetary formation models (the planetessimal accretion model and the gravitational collapse model). At extreme compressions, matter can be squeezed so close together that the electronic orbitals become grossly distorted, leading to pressure ionization. Theories of this regime are highly uncertain, and measurements would be of great benefit.
If matter is pushed even more tightly together, the electron fluid becomes dominated entirely by the degeneracy pressure, whereas the ions still behave classically. These are the theoretical conditions for the well-known “one-component plasma.” Probing this regime tests fundamental theories of very dense, highly degenerate matter. In particular, whether a first-order plasma phase transition exists could be conclusively settled. Also, in a system with a mixture of H and He gases that is compressed until the H becomes metallic, one may be able to determine whether He comes out of solution, a phenomena that is of critical importance to planetary interior models.
Nuclear Burn
If the inertial confinement fusion programs succeed in generating a standard ignition capsule testbed, controlled tests of quantities that affect the nuclear burn wave will become possible. Questions pertaining to the burn dynamics of Type Ia supernovae (SNe) may be accessible, such as how the burn transitions from a deflagration to a detonation, and what role hydrodynamic mixing plays in this. Perhaps even more fundamental is observing nuclear reactions under the appropriate conditions of density, temperature, and electronic screening. Experiments here might allow important thermonuclear reaction rates to be measured under conditions in which plasma screening effects have variable levels of significance: weak screening (Γ≪1), the intermediate regime (Γ≈1), strong screening (Γ≫1), and the
pycnonuclear regime (Γ>Γsolid≈178). (The corresponding densities and temperatures to these regimes are shown in Figure 3.3.) This would have major impact on stellar modeling. Here, Γ is the ratio of the coulomb interaction energy between neighboring particles and the thermal energy per particle (kT).
Opacities
Measurements of the opacities of materials under scaled conditions relevant to Type Ia SNe would be highly beneficial. The question of the rate of expansion of the universe relies upon “standard candle” observations of Type Ia supernovae light curves. The shape-brightness correction is thought to be due to opacities of dense, high-temperature plasma. Some of these assumptions could be checked by direct experimental measurements. Measuring the opacity of iron at conditions relevant to the core of the Sun would check the theoretical models of continuum lowering, as well as determine a fundamental parameter that controls the heat flow within the Sun and hence affects the internal structure of the Sun. With a combination of convergent implosion geometry and ultraintense short-pulse heating beams, it may be possible to create matter at 100 g/cm3 at 1-keV temperature in order to study its opacity, with relevance to the opacity at the center of the Sun.
High-Pressure Physics
New states and phases of matter can be created and probed at ultrahigh pressures, using carefully shaped compression pulses and time-resolved lattice structure diagnostics. The time scale for specific phase transitions can also be measured. The time scale for specific phase transitions, which can vary from subpicosecond to tens of nanoseconds or longer, can also be measured.
With carefully shaped drive pulses, it may be possible to accelerate solid-state microflyer plates to velocities in excess of 100 km/s. This would open up new regimes of impact and microcratering studies of possible relevance to shielding Earth-orbiting satellites from space debris, as well as cratering theories.
Parametric Instabilities
At high intensities, a whole variety of parametric instabilities can be investigated (stimulated Raman scattering, stimulated Brillouin scattering, and so on) in large-scale plasmas at high temperatures. These are discussed in Chapter 4.
Generating High Energy Density Conditions in the Laboratory
Laser-Produced Plasmas
High-energy lasers have been one of the workhorses of high energy density experiments. They typically have a flexibility that allows a wide range of high energy density conditions to be achieved. The pulse duration, focal spot size, energy, and, in the case of multiple beam systems, the pointing can all be varied to optimize the experimental conditions. Lasers with energies of even a few joules and nanosecond durations can produce high energy density conditions in targets. Multibeam lasers with energies in the kilojoule range have been used to produce extremely high energy density conditions. Many of these conditions are described in this chapter, with astrophysically relevant high energy density conditions described in Chapter 2. The largest currently operating laser system is the 60-beam, 30-kJ 0.35-µm wavelength OMEGA laser system at the University of Rochester. It can be configured in many ways, allowing a wide variety of high energy density research to be carried out. This research includes inertial confinement fusion (as described above) in both direct- and indirect-drive modes, strongly shocked materials, the evolution of hydrodynamic instabilities relevant to both laboratory and astrophysical plasmas, material opacities under extreme conditions, and generation of intense x-ray radiation sources. The National Ignition Facility, currently under construction at Lawrence Livermore National Laboratory, will extend the available laser energy range by almost 2 orders of magnitude, producing ~2 MJ of laser energy in 192 beams at 0.35-µm wavelength. It will maintain the flexibility afforded by a multibeam laser system but will generate much more extreme conditions than currently possible, including the possibility of obtaining fusion ignition.
Lasers couple their energy to a solid material or a plasma primarily through the collisional and/or noncollisional absorption of the light in the coronal region of the plasma. Electromagnetic radiation cannot propagate at electron densities higher than its wavelength-dependent critical electron density (ncr~1021 cm−3/λ2 µm2). This is a relatively low density region at the edge of a target. Thermal conduction carries the laser energy into the higher density regions. The next step depends on whether the goal is to directly couple the laser energy to the target (direct drive) or to convert the energy to x rays that are subsequently coupled to the target (indirect drive). In direct drive, the hot, high-density region expands (ablates), causing a pressure to be applied to the remaining target material. This ablation process is similar to the process that drives a rocket, acting through the conservation of momentum. This pressure can launch shock waves into the material, bringing it to higher pressure and/or accelerating it. In indirect drive, the laser energy is converted to x rays, often in an x-ray oven (hohlraum) that produces nearly blackbody radiation
with temperatures up to hundreds of electronvolts. This x-ray bath can subsequently couple to a target, producing shock waves and acceleration through the ablation process. The x rays can also be used directly to study the opacity of materials under extreme conditions.
Lasers with energies of a few joules or more can also be used to create x-ray lasers that provide a further extension of the HED physics conditions that can be created.
High-Intensity Laser-Matter Interactions
A second class of lasers for HED physics experiments is short-pulse high-intensity laser systems. “Short pulse” typically means a few picoseconds or less and “high intensity” is typically 1016 W/cm2 or greater. Intensities as high as ~1021 W/cm2 have been achieved. The number of such systems has expanded rapidly in the past decade and a half since the revolutionary development of chirped pulse amplification in the late 1980s. This technique involves stretching a pulse, amplifying it, and recompressing it to its original pulse duration. This increases the peak power and focused intensity by many orders of magnitude. There are many applications of this technology (see Chapter 4), from studies of relativistic effects in laser-plasma interactions, to the generation of intense x-ray, electron, and ion sources for both radiography and fusion applications, to the generation of electron-positron pairs and the generation of radioactive isotopes. These lasers can be coupled to other technologies, such as electron beams, to generate short bursts of Compton scattered x rays, or to a high energy density system (laser or pulsed power) to study the fast ignition approach to inertial confinement fusion, or to a target for ultrafast x-ray radiography.
The shortest pulse durations available are just a few optical cycles (~10−15 s), giving interaction times comparable to the fastest material response time. The largest high-intensity laser system was the recently decommissioned Nova petawatt-laser facility at Lawrence Livermore National Laboratory, which produced ~600 J in 0.45 ps and peak intensities of a few times 1020 W/cm2. More modest energy systems (up to tens of joules) that can approach similar intensity levels can be built on a few optical tables (4×8 feet), making them suitable for university-scale research.
There are unique regimes of high energy density plasma physics that can be accessed in experiments on very modest-scale, short-pulse lasers, with laser energies as low as tens of millijoules per pulse. This remarkable trick involves laser interactions with a jet of atomic or molecular clusters. An intense laser interacting with this gas of clusters sees localized regions of solid density in which the laser absorption is nearly 100 percent. This absorption causes ionization within the cluster and the ejection of electrons, which triggers a “coulomb explosion” owing to the close-
packed configuration of positively charged ions. These localized pockets of plasma can be very hot due to the heating from a laser plasma resonance. The hot balls of plasma expand rapidly until they encounter their cluster neighbors, which are also exploding. The end result can be the production of multikiloelectronvolt ions, high-Mach-number blast waves, and even nuclear fusion. A whole range of unique high energy density physics can thus be accessed with tabletop lasers suitable for university-scale laboratories.
Pulsed-Power Plasmas
“Pulsed power generators” deliver 105~107 A to low-impedance loads generating high energy density conditions in a number of different ways. The energy can be directly deposited in a plasma; it can be used to compress a preexisting plasma; it can be converted into extremely large fluxes of x rays that subsequently are coupled to a target material; or the magnetic energy can be used directly to launch shock waves in materials or to launch flyer plates that create high energy density conditions in a target. The largest pulsed-power systems can deliver energies orders of magnitude larger than the energy in current laser systems (though NIF will be comparable), allowing much larger samples to be driven to high energy density conditions. The pulse durations are typically 10−8 to 10−7 s, an order of magnitude or more longer than high-energy laser systems. Because of the longer durations of the pulsed-power sources, peak pressures of tens of megabars are currently achieved with both types of HED drivers (with higher pressures expected to be available on the NIF). While the pressures and peak radiation temperatures (200~300 eV) are comparable (though slightly lower on pulsed-power devices), a pulsed-power device can deliver more energy to a larger target.
High Energy Density Z-pinches
A Z-pinch is a technique that converts the energy of the electrical pulse in a pulsed-power system to kinetic energy in a magnetically driven implosion of a plasma column. This thereby generates a hot, dense “Z-pinch” plasma that, in the case of the Z-machine at Sandia National Laboratories, Albuquerque, produces x-ray pulses <10 ns long with >1 MJ total radiated energy. The pinch is caused by a self-generated j×B body force due to the axial current density, j, flowing in the plasma and the resulting self-magnetic field, B, that is in the azimuthal direction in a cylindrical plasma column, and this force compresses the plasma to the axis. The spatial-scale size of the resulting plasma is determined by the initial density and spatial scale of the load. Application of pulsed-power systems to dense Z-pinches and the achievement of high energy density conditions have occurred with single
exploding wire experiments, cylindrical wire-arrays, and gas-puff Z-pinch experiments. Even the lowest density of these plasmas, that generated by a gas-puff Z-pinch, presents unique opportunities for generating strongly radiative plasmas that have important applications. For example, at low enough density for collisional effects to be negligible, important opacities and photoionization rates that are very relevant to astrophysics can be measured directly.
A gas-puff Z-pinch starts with a centimeter-scale cylindrical gas puff at a pressure in the 102 to 103 pascal (Pa) range, in order to break down quickly when the pulsed-power generator voltage pulse reaches it. To be effective as a radiator, the gas that is imploded by the j×B force has a high atomic number, which increases the bremsstrahlung yield of the collisions between electrons and ions that are responsible for the x-ray radiation. With a 100- to 200-ns, ~1-MA current source, a few centimeters diameter gas-puff Z-pinch can be imploded to ~1 mm diameter and reach an ion density 20 to 50 times the original gas density. The ohmic and compressional work heats the electrons and generates highly charged ions. Electron densities exceeding 1020/cm3 and temperatures of several hundred electronvolts are achieved in plasmas that are a few centimeters long and ~1 mm diameter.
Plasmas generated from fine metal wires and insulating fibers (including fibers made of frozen hydrogen) start from solid density and are exploded by the high-current pulse to form a rapidly expanding plasma. The wire or fiber size is chosen to be small enough that the plasma formation phase takes only a few nanoseconds. As the material expands, the current (and self-magnetic field) is still rising, and the expansion can be arrested by the increasing j×B force. Current-driven instabilities limit the lifetime of all Z-pinch experiments, preventing long-time magnetic confinement of these dense Z-pinch plasmas.
In the case of the metal wire Z-pinch, radiation can play a major role in allowing the plasma to collapse to a small radius. For example, starting with a single fine wire (~5 to 50 µm initial diameter), the implosion starts with a plasma that has expanded to ~1 mm diameter, and the density can become high enough in the imploded plasma that radiation losses can exceed the rate of ohmic and compressional heating. In that case, as the plasma implodes, it cools ever more rapidly as well as increasing in density, which further increases the radiation loss. This process is known as radiative collapse. Single-wire Z-pinches can, in fact, form micropinches, that is, very small spots at random locations along the wire length where intense kiloelectronvolt x-ray emission occurs, most likely a result of the “sausage instability.” The final radius and density reached in those micropinches may be determined at least in part by radiative cooling of the imploding plasma until it becomes optically thick to its own emission.
The conditions in exploding wire micropinches have not, in fact, been directly measured in single-wire Z-pinch experiments, because the location of a micropinch
is not known in advance. However, the X-pinch configuration, in which two wires cross and touch at a single point, guarantees that a micropinch will be generated in a known location—close to the original cross point of the wires, where the sum of the current in the two wires acts on the plasma. These micropinches are typically in the ion density range 1020 to 1022/cm3, or even higher, and have electron temperatures of a few hundred electronvolts to 2 keV. Their size is much smaller than 1 mm, and may be of the order of 1 µm. The plasma remains hot and dense for about 50 to 80 ps.
The gas-puff and single metal wire (or crossed wire) Z-pinches are efficient radiation sources, and can be used for fundamental studies of atomic processes in dense plasmas. They can also be used to validate atomic physics computer codes and radiative-MHD codes. In addition, the X-pinch can be used for x-ray radiography.
A large number of wires in the form of a cylindrical wire-array is necessary to drive a hohlraum to a radiation temperature of interest for inertial confinement fusion or other high energy density science applications requiring megajoules of x rays. This is partly because a high-current pulsed-power generator does not couple energy efficiently into a small number of wires. In addition, arrays with large numbers (300 or even more) of wires have been found to generate a shorter, more powerful radiation pulse upon imploding to the axis than do arrays with a smaller number of wires. The Z-machine at Sandia, with 20-MA peak current and a rise time of about 100 ns, has produced plasmas that radiate close to 2 MJ in less than 10 ns starting from several hundred tungsten (W) wires. Hohlraum temperatures of 150 to 200 eV have been produced. The plasma itself in such a test is estimated to be ~1020 ions/cm3 when assembled on axis, with the W ions being ≥50 times ionized.
Ultrahigh Magnetic Pressures from Pulsed Power
With 20 MA carried in a 1-cm-diameter cylindrical structure, the magnetic field will be 4 MG (400 T), corresponding to a magnetic pressure of 0.6 Mbar (6×105 atm). By using rectangular conductors instead of cylinders and displacing the inner one so that only one face is close to the external conductor, the current per unit width can be increased to close to 7 MA/cm in 1.5-cm-wide conductors. The resultant 800-T magnetic field produces magnetic pressures of up to 2.5×1011 P (or 2.5 Mbar). This high pressure can be used directly to launch flyer plates for isentropic compression experiments, or to drive strong-shock waves into materials.
Magnetized Target Physics
Another way that pulsed power can be used to generate high energy density conditions is by compressing a preformed, magnetically confined plasma structure.
In one example, the magnetized target plasma is a field-reversed plasma configuration (FRC) that is produced within a solid, cylindrical conductor. That conductor can be imploded by a high current on a microsecond time scale. The intent is that a stable plasma configuration, the FRC, can benefit from the enormous pressures that can be exerted by a high current without being driven unstable if the current is carried by a collapsing metal conductor instead of the plasma itself. If the inner surface of the imploding conductor remains solid, it will also remain stable. The plasma pressure that can be achieved can substantially exceed the applied magnetic-field pressure as follows. The external magnetic pressure drives the liner inward, converting the magnetic-field energy into kinetic energy of the liner. The liner accelerates inward until the compression of the FRC is sufficient to produce a back-pressure that approximately equals the drive pressure, at which time the liner begins to slow down. It comes to a halt only after all of its inward kinetic energy has been converted to magnetic plus thermal energy of the FRC, taking into account energy loss due to magnetic-field diffusion into the liner. Estimates using reasonable choices of physical parameters, including magnetic and particle diffusion coefficients, suggest that a 30-MA-current driver, such as the Atlas facility, could achieve 1-cm-radius, several-centimeters-long plasmas at 1 Mbar (1011 P). This corresponds to a density of 6×1019/cm3 at 10-keV temperature, a very interesting plasma for producing deuterium-tritium fusion reactions.
Intense Ion Beams (Heavy and Light)
Intense ion beams can be produced using pulsed-power accelerators or using conventional accelerator technology. The former case is limited to 10 to 20 MeV by the nature of the technology, and high power density is achieved by focusing a beam that might be produced at the mega-ampere level. Intensities achieved using PBFA II Particle Beam Accelerator at Sandia National Laboratories, Albuquerque, before it was converted to the Z-machine exceeded 1012 W/cm2. Heavy ion beams can be generated from conventional ion sources at the ~1-MeV and ~1-A level for about a few microseconds. The power density can then be increased by merging separately generated heavy ion beams, acceleration to the gigaelectronvolt level, and axial bunching. It is expected to be possible to produce beams at 1 to 10 GeV and 104 A for ~10 ns and to focus them to ~1015 W/cm2, as is required for inertial confinement fusion, but the proof-of-principle experiments for this are still in the planning stage (as discussed earlier in this chapter).
Because the range of ions at the few megaelectronvolts per nucleon energy level is in the micron range, intense ion beams can be used for many of the same materials science applications for which nanosecond lasers are used, including generating ablation plasmas and driving shock waves into solid materials. Ions have
an advantage in that they are absorbed in the volume of a material, penetrating to a depth that is determined by the target material and their energy, whereas a laser interacts with the surface of a solid target and depends on the state of the plasma on the surface.
The beams themselves are high energy density plasmas in their own right. Intense light ion beams must be very close to charge neutral or they cannot propagate, and so they are essentially neutral plasmas moving at high speed in the laboratory frame. A proton beam at 4 MeV and 1 MA/cm2 represents an energy density of about 3×108 J/m3, although it is largely in directed kinetic energy rather than thermal energy. In a heavy ion beam entering an inertial confinement fusion target chamber, the kinetic energy of the individual ions may be high enough that charge neutrality is not a necessity for propagation. In that case, the kinetic energy density and the energy densities in the electric and magnetic fields are large. For lead ions at 1 GeV and 100 kA focused to 1 cm2, the kinetic energy density is ~1010 J/m3.
Intense ion beams and their associated self-magnetic fields can also be used in magnetic confinement fusion to generate favorable magnetic confinement configurations.
High-Energy Electron Beams
Similar to ion beams, electron beams can be produced using pulsed-power generators or conventional accelerators. Because the space-charge limit is much higher for electrons than ions in an accelerating gap (by the square root of the ion-to-electron mass ratio), pulsed-power generators can produce electron beams reaching 106 A/cm2 or even more in a 1-MV accelerating gap with self-focusing caused by anode plasma production. Such beams exceed the so-called Alfvén current limit and cannot propagate in vacuum. Because of their large electrostatic and magnetic energy densities, they must be charge and current neutralized. Intense electron beams can, in principle, be used to deliver energy some distance away from the source if their self-fields are neutralized. In an intense electron beam (e.g., 1 MA at 1 to 20 MeV), the self-fields assure that there is as much or more kinetic energy in transverse motion as there is in the direction of propagation. Surface ablation (and shock wave generation) can easily be achieved in solid density materials by focused intense electron beams.
High energy density electron beams can also be produced by conventional accelerator technologies, such as the 50-GeV electron beam produced at the Stanford Linear Accelerator Center. The interaction of these beams with plasmas is described in Chapter 4.
X-ray Lasers
X-ray lasers provide an example of using one type of high energy density system to produce another that can then be used in high energy density experiments. Energy deposited in a plasma by a laser or pulsed-power source leads to a population inversion resulting in x-ray lasing at wavelengths as short as ~40 Å. Because of their short wavelength, soft x-ray lasers have a significantly higher critical electron density (see the subsection above on “Laser-Produced Plasmas”) than conventional visible or UV lasers have, and they can propagate through high-density plasmas. They can also be used to volumetrically heat solid materials and high-density plasmas.
Recent developments in soft x-ray laser research have been directed toward utilizing higher-power technology to reduce the pumping source size to tabletop dimensions. Collisional excitation schemes have been very successful and have been adopted worldwide. These include fast capillary discharges and picosecond laser-driven transient schemes. These x-ray lasers operate in the high-efficiency saturation regime with typical pulse durations in the picosecond to nanosecond regime, output energies of tens to hundreds of microjoules, and high repetition rates (a few hertz to 1 shot every few minutes). These x-ray sources have peak powers and brightnesses higher than those of present-day synchrotrons but much lower repetitions rates. They have been used for many applications, including the interferometry of millimeter-scale dense plasmas, characterization of optics, and imaging of biological samples. Future directions include the development of ultrafast x-ray laser schemes operating below 50 Å and the determination of material properties under extreme conditions. The main advantages of these x-ray lasers are their scalability to shorter wavelengths with higher output energy that would allow them to be developed as unique diagnostic tools for picosecond interferometry of other high energy density conditions such as those that the NIF will generate.
Gas Guns and Diamond Anvils
A fundamental goal of geophysics is a basic understanding of the structure and dynamics of Earth’s interior in general and of the generation of Earth’s magnetic field in particular. Somewhere embedded in the churning, twisting flow patterns of the core-mantle system lies the cause for the dramatic reversals of the dipole geomagnetic field, as shown in paleomagnetic reversal records. The energy source for this dynamo is a combination of heat flow out of the solid inner core and the enhanced rotation rate of the inner core compared to the mantle, which is separated from the inner core by a liquid outer core. The result of this inner turmoil at Earth’s surface is as dramatic as the turmoil itself: plate tectonics, earthquakes, volcanoes, and—perhaps triggered by the magnetic-field reversals—possible global climate changes.
Much progress has been made in understanding Earth’s interior magnetorotational dynamics. With the advent of supercomputers, three-dimensional MHD models have begun to reproduce some of the dynamics thought to exist deep below our feet. These simulations have even predicted magnetic-field reversals. Such large-scale three-dimensional MHD code simulations, however, can only be as reliable as the input information, such as the material properties—material strength, phase, melt point, viscosity, and conductivity—at very high pressures (0.1 to 3.6 Mbar), high temperatures (1000 to 6000 K), and high densities.
This leads to the obvious question: How can the properties of the relevant materials be ascertained at such extreme conditions? The answers to questions such as these come from high-pressure laboratory experiments. There are several experimental avenues to such high-pressure conditions. The first, the diamond anvil cell, is the “workhorse” for establishing the phase diagrams of materials at pressures up to several megabars. These devices are essentially a high-tech device that compresses thin samples (10 to 100 µm) between two flat diamond anvil surfaces. When combined with a bright source of x rays in the kiloelectronvolt energy range, such as that supplied by a synchrotron light source, this setup is an extremely powerful tool for determining the phases of materials.
Experiments on diamond anvil cells are static, with strain rates of <10−6 s−1. Alternate experimental approaches include gas guns or powder guns. These devices are essentially a large-scale gun barrel. When detonated, a macroscopic “bullet” or sabot is accelerated out the end, impacting a sample, causing shock compression. This allows the equation of state of the shock-compressed sample to be determined with high accuracy, making gas guns a workhorse for dynamic or Hugoniot equation-of-state measurements. Pressures accessible by gas gun experiments can also reach several megabars.
High explosives are a variation on this theme of dynamic experiments. This technique is not as widely used as gas guns are, owing to lower precision. However, high-explosive-driven integral experiments are possible in a wide variety of geometries. Typical pressures achievable are several hundred kilobars.
Diagnostics for High Energy Density Laboratory Systems
As the technologies to produce high energy density conditions have evolved, so have the abilities to diagnose and understand these conditions. This has included development of (1) advanced diagnostics and (2) target fabrication techniques, as well as (3) advances in numerical simulation capability. These technologies form a triad, without which advances in understanding high energy density physics conditions would be severely limited. A few examples of diagnostic development are
described in this section, and the other two legs of the triad are described in the subsequent sections.
Many of the advanced diagnostic techniques have been developed as part of the inertial confinement fusion program. As described in the beginning of this chapter, short spatial and temporal scales are characteristic of ICF implosions. The need to diagnose these experiments has led to impressive developments, including time-resolved x-ray spectroscopy and imaging at picosecond time scales with multikiloelectronvolt photon energies. Diagnosis of nuclear reaction products includes detailed spectral and temporal measurements of neutron and charged particle spectra from primary, secondary, and tertiary reactions.
For laser and pulsed-power facilities to be attractive to users for high energy density plasma physics experiments, or for secondary experiments using the high energy density plasmas as drivers, the facilities must have excellent diagnostic systems providing information about the plasma conditions as a function of time. The diagnostics needed by a particular user might include experiment-specific instruments as well, such as shock-breakout instruments when a shock wave is generated in a thin plate attached to a high-temperature hohlraum or by the extremely high magnetic pressure that can be produced by the Z-machine. Another diagnostic requirement for experiments involving high-optical-depth materials is imaging with very high energy backlighter x rays (tens of kiloelectronvolts to even megaelectronvolts), to be able to radiographically see through these targets.
Laser Diagnostics
High energy density facilities rely on a large number of diagnostics to understand the laser or pulsed-power system performance, as well as the laser target interactions or pulsed-power system-driven plasma dynamics. Because of the relatively short time scales of interest (a few nanoseconds or less), much of the emphasis has been on the development of high temporal-resolution diagnostics. These include visible and x-ray streak cameras (producing a continuous record) and time-gated imaging detectors (producing two-dimensional information snapshots). The latter can be used to make movies with ~50-ps frame times and ~50-ps resolution (an example is shown in Figure 3.1). For even better time resolution, short-pulse lasers are often used in a pump-probe scheme, in which the interaction is probed with a second laser, the arrival time of which is varied to build up a time-resolved measurement. Any pump-probe technique using ultrafast lasers is sensitive to the exact pulse shape (prepulse and intensity contrast) of the beam.
Imaging of Target Nonuniformities
The evolution of hydrodynamic instabilities is of paramount importance to understanding inertial confinement fusion and high energy density conditions in general. As energy is deposited in a plasma, shock waves can be launched and the system can be accelerated, leading to conditions in which the hydrodynamic motion is unstable. Diagnostic imaging of perturbed, high-density targets allows the evolution of these instabilities to be measured and compared with numerical simulations and theoretical predictions. Constraints are many and varied, with a goal of simultaneously resolving the space and time evolution of the perturbations with time windows, spatial amplitudes, and perturbation wavelengths that are as small as possible. Here an illustrative diagnostic example for hydrodynamic experiments typical of those performed on the OMEGA or NIKE laser is considered. The diagnostic requires the following: fields of view of more than 1 mm, perturbation amplitude modulations that range from 0.25 µm to tens of microns of solid plastic, objects with diameters of 5 µm or less, and precise time gates that are less than 50 ps. The fundamental enabling diagnostic technology that provides imaging of target mass perturbations in these regimes is x-ray backlighting. The flexibility of high energy density drivers allows part of the energy to be used to generate the probing (backlighting) x-ray radiation. Time resolution is obtained with the help of a framing or streak camera as a detector, or by using an ultrafast laser to generate a short x-ray pulse. To compensate for poor spatial resolution of available detectors, high image magnification (about 10× to 20×) is generally used, which, in turn, requires high system throughput. Experiments with thick targets (e.g., 40 to 100 µm of solid plastic) also require a high efficiency of the diagnostics and a high energy of the probing radiation. For any backlighting scheme, there are two other general requirements: (1) small size of the backlighter source and (2) filtration of imaging radiation from the self-emission of the object. The surface brightness of the backlighter must be larger than the object brightness only in the bandwidth of the spectral line being used to image the object. Examples of x-ray imaging and radiography of HED plasmas produced by lasers and pulsed-power machines are shown in Figures 3.7 through 3.10. High-energy petawatt laser systems may allow high-energy x-ray backlighting of thicker samples at higher x-ray photon energies than are possible with current long-pulse laser systems. Directed jets of protons generated when these lasers interact with matter should allow very opaque targets to be radiographically diagnosed.
There are now available a range of imaging systems that couple well to the x-ray backlighting technique, and which meet many of the criteria described above. These include Kirkpatrick-Baez microscopes, gated x-ray pinhole cameras, point projection imaging, and curved-crystal monochromatic imagers.
Nuclear Reaction Diagnostics
The increased availability of high energy density systems has significantly expanded the range of nuclear and charged particle diagnostics that are used to study them. Part of this expansion is due to the larger energy of the high energy density systems, which produce higher nuclear yields, allowing lower cross-section processes to be observed. In the past, ICF implosions were diagnosed with neutron detectors that measured the primary neutron fusion yield (e.g., D+D→He3+n or T+p) and the secondary (two-step) reaction (D+T→He4+n). As the energy coupled into the implosions has increased, a large number of lower probability reactions have begun to be detectable (e.g., the secondary reaction D+He3→He4+p). This has led to the development of a wide array of new neutron and charged particle diagnostics that can provide significantly more information about the target characteristics.
The higher nuclear reaction yields associated with current and future ICF implosions lead to the opportunity to measure astrophysically relevant nuclear reaction rates under conditions that are close to those in astrophysical objects. Nuclear reaction cross-sections are typically measured in beam-target experiments with beam energies of hundreds of kiloelectronvolts or megaelectronvolts. These rates are then extrapolated to the multikiloelectronvolt temperature conditions in stars. Multikiloelectronvolt temperatures are achieved in ICF implosions. The nuclear reaction yields of solar-relevant processes can be measured, providing more accurate reaction rates for stellar processes. An example that may be possible on the OMEGA laser system is to measure the rate of 3He+3He→4He+2p reactions, if the distribution function is sufficiently Maxwellian. The NIF will extend the opportunities for measuring nuclear reaction rates relevant to stellar processes. A particularly intriguing possibility is the potential to use the bursts of 1019 neutrons from the D+T→α+n thermonuclear yield from an igniting ICF capsule to study reactions relevant to the s, p, and r astrophysical nucleosynthesis processes. For example, the neutron flux from an igniting capsule is high enough to drive 10 to 20 percent of dopant nuclei, say 89Y, into excited states via (n,n′) reactions, and trigger multiple step reactions on those excited states with lifetimes >1 ps.
Special Needs for Pulsed-Power System Diagnostics
The diagnostics needed to study the high energy density plasmas made in pulsed-power systems are essentially the same as those used in comparable laser-based experiments, with the additional need to operate in a high-radiation environment. For example, the bremsstrahlung background at the Z-machine can be 106 rads/s as a result of “stray electrons” accelerated in the vacuum feed to the Z-pinch load. In addition, there is the electromagnetic noise generated by the machine, as well as ground motion resulting from the self-closing water switches in
the pulsed-power system. Thus, every diagnostic instrument must be placed as far from the vacuum chamber as possible; it may have to be decoupled from the ground motion, and it must be collimated and shielded as well as possible. This said, the extremely interesting and relatively large-volume plasmas generated by the Z-machine and their many applications to high energy density science place a premium on having a large set of diagnostics in place for users. Although smaller pulsed-power machines produce less troublesome background, they also produce much smaller signals. Therefore, the same care in shielding diagnostics from background x rays and electromagnetic noise is necessary on smaller facilities as on the Z-machine. It is noteworthy that the relativistic electron beams generated by petawatt lasers and high irradiance CO2 lasers can produce large electromagnetic noise pulses that require the same attention to detail in shielding and collimation of detector channels as are required of pulsed-power experiments.
Beam Diagnostics
Intense electron and ion beams generate dense plasmas on surfaces if the deposited energy in a ≤1-µs pulse reaches ~1 kJ/g. Thus, any material placed in the path of such a beam will be rapidly ionized, making it difficult to measure beam properties such as current density and total beam momentum or energy. For example, small apertures in Faraday cups for intense ion beams can be completely blocked by plasma in just a few nanoseconds, and results from a pendulum that is intended to measure the impulse delivered by a beam to a target can be misinterpreted because of the large impulse due to an ablating plasma. The net result is that substantial numerical modeling is often necessary in order to elicit useful information from intense beam diagnostic systems that are straightforward to interpret at more modest energy densities. Beam propagation in a gas or plasma introduces similar problems for direct measurements because, for example, the resulting reverse current induced in the plasma or gas after breakdown can partially or completely eliminate the self-magnetic field of the beam current. Therefore, alternate diagnostic methods must be used to monitor beam properties, such as the intensity of x rays induced in a thin foil as the beam passes through it, for electrons, and nuclear reactions that yield an easily observed reaction product, for ions. Laser-based measurements, including interferometry, laser-induced fluorescence spectroscopy, and laser scattering can provide information on the background plasma and/or the beam.
Advances in Target Fabrication
Target fabrication is an essential enabling technology for high energy density physics. Targets have advanced enormously over the past three decades, not by
slow evolution but in true paradigm shifts from early low-tech endeavors to the sophisticated precision materials of today.
The evolution of high energy density systems, both in energy scale and complexity, together with the evolution of diagnostic capabilities and numerical simulations, has led to a concomitant need for more sophisticated and complex targets. Sophistication and control are needed to fabricate targets capable of supporting the intellectual challenges of high energy density plasmas. The extreme complexity of today’s targets was achieved as a result of multiple breakthroughs in new technologies and materials science. A critically important step in order to create high-quality spherical shells was that of combining two processes. One process involves density-matched microencapsulation via a droplet generator to produce shells with a highly spherical outer surface. The other process involves a decomposable mandrel technique that allows the actual target shell to be coated onto the mandrel (which is then decomposed and removed). The result is a highly spherical shell with a highly uniform wall that is vital so that defects in the target do not dominate implosion dynamics.
Hohlraums have likewise undergone several stepwise progressions in their manufacture, culminating with today’s precision diamond-turning machines that routinely control tolerances to a few microns on complex parts. The ultraprecision characterization of targets continues to evolve with interference microscopy that allows the diameter, wall thickness, and first mode deviations to be measured quickly with modest computing capability. An atomic force microscope traces the shell diameter providing multidimensional quantitative surface analysis for use in simulation codes. Success in the generation of large x-ray fluxes with pulsed-power devices has led to significant advances in the construction of wire arrays and more complicated targets used for equation-of-state studies. The flexibility engendered by high energy density systems has led to even more complicated targets, some that lack any symmetry, others that might be designed to enable multiple backlighting sources, and all requiring extreme precision throughout the manufacturing process.
An important future goal of high energy density physics requiring advances in target fabrication is the production of energy from inertial fusion. Providing billions of precision targets at the low cost needed for energy production will require an intimate understanding of the relevant materials science and additional breakthroughs in the way targets are fabricated. Standardized efficient industrial production technologies must be combined with existing knowledge in the field. An example is the use of fluidized beds to coat hundreds of thousands of targets at once. Initial experiments indicate that one fluidized bed can supply half of the 500,000 targets per day required by a 1,000-MWe power plant. Additional quantum leaps in the way that targets are manufactured will require a continued effort from industry, national laboratories, and universities, each bringing its unique strengths to this
highly challenging field. The high-repetition-rate (driver, targets, and so on) capabilities developed for inertial fusion energy would also be beneficial for many high energy density experiments.
High-Performance Computing
Computational capabilities have been revolutionized in recent years, bringing physical phenomena within the scope of numerical simulation that were out of reach only a few years ago. The Department of Energy’s Advanced Strategic Computing Initiative (ASCI) has played a major and multifaceted role in this revolution, as has the continued evolution of microprocessor and other technologies. High-performance computing today is typified by large parallel platforms with 30 gigaflops (Gflops) of sustained performance. High-speed connections enable centralized visualization systems for tasks ranging from debugging to processing of large database results. With the ability to perform highly resolved, multidimensional computations, advanced scientific computing has become an enabling tool for first-principles explorations of high energy density phenomena. Both theory and experiments now typically rely on numerical simulation that comprises an essential component of more-integrated research programs. Ultimately, inputs from theory, laboratory experiments on equations of state, dynamics, explorations of scaled phenomena, and so on, must be integrated in comprehensive computer simulation codes. These incorporate the physics, hydrodynamics, radiation, and other manifestations of high energy density phenomena, along with appropriate algorithms, and explicit or implicit models, in a software environment that must cater to the multiprocessor environment on which it runs. Numerical simulation can now rightfully be considered as an important component in high energy density science discovery.
Large, multidimensional data sets for and from such simulations require preprocessing before they can serve as inputs, postprocessing to digest the results, and, not least, computer visualization. Both the input data that specify initial and boundary conditions and the output data must also be compared against a host of diagnostic data for validation and other purposes. Ideally, this is an integrated, iterative, closed-loop process, with experiment, simulation, and theory each suggesting the next step(s).
The ever-increasing simulation needs of high energy density physics, discussed elsewhere in this report, suggest the need for an assessment of the necessary improvements and capabilities. Even if Moore’s law persists for the next decade or so, with DOE’s Advanced Strategic Computing Initiative continuing to drive advances at an even greater pace, a number of problems exist that simulations will not be able to completely solve. High-Reynolds-number, radiatively coupled turbulence, in either laboratory or astrophysical environments, for example, is likely to remain beyond
the reach of direct numerical simulation—that is, through a solution of the equations of motion with no approximations—for the foreseeable future. The difficulty arises from the combination of the large required spatial and temporal dynamic range and from the three-dimensional dynamics. Considerable insights can, however, be gleaned from simulations that advance the envelope in this fashion, exploiting increases in computational power with simulations relying on the fewest approximations possible. High energy density simulation codes include advection algorithms for the simulation of shocks and also vortical- and magnetic-field-driven instabilities, equation-of-state models that extend from solid to plasma regimes, and detailed electron and radiation transport and opacity packages that can provide an adequate estimate of the energy transport for the full range of high energy density temperatures and densities. Furthermore, some of these codes model the intense electromagnetic wave/particle interaction of high-intensity beams, from plasma coronal nascence through high-density heating. While no codes include all of these effects simultaneously, relevant parts of high energy density physics problems can be simulated, yielding results with predictive value. Such simulations advance our understanding of complex phenomena, yield insights that are fundamental in interpreting and designing experiments, and provide data for new theories and models.
Hardware and computation algorithm advances are required in order to continue to address these problems. Given a span of phenomena in a typical high energy density problem, simulations become tractable as more physics is modeled rather than simulated at every point in space and time. While in a way this is always the case—we rely on continuum and other approximations to simulate hydrodynamics—the complexity of high energy density problems requires an increase in the level of modeling and abstraction. Physics-based subgrid-scale and other phenomenological models that permit a reduction in the number of grid points on which the dynamics must be solved can potentially achieve this. Such models will rely on theoretical advances and special, well-characterized experiments that probe dynamics at small scales and validate the simulations that have incorporated the subgrid-scale models.

















































