4
METHODS, THEORIES, AND TOOLS
Various tools are commonly used to aid designers, and several additional theories offer more analytically rigorous support to engineering designers. Concurrent engineering may be the most practical method to improve the design process, and other common tools are used to obtain input from stakeholders in the design process (the Pugh Method, Quality Function Deployment, Decision Matrix techniques, and the Analytical Hierarchy Process). These tools incorporate relatively high levels of subjective judgment. An additional set of tools address variability, quality, and uncertainty in the design process (Projected Latent Structure, the Taguchi method, and Six Sigma). These tools are more analytical and are typically coupled to the processes used to produce products. Still other tools are used to generate alternatives for designers (artificial intelligence and TRIZ). Design theories also exist (Dym’s, Suh’s Axiomatic, Yoshikawa’s, and a Mathematical Framework) that are less widely used but offer more rigorous analytical bases. Finally, certain other tools are used primarily in the fields of management science and economics, and are being explored in current research for applicability to decision making in engineering design.
This review is illustrative rather than exhaustive given the voluminous existing literature about each tool and theory. Series of individuals and groups are devoted to research and application for each separate tool or theory mentioned here. Subjective comments on the applicability or limitations of the tools and theories are of course based only on the committee’s knowledge of the tools and of the relevant literature.
CONCURRENT ENGINEERING
Concurrent engineering is defined as “a systematic approach to the integrated, simultaneous design of products and their related processes, including manufacture and support. This approach is intended to cause the developers, from the outset, to consider all elements of the product life cycle from conception through disposal, including quality, cost, schedule, and user requirements” (Winner et al, 1988). According to Dean and Unal (1992) concurrent engineering consists of getting the right people together at the right time to identify and resolve design problems. Concurrent engineering includes designing for assembly, availability, cost, customer satisfaction, maintainability, manageability, manufacturability, operability, performance, quality, risk, safety, schedule, social acceptability, and all other attributes of the product Table 4–1 highlights the contrast between concurrent engineering and conventional engineering design.
The concurrent engineering environment has the following characteristics:
-
Reduced cycle time
-
Overlapping of functional activities
-
Collaboration in functional decisions
-
Concurrent evolution of system and Component decisions
-
Critical sequencing
Concurrent engineering strives to meet the need for continually shorter product development cycles and the need to represent the inputs of all stakeholders. Decision-making tools and processes continue to evolve to support making the best decisions in this environment. In the concurrent environment functional activities such as engineering and manufacturing are done simultaneously. This is contrasted with a traditional serial process in which the design team finishes its work before the drafting department prepares and releases the drawings, at which time manufacturing starts. Because of the overlapping of functional activities, cycle times may be greatly reduced and decisions become highly interdependent. This environment causes many decisions to be made without complete information, which has led to the development of methods to share product requirements, to assess risks effectively, and to develop abatement plans. System and component trades must be made concurrently, which requires effective methods for flow-down and tracking of requirements, as well as flow up and tracking of status. The tight schedules resulting from reduced cycle times require disciplined scheduling and monitoring of key decisions as well as management of the required sequencing and the downstream impact of design decisions. Cross-functional decision making requires integrated, highly reliable, and readily accessible databases.
Table 4–1 Comparison Between Concurrent Versus Linear (Serial) Engineering
|
Concurrent Engineering |
Linear (Serial) Engineering |
|
Parallel design of products and processes |
Sequential design |
|
Multifunctional team |
Independent designer |
|
Concurrent consideration of product life cycle |
Sequential consideration of product life cycle |
|
Total quality management tools |
Conventional engineering tools |
|
All stakeholder inputs |
Customer and supplier not involved |
The tools and methods being developed to support this environment, most of which are computer based, can be categorized as follows:
-
LAN- and Web-based management tools. Often an individual decision (say, material selection for a component) is dependent on a higher level system requirement (say, operation in a corrosive environment). Without good management tools the individual decision maker may be unaware of the requirement These management tools usually include a function for informing the individual decision maker of multi-level critical decision dates and status. An informative interconnected data management system is essential
-
Tools and processes for assessing risks and developing risk abatement plans. Because of compressed cycles and overlapping functional activities, decisions must be made with incomplete information or data. For example, manufacturing of components may begin before the final product drawing is complete and issued. There is inherent risk in starting manufacturing prior to drawing release as a change in definition may result in rework or scrap. Tools need to be developed to aid the decision maker to assess the risks and develop suitable abatement plans. Work with design structure matrices is a good start in this area. When these situations are routine occurrences, as with the above example, standard abatement plans may be developed.
-
Automated analysis tools for rapid evaluation of alternatives. The accuracy of decisions and reduction of risk can be greatly improved by the quantification of alternatives. Many tools exist or are under development to automate or Modify analysis to improve cycle time and efficiency. Parametric Modeling, Design of Experiments, and Automatic Finite Element Meshing are examples.
-
Data-sharing tools. In a cross-functional concurrent decision making environment with compressed cycle times, data must be readily available to all decision makers. Data must be accurate, timely, complete, easily accessed, and in many cases, configuration controlled. The data must be informative, not merely numerous. An excellent example of a shared database is the use of three-dimensional solid models for distributing geometric information for drawing, tooling, manufacturing, and customer appraisal analysis.
As decisions are made in the concurrent environment, the impact of each decision on the product is evaluated. This makes the concurrent engineering environment not only contextual but also a fundamental part of the decision process. As a process rather than a decision tool, it requires a wide variety of supporting tools as described above and in the following sections. Through continual feedback, the concurrent environment decision process facilitates evaluation and modification of decisions whenever undesirable or unexpected consequences result.
TOOLS TO OBTAIN STAKEHOLDER INPUT
THE PUGH METHOD
Stuart Pugh, University of Strathclyde, is the author of two books discussing the problems of engineering design (Pugh, 1990, 1996). The second book (Pugh, 1996) is largely a compendium of his many papers.
Pugh (1990) developed the product development process and a set of discipline-independent methodologies to carry out the process, such as customer surveys, the product design specification document, and the method of controlled convergence. In the Pugh method a decision matrix is prepared with columns to identify design concepts (Variant) and the rows to represent criteria. A design team chooses both concepts and criteria. One of the column concepts is chosen as a datum against which all others are to be judged. In the matrix cells for each row criteria a plus (+), zero (0), or minus (−) sign is then used to indicate whether the concept is better, equivalent, or less than that of the datum. For each concept the number of plus and minus signs is noted and the best concept is selected. Omitted concepts with unique plus cells are especially studied to provide insight. New concepts (variants or designs) are now formed, criteria modified and added, a new datum selected, and the process repeated. The process requires continuous elaboration until the datum column becomes uniquely best. This variant initiates the final detailed design process.
Pugh argues against ranking or weighting of either concepts or criteria beyond the simple plus (+), zero (0), and minus (−). In defense of his matrix approach to engineering design Pugh states, “The matrix does not make the decisions: it is simply a procedure for controlled convergence onto the best possible concept and is not composed for absolutes in the mathematical sense; the decisions remain with the user” (Pugh, 1990). The committed agrees with the method’s creator that his method should not be used to make decisions.
QUALITY FUNCTION DEPLOYMENT
Quality Function Deployment (QFD) has its Origins in Japan in the late 1960s, during an era when Japanese industries broke from their post-World War II mode of product development through imitation and moved on to product development based on originality (Akao, 1997). It provides a synthesis of the concepts and tools required to translate customer aspirations into the final technical and manufacturing activities needed to produce a quality product. QFD is a matrix management tool meant to translate the factor termed the “voice of the customer” into items that can be measured, assessed, and improved. It is particularly useful in finding gaps in a developing program and offering opportunities for new ideas to enter a design activity.
Don Clausing of the Massachusetts Institute of Technology is largely responsible for the introduction of QFD methodology to U.S. industry in the early 1980s. The blending of the ideas of QFD with those of Pugh’s Total Design theory is often called EQFD (Enhanced QFD) (Clausing and Pugh, 1991).
Quality Function Deployment is used to identify critical customer attributes and to create a specific link between customer attributes and design parameters. Matrices are used to organize information to help marketers and design engineers Visualize and answer three primary questions:
-
What attributes are critical to our customers?
-
What design parameters are important in meeting those customer attributes?
-
What should the design parameter targets be for the new design?
QFD constructs, in a fashion similar to Pugh, an evaluation matrix at each stage of product development both to display relevant states of knowledge and to provide a mechanism for decisions. This matrix correlates the identified customer needs called “the whats” (rows) to the engineering specifications called “the hows” (columns). Ideally, a Cross-functional team made up of members from the core functions in product development should develop the matrix. The matrix rows are usually descriptive verbalizations of the customer’s wants. The matrix columns are more likely to be quantitative measures of engineering requirements. The engineering measures are frequently correlated, or represent incompatible desiderata, and an additional triangular array is often placed atop the matrix displaying these associations. The schema, often called the “House of Quality,” is illustrated in Figure 4–1.
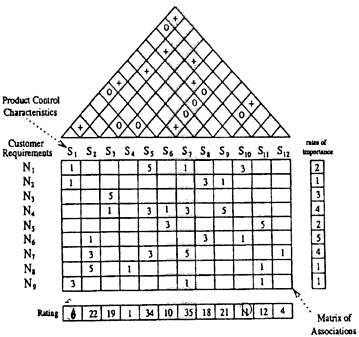
Figure 4–1 The House of Quality. Source: Carriere and Finster (1989).
The first step in building a House of Quality is to construct an evaluation matrix indicating how each engineering specification affects each customer need. Many cells of the matrix may be empty (blank), while others will contain a score testifying to the importance of the row-column association. Information on technical difficulties and cost can also be displayed. An additional step is to construct the “roof” for the house, a triangular matrix displaying relationships among engineering specifications. For instance, specifications for take-off weight for a commercial aircraft will strongly affect the required take-off distance. The roof of the House of Quality also provides a good indicator
of design trade-offs to consider in the future. Additional information matrices may be attached to the “house.” For example, information on customer perceptions of competing products and competitive benchmark data can provide “wings” and “cellars.”
The essential motivation for constructing a House of Quality schema is to provide a viewer, new or old to the design problem, a quick and thorough appraisal of its scope. It is an aid to the decision-making process.
The House of Quality can be used as a stand-alone tool to generate answers to a particular development problem. Alternatively, it can be applied in a more complex system in which a series of decision tools are used. The procedure is illustrated in Figure 4–2.
Figure 4–2 A cascade of evaluation matrices. Procedure adapted from Hauser and Clausing (1988).
The use of evaluation matrices is only a part of a larger philosophy implied by QFD. QFD also emphasizes the importance of teamwork by diverse experts. Moreover, customers are not viewed solely as those who will use the final product but also as those at the receiving end of each stage of the creation of the final product.
DECISION MATRIX TECHNIQUES
Decision matrix techniques are used to define attributes, weight them, and appropriately sum the weighted attributes to give a relative ranking among designs. An example of the framework for such a process is shown in Figure 4–3.
The advantages of this method are as follows:
-
The method encourages team interaction (causes the design team to consider attributes of a variety of potential solutions and their relative importance and thus a good way to help calibrate the team).
-
Analysis can be performed relatively quickly.
-
The method can identify non-viable design variant options and remove them from further consideration.
Disadvantages of this method are the following:
-
Criteria may have interdependencies.
-
Risk must be overtly addressed as an additional criterion.
-
Subjective weighting often reflects the design team’s opinion rather than the customer’s view.
-
It is not a stand-alone decision tool.
-
Sometimes it is used merely to rationalize decisions.
|
|
|
Concept Variants |
|||||
|
|
|
Concept 1 |
Concept 2 |
Concept 3 |
|||
|
Criteria |
Weights |
Value |
WV |
Value |
WV |
Value |
WV |
|
Criterion 1 |
|
|
|
|
|
|
|
|
Criterion 2 |
|
|
|
|
|
|
|
|
Criterion 3 |
|
|
|
|
|
|
|
|
Criterion 4 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sum: |
|
|
|
|
|
|
|
|
Weighted Sum: |
|
|
|
|
|
|
|
Figure 4–3 General format of the decision matrix.
The decision matrix is prepared using technical or economic criteria (or both). When all row criteria are not be considered equally important they are weighted individually. For every column concept (variant) each criterion is assigned a value, typically on a scale of 1 to 10. The final weighted value for all matrix cells is found by multiplying the criteria weights by their corresponding design variant value. The sums of both the values and the weighted values are then found for each concept variant.
The “Weighted Sum of Attributes” decision matrix shown in Figure 4–4 is an example typical of frequently encountered design decisions in which a variety of concepts are viable but vary considerably in their ability to meet conflicting requirements. In the example, for instance, all the concepts will provide attachment, but only one has loose parts. To help reach a decision, as only one concept will be used, the decision matrix shown in Figure 4–4 was prepared. As is often the case with this tool, (1) the weighted sums are not highly differentiated; (2) the weighting changes the decision relative to the unweighted sums, thus demonstrating the need for careful selection of the weights; and (3) the values often have to be normalized to prevent the dominance of one key requirement due to its high values. In the current example, if the parts count were in the hundreds of parts, its value would dwarf other considerations, unless of course, it was assigned a very low weight.
Figure 4–4 Decision matrix for access door attachment.
This example does not indicate a clear winner, merely that one choice (Quick-Nuts) can be eliminated, provided the weightings and assigned values are reasonable. The matrix evaluation
nevertheless can still be a useful tool. Further consideration of the weightings and playing “what if” will at least allow the decision maker to understand which requirements have been emphasized in the selection of a concept and which requirements may need careful attention in detail design. As part of playing “what if,” sensitivity studies can also be conducted by perturbing the values with varying ranges or probability distribution functions. The “Weighted Sum of Attributes” decision matrix is an important decision tool, but its limitations need to be well understood by the decision maker.
ANALYTIC HIERARCHY PROCESS
The Analytic Hierarchy Process (AHP) is a methodology for multi-criteria analysis and decision making developed by Thomas L.Saaty (1980, 1987). It can help decision makers to:
-
examine a complex problem with a number of possible solutions,
-
evaluate and prioritize alternatives, and
-
organize the information and judgments used in decision making.
The analytic hierarchy process allows the relative independent judgments made by people to be used in a more formalized decision making process. The basic idea assumes it is much easier for a person to say a car is much bigger than a motorcycle than it is to say how many times it is larger, or even exactly what is meant by “larger.” It is similar in approach to the Pugh method of employing plus (+), zero (0), and minus (−) judgments. The word “hierarchy” in the name reflects the notion that these judgments may be made at several levels and then combined to provide an overall evaluation. While proponents of the process claim it has many uses even beyond decision making, the focus of this discussion is on its use as a decision aid.
At each level of the hierarchy the process proceeds by having the user establish rough pair-wise comparisons between attributes by using such comparatives as “more important” and “much more important.” These pair-wise comparisons, often redundant, are used to produce a relative weighting of the various attributes. This process is repeated at the next level in a manner demonstrated by example to provide an overall evaluation.
A general form of a hierarchical model of a decision problem is a pyramid with a broad overall objective at the highest level. Lower levels list the criteria and respective subcriteria used to choose among alternatives. At the lowest level are the alternatives to be evaluated.
Consider the example of selecting an automobile to purchase. Presume the attributes of interest are comfort, performance, and safety. At the highest level of the hierarchy the user would be asked to judge, for example, whether comfort is more important than performance, equivalent to performance, or less important than performance. Then a similar set of comparisons would be made between performance and safety, and finally, another set of comparisons between comfort and safety. These would be manipulated to provide the relative weights, usually in the form of percentages, to be assigned to comfort, performance, and safety in purchasing the car.
The next step is to address which car best meets the criteria. Suppose three cars are under consideration: A, B, and C. The user would be asked to compare car A with car B with respect to comfort; then A to C with respect to comfort; and finally B to C with respect to comfort. After the averaging process, these comparisons would result in the relative percentage weightings of the three cars with respect to comfort. The same judgments would then be made with respect to performance. Is A much better than B with respect to performance, equivalent to B in performance, etc. Then A would be compared to C, and B would be compared to C with respect to the same performance attribute. After the averaging process, the relative Weights of the three cars would be obtained with respect to performance. Finally, the same procedure would be carried out for safety. Now it can be said for car A what percentage of the values for comfort, performance, and safety it should receive; and the same computation can be done for cars B and C. For each car, multiplying the car’s
percentage of each value attribute by the percentage the value represents with respect to a desirable car and summing overall attributes will provide for each car the percentage of overall value attributable to it. In one case, car A could have 55 percent of total value, car B could have 30 percent of total value, and car C could have 15 percent of total value. Proponents of the process would say this is an argument for purchasing car A.
The procedure, as can be seen, is very easy to perform because it uses only simple judgments. The problem is determining the strength of the recommendation of car A because it is highest on this scale. Additional difficulties occur when a large number of alternatives require paired comparisons, because k alternatives require k (k−1)/2 pairs. Moreover, care should be taken to ensure that some of the paired comparisons do not contradict each other.
The axiomatic structure of this process does not guarantee the alternative with the highest rating will be the most preferred alternative. Unfortunately, it can be shown that the addition of a new alternative may change the ranking of existing alternatives, a property seen as undesirable in a decision process. The analytic hierarchy process has difficulty with uncertainty, which it can handle only in an approximate way. The process therefore provides no basis for valuing the elimination or reduction of uncertainty.
The main advantage of the analytic hierarchy process is ease of understanding and application. It may have real value in making decisions with robust influence factors, where there is no possibility of a major loss and where the complete set of alternatives is known a priori.
The difficulty with the analytic hierarchy process, in addition to the theoretical features mentioned above, is that it cannot answer the questions necessary to build confidence in the selection of an alternative. The very simplicity of the process limits its ability to answer hard questions.
TOOLS AND METHODS TO ADDRESS VARIABILITY, QUALITY, AND UNCERTAINTY
Once the decisions have been made and product design concept finalized, the next steps are to translate the concept to reality. This section deals with decision-making tools, which are methods to address the quality of the design process, to address the variability in the process, and to convert the concept to final product. The general process of making decisions is greatly affected by the context (see Figure 2–1) in which the decisions are made. Design decision making in the context of variation can be conceptualized as shown in Figure 4–5.
The context of variation in Figure 4–5, similarly to Figure 2–1, has been segmented by the categories of input, output, controllable design parameters, and uncontrollable (noise) parameters. In Figure 4–5, the context is related to variation; therefore, the above four categories provide a context for decisions in which the variation needs to be considered in decision making.
While there may be variation in the input requirements, the primary variation to be considered is in the design, environmental, and manufacturing parameters. An example of variation in a design parameter is the seal clearance in a shaft. Examples of variation in environmental and manufacturing parameters are ranges in the line voltage a product Will see in use or differences in the ability of machines to meld tolerances. As a result of such Variations, the performance of individual product units will vary with respect to the design target. If the output variation is too great or the mean is not appropriately centered near the design target, then some of the units will not perform acceptably. The decision process must adequately consider variation in design, manufacturing, and environmental parameters to ensure products delivered to the user will perform within specified limits of design intent.
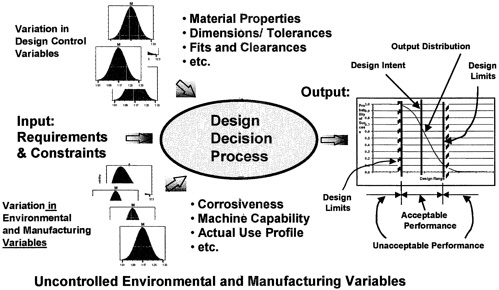
Figure 4–5 Decision making in the context of variation.
The consideration given to variation in the design process differs depending on whether the variation is in a design-controlled parameter or in manufacturing- and environmental- uncontrolled parameters. In the context of design decision making for products, the design parameters in Figure 4–5 are controllable whereas the environmental and manufacturing parameters are for the most part uncontrollable or at least contain an element of random variation (noise). The strategy in the design decision process for controllable design parameters is to use analysis, including statistical tools such as “Design of Experiments,” to select values (settings) for these parameters such that the product performance is within acceptable limits. The noise variation of environmental and manufacturing parameters cannot be changed or controlled by selection of parameter values as can be done with design parameters. The variation in environmental and manufacturing parameters either is known or can be measured and included in sensitivity analysis of design parameters. Experience has shown that inclusion of environmental and manufacturing noise variation in design decisions is crucial for products to consistently meet the design intent.
In summary, design decision making in the context of variation can significantly contribute to the success of a product from the standpoint of customer satisfaction (market share) and economic viability (profit to business). Employing “Design of Experiments” or similar methods enables one to rapidly quantify product performance and economic viability across a broad design space. Including variability or noise parameters in the design and decision process, as illustrated in Figure 4–5, enables the designer to quantify the sensitivity of the product to variation and determine the probability of success for achieving objectives relative to design limits. Additionally, for those controllable noise variables, product performance and cost trade-offs can be quantified in terms of design intent and probability of success. In total then, the process conceptualized in Figure 4–5 enables design decision making based not only on deterministic assessment but also on the inherent, real-world characteristics of product design.
PROJECTED LATENT STRUCTURE
Also called Partial Least Squares or PLS, Projected Latent Structure is a method for constructing predictive models when controllable variables are many and highly redundant. The emphasis is on predicting the responses and not necessarily on trying to understand the underlying relationships among the variables. PLS is not usually appropriate for screening out factors with a negligible effect on the response. However, when prediction is the goal and there is no practical need to limit the number of measured factors, PLS can be a useful tool (Tobias, 1995). The original mathematics of PLS is the work of Herman Wold (Wold, 1985). Svante Wold and B.Kowalski (Wold, 1978; Beebe and Kowalski, 1987) are given credit for establishing the field of “chemometrics,” based largely upon PLS methodology. In chemometrics the X factors (Controllable variables) may include the many spectroscopic measures taken on samples drawn from a chemical process, along with associated measures of temperatures, pressures, concentration, and flow rates. The Y responses (the behavior of other variables) in turn may represent the mass, volume, viscosity, density, flow rates, and other quality measures on intermediates and final products, once again gathered across many samples. The objective of PLS is to analyze the data sets X and Y in the hope of discovering one or more signs of structure (low dimensional linear relations) while recognizing X and Y may both have structural aspects unrelated to one another. The idea of PLS is to extract latent factors, accounting for as much variation as possible while modeling the response well. PLS has been successfully applied in the chemical process industries. The opportunity to explore applications of PLS to the design and assembly of hardware appears unexploited to date.
TAGUCHI METHOD
In Japan in the early 1960s, Genichi Taguchi began an introduction of statistical patterns of experiments (the fractional factorial, orthogonal arrays, and response surface “experimental design”) as aides in the design and manufacture of products (Taguchi, 1988). Several concepts were involved.
-
Quality should be measured by the deviation from a specified target value, rather than by conformance to preset tolerance limits.
-
A defined loss function should be established to provide a financial measure of customer dissatisfaction with a product’s performance as it deviates from a target value.
-
Process parameters are not constants and their intrinsic variability will be reflected in the variability of the product.
-
The product user’s environment adds further variability challenges to quality performance.
-
Engineering design must provide a robust product that is on target and simultaneously insensitive to variability arising from both the process and the environment.
Taguchi argues for the application of statistical methods throughout the entire engineering design process, from product concept to customer usage. He was among the first to emphasize the importance of statistical planning and analysis of experiments to identify and measure sources of variability and sensitivity to assist in resolving the problems of design engineering. Of particular note is Taguchi’s development of parameter design wherein non-linearity in response is used to decrease the sensitivity of that design to a given level of noise variability in manufacturing and use. Taguchi’s great contribution to the practice of engineering design is his emphasis on the need to study the sensitivity of product responses to variability in both manufacturing and environmental factors (Ross, 1996).
SIX SIGMA
In statistics the Greek letter sigma is used to identify the standard deviation, as a measure of the variability of measurements. When measurements are reasonably approximated by a normal distribution located on target, then the interval of target plus or minus two sigma will contain approximately 95 percent of all the measurements. If this interval also defines product specifications, then 5 percent of the product will be defective. When the specification limits are set at target plus or minus six sigma, this results in only 3.4 defects per million outputs. However, the terminology “six sigma” has come to mean far more than a simple counting of defects. It now identifies an entire quality culture of strategies, statistics, and tools for improving a company’s bottom line (Pyzdek, 2001).
The Six Sigma concept was introduced by Mikel Harry at Motorola in the 1980s. Many other corporate giants, including Texas Instruments and General Electric, have adopted it since then. The tools utilized in Six Sigma include problem statement development, brainstorming, histograms, fish-bone diagrams, process mapping, measurement-systems analysis, graphical analysis, capability analysis, hypothesis testing, regression analysis, analysis of variance, supply-chain management, design of experiments, statistical process control, and failure-mode-effects analysis.
METHODS AND TOOLS FOR GENERATING ALTERNATIVES
Generating alternatives to meet the requirements of a product is an inherent part of the design process. In the simplest form a single designer can Consult design guides for past practices and select a reasonable option. More creative designers could examine other fields to adopt new ideas or imagine a novel solution to the problem.
Group practice, in its simplest form, includes brainstorming to generate design alternatives. Newer tools draw on a range of computational capability to enhance the generation of options. Generally, the techniques can identify alternatives by employing a very large set of data using several methods or tools, possibly including artificial intelligence. A few of these techniques are summarized here.
DESIGN INFORMATION SYSTEMS, SUPPORT SYSTEMS, AND ENVIRONMENTS
Design decision making involves more than methods and tools for addressing decision events. Decisions usually occur in information-rich environments involving a range of stakeholders and disciplines. A wide variety of efforts have been developed aimed at supporting designers to make decisions in such rich contexts.
These efforts usually are pursued under the rubric of decision support, often involving many of the methods and tools discussed elsewhere in this report, but also frequently involving various levels of artificial intelligence. Gero and Sudweeks (1996, 1998), in two recent proceedings of the biennial International Conference on Artificial Intelligence in Design, provide a broad view of the many efforts in this area, which include design processes (decision-driven process models, cognitive theories of design decision making), knowledge management (representation, acquisition, sharing), decision support (reasoning, structure generation, form generation, component selection, optimization), and design support (interactive tools, collaboration support).
Figure 4–6 indicates the scope of this field, gleaned from an analysis of the papers included in these volumes. Traditionally, the focus has been on detailed design and automated decision making. However, current research is moving toward conceptual design and problem formulation, with necessary emphasis on decision support and, consequently, provision of information and knowledge
needed for making design decisions. Gero and Sudweeks assert, “Computer-aided decision making will produce better designs.”
|
Support/Focus |
Detailed Design |
Conceptual Design |
Problem Formulation |
|
Information/Knowledge |
|
|
|
|
Decision Support |
|
|
|
|
Decision Making |
|
|
|
Figure 4–6 Scope of artificial intelligence in design.
Numerous efforts have been undertaken to integrate much of the above into design environments. The long series of studies by Cody, Rouse, and Boff (1995) is a good example of work in this area. Analyses of the results of studying hundreds of designers yielded the requirements for the architecture of an interactive design environment, supported by an artificially intelligent Designer’s Associate.
Evaluation of a series of prototypes led to an important insight. Specifically, the cost of developing and maintaining the knowledge bases associated with what the Designer’s Associates envisioned would be prohibitive. Simply, there would be too much data and information to compile and maintain. This led to the recommendation to develop more focused support systems where the embedded knowledge required would be far less Comprehensive.
One direct result of this conclusion is the Product Planning Advisor (<http://www.ess-advisors.com/Products/Software/software.htm>), Which supports design teams in formulating and evaluating alternative functions/features of product Concepts relative to market models, as well as both current and likely competitive offerings. This much more focused design support tool combines intelligent support with multi-stakeholder, multi-attribute market models and quality function deployment representations of relationships among product functions/features and stakeholders’ attributes. The Product Planning Advisor has been employed in hundreds of product planning efforts, many involving top high-technology companies.
Artificial intelligence (AI) developers have, at various stages in its history, promised comprehensive automated decision making. AI as a Category includes such approaches as neural networks, expert systems, genetic algorithms, intelligent agents, and fuzzy logic. More realistically, however, for all but routine design decisions, AI can best provide powerful knowledge-based support of design decision making, rather than automated decision making. It does this in part by building on an understanding of human decision making in design contexts and tailoring support to enhance human abilities (e.g., pattern recognition) and overcome human limitations (e.g., errors). Thus, AI is not used to automate human decision making; rather the theory determines how AI can best assist decision making. Some recent attempts to exploit AI for the purpose of generating new design alternatives show promise.
TRIZ
TRIZ, a Russian acronym that translates to Theory of Inventive Problem Solving, describes a process to encourage creativity. The theory is based on the presumption that a conflict between two objectives creates a need for creativity. For example, the design has to be light and strong. The developer of the process reviewed hundreds of thousands of patents to see what ideas were used to reconcile these conflicting objectives. He developed a matrix that showed, for the intersection of conflicting objectives, alternatives used in existing patents. Some of the intersections are relatively sparse; others have several suggestions. The intent is that one of the suggestions might spark the creativity of the person facing the design problem. TRIZ was created by Genrich S.Altshuller in
Russia (Altshuller, 1988). He and his coworkers analysed about 1.5 million patents and worked out a methodology to resolve the technological problems,
The salient TRIZ principles are as follows:
-
All engineering systems have uniform evolution in the direction of increased ideality. Many others (such as economic and educational systems) have the same evolutionary trends.
-
Any innovative problem represents a conflict between new requirements and an old system.
TRIZ is composed of various systematic techniques including inventive principles; psychological inertia overpass system; physical, chemical, and geometric effects; substrate-field and functional analysis; technological ideality concept; and technology forecasting. It helps find a quasi-ideal solution to innovative problems through the resolution of hidden conflict based on inferred knowledge of system evolution.
TRIZ is more than a methodology. It represents a unique way to enhance creativity by getting individuals to think far beyond their own experience, to reach across other disciplines, and to resolve problems using knowledge extracted from other areas of business, science, or technology.
FORMAL METHODS FOR REPRESENTING DESIGN PROBLEMS
This section covers some limited formal methods and theories for representing design problems. They are selected as representatives from different schools of thought in approaching design problems: traditional engineering, decision theory, and artificial intelligence.
ENGINEERING DESIGN: A SYNTHESIS OF VIEWS
Dym (1994) attempts to articulate what is meant by engineering design, how it can be discussed both for designed artifacts and for the process of design, and what areas are amenable to, and perhaps most require, formal research approaches. The central thesis elevates representation as the key element in design. In addition, recent research in AI aimed at rendering design computable is purported to provide new techniques for design representation to enable improved understanding of design concepts and processes.
Design activities encompass a spectrum from routine design of familiar parts and devices, through variant design requiring some modification in form or function, to truly creative design of new artifacts. The spectrum of design concerns includes some processes susceptible to thoughtful analysis—in other words, cognitive processes. One principal consequence of this recognition is the need to focus on the languages of engineering design. On the other hand, creative designs are almost certainly not susceptible to encapsulation with current representation technologies and, therefore, cannot be modeled.
For the last half of the twentieth century mathematics was the language of engineering, owing in part to the central role of mathematics in physical sciences modeling. Engineers understand that much of what they really know cannot be expressed in mathematics alone. Engineers use graphics and pictures, as well as words, although often in a very structured way (e.g., in specifications and codes, in heuristics or rules of thumb). Designers and modelers of cognitive design processes understand that many languages of design have been devised and used.
Design knowledge includes information about such features as design procedures and shortcuts, as well as about designed artifacts and objects and their attributes. Designers think about design processes when they begin to create sketches and drawings to represent the objects they are designing. A complete representation of designed objects and their attributes requires a complete
representation of design concepts that may be less easy to describe or represent than physical objects (e.g., design intentions, plans, behavior).
The languages or representations used in design include:
-
verbal or textual statements to articulate design projects, describe objects, describe constraints or limits, communicate between different members of design and manufacturing teams, and document completed designs;
-
graphical representations to provide pictorial descriptions of designed artifacts such as sketches, renderings, and engineering drawings;
-
mathematical or analytical models to express some aspect of an artifact’s function or behavior, which is in turn often derived from some physical principle(s) that can be expressed mathematically;
-
numbers to represent discrete-valued design information (e.g., part dimensions); and
-
continuously varied parameters in design calculations or within algorithms representing a mathematical model.
Different languages are used to represent engineering and design knowledge at different times, and the same knowledge is often cast in different languages in order to serve different purposes. For example, fundamental structural-mechanics knowledge can be expressed analytically, as in formulas for the vibration frequencies of structural columns; numerically, as in discrete minimum values of structural dimensions or in finite element meshing algorithms for calculating stresses and displacements; and in terms of heuristics or rules of thumb, as in the knowledge that the first-order earthquake response of a tall, slender building can be modeled as a cantilever beam whose foundation is excited. Therefore, designers must realize that what they need to know is not just a set of formulas; they must know how to apply knowledge in different forms to serve different purposes. This means designers must master the languages of engineering design.
SUH’S AXIOMATIC DESIGN
This theory (Suh, 1990) describes design as a mapping between what designers want to achieve and how they achieve it. The framework of axiomatic design views design as a collection of mappings between four domains: the customer domain, the functional domain, the physical domain, and the process domain. In each domain the design is specified using different elements: customer attributes (CAs), functional requirements (FRs), design parameters (DPs), and process variables (PVs). In addition there are constraints (Cs). The design process starts with the identification of customer needs and attributes, and formulates them as FRs and constraints. These FRs are then mapped onto the physical domain by conceiving a design embodiment and identifying the DPs. There may be more than one solution to this mapping. Each DP is then mapped onto a set of PVs to define it. Each DP typically introduces new FRs, DPs, and PVs, and so the mapping process iterates by zigzagging between domains, until the design can be implemented without further composition. In principle this approach takes a broad view of design, but the axioms and methods are almost entirely about mapping from the functional to the physical domain, so they do not address all aspects of design. The principles of this theory potentially apply to a variety of design problems, including mechanisms, software, and organizations.
Based on Nam Suh’s experience and observations about existing designs and his assessment of successful and unsuccessful designs, he proposes two axioms:
-
Axiom 1, the Independence Axiom: Maintain the independence of functional requirements. This means that when two or more functional requirements exist, the design solution must be such that each one of the FRs can be satisfied without affecting the other FRs. That in turn means a designer must create a design (or design parameters) able to satisfy each FR independently
-
of the other FRs. Thus, this first axiom establishes a requirement about the design to guide the creative process and any decisions among alternatives.
-
Axiom 2, the Information Axiom: Minimize the information content. Suh defines information as the logarithm of inverse probability of meeting the functional requirement. Among designs satisfying Axiom 1, Suh’s axiomatic design approach states that the best design is the one with the minimum information or maximum probability of meeting the functional requirements, considering tolerances and nominal requirements.
In addition to these two axioms (and numerous associated theories and corollaries), Suh through case studies and examples essentially outlines a design methodology consistent with his axioms. The methodology involves techniques for zigzagging between functional requirements and design parameters and the use of matrix algebra to assess independence. The theoretical framework has some appeal to experienced designers who recognize that achieving conflicting functional requirements with one design parameter (independence axiom violation) is the source of some badly compromised designs and that the information content embedded in the functional requirements might be a valid assessment of such complexity. Suh’s axiomatic approach represents a substantial and potentially useful addition to design methods, but the technique has not shown significant practical application, as is discussed below. Moreover, the theoretical basis has some apparent limitations. It is not clear that Suh’s assertion is correct that an ideal design always has an equal number of functional requirements and design parameters.
On the one hand, although we can agree that independence is desirable, design constraints such as manufacturability, low cost, and ease of use may at times conflict with independence or for objective reasons override independence. The best design, therefore, may have more functional requirements than design parameters. On the other hand, there are cases where decreased sensitivity to variations in use or manufacturing may be particularly important and can be improved by having more design parameters than functional requirements, Thus the independence axiom can result in a useful assessment tool but is not a requirement for all good designs. Further development of the information definition may also be needed to best meet customer needs rather than simply meeting the given tolerances.
In summary, the axioms while useful do not appear to constitute a complete and optimal design method. This could be why the best practical applications to date use axiomatic design in combination with other design methods. One can use the independence axiom in combination with robust Taguchi methods to examine which design parameters to use in achieving a robust design. One could also use axiomatic principles to assess concepts created by TRIZ methodology (Mann, 1999).
YOSHIKAWA’S GENERAL DESIGN THEORY
Yoshikawa and his associates began in the late 1970s to publish papers on a general theory of design. This work attempts to address design in a rather complete fashion by defining design as “creating artificial things [that] have not existed in the real world previously.” Some of these papers have focused on how the approach might be applied to extending computer-aided design (CAD) systems to include engineering and simulation information. Although a formal mathematical basis is sketched, this approach remains largely philosophical with some interesting general observations about the nature of design. This approach has resulted in no new design methods or engineering design tools, nor (as yet) has it seemed to directly add new tools to the intelligent CAD area.
A MATHEMATICAL FRAMEWORK FOR ENGINEERING DESIGN
The decision-based design view of engineering design states that much of design consists of decision-making activities, and that decision support methods used in engineering design should reliably produce good advice. This is a non-trivial condition that demands that design methods adhere to the mathematics of decision theory. Only in this way can paradoxical results, in which a design method might recommend even the worst design alternative, be prevented. Rigorous decision theory has developed over the last 300 years and has its roots in the work of many mathematicians and economists, including Daniel Bernoulli, Charles Lutwidge Dodgson (Lewis Carroll), John von Neumann, Oskar Morgenstern, and Kenneth Arrow. Hazelrigg (1998, 1999) uses the results of these mathematicians and economists to lay out a decision theory-based framework for engineering design, thereby extending the earlier work of such people as Myron Tribus (1969), Richard de Neufville (1990), and Andrew Sage (1977).
The purpose of Hazelrigg’s framework is to provide a self-consistent method for rank ordering alternatives in the context of engineering design. The framework recognizes some key aspects of design, in the context of decision theory, that other methods fail to consider: (1) that all design decisions are made under conditions of significant uncertainty and risk; (2) that the preferences of key importance in a decision are those of the decision maker (not those of the customers or stakeholders); and (3) that alternatives must be ranked on a valid and validated real scalar measure. Thus, Hazelrigg uses the preference of the company CEO or other decision authority as the basis for a valid scalar measure (typically net present value of cash flow generated by a design), together with von Neumann-Morgenstern utility theory to assure validity of the measure under uncertainty and risk.
Hazelrigg adds two axioms to those of von Neumann and Morgenstern, although the first can be derived from the von Neumann-Morgenstern axioms and is presented only for convenience. The two additional axioms are as follows:
-
Axiom 1, the Axiom of Deterministic Decision Making: Given a defined set of alternatives from which to choose, each with a known and deterministic outcome, the decision maker’s preferred choice is the alternative whose outcome is most preferred.
-
Axiom 8, the Axiom of Reality in Engineering Design: All engineering designs are selected from among the set of explicitly considered potential designs.
The von Neumann-Morgenstern axioms provide a basis for comparison of known alternatives. They do not provide a basis for comparison of a known alternative with an unknown alternative, and some engineers thus argued that Hazelrigg’s framework is not valid. The addition of Axiom 8, which states that any chosen engineering design is a known option included in the set of options under consideration for selection (this should be intuitively obvious, as we do not produce products we never imagined), assures that the von Neumann-Morgenstern results apply to engineering design.
The von Neumann-Morgenstern axioms provide two results of consequence:
-
The Expected Utility Theorem. Given a pair of alternatives, each with a range of possible outcomes and associated probabilities of occurrence, the preferred choice is the alternative with the highest expected utility.
-
The Substitution Theorem. A decision maker is indifferent between a lottery and a certainty outcome whose utility is equal to the expected utility of the lottery, and for purposes of analysis, the two may be substituted one for the other.
Early applications of these ideas to engineering design include Greenberg and Hazelrigg (1974). Recent applications of utility theory exist, for example, Thurston et al. (1994); and many other recent papers apply decision theory to engineering design, but they largely fail to consider uncertainty and
the decision maker’s attitudes toward risk. Marston and Mistree (1997) use the von Neumann and Morgenstern axioms, but advocate additional areas (such as subjectivity in options and in designer preferences) to be included in design theory. A recent paper by Thurston (2001) assesses the appropriateness and usefulness of decision-based design. Of course, the desirability of a design to customers, as expressed in willingness to pay, is an important consideration in formulating an objective function—usually profits for the designer's company.
The Nobel laureate Kenneth Arrow in 1951 provided results of extreme importance to engineering design. Arrow states six conditions that should be satisfied by a selection method, such as the following: If, under all conditions and by every measure, alternative A is preferred to alternative B, then the selection method should not choose B over A. He goes on to prove that, in the case of three or more alternatives and three or more selection criteria (voters, for example), no selection method can be assured of giving a valid result. Arrow’s Impossibility Theorem points to the dangers of naive multi-criteria decision methods that comprise many engineering design selection methods. Based on Arrow’s result, Haunsperger and Saari (1991) have provided numerous paradoxical examples illustrating how naive decision support methods fail.
An early application of these ideas to engineering design can be found in Dyer and Miles (1976). Recent work by Allen (2001) points out, in the context of the von Neumann and Morgenstern setting for decision making under uncertainty, that a weakening of Arrow’s axioms permits a possibility result for group decisions with risk aversion. Scott and Antonsson (1999) argue that despite the common participation of many individuals in the design process, engineering design is closer to multiple criteria decision making than to social choice theory, so Arrow’s theorem need not apply.
DECISION MAKING IN MANAGEMENT SCIENCE AND ECONOMIC FIELDS
The fields of management science, game theory, and economics commonly use decision-making techniques, and some of these may have application to engineering design. In fact, many opportunities exist for cross-application of decision-making tools among unrelated fields. Operations research has developed numerical methods useful in computational economics and game theory. Constrained optimization packages for linear programming, integer programming, and non-linear programming are well known. Fixed-point algorithms can be used to find equilibria in economies and games.
DECISION MAKING IN ECONOMICS
The academic discipline of economics lies behind the business side of engineering design and technology management. Using economics terminology, engineering design consists of product selection and technology choice. Economists use techniques from constrained optimization, decision theory, game theory, and microeconomics (the study of resource allocation) in general to solve such problems. The methodology used in economics also typically differs somewhat from that used in engineering.
Economics tends to focus on the development of an overriding general framework for analysis of a wide variety of applied problems and policy issues. Such a framework involves the elucidation of a fully consistent general model from fundamental principles, starting with constrained optimization. A goal is to rigorously examine the implications of appropriate assumptions. Numerical work should be preceded by a precise statement of the equilibrium concept or constrained optimization problem (i.e., the objective function and feasible set) and by a careful examination of the conditions under which the model has a solution. Note the term “model” refers to the general and rigorous framework. The model includes the abstract exogenous information, assumptions, and definitions.
The basic product selection problem can be cast as a constrained optimization problem along the following lines. Once a firm has made its product selection decision, the firm’s profits (revenues minus costs, where revenues depend on demand) depend on its costs, the price at which the product is sold, and the number of units of the product produced and sold. Of course, profits also depend on the selection of products manufactured and sold by all other firms and their respective prices. Given the products of all other firms and their prices, one could construct the profit function for each feasible product choice and find its maximum value, subject to price and quantity being consistent with market demand. Then one could pick the product for which maximum profits are greatest. (This assumes other firms do not strategically alter their decisions in response to the product choice of the firm in question.) This extension can be analysed with game theory. Engineering considerations enter through the feasibility constraints faced by firms and through their cost functions (which depend on the production technology, the quantity manufactured, and input prices) for each possible product. The basic question reduces to a (highly non-trivial) constrained optimization problem. (The case of a multi-product firm is more difficult to analyze, but the same principles can be applied.)
Decision making in economics, whether for consumers or firms, is based on constrained optimization; however, the objective functions and constraints faced by consumers are different from those for firms.
The consumer’s decision problem starts from preferences—essentially, data in the form of a yes or no answer to the question of whether some combination of items to be consumed is at least as good as some other combination of items. Standard rationality assumptions on preferences are well known and give rise to utilities. The following axioms are typically used to study individual choice behavior in economics:
-
Symmetry: X is at least as good as X.
-
Consistency (transitivity): If X is at least as good as Y and Y is at least as good as Z, then X is at least as good as Z.
-
Decisiveness (completeness): Either X is at least as good as Y or Y is at least as good as X (or both).
-
No drastic changes (continuity): If X is strictly better than Y, then X1 is strictly preferred to Y1 whether X1 is sufficiently close to X and Y1 is sufficiently close to Y.
-
More is better (monotoricity): If X is greater than Y, then X is as least as good as Y.
Frequently an additional axiom stating that variety is strictly desirable (strict convexity) is added in order to guarantee that optimal choices are unique. Utility functions summarize the preference relation such that the utility associated with one combination exceeds the utility of another combination if and only if the first combination is strictly better according to the consumer’s preference. The consumer’s constraints reflect affordability (given all prices and income) and survivability (minimum quantities of food, shelter, and the like may be required).
If uncertainty is involved, preferences over lotteries (randomizations over combinations of items to be consumed) are the appropriate fundamental concept. Rationality axioms lead to cardinal utility representation (see von Neumann and Morgenstern, 1980). Cardinal utilities reflect attitudes toward risk and are unique (given the preferences over lotteries) up to multiplication by a positive constant and addition of a constant.
For firms, profits are the appropriate objective functions in simple cases. A sole entrepreneur should maximize expected utility of profits when uncertainty is present. In intertemporal settings, the firm should maximize the present discounted value of profits or the expected utility of profits. If shares of the firm are traded, the basic goal is to maximize the firm’s market value, although
complications (such as shareholder purchase of significant amounts of the firm’s output) can cause the objective to change. The firm’s constraints are derived from its available production technology, which when combined with all input prices, determines costs and from that aggregate, demand for its products.
The interactions and interdependencies among individuals, firms, and products can be captured by market equilibrium. When strategic aspects of individual and firm behavior matter, game theory provides a rigorous analytical tool.
GAME THEORY
Game theory is the study of formal models of strategic behavior in which the payoff or utility received by a player (individual or firm) can depend not only on the player’s own decisions but possibly also on the decisions of all other players. Game theoretic models are classified into cooperative and non-cooperative games.
A non-cooperative game is specified by a set of players, a strategy set for each player, and a payoff function (or utility depending on the strategies chosen by all the players) for each player. A Nash equilibrium is defined by the principle that each player chooses a strategy to optimize his or her own payoff given the decisions of all other players. Well-known conditions guarantee that a game has a Nash equilibrium, which may require randomized strategies. When there are multiple Nash equilibria, refinement concepts can narrow the equilibrium set. Non-cooperative games were introduced into the engineering design literature by Vincent (1983) for the study of collaboration within teams.
In a cooperative game, players can communicate and make binding agreements within coalitions (non-empty subsets of players), but cooperative games do not analyze the formation of coalitions. Many solution concepts are available, some of which are defined axiomatically.
SUMMARY OF METHODS, THEORIES, AND TOOLS
Table 4–2 provides a cursory rating of several tools with respect to potential values in current use, concept creation, concept development, selection among alternative concepts, and ease of use. Some decision analysis and applied decision theories are also included in this comparison. Concurrent engineering is included here as a tool, but it is more of an operating philosophy. It has its primary basis in the economics of product and process development, whereas the other approaches with a primary basis in economics build on theories of preferences (e.g., von Neumann-Morgenstern axioms).
The “ease of use” criterion is used in two ways to describe the tools and methods, encompassing both conceptual difficulty and execution difficulty. For example, QFD is overwhelming to execute if pursued fully, not because it is conceptually difficult but because filling in the huge number of cells in the matrices becomes daunting. Suh, however, is Conceptually difficult. Mathematically rigorous approaches can often be conceptually difficult to employ (e.g., in terms of understanding and justifying assumptions and perhaps overly narrow problem definition). On the other hand, broadly applicable methods, including Concurrent Engineering and QFD, face difficulty in some applications because of the very breadth they address.
Table 4–2 Summary of Tools and Applications Examined
|
|
Primary Basis |
Ratingsa—Potential Value for: |
||||||||||
|
|
Knowledge Engineering |
Logic/Set Theory |
Matrix Algebra |
Probability |
Statistics |
Economics |
Current Utilization |
Concept Creation |
Concept Development |
Selection Among Alternative Concepts |
Ease of Use |
|
|
Practical |
Concurrent Engineering |
|
X |
4 |
2 |
4 |
4 |
1 |
||||
|
Qualitative |
Decision Matrix |
|
X |
|
X |
4 |
1 |
2 |
4 |
5 |
||
|
|
Pugh Method |
|
X |
|
3 |
4 |
5 |
1 |
2 |
|||
|
|
QFD |
|
X |
|
2 |
2 |
4 |
2 |
1 |
|||
|
|
AHP |
|
X |
|
3 |
1 |
2 |
4 |
|
|||
|
|
Product Plan Advisor |
X |
|
X |
X |
|
3 |
2 |
3 |
4 |
3 |
|
|
Statistical |
PLS |
|
X |
X |
|
1 |
3 |
3 |
2 |
1 |
||
|
|
Taguchi Method |
|
X |
X |
|
4 |
1 |
4 |
4 |
2 |
||
|
|
Six Sigma |
|
X |
X |
|
3 |
3 |
3 |
3 |
2 |
||
|
Creative |
AI Support |
X |
|
2 |
4 |
2 |
2 |
2 |
||||
|
|
TRIZ |
X |
|
3 |
3 |
1 |
1 |
3 |
||||
|
Axiomatic |
Suh’s Theory |
|
X |
X |
|
2 |
2 |
3 |
5 |
1 |
||
|
|
Yoshikawa Theory |
|
X |
|
1 |
1 |
1 |
1 |
1 |
|||
|
|
Math Framework |
|
X |
|
X |
X |
X |
1 |
1 |
1 |
5 |
3 |
|
Validating |
Game Theory |
|
X |
|
X |
1 |
1 |
1 |
3 |
2 |
||
|
|
Decision Analysis |
|
X |
|
X |
|
X |
3 |
1 |
4 |
5 |
3 |
|
aRating by several members of the committee: 1=low; 5=high. |
||||||||||||
The “selection among alternative concepts” criterion has multiple interpretations. The multi-attribute matrix-oriented techniques are often used to select among overall product concepts, while the statistical methods are more typically used to select among process alternatives and among more detailed design differences. This criterion demonstrates the main strength for some of the more mathematically rigorous approaches. Not surprisingly such approaches have little basis for generating alternatives. In contrast, knowledge-based approaches such as AI and TRIZ are much better for generating alternatives than for choosing among them. Approaches such as QFD and Pugh attempt to aid in both.
Cooper et al. (2000) state, “The choice of tool may not be that critical; indeed, the best performers use an average of 2.4 tools each—no one tool can do it all!” One could use Table 4–2 and the discussion in this chapter as a guide to choosing approaches for design application. For example, effective choices include:
-
Concurrent engineering as an overall framework for decreasing costs and time to market;
-
TRIZ for generating alternatives;
-
Some form of Decision Matrix Technique for initial screening of ideas;
-
Six Sigma for process design and evaluation with emphasis on quality control;
-
Decision Analysis for making major investment decisions and for selection among viable concepts; and
-
Taguchi and axiomatic methods for reliable, robust design development.
Design is an intellectual activity of the human brain and is therefore difficult to understand or even to describe using mathematical theories. Because all human intellectual activity includes decision making, decision making is an integral and inherent part of any design process. A variety of tools, methods, and theories have been developed over time to help describe and facilitate decision making processes, and some of these have been applied to various aspects of design, but none approach a general and useful theory fundamental to all areas of design.
In current practice each of these formal approaches to representing design processes is valuable yet individualistic. Specific theories do not currently acknowledge or make reference to others, making it difficult to determine the compatibility or contradictions among them. This lack of coordination impedes the teaching and general reduction to practice of potentially useful tools. Although some work is being conducted to understand the connections among these theories (Jin and Lu, 1998), much more is needed.
The validation of individual theories is anecdotal and difficult to justify across the wide range of design processes. Each of the tools described here must take into account the uncertainty of the data input. This data may come from actual measurements, from analysis of historical data, from solicited expert opinions, or from moderated opinions of potential users. Much of this input data depends on the ability of humans to judge attributes, and on how their judgment is affected when the number of attributes becomes large or complex. This variable makes validation of designs and design tools difficult.
Each methodology can clearly be an intellectual activity of value provided its potential applicability and limitations are well understood. However, comparison and contrast of the results of each tool can provide additional insight to the designer, and tools used in tandem may result in incalculable synergies. While the value of a single tool with applicability across every design query might be desirable, today’s designers must use what is available.
In summary, as in all human activities, the tools and methods used in design are the ones that have the most utility given the constraints imposed by time and other resources available. Box (1979) has stated that “all models are wrong, some are useful,” to which the committee adds the codicil, “all tools are useful, some are appropriate.”
REFERENCES
Akao, Y. 1997. QFD: Past, present, and future. Proceedings of the Third Annual International QFD Symposium. Sweden: Linköping University.
Allen, B. 2001. On the possibilities for optimal collaborative engineering design under uncertainty. In Proceedings of Optimization in Industry II-1999, New York: ASME Press.
Altshuller, G. 1988. Creativity as an Exact Science, New York: Gordon and Breach.
Arrow, K.J. 1963. Social Choice and Individual Values. 2nd Edition. New York: Wiley.
Beebe, K.R., and B.R.Kowalski. 1987. An introduction to multivariate calibration and analysis. Analytical Chemistry 59(17):1007a-1017a.
Box, G. 1979. Robustness in Statistics, eds. R.L.Launer and G.M.Wilkenson, p. 202. New York: Academic Press.
Carriere, J., and M.Finster. 1989. An Interpretation of the House of Quality Based on Decision Theory. Technical Report 858. Department of Statistics, University of Wisconsin.
Clausing, D., and S.Pugh. 1991. Enhanced quality function deployment. Proceedings of the International Conference on Design Productivity, February 6–8, Honolulu, pp. 15–25.
Cody, W.J., W.B.Rouse, and K.R.Boff 1995. Designers’ associates: Intelligent support for information access and utilization in design . Human/Technology Interaction in Complex Systems, vol. 7, ed. W.B.Rouse, p. 173. Greenwich, Conn.: JAI Press.
Cooper, R.G., S.J.Edgett, and E.J.Kleinschmidt. 2000. New problems, new solutions: Making portfolio management more effective. Research Technology Management 43(2):18–33.
Dean, E.B., and R.Unal. 1992. Elements of designing for cost. AIAA 1992 Aerospace Design Conference, Irvine, Calif., February 3–6. Publication number AIAA-92–057. Reston, Virginia: AIAA Press.
de Neufville, R. 1990. Applied Systems Design. New York: McGraw-Hill.
Dyer, J.S., and R.F.Miles, Jr. 1976. An actual application of collective choice theory to the selection of trajectories for the Mariner Jupiter/Saturn 1977 project. Operations Research 24:220–224.
Dym, C.L. 1994. Engineering Design: A Synthesis of Views. Cambridge, England: Cambridge University Press.
Gero, J.S., and F.Sudweeks, eds. 1996. Artificial Intelligence in Design ‘96. Dordrecht: Kluwer.
Gero, J.S., and F.Sudweeks, eds. 1998. Artificial Intelligence in Design ‘98. Dordrecht: Kluwer.
Greenberg, J.S., and G.A.Hazelrigg. 1974. Methodology for reliability-cost-risk analysis of satellite networks. Journal of Spacecraft and Rockets 2(9):650–657.
Haunsperger, D.B., and D.Saari. 1991. The lack of consistency for statistical decision procedures. The American Statistician 45:252–255.
Hauser, J.R., and D.Clausing. 1988. The House of Quality. Harvard Business Review, May-June, pp. 63–73.
Hazelrigg, G.A. 1998. A framework for decision-based engineering design. Journal of Mechanical Design 120:653–658.
Hazelrigg, G.A. 1999. An axiomatic framework for engineering design. Journal of Mechanical Design 121:342–347.
Jin, Y., and S.Lu. 1998. Toward a better understanding of engineering design models. Universal Design Theory, eds. H.Grabowski, S.Rude, and G.Grein, pp. 71–86. Aachen, Germany: Shaker Verlag.
Mann, D. 1999. Axiomatic design and TRIZ: Compatibilities and contradictions. The TRIZ Journal, June. Available on-line at <http://www.triz-journal.com/>.
Marston, M., and F.Mistree. 1997. A decision based foundation for systems design: A conceptual exposition. Proceedings of the CIRP 1997 Conference on Multimedia Technologies for Collaborative Design and Manufacturing, October 8–10, Los Angeles, Calif., pp. 1–11.
Pugh, S. 1990. Total Design: Integrated Methods for Successful Product Engineering. Wokingham, England: Addison-Wesley.
Pugh, S. 1996. Creating innovative products using total design: The living legacy of Stuart Pugh, eds. D.Clausing and R.Andrade. Reading, Mass.: Addison-Wesley.
Pyzdek, T. 2001. The Six Sigma Handbook. New York: McGraw-Hill.
Ross, P.J. 1996. Taguchi Techniques for Quality Engineering. New York: McGraw-Hill.
Saaty, R.W. 1987. The analytic hierarchy process—what it is and how it is used. Mathematical Modelling 9(3–5):161–176.
Saaty, T.L. 1980. The Analytic Hierarchy Process, New York: McGraw-Hill.
Sage, A.P. 1977. Methodology for Large Scale Systems. New York: McGraw-Hill
Scott, M.J., and E.K.Antonsson. 1999. Arrow’s theorem and engineering decision making. Research in Engineering Design 11(4)218–228.
Suh, N.P. 1990. The Principle of Design. Oxford, England: Oxford University Press.
Taguchi, G. 1986. Introduction to Quality Engineering: Designing Quality into Products and processes. Dearborn, Mich.: American Supplier Institute.
Taguchi, G. 1988. Introduction to Quality Engineering: Designing Quality into Products and Processes. Japan: Asian Productivity Organization.
Taguchi, G., and Y.Wu. 1980. Introduction to Off-line Quality Control. Nagoya, Japan: Central Japan Quality Control Association.
Tobias, D.R. 1995. An introduction to partial least square regression. Proceedings of the 20th SUGI Conference, April 2–5, Orlando, Florida.
Thurston, D.L., J.V.Carnaham, and T.Liu. 1994, Optimization of design utility. ASME Journal of Mechanical Design 116(3):801–808.
Thurston, D.L. 2001. Real and misconceived limitations to decision based design with utility analysis. ASME Journal of Mechanical Design 123(2):176–182.
Tribus, M. 1969. Rational Descriptions, Decisions, and Designs. Elmsford, N.Y.: Pergamon Press.
Vincent, T.L. 1983. Game theory as a design tool Journal of Mechanisms, Transmissions, and Automation in Design 105:165–170.
von Neumann, J., and O.Morgenstern. 1980. The Theory of Games and Economic Behavior. Reprint. Princeton, N.J.: Princeton University Press.
Winner, R.I., J.P.Pennell, H.E.Bertrand, and M.M.G.Slusarezuk. 1988. The Role of Concurrent Engineering in Weapons System Acquisition, IDA Report R-338. Alexandria Va.: Institute for Defense Analyses.
Wold, S. 1978. Cross-validatory estimation of the number of components in factor and principal components models. Technometrics 20(4):397–405.
Wold, H. 1985. Partial least squares. Encyclopedia of Statistical Sciences, vol. 6, eds. S.Kotz and N.L.Johnson, pp. 581–591. New York: Wiley.
Yoshikawa, H. 1981. General design theory and a CAD system. Man-Machine Communication in CAD/CAM, eds. T.Sata and E.Warman. Amsterdam: North-Holland.
























