Fuel Cells That Run on Common Fuels
JOHN M. VOHS
Department of Chemical and Biomolecular Engineering
University of Pennsylvania
Philadelphia, Pennsylvania
A fuel cell is a device that converts energy stored in chemical bonds in a fuel directly into electricity with high efficiency (Carette et al., 2000; Minh 1993). Unlike conventional methods of producing electricity, such as steam turbines, the efficiency of a fuel cell is not limited by the Carnot cycle; therefore, fuel cells can have energy-conversion efficiencies of 60 to 80 percent. This makes fuel cells environmentally friendly energy-conversion devices, and they have been proposed for use in applications ranging from large-scale power production to transportation to battery replacement.
Fuel cells were invented more than 150 years ago, but their commercialization has been very slow. To date, they have been used primarily in space vehicles, but these systems are quite costly and not suitable for commercial applications. In the last decade, however, there has been a dramatic increase in research, and it is now clear that fuel cells will enter the commercial marketplace in the not too distant future. Currently, most attention is focused on two types of fuel cells, polymer-electrolyte membrane (PEM) fuel cells and solid-oxide electrolyte fuel cells (SOFCs) (Carrette et al., 2000; Minh 1993). PEM systems use a proton-conducting polymer as the electrolyte and operate at low temperatures; SOFCs use an oxygen ion-conducting ceramic membrane as the electrolyte and operate at temperatures of 700 to 1,000°C.
In a PEM system, the charged species transported through the electrolyte are protons (H+); thus, H2 must be used as the fuel. This requirement presents many challenges for developers of PEM systems because hydrogen is difficult to store and costly to produce. The only viable source of hydrogen today is from the reforming of hydrocarbons (Ogden 2002). PEM systems also require high-puri-
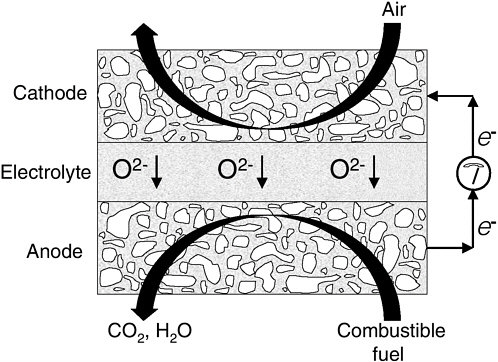
FIGURE 1 Schematic drawing of an SOFC.
ty H2, because parts-per-million levels of carbon monoxide (CO) and sulfur poison the precious metal catalysts in the anode.
The species transported through the electrolyte in SOFCs are O2- ions. This makes SOFCs more fuel flexible, and, in theory, any combustible gas could be used as the fuel. A schematic drawing of an SOFC is shown in Figure 1.
The cell is composed of a thin, dense layer of an oxygen ion-conducting electrolyte, typically yttria-stabilized zirconia (YSZ), and a porous anode and cathode. To obtain appreciable oxygen ion conductivity in the electrolyte, the system must operate at high temperatures. The cathode is composed of an electronically conducting oxide, such as strontium-doped LaMnO3 (LSM). The cathode is exposed to air and reduces O2 to O2- ions using electrons supplied by the external circuit according to the following half-cell reaction:
1/2 O2 + 2 e−→ O2- (1)
The anode catalyzes the oxidation of the fuel using O2- ions delivered through the electrolyte-producing electrons that flow through the external circuit to the cathode. If H2 is used as the fuel, the anode half-cell reaction is as follows:
H2 + O2- → H2O + 2 e- (2)
In conventional SOFCs, the anode is almost always composed of a porous composite of nickel (Ni) and YSZ.
At equilibrium, the cell potential (i.e., the voltage difference between the anode and cathode) is given by the Nernst equation. For the two half-cell reactions shown above the Nernst equation in terms of the partial pressures of H2 and H2O at the anode, the partial pressure of O2 at the cathode and Faraday’s constant, F, is as follows:
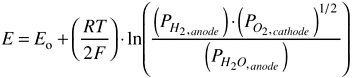
(3)
The open-circuit voltage for the cell, Eo, is determined by the standard Gibbs free-energy change for the overall reaction. Under operating conditions, when current flows from the anode to the cathode through an external load, the cell potential is less than the theoretical potential given by Eq. 3 because of various losses, such as the resistance to oxygen ion flow across the electrolyte. Because the work that can be performed by the electrons is directly proportional to the potential, the efficiency of the cell decreases as the amount of current used increases.
SOFCs have some fuel flexibility. The Ni current collector in the anode is a good hydrogen-oxidation catalyst and is not poisoned by CO. Indeed, CO can even be used as the fuel. Thus, the most common fuel for an SOFC is a hydrogen-rich synthesis gas (a mixture of CO and H2), which can be produced by reacting methane with steam. Because Ni is an excellent catalyst for this so-called steam-reforming process, it is possible to perform this reaction within the anode by cofeeding steam with natural gas. It is much more difficult, however, to reform higher hydrocarbons, such as those found in common liquid fuels like gasoline or diesel. These fuels require a separate, partial oxidation (POX) reactor in which the fuel is partially oxidized using air to produce a CO/H2 mixture. It is important to note that hydrocarbon reforming significantly decreases electrical efficiency. For example, the use of a POX reactor decreases the amount of electrical energy that can be extracted from the fuel by ~30 percent (this energy is converted to heat in the POX reactor).
Although SOFCs that rely on reforming of hydrocarbons to produce synthesis gas are a viable technology, it would be much simpler and more efficient if the reforming step could be avoided and the fuels used directly. Thus, one would prefer to have an anode half-cell reaction that involves the direct oxidation of a hydrocarbon fuel, such as the following:
CnH2n+2 + (3n+1) O2− → n CO2 + (n+1) H2O + (6n+2) e− (4)
The primary reason that this approach is not used in conventional SOFCs is that at high temperatures, decomposition of hydrocarbons to produce graphite or coke is thermodynamically favorable. Most metals catalyze this decomposition reaction. Ni is particularly active, and, when exposed to dry hydrocarbons at temperatures above 700°C, a fibrous layer of coke grows away from the surface of the metal. In a fuel cell, this produces rapid deactivation. This is demonstrated in Figure 2, which shows the current output of an SOFC with a Ni/YSZ cermet anode as a function of time. The cell was initially operated on H2 and exhibited stable performance. After 60 minutes the fuel was switched to pure CH4. Note that the cell rapidly deactivated, and after an additional 60 minutes, the cell was completely inactive. The deactivation was irreversible; the cell remained inactive when the fuel was switched back to H2. Examination of the cell after this run revealed that the anode compartment was completely filled with coke.
Although the results presented in Figure 2 are discouraging, catalytic sci-
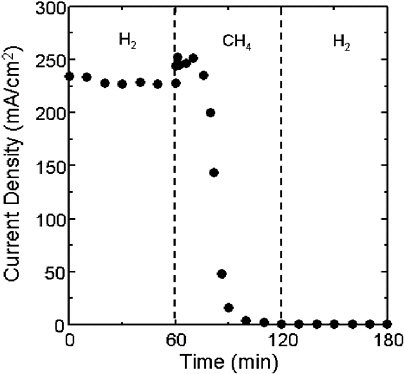
FIGURE 2 Performance of an SOFC with an Ni/YSZ anode as a function of time and fuel composition. Source: Park et al., 1999. Reprinted with permission.
ence provides clues to methods of overcoming the problem of anode fouling. Solving this problem has been the primary focus of our research for the past decade. Coke formation from hydrocarbons is thermodynamically favorable at high temperatures; however, this reaction proceeds very slowly in the absence of a catalyst. Thus, the key to producing an SOFC anode that is active for the direct oxidation of hydrocarbons is to use materials that do not catalyze carbon-deposition reactions. A catalyst for the oxidation of the hydrocarbons is still necessary, and the anode must be electronically conductive. Although most metals will catalyze carbon deposition from hydrocarbons, the noble metals, copper (Cu), silver (Ag), and gold (Au), are notable exceptions. We chose Cu to provide electrical conductivity in our anode design. Because Cu is inactive for hydrocarbon oxidation, a separate oxidation catalyst was also incorporated into the anode. Ceria (CeO2) was chosen to provide this function. Ceria is an excellent hydrocarbon-oxidation catalyst, and unlike most metals, it does not catalyze coke formation.
Although the rationale for using a Cu/CeO2/YSZ composite anode is relatively straightforward, synthesizing an anode with this composition presents several challenges. The most common method of fabricating Ni/YSZ anodes is to press a mixture of NiO and YSZ powders to form a wafer and then anneal the mixture at high temperatures in air to produce a dense NiO/YSZ composite. This is followed by annealing in H2 to reduce the NiO to Ni. This step also makes the anode highly porous. Tape casting, tape calendaring, and similar ceramics-processing methods are often used in place of the pressing step for the NiO-YSZ mixture. The initial annealing step must be carried out at a temperature higher than 1,300°C to sinter the YSZ component and achieve good ionic connectivity in the oxide phase. Unfortunately, because of the low melting temperatures of Cu2O and CuO (1,235°C and 1,326°C, respectively), Cu/CeO2/ YSZ cermets cannot be produced in a similar way.
To avoid these problems, we have developed several novel fabrication methods in which the porous YSZ part of the anode cermet is prepared first, and the Cu and CeO2 are added in separate steps that do not require high temperatures. The simplest method uses dual-tape casting, as shown in Figure 3 (Park et al., 2001). In this approach, an aqueous slurry containing YSZ powder and organic binders is cast into a film. Upon annealing in air at 1,500°C, the binders are burned out, and the oxide particles sinter to form a dense layer. Pore formers, such as graphite or polymer beads, can be added to the green tape to introduce porosity. The pore formers are oxidized during the annealing step and this gasification process produces pores in the sintered tape. With the appropriate choice of conditions, YSZ with porosity as high as 80 percent can be produced. In dual-tape casting, a second layer, which can have a different composition, is spread onto the first green layer. In Figure 3, the first layer becomes the dense electrolyte, while the second layer with pore formers becomes the anode. Cu and CeO2 are added to the porous anode layer by impregnating it with aqueous
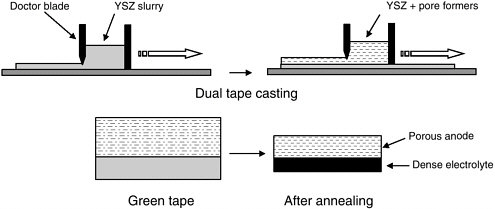
FIGURE 3 Schematic drawing of the tape-casting process used in the synthesis of an SOFC.
solutions of Cu(NO3)2 and Ce(NO3)3 followed by annealing at moderate temperatures (< 900°C) in H2 and then air to produce metallic Cu and CeO2. In a separate step, an LSM slurry is applied to the exposed surface of the electrolyte to form the cathode.
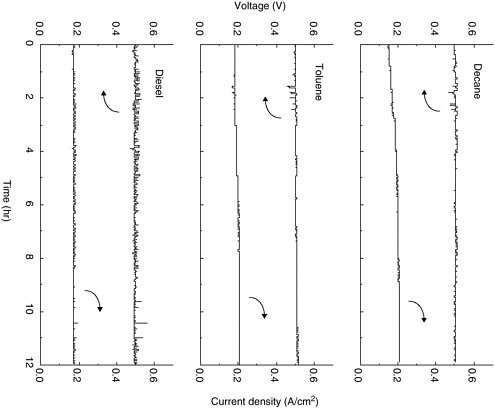
It has been shown that SOFCs with Cu/CeO2/YSZ anodes are highly resistant to fouling via carbon deposition and are remarkably fuel flexible (Kim et al., 2001; Park et al., 2000). This is apparent in Figure 4, which shows current density and voltage versus time for a fuel cell with a Cu/CeO2/YSZ anode operating on decane (C10H22), toluene (C7H8), and a synthetic diesel (Kim et al., 2001). Note that stable operation is achieved for all three fuels. Tests of up to three weeks in duration have been performed to demonstrate the long-term stability of these anodes.
The direct oxidation of hydrocarbon-based fuels in an SOCF has many significant advantages over H2-powered fuel cell systems. One of the most important is increased efficiency. As noted above, reforming hydrocarbons to produce H2 can decrease overall system efficiencies by as much as 30 percent. Direct oxidation of hydrocarbons also greatly simplifies fuel cell systems by eliminating the need to cofeed water when using methane, eliminating the need for external hydrocarbon reformers, and eliminating the need to store and transport H2. Direct oxidation has the added advantage that the current infrastructure for the production and distribution of hydrocarbon-based fuels could be used. Although further development is necessary, fuels cells that rely on the direct oxidation of hydrocarbons may play an important role in the commercialization of fuel cell technologies.
ACKNOWLEDGMENTS
The research described in this paper was supported by the Defense Advanced Research Projects Agency and the Office of Naval Research. The author would also like to thank Prof. Raymond Gorte for his collaborations on the work described in this paper.
REFERENCES
Carrette, L., A. Friedrich, and U. Stimming 2000. Fuel cells: principles, types, fuels, and applications. ChemPhysChem 1(4): 162-193.
Kim, H., S. Park, J.M. Vohs, and R.J. Gorte. 2001. Direct oxidation of liquid fuels in a solid oxide fuel cell. Journal of the Electrochemical Society 148(7): A693-A695.
Minh, N.Q. 1993. Ceramic fuel-cells. Journal of the American Ceramic Society 76(3): 563-588.
Ogden, J.M. 2002. Hydrogen: the fuel of the future? Physics Today 55(4): 69-75.
Park, S., R. Craciun, J.M. Vohs, and R.J. Gorte. 1999. Direct oxidation of hydrocarbons in a solid oxide fuel cell: I. methane oxidation. Journal of the Electrochemical Society 146(10): 3603-3605.
Park, S., J.M. Vohs, and R.J. Gorte. 2000. Direct oxidation of hydrocarbons in a solid-oxide fuel cell. Nature 404: 265-267.
Park, S., R.J. Gorte, and J.M. Vohs. 2001. Tape cast solid oxide fuel cells for the direct oxidation of hydrocarbons. Journal of the Electrochemical Society 148(5): A443-A447.
Dimension-Dependent Properties of Macromolecules in Nanoscopic Structures
JUAN J. DE PABLO AND PAUL F. NEALEY
Department of Chemical Engineering
University of Wisconsin-Madison
Many materials exhibit size-dependent properties as system dimensions approach the atomic or molecular level. For example, metal and semiconducting nanoclusters with dimensions of a few nanometers exhibit remarkable optical, electrical, mechanical, catalytic, and magnetic properties (Murray et al., 2000). Nanocluster properties differ significantly from corresponding bulk properties; they depend on the quantum-level electronic structure of the ensemble and the ratio of surface to bulk atoms, and they provide the foundation for a wide range of innovative nanotechnologies. Unfortunately, much less is known about the properties of amorphous, polymeric materials in nanoscopic structures. Because the characteristic dimensions typically associated with polymeric molecules are on the order of 5- to 10-nm, it is natural to expect size-dependent properties in polymeric structures with dimensions from 10 to 100 nm.
Evidence for dimension-dependent properties of amorphous polymers has been observed in measurements of the glass transition temperature, Tg. Experiments by several research groups, including ours, report that the Tg of polymer films with nanoscopic dimensions can be significantly different from the corresponding bulk value (Forrest and Dalnoki-Veress, 2001). Based on seminal experiments by Forrest et al. (1996), it is now widely perceived that the Tg of freestanding, ultrathin films is substantially lower than that of the bulk material. Our recent simulations suggest that polymer chains or chain segments near the free surfaces of the films have greater mobility than the polymer in the interior of the film (Torres et al., 2000). We postulate that as the film thickness decreases, the fraction of the film with higher mobility increases, thereby resulting in the observed monotonic decrease with film thickness (Jain and de Pablo, 2000). In contrast, Tg for supported, ultrathin films has been observed to increase or de
crease with respect to the bulk value, depending on the substrate. Recently, we have shown that the interfacial energy, γsl, between the substrate and the polymer is a significant parameter that governs the Tg of supported, ultrathin films (Fryer et al., 2001). The Tg of the films was characterized using local thermal analysis (a technique we developed at the University of Wisconsin [Fryer et al., 2000 ]), ellipsometry, and x-ray reflectivity. We have also demonstrated that the Tg of a 100-nm film of a model-resist resin, poly(4-hydroxystyrene) (PHS), is elevated above the bulk Tg by as much as 55°C by grafting the polymer to the substrate (Tate et al., 2001).
In the bulk, transport properties such as diffusion coefficients increase by several orders of magnitude in the narrow range of temperature over which the material undergoes a transition from a glass to a rubber (Nealey et al., 1993, 1994). Similarly, mechanical properties such as the Young’s modulus decrease by 2 to 4 orders of magnitude over this same temperature range. Although the dimension dependence of Tg is now fairly well documented, less is known about mass transport and mechanical properties of polymers that are also likely to be dimension dependent. It is difficult to interpret consistently the current literature on diffusion in supported, thin films. Several studies report that chain diffusion slows in thin films (Frank et al., 1996) while dye diffusion has been reported to increase significantly (Tseng et al., 2000). We are not aware of any published reports on dimension-dependent mechanical properties of amorphous polymers.
In most commercial applications of films and coatings, the thickness of the polymer does not approach the sub-100 nm scale, and the dimension-dependent phenomena referred to above do not affect the properties, processing, or usefulness of the materials. However, in the microelectronics industry, the largest section of the U.S. economy, dimension-dependent properties of polymer nanostructures are anticipated to pose significant challenges, particularly with sub-100 nm patterning of photoresist materials (consisting of a polymer and photo-sensitive additives) by advanced lithography. To reach critical patterning dimensions of less than 100 nm, for example, the industry may be forced to use ultrathin films of polymer photoresist in conjunction with 157 nm and extreme ultraviolet (13.4 nm) lithography, due to the opacity of organic materials at these wavelengths (Brodsky et al., 2000; Stewart et al., 2000). In these systems, resist formulations and processing conditions may have to be optimized as a function of thickness for control over the transport of small molecules (e.g., photo-generated acids in films of chemically amplified photoresists), particularly during postexposure annealing (or “bake”) (Fryer et al., 1999; Postnikov et al., 1999). The thermophysical and mass-transport properties of the films affect the sensitivity, resolution, contrast, and line-edge roughness of the photoresist. Optimization may be difficult because diffusion coefficients of probe molecules change by orders of magnitude as the temperature is varied within 15oC of Tg.
Dimension-dependent mechanical properties may pose the greatest challenges to the lithographic process and to nanofabrication techniques in general.

FIGURE 1 Collapse behavior of photoresist structures (Apex-E, pitch = 400 nm, line-width = 200 nm).
In the bulk, the mechanical properties and the glass transition of a material are related; the shear modulus, for example, increases substantially as the temperature is decreased below Tg. It is therefore natural to anticipate similar relations in nanoscopic structures. When the distance between patterned resist structures (or MEMS [microelectromechanical systems] components) decreases, tremendous capillary forces are produced during drying of rinse liquids (e.g., water, after wet chemical processing) (Cao et al., 2000). These forces can cause the structures to collapse (see Figure 1) (Cao et al., 2000; Goldfarb et al., 2000; Namatsu et al., 1999). For arrays of dense (1:1) and semidense (1:2-1:5) lines with widths of 100 to 200 nm and aspect ratios of 3 to 4, we have shown that the susceptibility to collapse is strongly dependent on the aspect ratio and that the critical aspect ratio of collapse is inversely proportional to the distance between structures (Cao et al., 2000). These observations are consistent with models of capillary forces that predict that the force acting on the resist structures is inversely proportional to the distance between structures. They are also consistent with beam-bending models that predict that the maximum deformation of the resist structure in response to the imposed force is proportional to the aspect ratio cubed and is inversely proportional to the stiffness (Young’s modulus).
The focus of our efforts over the last few years has been to fill a serious gap that hinders the development of nanotechnology and to develop a fundamental understanding of the properties of nanostructured polymeric materials. Through a combination of theoretical and experimental work, we have attempted to acquire a fundamental understanding of transport and mechanical properties of nanostructured polymers, because precisely these properties often determine their usefulness in coating, packaging, MEMS, microelectronic, and nanotechnology
applications in general. We believe describing these systems with molecular-level models is essential to interpreting experimental results, guiding experimental design, and identifying new size-dependent phenomena. One broad objective of our research has been to determine the scale, if any, at which continuum-level representations of a material become inadequate.
MECHANICAL PROPERTIES OF NANOSTRUCTURED POLYMER SYSTEMS
One of the major aims of our research has been to quantify the mechanical properties of three-dimensional polymer nanostructures. Possible techniques to make these measurements include surface acoustic wave (SAW) analysis and scanning probe techniques. Unfortunately, the SAW techniques yield high-frequency mechanical properties that are difficult to extrapolate to the more relevant static or low-frequency regime. Scanning probe techniques, such as measuring the torsion of a cantilever required to push over a photoresist structure with dimensions of 100 to 200 nm are not convenient because of the gross mismatch in stiffness between standard cantilever beams and the polymer. To circumvent these problems, we have developed a formalism in which well defined forces are imposed on three-dimensional polymer nanostructures using simple and elegant principles from the classical thermodynamics of surface tension.
Test structures of poly-(methylmethacrylate) (PMMA) have been patterned using advanced lithographic techniques (electron-beam lithography). Images of sample structures and the principles of our experiments are depicted in Figure 2. The difference between the pressure in the liquid between structures and the pressure of the atmosphere is given by the Laplace equation; it is inversely proportional to the distance between the structures, assuming that gravitational effects are negligible at this scale and that the curvature of the meniscus can be modeled as a cylindrical surface (determined by the contact angle of the fluid in contact with the polymer). The net force on the structures is determined by the difference in pressure on the opposing walls of the structures times the surface area of the walls. Known forces can be applied by carefully choosing the dimensions and geometry of the system and slowly drying the structures initially immersed in liquid. The deformation behavior of the structures in response to the imposed force cannot be monitored in real time; the force increases as the distance between structures decreases (after deformation begins); and we don’t yet have analytical techniques to monitor the deformation of the nanostructures. Instead, we observe whether the structures are collapsed or not after complete drying and the severity of collapse as parameterized by the normalized collapse length (touching length of the beams/initial beam length) to calculate the mechanical properties of the structures with appropriate continuum-level and molecular-level models of the collapse process (see below). Our results confirm
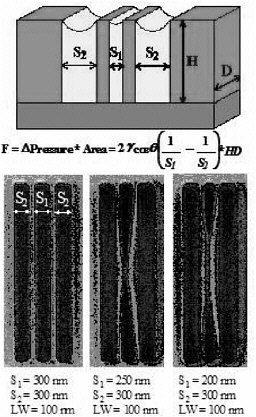
FIGURE 2 Schematic and scanning electron microscope (SEM) images of test structures in which well-defined capillary forces are applied to the walls of three-dimensional polymer nanostructures.
that the severity of collapse of 100-nm test structures scales with the initial capillary force for a number of different combinations of structure spacings.
Structures such as those depicted above have been patterned with linewidths from 300 nm to 90 nm, aspect ratios from 4 to 8, and distances or spacings between structures also in the 100- to 400-nm regime. A critical aspect ratio for collapse has been extracted from these experiments. Experimental critical aspect ratio data have been compared to those predicted using a simple continuum elastoplastic model of the polymeric material, with bulk values of the yield stress and the Young’s modulus. Figure 3 shows some of our results for nanoscopic structures having widths as small as 100 nm; the agreement between continuum-level predictions using bulk material properties and experimental data is quantitative. Note, however, that below 100 nm, preliminary experimental results suggest that mechanical properties start to deviate from the bulk. Unfortunately experiments on smaller structures become increasingly difficult, and to anticipate the behavior of ultrasmall nanoscopic structures we must turn to molecular simulations.
Molecular simulations of virtual bending experiments of ultrasmall structures can be performed by applying a lateral force to a feature; the resulting deflection is measured to extract a modulus of elasticity. Simulations of a coarse-grained model of polystyrene have revealed that the Young’s modulus of poly
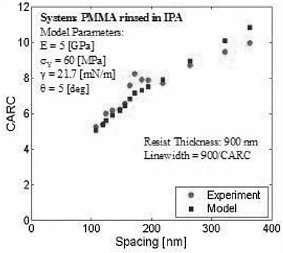
FIGURE 3 Critical aspect ratio for collapse (CARC) for PMMA rinsed in isopropyl alcohol. The material properties, surface tension, and contact angle were all determined from independent experiments on bulk samples.
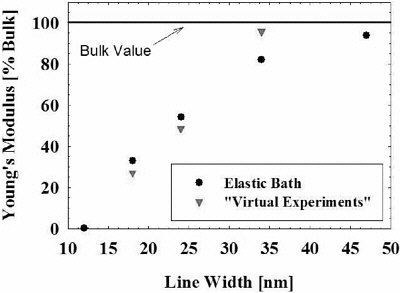
FIGURE 4 Young’s modulus (normalized with respect to the bulk value) of nanoscopic structures (lines) as a function of width. The triangular symbols correspond to simulated bending and the circular symbols are from strain fluctuations in an elastic bath.
styrene exhibits a pronounced decrease below 50 nm (see Figures 4 and 5) (Boehm and de Pablo, 2002). The model used in our simulations consists of spherical Lennard-Jones interaction sites interconnected by harmonic bonds. This remarkable size-induced softening is reminiscent of a glass-to-rubber transition in the bulk, but it has not been considered before. A second intriguing result of our
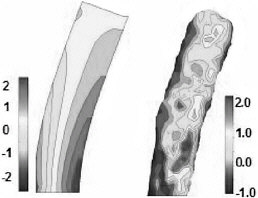
FIGURE 5 Cross-section view of the distribution of reduced normal stresses in a nanoscopic structure. The aspect ratio is 4, and the width is approximately 20 nm. The figure on the left corresponds to finite-element calculations, and that on the right corresponds to molecular simulations of a coarse-grained polymeric model.
simulations is that the spatial density and stress distributions in molecular nanostructures are markedly different from those predicted by continuum mechanics. Figure 5 shows the distribution of normal stresses in a polymeric line with a width of 20 nm and an aspect ratio of 4. On the left, we show numerical finite-element results from our elasticity-theory continuum analysis. On the right, we show the results of molecular simulations for a material with exactly the same bulk mechanical constants. Clearly, the stress distribution from continuum mechanics is unable to capture the phenomena at play in nanostructures; for the models considered in our work, the assumption of a mechanical continuum starts to deviate from the continuum observed in molecular models of nanoscopic polymeric structures between 50 and 70 nm.
The virtual bending experiments described above have the advantage that they mimic precisely a deformation experiment using an atomic force microscope. Unfortunately, these calculations are particularly demanding and are subject to large statistical uncertainty. To eliminate this problem, we have implemented novel simulation techniques in which nanoscopic lines are immersed in elastic media with well-defined mechanical properties (Van Workum, 2002). The elastic constants of the lines are inferred from simulations of the resulting composite material. These simulations have allowed us to determine all of the elastic constants of a nanoscopic structure from a single simulation and enabled the study of the development of anisotropy as we reach small dimensions. As illustrated in Figure 6, these calculations have shown that the elastic constants of nanoscopic structures are highly anisotropic.
Recently we have also developed a stress-fluctuation-based formalism to evaluate local elastic constants from molecular simulations. One of the assumptions implicit in continuum-level models of a pure material is that the moduli of elasticity are homogeneous throughout the system. This might not be the case, however, in glassy, amorphous polymeric systems. Figure 7 shows a cross section of a nanoscopic polymeric structure. The density distribution is shown on the left; density fluctuations are relatively small (a few percent) and are distribut
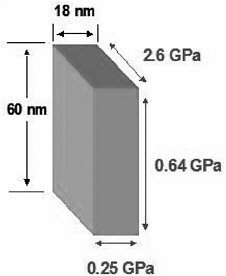
FIGURE 6 Elastic moduli of a nanoscopic polymeric structure determined from simulations of strain fluctuations. The bulk value is 3 Gpa.

FIGURE 7 Cross-sectional view of the local density (left) and local elastic constant (right) distribution of a model polymeric nanostructure. The density is shown in reduced (Lennard-Jones) units, and the elastic constants are shown as a percentage of the bulk value.
ed uniformly throughout the structure. The local elastic modulus corresponding to the stress that arises upon vertical compression (in the direction normal to the substrate) of the structures is shown on the right. Near the air-polymer interface the material exhibits a gradual softening. Near the polymer-substrate interface the material undergoes a pronounced layering, which gives rise to large local elastic moduli. In the core of the structure, however, the local elastic constants
of nanoscopic polymeric structures reveal distinct “soft” and “hard” domains. These domains have characteristic dimensions of approximately 2 to 4 nm and may be related to the so-called “dynamic heterogeneities” that have been postulated in the literature to explain experimental data for bulk, polymeric glasses (Ediger and Skinner, 2001).
CONCLUSIONS
Our experiments and simulations to date have revealed that, above approximately 100 nm, the mechanical behavior of nanoscopic polymeric structures can be described using continuum formalisms and bulk material properties. At smaller length scales, our results suggest that amorphous polymeric structures exhibit dimension-dependent, anisotropic, elastic constants. Furthermore, our calculations of local elastic constants indicate the existence of mechanical inhomogeneities on the scale of a few nanometers.
The calculations we have performed to date have been carried out on extremely simple polymer models, and our experiments have been limited to structures of approximately 100 nm. The extent to which specific interactions, temperature, molecular weight, and plasticizers influence the behavior described here remains unknown and is likely to become a fertile area of research in the years to come. Fundamental understanding of factors leading to size-dependent mechanical properties will result in strategies to improve the mechanical properties of nanoscopic polymer structures and eliminate collapse.
REFERENCES
Boehme, T., and J.J. de Pablo. 2002. Evidence for size-dependent mechanical properties from simulations of nanoscopic polymeric structures. Journal of Chemical Physics 116(9): 9939-9951.
Brodsky, C., J. Byers, W. Conley, R. Hung, S. Yamada, K. Patterson, M. Somervell, B. Trinque, H.-V. Tran, S. Cho, T. Chiba, S.-H. Lin, A. Jamieson, H. Johnson, T. Vander Heyden, and C.G. Wilson. 2000. 157 nm resist materials: progress report. Journal of Vacuum Science and Technology B 18(6): 3396-3401.
Cao, H.B., P.F. Nealey, and W.D. Domke. 2000. Comparison of resist collapse properties for deep ultraviolet and 193 nm resist platforms. Journal of Vacuum Science and Technology B 18(6): 3303-3307.
Ediger, M.D., and J.L. Skinner. 2001. Single molecules rock and roll near the glass transition. Science 292(5515): 233-234.
Forrest, J.A., K. Dalnoki-Veress, J.R. Stevens, and J.R. Dutcher. 1996. Effect of free surfaces on the glass transition temperature of thin polymer films . Physical Review Letters 77(10): 2002-2005.
Forrest, J.A., and K. Dalnoki-Veress. 2001. The glass transition in thin polymer films. Advances in Colloid and Interface Science 94(1-3): 167-196.
Frank, B., A.P. Gast, T.P. Russell, H.R. Brown, and C. Hawker. 1996. Polymer mobility in thin films. Macromolecules 29(20): 6531-6534.
Fryer, D.S., S. Bollepali, J.J. de Pablo, and P.F. Nealey. 1999. Study of acid diffusion in resist near the glass transition temperature. Journal of Vacuum Science and Technology B 17(6): 3351-3355.
Fryer, D.S., P.F. Nealey, and J.J. de Pablo. 2000. Thermal probe measurements of the glass transition for ultrathin polymer films as a function of thickness. Macromolecules 33(17): 6439-6447.
Fryer, D.S., R.D. Peters, E.J. Kim, J.E. Tomaszewski, J.J. de Pablo, P.F. Nealey, C.C. White, and W.-I. Wu. 2001. Dependence of the glass transition temperature of polymer films on interfacial energy and thickness. Macromolecules 34(16): 5627-5634.
Goldfarb, D.L., P.F. Nealey, J.P. Simons, W.M. Moreau, and M. Angelopoulos. 2000. Aqueousbased photoresist drying using supercritical carbon dioxide to prevent pattern collapse. Journal of Vacuum Science and Technology B 18(6): 3313-3317.
Jain, T.S., and J.J. de Pablo. 2002. Monte Carlo simulation of freestanding polymer films near the glass transition temperature. Macromolecules 35(6): 2167-2176.
Murray, C.B., C.R. Kagan, and M.G. Bawendi. 2000. Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies. Annual Review of Materials Science 30: 545-610.
Namatsu, H., K. Yamazaki, and K. Kurihara. 1999. Supercritical drying for nanostructure fabrication without pattern collapse. Microelectronic Engineering 46(1-4): 129-132.
Nealey, P.F., R.E. Cohen, and A.S. Argon. 1993. Solubility and diffusion of polybutadiene in polystyrene at elevated temperatures. Macromolecules 26(6): 1287-1292.
Nealey, P.F., R.E. Cohen, and A.S. Argon. 1994. Effect of gas pressure on the solubility and diffusion of polybutadiene in polystyrene. Macromolecules 27(15): 4193-4197.
Postnikov, S.V., M.D. Stewart, H.V. Tran, M.A. Nierode, D.R. Medeiros, T. Cao, J. Byers, S.E. Webber, C.G. Wilson. 1999. Study of resolution limits due to intrinsic bias in chemically amplified photoresists. Journal of Vacuum Science and Technology B 17(6): 3335-3338.
Stewart, M.D., K. Patterson, M.H. Somervell, and C.G. Wilson. 2000. Organic imaging materials: a view of the future. Journal of Physical Organic Chemistry 13(12): 767-774.
Tate, R.S., D.S. Fryer, S. Pasqualini, M.F. Montague, J.J. de Pablo, and P.F. Nealey. 2001. Extraordinary elevation of the glass transition temperature of the polymer films grafted to silicon oxide substrates. Journal of Chemical Physics 115(21): 9982-9990.
Torres, J.A., P.F. Nealey, and J.J. de Pablo. 2000. Molecular simulation of ultrathin polymeric films near the glass transition . Physical Review Letters 85(15): 3221-3224.
Tseng, K.C., N.J. Turro, and C.J. Durning. 2000. Molecular mobility in polymer thin films. Physical Review E 61(2): 1800-1811.
Van Workum, K. 2002. Mechanical properties of polymeric nanostructures. PhD Thesis, University of Wisconsin.
The Role of Computational Fluid Dynamics in Process Industries
DAVID LEE DAVIDSON
Solutia, Inc.
Cantonment, Florida
Continuum mechanics, one of our most successful physical theories, is readily applicable to the process industries. In continuum mechanics, the existence of molecules is ignored, and matter is treated as a continuous medium. The continuum hypothesis is valid, provided the equations of continuum mechanics are applied at sufficiently large length scales and time scales that the properties of individual molecules are not noticed. The mapping of the laws of mass, momentum, and energy conservation to the continuum results in field equations that describe the dynamics of the continuum. These field equations, variously known as the equations of motion, the equations of change, or simply the conservation equations, are nonlinear, partial differential equations that can be solved, in principle, when combined with the appropriate constitutive information1 and boundary conditions.
Continuum mechanics is the mechanical analog of classical electrodynamics, in which a set of field equations (Maxwell’s equations) describe the dynamics of the relevant variables of the electrical and magnetic fields. Whereas Maxwell’s equations are linear unless the constitutive behavior is nonlinear, the equations of continuum mechanics are nonlinear, regardless of the constitutive behavior of the materials of interest. The inherent nonlinearity of the conservation equations, which is due to convective transport of momentum, energy, and
chemical species, is responsible for certain fluid mechanical phenomena, such as turbulence, that have no electrodynamic analog and that complicate solution of the conservation equations.
Analytical solutions (e.g., obtained by eigenfunction expansion, Fourier transform, similarity transform, perturbation methods, and the solution of ordinary differential equations for one-dimensional problems) to the conservation equations are of great interest, of course, but they can be obtained only under restricted conditions. When the equations can be rendered linear (e.g., when transport of the conserved quantities of interest is dominated by diffusion rather than convection) analytical solutions are often possible, provided the geometry of the domain and the boundary conditions are not too complicated. When the equations are nonlinear, analytical solutions are sometimes possible, again provided the boundary conditions and geometry are relatively simple. Even when the problem is dominated by diffusive transport and the geometry and boundary conditions are simple, nonlinear constitutive behavior can eliminate the possibility of analytical solution.
Consequently, numerical solution of the equations of change has been an important research topic for many decades, both in solid mechanics and in fluid mechanics. Solid mechanics is significantly simpler than fluid mechanics because of the absence of the nonlinear convection term, and the finite element method has become the standard method. In fluid mechanics, however, the finite element method is primarily used for laminar flows, and other methods, such as the finite difference and finite volume methods, are used for both laminar and turbulent flows. The recently developed lattice-Boltzmann method is also being used, primarily in academic circles. All of these methods involve the approximation of the field equations defined over a continuous domain by discrete equations associated with a finite set of discrete points within the domain and specified by the user, directly or through an automated algorithm. Regardless of the method, the numerical solution of the conservation equations for fluid flow is known as computational fluid dynamics (CFD).
CFD was initially done without automation because the need to solve these equations (e.g., in aircraft design) preceded the development of electronic computers by several decades. With the advent of electronic computers, more ambitious numerical calculations became possible. Initially, CFD codes were written for specific problems. It was natural to generalize these codes somewhat, and eventually, particularly as computational resources became more readily available, general-purpose CFD codes were developed. It was then recognized that a business could be built upon the development and licensing of these codes to industrial, academic, and government users. Today, many of the general-purpose commercial codes are quite sophisticated, cost a tiny fraction of their development cost, and are probably the mainstay of the industrial application of CFD.
Four steps are required to apply a general-purpose CFD code to an industrial problem. First, the domain must be defined. This amounts to constructing the
geometry for the problem,2 which is typically done using a computer-assisted design (CAD)-like preprocessor.3 Within the preprocessor, relevant physics are defined, appropriate models are specified, boundary and initial conditions are applied, and solver parameters are specified. Because the conservation and constitutive equations must be discretized on the specified geometry, the domain discretization must be specified. This process, known as meshing or grid generation, is the second step in the application of a CFD code to an industrial problem. Meshing can be accomplished using two basic protocols: (1) structured meshing, which involves creating an assembly of regular, usually hexahedral (quadrilateral in two dimensions) elements or control volumes throughout the domain; and (2) unstructured meshing, which involves filling the geometry with control volumes, often tetrahedrons and prisms, in an irregular fashion. Unstructured mesh generators are usually simpler to use with complicated geometries and involve some degree of automation. For example, the user may specify one or more measures of surface grid density, and the mesh generator will fill the volume with elements according to some algorithm. In the third step, the equations are discretized over the specified grid, and the resulting nonlinear4 algebraic equations are solved. The development of solvers is still an active area of research, the goal being to improve the likelihood and rate of convergence. The fourth step, after satisfactory convergence is obtained, is to interrogate the solution to obtain the desired information. That information may be a single number extracted from the solution data set, an animation illustrating the transient macroscopic behavior of the entire flow field, or anything in between. Because the data sets can be quite large,5 robust tools for data set interrogation are often required. These are usually provided with the commercial CFD codes, but one leading commercial tool is a stand-alone CFD postprocessor (FIELDVIEW, 2002).
CURRENT INDUSTRIAL APPLICATIONS
CFD is routinely used today in a wide variety of disciplines and industries, including aerospace, automotive, power generation, chemical manufacturing, polymer processing, petroleum exploration, medical research, meteorology, and astrophysics. The use of CFD in the process industries has led to reductions in
the cost of product and process development and optimization activities (by reducing down time), reduced the need for physical experimentation, shortened time to market, improved design reliability, increased conversions and yields, and facilitated the resolution of environmental, health, and right-to-operate issues. It follows that the economic benefit of using CFD has been substantial, although detailed economic analyses are rarely reported. A case study of the economic benefit of the application of CFD in one chemical and engineered-material company over a six-year period conservatively estimated that the application of CFD generated approximately a six-fold return on the total investment in CFD (Davidson, 2001a).
CFD has an enormous potential impact on industry because the solution of the equations of motion provides everything that is meaningful to know about the domain. For example, chemical engineers commonly make assumptions about the fluid mechanics in process units and piping that lead to great simplifications in the equations of motion. An agitated chemical reactor may be designed on the assumption that the material in the vessel is completely mixed, when, in reality, it is probably not completely mixed. Consequently, the fluid mechanics may limit the reaction rather than the reaction kinetics, and the design may be inadequate. CFD allows one to simulate the reactor without making any assumptions about the macroscopic flow pattern and thus to design the vessel properly the first time. Similarly, the geometrically complicated parts required for melt spinning can be designed with CFD rather than rules-of-thumb or experiments, resulting in “right the first time” designs (Davidson, 2001b). Commercial publications (e.g., CFX Update, Fluent News, and Applications from the Chemical Process Industry) are filled with case studies illustrating how CFD was applied to the design of a particular unit, the optimization of a particular process, or the analysis of a particular phenomenon with good results.
AREAS OF RESEARCH
There are, of course, limitations to the application of CFD, and active research is being done to overcome them. The primary limitation is in the area of turbulent flow. Turbulent flows are solutions to the equations of motion and can be computed directly, at least in principle. This approach, known as direct numerical simulation, requires a spatial grid fine enough to capture the smallest length scale of the turbulent fluid motion (the Kolmogorov scale) throughout the domain of interest and a correspondingly small time step. In typical problems of industrial interest, the ratio of the length scale of the domain to the Kolmogorov length scale is so large that the required grid is prohibitively large. Available computational resources are usually inadequate for this task except for relatively simple problems.
Consequently, industrial practitioners of CFD use turbulence models, usually by solving the Reynolds-averaged equations, that is, equations generated by
averaging the equations of motion over a time scale that is much larger than the time scale of the turbulent fluctuations but much smaller than the smallest time scale of interest in the application. This procedure results in a set of equations that have the same form as the original equations of motion, but with time-averaged quantities in place of instantaneous quantities, plus one additional term that arises from the nonlinear convective terms in the original equations of motion. In the Reynolds-averaged momentum-conservation equation, for example, this additional term has the form of an additional stress, known as the Reynolds stress. This term is modeled based on the time-averaged quantities of the flow field. A variety of turbulence models are available (Wilcox, 1998), but the workhorse model of industrial CFD is the so-called k-epsilon model, which was introduced several decades ago (Casey and Wintergerste, 2000; Launder and Spalding, 1974). These turbulence models can lead to significant inaccuracies, and CFD practitioners must use them carefully.
Large eddy simulation (LES) is an alternative approach to turbulence modeling. Turbulent flows are characterized by an eddy cascade, in which large eddies transfer their kinetic energy to smaller eddies, which in turn transfer kinetic energy to even smaller eddies, and so on until, at the Kolmogorov scale, the kinetic energy is transformed into heat. LES attempts to solve for the larger eddies directly while modeling the smaller eddies. Although LES is more computationally intensive than other kinds of turbulence modeling, it has been applied to industrial-scale problems (Derksen, 2001).
The second great limitation of CFD is dispersed, multiphase flows. Multiphase flows are common in industry, and consequently their simulation is of great interest. Like turbulent flows, multiphase flows (which may also be turbulent in one or more phases) are solutions to the equations of motion, and direct numerical simulation has been applied to them (Miller and Bellan, 2000). However, practical multiphase flow problems require a modeling approach. The models, however, tend to ignore or at best simplify many of the important details of the flow, such as droplet or particle shape and their impact on interphase mass, energy, and momentum transport, the impact of deformation rate on droplet breakup and coalescence, and the formation of macroscopic structures within the dispersed phase (Sundaresan et al., 1998).
ENTERPRISE-WIDE ACCESS
Although the commercial CFD industry has greatly simplified the use of CFD codes by providing CAD-like preprocessors, automatic mesh generation, graphical user interfaces for all aspects of model definition, and on-line documentation, the industrial practice of CFD is still primarily in the hands of specialists. Regular use of a general-purpose code requires significant expertise in transport phenomena, an understanding of the capabilities and limitations of the modeling approaches used to handle turbulence and dispersed multiphase flows,
an understanding of the relationship between mesh quality, convergence, and solution accuracy, and proficiency with the various means of interacting with the CFD code, including the graphical user interface, advanced command languages (when available), and user-accessible FORTRAN subroutines.6 For these reasons, attempts to train large numbers of engineers in the use of CFD have not been very successful (Davidson, 2001a). Nevertheless, the potential benefit of a much broader CFD user base is very great. In our opinion, CFD should be accessible to every person in the enterprise who makes decisions the outcomes of which are governed by the laws of physics, from the CEO who makes strategic business decisions based on business goals to the operator who adjusts valve positions to meet process goals.
We believe that this can be achieved through the development of so-called “digital experts,” stand-alone CFD (and other) applications that would be integrated into commercial CFD codes (as appropriate) and wrapped in interfaces that speak the language of the industrial application, not the language of CFD. Digital experts would automate geometry construction, mesh generation, solver selection, and other processes behind the scenes. In addition, they would contain all of the algorithms necessary to nurse the CFD codes to solution automatically, without having to ask the user to define satisfactory convergence, for example. Finally, they would extract the essential ingredients from the complete CFD solution and present them to the user in a convenient and familiar format, so the user would not have to be concerned with interrogation of the flow field by computation or visualization. A discussion of one digital expert that has been developed for melt-fiber spinning has been published (Davidson, 2001b).
The decision to develop an industrial digital expert is based on the relationship between development cost and benefit. Recently, a commercial product has become available with the potential to change that relationship significantly. EASA™ (Enterprise Accessible Software Applications from AEA Technology), which was designed to help industrial practitioners develop digital experts, solves a number of problems for industrial developers, including construction of the graphical user interface, accessibility of the final product (the digital expert or EASAp) over the enterprise intranet, and the orchestration of computations on a heterogeneous computer network (Dewhurst, 2001). In essence, EASA allows an industrial CFD specialist to put bullet-proof digital experts in the hands of his or her coworkers, with a consistent interface tailored to the user.
SUMMARY
CFD is a powerful tool for solving a wide variety of industrial problems. Commercial general-purpose codes have the potential to solve a very broad spectrum of flow problems. Current research is concentrated on overcoming the principle weaknesses of CFD, namely how it deals with turbulence and dispersed multiphase flows. Development work on solver algorithms, meshing, and user interface generation are ongoing, with the objectives of improving accuracy, reducing solution time, and increasing accessibility. In spite of the limitations of CFD, the economic value of industrial applications has been demonstrated in a variety of industries, and its value as a research tool has been accepted in many areas, such as meteorology, medicine, and astrophysics. In industry, CFD is presently primarily in the hands of specialists, but the development of digital experts and tools to facilitate the development of digital experts may revolutionize the way industry uses CFD by providing ready access throughout the enterprise. This would result in significant gains in productivity and profitability.
REFERENCES
Casey, M., and T. Wintergerste, eds. 2000. Best Practice Guidelines. Brussels: European Research Community on Flow, Turbulence and Combustion.
Davidson, D.L. 2001a. The Enterprise-Wide Application of Computational Fluid Dynamics in the Chemicals Industry. Proceedings of the 6th World Congress of Chemical Engineering. Available on Conference Media CD, Melbourne, Australia.
Davidson, D.L. 2001b. SpinExpert: The Digital Expert for the Design and Analysis of Fiber Spinning Operations. Pp. 219-226 in Proceedings of the 3rd International ASME Symposium on Computational Technology (CFD) for Fluid/Thermal/Chemical/Stress Systems and Industrial Applications. Atlanta, Ga.: American Society of Mechanical Engineers.
Derksen, J.J. 2001. Applications of Lattice-Boltzmann-Based Large-Eddy Simulations. Pp. 1-11 in Proceedings of the 3rd International ASME Symposium on Computational Technology (CFD) for Fluid/Thermal/Chemical/Stress Systems and Industrial Applications. Atlanta, Ga.: American Society of Mechanical Engineers.
Dewhurst, S. 2001. An exciting new way to deploy your CFD. CFX Update 21: 6.
FIELDVIEW. 2002. Intelligent Light Website. Available online at: <http://www.ilight.com>.
Launder, B.E., and D.B. Spalding. 1974. The numerical computation of turbulent flow. Computational Methods in Applied Mechanics and Engineering 3: 269–289.
Miller, R.S., and J. Bellan. 2000. Direct numerical simulation and subgrid analysis of a transitional droplet laden mixing layer. Physics of Fluids 12(3): 650–671.
Sundaresan, S., B.J. Glasser, and I.G. Kevrekidis. 1998. From bubbles to clusters in fluidized beds. Physical Review Letters 81(9): 1849–1852.
Wilcox, D.C. 1998. Turbulence Modeling for CFD. La Canada, Calif.: DCW Industries Inc.
SUGGESTED READINGS
Anderson, D.A., J.C. Tannehill, and R.H. Pletcher. 1984. Computational Fluid Mechanics and Heat Transfer. New York: Hemisphere Publishing Corp.
Batchelor, G.K. 1977. An Introduction to Fluid Dynamics. London: Cambridge University Press.
Berg, P.W., and J.L. McGregor. 1966. Elementary Partial Differential Equations. Oakland, Calif.: Holden-Day.
Bird, R.B., W.E. Stewart, and E.N. Lightfoot. 1960. Transport Phenomena. New York: John Wiley & Sons.
Carslaw, H.S., and J.C. Jaeger. 1959. Conduction of Heat in Solids. Oxford, U.K.: Clarendon Press.
Chandrasekhar, S. 1981. Hydrodynamic and Hydromagnetic Stability. New York: Dover Press.
Crochet, M.J., A.R. Davies, and K. Walters. 1984. Numerical Simulation of Non-Newtonian Flow. Amsterdam: Elsevier Science Publishers.
Jackson, J.D. 1975. Classical Electrodynamics. New York: John Wiley & Sons.
Schowalter, W.R. 1978. Mechanics of Non-Newtonian Fluids. Oxford, U.K.: Pergamon Press.
Van Dyke, M. 1975. Perturbation Methods in Fluid Mechanics. Stanford, Calif.: Parabolic Press.
Whitaker, S. 1984. Introduction to Fluid Mechanics. Malabar, Fla.: Krieger Publishing Co.