Appendix E
Computational Modeling and Simulation of Epidemic Infectious Diseases
Donald S. Burke, M.D.
Bloomberg School of Public Health
Johns Hopkins University
I simply wish that, in a matter which so closely concerns the well-being of mankind, no decision shall be made without all the knowledge which a little analysis and calculation can provide.
Daniel Bernoulli, on smallpox inoculation, 1766
HISTORICAL FOUNDATIONS
Mathematics and statistics have been essential to the theory and practice of infectious disease control since 1766, when Bernoulli analyzed life expectancies and death rates in his evaluation of variolation as a public health tool (Dietz, 2000). Subsequently, Philip-Charles Alexandre Louis in France and William Farr in Britain melded quantitative epidemiological measurements with philosophical concepts of social justice, a synthesis from which the statistical hygienic movement was born (Lilienfeld, 1980). The second era of epidemiology arose at the turn of the twentieth century with the proof of the germ theory and the development of mechanistic mathematical models, first by the brilliant Ronald Ross, who used his own malaria field research data to guide the construction of sophisticated mathematical models (Serfling, 1952). In the 1930s Kermack and McKendrick formulated the now familiar “S-E-I-R” (susceptible, exposed, infected, and removed) deterministic differential equations models for the transmission of infectious diseases (Serfling, 1952). Stochasticity—the role of chance— was subsequently added to the models.
In its third era (the past few decades), epidemiology has moved away from its classical foundations in infectious diseases to focus on chronic diseases, and, of necessity, reverted to an emphasis on statistical identification of risk factors rather than elucidation of mechanisms and dynamics. Some leaders in the field rue this development. Dr. Mervin Susser, a highly respected statesman–epidemiologist, recently admonished his fellow epidemiologists to adopt a multilevel, systems analysis, “eco-epidemiology” approach (Susser and Susser, 1996a, 1996b). Others have argued that modern epidemiology must fully embrace new powerful computational technologies to analyze, model, and simulate the dynamics of disease generation and propagation (Koopman, 1996).
TOWARD A NEW SCIENCE OF EXPERIMENTAL EPIDEMIOLOGY
Epidemiology is not commonly considered to be an experimental science. The discipline concerns itself with large populations of ill (or potentially ill) humans, and rigorously controlled experimental designs are rarely practical or ethical. When prospective epidemiological studies are undertaken, as in Phase III efficacy trials of vaccines, study population size limitations are such that usually only one new intervention can be evaluated. Mathematical and statistical modeling is invaluable in the design and interpretation of epidemiological studies, but is not well suited to simulation of interventions and outcomes. Extraordinary increases in the speed and memory of inexpensive computer processors now make it possible to create and run computations that were impossible only a few years ago, giving rise to computational simulations of unimagined speed, granularity, and stochasticity. Such simulations could serve as dry “laboratories” for a new science of experimental epidemiology in which new population-level interventions could be designed, evaluated, and iteratively refined on simulated epidemics, with tangible benefits for real-world epidemic prevention and control efforts. Successful development of this new science will require interdisciplinary collaborations between epidemiologists and other computationally oriented academic disciplines (Levin et al., 1997). Indeed, some exciting developments have already appeared at these epidemiological/computational interfaces and are briefly reviewed here. They include harmonic decomposition, agent-based modeling, network modeling, and creation of digital organisms.
Harmonic Decomposition Analysis
The tempo, mode, and spatial distribution of an epidemic infectious disease are well understood to reflect external forcing events (e.g., weather or climate), host immune factors (e.g., herd immunity), microbial evolu-
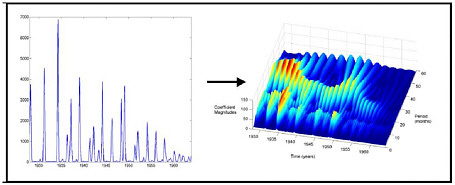
FIGURE E-1 Continuous wavelet transform decomposition of 1928–1964 Baltimore measles time series data showing that the incidence curve is decomposable into a shorter component with a periodicity of 12 months, and a longer component with a variable periodicity of 24–36 months. The longer component correlates closely with changes in birth rates.
tion, and population-level control efforts, as well as the complex dynamic interplay among these factors. Recently, new analytic techniques borrowed from physics, such as Fourier analysis and wavelet analysis, have permitted the decomposition of temporo-spatial epidemic harmonics (the aggregate signal) into modes, each of which may reflect only one of the underlying factors. For example, Fourier analysis has been used to decompose dengue and malaria data sets to reveal the weather-independence of interepidemic variability (Rogers et al., 2002; Hay et al., 2000). Of special interest is demonstration of the power of wavelet analysis to decompose measles epidemic harmonics to reveal recurrent spatial spreading patterns not evident in the undecomposed epidemic data. Such preliminary successes with decompositional techniques suggest they will make it possible to analyze and explain the dynamics of many infectious diseases (Grenfell et al., 2001; Strebel and Cochi, 2001).
Agent-Based Models
Agent-based computational models are computer programs in which a population of individual entities is created, and each individual is endowed with simple rules for interactions with the environment and with other individuals (Holland, 1995). Agents are typically programmed as two-dimensional entities that are distributed across a two-dimensional surface in proximity to other similar agents (but there is no inherent limit on this dimensionality). As the model runs, agents move over the surface and inter-
act with each other. As has been generally observed in the field of complexity studies, remarkably complex behaviors can emerge at a group level from very simple rules governing interagent behaviors. Indeed, Wolfram (2002) suggested that one simple variety of agent-based computational models, termed cellular automata (immobile, identical, grid-based agents), can be used to model all manner of complex scientific phenomena. To date, agent-based models have been used primarily in social and economic modeling. Epstein and Axtell (1996) made an early seminal contribution, and, more recently, a full supplement of the Proceedings of the National Academy of Sciences was devoted to agent-based modeling in the social sciences (Bankes, 2002). A few promising studies have appeared in which agent-based modeling is used to examine infectious diseases (e.g., influenza) and the immune response (Hofmeyr and Forrest, 2000). The rapid rise in freely available computational power should permit the development of a wide variety of infectious disease agent-based simulations (Swarm Development Group website).
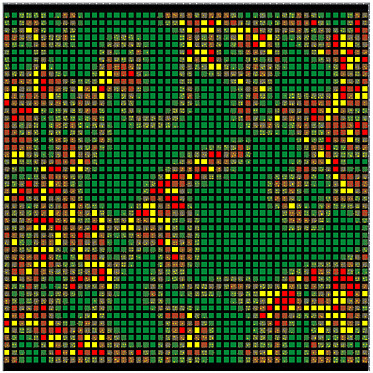
FIGURE E-2 Visual display of a two-dimensional agent-based model. Each square represents an individually programmable, mobile agent. Color-coding allows easy visual tracking of agents with different properties.
Network Models
Social networks have long been known to play a major role in determining the rate and pattern of epidemic spread of microbial diseases in human societies. Attention has focused in particular on the role of population heterogeneities and subnetworks in the spread of sexually transmitted diseases, especially HIV/AIDS; however, little work has been done on the role of network topology in the spread of other infectious diseases. More recently, physicists and computer scientists have become concerned about the spread of infectious agents (e.g., computer viruses, worms, etc.) through the Internet and the World Wide Web.
This welcome new interest in network topology has spawned a minor revolution in network modeling. It is now clear that many natural and human-made networks, from actors (the Kevin Bacon game) to the U.S. electrical power grid to the Internet, all follow a “scale-free” distribution (Barabasi, 2002). The observation that a wide variety of unplanned network topologies may follow a stereotyped pattern has led to research on how networks add nodes and grow (the “emergence” of networks); the factors involved are just beginning to be understood. Furthermore, the crucial role of occasional long-distance internodal connections in shortening global mean path lengths (the “small world” phenomenon) and accelerating epidemic spread has come to be appreciated (Watts, 1999). Recent

FIGURE E-3 Internet routing map (80,000 nodes). See http://www.cs.bell-labs.com/~ches/map/.
work on the tolerance of various abstract network topologies to errors or attacks has been convincingly modeled, and general strategies for improving network stability have been proposed. It appears clear that network models inspired by the Internet will productively inform the modeling of microbial pathogen networks (Albert et al., 2000; Pastor-Satorras and Vesignani, 2001; Lloyd and May, 2001).
Digital Microbes
Evolutionary principles have been widely incorporated into machine learning, artificial intelligence, and computer programming for decades. Indeed, in genetic algorithms—the first and now a standard evolutionary computation technique—code strings are iteratively mutated, recombined, and selected for fitness, just as if they were nucleic acid strings evolving in nature (Burke et al., 1998). Genetic algorithms are now widely employed by computer programmers to solve practical computationally intensive problems, such as protein folding, but only a few studies have appeared in which evolving code strings are used to simulate microbial evolution and adaptation. Preliminary studies suggest that the rules governing code string evolution may be independent of the stuff from which the evolving code strings are made, and that experiments on digital microbes—with code string evolution and epidemiology “in silicon”—may be a productive way to understand and solve problems that are difficult to study in nature (Ray, 1995; Wilke et al., Adami et al., 2000; Radman et al., 1999).
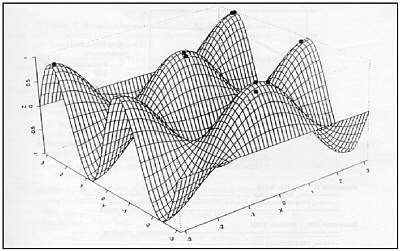
FIGURE E-4 Representation of evolving bit strings in a fitness landscape. In this example populations of strings are shown as dots colonizing local fitness optima in sequence space.
BIOTERRORISM MODELS
An immediate problem facing the United States is whether to reinstitute routine smallpox vaccination of the entire population. Rational alternatives would be to withhold routine vaccination, and use smallpox vaccine only in “ring immunization” of contacts once cases had appeared, or immediately preimmunize some subset of the population and be prepared to implement ring immunization. Critics of modeling argue that models cannot provide clear evidence for or against any option; advocates counter that the purpose of modeling and simulation is not to provide an answer, but to furnish a tool for improving the decision-making process. Indeed, all decisions are based on models (mental or otherwise), but the use of computational models forces all assumptions to be made explicit, and permits a search for nonlinear intervention effects that may not be discovered using intuitive mental models. Particularly in dealing with a hypothetical threat such as smallpox, models and simulations can allow the testing of intervention strategies in silicon that simply cannot be tested in advance, and could never be tested in a real-world bioterrorism emergency.
NEW NATIONAL INITIATIVE IN COMPUTATIONAL EPIDEMIOLOGY
The Center for Discrete Mathematics and Theoretic Computer Science, created by the National Science Foundation, recently established a five-year special focus on computational and mathematical epidemiology (Center for Discrete Mathematics and Theoretic Computer Science webpage, 2001). The objectives are to develop and strengthen collaborations and partnerships between mathematical scientists (mathematicians, computer scientists, operations researchers, statisticians) and biological scientists (biologists, epidemiologists, clinicians), and to identify and explore methods in mathematical science—especially discrete mathematics and algorithms, models, and concepts developed in the field of theoretic computer science— not yet widely used in studying epidemiological problems.
REFERENCES
Adami C, Ofria C, Collier TC. Evolution of biological complexity. Proc Natl Acad Sci 97: 4463–4468 (2000).
Albert R, Jeong H, Barabasi A-L. Error and attack tolerance of complex networks. Nature 406: 378–382 (2000).
Bankes SC. Agent-based modeling: A revolution? Proc Natl Acad Sci 99 (Suppl 3): 7199– 7200 (2002).
Barabasi A-L. Linked: The new science of networks. (2002).
Burke DS, De Jong KA, Grefenstette JJ, Ramsey CL, Wu AS. Putting more genetics into genetic algorithms. Evol Comput 6: 387–410 (1998).
Center for Discrete Mathematics and Theoretical Computer Science. http://www.isd.atr.co.jp/~ray.pubs/tierra.
Dietz K, Heesterbeek JAP. Bernoulli was ahead of modern epidemiology. Nature 408: 513– 514 (2000).
Epstein JM, Axtell RL. Growing artificial societies. Social science from the bottom up. MIT Press, Cambridge, MA (1996).
Grenfell BT, Bjornstad ON, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature 414: 716–723 (2001).
Hay SI Myers MF, Burke DS, et al. Etiology of interepidemic periods of mosquito-borne disease. Proc Natl Acad Sci 97: 9335–9339 (2000).
Hofmeyr SA, Forrest S. Architecture for an artificial immune system. Evol Comput 8: 443– 473 (2000).
Holland JH. Hidden order: How adaptation builds complexity. Addison Wesley (1995).
Koopman JS. Emerging objectives and methods in epidemiology. Am J Public Health 86: 630–632 (1996).
Levin SA, Grenfell B, Hastings A, Perelson AS. Mathematical and computational challenges in population biology and ecosystems science. Science 275: 334–343 (1997).
Lilienfeld AM (Ed). Aspects of the history of epidemiology: times, places, and persons. Johns Hopkins University Press, Baltimore (1980).
Lloyd AL, May RM. Epidemiology: How viruses spread among computers and people. Science 292: 1316–1317 (2001).
Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Let 86: 3200–3203 (2001).
Radman R, Matic I, Taddei F. Evolution of evolvability. Ann N Y Acad Sci. 870: 146–155 (1999).
Ray TS. Evolution, ecology, and optimization of digital organisms. http://www.isd.atr.co.jp/ray/pubs/tierra. 1995.
Rogers D, Randoph S, Snow RW, Hay SI. Satellite imagery in the study and forecast of malaria. Nature 415: 710–715 (2002).
Serfling RE. Historical review of epidemic theory. Human Biology 24: 145–166 (1952).
Strebel PM, Cochi SL. Waving goodbye to measles. Nature 414: 695–696 (2001).
Susser M, Susser E. Choosing a future for epidemiology: I. Eras and paradigms. Am J Pub Health 86: 668–673 (1996a).
Susser M, Susser E. Choosing a future for epidemiology: II. From black box to Chinese boxes and eco-epidemiology. Am J Pub Health 86: 674–677 (1996b).
Swarm Development Group. http://www.swarm.org.
Watts D. Small worlds. The dynamics of networks between order and randomness (1999).
Wilke CO, Wang JL, Ofria C, Lenski RE, Adami C. Evolution of digital organisms at high mutation rates leads to survival of the flattest.
Wolfram S. A new kind of science. Wolfram Media (2002).








