V Committee’s Findings Related to NTPR Dose Reconstruction Program
The committee’s evaluation of the NTPR dose reconstruction program considered not only the validity of central and upper-bound estimates of dose for the assumed exposure scenarios obtained in dose reconstructions, but also the approaches used to determine the veteran’s exposure scenario. The committee’s findings regarding scenario determinations, estimates of external and internal doses and related uncertainty, and estimates of total organ doses from all pathways are discussed below, with examples taken from the 99 individual dose reconstruction cases sampled and from reconstructions for other veterans who provided written consent for use of their records. In parallel with the discussions in Chapter IV, Section V.A discusses scenario determination, Section V.B the estimation of external dose, Section V.C the methods of estimating internal dose, Section V.D the dose reconstructions for occupation forces in Japan, and Section V.E the estimates of uncertainty and upper-bound doses from all radiations and exposure pathways combined. Section V.F summarizes the committee’s findings regarding dose and uncertainty estimates obtained by the NTPR program.
V.A DETERMINATION OF EXPOSURE SCENARIOS
V.A.1 Introduction
As discussed in Section I.C, the most important part of the dose reconstruction process is the determination of a participant’s exposure scenario. Because exact histories do not exist for individual veterans, the analyst often has to reconstruct a scenario or a set of possible scenarios on the basis of plausible assump
tions. Problems arise because “plausibility” can be subjective. It is often difficult, 50 years after most of the atmospheric tests, to verify even a veteran’s participation status with certainty. For example, the original list of veterans provided for the earlier Five Series study (see Section I.B.6) was to have indicated all participants in five test series, but it erroneously omitted more than 20,000 participants and included some 8,000 who were later determined to be nonparticipants.
The committee was generally impressed with the extensive historical research carried out by JAYCOR to document the whereabouts and roles of veterans who took part in the testing program. JAYCOR had to locate and piece together deteriorating, obscure, and often almost-unreadable records (morning reports, ship logs, unit histories, and so on) from diverse archival sources. With such sources, the dates of arrival and departure, where a veteran was quartered, and so on, could usually be documented. In contrast, the veteran’s specific duties and the time he spent in various locations (such as on contaminated ships) were typically difficult to document with certainty.
Procedures to be followed by the NTPR program for dose reconstructions, as laid out in 32 CFR 218.3, specify that “possible variations in the activities, as well as possible individual deviations from group activities, with respect to both time and location, are considered in the uncertainty analysis of the radiation dose calculations.” There is also an expectation that a veteran will be given the benefit of the doubt in determinations used to adjudicate a claim for a nonpresumptive disease under 38 CFR 3.311. As stated in 38 CFR 3.102, “when, after careful consideration of all procurable and assembled data, a reasonable doubt arises regarding service origin, the degree of disability, or any other point, such doubt will be resolved in favor of the claimant” (see also Section I.C.3.2).
In many of the records examined by the committee, however, the participant did not appear to have been given the benefit of the doubt regarding the assumed exposure scenario or film-badge dose, including the time and place of exposure. In reviewing the 99 cases, which were randomly sampled within strata, the committee found at least 20 in which a veteran’s external exposure scenario appeared to be incorrect, incomplete, or suspect (for example, see cases #15, 22, 27, 32, 33, 37, 40, 47, 53, 73, 77, 81, 83, 84, 87, 88, 89, 93, 97, 98, and 99). The inaccuracies were often due to insufficient follow-up by an analyst with the participant or other members of his unit. Examples are discussed below.
One tendency the committee saw in the 99 cases was for the analyst to assume that an activity that allegedly violated radiation safety (rad-safe) or operational guidelines in place at the time did not happen. For example, an analyst often assumed that decontamination crews did not stay longer than the allowed times on contaminated ships, that radiation safety monitors and other personnel did not go beyond the 10 R h−1 demarcation line, or that badges that were issued and then returned had, in fact, been worn (not left in a drawer). If the date of issue of a film badge was missing, it was often assumed to have been the recorded date of turn-in of the veteran’s previous badge.
Such pragmatic assumptions reflect the analyst’s need to complete the calculations and seem also to reflect a tendency to idealize human behavior, particularly military behavior. Such assumptions tend to deny that chaos, confusion, and a perceived need among leaders to ignore rules to complete the task at hand may drive what happens in the field, particularly when a nuclear weapon has just been detonated. The commander of a decontamination crew may have been focused on getting a ship decontaminated and may have considered the rad-safe guidelines to be unnecessarily restrictive and thus not to be taken literally. The rad-safe limit line was not “drawn in the sand,” and forward units were sometimes unsure about their exact location relative to that line and to ground zero. Communication of radiation intensity from rad-safe monitoring personnel to commanding officers in the field was sometimes unreliable.
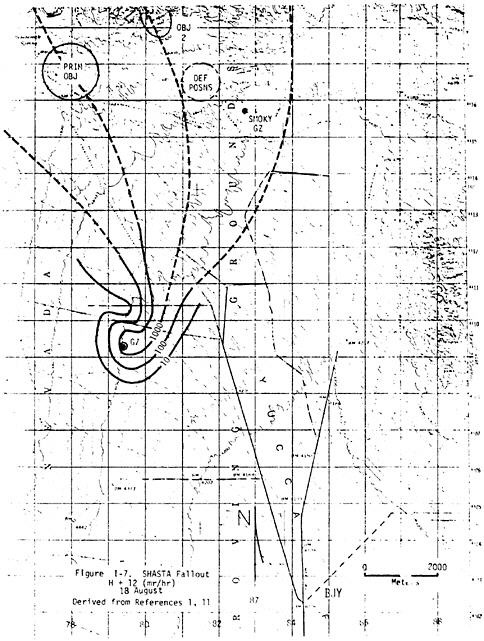
Generic estimates of shielding and time spent indoors versus outdoors used to estimate external dose are questionable for some participants. For example, some participants on ships claimed that because of the heat they slept on deck, where they would not have been shielded at all (see case #28). The assumed 50% shielding factor for participants on Pacific islands may be too high for those who were billeted in tents or thin metal structures that may have had many open windows at night (see Figures V.A.1 and V.A.2). Thus, as discussed later in this chapter, generic dose estimates on ships and islands may not be reasonable estimates of the doses to some unit members.

FIGURE V.A.1 Typical metal buildings used at Enewetak during Operation CASTLE.

FIGURE V.A.2 Tents on Parry Island at Operation CASTLE.
Some sources of information about veterans were not used as well as they might have been. For example, it is not apparent that information in “File A” (see Section I.B.3) for individual veterans was always considered. Additionally, the veteran himself and his buddies were rarely contacted, nor were civilian radiation-safety personnel who often accompanied participant groups during planned activities. That approach might reflect a difference in worldview between a researcher and a claims adjudicator or government contractor, but it is our view that additional and sometimes useful information could have been obtained from the veterans themselves. The questionnaire that was administered in the early days of the NTPR program was very sketchy. It included such questions as “Were you issued a badge?” and “Did you wear it?” When questions came up in the scenario reconstruction about what specific activities a veteran was involved in, the veteran apparently was almost never asked for clarification. The committee’s impression is that the contractor assumes that the veteran himself should not be regarded as a reliable source of information. When, on occasion, a veteran came forward with an account of what happened on the sometimes-chaotic day of a weapon test, his story may have been discounted by the analyst and may not even have influenced the calculation of uncertainty, that is, the assigned upper bound of the dose. Examples illustrative of those points are detailed below.
V.A.2 Discussion of Selected Cases Illustrating Scenario Determination Problems
In this section, we discuss some of the 99 sampled cases and additional files submitted by veterans. These cases are listed in Appendix B.
Case #22: The participant claimed that he was present at Operation IVY. However, his service records had been damaged, and his claim that he participated in IVY could not be verified. He was not given the benefit of the doubt in evaluating his claim for a nonpresumptive disease, and no dose was calculated for possible participation in IVY. Nor was the estimated upper bound of his assigned total dose (from his participation in other test series) adjusted to reflect his possible participation in IVY. He was not contacted to investigate his claim further.
Case #53: This case provides a good example of inconsistent application of assumptions used in estimating the external dose and upper bound from boarding target ships at Operation CROSSROADS. The dose memorandum states that the veteran was given the benefit of the doubt by assuming that he participated in two-thirds of the target-ship boardings by his unit. However, the calculations in the case file are based on only one-third of the boardings. In other cases involving target-ship boarding (for example, cases #45 and 49), the veterans were usually given the benefit of the doubt by assuming that they participated in all boardings (see Figure V.A.3).

FIGURE V.A.3 Sailors sweeping deck of ship.
Case #77: This veteran was a member of the 50th Chemical Platoon at Operation TEAPOT, and much of his film-badge information has been lost. From film-badge data summaries that have been found, it is known that several members of the 50th Chemical Platoon, which made up the Desert Rock Radiological Safety (Rad-Safe) Section for TEAPOT, received external doses that greatly exceeded the operational limit of 6 rem, but it is not known who those individuals were. The veteran in question was informed that a reconstructed dose of 3.12 rem was his “most probable dose,” but he was given the benefit of the doubt by assigning him the operational limit of 6 rem instead. The fact that no upper bound was provided implies that the dose of 6 rem would be considered as a 95th percentile of this veteran’s dose in any adjudication process (the veteran did not file a claim for compensation).
The veteran’s personal narrative was provided to the analyst. He stated that he was assigned as rad-safe monitor for two colonels from the Pentagon, who were “dressed in silver suits covering every part of their body, including shoes. They taped all seams with a tape comparable in appearance with duct tape. I watched all this while wearing only a T-shirt and fatigue pants. I was curious as to what they knew, what I didn’t know, and what they weren’t telling me.” He goes on to describe what happened next (apparently, this incident occurred at Shot MET):
About ten (10) minutes after detonation of the 22 kiloton device, I entered the blast area to find instruments the two Colonels had placed in the area. (We had previously met to acquaint me with the location and critique the recovery.) When I arrived at the site it was very dark, dusty and windy. I can’t recall the exact readings, but they were high. I returned to meet the Colonels, who had driven their van onto a road leading into the site. I reported that the recovery area was very hot, and they would have to work very quickly. I led them back to the instrument location. They recovered their instruments and packed them into boxes. In the recovery area fires were still burning. There was a lot of smoke and dust, and the mushroom cloud was still visible. The ground around us was black. The winds were strong. We had passed several mannequins burning, and I learned later this was a test of fireproof clothing. The mannequins burned and the clothes did not. We were several minutes in the area. We then left and I never saw the two Colonels again. I stopped to brush myself off, as I was covered with dust. I made a note of the time spent in the area. I remember thinking that the two Colonels had exceeded 5 Roentgens – more like 6 – and that my double trip into the area would place me even higher. (For example, see Figure V.A.4.)
The veteran goes on to give details about several other tests, one of which again suggests the potential for an inhalation dose:
One of the major studies undertaken by the 50th Chemical Platoon was to try to correlate a radiation pattern between the ground and the air. In order to be sure these readings from the air were accurate, it was necessary to have men on the

FIGURE V.A.4 US Army observers examining dummies set up about 3,000 yards from ground zero during dry run for Operation TEAPOT Shot MET.
ground to check them. As part of this group, I was assigned to be a ground monitor. The exercise took place at a site where a nuclear detonation had occurred. I am unsure of the exact reading, but our location was radioactive enough to gather data from aircraft flyovers.
After the first series, it was decided that the aircraft probe was not accurate. We stopped for a couple of days while a lead shield was built to protect the probe in the aircraft from every angle except straight down. We then spent a few more days testing this new device. Adjustments were made, and we were in and out of the area several more times. We took readings all the way to ground zero.
This exercise was the dirtiest of my stay. Every day we were covered with dust from our travels through the test site. We had no protection and were inhaling dust constantly. I remember thinking our lungs must have looked like our clothes. I do not remember if we had film badges.
He then describes an operation (apparently at Shot APPLE-II) in which he became disoriented near ground zero:
During the test known as the Survival City Shot, I was assigned to locate a large group of military vehicles. I made several trips through the area prior to the test to orient myself to the location of these vehicles. They consisted primarily of 2 1/2 ton – 3/4 ton trucks and jeeps.
I especially remember the layout of Survival City with its city street and completely furnished houses. There were even families of mannequins set in the houses. There was a two story brick building which had been built especially for the test. It was kind of a landmark because it was the tallest structure on the desert except for the bomb towers. Farther from ground zero was a completely equipped mobile home park. A large number of civil defense people were at this test.
I entered the test site shortly after the blast, with a team, seeking the ten Roentgen line [10 R h−1]. I could not find the vehicles. They had been parked less than a mile from ground zero. The ground was black, the two story building was gone, and I became disoriented for a few minutes as I drove around looking for some trace of the vehicles. While I was looking, a call came over the radio that all troops were being pulled from the area due to a wind shift. When I found my way back I had been inside the ten roentgen line. I did not stop my jeep to take a reading. I was alone at this time, and was relieved to find my way back. I believe my exposure was quite high for this event. It was very windy, with dust and smoke. I had no protective clothing or equipment.
The analyst only peripherally considered this narrative in the dose reconstruction. Regarding the first account, about accompanying the two colonels after Shot MET, the analyst writes that the veteran “did not provide sufficient information to identify the specific project that he supported on shot day.” Because the veteran commented on seeing burning mannequins, the analyst decided to assign him to Project 40.20, the Clothing Test Project, and accordingly assigned him a dose of 0.20 rem appropriate to that group, apparently discounting the veteran’s statement that “I learned later this was a test of fire-proof clothing.” Evidently, no inhalation dose was considered.
Regarding the project to assess the correlation between readings on the ground and air-based readings, the analyst comments that although the veteran described this as a “major study,” “such a project is not listed, per se, among the Desert Rock projects at operation TEAPOT.” The closest documented match that the analyst could find was Project 40.19, CBR Defense Team Training, and the veteran’s dose from that activity was accordingly based on a reconstruction that had been done for that group, with the comment that his “dose resulting from this activity was certainly less than 1.7 rem.” Again, no inhalation exposure was considered, nor was any allowance made for the possibility that the veteran’s account may reflect an activity that was not represented in other surviving records from the time. A note in the file states that because this veteran was a PFC (private first class) at the time, he could not have been involved in CBR team training and, therefore, the dose of 1.7 rem noted above should be subtracted from his dose. However, the 1.7-rem piece of his dose was not replaced with a more accurate estimate.
Regarding the third narrative, related to Survival City in connection with Shot APPLE-II, the analyst found other records that supported the veteran’s
claim that he was involved. However, some details of the veteran’s account were evidently discounted. The analyst’s report states that:
the scenario is questionable since rad-safe monitors did not travel alone in jeeps and there was no reason to send anyone into the shot area to ‘search for’ the test vehicles since their locations were well known. Moreover, it was not the function of the 50th Chemical Platoon to locate vehicles, but merely to accompany project personnel who were to evaluate damaged vehicles.
The analyst goes on to assign the veteran a dose for this shot on the basis of a reconstruction that had been done for 573rd Ordnance Company personnel and accompanying rad-safe monitors.
In the end, the analyst made an argument that the veteran’s overall dose could not have exceeded the operational limit of 6.0 rem. The argument was based on information that seven members of the 50th Chemical Platoon evidently did exceed the limit and were restricted from further radiation-related work, but this veteran evidently was not restricted. The analyst states that “the dose calculation … does not consider [the veteran’s] allegation that he became disoriented while searching for some test vehicles and spent a few minutes in a high-radiation area. The dose resulting from such an excursion cannot be estimated without more specific information.”
This narrative illustrates two points. First, if given the opportunity, veterans sometimes can provide detailed and compelling accounts about their experiences. The men who participated in these atomic tests knew that they were making history at the threshold of the nuclear age. Although memory is not totally reliable, such experiences are not easily forgotten. Second, although it is inherently difficult for an analyst to take scenario uncertainty into account quantitatively, a better effort could be made to acknowledge that such uncertainty exists and to account for it. Although the committee did not try to recompute the veteran’s dose, there was consensus that his true external dose could have greatly exceeded the assigned 6 rem, and that there was also the potential for substantial inhalation dose and beta dose to the skin, exposure routes that were not considered.
Contributed case: Another example, not among the 99 sampled cases but a record that was randomly pulled from the Science Applications International Corporation (SAIC) files and then used with the permission of the veteran, concerns an Air Force helicopter technician. In this case, assumptions made throughout the dose reconstruction did not appear to give the veteran the benefit of the doubt. Other personnel involved, whose names and ranks were provided to the analyst by the veteran, could have provided supplemental information, but the record does not indicate that any follow-up contacts were attempted. The case is particularly interesting because it involved highly unusual, or possibly unique, conditions of exposure, which can place considerable demands on the analyst in developing an exposure scenario that fits the particular circumstances.
The veteran had been trained in maintenance of F-84G aircraft that were used for cloud sampling after nuclear detonations in the South Pacific (see Figure V.A.5). He arrived at Kwajalein on September 30, 1952, and was present for both detonations in Operation IVY. After Shot MIKE (November 1, 1952), two F-84G sampler planes had to leave the radioactive cloud because one got into trouble and “went into a spin” and the other followed it. The first one could not return to land and the pilot went down in the sea with his plane. The other plane just made it to Enewetak but had a rough landing, blowing out two of its tires. The veteran was flown to Enewetak to change the wheels and tires, refuel the plane, and use a power source to restart its engine so that it could return to Kwajalein. The downed F-84G must have still been holding its very hot air samplers on its wings and nose. On his return to Kwajalein, the veteran recalled that he required more than 4 h of showering before the Geiger-counter reading on him came down to acceptable levels.
The veteran’s initial dose reconstruction, as reported to him in 1983, assigned him a dose of 0.000 rem. He complained right away. In 2000, he filed a claim for service-connected disability. The analysts revisited the calculations at that time, and a revised dose assessment was reported.
The second dose reconstruction began with the fact that 4 days after Shot MIKE, the external exposure rate at 4 in. from the pylon of the F-84G that he had serviced was recorded as 0.10 R h−1. That was extrapolated back in time (on the basis of a decay rate of t−1.2) to the time when the veteran would have been on Enewetak changing the tires, but this extrapolation evidently did not take into

FIGURE V.A.5 F-84G cloud-sampling aircraft.
account the presence of cloud samples while the veteran was working on the plane and the likelihood that the plane lost some of its radioactivity in a washdown after its return to Kwajalein. It was assumed that it had taken him 1 h of work close to the hot plane to get both tires changed, refuel it, and restart it. It was assumed that the veteran spent that time near the landing gear at a distance of 1 m from the contaminated fuselage (“his arms being extended”). The landing gear and blown tires were assumed to be uncontaminated because they would have been “tucked inside” the plane.
The committee did not attempt to do a dose reconstruction for the veteran, but the committee took issue with every assumption that was applied and considers the assigned upper bound of 0.8 rem to be much too low to adequately reflect the uncertainties in scenario definition and estimation of dose. The extrapolation of the measured exposure rate backward in time is complicated by the fact that the plane would have had its highly radioactive air samplers removed immediately on its return and the possibility that it cooled off during the 2-h flight back to Kwajalein and was hosed down before day 4 to begin its decontamination.
Elsewhere in the dose reconstruction report, the analyst calculates doses that the veteran might have received in later work where he decontaminated F-84s, mentioning that the planes were routinely decontaminated within a day of their return from flying through the mushroom cloud. The analyst states that:
During the mornings following both shots (2 November and 17 November) the F-84G aircraft were moved to a decontamination ramp at Kwajalein, where they would be thoroughly scrubbed and washed down. The average radiation intensity upon landing of the F-84G’s was 2.5 [R h−1]. As the readings were taken of various aircraft parts, the average was likely indicative of radiation levels at 4 inches from the surfaces of aircraft components that personnel were likely to spend the majority of their time maintaining. Engine/intake area decontamination effectiveness was about 50 percent; smooth surfaces were about 95-98 percent. The highest surface contamination zones on the aircraft were leading edges, air intakes, and engines.
Even if the wings were decontaminated with an effectiveness of only 90%, it follows that the measured reading of 0.1 R h−1 on day 4 should have been multiplied by 10 before extrapolating it back to shot-day levels. On that basis, it seems reasonable to suppose that the estimated dose during the tire-changing event was too low by at least a factor of 10. Again, this conclusion does not take into account the presence of air samplers, which would increase the extent of underestimation of the veteran’s dose.
Other assumptions made in the scenario reconstruction do not seem to give the veteran the benefit of the doubt. The assumption that the landing gear and tires were not contaminated seems doubtful. Potentially, the well in which the landing gear is housed during flight may serve as a trap for radioactive particles. The metal cover over the wheel well swings down when the landing gear is extended, and the cover presumably was contaminated. Finally, the assumption
that it took 1 h to complete the maintenance of this plane (with a half-hour spent away from it) is not well established by the record.
This example shows that despite assertions by the NTPR program, assumptions about exposure scenarios used in reconstructing doses are not necessarily “high-sided” and do not necessarily give the benefit of the doubt to the veteran.
Case #73: In other examples among the cases reviewed by the committee, assumptions applied did not seem to give the veteran the benefit of the doubt. In this case, an assumption was made that because there was no record of badging for some missions and the analyst believed that the policy would have been to badge all participants with potential for exposure, the veteran must not have had the potential for any measurable exposure during his missions. The case involved a participant in the CROSSROADS test series who was stationed aboard the USS Prinz Eugen. He was cited for outstanding work in removing ammunition from contaminated vessels under difficult and hazardous conditions. In the reconstructed scenario, the veteran was assumed to have done decontamination work for only 4-h shifts every second day; little basis for the assumption was offered. When there were gaps between days with badging, the veteran evidently was assumed to have zero dose. As discussed in Section IV.B.2, doses on ships are assigned on the basis of the mean exposure rate recorded on known dates on the ship with allowance for decay according to the fitted time course and extrapolation backward in time based on the physics of radioactive decay. No original badge records are included in the file, nor does the file document the radiation levels on the dozen target ships this veteran had worked on. Little information came directly from the veteran, as the file includes only a brief questionnaire with his terse responses. Very little uncertainty was assigned to the estimated dose for the veteran. The estimated dose and upper bound in this case do not adequately reflect plausible conditions of exposure and uncertainties in estimating the veteran’s dose.
Case #47: Another veteran participated in Operations CASTLE and IVY. Many film badge records of CASTLE evidently were lost, and the records of many participants do not include dates of issue or turn-in. The records also show confusion over who was wearing a particular badge, and the veteran in this case evidently wore more film badges than could be found. A memorandum in the case file to VA states that “at this point, there is reason to suspect the entire CASTLE database as having the potential for serious errors that could be very embarrassing in litigation.” The veteran’s main responsibility was driving people from place to place on the islands. His story about his experiences included a statement that he was flown over ground zero 6 days after the blast and a claim that he visited an island about 15 miles from ground zero 3 days after a test, stayed for about 8 h, and was then ordered off the island because of concern about his radiation dose. Those stories were discounted and were not used in the sce-
The general who was contacted stated that the usual practice had been to leave the “permanent” badge behind on missions for which a mission badge was issued. (This is in contrast to a report on the REDWING test series (Bruce-Henderson et al., 1982), which states that permanent badges were to be worn at all times.) If that was the usual procedure, dose estimation should routinely have added mission badges to permanent badges (in line with giving the veteran the benefit of the doubt) rather than treating them as redundant measures and ignoring them, as was usually done (see Section V.B.1.1).
Case #55: Occasional difficulties in reading original film-badge data were not always resolved in a way that gave the veteran the benefit of the doubt. For example, the veteran in this case has a record for a badge issued July 7, 1956, that seems to indicate a reading of 3.105 rem, but the analyst apparently believed that the handwritten number “3” could also have been a “2.” It was originally treated as a “3” but was treated in the final dose assessment as a “2.” Nevertheless, uncertainty of less than 1 rem was assigned to the dose estimate.
Case #40: Another example of a scenario reconstruction that did not appear to give the veteran the benefit of the doubt involved a participant who served with the Army as a smoke-generator specialist in Operation UPSHOT-KNOTHOLE at the NTS and was present during a fallout event at Camp Mercury. He contacted the program initially in 1989 to request information on his dose. He was part of a group of 17 men who carried out two experiments in spring 1953 to determine whether smoke screens can protect against thermal radiation (heat). One of the experiments was associated with Shot ENCORE (May 8, 1953), and the other with Shot GRABLE (May 25, 1953); they had the same intended ground zero. His group had to go out to the site during the hours before detonation and set up hundreds of smoke pots and smoke generators along specified lines near the intended ground zero, trigger the smoke-generation system remotely at the time of the blast, and then collect all the contaminated equipment on shot day. The file includes no statement from the veteran about his precise role in the experiments, and no badge data exist for him though others in his unit had measurable doses ranging up to 0.9 rem. On the basis of that information and a presumption that badge records for this test series are essentially complete, a letter from DTRA to the veteran states that according to rad-safe requirements at the time of UPSHOT-KNOTHOLE, he would not have been allowed in an area with radiation intensity above 0.01 R h−1 without a badge.
Case #37: A photographer for the Army who served in Operations TEAPOT (1955) and PLUMBBOB (1957) might not have been given the benefit of the doubt. One uncertainty concerned his date of arrival at the NTS. On the same day (August 21, 2000), the same person at JAYCOR evidently wrote two memoranda to the same analyst at SAIC, one stamped “Received” citing the veteran’s date of arrival at Camp Desert Rock as March 23, 1955, and one not stamped “Received” giving his date of arrival as April 18, 1955. The analyst evidently treated April 18 as the correct date, thereby excluding the possibility that the veteran participated in the several shots in TEAPOT that fell between those dates. Additional uncertainty attends his dates of participation in 1957. The file contains no direct statement from the veteran, but there is a note that he claimed that he was present by special orders (of which he had a numbered record, issued April 19, 1955) in a tank at ground zero within 1 h of a detonation. Evidently, some records related to these special orders have survived, but they are not in the SAIC file. The mission would probably have occurred at Shot APPLE-II, which took place on May 5, 1955. No film badge record remains for estimating the veteran’s dose. There was apparently also a question regarding the veteran’s unit. An initial dose assessment gave him the benefit of the doubt by assuming that he was a member of the most highly exposed unit, but a later assessment reduced his dose by assigning him a weighted average of the doses to the various units participating in the exercise.
Case #87: A number of veterans had a clear potential for skin contamination. One Army veteran operated earth-moving equipment during Operation UPSHOT-KNOTHOLE and later developed skin cancer (see Figure V.A.6). Earth-moving was required in building roadways, setting up target areas, clearing sites after shots, and digging trenches in preparation for new tests. This kind of work was presumably very dusty in the Nevada desert, and there were regular opportunities for both skin dose (through being dirty all day) and inhalation of radioactive dust produced by resuspension of radionuclides in previously deposited fallout. The veteran also was an observer in the trenches during shots. In the dose reconstruction, the veteran seems to have been assigned a generic dose on the basis of averaging the daily person-time that engineering units would have spent in clearing operations and estimating the probability that each member participated. In short, an average dose for the unit was calculated and assigned to the veteran. However, there may have been considerable variation in dose among the participants in this work, and the unavoidable uncertainty about what this particular veteran was assigned to do remains unaccounted for, given that the assigned upper-bound dose is within a factor of 2 of the central estimate.

FIGURE V.A.6 Photograph of a bulldozer clearing a path through a contaminated area.
Case #99: The uncertainty in scenario reconstruction sometimes goes beyond the specific tasks and conditions that a veteran experienced and goes to some basic questions: Was he even there? Which series was he present for? For example, one veteran who was a major in the Army filed a claim in 1980, alleging participation in Operation UPSHOT-KNOTHOLE. He was evidently an ordnance officer with the Special Weapons Command. His presence at the NTS initially could not be verified, although he claimed to have witnessed 21 shots. No film-badge records were found, so the dose was based entirely on reconstruction. The analyst made some educated guesses about what the veteran’s responsibilities might have been and credited him with being present at 11 shots, describing this approach as “high-sided” despite the veteran’s claim that he was present at 21 tests. (The analyst clearly was frustrated by this case and offered in a memorandum that the veteran also may have been present at another series of tests, perhaps TUMBLER-SNAPPER.) Because the veteran’s case was analyzed in 1983, he was assigned a dose but not an upper bound.
Case #84: Another case in which some basic facts are unclear involves an Army sergeant who participated in Operation UPSHOT-KNOTHOLE. The veteran had no film-badge data, so his estimated dose was based entirely on a generic (unit)
Case #93: A personal account that was discredited concerned a veteran who had worked as a laundryman for the Army at Operation BUSTER-JANGLE (1951). He stated that he wore a badge for both shots that he witnessed, but no records of his film-badge readings remain. The scenario reconstruction discredited his account of being about 2 miles from ground zero and instead assumed that he participated only as an observer in Shots UNCLE and SUGAR, which would have put him many miles from ground zero and beyond the range where measurable exposure would have occurred. The analyst documented that the veteran was on a 20-day emergency leave and accordingly could have been present only at Shots SUGAR and UNCLE. However, an error may have been made in the assumptions. His original emergency leave was effective October 17, 1951. A 10-day extension was granted on October 27 but seems to have been modified in a later morning report to add 10 days of leave but to begin it effective November 6 rather than October 27. With those assumptions, the modified account of the dates would fit better with the veteran’s own account because he could have been present as a witness at Shots DOG (November 1) and EASY (November 5). The veteran’s actual dose therefore could have been much higher than the dose that he was assigned.
V.A.3 Conclusions on Adequacy of Scenario Determinations
The preceding discussion clearly illustrates that dose reconstructions performed in the NTPR program often fail to adequately establish the exposure
scenarios that are the basis of the veterans’ dose estimates. The committee found clear examples in which a veteran’s location and duration of exposure were not unambiguously determined, a veteran was not given the benefit of the doubt with respect to his exposure scenario, adequate follow-up with a veteran or members of his unit was not carried out to define the scenario, or some potential exposure pathways were not considered. The following sections, which discuss the committee’s findings with respect to the methodology used in the NTPR program to reconstruct external and internal doses and related uncertainties, provide further examples where uncertainty in the exposure scenario impacts estimated doses and upper bounds.
The committee recognizes that development of exposure scenarios can be challenging, given the lack of information on a veteran’s activities and exposure environment in many cases. However, in accordance with applicable regulations, a veteran must be given the benefit of the doubt in the development of an exposure scenario. In the committee’s view, that means that an analyst must consider plausible conditions of exposure that are consistent with available information, including statements by a veteran and other people with knowledge of the veteran’s activities, and then select a plausible exposure scenario that results in the highest estimate of dose to the veteran. Selection of exposure scenarios should not be constrained by rad-safe guidelines or plans of operation when there is evidence that they were not followed. The committee’s evaluation of individual cases discussed in this section suggests that selection of plausible exposure scenarios based on giving the veteran the benefit of the doubt is not an unreasonably burdensome task. If that approach is not followed, it is unlikely that credible upper bounds of doses will be obtained in many dose reconstructions, as intended by the NTPR program.
V.B EXTERNAL DOSE ESTIMATION
V.B.1 Introduction
Reconstruction of external doses by the NTPR program includes gamma doses estimated from film-badge data and scientific dose reconstructions in cases in which film-badge data are not available. Neutron dose is generally considered separately because film badges were relatively insensitive to neutrons. Beta skin and eye doses are also considered separately. Thus, the committee’s findings with respect to both the central and the upper-bound estimates will be discussed separately for dose reconstructions based primarily on gamma exposure measured with film badges and for gamma doses estimated from unit dose reconstructions. Neutron and beta dose reconstructions in the NTPR program are also discussed separately. External doses based on film-badge data are discussed in Section V.B.2, reconstructed external gamma doses in Section V.B.3, and a summary of the committee’s findings regarding external gamma dose estimates in Section
V.B.4. Neutron doses are discussed in Section V.B.5, and beta skin and eye doses in Section V.B.6.
As discussed in Section II.B, the committee, in responding to its charge, reviewed 99 randomly selected dose reconstructions in detail, including the supporting documentation in the SAIC files. A number of other dose reconstructions submitted by veterans were also examined. Committee members reviewed many of the data and reports on which the estimated doses for those cases were based, including published reports describing the generic unit dose reconstructions and unpublished internal memoranda. Additional information was obtained from formal replies by DTRA to written questions from the committee (see Appendix D) and presentations by NTPR program and VA staff at open committee meetings.
In 29 of the 99 cases examined by the committee, the veteran’s reported external gamma dose was based primarily on film-badge data; 21 of these were for participants at Pacific tests. Upper bounds were reported for all but four of the 29. In 51 of the 99 cases, the veteran’s external gamma dose was based primarily on his unit’s generic dose reconstruction (22 associated with NTS testing and 29 with Pacific testing). In 14 of the 99, all Pacific-test cases, the veteran’s dose reconstruction was based on a mixture of film-badge data and generic unit doses; the generic doses were modified as necessary to reflect the veteran’s specific exposure scenario. Five of the 99 cases involved unbadged participants and activities that were not covered by a unit dose reconstruction.1 In 19 of the 99 cases (14 Pacific and five NTS), all for claims filed before 1994, no upper bound was reported. Of the 99 cases, 66 involved primarily Pacific tests and 30 primarily NTS tests, but six people participated in tests at both sites, and a few received comparable doses at the two sites. A neutron dose was reported in three of the 99 cases in the random sample. However, some test participants, not among the 99 cases, received significant neutron doses (Goetz et al., 1981).
In 27 of the 99 cases, a claim or other indication of skin or eye disease was indicated. Beta doses were calculated for nine post-1998 claims, but beta doses were not reported for 18 cases of claims of skin or eye disease before 1998.
The committee’s detailed evaluation of methods used in the NTPR program to obtain central and upper-bound estimates of the dose from external exposure based on film-badge data and unit dose reconstructions is discussed below. The conclusions are illustrated with examples from the 99 cases examined by the committee and with examples from additional information submitted to the committee by test participants.
V.B.2 External Gamma Doses Based on Film-Badge Data
V.B.2.1 Central Estimates
As discussed in Section IV.B.1, external doses estimated by the NTPR program from film-badge readings are generally biased high compared with estimates based on National Research Council (NRC, 1989) committee recommendations and thus favor the veterans. However, the veteran is not always given the benefit of the doubt regarding allegedly damaged film badges, overlapping mission and permanent badges, and when and how long badges were worn.
The committee found that there was sometimes inconsistency in replacing allegedly suspect film-badge data with a reconstructed dose, particularly for the REDWING test series and for dose assessments before 1995. NTPR program policy regarding REDWING badges changed over time but in early 1995 was clarified to require replacement of all suspect film-badge data with a dose reconstruction if it was feasible (Schaeffer, 1995). As documented in the NRC (1989) report, many of the film badges issued early in the series and worn for more than a few weeks apparently suffered damage that caused the film to appear to record a higher dose—up to several hundred millirem more than actually received. However, later batches of film badges were waterproofed and were not subject to the same problems. Some of the data from the later badges may also have been discarded in favor of reconstructed doses, even for assessments before 1995. Ten of the 99 sample cases involved film-badge data from the REDWING series, and in eight of these the total external dose was based primarily on these data. In 8 of the 10 cases, some film-badge data were determined to be questionable, and the doses were replaced with reconstructed doses; however, in 2 (cases #35 and 42), data were accepted even though the badge was deemed possibly damaged. In three cases (cases #54 in 1995, #82 in 1956, and #55 in 1994), a possibly damaged film-badge reading was accepted but treated as an upper bound. Some of the badges whose data were replaced were rated highly suspect on reanalysis (see case #55), but others were deemed merely questionable (see case #82). However, the fact that case #42 was from 1996 suggests that the policy was not administered uniformly even after clarification.
The committee believes that the present policy of disregarding data for badges rated questionable on reanalysis, as opposed to highly suspect, should be reexamined. Even badges that exhibit slight damage, such as the absence of a distinct filter image, can be analyzed to provide a reasonable dose estimate (NRC, 1989). For example, in case #44 (1998), a potentially damaged badge was reanalyzed, and the originally reported dose of 0.97 R was revised to 0.46 R. However, the analyst replaced the film-badge dose with a reconstructed dose of 0.17 rem. Unless there is clear evidence that a film badge is so highly damaged as to provide a completely unrealistic dose estimate, a policy of accepting the data is more prudent than replacing them with a reconstructed dose. In most cases the
data were already recorded in the veterans’ medical records, and often they were reported to the veterans in previous NTPR program reports, so the practice of replacing them with lower reconstructed values does not give the veterans the benefit of the doubt as required by law; it also detracts from the credibility of the dose reconstruction process by giving the appearance that the tendency of DTRA is to reduce previously reported doses whenever possible.2 The committee notes, however, that in most of the REDWING cases examined, the impact on the estimate of total external dose would have been minor.
Instances of uncertainty regarding when a badge was issued and turned in were common (see cases #10, 35, 47, 54, 74, and 97). In many cases, original film-badge records were available, but the fields for date of issue and return had never been filled in. Because reconstructed doses were calculated to account for periods when a person was not badged, incorrect assumptions regarding the period covered by a film-badge dose could have resulted in underestimation of a total dose.
The committee found one case (#32) in which previously reported badge results were in the file but were not used in the dose assessment. Cases in which suspicious data indicated possibly incorrect doses also were found. For example, in case #35, the veteran’s film-badge reading was considerably lower than the unit average.
A mission badge was usually assumed to have been worn concurrently with a permanent badge if a permanent badge had been issued, although there is some indication that this was not always true (see discussion of case #47 in Section V.A.2). If the mission-badge dose was lower than the permanent-badge dose, the mission-badge dose was assumed to be included in the permanent-badge dose, and only the dose from the permanent badge was used. If the total dose determined from mission badges exceeded that from the permanent badge, the higher dose was used. It is possible that veterans did not wear mission badges continuously between the time they were issued and the time they were turned in, so in many instances a veteran should have been given the benefit of the doubt and the mission-badge and permanent-badge readings should have been summed.
In many cases, a participant was issued a mission badge but not a permanent badge. His dose for the period not covered by the mission badge was based on a unit dose reconstruction. For example, in case #11, mission badges were issued to a participant who serviced cloud-sampling aircraft; he was not issued a permanent badge. It was assumed that his mission badges accounted for his dose from fallout on the island during the period when the badges were assigned and his reconstructed dose from fallout was modified (on the basis of his unit dose reconstruction) to reflect this, even though he may not have worn the mission badges for the entire period. Therefore, his total dose may well have been underestimated. The committee identified at least eight cases in its sample of 99 in
which either the mission-badge data were considered to be included in the permanent-badge data or the mission-badge data were assumed to include fallout doses on islands or ships (see cases #10, 11, 16, 32, 38, 44, 92, and 97).
If film badges were generally issued for particular types of mission activities and no data were located, the analyst often assumed that the absence of badge data indicated that the participant did not engage in a mission-related activity and assigned a reconstructed generic dose estimate. The veteran generally is not given the benefit of the doubt even when there is some evidence that he participated in such additional radiation-risk activities on the basis of his general duties or frequency of available mission-badge data. That considerable film-badge data are known to have been lost suggests that the inability to locate such data or extant film does not imply that a permanent or mission badge was not issued or worn during some periods of possible radiation exposure and that the participant therefore could not have been exposed. For example, in case #40, the analyst assumed that the participant was not exposed in high-radiation areas because no film-badge data could be found, even though an earlier assessment had given him the benefit of the doubt and assigned a higher dose (see discussion of this case in Section V.A.2). The participant was not contacted to inquire whether he wore a badge and whether he actually had entered a high-radiation area.
The committee found instances in the 99 sampled cases in which apparently no effort was made to search for film-badge data (for example, see cases #33, 36, and 38). For example, case #38 involved a supply supervisor stationed on Enewetak Island who claimed that he wore a dosimeter. According to his service record, he had previously been assigned a dose of 0.15 rem. That dose might have been based on a film-badge reading, but apparently no effort was made to determine its origin, and this dose increment is assumed to be included in his reconstructed dose rather than being added to it.
The committee found at least 10 instances (cases #21, 22, 27, 38, 40, 81, 87, 93, 94, and 98) in which participants claim to have been issued a film badge but no badge or data could be located. As discussed earlier, film badges and data are known to have been lost and to be no longer available.
For some veterans, some film-badge data were found. That suggests that they did participate in some activities that required badges and that other badge data could have been lost. The committee identified numerous cases in which mission-badge data could have been lost (for example, cases #9, 10, 17, 27, 32, 33, 36, 40, 44, 47, 54, 59, 92, and 99). In case #10, it is clear that the participant did not return all film badges.
Reconstructed doses were usually estimated only for periods for which no film-badge data were found. In its 99 sampled cases, the committee found frequent occurrences of re-evaluation of film-badge data because readings appeared to be anomalously high; many of these, as discussed previously, were for Operation REDWING. The committee found only one example of replacement of an obviously incorrect film-badge reading (zero) with a reconstructed dose (case
#97). There might be a greater tendency to question high readings than to question low readings, inasmuch as damaged film badges were known generally to read high. However, low readings might result from failure to wear badges when they were supposed to be worn or from incorrectly recorded data.
A veteran’s estimated dose apparently was not routinely compared with that of others in his unit with similar duties and more complete film-badge records. The committee noted several cases in which such a comparison would have been appropriate (for example, cases #24, 25, 35, 38, 58, 68, and 69). For example, in case #24, the participant’s recorded film-badge reading was the lowest of all recorded badge data for his unit.
Doses based on film-badge data are assumed to be definitive for the period covered if such data are available, even though the film-badge data may not agree with a reconstructed dose. Considering that the ratios of the upper-bound dose to the central estimate that the NTPR program provides for “scientific dose reconstructions” are often much lower than the corresponding ratios that it applies to film-badge data, that practice seems contradictory. The committee found that in many cases, the policy does not give the veteran the benefit of the doubt regarding his potential total and upper-bound external dose, particularly if readings from slightly damaged film badges were replaced with reconstructed doses, if possible mission-badge data were not located, if incorrect dates were used for periods when the badges were worn, if badges were not always worn continuously as required, or if incorrect badge data were used. The additional uncertainty in doses based on film-badge data should be reflected in estimated upper bounds, and this is discussed in more detail below.
V.B.2.2 Upper Bounds
As discussed in Section IV.B.1, the NTPR program estimates the upper bound of an external dose for a single film-badge reading as recommended in the NRC (1989) report. However, it estimates a slightly lower uncertainty in the sum of multiple film-badge readings than if the most extreme method suggested in the NRC (1989) report had been used. The mean dose estimated by the NTPR program is inflated by about 30% relative to the National Research Council recommendation, because a correction to convert exposure in roentgen to equivalent dose in rem is not applied. Consequently, the upper bound of the sum of multiple-badge data calculated by the NTPR program is still almost always greater than if even the extreme National Research Council recommendation for calculating an upper bound had been followed precisely.3 Thus, a dose estimate and upper
bound obtained by the NTPR program based primarily on film-badge data should be on the high side if the participant was badged during all periods of potential exposure.
However, the reported film-badge data may not provide an accurate and complete record of a veteran’s dose for the period supposedly covered. The upper-bound estimate does not reflect the possibility that the veteran did not wear his badge at all times, that mission badges were issued but not turned in or the data were lost, or that the interval when the film badge was purportedly worn is incorrect. As discussed earlier, the committee found that records indicating when badges were issued and turned in were often ambiguous or had no entries in the date fields. Assumptions had to be made on the basis of reasonable likelihood. However, the possibility that the assumptions were not always correct is not reflected in the upper-bound calculations. Furthermore, no additional uncertainty is assumed to account for the possibility that incorrect data were reported or that a reading was assigned to the wrong individual because of, for example, clerical errors or switching of data. There appears to be considerable evidence that film-badge data were lost, badges were lost, and badges were issued but not always worn. That suggests that for many veterans whose reported doses are based primarily on film-badge data, the upper bound assigned may not truly reflect a credible 95th percentile of the possible dose.
Finally, the NTPR program uses the same uncertainty estimates for a dose estimate based on a cohort badge as for one based on an individual badge. (Recall that “cohort” badging was used when several representative unit members were badged and that the data from such badges were attributed to others in the unit.) The assigned uncertainty clearly should be increased when a dose is based on a cohort badge to reflect the likely variations in doses among the members of the unit. Cohort-badge data were included in the dose estimates in at least six of the 99 cases examined by the committee (cases #6, 9, 15, 26, 39, and 68). In at least one of those (case #15), the committee found that the cohort dose probably considerably underestimated the dose to the participant, who probably entered areas with much higher exposure rates than an average member of the cohort.
In summation, among the 99 random cases reviewed, the committee found a number in which an increased upper-bound estimate of doses based partly or primarily on film-badge data might well be warranted.
V.B.3 Reconstructed External Gamma Doses
V.B.3.1 Central Estimates
The committee examined the methods and models used to estimate average external gamma doses assigned to units on the basis of cohort film-badge data or radiation-survey data combined with assumptions about a unit’s activities. In many of the unit dose reconstructions, the analysis was thorough and comprehen-
sive. As in a previous National Research Council study (NRC, 1985b), the committee has concluded that the methods used to estimate average doses from external exposure to gamma rays are generally acceptable and, if adequate input data are available, provide credible estimates of the average dose to members of a unit.4
Many of the unit dose reconstructions include a comparison of the mean unit dose with available film-badge data. The mean reconstructed doses generally agree fairly well with the mean of the film-badge data. However, the film-badge data are often sparse, and the variability in the film-badge data is often greater than the estimated uncertainty in the mean unit dose. That result is attributed to the fact that many of the film badges were issued to participants who were expected to receive higher doses, such as radiation monitors, so the higher doses do not reflect doses to ordinary participants. However, the estimated uncertainty should still reflect the possibility that not all participants with a potential for high doses had a (surviving) film-badge record.
In many cases, the unit dose estimates are based on sparse survey data and questionable assumptions regarding exposure scenarios, particularly for exposure on some ships, so the dose to some individuals in the unit could substantially exceed the mean. For some smaller units, in which the specific daily activities of individual members could not be precisely determined, daily average doses to members of a subunit were estimated by using a daily weighted average of doses for various radiation-risk activities that was based on previous dose reconstructions, manpower requirements for each activity, and morning-report unit strengths (Ortlieb, 1995).
External dose estimates based on reconstructed doses depend on the validity of assumed exposure scenarios and the inclusion of doses from all possible exposures. However, as discussed below, doses to the most exposed people in many units may not have been realistically estimated in generic dose reconstructions, particularly if the exposure scenario for some did not conform to that assumed for the unit as a whole.
V.B.3.2 Upper Bounds
As described in Section IV.D.2, the unit dose reports generally provide a discussion of the uncertainty in the central or “best” estimate of the dose to a representative member of the unit. As discussed in Section IV.E.2.2, the estimated uncertainty does not reflect the possible upper-bound dose to any individual in the unit but rather the distribution of possible doses about this central estimate. Departures by individuals from the assumed group scenario are not
considered in estimating uncertainty. This uncertainty analysis is asserted to be “high-sided” because it estimates space-time scenarios in a manner that overestimates exposures, particularly for NTS observer and maneuver units. However, the ratio of the 95th percentile upper-bound dose to the central estimate for external gamma-ray dose based on unit reconstructions is often very low, with the upper bound sometimes only 10 to 20% above the central estimate. Uncertainties of that magnitude are not consistent with uncertainty ranges generally estimated for other dose reconstructions of external radiation exposure based on similar types of data (Henderson and Smale, 1990; Simon et al., 1995). The ratios of reconstructed upper-bound doses to central estimates are often even lower than the ratios based on film-badge data, even though film-badge data, if available, are assumed to provide the most reliable dose estimates and are considered the doses of record.
In many cases, the calculated upper bounds, even though alleged to be “high-sided” estimates, appear to be completely unreasonable. For example, the 95th percentile upper bound estimated for Operation UPSHOT-KNOTHOLE, Shot SIMON maneuver units (Edwards et al., 1985) is only 10% above the “best” estimate (see Table IV.B.1). As discussed in Section IV.B.2, that estimate results from assuming that the uncertainty in the radiation field could be neglected, that the central estimate is itself “high-sided,” and that all the uncertainty is due to uncertainty in march speed and stay times. But the resulting total uncertainty estimate is less than the uncertainty in the measurement of exposure rate in the field with available survey meters (Brady and Nelson, 1985).
Similarly, the 95th percentile upper bounds calculated for some Pacific test series unit dose reconstructions also appear to be unreasonably low. For example, the upper bound for doses incurred in boarding or decontaminating target vessels during Operation CROSSROADS is estimated to be only 20% above the mean dose (Weitz et al., 1982), and the upper-bound dose for seamen and island residents from fallout during Operations GREENHOUSE and CASTLE also was generally estimated to be only about 10-20% above the mean dose (Thomas et al., 1982; 1984).
Because uncertainty analyses reported in the unit dose reports are complex and because detailed data and calculations are usually not included in the reports, it was not possible to examine all the specific calculations, assumptions, and supporting data in detail. However, as discussed below, the committee has concluded that the reported upper bounds are not always credible estimates of the 95th percentile dose to all members of the unit.
V.B.3.2.1 NTS unit dose reconstructions
For NTS test observers and maneuver troops, the estimated upper bound of an external gamma dose is based on assumptions that the radiation field was well documented, that the times spent by the troops in various locations were fairly
well known, and that all participants followed rules (for example, stayed down in trenches for a specified time after a shot and did not venture into areas marked as exceeding mission exposure-rate limits) (Frank et al., 1982; Edwards et al., 1985). The doses were often intended to be “high-sided” by maximizing the time that troops were assumed to have spent at the highest allowed exposure rate (Goetz et al., 1981). That conclusion assumes that there was no error in establishing and marking the lines reflecting the limits and that extrapolations of survey data over time were correctly made with appropriate radioactive-decay factors.
However, monitors with troops at the NTS may have failed to do their job properly, instruments may not have been properly calibrated, and officers may have ignored monitor readings or delayed their response. As discussed in Section V.A, it is clear that procedures were not always adhered to and that errors were made.
The assumption that radiation fields were always well characterized is also questionable. With regard to the Marine Corps maneuvers at Operation UPSHOT-KNOTHOLE, Shot BADGER (Frank et al., 1982), the unit dose reconstruction report notes that: “a major obstacle to the preparation of this report was the lack of systematic radiological survey data for the area of Brigade operations.” For Army maneuver units at UPSHOT-KNOTHOLE (Edwards et al., 1985), isopleths estimated by the US Atomic Energy Commission were used to generate space-time models of exposure rate because original survey data were not available.
Assumptions regarding locations of troops vs time are often asserted to be without error or “high-sided,” although the assertions include such words as likely, supposed to, and probably (Frank et al., 1982; Edwards et al., 1985). Finally, departures by individuals from the assumed group scenario are not considered in estimating uncertainty (see Appendix F for discussion of a case in which an actual exposure scenario probably did not correspond to the scenario assumed in a unit dose reconstruction).
V.B.3.2.2 Pacific test site unit dose reconstructions—exposure to fallout
Upper-bound estimates of external gamma dose from fallout for participants in many of the earlier Pacific test series assume that participants were exposed at random locations when on deck or outdoors on a contaminated island or ship, rather than at or near a fixed duty station where the external exposure rate may have been higher or lower than the mean. Estimates of the time that veterans may have been indoors or below decks and of the shielding provided by tents and buildings on islands may also have been overestimated for some participants. Furthermore, generic upper-bound estimates are often incorrectly assigned when calculating the dose to a participant who was exposed for only a fraction of the time assumed in the unit dose reconstruction (for example, when a participant was exposed for only a fraction of the interval assumed in the generic dose reconstruction and the dose was prorated with the same fractional error).
The assumption that each exposure outdoors or on deck was at a random location results in too low an upper bound. It is far more likely that a participant’s assigned duties placed him repeatedly at particular places on a ship or island, and it is unlikely that he was in entirely different areas on the same day. If, for example, the participant was a member of a decontamination crew, his duty location might more likely be in a high-activity area than in an area with an exposure rate reflected by the mean of all the survey data. Even if a participant was not a crewmember, there is no reason to believe that his topside or island activities would place him in completely random locations during the first few days, when most of the dose would be incurred. For personnel billeted on islands, even though the indoor dose is reduced by an assumed 50% shielding factor, it is not negligible, and the indoor location was likely to be repeated rather than random, although his outdoor locations might have been more varied.
The upper-bound gamma doses from exposure to fallout at the Pacific test sites are generally based on a default 50% coefficient of variation (CV) in the mean exposure rate on an island or ship. However, the 50% CV estimate is itself highly uncertain for most events, and that uncertainty is not considered in estimating upper bounds. The CV estimate includes a component representing the variance due to the measurement itself,5 so it does not just represent the variability with location.
Even accepting the 50% CV estimate as reasonable, or a modified value for ships with few data or for which better information is available, a more reasonable upper-bound estimate can be obtained by assuming reasonable uncertainty distributions of parameter values and estimating the total uncertainty stochastically with a Monte Carlo calculation. In contrast with the method used in the NTPR program, we make the pessimistic assumption that the participant was exposed at the same indoor and outdoor locations for the entire period of exposure.
The uncertainty due to time topside on a ship (or outdoors on a residence island) versus inside and the shielding factor, uncertainty in the decay rate, and uncertainty in converting free-in-air exposure to dose must also be considered. Let
I = ∫{[E(t0) × SF × IN] + [E(t0) × OUT]} × t−x × FBE dt.
The integral is over the period of exposure t1 measured from the time of the test to some time T when the veteran left the test site area, and t0 is the time of the measurements of exposure rate. (If the period of exposure is not continuous, the integral can be written as a sum of integrals.) In the equation, I is the integrated dose, E(t0) is the mean of the survey exposure rates measured at time t0, SF is a
Evaluation of the integral given above provides the following expression for the total gamma dose received over the interval from t1 to T:
I = {[E(t0) × SF × IN] + [E(t0) × OUT]} × t0x × [(t11−x – T1−x)/(x − 1)] × FBE.
The upper bound or variance in the total dose calculated from the above equation can be estimated by assigning an uncertainty distribution to each variable. An estimate of the total variance and 95th percentile upper bound was obtained with a Monte Carlo simulation by using the following assumptions:
|
E(t0) |
= 1 R h−1, lognormally distributed with a CV of 0.5 (the indoor and outdoor exposure rates are sampled independently in the Monte Carlo simulation). |
|
SF |
= 0.1 (ships), lognormally distributed with a geometric standard deviation (GSD) of 1.5; SF = 0.5 (islands), normally distributed with an SD of 0.1 (the NTPR program assumes an SD of 0.05). |
|
OUT |
= 0.4 for ships (as assumed by the NTPR program), lognormally distributed with a GSD of 1.4; OUT = 0.6 for islands (as assumed by the NTPR program), lognormally distributed with a GSD of 1.4. |
|
FBE |
= 0.7 rem R−1, normally distributed with an SD of 0.05 (consistent with the NTPR program’s estimated uncertainty). |
|
x |
= 1.2, normally distributed with an SD of 0.1 to account for the variability in x from shot to shot as well as with time after a particular shot. An SD of 0.1 is consistent with data presented in various DNA and SAIC reports; for example, Thomas et al. (1984) estimate a 90% confidence interval of ± 0.2 on the basis of observations. |
The following compares the normalized results in rem for the 95th percentile upper bound (UB) from this Monte Carlo (MC) analysis for an exposure from t0 = t1 = 9 h to T = 120 h with the approximate upper bounds that would be reported by the NTPR program for similar scenarios:
|
|
Dose |
UB-MC |
NTPR-UB |
|
Ship |
6 |
13 |
~7 |
|
Island |
10 |
19 |
~12 |
Similar comparisons could be expected for other intervals.
From the Monte Carlo analysis, it seems clear that a realistic 95th percentile upper-bound estimate of the dose from a single event could be a factor of 2 or more above the mean dose even if the 50% CV for E0 is valid, and it could be even higher if the CV is based on little real data.6
Even assuming that a participant’s location when outdoors or topside varied enough that he was unlikely to have been exposed always at the same exposure rate, thus giving the above analysis of a “high-sided” estimate of his upper-bound dose, it seems clear that the assumption by the NTPR program that he would be exposed completely randomly to the entire distribution of measured exposure rates provides too low an upper-bound estimate. That conclusion is supported by available film-badge results for Operations GREENHOUSE and CASTLE. An SAIC memorandum regarding film-badge data for seamen on the USS Curtiss indicates that the highest film-badge readings were a factor of 2–3 above the mean for various exposure periods (reference CIC-67763, available through http://www.osti.gov/opennet/). A similar memorandum regarding film-badge data for servicemen on Parry Island during Shot DOG indicates that the mean was 0.9 R with a range of 0.56-1.4 R (CIC-58845, available through the same Web site). In both cases, the highest film-badge dose was well above the estimated upper bound for reconstructed doses, which was only about a factor of 1.2 above the mean. Data included in the file for case #68 indicate that the upper end of the range of film-badge readings on the USS Estes (CASTLE series) is much higher than the upper bound estimated for the reconstructed dose to members of the crew.7
Additional exposure to nonbadged crewmembers participating in decontamination activities is not considered in the above analysis. Personnel assigned to decontaminate ships would be likely to receive higher than the average exposure rate for the ship. It is true that weathering and decontamination activities may have reduced the exposure rate somewhat compared with an exposure rate based only on the initial survey data and default decay rate. However, the survey results on ships were often taken during or after the initial decontamination activities, and on-deck activity was generally restricted until decontamination was over.
Finally, the NTPR program does not apply its own uncertainty model correctly. For example, for Operation GREENHOUSE, as discussed earlier, the calculated upper bound is about 20% above the mean for a person exposed over
|
6 |
Exposure to multiple events based on additional survey data would reduce the upper bound somewhat depending on the relative fallout levels. However, it is also not clear that the NTPR program properly accounts for the additional variance due to subtracting residual exposure rates from previous events to obtain the appropriate E0. Any instrument bias in the measurements (assumed to be small relative to the CV) would result in a corresponding bias in the estimated dose. |
|
7 |
As discussed in Section IV.B.2, the NTPR program believes that the higher film-badge data reflect doses to personnel whose duties were more likely to result in high radiation exposure and, thus, do not reflect the upper bound for most unit members. The data do, however, call into question whether unit members are being given the benefit of the doubt in estimating the upper-bound dose. |
the entire series (several months) to fallout from several tests. However, it is assumed that this 20% factor applies to a person exposed over a shorter period when the dose is calculated by integration with the t−1.2 rule, rather than by summing the daily doses and variances for the shorter period (see case #4).8
V.B.3.2.3 Pacific test site unit dose reconstructions—exposure on contaminated target ships
The committee believes that upper-bound estimates of external doses received when boarding target ships in Operation CROSSROADS are unreasonably low. The available data used to calculate the mean exposure-rate curves for each ship are not given, but it is asserted that the upper bound of a total dose is less than a factor of 1.2 above the mean. The original unit dose reconstruction (Weitz et al., 1982) assumed a factor of 1.5. However, that was changed in 1986. The rationale was that the reported averages generally fell within a factor of 1.5 of the trend lines for the daily doses (see Figure IV.B.1) and that an uncertainty factor (ratio of upper bound to mean) of 1.2 better represented the standard error of the mean, which is asserted to be a more appropriate estimate of the error for multiple boardings (Schaeffer, 2002b). As was the case with exposure to fallout during later test series, that assertion is based on assuming random locations during each boarding even if the participant was exposed only for one boarding period (Schaeffer, 2002b) rather than allowing for variation across the measured exposure rates on the ship.9 It is even less likely that a nonbadged participant’s location when he was engaging in inspection or decontamination activities aboard a contaminated target ship would be random than for a participant exposed to fallout on an island or ship during later test series. Furthermore, as discussed below, variations in exposure rate with location on target ships were in most cases probably greater than that measured on ships exposed to fallout during later test series.
The committee examined data on the range of exposure rates on target ships. The data suggested large variations with location on contaminated ships (B2, 1946). Table V.B.1 is an excerpt of those data, showing the average and maximum exposure rates measured on a few target ships. The ratio of the maximum exposure rate to the average suggests a CV well above 50%. For most ships, the available data are sparse, and it is not clear how the mean was determined. Extensive survey data are available, however, for one ship, the USS Salt Lake City (B2, 1946). For the Salt Lake City, the mean exposure rates on deck (topside) ranged from an average of about 0.4 R d−1 near the bow to >10 R d−1 in other open
TABLE V.B.1 Radiation Levels on Selected Target Ships in Roentgen per 24 h (B2, 1946)
|
Shipa |
H+day |
Reported Mean |
Topside Maximum |
|
Parche |
8 |
4 |
7.5 |
|
Pensacola |
8 |
10 |
50 |
|
Salt Lake City |
10 |
3 |
150 |
|
Mugford |
8 |
3 |
30 |
|
Prinz Eugen |
9 |
4 |
60 |
|
Skate |
7 |
4 |
30 |
|
Tuna |
7 |
4 |
30 |
|
aParche, Skate, and Tuna were submarines, but only Tuna was submerged. Other unpublished data suggest that the topside variation in exposure rates was somewhat lower on Tuna than on other ships. |
|||
areas amidships and up to 150 R d−1 for hotspots. Although data for other ships are more limited, data from B2 (1946) and transcripts of radio communications available from the Department of Energy Coordination and Information Center (CIC documents #57001, 57004, 57007, 57020, 57023, 57032, 57033, 57044, 57046, and 57047, which are available through http://www.osti.gov/opennet/) indicate similar variability in exposure rates, excluding hotspots, and suggest that the reported averages and the variations about the means are also very uncertain in that they depend on the number and location of the measurements.10
As discussed previously, doses to seamen boarding target ships are based on the average below-decks, topside and amidships daily dose curves constructed for each ship. Average below-deck exposure rates are small fractions of topside values (Weitz et al., 1982). The target-ship dose calculations by the NTPR program generally average topside and below-deck doses instead of assuming a worst-case scenario that the subject was always topside (Figure V.B.1), barring evidence to the contrary (see case #53).
In some cases, a veteran is given the benefit of the doubt and is assumed to have participated in all boardings (see cases #45, 48, and 49). In other cases, however, that assumption was not made. Thus, in cases #45, 48 and 49, the veteran was given a higher dose for service on possibly less contaminated ships than the veteran in case #53 (see discussion of case #53 in Section V.A.2).
The uncertainty in doses from boarding target vessels clearly does not adequately reflect the uncertainty in the average exposure rate or the variability in exposure rate with location. It also does not reflect the uncertainty in the number of boardings and the location when aboard. Limited film-badge data confirm that. In case #53, the veteran was assigned a reconstructed dose from boarding the USS Skate after Shot BAKER of 0.51 rem, with an upper bound of 0.6 rem, but film-badge data for 82 members of the Skate crew for August indicated a maxi

FIGURE V.B.1 Damaged quarterdeck on USS Pensacola.
mum film-badge dose of 1.1 rem (10 other badges were not turned in or were unreadable).
The committee thus finds that the upper-bound estimates of external gamma dose to participants who boarded target ships during Operation CROSSROADS are likely to be considerably underestimated.
An upper bound for being alongside target ships is estimated as a factor of 1.5 above a central estimate on the basis of survey data taken at a distance of 6 ft from the target. However, the data often vary by about a factor of 2 from port versus starboard, and this suggests that the upper bound may also be too low. The contribution to dose from being alongside a target ship was generally a significant fraction of the total dose to most seamen other than those boarding the targets or those who were members of engineering units and thus were exposed to contaminated piping (Weitz et al., 1982).
V.B.3.2.4 Pacific unit dose reconstructions—summary
Most of the uncertainty in the calculated external gamma dose to participants on ships and islands is due to variations in the measured exposure rate. That the
data are limited suggests that a higher uncertainty should be estimated that allows for the variability in exposure rate with location. Furthermore, the NTPR program assigned default mean exposure rates and corresponding uncertainties (CVs) to islands and ships for which no monitoring data were available, on the basis of the mean and CV estimated for nearby ships for which measurements were available. The committee believes that a higher CV than the mean for nearby ships should be applied on ships for which no data were available to reflect the additional uncertainty in the mean and variance.
The upper-bound calculations for fallout-contaminated ships and islands and the upper bounds for the CROSSROADS target-ship dose calculations are cases in which the NTPR program’s uncertainty analysis clearly is flawed. Those exposure scenarios affect a large fraction of the dose assessments that are based primarily on the unit dose reconstructions carried out for the CROSSROADS, CASTLE, GREENHOUSE, and IVY test series in the Pacific. A considerable fraction (about 25%) of the 99 sampled cases examined by the committee involved either exposure to fallout on ships or islands in the Pacific or exposure from boarding CROSSROADS target ships by nonbadged personnel. About 20% of the individual dose assessments carried out by SAIC for DTRA have involved participants in the CROSSROADS tests, and this reflects the large number of participants in that exercise. About 25% of the individual dose assessments have involved participants exposed to fallout on islands or ships at the Pacific test sites during Operations GREENHOUSE, CASTLE, and IVY before the period when all participants were issued film badges.
V.B.4 Summary of Findings on Estimates of External Gamma Dose
V.B.4.1 Central Estimates
Estimates of the most likely total external gamma doses to individual participants are usually based on film-badge data, unit dose reconstructions, or both and are generally credible, provided that the assumed exposure scenario is reasonable. However, as discussed above and in Section V.A, it appears that in many cases a plausible set of exposure scenarios for the participant was not fully considered. The unit dose reconstructions estimate the average dose to members of the unit. However, some members of a unit may have had doses well above the average. The committee believes that the dose reconstruction process should give a participant the benefit of the doubt by assuming, without strong evidence to the contrary, that he was a member of the most critically exposed population in the unit. The upper bound assigned to the central estimate should reflect a credible maximum (for example, the 95th percentile) of the dose to such members.
Although most individual dose reconstructions are based on unit dose reconstructions, many also involved some modifications based on unique circum-
stances or duties. In many cases, the doses for those duties were estimated on the basis of few data regarding exposure rates and time exposed. Examples include workers in laundries where contaminated clothing was washed, small-boat operators that ferried troops between contaminated islands or ships, and workers who prepared trenches for observers in previously contaminated areas. Often, the corresponding estimates were based on assumptions that were intended to “high-side” the estimate and were deemed to be upper-bound estimates. Generally, the doses from such activities were relatively low, but it is not clear that the estimates always reflected at least the 95th percentile of possible doses.
V.B.4.2 Upper Bounds
Upper-bound estimates of external gamma dose provided by the NTPR program are based primarily on film-badge data or unit dose reconstructions, as discussed above. If a reported dose is based primarily on film-badge data that adequately and reasonably account for all possible external exposures, the reported upper-bound estimates are probably reasonable and even higher than the 95th percentile goal. However, upper bounds based primarily on unit dose reconstructions are, in general, likely to have been underestimated, often substantially.
The upper-bound estimates do not generally include uncertainty due to a possibly incorrect exposure scenario (such as neglect of possible additional exposures or errors in time exposed because of missing or incorrect records). Upper-bound estimates therefore are not credible unless the scenario is correctly specified.
Some of the unit dose reconstructions reviewed by the committee, particularly for smaller units in which the specific daily activities may have varied and were not well known, did not attempt to determine both a central (“best”) estimate and an upper bound. Instead, the central estimate is alleged to be “high-sided” on the basis of the scenario and exposures assumed (for example, see Ortlieb, 1995), and the estimate is treated as an upper bound when it is combined with other reconstructed or film-badge doses.
Upper bounds estimated from film-badge data and from reconstructed doses are combined in quadrature, assuming that they are uncorrelated, to arrive at an estimate of the upper bound in the total dose. To the extent that the individual upper-bound estimates are credible and all doses and potential uncertainties are included, the upper-bound estimate for the sum is credible, provided that uncertainties in the increments of dose are independent—that is, not correlated—which they may not be because of repetitiveness of behavior and work responsibilities. However, as discussed above, the committee has found a number of instances in which the uncertainty estimates in unit dose reconstructions are not credible and will not adequately reflect the true upper bound (95th percentile) of the dose to an individual participant. The committee has also identified situations in which
uncertainty in the exposure scenario, film-badge issuance, and lack of benefit of the doubt suggest a much higher upper bound of the reported doses for individuals, even if they are based primarily on film-badge data.
On the basis of its review, the committee has concluded that reported upper-bound doses of external gamma radiation based primarily on unit dose reconstructions were often markedly underestimated compared with upper bounds that would be obtained if more credible assumptions about parameter values and uncertainties had been used. Of the 50 cases in the 99-case random sample in which a reported upper bound was based partly on a generic (unit) dose reconstruction, the committee has concluded that the upper bounds of about 30 Pacific test-site cases may be underestimated, often by a factor of 2-3 or even more. Reported upper-bound estimates based primarily on film-badge data probably are reasonably “high-sided,” provided that the film-badge data accounted for all possible doses. The committee believes that failure to allow for the possibility that the badge was not always worn, that the times worn are incorrect, or that not all badge data have been accounted for makes it likely that many of the reported upper bounds based only or primarily on film-badge data also underestimate a credible upper bound (95th percentile) dose. Of the 25 cases in which the reported upper bound is based almost entirely on film-badge data, several may also warrant a higher value to give the benefit of the doubt to the participant. Thus, the committee has concluded that the estimated upper bounds reported by the NTPR program for most of the 99 cases examined do not represent a credible estimate of the 95th percentile upper bound in the dose from external gamma radiation exposure.
V.B.5 Neutron Dose Estimates
V.B.5.1 Central Estimates
Most test participants were not exposed to neutrons, except for observers in trenches at NTS tests and a few cloud-sampling personnel. For most participants who were exposed to neutrons, the doses were very low. However, a small number of volunteer observers in trenches very close to ground zero did receive substantial neutron (and gamma) doses during some NTS tests (Goetz et al., 1981).
Estimates of equivalent dose from exposure to neutrons must take into account the increased biological effectiveness of these radiations compared with gamma rays. As discussed in Section IV.B.3, the NTPR program has assumed a quality factor of 13 or 8.5 to represent this effect. These QFs apply at low doses of neutrons. Kocher et al. (2002) recently surveyed the available data and estimated radiation effectiveness factors (REFs) for neutrons, which represent the biological effectiveness in inducing cancer and other stochastic effects in humans relative to the effectiveness of gamma rays. For acute exposure to fission neutrons at low doses received by participants at atomic tests, a median REF of about 15 for induction of solid tumors would be obtained on the basis of the analysis by
Kocher et al.11 If it is taken into account that the spectrum of neutrons to which participants were exposed included neutrons of lower energy than fission neutrons, because of scattering in air, and that REFs for lower-energy neutrons are lower than REFs for fission neutrons, the median REF for fission neutrons and solid tumors estimated by Kocher et al. indicates that the QFs adopted by the NTPR program are reasonable. That is, the assumptions about QF yield reasonable central estimates of neutron equivalent doses to participants. However, as discussed below, the committee has concluded that current estimates of upper-bound neutron doses by the NTPR program may be too low.
V.B.5.2 Upper Bounds
Reported upper bounds of external dose from exposure to neutrons are based on generally accepted radiation-transport calculations and reasonable corrections to account for shielding by trenches, vehicles, and so on. However, estimated upper bounds of neutron doses do not include any uncertainty in the neutron QF. A review of available data in 1986 by the International Commission on Radiation Units and Measurements (ICRU, 1986) indicated that a credible upper bound of QF could be at least a factor of 5 above a central estimate. Later reviews by the National Council on Radiation Protection and Measurements (NCRP, 1990) and the UK National Radiological Protection Board (Edwards, 1997; 1999) also indicated that there is substantial uncertainty in the biological effectiveness of neutrons.
Kocher et al. (2002) reviewed the available data and estimated probability distributions of REFs for fission neutrons. For induction of solid tumors, the probability distribution of REF is lognormal and has a 95% confidence interval between 2.0 and 3.0; the 50th percentile (median) is 7.7. That REF applies at high acute doses of the reference high-energy gamma rays. Thus, to account for the dependence of the relative biological effectiveness (RBE) of neutrons on the dose and dose rate of the reference gamma rays and to be comparable to the QFs at low doses assumed by the NTPR program, the probability distribution of REF should be multiplied by a factor of about 2.12 The resulting 95th percentile of the probability distribution of equivalent dose, appropriate for exposure to fission neu
trons and induction of solid tumors, is about 50, or about a factor 3 above the median.
On the basis of the probability distribution of REF for fission neutrons and solid tumors described above, and taking into account the energy dependence of REF and its uncertainty (Kocher et al., 2002), a credible upper bound (95th percentile) of neutron equivalent dose could be a factor of about 3-5 higher than the QFs of 13 and 8.5 assumed by the NTPR program. Consequently, the upper bound of a combined neutron and gamma dose reported by the NTPR program may not represent a credible upper bound (95th percentile) of the total equivalent dose. For the few participants who were exposed to neutrons,13 the committee has concluded that the NTPR program should revise the upper-bound estimates of neutron dose to include the uncertainty in biological effectiveness.
V.B.6 Beta Skin and Eye Dose Estimates
V.B.6.1 Introduction
Skin cancer was one of the most cited medical issues in the 72 (of 99) sampled individual dose reconstructions that included VA claims. However, for most of the cases involving skin cancer, no beta dose was calculated; beta dose was not routinely calculated in such cases until 1998.
The method for assessing beta dose is discussed in Section IV.B.4. Beta doses from standing on contaminated ground are calculated from upper-bound gamma doses by applying tabulated beta-to-gamma dose ratios that depend on the height above ground, the time after detonation, and whether the shot was at the NTS or in the Pacific. Beta doses from skin contamination and immersion in air or water are calculated by using dose coefficients (beta equivalent-dose rates per unit concentration of radionuclides in the source region). The current method of assessing beta-particle dose from sources outside the body is described in Barss (2000). The Barss report can be considered to have generally documented the method used in 1998 and 1999 and to present the method used after its publication in January 2000.
Of the 99 individual dose-reconstruction cases in the committee’s sample, 27 included a claim or other indication of skin or eye disease (cases #2, 4, 9, 12, 17, 18, 19, 20, 25, 28, 29, 35, 38, 39, 40, 54, 55, 64, 65, 66, 70, 71, 87, 88, 93, 96, and 97). Most involved skin cancer and some indicated the type of skin cancer (such as basal cell or melanoma). Three claims or indications were for other skin conditions: rash and spots (case #87), skin disability (case #88), and incurable skin disease (case #54). Three cases were for cataract (cases #19, 39, and 67), and
there was one case of macular degeneration (case #71). In case #64, both skin and eye doses were recorded explicitly, but the file did not indicate the diseases involved. Of the 27 cases, skin or eye dose was recorded explicitly in nine files for which the claim or other indication of skin or eye disease occurred in 1998 or later (cases #9, 12, 25, 39, 40, 64, 66, 96, and 97). The other 18 files—for claims or other indications of skin or eye disease that occurred before 1998—did not provide explicit skin or eye doses. That distribution is consistent with information provided by the NTPR program (Schaeffer, 2002c): skin dose assessments were not performed routinely before 1998. Table V.B.2 summarizes the nine files that state explicit skin or eye doses, and some representative assessments are discussed below.
V.B.6.2 Summaries of Selected Skin and Eye Dose Assessments
In case #9, the beta dose calculations appear to have been performed with mathematical software, and the data and calculations were annotated. The beta-to-gamma dose ratio method described in Barss (2000) and Section IV.B.4 was used for the beta dose to the skin and lens of the eye from exposure to contaminated surfaces outside the body. Before the beta-to-gamma dose ratios were applied, the upper bound of each component of the gamma dose was determined by multiplying the estimated gamma dose by an upper-bound factor (ratio of upper bound to central estimate). Upper-bound factors of 1.2–1.6 appear to have been used for gamma doses obtained from film badges and reconstructions. A substantial portion of the beta dose to the upper arms and forearms was ascribed to two 1-min exposures to highly contaminated towlines. The assumed distances were 20 cm for the forearm and 40 cm for the upper arm. No uncertainties were ascribed to the exposure time or the distances. The calculated doses would be very sensitive to errors in the determinations of such small times and distances. Although Barss (2000) includes methods for determining beta dose from standing in descending fallout and from skin contamination, there did not appear to be any consideration of those pathways in this case. That could have been appropriate, but it would have been useful to discuss the reasons for not including them.
In case #64, the file contains no narrative describing the dose assessment or detailed calculations. The gamma dose was determined to be 0.7 rem from ship dose tables, and the neutron dose was determined to be zero on the basis of references. As indicated in Table V.B.2, the upper-bound gamma dose was set to 1.6 rem, but without explanation. There were no beta dose calculations, but the skin and eye doses were also set to 1.6 rem, implying a beta-to-gamma dose ratio of 1. There was no consideration of skin contamination or immersion dose. The veteran performed basic seamanship and watch duties on the USS Allen M. Sumner and the USS Moalem. If he worked outside on contaminated ships, some beta dose would be expected from contaminated surfaces and possibly from skin contamination or descending fallout.
TABLE V.B.2 Summary of Nine Cases in Committee’s Random Sample in Which Skin or Eye Doses Were Reported
|
Case # |
Condition |
Claim or Inquiry Date |
Assessment Date |
External Upper Bound Dose |
Skin-dose location |
|
9 |
Skin cancer |
2/25/00 |
12/13/00 |
5.2 |
Head, face, neck Upper arm Forearm Back |
|
12 |
Skin cancer |
8/18/99 |
10/8/99 |
3.7 |
Lower leg |
|
25 |
Skin cancer |
8/11/00 |
10/6/00 |
1.5 |
Face (forehead) |
|
39 |
Cataract |
6/15/00 |
9/5/00 |
7.3 |
N/A |
|
40 |
Skin cancer |
10/19/98 |
7/15/99 |
0.2 |
Face |
|
64 |
Unknown |
12/23/98 |
1/1/99 |
1.6 |
Not stated |
|
66 |
Skin cancer |
12/23/98 |
1/3/99 |
1.8 |
Face, back, arms |
|
96 |
Skin cancer |
4/3/98 |
8/12/98c |
4.3 |
Arm |
|
97 |
Cataract |
3/19/99 |
4/14/99 |
1.9 |
N/A |
|
aMethods: A, Barss (2000); B, Lorence et al. (1989) and Finn et al. (1979); C, no method cited. bReferences were not provided for the beta component of the eye dose, but the methods of Barss (2000) appear to have been used. cDate of transmittal letter; dose-assessment narrative was undated. |
|||||
|
Dose (rem) |
|
||
|
Skin |
Lens of eye |
Methoda |
Comment |
|
30.3 |
8.7 |
A |
“Date pair/upper bound request” in response to VA inquiry; no narrative dose assessment in file; calculations performed with mathematical software and annotated |
|
30.1 |
|||
|
55.5 |
|||
|
8.5 |
|||
|
77.5 |
N/A |
B |
“Upper bound request” in response to VA inquiry; no narrative dose assessment in file; calculations performed with mathematical software and annotated |
|
7.1 |
N/A |
A |
“Date pair/upper bound request” in response to VA inquiry; no narrative dose assessment in file; calculations performed with mathematical software and annotated |
|
N/A |
25.5 |
Ab |
“Date pair/upper bound request” in response to VA inquiry; no narrative dose assessment in file; calculations performed with mathematical software and annotated |
|
0.3 |
N/A |
B |
Update of previous dose assessment based on request from veteran’s family member; beta skin dose specifically requested by JAYCOR; update included detailed narrative and spreadsheet calculations |
|
1.6 |
1.6 |
C |
“Upper bound request” in response to personal inquiry; no narrative dose assessment in file; external dose determined by reference to previous reports; no indication of how skin and eye doses were assessed |
|
1.8 |
N/A |
C |
“Upper bound request” in response to personal inquiry; no narrative dose assessment in file; external dose determined by reference to previous reports; no indication of how skin and eye doses were assessed |
|
35 |
N/A |
B |
Radiation dose assessment in response to VA inquiry; this update to the veteran’s dose included narrative; two assessments were performed with mathematical software and annotated |
|
N/A |
2.4 |
B |
“Upper bound request” in response to personal inquiry; no narrative dose assessment in file; external dose determined by reference to previous reports; eye beta dose calculations performed with mathematical software and annotated |
In case #96, the file contained two dose assessments. The calculations in the first assessment appear to have been performed with mathematical software, and the data and calculations were annotated and easy to follow, compared with other assessments. For gamma doses, comparisons were made between the individual calculations for the veteran and the island gamma doses from published reports. The comparisons were well documented, and the two approaches gave results in good agreement. This assessment, which was performed on June 8-15, 1998, preceded publication of Barss (2000), but the method of assessing beta doses, which was based on multiplying gamma doses by beta-to-gamma dose ratios, appears to be fundamentally the same. Although the narrative report cited Lorence et al. (1989) and Finn et al. (1979) for the beta dose assessment, the calculation itself cited the Barss file using the Stiver method, which was probably the documentation of application of the fundamental references to beta dose assessments. The beta-to-gamma dose ratios in the table used in the assessment for the 1-m distance from the source assumed for the arm were identical with those given in Table 2 of the Barss report, which was identified as intended for historical development only. Discussions in the Barss report indicate that the data in Table 2 were based on erroneous assumptions and that using better assumptions lowers the beta-to-gamma dose ratios by a factor of about 2. Revised tables are provided in the Barss report and are identified as the ones to be used. The upper-bound gamma dose was calculated to be 4.1 rem, and the upper-bound skin dose to the arm was assessed to be 95.2 rem.
A second, undated assessment in case #96 was performed by using “new beta/gamma ratios of 7/13/98.” The ratios in this table are lower than those used in the first assessment, described above, but are still slightly higher than those later recommended for use by Barss (2000). Although annotated, this calculation was not as easy to follow as in the first assessment. The beta-to-gamma dose ratios used in the second assessment for the 1-m distance from the source assumed for the arm were roughly a factor of 2 lower than those used in the first assessment for the same distance and closer to those later published in Barss (2000). The results of the second assessment were an upper-bound gamma dose of 4.3 rem and an upper-bound skin dose of 35 rem. The skin dose was checked against island gamma doses in published reports and found to be in good agreement (32.4 rem). The dose-assessment narrative reported the upper-bound gamma dose as 4.3 rem and the skin dose as “as much as 35” rem.
V.B.6.3 Discussion and Conclusions Regarding Estimate of Skin Doses
From the committee’s reviews of the 99 sampled cases, it is not evident that skin or clothing contamination is being considered as a pathway for beta dose to the skin. If skin or clothing contamination was considered and dismissed, the consideration was not documented in any of the seven cases for which the beta-particle components of skin doses were calculated. However, there are examples
in which participants had to take multiple showers to decontaminate their bodies (see cases #9 and 26) and situations in which soil, presumably contaminated with fallout, was brushed from their clothing and bodies with brooms (for example, see document submission from veteran Frank Bushey in Appendix C). The committee regards neglect of skin contamination as an important problem in dose reconstructions for maneuver troops and close-in observers at the NTS who filed claims for skin cancer. In the Pacific, “minor radiation burns” were seen on personnel who were below decks on the USS Phillip when vents were opened during a period of fallout to reduce intolerably high temperatures (Martin and Rowland, 1982). The committee also notes that a contemporary report (Morgan, 1946) indicated that contamination was found frequently on the clothing and bodies of persons on ships.
Beta-particle doses from standing on contaminated ground are calculated by applying a beta-to-gamma dose ratio to an upper-bound gamma dose. As noted earlier, the committee is concerned that uncertainties in gamma doses may be underestimated in some cases and could lead to underestimates of upper-bound gamma doses and, consequently, to underestimates of beta-particle doses.
The committee also notes that uncertainties are not estimated for the beta-to-gamma dose ratios, although Barss (2000) argues that the ratios are overestimates. However, beta-to-gamma dose ratios depend on the time since detonation and the distance from the source to the exposed tissue. Errors in those quantities may result in substantial underestimation or overestimation of beta-to-gamma dose ratios.
On the basis of the foregoing, the committee found that the beta components of skin doses are questionable. For most of the unit dose reconstructions, beta doses were not calculated, because the method had not been developed. Furthermore, letters to VA by the NTPR program as late as 1997 implied that doses of around 1,000 rem were needed to cause statistical increases in skin cancer (Schaeffer, 1997). The NTPR program also indicated that no evidence suggested that skin cancer was associated with the much lower radiation doses (external or internal) received by participants in atmospheric nuclear testing. That conclusion, however, was apparently based on skin dose calculations that were too low because they did not include a contribution from beta particles and, as discussed below, the assumption that around 1,000 rem was required to induce skin cancer is no longer supported by scientific evidence.
In 1989, NCRP used a linear coefficient, based on recent epidemiological studies, to estimate the cancer risk posed by small radioactive particles on the skin (NCRP, 1989). NCRP noted that skin exposed to ultraviolet (UV) radiation was more susceptible to radiation-induced cancer than UV-protected skin. Most atomic veterans served in Nevada and the South Pacific, places with high solar indexes, so they undoubtedly had UV exposures to some areas of skin.
In 1990, the National Research Council reviewed the relationship between radiation and skin cancer in the fifth report on Biological Effects of Ionizing Radiation (BEIR V) (NRC, 1990). On the basis of a study of persons treated for
ringworm with radiation, the report noted that tumors began to appear about 20 years after exposure and were not limited to the most heavily irradiated parts of the scalp. Tumors tended to occur more commonly at the margins of the scalp and in neighboring areas of skin that were not covered by hair or clothing. An excess of skin cancers was detected even on the cheeks and the neck, where the doses were estimated to have been only 0.12 and 0.09 Gy (12 and 9 rad), respectively. The distribution of tumors suggested that the carcinogenic effects of X rays were increased by exposure to UV radiation.
In 1991, the ICRP stated in Publication 59 (ICRP, 1991b) that “although it has traditionally been thought that there was little if any risk of skin cancer below 10 Gy [1,000 rad], there are now several sets of data indicating excess skin cancer following doses of a few grays [a few hundred rad], with one study suggesting risk below 1 Gy [100 rad]. The evidence does not indicate that the risk per unit dose is greater at higher doses than at lower [doses].” The ICRP also noted that risks were greater for UV-irradiated skin.
Thus, by 1991, there was ample indication from authoritative national and international bodies that skin cancer could be caused by doses much lower than 1,000 rad and that UV-exposed skin was particularly sensitive. However, it was not until 1998 that this information began to be incorporated in dose reconstructions for atomic veterans who filed claims for skin cancer.
V.C EVALUATION OF METHODS OF ESTIMATING INTERNAL DOSE
V.C.1 Introduction
Doses due to intakes of radionuclides produced in a nuclear detonation often are considered to be unimportant when compared with doses due to external exposure. That is especially the case in exposure scenarios involving inhalation of fallout particles at locations relatively close to ground zero and shortly after detonation (NRC, 1985b; Levanon and Pernick, 1988; IOM/NRC, 1995). Such an exposure scenario is important for many participants in nuclear tests at the NTS and in the Pacific. The unimportance of the inhalation hazard posed by fallout shortly after a detonation, compared with the hazard posed by external exposure, is attributed to such factors as: the presence of much greater activities of short-lived photon-emitting radionuclides that tend to result in high external doses per unit activity but much lower inhalation doses, compared with the activities of longer-lived radionuclides for which inhalation doses per unit activity often are considerably higher; the dominance of large, essentially nonrespirable particles in fallout relatively close to ground zero; and the insolubility of fallout particles, which can substantially reduce the extent of absorption of inhaled radionuclides into the body. However, there are exposure scenarios for participants at the NTS and in the Pacific in which activities of longer-lived radionuclides compared with
shorter-lived radionuclides are much higher than in fresh fallout (for example, when exposures occurred a few weeks or more after a detonation), and internal exposure in these cases can contribute significantly to the total dose received by an organ or tissue of concern; see, for example, dose estimates for occupation forces in Japan given in Table IV.D.1.
This section presents the committee’s evaluation of methods used in the NTPR program to estimate internal doses to atomic veterans. Methods of estimating internal dose and the approach to addressing uncertainty are discussed in Sections IV.C and IV.E.4, respectively. Discussions in this section mainly concern methods of estimating doses due to inhalation of radionuclides. Intakes by inhalation are expected to be the most important in determining internal doses to atomic veterans, and only inhalation has been considered routinely in dose reconstructions. Additional discussions and evaluations of the low-level internal dose screen and a bioassay program mentioned in Section IV.C.1 are presented in Sections VI.C and VI.D, respectively.
Data that can be used to estimate inhalation doses to atomic veterans, including data on concentrations of radionuclides in air at times and locations of exposure or amounts of radionuclides excreted in urine or feces, generally are lacking (see Section IV.C.1). Given the lack of relevant data, the basic approach to estimating inhalation doses in the NTPR program has been to use assumptions that are intended to result in substantial overestimates of dose to most participants. In contrast to the approach to assessing external dose from exposure to photons, in which a central (best) estimate and an upper 95th percentile of possible doses are obtained, only a single estimate of inhalation dose, which is intended to be an upper bound (at least a 95th percentile), is obtained in all dose reconstructions for atomic veterans. Thus, the committee’s evaluation of methods used in the NTPR program to estimate inhalation doses essentially involves an assessment of whether the methods are likely to yield credible upper bounds (at least a 95th percentile) of possible doses.
This section is divided into four parts. First, we summarize findings of a previous committee of the National Research Council that reviewed methods of estimating inhalation doses to atomic veterans; second, we discuss our own evaluation of methods of estimating inhalation doses; third, we consider the potential importance of ingestion exposures of atomic veterans (as noted in Section IV.C.3, ingestion of radionuclides is rarely taken into account in dose reconstructions); and fourth, we summarize our principal findings from our evaluation of methods of estimating internal doses used in the NTPR program and conclusions based on the findings.
V.C.2 Findings of Previous National Research Council Review
In the middle 1980s, a committee of the National Research Council conducted the first external scientific review of methods used in the NTPR program
to estimate doses to atomic veterans (NRC, 1985b). That committee’s review of methods of estimating internal doses focused mainly on inhalation doses because, as noted above, ingestion usually was considered to be relatively unimportant and had been included in dose reconstructions only rarely.
At the time of the first National Research Council review, methods of estimating inhalation doses to atomic veterans were largely the same as the methods that have been used since then (Egbert et al., 1985; Barrett et al., 1986). As described in Section IV.C.2, inhalation doses were estimated on the basis of estimates of concentrations of radionuclides in air at locations and times of exposure that were inferred from measurements of external photon exposure with film badges worn by veterans or field instruments, assumed resuspension factors, assumed breathing rates, and other assumptions about the physical and chemical composition of fallout particles or neutron-activated materials in soil.
The 1985 committee generally took a dim view of methods of estimating inhalation doses on the basis of measurements of external photon exposure. The committee stated, for example, that “these methods involve assumptions about relationships between airborne and deposited fallout that are not scientifically valid, and their reliability, even for establishing upper limits of internal radiation doses, is unknown” (NRC, 1985b). Other statements also questioned the credibility and defensibility of the methods. The committee’s report did not discuss the basis of the findings in detail. However, the committee’s concerns apparently included the methods’ insensitivity to the presence of beta- and alpha-emitting radionuclides that are important contributors to inhalation dose, such as 90Sr and plutonium, and the possibility that internal dosimetry models used to estimate doses per unit activity of radionuclides inhaled (inhalation dose coefficients) would not apply to the physical and chemical forms of fallout particles, especially in cases of exposure to large, highly insoluble particles in descending fallout. The committee argued that methods of estimating internal doses to atomic veterans needed to be validated with bioassay testing.
In spite of the 1985 committee’s concerns about methods of estimating inhalation doses in the NTPR program, however, it also concluded that the methods “tended to overestimate possible internal doses” and, particularly in cases of inhalation of descending fallout, “probably resulted in large overestimates of radiation exposures” (NRC, 1985b). Those findings also were not discussed in detail, but they apparently were based, at least in part, on the use in dose reconstructions of an assumption that all fallout was in the form of small particles that were respirable when most of the activity in fallout at locations of participant exposure was in the form of large, essentially nonrespirable particles.14
|
14 |
An option of estimating doses due to inhalation of large, essentially nonrespirable particles (AMAD, 20 μm) was later included in the FIIDOS computer code (Egbert et al., 1985) (see Section IV.C.2.2.1). |
The 1985 committee concluded that inhalation exposures had only a “minor impact on total doses expected” (NRC, 1985b). The committee’s concerns about methods of estimating inhalation doses thus did not appear to be important with regard to the potential for significant doses to atomic veterans. The view that inhalation doses generally were overestimated in the NTPR program and were unimportant was echoed in a later study (IOM/NRC, 1995).
V.C.3 Evaluation of Methods of Estimating Inhalation Dose
The present committee’s evaluation of methods used in the NTPR program to estimate inhalation doses focuses on the question of whether the methods are likely to provide credible upper bounds of possible doses (see Section IV.E.4). The committee’s evaluation is divided into three parts. The first part discusses assumptions used in estimating inhalation doses that, in the committee’s opinion, tend to result in overestimates of dose. The second part discusses assumptions that, in the committee’s opinion, tend to result in substantial underestimates of inhalation doses, and it also considers assumptions that have substantial uncertainty and the importance of that uncertainty in obtaining credible upper bounds of inhalation doses. The third part summarizes the committee’s evaluation of methods of estimating inhalation doses used in the NTPR program.
V.C.3.1 Assumptions Tending to Overestimate Inhalation Dose
The committee found that several assumptions used to estimate inhalation doses in the NTPR program should tend to result in overestimates of possible doses. In the following discussion, assumptions related to estimating inhalation dose coefficients (equivalent doses to specific organs or tissues per unit activity of radionuclides inhaled) are considered first and are followed by assumptions related to estimating inhalation exposures (intakes of radionuclides in air); these are the two components of models used to estimate inhalation doses (see Section IV.C.2).
[1] In exposure scenarios in which inhaled particles are assumed to be respirable (that is, when a particle size, AMAD, of 1 μm is used), organ-specific inhalation dose coefficients used in the NTPR program often (but not always) are higher than values for the same particle size currently recommended for use in radiation protection of workers by ICRP.
An AMAD of 1 μm often is assumed, for example, in scenarios involving suspension of activation products in soil or resuspension of fallout particles that were deposited on the ground or other surfaces, especially when this assumption results in higher estimates of dose than would an assumed particle size of 20 μm (see Section IV.C.2.2.1).
As noted in Section IV.C.2.2, all inhalation dose coefficients used in dose reconstructions were based on dosimetric and biokinetic models described in ICRP Publication 30 (ICRP, 1979a). Those models represented the state-of-the-art in estimating internal dose when methods of estimating internal doses to atomic veterans (Egbert et al., 1985) were developed.
Beginning in the late 1980s, ICRP developed a new set of dose coefficients for inhalation and ingestion of radionuclides (ICRP, 1989; 1993; 1994a; 1995; 1996a; 1996b) to replace values recommended in ICRP Publication 30.15 The dose coefficients and associated dosimetric and biokinetic models constitute ICRP’s current recommendations on methods of calculating dose from intakes of radionuclides for purposes of radiation protection (see also ICRP, 2002).
ICRP’s current recommendations on inhalation (and ingestion) dose coefficients incorporate three important changes in methods of calculating internal dose. First, the earlier model used to estimate deposition, retention, translocation, and absorption of inhaled radionuclides and doses to tissues of the respiratory tract (ICRP, 1979a) was replaced by a new and more complex respiratory-tract model (ICRP, 1994b). Second, new biokinetic models to describe the behavior of radionuclides after absorption into blood from the respiratory or gastrointestinal (GI) tract were developed for many chemical elements.16 Third, when radioactive decay products are produced in the body after intakes of a parent radionuclide, separate biokinetic models are used for the particular chemical elements of concern.17 In addition, assumed GI-tract absorption fractions and deposition fractions of absorbed activity in different organs or tissues are changed for some radionuclides.
A comparison of dose coefficients for inhalation of radionuclides in respirable form (AMAD, 1 μm) often used in dose reconstructions for atomic veterans with values for workers for the same particle size currently recommended by ICRP (2002) is given in Tables V.C.1 and V.C.2.18 Radionuclides listed in these tables include selected shorter-lived and longer-lived fission products, activation
|
15 |
Dose coefficients given in ICRP Publication 56 (ICRP, 1989) were superseded by values given in later reports. |
|
16 |
The new biokinetic models are physiologically based—that is, translocation and retention are modeled with more realistic representations of physiologic compartments in the body, and cycling among various compartments is taken into account—in contrast to the more empirical approach used previously of modeling retention by fitting of retention or excretion data over time with simple exponential functions (ICRP, 1979a). |
|
17 |
The approach to biokinetic modeling of decay products now used by ICRP was incorporated in earlier dose coefficients in the ORNL reports (Killough et al., 1978b) but not in dose coefficients given in ICRP Publication 30 (ICRP, 1979a) or by Eckerman et al. (1988) (see Section IV.C.2.2). |
|
18 |
For purposes of evaluating compliance with dose limits for occupational exposure, ICRP now recommends that a default particle size (AMAD) of 5 μm should be assumed in the absence of information on actual particle sizes (ICRP, 1994a). In the present report, however, current ICRP recommendations based on a particle size of 1 μm are used to be consistent with the assumption for inhalation of respirable particles used in all dose reconstructions. |
products, and transuranium radionuclides that often should be among the most important in estimating inhalation doses at various times after a detonation. Not included in the tables is 131I, for which the dose coefficient for the thyroid currently recommended by ICRP (1994a) is about a factor of 2 less than the value used in dose reconstructions, and 137Cs, for which the current dose coefficients for all organs and tissues are slightly lower than the values used in dose reconstructions. The data in these tables illustrate that doses per unit activity inhaled tend to be substantially higher for longer-lived radionuclides than for shorter-lived radionuclides (see Section V.C.1).
The data in Tables V.C.1 and V.C.2 indicate that dose coefficients for inhalation of radionuclides attached to respirable particles (AMAD, 1 μm) used in the NTPR program tend to be higher than values for the same particle size currently recommended by ICRP. That is the case especially for the lung and respiratory lymphatic tissues, but for some radionuclides substantial differences are also
TABLE V.C.1 Comparison of Dose Coefficients for Inhalation of Radionuclides in Respirable Form (AMAD, 1 μm) Used in NTPR Program with Values for Same Particle Size Currently Recommended by ICRP: I. Shorter-Lived Radionuclides
|
|
Dose coefficient (rem μCi−1)a |
|||||||
|
Nuclideb |
Lungc |
Lymph tissued |
Large intestinee |
Red bone marrow |
Bone surfaces |
Liver |
Bladder Wall |
|
|
24Na |
4.6E-3 |
2.5E-2 |
3.8E-4 |
1.0E-3 |
1.2E-3 |
8.1E-4 |
5.3E-4 |
|
|
(15.0 h) |
(5.2E-4) |
(4.1E-4) |
(4.4E-4) |
(5.6E-4) |
(7.8E-4) |
(3.7E-4) |
(5.6E-4) |
|
|
56Mn |
2.0E-3f |
|
3.8E-5f |
3.0E-5f |
|
|||
|
(2.6 h) |
(1.3E-3) |
(8.5E-5) |
(3.7E-4) |
(3.7E-5) |
(3.0E-5) |
(4.1E-5) |
(2.2E-5) |
|
|
91Sr |
4.3E-3 |
2.9E-2 |
2.6E-3 |
4.1E-4 |
4.4E-4 |
4.1E-4 |
2.6E-4 |
|
|
(9.6 h) |
(1.9E-4) |
(9.6E-5) |
(1.9E-3) |
(4.8E-4) |
(5.2E-4) |
(9.6E-5) |
(5.6E-4) |
|
|
93Y |
1.4E-2 |
1.4E-2 |
6.4E-3 |
1.1E-4 |
1.7E-4 |
2.3E-4 |
1.4E-5 |
|
|
(10.2 h) |
(5.6E-3) |
(1.9E-5) |
(7.0E-3) |
(6.7E-6) |
(4.8E-6) |
(6.3E-6) |
(5.6E-6) |
|
|
97Zr |
2.1E-2 |
2.2E-2 |
1.6E-2 |
4.0E-4 |
3.8E-4 |
3.9E-4 |
2.4E-4 |
|
|
(16.7 h) |
(1.2E-2) |
(4.8E-4) |
(1.4E-2) |
(2.9E-4) |
(2.4E-4) |
(1.6E-4) |
(1.8E-4) |
|
|
143Ce |
1.6E-2 |
1.9E-2 |
1.6E-2 |
1.2E-4 |
7.7E-5 |
2.0E-4 |
7.6E-5 |
|
|
(33.0 h) |
(1.5E-2) |
(2.5E-4) |
(9.3E-3) |
(1.6E-4) |
(1.9E-4) |
(6.3E-4) |
(5.6E-5) |
|
|
239Np |
1.0E-2 |
1.9E-2 |
1.2E-2 |
1.8E-4 |
9.1E-4 |
2.9E-4 |
7.3E-5 |
|
|
(2.4 d) |
(2.2E-2) |
(2.9E-4) |
(7.0E-3) |
(1.7E-4) |
(1.9E-3) |
(1.2E-4) |
(7.8E-5) |
|
|
aFirst entry is value from Table 5a of Egbert et al. (1985) based on ORNL reports (Killough et al., 1978a; Dunning et al., 1979) and often used in dose reconstructions for atomic veterans, except as noted; values are based on dosimetric and biokinetic models in ICRP Publication 30 (ICRP, 1979a). Second entry, in parentheses, is value for AMAD of 1 μm currently recommended for adult workers by ICRP (2002). All values apply to radionuclides in oxide form (Eckerman et al., 1988). bEntry in parentheses is radionuclide half-life. cDose coefficients for lung are calculated as described in Section V.C.3.1, comment [7]. dLymphatic tissues that drain bronchial and pulmonary regions of lung. eWall of lower large intestine. fValue from Eckerman et al. (1988). |
||||||||
TABLE V.C.2 Comparison of Dose Coefficients for Inhalation of Radionuclides in Respirable Form (AMAD, 1 μm) Used in NTPR Program with Values for Same Particle Size Currently Recommended by ICRP: II. Longer-Lived Radionuclides
|
|
Dose coefficient (rem μCi−1)a |
||||||
|
Nuclideb |
Lungc |
Lymph tissued |
Large intestinee |
Red bone marrow |
Bone surfaces |
Liver |
Bladder Wall |
|
60Co |
1.3 |
1.2E1 |
2.9E-2 |
6.4E-2 |
5.1E-2 |
1.2E-1 |
1.1E-2 |
|
(5.3 y) |
(6.3E-1) |
(5.9E-1) |
(1.7E-2) |
(4.4E-2) |
(3.3E-2) |
(7.0E-2) |
(4.4E-3) |
|
89Sr |
6.6E-3 |
7.6E-2 |
1.4E-2 |
1.3E-2 |
2.7E-2 |
2.2E-3 |
1.1E-3 |
|
(50.5 d) |
(7.4E-4) |
(6.7E-4) |
(1.4E-2) |
(1.6E-2) |
(2.0E-2) |
(6.7E-4) |
(2.3E-3) |
|
90Sr |
9.9E-3 |
1.4E-1 |
1.4E-2 |
1.1 |
2.2 |
1.5E-2 |
7.3E-3 |
|
(28.8 y) |
(2.3E-3) |
(2.2E-3) |
(1.9E-2) |
(5.9E-1) |
(1.4) |
(2.2E-3) |
(4.8E-3) |
|
95Zr |
6.9E-2 |
2.3E-1 |
1.6E-2 |
5.5E-3 |
7.8E-3 |
4.7E-3 |
1.6E-3 |
|
(64.0 d) |
(1.1E-1) |
(1.9E-2) |
(8.9E-3) |
(8.5E-3) |
(4.4E-2) |
(3.6E-3) |
(4.1E-4) |
|
106Ru |
3.8 |
3.4E1 |
1.4E-1 |
9.4E-3 |
1.0E-2 |
1.2E-2 |
3.9E-3 |
|
(373 d) |
(1.9) |
(3.5E-1) |
(7.8E-2) |
(3.6E-3) |
(3.1E-3) |
(4.4E-3) |
(2.3E-3) |
|
144Ce |
2.9 |
2.2E1 |
1.3E-1 |
9.0E-3 |
1.5E-2 |
8.1E-2 |
2.9E-4 |
|
(285 d) |
(1.4) |
(2.1E-1) |
(7.0E-2) |
(4.1E-3) |
(7.0E-3) |
(2.0E-2) |
(2.7E-4) |
|
152Eu |
2.7 |
6.1E1 |
5.6E-2 |
1.3E-1 |
2.0E-1 |
9.8E-1 |
1.4E-2 |
|
(13.5 y) |
(2.1E-1) |
(1.2E-1) |
(5.6E-2) |
(2.4E-1) |
(6.7E-1) |
(9.6E-1) |
(2.3E-2) |
|
239Puf |
5.8E2 |
4.1E4 |
1.1E-1 |
3.0E2 |
4.2E3 |
8.0E2 |
2.9 |
|
|
(2.9E2) |
(3.0E3) |
(1.1) |
(3.1E1) |
(6.3E2) |
(1.3E2) |
(1.1) |
|
aFirst entry is value from Table 5a of Egbert et al. (1985) based on ORNL reports (Killough et al., 1978a; Dunning et al., 1979) and often used in dose reconstructions for atomic veterans; values are based on dosimetric and biokinetic models in ICRP Publication 30 (ICRP, 1979a). Second entry, in parentheses, is value for AMAD of 1 μm currently recommended for adult workers by ICRP (2002). All values apply to radionuclides in oxide form (Eckerman et al., 1988). bEntry in parentheses is radionuclide half-life. cDose coefficients for lung are calculated as described in Section V.C.3.1, comment [7]. dLymphatic tissues that drain bronchial and pulmonary regions of lung. eWall of lower large intestine. fDose coefficients apply to any mixtures of 239Pu and 240Pu, which have half-lives of 24,100 and 6,560 y, respectively. |
|||||||
found for other organs and tissues. In some cases, however, the ICRP’s current dose coefficient is substantially higher than the value used in the NTPR program. The increase by a factor of 10 for plutonium and the lower large intestine wall is discussed in Section V.C.3.2, comment [3].
Differences in dose coefficients for the lung shown in Tables V.C.1 and V.C.2 are due to a number of factors, including: substantial differences in dose coefficients for respiratory lymphatic tissues combined with a change in how the dose to these tissues is incorporated into the dose to the lung (see comment [7] in this section); differences in dosimetric models for radiosensitive tissues in airways of the respiratory tract; differences in assumptions about deposition fractions of inhaled 1-μm particles in different regions of the respiratory tract, includ
ing a separate accounting of depositions resulting from breathing through the mouth or nose in the new respiratory-tract model; and differences in models that describe clearance of radionuclides from the respiratory tract by mechanical transport of particles or absorption into blood, including a separate accounting of the two competing processes in the new model. For inhalation of a long-lived, alpha-emitting radionuclide in insoluble form, such as plutonium, those factors are listed in approximate order of importance. A change in definition of “lung” in the ICRP models also has implications for estimating the probability of causation of lung cancers in atomic veterans; this issue is discussed in comment [7] in this section.
[2] In exposure scenarios in which inhalation of large particles is assumed (that is, when an AMAD of 20 μm is used), organ-specific dose coefficients used in the NTPR program often are higher than values that would be based on current ICRP recommendations.
In the NTPR program, an AMAD of 20 μm sometimes is assumed in estimating doses due to inhalation of descending fallout because large particles constitute a substantial fraction of fallout near the location of a detonation (Hicks, 1982; Levanon and Pernick, 1988). That is the case especially when an organ of concern in a dose reconstruction is the thyroid, an organ in the GI tract, or the prostate,19 and the assumption results in higher estimates of dose than would an assumed particle size of 1 μm. An assumption of large particles is also used in some cases in estimating inhalation doses due to resuspension of deposited fallout. On the basis of dose coefficients used in the NTPR program, an assumption of inhalation of large particles that are mainly deposited in the nose and throat and then swallowed greatly reduces estimates of dose to the lung but increases estimates of dose to organs of the GI tract and the dose to the thyroid from inhalation of 131I compared with an assumption that the inhaled materials are respirable (AMAD, 1 μm) (see Section IV.C.2.2.1).
Large-particle inhalation dose coefficients used in the NTPR program are calculated by assuming that all inhaled particles are deposited in the nose and throat and that 99% of the deposited activity is swallowed, with the remaining 1% absorbed into blood (ICRP, 1979a). Doses to organs of the GI tract result mainly from radionuclides that are swallowed and pass through the body, and these doses are estimated by using dose coefficients for ingestion of radionuclides. Doses to other organs depend on the total activity absorbed into blood from the nose and throat and the GI tract.
In ICRP’s current respiratory-tract model (ICRP, 1994b), the fraction of inhaled large particles (AMAD, 20-100 μm) that are deposited in the nose and throat is assumed to be about 0.5, in contrast to the previous value of 1.0 (ICRP,
1979a). Furthermore, about half the particles deposited in the nose and throat are assumed to be expelled by nose-blowing or -wiping (ICRP, 1994b). Thus, dose coefficients for inhalation of large particles used in the NTPR program may be too high by a factor of about 4. As indicated by comparisons in Tables V.C.3 and V.C.4, there usually is little difference between ingestion dose coefficients used in the NTPR program and those currently recommended by ICRP, especially in organs of the GI tract. Again, ingestion dose coefficients are applied to the large fraction of radionuclides attached to large particles that are deposited in the nose and throat and later swallowed. In cases of intakes of 131I, the ingestion dose coefficient for the thyroid currently recommended by ICRP is about 20% less than the value used in the NTPR program. Thus, taking into account differences in the models for deposition and exhalation of large particles in the nose and throat and differences in dose coefficients for ingestion, dose coefficients for inhalation of large particles used in the NTPR program should, in most cases, be higher than values that would be based on current ICRP recommendations.
TABLE V.C.3 Comparison of Dose Coefficients for Ingestion of Radionuclides Used in NTPR Program with Values Currently Recommended by ICRP: I. Shorter-Lived Radionuclides
|
|
Dose coefficient (rem μCi−1)a |
||||||
|
Nuclideb |
Kidneys |
Pancreas |
Large intestinec |
Red bone marrow |
Bone surfaces |
Liver |
Bladder Wall |
|
24Na |
1.4E-3 |
1.5E-3 |
7.3E-4 |
1.8E-3 |
2.2E-3 |
1.4E-3 |
1.0E-3 |
|
(15.0 h) |
(1.1E-3) |
(1.4E-3) |
(1.5E-3) |
(1.4E-3) |
(2.0E-3) |
(1.1E-3) |
(1.6E-3) |
|
56Mn |
|
|
2.0E-3d |
9.0E-5d |
3.9E-5d |
|
|
|
(2.6 h) |
(1.1E-4) |
(1.9E-4) |
(2.0E-3) |
(8.9E-5) |
(4.4E-5) |
(9.3E-5) |
(9.3E-5) |
|
91Sr |
3.4E-4 |
3.7E-4 |
1.6E-2 |
3.2E-4 |
2.3E-4 |
2.6E-4 |
3.1E-4 |
|
(9.6 h) |
(2.3E-4) |
(2.5E-4) |
(1.5E-2) |
(5.9E-4) |
(5.2E-4) |
(1.8E-4) |
(7.0E-4) |
|
93Y |
1.7E-5 |
2.0E-5 |
3.3E-2 |
1.7E-5 |
6.1E-6 |
1.2E-5 |
2.3E-5 |
|
(10.2 h) |
(1.8E-5) |
(1.9E-5) |
(3.2E-2) |
(1.6E-5) |
(7.4E-6) |
(1.2E-5) |
(2.3E-5) |
|
97Zr |
4.1E-4 |
4.0E-4 |
6.6E-2 |
4.8E-4 |
1.7E-4 |
3.0E-4 |
6.5E-4 |
|
(16.7 h) |
(4.1E-4) |
(3.7E-4) |
(6.7E-2) |
(4.4E-4) |
(2.0E-4) |
(2.9E-4) |
(6.7E-4) |
|
143Ce |
1.0E-4 |
1.1E-4 |
4.3E-2 |
1.9E-4 |
5.9E-5 |
7.6E-5 |
2.1E-4 |
|
(33.0 h) |
(1.0E-4) |
(1.0E-4) |
(4.4E-2) |
(1.3E-4) |
(7.8E-5) |
(8.1E-5) |
(2.1E-4) |
|
239Np |
7.8E-5 |
8.0E-5 |
2.9E-2 |
1.7E-4 |
7.6E-5 |
6.7E-5 |
1.8E-4 |
|
(2.4 d) |
(7.8E-5) |
(7.4E-5) |
(3.2E-2) |
(9.6E-5) |
(9.3E-5) |
(5.2E-5) |
(1.7E-4) |
|
aFirst entry is value from Table 4a of Egbert et al. (1985) based on ORNL reports (Killough et al., 1978a; Dunning et al., 1979) and often used in dose reconstructions for atomic veterans, except as noted; values are based on dosimetric and biokinetic models in ICRP Publication 30 (ICRP, 1979a). Second entry, in parentheses, is value currently recommended for adult workers by ICRP (1994a; 2002). All values assume GI-tract absorption fraction that applies to radionuclides in oxide form (Eckerman et al., 1988). bEntry in parentheses is radionuclide half-life. cWall of lower large intestine. dValue from Eckerman et al. (1988) or DOE (1988). |
|||||||
TABLE V.C.4 Comparison of Dose Coefficients for Ingestion of Radionuclides Used in NTPR Program with Values Currently Recommended by ICRP: II. Longer-Lived Radionuclides
|
|
Dose coefficient (rem μCi−1)a |
||||||
|
Nuclideb |
Kidneys |
Pancreas |
Large intestinec |
Red bone marrow |
Bone surfaces |
Bladder Liver |
Wall |
|
60Co |
5.7E-3 |
5.9E-3 |
4.0E-2 |
5.4E-3 |
4.0E-3 |
6.8E-3 |
6.2E-3 |
|
(5.3 y) |
(5.2E-3) |
(5.2E-3) |
(4.1E-2) |
(4.8E-3) |
(4.1E-3) |
(8.5E-3) |
(6.3E-3) |
|
89Sr |
8.6E-4 |
8.6E-4 |
8.7E-2 |
5.2E-3 |
1.1E-2 |
8.6E-4 |
4.3E-4 |
|
(50.5 d) |
(7.4E-4) |
(7.4E-4) |
(8.1E-2) |
(1.8E-2) |
(2.2E-2) |
(7.7E-4) |
(2.5E-3) |
|
90Sr |
6.0E-3 |
6.0E-3 |
7.8E-2 |
4.3E-1 |
8.6E-1 |
5.7E-3 |
3.0E-3 |
|
(28.8 y) |
(2.4E-3) |
(2.4E-3) |
(8.1E-2) |
(6.7E-1) |
(1.5) |
(2.4E-3) |
(5.6E-3) |
|
95Zr |
4.2E-4 |
3.9E-4 |
2.9E-2 |
6.6E-4 |
3.3E-4 |
3.0E-4 |
9.0E-4 |
|
(64.0 d) |
(4.4E-4) |
(4.1E-4) |
(2.9E-2) |
(7.8E-4) |
(1.9E-3) |
(3.0E-4) |
(4.1E-4) |
|
106Ru |
8.3E-3 |
8.3E-3 |
2.6E-1 |
8.3E-3 |
9.6E-3 |
8.3E-3 |
4.4E-3 |
|
(373 d) |
(5.6E-3) |
(5.6E-3) |
(2.6E-1) |
(5.6E-3) |
(5.6E-3) |
(5.6E-3) |
(6.3E-3) |
|
144Ce |
2.4E-4 |
3.0E-5 |
2.5E-1 |
1.4E-4 |
1.5E-4 |
7.4E-4 |
7.3E-5 |
|
(285 d) |
(7.4E-5) |
(7.0E-5) |
(2.4E-1) |
(7.0E-4) |
(1.2E-3) |
(3.6E-3) |
(1.1E-4) |
|
152Eu |
1.2E-3 |
6.6E-4 |
6.3E-2 |
9.8E-4 |
6.9E-4 |
2.6E-3 |
1.1E-3 |
|
(13.5 y) |
(1.2E-3) |
(1.2E-3) |
(3.7E-2) |
(2.2E-3) |
(4.1E-3) |
(5.9E-3) |
(1.6E-3) |
|
239Pud |
6.3E-2 |
3.6E-3 |
2.0E-1 |
1.9E-1 |
2.6 |
4.9E-1 |
1.8E-3 |
|
|
(2.5E-3) |
(1.0E-3) |
(2.0E-1) |
(2.9E-2) |
(5.9E-1) |
(1.3E-1) |
(1.0E-3) |
|
aFirst entry is value from Table 4a of Egbert et al. (1985) based on ORNL reports (Killough et al., 1978a; Dunning et al., 1979) and often used in dose reconstructions for atomic veterans; values are based on dosimetric and biokinetic models in ICRP Publication 30 (ICRP, 1979a). Second entry, in parentheses, is value currently recommended for adult workers by ICRP (1994a; 2002). All values assume GI-tract absorption fraction that applies to radionuclides in oxide form (Eckerman et al., 1988). bEntry in parentheses is radionuclide half-life. cWall of lower large intestine. dDose coefficients apply to any mixtures of 239Pu and 240Pu, which have half-lives of 24,100 and 6,560 y, respectively. |
|||||||
[3] An assumption that inhaled particles are respirable (AMAD, 1 μm) should result in large overestimates of dose to the lung if most of the inhaled materials were large particles. Doses to other organs and tissues, except those in the GI tract in many cases, also should be overestimated.
Some dose reconstructions for atomic veterans assume that inhaled particles were respirable even when a substantial fraction of inhaled material probably consisted of large particles. As noted above and discussed in Section IV.C.2.2.1, an assumption of respirable particles often is used when the organ or tissue of concern is not the thyroid, an organ in the GI tract, or prostate, even in cases of inhalation of mostly large particles in descending fallout. Inhalation of large particles also could be important in other scenarios, such as exposure to fresh
fallout that was resuspended by gentle disturbances that did not pulverize fallout particles.
An assumption that inhaled materials were respirable when the materials probably consisted mainly of large particles should result in large overestimates of dose to the lung, because lung doses are proportional to the fraction of inhaled material that is deposited in the bronchial and pulmonary regions and this deposition fraction is small for large particles. In the ICRP’s current respiratory-tract model (ICRP, 1994b), the total deposition in all tissues making up the lung is about 15% when inhaled particles are assumed to be respirable (AMAD, 1 μm); but when large particles are inhaled, the fraction deposited in the lung ranges from about 1.5% at an AMAD of 20 μm to less than 0.05% at an AMAD of 100 μm. In the respiratory-tract model used in the NTPR program (ICRP, 1979a), the deposition fraction in tissues making up the lung is assumed to be 33% at an AMAD of 1 μm and zero at an AMAD of 20 μm or greater. Thus, dose to the lung could be overestimated by more than a factor of 10 when inhalation of respirable particles is assumed but most inhaled materials were large particles.
A comparison of inhalation dose coefficients in Tables V.C.1 and V.C.2, which apply to respirable particles, with the corresponding ingestion dose coefficients in Tables V.C.3 and V.C.4, which describe much of the dose from inhalation of large particles, indicates that an assumption of respirable particles when large particles are inhaled also could result in substantial overestimates of dose to organs and tissues other than those in the respiratory and GI tracts. The extent of overestimation depends on the radionuclides inhaled and their relative activities. However, plutonium is an exception (see Section V.C.3.2, comment [3]).
[4] The extent of absorption of inhaled radionuclides into blood from the respiratory tract or, when swallowed, from the GI tract assumed in dose reconstructions may be overestimated for refractory radionuclides—such as plutonium and isotopes of yttrium, zirconium, and rare-earth elements—in fallout particles, especially when large particles are inhaled.
In the respiratory-tract model used in the NTPR program (ICRP, 1979a), radionuclides that are not in gas or vapor form are assumed to be attached to surfaces of inhaled particles, from which they can be detached and dissolved in the respiratory and GI tracts, and the solubility of radionuclides is assumed to depend only on their chemical form, independent of the chemical composition of the particles to which they are attached. In fallout particles, however, refractory radionuclides— such as plutonium and isotopes of yttrium, zirconium, and rare-earth elements—are distributed approximately uniformly throughout the particle volume, rather than attached to surfaces (see Section IV.C.2.1.2). Furthermore, fallout particles that contain refractory materials should be highly insoluble, perhaps more so than insoluble chemical forms of radionuclides included in the ICRP models.
Thus, when fallout particles are inhaled, absorption of refractory radionuclides into blood from the respiratory or GI tract before the particles are elimi-
nated from the body may be substantially less than assumed in the NTPR program, especially in cases of inhalation of large fallout particles that contain a relatively high proportion of refractory radionuclides. Reductions in absorption would result in corresponding reductions in doses to organs and tissues other than those in the respiratory and GI tracts.
[5] Dosimetry models for internal emitters assumed in dose reconstructions may overestimate doses to organs and tissues of the respiratory and GI tracts when large fallout particles that contain refractory radionuclides that emit alpha particles, such as plutonium, are inhaled.
In dosimetry models for radionuclides in the body used in dose reconstructions (ICRP, 1979a), which provide estimates of doses to target tissues per disintegration of a radionuclide at a site of deposition or transit, emitted radiation is assumed not to be attenuated or absorbed in particles to which radionuclides are attached. That assumption is reasonable when radionuclides are attached to surfaces of small particles. However, doses to organs and tissues of the respiratory and GI tracts could be substantially lower than calculated with ICRP’s dosimetry models for internal emitters when large fallout particles that contain refractory radionuclides that emit alpha particles, such as plutonium, are inhaled. In such cases, most of the energy of emitted alpha particles would be absorbed in the fallout particles, rather than surrounding tissues, because of the very short range of alpha particles of a few μm or less. As noted above, this effect could persist during the time that large fallout particles remain in the body, because of their insolubility.
[6] Dose coefficients for inhalation of radionuclides used in the NTPR program are committed doses; that is, they represent total doses received in specific organs and tissues over a period of 50 years after intake. In organs and tissues other than those in the lung (excluding lymphatic tissues) and GI tract, use of 50-year committed doses can result in substantial overestimates of the dose that could have caused a cancer in an exposed person when an inhaled radionuclide is long-lived and tenaciously retained in the body and the cancer of concern occurred well within 50 years.
Use of 50-year committed doses from intakes of radionuclides is standard practice in radiation protection of workers. That approach takes into account that an acute intake of a radionuclide can result in a dose that is received over many years (see Section IV.C.2.2).20
In dose reconstructions for atomic veterans who file a claim for compensation, the quantity of interest is the dose received in an organ or tissue of concern
before a cancer occurred at that site, not the 50-year committed dose used in radiation protection. When an inhaled radionuclide has a half-life or biological half-time in the body of a few years or less, there is little difference between the dose received before the time of occurrence of a cancer, assuming that the cancer did not occur before a minimum latent period after intake, and the 50-year committed dose resulting from a given intake. However, when a radionuclide is long-lived and tenaciously retained in the body, there can be a significant difference between the dose received before a cancer occurred and the 50-year committed dose. In inhalation exposures of atomic veterans, the difference is potentially important mainly for plutonium and, to a lesser extent, 90Sr. The difference between the dose received and the 50-year committed dose is most important for organs and tissues other than those in the respiratory and GI tracts, excluding respiratory lymphatic tissues where long-lived and insoluble radionuclides are assumed to be tenaciously retained (ICRP, 1979a; 1994b).
Consider a hypothetical example in which the disease of concern in an atomic veteran is bone or liver cancer and the dose to bone surfaces or liver was due primarily to inhalation of insoluble plutonium. Suppose that the cancer was diagnosed 35 years after exposure and that the latent period for the cancer is 10 years (Eckerman et al., 1999). In this case, the dose that could have caused the cancer is the dose received within the first 25 years after exposure, and use of 50-year committed doses to bone surfaces or liver would overestimate the dose that could have caused the cancer, mainly because of the biological half-time of plutonium in bone or the liver of several decades (ICRP, 1979a; 1993; 2002). The retention half-time of insoluble plutonium in the lung of a few years when inhaled particles are respirable (AMAD, 1 μm) is less important. Thus, even if inhaled plutonium were rapidly transferred to bone or liver, the 50-year committed dose would overestimate the dose received in the first 25 years by about a factor of 2, and the degree of overestimation would increase somewhat if the inhaled plutonium was respirable and the low rate of absorption of insoluble forms of inhaled plutonium from the respiratory tract into blood is taken into account.21
Again, the difference between the 50-year committed dose and the dose received in an organ or tissue is potentially important only if the dose was due mainly to intakes of long-lived radionuclides that are tenaciously retained in the body. Thus, the importance of this difference in dose reconstructions for atomic veterans depends on the activities of particular radionuclides inhaled.
The committee also notes, however, that use of 50-year committed doses from inhalation of long-lived radionuclides that are tenaciously retained in the body, such as plutonium, could result in underestimates of the dose that could
have caused a veteran’s cancer in two situations. The first is illustrated by the example discussed above. In that example, if plutonium is an important contributor to dose and a cancer occurs more than 60 years after exposure, the 50-year committed dose would underestimate the relevant dose. That situation could occur in the future as the population of surviving atomic veterans ages.
The second situation involves cancers for which VA may have assumed that there is no appreciable increase in risk beyond some time after a radiation exposure. For example, studies of the Japanese atomic-bomb survivors indicate that there is little risk of a radiation-induced leukemia beyond about 25 years after exposure (see Section III.E), and a similar assumption may be made for a few other cancers, including lymphoma and multiple myeloma. However, there is an important difference between exposures of the Japanese atomic-bomb survivors and exposures of some atomic veterans that should be taken into account in applying assumptions about decreases in cancer risk at times long after exposure of the veterans. Essentially all of the dose to the atomic-bomb survivors was received at the time of the bombings or shortly thereafter, and there was little exposure due to inhalation of long-lived fission products and plutonium. In contrast, an atomic veteran who inhaled substantial amounts of plutonium and other long-lived radionuclides that are tenaciously retained in the body continued to receive a dose to bone marrow and lymphatic tissues long after the time of intake. Therefore, the practice in the NTPR program of assigning the entire 50-year committed dose from inhalation of plutonium and other long-lived radionuclides to the year of intake, which ignores that the dose is protracted over many decades after an intake, would greatly underestimate the dose that could have caused a veteran’s cancer if the risk of that cancer is assumed to be negligible beyond some time after exposure and the veteran’s cancer occurred at such a time.
[7] Dose coefficients for the lung used in the NTPR program could overestimate doses to particular tissues in the respiratory tract where lung cancers occur.
In the respiratory-tract model used by the NTPR program (ICRP, 1979a), dose coefficients for the lung represent the average dose to the tracheobronchial tree, pulmonary region, and pulmonary lymphatic tissues. That is, dose to the lung is calculated as the total energy absorbed in the three regions divided by an assumed total mass of tissue of 1,000 g.
Most lung cancers occur in the bronchial region, which also is the region where most excess lung cancers in the Japanese atomic-bomb survivors have occurred (ICRP, 1994b). In the respiratory-tract model used in dose reconstructions (ICRP, 1979a), calculated doses to the lung overestimate doses to the tracheobronchial tree in cases of inhalation of insoluble (Class Y) longer-lived radionuclides in respirable form (AMAD, 1 μm) by about a factor of 3 because of the influence of the relatively high dose to lymphatic tissues on the average dose in all tissues considered (see Table V.C.2). The difference is smaller when shorter-
lived radionuclides are inhaled, because of the smaller influence of doses to lymphatic tissues (see Table V.C.1).
In ICRP’s current respiratory-tract model (ICRP, 1994b), dose to the lung is calculated as a weighted average of doses to the bronchial region, bronchiolar region, alveolar-interstitial region, and lymphatic tissues draining these regions, with the dose to lymphatic tissues given a weight of 0.001 and doses to the other three regions each given a weight of 0.333. Thus, the current model gives much less weight to the dose to lymphatic tissues, and the result is that the average dose to all tissues in the bronchial region is about the same as the weighted-average dose to the lung.
[8] Assumptions about resuspension of radionuclides in fallout that was deposited on the ground or suspension of neutron-induced activation products in surface soil used in dose reconstructions should, in some cases, tend to result in overestimates of concentrations in air relative to concentrations on the ground.
Resuspension of fallout deposited on the ground or suspension of activation products in surface soil is important in many scenarios for inhalation exposure of atomic veterans. Resuspension factors normally used in dose reconstructions for these scenarios are discussed in Sections IV.C.2.1.3 and IV.C.2.1.4 and are summarized in Table IV.C.2.
In some exposure scenarios at the NTS or on residence islands in the Pacific, resuspension or suspension of radionuclides on the ground occurred mainly as a result of normal wind stresses or walking and other activities that did not involve vigorous disturbance of surface soil. In those cases, a resuspension factor of 10−5 m−1 often is assumed in dose reconstructions (see cases #8, 21, 22, 23, 27, 36, 38, 43, 47, 96, and 98), although a lower resuspension factor of 10−6 m−1, or even zero, sometimes is assumed when deposited fallout was aged for some time (see cases #31, 58, 63, 78, and 94). The latter assumptions are based on studies that showed that weathering of deposited materials generally reduced the resuspension factor over time (for example, see Anspaugh et al., 1975). As discussed in Sections IV.C.2.1.3 and IV.C.2.1.7, resuspension factors assumed in dose reconstructions are intended to overestimate airborne concentrations of radionuclides relative to concentrations on the ground.
The resuspension factor that should be applied to a particular exposure scenario is a highly uncertain parameter (see Section IV.C.2.1.3), and its value depends on the disturbance that causes resuspension. Data summarized in Table 12.7 of Sehmel (1984) indicate that resuspension factors at a height of 1 m above ground caused by normal wind stresses vary over a range of about 10−10 to nearly 10−4 m−1, with most of the values being less than 10−5 m−1, often by a factor of 10 or more; 1 m is the standard height at which resuspension factors normally are determined. Higher resuspension factors usually apply to freshly deposited materials, although very low values were obtained in some controlled tracer studies.
Most studies of the effects of walking on resuspension, as summarized in Table 12.9 of Sehmel (1984), were conducted in indoor environments, and results of such studies probably are not applicable outdoors. In the few studies outdoors, resuspension factors at a height of 1 m above ground caused by walking were in the range of about 10−8 to 10−5 m−1.22
On the basis of information summarized above, the committee has concluded that resuspension factors used in the NTPR program should tend to overestimate airborne concentrations of radionuclides relative to concentrations on the ground in exposure scenarios in which resuspension or suspension of radionuclides is caused by normal wind stresses, walking, or other actions that do not involve vigorous disturbance of surface soil. That conclusion applies, for example, to resuspension of fresh or aged fallout or suspension of activation products in soil at the NTS and to resuspension of fallout on residence islands in the Pacific under the stated conditions of disturbance. As noted above, resuspension factors of 10−5 or 10−6 m−1 often are assumed in these scenarios. A resuspension factor of 10−5 m−1 that is normally assumed in scenarios at the NTS involving suspension of activation products in soil also should be a considerable overestimate under the stated conditions of disturbance because suspended materials are part of soil rather than deposited loosely on the ground surface, as is fallout.
The committee also cautions, however, that a resuspension factor of 10−5 or 10−6 m−1 may not be an overestimate during normal, nonvigorous activities on contaminated ships in the Pacific, nor does the conclusion discussed above apply to other exposure scenarios at the NTS in which resuspension is caused by more vigorous disturbances of deposited fallout. Those issues are discussed in the following section.
In summary, the committee has identified several assumptions used in the NTPR program to estimate inhalation dose coefficients and concentrations of radionuclides in air that, in the committee’s opinion, should tend to result in overestimates of inhalation doses to atomic veterans; these assumptions are briefly restated in Table V.C.5. The committee also emphasizes, however, that the discussions of these assumptions should not be used to draw conclusions about whether estimates of inhalation doses to atomic veterans provide credible upper bounds without also considering the importance of uncertainties in these assumptions and the importance of other countervailing assumptions used in the NTPR program that may tend to result in underestimates of inhalation doses. Those other issues are discussed in the following section, and the committee’s overall evaluation of methods of estimating inhalation doses used in the NTPR program is presented in Sections V.C.3.3, V.C.5, and V.C.6.
TABLE V.C.5 Summary of Assumptions Used to Estimate Inhalation Doses in NTPR Program That Should Tend to Result in Overestimates of Dosea
|
Dose coefficients (organ-specific equivalent doses per unit activity of radionuclides inhaled) • Dose coefficients for respirable particles (AMAD, 1 μm) often are higher than values for same particle size currently recommended for workers by ICRP. • Dose coefficients for large particles (AMAD, 20 μm) often are higher than values based on current ICRP recommendations. • Assumption of respirable particles overestimates dose to lung and many other organs when most inhaled materials are large particles.b • Assumed absorption of refractory radionuclides (for example, plutonium and isotopes of yttrium, zirconium, and rare-earth elements) from respiratory or GI tract may be overestimated, especially when large particles are inhaled. • Dose to respiratory and GI tracts may be overestimated when large particles containing alpha-emitting refractory radionuclides (for example, plutonium) are inhaled. • Use of 50-year committed doses may overestimate relevant doses from intakes of long-lived radionuclides that are tenaciously retained in the body (for example, plutonium).c • Dose coefficients for the lung may overestimate dose to tissues in respiratory tract where lung cancers occur.d |
|
Methods used to estimate inhalation exposures (intakes of radionuclides in air) • Resuspension factors applied to fallout deposited on ground or to neutron-induced activity in soil may overestimate airborne concentrations in some scenarios.e |
|
a Assumptions are discussed in detail in Section V.C.3.1. b For most radionuclides, assumption of respirable particles when large particles are inhaled does not overestimate dose to organs of GI tract. c Relevant dose is dose received before disease of concern in exposed person occurs, taking into account latent period between radiation exposure and earliest onset of disease. However, as discussed in Section V.C.3.1, comment [6], use of 50-year committed doses may underestimate relevant doses in some cases. d Most lung cancers, including cancers caused by radiation, occur in bronchial region. e Conclusion applies mainly to scenarios in which resuspension of fallout deposited on the ground or suspension of neutron-induced activity in soil is caused by normal wind stresses or walking and other activities that do not involve vigorous disturbance of surface soil. |
V.C.3.2 Assumptions With Substantial Uncertainty or Tending to Underestimate Inhalation Dose
The committee also is concerned that some assumptions used to estimate inhalation doses in the NTPR program may not tend to overestimate actual doses and thus may not lead to credible estimates of upper bounds for use in evaluating claims for compensation.
The committee’s concerns are of two kinds. The first is that, in some cases, assumptions about scenarios of inhalation exposure or estimates of parameter values probably result in substantial underestimates of possible doses, provided that other assumptions used in estimating inhalation dose are reasonable. The second concern is that uncertainties in assumptions, models, and parameter val-
ues used to estimate inhalation doses have not been considered in the NTPR program. As discussed in Section IV.E.4, all estimates of inhalation dose are presented as single values without uncertainty. The justification for that approach is essentially that estimates of inhalation dose are based on assumptions that are sufficiently biased on the high side that the estimates themselves can be considered upper bounds of possible doses. However, the committee is concerned that that may not be the case when uncertainties in assumptions are considered, even when assumed exposure scenarios are reasonable. The two types of concerns are related, in that they both are important in evaluating whether estimates of inhalation doses obtained in the NTPR program are credible upper bounds. As in the previous section, assumptions concerned with estimation of inhalation dose coefficients (organ-specific equivalent doses per unit activity of radionuclides inhaled) are considered first, followed by assumptions concerned with estimation of inhalation exposures (intakes of radionuclides in air).
[1] Dose coefficients for inhalation of radionuclides used in the NTPR program are based on dosimetric and biokinetic models that have substantial uncertainty. As a result, credible upper bounds of inhalation dose coefficients may be substantially higher than values used in dose reconstructions, even though the assumed dose coefficients often are higher than values currently recommended by ICRP.
Dose coefficients for inhalation of radionuclides used in the NTPR program are standard values developed by ICRP. These dose coefficients apply to so-called Reference Man, which is an anatomic, physiologic, and metabolic representation of an average adult (ICRP, 1975). Dose coefficients for Reference Man are assumed to be appropriate for use in radiation protection (that is, in evaluating compliance with dose limits for workers and other requirements).
However, there is substantial uncertainty in inhalation dose coefficients developed by ICRP. The uncertainty results, first, from uncertainty in dosimetric and biokinetic models used to calculate dose coefficients and in data incorporated in the models and, second, from the variability in anatomic, physiologic, and metabolic characteristics among people. Those sources of uncertainty in dose coefficients should be acknowledged and addressed in dose reconstructions for atomic veterans if credible upper bounds of inhalation dose are to be obtained. The approach taken in the NTPR program essentially has been to argue, first, that its methods of estimating inhalation dose, especially assumptions about resuspension factors used to estimate airborne concentrations of radionuclides relative to concentrations on the ground or other surfaces, generally are sufficiently biased on the high side that they compensate for uncertainty in dose coefficients,23
and, second, that information on uncertainty in dose coefficients was not available for use in dose reconstructions (for example, see Goetz et al., 1987).
The first analysis of uncertainty in dose coefficients was concerned with dose to the thyroid of an adult from ingestion of 131I (Dunning and Schwarz, 1981); the results also apply to inhalation of 131I. The analysis showed that when data on the variability in thyroid mass, fractional uptake of absorbed iodine in the thyroid, and retention half-time of iodine in the thyroid are taken into account, the 95th percentile of the dose per unit activity intake in an adult exceeds the median (50th percentile) by a factor of 3. The results of that uncertainty analysis could have been taken into account, but were not, in a later dose reconstruction for a small group of veterans on Rongerik Atoll in the Marshall Islands who were exposed to high levels of fallout after Operation CASTLE, Shot BRAVO and received an estimated equivalent dose of 190 rem to the thyroid from intakes of 131I (Goetz et al., 1987).
More recently, Bouville et al. (1994) published an analysis of the reliability of dose coefficients for inhalation and ingestion of selected radionuclides; the analysis was adopted in a later report of NCRP (1998). The results of that analysis are summarized in Table V.C.6. An uncertainty factor of 10, for example, means that the 95th percentile of a subjective probability (uncertainty) distribution of the effective dose per unit activity intake by healthy adult males is a factor of 10 higher than the value recommended by ICRP.
Estimates of reliability (uncertainty) in dose coefficients summarized in Table V.C.6 apply to the effective dose, which is a weighted average of equivalent doses to different organs and tissues defined in ICRP Publication 60 (ICRP, 1991a) and is similar to the effective dose equivalent calculated in some dose reconstructions for atomic veterans (see Section IV.C.2). In specific organs and tissues of concern when a veteran files a claim for compensation, the uncertainty in an inhalation dose coefficient could be larger than the uncertainty in the effective dose coefficient. That is the case, for example, in estimating dose to radio-sensitive tissues of the skeleton (bone surfaces and bone marrow) when the important radionuclides inhaled include 90Sr or plutonium (Eckerman et al., 1999). Estimates of dose to the walls of organs of the GI tract from ingestion of alpha-emitting radionuclides (such as plutonium) also have large uncertainty (ICRP, 1979a).
Uncertainty in inhalation dose coefficients of the magnitude indicated in Table V.C.6 clearly is important when methods of estimating inhalation dose used in the NTPR program are intended to provide credible upper bounds. Depending on the particle size of inhaled materials, the organ or tissue of concern, and the important radionuclides inhaled, this source of uncertainty may not be fully compensated by assumptions embodied in dose coefficients used in the NTPR program that should tend to overestimate dose, including that the dose coefficients are higher in many cases than values currently recommended by ICRP.
TABLE V.C.6 Estimated Reliability of Effective Dose Coefficients for Selected Radionuclides, Relative to Values Recommended in ICRP Publication 30a
|
Radionuclide |
Route of Intakeb |
Uncertainty Factorc |
|
High reliability |
||
|
3H (HTO) |
Ingestion |
2 |
|
14C (CO2) |
Inhalation |
2 |
|
137Cs |
Inhalation or ingestion |
2 |
|
90Sr |
Inhalation or ingestion |
3 |
|
131I |
Inhalation or ingestion |
3 |
|
140La |
Ingestion |
3 |
|
Intermediate reliability |
|
|
|
140La, 210Pb |
Inhalation |
5 |
|
14C (CO2) |
Ingestion |
5 |
|
60Co, 144Ce |
Inhalation |
5 |
|
210Pb, 230Th |
Inhalation |
5 |
|
234U |
Inhalation |
5 |
|
55Fe, 95Nb |
Inhalation or ingestion |
5 |
|
140Ba, 226Ra |
Inhalation or ingestion |
5 |
|
Low reliability |
|
|
|
210Po |
Ingestion |
10 |
|
60Co, 210Pb |
Ingestion |
10 |
|
230Th, 234U |
Ingestion |
10 |
|
95Zr, 106Ru |
Inhalation or ingestion |
10 |
|
125Sb |
Inhalation or ingestion |
10 |
|
237Np, 239Pu |
Inhalation or ingestion |
10 |
|
241Am, 244Cm |
Inhalation or ingestion |
10 |
|
144Ce |
Ingestion |
10 |
|
aEstimates given by Bouville et al. (1994) and NCRP (1998). Effective dose is weighted average of equivalent doses to different organs and tissues (ICRP, 1991a). bInhaled materials are assumed to be attached to respirable particles (AMAD, 1 μm), except that 3H (HTO) and 14C (CO2) are assumed to be in vapor and gaseous form, respectively. cRatio of the upper limit of a 90% confidence interval of a subjective probability distribution of the effective dose per unit activity intake by healthy adult males to the effective dose coefficient recommended by ICRP; that is, the 95th percentile of an assumed probability distribution exceeds ICRP’s recommended value by the uncertainty factor (see Section V.C.3.2, comment [1]). |
||
[2] Dose coefficients for inhalation of alpha-emitting radionuclides, such as plutonium, used in dose reconstructions incorporate an assumption that the biological effectiveness of alpha particles is 20 times that of photons and electrons, without uncertainty. However, a credible upper-bound estimate of the biological effectiveness of alpha particles is substantially higher than the assumed value.
Dose coefficients for inhalation of alpha-emitting radionuclides used in dose reconstructions incorporate a standard assumption recommended by ICRP (1977;
1991a) and NCRP (1987b; 1993) that alpha particles are 20 times more effective in inducing stochastic biological effects (cancers and severe hereditary effects) than photons and electrons. That is, in calculating equivalent doses in organs and tissues, absorbed doses of alpha particles are multiplied by a factor of 20. That factor is applied without uncertainty in radiation protection. However, available information on the relative biological effectiveness (RBE) of alpha particles indicates that there is considerable uncertainty in the particular value that should be used to estimate equivalent doses in humans. That uncertainty should be addressed if credible upper bounds of doses from inhalation of alpha-emitting radionuclides, such as plutonium, are to be obtained in dose reconstructions.
A review and analysis of data on the biological effectiveness of alpha particles in inducing lung tumors in various animals was published by ICRP (1980b) at about the time the NTPR program began; the review included information on uncertainty in estimates of biological effectiveness. On the basis of the combined data from studies that used soluble or insoluble chemical forms of alpha-emitting radionuclides, ICRP concluded that the RBE of alpha particles was in the range of about 6-40. However, when only the data from studies using insoluble plutonium oxide were considered, the RBE was in the range of about 10-100. The latter estimate of uncertainty is more relevant to dose reconstructions for atomic veterans in that plutonium and other alpha-emitting radionuclides in fallout are expected to be relatively insoluble.
Later analyses of data on the biological effectiveness of alpha particles were presented by NCRP (1990) and the UK National Radiological Protection Board (Muirhead et al., 1993). The analyses indicate that a central estimate of the RBE of alpha particles obtained from various studies that are relevant to induction of cancer in humans is in the range of about 5-60. That range would be substantially broader if uncertainty in the individual determinations of biological effectiveness were taken into account.
On the basis of analyses by ICRP (1980b), NCRP (1990), and Muirhead et al. (1993) discussed above, Kocher et al. (2002) developed a subjective probability (uncertainty) distribution of the so-called radiation effectiveness factor (REF) for alpha particles in inducing solid tumors in humans; an REF in humans represents data on the RBE of alpha particles in other organisms.24 Probability distributions of REFs for all radiation types developed by Kocher et al. (2002) will be used in estimating equivalent doses to workers at DOE facilities for the purpose of evaluating claims for compensation for radiation-related diseases.
The probability distribution of REF for alpha particles and solid tumors developed by Kocher et al. (2002) has a 95% confidence interval of 3.4-100; the
central estimate (50th percentile) is 18.25 That confidence interval encompasses an estimate of uncertainty by the US Environmental Protection Agency (EPA, 1999). On the basis of the uncertainty estimated by Kocher et al., a credible upper bound of the biological effectiveness of alpha particles, as represented by the 95th percentile, is about 76, or a factor of nearly 4 greater than the value 20 used in dose reconstructions. An uncertainty of such magnitude clearly is important.
[3] Dose coefficients for inhalation of plutonium used in dose reconstructions may underestimate doses to organs of the GI tract by a substantial amount in scenarios in which an appreciable fraction of inhaled materials are respirable (AMAD, 1 μm).
In dose reconstructions for atomic veterans, doses to organs of the GI tract due to inhalation of radionuclides usually are calculated by using dose coefficients for large particles (AMAD, 20 μm). That choice is made because, on the basis of dose coefficients for inhalation and ingestion used in the NTPR program, an assumption of large particles generally results in higher estimates of dose to these organs than an assumption of respirable particles (AMAD, 1 μm); see Section IV.C.2.2.1 and dose coefficients for the wall of the lower large intestine based on ICRP Publication 30 (ICRP, 1979a) given in Tables V.C.1 through V.C.4.
On the basis of dose coefficients for inhalation and ingestion of radionuclides by adult workers currently recommended by ICRP (1994a; 2002), an assumption of inhalation of large particles still results in higher estimates of dose to organs of the GI tract in most cases (see Tables V.C.1 through V.C.4). However, insoluble plutonium is an exception. In this case, current ingestion dose coefficients for organs of the GI tract are little changed from the values used in dose reconstructions, but inhalation dose coefficients for these organs, assuming an AMAD of 1 μm, are a factor of about 10 higher in the current recommendations. As a result of that increase, the usual assumption of large particles would result in an underestimate of dose to organs of the GI tract from inhalation of insoluble plutonium by a factor of about 5 in scenarios in which inhalation of respirable particles is likely. The importance of this underestimation of dose depends on intakes of plutonium relative to intakes of other radionuclides and the magnitude of the dose.
The increase in dose coefficients for organs of the GI tract from inhalation of insoluble plutonium and the counterintuitive result that the dose to these organs from inhalation is higher than the dose from ingestion of insoluble plutonium is due to a significant change in the biokinetic model for systemic plutonium. In the model used in the NTPR program (ICRP, 1979a), all plutonium absorbed into
blood from the respiratory or GI tract is assumed to be deposited only in bone, liver, or gonads. In ICRP’s current model, however, so-called soft tissue compartments are also included, and 14% of all plutonium absorbed into blood is assumed to be deposited uniformly in these tissues, which include all organs of the GI tract (ICRP, 1993). Furthermore, the residence half-time of plutonium in the soft-tissue compartment is many decades. Thus, in the current model, the higher dose to organs of the GI tract from inhalation of insoluble, respirable plutonium than from ingestion is due to three factors: the greater absorption of plutonium from the respiratory tract than from the GI tract, where the absorption fraction is only 10−5 (ICRP, 1993; 2002); the low doses to walls of the GI tract during passage of ingested plutonium, because of the short range of alpha particles in matter and short transit time of material in the GI tract (ICRP, 1979a); and deposition of a small but important amount of absorbed plutonium in tissues of GI tract, where it remains for many years.
[4] Methods used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces on the basis of measurements of external photon exposure with film badges or field instruments involve potentially important sources of error and uncertainty that have not been evaluated. An overall bias of the methods toward overestimation or underestimation of concentrations of radionuclides in deposited fallout in all exposure scenarios is difficult to determine from documentation of the methods. However, an assumption of no fractionation of radionuclides in fallout except for removal of noble gases, which has been used in all dose reconstructions, should result in substantial underestimates of concentrations of important refractory radionuclides, such as plutonium, in deposited fallout at locations relatively close to detonations where many participants were exposed, especially at the NTS. In addition, an assumption that the source region is infinite in extent, which is used to relate measured external exposures to concentrations of radionuclides on the ground or other surfaces, is probably not valid in cases of fallout on ships in the Pacific, and concentrations of radionuclides in deposited fallout may be substantially underestimated in these cases.
Scenarios involving inhalation of radionuclides in descending fallout or in fallout that was deposited on the ground or other surfaces and then resuspended in the air are important in dose reconstructions for many participants at the NTS or in the Pacific. In all such scenarios, inhalation doses are estimated in the NTPR program on the basis of estimates of concentrations of radionuclides in deposited fallout. The following discussion concerns methods used in the NTPR program to estimate those concentrations. Assumptions about resuspension factors that are used to estimate concentrations of radionuclides in air breathed by exposed people relative to concentrations on the ground or other surfaces are considered separately in later comments in this section.
Methods used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces are described in Section IV.C.2.1. These estimates depend essentially on two types of data: relative activities of radionuclides in an atmospheric cloud immediately after a detonation, which are estimated from cloud sampling data and calculations of relative activities of fission and activation products produced by the weapon type of concern; and external photon exposures or exposure rates due to deposited fallout, which are estimated from readings of film badges worn by participants or field instruments. All other aspects of the methods involve assumptions about how those data are related to concentrations of radionuclides in deposited fallout. Specifically, on the basis of an assumption about relative activity concentrations of radionuclides on the ground or other surfaces compared with estimated relative activities in the cloud (fractionation of radionuclides) and calculations of external exposure rates per unit concentration of radionuclides on the surface, the desired concentrations on the surface, SA, are estimated as (SA/I) × I, where I is a measured exposure rate due to all radionuclides and (SA/I) is the reciprocal of the calculated exposure rate per unit concentration for the assumed mixture of radionuclides on the surface.
As discussed in Section V.C.2, a previous committee of the National Research Council concluded that methods of estimating radionuclide concentrations in fallout deposited on the ground or other surfaces based on measurements of external photon exposure are not scientifically valid and that their reliability is unknown (NRC, 1985b). The present committee agrees with the previous conclusion that the reliability of the methods is unknown but does not consider the methods to be generally invalid. Relative activities of radionuclides in an atmospheric cloud can be estimated reasonably well from data from cloud sampling and calculations of relative amounts of fission and activation products produced by detonation of a weapon type of concern. If fractionation of radionuclides in the cloud is properly taken into account (see Section IV.C.2.1.2), relative activity concentrations of radionuclides in deposited fallout can be estimated from relative activities in the cloud. Well-established calculation methods can then be used to estimate external exposure rates due to assumed relative activity concentrations of radionuclides in deposited fallout. Finally, measurements of external exposures or exposure rates can be used to normalize calculated exposure rates due to an assumed mixture of radionuclides in deposited fallout to obtain estimates of absolute activity concentrations (Ci m−2) of each radionuclide.
Thus, the committee has concluded that methods used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces are valid, at least in principle, even with regard to estimating concentrations of beta- and alpha-emitting radionuclides, such as 90Sr and plutonium, that can be important contributors to inhalation dose but are not detected by measurements of external photon exposure. However, the reliability of the methods depends on the validity of data and assumptions used to estimate relative
activity concentrations of radionuclides in deposited fallout and the validity of assumptions used to calculate external exposure rates per unit concentration of radionuclides on a surface.
The committee is concerned that important sources of error and uncertainty in methods used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces based on measurements of external photon exposure have not been evaluated. Therefore, the reliability of the methods has not been demonstrated, and uncertainty in the calculations has not been quantified. The committee’s principal concerns involve two issues: fractionation of radionuclides in an atmospheric cloud, which determines relative activities of radionuclides in deposited fallout at specific locations compared with estimated relative activities in the cloud; and calculation of external photon exposure rates per unit concentration of radionuclides on a surface in cases of fallout on ships in the Pacific.
Methods used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces assume that fractionation of radionuclides in an atmospheric cloud does not occur, except for removal of noble gases (see Section IV.C.2.1.1). However, fractionation is important in determining relative activities of radionuclides in deposited fallout. Although the discussion of fractionation in Section IV.C.2.1.2 is an idealized representation of a complex process (Freiling et al., 1964), neglect of fractionation generally results in underestimates of relative activities of refractory radionuclides—such as plutonium and shorter-lived isotopes of yttrium, zirconium, and rare-earth elements—in fallout at locations relatively close to detonations where considerable resuspension occurred and many participants were exposed and similar overestimates of relative activities of volatile radionuclides, such as 131I and isotopes of strontium. Neglect of fractionation is an important concern, in part, because plutonium probably posed the greatest long-term inhalation hazard at the NTS and in the Pacific.
Data discussed by Hicks (1982) and Freiling et al. (1964) indicate that fractionation typically alters the relative activities of refractory and volatile radionuclides in local fallout, compared with initial activities in an atmospheric cloud, by a factor of about 3-4. In a few shots, however, the effect was as large as a factor of 100 or even more (Freiling et al., 1964). Thus, activities of plutonium and other refractory radionuclides in deposited fallout could be underestimated substantially when fractionation is not taken into account, and activities of volatile radionuclides could be overestimated to a similar extent. That is the case especially at the NTS because all fallout there probably contained a substantial fraction of large particles in which most of the activity of refractory radionuclides but relatively little of the activity of volatile radionuclides was found (Hicks, 1982). Furthermore, there is substantial uncertainty in the extent of fractionation at any shot. There also is some uncertainty in estimates of relative activity concentrations of radionuclides in an atmospheric
cloud and in film-badge or field-instrument measurements of external photon exposures from radionuclides deposited on a surface. However, the extent of fractionation and its uncertainty probably is the most important factor affecting the reliability of methods of estimating concentrations of radionuclides in deposited fallout in all exposure scenarios. The committee also notes that the extent of fractionation cannot be estimated reliably from measured external exposures, because relative activities of photon-emitting radionuclides in deposited fallout can vary widely and still give approximately the same reading on a film badge or field instrument and approximately the same dependence of exposure rate on time after a detonation.
In the method used in the NTPR program to calculate external photon exposure rates per unit concentration of radionuclides deposited on the ground or other surfaces, the surface is assumed to be uniformly contaminated and infinite in spatial extent, and the source region is modeled to take into account a small shielding effect of about 0.7 due to ground roughness (Egbert et al., 1985; Barrett et al., 1986). Those assumptions are reasonable in cases of fallout deposited at the NTS or on residence islands in the Pacific because external exposure at a given location was due almost entirely to sources within a few tens of meters and fallout usually was widespread and did not vary irregularly over such small distances. The method of calculation is unlikely to significantly overestimate exposure rates per unit concentration of radionuclides in fallout deposited at the NTS or on residence islands in the Pacific and therefore probably does not significantly underestimate concentrations corresponding to a measured exposure rate.
The assumption of an infinite and uniformly contaminated source region is also used to calculate external exposure rates per unit concentration of radionuclides in fallout deposited on ships in the Pacific (Egbert et al., 1985; Barrett et al., 1986; Goetz et al., 1991). On ships, however, the area of the source region, either on deck or below, is substantially less than the area in an infinite source region that would contribute in an important way to a calculated exposure rate at a given location; as noted above, sources at distances out to a few tens of meters contribute to external exposures due to a surface source of infinite extent. Thus, concentrations of radionuclides in fallout deposited on ships that would result in a given exposure rate are higher than calculated concentrations that would yield the same exposure rate when an infinite source is assumed, and an assumption of an infinite source region results in underestimates of concentrations of radionuclides in fallout on ships. Shielding provided by superstructures on decks of many ships and shielding provided by structures below decks further limit the area of the source region that contributes significantly to a measured exposure rate at a given location, thus increasing the extent of underestimation of concentrations of radionuclides in fallout on ships. On target ships at Operation CROSSROADS, estimation of surface activities of radionuclides that could be resuspended in the air on the basis of measurements of external exposure rates is further complicated by the presence of substantial contamination of hulls and piping inside the hulls.
On the basis of considerations discussed above, the committee has concluded that an assumption of an infinite source region in calculating external exposure rates per unit concentration of radionuclides on a surface probably is not valid in cases of fallout on ships in the Pacific and that concentrations of radionuclides in deposited fallout may be substantially underestimated in these cases. In any event, the reliability of the method used to calculate exposure rates per unit concentration in cases in which fallout is deposited over an area of finite extent has not been evaluated in the NTPR program.
[5] In estimating inhalation doses in scenarios involving exposure to descending fallout, the resuspension factor used to estimate concentrations of radionuclides in descending fallout based on estimated concentrations on the ground or other surfaces may underestimate airborne concentrations relative to concentrations on the surface when exposure did not occur during the entire period of fallout.
The method used in the NTPR program to estimate concentrations of radionuclides in descending fallout is based on estimates of concentrations in fallout deposited on the ground or other surfaces and an assumed “effective” resuspension factor of 10−4 m−1 (see Section IV.C.2.1.5). The resuspension factor is based on an assumption that fallout descended from a height of about 104 m (10 km), and the method assumes implicitly that descending fallout is distributed uniformly over that height. When exposure is assumed to occur during only part of the period of descent, inhalation dose is assumed to vary linearly with exposure time (that is, the dose rate is assumed to be constant).
The committee finds that the concept underlying the method of estimating concentrations of radionuclides in descending fallout relative to estimated concentrations on the ground or other surfaces is reasonable, because a concentration in deposited fallout results from descent of an average concentration in air over some height, where the appropriate average concentration in air is inversely proportional to the assumed height. Furthermore, the assumed height is unimportant provided that the assumed average concentration in air yields the correct concentration in deposited fallout. Thus, average concentrations of radionuclides in descending fallout relative to concentrations in deposited fallout should not be underestimated when exposure is assumed to occur during the entire period of descent.
However, that conclusion may not be reasonable in all cases of exposure to descending fallout. Rates of descent of fallout vary greatly with particle size (Sehmel, 1984), as do the relative amounts of refractory and volatile radionuclides (see Section IV.C.2.1.2). As a result, dose rates due to inhalation of descending fallout vary with time during the period of descent. Therefore, in scenarios in which exposure to descending fallout was assumed to occur during only part of the period of descent, average dose rates above (or below) the average dose rate over the entire period of descent could occur. Similarly, on residence
islands or ships in the Pacific, doses due to inhalation of descending fallout could be underestimated or overestimated even when a participant was present during the entire period of descent, because inhalation exposure sometimes was assumed to occur during only the fraction of the time that a participant was assumed to spend outdoors (see case #5).
A further difficulty with the method is that, in some cases, fallout probably descended from a height considerably less than 10 km. In such cases, inhalation exposures could be underestimated if the assumed duration of exposure is less than the assumed period of descent from a height of 10 km. That situation could occur, for example, if fallout originated in the stem of a mushroom cloud produced in a detonation, as probably happened at Operation PLUMBBOB, Shot SMOKY (see Appendix F).
[6] In estimating inhalation doses in scenarios involving resuspension of deposited fallout at the NTS or on islands in the Pacific, the presence of aged fallout that was deposited more than a few months before exposure usually is not taken into account, and the presence of fallout from all prior shots is ignored in some cases. Thus, even in scenarios in which an assumed resuspension factor is a credible upper bound, inhalation doses could be underestimated substantially, especially in cases of exposure at the NTS at times relatively late in the period of aboveground testing.
The possibility of substantial inhalation exposure due to resuspension of aged fallout is an important concern at the NTS and on islands in the Pacific. The concern arises from two considerations. First, concentrations of plutonium and other longer-lived radionuclides, for which doses per unit activity inhaled are the highest and the inhalation hazard thus is the greatest, persisted in aged fallout with little depletion due to decay. Second, at times relatively late in the period of aboveground testing, areas where participants were exposed often were affected by fallout from several prior shots, and concentrations of plutonium and other longer-lived radionuclides on the ground at locations of exposure could be substantially higher than those due to fallout from a single shot. An additional important problem discussed in comment [4] above is that concentrations of plutonium, which probably is the most important longer-lived radionuclide in deposited fallout, may be substantially underestimated by the NTPR program because of neglect of fractionation.
In dose reconstructions for participants on islands in the Pacific, inhalation exposures due to resuspension of deposited fallout are taken into account for periods up to 2,500 h (about 3.5 months) after fallout occurred (Goetz et al., 1991). Thus, fallout from shots that occurred more than 2,500 h before an exposure of concern apparently is not taken into account (see cases #58, 63, and 94). The committee also found evidence that at times of a month or more after fallout was deposited, a resuspension factor of 10−6 m−1 was used in some cases to estimate airborne concentrations of radionuclides, rather than the standard value
of 10−5 m−1 often used on residence islands (see cases #16, 31, and 78). Use of a time cutoff and a lower resuspension factor for aged fallout was based on an argument that aged fallout is much less susceptible to resuspension than freshly deposited material, although no data are presented to support the argument. As discussed in Section V.C.5, however, the committee does not believe that neglect of resuspension of aged fallout on islands in the Pacific has important consequences for dose reconstructions; that is, potential inhalation doses do not appear to be high.
In dose reconstructions for participants at the NTS, the presence of fallout from previous shots was taken into account in some cases (Barrett et al., 1986); see Section IV.C.2.1.1 and Table IV.C.1 (see also cases #21, 23, 27, 80, and 87). The NTPR program judged the importance of fallout from previous shots on the basis of available data on fallout patterns after each shot at the NTS. An example of an assumed fallout pattern from Operation PLUMBBOB Shot SHASTA at locations of participants at the later PLUMBBOB Shot SMOKY (Goetz et al., 1979) is shown in Figure V.C.1. In all cases except as noted in footnote a in Table IV.C.1, fallout from previous shots that was assumed to affect the area at a later shot occurred within 3 months, and fallout that occurred earlier (usually in prior test series) was ignored. To provide a frame of reference for the information in Table IV.C.1, the following discussions, and later discussions in this report, locations of all shots in Operations BUSTER-JANGLE, TUMBLER-SNAPPER, UPSHOT-KNOTHOLE, TEAPOT, and PLUMBBOB at the NTS are shown in Figures V.C.2 through V.C.6.
The committee believes that the presence of prior fallout has been neglected in some cases at the NTS where it is potentially important. Consider first the shots listed in Table IV.C.1 at which fallout from one or more previous shots has been taken into account in dose reconstructions. On the basis of locations of shots and fallout patterns given by Hawthorne (1979), the committee notes the following two examples.
-
The area near UPSHOT-KNOTHOLE Shot HARRY also was affected by fallout from TUMBLER-SNAPPER Shot GEORGE (June 1, 1952) because of its nearby location and considerable onsite fallout.
-
The area near PLUMBBOB Shots LASSEN, WILSON, OWENS, WHEELER, CHARLESTON, and MORGAN, which were detonated at the same location, also was affected by fallout from BUSTER-JANGLE Shot SUGAR (Nov. 19, 1951) because of its nearby location and considerable onsite fallout. It also is likely that the area near those PLUMBBOB shots was affected by fallout from TUMBLER-SNAPPER Shot GEORGE (June 1, 1952) and TEAPOT Shot APPLE I (March 12, 1955) because of their directions of plume travel and onsite fallout. Finally, onsite fallout from Shot WILSON affected the area near the later PLUMBBOB shots at the same location.
In reviewing various documents, including the 99 randomly selected cases of individual dose reconstructions, the committee also encountered cases not included in Table IV.C.1 in which fallout from previous shots apparently impacted the area near a shot of concern but was not considered in dose reconstructions. Those cases are described as follows (examples from the randomly selected dose reconstructions are included in parentheses).
-
The area near UPSHOT-KNOTHOLE Shot NANCY (March 4, 1953) was affected by fallout from TUMBLER-SNAPPER Shot FOX (May 25, 1952) because of its detonation at the same location and considerable onsite fallout. It also is likely that this area was affected by fallout from TUMBLER-SNAPPER Shot EASY (May 7, 1952) because of the direction of plume travel and onsite fallout (cases #7, 29, 84, 86, and 87).
-
The area near UPSHOT-KNOTHOLE Shot SIMON (Apr. 25, 1953) was affected by fallout from TUMBLER-SNAPPER Shot EASY (May 7, 1952) because of its detonation at the same location and considerable onsite fallout (cases #30, 51, and 81).
-
The area near TEAPOT Shot APPLE II (May 5, 1955) was affected by fallout from TUMBLER-SNAPPER Shot EASY (May 7, 1952) and UPSHOT-KNOTHOLE Shot SIMON (Apr. 25, 1953) because of their detonation at the same location and considerable onsite fallout (cases #37, 77, 83, and 90).
-
The area near PLUMBBOB Shot HOOD (July 5, 1957) was affected by fallout from prior Shots SUGAR, GEORGE, APPLE I, and WILSON (see second bullet in previous paragraph) and by fallout from Shot BOLTZMANN listed in Table IV.C.1 that was accounted for at other PLUMBBOB shots because Shot HOOD was detonated at the same location as Shots LASSEN, WILSON, OWENS, WHEELER, CHARLESTON, and MORGAN.
That list is not intended to be exhaustive, and other shots presumably could be identified whose ground areas were affected by fallout from previous shots.
The lack of consideration of the impact of fallout from prior shots in the area of PLUMBBOB Shot HOOD noted above seems particularly inexplicable, given that the existence of some prior fallout was considered at all other PLUMBBOB shots at the same location during the same period. That the omission of Shot HOOD from Table IV.C.1 is not an oversight by the NTPR program is indicated by an assumption used in unit dose reconstructions for participant groups in forward areas after the shot that the groups were exposed to suspended neutron-induced radioactive material “in the absence of a fallout field” (see Section 3 and Tables 35 and 37 through 40 of Barrett et al., 1986). An assumption that there were no fission products or plutonium on the ground at the time and location of Shot HOOD is unsupportable, and it clearly results in underestimates of inhalation doses to participant groups in forward areas at that shot, without regard for the particular disturbances that caused resuspension of surface materials. An
example analysis of potential inhalation doses in forward areas after detonation of Shot HOOD is given in Appendix E.
More generally, extensive measurements of concentrations of radionuclides in surface soil at the NTS that were made during the 1980s (McArthur and Kordas, 1983; McArthur and Kordas, 1985; McArthur and Mead, 1987; McArthur and Mead, 1988; McArthur and Mead, 1989; McArthur, 1991; IT and DRI, 1995) indicate that by the times of later test series, large areas of the NTS had received substantial fallout. The extent of substantial fallout is indicated, for example, by the distribution of 137Cs shown in Figure V.C.7. Thus, without the need to consider locations of particular shots and associated directions of fallout patterns and the extent of fallout, as has been done in dose reconstructions (Barrett et al., 1986) and in the committee’s evaluation as given above, it is virtually certain that participants, including maneuver troops and observers, who engaged in activities in any of several areas, especially in the northeast quadrant of the NTS where most shots were detonated, during later periods of atomic testing received inhalation doses due to resuspension of previously deposited fallout. The magnitude of possible doses depends, of course, on the particular locations and times of exposure, activities of the participants, and the nature of the disturbances that caused resuspension.
Neglect of resuspension of previously deposited fallout in many dose reconstructions for participants at the NTS perhaps was based on an assumption that the resuspension factor would decrease substantially over time, as indicated by data obtained at the site (Anspaugh et al., 1975). However, fallout in many areas of the NTS increased over time as more shots affected the areas, and there undoubtedly were scenarios in which the resuspension factor did not decrease substantially over time. An example is exposures during assaults or marches behind armored vehicles (see case #88). A high resuspension factor of 10−3 m−1 normally is assumed during such activities (see Table IV.C.2), and the vigorous action of vehicle treads most likely resuspended aged and fresh fallout about equally. It also is not obvious that a pronounced decrease in the resuspension factor over periods of a few years would apply to resuspension caused by walking or other light activities, especially if large groups of participants were involved, because measured resuspension over long periods at the NTS (Anspaugh et al., 1975) probably was caused mainly by wind stresses rather than human activities.
On the basis of considerations discussed above, neglect of prior fallout clearly is a potentially important source of underestimation of upper bounds of inhalation doses to many participants at the NTS, especially if participants were exposed in forward areas during later periods of atomic testing. The presence of prior fallout is especially important in scenarios in which higher resuspension factors of 10−3 or 10−4 m−1 are assumed (see Table IV.C.2), given that plutonium probably was the principal long-term inhalation hazard and that concentrations of plutonium in fallout at the NTS are substantially underestimated in dose reconstructions because of neglect of fractionation (see comment [4] above).
[7] In dose reconstructions for participants at the NTS, resuspension of previously deposited fallout by the blast wave produced by a detonation generally has been ignored. Neglect of effects of a blast wave on resuspension could result in underestimation of upper bounds of airborne concentrations of radionuclides in previously deposited fallout relative to concentrations on the ground by a factor of about 100 or more in some exposure scenarios.
When a nuclear weapon is detonated above ground, a blast wave is produced in which the wind speed close to the location of the detonation can reach several hundred miles per hour (1 mph = 1.6 km h−1) and the wind speed at distances of about 1 mile (1.6 km) can be about 180 mph (Glasstone and Dolan, 1977). Wind speeds of such magnitude can result in extensive resuspension of radionuclides in fallout that was deposited after previous shots. Depending on the height and yield of a detonation, a blast wave can produce a dense cloud of dust at distances up to about 6 miles (10 km). The effect of a blast wave is evident in photographs taken after detonations at the NTS; an example is shown in Figure V.C.8.
The potential importance of a blast wave on resuspension of previously deposited fallout at the NTS is indicated by the following considerations. First,

FIGURE V.C.8 Photograph taken shortly after detonation of Operation PLUMBBOB, Shot PRISCILLA showing formation of dust cloud along the ground by blast wave produced by the detonation.
the resuspension factor associated with a blast wave should be substantially higher than values that apply to other, less vigorous disturbances, such as walking, that often are considered in dose reconstructions. If the height of the dust cloud caused by a blast wave is assumed to be about 100 m and it is further assumed that all radionuclides on the ground surface are resuspended by a blast wave, the resuspension factor is 1/(100 m), or 10−2 m−1. Thus, even if only 10% of the radionuclides in deposited fallout were resuspended by a blast wave, the resuspension factor would be 10−3 m−1. A credible upper bound in the range of 10−2-10−3 m−1 seems reasonable when one considers that values as high as 10−3-10−4 m−1 caused by vehicular and pedestrian traffic have been reported (Sehmel, 1984). The committee also notes that a resuspension factor of 10−3 m−1 is assumed in some exposure scenarios that involved vigorous disturbances of surface soil (see Table IV.C.2) and that a value of 10−2 m−1 was assumed in an unusual scenario involving short-term exposures during a localized dust storm (see Section IV.C.2.1.3). A credible upper bound of the resuspension factor associated with a blast wave should be at least as high as the value assumed by the NTPR program in these other cases of unusually high resuspension.
Second, a substantial fraction of materials resuspended by a blast wave should be in the form of small, respirable particles. Although fresh fallout at the NTS consisted primarily of large, essentially nonrespirable particles as a result of fractionation, particle sizes probably were reduced by wind stresses and other natural disturbances (NCRP, 1999), and a blast wave itself should tend to pulverize larger particles on the ground.
Third, smaller resuspended particles have low fall velocities. At the low wind speeds that occurred at ground level at the time of most detonations at the NTS (Hawthorne, 1979), the deposition velocity of small particles is expected to be about 10−2 cm s−1 (Sehmel, 1984). That estimate agrees with a study at the NTS in which deposition velocities of respirable particles in the range of 3 × 10−1 to 3 × 10−3 cm s−1 were inferred (Luna et al., 1969). If the deposition velocity is assumed to be 10−2 cm s−1 and the height of the dust cloud is assumed to be 100 m, the time required for dust to settle is 106 s, or approximately 10 days. That estimate is comparable to measured half-times of several tens of days for settling of resuspended radionuclides at the NTS, as summarized in Table 12.8 of Sehmel (1984). Thus, when resuspension was caused by a blast wave, most of the resuspended material that was respirable probably remained airborne during periods of possible inhalation exposure in forward areas after a detonation.
Fourth, since weapons were detonated at times of calm winds or low wind speeds at ground level (Hawthorne, 1979), and the dust cloud caused by a blast wave often covered a wide area, it is reasonable to presume that the cloud usually was not completely blown away from forward areas where exposures occurred for up to a few hours after a detonation.
A blast wave undoubtedly occurred at most aboveground shots at the NTS, the exceptions being detonations at high altitudes, safety shots, and misfires. The
extent of the resulting dust cloud presumably depended, for example, on the height of the detonation above ground and yield, but there were some blast-wave effects at most shots. There is little doubt that many participants who engaged in activities in forward areas after a shot encountered a dust cloud caused by the blast wave. Reports of activities of participant groups and individual dose reconstructions reviewed by the committee sometimes referred to high dust levels (see cases #21, 27, and 77), and levels sometimes were so high that a planned activity was delayed or canceled (see case #21 and Appendixes E and F). The presence of high dust levels in areas where participant groups engaged in activities is also indicated by the routine procedure after many operations of using brooms to brush accumulated soil from participants’ clothing, as shown in Figure V.C.9, even when participants had engaged in activities, such as walking, that should not have caused extensive resuspension (see Goetz et al., 1981; U.S. Army, 1957).

FIGURE V.C.9 Illustration of procedure for routine decontamination of participants (maneuver troops) after operations in forward areas at NTS.
Thus, neglect of the effects of a blast wave on resuspension at the NTS could result in underestimation of upper bounds of airborne concentrations of radionuclides in previously deposited fallout relative to concentrations on the ground by a factor of about 100 or more in some scenarios. That is especially the case when a resuspension factor of 10−5 m−1 or less is assumed in dose reconstructions, as in scenarios in which resuspension after detonations was assumed to be caused by walking or other light activities. In addition, the frequent neglect of aged fallout that contained substantial amounts of important long-lived radionuclides, such as plutonium, and the likelihood discussed in comment [4] that concentrations of plutonium in fallout deposited at the NTS have been underestimated substantially, because of neglect of fractionation, could increase the extent of underestimation of upper bounds of airborne concentrations of radionuclides to which participants in forward areas were exposed by another factor of perhaps as much as 10 in the worst cases. Therefore, regardless of uncertainties in estimating inhalation doses due to blast-wave effects, it is virtually certain that inhalation doses to many participants in forward areas at the NTS have been greatly underestimated by the NTPR program.
An example analysis to investigate potential inhalation doses due to blast-wave effects in forward areas at Operation PLUMBBOB, Shot HOOD is presented in Appendix E. The results of that analysis indicate that upper bounds of equivalent doses to some organs well above 1 rem are plausible in some cases and, therefore, that blast-wave effects at the NTS are potentially important. In its review of randomly selected dose reconstructions for individual veterans, the committee encountered many cases in which consideration of blast-wave effects could be important for obtaining credible upper bounds of dose to participants at the NTS from all exposure pathways combined.26
[8] In several individual dose reconstructions reviewed by the committee, an internal dose of zero was assigned even though a substantial external dose was estimated and inhalation exposure was plausible. Regardless of the magnitude of possible inhalation doses, assigning a zero dose does not conform to the stated policy that the veteran will be given the benefit of the doubt in estimating dose, and it does not provide a credible upper bound.
In its review of 99 randomly selected individual dose reconstructions, the committee found four cases (cases #7, 29, 89, and 99) in which a veteran filed a claim for compensation for cancer in an internal organ, the veteran was a confirmed member of a participant group that engaged in activities in the forward area at one or more shots at the NTS, the veteran was assigned an external dose of
about 1–4 rem, and the group’s activities probably took place in an area of fallout from prior shots, but the veteran was not assigned an internal dose. Indeed, in one of those cases (case #99), the presence of fallout from previous shots was acknowledged but not taken into account in estimating dose. In another case of a participant who served on boarding parties on contaminated ships at Operation CROSSROADS (case #49), an internal dose was calculated, but the assigned dose was zero. An assignment of no internal dose in such cases is difficult to understand.
The committee also encountered cases in which a veteran filed a claim for compensation for an unspecified disease or a dose reconstruction was requested without the filing of a claim and the veteran was assigned an external dose of about 1–6 rem, but the veteran was assigned no internal dose (see cases #1, 28, 30, 34, 52, 54, 55, 56, 64, 72, 74, 77, and 92). In some of those cases, the potential for a substantial internal dose was clear—for example, when a veteran was a member of a radiation-safety team or other group that engaged in activities in contaminated forward areas after a detonation at the NTS (cases #1, 30, and 77), or a veteran spent considerable time on residence islands in the Pacific (cases #52, 54, 55, and 56). It was not possible to receive external doses of a few rem on the ground at the NTS or in the Pacific without any internal exposure.
In addition, estimates of inhalation dose in some unit dose reconstructions for participant groups almost certainly are much too low. One such case mentioned in the previous comment and discussed in Appendix E involves exposures at Operation PLUMBBOB, Shot HOOD.
[9] Resuspension factors used in the NTPR program to estimate inhalation doses from exposure to fallout deposited on ships may not represent credible upper bounds of actual resuspension factors in many cases.
Resuspension factors normally used to estimate inhalation doses to participants from exposure to fallout deposited on ships in the Pacific are summarized in Table IV.C.3. During normal activities (that is, excluding decontamination and ammunition loading and unloading), the assumed resuspension factor is 10−5 or 10−6 m−1, with the higher value applied to exposures below decks and the lower value applied to exposures on deck. Assumed resuspension factors on ships were based on a review of data obtained in indoor and outdoor environments (Phillips et al., 1985). The committee believes, however, that credible upper bounds of resuspension factors during normal activities on ships could be substantially higher.
In indoor environments, data reviewed by Sehmel (1984) but not considered by Phillips et al. (1985) indicate that a credible upper bound of the resuspension factor could be 10−2 m−1 or higher, and values above 10−4 m−1 are not uncommon. Such high values are reported even in cases in which the stress that caused the resuspension—such as walking, changing clothes, or several people moving in a room—did not involve vigorous activity, and high values occurred in both ventilated and unventilated rooms.
The committee believes that resuspension factors during walking and other normal activities on decks of ships could be substantially higher than values observed under similar conditions on land. Fallout particles probably do not adhere to smooth deck surfaces to nearly the extent that they do in surface soil; this may be an important reason for the high resuspension factors observed indoors. The committee also recognizes, however, that the possibility of high resuspension factors for fallout deposited on decks of ships may be mitigated by several factors, including the generally damp conditions on ships in the Pacific due to the high humidity, frequent rains, and periodic swabbing of decks; the propensity for loose particles that could be moved by the wind to accumulate in nooks, crannies, and cracks, where resuspension is less likely; and the small area of contamination on a ship, which increases natural dilution and the chance of the winds blowing resuspended material away from locations of participants before exposure occurs, compared with exposure to large areas of contamination on land. Thus, although assumed resuspension factors summarized in Table IV.C.3 may not be credible upper bounds on ships in the Pacific, it seems likely that the possible degree of underestimation of resuspension is greater below decks than on deck.
[10] In dose reconstructions for participants on residence islands in the Pacific, exposures to descending or resuspended fallout during the fraction of the time spent indoors normally are ignored; that is, concentrations of radionuclides in indoor air are assumed to be zero. That assumption does not provide a credible upper bound of possible inhalation doses indoors. Inhalation doses during the fraction of the time spent below decks on ships in the Pacific also may be underestimated in some cases.
The committee’s review of dose reconstructions for veterans who served on residence islands in the Pacific, as included in the 99 randomly selected cases, indicates that inhalation of descending or resuspended fallout normally is assumed not to occur during the fraction of the time spent indoors (see cases #16, 43, and 78). The indoor exposure time on residence islands normally is assumed to be 40%.
The committee agrees that concentrations of radionuclides on residence islands in the Pacific probably were lower in indoor air than outdoors. Furthermore, an assumption that a person was exposed outdoors for 100% of the time while on a residence island would not increase estimated inhalation doses by a large amount. However, an assumption of no inhalation exposure indoors is unreasonable, given that windows and doors of buildings on residence islands presumably were open much of the time to promote ventilation, and it does not provide a credible upper bound of possible inhalation doses in these cases.
In some dose reconstructions for participants who served on ships in the Pacific, the inhalation dose during the fraction of the time spent below decks also is assumed to be zero (see cases #6, 24, 25, and 44). Especially in cases of
exposure during known periods of fallout on ships, this assumption takes into account that forced-air ventilation systems often were turned off in an effort to minimize contamination below decks. However, it is unreasonable to assume that ventilation systems were always turned off during periods of substantial fallout and that there was no contamination below decks. At Operation CASTLE, for example, forced-air ventilation systems were sometimes left on during periods of fallout to maintain tolerable temperatures below decks (Martin and Rowland, 1982). Thus, inhalation doses to participants during periods spent below decks on ships probably were underestimated in some cases.
In summary, the committee has identified several assumptions used in the NTPR program to estimate inhalation dose coefficients and concentrations of radionuclides in air that have substantial uncertainty that has not been taken into account in dose reconstructions, and the committee has also identified several assumptions that should tend to result in underestimates of inhalation doses to atomic veterans; these assumptions are briefly restated in Table V.C.7. Additional concerns about situations in which use of 50-year committed doses and assignment of committed doses to the year of intake could result in underestimates of the dose that could have caused a veteran’s cancer are discussed in Section V.C.3.1, comment [6]. The committee also emphasizes, however, that the discussions of assumptions summarized in Table V.C.7 should not be used to draw conclusions about whether estimates of inhalation dose to atomic veterans in particular scenarios provide credible upper bounds without consideration of the importance of assumptions discussed in the previous section that should tend to result in overestimates of inhalation doses. The committee’s overall evaluation of methods of estimating inhalation doses used in the NTPR program is presented in the following section and in Sections V.C.5 and V.C.6.
V.C.3.3 Evaluation of Methods of Estimating Inhalation Dose
The committee found that several assumptions used in dose reconstructions for atomic veterans should tend to result in overestimates of inhalation doses to participants at the NTS or in the Pacific. Those assumptions are discussed in Section V.C.3.1 and summarized in Table V.C.5. Nearly all the assumptions concern dose coefficients for inhalation of radionuclides used in all dose reconstructions, but one assumption concerns resuspension factors that are applied in estimating airborne concentrations of radionuclides in some exposure scenarios.
The committee also found, however, that several assumptions used in dose reconstructions for atomic veterans have substantial uncertainty that has not been taken into account in the NTPR program and that several other assumptions should tend to result in underestimates of inhalation doses to participants at the NTS or in the Pacifics. Those assumptions are discussed in Section V.C.3.2 and summarized in Table V.C.7. Most of the assumptions concern methods used to estimate airborne concentrations of radionuclides in various scenarios, but im
TABLE V.C.7 Summary of Assumptions Used to Estimate Inhalation Doses in NTPR Program That Have Substantial Uncertainty That Is Not Taken into Account or Should Tend to Result in Underestimates of Dose
|
Dose coefficients (organ-specific equivalent doses per unit activity of radionuclides inhaled)a • Uncertainties in dose coefficients due to uncertainties in dosimetric and biokinetic models are not taken into account. • Uncertainty in dose coefficients for alpha-emitting radionuclides due to uncertainty in biological effectiveness of alpha particles is not taken into account. • Dose coefficients for organs of GI tract from inhalation of plutonium may be underestimated when inhaled materials are respirable (AMAD, 1 μm). |
|
Methods used to estimate inhalation exposures (intakes of radionuclides in air) • Sources of error and uncertainty in methods of estimating radionuclide concentrations in deposited fallout based on measured external photon exposures have not been evaluated, and reliability of methods is unknown. The assumption of no fractionation (except for removal of noble gases) should result in substantial underestimates of concentrations of refractory radionuclides (such as plutonium), and the method of calculating external exposure rates per unit concentration of radionuclides on a surface probably is not valid for fallout deposited on ships in Pacific and should result in underestimates of concentrations in these cases. • Resuspension factor used to estimate radionuclide concentrations in descending fallout may result in underestimates of exposure when exposure did not occur during entire period of fallout. • Presence of fallout deposited more than a few months before exposure usually is ignored, especially late in period of atomic testing at NTS, when buildup of plutonium and longer-lived fission products from many prior shots was extensive. • Effect of blast wave from detonations at NTS on resuspension of substantial fraction of previously deposited fallout over large areas generally is ignored. • In some dose reconstructions for veterans who filed claim for compensation for cancer in internal organs and received substantial external dose, inhalation dose of zero was assigned even though inhalation exposure almost certainly occurred. • Resuspension factors applied to fallout deposited on ships in Pacific, especially below decks, may be too low. • Inhalation dose during time spent indoors on residence islands in Pacific is assumed to be zero; some inhalation doses below decks on ships also may be underestimated. |
|
aAdditional discussions of situations in which use of 50-year committed doses from inhalation and assignment of committed doses to the year of intake could result in underestimates of the dose that could have caused a veteran’s cancer are given in Section V.C.3.1, comment [6]. |
portant sources of uncertainty in dose coefficients also have not been taken into account.
The basic question in evaluating methods used in the NTPR program to estimate inhalation doses is whether the methods provide credible upper bounds of doses from this intake pathway (see Section IV.E.4). The question is difficult to answer in general terms, especially in the more important cases of exposure to fallout. Participants were exposed to airborne radionuclides in descending or resuspended fallout under a wide variety of conditions, especially at the NTS, and
the importance of different sources of overestimation or underestimation of inhalation dose depends on the conditions of exposure. Therefore, estimates of inhalation dose obtained in dose reconstructions, which are intended to be upper bounds, probably provide credible upper bounds in some cases; they almost certainly do not in other cases, and it is difficult to determine one way or the other in the rest.
Another complicating factor is that the committee could not fully evaluate methods used by the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces on the basis of assumptions about the composition of fallout and external photon exposures measured with film badges or field instruments. Those methods are important because estimated concentrations in fallout are used to calculate inhalation dose in most cases. Therefore, although some assumptions embodied in the methods of estimating concentrations of radionuclides in fallout are likely to be overpredictive or underpredictive, it often is difficult to judge whether the net effect of all such assumptions is that estimated inhalation doses from exposure to descending or resuspended fallout tend to be overestimates or underestimates and by how much.
An example of a scenario in which credible upper bounds of inhalation dose probably are obtained in dose reconstructions involves exposure to descending fallout throughout the period of descent. Such exposures occurred, for example, on residence islands in the Pacific (see cases #3, 5, 8, 16, 22, 32, 38, 43, 47, 58, 60, 63, 78, and 96). Suppose that a participant who was exposed mainly to descending fallout filed a claim for compensation for a cancer in an internal organ other than the lung or an organ in the GI tract (such as the kidney). Several assumptions used in such a case should result in substantial overestimates of inhalation dose. Assumed dose coefficients for those organs usually apply to a particle size (AMAD) of 1 μm, even though most particles in descending fallout presumably were large and essentially nonrespirable, and dose coefficients for inhalation of respirable particles used by the NTPR program often are at least a factor of 2 higher than values for inhalation of large particles based on current ICRP recommendations. Because fractionation of radionuclides in fallout is ignored in all dose reconstructions, doses due to inhalation of volatile radionuclides attached to particle surfaces should be overestimated by a factor of about 3 or more. Doses due to inhalation of refractory radionuclides may also be overestimated substantially, even though their amounts in fallout probably are underestimated by a factor of about 3 or more because of neglect of fractionation; refractory radionuclides are dispersed mainly throughout the volume of large and highly insoluble fallout particles and therefore may be absorbed from the respiratory and GI tracts into blood to only a small extent before the particles are eliminated from the body. If the radionuclide composition in an atmospheric cloud is reasonably well characterized on the basis of cloud sampling data, the several factors that should tend to result in overestimates of inhalation dose probably are sufficient to compensate for uncertainties in all dose coefficients amounting to a factor of
about 3-10 about a central estimate, owing to uncertainties in dosimetric and biokinetic models and the uncertainty in the biological effectiveness of alpha particles of a factor of about 4. Estimates of inhalation dose to the lung should also be credible upper bounds when descending fallout is assumed to consist of small (1-μm) particles. These discussions and summaries in Appendix B of estimated upper-bound doses for the specific cases identified above indicate that upper bounds of organ equivalent doses in scenarios involving exposure to descending fallout usually were low (that is, less than 1 rem).
A clear example of when estimates of inhalation dose obtained in dose reconstructions almost certainly do not provide credible upper bounds involves a scenario for exposure to resuspended fallout at the NTS. Participants who engaged in activities in forward areas within a few hours after a shot almost certainly were exposed to previously deposited fallout that was resuspended to a large extent by the blast wave produced by the detonation. However, effects of a blast wave have been ignored in all dose reconstructions, so the upper bound of the resuspension factor probably has been underestimated by more than a factor of 100 in scenarios in which resuspension is assumed to be caused by walking or other light activities. In addition, plutonium probably was the most important inhalation hazard in previously deposited fallout and, as noted above, concentrations of plutonium in fallout at the NTS probably are underestimated by a factor of about 3 or more because of neglect of fractionation. Furthermore, fallout that occurred more than a few months before a shot of concern generally has been ignored, but many prior shots contributed to fallout at the NTS toward the end of the period of aboveground testing. Therefore, unless concentrations of plutonium in fallout are overestimated by the NTPR program by substantially more than a factor of 100—which seems highly unlikely considering the interest in measuring plutonium in cloud samples—biases in other assumptions that tend to result in overestimates of inhalation dose almost certainly are not sufficient to compensate for neglect of blast-wave effects in all dose reconstructions at the NTS. Furthermore, as noted in Section V.C.3.2, comment [7], upper bounds of organ equivalent doses in this scenario could be substantially above 1 rem in some cases.
As an example of how it can be difficult to determine whether estimated inhalation doses are credible upper bounds, consider a scenario in which participants walked or engaged in other light activity in an area contaminated by fallout. This type of scenario occurred before some shots at the NTS (see cases #1, 7, 23, and 87). Suppose that lung cancer is the disease of concern, and consider the dose to the lung from plutonium only. The dose coefficient for the lung for inhalation of respirable particles (AMAD, 1 μm) used in dose reconstructions is based on ICRP Publication 30 (see Table V.C.2), the assumed breathing rate is 1.2 m3 h−1, and the assumed resuspension factor, which is intended to be an upper bound, often is 10−5 m−1. An intended upper bound of the inhalation dose (rem h−1) per unit activity concentration of plutonium on the ground used in dose reconstructions is proportional to the product of those three factors, or 7 × 10−3. This factor
is applied to an estimated concentration of plutonium on the ground, which is based on an assumption of no fractionation in fallout.
Now, consider the effects of bias and uncertainty on the estimate of dose from inhalation of plutonium given above. We make the following assumptions:
-
When inhalation of respirable particles (AMAD, 1 μm) is assumed, the central estimate of the dose coefficient for the lung should be reduced by a factor of 2 to conform to current ICRP recommensdations (see Table V.C.2).
-
The uncertainty in the dose coefficient due to uncertainties in dosimetric and biokinetic models is represented by a lognormal probability distribution with a 90% confidence interval that spans a factor of 10 above and below the central estimate (see Table V.C.6).
-
The uncertainty in the biological effectiveness of alpha particles relative to photons and electrons is described by a lognormal probability distribution with a 50th percentile at 18 and a 97.5th percentile at 100 (see Section V.C.3.2, comment [2]).
-
Only a fraction of resuspended plutonium is in respirable form, with the dose to the lung from inhalation of large particles assumed to be essentially zero, and the uncertainty in this fraction is described by a uniform probability distribution over the range of 0.2-0.8.
-
On the basis of a review of available data (EPA, 1997), the uncertainty in the breathing rate that applies during light activity is described by a lognormal probability distribution with a 90% confidence interval of 0.6–1.4 m3 h−1.27
-
Fractionation increases the concentration of plutonium on the ground compared with the concentration assumed in dose reconstructions by an uncertain factor that is described by a lognormal probability distribution with a 90% confidence interval of 2-4.
-
The uncertainty in the resuspension factor under conditions of walking or other light activity is described by a lognormal probability distribution with a 90% confidence interval of 10−8-10−5 m−1 (see Section V.C.3.1, comment [8]).
-
By multiplying those probability distributions with Latin Hypercube sampling techniques and the Crystal Ball® 2000 software (Decisioneering, 2001),28 we obtain the following results:
-
The central estimate (50th percentile) of the probability (uncertainty) distribution of the result is 1 × 10−4.
|
27 |
The committee notes that the NTPR program generally assumes a single breathing rate, with no uncertainty, in a given scenario (see Section IV.C.2). Assumed breathing rates probably underestimate upper bounds when uncertainties in breathing rates for various activities (EPA, 1997) are considered. However, neglect of uncertainties in breathing rates is not an important concern, because they clearly are small compared with uncertainties in other parameters used in calculating inhalation doses to atomic veterans, including dose coefficients and resuspension factors. |
|
28 |
Crystal Ball® 2000 is licensed by Decisioneering, Inc., 1515 Arapahoe St., Suite 1311, Denver, Colorado 80202. |
-
The estimate of 7 × 10−3 based on input parameters assumed in dose reconstructions, which is intended by the NTPR program to be an upper bound (at least a 95th percentile), lies between the 75th and 80th percentiles of the probability distribution based on assumed uncertainties in the parameters.
-
The 95th percentile of the probability distribution of the result is 9 × 10−3, which is a factor of about 1.3 greater than the presumed upper bound obtained in dose reconstructions.
The analysis described above is not intended to be definitive and should not be taken as such. Fractionation of plutonium may be misrepresented in the analysis (for example, the assumed upper bound of the probability distribution describing fractionation could be too low), and other uncertainties, such as uncertainties in the duration of exposure and the nature of work activities, would need to be considered. Nonetheless, the results suggest that an estimate of inhalation dose based on estimates of input parameters used in dose reconstructions is more likely than not to overestimate actual doses in the assumed scenario. In contrast, that estimate is slightly less than an estimated upper bound (95th percentile) of a probability distribution of inhalation dose based on assumed uncertainties in input parameters. Thus, when possible errors in estimating concentrations of plutonium in fallout and the need to include uncertain contributions to dose from resuspension of other radionuclides in fallout are considered, it is difficult to draw a definitive conclusion about whether estimates of inhalation dose obtained by the NTPR program for this scenario provide credible upper bounds. However, as indicated by discussions in Appendix E.5 and summaries in Appendix B of estimated doses for the specific cases identified at the beginning of this example, upper bounds of organ equivalent doses in scenarios in which resuspension of previous fallout was caused only by walking or other light activity almost certainly were low (substantially less than 1 rem).
Further summary discussions of the committee’s evaluation of methods used to estimate inhalation doses to atomic veterans are given in Sections V.C.5 and V.C.6.
V.C.4 Evaluation of Potential Ingestion Doses
Ingestion of radionuclides is rarely considered in dose reconstructions for atomic veterans, and ingestion doses are not estimated in any randomly selected cases reviewed by the committee (for example, see Section IV.C.3).29 Thus, with
rare exceptions (see Goetz et al., 1987), ingestion is considered to be unimportant compared with inhalation and external exposure.
As noted in Section I.D, atomic veterans have expressed concern about ingestion doses they might have received. This section discusses the potential importance of ingestion exposures of atomic veterans. The potential importance of ingestion is assessed on the basis of assumed exposure scenarios at the NTS and in the Pacific.
V.C.4.1 Example Analysis of Potential Ingestion Doses at the NTS
Two scenarios of ingestion exposure at the NTS are considered. The first involves ingestion of contaminated soil that was transferred to the hands and then swallowed. This scenario could occur when participants engaged in such activities as digging trenches (see case #87) or installing or removing displays or electronic equipment in contaminated areas (see case #1). This scenario is used to investigate possible doses due to ingestion of longer-lived radionuclides in fallout.
A bounding estimate of potential doses due to ingestion of contaminated soil at the NTS is obtained on the basis of the following assumptions. Data given by McArthur (1991) and companion reports (see Section V.C.3.2, comment [5]) indicate that concentrations of plutonium in surface soil at the end of the period of atomic testing exceeded 500 pCi g−1 at a few locations and that the highest concentrations of 90Sr and 137Cs exceeded about 500 and 200 pCi g−1, respectively. On the basis of an estimate that an adult ingests soil at 20 mg h−1 while gardening (EPA, 1997), we assume that a soil-ingestion rate of 100 mg h−1 is a credible upper bound for a participant who worked in contaminated soil at the NTS.30 On the basis of those assumptions, the intake rate would be about 50 pCi h−1 for plutonium and 90Sr and 20 pCi h−1 for 137Cs. If ingestion dose coefficients for workers currently recommended by ICRP (1994a; 2002) are assumed, a central estimate of the dose to any organ would not exceed 0.1 mrem h−1. Taking into account uncertainties in ingestion dose coefficients (see Table V.C.6), a credible upper bound would not exceed about 1 mrem h−1. Thus, an assumption of reasonable exposure times would give total doses to any organ of no more than about 10 mrem. The assumed radionuclide concentrations in soil are at the upper end of measured concentrations at the NTS and the assumed soil-ingestion rate should be an overestimate, so it is reasonable to conclude that ingestion of radionuclides in soil is not an important concern at the NTS. That conclusion also takes into account that concentrations of shorter-lived radionuclides presumably were not high when digging and other such activities were undertaken.
A second credible exposure scenario that is used to investigate doses due to ingestion of shorter-lived radionuclides in fallout involves participants at the NTS who consumed contaminated milk that was produced near St. George, Utah. A bounding estimate of potential ingestion doses in this scenario is obtained from estimates of ingestion doses to adults who lived near St. George. After Operation UPSHOT-KNOTHOLE, Shot HARRY, which resulted in unusually high levels of fallout near St. George, central estimates of absorbed doses to an adult due to ingestion are 4.3 rad to the thyroid; 0.12 and 0.3 rad to the upper and lower large intestine wall, respectively, and 0.07 rad or less to all other organs (Ng et al., 1990).31 Doses to participants at the NTS due to consumption of contaminated milk obtained from St. George would have been far less, because doses at St. George due to fallout from Shot HARRY were considerably higher than doses due to fallout from other shots and the amount of contaminated milk consumed by participants at the NTS would have been a small fraction of the total diet of locally grown foods consumed by residents near St. George. Thus, it is reasonable to conclude that ingestion of shorter-lived radionuclides also is not an important concern at the NTS.
V.C.4.2 Example Analysis of Potential Ingestion Doses in the Pacific
As in the previous section, two scenarios for ingestion exposure on residence islands in the Pacific are considered here. The first scenario involves ingestion of locally produced terrestrial and aquatic foodstuffs that were contaminated by fallout. Although participants on residence islands consumed mainly imported foods, such items as coconut milk and seafood obtained from lagoons presumably were consumed on occasion. This scenario is used to investigate possible doses due to ingestion of longer-lived radionuclides in fallout.
A bounding estimate of potential doses due to ingestion of locally produced foodstuffs is based on assessments of dose to native Marshall Islanders today. Doses to natives should be far higher than potential doses to atomic-test participants because a far greater fraction of foodstuffs consumed by native populations is obtained locally. An assessment of ingestion doses to residents of northern Marshall Islands (Robison et al., 1997b) indicates that the highest annual effective dose to a resident of Enewetak Atoll is about 0.03 rem. The atoll was the location of residence islands for participants. The estimated dose to native residents assumes that only local foods are consumed. Ingestion doses result mainly from intakes of 137Cs because of its high accumulation in terrestrial and aquatic foodstuffs in environments with low concentrations of potassium (Whicker and Schultz, 1982), with minor contributions from intakes of 90Sr and insignificant
contributions from plutonium; doses to any organ are about the same as the effective dose. An assessment of ingestion doses to Marshall Islanders who might resettle on Bikini Atoll (Robison et al., 1997a) indicates that annual equivalent doses to different organs would be about 0.3-0.4 rem if 20% of the caloric content of the diet is obtained from local foods. Contamination on Bikini Atoll is substantially higher than on islands where participants resided (Robison et al., 1997b). Finally, an assessment of exposures of residents of Bikini, Enewetak, Rongelap, and Utirik Atolls using whole-body counting (Sun et al., 1997a) indicated that annual internal doses to all organs from intakes of 137Cs were less than 0.02 rem.
Concentrations of 137Cs and 90Sr on residence islands during the period of atomic testing were higher, by a factor of 2-3, than concentrations when the dose assessments described above were performed because of radioactive decay. Nonetheless, the results indicate that potential doses to participants on residence islands in the Pacific due to ingestion of longer-lived radionuclides were very low, perhaps a few mrem or less, given that only a small fraction of the caloric content of a participant’s diet would have been obtained from local foods and relatively few participants spent more than a few months on residence islands.
A second credible exposure scenario used to investigate potential doses due to ingestion of shorter-lived radionuclides in fallout in the Pacific involves participants who ingested fallout particles that were deposited directly on food and water as they were being consumed. This scenario is investigated using the following analysis. Service personnel on Rongerik Atoll received high doses after Operation CASTLE, Shot BRAVO. A dose reconstruction for them gave the following results (Goetz et al., 1987). First, estimated external doses are about 30-50 rem. Second, estimated internal doses are 190 rem to the thyroid, 76 rem to the lower large intestine wall, 44 rem to the upper large intestine wall, 13 rem to the small intestine wall and lung, and from 0.6 to about 6 rem to all other internal organs. Those doses were due mainly to shorter-lived radionuclides in fallout that occurred within 1 day of detonation. Furthermore, on the basis of the consideration that most of the fallout on Rongerik was in the form of large particles, the analysts concluded that internal doses were dominated by ingestion that resulted from deposition of fallout on foods while they were being consumed and that intakes by inhalation were relatively unimportant.32
Dose reconstructions reviewed by the committee indicate that estimated external doses to most participants who were stationed on residence islands are less than 1 rem. If the ratios of internal to external doses to personnel on Rongerik Atoll given above are assumed to apply to participants on residence islands and if
|
32 |
It should be noted that as a result of an assumption that ingestion intakes were dominant, estimated internal doses to some organs and tissues are similar to estimated external doses. That result differs from the expectation that when ingestion is unimportant, doses from inhalation of descending fallout normally should be substantially less than external doses (see Section V.C.1). |
internal doses on Rongerik are assumed to be due entirely to ingestion, ingestion doses on residence islands would not have exceeded a few rem to the thyroid, about 1-2 rem to the large intestine walls, and a fraction of a rem to all other internal organs. Those results should greatly overestimate ingestion doses on residence islands if precautions about eating were taken during known periods of fallout.
V.C.4.3 Summary of Evaluation of Ingestion Doses
The committee acknowledges the concerns of atomic veterans about doses they may have received from ingestion of radionuclides. However, on the basis of an analysis of bounding scenarios for ingestion exposure of participants at the NTS and on residence islands in the Pacific, doses to specific organs and tissues due to ingestion of radionuclides probably were low, especially compared with doses from external exposure, except in rare circumstances. Ingestion doses to most participants probably were around a few mrem or less. Doses of that magnitude are unimportant, so neglect of intakes of radionuclides by ingestion in dose reconstructions for atomic veterans does not appear in most cases to be an important concern with regard to evaluating claims for compensation for radiation-related diseases.
A conclusion that ingestion doses to most atomic veterans were very low may seem unreasonable, especially at the NTS, given the considerable attention that has been paid to ingestion exposures of the US population due to fallout from atmospheric weapons tests at the NTS (NCI, 1997; IOM/NRC, 1999). However, even in the population of the US, doses to most organs and tissues due to ingestion of radionuclides in fallout were substantially less than doses from external exposure (Anspaugh and Church, 1986; Anspaugh et al., 1990; Till et al., 1995; Whicker et al., 1996; UNSCEAR, 2000). The one exception was doses to the thyroid from ingestion of 131I in milk, but even in such cases the principal concern was doses to infants and children who consumed large quantities milk, and doses to adults who drank milk were substantially less. Therefore, ingestion doses normally would have been a concern at the NTS only if participants drank large quantities of milk that had been contaminated by high levels of fallout from recent atmospheric tests. That situation is not known to have occurred at the NTS, and it generally was not a concern in the Pacific, given the absence of sources of milk near the locations of Pacific tests.
V.C.5 Summary of Principal Findings Related to Estimation of Internal Dose
The committee’s evaluation of methods used in the NTPR program to estimate internal doses to atomic veterans focused on methods of estimating inhalation dose. As discussed above, the committee has concluded that internal expo-
sures of most participants were due mainly to inhalation and that intakes by ingestion usually were insignificant.
The committee recognizes that estimation of inhalation doses to atomic veterans is difficult. Given the lack of data on airborne concentrations of radionuclides at locations and times of exposure and data on amounts of radionuclides excreted in urine or feces, inhalation doses can be estimated only by using indirect methods that involve substantial uncertainty. It also is likely that in some exposure scenarios, such as those involving exposure to suspended neutron-activation products in soil at the NTS or exposure to descending fallout at the NTS or on residence islands in the Pacific, inhalation doses were inconsequential compared with external doses that could be monitored with film badges or field instruments. In scenarios in which inhalation doses should be much lower than external doses, uncertainties in methods used by the NTPR program to estimate inhalation dose are unlikely to be important.
The committee’s detailed evaluation of methods used in the NTPR program to estimate inhalation doses to atomic veterans is given in Section V.C.3 and summarized in Tables V.C.5 and V.C.7. In some respects, the methods should tend to overestimate inhalation doses. In other respects, however, the methods involve substantial uncertainty or they should tend to underestimate inhalation doses to such an extent that it is often difficult to determine whether estimated doses to atomic veterans are credible upper bounds, as intended by the NTPR program. Furthermore, the committee has identified exposure scenarios in which neglect of resuspension of previously deposited fallout by the blast wave produced in most detonations at the NTS almost certainly has resulted in underestimation of upper bounds of inhalation doses by a factor of at least 100. Such scenarios are important because thousands of participants at the NTS could have been exposed to substantial airborne concentrations of fallout that was resuspended by a blast wave. The committee also identified other cases in which an inhalation dose of zero was assigned to an organ in which a veteran’s cancer occurred but there is little doubt that there was some inhalation exposure.
On the whole, the committee has concluded that methods used in the NTPR program to estimate inhalation doses to atomic veterans have important shortcomings that center around three issues.
[1] Most estimates of inhalation dose to participants at the NTS and in the Pacific depend on estimates of concentrations of radionuclides deposited on the ground or other surfaces or distributed over a depth in surface soil at locations and times of exposure. Those estimates are based, in part, on measurements of external photon exposure with film badges worn by participants or field instruments, combined with calculations of external exposure rates per unit concentration of radionuclides on the surface. However, especially in scenarios involving exposure to descending or resuspended fallout, the reliability of the methods of estimating concentrations of radionuclides
Methods of estimating inhalation doses based, in part, on measured external photon exposures were criticized by a previous committee of the National Research Council (NRC, 1985b). The essence of the criticism was that the methods lacked scientific credibility and that their reliability is therefore unknown. Similarly, on the basis of an evaluation of simultaneous measurements of airborne concentrations and ground deposition at the same locations near the NTS during periods of atomic testing, Cederwall et al. (1990) concluded that the relationship between airborne and surface concentrations of fallout is too complex to be treated adequately by simple approaches, such as use of a deposition velocity. The present committee shares those concerns about the reliability of methods used in the NTPR program to estimate concentrations of radionuclides that are potentially important contributors to inhalation dose.
The previous National Research Council committee suggested that urinanalysis should be used to assess the validity of methods used in the NTPR program to estimate internal dose (NRC, 1985b). The present committee also believes that some indication of reliability is essential if estimates of inhalation dose are to be considered credible. However, because of experience with a bioassay program that was recently undertaken to assess internal exposures to plutonium and difficulties with the use of present-day measurements to estimate intakes that occurred many years ago, as discussed in Section VI.D, the committee believes that urinanalysis is not likely to provide useful information on the reliability of methods used to estimate inhalation doses to atomic veterans.
A potentially more fruitful approach would be to compare estimated radionuclide concentrations in deposited fallout or in neutron-activated soil used in the NTPR program with measurements that were made at the NTS or in the Pacific after the period of atomic testing ended. As noted in Section V.C.3.2, comment [6], radionuclide concentrations in surface soil over portions of the NTS that were affected by fallout were measured extensively during the 1980s. Important constituents of fallout on which data were obtained are 241Am, 238Pu, 239,240Pu, 60Co, 90Sr, and 137Cs. Although data on shorter-lived radionuclides in fallout are lacking, measurements of longer-lived constituents and knowledge of the relative activities of different fission and activation products that were produced in each shot presumably could be used to assess the reliability of estimated concentrations of all radionuclides in deposited fallout that are used in dose reconstructions. An illustration of the importance of those data is provided by an analysis presented in Appendix E. In addition, later measurements of 152,154,155Eu in surface soil could be used to assess the reliability of estimated concentrations of activation products at the NTS.
Similarly, concentrations of radionuclides in fallout deposited on residence islands in the Pacific have been estimated in many studies, some of which began
during the period of atomic testing (see, for example, Wilson et al., 1975; Robison et al., 1997b; Simon and Graham, 1997; Donaldson et al., 1997). Those data could be used to assess the reliability of estimated concentrations of radionuclides in fallout deposited on residence islands that are used in dose reconstructions and the potential importance of inhalation doses, and they may also be useful in assessing the reliability of estimated concentrations of radionuclides in fallout on ships. The potential importance of the data is illustrated by the following example. On residence islands at Enewetak Atoll, the total deposition of plutonium reported by Wilson et al. (1975) is about 0.3-25 nCi m−2. If we assume that those data define a 90% confidence interval of plutonium concentrations and use the same assumptions about uncertainties in parameter values as in the example analysis of a scenario involving resuspension caused by walking or other light activities discussed in Section V.C.3.3—except that an assumption about fractionation is not needed when concentrations of plutonium on the ground are measured—we find that a central estimate of inhalation dose to the lung is about 10−4 mrem h−1, and an upper bound (95th percentile) of a probability (uncertainty) distribution is about 0.02 mrem h−1. Those results indicate that inhalation doses due to resuspension of longer-lived radionuclides in fallout deposited on residence islands in the Pacific are unlikely to be important in most cases. That conclusion is supported by later assessments of doses to native Marshall Islanders from inhalation of plutonium (Robison et al., 1997b; Sun et al., 1997b). Knowledge of amounts of shorter-lived radionuclides in fallout relative to plutonium could be used to infer possible inhalation doses due to resuspension of all radionuclides deposited on residence islands.
The committee is particularly concerned about two assumptions used in the NTPR program to estimate concentrations of radionuclides in fallout deposited on the ground or other surfaces. The first is an assumption of no fractionation of radionuclides in fallout except for removal of noble gases. That assumption almost certainly results in substantial underestimates of concentrations of refractory radionuclides (such as plutonium) in fallout at the NTS and in the Pacific. An assumption of no fractionation is especially important at the NTS because accumulation of fallout plutonium during the period of atomic testing presented an important inhalation hazard to thousands of participants who engaged in activities in forward areas. The second is an assumption, used to calculate external exposure rates per unit concentration of radionuclides in deposited fallout, that the source region is a surface of infinite extent. That assumption is reasonable at the NTS and on residence islands in the Pacific, but it probably results in underestimates of concentrations of radionuclides in fallout deposited on ships.
Estimates of concentrations of radionuclides on the ground or other surfaces used in dose reconstructions are of crucial importance because calculated inhalation doses in most scenarios depend on those estimates. The committee is not aware of any efforts by the NTPR program to assess the reliability of those estimates at the NTS or in the Pacific. If a key element of a method on which
estimates of dose depend has unknown reliability, all estimates of dose based on the method are called into question unless it can be demonstrated by other means that the method as a whole most likely results in substantial overestimates of dose. The committee does not believe that it has been demonstrated that the method as a whole tends to overestimate inhalation doses.
[2] An important deficiency in dose reconstructions for many participants at the NTS is the lack of consideration of resuspension of previously deposited fallout by the blast wave produced in aboveground detonations. When combined with the frequent neglect of aged fallout that accumulated at the NTS during the period of atomic testing and the general neglect of fractionation in fallout, neglect of resuspension caused by a blast wave could result in underestimates of upper bounds of inhalation doses by a factor of at least 100 in some scenarios in which participants engaged in activities in forward areas within a few hours after a shot, and perhaps by a factor of as much as 1,000 in the worst cases.
The issue of neglect of resuspension caused by the blast wave produced in a detonation in all dose reconstructions at the NTS and the possible degree of underestimation of upper bounds of inhalation dose in some scenarios due to neglect of blast-wave effects are discussed in Section V.C.3.2, comment [7]. The committee believes that neglect of effects of a blast wave on inhalation exposures of participants in forward areas after detonations at the NTS, combined with the frequent neglect of aged fallout that accumulated during the period of atomic testing at the NTS and neglect of fractionation in fallout, is an important deficiency for which there is no apparent explanation. The potential importance of resuspension caused by a blast wave on inhalation doses is demonstrated by an analysis in Appendix E. Neglect of blast-wave effects is important not only because of the likelihood of large underestimates of inhalation dose but also because thousands of participants at the NTS (maneuver troops and close-in observers) probably were exposed to fallout that was resuspended by a blast wave, and credible upper bounds of doses to organs of concern could have exceeded 1 rem in many cases.
[3] Dose coefficients for inhalation of radionuclides (equivalent doses to specific organs and tissues per unit activity intake) have substantial uncertainty that has not been taken into account in the NTPR program. In the worst cases, such as the dose coefficient for the lung from inhalation of plutonium, a credible upper bound of a dose coefficient based on current ICRP recommendations and a full accounting of uncertainty is more than a factor of 10 higher than values used in dose reconstructions for atomic veterans.
Dose coefficients for inhalation of radionuclides are uncertain because of uncertainty in the associated dosimetric and biokinetic models and in the biological effectiveness of alpha particles. Evaluations of those uncertainties have been
available for use in dose reconstructions at least since 1994 (see Section V.C.3.2, comments [1] and [2]). The conclusion that the upper bound of a dose coefficient for inhalation could be underestimated by a factor of more than 10 in the worst cases takes into account the presumed bias of most dose coefficients used in dose reconstructions to overestimate dose when a particle size (AMAD) of 1 μm is assumed (see Tables V.C.1 and V.C.2).
The substantial uncertainty in dose coefficients is important because it affects all calculations of inhalation dose to participants. Uncertainty in dose coefficients should be acknowledged and taken into account in the NTPR program if credible upper bounds of inhalation doses to atomic veterans are to be obtained.
V.C.6 Conclusions on Credibility of Estimated Upper Bounds of Inhalation Dose
All estimates of inhalation dose to atomic veterans obtained in the NTPR program are reported as single values without uncertainty, and those estimates are intended to provide upper bounds of possible inhalation doses. Thus, the key question in evaluating methods of estimating inhalation doses used in dose reconstructions is whether the methods provide credible upper bounds. If they do, estimates of inhalation dose to atomic veterans are appropriate for use in evaluating claims for compensation for radiation-related diseases. However, if estimates of inhalation dose are substantially less than credible upper bounds, the veterans are not given the benefit of the doubt and, depending on the magnitude of possible doses from all exposure pathways, their claims for compensation may not be evaluated fairly; that is, a veteran’s claim could be denied even though a credible upper-bound estimate of dose, taking all exposure pathways and uncertainties into account, would qualify the veteran for compensation.
As discussed in Section V.C.3.3, the committee does not believe that the question of whether estimates of inhalation dose obtained in the NTPR program are credible upper bounds can be given a single answer that applies to all exposure scenarios for participants at the NTS and in the Pacific. However, partly on the basis of conclusions obtained in previous reviews by committees of the National Research Council (see Section V.C.2), the NTPR program has often claimed that its methods of calculating inhalation dose provide overestimates of dose (the doses are “high-sided”), the implication being that the claim applies generally (see, for example, Schaeffer, 2001b). Therefore, the question is whether the methods of estimating inhalation doses provide credible upper bounds in all or nearly all cases.
The present committee’s review of methods of estimating inhalation dose used in the NTPR program has been considerably more extensive than previous reviews by other committees of the National Research Council. The present committee considered many issues involved in estimating inhalation doses that were not evidently considered in previous reviews. Furthermore, the present committee had
access to documentation of methods that was not available when the first review was conducted in 1985; and for the first time, extensive and detailed evaluations of dose reconstructions for individual veterans who filed a claim for compensation or who requested information on their doses were conducted.
On the basis of its review, the present committee has reached a different conclusion about methods of estimating inhalation dose used in the NTPR program from the one based on previous reviews. Its conclusion is summarized as follows: Methods used in the NTPR program to estimate inhalation doses to atomic veterans do not consistently provide credible upper bounds. Furthermore, the extent of underestimation of upper bounds is a factor of at least 100 in important scenarios involving maneuver troops and close-in observers at the NTS who were exposed to old fallout that was resuspended by the blast wave produced in a detonation.
There are some important scenarios in which estimates of inhalation dose obtained in dose reconstructions probably are credible upper bounds, as intended by the NTPR program. An example of such a scenario discussed in Section V.C.3.3 is exposure to descending fallout throughout the period of descent on residence islands in the Pacific when cancer in an internal organ other than an organ in the GI tract is the disease of concern, although an unequivocal conclusion is difficult even in this scenario because of the unknown reliability of methods used by the NTPR program to estimate concentrations of radionuclides in descending fallout. It also seems likely that estimates of inhalation dose in scenarios at the NTS involving suspension of neutron-activation products in surface soil are credible upper bounds, given that assumed resuspension factors are likely to be considerable overestimates for radioactive materials that are fixed in soil. Estimates of inhalation doses to occupation forces in Japan discussed in Section IV.D also should be credible upper bounds if they are based on an assumption that exposure occurred only at locations of highest fallout.
However, the types of exposure scenarios for which estimates of inhalation dose obtained in dose reconstructions probably are credible upper bounds are somewhat limited. In many frequently occurring scenarios, such as scenarios of exposure to previously deposited fallout in forward areas at the NTS, the committee believes that uncertainties in assumptions used to estimate inhalation dose are sufficiently important that doses estimated by the NTPR program may not be credible upper bounds even if some parameter values used in the calculations, especially resuspension factors, are credible upper bounds. Even in scenarios involving exposure to descending fallout, exposure during the entire period of fallout probably was a rare occurrence at the NTS, in which case concentrations of radionuclides in air could be underestimated, depending on when exposure occurred; and the committee again notes that concentrations of radionuclides in fallout that descended on ships in the Pacific may be underestimated. Furthermore, in some dose reconstructions, it is evident to the committee that upper bounds of inhalation doses to atomic veterans have been underestimated by large
factors. The most obvious cases involve exposure scenarios for participants in forward areas at the NTS, including maneuver troops and close-in observers, in which resuspension of substantial amounts of previously deposited fallout by the blast wave produced in a detonation has been ignored even though exposure to relatively high concentrations of resuspended radionuclides caused by the blast wave almost certainly occurred. For example, when the NTPR program has assumed that resuspension of previously deposited fallout was caused by walking or other light activity in cases in which blast-wave effects probably occurred but were ignored, the committee believes that upper bounds of inhalation doses are underestimated by a factor of at least 100, and perhaps by a factor of as much as 1,000 in the worst cases. Furthermore, in such cases, upper bounds of equivalent doses to some organs and tissues could have been substantially above 1 rem.
Of paramount importance is the issue of whether deficiencies in methods of estimating inhalation dose identified by the committee could have affected decisions about compensation of atomic veterans. The committee believes that possible underestimation of upper bounds of inhalation doses by the NTPR program is unlikely to be important for most participants in the Pacific or occupation forces in Japan. Inhalation doses to most of those participants probably were too low for possible underestimation of upper bounds to have affected decisions about compensation. The committee also believes that neglect of possible ingestion doses in dose reconstructions is unlikely to be important for most participants at any site. However, the neglect of blast-wave effects, combined with the frequent neglect of aged fallout that accumulated during the period of atomic testing at the NTS and neglect of fractionation in fallout, is an important concern for thousands of participants who were exposed in forward areas at the NTS shortly after a detonation. On the basis of an example analysis of the effects of a blast wave on inhalation doses (see Appendix E) and screening doses that have been used in evaluating claims for compensation (see Section III.E), use of credible upper bounds of inhalation doses in scenarios involving resuspension by a blast wave could have changed decisions not to grant compensation in some cases, depending on the disease of concern (for example, lung cancer in a nonsmoker).
The question of the importance of deficiencies in methods of estimating inhalation doses in the NTPR program with respect to evaluating claims for compensation for radiation-related diseases is discussed further in Sections VI.F and VII.C.
V.D DOSE RECONSTRUCTION FOR OCCUPATION FORCES IN JAPAN
As discussed in Section IV.D, the upper-bound external dose for the 195,000 troops who participated in the occupation of Japan or were prisoners of war at or near Hiroshima or Nagasaki was estimated, on the basis of very pessimistic assumptions, to be always less than 1 rem, even though the likely dose to most
participants was at least a factor of 10 lower (McRaney and McGahan, 1980). The dose from ingestion of contaminated food or water or inhalation of resuspended debris was also found to be insignificant. The highest possible dose is for a participant who was present throughout the entire operation and spent 8 h d−1 at the location of highest exposure rates. However, most troops were rotated, troops were billeted well away from contaminated areas, and the highest exposure rates occurred over an area of only about 0.1 km2. In examining a sample of 12 cases, the committee found that detailed calculations of worst-case upper-bound doses were carried out for most of the veterans, and the calculations included both internal and external doses. In those cases, the calculated upper bound was considerably less than the overall generic upper-bound value of 1 rem. The one exception was a person with a calculated upper-bound dose of 0.62 rem. At the other extreme, three veterans were given an upper-bound dose of zero because they did not have an opportunity to be close to contaminated sites (for example, they remained on board a ship in the Nagasaki harbor). In one case, the veteran was in a different part of Japan.
The committee concurs with the assessment by the NTPR program that the dose to even the most exposed of the occupation troops in Japan from both internal and external exposure was probably well below 1 rem.
V.E COMMITTEE EVALUATION OF METHOD OF ESTIMATING UNCERTAINTY IN DOSE AND UPPER BOUNDS
As stated in Section II.A, dose reconstruction is an inexact science. Uncertainties in quantifying dose arise from uncertainties in the various components that must be brought together to calculate a dose: in reconstruction of the activity scenario, in characterization of the radiation environment through time and space, in parameters assumed for calculations (such as resuspension factors and decay factors for radiation fields), in characterization of the mixture of radionuclides produced by a particular detonation, and in quantifying exposures through various routes (such as inhalation, ingestion, and dermal exposure).
Clearly, uncertainties in the dose assigned to an atomic veteran are highly relevant to the adjudication process, particularly for diseases not categorized as “presumptive,” that is, diseases whose probability of causation is evaluated, because those uncertainties can inform the decision regarding the merits of a claim for service-connected disability. According to 32 CFR 218.3, which describes the approach to dose reconstruction used in the NTPR program: “Due to the range of activities, times, geometries, shielding, and weapon characteristics, as well as the normal spread in the available data pertaining to the radiation environment, an uncertainty analysis is performed. This analysis quantifies the uncertainties due to time/space variations, group size, and available data. Due to the large amounts of data, an automated (computer-assisted) procedure is often used to facilitate the
data-handling and the dose integration and to investigate the sensitivity to variations in the parameters used.”
However, the committee did not see evidence in the case files that this kind of thorough uncertainty analysis was often done, although Monte Carlo methods can bring together sources of uncertainty in this way. The standard operating procedures (SOPs) document provided to the committee (DTRA, 1997) provides almost no information about how uncertainty is quantified by the NTPR program, and this complicated the committee’s review of methods used. The unit dose reports do provide uncertainty estimates, but they are usually estimates of the uncertainty in the average unit dose and, as discussed earlier, they may not provide a credible estimate of the uncertainty in the dose to the most exposed individuals in the unit. Furthermore, they often provide little detail regarding the specific method used, the exact correlations assumed or neglected, and the specific data used to calculate the upper bounds. Often, the reports acknowledge that the procedures used to combine various sources of uncertainty are based on approximate methods.
The NTPR program’s intention with an upper-bound calculation is to provide at least a 95th percentile of the dose, that is, a dose that is intended to ensure that we can be at least 95% confident that the true dose is lower. Upper bounds estimated from film-badge data and from reconstructed gamma and neutron doses are combined in quadrature, assuming that they are uncorrelated, to arrive at an estimate of the upper bound in the total external dose. To the extent that the individual upper-bound estimates are credible and all doses and potential uncertainties are included, the upper-bound estimate for this sum is credible, provided that uncertainties in the increments of dose are independent—that is, not correlated—which they may not be because of repetitiveness of behavior and work responsibilities. If the components being summed are positively correlated, then the quadrature method will systematically underestimate the upper bound for the aggregated dose. Another problem arises in the context of combining uncertainties across different types of radiation. In recent years, after it became routine to report an upper bound for the external gamma plus neutron dose to VA, the sum of the estimated upper bounds of the gamma and neutron doses and the estimated “high-sided” internal organ dose has been used as the dose of record in evaluating probability of causation of a veteran’s claimed disease in the adjudication process. Summing upper bounds of external and internal doses would generally result in an overestimate of the upper bound of the total organ dose. However, as discussed earlier in this chapter, the committee found that in many cases the estimated upper bounds for external gamma and neutron dose were not credible and the “high-sided” estimates of internal and beta skin doses may not always reflect the 95th percentile dose (that is, a credible 95th percentile could be considerably higher).
To the extent that the external gamma-plus-neutron dose upper bounds and inhalation dose estimates are reasonable estimates of at least 95th percentile or higher doses, the VA practice of summing the reported upper-bound external
dose and the “high-sided” inhalation dose will result in a high-sided estimate of the 95th percentile upper bound of the total organ dose.33 Although external and inhalation dose estimates are sometimes correlated to some extent, such as when both are based on the same exposure-rate measurement, most of the pertinent uncertainties involved are independent of each other. The estimated beta skin dose calculated by the NTPR program is directly related to the reported upper bound in gamma external dose. Thus, summing the reported beta dose estimate with the reported upper-bound gamma dose estimate will result in a credible estimate of the upper bound of the skin dose when the beta and gamma dose estimates both are credible upper bounds.
The committee acknowledges that calculation of an upper-bound dose is itself an uncertain process. Furthermore, it is not clear how one ought to quantify effects of uncertainties in an activity scenario. For example, for external radiation exposure, NTPR program policy guidelines sometimes seem to target a best or even “high-sided” central estimate together with a 95th percentile upper-bound dose, and at other times seem to opt for only a “high-sided” estimate, in accordance with the benefit-of-the-doubt provision. For internal dose, the policy of the NTPR program is to provide a “high-sided” estimate that supposedly incorporates benefit of the doubt with respect to the exposure scenario. However, as discussed elsewhere in this chapter, the committee has concluded that assumed exposure scenarios often did not give the veteran the benefit of the doubt.
V.F SUMMARY OF COMMITTEE FINDINGS REGARDING DOSE AND UNCERTAINTY ESTIMATES BY NTPR PROGRAM
The central (“best”) estimates of external gamma and neutron doses to participants obtained by the NTPR program based on film-badge data and/or unit dose reconstructions are generally credible, provided that the assumed exposure scenario is reasonable. However, the committee has documented numerous examples in which the NTPR program has failed to establish the participant’s exposure scenario adequately; that is, plausible scenarios could be developed, on the basis of available information, that would have resulted in higher estimates of dose.
The committee finds that estimates of uncertainty in external dose obtained by the NTPR program in unit dose reconstructions often are not credible and do not adequately reflect the upper bound (95th percentile) in the external dose to an individual participant, because deviations in individual exposure scenarios from the assumed group exposure scenario are not considered. Furthermore, the committee has identified a number of situations in which uncertainty in film-badge issuance dates, interpretation of data, and failure to give the veteran the benefit of
the doubt suggest the possibility of a much higher credible upper bound of the dose to an individual than reported by the NTPR program, even when the dose is based primarily on film-badge data. Upper-bound estimates of external dose should include consideration of the possibility of incorrect exposure scenarios, possibly missing or erroneous film-badge data, the impact of limited survey data, and other such factors. To give the veteran the required benefit of the doubt, some method should be devised to increase upper-bound estimates of external dose when there is reason to believe that any of those events may have occurred.
The committee has concluded that, contrary to claims by the NTPR program, calculated internal doses from inhalation are not always “high-sided.” The committee has identified scenarios for which the method used by the NTPR program to estimate inhalation dose probably provides credible upper bounds (95th percentiles of possible doses or above). However, the committee has also identified important scenarios for which estimates of inhalation dose obtained by the NTPR program probably underestimate upper bounds by as much as a factor of 100 or more. Furthermore, organ equivalent doses could be substantial in some of those cases.
The committee found that beta doses to the skin and lens of the eye, although claimed by the NTPR program to be “high-sided,” may not represent a credible estimate of the 95th percentile beta dose. Furthermore, beta doses from direct contamination of skin or clothing apparently have not been considered in dose reconstructions in any cases in which a veteran filed a claim for skin cancer.
The committee believes that upper bounds of neutron doses reported by the NTPR program are not credible, because of neglect of the uncertainty in the biological effectiveness of neutrons. When neutron doses were important, estimated upper bounds of the combined gamma-plus-neutron doses obtained by the NTPR program may be low by as much as a factor of 5.
The committee thus has concluded that the external gamma and neutron dose upper bounds and “high-sided” internal and beta skin and eye doses reported by the NTPR program often do not represent a credible estimate of the 95th percentile upper bound of the possible dose to an individual participant.
As discussed in Section III.E, VA uses the sum of the reported external-dose upper bound and organ internal dose to evaluate the probability of causation of a claimed radiation-related disease. By using the upper-bound dose estimate to evaluate probability of causation, rather than the best (central) estimate, VA intends to give the veteran the benefit of the doubt. However, to the extent that the reported doses do not provide credible estimates of 95th percentile upper bounds of organ total equivalent doses, evaluations of probability of causation may be less favorable to the veteran than intended. Implications of the committee’s findings with regard to evaluating claims for compensation are discussed further in Section VI.F.