4
Content Analysis
Crucial to any curriculum is its content. For purposes of this evaluation, an analysis of the content should address whether the content meets the current and long-term needs of the students. What constitutes the long-term needs of the students is a value judgment based on what one sees as the proper goals and objectives of a curriculum. Differences exist among well-intentioned groups of individuals as to what these are and their relative priorities. Therefore, an analysis of a curricular program’s content will be influenced by the values of the person or persons conducting the content analysis. Moreover, if the analysis considers a district, state, or national set of standards, other differences can be expected to emerge. In this chapter, we examine how to conduct the content analysis in order to identify a set of common dimensions that may help this methodology to mature, as well as to bring forth the difference in values. A curriculum’s content must be compatible with all students’ abilities, and it must consider the abilities of, and the support provided to, teachers.
An analysis of a curriculum’s content should extend beyond a mere listing of content to include a comparison with a set of standards, other textual materials, or other countries’ approaches or standards. For the purposes of this study—reviewing the evaluations of the effectiveness of mathematics curricula—content analyses will refer to studies that range from documenting the coverage of a curriculum in relation to standards to more extended examinations that also assess the quality of the content and presentation. Clarity, consistency, and fidelity to standards and their relationship to assessment should be clearly identifiable, basic elements of any
TABLE 4-1 Distribution of the Content Analysis Studies: Studies by Type and Reviews by Grade Band
|
Type of Study |
Number of Reviews |
Number of Studies |
Percentage of Total Studies by Program Type |
|
NSF supported |
|
19 |
53 |
|
Elementary |
10 |
|
|
|
Middle |
20 |
|
|
|
High |
13 |
|
|
|
Total |
43 |
|
|
|
Commercially generated |
|
1 |
3 |
|
Elementary |
3 |
|
|
|
Middle |
8 |
|
|
|
High |
0 |
|
|
|
Total |
11 |
|
|
|
UCSMP |
|
10 |
28 |
|
UCSMP (high school) |
12 |
|
|
|
Total |
12 |
|
|
|
Not counted in above |
|
6 |
16 |
|
Total |
|
36 |
100 |
reasonable content analysis. The remainder of the chapter reviews primary examples of content analysis and delineates a set of dimensions for review that might help make the use of content analysis evaluations more informative to curriculum decision makers.
We identified and reviewed 36 studies of content analysis of the supported and commercially generated National Science Foundation (NSF) mathematics curricula. Each study could include reviews of more than one curriculum. Table 4-1 lists how many studies were identified in each program type (NSF-supported, University of Chicago School Mathematics Project [UCSMP], and commercially generated), the total number of reviews in those studies, and the breakdown of those reviews by elementary, middle, or high school. These reviews allowed us to consider various approaches to content analysis, to explore how those variations produced different types of results and conclusions, and to use this information to make inferences about the conduct of future evaluations.
The content analysis reviews were spread across the 19 curricular programs under review. The number of reviews for each curricular program varied considerably (Table 4-2); hence our report on these evaluations draws on reports by some programs more than others.
Table 4-3 identifies the sources of the studies by groups that produced multiple reviews. Those classified as internal were undertaken directly by an author, project evaluator, or member of the staff of a publisher associated with the curricular program. Content analyses categorized as external
TABLE 4-2 Content Counts by Program
|
|
Number of Reviews by Program |
|||
|
Curriculum Name |
0 |
1 |
2-5 |
>5 |
|
Everyday Mathematics |
|
|
|
7 |
|
Investigations in Data, Number and Space |
|
|
2 |
|
|
Math Trailblazers |
|
1 |
|
|
|
Connected Mathematics Project |
|
|
|
8 |
|
Mathematics in Context |
|
|
|
7 |
|
Math Thematics |
|
|
5 |
|
|
MathScape |
|
1 |
|
|
|
MS Mathematics Through Applications Project |
0 |
|
|
|
|
Interactive Mathematics Project |
|
|
4 |
|
|
Mathematics: Modeling Our World (ARISE) |
|
|
2 |
|
|
Contemporary Mathematics in Context (Core-Plus) |
|
|
3 |
|
|
Math Connections |
|
|
2 |
|
|
SIMMS |
|
|
2 |
|
|
Addison Wesley/Scott Foresman |
|
|
2 |
|
|
Harcourt Brace |
|
1 |
|
|
|
Glencoe/McGraw-Hill |
|
|
2 |
|
|
Saxon |
|
|
|
6 |
|
Houghton Mifflin/McDougal Littell |
0 |
|
|
|
|
Prentice Hall/UCSMP |
|
|
|
14 |
|
Total number of times a curriculum is in any study |
68 |
|
|
|
|
Number of evaluation studies |
36 |
|
|
|
were written by authors who were neither directly associated with the curricula nor with any of the sources of multiple studies.
In this chapter (and in subsequent chapters) we report examples of evaluation studies and describe their approaches and statements of findings. It must be recognized that the committee does not endorse or validate the accuracy and appropriateness of these findings, but rather uses a variety of them to illustrate the ramifications of different methodological decisions. We have carefully selected a diverse set of positions to present a balanced and fair portrayal of different perspectives. Knowing the current knowledge base is essential for evaluators to make progress in the conduct of future studies.
TABLE 4-3 Number of Reviews of Content by Program Type
LITERATURE REVIEW
We identified four sources where systematic content analyses were conducted and applied across programs. They were (1) the U.S. Department of Education’s review for promising and exemplary programs; (2) the American Association for the Advancement of Science (AAAS) curricular material reviews for middle grades mathematics and algebra under Project 2061; (3) the reviews written by Robinson and Robinson (1996) on the high school curricula supported by the National Science Foundation; and (4) the reviews of grades 2, 5, 7, and algebra, available on the Mathematically Correct website. We begin by reviewing these major efforts and identifying their methodology and criteria.
U.S. Department of Education
The U.S. Department of Education’s criteria for content analysis evaluation—Quality of Program, Usefulness to Others, Educational Significance, and Evidence of Effectiveness and Success (U.S. Department of Education, 1999)—included ratings on eight criteria structured in the form of questions:
-
Are the program’s learning goals challenging, clear, and appropriate; is its content aligned with its learning goals?
-
Is it accurate and appropriate for the intended audience?
-
Is the instructional design engaging and motivating for the intended student population?
-
Is the system of assessment appropriate and designed to guide teachers’ instructional decision making?
-
Can it be successfully implemented, adopted, or adapted in multiple educational settings?
-
Do its learning goals reflect the vision promoted in national standards in mathematics?
-
Does it address important individual and societal needs?
-
Does the program make a measurable difference in student learning?
American Association for the Advancement of Science
AAAS’s Project 2061 (http://www.project2061.org) developed and used a methodology to review middle grades curricula and subsequently algebra materials. In describing their methods, Kulm and colleagues (1999) outlined the training and method. After receiving at least three days of training before conducting the review, each team rated a set of algebra or middle grades standards in reference to the Curriculum and Evaluation Standards for School Mathematics from the National Council of Teachers of Mathematics (NCTM) (1989). In algebra, each review encompassed ideas from one area of algebra: functions, operations, and variables. Similarly in middle grades, particular topics were specified. Each team used the same idea set to review a total of 12 textbooks or sets of textbooks over 12 days. Two teams reviewed each book or set of materials.
The content analysis procedure is outlined on the AAAS website and summarized below:
-
Identify specific learning goals to serve as the intellectual basis for the analysis, particularly to select national, state, or local frameworks.
-
Make a preliminary inspection of the curriculum materials to see whether they are likely to address the targeted learning goals.
-
Analyze the curriculum materials for alignment between content and the selected learning goals.
-
Analyze the curriculum materials for alignment between instruction and the selected learning goals. This involves estimating the degree to which the materials (including their accompanying teacher’s guides) reflect what is known generally about student learning and effective teaching and, more important, the degree to which they support student learning of the specific knowledge and skills for which a content match has been found.
-
Summarize the relationship between the curriculum materials being evaluated and the selected learning goals.
The focus in examining the learning goals is to look for evidence that the materials meet the following objectives:
-
Have a sense of purpose.
-
Build on student ideas about mathematics.
-
Engage students in mathematics.
-
Develop mathematical ideas.
-
Promote student thinking about mathematics.
-
Assess student progress in mathematics.
-
Enhance the mathematics learning environment.
Features of AAAS’s content analysis process include opting for a careful review of a few selected topics, chosen prior to the review, that are used consistently across the textbooks reviewed, and requiring that particular page numbers and sections are referenced throughout the review. The evaluation reviews are available on the website.
Robinson and Robinson
Robinson and Robinson (1996) reviewed the integrated high school curricula by defining and using a set of threads to review a set of integrated curricula. These threads, which included algebra/number/function, geometry, trigonometry, probability and statistics, logic/reasoning, and discrete mathematics, were effective in bringing together the structure of an integrated curricula. They further identify commonalities among the curricula, including what is meant by integrated and context-rich, what pedagogies are used, choices of technology, and methods of assessment.
Mathematically Correct
On the Mathematically Correct website, reviews of curricular materials are made available, often via links to other sites viewed as similarly aligned; we collected those pertaining to the relevant curricula. A set of reviews of 10 curricular programs for grades 2, 5, and 7 by Clopton and colleagues presented a systematic discussion of the methodology where the reviewers selected topics “designed to be sufficient to give a clear impression of the features of the presentation and an assessment of the mathematical depth and breadth supported by the program” (1999a, 1999b, 1999c). Ratings on programs focused on mathematical depth, the clarity of objectives, and the clarity of explanations, concepts, procedures, and definitions of terms. Other foci included the quality and sufficiency of examples and the efficiency of learning. In terms of student work, the focus was on the quality and sufficiency of student work and its range, depth, and scope. Clopton et al.’s studies used the Mathematically Correct and the San Diego Standards that were in force at the time. For example, for fifth grade, they selected multiplication and division of whole numbers, decimal multiplication and division, area of triangles, negative numbers and powers, exponents, and scientific notation where a detailed rationale is provided for the selection of each topic. Each textbook was rated according to the depth of study of the topics, ranging from 1 (poor) to 5 (outstanding). Two dimensions of that judgment were identified: quality of the presentation (clarity of objectives,
explanations, examples, and efficiency of learning) and quality of student work (sufficiency, range, and depth). No procedure was outlined for how reviewers were trained or how differences were resolved.
Other Sources of Content Analysis
The rest of the studies categorized as content analyses varied in the extent of specificity on methodology. A number of the reviews were targeted directly at teachers to assist them in curricular decision making. The Kentucky Middle Grades Mathematics Teacher Network (Bush, 1996), for example, reviewed four middle grades curricula using groups of teachers. They selected four general content areas (number/computation, geometry/ measurement, probability/statistics, and algebraic ideas) from the Core Content for Assessment (Kentucky Department of Education, 1996) and asked teachers to evaluate the materials based on appropriateness for grade levels and quality of content presentation. They were also asked to evaluate the pedagogy. Although these reviews identified missing content strands and produced judgments of general levels of quality, we found them to be of limited rigor for use in our study; in particular, this was because of their lack of specificity on method. Other content analyses ranged from those by authors explaining the design and structure of the materials (Romberg et al., 1995) to those by critics of particular programs focusing on only the areas of concerns, often with sharp criticisms.
We identified one study by Adams et al. (2000) (subsequently referred to as the “Adams report”) entitled Middle School Mathematics Comparisons for Singapore Mathematics, Connected Mathematics Program, and Mathematics in Context that used the National Council of Teachers of Mathematics (NCTM) Principles and Standards for School Mathematics 2000 as a comparison. Their method of content analysis is based on 72 questions that compare the curricula against the 10 overarching standards (number, algebra, geometry, measurement, data and probability, problem solving, reasoning and proof, communication, connection, and representation) and 13 questions that examine six principles (equity, curriculum, teaching, learning, assessment, and technology). Further information from each of these four sources of content analysis will be referenced in the discussion of the reviews in subsequent sections.
DIMENSIONS OF CONTENT ANALYSES
As we discovered by examining the available reports, the art and science of systematic content analysis for evaluation purposes is still in its adolescence. There is a clear need for the development of a more rigorous paradigm for the planning, execution, and evaluation of content analyses.
This conclusion is supported by a review of the results of the content analyses; the ratings of many curricular programs vacillated from strong to weak, with little explanation for the divergent views.
In Chapter 3, we identified content analyses as a form of connoisseurial assessment (Eisner, 2001). Variations among experts can be expected, but they should be connected to differences in selected standards, philosophies of mathematics or learning, values, or selection of topics for review. Each of these influences on the content analysis should be explicitly articulated to the degree possible as part of an evaluation report, a form of “full disclosure” of values and possible bias. Faced with the current status of “content analysis,” we recognized that rather than specifying methods for the conduct of content analyses to produce identical conclusions, we needed to assist evaluators in providing decision makers with clearer delineation of the different dimensions and underlying theories they used to make their evaluations.
A review of the research literature provided relatively few systematic studies of content analysis. However, we did find three studies that were applicable to our work: (1) an international comparative analysis and distribution of mathematics content curricula across the school grades that was conducted in the Third International Mathematics and Science Study (TIMSS) (Schmidt et al., 2001), (2) a project by Porter et al. (1988) concerning content determinants where they demonstrated variations in emphases in a variety of textbooks in the early 1980s, and (3) where Blank (2004) developed tools to map the content dimensions of curriculum and compared this with the relative emphases in the assessments.
To strengthen our deliberations on this issue, we collected testimony from educators and invited scholars to comment on what constitutes a useful content analysis, and illustrations are cited in text boxes. Our review of the literature, analysis of the submitted evaluations, and consideration of the responses confirmed our belief that uniform standards or even a clear consensus on what constitutes a content analysis do not exist. We saw our work as a means to contribute to the development of clearer methodological guidelines through a synthesis of previous studies and the deliberations of the committee. In the next sections, we discuss participation in content analyses, the selection of standards or comparative curricula, and the inclusion of content and/or pedagogy. We then identify a set of dimensions of content analyses to guide their actual conduct.
Participation in Content Analyses
A key dimension of content analysis is the identity of the reviewer(s) (Box 4-1). We recognized the importance of including members of the mathematical sciences community in this process, including those in both
|
BOX 4-1 “Whether or not a curriculum is mathematically viable would ultimately depend on the judgment of some mathematicians. As such, good judgment rightfully should play a critical role.”—Hung Hsi Wu, University of California, Berkeley “Neither mathematicians nor educators are alone qualified to make these judgments; both points of view are needed. Nor can the work be divided into separate pieces (the intended and achieved curriculum), one for mathematicians to judge and one for educators. The two groups must cooperate.”—William McCallum, University of Arizona “The qualifications needed to make valid judgments on the quality of content in terms of focus, scope, and sequencing over the years are much more stringent than seems to be commonly appreciated. In mathematics, for example, someone with only a Ph.D. in the subject is unlikely to be qualified to do this unless, over the years, he or she has made significant contributions in many areas of the subject and has worked successfully in applying mathematics to outside subjects as well.”—R. James Milgram, Stanford University |
pure and applied mathematics (Wu and Milgram testimony at the September 2002 Workshop). There was agreement among respondents that the expertise of mathematics educators is needed to ensure careful considerations of student learning and classroom practices (McCallum testimony at the September 2002 Workshop). Although we found some debates between the parties, our reviews also revealed that mathematicians and mathematics educators shared a common goal of an improved curriculum. Controversy in this direction provides increased impetus for establishing methodological guidelines and bringing to the surface the underlying reasons for disputes and disagreements.
We found it particularly helpful when a content analysis was accompanied by a clear statement of the reviewer’s expertise. Adams et al. (2000, p. 2), for example, disclosed their qualifications early on, writing, “Another point to consider is our expertise, both what it is and what it is not. The group that created this comparison consists entirely of people who combine high-level training in mathematics with an interest in education but who have neither direct experience of teaching in the American K-12 classroom nor the training for it.” Most reviews, however, did not discuss reviewers’ credentials. We did not find, for example, a similar statement by experts in education identifying their qualifications in mathematics. Other reviews, such as the one by Bush (1996), were conducted by panels of teachers. The involvement of teachers and/or parents in content analysis should prove to
be a valuable means of feedback to writers and a source of professional development to the teachers.
The Selection of Standards or Comparative Curricula
At the most general level, the conduct of a content analysis requires identifying either a set of standards against which a curriculum is compared or an explicitly contrasting curriculum; the analysis should not rely on an imprecise characterization of what should be included. Common choices include the original or the revised NCTM Standards, state standards or other standards, or comparative curricula as a means of contrast. The strongest evaluations, in our opinion, used a combination of these two approaches along with a rationale for their decisions.
The choice of comparison can have a crucial impact on the review. For example, the unpublished Adams report succinctly showed how conclusions from content analysis of a curriculum can vary with changes in the adopted measures, varying goals, and philosophies. This report, prepared for the NSF, stood out as being particularly complete and carefully researched and analyzed in its evaluations. To appraise the NSF curricula, they evaluated Connected Mathematic Project (CMP) and Mathematics in Context in terms of the 2000 NCTM Principles and Standards for School Mathematics. These two programs were chosen, in part, because evidence by AAAS’s Project 2061 suggested they are among the top of the 13 NSF-sponsored projects studied.
An interesting and valued feature in the Adams report was that these programs were compared with the “traditional” Singapore mathematics textbooks “under the authority of a traditional teacher” (Adams et al., 2000, p. 1). To explain why Adams selected the Singapore program as the “traditional approach” measure of comparison, recall that the performance of students from the United States on TIMSS “dropped from mediocre at the elementary level through lackluster at the middle school level and down to truly distressing at the high school level.” On the other hand, of the 41 nations whose students were tested, those from Singapore “scored at the very top” (Adams et al., 2000, p. 1). We found that this comparison component of the Adams study with a top-ranked traditional program provides a valuable and new dimension absent from most other studies. Because the United States is at the forefront of scientific and technological advances, the Singapore comparison dimension cannot be ignored: content analysis studies that make comparisons across a variety of types of curricular material must be encouraged and supported.
The Adams report demonstrated the importance of the selection of the standards and the comparative curricula in their reported results. When
these NSF programs were compared to the NCTM Principles and Standards for School Mathematics (PSSM), they showed strong alignment; when contrasted with the Singapore curriculum, they revealed delays in the introduction of basic material.
Once the participants, standards, and comparison curricula are selected and identified, other factors remains that are useful in creating the necessary types of distinctions to conduct the content analyses. In the next section, we identify some of these additional considerations.
Inclusion of Content and/or Pedagogy
A major distinction among content analyses was whether the emphasis was on the material to be taught, or the material and its pedagogical intent. In response to criticisms of American programs, which are described as “a mile wide and an inch deep” (Schmidt et al., 1996), a focus on the identification and treatment of “essential ideas” provides one way to approach the content dimension of content analysis (Schifter testimony at the September 2002 Workshop). Another respondent proposed a three-part analysis to determine whether (1) there are clearly stated objectives to be achieved when students learn the material, (2) the objectives are reasonable, and (3) the objectives will prepare students for the next stages of learning (Milgram testimony at the September 2002 Workshop).
Alternatively, some scholars believe a content analysis should include an examination of pedagogy citing the need to examine both the content and how it is intended to be taught (Gutstein testimony at the September 2002 Workshop). Some scholars expressed the view that the content analysis must be conducted in situ in recognition that the content of a curriculum emerges from the study of classroom interactions, so examination of materials alone is insufficient (McCallum testimony at the September 2002 Workshop). This approach is not simply a question of whether material was taught and how well; it reflects a concern that instructional practices can modify the course of the content development, especially when using activity-based approaches that rely on the give and take of classroom interactions to complete the curricula. Such studies, often called design experiments (Cobb et al., 2003), do not entail full-scale implementation, only pilot sights or field tests. Typically, these student-oriented approaches rely more heavily on teachers’ content knowledge and judgment and hence are difficult to analyze in the absence of their use and without information about the teacher’s ability. Decisions to include or exclude pedagogy in a content analysis and to study the materials independently or in situ are up to the reviewer, but the choice and reasons for it should be specified. For examples of viewpoints from experts, see Box 4-2.
|
BOX 4-2 “A useful content analysis would … identify the essential mathematical ideas that underlie those topics … [one must determine if] those concepts [are] developed through a constellation of activities involving different contexts and drawing upon a variety of representations, and so one must follow the development of those concepts through the curriculum…. A curriculum should include enough support for teachers to enact it as intended. Such support should allow teachers to educate themselves about mathematics content, students’ mathematical thinking, and relevant classroom issues…. It might help … teachers analyze common student errors in order to think about next steps for those who make them. And it might help teachers figure out how to adjust an activity to make it more accessible to struggling students without eliminating the significant mathematics content, or to extend the activity for those ready to take on extra challenge.”—Deborah Schifter, Education Development Center “To begin, one must understand that mathematics is almost unique among the subjects in the school curriculum in that what is done in each grade depends crucially on students having mastered key material in previous grades. Without this background, students simply cannot develop the understanding of the current year’s material to a sufficient depth to support future learning. Once this failure happens, students typically start falling behind and do not recover.”—R. James Milgram, Stanford University “Mathematics is by definition a coherent logical system and therefore tolerates no errors. Any mathematics curriculum should in principle be error-free.”—Hung Hsi Wu, University of California, Berkeley [A content analysis requires] “looking both at the mathematics that goes into it and at how well the mathematics takes root in the minds of students. Both are necessary: topics that are mentioned in the table of contents but unaccompanied by a realistic plan for preparing teachers and reaching students cannot be said to add to the content of a curriculum, nor can activities that work well in the classroom but are mathematically ill conceived.”—William McCallum, University of Arizona “One very important [issue of vital importance to mathematics education that is not captured by broad measures of student achievement] is the maintenance of a challenging high-quality education for the best students. The primary object of concern these days in mathematics education seems to be the low-achieving student, how to raise the floor. Certainly, this is the spirit evoked by No Child Left Behind. This is a very important issue, but it should not blind us to the fact that the old system, the system often denigrated today, is the one which got us where we are, to a society transformed by the impact of technology…. The percentage of people who need to be highly competent in mathematics has always been and will continue to be small, but it will not get smaller. We must make sure that mathematics education serves these people well.”—Roger Howe, Yale University |
The Discipline, the Learner, and the Teacher as Dimensions of Content Analysis
Curricular content analysis involves an examination of the adequacy of a set of materials in relation to its treatment of the discipline, learner(s), and the teacher. Learning occurs through an interaction of these three elements. Beyond being examined independently, an analysis must consider how they interact with one another. Following this triadic scheme, we specified three dimensions of a content analysis to be more informative to curricula decision makers:
-
Clarity, comprehensiveness, accuracy, depth of mathematical inquiry and mathematical reasoning, organization, and balance (disciplinary perspectives).
-
Engagement, timeliness and support for diversity, and assessment (learner-oriented perspectives).
-
Pedagogy, resources, and professional development (teacher- and resource-oriented perspectives).
We discuss each dimension and how it has been addressed in the various content analyses under review. Elements of the dimensions overlap and interact with each other, and no dimension should be assumed as logically or hierarchically prior to the others, except as indicated within a particular content analysis. A content analysis neglecting any dimension would be considered incomplete.
Dimension One: Clarity, Comprehensiveness, Accuracy, Depth of Mathematical Inquiry and Mathematical Reasoning, Organization, and Balance
A major goal of developing standards is to provide guidance in the evaluation of curricular programs. Thus, in determining curricular effectiveness at a basic level, one wants to ascertain if all the relevant topics are covered, if they are sequenced in a logical and coherent structure, if there is an appropriate balance and emphasis in the treatment, and if the material appropriately meets the longer term needs of the students. The many ways to do this means there is a significant element of judgment in making this assessment. Nonetheless, it is likely that some curricula do a better job than others, so distinctions must be drawn.
In developing a method to determine these factors, many content analyses found that determining comprehensiveness can be difficult if curricular programs offer too many disjointed and overlapping topics. This finding motivated a call for the clarity of objectives or the identification of the
major conceptual ideas (Milgram testimony; Schifter testimony). With a clear specification of objectives, a reviewer can search for missing or superfluous content. A common weakness among content analyses, for example, was failure to check for comprehensiveness. In mathematics, comprehensiveness is particularly important, as missing material can lead to an inability to function downstream. In a content analysis of the Connected Math Program, Milgram (2003) wrote:
Overall, the program seems to be very incomplete, and I would judge that it is aimed at underachieving students rather than normal or higher achieving students…. The philosophy used throughout the program is that students construct their own knowledge and that calculators are to always be available for calculation.
This means that
-
standard algorithms are not introduced, not even for adding, subtracting, multiplying, and dividing fractions
-
precise definitions are never given
-
repetitive practice for developing skills, such as basic manipulative skills, is never given
Likewise, Adams et al. (2000, p. 14), critiqued Mathematics in Context on similar dimensions:
Our central criticism of Mathematics in Context curriculum concerns its failure to meet elements of the 2000 NCTM number strands. Because MiC is so fixated on conceptual underpinnings, computational methods and efficiency are slighted. Formal algorithms for, say, dividing fractions are neither taught nor discovered by the students. The students are presented with the simplest numerical problems, and the harder calculations are performed using calculators. Students would come out of the curriculum very calculator-dependent…. To us, this represents a radical change for the old “drill-and-kill” curricula, in which calculation was over-emphasized. The pendulum has, apparently, swung to the other side, and we feel a return to some middle ground emphasizing both conceptual knowledge and computational efficiency is warranted.
As an example of the positive impact of content analyses, the authors have indicated that in response to criticisms and the changes advised by PSSM, plans are being made to strengthen these dimensions in subsequent versions (Adams et al., 2000).
Accuracy was selected as one of our primary criteria because all consumers of mathematics curricula expect and demand it. The elimination of errors is of critical importance in mathematics (Wu testimony at the Sep-
tember 2002 Workshop). Some content analyses claimed that materials had too many errors (Braams, 2003a). Virtually no one disputes that curricular materials should be free from errors; all authors and publishers indicated that errors should be quickly corrected, especially in subsequent versions. It appears that not all content analyses paid appropriate attention to the accuracy issue. For example, Richard Askey, University of Wisconsin, in commenting on the Department of Education reviews to the committee during his September 17, 2002, testimony, pointed out that “In these 48 reviews, no mention of any mathematical errors was made. While a program could be promising and maybe even exemplary and contain a significant number of mathematical errors, the fact that no errors were mentioned strongly suggests that these reviews were superficial at best.”
It surfaced over time that some of the debate over the quality of the materials focused on the relative importance of different types of mathematical activity. To assist in deliberations, we chose to stipulate a distinction between mathematical inquiry and mathematical reasoning. Mathematical inquiry, as used in the report, refers to the elements of intuition necessary to create insight into the genesis and evolution of mathematical ideas, to make conjectures, to identify and develop mathematical patterns, and to conduct and study simulations. Mathematical reasoning refers to formalization, definition, and proof, often based on deductive reasoning, formal use of induction, and other methods of establishing the correctness, rigor, and precise meaning of ideas and patterns found through mathematical inquiry. Both are viewed as essential elements of mathematical thought, and often interact. Making too strong a distinction between these two elements is artificial.
Frequent debates revolve around the balance between mathematical inquiry and mathematical reasoning. For example, when content material has weak or poor explanations, does not establish or is not based on appropriate prerequisites, or fails to be developed to a high level of rigor or lacks practice in effective choices of examples, issues of mathematical reasoning are often cited as missing. At the same time, rather than focusing solely on the treatment of a particular topic at one particular point in the material, it is essential to follow the entire trajectory of conceptual development of an idea, beginning with inquiry activities, and ensuring that the subsequent necessary formalization and mathematical reasoning are provided. Moreover, one must determine in a content analysis whether a balance between the two is achieved so that the material both invites students’ entry and exploration of the origin and evolution of the ideas and builds intuition, and ensures their development of disciplined forms of evidence and proof.
To illustrate this tension and the need for careful communication and exchange around these issues, we report here two viewpoints, one pre-
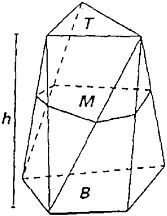
FIGURE 4-1 Prismoidal figure.
SOURCE: Contemporary Mathematics in Context: A Unified Approach (Core-Plus), Course 2, Part A, p. 137.
sented orally to the committee at one of the workshops and the other subsequently sent to the committee. Richard Askey (University of Wisconsin), who has examined curricular adequacy, responded at the Workshop to our question as to whether the program’s content reflects the nature of the field and the thinking that mathematicians use. He discussed the importance of careful examination of content for errors and inadequate attention to rigor and adequacy, focusing on Core-Plus curriculum’s treatment of formula for the volume of a number of common three-dimensional shapes. In Core-Plus, 9th-grade students are introduced to a table of values that represent the volume of water contained in a set of shapes (including a square pyramid, a triangular pyramid, a cylinder, and a cone) as the height increases from 0 to 20 cm. Using the data and a calculator, the students fit a line to produce the inductive observation that the volume of a cone is approximately one-third the volume of a cylinder with identical height and base. Askey’s stated objection was “The geometric reasoning for the factor of 1/3 [is] never mentioned in Core-Plus.”
A follow-up discussion of volume is presented on the next page, where the authors provide a formula for a prismoidal 3-D figure (Figure 4-1). To calculate its volume, a formula is given:
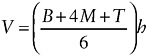
In the formula, B is the area of the cross-section at the base, M is the area of the cross-section at the “middle,” T is the area of the cross-section at the top, and h is the height of the space shape.
The authors of Core-Plus informally explain this formula as a form of a weighted average, then use it to derive the formula for the particular cases of a triangular prism, a cylinder, a sphere, and a cone. They end with problems asking students to estimate volumes of vases or bottles.
Askey’s objections were stated as:
A few pages later, a result which was standard in high school geometry books of 100 years ago and of some as late as 1957 (with correct proofs) is partially stated, but no definition is given for the figures the result applies to, nothing is written about why the result is true, and it is applied to a sphere. The correct volume of sphere is found by applying this formula, but the reason for this is not that the formula as stated applies to a sphere, but because the formula is exact for any figure where the cross-sectional area is a quadratic function of the height, which is the case for a sphere as well as the figures which should have been defined in the statement of the prismoidal formula. To really see that the use of this formula for a sphere is wrong, consider the two-dimensional case. The corresponding formula is a formula for the area of a trapezoid, and one does not get the right formula for the area of a circle by applying a formula for the area of a trapezoid, unless one uses an integral formula for area. The prismoidal formula is just Simpson’s rule applied to an integral. The idea that you can apply formulas at will is not how mathematicians think about mathematics.
The committee received a letter in response to Askey’s assertions from Eric Robinson (Department of Mathematics, Ithaca College), who wrote:
One panelist used two examples for the Core-Plus curriculum in his presentation to suggest a general lack of reasoning in the curricula. These examples had other intents. The criticism in the first example has to do with the lack of geometric derivations of the factor of 1/3 in the formula for the volume of a cone…. In Core-Plus, when students explore examples, they collect “data.” They have studied some of the statistics strand earlier in the curriculum, where, among other things, they look for patterns in data. Here, and in other places in the curriculum, there is a nice tie between the idea of statistical prediction and conjecture. Students would understand the difference between a conjecture and a result that was certain. They wouldn’t interpret it as being “able to do anything they want”. The intent here is to tie together some ideas the students have been studying; patterns in data, linear models and volume. It is also intended to suggest a geometric interpretation of the coefficient of x in the symbolic representation of the linear model. It is not intended to be derivation of formulas for any of the solids mentioned…. The second example mentions references on the prismoidal formula. The intent of that particular
exercise is to see if students can translate information from a visual setting to a symbolic expression. The intent, here, is not the derivation of the cone or prismoidal formulas. Intent matters.
These differing views about content provide a valuable window into the challenges associated with the evaluation of content analyses. In the committee’s view, Askey seeks to have more attention paid to issues of mathematical reasoning and abstraction: formal introduction, complete specification of restriction of formula application, and proof. Robinson values mathematical inquiry: conjecturing based on data, the development of visual reasoning, statistical prediction, and successive thematic approaches to strengthen intuition. Robinson further argues against isolated review of the treatment of topics because “students are continually asked to provide justification, explanation, and evidence, etc., in various ways that focus on obtaining insight needed to answer a question or solve a problem. Student justification increases in rigor as students ascend through the grades.”
The example illustrates that content analysts can reasonably have different views about the optimal balance of mathematical reasoning and inquiry, and the debates over content have mathematically and pedagogically sophisticated arguments on both sides. We encourage discussions in line with the differing Askey and Robinson views, at the level of particular example and with careful and explicit articulation of reason and logic. More precise methodological distinctions can be useful in facilitating such exchanges.
Examining the organization of material is another part of content analysis. For some, an analysis of the logical progression of concept development determines the sequence of activities, usually in the form of a Gagne-type hierarchical structure (Gagne, 1985). In reviewing Saxon’s Math 65 treatment of multiplication of fractions, Klein (2000) illustrates what is called an “incremental approach”:
Multiplication of fractions is explained in the Math 65 text using fraction manipulatives. Pictures in the text, beginning on page 324, help to motivate the procedure for multiplying fractions. This approach is perhaps not as effective as the area model used by Sadlier’s text, however, it leads in a natural way to an intuitive understanding of division by fractions, at least for simple examples. On page 402 of the Math 65 text, the notion of reciprocals is introduced in a clear, coherent fashion. In the following section, fraction division is explained using the ideas of reciprocals as follows. On page 404, the fraction division example of 1/2 divided by 2/3 is given. This is at first interpreted to mean, “How many 2/3’s are in 1/2?” The text immediately acknowledges that the answer is less than 1, so the question needs to be changed to “How much of 2/3 is in 1/2?” This question is supported by a helpful picture. The text then reminds the
students of reciprocals and reduces the problem to a simpler one. The question posed is, “How many 2/3’s are in 1?” This question is answered and identified as the reciprocal, 3/2. The text returns to the original question of 1/2 divided by 2/3. It then argues that the answer should be 1/2 times the answer to 1 divided by 2/3. The development proceeds along similar well-supported arguments from this point. Although this treatment of fraction division is clearer than what one finds in most texts, it would be improved with further elaboration on the problem 1 divided by 2/3. Here, the inverse relationship between multiplication and division could be invoked with great advantage. 1 divided by 2/3 = 3/2 because 3/2 × 2/3 = 1.
Some curricula use a spiral or thematic approach, which involves the weaving of content strands throughout the material with increased levels of sophistication and rigor. In the Department of Education review (1999), Everyday Math was commended for its depth of understanding when a reviewer wrote, “Mathematics concepts are visited several times before they are formally taught…. This procedure gives students a better understanding of concepts being learned and takes into consideration that students possess different learning styles and abilities” (criterion 2, indicator b). In contrast, Braams (2003b) reviewed the same materials and wrote, “The Everyday Mathematics philosophical statement quoted earlier describes the rapid spiraling as a way to avoid student anxiety, in effect because it does not matter if students don’t understand things the first time around. It strikes me as a very strange philosophy, and seeing it in practice does not make it any more attractive or convincing.” We know of no empirical studies that shed light on the differences in these assertions of preference.
Finally, the issue of balance referred to the relative emphasis among choices of approaches used to attain comprehensiveness, accuracy, depth of mathematical inquiry and reasoning, and organization. Curricula are enacted in real time, and international comparisons show that American textbooks are notoriously long, providing the appearance of the ability to cover more content than is feasible (Schmidt et al., 1996). In real time, curricular choices must be made and curricular materials reflect those choices, either as written or as enacted. In reference to mathematics curricula, decisions on balance include: conceptual versus procedural, activities versus practice, applications versus exercises, and balance among selected representations such as the use of numerical data and tables, graphs, and equations.
The level of use and reliance on technology is another consideration of balance, and many content analyses comment directly on this. Analyses of curricular use of technologies fell into two categories: the use of calculators in relation to computations and the use of technologies for modeling and simulation activities, typically surrounding data use.
For some reviewers, the use of calculators is questioned for its effects on computational fluency. In summarizing their reviews of the algebra materials, Clopton et al. (1998) wrote:
In general, the material in the bulk of the lessons would receive moderately high marks for presentation and student work, but many of the activities and the heavy use of calculators lead to serious concerns and a lowering of both presentation and student work subscores. In general, but not always, nearly every one of the books in this category would be improved substantially with removal of most discovery lessons and the over use of calculators.
In the review of UCSMP, the statement was made, “The use of technology does not generally interfere with learning, and there is a decided emphasis on the analytic approach” (Clopton et al., 1998).
Other reviewers value the use of technologies as a positive asset in a curriculum and make finer distinctions about appropriate uses. It is valuable to consider whether certain kinds of problems and topics would be eliminated from a curriculum without the use and access to appropriate technology, such as problems using large or complex databases. For example, although AAAS reviews (1999a) do not have a criteria addressing technology in isolation, they include it in a category referred to as “Providing Firsthand Experiences.” In reviewing the Systemic Initiative for Montana Mathematics and Science (SIMMS) Integrated Mathematics: A Modeling Approach Using Technology materials, they write, “Activities include graphing tabular data, creating spreadsheets and graphs, collecting data using calculators, and comparing and predicting values of such things as congressional seat apportionment and nutritional values. Although the efficiency of doing some activities depends heavily on the teachers’ comfort level with the technology, these firsthand experiences are efficient when compared to others that could be used.” A discussion of the balance of the use of technology is a useful way for a reviewer to indicate his or her stance on the appropriate place of technology in the curriculum. In content analyses, we indicated that rather than making statements that indicated either complete rejection or unbridled acceptance of technological use, a more useful approach is to more clearly identify effects on particular mathematical ideas in terms of gains and losses. A fuller discussion of a range of technology beyond calculators should be included in content analyses.
Another issue of organization is determining how much direct and explicit instructional guidance to include in the text. Discovery-oriented or student-centered materials may choose to include less explicit content development in text, and rely more heavily on the tasks to convey the concepts. Although this provides the opportunity for student activity, it relies more heavily on the teachers’ knowledge. In this sense, curriculum materials may vary between serving as a reference manual and a work or activity
book. Perhaps it would resolve many of these disputes if both types of curricular resources were distinctively provided to schools as different types of resources.
As an example of debates on issues of balance, Adams et al. (2000, p. 12) wrote:
CMP admits that “because the curriculum does not emphasize arithmetic computations done by hand, some CMP students may not do as well on parts of the standardized tests assessing computational skills as students in classes that spend most of their time on practicing such skills. This statement implies we have still not achieved a balance between teaching fundamental ideas and computational methods.”
Earlier in the paragraph, the authors established their position on the issue, writing, “In our opinion, concepts and computations often positively reinforce one another.”
Likewise, Adams et al. (2000, p. 9) critiqued the Singapore materials for their lack of emphasis on higher order thinking skills, writing:
While the mathematics in Singapore’s curriculum may be considered rigorous, we noticed that it does not often engage students in higher order thinking skills. When we examine the types of tasks that the Singapore curriculum asks students to do, we see that Singapore’s students are rarely, if ever, asked to analyze, reflect, critique, develop, synthesize, or explain. The vast majority of the student tasks in the Singapore curriculum is based on computation, which primarily reinforces only the recall of facts and procedures. This bias towards certain modes of thinking may be appropriate for an environment in which students’ careers depend on the results of a standardized test, but we feel it discourages students from becoming independent learners.
It is possible that at its crux, the debate involves the question of whether higher level skills are best achieved by the careful sequence and accumulation of prerequisite skills or by an early and carefully ordered sequence of cognitive challenges at an appropriate level followed by increasing levels of formalization. Empirical study is needed to address this question. Adjustments in balance may be a long-term outcome of a more carefully articulated set of methods for content analysis.
In summary, the first dimension of content analysis is derived fairly directly from one’s knowledge of and perspective on the discipline of mathematics. There is no single view of coherence of mathematics as illustrated by the variations among the examples presented. For some, mathematics curricula derive their coherence from their connection to a set of concepts ordered and sequenced logically, carefully scripted to draw on students’ prior knowledge and prepare them for future study, with extensive examples for practice. For others, the coherence is derived from links to
applications, opportunities for conjecture, and subsequent developmental progress toward rigor in problem solving and proof, increasing formalization and providing fewer, but more elaborate, examples.
Dimension Two: Engagement, Timeliness and Support for Diversity, and Assessment
A review of the content analyses reveals very different views of the learner and his/her needs. Clearly, all reviewers claim that their approach best serves the needs of the students, but differences in how this is evaluated emerge among content analyses.
The first criterion we categorized in this dimension is student engagement. It was selected to capture a variety of aspects of attention to students’ participation in the learning process that may vary because of considerations of prior knowledge, interests, curiosity, compelling misconceptions, alternative perspectives, or motivation. There is a solid research base on many of these issues, and content analysts should establish how they have made use of these data.
The reviews by AAAS provide the strongest examples of using criteria focused on the reviewer’s assessment of levels and types of student participation. They analyze the material in terms of its success in providing students with an interesting and compelling purpose, specifying prerequisite knowledge, alerting teachers to student ideas and misconceptions, including a variety of contexts, and providing firsthand experiences. For example, for the Mathematics: Modeling Our World (ARISE) materials, their review states:
For the three idea sets addressed in the materials [as specified by their methodology], there are an appropriate variety of experiences with objects, applications, and materials that are right on target with the mathematical ideas. They include many tables and graphs, both in the readings and in the exercises; real-world data and content; interesting situations; games; physical activity; and spreadsheets and graphing calculators. Each unit begins with a short video segment and accompanying questions for student response, designed to introduce the unit and provide a context for the mathematics. (Section III.1 Providing Variety of Contexts (2.5)—http://www.project2061.org/tools/textbook/algebra/Mathmode/instrsum/COM_ia3.htm)
For the same materials, the reviewers wrote the following concerning their explicit attention to misconceptions:
For the Functions Idea Set, the material explicitly addresses commonly held ideas. There are questions, tasks, and activities that are likely to help students progress from their initial ideas by extending correct commonly held ideas that have limited scope…. There is no evidence of this kind of
support being provided for the other two idea sets. Although there are some questions and activities related to the Operations Idea Set that are likely to help students progress from initial ideas, students are not asked to compare commonly held ideas with the correct concept. (Section II.4 Addressing Misconceptions (0.8)–http://www.project2061.org/tools/textbook/algebra/Mathmode/instrsum/COM_ia2.htm)
For Saxon, for the same two questions, the AAAS authors wrote:
The experiences provided are mainly pencil and paper activities. The material uses a few different contexts such as calculators and fraction pieces, and in grade six there are three lessons using fraction manipulatives. In grade seven, students put together a flexible model and later work with paper and pencil measurements. A lesson in grade seven on volume of rectangular solids uses a variety of drawings and equations that are right on target with the benchmark, but there is no suggestion that the students actually use sugar cubes, as referenced to build a figure. For the algebra graphs and algebra equation concepts, no variety of contexts is offered. Most firsthand experiences are found in the supplementary materials where students are given a few opportunities to do measurements, work with paper models of figures, collect data, and construct graphs. (Instructional Category III, Engaging Students in Mathematics—http://www.project2061.org/tools/textbook/matheval/13saxon/instruct.htm)
In relation to building on student ideas about mathematics, the same authors wrote:
While there is an occasional reference to prerequisite knowledge, the references are neither consistent nor explicit. In the instances where prerequisite knowledge is identified, the reference is made in the opening narrative that mentions skills that are taught in earlier lessons. The lessons often begin a new skill or procedure without reference to earlier work. There are warm-up activities at the beginning of lessons that provide practice for upcoming skills, but they are not identified as such. There is no guidance for teachers in identifying or addressing student difficulties. (Instructional Category II, Building on Student Ideas about Mathematics—http://www.project2061.org/tools/textbook/matheval/13saxon/instruct.htm)
The next set of passages demonstrates that not all reviewers see the most important source of student engagement as being through the use of context or building on prior knowledge, but rather by the careful choice of student example, sequencing of topic, and adequate and incremental challenge. An example of a content analysis with this focus was found in the reviews of UCSMP by Clopton et al. (1998). The two relevant criteria for review were “the quality and sufficiency of student work” and “range of depth and scope in student work.” Summarizing these two criteria under the subtitle of exercises, they wrote:
The number of student exercises is very low, and this is the most blatant negative feature of this text. These exercises are most typically at basic achievement levels with a few moderately difficult problems presented in some instances. For example, the section on solving linear systems by substitution includes six symbolic problems giving very simple systems and three word problems giving very simple systems. The actual number of problems to be solved is less than it appears to be as many of the exercise items are procedure questions. The extent, range, and scope of student work is low enough to cause serious concerns about the consolidation of learning. (Section 3: Overall Evaluation—exercises–http://mathematicallycorrect.com/a1ucsmp.htm)
One can see very different views of engagement in these varied comments, and hence, one would expect varied ratings based on one’s meaning for the term.
A persistent criticism found in certain content analyses, but not in others, involves their timeliness and support for diversity. We interpret this criterion to apply to meeting the needs of all students, in terms of the level of preparation (high, medium, and low), the diverse perspectives, the cultural resources and backgrounds of students, and the timeliness of the pace of instruction.
As one illustration of the issues subsumed in this criterion, material may be presented so late in the school program that it could jeopardize options for those students going to college or planning a technically oriented career. To support Askey’s remark that a “content analysis should consider the structure of the program, whether essential topics have been taught in a timely way,” in testimony to the committee, he provided an example where the tardiness in presentation could affect college options. “For Core-Plus, I illustrated how this has not been done by remarking that (a+b)2 = a2 + 2ab + b2 is only done in grade 11. This is far too late, for students need time to develop algebra skills, and plenty of problems using algebra to develop the needed skills.” Christian Hirsch, Western Michigan University and author of Core-Plus, responded in written testimony, “the topic is treated in CPMP Course 3, pages 212-214 for the beginning of the expansion/factorization development,” and that “students study Course 3 in grade 11 or grade 10, if accelerated.” Yet including timeliness raises the legitimate issue of whether such a delay in learning this material could put students at a disadvantage when compared with the growing number of students entering college with Advanced Placement calculus and more advanced training in mathematics.
Although absent from some studies, this timeliness theme is consistent through those content analyses that focused on the challenge of the mathematics. To illustrate how this issue can be studied in a content analysis, Adams and colleagues (2000, p. 11) point out, “we find that CMP students are not expected to compute fluently, flexibly and efficiently with fractions,
decimals, and percents as late as eighth grade. Standard algorithms for computations with fractions…. are often not used…. [While] CMP does a good job of helping students discover the mathematical connections and patterns in the algebra strand, [it] falls short in a follow-through with more substantial statements, generalizations, formulas, or algorithms.” In an 8th-grade unit, “CMP misses the opportunity to discuss the quadratic formula or the process of completing the square.”
Other examples (AAAS, 1999b, Part 1 Conclusions [in box]—http://www.project2061.org/matheval/part1c.htm; Adams et al., 2000, p. 12) could be offered, but the critique permits one to see why the issue of balance is crucial in content analyses, as one examines whether emphasis on discovery approaches and new levels of understanding can carry the cost of a lack of basic knowledge of facts and standard mathematical algorithms at an early age. In addition to timeliness for all students, in many content analyses, there is expressed concern for the most mathematically inclined students to receive enough challenges. For example, Adams et al. (2000, p. 13) wrote that in Mathematics in Context:
Alongside each lesson are comments about the underlying mathematical concepts in the lesson (“About the Mathematics”) as well as how to plan and to actually teach the lesson. A nice feature is that these comments occur in the margins of the Teachers’ Guides…. On the other hand, these comments often contain some useful mathematical facts and language that could be, but most likely wouldn’t be, communicated to the students; in particular high-end students could benefit from these insights if they were available to them. In addition, the lack of a glossary hides mathematical terminology from the students, a language which they should be beginning to negotiate by the middle grades. Exposure to the precise terminology of mathematics is crucial for students at this stage, not only as a means of exemplifying the rigor of mathematics, but as a way to communicate their discoveries and hypotheses in a common language, rather than the idiosyncratic terms that a particular student or class may develop.
As a result of comments such as these, the authors summarize by stating, “high-end students may not find this curriculum very challenging or stimulating” (p. 14).
In the content analyses, support for diversity was typically addressed only in terms of performance levels, and even then, high performers were identified as needing the most attention (Howe testimony). In contrast, other researchers focused on the importance of providing activities that can be used successfully to meet the needs of a variety of student levels of preparation, scaffolding those needing more assistance and including extensions for those ready for more challenge (Schifter testimony). Furthermore, there are other aspects of support for diversity to be considered, such as language use or cultural experiences. More attention in these content analy-
ses must be paid to whether the curriculum serves the diverse needs of students of all ability levels, all language backgrounds, and all cultural roots. Most of the analyses remained at the level of attention to the use of names or pictures portraying occupations by race and gender (AAAS, 1999b; Adams et al., 2000; U.S. Department of Education, 1999). The cognitive dimensions of these students’ needs, including remediation, support for reading difficulties, and frequent assessment and review, are less clearly discussed.
Support for diversity in content analyses represents the biggest challenge of all. Scientific approaches have relied mostly on our limited understanding of individual learning and age-dependent cognitive processes. Moreover, efforts to understand these processes have focused at the level of the individual (the “immunology” of learning), while the impact of population forces (i.e., that is, the extrapolation of individual processes at a higher level) on learning is poorly understood (girls, as a group, in 7th and 8th grades are inadequately encouraged to excel in mathematics). Population-level processes can enhance or inhibit learning. These processes may be the biggest obstacle to learning, and curriculum implementations that do not address these forces may fail regardless of the quality discipline-based dimensions of the content analysis, hence the need for learner- and teacher-based dimensions in our framework. The grand challenge is that models that rely solely on traditional scientific approaches may not be successful if the goal is to promote learning in a highly heterogeneous (at many levels) society. Innovative scientific approaches that attend to the big picture and the impact of nonlinear effects at all levels must be adopted.
Within the second dimension (Engagement, Timeliness and Support for Diversity, and Assessment), the final criterion concerns how one determines what students know, or assessment. An essential part of examining a curriculum in relation to its effects on students is to examine the various means of assessment. Examining these effects often reveals a great deal about the underlying philosophy of the program.
The quality of attention to assessment in these content analyses is generally weak. In the Mathematically Correct Reviews (Clopton et al., 1998, 1999a, 1999b, and 1999c), assessment is referred to only in terms of “support for student mastery.” In the Adams report, which was quite strong in most respects, only two questions are discussed: Does the curriculum include and encourage multiple kinds of assessments (e.g., performance, formative, summative, paper-pencil, observations, portfolios, journals, student interviews, projects)? Does the curriculum provide well-aligned summative assessments to judge a student’s attainment? The responses were cursory, such as “This principle is fully met. Well-aligned summative assessments are given at the end of each unit for the teacher’s use.” The exception to this was found in AAAS’s content analyses, where three differ-
ent components of assessment are reviewed: Are the assessments aligned to the ideas, concepts, and skills of the benchmark? Do they include assessment through applications and not just require repeating memorized terms or rules? Do they use embedded assessments, with advice to teachers on how they might use the results to choose or modify activity? The write-ups for each curriculum show that the reviewers were able to identify important distinctions among curricula along this dimension. For example, in reviewing the assessment practices for each of these three questions concerning the Interactive Mathematics Program (IMP), the reviewers wrote:
There is at least one assessment item or task that addresses the specific ideas in each of the idea sets, and these items and tasks require no other, more sophisticated ideas. For some idea sets, there are insufficient items that are content-matched to the mathematical ideas…. (Section VI.1: Aligning Assessment (2.3)—http://www.project2061.org/tools/textbook/algebra/Interact/instrsum/IMP_ia6.htm)
All assessment tasks in this material require application of knowledge and/or skills, although ideally would include more applications assessments throughout, and more substantial tasks within these assessments…. Assessment tasks alter either the context or the degree of specificity or generalization required, as compared to similar types of problems in class work and homework exercises.
The material uses embedded assessment as a part of the instructional strategy and design…. The authors make a clear distinction between assessment and grading, indicating that assessment occurs throughout each day as teachers gauge the learning process…. In spite of all these options for embedded assessment throughout the material, there are few assessments that provide opportunities, encouragement, or guidance for students on how to further understand the mathematical ideas.
AAAS reviews include one additional criterion that is essential to discussions of assessment. It is referred to as “Encouraging students to think about what they have learned” (AAAS, 1999a). The summary of the reviews for IMP is provided to assist in understanding how this criterion adds to one’s understanding of the curricular program and suggest places for improvement.
The material engages students in monitoring their progress toward understanding the mathematical ideas, and only does so primarily through the compilation of a portfolio at the end of each unit…. Personal growth is a part of each portfolio as students are encouraged to think about their personal development and how their ideas have developed or changed throughout the unit. However, these reflections are generally very generic, rather than specific to the idea sets. (V.3: Encouraging Students to Think about What They’ve Learned (1.6)—http://www.project2061.org/tools/textbook/algebra/Interact/instrsum/IMP_ia5.htm)
Dimension Three: Pedagogy, Resources, and Professional Development
A successful curriculum is impossible if it does not pay attention to the abilities and needs of teachers, and thus pedagogy must be a component in a content analysis. Bishop (1997) asserted that “Some elementary school teachers are ill prepared to teach mathematics, and very inexperienced teachers can seriously misjudge how to present the material appropriately to their classes.” This concern was often repeated in testimony that we heard from teachers, educators, and textbook publishers. Other researchers saw the curriculum as a vehicle to strengthen teachers’ content knowledge and design materials with this purpose in mind (Schifter testimony). The question that arises is how such concerns should affect the conduct of content analyses.
One issue is that such analyses should report on the expectations of the designers for professional development. It is clear that programs which introduce new approaches and new technologies will require more professional development for successful implementation. Testimony indicates that even for more traditional curricula, professional development is needed. Deeper understanding is possible only through added support; if stipulated, such requirements should be reported in content analyses. Expanding on this theme, Adams et al. (2000) offer a potential explanation for the poorer U.S. TIMSS performance by commenting that “we must acknowledge that Singapore’s educational system—the curriculum, the teachers, the parental support, the social culture, and the strong government support of education—has succeeded in producing students who as a whole understand mathematics at a higher level, and perform with more competence and fluency, than the American students who took the [TIMSS] tests.” On the other hand, “[s]imply adopting the middle-grades Singapore curriculum is not likely to help American students move to the top.” The issue is far more complex because it also involves teacher development. As the Adams report argued, “The most striking difference between the educational systems of [the United States and Singapore] is in governmental support of education. For example, the government encourages every teacher to attend at least 100 hours of training each year, and has developed an intranet called the ‘Teachers’ Network,’ which enables teachers to share ideas with one another” (Adams et al., 2000, p. A-3). Although this issue of teacher development is addressed in some of the content analyses, it is so crucial that it should be addressed in most of them.
The second criterion in this dimension concerns resources, and they, too, must be explicitly considered in content analyses. The Adams report described the important differences between Singapore and the United States in the kind of students being tested and the mathematical experiences they
bring to the classroom. As an illustration, the report described how Singapore students are filtered according to talent and how they receive enrichment programs. This information is critical to making an informed comparison, not only about the curriculum itself, but about the assumptions it makes about the environment in which it is to be used. It further helps one to assess the assumptions about resources for curricular use.
Conclusions
In reviewing the 36 content analyses, we determined that although a comprehensive methodology for the conduct of content analyses was lacking, elements were distributed among the submissions. We summarized the content analyses and reported the results when those results could be used inferentially to inform the subsequent conduct of content analyses. We recognized that no amount of delineation of method would produce identical evaluations, but suggested rather that delineation of dimensions for review might help to make content analysis evaluations more informative to curriculum decision makers. Toward this end, we recognized the importance of involvement by mathematicians and mathematics educators in the process, and called for increased participation by practitioners. We discussed the need for careful and thoughtful choices on the standards to be used and the selection of comparative curricula. We acknowledged that some content analysts would focus on the materials a priori, and others would prefer to conduct analysis based on curricular use in situ.
We identified three dimensions along which curricular evaluations of content should be focused:
-
Clarity, comprehensiveness, accuracy, depth of mathematical inquiry and mathematical reasoning, organization, and balance (disciplinary perspectives).
-
Engagement, timeliness and support for diversity, and assessment (learner-oriented perspectives).
-
Pedagogy, resources, and professional development (teacher- and resource-oriented perspectives).
In addition, we recognized that each of these dimensions can be treated differently depending on a reviewer’s perspectives of the discipline, the student, and the resources and capacity in schools. A quality content analysis would present a coherent and integrated view of the relationship among these dimensions (Box 4-3).
Differences in content analyses are inevitable and welcome, as they can contribute to providing decision makers with choices among curricula. However, those differences need to be interpreted in relation to an under-
|
BOX 4-3
|
lying set of dimensions for comparison. Therefore, we have provided an articulation of the underlying dimensions that could lead to a kind of consumer’s guide to assist the readers of multiple sources of content analysis. One would expect that just as one develops preferences in reviewers (whether they are reviewing books, wine, works of art, or movies), one will select one’s advisers on the basis of preferences and preferred expertise and perspectives. Second, with a more explicit discussion of methodology, reviewers with divergent perspectives may find more effective means of identifying and discussing differences. This might involve the use of panels of reviewers in discussion of particular examples with contrasting perspectives.
In these content analyses—over time and particularly in the solicited letters—we see evidence that the polarization that characterizes the mathematics education communities (mathematicians, mathematics educators, teachers, parents) could be partially reconciled by more mutual acknowledgment of the legitimacy of diverse perspectives and the shared practical need to serve children better. It is possible, for example, that based on critical content analyses, subsequent versions of reform curricula could be revised to strengthen weak or incomplete areas, traditional curricular materials could be revised to provide more uses of innovative methods, and new hybrids of the approaches could be developed.
At the same time, while the issue of content analysis is critical from philosophical, academic, and logical viewpoints, it is not clear what degree or type of impact current content changes have on student learning and
achievement when curricula are implemented in classrooms. Learning is taking place in a complex dynamical system, and one should consider whether the correction of current curricular deficiencies, a process that obviously must be carried out, is the key pressure point for changing the educational system. Will curricular content changes by themselves actually reduce the disparities in learning that have been documented in many studies? Answers to analogous questions exist in other fields. For example, although detailed understanding of the immunology of HIV (resulting in the development of a robust vaccine) may be the key in the long run, as of today, human behavior along with cultural practices and norms are the drivers (pressure points) of the HIV epidemic. Efforts to alter behavior and cultural practices and norms, at this point, are most likely to have immediate impact on HIV transmission dynamics. Furthermore, changes in the social landscape will have a beneficial impact on the transmission dynamics and control of many sexually transmitted diseases. Analogously, in examining curricular effectiveness the role of content analyses, while critical, is not the only pressure point in the system and may interact in fundamental ways with other pressure points. Therefore it is essential to consider methods and approaches that take into account the possible impact and implications of changing and evolving landscapes on a curriculum’s implementation and effectiveness. The landscape shift illustrated in the 5-year longitudinal study by Carroll (2001) of Everyday Mathematics highlights some of these challenges. The next two chapters, on comparative studies and case studies, add indirect consideration of other influences on the curricular effectiveness.
Nonetheless, as we transition to these, we emphasize the importance of content analysis in relation to comparative and case studies. For example, content analyses can offer insights into the designs of comparative analyses. A thorough content analysis provides a clear articulation of the program theory from one point of view. From a set of such reviews, researchers can identify contentious issues that merit further basic research. One could examine questions such as, Do clear, concise materials used as primary texts lead to stronger conceptual development than engaging, active challenges and tasks? or Does the introduction of formal definitions facilitate further and deeper understanding and mastery of new material? How and when does this work? Research is needed to determine whether analyses of the intended curricula are validated by the empirical outcomes of the enacted curricula. Content analyses are also valuable to inform the conduct of comparative studies. A content analysis can help an evaluator to select appropriate outcome measures, to measure particularly important content strands, and to concentrate on the essential aspects of implementation and professional development. For these multiple reasons, careful and increasingly sophisticated content analysis will make important contributions to the evaluation of the effectiveness of a curricular program.































