6
Achieving Intelligence
One of the great aspirations of computer science has been to understand and emulate capabilities that we recognize as expressive of intelligence in humans. Research has addressed tasks ranging from our sensory interactions with the world (vision, speech, locomotion) to the cognitive (analysis, game playing, problem solving). This quest to understand human intelligence in all its forms also stimulates research whose results propagate back into the rest of computer science—for example, lists, search, and machine learning.
Going beyond simply retrieving information, machine learning draws inferences from available data. Mitchell describes the application of classifying text documents automatically and shows how this research exemplifies the experiment-analyze-generalize style of experimental research.
One of the exemplars of intelligent behavior is natural-language processing in all its forms—including speech recognition and generation, natural-language understanding, and machine translation. Lee describes how, in the area of statistical natural-language understanding, the commitment to an empirical computational perspective draws meaning from data and brings interdisciplinary contributions together.
Games have frequently provided settings for exploring new computing techniques. They make excellent testbeds because they are usually circumscribed in scope, have well-defined rules, employ humanperformance standards for comparison, and are not on the critical path to
make-or-break projects. In addition, they are engaging and appealing, which makes it easy to recruit early users. Koller and Biermann examine the history of computer science endeavors in chess and checkers, showing how success depends both on “smarts” (improved representations and algorithms) and sheer computer power.
THE EXPERIMENT-ANALYZE-GENERALIZE LOOP IN COMPUTER SCIENCE RESEARCH: A CASE STUDY
Tom Mitchell, Carnegie Mellon University
Much research in computer science involves an iterative process of attacking some new application problem, developing a computer program to solve that specific problem, and then stepping back to learn a general principle or algorithm, along with a precise description of the general class of problems to which it can be applied. This experiment-analyze-generalize loop lies at the heart of experimental computer science research, and it is largely responsible for the continuous growth over several decades in our knowledge of robust, effective computer algorithms. Here we illustrate the approach with a case study involving machine-learning algorithms for automatically classifying text. In particular, we see how attempts to train a text classifier for classifying Web pages led to a fundamental insight into a new class of learning algorithms.
Automatically classifying text documents such as e-mails, Web pages, and online memos is a problem of obvious importance. It would clearly be useful for computers to automatically classify e-mails into categories such as “spam,” “meeting invitations,” and so on, or to automatically classify Web pages into categories such as “personal home page,” “product announcement,” and others. Computer scientists have studied the problem of automatic text classification for a number of years, over time developing increasingly effective algorithms that achieve higher classification accuracy and accommodate a broader range of text documents.
Machine Learning for Text Classification
One approach to developing text classification software involves machine learning. In most software development, programmers write detailed algorithms as line-by-line recipes to be executed by the computer. In contrast, machine learning involves training the software by instead showing it examples of inputs and outputs of the desired program. The computer then learns (estimates) the general input-output function from the examples provided. For instance, to train a program to classify Web pages into categories such as “personal home page” or “product description,” we would present a set of training examples consisting of individual Web pages (example inputs) and the correct classification for each (example outputs). The machine-learning system uses these training examples to produce a general program that achieves high accuracy on these examples, and presumably on novel future inputs as well. While it
is unrealistic to expect perfect classification accuracy over novel future examples, in fact these accuracies for many text classification problems are well above 90 percent, and are often higher than those that can be achieved by manual programming (because humans generally don’t know the general classification rule either!).
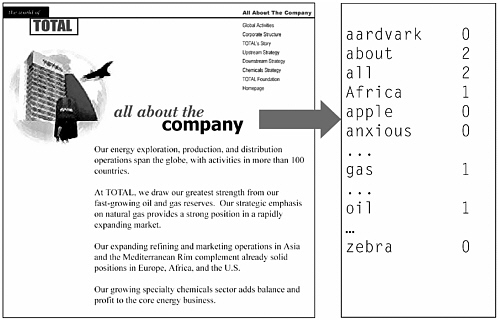
What kind of machine-learning approach can analyze such training examples to learn the correct classification rule? One popular machine learning approach is a Bayesian classifier employing a bag-of-words representation for Web pages. The bag-of-words representation, depicted in Figure 6.1, describes each text document by the frequency of occurrence of each word in the document. Although this representation removes information such as the exact sequence in which words occur, it has been found to be highly effective for document classification.
Once the training-example Web pages are described in terms of their word frequencies, the classifier can calculate from these training examples the average frequency for each word, within each different class of Web pages. A new document can then be automatically classified by first observing its own word frequencies and then assigning it to the class whose average frequencies are most similar to its own. The naive Bayes classifier uses this general approach. More precisely, it uses the training data to estimate the probability P(wi|cj) that a word drawn at random from a random document from class cj will be the word wi (e.g., P(“phone”|home page) is the probability that a random word found on a random home page will be the word “phone”). Thousands of such probability terms are estimated during training (i.e., if English contains approximately 105 words, and if we consider only two distinct classes of Web pages, then the program will estimate such 2 × 105 probabilities). These learned probabilities, along with the estimated class priors, are then used to classify a new document, d, by calculating the probability P(wi|d) that d belongs to the class cj based on its observed words. Figure 6.2 summarizes the training and classification procedures for the naive Bayes classifier (this type of Bayes classifier is called “nave” because it makes the assumption that words occur independently within documents of each class, and “Bayesian” because it uses Bayes rules along with the learned probability terms to classify new documents).
Improving Accuracy by Learning from Unlabeled Examples
Although the naive Bayes classifier can often achieve accuracies of 90 percent or higher when trained to discriminate classes of Web pages such as “personal home page” versus “academic course Web page,” it often requires many hundreds or thousands of training examples to reach this accuracy. Thus, the primary cost in developing the classifier involves
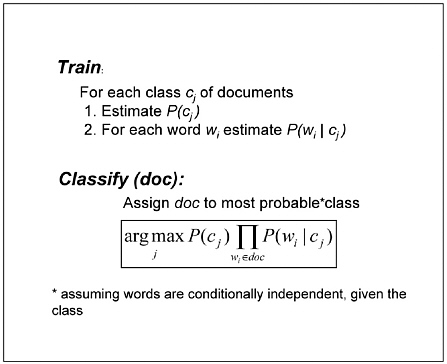
FIGURE 6.2 Naïve Bayes Learner based on the bag-of-words representation from Figure 6.1.
hand-labeling the training examples. This leads to the interesting question: Can we devise learning methods that achieve higher accuracy when given unlabeled examples (e.g., additional Web pages without their classification) in addition to a set of labeled examples? At first it may seem that the answer must be no, because providing unlabeled examples amounts to providing an example input to the program without providing the desired output. Surprisingly, if the text documents we wish to classify are Web pages, then we shall see that the answer is yes, due to a particular characteristic of Web pages.
The characteristic that makes it possible to benefit from unlabeled data when learning to classify Web pages is illustrated in Figure 6.3. Note first that Web pages typically appear on the Web along with hyperlinks that point to them. We can therefore think of each example Web page as being described by two sets of features: the words occurring within the page (which we will call X1) and the words occurring on hyperlinks that point to this page (which we will call X2). Furthermore, in many cases the X1 features alone are sufficient to classify the page without X2 (i.e., even
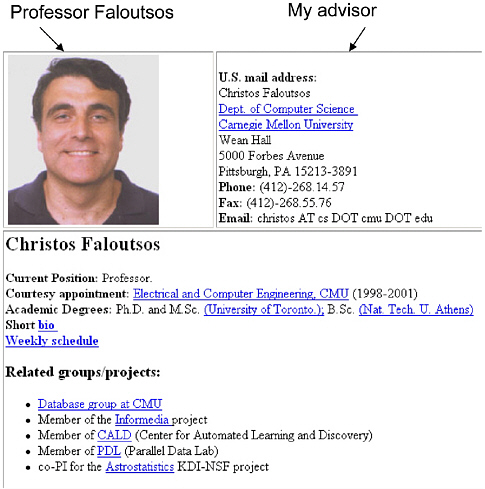
FIGURE 6.3 Redundantly sufficient features for classifying Web pages. Note that the class of this Web page (“faculty home page”) can be inferred from either (a) the words on the Web page or (b) the words on the hyperlinks that point to the page. In such cases we say that these two feature sets are “redundantly sufficient” to classify the example.
when ignoring the hyperlinks, it is obvious that the Web page of Figure 6.3 belongs to the class “faculty home page”). Similarly, the X2 features taken alone may also be sufficient to classify the page (i.e., if the hyperlink pointing to the page contains the words “Professor Faloutsos,” the page is most probably a “faculty home page”). In short, we say in this case that the features describing the example Web pages are redundantly sufficient
to perform the classification. Furthermore, notice that the hyperlink words tend to be quite independent of the exact words on the page, given the class of the page (in part because the hyperlinks and the pages to which they point are often written by different authors).
This characteristic of Web pages suggests the following training procedure for using a combination of labeled and unlabeled examples: First, we use the labeled training examples to train two different naive Bayes classifiers. One of these classifiers uses only the X1 features; the other uses only the X2 features. The first classifier is then applied to the unlabeled training examples, and it selects the example d that it is most confident in classifying (i.e., the example that yields the highest probability P(cj|d)). It is then allowed to assign that label to this previously unlabeled example, and the second classifier is now retrained using this new labeled example along with the original labeled examples. The identical process can be executed reversing the roles of the two classifiers, using each to train the other. This process is called co-training. Furthermore, the process can be repeated many times, each time assigning a few most-confident labels to the initially unlabeled examples.
Does this learning algorithm work in practice? It does. Blum and Mitchell,1 for example, describe experiments using co-training to classify Web pages into the categories “academic course home page” or not. Starting with just 12 labeled Web pages, they found that co-training with an additional 788 unlabeled Web pages reduced the classification error rate by a factor of two, from 11 percent to 5 percent.
Analyze the Specific Solution to Generalize the Principle
Given the empirical success of this co-training algorithm for classifying Web pages, it is natural to ask: What is the general class of machine-learning problems for which unlabeled data can be proven to improve classification accuracy? Intuitively, the reason co-training works when learning to classify Web pages is that (1) the examples can be described by two different sets of features (hyperlink words, page words) that are redundantly sufficient, and (2) the two features are distributed somewhat independently, so that an example with an easy-to-classify hyperlink is likely to point to a Web page of average classification difficulty. We can
therefore train two classifiers, using each to produce new, high-confidence labels for training the other.
Blum and Mitchell make this intuitive characterization more precise and formal.2 They prove that for the class of learning problems they define, one can learn successfully from a small set of labeled examples and a larger volume of unlabeled examples. The essence of their characterization is as follows. In general, one can view the problem of learning a classifier as the problem of estimating some unknown classifier function f : X → Y given only a set of labeled input-output examples ![]() and a set of unlabeled examples {xi} with unknown output. The co-training problem setting can then be defined as a special case of learning a classifier, where (1) the input instances X can be described as X1 × X2 (i.e., X1 = hyperlink words, X2 = Web page words), and where (2) one can compute f based on either X1 or X2 (formally, there exist functions g1 and g2 such that f(x) = g1(x1) = g2(x2) for any x =
and a set of unlabeled examples {xi} with unknown output. The co-training problem setting can then be defined as a special case of learning a classifier, where (1) the input instances X can be described as X1 × X2 (i.e., X1 = hyperlink words, X2 = Web page words), and where (2) one can compute f based on either X1 or X2 (formally, there exist functions g1 and g2 such that f(x) = g1(x1) = g2(x2) for any x = ![]() x1,x2
x1,x2![]() . They then go on to characterize the impact of unlabeled data on learning behavior in several situations. For example, they show that if one makes the additional assumption that X1 and X2 are conditionally independent given the class Y, then any function that is learnable from noisy labeled data can also be learned from a small set of labeled data that produces better-than-random accuracy, plus unlabeled data.
. They then go on to characterize the impact of unlabeled data on learning behavior in several situations. For example, they show that if one makes the additional assumption that X1 and X2 are conditionally independent given the class Y, then any function that is learnable from noisy labeled data can also be learned from a small set of labeled data that produces better-than-random accuracy, plus unlabeled data.
Summary
This case study shows how the attempt to find more accurate learning algorithms for Web page classification motivated the development of a specialized algorithm, which in turn motivated a formal analysis to understand the precise class of problems for which the learning algorithm could be proven to succeed. In fact, the insights provided by this analysis have, in turn, led to the development of more accurate learning algorithms for this class of problems (e.g., Collins and Singer,3 and Muslea et al.4). Further-
more, it made it apparent that the co-training algorithm published by Blum and Mitchell was in fact similar to an earlier algorithm by Yarowski5 for learning to disambiguate word senses (e.g., learning whether “bank” refers to a financial institution, or a place near a river). In Yarowski’s case, the features X1 and X2 are the linguistic context in which the word occurs, and the document in which it occurs.
This case study illustrates the useful interplay between experiment and theory in advancing computer science. The advance in our understanding of the science of computation can be described in this case using statements of the form “for problems that exhibit structure S, algorithm A will exhibit property P.” In some cases we have only experimental evidence to support conjectures of this form, in some cases analytical proofs, but in many cases a blend of the two, and a family of related statements rather than a single one.
Of course the interplay between experiment and analysis is generally messy, and not quite as clean as post facto reports would like to make it appear! In many cases the formal models motivated by specific applications do not fully capture the complexities of the application. In our own case study, for instance, the assumption that hyperlink words can be used to classify the Web page they point to is not quite valid—some hyperlink words such as “click here” provide no information at all about the page they point to! Nevertheless, theoretical characterizations of the problem are useful even if incomplete and approximate, provided they capture a significant problem structure that impacts on the design and performance of algorithms. And the experiment-analyze-generalize cycle of research often leads to a second and third generation of experiments and of theoretical models that better characterize the application problems, just as current theoretical research on using unlabeled data is now considering problem formalizations that relax the assumption violated by the “click here” hyperlinks.
“I’M SORRY DAVE, I’M AFRAID I CAN’T DO THAT”: LINGUISTICS, STATISTICS, AND NATURAL-LANGUAGE PROCESSING CIRCA 2001
Lillian Lee, Cornell University
It’s the year 2000, but where are the flying cars? I was promised flying cars.
—Avery Brooks, IBM commercial
According to many pop-culture visions of the future, technology will eventually produce the Machine That Can Speak to Us. Examples range from the False Maria in Fritz Lang’s 1926 film Metropolis to Knight Rider’s KITT (a talking car) to Star Wars’ C-3PO (said to have been modeled on the False Maria). And, of course, there is the HAL 9000 computer from 2001: A Space Odyssey; in one of the film’s most famous scenes, the astronaut Dave asks HAL to open a pod bay door on the spacecraft, to which HAL responds, “I’m sorry Dave, I’m afraid I can’t do that.”
Natural-language processing, or NLP, is the field of computer science devoted to creating such machines—that is, enabling computers to use human languages both as input and as output. The area is quite broad, encompassing problems ranging from simultaneous multi-language translation to advanced search engine development to the design of computer interfaces capable of combining speech, diagrams, and other modalities simultaneously. A natural consequence of this wide range of inquiry is the integration of ideas from computer science with work from many other fields, including linguistics, which provides models of language; psychology, which provides models of cognitive processes; information theory, which provides models of communication; and mathematics and statistics, which provide tools for analyzing and acquiring such models.
The interaction of these ideas together with advances in machine learning (see Mitchell in this chapter) has resulted in concerted research activity in statistical natural-language processing: making computers language-enabled by having them acquire linguistic information directly from samples of language itself. In this essay, we describe the history of statistical NLP; the twists and turns of the story serve to highlight the sometimes complex interplay between computer science and other fields.
Although currently a major focus of research, the data-driven, computational approach to language processing was for some time held in deep disregard because it directly conflicts with another commonly held viewpoint: human language is so complex that language samples alone seemingly cannot yield enough information to understand it. Indeed, it is often said that NLP is “AI-complete” (a pun on NP-completeness; see
Kleinberg and Papadimitriou in Chapter 2), meaning that the most difficult problems in artificial intelligence manifest themselves in human language phenomena. This belief in language use as the touchstone of intelligent behavior dates back at least to the 1950 proposal of the Turing Test6 as a way to gauge whether machine intelligence has been achieved; as Turing wrote, “The question and answer method seems to be suitable for introducing almost any one of the fields of human endeavor that we wish to include.”
The reader might be somewhat surprised to hear that language understanding is so hard. After all, human children get the hang of it in a few years, word processing software now corrects (some of) our grammatical errors, and TV ads show us phones capable of effortless translation. One might therefore be led to believe that HAL is just around the corner.
Such is not the case, however. In order to appreciate this point, we temporarily divert from describing statistical NLP’s history—which touches upon Hamilton versus Madison, the sleeping habits of colorless green ideas, and what happens when one fires a linguist—to examine a few examples illustrating why understanding human language is such a difficult problem.
Ambiguity and Language Analysis
At last, a computer that understands you like your mother.
—1985 McDonnell-Douglas ad
The snippet quoted above indicates the early confidence at least one company had in the feasibility of getting computers to understand human language. But in fact, that very sentence is illustrative of the host of difficulties that arise in trying to analyze human utterances, and so, ironically, it is quite unlikely that the system being promoted would have been up to the task. A moment’s reflection reveals that the sentence admits at least three different interpretations:
-
The computer understands you as well as your mother understands you.
-
The computer understands that you like your mother.
-
The computer understands you as well as it understands your mother.
That is, the sentence is ambiguous; and yet we humans seem to instantaneously rule out all the alternatives except the first (and presumably the intended) one. We do so based on a great deal of background knowledge, including understanding what advertisements typically try to convince us of. How are we to get such information into a computer?
A number of other types of ambiguity are also lurking here. For example, consider the speech recognition problem: how can we distinguish between this utterance, when spoken, and “. . . a computer that understands your lie cured mother”? We also have a word sense ambiguity problem: how do we know that here “mother” means “a female parent,” rather than the Oxford English Dictionary-approved alternative of “a cask or vat used in vinegar-making”? Again, it is our broad knowledge about the world and the context of the remark that allows us humans to make these decisions easily.
Now, one might be tempted to think that all these ambiguities arise because our example sentence is highly unusual (although the ad writers probably did not set out to craft a strange sentence). Or, one might argue that these ambiguities are somehow artificial because the alternative interpretations are so unrealistic that an NLP system could easily filter them out. But ambiguities crop up in many situations. For example, in “Copy the local patient files to disk” (which seems like a perfectly plausible command to issue to a computer), is it the patients or the files that are local?7 Again, we need to know the specifics of the situation in order to decide. And in multilingual settings, extra ambiguities may arise. Here is a sequence of seven Japanese kanji characters:
Since Japanese doesn’t have spaces between words, one is faced with the initial task of deciding what the component words are. In particular, this character sequence corresponds to at least two possible word sequences, “president, both, business, general-manager” (= “a president as well as a general manager of business”) and “president, subsidiary-business, Tsutomu (a name), general-manager” (= ?). It requires a fair bit of linguistic information to choose the correct alternative.8
To sum up, we see that the NLP task is highly daunting, for to resolve the many ambiguities that arise in trying to analyze even a single sentence requires deep knowledge not just about language but also about the world. And so when HAL says, “I’m afraid I can’t do that,” NLP researchers are tempted to respond, “I’m afraid you might be right.”
Firth Things First
But before we assume that the only viable approach to NLP is a massive knowledge-engineering project, let us go back to the early approaches to the problem. In the 1940s and 1950s, one prominent trend in linguistics was explicitly empirical and in particular distributional, as exemplified by the work of Zellig Harris (who started the first linguistics program in the United States). The idea was that correlations (co-occurrences) found in language data are important sources of information, or, as the influential linguist J.R. Firth declared in 1957, “You shall know a word by the company it keeps.”
Such notions accord quite happily with ideas put forth by Claude Shannon in his landmark 1948 paper establishing the field of information theory; speaking from an engineering perspective, he identified the probability of a message’s being chosen from among several alternatives, rather than the message’s actual content, as its critical characteristic. Influenced by this work, Warren Weaver in 1949 proposed treating the problem of translating between languages as an application of cryptography (see Sudan in Chapter 7), with one language viewed as an encrypted form of another. And Alan Turing’s work on cracking German codes during World War II led to the development of the Good-Turing formula, an important tool for computing certain statistical properties of language.
In yet a third area, 1941 saw the statisticians Frederick Mosteller and Frederick Williams address the question of whether it was Alexander Hamilton or James Madison who wrote the various pseudonymous Federalist Papers. Unlike previous attempts, which were based on historical data and arguments, Mosteller and Williams used the patterns of word occurrences in the texts as evidence. This work led up to the famed Mosteller and Wallace statistical study that many consider to have settled the authorship of the disputed papers.
Thus, we see arising independently from a variety of fields the idea that language can be viewed from a data-driven, empirical perspective—and a data-driven perspective leads naturally to a computational perspective.
A “C” Change
However, data-driven approaches fell out of favor in the late 1950s. One of the commonly cited factors is a 1957 argument by linguist (and student of Harris) Noam Chomsky, who believed that language behavior should be analyzed at a much deeper level than its surface statistics. He claimed,
It is fair to assume that neither sentence (1) [Colorless green ideas sleep furiously] nor (2) [Furiously sleep ideas green colorless] . . . has ever occurred. . . . Hence, in any [computed] statistical model . . . these sentences will be ruled out on identical grounds as equally “remote” from English. Yet (1), though nonsensical, is grammatical, while (2) is not.9
That is, we humans know that sentence (1), which at least obeys (some) rules of grammar, is indeed more probable than (2), which is just word salad; but (the claim goes), since both sentences are so rare, they will have identical statistics—i.e., a frequency of zero—in any sample of English. Chomsky’s criticism is essentially that data-driven approaches will always suffer from a lack of data, and hence are doomed to failure.
This observation turned out to be remarkably prescient: even now, when billions of words of text are available online, perfectly reasonable phrases are not present. Thus, the so-called sparse data problem continues to be a serious challenge for statistical NLP even today. And so, the effect of Chomsky’s claim, together with some negative results for machine learning and a general lack of computing power at the time, was to cause researchers to turn away from empirical approaches and toward knowledge-based approaches where human experts encoded relevant information in computer-usable form.
This change in perspective led to several new lines of fundamental, interdisciplinary research. For example, Chomsky’s work viewing language as a formal, mathematically describable object has had a lasting impact on both linguistics and computer science; indeed, the Chomsky hierarchy, a sequence of increasingly more powerful classes of grammars, is a staple of the undergraduate computer science curriculum. Conversely, the highly influential work of, among others, Kazimierz Adjukiewicz, Joachim Lambek, David K. Lewis, and Richard Montague adopted the lambda calculus, a fundamental concept in the study of programming languages, to model the semantics of natural languages.
The Empiricists Strike Back
By the 1980s, the tide had begun to shift once again, in part because of the work done by the speech recognition group at IBM. These researchers, influenced by ideas from information theory, explored the power of probabilistic models of language combined with access to much more sophisticated algorithmic and data resources than had previously been available. In the realm of speech recognition, their ideas form the core of the design of modern systems; and given the recent successes of such software—large-vocabulary continuous-speech recognition programs are now available on the market—it behooves us to examine how these systems work.
Given some acoustic signal, which we denote by the variable a, we can think of the speech recognition problem as that of transcription: determining what sentence is most likely to have produced a. Probabilities arise because of the ever-present problem of ambiguity: as mentioned above, several word sequences, such as “your lie cured mother” versus “you like your mother,” can give rise to similar spoken output. Therefore, modern speech recognition systems incorporate information both about the acoustic signal and the language behind the signal. More specifically, they rephrase the problem as determining which sentence s maximizes the product P(a|s) × P(s). The first term measures how likely the acoustic signal would be if s were actually the sentence being uttered (again, we use probabilities because humans don’t pronounce words the same way all the time). The second term measures the probability of the sentence s itself; for example, as Chomsky noted, “colorless green ideas sleep furiously” is intuitively more likely to be uttered than the reversal of the phrase. It is in computing this second term, P(s), where statistical NLP techniques come into play, since accurate estimation of these sentence probabilities requires developing probabilistic models of language. These models are acquired by processing tens of millions of words or more. This is by no means a simple procedure; even linguistically naive models require the use of sophisticated computational and statistical techniques because of the sparse data problem foreseen by Chomsky. But using probabilistic models, large datasets, and powerful learning algorithms (both for P(s) and P(a|s)) has led to our achieving the milestone of commercial-grade speech recognition products capable of handling continuous speech ranging over a large vocabulary.
But let us return to our story. Buoyed by the successes in speech recognition in the 1970s and 1980s (substantial performance gains over knowledge-based systems were posted), researchers began applying data-driven approaches to many problems in natural-language processing, in a turn-around so extreme that it has been deemed a “revolution.” Indeed,
now empirical methods are used at all levels of language analysis. This is not just due to increased resources: a succession of breakthroughs in machine-learning algorithms has allowed us to leverage existing resources much more effectively. At the same time, evidence from psychology shows that human learning may be more statistically based than previously thought; for instance, work by Jenny Saffran, Richard Aslin, and Elissa Newport reveals that 8-month-old infants can learn to divide continuous speech into word segments based simply on the statistics of sounds following one another. Hence, it seems that the “revolution” is here to stay.
Of course, we must not go overboard and mistakenly conclude that the successes of statistical NLP render linguistics irrelevant (rash statements to this effect have been made in the past, e.g., the notorious remark, “every time I fire a linguist, my performance goes up”). The information and insight that linguists, psychologists, and others have gathered about language is invaluable in creating high-performance broad-domain language understanding systems; for instance, in the speech recognition setting described above, a better understanding of language structure can lead to better language models. Moreover, truly interdisciplinary research has furthered our understanding of the human language faculty. One important example of this is the development of the head-driven phrase structure grammar (HPSG) formalism—this is a way of analyzing natural language utterances that truly marries deep linguistic information with computer science mechanisms, such as unification and recursive datatypes, for representing and propagating this information throughout the utterance’s structure. In sum, although many challenges remain (for instance, while the speech-recognition systems mentioned above are very good at transcription, they are a long way from engaging in true language understanding), computational techniques and data-driven methods are now an integral part both of building systems capable of handling language in a domain-independent, flexible, and graceful way, and of improving our understanding of language itself.
Acknowledgments
Thanks to the members of and reviewers for the CSTB fundamentals of computer science study, and especially Alan Biermann, for their helpful feedback. Also, thanks to Alex Acero, Takako Aikawa, Mike Bailey, Regina Barzilay, Eric Brill, Chris Brockett, Claire Cardie, Joshua Goodman, Ed Hovy, Rebecca Hwa, John Lafferty, Bob Moore, Greg Morrisett, Fernando Pereira, Hisami Suzuki, and many others for stimulating discussions and very useful comments. Rie Kubota Ando provided the Japanese example. The use of the term “revolution” to describe the re-ascendance
of statistical methods comes from Julia Hirschberg’s 1998 invited address to the American Association for Artificial Intelligence. The McDonnell-Douglas ad and some of its analyses were presented in a lecture by Stuart Shieber. All errors are mine alone. This paper is based on work supported in part by the National Science Foundation under ITR/IM grant IIS-0081334 and a Sloan Research Fellowship. Any opinions, findings, and conclusions or recommendations expressed above are those of the author and do not necessarily reflect the views of the National Science Foundation or the Sloan Foundation.
Bibliography
Chomsky, Noam, 1957, “Syntactic Structures,” Number IV in Janua Linguarum. Mouton, The Hague, The Netherlands.
Firth, John Rupert, 1957, “A Synopsis of Linguistic Theory 1930-1955,” pp. 1-32 in the Philological Society’s Studies in Linguistic Analysis. Blackwell, Oxford. Reprinted in Selected Papers of J.R. Firth, F. Palmer (ed.), Longman, 1968.
Good, Irving J., 1953, “The Population Frequencies of Species and the Estimation of Population Parameters,” Biometrika 40(3,4):237-264.
Harris, Zellig, 1951, Methods in Structural Linguistics,University of Chicago Press. Reprinted by Phoenix Books in 1960 under the title Structural Linguistics.
Montague, Richard, 1974, Formal Philosophy: Selected Papers of Richard Montague, Richmond H. Thomason (ed.),Yale University Press, New Haven, Conn.
Mosteller, Frederick, and David L. Wallace, 1984, Applied Bayesian and Classical Inference: The Case of the Federalist Papers, Springer-Verlag. First edition published in 1964 under the title Inference and Disputed Authorship: The Federalist.
Pollard, Carl, and Ivan Sag, 1994, Head-driven Phrase Structure Grammar, University of Chicago Press and CSLI Publications.
Saffran, Jenny R., Richard N. Aslin, and Elissa L. Newport, 1996, “Statistical Learning by 8-Month-Old Infants,” Science 274(5294):1926-1928, December.
Shannon, Claude E., 1948, “A Mathematical Theory of Communication,” Bell System Technical Journal 27:379-423 and 623-656.
Turing, Alan M., 1950, “Computing Machinery and Intelligence,” Mind LIX:433-460.
Weaver, Warren, 1949, “Translation,” Memorandum. Reprinted in W.N. Locke and A.D. Booth, eds., Machine Translation of Languages: Fourteen Essays,MIT Press, Cambridge, Mass., 1955.
For Further Reading
Charniak, Eugene, 1993, Statistical Language Learning,MIT Press, Cambridge, Mass.
Jurafsky, Daniel, and James H. Martin, 2000, Speech and Language Processing: An Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition, Prentice Hall. Contributing writers: Andrew Keller, Keith Vander Linden, and Nigel Ward.
Manning, Christopher D., and Hinrich Schütze, 1999, Foundations of Statistical Natural Language Processing,MIT Press, Cambridge, Mass.
COMPUTER GAME PLAYING: BEATING HUMANITY AT ITS OWN GAME
Daphne Koller, Stanford University, and Alan Biermann, Duke University
The idea of getting a computer to play a complex game such as checkers or chess has been present in computer science research from its earliest days. The earliest effort even predated real computers. In 1769, Baron Wolfgang von Kempelen displayed a chess-playing automaton called “Turk.” It drew a lot of attention, until people realized that the cabinet of the “machine” concealed a human dwarf who was a chess expert.
The first real attempt to show how a computer could play a game was by Claude Shannon, one of the fathers of information science. The basic idea is to define a game tree that tells us all of the possible move sequences in the game. We can then ask, at each point in the tree, what a rational (selfish) player would do at that point. The answer comes from an analysis of the game tree beginning at the end of the tree (the termination of the game). For example, assume that one player has black pieces and the other white pieces. We can mark each game termination point as B—black wins, W—white wins, or D—draw. Then we can work our way from the termination points of the game backwards: If the white player, at her turn, has a move leading to a position marked W, then she can take that move and guarantee a win; in this case, this position is labeled with W. Otherwise, if she has a move leading to a position marked D, then she can force a draw, and the position is labeled with D. If all of her moves lead to positions marked B, then this position is a guaranteed win for black (assuming he plays optimally), and it is marked with B. Similar propagation rules apply to positions controlled by the black player. Thus, assuming perfect play by each player, we can completely understand the win potential of every board position.
This procedure is a great theoretical tool for thinking about a game. For example, it shows that, assuming both players play perfectly, we can determine without playing a single move which of the players will win, or if the game has a forced draw. We simply carry out the above procedure and check whether the initial position is marked with a B, a W, or a D. Unfortunately, for almost all realistic games, this procedure cannot be carried out because the size of the computation is too large. For example, the game tree for chess has approximately 10120 trajectories. As Shannon points out, a computer that evaluated a million positions per second would require over 1095 years just to decide on its first move!
Shannon’s idea was to explore only part of the game tree. At each position, the computer looks forward a certain number of steps, and then somehow evaluates the positions reached even if they are not wins or losses. For example, it can give a higher score to positions where it has more pieces. The computer then selects an optimal move relative to that myopic perspective about the game.
Turing, the inventor of the Turing machine (see “Computability and Complexity” by Kleinberg and Papadimitriou in Chapter 2) was the first to try and implement this idea. He wrote the first program capable of playing a full game of chess. But this program never ran on a computer; it was hand-simulated against a very weak player, who managed to beat it anyway.
The first attempt to get an actual computer to play a full-scale real game was made by Arthur Samuel. In the mid-1940s, Samuel was a professor of electrical engineering at the University of Illinois and became active in a project to design one of the first electronic computers. It was there that he conceived the idea of a checkers program that would beat the world champion and demonstrate the power of electronic computers. Apparently the program was not finished while he was at the University of Illinois, perhaps because the computer was not completed in time.
In 1949, Samuel joined IBM’s Poughkeepsie Laboratory and worked on IBM’s first stored program computer, the 701. Samuel’s work on checkers was not part of his job. He did the work in his spare time, without telling his supervisors. He got the computer operators (who had to authorize and run all computer programs) to run his program by telling them it was testing the capabilities of the 701. This program was one of the first programs to run on IBM’s very first production computer. The computer spent its days being tested for accounting and scientific computation, and its nights playing checkers.
Interestingly, Samuel’s justification for using the machine was actually valid. Indeed, because his checkers program was one of the earliest examples of non-numerical computation, Samuel greatly influenced the instruction set of early IBM computers. The logical instructions of these computers were put in at his instigation and were quickly adopted by all computer designers, because they are useful for most non-numerical computation.
Samuel’s program was the first to play checkers at a reasonable level. It not only implemented Shannon’s ideas; it also extended them substantially by introducing new and important algorithmic ideas. For example, Shannon’s original proposal was to search all of the paths in the game up to a given depth. Samuel’s program used a more sophisticated algorithm, called alpha-beta pruning, that avoided exploring paths that it could prove were suboptimal. This algorithm allowed Samuel to almost double the number of steps that it looked into the future before making the decision.
Alpha-beta pruning allowed Samuel’s program to prune large numbers of paths in the tree that would never be taken in optimal play. Consider the example in Figure 6.4. Here, the machine, playing white, has two moves, leading to positions A and B. The machine examines the paths that continue beyond position A and determines that the quality (according to some measure) of the best position it can reach from A is 10. It then starts evaluating position B, where the black player moves. The first move by black leads to position B1; this position is evaluated, by exploring the paths below it, to have a value of 5 (to white). Now, consider any other move by black, say to B2. Either B2 is worth more than 5, or less than 5. If it is worth more than 5, then it is a better position for white, and black, playing to win, would not take it. If it is worth less than 5, then black will take it, and the result will only be worse for white. Thus, no matter what, if the machine moves to position B, it can expect to end up with a position valued at 5 or less. As it can get 10 by moving to position A, it will never move to B. And it can determine this without ever exploring B2, B3, . . ., B12, or any of their descendants. This powerful idea coupled with other mechanisms enabled the search routines to run hundreds or even thousands of times faster than would have otherwise been possible.
Besides having sophisticated search capability, Samuel’s program was the first program that learned by itself how to perform a task better. Samuel himself was a mediocre checkers player. But he was a very smart computer scientist. He came up with a method by which the computer could
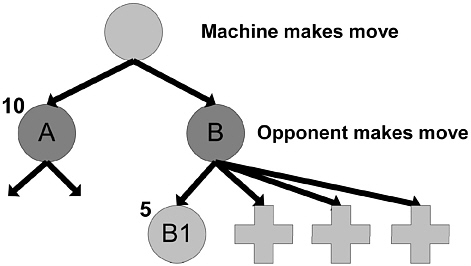
FIGURE 6.4 The alpha-beta search procedure makes move A without examining any of the paths marked +.
gradually improve its play as it played more and more games. Recall that the computer has to evaluate each non-terminal position. One could, for example, count the number of pieces of each type on the board and add them up with appropriate weights. But is a king worth twice as much as a regular piece, or perhaps five times as much? Samuel came up with the following idea: let’s learn these weights by seeing which set of weights leads to better play. Thus, the computer would play using one set of weights, and after seeing whether it won or lost the game, it would go and adjust the weights to get a more correct evaluation of the positions it had encountered along the way. If it won, it would aim to increase its valuation for these positions, and if it lost, it would decrease them. Although no single run is reliable in determining the value of a position (a bad position might, by chance, lead to a win), over time the valuations tended to get better. Although the computer started out playing very poor checkers, it ended up playing better than Samuel.
Samuel’s program, even today, is a very impressive achievement, since the 701 had 10 kilobytes of main memory and used a magnetic tape (and not a disk) for storage. Thus, it had less memory than one of the musical greeting cards that one can buy at the store for a few dollars.
When it was about to be demonstrated, Thomas J. Watson, Sr., the founder and president of IBM, remarked that the demonstration would raise the price of IBM stock 15 points. It did. Samuel’s program and others generated a lot of excitement, and many people were led to believe that computers would soon be better than any human player. Indeed, in 1957, Allen Newell and eventual Nobel-prize winner Herbert Simon predicted that in 10 years, a computer would be world chess champion. Unfortunately, these predictions were premature. Impressive as Samuel’s achievement was, it was not a very good checkers player. Although it was able to beat Samuel, most competent checkers players beat it without much strain.
Perhaps an early failure was to be expected in this new science, and people began to write much better programs. This effort was carried over to the more popular game of chess, and a number of individuals around the country began bringing their programs to an annual chess tournament. It was fun to see computers play against each other, but the nagging fact remained: against humans these programs did not offer much competition.
These events led to much thought. What was going on here? The answer seemed to be in the nature of the games of checkers and chess. Researchers realized that the game trees were growing in size at an exponential rate as one looks further ahead in the sequences of possible moves. Computer programs were wasting their time doing a uniform search of every possible move sequence while humans searched only selected paths. Humans had knowledge of which paths were likely to yield interesting
results, and they could look much deeper than machines. That is how humans could win.
It seemed obvious that the way to get machines to defeat humans was to design the programs to play more like people: rather than using a lot of computer cycles to explore all these irrelevant paths, the computer should spend more time thinking about which paths to explore. Like people, machines should invest their resources only in selected paths and they should look very far down them. During the 1970s, the annual chess tournament featured many programs that followed this theory: build in a mechanism that simulates a human’s ability to search the interesting paths, and create an ability in the machine to see very far into the future moves of the game. It was quite common for program designers to analyze a clever move by their program and brag about the long search that was used to find it. Only a fool who did not understand the modern lessons of game playing would try a uniform search algorithm.
But the next surprise came from a chess program developed at Northwestern University by David Slate, Larry Atkin, and others. They created a uniform search algorithm despite the common wisdom and won the annual tournament. At first, people felt it was just luck, but when the result was repeated a few times, they had to take notice. Why did the uniform search program defy all reason and defeat selected path programs that look much deeper? The answer came from a new rationalization: a program doing uniform search to a fixed depth plays perfectly to that depth. It never makes a mistake. Yet a selective search program does make an occasional mistake within that depth, and when it does the uniform search program grabs the advantage. Usually the advantage is enough to win the game. So uniform search programs dominated the field, and variations on them still are being used.
But the question remained: when would these programs finally become good enough to defeat humans? Although the Simon-Newell prediction asserted 10 years from 1957, the reality was that it took 40 years. A computer first became world champion in 1997, when IBM’s Deep Blue defeated Garry Kasparov. In a match that involved six games, Deep Blue won two games, lost one, and tied three. The ultimate goal of a 40-year quest had been achieved. But examine for a moment the computational resources that were brought against the human player. Deep Blue ran on the powerful RS/6000 machine running 32 processors in parallel and also had special-purpose circuitry to generate chess moves. Deep Blue benefited greatly from harnessing Moore’s law (see Hill in Chapter 2). This giant machine examined 200 million chess moves per second! But a lot of computer cycles were not the only factor in Deep Blue’s victory. The Deep Blue team had spent years building special chess knowledge into the software and hardware of the system, and the system’s play had been
criticized regularly by chess masters during its development and improved through many redesigns and modifications. Only through this coordinated and long-term effort was the win possible.
The years also proved the importance of the learning techniques developed by Samuel in his checkers program. For example, the world’s best backgammon program, one which plays at world-champion level, is a program developed by Gerry Tesauro (also at IBM). The main idea in this program is not search: search does not work well in backgammon, where even a single play of the game involves thousands of different possible successor states. The main idea in this program is a learning algorithm that learns to evaluate the quality of different positions. This program’s evaluation was so good that it changed the evaluation of certain positions, and therefore changed the way in which experts play the game!
This story teaches us very much about game playing. But it also teaches us about the nature of computation and the nature of human problem solving. Here are some of the major lessons:
-
Our intuitions and thoughtful insights into a process as complicated as playing one of these board games are very unreliable. We learn things in information science by writing a program and observing its behavior. We may theorize or estimate or consult our experts at length on some problems, but often we cannot find the answer without doing the experiment. On numerous occasions, we found the experts were wrong and the world of experiment held an amazing lesson for us.
-
The process of decision making in games is vastly more complex than we imagined. It was a combination of increased computer speed combined with decades of research on search and evaluation methods that eventually made it possible to defeat a great chess champion. It was not clear in the early days how much of either of these—machine speed or quality of search—would be needed, and it is a profound lesson to observe how much of each was required. This provides us with plenty of warning that when we examine other decision processes such as in economic, political, or medical diagnosis situations, we may find similar difficulties.
-
It is not always the case that to achieve human-level performance, a computer should use the same techniques that a human does. The way a computer does computation is inherently different from the way the brain works, and different approaches might be suitable for these two “computing architectures.” However, the performance of Deep Blue also shows that quantity (a large amount of computer cycles) might occasionally lead to quality—a performance that might be at the level of a human, or indeed indistinguishable from that of a human. (In the match between Deep Blue and Kasparov, several of Kasparov’s advisors accused IBM of cheating by having human players feeding moves to Deep Blue.) But is this much
-
brute-force computation really necessary in order to play high-quality chess? We have the feeling that there must be a more efficient use of machines that will do the same job. But we have no idea what it is. Perhaps, in order to solve that problem, we need to really understand how intelligence works and how to implement it within a computer.
-
Rather than designing a program in its entirety, it may be better to let the computer learn for itself. There is a lot of knowledge that people might have based on their experience but do not know how to make explicit. Sometimes there is simply no substitute for hands-on experience, even for a computer.
-
The research in game playing over the years has had ramifications for many other areas of computing. For example, computer chess research at IBM demonstrated computing technology that has also been used to attack problems related to computations on environmental issues, modeling financial data, the design of automobiles, and the development of innovative drug therapies. Samuel’s ideas on how to get programs to improve their performance by learning have provided a basis for tackling applications as diverse as learning to fly a helicopter, learning to search the Web, or learning to plan operations in a large factory.