2
Molecular and Cellular Responses to Ionizing Radiation
Since the early years of radiobiology the cellular effects of ionizing radiation have been studied in the context of induced chromosomal aberrations, and early models of radiation action were largely based upon such studies (Savage 1996). In the 1970s, somatic cell genetic techniques were developed to allow the quantification and characterization of specific gene mutations arising in irradiated cultures of somatic cells. In more recent years, findings of persistent postirradiation genomic instability, bystander effects, and other types of cellular response have posed additional questions regarding the mechanisms underlying the cytogenetic and mutagenic effects of radiation and their potential to contribute to radiation tumorigenesis.
This chapter considers the general aspects of dose-response relationships for radiobiological effects and subsequently reviews the largely cellular data on a range of radiobiological end points. The main focus of the review is the issue of cellular effects at low doses of low-LET (linear energy transfer) radiation. Many of the conclusions reached from this review, when aggregated with those of Chapters 1 and 3, contribute to the judgments made in this report about human cancer risk at low doses and low dose rates.
GENERAL ASPECTS OF DOSE-RESPONSE RELATIONSHIPS
Any effect of radiation exposure must be quantified in relation to the effect observed in a control population. In this way the dose to an irradiated population is considered in the context of, among other factors, the natural background radiation received. For low-LET radiation an absorbed dose of 1Gy1 (1000 mGy) corresponds to an equivalent dose of 1 Sv (1000 mSv). Because this report focuses on low-LET radiation, reference is mostly to grays and not to sieverts. Low-LET background radiation worldwide is responsible for an average annual effective dose per person of about 0.9 mGy per year (UNSCEAR 2000b). This includes an estimated 0.48 mGy from external terrestrial radiation to the body, 0.28 mGy from cosmic radiation (excluding the neutron component), and 0.17 mGy from radioisotopes in the body. For the purposes of this report, it does not include background radiation of about 1.2 mSv delivered to the lungs from radon and radon progeny or other high-LET radiation. Radon is the subject of the BEIR VI report (NRC 1999).
The maximal permissible levels that are recommended in the United States by the National Council on Radiation Protection and Measurements (NCRP) for people exposed to radiation other than background radiation and from medical applications are 1 mSv per year for the general population and 50 mSv per year for radiation workers employed by nuclear-related industries (Federal Register 1987). Considering the levels of background radiation, the maximal permissible levels of exposure of radiation workers now in effect, and the fact that much of the epidemiology of low-dose exposures includes people who in the past have received up to 500 mSv, the BEIR VII committee has focused on evaluating radiation effects in the low-dose range <100 mGy, with emphasis on the lowest doses where relevant data are available. Effects that may occur as the radiation is delivered chronically over several months to a lifetime are thought to be most relevant.
An effect (E) (for example chromosomal aberrations, mutations, or animal carcinogenesis) induced by an acute dose of low-LET radiation delivered over a few minutes has been described by the relationship E = αD + βD2, where D = dose; this is a linear-quadratic dose-response relationship curving upward (Lea 1946; Cox and others 1977). Theoretically, the α term represents the single-hit intratrack component, and β represents the two-hit intertrack component. An alternative interpretation is that the D2 term may arise from multiple tracks that would increase the overall burden of damage in a cell and thereby partially saturate a repair
system and reduce the probability of repair of particular damage from a track (UNSCEAR 1993). However, there is no experimental evidence to support this model. As the dose is reduced, the β term becomes less important, and the dose-response relationship approaches linearity with a slope of α. For doses delivered in multiple fractions or at low dose rates, in which case the effects during the exposure period are independent and without additive or synergistic interactions, the dose-response relationship should also be linear with a slope of α. Theoretically, the value of α should be the same for high and low dose rates and for single or multiple doses, and there should be a limiting value, α1, so that reducing the dose rate further would not reduce the α term (see Figure 2-1 for an illustration of these concepts).
For extrapolating data from acute high-dose-rate experiments to results expected for low doses and low-dose-rate experiments, the dose and dose-rate effectiveness factor, DDREF, is estimated (see Figure 2-1). The DDREF is estimated by comparing the linear extrapolation (curve B) of the induced incidence for a set of acute dose points (curve A) with the linear curve (D) for low dose rate. The DDREF is equal to the slope αL for curve B divided by the slope α1 for curve D. If only acute high-dose data are available, the slope (α1) for the linear extrapolation of the data for acute doses that approach zero (tangent to curve A) is used. This is the dose effectiveness factor (DEF), which is assumed and shown (Cornforth and others 2002) to be equal to the dose-rate effectiveness factor (DREF). Therefore, the term DDREF is used to estimate effects for either low doses or low dose rates. This value for DDREF can be estimated from a fit of the acute data using the relationship described above (i.e., E = αD + βD2). Thus, the DDREF = [(αD + βD2)/D]/(αD/D)=(αD + βD2)/αD, which equals 1 + Dβ/α or 1 + D/(α/β). D is the dose at which the response for acute irradiation is divided by the response for low-dose-rate irradiation to obtain the DDREF, and the relationship shows that DDREF will increase with the dose at which the curves A and D are compared. Note, the contribution from the β term (βD2) equals the contribution from the α term (αD) (i.e., βD2 = αD, when D = α/β). For this dose equal to α/β, the incidence for curve D is equal to the difference between the incidence for curve A and the incidence for curve D; thus, curve A intersects the linear curve B at the dose equal to α/β. For example, if α/β equals 1 Gy, the DDREF for a dose of 1 Gy would theoretically equal (1 + 1/1) or 2; for a dose of 0.5 Gy, the DDREF would equal 1.5, and for a dose of 2 Gy, it would equal 3. If α/β equals 2 Gy, curves A and B would intersect at 2 Gy where the DDREF equals 2; at doses less than or greater than 2 Gy, the DDREF would be less than or greater than 2, respectively. This concept is illustrated with experimental data in Figure 2-8; for the induction of HPRT (hypoxanthine-guanine phosphoribosyl transferase) muta-
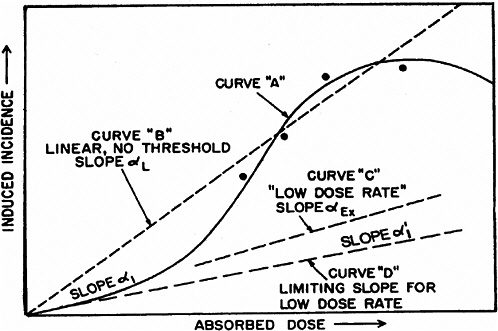
FIGURE 2-1 Schematic curves of incidence versus absorbed dose. The curved solid line for high absorbed doses and high dose rates (curve A) is the “true” curve. The linear, no-threshold dashed line (curve B) was fitted to the four indicated “experimental” points and the origin. Slope α1 indicates the essentially linear portion of curve A at low doses. The dashed curve C, marked “low dose rate,” slope αEx, represents experimental high-dose data obtained at low dose rates. SOURCE: Reproduced with permission of the National Council on Radiation Protection and Measurements, NCRP Report No. 64 (NCRP 1980).
tions in mouse splenic T lymphocytes, the DDREF was ~1.5 at 1 Gy and ~4 at 5 Gy. Also, in Figure 10-2, dose-response curves for the incidence of solid cancers in Japanese A-bomb studies were constructed over the dose range of 0–1.5 Sv, assuming α/β = 1.45 Sv and α/β = 3.33 Sv, and DDREF values were calculated by dividing the slope of curve B by the slope of curve D. These slope ratios give DDREF values of 1.8 for α/β = 1.45 Sv and 1.3 for α/β = 3.33 Sv.
Several factors may affect the theoretical dose-response relationships described above, namely: variations in radiosensitivity during the cell cycle; induction of an adaptive response to an initial exposure, which can reduce the effect of later exposures; a bystander effect that causes an irradiated cell to have an effect on a nearby unirradiated cell; the induction of persistent genomic instability; and hyper-radiation sensitivity in the low-dose region. Except for the cell cycle, these factors have been identified and studied since the BEIR V report (NRC 1990). These factors, together with data on the induction of gene/chromosomal mutations in somatic cells are discussed in subsequent sections of this chapter.
INDUCTION OF CHROMOSOME ABERRATIONS
Early studies on the mechanisms of chromosome aberration induction summarized by Savage (1996) lead to the following conclusions: Primary radiation-induced break-type lesions can (1) reconstitute without morphological change to chromosomes; (2) rejoin illegitimately with another break close in time and space to produce an intra- or interchromosomal aberration visible at the subsequent mitosis; or (3) remain “open,” leading to a simple break at mitosis. These early conclusions, based primarily on work with plant cells, are supported by subsequent studies with mammalian cells. The quantitative cytogenetic systems developed over the years, particularly in G0 human lymphocytes, have been utilized in studies on the effects of dose, dose rate, and radiation quality. From a mechanistic viewpoint there is compelling evidence that the induction and interaction of DNA double-strand breaks (DNA DSBs or, more correctly, double-stranded lesions) is the principal mechanism for the production of chromosome aberrations. The fundamental arguments supporting this widely accepted conclusion have been discussed in depth (Bender and others 1974; Scott 1980; Cornforth and Bedford 1993; Natarajan and Obe 1996). Of particular note are the data showing excess aberrations following the introduction of DNA DSB-inducing restriction endonucleases into cells (Bryant 1984; Obe and others 1985; Morgan and Winegar 1990). The increased chromosomal radiosensitivity in cells genetically deficient in processes associated with DNA DSB repair, reviewed by ICRP (1998), also supports this conclusion.
The biophysical modeling of the dose-response and LET dependence for chromosome aberration induction has been a major focus in radiobiological research for many years. In the following paragraphs, a brief outline is provided of the current state of knowledge of the mechanisms that are believed to play a role in the induction of chromosomal aberrations (see Bedford and Dewey 2002 for a detailed discussion). Aberrations formed following irradiation of cells in the G0/G1 phase of the cell cycle are dicentric exchanges, centric rings, and monocentric exchanges (translocations). The vast majority of studies show that the dose-response for low-LET radiation is curvilinear and fits well to the equation αD + βD2. At high doses, saturation effects occur, and the dose-response tends to turn down; for human lymphocytes, saturation occurs at doses greater than 4–5 Gy. The linear coefficient α, representing the initial slope of the dose-response, increases with the LET of the radiation, reaches a maximum at ~70 keV μm−1, and then falls. The quadratic coefficient β is approximately constant up to around 20 keV μm−1 but reduces at higher LET (>100 keV μm−1). A reduction in low-LET dose rate reduces aberration yields in a dose-dependent manner; the value of α is unaffected, but the value of β decreases (Edwards and others 1989).
A current explanation of the above dose-response characteristics is that DNA DSBs are the principal causal events for aberration induction and that these are induced with linear kinetics at around 30 DNA DSBs Gy−1. Correct repair and misrepair processes operate in competition for these DNA DSBs, with the majority of breaks restituting correctly and a small fraction taking part in misrepair-mediated chromosomal exchanges (Hlatky and others 1991). The fraction of misrepair events is suggested to be dose dependent, with the close proximity of DNA DSBs promoting exchanges and thereby imposing curvature on the low-LET dose response. The two-track component of DNA lesion production and interaction increases as a quadratic function of dose and produces biophysical curvature on the dose-response. However, the concept of proximity-promoted interaction of lesions gives more weight to lesions arising along the path of single tracks. Such proximity effects have been reviewed (Sachs and others 1997). Modeling procedures of this type, while providing a coherent explanation of low-LET dose-response, are insufficient to account fully for high-LET effects (Moiseenko and others 1997). An additional factor considered in some modeling of dose- and LET-dependent responses is the possibility that some exchanges might involve interaction of a DNA DSB with an undamaged DNA site (i.e., recombinational-like DNA misrepair). It seems likely that a variety of repair and misrepair options are available to the cell and that their relative importance is LET dependent; this feature may relate to the complexity of a significant fraction of initial DNA DSBs (see Chapter 1).
Dose and LET dependence also apply to the morphological complexity of the induced chromosomal aberrations themselves. The development of fluorescence in situ hybridization (FISH) methods of chromosome painting has allowed aberration complexity to be studied in detail. In brief, aberration complexity reflects the number of DNA DSBs in-
volved in a given chromosomal exchange event; not surprisingly, aberration complexity becomes most apparent at high doses of low-LET radiation and at all doses of high-LET radiation (Finnon and others 1995, 1999; Griffin and others 1995; Anderson and others 2000). The precise mechanism of formation of these complexes remains uncertain, but multiple pairwise exchanges involving the same chromosomes play some part (Edwards and Savage 1999). However, cyclic exchanges involving three and four breaks are not uncommon, implying that the interaction of multiple DNA DSBs can occur. Recent studies using multicolor mFISH analyses further emphasize the complexity of many radiation-induced chromosomal exchanges produced after high acute doses of radiation (Loucas and Cornforth 2001). These mFISH analyses also show that even after exposure at very low dose rates, the formation of complex chromosomal exchanges is not completely eliminated (Loucas and others 2004).
Combining FISH painting and premature chromosome condensation techniques (Darroudi and others 1998) has also facilitated studies on the rate of formation of aberrations. In these studies (Darroudi and others 1998; Greinert and others 2000) a substantial portion of exchanges have been shown to form rapidly, although some require several hours. There is some evidence that those aberrations forming rapidly tend to be incomplete exchanges, which suggests a time dependence for pairwise exchange (Alper and others 1988) of DNA DSBs. The general picture that emerges from these biophysical studies is that the misrepair events of radiation-induced DNA DSBs that lead to chromosome aberrations are probably associated with the dominant postirradiation function of the nonhomologous end joining (NHEJ) repair processes described in Chapter 1.
Overall, biophysical approaches to the modeling of dose-response for chromosomal aberrations, although not without some uncertainties on mechanisms, imply that the single-track component of radiation action will dominate responses at low doses and low dose rates (i.e., the dose-response for all forms of aberrations will be linear at low doses and low dose rates). Considerable effort has been expended to test this proposition, and in a very large multicenter study using assays of dicentric aberrations in human lymphocytes, the linearity of the response was evident down to at least 20 mGy of low-LET radiation (Lloyd and others 1992), which is illustrated in Figure 2-5. Below that dose, the statistical power of the data was not sufficient to exclude the theoretical possibility of a dose threshold for radiation effects.
Another important feature of the chromosomal response to radiation is the postirradiation period during which initial DNA damage is fixed and then expressed in the form of aberrations such as dicentric chromosomes. On the basis of direct observation and theory, the conventional cytogenetic view is that all such chromosomal damage sustained within a given cell cycle will be fixed and then expressed at the first postirradiation mitosis. Accordingly, Carrano and Heddle (1973) predicted that the dicentric aberration frequency will fall by a factor of around 2 per cell division on the basis that at each mitotic anaphase, a given dicentric has an equal chance of falling free or producing a lethal anaphase bridge. This prediction has been tested as part of a recent study (Pala and others 2001) that showed dicentric yields falling by up to a factor of 4 between the first and second postirradiation cell division. It seems therefore that the vast majority of initial unrepaired and misrepaired lesions are expressed as chromosomal damage at the first division. Cells carrying unbalanced chromosomal exchanges (dicentrics) or substantial chromosomal losses are not expected to contribute to the viable postirradiation population. By contrast, cells carrying small deletions or balanced exchanges such as reciprocal translocations are likely to remain viable, and some may have the potential to contribute to tumor development.
Later in the chapter this conventional view is contrasted with data implying that in some circumstances, a certain fraction of irradiated cells can express chromosomal damage over many cell cycles (i.e., persistent genomic instability). The proposition that this induced instability phenotype can contribute to tumorigenesis is explored in Chapter 3.
INDUCTION OF GENE MUTATIONS IN SOMATIC CELLS
Ionizing radiation is known to induce a broad range of potentially mutagenic lesions in DNA ranging from damaged DNA bases to frank DNA breaks and chemically complex lesion clusters (see Chapter 1). Not unexpectedly, molecular analyses of radiation-induced somatic mutations at a number of loci provide evidence of induction of point mutations in single genes and of small and large deletions that may encompass a number of physically linked genes (Sankaranarayanan 1991; Thacker 1992). An important factor in the induction and recovery of deletion-type, multilocus mutations is the degree to which multiple gene loss may be tolerated by the cell. There is good evidence that such tolerance is highly dependent on the genetic context of the mutation (i.e., its position in respect to essential genes and, for autosomal loci, the genetic status of the second gene copy on the homologous chromosome). These issues are discussed in depth elsewhere (Thacker 1992); here it is sufficient to note that genetic context can result in up to a twentyfold change in induced mutation frequencies in autosomal genes (Bradley and others 1988; Amundson and Liber 1991). There is strong molecular evidence that in most circumstances, a DNA deletion mechanism dominates mutagenic response after ionizing radiation (Sankaranarayanan 1991; Thacker 1992), and it is for this reason that the genetic context of the mutation is of great importance. In illustration of this, radiation mutagenesis in cells hemizygous (one gene copy deleted) for autosomal APRT (adenine phosphoribosyltransferase) is constrained by the proximity of an essential sequence; induced mutation frequencies are relatively low,
and only ~20% of induced mutations are of the deletion or rearrangement type (Miles and others 1990)—many deletions will have led to cell death. By contrast, radiation mutagenesis at the X-linked HPRT gene is much less constrained by neighboring sequence; induced mutation frequencies are substantially higher, and ~70% of induced mutations show HPRT deletion or rearrangement (Thacker 1986)—many more will have been tolerated (Bedford and Dewey 2002). Stated simply, gene loss mutations are characteristic of radiation, but their recovery in viable cells can be a major limiting factor. Also, gene amplification can result from the process of DSB repair (Difilippantonio and others 2002). As shown later, these features are important for consideration of carcinogenic mechanisms and are also discussed in respect of germline mutagenesis.
Deletion and rearrangement of APRT, HPRT, and other target genes do occur spontaneously but are generally less frequent than point mutation; in the case of most chemical mutagens, there is a strong bias toward the induction of point mutations (Thacker 1986; Miles and others 1990; Sankaranarayanan 1991).
Studies of the effect of radiation quality on the induction of gene mutations show a relationship similar between relative biological effectiveness (RBE) and LET to that noted for chromosome aberration induction. Mutagenic effectiveness peaks at a LET of 100–200 keV μm−1, with maximum RBE values usually in the range of 7–10 based largely on initial slopes of the dose-response (Cox and Masson 1979; Thacker and others 1979; Thacker 1992). Molecular analyses broadly suggest that a DNA deletion mechanism predominates for all radiation qualities (Thacker 1986; Gibbs and others 1987; Aghamohammadi and others 1992; Jostes and others 1994), but there are some conflicting data on this issue.
DNA sequence data for radiation-induced intragenic deletions in APRT and larger deletions encompassing HPRT indicate the frequent involvement of short direct or inverted DNA repeats at deletion breakpoints (Miles and others 1990; Morris and Thacker 1993). The presence of these short repeats is highly suggestive of an important role for illegitimate recombination processes in mutagenesis and, as for chromosome aberration induction, the involvement of DNA DSBs and error-prone NHEJ repair. Evidence for a close relationship between gene mutations and chromosome aberrations is that several induced gene mutations are associated with macroscopic region-specific chromosomal deletions or rearrangements (Cox and Masson 1978; Thacker and Cox 1983; Morris and Thacker 1993).
If, as molecular data suggest, error-prone NHEJ repair of DNA DSBs is the principal source of radiation-induced gene mutations, then a linear dose-response would be anticipated at low doses. For technical reasons, dose-response relationships for gene mutations are far less precise than those for chromosome aberrations. In general, however, a linear or linear-quadratic relationship provides a satisfactory description of the dose-response down to ~200 mGy (Thacker 1992) and, from limited data, at lower doses. The exceptions to this are the data from a particularly sensitive in vivo system that scores reversion mutations (as hair color changes) at the pink-eyed unstable (Bonassi and others 1995) locus in the mouse. Using this system, a linear nonthreshold low-LET dose response has been obtained at doses down to 10 mGy (Schiestl and others 1994), but as discussed later in this chapter, that system is probably reflecting a mutagenic component from the induction of genomic instability.
Studies of radiation-induced gene mutation in radiosensitive mutant cell lines indicate that increased mutability can be associated not only with defective repair of DNA DSB but also with processes that affect the regulation of DNA repair (Thacker and others 1994). Finally, in studies on the effects of low-dose-rate, low-LET radiation and other cellular repair-related factors (Thacker 1992), there is consistent evidence for potentially increased efficiency of repair of pre-mutagenic lesions at low dose rates, but none of these studies specifically suggest the presence of a low-dose threshold. The following sections consider specific aspects of cellular response relating to cell cycle effects, adaptive responses to radiation, the transfer of damage signals between cells (bystander effects), induced and persistent genomic instability, low-dose hyper-radiation sensitivity, and other aspects of dose-response.
RADIATION-INDUCED GENOMIC INSTABILITY
Radiation-induced genomic instability has been defined as the manifestation of genetic damage in a certain fraction of irradiated cells over many cell cycles after they were irradiated (Little 2003). This persistent instability is expressed as chromosomal rearrangements, chromosomal bridge formation, chromatid breaks and gaps, and micronuclei (Grosovsky and others 1996; Murnane 1996; Poupon and others 1996; Limoli and others 1997a; Suzuki and others 1998) in the progeny of cells that survive irradiation. Reduction in cell cloning efficiency several generations after irradiation is called delayed lethality; it is supposedly a manifestation of genomic instability associated with an increase in lethal mutations (Seymour and Mothersill 1997). Also, gene mutations, such as HPRT mutations, that arise de novo several generations after irradiation are thought to be another manifestation of genomic instability. The spectrum of these de novo mutations resembles that of spontaneous mutations (i.e., primarily point mutations instead of deletions that are induced directly by irradiation; Little and others 1997). There is controversy, however, as to whether all of these different end points represent the same fundamental chromosomal alterations that result in genomic instability (Chang and Little 1992; Morgan and others 1996; Limoli and others 1997a; Little 1998; Mothersill and others 2000a). However, the similarity in the frequencies of genomic instability induced in X-irradiated cells, (3 to 19) × 10−5 per cell/mGy,
and the frequencies of chromosomal aberrations induced directly by irradiation may suggest that the induction of chromosomal aberrations is a primary event that plays a major role in radiation-induced genomic instability (data presented in section “Observed Dose-Response Relationships at Low Doses”).
There is controversy concerning the fundamental radiation target and lesions that result in genomic instability. Evidence that the nucleus is the target (Limoli and others 1997b; Kaplan and Morgan 1998) is that 125IdU (iododeoxyuridine) disintegrations in the DNA resulted in chromosomal instability, whereas 125I disintegrations in the cytoplasm and cellular membrane did not. Furthermore, incorporation of BrdU (bromodeoxyuridine) into DNA increased the amount of radiation-induced chromosomal instability (Limoli and others 1999), which argues for DNA as the target. However, since restriction enzymes that produced DSBs in DNA (Kinashi and others 1995), mutations (Phillips and Morgan 1994), and chromosomal aberrations (Bryant 1984) did not induce chromosomal instability (Limoli and others 1997b), the hypothesis was presented that DSBs themselves are insufficient and that complex clustered damage in the DNA, such as that from 125I disintegrations, is required. There is also some evidence that genomic instability results from complex chromosomal abnormalities created de novo by rearrangements that generate unstable combinations of DNA sequences (Murnane 1990), such as inverted repeats or associations of euchromatin with heterochromatin (Grosovsky and others 1996). Nevertheless, since the amount of instability induced by 125I disintegrations in the DNA was relatively low (maximum of 4–9% unstable clones; Kaplan and Morgan 1998; Griffin and others 2000), the possibility was suggested that targets in addition to DNA might be involved (Limoli and others 2001). At the least, damage and/or errorprone repair in DNA is probably involved in radiation-induced genomic instability because mutant cells deficient in the repair enzymes needed for NHEJ are most sensitive to the induction of radiation-induced instability (Little 2003) and especially genomic instability induced by DNA DSBs (Difilippantonio and others 2002).
There are also data indicating that reactive oxygen species (Limoli and others 2001; Little 2003), potentially persistent over several generations, may play an important role in ongoing genomic instability. In addition, alterations in signal transduction pathways may be involved (Morgan and others 1996), and alterations in nucleotide pools have been shown to lead to genomic instability (Poupon and others 1996). Another possibility is that damage to centrosomes might be an important target because centrosome defects are thought to result in genomic instability through missegregation of chromosomes (Pihan and others 1998; Duensing and others 2001) that would result in aneuploidy (Duensing and Munger 2001). However, as reported recently (Hut and others 2003), centrosomal damage can result from incompletely replicated or damaged DNA.
Because chromosomal instability has been associated with breakage-fusion-bridge (B/F/B) cycles (Fouladi and others, 2000; Gisselsson and others 2000; Lo and others, 2002a, 2002b; Little 2003), the roles of telomeres may be particularly relevant. See Mathieu and colleagues (2004) and Murnane and Sabatier (2004) for reviews. Chromosome instability can also be initiated by DSBs that result in the loss of a telomere that protects the chromosome end and prevents chromosome fusion. A single DSB introduced at a telomere with the I-SceI endonuclease in mouse embryonic stem (ES) cells (Lo and others, 2002a) and spontaneous telomere loss in a human tumor cell line (Fouladi and others, 2000; Lo and others, 2002b) were found to result in sister-chromatid fusion and chromosome instability. Chromosome instability can be associated with prolonged B/F/B cycles; these cycles arise as a consequence of breakage of fused sister chromatids when their centromeres are pulled in opposite directions during anaphase, with subsequent re-fusion in the next cell cycle. These B/F/B cycles result in extensive DNA amplification and cease only when the chromosome acquires a new telomere, often by nonreciprocal translocations from another chromosome. However, because the nonreciprocal translocations provide telomeres that stabilize the marker chromosome, those chromosomes that donate the nonreciprocal translocations can become unstable due to the loss of their telomeres. Then, a subsequent nonreciprocal translocation can serve to transfer instability to another chromosome (Murnane and Sabatier 2004; Sabatier and others 2005). Thus, the loss of a single telomere can result in transfer of instability from one chromosome to another, leading to extensive genomic instability.
The importance of telomere loss as a mechanism for chromosome instability through B/F/B cycles in cancer has been emphasized by the demonstration that telomerase-deficient mice that are also deficient in p53 have a high cancer incidence (Artandi and others 2000; Chang and others 2001; Rudolph and others 2001). The analysis of the tumor cells from these mice demonstrated the presence of chromosome rearrangements typical of B/F/B cycles, including gene amplification and nonreciprocal translocations commonly seen in human cancer. It is possible that the genomic instability observed for chromosomal aberrations, HPRT mutations, and longer telomere terminal restriction fragment lengths in X-irradiated CHO cells (Romney and others 2001) is also a manifestation of nonreciprocal translocations that lead to telomere loss.
A question that has to be addressed is the relevance of radiation-induced genomic instability for radiation-induced cancer, and a corollary of this question is the relationship among expression of p53, radiation-induced apoptosis, and radiation-induced genomic instability. The “guardian-of-the-genome” hypothesis postulates that either cell cycle arrest allows additional time for repair of DNA damage or, alternatively, apoptosis eliminates damaged cells, thereby preventing progeny from manifesting genomic instability and ulti-
mately carcinogenesis (Lane 1992; Kemp and others 1994; White and others 1994; Levine 1997; Lengauer and others 1998). Evidence has been presented that radiation-induced apoptosis can occur via p53-dependent and p53-independent mechanisms (Strasser and others 1994) initiated by damage in the nucleus (Guo and others 1997) or cytoplasm-membrane (Haimovitz-Friedman 1998). This damage results in cells undergoing apoptosis either during interphase without attempting division (Endlich and others 2000), several hours after they have divided a few times (Forrester and others 1999), or during an aberrant mitosis (Endlich and others 2000). The signal transduction pathways (White and Prives 1999) resulting in radiation-induced apoptosis involve the nucleus and cytoplasm with alterations in mitochondrial electron transport (Voehringer and others 2000) and release of cytochrome c from the mitochondria, which initiates caspase cleavage (Finucane and others 1999) and terminates in activation of a nuclease responsible for internucleosomal digestion of DNA (Wyllie 1998).
In accord with the guardian-of-the-genome hypothesis, mouse tumors undergoing apoptosis in a p53-independent manner contained abnormally amplified centrosomes, aneuploidy, and gene amplification (Fukasawa and others 1997). Also, a decrease in radiation-induced apoptosis associated with nonfunctional p53 or expression of Bcl2 correlated with an increase in mutagenesis (Xia and others 1995; Cherbonnel-Lasserre and others 1996; Yu and others 1997). However, the latter correlation might be due not to p53-mediated’s enhancement of radiation-induced apoptosis (Xia and others 1995) but instead to p53-mediated’s suppression of homologous recombination (Sturzbecher and others 1996), which in turn might suppress genomic instability and a hypermutable phenotype. However, there is evidence that radiation-induced genomic instability is independent of p53 expression (Kadhim and others 1996). Furthermore, when the guardian-of-the-genome hypothesis was tested in lymphocyte cultures that were irradiated under different dose-rate and mitogen-treatment conditions, postradiation incubation allowing apoptotic processes to remove damaged cells did not prevent the development of chromosomal instability during long-term cell proliferation over 51–57 days (Holmberg and others 1998). Thus, the relationship between radiation-induced genomic instability, radiation-induced apoptosis, and radiation-induced cancer is uncertain (discussed at length in Chapter 3). Furthermore, radiation-induced genomic instability could not be induced in normal diploid human fibroblasts (Dugan and Bedford 2003) and may be related to confounding in vitro stress factors (Bouffler and others 2001) or to the cells being partially transformed. Finally, as discussed in Chapter 3, it may be that genomic instability plays a more important role in tumor progression than in tumor initiation.
Data are critically needed for the definition of molecular targets and processes responsible for genomic instability in order to define and understand the dose-response relationship for genomic instability and especially why, in some cellular systems, the induction frequency saturates with only about 10–30% of the surviving cells manifesting genomic instability (Little 1998; Limoli and others 1999) (data presented in Table 2-1). It may be that only a certain fraction of the cells, or those in a certain part of the cell cycle, are susceptible to radiation-induced genomic instability. Until the molecular mechanisms responsible for genomic instability and its relationship to carcinogenesis are understood, the extrapolation of dose-response data for genomic instability to radiation-induced cancers in the low-dose range <100 mGy is not warranted.
CELL CYCLE EFFECTS
In a number of mammalian cell lines, cells irradiated in mitosis or late G2 are most susceptible, cells in G1 are intermediate in susceptibility, and cells in middle to late S phase and early G2 are most resistant to the induction of cell lethality, chromosomal aberrations, and mutations (Sinclair and Morton 1963; Terasima and Tolmach 1963; Dewey and others 1970; Burki 1980; Jostes and others 1980; Watanabe and Horikawa 1980; Chuang and Liber 1996; Leonhardt and others 1997). Also, cells irradiated at the G1/S transition are often observed to be more radiosensitive than cells in G1 or S. However, exceptions have been observed, such as little variation in radiosensitivity during the cell cycle (Henderson and others 1982) and greater sensitivity of cells in late S than of cells in G1 (Thompson and Humphrey 1968; Guo and others 1997; Furre and others 1999). Since radioresistance during late S phase has been attributed to error-free repair of DNA DSBs by homologous recombination when sister chromatids have been replicated (Rothkamm and Lobrich 2003; Rothkamm and others 2003), the lack of radioresistance during late S phase in some cell lines may be attributed to their inability to carry out repair by homologous recombination. Those effects have been observed in connection with relatively high acute doses of 1.5–10 Gy (1500-10,000 mGy), but how such variations in radiosensitivity during the cell cycle may affect responses to low doses up to 100 mGy is not known. Also, there are no reports of studies to determine whether there may be variations in radiosensitivity during the cell cycle for induction of genomic instability. However, studies with cell lines have indicated that cells are most susceptible to malignant transformation in vitro when they are irradiated with high-LET radiation or low-energy X-rays in late G2/M (Cao and others 1992, 1993; Miller and others 1992).
The inverse dose-rate effect (Crompton and others 1990; Amundson and Chen 1996), in which cells at first become more radioresistant and then more radiosensitive again as the dose rate of low-LET radiation is decreased below about 1–10 mGy/min, has been attributed to the arrest of cells in a radiosensitive G2 phase of the cycle (Mitchell and others 1979; Furre and others 1999). However, evidence has been
presented that the inverse dose-rate effect can be observed when cells do not arrest in G2 and, instead, correlates with low-dose hyper-radiation sensitivity (HRS; Mitchell and others 2002). This conclusion may be consistent with recent results from the same research group (Marples and others 2003), which reported that HRS for acute radiation doses was attributed to cells in radiosensitive G2 failing to arrest before mitosis. For high-LET radiation, the inverse dose-rate effect has been attributed to the traversal of cells through a radiosensitive G2 phase (Brenner and others 1996; Elkind 1996; Tauchi and others 1999). Such an inverse dose-rate effect has been reported for cell lethality and mutations induced by low-LET radiation and for transformation induced by high-LET radiation.
Vilenchik and Knudson (2000) hypothesized that the increase in mutability observed below a dose rate of 1 mGy/min for mouse spermatogonia and 10 mGy/min for cells in vitro is not caused by variations in radiosensitivity during the cell cycle but rather by a diminished activation of error-free repair at very low dose rates inasmuch as the rate of induced DNA damage (signal) is lower than the background rate of spontaneous DNA damage (noise). This interpretation of the data remains controversial, particularly since there is evidence that argues against the inducibility of DNA repair genes. However, Collis and colleagues (2004) reported recently that DNA damage introduced at a very low dose rate of 0.33 or 1.5 mGy/min produced less activation of the radiation damage sensor ATM (ataxia-telangiectasia-mutated), as detected by H2AX foci, than activation at a high dose rate of 750 mGy/min. Furthermore, this reduction of ATM activation was observed after irradiation in Go/G1, S, and G2/M, and correlated with enhanced cell killing. For a discussion of the expression of particular genes involved in DNA repair and controlling checkpoints in the cell cycle, see “DSB Signal Transduction and Inducible Repair” in Chapter 1, along with Figure 1-10.
Although some small transient effects on cell cycle progression have been reported for doses of 20–100 mGy (Puck and others 1997; Amundson and others 1999b), no inverse dose-rate effect would be expected at these dose levels (Brenner and others 1996), and if it did exist, it would be difficult to demonstrate. However, at approximately 100 mGy, an inverse dose-rate effect of fission-spectrum neutrons has been observed between 4 and 100 mGy/min for neoplastic transformation of C3H 10T1/2 cells (Hill and others 1982, 1984) and between 10 versus 250 mGy/min and 0.0083 versus 0.083 mGy/min for induction of lung adenocarcinomas and mammary adenocarcinomas in mice (Ullrich 1984). Apparently, these inverse dose-rate effects could not be explained by perturbations in the cell cycle, and for mammary tumors, the effect was associated with an increased probability of progression of carcinogen-altered cells rather than an increased number of initiated cells (Ullrich 1986). Furthermore, an inverse dose-rate effect was not observed for the induction of ovarian tumors, for which the response to dose at low dose rates was much lower than that at high dose rates (Ullrich 1984). How these data on high-LET fission neutrons can be extrapolated to low-LET radiation is unknown, especially because the RBE for these carcinogenic effects has been estimated to be as high as 10 or more. This means that the equivalent doses and equivalent dose rates mentioned above, when expressed in millisieverts, would be at least 10 times greater than the values expressed in milligrays.
Furthermore, when the same tumors were induced in mice by low-LET radiation at doses of 0.1–6.0 Gy, no inverse dose-rate effect was observed between 0.04 and 0.6 mGy/min; these low dose rates always had a dose-response relationship significantly below that observed for acute high-dose-rate irradiation (Ullrich and others 1976, 1987; Ullrich and Storer 1979a, 1979b, 1979c; Ullrich 1983). Similar observations were reported for neoplastic transformation of C3H 10T1/2 cells by low-LET radiation, for which the dose-response relationship for a low dose rate of 1 mGy/min was much below that observed for an acute high dose rate of 1.0 Gy/min (Han and others 1980). The lack of a low-LET inverse dose-rate effect for tumor induction and neoplastic transformation in vitro contrasts with the inverse dose-rate effect seen for cell killing and induction of mutations that is sometimes attributed to perturbations in cell cycle progression. However, results obtained with mammalian cell lines, in particular those for neoplastic transformation, should be interpreted with great caution if they are to be used in estimating radiation risk to humans.
ADAPTIVE RESPONSE
Organisms, such as bacteria, that live in a highly changeable environment have multiple mechanisms for adapting to environmental stress. The bacterium Escherichia coli has two distinct, inducible, redox-regulated transcriptional switches involving the soxRS and oxyR transcription factors, which respond to exposure to superoxide and hydrogen peroxide, respectively (Demple 1991; Choi and others 2001). After exposure to ionizing radiation, these factors re-program the cellular transcription pattern with increased expression of proteins that inactivate reactive oxygen species and some DNA repair enzymes that process oxidative DNA damage. As a consequence, E. coli cells exhibit a distinct adaptive response to oxidative stress: exposure to a low dose of active oxygen makes the cells more resistant to later exposures for some finite period. In that situation, there is a clear threshold value for deleterious effects of ionizing radiation. However, the soxRS and oxyR gene regulons have not been conserved during evolution, and human cells, which exist in a much more stable cellular environment than bacteria, do not appear to have counterparts. Thus, humans do not have an adaptive response to oxidative damage similar to the well-characterized systems in bacteria.
A broad perturbation of DNA transcription is observed in human cells after exposure to ionizing radiation; it involves the activation of transcription factors, such as NF-kappaB and c-jun/c-fos. After exposure of human lymphoblastoid cells to 5 Gy of radiation, 2–3% of the genes exhibit more than a 50% change in induction or repression (Tusher and others 2001). These genes include several involved in cell cycle control. No genes involved in repair of DNA DSBs generated by ionizing radiation were induced (Tusher and others 2001; Wood and others 2001). It should also be noted that the base-excision repair enzymes involved in the removal of oxidative damage are not induced by low doses of ionizing radiation in human cells (Inoue and others 2004). These studies have provided no support for a general adaptive repair response in human cells to counteract DNA DSB formation that can result in cell death or mutagenesis.
A different type of apparent adaptive response has been well documented for the induction of chromatid-type breaks and mutations in human lymphocytes stimulated to divide. In most studies, a priming or adaptive dose of about 10 mGy significantly reduces the frequency of chromosomal aberrations (Shadley and others 1987; Wolff 1992a, 1996) and mutations (Kelsey and others 1991) induced a few hours later by 1–3 Gy. However, when the priming dose was 10 mGy, the adaptive response for chromosomal aberrations was reduced significantly as the priming dose rate was reduced from 50 mGy/min to 6.4 mGy/min (Shadley and Wiencke 1989). Adaptive responses of this type were reviewed by UNSCEAR (1994).
Although alterations in cell cycle progression have been implicated in the mammalian cell adaptive phenomenon (Aghamohammadi and Savage 1991), carefully controlled studies indicate that the priming dose induces radioresistance for induction of chromosomal aberrations in human lymphocytes (Wolff 1996); priming doses less than 5 mGy, or greater than about 200 mGy, yield very little if any adaptation (Wolff 1992b). The induction and magnitude of the adaptive response in human lymphocytes are highly variable among people (Bose and Olivieri 1989; Sankaranarayanan and others 1989; Shadley and Wiencke 1989; Hain and others 1992; Vijayalaxmi and others 1995; Upton 2000), and the adaptive response could not be induced when lymphocytes were given the priming dose during G0 (Shadley and others 1987). Although inhibitor and electrophoretic studies (Youngblom and others 1989; Wolff 1992b) suggest that alterations in transcribing messenger RNA and synthesis of proteins are involved in the adaptive response in lymphocytes, no specific signal transduction or repair pathways have been identified. Finally, humans exposed occupationally (Barquinero and others 1995) or to iodine-131 (131I) for treatment of thyroid disease (Monsieurs and others 2000) or as children after Chernobyl (Tedeschi and others 1995) varied in their ability to demonstrate an apparent adaptive response for chromosomal aberrations (Padovani and others 1995; Tedeschi and others 1996). This variability may relate to the genetic variation reported for radiation-induced transcriptional changes (Correa and Cheung 2004).
Adaptive responses to radiation observed in other cellular systems for induction of cell lethality, chromosomal aberrations, mutations (Zhou and others 1993; Rigaud and others 1995), and defects in embryonic development provide little information that can be used to suggest that the dose-response curve in the dose range 0–100 mGy will be less steep than that described by the limiting value of α mentioned above. When mouse embryos were exposed to a priming dose of about 10 mGy and evaluated for chromosomal aberrations or defects in development induced by a challenge dose several hours later, the results were highly variable for the induction of an adaptive response (Muller and others 1992; Wojcik and others 1992; Wolff 1996; Wang and others 1998). Studies of radiation-induced mutagenesis also had variable results. Adaptation not only decreases the frequency of mutants induced by a challenge dose but also appears to alter the types of mutants. Adaptation of human lymphoblastoid cells to a challenge dose of 4 Gy 6 h after 20 mGy decreased the proportion of HPRT mutants of the deletion type relative to small point mutations (Rigaud and others 1995). In contrast, adaptation of human-hamster hybrid AL cells to a challenge dose of 3 Gy after a priming dose of 40 mGy increased the proportion of complex unstable mutations (Ueno and others 1996). An extensive study (Sasaki 1995) of chromosomal aberrations, HPRT mutations, and cell killing demonstrated adaptation in quiescent cultured m5S mouse embryonic skin cells preexposed in G1 to 10–50 mGy; cells exposed 4 h later to doses greater than 2 Gy were significantly more resistant than nonadapted cells for all three end points (see Figure 2-2 for cell-killing results). The adaptation phenomenon appeared to involve a protein kinase C signaling pathway. In addition, the lack of an adaptive response in a tumorigenic variant, clone 6110, and restoration of the adaptive response obtained by introducing human chromosome 11 (five other chromosomes had no effect) further suggested that interference of signaling pathways may alter adaptive responses in malignant cells. The observation (Broome and others 2002) that a priming dose as low as 1 mGy induced an adaptive response in a nontransformed human fibroblast cell line for micronuclei induced by a challenge dose of 2 Gy has to be confirmed for other systems and end points, such as mutation induction. Also, the large variation in adaptive response for radiation-induced micronuclei in human lymphoblastoid cell lines must be considered (Sorensen and others 2002). Most important, the adaptive response has to be demonstrated for both priming and challenging doses in the low-dose range <100 mGy, and an understanding of the molecular and cellular mechanisms of the adaptive response is essential if it is to have relevance for risk assessment.
Studies of adaptation for malignant transformation in vitro provide conflicting information and might not be relevant to malignant transformation in vivo. Although the
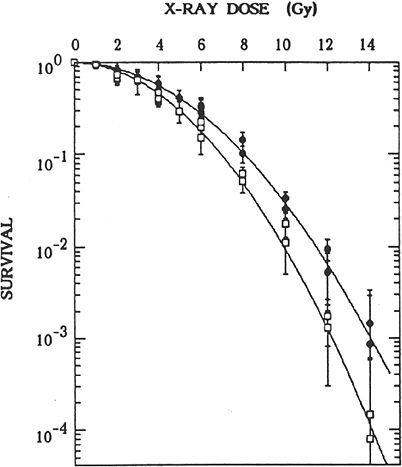
FIGURE 2-2 Effects of preirradiation on clonogenic survival of mouse m5S cells. Closed symbols represent results in cells in G1 preirradiated with 20 mGy of X-rays 5 h before graded doses of acute radiation. Open symbols represent results in cells in G1 given graded doses of acute radiation only. Statistical errors are standard errors of the mean based on variation in the number of recovered colonies in irradiated dishes (this does not include propagation of error in plating efficiency of nonirradiated controls). SOURCE: Sasaki (1995).
morphologic transformation frequency of m5S adapted mouse embryonic skin cells that had received 20 mGy was about half the spontaneous frequency of 3 × 10−5 observed in nonprimed cells, the adapted cells exposed 5 h later to a challenge dose of 1 Gy were more susceptible to morphologic transformation than the nonadapted cells (Sasaki 1995). These transformation results, however, contrast with results in mouse C3H 10T1/2 cells that were exposed in plateau phase to a challenge dose of 4 Gy 5 h after a priming dose of 100 or 670 mGy (i.e., adapted cells were more resistant to malignant transformation than nonadapted cells; Azzam and others 1994). Furthermore, the priming dose of 100 or 670 mGy caused an increase by a factor of 2–5 in the transformation frequency relative to the frequency of about 3 × 10−4 observed for nonirradiated cells. When the same group of investigators exposed the same C3H 10T1/2 cells in plateau phase to priming doses of 1, 10, or 100 mGy, the neoplastic transformation frequency was lower by a factor of 3–4 than the spontaneous frequency (Azzam and others 1996). The reduction was observed only when the cells were trypsinized and replated 24 h after irradiation for the transformation assay; trypsinization and replating immediately after irradiation did not alter the frequency. Similar results have been reported by Redpath and coworkers (Redpath and Antoniono 1998; Redpath and others 2001): the malignant transformation frequency was reduced by about half when human hybrid cells approaching confluence were trypsinized and replated 24 h after a priming dose of 10 mGy; again, no statistically significant reduction in transformation frequency was observed when the cells were trypsinized and replated immediately after irradiation.
The validity of extrapolating any of the results from in vitro neoplastic transformation systems to malignant transformation in vivo may be questioned for the following reasons. First, the effects associated with variations in time of trypsinization and replating after irradiation must be understood (Schollnberger and others 2002). Second, the measured neoplastic transformation frequency depends on both the density of viable cells plated (Bettega and others 1989) and the number of generations before the cells become confluent (Kennedy and others 1980). Third, when priming doses of 1–100 mGy resulted in a decrease in the neoplastic transformation frequency, the spontaneous transformation frequency was unusually high in one case (Azzam and others 1994), and a Hela X skin fibroblast human hybrid cell system was used in the other (Redpath and Antoniono 1998). Fourth, studies of malignant transformation in immortalized (already-transformed) cell lines may have little relevance to malignant transformation of normal nonimmortalized cells, especially in vivo, where complex interactive processes can occur (Harvey and Levine 1991; Kamijo and others 1997).
For several mammalian cell lines in culture, adaptive responses for cell lethality after doses of 200–600 mGy (Marples and Joiner 1995; Joiner and others 1996; Marples and Skov 1996; Wouters and others 1996; Skov 1999) and for enhanced removal of thymine glycols after a dose of 2 Gy (Le and others 1998) have been observed 4–6 h after a priming dose of 200 mGy. In Chinese hamster V79 cells, the rate of repair of DNA DSBs induced by 1.5 or 5.0 Gy was increased 4 h after a priming dose of 50 mGy (Ikushima and others 1996).
The adaptive responses of mammalian cells described above, at least for cell survival and repair of DNA strand breaks (Robson and others 2000), may be associated in part with the downregulation of a gene DIR1 90 min after doses of 50–1000 mGy. This gene codes for proteins (Robson and others 1997, 1999, 2000) similar to a family of heat shockrelated proteins (HSPs) known as immunophilins with tetrapeptide repeats (TPRs). TPR-containing proteins, such as cell cyclin proteins cdc23, cdc27, and cdc16, have been reported to form complexes in vivo, and the TPR domain is thought to be involved in binding HSP90 and HSP70. Less binding of HSP70 and the induction of other members of the HSP70 family by low doses of radiation (Sadekova and
others 1997) might result in adaptation through the same mechanisms.
The recent microarray expression studies (Yin and others 2003) that demonstrated downregulation of the large HSPs 30 min after irradiating the mouse brain with 100 mGy may support these conjectures. Also, the radiation-induced downregulation of CDC16, which belongs to the anaphasepromoting complex, was enhanced by an adaptive dose of 20 mGy (Zhou and Rigaud 2001). In fact, regulation of repair and cell cycle progression may be achieved by differential complex formation (Eckardt-Schupp and Klaus 1999). For instance, PCNA (proliferating cell nuclear antigen) expression, which is modulated by p53 in response to radiation, may play an important role in regulating and coordinating cell cycle progression, DNA replication, translesion synthesis, and DNA excision repair, depending on its partner proteins. Within minutes after ionizing radiation, the immediate-response genes transcription factors such as c-jun, c-fos, and NF-kB are turned on, possibly thwarting the general downregulation of transcription after irradiation and allowing privileged transcription of special genes. The sensors for these fast responses are in membranes, and they initiate signal transduction by several cascades of protein kinases (Eckardt-Schupp and Klaus 1999) that may involve reactive oxygen intermediates (Mohan and Meltz 1994; Hoshi and others 1997). Therefore, adaptation in mammalian cells probably involves induction of signal transduction pathways (Stecca and Gerber 1998) rather than induction of DNA repair enzymes.
There is much variability and heterogeneity in the ability to induce adaptive responses that usually require a priming dose of 10–200 mGy and a large challenge dose of 1–2 Gy. Challenge doses of this magnitude probably have little relevance to risk assessment for low radiation doses of 1–100 mGy. Furthermore, the molecular pathways associated with the phenomenon have not been delineated. Available data indicate that the adaptive response results from DNA damage that can be induced by 3HTdR (triliated thymidine) incorporated into DNA, by H2O2, and by restriction enzymes (Wolff 1992b; Sasaki 1995; Belyaev and Harms-Ringdahl 1996). The ability to induce an adaptive response appears to depend on the genotype (Wojcik and others 1992), which may relate to genetic variation reported for radiation-induced transcriptional changes (Correa and Cheung 2004). In fact, the effect of the genotype on the adaptive response has been demonstrated most conclusively in Drosophila melanogaster (Schappi-Bushi 1994).
A priming dose has been reported to reduce chromosomal damage in some chromosomes and increase it in others (Broome and others 1999). Data are needed, particularly at the molecular level, on adaptation induced when both priming and challenging doses are in the low-dose range <100 mGy; relevant end points should include not only chromosomal aberrations and mutations but also genomic instability and, if possible, tumor induction. In vitro and in vivo data are needed on delivery of the priming and challenge doses over several weeks or months at very low dose rates or with fractionated exposures.
Finally, we should be concerned about the cumulative effect of multiple low doses of less than 10 mGy. Such data have not yet been obtained, in particular those explaining the molecular and cellular mechanisms of the adaptive response. Therefore, it is concluded that any useful extrapolations for dose-response relationships in humans cannot be made from the adaptive responses observed in human lymphocytes or the other cellular systems mentioned above. In fact, a study (Barquinero and others 1995) reporting that an average occupational exposure of about 2.5 mGy per year over 7–21 years resulted in a variable adaptive response for chromosomal aberrations induced in human lymphocytes by a large challenge dose of 2 Gy also reported that the incidence of spontaneous aberrations was increased significantly by the occupational exposure. Barquinero and colleagues (1995) also cite six reports indicating that basal rates of chromosomal abnormalities are in general higher in exposed human populations; recent papers (Tanaka and others 2000; Tawn and others 2000a, 2004; Burak and others 2001; Liu and others 2002; Maffei and others 2004) present similar information. Therefore, based on current information, the assumption is unwarranted that any stimulatory effects of low doses of ionizing radiation substantially reduce long-term deleterious radiation effects in humans.
BYSTANDER EFFECTS
A factor that could have a significant effect on the dose-response relationship is the bystander effect that irradiated cells have on nonirradiated cells. Recent comprehensive reviews of bystander effects observed in vitro (Morgan 2003a) and in vivo (Morgan 2003b) emphasized their possible mechanisms, implications, and variability. In addition, reviews have been published recently on the relationship between the bystander effect, genomic instability, and carcinogenesis (Little 2003; Lorimore and others 2003). Observations that irradiated cells or tissues could have deleterious effects on nonirradiated cells or tissues were reported many years ago (Bacq and Alexander 1961) and were termed abscopal effects. As an example of such an effect, plasma from patients who underwent localized radiation therapy induced chromosomal aberrations in lymphocytes from nonirradiated patients (Hollowell and Littlefield 1968; Littlefield and others 1969). A bystander effect has been demonstrated conclusively for cells in culture exposed to high-LET radiation, usually α-particles. Little and colleagues estimated that a single α-particle traversing a cell can induce HPRT mutations (Nagasawa and Little 1999), sister-chromatid exchanges (Nagasawa and Little 1992), upregulation of p21 and p53, and downregulation of cyclin B1, cdc2, and rad51 (Azzam and others 1998) in unirradiated cells. At least for the bystander effect on signal transduction
pathways and induction of mutations, the irradiated and nonirradiated cells had to be in contact with each other through gap junctions. Hall and colleagues demonstrated the same bystander phenomenon for cell killing, induction of mutations (Zhou and others 2000), micronuclei formation (Hall 2000), and malignant transformation (Sawant and others 2001a); the magnitude of the bystander effect increased with the number of α-particles traversing the nuclei (Sawant and others 2001a).
For malignant transformation, the frequency when only 10% of the cells were traversed by an α-particle was as great as when every cell was exposed to an α-particle; furthermore, nonirradiated cells did not have to be in contact with irradiated cells. However, the same group subsequently reported that gap junctions appeared to be required for another bystander effect resulting in cell lethality in nonhit cells (Sawant and others 2002). The group also showed that irradiating the cytoplasm with α-particles (Wu and others 1999) induced mutations (small deletion and base-pair alteration mutations) that resembled those occurring spontaneously, not the larger deletions observed when the nucleus was irradiated to induce mutations in both irradiated and nonirradiated cells (Zhou and others 2000). Lorimore and colleagues (1998) have observed a similar bystander effect: delayed chromosomal aberrations associated with genomic instability when cells were exposed to α-particles. Prise and colleagues (1998) have observed a bystander effect for genomic instability associated with the formation of micronuclei 20–30 generations after individual cells were irradiated with a charged-particle microbeam. Their subsequent studies with primary human fibroblasts (Belyakov and others 2001) showed that even though a single cell had been targeted, an additional 80–110 cells had micronuclei; the yield of cells that had excess micronuclei was independent of the number of charged particles delivered to the targeted cell.
The molecular mechanisms proposed for the bystander effects described above are speculative (see Chapter 1 “DSB Signal Transduction and Inducible Repair” for a discussion of possible repair and signal transduction pathways that may be involved). Activation of the p53-mediated DNA damage response pathway in bystander cells has led to speculation (Grosovsky 1999) that reduced replication fidelity or increased recombinational activity might lead to the genetic effects that occur in these cells. However, α-particle-induced chromosomal instability was reported to be independent of the p53 status of the cells (Kadhim and others 1996). The bystander phenomenon may involve the diffusion of cytokines or long-lived reactive oxygen species (ROS; Narayanan and others 1997, 1999; Lorimore and others 1998; Wu and others 1999; Azzam and others 2002; Morgan 2003a, 2003b) including any products formed by reaction with hydrated electrons or OH• radicals (Ward 2002). Also, the diffusion of paracrine proapoptotic or antiapoptotic factors induced by upregulation of p21 (Chang and others 2000) may be involved. Because CDC2 is downregulated by α-particles, there may be reduced phosphorylation of connexin 43 by CDC2 and thus increased membrane permeability (Azzam and others 1998). This hypothesis is supported by the observation that membrane signaling is involved in the bystander effect for sister-chromatid exchanges and HPRT mutations induced indirectly by α-particles (Nagasawa and others 2002).
Regardless of the molecular mechanisms involved, the bystander effects observed with high-LET particles may have important implications for low doses of high-LET radiation. According to Sawant and others (2001a), “These results, if applicable in vivo, would have significant consequences in terms of radiation risk extrapolation to low doses, implying that the relevant target for radiation oncogenesis is larger than an individual cell, and that the risk of carcinogenesis would increase more slowly, if at all, at higher doses—an effect seen in vivo, as well as epidemiologically. Thus, a simple linear extrapolation of radiation risk from high doses (where they can be measured) to lower doses (where they must be inferred) would be of questionable validity.” In other words, it is speculated that there could be a convex, downward-curving dose-response relationship at low doses, and that extrapolation of data from high doses could lead to an underestimate of the effect at low doses of high-LET radiation.
A most critical question, however, is whether these types of bystander effects exist for low-LET radiation doses <100 mGy, which are the focus of this report. For α-particles and other high-LET radiation used in bystander studies, the dose to the nucleus was calculated to be 130–500 mGy per α-particle traversal, depending on the size and shape of the cell and its nucleus (Azzam and others 1998); that is, a flattened cell nucleus would have a much lower dose from high-LET radiation than a spherical rounded cell nucleus because of the geometry of the nucleus in relation to the radiation source (Clutton and others 1996a, 1996b). For low-LET radiation (assuming an RBE of 3), the dose corresponding to that from the high-LET radiation would be 0.39–1.5 Gy. Because the bystander effect resulting from an α-particle traversal through an irradiated cell was lower by a factor of 3–5 than the direct effect on the irradiated cell and because the magnitude of the bystander effect appeared to increase as the number of traversals through the cell increased (Sawant and others 2001a), one might expect that the same type of bystander effect would not be observed in the low-dose range <100 mGy for low-LET radiation. In fact, data indicate that the bystander effect for induced expression of p53 was much greater and persisted much longer after α-irradiation than after X-irradiation (Hickman and others 1994).
In human keratinocytes, a bystander effect for cell lethality that required cell-to-cell contact with gap junctions has been reported for γ-ray doses of 500 mGy and above (Mothersill and Seymour 1997). In the same dose range, a bystander effect that did not require cell-to-cell contact was
observed when cell culture medium from irradiated cells was added to nonirradiated cells (Mothersill and Seymour 1998a). The observed bystander effect is specific for keratinocytes because it was not observed for fibroblasts. The effect is eliminated by heating the medium at 70°C for 30 min, and there is some evidence that an alteration in energy metabolism and induction of apoptosis are involved (Mothersill and others 2000b). Furthermore, the bystander effect from transfer of medium varies among cell lines (Mothersill and others 2000b; Seymour and Mothersill 2000), and its contribution to cell lethality has been reported either to plateau with about 40% of human keratinocytes killed at 30–60 mGy (Seymour and Mothersill 2000) or to increase at doses over 1 Gy delivered to CHO (Chinese hamster ovary) cells (Mothersill and others 2000b). Finally, bystander cell killing reported for a dose as low as 10 mGy appears to be greater for delayed cell lethality quantified by cloning efficiency at about 14 d after irradiation than for initial cell lethality quantified by cloning efficiency determined immediately after irradiation (Seymour and Mothersill 2000). Delayed lethality is supposedly a manifestation of genomic instability associated with an increase in lethal mutations in cells that survive irradiation (Seymour and Mothersill 1997).
In another study, a low-LET radiation bystander effect that required gap junctions was observed in a three-dimensional Chinese hamster culture model (Bishayee and others 1999). The bystander effect that caused cell lethality in the nonirradiated cells became apparent only after the irradiated cells had undergone 1000–2000 disintegrations of 3HTdR in the DNA, that is, at a very high dose of about 2.5–5.0 Gy (Dewey and others 1965).
Several issues should be considered in relation to the bystander effect. First, in contrast with the results summarized above that involved enhancement of damage, a bystander effect was reported to increase survival (Dent and others 1999) when medium from γ-irradiated mammary carcinoma cells was transferred to nonirradiated cells 120 min after a dose of 2 Gy. Apparently, the soluble TGF-α (transforming growth factor-α) that was released induced secondary activation of EGFR (epidermal growth factor receptor), MAPK (mitogen-activated protein kinase), and JNK (c-jun N-terminal kinase), which resulted in an increase in survival. Thus, as reviewed by Waldren (2004) both beneficial and detrimental effects may result from the bystander effect. A similar observation was reported for normal human diploid lung fibroblasts exposed to low doses of α-particles; the observed enhancement of cell growth was hypothesized to result from an ROS-caused increase in TGF-β (Iyer and Lehnert 2000). Second, there is a suggestion that an adaptive response induced by a priming dose of 1 mGy for reducing radiation-induced micronuclei was due in part to a bystander effect (Broome and others 2002). However, the bystander effect of a priming dose has not been found to induce a radioprotective or adaptive response for chromosomal aberrations or cell killing (Wolff 1992b; Mothersill and Seymour 1998a). Third, an adaptive response induced by irradiating a cell directly may cancel out at least part of the bystander effect; this was observed for cell lethality when mouse C3H 10T1/2 cells were irradiated with 20 mGy of X-rays 6 h before α-particle irradiation (Sawant and others 2001b). Fourth, molecular mechanisms responsible for the bystander effect of low-LET radiation, as well as high-LET radiation, that may include genetic variation in transcriptional response to radiation exposure (Correa and Cheung 2004), have not been delineated. Fifth, recent results (Prise and others 2003) suggest that a bystander effect for cell lethality from soft X-ray irradiation (LET of 25–30 keV/μ) might be observed down to 50 mGy but not below. Sixth, until molecular mechanisms of the bystander effect are elucidated, especially as related to an intact organism, and until reproducible bystander effects are observed for low-LET radiation in the dose range of 1–5 mGy, where an average of about one electron track traverses the nucleus, a bystander effect of low-dose, low-LET radiation that might result in a dose-response curving either upwards or downwards should not be assumed.
HYPER-RADIATION SENSITIVITY AT LOW DOSES
Another factor that can cause the dose-response to deviate from the alpha-beta model is HRS that has been reported for cell lethality induced by low-LET radiation at doses up to 200 mGy (Joiner and others 1996; Skov 1999; Figure 2-3). In this dose range, survival can decrease to 85–90%, depending on the cell line, which is significantly lower than survival predicted by the value of α determined from survival values above 1–2 Gy. HRS might be associated with a bystander effect, but a recent study (Mothersill and others 2002) suggests that it is not. Although the magnitude of HRS varies, there is some evidence that it also occurs for fractionated doses of about 400 or 500 mGy both in vitro (Smith and others 1999; Short and others 2001) and in vivo for kidney and skin (Joiner and others 1996) and for glioma cell lines irradiated with multiple fractions of 700–800 mGy (Beauchesne and others 2003). Furthermore, an observed inverse dose-rate effect was attributed to HRS seen for low acute doses (Mitchell and others 2002), and recent cell cycle studies (Mitchell and others 2002; Marples and others 2003; Short and others 2003) suggest that HRS may be related to cells not arresting in radiosensitive G2. Since a high proportion of the target stem-like cells in humans would be noncycling G0 cells (see Chapter 3, “General Aspects of Dose-Response”), the last two observations, if generally true, would suggest that neither HRS nor the inverse dose-rate phenomenon should have any significant effect on the dose-response for cancer induction in humans.
Molecular mechanisms involved in HRS have been described in only a preliminary way. However, HRS for cell lethality up to 200 mGy was not observed in radiosensitive
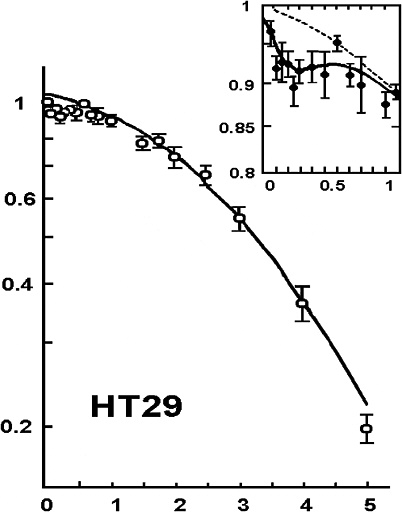
FIGURE 2-3 Illustrative example of hyper-radiation sensitivity for low doses. Example is from HT29 cells given graded doses of X-rays. SOURCE: From Joiner and colleagues (1996).
AT and XR-V15B cell lines (Skov 1999) or with high-LET radiation (Lambin and others 1993). For doses above 50–200 mGy, for which HRS is no longer observed, the flattening of the survival curve between 500 and 1000 mGy may be related to DNA PKcs activity (Marples and others 2002) or to the downregulation of the DIR1 gene (Robson and others 1997, 1999); this downregulation has been shown to correlate with an increase in rate of repair of DNA single-strand breaks (Robson and others 2000; Collis and others 2004; Marples and others 2004).
DNA damage introduced at a very low rate may not activate the radiation damage sensor ATM (Collis and others 2004). Consequently, exposure to low levels of chronic radiation may cause more cell damage than estimated from extrapolation of higher doses. This hypersensitivity to killing could serve to eliminate cells that have received DNA damage and potentially carcinogenic changes to their genome. Alternatively, it cannot presently be excluded that some of these cells may survive and proliferate as clones of mutated cells. It is important to note that the effect of cellular hypersensitivity to killing by very low chronic doses of ionizing radiation is a modest effect that has been detected only in some, but not all, human cell lines investigated.
Studies of other end points have provided some additional evidence of HRS. In a signal transduction study that used γ-ray doses of 20, 50, 100, 250, and 500 mGy, there was a suggestion of HRS up to 200 mGy for radiation-induced transcription of MDM2, ATF3, and BAX in a human myeloid tumor line (Amundson and others 1999b; Figure 2-4).
Similar observations over the same dose range were reported (Yang and others 2000) for X-ray induction of protein-8 (XIP8) in human MCF-7:W58 breast cancer cells; this protein as it complexes with Ku70/Ku80 appears to be an important cell-death signal. HRS was also observed in mice as gene deletions that reverted unstable mutations in melanocytes exposed to 10 mGy of X-radiation (Schiestl and others 1994); that is, there was a threefold effect at 10 mGy and a twelvefold effect at 1 Gy. The frequency of gene deletions was about 100 times higher than the frequency of other
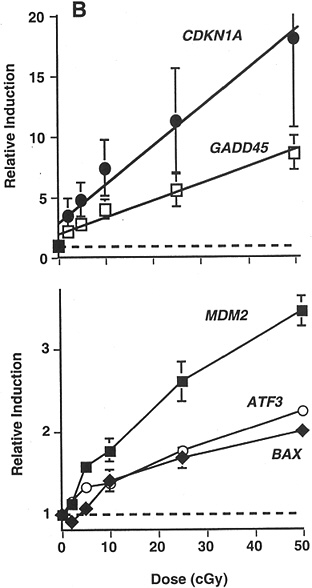
FIGURE 2-4 Maximal induction of CDKN1A (●), GADD45 (□), MDM2 (■), ATF3 (○), and BAX (◆) by low doses of γ-rays. Points are averages of four independent experiments; error bars are standard errors. Dashed line indicates basal level in untreated controls; solid lines were fitted by linear regression through the data. SOURCE: From Amundson and colleagues (1999b).
recessive mutations at other coat color loci; therefore, the authors speculated that the deletions resulted from nontargeted effects, such as increased recombination frequencies (i.e., genomic instability) in the proliferating melanocytes.
In summary, there are data suggesting HRS for cell lethality and signal transduction up to 200 and some data suggesting HRS for mutagenesis or genomic instability at up to 50 mGy. However, it is not clear (Malaise and others 1994; Skov 1999) whether HRS for cell lethality would cause an increase in deleterious effects in surviving cells or would actually decrease deleterious effects by increased killing of damaged cells. Also, it is not known what effect HRS for signal transduction pathways (such as that illustrated in Figure 2-4) will have in mitigating or increasing deleterious effects. Most important, it is not known if HRS plays a role when radiation doses <100 mGy are delivered over weeks to months, which could be relevant for low doses of low-LET radiation delivered to radiation workers.
OBSERVED DOSE-RESPONSE RELATIONSHIPS AT LOW DOSES
At the time of publication of the BEIR V report (NRC 1990) and during the next several years, dose-response relationships for induction of chromosomal aberrations and gene mutations by acute doses of low-LET X-irradiation were described quite satisfactorily down to ~200 mGy by the linear quadratic (alpha-beta) relationship discussed earlier. In general, low dose rates and fractionated doses reduced the induction frequencies by factors of about 2 or more, but the results were variable and included a few reports of inverse dose-rate effects (Thacker 1992). In this section, more recent experiments conducted with mammalian cellular systems that have measured frequencies of various events resulting from relatively low doses and low dose rates of X-rays or γ-rays are reviewed (Table 2-1). The objective is to summarize data acquired primarily since the 1990 BEIR V report that provide information on the shape of the dose-response curve down to 100 mGy. Whenever possible, these data will be related to human exposures, although caution should be exercised whenever attempting to extrapolate from in vitro systems to the human.
Normal human fibroblasts irradiated in plateau phase with doses of 109–6000 mGy gave a linear dose-response relationship for the induction of chromosomal aberrations detected by premature chromosomal condensation immediately after irradiation (Darroudi and others 1998); the slope was 6 × 10−3 fragments per cell per milligray (Cornforth and Bedford 1983). When the cells entered metaphase and were scored for chromosomal dicentrics and rings after repair or misrepair of DNA damage had occurred (released from confluence after potentially lethal damage repair had occurred), a β-component was apparent, and the α-component decreased to 5.8 × 10−5 aberrations per cell per milligray (Cornforth and Bedford 1987). Six laboratories collaborated in quantifying the frequency of chromosomal aberrations in human lymphocytes exposed to eight different acute doses from 3 to 300 mGy; a linear dose-response relationship was observed above 20 mGy, with a slope of 2.9 × 10−5 chromosomal aberrations per cell per milligray (Lloyd and others 1992; Figure 2-5).
Below 20 mGy, however, the data could not distinguish between a linear and a threshold model. When immortalized human lymphocytes were irradiated in G2 with four different doses from 50 to 500 mGy, a linear dose-response relationship was observed, with a slope of 2.5 × 10−5 chromosomal aberrations per cell per milligray (Puck and others 1997). These results are similar to those obtained with primary human skin fibroblasts (Cornforth and others 2002), irradiated while the cells were arrested in G0. For total aberrations per cell, an α-component of (5.8 ± 2.4) × 10−5/mGy for acute radiation corresponded to a linear dose-response relationship of (4.9 ± 2.0) × 10−5/mGy for low-dose-rate irradiation (0.5 or 1 mGy/min) between 300 and 6000 mGy. For dicentrics, the frequency was (1.9 ± 1.2) × 10−5/mGy for the low dose rate (LDRs). These LDR coefficients correspond to the limited slope (curve D) in Figure 2-1.
An extensive aberration study was conducted in which mice were irradiated daily for 21, 42, or 63 d at doses of 6.4, 18.5, or 55 mGy; lymphocyte cultures set up two weeks after irradiation was completed yielded a linear dose-response (1.2 × 10−5 chromosomal translocations per cell per milligray), with no evidence of either an adaptive or a supralinear response (Tucker and others 1998) (see Figure 2-6 in which the frequencies determined for painted chromosomes were corrected for the whole genome). The DDREF for acute exposures of 1–3 Gy was about 4–6 (see “General Aspects of Dose-Response Relationships” for definition of DDREF). Most important, the induced frequency of chromosomal translocations was not significantly different from that reported in workers at the Sellafield Nuclear Facility who were occupationally exposed to lifetime cumulative doses of more than 500 mSv, that is, (1.0 ± 0.25) × 10−5/mGy for smokers (Tawn and others 2000a). A subsequent analysis by Tawn and colleagues (2004) reported a linear dose-response between 50 and 1000 mSv of (1.11 ± 0.19) × 10−5 translocations per cell per millisievert.
In addition, the α-component is 1.9 × 10−5/mGy for the frequency of chromosomal translocations in lymphocytes of cleanup workers of the Chernobyl nuclear accident who received an estimated average dose of 95 mGy over 6–13 years (Jones and others 2002). These values are similar to the frequency of dicentrics (1.4 × 10−5/mGy) observed in people who were exposed to 100 ± 124 mGy of cobalt-60 over about 10 years (Liu and others 2002) and for Mayak nuclear workers exposed over 1–5 years (0.5–0.9 × 10−5/mGy for translocations; Burak and others 2001). Note that in the seven studies above, the dose-response relationships are consistent with a linear no-threshold model in which the aberration frequencies per milligray are similar.
TABLE 2-1 Dose-Response Relationships at Relatively Low Doses
|
End Point |
Dose Range, mGy |
Curve Shape |
Frequency of Events per Viable Cell per Milligray |
Comments and References |
|
|
Human fibroblasts in G0 |
Immediate PCC fragments |
109–6000 (acute) |
Linear |
6 × 10−3 |
LNTc extrapolates to 5 mGy (Cornforth and Bedford 1983) |
|
Human fibroblasts in G0 α-component-metaphase |
Chromosome dicentrics and rings |
1000–12,000 (acute) |
Upward curvature |
5.8 × 10−5 |
(Cornforth and Bedford 1987) |
|
Immortal human lymphocytes in G2 |
Chromatid gaps |
50–500 (acute) |
Linear |
2.5 × 10−5 |
LNT > ~50 mGy (Puck and others 1997) |
|
Human lymphocytes in G0 (six laboratories) |
Chromosome dicentrics |
3–300 (acute) |
Linear |
2.9 × 10−5 |
LNT > ~20 mGy (Lloyd and others 1992) |
|
Human primary fibroblasts in G0 (acute α-component) |
Chromosome aberrations |
1000–6000 (acute) |
Upward curvature |
5.8 × 10−5 |
α-Component for acute corresponds to linear dose-response for LDR (Cornforth and others 2002) |
|
Human primary fibroblasts in G0-0.5 or 1 mGy/min |
Chromosome aberrations |
300–6000 (LDR) |
Linear |
4.9 × 10−5 |
LNT > 300 mGy (Cornforth and others 2002) |
|
Mice—daily doses of 6.4, 18.5, or 55 mGy for 21, 42, or 63 d, respectively |
Chromosome translocations |
100–3500 (LDR) |
Linear |
1.2 × 10−5 |
LNT > ~100 mGy DDREFd of 4–6 for 1–2 Gy acute exposure (Tucker and others 1998) |
|
Nuclear workers at Sellafield—lymphocyte cultures |
Chromosome translocations |
50–1000 (LDR) |
Linear |
1.1 × 10−5 |
LNT > 50 mGy (Tawn and others 2000a, 2004) |
|
Cleanup workers at Chernobyl—lymphocyte cultures |
Chromosome translocations |
~95 (LDR) |
? |
1.9 × 10−5 |
Increase of 30% (10–53% p < .002) relative to controls (Jones and others 2002) |
|
Chinese hamster cells with human chromosome 11 |
Loss of antigen on chromosome 11 |
250–1500 (acute) |
Linear |
7 × 10−6 |
LNT > ~ 250 mGy (Puck and Waldren 1987) |
|
TK6 human lymphoblasts—daily doses of 10, 25, 50, or 100 mGy for 1 month |
HPRT mutations |
50–2000 (LDR) |
Linear |
6 × 10−9 |
LNT > ~50 mGy (Grosovsky and Little 1985) |
|
Mice—T lymphocytes in spleen—chronic at 0.69 mGy/min or 0.1 mGy/min |
HPRT mutations |
300–6000 (LDR) |
Linear |
3 × 10−9 |
LNT > ~300 mGy DDREF of ~1.5 for acute <2 Gy (Lorenz and others 1994) |
|
Cleanup workers at Chernobyl—lymphocyte cultures |
HPRT mutations |
~95 (LDR) |
? |
5 × 10−8 |
Increase of 41% (19–66% p < .001) relative to controls (Jones and others 2002) |
|
Chinese hamster cells with human chromosome 11 |
Genomic instability Translocations on chromosome 11 |
1000–10,000 (acute) |
Linear |
3 × 10−5 |
Based on percent unstable clones with BrdU saturates at 30% (Limoli and others 1999) |
|
Chinese hamster cells (CHO) |
Genomic instability de novo HPRT mutations |
2000 |
? |
5 × 10−5 |
Based on percent unstable clones; from 4 to 12 Gy saturates at 20% (Little 1998) |
|
Melanocytes in irradiated mice |
Genomic instability gene deletions |
10–1000 |
Linear |
8 × 10−5 |
LNT > 10 mGy, but supralinear from 0 to 10 mGy (Schiestl and others 1994) |
Three mutation experiments have yielded a linear dose-response relationship. First, the loss of an antigen marker on human chromosome 11 integrated in Chinese hamster cells and exposed to four different doses from 250 to 1500 mGy yielded a linear dose-response relationship with a slope of 7 × 10−6 mutants per viable cell per milligray (Puck and Waldren 1987). The relatively high frequency is due to the large target size because of the large distance between the antigen marker and essential genes on chromosome 11 (see “Induction of Gene Mutations in Somatic Cells”).
Second, human lymphoblast cells (TK6) exposed to one acute dose or to daily doses of 10, 25, 50, or 100 mGy for up to one month, with samples taken every 5 d, yielded a linear dose-response relationship for induction of HPRT or TK mutations (Figure 2-7). Over a total dose range of 50–2000 mGy, the slope for HPRT mutations was 6 × 10−9 mu-
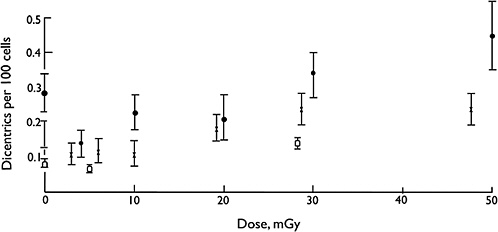
FIGURE 2-5 Dicentric yields as a function of dose; ●, Pohl-Ruling and others (1983); ![]() , Lloyd and others (1992), experiment 1; □ experiment 2. SOURCE: From Lloyd and colleagues (1992).
, Lloyd and others (1992), experiment 1; □ experiment 2. SOURCE: From Lloyd and colleagues (1992).
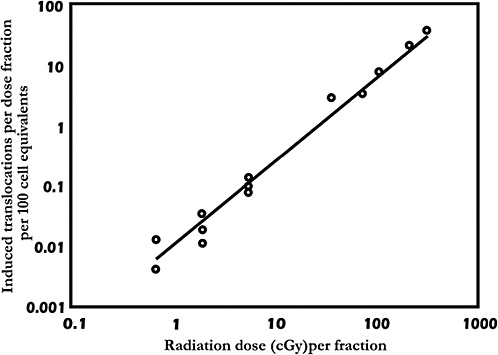
FIGURE 2-6 Induced translocations (observed frequency less control value) per dose fraction as a function of radiation dose per fraction. The line is the least-squares regression fit, with Y = 0.0121X1.367; R2 = 0.98. Five points on the upper part of the line represent the acute exposures (DDREF of 4–6), and the three sets of values on the lower portion of the line are from mice that received fractionated exposures. SOURCE: From Tucker and others (1998).
tants per viable cell per milligray (Grosovsky and Little 1985).
Third, mice were irradiated with total doses of 300–6000 mGy applied at an acute dose rate of 500 mGy/min or at a low dose rate of 1000 mGy/d (0.69 mGy/min) or 1000 mGy per week (0.1 mGy/min; Lorenz and others 1994). At 8–10 weeks after irradiation was completed, the frequency of HPRT mutants in splenic T lymphocytes for the LDRs was described by a linear dose-response relationship that had a slope of 3 × 10−9 mutants per viable cell per milligray. This is about one-tenth the frequency of HPRT mutants observed in lymphocytes of cleanup workers of the Chernobyl nuclear accident who received an estimated average dose of 95 mGy over 6–13 years (Jones and others 2002). An interesting observation in the mouse experiments was that an inverse dose-rate effect was not observed; the mutation frequency for 0.1 mGy/min was the same as that for 0.69 mGy/min. From a summary of data for radiation-induced mutations as function of dose rate (Vilenchik and Knudson 2000), an inverse dose-rate effect would not be expected if the induction of HPRT mutations in T lymphocytes in the spleen corresponded to the induction of specific locus mutations in spermatogonia. However, if they corresponded to the induction of HPRT mutations in cells in vitro, the mutation frequency for 0.1 mGy/min should have been about half that for 0.69 mGy/min.
By dividing the HPRT mutation frequencies for acute irradiation by the frequencies for LDR irradiation (obtained in the mouse T-lymphocyte experiment of Lorenz and others 1994 described above), the DDREF was 3–5 for acute doses greater than 3 Gy and about 1.5 for acute doses less than 2 Gy (Figure 2-8). The DDREF points (averages of 1.0) plotted for each of the LDRs were obtained by dividing the mutation frequencies for each total dose by the product of 3 × 10−6 mutants per viable cell per gray (value for LDRs) times the total dose. The range of DDREF values for acute doses are similar to those obtained for the same dose ranges in transformation in vitro (Han and others 1980) and animal carcinogenesis and life-shortening experiments (Ullrich and Storer 1979a; Ullrich and others 1987). (For definition and illustration of DDREF, see “General Aspects of Dose-Response Relationships.”)
Overall, the dose-response for radiation-induced genomic instability is quantitatively similar to that for radiation-induced chromosomal aberrations, with the exception that the frequency for genomic instability saturates between 4 and 12 Gy (Little 1998; Limoli and others 1999), while the frequency for chromosomal aberrations continues to increase with dose. After 10 Gy, 30% of the CHO clones were unstable for chromosomal aberrations, which was the saturation level reached after 4 Gy when the cells had incorporated BrdU (Limoli and others 1999). Furthermore, when induc-
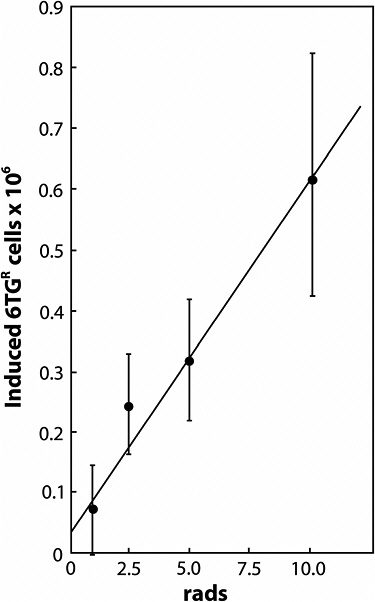
FIGURE 2-7 Frequency of 6TGR cells induced by 1–10 rads (0.01–0.1 Gy) of X-rays in TK6 human lymphoblastoid cells. Data points (with standard deviations) are from regression analyses of mutations induced per day at various dose rates (1–10 rads/d; 0-30 d) as described in Grosovsky and Little (1985).
tion of genomic instability was assayed as chromosomal aberrations in mammary epithelial cells at 25 population doublings after the cells had been irradiated in vitro or in vivo (Ullrich and Davis 1999), a downward-curving dose-response curve was observed between 0 and 0.25 Gy, with the response saturating between 1 and 3 Gy at about 0.35 aberration per cell. The percentage of CHO clones (containing a human chromosome 4) that were stable for chromosomal translocations in chromosome 4, had a linear dose-response of 3 × 10−5 events per irradiated cell per milligray between 1 and 10 Gy (Limoli and others 1999). For HPRT mutations in CHO cells, the percentage of clones that were unstable for de novo HPRT mutations was 5 × 10−5 events per irradiated cell per milligray, based on 10% being unstable after 2 Gy (Little 1998). Between 4 and 12 Gy, the percentage of unstable clones remained the same at 10–20%. For irradiated human blood lymphocytes stimulated with PHA (phytohemagglutinin) and analyzed 51–57 d after irradiation, the frequency of de novo aberrations was (3 to 10) × 10−5 chromosomal aberrations per cell per milligray (Holmberg and others 1998).
Genomic instability was also observed in mice as gene deletions in melanocytes exposed to X-irradiation (Schiestl and others 1994a), with a threefold increase at 0.01 Gy and a twelvefold increase at 1.0 Gy. The frequency of gene deletions was about 100 times higher than mutation frequencies; therefore, the authors speculated that the deletions resulted from nontargeted effects, such as an increased recombination frequency or genomic instability in the proliferating melanocytes. The dose-response was linear between 0.01 and 1.0 Gy and had a slope of 8 × 10−5 events per cell per milligray. Note that the three values listed above for the frequencies of radiation-induced instability (3–10 × 10−5 events per cell per milligray) are of the same order of magnitude as the frequency of chromosomal aberration induced directly by irradiation (1–4 × 10−5 events per cell per milligray; Table 2-1).
A malignant transformation experiment with primary hamster embryo cells exposed to five different doses from 0.03 to 1.5 Gy yielded a linear dose-response curve that had a slope of 4 × 10−6 transformants per viable cell per milligray (Borek and others 1983). An extensive collaborative study involving six laboratories that quantified malignant transformation of immortalized mouse C3H 10T1/2 cells exposed to
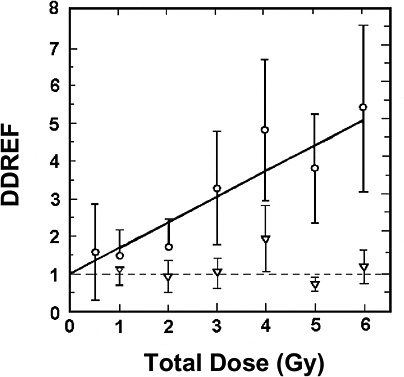
FIGURE 2-8 DDREF for low-LET 137Cs γ-rays: (○) dose rates 0.5 Gy/min; (∇) dose rates 1 Gy/d (0.69 mGy/min) to 1 Gy per week (0.10 mGy/min). SOURCE: From Lorenz and colleagues (1994).
seven different doses from 0.25 to 5.0 Gy reported a linear dose-response with a slope of 8 × 10−8 transformants per viable cell per milligray (Mill and others 1998). A study conducted with a human Hela hybrid cell system (Redpath and others 2001) reported a frequency of 4 × 10−8 transformants per viable cell per milligray beyond a threshold of ~0.3 Gy; however, the results were greatly dependent on the time the cells were trypsinized and plated after irradiation for the transformation analysis. Note that these results for transformation are quite variable and that the frequencies are ten- to a thousandfold lower than the frequencies for radiation-induced genomic instability. However, as discussed earlier under adaptive response, studies of malignant transformation in immortalized (already-transformed) cell lines may have little relevance to malignant transformation of normal nonimmortalized cells, especially in vivo where complex interactive processes can occur.
In summary, results of experiments that quantified chromosomal aberrations, malignant transformations, or mutations induced by relatively low total doses or low doses per fraction suggest that the dose-response relationship over a range of 20–200 mGy is generally linear and not affected significantly by either an adaptive or a bystander effect (Table 2-1). No data are available in this dose range for radiation-induced genomic instability. The question of the shape of the dose-response relationship up to about 20 mGy remains, although several of the dose-response relationships described above appear to be consistent with extrapolation linearly down to about 5 mGy. As has been pointed out (Cornforth and Bedford 1983), a macroscopic X-ray dose of about 5 mGy would, on the average, result in one to two electron tracks crossing the nucleus of each cell. Since the tracks are produced randomly, the proportion of nuclei traversed by zero, one, or two electron tracks would be about 0.37, 0.37, and 0.18, respectively. For lower doses, a larger and larger proportion of cell nuclei would receive no dose (track) at all. The nuclei that would receive a track would all receive (on the average) the same dose because the proportion receiving two or more tracks would diminish rapidly. Therefore, unless interactions among neighboring or surrounding cells influence the response, if 5 mGy produces an effect and if the effect is linear above 5 mGy, the dose-response curve must also be linear from 0 to 5 mGy. In addition to the existence of biological information at these very low dose levels, the committee concluded that the biophysical characteristics of the interaction of low-LET radiation with DNA, coupled with the characteristics of DNA repair, argue for a continuation of the linear response at lower doses. However, if a single electron track traversing a cell’s nucleus could induce an adaptive or bystander effect, the dose-response relationship below 5 mGy might deviate from linearity depending on whether cellular effects are decreased or increased. In the committee’s judgment, there is no evidence for either an adaptive response or a bystander effect for doses below 5 mGy.
Furthermore, the calculated value of 5 mGy for an average of one electron track per nucleus depends on the size and shape of the nucleus, as well as on the energy of the radiation (Rossi and Zaider 1996; Edwards and Cox 2000). For example, the calculated doses for an average of one electron track per nucleus are as follows: about 5 mGy for 60 keV and a 6-μm diameter sphere, about 4 mGy for 60 keV and a 7-μm sphere, about 3 mGy for 300 keV and a 6-μm sphere, and about 2 mGy for 300 keV and a 7-μm sphere. For the very low doses for which important signal transduction events may result from ionizations in either the nucleus or the cytoplasm, the volume of the whole cell might be most appropriate for these types of calculations. Possibly, the shape of the dose-response relationship up to 5 mGy might be determined with in vitro and in vivo experiments in which multiple doses of about 1–5 mGy are delivered over a long period. However, the question must be addressed rigorously by defining the molecular processes responsible for the end points in question at these very low doses.
SUMMARY
This chapter discusses the biological effects of the ranges of radiation dose that are most relevant for the committee’s deliberations on the shapes of dose-response relationships. Considering the levels of background radiation, the maximal permissible levels of exposure of radiation workers now in effect, and the fact that much of the epidemiology of low-dose exposures includes people who in the past have received up to 500 mGy, the committee has focused on evaluating radiation effects in the low dose range of <100 mGy, with emphasis on the lowest doses when relevant data are available. Effects that may occur as the radiation is delivered chronically over several months to a lifetime are thought to be most relevant.
Considerable emphasis has been placed on the dose-response and mechanisms for inducing chromosomal aberrations and gene mutations because, as discussed in Chapter 3, there is evidence that the induction of cancer is associated with these cellular responses. The general pictures that emerge from biophysical studies is that the misrepair of radiation-induced DNA DSBs that lead to chromosome aberrations are probably associated with the dominant postirradiation function of nonhomologous end joining repair processes described elsewhere is this report. Overall, biophysical approaches to the modeling of dose-response for chromosome aberrations, although not without some uncertainties on mechanisms, imply that the single-track α-component of radiation action will dominate at low doses and LDRs (i.e., the dose-response for all forms of aberrations will be linear at low doses and LDRs). Also, as observed, the response at LDRs and low doses, or after fractionated doses, should be lower by a DDREF; then the response to a single acute high-dose-rate exposure for which the two-hit β-component becomes important. In certain
cases, an inverse dose-rate effect for cell lethality and mutations has been reported for which the effect at very low dose rates is as high or higher than for single, acute, high-dose-rate exposures. The ability to demonstrate this phenomenon, however, is variable, and no mechanisms have been clearly identified to explain such effects.
Several factors may affect the theoretical dose-response relationships described above: variations in radiosensitivity during the cell cycle; induction of an adaptive response to an initial exposure, which can reduce the effect of later exposures; a bystander effect that causes an irradiated cell to have an effect on a nearby unirradiated cell; the induction of persistent genomic instability; and HRS in the low-dose region. Except for the cell cycle, these factors have been identified and studied since the BEIR V report (NRC 1990). These factors together with quantitative data on the induction of gene or chromosomal mutations in somatic cells are discussed.
Radiation genomic instability has been demonstrated by the manifestation of chromosomal damage in a certain fraction of irradiated cells over many cell cycles after they were irradiated. Data are critically needed for the definition of molecular targets and processes responsible for genomic instability in order to define and understand the dose-response relationship, and especially why the induction frequency saturates with only about 10–30% of the surviving cells manifesting genomic instability. A possibility that has not been investigated is that only a certain fraction of the cells, such as those in a certain part of the cell cycle, are susceptible to radiation-induced genomic instability. Because chromosomal instability has been associated with breakage-fusion-bridge cycles, the role of telomeres may be particularly relevant. Chromosome instability can also be initiated by DSBs that result in the loss of a telomere that protects the chromosome end and prevents chromosome fusion. Furthermore, from limited data, the similarity in the frequencies of genomic instability induced in X-irradiated cells and the frequencies of chromosomal aberrations induced directly by irradiation may suggest that the induction of chromosomal aberrations is a primary event that plays a major role in radiation-induced genomic instability. There is also some evidence that reactive oxygen species may play a role. However, until the molecular mechanisms responsible for genomic instability and its relationship to carcinogenesis are understood, extrapolation of the limited dose-response data for genomic instability to radiation-induced cancers in the low-dose range <100 mGy is not warranted.
An apparent adaptive response has been well documented for cell lethality, chromosomal aberrations, mutations, and in vitro transformation. The phenomena are illustrated by a reduction in response to a challenge dose of about 1 Gy delivered a few hours after a low priming dose of about 10–20 mGy. There is much variability in the ability to demonstrate the adaptive response, however. Data are needed, particularly at the molecular level, on adaptation induced when both priming and challenging doses are in the low-dose range <100 mGy; relevant end points should include not only chromosomal aberrations and mutations but also genomic instability and, if possible, tumor induction. Studies of the adaptive response for malignant transformation in immortalized (already-transformed) cell lines may have little relevance to malignant transformation of normal nonimmortalized cells, especially in vivo, where complex interactive processes can occur. In vitro and in vivo data are needed on the delivery of priming and challenge doses over several weeks or months at very low dose rates or with fractionated exposures. Specifically, an adaptive response resulting from the cumulative effect of multiple low doses of less than 10 mGy should be determined. Such data have not yet been obtained, particularly those explaining the molecular and cellular mechanisms of the adaptive response. Thus, it is concluded that any useful extrapolations for dose-response relationships in humans cannot be made from the adaptive responses observed in human lymphocytes or other mammalian cellular systems. Therefore, at present, the assumption that any stimulatory effects of low doses of ionizing radiation substantially reduce long-term deleterious radiation effects in humans is unwarranted.
A bystander effect in which an irradiated cell induces a biological response in a neighboring unirradiated cell has been observed with high-LET radiation for inducing cell lethality, chromosome aberrations, sister-chromatid exchanges, mutations, genomic instability, signal transduction pathways, and in vitro transformation. There is some evidence that long-lived reactive oxygen species or the diffusion of cytokines plays a role in the bystander effect. For low-LET radiation, the bystander effect has been limited to cell lethality and lethal mutations associated with reduced cloning efficiency. Recent results suggest that a bystander effect for cell lethality from soft X-ray irradiation might be observed down to 50 mGy but not below. Until molecular mechanisms of the bystander effect are elucidated, especially as related to an intact organism, and until reproducible bystander effects are observed for low-LET radiation in the dose range of 1–5 mGy, where an average of about one electron track traverses the nucleus, a bystander effect of low-dose, low-LET radiation that might result in modification of the dose-response should not be assumed.
HRS is a phenomenon for which doses less than about 200 mGy produce a dose-response for cell lethality that is steeper than that predicted from the classic D + D2 model. There are data suggesting HRS for cell lethality and signal transduction at up to 200 mGy and some data suggesting HRS for mutagenesis or genomic instability at up to 50 mGy. Furthermore, from limited data from only one laboratory, an observed inverse dose-rate effect for cell lethality was attributed to HRS seen for low acute doses, and cell cycle analysis suggested that HRS may be related to cells not arresting in radiosensitive G2. Since a high proportion of the target stem-like cells in humans would be noncycling, the last two observations, if generally true, would suggest that neither HRS
nor the inverse dose-rate phenomenon should have any significant effect on the dose-response for cancer induction in humans. Furthermore, molecular mechanisms associated with the two phenomena have not been delineated, and it is not known whether HRS for cell lethality would cause an increase in deleterious effects in surviving cells or would actually decrease deleterious effects by increased killing of damaged cells. Also, it is not known what effect HRS for signal transduction pathways will have in mitigating or increasing deleterious effects. Most important, it is not known if HRS plays a role when radiation doses <100 mGy are delivered over weeks to months, which could be relevant for low doses of low-LET radiation. Finally, until the molecular mechanisms responsible for HRS are understood, its role in low-dose radiation carcinogenesis is uncertain.
Results of experiments that quantified chromosomal aberrations, malignant transformation in vitro, or mutations induced by relatively low total doses or low doses per fraction indicate that the dose-response relationship over a range of 20–100 mGy is most likely to be linear and not affected significantly by either an adaptive or a bystander effect. No data are available in this dose range for radiation-induced genomic instability. Furthermore, as stated previously, studies of malignant transformation in immortalized (already-transformed) cell lines may have little relevance to malignant transformation of normal nonimmortalized cells, especially in vivo where complex interactive processes can occur. However, the results from these in vitro transformation studies may have relevance for effects involved in promoting the immortalization process, possibly through the induction of genomic instability. Thus, the question of the shape of the dose-response relationship up to about 20 mGy remains, although several of the dose-response relationships described above appear to be consistent with extrapolation linearly down to about 5 mGy. The shape of the dose-response relationship up to 5 mGy might be determined with in vitro and in vivo experiments in which multiple doses of about 1–5 mGy are delivered over a long period. However, this question should be addressed rigorously by defining the molecular processes responsible for the end points in question at these very low doses.






















