7
Scientific Evidence for Causation in the Population
INTRODUCTION
This chapter describes the kinds of scientific evidence used for establishing a general causal relationship between exposure and disease, an important input to presumptive service-connection decisions. Unlike individual service-connection claims, in which a particular veteran has to make a case that a particular condition affecting him or her was caused by or aggravated by military service, a presumptive service connection applies to a group, or population of veterans. Presumptive service connections remove the burden of proof from individual veterans, but establishing presumptions necessitates an assessment of the scientific evidence for population causal claims (i.e., was some group of veterans exposed to conditions or substances that aggravated existing or caused new health problems after service separation). More specifically, the goal is often to establish whether, in a population of individuals, exposures received by members of the population resulted in a change in the frequency of occurrence or in the average severity of a disease. For example, we might ask whether the frequency of non-Hodgkin’s lymphoma (NHL) among Vietnam veterans who were exposed to benzene during service is higher than the frequency among those who were not. If so, then we might assert that exposure to benzene is capable of causing NHL. The causal claim about the population does not mean that every veteran exposed to benzene during service will develop NHL or that every case of NHL would not have happened but for benzene exposure. On the population level, causal claims typically involve how risk (the probability of disease) changes in response to exposure.
In this chapter we will focus on the scientific issues involved in establishing these sorts of causal claims. We will review the issues facing scientists or others who review evidence to collectively decide on population causal claims. The next chapter provides a framework for doing so. At the start of this chapter, we discuss the types of scientific information considered in evaluating the strength of evidence for inferring causation. Then we discuss how epidemiologists define and assess association and how association differs from causation. This distinction is essential to understanding prior approaches to presumptive disability decision making and also this Committee’s proposed approach. In Appendix J, we offer an extended discussion of what we mean by causation and how it is modeled statistically. We have placed this material in an appendix, not as a reflection of its importance, but because the topic is too complicated to cover in a short section.
Next we discuss the scientific strategies used to establish association, and lastly we discuss the scientific strategies used to move beyond just determining the presence of an association to inferring causation. We conclude the chapter by discussing uncertainty—both with respect to association and with respect to causation. We leave to the next chapter a discussion of strategies for synthesizing potentially diverse sources of evidence into a single overall judgment of the strength of evidence for a causal claim.
SOURCES OF EVIDENCE
Evidence about population causal claims (hereafter just “causal claims”) comes from a variety of sources. In some cases, we have extensive knowledge about the mechanism by which exposure causes disease. For example, we do not need a randomized clinical trial to establish that bullet or shrapnel wounds have a deleterious effect on health. In other cases, such as low levels of exposure to lead and cognitive deficits in children, we know much less about the mechanisms and turn to other types of scientific evidence including findings of epidemiologic studies. Any scientific assessment of a causal claim combines the mechanistic knowledge and statistical evidence from epidemiologic studies. In this section we briefly survey the types of statistical evidence used to establish causal claims, and then we sketch the types of toxicologic, biologic, and mechanistic knowledge used to support or reject causal claims. By statistical evidence we mean the quantitative relationships between a set of measured variables in a sample. Case reports about individual patients may be useful for suggesting etiologic hypotheses, particularly with exposures that are followed quickly by disease onset.
Randomized Clinical Trials
The most persuasive human evidence for establishing a causal relationship comes through experimental studies in which investigators control exposure. Randomized clinical trials (RCTs) are the counterpart in humans to the controlled laboratory experiment with animals. In clinical trials, the exposure (usually considered as potentially beneficial, such as a new medication) is allocated randomly to the study population in such a way that the treated and untreated groups are otherwise equivalent, at least in expectation. If the randomization process has been successful, then any differences between the treated and comparison groups should reflect a causal relationship between treatment and disease (or outcome) risk. Randomization assures comparability of the two groups on factors that may affect the occurrence of the outcome.
Although the RCT is simple in concept, proper execution in human populations is often quite challenging and complicated. Even if randomization is successful in assuring comparability of exposed and comparison groups, validity of results for causal inference is not assured. For example, there are powerful placebo effects that operate in humans, which can be eliminated, in some instances, by concealing treatment status from the study participants. More subtle problems can arise when the doctors or others administering the treatment and collecting the outcome data are aware of treatment status. This potential for bias has prompted the use of the “double-blind” design, in which neither the study personnel in contact with participants nor the participants themselves know the treatment status. A refinement of this design is the crossover study, in which treatment and nontreatment are given in random order to each participant, allowing each person in the study group to be his or her own control. This design illustrates the kind of evidence we would like to have to draw causal claims, since we directly observe the response of the same person when they are treated and not treated, so that the treatment can be reasonably inferred to be the “cause” of any differences in response under the two conditions. Unfortunately, crossover trials are a practical approach only for studying short-term responses to agents for non-fatal conditions, so that they cannot be used for assessing effects of environmental exposures on chronic diseases.
In most other designs, including RCTs of standard design and most observational studies, we have to base such conclusions on differences in rates between exposed and unexposed groups of different individuals, rather than on the responses of the same individual in exposed and unexposed states. Interpretation of differences in outcome frequency as a causal effect when comparisons are made between different groups requires a form of inference known as “counterfactual.” Using the counterfactual (i.e.,
counter to the facts) we infer what would have happened in the exposed group had the exposure been some alternative by making a comparison with the outcomes of others who actually experienced the different exposure. The counterfactual approach needs comparability of the exposed and comparison groups.
RCTs and other experiments involving humans are ethically limited in the range of questions to which they can be applied. Many of the major questions of public health—for example, the effects of air pollution or pesticides on human health—cannot be addressed through RCTs because it is not ethical to expose humans experimentally to substances in quantities that are presumed harmful. For such questions, we are limited to passively observing the health of people “naturally” exposed—that is, to observational studies. Nonetheless, the model of the RCT remains useful as a framework for considering limitations of findings of observational studies. Randomized interventions can be ethically carried out to reduce exposure to harmful agents (e.g., tobacco use).
Observational Studies
In an observational study, the investigator does not control exposure of the people in the study and does not intervene in any way in the population under study. Although observational studies may lack the comparability of exposed and non-exposed characteristic of controlled experiments, they are nonetheless capable of providing evidence about the relationship between exposure and health and are generally the only option available to obtaining human evidence of the effect of potentially harmful exposures.
Broadly speaking, observational study designs fall into three categories: cross-sectional studies, cohort studies, and case-control studies. In cross-sectional studies, a variety of factors are recorded at a particular point in time. In cohort studies, persons exposed or unexposed to a given factor are observed over a period of time for health effects related to the exposure. The case-control study compares persons with a given disease (cases) to those without the disease (controls) with regard to their history of exposure. Each of these general designs has appropriate analytic strategies, and each design has its own strengths and weaknesses. There are variations of each of these approaches, and a few additional approaches as well (for example, case-crossover studies). These designs are well described in standard epidemiologic references.
One general difficulty of observational studies, regardless of design, is that exposure is not randomized. Rather, exposure status may be determined by where people live or work, what they eat, what social group they belong to, or by a host of other factors that can be associated with disease risk. As a consequence of these other factors, associations between expo-
sures and disease risk may occur even if the exposure does not cause the disease. Conversely, no association may be measured when the exposure actually does cause disease because these factors act to reduce the effect.
Toxicologic, Mechanistic, and Biologic Knowledge
In addition to randomized clinical trials and observational studies, which provide statistical evidence of a relationship between exposure and disease, a wide variety of other types of scientific evidence may be crucial for inferring a causal relationship between exposure and disease (IOM, 2006a,b; IOM/NRC, 2005). Controlled laboratory experiments with animals and research in in vitro systems and other relevant biological, physical, or even social data can be used to assess the likelihood that a given substance or circumstance can cause a particular human health effect. Approaches to assessing the combined evidence from human and animal investigations, as well as from in vitro systems, have been formulated by a number of agencies including the International Agency for Research on Cancer (IARC, 2006b), the Institute of Medicine (IOM) (IOM, 2006b; IOM/NRC, 2005), and the Environmental Protection Agency (EPA, 2005). These formalized approaches offer guidance on assessment of evidence and relative weighting of various lines of evidence.
Even without statistical evidence from epidemiologic studies, the findings of animal studies and mechanistic investigations on how an agent causes a health effect can be sufficiently convincing to support a causal conclusion. For example, IARC identified benzo(a)pyrene as a human carcinogen primarily based on non-epidemiologic evidence (Straif et al., 2005). However, we infrequently amass this level of biological understanding for agents affecting human health. More typically, non-epidemiologic lines of research are considered to support the conclusion that a substance, or chemical, “probably” causes, or is “likely” or “reasonably anticipated” to cause an adverse effect such as cancer or other health endpoints (e.g., EPA, 2005; IARC, 2006b; NTP, 2005; NTP CERHR, 2003, 2005). When there are epidemiologic findings supporting an association between an agent and disease, however, experimental or other biological evidence may provide sufficient weight and understanding for scientists to conclude that the association is due to a causal relationship. For example, in several species the agent may produce the same effect as observed in human studies, and by a mechanism that is conserved and relevant across species with key features of the mechanism observed through experiments in human cell lines or other systems.
As a case in point, epidemiologic, animal, and mechanistic data were all considered in establishing that industrial exposure to butadiene can cause lymphohematopoietic cancers (IARC, 1999). Epidemiologists showed that
styrene-butadiene exposed rubber workers had elevated lymphohematopoietic cancer rates. Toxicologists showed that potentially carcinogenic metabolites of butadiene in butadiene-exposed workers activated potential oncogenes, providing mechanistic knowledge on carcinogenesis, and biologists induced tumors in mice and rats, both with exposure to butadiene and to a known metabolite that occurs in humans and mice and rats, providing animal evidence.
Formaldehyde provides a contrasting example. IARC (2006a, sec. 5-2) noted that epidemiologic studies found “strong but not sufficient evidence for a causal association” between formaldehyde exposure and leukemia. Their interpretation of the finding as causal was guarded because of some limitations in the several positive studies (e.g., small numbers of deaths) and lack of finding of effect in a high-quality study. There was uncertainty with regard to possible underlying mechanisms. The IARC monograph noted lack of good rodent models for human acute myeloid leukemia. It also considered various possible mechanisms, “such as clastogenic damage to circulatory stem cells” (IARC, 2006a, sec. 5-4). Unable to identify a mechanism for the induction of leukemia in humans from formaldehyde and data to support it, IARC did not conclude that formaldehyde was a known cause of human leukemia. Golden et al. (2006) have advanced arguments that the relationship could not be causal. For example, they argued that inhaled formaldehyde is so reactive that it is unlikely to travel as formaldehyde from the upper airways to the bone marrow; also they argued that “there is no indication that formaldehyde is toxic to the bone marrow/hematopoietic system” as are other known leukemogens benzene, ionizing radiation, and chemotherapeutic agents (Golden et al., 2006, p. 146).
ASSOCIATION AND CAUSATION
Association
Absent strong mechanistic understanding, the first step towards establishing a causal relationship between exposure experienced by people and a disease is to establish a statistical association between exposure and the disease. Exposure and disease are positively associated in a group if the incidence of disease among those exposed is higher than the incidence among those not exposed. For example, in the early 1950s Doll and Hill demonstrated that tobacco smoking and lung cancer mortality were associated. In a cohort of British physicians, lung cancer mortality was much higher among people who smoked 25 g of tobacco daily compared with those who didn’t smoke (Doll and Hill, 1954, p. 1530). Even though a detailed mechanism between inhaling smoke and contracting lung cancer was not evident, a vague but plausible mechanism based on the carcinogenic proper-
ties of tobacco tar allowed scientists to hypothesize that the association was produced by a causal relationship. Had there been no observed difference in lung cancer mortality between smokers and nonsmokers, they would have likely assumed that smoking had no causal influence on lung cancer.
The strength of association between exposure and disease is typically measured with a statistic called the relative risk (RR). RR is the ratio of the incidence of disease among the exposed over the incidence in the unexposed:
An RR of 1.0 means that the frequency of disease among the exposed is the same as among the unexposed. An RR of 10 means that the rate of disease among the exposed is 10 times as high as among the unexposed.
A high RR does not imply a high absolute risk in the population. If, for example, one in a million unexposed individuals and 10 in a million exposed individuals get the disease, then the RR is 10, even though the chances of getting the disease among those exposed is only 1 in 100,000.
Another measure of association, commonly used in case-control studies, is the odds ratio (OR):

From this formula, it can readily be seen that the OR, expressed in the first line as the odds of exposure in cases divided by the odds of exposure in controls, is also (second line) the odds of disease in the exposed divided by the odds of disease in the unexposed. The OR has the desirable property of being approximately equal to the RR if the disease is rare (Greenland and Thomas, 1982). This is true even though the absolute risks in exposed and unexposed cannot be estimated from case-control studies.
Association Is Not Causation
Association is not the same as causation. It is prima facie evidence for causation, but not sufficient by itself for proving a causal relationship between exposure and disease. For example, although they did not record its presence, Doll and Hill would presumably have found a high positive
association between having tar-stained fingers and lung cancer mortality in their study. Clearly having tar stains on one’s fingers does not by itself cause lung cancer, but it could be associated with lung cancer risk because heavier smokers, at greater risk for lung cancer, would also be more likely to have tar-stained fingers.
Unlike associations, causal claims support making counterfactual claims, that is, claims about what the world would have been like had something been different, or changed. For example, what would have been the rate of lung cancer mortality among a group of smokers had they been prevented from smoking? For this, the counterfactual claim would be the rate of lung cancer mortality among never smokers. What would have been the rate of lung cancer mortality among those with tar-stained fingers had we eliminated their stains with special soap? Although tar stains and smoking are both associated with lung cancer, we can answer these questions because we know the causal mechanisms: smoking is a common cause of tar stains and lung cancer, but tar stains by themselves have no effect on lung cancer mortality. Service-connection claims require the same attention to counterfactual questions: what would have been the rate of adult-onset type 2 diabetes had Vietnam veterans not been exposed to Agent Orange, for example.
Claims about association alone do not support the sorts of claim that must underlie presumptive service connections, while causal claims do. We call an association that arises in a population from an exposure that causes disease a causal association. Associations are termed spurious if they arise for some other reason. For example, the association between tar-stained fingers and lung cancer is spurious.
Spurious associations can arise in many ways. One is from a common factor (confounder) that is associated with the exposure under study and also a cause of the disease of interest, and another is from reverse causality (the disease is a cause of exposure) as depicted in Figure 7-1.
In the context of presumptive service connections, exposure typically occurs prior to the medical condition under consideration. Thus, we can almost always rule out the possibility that a medical condition was a cause of exposure, but the development of disease may influence apparent exposure. For example, it has been speculated that early subclinical manifestations of diabetes could increase storage of polychlorinated biphenyls (PCBs) in the body, leading to apparent associations of PCBs with diabetes even when the exposure is measured years before the emergence of the disease. More intuitively, people developing asthma might choose to not have cats if the presence of a cat exacerbated their asthma. The inverse association that would be observed between asthma and cat ownership would represent reverse causation and not a causal, protective effect of cats on risk for asthma. Thus, reverse causation may produce a spurious association even with carefully collected prospective data.
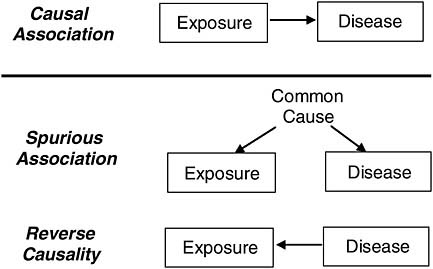
FIGURE 7-1 Causal and spurious associations.
If we can measure potential confounders (i.e., common causes) that might give rise to spurious association, then statistical adjustment can be used to remove the part of the observed association that arises spuriously from confounders. We discuss this strategy in a later section.
There is also the possibility that exposure causes disease, but that the two are not associated in the population under study. For example, if a confounder produces negative association between exposure and disease, but the true causal relationship produces positive association, and the two associations (true and confounded) are of roughly same magnitude, then the observed association will be small as represented in Figure 7-2. Note that dropouts are excluded from this example. Fortunately, because hiding a causal association requires a spurious association of similar magnitude but opposite sign as the causal association, this situation occurs infrequently.
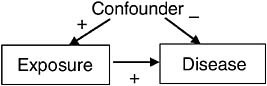
FIGURE 7-2 Scenario for causation without association.
The Problem of Bias
Even if confounding and reverse causation can be ruled out (or statistically controlled for, as we discuss below), observational studies might still be affected by other forms of bias, including information bias and selection bias. Bias in this context does not suggest prejudice on the part of the researcher, but rather denotes systematic error arising from the collection of information or the selection of participants that produces an observed association not attributable to an underlying causal relationship between exposure and disease. For example, systematic error might occur in a case-control study of patients with pancreatic cancer in which most of the cases have died before they could be interviewed. If the interviewer relies on family members for information about exposures of the dead person but on living controls themselves, then the quality of the exposure information is likely to differ for the cases and the controls. Differential quality of data for cases and controls can in turn easily distort the true association between an exposure and a disease. This would be an example of information bias, a broad class of bias that relates to the quality of data collected. Another kind of bias is selection bias, which occurs when the selection process by which the study sample is derived distorts the relationship between exposure and outcome. For example, suppose half of the patients in the treatment arm of an RCT drop out of the study from side effects, while no one from the control arm drops out, and suppose that the dropouts are the ones who began the study in worse health. Even if the treatment has no benefit whatsoever on the outcome, the treated group will appear to fare better than the untreated group. Once possible biases are identified, their possible impact on the results can be assessed through sensitivity analysis (discussed below).
EVIDENCE FOR ASSOCIATION
Although it is not sufficient for establishing causation, association is nevertheless prima facie evidence for causation, and the lack of association is prima facie evidence for lack of causation. Thus, if mechanistic knowledge is insufficient to settle the issue, a first stage in any evidence-based approach to presumptive service connection is to empirically establish and quantify the level of association in the service population under consideration, or in similarly exposed populations.
Epidemiologists (e.g., Rothman, 2002) use risk measures such as the RR and the OR to quantify the association between exposure and disease in a population. Other measures might also be of interest, such as the attributable fraction (AF)—the proportion of disease in either the total population or an exposed subgroup that is caused by exposure—which is
particularly relevant for compensation policy (see next chapter). This report uses the terminology service-attributable fraction (SAF) when the subgroup of interest is a military population. More complex conceptual and statistical models are needed when there are several risk factors to be considered in combination, as will be discussed later in this chapter.
Risk measures are estimated by applying statistical techniques to data from a particular sample drawn from the population of interest (e.g., a study of 1,000 randomly selected veterans of a particular conflict). The result of this process is an estimate of the population risk measure (e.g., the RR), together with a measure of the uncertainty in those estimates (a standard error or confidence interval) caused by the inherent variability in a random sampling process. Note that these uncertainty estimates usually account only for random variation, not the consequences of any bias.
Statistical techniques are also used to test specific hypotheses, particularly the null hypothesis that there is no association between exposure and disease in the population. The null hypothesis is of particular interest—unless it can be rejected, there is insufficient empiric evidence to conclude the existence of an association in the population.
The statistical tests related to the null hypothesis are referred to as significance tests, and the test results are commonly expressed in the form of a P value, the probability of observing a sample result at least as extreme as that observed in the sample if the null hypothesis were true. Note that the P value does not provide the probability that the null hypothesis is true given the observed data. That would require specification of one’s prior belief in the null hypothesis before seeing the data. Additionally, failing to find the P value needed to reject the null hypothesis at some level of probability does not exclude the possibility of an association. There should be enough precision to rule out a counter explanation that the study was inadequate to detect a meaningful effect size.
EVIDENCE FOR GOING BEYOND ASSOCIATION TO CAUSATION
If an association has been established, the next (and more difficult) task is to assess the evidence for causation by trying to eliminate alternative explanations to causality for the association. For example, tobacco companies and some academic researchers initially dismissed the association between smoking and lung cancer by proposing explanations other than causation. Arguments were advanced such as: perhaps a poor economic background would expose someone to conditions besides smoking that would lead to lung cancer and would also make them more likely to smoke or perhaps there are genes that dispose people to smoke and also to be more susceptible to lung cancer. Only after some years of epidemiologic research, animal studies, and scientific debate did the scientific community
reject all alternative explanations and conclude that the association between smoking and cancer is causal. Postulating and eliminating alternatives are core skills in observational research. This process can use data from many sources, including the basic sciences and toxicology. If reasonable alternatives are possible, then we cannot move beyond association to a firm causal conclusion.
Experimental Control: Inferring Causation in RCTs
Randomized clinical trials remove two of the possible alternative explanations of an observed association: confounding and reverse causality. By assigning treatment (exposure) randomly, the design removes the influence of any confounder that might influence exposure (Figure 7-3a), and the influence of the outcome on exposure, if there is any (Figure 7-3b). Done properly, and setting aside the play of chance, only a causal relationship from exposure to health outcome should produce observed association in an RCT (Figure 7-3c). However, RCTs are generally not possible for the kinds of causal questions facing VA in presumptive disability decision making.
Statistical Control: Inferring Causation from Observational Studies
Adjusting for Confounding
When associations are found in observational studies, the first approach for removing spurious associations from confounders is statistical control of characteristics that may differ between exposed and unexposed persons (i.e., adjustment). Multiple regression models are one way to estimate the association between exposure and outcome after adjusting for charac-
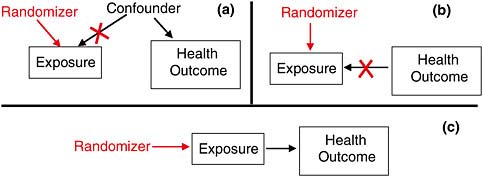
FIGURE 7-3 The power of randomization.
teristics of participants that might confound the results. If investigators have successfully measured characteristics that distort the results, then adjustment of these factors will help separate a spurious from a causal association.
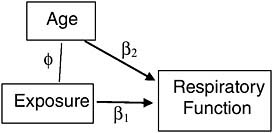
For example, suppose we conduct an observational study of veterans, each exposed during service to some level of a toxin that can permanently degrade respiratory function. Suppose further that older veterans are more likely to have been exposed to more of the toxin, as it was used more frequently in the early segment of a war. Since age (after military service) also naturally degrades respiratory function, it is a confounder of the association between the exposure and respiratory function in this study (Figure 7-4) and must be included as a covariate in a multiple regression to adjust for its biasing effect. If age is the only such confounder in the study, and it is measured accurately, then we can indeed separate the spurious from the causal association statistically.1
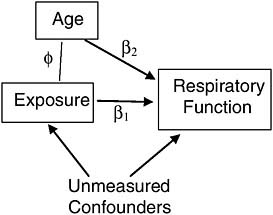
Two problems are common in such an approach, however. First, unlike randomization, which can eliminate the influence of all confounders without having to identify and measure any of them, appropriate statistical adjustment for confounders requires identifying and measuring all of them. If, for example, age were not the only confounder of the association of exposure with respiratory function (Figure 7-5), then the association between exposure and respiratory function, statistically adjusted for age, would still combine both spurious and causal association, and thus present a misleading estimate of the effect of exposure on respiratory function.
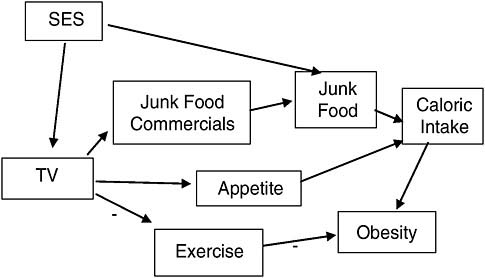
Deciding which variables to control for in a statistical analysis of the association between exposure and disease depends upon knowledge about the possible mechanisms connecting them. For example, dozens of observational studies, some involving thousands of subjects, have shown an association between watching TV and childhood obesity (IOM, 2006a). Can we move beyond an association and say that watching TV causes childhood obesity?
These studies include a variety of statistical adjustments, depending on the mechanisms the researchers consider important. The primary mechanisms thought to connect TV and obesity are shown in Figure 7-6. Thus, several studies controlled for socioeconomic status (SES), as a child from a low socioeconomic status home might be allowed to watch more TV and also allowed to eat a higher proportion of high-calorie/low-nutrition foods
(“junk” foods). Several studies attempted to separate out the potential contribution of TV to obesity through replacing or suppressing exercise, which in turn would lead to more obesity, or by increasing caloric intake, either through increasing exposure to food marketing, or by increasing appetite through other means (e.g., people like to snack when they are relaxing passively in front of a TV). Being able to identify these mechanisms allows us to identify and control for potential sources of spurious association and also to tease apart the importance of a variety of possible mechanisms.
Measurement Error
A further problem in adjusting for spurious associations involves measurement error. If a confounder has been included in the statistical analysis as a covariate but has been measured poorly, then the included variable is only a surrogate for the true variable. This is equivalent to partially omitting the variable and thus does not allow all confounding bias to be removed from the estimate of the causal association (Kennedy, 2003). The more measurement error in the confounding variables the greater the potential for incomplete control of bias.
Another problem similar to measurement error occurs when covariates are measured too coarsely. If, for example, TV was not measured in minutes per day, but rather as high, medium, and low, then differences in TV watching levels within these coarse categories could still affect the probabilities of exposure to junk food commercials. Statistically adjusting for this imprecise measure of TV would fail to remove all confounding.
To summarize, statistically adjusting for confounders can separate the causal from the spurious association between exposure and disease, but it can do so completely only if all confounders have been identified, measured accurately, and represented in a valid statistical model. Thus, in assessing a report on a study that claims that adjustment for confounding has been made, the adjusted association estimates the causal association if the study has
-
included all reasonable confounders,
-
measured them with reasonable precision and accuracy, and
-
used them in a valid statistical model.
Instrumental Variables
An alternative to measuring and adjusting for confounders is instrumental variable estimation, a technique favored by econometricians (Kennedy, 2003) but not yet widely used in epidemiology (Greenland, 2000). An instrumental variable must be related directly to the putative cause but independent of all
potential confounders. Under this condition, we can separate variation in the cause that might spuriously come from the confounders or from reverse causation from true variation in the cause that will translate to variation in the effect. By using the instrument to show how much of the variation is not from the confounders and not from reverse causation, we can then statistically adjust the observed association between cause and effect without even measuring the confounders or being concerned about reverse causation.
An example of an instrumental variable might be distance from the hypocenter for veterans of a nuclear weapons test. The true causal variable here would be their ionizing radiation exposure. For some participants this may have been measured by a film badge dosimeter, but these measurements are incomplete and inaccurate. However, one could use the mean of the measured doses for all participants located at the same distance from the hypocenter as an instrumental variable for assigning dose to all participants, and then examine the relationship between these assigned doses and subsequent cancer risk. Assuming a Service member’s assignment to a particular location during the test was effectively at random with respect to potential confounders (Service members weren’t assigned to locations based on their future cancer risks), this would be expected to yield an unbiased assessment of the exposure-response relationship (Figure 7-7).
Although instrumental variable estimation is a potentially powerful strategy for separating causal from spurious association, it depends heavily on the availability of an informative instrumental variable and on the untestable assumption that the instrument is independent of all the other potential confounders and not an independent risk factor for disease given radiation dose. Thus, its practical applications in epidemiologic research are limited.
Other Guides to Causal Knowledge
There have been several attempts to create sets of criteria to guide scientific judgments when moving beyond observed association to causa-
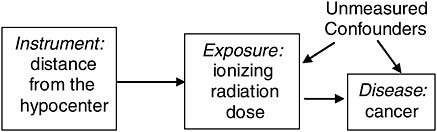
FIGURE 7-7 Instrumental variable.
tion. Some of these criteria can be traced to the “canons of inference” proposed by John Stuart Mill (1862). In the early days of microbiology, Koch developed his famous “postulates” as formal criteria for establishing a causal association of a clinical infectious disease with a microorganism. Koch’s postulates include the identification of the suspect causal organism in people with the disease and the causation of the illness in an animal by infection with the organism (Koch, 1884). Unfortunately, such experimentally based criteria are of little help in establishing the causality of an environmental exposure with a chronic disease. The version of the criteria most familiar to epidemiologists and other public health researchers is the Bradford-Hill criteria, which are: the strength of the association, consistency, specificity, temporality (logical time sequence), dose-response (biologic gradient), plausibility, coherence, experimental evidence, and analogy (Hill, 1965). Although each of these criteria has limitations or exceptions, they can be useful guides to assessing the overall evidence. For example, see the introductory chapter in the 2004 Surgeon General’s report on smoking (DHHS/CDC, 2004).
As we discussed above, background knowledge about the biologic mechanisms by which an exposure might or might not cause disease can prove crucial in establishing a causal claim or its negation. The tools of experimental biology have been extraordinarily valuable in developing insights into human physiology and pathology. Such laboratory tools have been extended to explore the effects of putative toxins on human health, especially through the study of model systems in other species. The field of toxicology has flourished in recent decades, allowing arguments of plausibility to be developed for a range of environmental toxicants. At the same time, species can differ in fundamental aspects of physiology (e.g., metabolism, hormonal regulation) that limit extrapolation from one species to another.
REALISTIC CAUSAL INFERENCE
Multifactorial Causation
Epidemiologists have long recognized that most chronic diseases, such as cancer or coronary heart disease, result from a complex “web of causation,” whereby one or more external agents (exposures) taken into the body initiate a disease process, the outcome of which could depend upon many factors including age, genetic susceptibility, nutritional status, immune competence, social factors, and others. Exposures may occur over an extended period of time with some cumulative effect, and exposure to multiple agents together could result in synergistic or antagonistic effects different from what might result from each separately. These general notions were formal-
ized by Rothman (1976) in a “sufficient component causes model,” which postulates that disease can result from a number of different constellations of causal factors, each of which may comprise several components (e.g., exposure plus susceptibility plus timing) that are all necessary to make them a complete cause. This framework is useful in thinking about exposure to multiple causal factors. For example, consider the diagram in Figure 7-8.
Consider the data from a hypothetical epidemiologic study of veterans exposed to some particular exposure illustrated in Table 7-1. In this hypothetical example, smoking is a much larger contributor to risk than is the military exposure of the participants, but the two factors are not confounded, since among the population at risk, the proportion of smokers is the same in the exposed and unexposed. It is also evident that the two effects on risk are multiplicative, since individuals with both factors Background causes Radiation alone Smoking aloneRadiation and smoking jointly
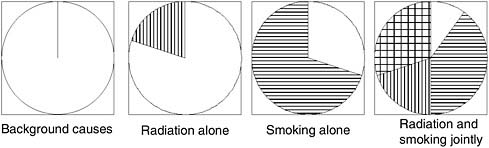
FIGURE 7-8 Rothman’s sufficient component causes model.
NOTE: Each circle represents a different constellation of factors that is sufficient to produce disease; within any circle, the sectors represent specific factors that are all necessary to comprise a complete cause. Blank space represents host susceptibility plus background exposures; vertical bars, ionizing radiation; horizontal bars, tobacco smoking; cross-hatched, joint action of smoking and radiation.
SOURCE: Rothman, 1976.
TABLE 7-1 Hypothetical Example of Military Radiation Exposure, Smoking, and Cancer
|
Military Radiation Exposure |
Smoking Habit |
Number at Risk |
Cancer Cases |
Relative Risk |
|
No |
Never |
1,000 |
10 |
1 |
|
No |
Current |
1,000 |
100 |
10 |
|
Yes |
Never |
1,000 |
30 |
3 |
|
Yes |
Current |
1,000 |
300 |
30 |
have an RR of 30, the product of the RR for smoking (10) and for military exposure (3). In other exposure situations, the pattern of combined effects could be less than multiplicative, or greater. Two specific models have special relevance to compensation policy. The first is the multiplicative model just illustrated, which can be represented mathematically as
where RRE is the RR for exposed nonsmokers relative to nonexposed non-smokers, and RRS is the RR for unexposed smokers relative to unexposed nonsmokers. Under this model, the effect of exposure is the same in both nonsmokers (RRE|NS = 3) and smokers (RRE|S = 30/10 = 3). The other important situation is an additive model of the form:
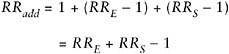
In other words, the risk from exposure to both factors is the background risk plus the sum of the additional risks from each factor separately. Thus, in our hypothetical example, if the single-factor risks were as before, we would have expected an RR for exposed smokers of 1 + (10 − 1) + (3 − 1) = 12, rather than 30 as above. Under this model, the excess RR (ERR = RR − 1) for exposure is the same in nonsmokers (ERRE|NS = 3 − 1 = 2) and smokers (ERRE|S = 12 − 10 = 2). Of course, the actual joint effect could be different from either of these specific models. The effect when both exposures are present could be less than additive (e.g., a joint RR of 11), greater than multiplicative (e.g., 50), or in between (e.g., 20).
Models for Interaction
Epidemiologists use the term interaction (or effect modification) to denote the departure of the observed joint risk from what might be expected based on the separate effects of the factors. However, any estimate of interaction is model specific, meaning it depends on what model of interaction we expect (multiplicative, additive, or some other). In claiming interaction, one must therefore specify the model for the combined effect from which the observed data deviate. For example, one could define a multiplicative interaction RR as
or an additive interaction RR as RRInt(add) = RRjoint − RRE − RRS+ 1. For the data illustrated in the table above, RRInt(mult) = 30/(3 × 10) = 1 and RRInt(add) = 30 − 3 − 10 + 1 = 18, indicating no departure from a multiplicative model but a large positive deviation from an additive model. Likewise, if the joint RR were 12, the multiplicative interaction RR would have been 0.4 and the additive interaction would have been 0, indicating a less than multiplicative joint effect and no departure from an additive model. These concepts have natural extensions to more than two risk factors, such as the inclusion of main effects and interactions in the widely used logistic regression model (which assumes a multiplicative model). The following chapter will describe how these parameters can be used to estimate the proportion of disease among exposed individuals that is attributable to the separate or joint action of each factor or other unknown factors, and the relevance and limitations of such estimates for attributing causation in individuals.
The previous example presumes that there is no causal connection between the military exposure and smoking—that prior smoking did not cause the individual’s exposure in the military or vice versa. If this assumption did not hold, a very different analysis would be required. For example, suppose a nonsmoking recruit received a serious battle wound leading to amputation, which subsequently caused him or her to take up smoking for self-medication, and he or she ultimately developed lung cancer. In this case, one might wish to estimate the direct effect of battle trauma on lung cancer risk and the indirect effect mediated through smoking. However, as a policy matter, one might conclude that both routes were ultimately the consequence of battle trauma and should not be distinguished for the purpose of deciding on compensation. In other words, an individual’s smoking history would be irrelevant.
UNCERTAINTY
The science of estimating the causal influence of an exposure on disease, especially in cases where controlled experiments are not feasible, is fraught with uncertainty. Dealing with uncertainty in a principled way is one of the goals of statistics, however, and it need not stop us from rational analysis. In this section we provide a framework for dealing with the uncertainty inherent in assessing population causal claims.
There are three levels of uncertainty in making a case for a service connection:
-
Uncertainty as to the correct causal model
-
Uncertainty as to the statistical (parameter) estimates within each model
-
Uncertainty about the specifics of a given individual within a group
The uncertainty about the correct causal model involves uncertainty about whether exposure in fact causes disease at all, about the set of confounders that are associated with exposure and cause disease, about whether there is reverse causation, about what are the correct parametric forms of the relations of the exposure and confounders with outcome, and about whether there are other forms of bias affecting the evidence. One currently used method for making this uncertainty clear is to draw a set of causal graphs, each of which represents a particular causal hypothesis, and then consider evidence insofar as it favors one or more of these hypotheses and related graphs over the others. We explain this approach in more detail in Appendix J.
Uncertainty about the model is not just limited to the qualitative causal structure; however, it also involves uncertainty about the parametric form of the model specified, the variables included, whether or not measurement error is modeled, and so on. When mechanistic knowledge exists, this sort of uncertainty is mitigated. Nevertheless, model uncertainty is perhaps the most important level of uncertainty.
By comparison, uncertainty about the parameter estimates (regression coefficients) for a given model is a well-studied problem. When the newspaper reports that a political poll is accurate to “within 3 percentage points,” it is attempting to report the uncertainty about the estimates reported by the poll. When a regression analysis produces an OR with a confidence interval (or a P value for the null hypothesis that the adjusted association is 0), it is quantifying the uncertainty caused by the random variation that we can expect from one sample to another. The important point is that these reports of uncertainty are conditional on the model being a sufficiently adequate approximation to reality so that the inferences drawn are valid. The overall scientific inference involves uncertainty about the model and uncertainty about the parameter estimates given each model. It would be misleading to neglect the uncertainty in the model, and act as if the P values and confidence intervals delimit and make precise our overall scientific uncertainty.
Beyond model uncertainty and parameter estimate uncertainty, we still face uncertainty in applying causal models to individuals. Typically, causal models will provide a prediction about the chances or severity of a disease, given a particular level of exposure and particular levels of the covariates, such as age or social class. For a given individual, we might be highly uncertain about the level and duration of exposure, as well as uncertain about the levels of covariates. This level of uncertainty is also important to presumptive service-connection claims, as will be discussed in the following chapter.
There are two systematic, quantitative approaches for including uncertainty about the model into an assessment of overall uncertainty about a
causal inference. The first is sensitivity analysis, and the second is model averaging. In sensitivity analysis we attempt to quantify the sensitivity of the parameter estimate to assumptions about the model. In model averaging, we attempt to provide an overall uncertainty to our estimate by calculating the estimate of a common parameter or target and its uncertainty for each model we consider plausible, and then by weighting the estimates and the uncertainties by the likelihood of each model. It is essential that the target have the same interpretation in each model, or the combination of the estimates has no meaning.
Sensitivity Analysis
In general, sensitivity analysis is the attempt to systematically explore the sensitivity of a particular parameter estimate, such as the size of the causal effect of exposure on disease, to any assumption made in the model that itself can be parameterized. For example, in estimating the effect of cumulative exposure to lead on a child’s IQ, cumulative lead exposure for a child can be estimated by measuring the concentration of lead in the child’s shed baby teeth. Although this is an improvement over blood lead, it still involves error. The estimate of the effect of lead on IQ is sensitive to the amount of measurement error for lead, and the measurement error can be parameterized by the proportion of the variance of the measure thought to come from actual lead as opposed to error. A sensitivity analysis can then be performed by estimating the effect under a progression of levels of this proportion. This provides an assessment of how sensitive the causal estimate is to various possibilities of measurement error, and provides a more specific statement of what we must assume about measurement error in order to reach the causal conclusion.
Paul Rosenbaum (2002), along with Charles Manski (1995), has developed a formal technique for dealing with unmeasured confounding or bias called sensitivity analysis. The essential idea is to make reasonable guesses as to the range of distortion introduced by possible bias, or the extent of the associations underlying the possible confounding, and then to use those ranges to estimate the extent to which the outcome is changed under those assumptions. If the outcome turns out to be highly sensitive to such perturbations, one cannot rule out the possibility that the observed association is an artifact. Greenland (1996) has advocated a more quantitative approach to directly modeling multiple sources of bias.
Model Averaging
Given the inevitable uncertainty about the true model form, one might ask how one should estimate the RR (or any other epidemiologic effect
parameter derived from it) and an “honest” confidence interval for it that allows for this possibility of model specification error. There is an extensive statistical literature on this question (see, for example, Leamer, 1978, for a review), but in practice the problem is frequently ignored. Frequently, an investigator conducts a number of different analyses and ends up reporting only a single best-fitting model, or the one model in which he or she holds the strongest belief, and reports confidence limits on the parameters of that model, as if it were the “true” model. Sometimes, an investigator may acknowledge this uncertainty about model form by reporting a range of alternative models in the spirit of sensitivity analyses. This can leave the reader uncertain as to which specific set of estimates to use, particularly if several models fit the data more or less equally well, yet yield different estimates and confidence intervals. There are, however, a number of formal approaches to this problem from both a frequentist and a Bayesian perspective.
Here we summarize briefly just one of them, known as Bayesian model averaging (Hoeting et al., 1999). Suppose we have a parameter of interest β (measuring the effect of interest) and a range of alternative models m = 1, … M, yielding estimates ![]() and variances estimates
and variances estimates ![]() of this same parameter under different models (for this purpose, we must assume that the parameter β has the same interpretation under each of the different models, i.e., the effect of exposure, conditional on different choices of adjustment variables). Let πm = Pr(M = m|D) denote the posterior probability of model m, conditional on the observed data D. Then a natural estimator of β that takes account of model uncertainty might be a simple weighted average of the model-specific estimators,
of this same parameter under different models (for this purpose, we must assume that the parameter β has the same interpretation under each of the different models, i.e., the effect of exposure, conditional on different choices of adjustment variables). Let πm = Pr(M = m|D) denote the posterior probability of model m, conditional on the observed data D. Then a natural estimator of β that takes account of model uncertainty might be a simple weighted average of the model-specific estimators, ![]() with variance
with variance ![]() This formal approach has seldom been applied in practice, although there are some examples in the epidemiologic literature. It also has some potential for misuse, as when many highly correlated variables are considered in the same model. In model averaging, we attempt to deal with model uncertainty by calculating the estimate of a common parameter or target and its uncertainty for each model we consider plausible, and then by weighting the estimates and the uncertainties by the likelihood of each model.
This formal approach has seldom been applied in practice, although there are some examples in the epidemiologic literature. It also has some potential for misuse, as when many highly correlated variables are considered in the same model. In model averaging, we attempt to deal with model uncertainty by calculating the estimate of a common parameter or target and its uncertainty for each model we consider plausible, and then by weighting the estimates and the uncertainties by the likelihood of each model.
SUMMARY
Presumptive service-connection decisions depend on population-level causal questions, such as “Were some cases of type 2 diabetes among Vietnam veterans caused by exposure to dioxin in Agent Orange during military service?” Assessing such claims scientifically involves review of statistical
evidence from epidemiologic studies, evidence from experiments in other animals, and mechanistic evidence from basic biologic science.
Because a statistical association between exposure and disease does not prove causation, plausible alternative hypotheses must be eliminated by careful statistical adjustment and/or consideration of all relevant scientific knowledge. Epidemiologic studies that show an association after such adjustment, for example through multiple regression or instrumental variable estimation, and that are reasonably free of bias and further confounding, provide evidence but not proof of causation. Mechanistic knowledge about how particular agents might produce adverse health effects provides further evidence. For example, ionizing radiation is known to cause mutations in DNA that can result in cancer. Animal studies may provide further evidence by showing that an agent may induce in several different species the same effect observed in human studies, and by a mechanism that is conserved across species with key features of the mechanism observed.
Uncertainty about a causal claim can arise because of uncertainty about which among a set of plausible models is correct, or because of uncertainty about study design and execution, or it can arise because of uncertainty caused by simple sampling variability, or it can arise because of uncertainty in the basic science required to analyze other evidence. The overall uncertainty about the claim in question is some combination of all of these uncertainties.
Additional information on causation and statistical causal methods can be found in Appendix J.
REFERENCES
DHHS/CDC (Department of Health and Human Services/Centers for Disease Control and Prevention). 2004. The health consequences of smoking: A report of the Surgeon General. http://www.cdc.gov/tobacco/data_statistics/sgr/sgr_2004/index.htm (accessed July 27, 2007).
Doll, R., and A. B. Hill. 1954. The mortality of doctors in relation to their smoking habits; A preliminary report. British Medical Journal 1(4877):1451-1455.
EPA (Environmental Protection Agency). 2005. Guidelines for carcinogen risk assessment. EPA/630/P-03/001B. Washington, DC: Environmental Protection Agency. http://www.epa.gov/IRIS/cancer032505.pdf (accessed March 1, 2007).
Golden, R., D. Pyatt, and P. G. Shields. 2006. Formaldehyde as a potential human leukemogen: An assessment of biological plausibility. Critical Reviews in Toxicology 36(2):135-153.
Greenland, S. 1996. Basic methods for sensitivity analysis of biases. International Journal of Epidemiology 25(6):1107-1116
Greenland, S. 2000. An introduction to instrumental variables for epidemiologists. International Journal of Epidemiology 29(4):722-729; Erratum 29(6):1102.
Greenland, S., and D. Thomas. 1982. On the need for the rare disease assumption in case-control studies. American Journal of Epidemiology 116(3):547-553.
Hill, A. B. 1965. The environment and disease: Association or causation? Proceedings of the Royal Society of Medicine 58:295-300.
Hoeting, J., D. Madigan, A. Raftery, and C. Volinsky. 1999. Bayesian model averaging. Statistical Science 14:382-401.
IARC (International Agency for Research on Cancer). 1999. IARC monographs on the evaluation of carcinogenic risk to humans: Re-evaluation of some organic chemicals, hydrazine and hydrogen peroxide. Vol. 71. http://monographs.iarc.fr/ENG/Monographs/vol71/volume71.pdf (accessed March 1, 2007).
IARC. 2006a. IARC monographs on the evaluation of carcinogenic risk to humans: Formaldehyde, 2-butoxyethanol and 1-tert-butoxypropan-2-ol. Lyon, France: International Agency for Research on Cancer. http://monographs.iarc.fr/ENG/Monographs/vol88/volume88.pdf (accessed August 22, 2007).
IARC. 2006b. IARC monographs on the evaluation of carcinogenic risk to humans: Preamble. Lyon, France: International Agency for Research on Cancer. http://monographs.iarc.fr/ENG/Preamble/CurrentPreamble.pdf (accessed March 1, 2007).
IOM (Institute of Medicine). 2006a. Food marketing to children and youth: Threat or opportunity. Washington, DC: The National Academies Press.
IOM. 2006b. Asbestos: Selected cancers. Washington, DC: The National Academies Press.
IOM/NRC (National Research Council). 2005. Dietary supplements: A framework for evaluating safety. Washington, DC: The National Academies Press.
Kennedy, P. 2003. A guide to econometrics. 5th ed. Cambridge, MA: MIT Press.
Koch, R. 1884. Die aetiologie der tuberkulose. Mittheilungen aus dem Kaiserlichen Gesundheitsamte 2:1-88.
Leamer, E. E. 1978. Specification searches: Ad hoc inference with nonexperimental data. New York: John Wiley & Sons.
Manski, C. 1995. Identification problems in the social sciences. Cambridge, MA: Harvard University Press.
Mill, J. S. 1862. A system of logic: Ratiocinative and inductive, being a connected view of the principle of evidence, and the methods of scientific investigation. 5th ed. London, UK: Parker, Son and Bowin.
NTP (National Toxicology Program). 2005. Report on carcinogens. 11th ed. Washington, DC: National Toxicology Program. http://ntp.niehs.nih.gov/index.cfm?objectid=32BA9724-F1F6-975E-7FCE50709CB4C932 (accessed March 1, 2007).
NTP CERHR (NTP Center for the Evaluation of Risks to Human Reproduction). 2003. NTP-CERHR Monograph on the Potential Human Reproductive and Developmental Effects of Di-n-Butyl Phthalate (DBP). Research Triangle Park, NC: NTP CERHR, U.S. Department of Health and Human Services.
NTP CERHR. 2005. Guidelines for CERHR Expert Panel Members. Research Triangle Park, NC: NTP CERHR, U.S. Department of Health and Human Services.
Rosenbaum, P. R. 2002. Observational studies. 2nd ed. New York: Springer-Verlag.
Rothman, K. J. 1976. Causes. American Journal of Epidemiology 104(6):587-592.
Rothman, K. J. 2002. Epidemiology: An introduction. Oxford, UK: Oxford University Press.
Straif, K., R. Baan, Y. Grosse, B. Secretan, F. E. Ghissassi, and V. Cogliano. 2005. Carcinogenicity of polycyclic aromatic hydrocarbons. Lancet Oncology 6(12):931-932.