Appendix J
Causation and Statistical Causal Methods
In this appendix we provide more detail about the meaning of general causal claims, and how the qualitative aspects of causal claims can be precisely modeled. Substantial progress has been made on this front in the last two decades (see Pearl, 2000; Spirtes et al., 2000).
INDIVIDUAL-VERSUS POPULATION-LEVEL CAUSAL CLAIMS
First, consider the difference between individual- and population-level causal claims. In legal contexts, the goal is often to establish whether one particular event was the cause of another particular event. For example, if a child who lives near a chemical factory contracts a rare cancer, a court might seek to establish whether or not a chemical spill adjacent to the child’s property was the “cause” of his or her particular cancer. By saying that the chemical spill caused the disease, we mean that the cancer would not have occurred had the spill not happened (“but for exposure” in legal terms). This is an individual-level causal claim. For cases in which a particular veteran seeks to service connect a particular disease or disability he or she has contracted after separation from the service is, if causation is the standard, an instance of establishing an individual-level causal claim.
In epidemiologic or scientific contexts, however, the goal is often to establish whether, in a population of individuals, generic sorts of exposures result in a change in the frequency or average severity of a disease. For example, an epidemiologist might ask whether the frequency of abnormal births among American women who were exposed to polychlorinated biphenyls (PCBs) during pregnancy is higher than the frequency among those who were not. If so, then epidemiologists might assert that exposure to PCBs during pregnancy is capable of causing birth defects. The causal claim about the population does not entail that every fetus whose mother is exposed to PCBs during pregnancy will develop birth defects, and it does not entail that every birth defect would not have happened but for PCB exposure. On the population level, causal claims typically involve how the probability distribution of the disease changes in response to exposure. When either Congress or the Department of Veterans Affairs seeks to presumptively service-connect a particular health condition or disability to a particular population of veterans, establishing a population-level causal claim is required.
CAUSATION AND COUNTERFACTUALS
Beginning in the 1970s, Rubin (1974) and many after him developed a formal theory of causal inference based on counterfactuals, which play an essential role in both individual- and population-level causal claims. On the individual level, for example, we might observe that a particular person was exposed to a chemical and later contracted a disease. The question we would like to answer is counterfactual: What would have happened had the same individual not been exposed to the chemical? Likewise, for other individuals who were not exposed, we might like to know what would have happened had they been exposed.
On the population level the questions are similar. We observe that a population of individuals, such as Gulf War veterans, were exposed to a variety of conditions and substances in their tour of duty in the Mideast and then exhibited a certain frequency of illness years later. The population question we would like to answer is counterfactual: What would the frequency of illnesses have been had the same population not been exposed to the conditions and substances they were exposed to in the Gulf War?
In Rubin’s framework, analyzing randomized clinical trials that involve assigning one group to treatment and another to control is a counterfactual missing data problem. For all the people in the treatment group, we are missing data on their response had they been assigned to the control group, and symmetrically for the control group.
INTERVENTION
Underneath these counterfactuals, however, is a subtle but crucial assumption about how the world should be imagined to have been different. Recall that “exposure to excessive radiation caused Mary to get leukemia” means that “had Mary not been exposed to excessive radiation she would not have gotten leukemia.” This makes sense if we envision a world identical to the one Mary did experience, but change it minimally by intervening to prevent her from being exposed to excessive radiation.
Consider a slightly different example, however. Suppose John smoked 30 roll-your-own cigarettes a day from age 25 to 50, had intensely tar-stained fingers during this period, and got lung cancer at the age of 51.
Sticking with common sense, we will assume that smoking caused John to have both tarstained fingers and lung cancer, but that having tar-stained fingers has no causal influence on getting lung cancer (Figure J-1). By the counterfactual theory, the following ought then to be true: “Had John not had tar-stained fingers, he would have gotten lung cancer anyway.” To make sense of this counterfactual, we might envision a world in which John still smoked, but either smoked packaged cigarettes that produced no finger stains or washed his hands with tar-
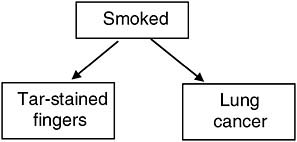
FIGURE J-1 Causal structure for smoking, tar-stained fingers, and lung cancer.
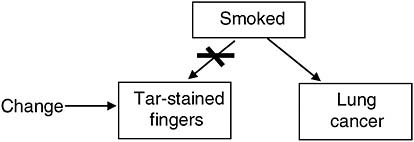
FIGURE J-2 Hypothetical intervention on finger tar stains.
solvent soap every night. Some might object and say: “What I think of when I hear ‘Had John not had tar-stained fingers’ is a situation in which he didn’t smoke—and in that case he wouldn’t have gotten lung cancer!” Again, to make sense of the counterfactual: “Had John not had tarstained fingers, he would have gotten lung cancer anyway,” we must imagine a world in which we directly change only whether John had tar-stained fingers and leave the rest of the story intact (Figure J-2).
Further, in such a world our hypothetical intervention destroys any influence smoking might have had on whether John had tar-stained fingers in the real world. If it didn’t, we could not make sense of the hypothetical.
These points apply directly to the same population claims we used above to illustrate presumptive service connection. When we ask the question, “What would the frequency of illnesses have been among Gulf War veterans had they not been exposed to the conditions and substances they were exposed to in the Gulf War?” we don’t mean to imagine a world in which these veterans never signed up for the armed forces because they were medically unfit for duty. Instead, we mean to imagine a world in which everything about them was the same, but they were prevented from being exposed to the conditions and substances they were exposed to in the Gulf War. This is the counterfactual that bears on presumptive service connection.
So a theory of causation must model hypothetical interventions that are tightly targeted, and, most importantly, describe how the world would react to any sort of ideal, hypothetical intervention or treatment we can imagine. Further, the theory ought to make the connection with statistical evidence clear. Over the last two decades, epidemiologists,1 computer scientists,2 philosophers,3 and statisticians4 have developed a theory of statistical causal inference that incorporates the virtues of Rubin’s counterfactual account but also models interventions and provides a clear connection to statistical evidence as it bears on causal claims. Below we present the briefest possible introduction to this theory. More detail is available in Robins (1986, 1988), Pearl (2000), Spirtes et al. (2000), Dawid (2004), Cox and Wermuth (2004), and many other sources.
CAUSAL STATISTICAL MODELS
The kind of causal theories and statistical evidence relevant to presumptive service-connection decisions involve a population and a set of variables, or factors. A population denotes a (potentially infinite) group of individuals, such as Vietnam War veterans, or American men over the age of 60, or all possible offspring of a heterozygous and homozygous pea plant. A set of variables describe properties of such individuals that might cause each other, such as exposed to Agent Orange (yes, no), smoked (no, lightly, heavily), lung cancer (yes, no), yearly income (in dollars), and so on.
The qualitative part of a causal theory, that is, which variables are causes of which other variables and which are not, can be represented with a causal graph, that is, a diagram involving arrows that connect the variables. See Neapolitan (2004), Pearl (2000), Spirtes et al. (2000), and Glymour and Cooper (1999). For example, consider the causal graph in Figure J-3.
To be concrete, let us assume that this model is meant to apply to a population of 4-year-old American children. Further, suppose the variables are the following:
-
Exposure (yes, no)—Yes, if exposed to another child who was within 2 days of symptomatic chicken pox.
-
Infection (yes, no)—Yes, if chicken pox virus was active in bloodstream.
-
Rash (yes, no)—Yes, if rash appeared.
Then each arrow in the causal diagram depicts a claim about direct causation relative to this set of variables and this population. In this case, the diagram claims that
-
exposure is a direct cause of infection, and
-
infection is a direct cause of rash, and
-
that no other direct causal claims hold among these variables in this population, including the claim that exposure is a direct cause of rash.
DEFINITION OF DIRECT CAUSATION
The presence of an arrow from one variable, such as exposure, to another, such as infection, means that, holding all the other variables in the system fixed, changing the assignment of exposure will result in some change in the probability of infection.5 The absence of an arrow, for example the absence of an arrow from exposure to rash, means that, holding the other variables (infection) fixed, changing the assignment of exposure will not result in any change in the probability of rash.
FIGURE J-3 Chicken pox.
Notice the role of possibly counterfactual interventions. When we say “holding fixed,” or “changing the assignment,” we are referring to hypothetical interventions in which we set or assign the value of a variable.
The quantitative part of a causal theory involves specifying a probability model that accords with the qualitative model. The full model with both graph and probability distribution is called a Causal Bayes Network. See Pearl (2000), Spirtes et al. (2000), and Neopolitan (2004). For each variable in the system, we express its probability distribution as a function of its direct causes. That is, we specify the way in which each effect responds to any set of values its direct causes might take on, and, since it is a population we are talking about, we need to express this response probabilistically. For example, in the chicken pox case, we might give the whole causal model—both its qualitative and quantitative parts—with a causal diagram and a table expressing the response structure for each variable (Figure J-4).
Because exposure has no immediate causes in our model, the hypothetical quantitative table just gives how probable it is for a 4-year-old American child to be exposed to another child who is infected and within 2 days of exhibiting chicken pox symptoms. Note that the numbers in this table are purely for illustration and do not reflect actual data. The probability of infection is given as a function of its immediate causes—in this case exposure. It claims that if a child is exposed to another child with chicken pox, then they have an 80 percent chance of becoming infected themselves, but if they are not exposed to another child with chicken pox, they have just a 3 percent chance of becoming infected.
We compute the joint probability distribution over the variables V as the product of the conditional probability of each variable on its direct causes:
Having the joint distribution allows us to compute the probability of any variable conditional on an observation for any other variable or set of variables. For example, in the chicken pox model, we can compute the probability of exposure conditional on observing that a child is infected or conditional on having a rash, or the probability of rash conditional on observing exposure, and so on.
Most importantly, these models allow us to explicitly represent hypothetical interventions. The rule is simple: add an “intervention” variable to the system and draw an arrow to the variables targeted by the intervention. If the intervention determines the probability of its targets—for example, a randomizer that assigns subjects to treatment or control—erase the other arrows that previously went into these targets, and change the quantitative model accordingly.
For example, suppose we wanted to model an intervention in which we assigned everyone in our population of 4-year-old children to be infected with the chicken pox virus (by injection). Then the resulting “intervened upon” system would be as shown in Figure J-5.
Computing the joint distribution after an intervention goes the same way as for preintervention systems, but the results will sometimes differ, and it is this difference that captures the causal part of the model. For example, in the chicken pox model prior to our intervention (Figure J-4), the probability of exposure given infection is higher than 0.1, as in P(Exposure = yes | Infection = yes) > 0.1, but in the intervened-upon version of the system (Figure J-5), P(Exposure = yes | Infection set = yes) = 0.1 = P(Exposure). This is because the intervention on infection eliminated the causal connection between exposure and infection, and thus changed their informational relationship as well.
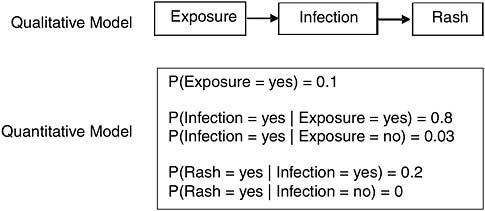
FIGURE J-4 Hypothetical statistical causal model for chicken pox.
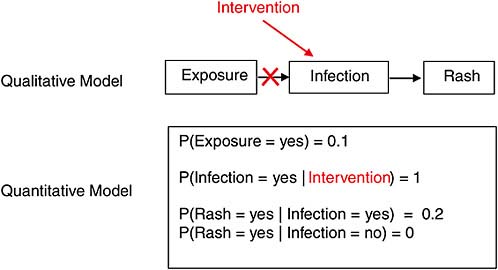
FIGURE J-5 Hypothetical intervention in the chicken pox system.
As this point cannot be emphasized enough, and as it underlies the difference between association and causation, consider another case in which two models agree about things prior to an intervention but differ about things after an intervention. Consider two distinct causal models of the relationship between a child’s exposure to environmental lead and their cognitive function measured by IQ (Figure J-6).
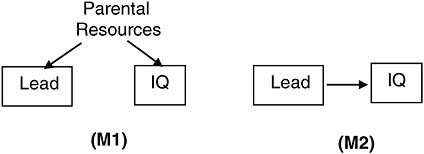
FIGURE J-6 Two hypothetical models of lead exposure and cognitive function.
In model 1 (M1), lead and IQ are effects of a common cause, parental resources, but have no influence on each other. We assume that parents with more resources will choose environments with less lead, and provide the stimulation necessary to increase their child’s measured IQ. In model 2 (M2), lead is a direct negative cause of IQ. Supposing that the level of parental resources remains unmeasured, it is easy to attach quantitative values for both models such that the probability distributions over the measured variables lead and IQ are identical. In that case, P(IQ | Lead)M1 = P(IQ | Lead)M2. That is, predictions about IQ from observations of lead exposure are implied to be identical in both models. Put another way, the association between lead and IQ implied by M1 can just as well be implied by M2 and vice versa.
It is not possible, however, for the models to agree about the relationship after a hypothetical intervention that sets the value of lead exposure: P(IQ | Leadset by intervention)M1 ≠ P(IQ | Leadset byintervention)M2. That is because a hypothetical intervention, or treatment, on lead, changes M1 in a way that makes lead and IQ independent, but leaves the causal dependence of lead and IQ unperturbed in M2 (Figure J-7).
So M1 and M2 can agree completely on the population we observe, but differ on the sorts of counterfactuals that underlie presumptive service connections. M2 supports counterfactuals of the sort: “Had Jonathan not been exposed to lead, he wouldn’t have scored below average on the IQ test,” but M1 does not. If M1 is true (and clearly that is a big if), then hypothetically changing the amount of lead Jonathan was exposed to leaves his IQ the same, for in M1 it is not lead that
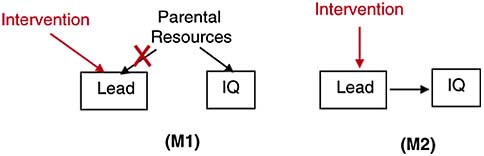
FIGURE J-7 Hypothetical postintervention models of lead and IQ.
causes IQ but parental resources. In all likelihood the “correct” model is a combination of M1 and M2: one in which any observed negative association between lead exposure and IQ is due to both a common cause and a direct causal influence.
Equipped with the correct causal model connecting military service (or a particular exposure in service) for an identified group and a health outcome, both qualitatively and quantitatively, we can compute the probability of this outcome in the counterfactual world in which the group was not exposed to the conditions and substances of military service and compare this to the probability of the outcome that we actually observed. This computation, of course, depends crucially on the model we consider “correct.”
For example, consider the three hypothetical causal models shown in Figure J-8. Suppose that we didn’t know which of these models was an accurate representation of the world. Suppose further that we collected a sample of 255 subjects, and for each recorded whether they had been exposed to some substance (Exposure), whether they had the disease in question (Health Outcome), and whether or not they showed evidence of some covariate, for example low income. We show purely hypothetical data table in Table J-1. The analysis of this dataset under the three models in Figure J-8 would yield three quite different estimates of the relative risk (RR) and any of the other epidemiologic parameters derived from it, for example, the population attributable risk (PAR). Under model M1, which asserts that Exposure causes Health Outcome and that the relationship is not confounded, we would ignore the covariate and estimate the RR from the crude odds ratio between exposure and disease, [(155/45) / (100/100)] = 3.44 (95% confidence interval [CI] 2.23-5.31). Under model M2, on the other hand, which asserts that Exposure is not a cause of Health Outcome at all, and that any observed association is due entirely to confounding, we would ignore the apparent association in the data and conclude based solely on the model that there was no causal association between exposure and disease (i.e., OR = 1.0). Finally, under model M3, which asserts that Exposure causes Health Outcome but that the two are also confounded, we would have to adjust for the confounder and obtain the adjusted OR = 3.03 (95% CI 1.93-4.73).
For these data, neither model M1 nor M2 fits the observed data very well, so we would need very compelling prior knowledge to accept them over M3. If, however, we had no recorded data on the covariate, then we could not distinguish between the three models.
TABLE J-1 Hypothetical Exposure and Health Outcome Data
|
Exposure |
Covariate |
Health Outcome = No Disease |
Health Outcome = Disease |
|
No |
No |
60 |
19 |
|
|
Yes |
40 |
26 |
|
|
Total |
100 |
45 |
|
Yes |
No |
40 |
39 |
|
|
Yes |
60 |
116 |
|
|
Total |
100 |
155 |
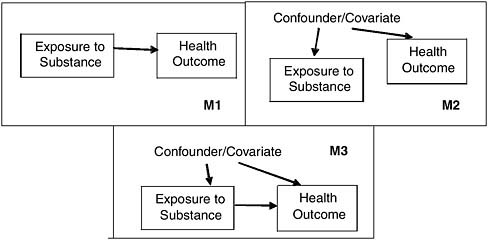
FIGURE J-8 Three hypothetical causal models connecting exposure/disease.
So given the correct causal model, and the knowledge that it is the right causal model, we can compute the quantities we need to entertain questions about service connection and presumptive service connection.
REFERENCES
Cox, D. R., and N. Wermuth. 2004. Causality: A statistical view. International Statistical Review 72:285-305.
Dawid, A. P. 2004. Probability, causality and the empirical world: A Bayes-de Dinetti-Popper-Borel synthesis. Statistical Science 19:44-57.
Glymour, C., and G. F. Cooper, eds. 1999. Computation, causation, and discovery. Menlo Park, CA: AAAI Press/Cambridge, MA: MIT Press.
Neapolitan, R. E. 2004. Learning Bayesian networks. Upper Saddle River, NJ: Pearson Prentice Hall.
Pearl, J. 2000. Causality: Models, reasoning, and inference. New York: Cambridge University Press.
Robins, J. M. 1986. A new approach to causal inference in mortality studies with sustained exposure periods—application to control of the healthy worker survivor effect. Mathematical Modelling 1986(7):1393-512 (errata appeared in Computers and Mathematics with Applications 1987(14): 917-921).
Robins, J. M. 1988. Confidence intervals for causal parameters. Statistics in Medicine 7:773-85.
Rubin, D. B. 1974. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology 56:688-701.
Spirtes, P., C. Glymour, and R. Scheines. 2000. Causation, prediction, and search. 2nd ed. Boston, MA: MIT Press.










