3
Strategies for Disease Containment
OVERVIEW
Given limited supplies of vaccines, antiviral drugs, and ventilators, non-pharmaceutical interventions are likely to dominate the public health response to any pandemic, at least in the near term. The six papers that make up this chapter describe scientific approaches to maximizing the benefits of quarantine and other nonpharmaceutical strategies for containing infectious disease as well as the legal and ethical considerations that should be taken into account when adopting such strategies. The authors of the first three papers raise a variety of legal and ethical concerns associated with behavioral approaches to disease containment and mitigation that must be addressed in the course of pandemic planning, and the last three papers describe the use of computer modeling for crafting disease containment strategies.
More specifically, the chapter’s first paper, by Lawrence Gostin and Benjamin Berkman of Georgetown University Law Center, presents an overview of the legal and ethical challenges that must be addressed in preparing for pandemic influenza. The authors observe that even interventions that are effective in a public health sense can have profound adverse consequences for civil liberties and economic status. They go on to identify several ethical and human rights concerns associated with behavioral interventions that would likely be used in a pandemic, and they discuss ways to minimize the social consequences of such interventions.
The next essay argues that although laws give decision makers certain powers in a pandemic, those decision makers must inevitably apply ethical tenets to decide if and how to use those powers because “law cannot anticipate the specifics of each public health emergency.” Workshop panelist James LeDuc of
the Centers for Disease Control and Prevention (CDC) and his co-authors present a set of ethical guidelines that should be employed in pandemic preparation and response. They also identify a range of legal issues relevant to social-distancing measures. If state and local governments are to reach an acceptable level of public health preparedness, the authors say, they must give systematic attention to the ethical and legal issues, and that preparedness should be tested, along with other public health measures, in pandemic preparation exercises.
LeDuc’s fellow panelist Victoria Sutton of Texas Tech University also considered the intersection of law and ethics in public health emergencies in general and in the specific case of pandemic influenza. In particular, Sutton identified several “choke points”—particularly thorny ethical and legal issues—that present barriers to pandemic mitigation. In addition to the problem of leadership, which is addressed in the next chapter, these issues include the role of interdisciplinary and intersectoral approaches in decision-making; the tradeoffs between personal freedom and public good that are implicit in social-distancing measures; the global implications of quarantine and travel restrictions; the need for consistency among various disease-control policies; and the definition of appropriate, measurable “triggers” for when to impose each potential countermeasure.
The third paper in this chapter considers quarantine, one of the most ethically and legally complex tactics used in combating pandemic disease. In this article, Martin Cetron of CDC and Julius Landwirth of Yale University describe the modern practice of quarantine and its potential implementation as outlined in the U.S. Department of Health and Human Services (HHS) plan for containing pandemic avian influenza. Whenever the possibility of using a quarantine is discussed, they observe, decision makers confront the central dilemma arising from the contrast between public health ethics, which emphasizes collective action for the good of the community, and therapeutic medicine, with its focus on the individual. The authors identify various means to address this tension and offer examples of how ethical considerations can be incorporated into pandemic preparedness plans.
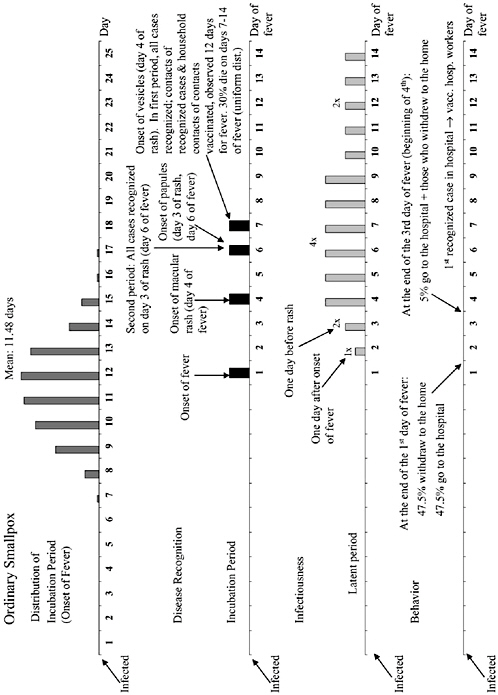
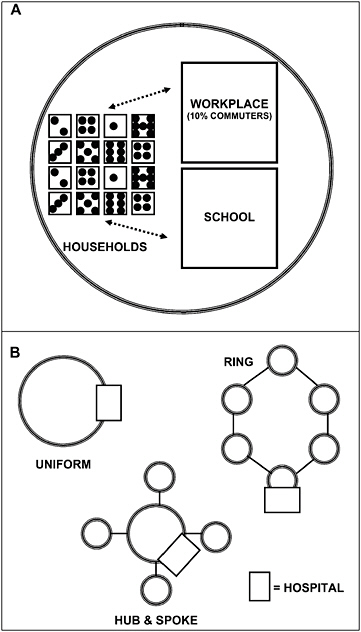
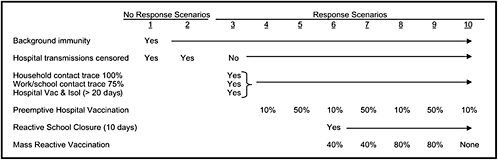
The chapter concludes with a three-part contribution by Joshua Epstein of the Brookings Institution: an informal discussion of the modeling process as it applies to infectious disease containment, followed by two publications in which such models are used to inform strategies for containing smallpox epidemics resulting from bioterrorism. Epstein and his group produce explicit models of disease, and, in the course of doing so, they examine and refine the assumptions upon which each model rests. Epstein observes that while models cannot replace human judgment, they can better inform our choices, and while they cannot eliminate uncertainty, models can identify crucial gaps in knowledge. To support these assertions, Epstein describes how his group collaborates with medical experts to produce disease scenarios and containment strategies (e.g., for smallpox) more robust than would be possible either through pure computation or through expert opinion alone.
Responding to Epstein’s presentation, workshop panelist Timothy Germann,
of Los Alamos National Laboratory, observed that models cannot address ethical and legal questions; instead models must be combined with ethical and legal judgments to make policy decisions. Epstein replied to that observation by pointing out the possibility that models of infectious disease containment could be shaped by legal and ethical considerations—introduced in the form of constraints—built into them, much as economic factors have been included in similar models. Moreover, he said, models sometimes provide information that can help resolve ethical dilemmas; for example, projections that reveal little difference in effectiveness between voluntary and mandatory quarantine.
PREPARING FOR PANDEMIC INFLUENZA: LEGAL AND ETHICAL CHALLENGES1
Lawrence O. Gostin, J.D.2
Georgetown University Law Center
Benjamin E. Berkman, J.D., M.P.H.3
Georgetown University Law Center
Introduction
Highly pathogenic influenza A (H5N1) has captured the close attention of policy makers who regard pandemic influenza as a national security threat. The virus is endemic in bird populations in Southeast Asia, with serious outbreaks also having now occurred in Africa, Europe, and the Middle East (WHO, 2006a, 2007a). Modeling4 suggests that the infection will eventually affect the
entire globe through transmission mechanisms involving both birds and humans (Longini et al., 2005). The majority of avian outbreaks in Southeast Asia have been attributed to the movement of poultry and poultry products (Chen et al., 2006; Rosenthal, 2006). Similarly, international trade and travel will play a major role in transmission in human outbreaks, and frequent and widespread travel will make it difficult to contain any pandemic in humans. Even if trade and travel are severely restricted in order to limit human transmission, migratory birds will likely spread the disease by infecting birds on other continents (Normile, 2006).
So far, however, the spread of the H5N1 strain has been confined mainly to animal populations. The virus is highly contagious among birds, and also highly pathogenic (Garrett, 2005), but because of a significant species barrier, the virus is still rare in humans (WHO, 2005b). The first confirmed cases of human infection were reported in 1997. As of May 16, 2007, 306 cases of the current wave of Influenza A (H5N1) have been reported, with 185 deaths (WHO, 2007b). Most cases are attributable to close contact with infected poultry or contaminated surfaces—e.g., poultry farms, markets, backyard pets, and cock-fighting venues (Thorson et al., 2006). A few cases of human-to-human transmission have occurred, principally involving intimate household contact, but the virus is of very limited transmission competence (WHO, 2006b). The virus appears highly pathogenic, with a reported death rate exceeding 50 percent (Wong and Yuen, 2006). However, because of the possibility of under-reporting, the exact prevalence, transmissibility, and fatality rates of H5N1 remain uncertain.
Recent evidence that the 1918 pandemic was caused by an avian influenza virus lends credibility to the theory that the current strain could develop pandemic potential (Taubenberger et al., 2005; Tumpey et al., 2005). Historically, the number of deaths during a pandemic has varied greatly, depending on the number of people who become infected, the virulence of the virus, and the effectiveness of preventive measures (WHO, 2005c). Accurate predictions of mortality are thus difficult to establish, and estimates differ considerably. A mild pandemic, comparable to those in 1957 and 1968, is likely to cause the deaths of from 89,000 to 207,000 people in the United States (Garrett, 2005; Global Security, 2006) and 2 million to 7.4 million people globally (WHO, 2005d). One study that extrapolates from the severe 1918 pandemic finds that, in the absence of intervention, an influenza pandemic could lead to 1.9 million deaths in the United States and 180 million to 369 million deaths globally (Osterholm, 2005).5 A different study, also based on 1918 data, concludes that an estimated 62 million people will die globally, with 96 percent of these deaths occurring in the developing world (Murray et al., 2006). An influenza pandemic would also result in massive economic disruption. At present, the principal economic effects are being experi-
enced in the rural areas of Southeast Asian countries and are fairly limited. They are mostly related to losses of poultry and to governmental control measures such as the culling of birds. Economic losses would become much higher if sustained human-to-human transmissions develops.
The two principal strategies for containing serious human outbreaks of influenza are therapeutic countermeasures (e.g., vaccines and antiviral medications) and public health interventions (e.g., infection control, social separation, and quarantine). Many of the barriers to effective interventions are technical and have been thoroughly discussed. This article focuses on the formidable legal and ethical challenges, which have yet to receive sufficient attention (Kotalik, 2005; Torda, 2006; Thomson et al., 2006; Kayman and Oblorh-Odjidja, 2006).6
Medical Countermeasures: Vaccines and Neuraminidase Inhibitors
Industrialized countries place great emphasis on scientific solutions. Vaccination and, to a lesser extent, antiviral medication (in particular, the neuraminidase inhibitors oseltamivir [Tamiflu©] and zanamivir [Relenza©]) are perhaps the most important medical interventions for reducing morbidity and mortality associated with influenza (Germann et al., 2006; Iton, 2006; Stohr and Esveld, 2004). There is also recent evidence from primate models that the 1918 H1N1 influenza strain, unlike contemporary strains, can cause an exuberant immune response, which suggests that immunity suppressants might be another means of combating at least some strains of the virus (Kobasa et al., 2007). The United States plans to devote over 90 percent of pandemic influenza spending to medical countermeasures (U.S. Congressional Budget Office, 2006; Spotswood, 2005).
Despite the promise of medical countermeasures, their use has been limited by a chronic mismatch between public health needs and private-sector control of production. Vaccine production, for example, has been unreliable even for seasonal influenza. The best way to ensure pandemic preparedness is to increase the baseline level of seasonal countermeasures. The World Health Organization (WHO) concluded that better use of vaccines for seasonal epidemics could help ensure that manufacturing capacity meets demand in a future pandemic (World Health Assembly, 2005; Gronvall and Borio, 2006). But even though this approach is good for the long-term, more immediate solutions are needed. Moreover, supply is difficult to increase because intellectual property concerns, regulatory hurdles, a lack of market incentives, limited production capacity, and fear of liability all act to curb entry into the market.
|
6 |
For an example of this lack of attention to law and ethics, see Department of Health and Human Services. 2006. Medical Offices and Clinics Pandemic Influenza Planning Checklist. [Online]. Available: http://www.pandemicflu.gov/plan/medical.html#3 [accessed January 30, 2007]. This document purports to be a “checklist to help medical offices and ambulatory clinics assess and improve their preparedness for responding to pandemic influenza.” However, it does not address the myriad legal and ethical issues that will arise. |
Even if these supply problems can be overcome, it is unlikely that sufficient medical countermeasures will be available to halt the spread of a pandemic. In particular, there will likely be a significant delay in the production of a vaccine. With current technology it will take at least 6 months from the onset of an outbreak, and possibly longer, for the first doses of vaccine to be available. Furthermore, there is no guarantee that medical countermeasures will be efficacious. Experimental H5N1 vaccines may not be effective against a novel human subtype, and the pathogen may become resistant to neuraminidase inhibitors.
Public Health Countermeasures
Given the limits of medical countermeasures, a broad range of public health would likely be employed against an influenza pandemic, from relatively innocuous techniques, such as disease surveillance and hygienic measures, to considerably more restrictive interventions, such as social distancing, travel restrictions, quarantine, and case isolation. There are reasons to believe that all of these will be effective to at least some degree (Markel et al., 2006), but evidence supporting their effectiveness is scarce (IOM, 2006). The hope is that public health interventions, while incapable of completely stopping the transmission of the virus, will be able to slow the pandemic. By reducing the rate of spread of the disease, public health countermeasures can buy time for the development of medical countermeasures while also helping to ensure that the health-care system does not become overwhelmed by a surge of patients (Cetron, 2006). Unfortunately, each type of public health intervention raises serious ethical and human rights concerns.
Public Health Surveillance
Surveillance is the backbone of public health, providing the data necessary to understand an epidemic threat and to inform the public, provide early warning, describe transmission characteristics and incidence and prevalence, and assist a targeted response. Surveillance strategies include rapid diagnosis, screening, reporting, case management reporting, contact investigations, and the monitoring of trends.
It is clear that surveillance is necessary to quickly identify and respond to a pandemic influenza outbreak. The revised International Health Regulations (IHR) require member states to notify WHO of all events which may constitute a “public health emergency of international concern.” Consequently, once a country identifies a signal suggesting human-to-human transmission, the country is expected to begin investigations immediately and simultaneously to notify WHO of the event. Surveillance thus comprises a crucial element of the early response to a forming pandemic.
But because governments must collect sensitive health information from patients, travellers, migrants, and other vulnerable populations, surveillance also
poses privacy risks (Bayer and Fairchild, 2002). The IHR requires states to keep data “confidential and processed anonymously as required by national law,” but in a crisis it can sometimes be necessary to disclose certain information without any undue delay. In such a situation, when the immediate use of the information is necessary for an important public health purpose, disclosure can be warranted, but the identity of the affected person should be protected as much as possible. A breach of the right to privacy can result not only in economic harms, such us unemployment or loss of insurance or housing, but also in social and psychological harms. For that reason, if information is released outside of the public health system, it is particularly important to avoid the inclusion of any uniquely identifiable characteristics, such as names, government identification numbers, fingerprints, or phone numbers. Cases should stay anonymous or encrypted when reasonably feasible. In every situation the rights to privacy and personal autonomy require that only the minimum amount of information necessary to achieve the goal should be released and to as few people as possible. Dignity and respect for the person should be protected.
Screening and testing can pose serious threats to a person’s privacy and bodily integrity. Ideally, public health officials should receive an individual’s informed consent before performing any medical tests, and education programs can help convince many people to agree to voluntary testing, but there may be rare times when mandatory testing is necessary to advance the public good. In such cases, interference with the right to bodily integrity and with the right to refuse testing may be permissible when the mandatory testing policy is clearly necessary and effective in protecting the public health, when it is performed by competent public health officials, and when the least intrusive means are used. At a minimum, compulsory testing should be limited to individuals known or at least suspected to be infected and should be done in a fair and nondiscriminatory way. The people whose privacy and autonomy are being infringed should be informed of the reasons for the infringement. And in all cases compulsion should be the last resort and used only if voluntary or less restrictive means are ineffective.
Community Hygiene and Hospital Infection Control
Hygienic measures to prevent the spread of respiratory infections are broadly accepted and have been widely used in both influenza pandemics (APHA, 1918) and also, although with uncertain benefits, the SARS outbreaks (WHO, 2003; CDC, 2005a). These hygienic methods include hand-washing, disinfection, the use of personal protective equipment (PPE) such as masks, gloves, gowns, and eye protection, and respiratory hygiene, such as the use of proper etiquette for coughs, sneezes, and spitting.
It is important that the public be informed of the need for hygienic measures, and that accurate information, including the uncertainty of the effectiveness of the recommended interventions, be provided. In past epidemics misinformation
has been rampant, and this has led to substantial public anxiety, to reliance on word of mouth for knowledge, and to the purchase of ineffective and expensive products (Rosling and Rosling, 2003). The situation raises issues of distributive justice because ineffective or inaccurate communications have the greatest effects on marginalized members of society, as they are the least likely to have access to alternative credible sources of information and are the people for whom wasting resources would have the greatest adverse effects (Gostin and Powers, 2006). Furthermore, a consideration for personal dignity implies that individuals should be provided with adequate information to make informed decisions about their own health. Public education campaigns should be grounded in the science of risk communication, as the acceptability of health measures is vital to community adherence. The information disseminated through public education campaigns should be accurate, clear, uncomplicated, not sensationalistic or alarmist, and as reassuring as possible (SARS Commission, 2006).7
Decreased Social Mixing/Increased Social Distance
Past experience shows that one consistent response to epidemics has been to decrease social mixing and increase social distance by such means as community restrictions and voluntary social separation (WHO, 2005d; Stern and Markel, 2004). There is some limited evidence that school closings do reduce seasonal influenza transmission (Heymann et al., 2004), and it is assumed—although but not proven—that other limits on social mixing also slow the spread of respiratory disease (World Health Organization Writing Group, 2006). Thus societies faced with pandemics have often closed public places (schools,8 childcare, workplaces, mass transit) and cancelled public events (sports, arts, conferences). As fear rises,rises,, the public itself may shun public gatherings. Predicting the effect of policies to increase social distance is difficult, as infected persons and their contacts may be displaced into other settings, and individuals may voluntarily separate in response to perceived risk. For these reasons, additional research needs to be conducted on behavior during epidemics and the effects of social distancing on transmission.
Social separation, particularly for long durations, can cause loneliness and emotional detachment, disrupt social and economic life, and infringe individual rights. Community restrictions raise profound questions about the government’s right to interfere in such areas as faith (by, for instance, limiting religious gatherings), family (with, for example, restrictions on funeral attendance), and pro-
|
7 |
The Canadian SARS Commission has evaluated crisis communication during that public health emergency. |
|
8 |
A review of state law authorizing school closure can be found at Hodge JG. 2006 (December 11). Assessing Legal Preparedness for School Closure in Response to Pandemic Flu or Other Public Health Emergencies. [Online]. Available: http://www.newfluwiki2.com/upload/Hodge.ppt [accessed January 30, 2007]. |
tection of the vulnerable (e.g., by making it more difficult to visit vulnerable individuals and provide them with food, water, clothing, or medical care).
Undoubtedly, most judicial systems would uphold reasonable community restrictions, but legal and logistical questions loom: Who has the power and under what criteria to order closings, and for what period of time? What threshold of disease should trigger closings, and should thresholds be different for different entities? Under what circumstances should compensation for closings be paid? What should the penalties be for non-compliance? Such questions about enforcement and the assurance of population safety are critically important, but for the most part they have not been answered.
One fear is that governments might put into effect restrictions on personal liberties that are unnecessary—implementing restrictions before they are needed, extending them past the end of the crisis, or enacting restrictions that do nothing to decrease influenza transmission. In such situations, closings would not meet the appropriate standards for either necessity or proportionality. Furthermore, it is important to remember that the cost of restrictive policies will be borne most heavily by those with the fewest resources, so errant social-distancing actions have distributive-justice implications. A final worry is that governments might use social distancing in a discriminatory fashion, scapegoating ethnic or religious minorities, or that governments might use social distancing as a pretext to crack down on dissidents who assemble to protest.
Ideally, questions of government authority and accountability should be answered by policy decisions made in an open and transparent process that encourages input from all portions of society and that is carried out before a pandemic hits. Governments should explicitly define who has the power to order social distancing strategies and for what period of time. Governments should also clearly state the criteria under which such power is exercisable and delineate the legitimate bases for any differential treatment. Penalties should be proportional to offenses and not based on irrational fears or discriminatory beliefs.
On the other hand, one must recognize that detailed pandemic influenza preparations will often not be the highest priorities for countries dealing with important and more immediate concerns. Furthermore, some countries lack the legal and governmental infrastructures to implement such an ideal plan as is outlined above. In such countries, completely determining issues of government authority and accountability prior to a pandemic may be extremely difficult. One should also note that pandemics are difficult to predict, and information acquired as a pandemic evolves may render some of what was previously believed about various social-distancing strategies obsolete.
At the very least, though, governments should dedicate themselves to non-discrimination and transparency before an influenza pandemic occurs. It is important that governments implement social-distancing policies fairly and with as broad involvement in planning as possible. This will not only make it more likely that the appropriate ethical considerations have been taken into account, but it
will also improve the likelihood that the public will accept social distancing as a means to slow disease transmission. And, since compliance with social-distancing instructions will be difficult to enforce, public acceptance will be critical to such a measure’s success.
Workplace and School Closings
Workplace and school closings present particularly difficult ethical issues. Apart from the uncertainty of their effectiveness, the most important issues center on the subject of distributive justice. Workplaces are vital to the livelihoods of both employers and employees, so closing them can cause severe financial hardships. In extreme cases, lost profits caused by closings may push companies to go out of business, leading to job losses and other economic hardships. Even for people who have an economic safety net, these problems can have a significant effect, but for people living at a subsistence level the effect of lost income can be far worse. If workplaces stay closed for a significant amount of time, such people may be unable to pay for shelter, food, or medicine. Similar issues are raised by school closings, which may require parents to stay at home in order to care for young children.
Ideally, public health authorities should work cooperatively with businesses, schools, and communities prior to an emergency in an effort to establish mutually agreeable closure procedures. Though governments should retain the legal power to enforce closings if absolutely necessary, it would be preferable to subsidize lost profits and incomes as necessary in order to create incentives for complying with closure requests. The latter approach was used extensively in countries affected by SARS for people placed in quarantine (Rothstein et al., 2003).
Practical constraints may sometimes make this approach impossible. The governments of many countries have more pressing needs than addressing a potential pandemic. Furthermore, some countries may be financially unable to provide compensation for closure. In 1918 each of the waves of the pandemic lasted for several months, and most locations were hit by multiple waves (Johnson and Mueller, 2002). The amount of resources needed to compensate for lost income or profits for this amount of time will be out of the reach of many of the world’s governments.
In light of these constraints, governments should at least make a serious effort to weigh the risks to health and welfare from workplace closings and other social-distancing measures against those risks of disease transmission that the closings might mitigate. In different locations the balance of risks may be resolved differently, depending on resources and the number of people living at or below a subsistence level. Countries should consider tactical closures if necessary, such as closing only those entities that most facilitate transmission. For example, schools have been identified as a primary driver of seasonal influenza (Germann et al., 2006), and some believe that closing schools will slow the
spread of a pandemic. Countries might also consider using closings as a means to buy time for other preparations; closings could be put in place until the level of disease in a community exceeds a predetermined level and then relaxed, with the hope of slowing the initial spread of disease through the community.
Provision of Necessities
If people are instructed to avoid public places, such as markets, stores, and pharmacies, or if those places are required to close, there will be a need for people to procure food, medicine, and other necessities in some other way. Similarly, shutting down mass transit may prevent people from being able to get to those facilities that do remain open, and it could prevent some people from being able to seek medical care. Such a situation also raises distributive-justice concerns since those people with the least resources will be least likely to be able to procure additional resources before closings occur.
Ideally governments would set up networks for the distribution of necessary provisions to citizens’ homes, with a particular focus on those most in need. Such distribution should be consistent and reliable, and it should provide necessities such as food and medicine for the duration of social-distancing measures. It should also be conducted in such a manner as to minimize interaction with potentially infectious people, and those people responsible for distributing provisions should use infection-control precautions to decrease the likelihood that they will spread disease. Transportation for medical care should be provided as needed by personnel who are apprised of the risks involved in transporting potentially infectious people; these personnel should be provided with protective equipment that will allow them to guard themselves from the disease and to avoid spreading it to others. Similarly, a program should be put in place for the removal of bodies from homes in a safe and efficient manner.
Resource constraints and logistical difficulties are likely to impede such a program in many areas. Many governments may lack the resources to provide food, medicine, and other necessities to its citizens during a pandemic. Even if the resources are available, the workforce needed to conduct distribution may be absent, especially at the height of a pandemic when a substantial number of people would be ill. Furthermore, there may not be enough people willing to interact closely with potentially infectious people to allow such a system to function. Shortages of personnel may be especially likely for medical transport and mortuary services.
At the very least, governments should do what they can to facilitate the provision of resources before an area is hit by disease. To the extent possible governments should give advance warning of disease and make recommendations about what food, medicine, and other supplies should be stockpiled and in what quantities. If they are able, governments should provide such necessities for people unable to afford them on their own. Governments should provide access to
medical care to the greatest extent possible, perhaps by reassigning public safety officers to this purpose. Governments should also provide a means by which people who have recovered from influenza—and who thus presumably would be immune—could volunteer to assist others in the provision of necessities.
International Travel and Border Controls
Transnational public health law has become increasingly important in global health, as evidenced by the WHO’s International Health Regulations and by national health agencies’ proposed communicable disease regulations (HHS, 2005a). These legal initiatives reflect WHO recommendations for border controls (WHO, 2004; IOM, 2005). Transnational containment measures can be far-reaching: entry or exit screening, reporting, health-alert notices, collection and dissemination of passenger information, travel advisories or restrictions, and physical examination or management of sick or exposed individuals. These kinds of powers were exercised in Asia and North America during the SARS outbreaks, although their effectiveness has not been established (Bell and WHO Working Group, 2004; St. John et al., 2005). The IHR also authorizes a variety of sanitary measures at borders and on conveyances, including inspection, fumigation, disinfection, pest extermination, and destruction of infected or contaminated animals or goods (HHS, 2005b). Although border protection is permitted, it can severely disrupt travel, trade, and tourism, and it should be balanced against the global economic impact.
Controls placed on international travel can also infringe upon civil liberties. The freedom of movement is a basic right protected by national laws and international treaties, but it is subject to limits when necessary for the public’s health (Shapiro v. Thompson, 1999). In particular, some of these limits can present serious risks to privacy. For example, containment measures may require the travel industry to collect and disclose passenger data (CDC, 2005b). Such infringements on privacy rights can be justified only if there is a genuine need to obtain high-quality surveillance data and if the infringements are carried out in accordance with the fair information practices described in the surveillance section above. To avoid discrimination and to ensure proportionality, public health officials should inform the affected individuals about the reasons for the infringement, the intended use of the information, and the extent to which third parties can have access to the data.
Given the transboundary nature of travel advisories as well as the economic impact they can have on affected countries, it should be left to the WHO to issue transparent and clearly justified travel recommendations in accordance with the revised IHR. It is the responsibility of individual countries to communicate all relevant information on the emergence of a public health threat to the international community. This responsibility is related to the surveillance duties and to the issues that accompany them. Ultimately, it is the responsibility of the national
government to use whatever policy instruments it has available to ensure that it can comply with the requirements of the new IHR.
Isolation and Quarantine
Isolation and quarantine are two of the oldest disease-control methods in existence and would likely be used in at least some instances during an influenza pandemic. While the terms “quarantine,” “isolation,” and “compulsory hospitalization” are often used interchangeably, they are, in fact, distinct. The modern definition of quarantine is the restriction of the activities of asymptomatic persons who have been exposed to a communicable disease, during or immediately prior to the period of communicability, to prevent disease transmission (Reich, 2003). In contrast, isolation is the separation, for the period of communicability, of known infected persons in such places and under such conditions as to prevent or limit the transmission of the infectious agent (Benenson, 1995). Quarantine and isolation can be accomplished by various means, including confining people to their own homes, restricting travel out of an affected area, and keeping people at a designated facility (Global Security, 2005). Whatever techniques are used, it is important to treat symptomatic, potentially infected, and non-exposed populations differently. For example, it would be inappropriate to place infected individuals in the same room as those who are only possibly exposed.
Quarantine and isolation are the most complex and controversial public health powers. Given that they involve a significant deprivation of an individual’s liberty in the name of public health, quarantine and isolation expose the tension between the interests of society in protecting the health of its citizens and the civil liberties of individuals, such as privacy, non-discrimination, freedom of movement, and freedom from arbitrary detention. Although these civil liberties are protected by both universal and regional human rights declarations and conventions, large-scale public health threats can require extraordinary measures by the government. Coercive public health powers such as quarantine and isolation can be legitimately justified if the public health interests of society are carefully balanced against the freedom of the individual (Gostin, 2007). To pass the balancing test, the benefits to the public should outweigh the burdens or harms that a quarantine may place on individuals. In addition each country should comply with the Siracusa principles, a set of internationally agreed-upon legal principles that establish the conditions under which restrictions on civil liberties are justified (United Nations Economic and Social Council, 1985). These principles hold that restrictions of liberty should be legal, proportionate, necessary, and accomplished by the least restrictive means that are reasonably available.
Measures as coercive as quarantine and isolation should only be used when a disease is known through extensive scientific study to be contagious and should be limited to people who have in fact been exposed to the disease. In cases of scientific uncertainty, however, resource and time restraints can make it neces-
sary for the government to take action without performing medical testing on each individual. There may be situations, for example, in which the availability of accurate tests and competent medical staff is limited. But at a minimum the state’s power should be exercised fairly and never as a subterfuge for discrimination. In a crisis situation, reasonable suspicion based on known contact with the pandemic virus can be sufficient to issue a quarantine or isolation order. However, to ensure the legitimacy of the measures taken, the decision to use restrictive measures must be made in an open, fair, and legitimate manner. The public has a right to know the legitimate public health reasons for restricting liberty. Public health authorities should fully and honestly disclose their reasons for action and allow community participation. Such transparency will enhance public trust and the acceptance of the proposed containment measures (Markovits, 2005; Heyman, 2005).
Quarantine and isolation should be voluntary whenever possible, and, when that is impossible, they should be enforced by the least intrusive means available. Research in the aftermath of SARS showed that people understood and accepted the need for restrictive measures. Many perceived it as their civic duty and were willing to sacrifice their right to freedom of movement (University of Toronto Joint Centre for Bioethics Pandemic Influenza Working Group, 2005). However, if governments expect full voluntary compliance, the decisions need to be made in an open and fair manner, and society should ensure that those who are quarantined or isolated receive adequate care and do not suffer unfair economic burdens.
When the protection of a community’s health requires that individual liberty and autonomy be restricted, the principle of reciprocity obliges society to provide those affected with the necessities of life. During quarantine, these necessities would include being housed in safe, humane conditions and receiving high-quality medical care and psychological support. Recent studies have confirmed that quarantine imposes some serious financial and psychological hardships on the affected individuals. About 30 percent of individuals quarantined for SARS, for example, suffered from posttraumatic stress disorder and depression (Hawryluck, 2004).
Distributive justice requires that officials limit the extent to which the personal and economic burdens of a public health threat fall unfairly upon individual citizens. A lack of resources and amenities should be addressed in the most fair and equitable possible way. Governments as well as national and international organizations should stockpile medical supplies and food. A pandemic influenza will require solidarity among nations and collaborative approaches that set aside traditional values of self-interest and territoriality.
Conclusion
Preparing for an influenza pandemic forces society to face a number of difficult challenges, many of which transcend the issue of mere scientific effective-
ness. Public health emergencies raise serious ethical issues which are central to society’s commitment to freedom and social justice. Even when effective, public health interventions can have serious adverse consequences on economic and civil liberties. It is vital that individual rights are only sacrificed when absolutely necessary to protect the public’s health. As such, laws must clearly establish the criteria under which governments can exercise emergency powers. These laws must also provide adequate due process and ensure that any infringements on individual rights are minimized.
The threat of an influenza pandemic is real. If the threat manifests itself, millions of lives will be lost. Such widespread death would be catastrophic, but the tragedy would be even worse if society ignores the ethical issues discussed above. It is crucial that society decide as soon as possible how it wants to respond to these ethical concerns so that in the event of a pandemic we are equipped— scientifically as well as ethically—to deal with its impact.
ETHICAL AND LEGAL CONSIDERATIONS IN PREPARING FOR PANDEMIC INFLUENZA9
James W. LeDuc, Ph.D.10
Centers for Disease Control and Prevention
Drue H. Barrett, Ph.D.11
Centers for Disease Control and Prevention
Anthony D. Moulton, Ph.D.12
Centers for Disease Control and Prevention
Richard A. Goodman, M.D., J.D., M.P.H.13
Centers for Disease Control and Prevention
Kathy Kinlaw, M.Div.14
Emory University
Robert J. Levine, M.D.15
Yale University
Introduction
A pandemic of influenza will be a global challenge that affects all sectors of society and places virtually every individual at risk, independent of social or economic status, ethnic origin, or gender. International travel will rapidly introduce novel influenza strains around the world. Major urban centers will be affected first, but soon thereafter the movement of residents will spread the disease to all but the most isolated communities. High infection rates may cause disruption of critical services across all sectors of society, and health-care facilities may be overwhelmed with seriously ill patients. Unless health-care workers are selectively protected, they may suffer disproportionately, which could lead to critical shortages of skilled health-care professionals and the further erosion of clinical care capacity. Antiviral drugs and protective vaccines will likely be in limited supply, necessitating difficult decisions on how to distribute these critical resources. Nonpharmaceutical interventions (NPIs)—including, for example, isolation of those infected, quarantine of those exposed, and other social-distancing measures—will be among the few options available to public health officials to limit the spread of infection and protect the largest number of individuals.
Preparation for pandemic influenza is a dynamic undertaking which involves many partners and different sectors of society. There must be careful preparation and coordination among all stakeholders, undertaken in a fully transparent and inclusive manner, in order to ensure equitable distribution and optimal benefit from limited supplies of antiviral drugs and vaccines. Further, successful implementation of social-distancing measures and other NPIs will require systematic attention to the important legal and ethical issues that their use raises.
Laws give public health agencies the power to act to protect the public’s health through the exercise of such measures as isolation and quarantine, but laws necessarily must leave room for discretion by decision makers because it is not possible to anticipate the specifics of each public health emergency. For this reason public health officials must apply ethical reasoning on matters for which the law does not provide precise guidance. In particular, such ethical considerations should inform officials’ deliberations when making difficult choices that directly affect the health and well-being of the populations they serve. In the pages that follow, we suggest ethical guidelines that will be relevant to efforts to prepare for and respond to a pandemic, discuss some of the legal issues that require consideration, and conclude with some general comments relevant to national and international preparedness efforts. It is important to recognize that scientific knowledge about effective pandemic influenza interventions is evolving rapidly. The issues and suggestions presented here, while intended to have broad applicability, nonetheless may need to be reassessed as scientific knowledge advances, as the results of various public health interventions become known, and as the pathogens under consideration themselves evolve over time.
Ethical Guidelines
In an attempt to establish systematic ethical guidelines to guide decision makers in preparing for and responding to pandemic influenza, the CDC asked the Ethics Subcommittee of the Advisory Committee to the Director, CDC, to prepare a set of guidelines for use in the prioritization and distribution of vaccines and antiviral drugs and also in the development of any interventions that might limit individual freedom and create social distancing.16 Table 3-1 outlines the general ethical considerations that the Ethics Subcommittee describes in its document. In preparing these guidelines, the subcommittee took into account the need to have ethical perspectives provide practical direction as well as the importance of having any proposed guidelines fully vetted by those involved in planning and responding to pandemic influenza.
It is clear that because of such factors as production capacity and the lead time required to identify viral strains there will not be sufficient amounts of antiviral drugs or vaccines to protect all those potentially at risk during an influenza pandemic (although recent increases in production capacity may limit shortages of one key antiviral drug). The existence of such shortages will require that the distribution of these limited resources be prioritized. Traditionally, interventions have been distributed to those individuals most at risk on the principle of attempting to limit serious illness and death as much as possible. During a pandemic, however, preserving the functioning of society may be a higher priority, which would require that those individuals who are essential to the provision of health care, the maintenance of public safety, or the functioning of key aspects of society receive priority in the distribution of vaccines, antivirals, and other scarce resources. Such an approach will require that diverse stakeholders be involved in affirming this priority, determining who is deemed essential, and establishing a distribution strategy.
There are a variety of other ethical considerations identified by the Ethics Subcommittee. There should, for instance, be a commitment to transparency throughout the influenza planning and response process. Furthermore, since public engagement and involvement are essential to building public will and trust, they should be evident throughout this process. Public health officials have a responsibility to maximize preparedness in order to minimize the necessity for making allocation decisions later, during the course of the pandemic. Ethical guidelines should be based on the best available scientific evidence, with the current knowledge base serving as a foundation for these guidelines. There should
|
16 |
The ethical guidance described in this article is based on the document developed by the Ethics Subcommittee of the Advisory Committee to the Director, CDC, Ethical Guidelines in Pandemic Influenza. The ethical guidelines document was prepared by Robert J. Levine and Kathy Kinlaw with input from other members of the Ethics Subcommittee and with assistance form Drue Barrett. The information was presented by James W. LeDuc to the IOM on September 20, 2006. A copy of Ethical Guidelines in Pandemic Influenza may be obtained at http://www.cdc.gov/od/science/phec/. |
TABLE 3-1 Ethical Guidelines in Pandemic Influenza
|
General Ethical Considerations |
|
Identification of clear planning goals |
|
Commitment to transparency |
|
Public engagement and involvement |
|
Maximizing of preparedness |
|
Sound guidelines based on best available scientific evidence |
|
Global involvement and cooperation |
|
Balancing of individual liberty and community interest |
|
Diversity in ethical decision making |
|
Fair process (procedural justice) |
|
SOURCE: CDC (2007). |
also be a commitment to ongoing scientific and ethical evaluation of interventions. The pandemic planning process should acknowledge the importance of working with and learning from preparedness efforts globally. The reasons for this collaboration include not only the potential of global involvement to benefit U.S. citizens (an “instrumental” reason) but also a recognition of global interdependence and the value of the common good.
It will be important in planning for pandemic influenza to balance individual liberties with community interests. Limits on individual freedom may be necessary to protect the community as a whole as well as those individuals whose liberty is restricted, yet individual liberty should be restricted with great care and only when alternative approaches are unlikely to be effective. In determining these restrictions, the guiding principles should include adopting the least restrictive practices, ensuring that restrictions are necessary and proportional to the need for protection, and ensuring that those affected by restrictions receive support from the community, such as job security and provision of necessities for the individuals and their families. Diverse public voices should be involved in determining the need for restrictions and in articulating their ethical justifications. Furthermore, planning and implementation should be done by decision makers who are impartial and neutral and who are consistent in applying standards, and those affected by the decisions should have a voice in making them—and, where feasible, agree in advance to the process. All who are affected by these decisions should be treated with dignity and respect.
Another important component of pandemic influenza planning will be resource allocation. The guidelines suggest that resource allocation should be designed to accomplish clearly articulated goals and be guided by criteria specified well in advance of a pandemic. The classic utilitarian approach of the greatest good for the greatest number is not appropriate for defining priorities in a pandemic influenza. Instead, the recommended approach is one that resembles utilitarianism in that it evaluates policies primarily in terms of their anticipated consequences but is tempered by the ethical principles of respect for persons,
nonmaleficence, and justice. Distribution plans should specify what scarce goods are involved, who is to decide about prioritization and distribution, who is eligible to be a recipient, and what moral criteria will be used to assign priorities to groups of individuals. Criteria that would generally not be ethically supported include “to each according to purchasing power,” “first come, first served,” or criteria such as race, ethnicity, religious belief, or any similar characteristics used to make discriminations that are invidious and not morally relevant. Normally, distribution based on an individual’s social worth is not morally acceptable; however, in planning for a pandemic, where the primary objective is to preserve the function of society, it may be necessary to identify certain individuals and groups as key to the preservation of society and to accord them a higher priority.
Social distancing and restrictions on personal freedom will be important tools for managing pandemic influenza. Such interventions can include the isolation of infected individuals; the quarantine of those heavily exposed, such as family members or close contacts; adjustments to school schedules or even the closing of schools and cancellation of public events; limiting travel; and restricting access to public venues. These interventions are founded on the premises that an individual sick with influenza is infectious only for a short time and that separating that person from the larger group of susceptible individuals during that time will likely interrupt further transmission of the disease. Putting any of these interventions into effect will involve restricting highly valued personal freedoms, so justification for any such restrictions must be carefully considered. The process for making decisions about these restrictions should be well thought out in advance and be done in a transparent manner by a group that is representative and diverse. Recent modeling of the effects of social-distancing measures at different stages of a pandemic suggests that voluntary compliance may be enough for such measures to succeed (IOM, 2006). Mandatory liberty-limiting and social-distancing interventions should be imposed only in situations where voluntary actions seem unlikely to be effective.
During a pandemic, centralized decision making will be necessary in a number of areas. Because this type of decision making represents a departure from customary public health practice, it will be important to create fair and equitable restrictions, and a process should be in place for objections to be heard, restrictions appealed, and new procedures to be considered. Local autonomy in decision making should be honored whenever there is no evidence that centralized decision making will contribute substantially to preserving the functioning of society and where the easing of restrictions is proportional and reasonable in particular communities (e.g., uniform duration of school closings may not be reasonable in communities where the influenza wave has already ended.) Communications about restrictions should begin early in the planning process, and the public should be clearly informed that restrictions on personal freedom are expected. Any liberty-limiting measure should be enacted only if the best available scientific evidence indicates that implementing the measure will achieve its
intended goal, that the limitation is proportional to the anticipated benefit, that no less restrictive measure is likely to be effective, and that failure to implement the measure is likely to result in grave harm to the functioning of society. Throughout the process, the need for limits on individual freedom must continue to be assessed and affirmed.
Legal Considerations
Many legal challenges will undoubtedly emerge during the course of the global response to a pandemic of influenza. These will vary among countries and, domestically, across states, provinces, and localities in response to variation in the laws, to officials’ competency in applying them, and to citizens’ willingness to comply with, or challenge, the legal mandates (Fidler and Cetron, 2007; Stier and Goodman, in press). The CDC Public Health Law Program has described the concept of public health legal preparedness for public health emergencies, such as pandemic influenza, and it has identified four core elements that affect public health legal preparedness: a) laws; b) competencies in applying these laws; c) coordination of legal powers across jurisdictions and sectors; and d) information about best practices in implementing law-based interventions (Moulton et al., 2003; Goodman et al., 2006). These elements are highly relevant to social distancing, for instance, and steps that might be taken to maximize the effectiveness of social-distancing measures are described in detail elsewhere in this report (Cetron and Landwirth, 2005, and reprinted earlier in this chapter).
Experts generally agree that, as part of their police powers, all states have legal authority to quarantine and isolate individuals. The specific authorities and abilities of given states and other jurisdictions to quarantine groups, suspend public meetings, close facilities, and impose curfews are less well known. Experts differ on whether adequate social distancing can be achieved voluntarily. Table 3-2 lists a variety of issues related to public health law that will influence the effectiveness of mandatory social distancing, arranged according to the framework of the four public health legal-preparedness core elements.
Table 3-3 presents a number of questions about and challenges relating to the level of legal preparedness for social distancing. For example, what are the status and adequacy of laws for isolating those known to be, or strongly suspected of being, infected with pandemic influenza? Are public health officials legally authorized to quarantine those who have been in close contact with infected individuals? What is the status of legal authority to close schools and public gatherings? Can commercial movements and travel be restricted legally? To what extent? Do laws confer immunity to liability for health-care providers who, during a declared public health emergency, perform services for which they are not licensed or against whom claims of negligence may be asserted? Are the pertinent school laws uniform across adjoining communities? Do states have legal authority to assist in enforcement of a federal quarantine?
TABLE 3-2 Selected Public Health Law-Related Issues and Needs for Effective Mandatory Social Distancing
|
Legal Authorities to:
|
|
Public and Private Officials Competent in:
|
|
Coordination of Legal Tools Across Jurisdictions and Sectors:
|
|
Information Resources on:
|
TABLE 3-3 Selected Challenges to Legal Preparedness for Social Distancing
|
Legal Authorities:
|
|
Competencies:
|
|
Coordination:
|
|
Information Resources:
|
With respect to legal-preparedness competencies: Are officials trained in the application of legal powers to put social-distancing interventions into effect? Are they adequately prepared to protect individual and property rights while implementing social-distancing interventions? Are judges aware of the legal powers that public health officials hold and of the legal precedents relevant to appeals that aggrieved citizens may put forward? Do hospital executives and other health-care providers (and their legal counsel) understand their legal responsibilities during an influenza pandemic? Are officials capable of effective communication with the public and the media about the need for, and legal basis of, social-distancing interventions?
As to the coordination of legal powers across jurisdictions and sectors, there are concerns that the laws of some states may not allow those states to assist in enforcing a federally declared quarantine of, for example, passengers arriving on an international flight. It is thought that few jurisdictions have protocols in place for a coordinated response by health-care, law enforcement, and public health agencies to an infectious disease outbreak. A notable exception is the tripartite agreement executed in 2004 by the New York City health and police departments and the Federal Bureau of Investigation (FBI) for joint investigations of suspected bioterrorist attacks.17
Regarding the core element of information on legal best practices, there are a number of important issues: Do public health, health-care, law enforcement, and other relevant officials have ready access to such information in deciding when to use legal authorities to support social distancing? Are judges informed about the specific legal powers that public health officials possess? Do the executives and legal counsels of private hospitals know about these powers and understand their implications for hospital operation during emergencies?
These core elements of public health legal preparedness for pandemic influenza should be tested in every community and state by conducting exercises and other approximations of an actual pandemic. Such tests can help local and state officials and their private-sector counterparts identify gaps in legal authorities for mandatory social distancing, in case it should be needed, and also help them ascertain whether protocols are in place to translate those powers into practice. Exercises can test whether information is available to all the relevant government and private organizations concerning their legally specified roles and responsibilities during a pandemic, including their communications with the public and the media. Exercises also should test how well the applications of nonpharmaceutical interventions are coordinated between the federal government and the states, across states, and throughout jurisdictions within each state.
These and other legal aspects of the preparation for and response to pandemic influenza offer options for the Institute of Medicine and other organizations to participate further. Such participation might include, for example, efforts to assist
|
17 |
Document available at http://www2.cdc.gov/phlp/docs/Investigations.PDF. |
local, state and federal agencies, including CDC and the U.S. Department of Justice, in identifying gaps in the four public health legal-preparedness core elements in states and communities and then working to strengthen those core elements. In this effort, federal agencies should partner with state and local public health leaders and their legal counsel, their health-care counterparts, the courts, and all others who will play critical roles in shaping, implementing, and adjudicating the response to pandemic influenza.
Closing Thoughts
The threat of pandemic influenza has focused national and global attention on public health and on the tools that will be required to address this serious global challenge, some of which have not been used extensively in modern times. Because the scientific data needed for informed decision making are incomplete, models have been used extensively to predict outcomes based on representative scenarios of an influenza pandemic. These increasingly sophisticated models have proven valuable in exploring the possible outcomes of various policy decisions (IOM, 2006). One aspect of model development is careful documentation of assumptions made while building the model. These assumptions allow model builders to estimate various possible outcomes in the absence of hard data. It is essential that policy makers pay close attention to the assumptions underlying the models being developed and to the basis for these assumptions. Well-founded assumptions can guide future research aimed at pinpointing the key elements in our intervention strategies, and careful refinement of the assumptions will yield models that more faithfully represent reality.
Although a great deal of money and effort has gone into purchasing antiviral drugs for the treatment of pandemic influenza, and although good progress is being made in vaccine development and production, there remains a strong likelihood that these and other important items will be in short supply, and this will necessitate hard choices as to who receives them and who does not. Thus there needs to be extensive discussion, planning, and preparation concerning the allocation decisions and liberty-limiting and social-distancing interventions that will certainly be necessary in a pandemic. These steps should be taken only if the best available scientific evidence implies that they are likely to be successful, if they are grounded in sound ethical and legal principles, and if the important decisions about them are taken through a process that is transparent, inclusive, and appropriately communicated to the general public.
PUBLIC HEALTH AND ETHICAL CONSIDERATIONS IN PLANNING FOR QUARANTINE18
Martin Cetron, M.D.19
Centers for Disease Control and Prevention20
Julius Landwirth, M.D., J.D.21
Yale University
Quarantine is one of the oldest, most effective, most feared, and most misunderstood methods of controlling communicable disease outbreaks. Its etymological roots are traceable to fourteenth century public health practices requiring ships arriving in Venice from plague-infected ports to sit at anchor for 40 days (hence, quar-antine) before disembarking their surviving passengers. While in recent times the use of quarantine has been more humane and scientifically based, the historical association with exile and death and the morally negative connotation of sacrifice of a few for the benefit of others remains as an undercurrent of public apprehension. Nevertheless, quarantine was recently implemented successfully in several countries as a socially acceptable measure during the SARS epidemic in 2003 (Cetron and Simone, 2004). It is an important component of the Department of Health and Human Services (HHS) Pandemic Influenza Plan issued in November, 2005 (HHS, 2006a).22
The purpose of this article is to review the modern public health approach to quarantine, outline highlights of current plans for its implementation in the event of an avian influenza pandemic, and consider the ethical principles that should be considered.
Definitions
Quarantine is the restriction of persons who are presumed to have been exposed to a contagious disease but are not ill. It may be applied at the individual, group, or community level and usually involves restriction to the home or designated facility. Quarantine may be voluntary or mandatory.
Isolation is the separation of ill persons with contagious diseases. It may be applied at the individual, group, or community level.
Quarantine of groups refers to quarantine of people who have been exposed to the same source of illness (e.g., at public gatherings, airline, school, workplace).
Working quarantine refers to persons who are at occupational risk of influenza infection, such as health-care workers, who may be restricted to their homes or designated facilities during off duty hours.
Community-wide quarantine refers to closing of community borders or the erection of a real or virtual barrier around a geographic area (cordon sanitaire).
Modern public health places quarantine within a broader spectrum of interventions generally referred to as “social distancing.”
The effect of successful measures to increase social distance is to convert a dynamic of exponentiation in the spread of an infectious agent to one of suppression in which the number of secondary cases from exposed persons is reduced to a manageable level. Time is the key variable in the success or failure of social distancing strategies, including the duration of communicability, whether or not communicability occurs before onset of symptoms, the number of resulting contacts, and the efficiency of or delays in contact tracing.
Globalization of travel and trade, and decreased travel time between distant places have further complicated these relationships. There are several hundred international ports of entry airports in the United States. Fortunately, 25 of these airports account for approximately 85 percent of international arrivals. Detailed recommendations for travel-related containment measures can be found in the full HHS report and will not be further elaborated here.
Principles of Modern Quarantine
In the months before adequate supplies of vaccines and antiviral agents are expected to be available, quarantine and isolation are likely to be the mainstays of containment strategies.
The HHS plan states that: The goal of quarantine is to protect the public by separating those exposed to dangerous communicable disease from the general population. It represents collective action for the common good that is predicated on aiding individuals who are already infected or exposed and protecting others from inadvertent exposure (HHS, 2006b).
Principles of modern quarantine and social distancing limit their use to situations involving highly dangerous and contagious diseases and when resources are reliably available to implement and maintain the measures. It encompasses a wide range of strategies to reduce transmission that may be implemented along a continuum based on phase and intensity of an outbreak.
For example, at a stage when transmission of a novel influenza virus is still limited, either abroad or in the area, and local cases are either imported or have clear epidemiological links to other cases, individual quarantine of close
contacts may be effective. At a more advanced phase of the pandemic, however, when virus transmission in the area is sustained and epidemiological links to other known cases is unclear, limiting quarantine to exposed individuals may be ineffective, and the strategy may need to expand to include community-based interventions that increase social distance. These include school closings, cancellation of public gatherings, encouraging non-essential workers to stay home, and reduced holiday transportation schedules. If these measures are believed to be ineffective, community-wide quarantine may need to be implemented.
The HHS guidelines cite two important principles designed to help ensure that those in quarantine are not placed at increased risk. First, quarantined individuals will be closely monitored, with daily visits as needed, in order to detect earliest onset of symptoms and separation from those who are well. Second, persons in isolation will be among the first to receive any disease-prevention interventions. In addition, the HHS plan recommends that they should be provided with all needed support services, including psychological support, food and water, and household and medical supplies.
Home quarantine is the preferred method of separation, whenever possible. Designated quarantine facilities may have to be identified for potentially affected persons who do not have access to an appropriate home environment, such as persons living in dormitories, travelers, the homeless, or if the configuration of the home is not suitable for the protection of the potentially infected person and other occupants.
Voluntary quarantine is the preferred first option before resorting to mandatory orders or surveillance devices. In this connection, it is noteworthy that quarantine does not require 100 percent compliance to be effective. Toronto Public Health officials reported only 22 orders for mandatory detainment among the approximately 30,000 persons who were quarantined (Upshur, 2003).
Legal and Ethical Considerations
Primary responsibility for public health matters within their borders rests with state and local governments. This includes isolation and quarantine. Applicable state laws, regulations and procedures vary widely. A recently developed Model State Emergency Health Powers Act attempts to promote greater interstate consistency in response to emergency public health situations (Center for Law and the Public’s Health, 2001). In the section on isolation and quarantine, the Model Act covers the principles and conditions governing implementation of quarantine; authorization of public health authorities to impose temporary quarantine by directive, with rights of appeal within 10 days; imposition of quarantine with notice following a public health authority court petition and hearing; and legal procedures for release from quarantine or relief from violations of conditions of quarantine. Although it has been criticized by some as being overly broad
in its coercive powers (Annas, 2002; Mariner, 2001) the Model Act has been adopted in whole or part in a number of jurisdictions.
The federal Public Health Service Act (U.S. Congress, 1946) gives the HHS secretary responsibility for preventing introduction, transmission, and spread of communicable diseases from foreign countries into the United States and within the United States and its territories/possessions. This authority is delegated to the Centers for Disease Control and Prevention (CDC), which are empowered to detain, medically examine, or conditionally release individuals reasonably believed to be carrying a communicable disease. The Public Health Service Act also provides that the list of diseases for which quarantine is authorized must first be specified in an executive order of the president, on recommendation of the HHS secretary (CDC, 2006). On April 5, 2005, influenza caused by a novel or reemergent strain that is causing or has the potential to cause a pandemic was added to that list (White House, 2005).
Although the discipline of public health has its origins several centuries ago, it is only relatively recently that ethical principles and codes to guide public health practice and policy have been formulated. The ethical principles at the heart of the more fully developed fields of medical and research ethics are grounded in the primacy of individual autonomy in clinical decision-making in the therapeutic setting and in consent for participation in the setting of human subjects research. They are guided by a fundamental moral axiom that individual persons are valued as ends in themselves and should never be used merely as means to another’s ends. Public health, on the other hand, emphasizes collective action for the good of the community.
The Principles of the Ethical Practice of Public Health, issued by the Public Health Leadership Society in 2002 (Public Health Leadership Society, 2002), states that community health should be achieved in a way that respects the rights of individuals and the community. Accompanying notes are instructive:
This principle identifies the common need in public health to weigh the concerns of both the individual and the community. There is no ethical principle that can provide a solution to this perennial tension in public health. We can highlight, however, that the interest of the community is part of the equation, and for public health it is the starting place in the equation; it is the primary interest of public health. Still, there remains the need to pay attention to the rights of individuals when exercising the police powers of public health (Public Health Leadership Society, 2002).
To address this potential dichotomy, the principles require ensuring opportunity for informed community participation in the development of policies, programs, and priorities, accessibility to basic resources and conditions necessary for health, and protection of confidentiality.
Principles of practice, law and ethics in the containment of outbreaks of infectious disease, especially use of quarantine, confront a common underlying concern, namely,
The individual fear and community panic associated with infectious diseases often leads to rapid, emotionally driven decision making about public health policies needed to protect the community that may be in conflict with current bioethical principles regarding care of individual patients (Smith et al., 2004)
In November 2005, the Council on Ethical and Judicial Affairs of the American Medical Association issued recommendations for the medical profession in the use of quarantine and isolation as public health interventions. Again, the tensions between the ethical imperatives of therapeutic medicine and public health are reflected in the following excerpts:
Quarantine and isolation to protect the population’s health potentially conflict with the individual rights of liberty and self-determination. The medical profession, in collaboration with public health colleagues, must take an active role in ensuring that those interventions are based on science and are applied according to certain ethical considerations…. Individual physicians should participate in the implementation of appropriate quarantine and isolation measures as part of their obligation to provide medical care during epidemics…. In doing so, advocacy for their individual patients’ interests remain paramount (Council on Ethical and Judicial Affairs, 2005).
An important rationale for acknowledging and attempting to ameliorate this tension in pandemic preparedness planning, including quarantine measures, is to reduce the potential for unfair distribution of burdens and benefits among various segments of society (Markovits, 2005). In an important contribution, Susan Kass has developed a six-step framework for ethical analysis specifically for public health (Kass, 2001). The application of this general framework to quarantine is discussed in detail elsewhere in these proceedings.
Ross Upshur has outlined four principles that must be met to justify quarantine (Upshur, 2002):
First, under the harm principle there must be clear scientific evidence of personto-person spread of the disease and the necessity of quarantine as a containment measure. Second, the least restrictive means should be implemented. Third, upholding the principle of reciprocity points to the community’s obligation to provide necessary support services for those in quarantine. Fourth, the obligation of public health authorities is to communicate the reasons for their actions and to allow for a process of appeal. In November 2004, the World Health Organization issued a checklist for influenza pandemic preparedness. It encourages planners to “consider the ethical issues related to limiting personal freedom, such as may occur with isolation and quarantine” (WHO, 2005a).
An instructive example of how ethical considerations can be incorporated into pandemic preparedness plans can be found in the Ontario Health Plan for an Influenza Pandemic (Ontario Ministry of Health and Longterm Care, 2005). The development of this plan included a collaboration with the Toronto Joint Centre for Bioethics, which produced a 15-point ethical guide for decision making for a pandemic (University of Toronto Joint Centre for Bioethics Pandemic Influenza Working Group, 2005). The guide identified four key ethical issues in pandemic preparedness planning, one of which was “restricting liberty in the interest of public health by measures such as quarantine.” The guide describes the following substantive and procedural ethical values at stake in addressing this issue:
-
Individual liberty: Isolation and quarantine should be proportional, necessary, relevant, equitably applied, and done by least restrictive means.
-
Protection of public from harm: Officials must weigh the imperative for compliance and review decisions.
-
Proportionality: Restrictive interventions should be limited to the actual level of risk to community.
-
Privacy: There must be a necessity for overriding the public’s protection.
-
Reciprocity: Support is needed for those facing a disproportionate burden in protecting public health, individual liberty (proportional, necessary, relevant, least restrictive means, equitably applied), protection of public from harm (weigh the imperative for compliance, review decisions), proportionality (restrictive interventions limited to actual level of risk to community), privacy (necessity for overriding for public’s protection), and reciprocity (support for those facing disproportionate burden in protecting public health).
Procedures should be reasonable, with reasons for decisions shared with stakeholders; open and transparent; inclusive, with stakeholder participation; responsive, subject to review and revision with experience; and accountable.
Based on these principles, the guide recommended the following:
-
Governments and the health-care sector should ensure that pandemic influenza response plans include a comprehensive and transparent protocol for the implementation of restrictive measures. The protocol should be founded upon the principles of proportionality and least restrictive means, should balance individual liberties with protection of public from harm, and should build safeguards such as the right of appeal.
-
Governments and the health-care sector should ensure that the public is aware of a) the rationale for restrictive measures, b) the benefits of compliance, and c) the consequences of noncompliance.
-
Governments and the health sector should include measures in their pandemic influenza preparedness plans to protect against stigmatization and to safe-
-
guard the privacy of individuals and/or communities affected by quarantine or other restrictive measures.
-
Governments and the health-care sector should institute measures and processes to guarantee provisions and support services to individuals and/or communities affected by restrictive measures, such as quarantine orders during a pandemic influenza emergency. Plans should state in advance what backup support will be available to help those who are quarantined (e.g., who will do their shopping, pay the bills, and provide financial support in lieu of lost income). Governments should have public discussions of appropriate levels of compensation in advance, including who is responsible for compensation.
Past experience has shown that voluntary cooperation and public trust are key ingredients of successful response to a public health emergency. They may be important antidotes to individual fear and community panic that may be engendered by infectious disease outbreaks. Careful attention to the ethical values at stake in public health decision making can help foster voluntary cooperation and public trust and should be a part of state and federal pandemic preparedness planning.
REMARKS ON THE ROLE OF MODELING IN INFECTIOUS DISEASE MITIGATION AND CONTAINMENT
The Brookings Institution
I have been invited to make some brief informal remarks about the modeling enterprise and its relevance to infectious disease mitigation and containment. I will try to be brief, and will certainly be informal, in the sense of dispensing with extensive citations. Following this paper are two published articles which serve as recent examples of my own modeling. I would refer you to these articles for complete references and technical details.
Implicit and Explicit Models
I would like to begin with a claim that most audiences find rather discomfiting. It is this: Everyone in the room is a modeler. You are all modelers. Anyone
who ventures a projection, or imagines how things might unfold in space and time, is running some model or other. It is just an implicit model in which the assumptions aren’t actually laid out, in which their internal consistency can’t really be tested, in which their consequences can’t be played out and examined very rigorously, in which their relation to data is unknown. But when you close your eyes and imagine an epidemic spreading, or any other social phenomenon, you are running some model or other. It is just an implicit model that you haven’t written down.
I am always amused when smug practitioners challenge me with the question: “Can you validate your model?” The appropriate retort, of course, is: “Can you ‘validate’ yours?” At least I can write mine down so that it can, in principle, be calibrated to data (if that is what you mean by “validate”).
Accordingly, I build explicit models, and we at NIH/MIDAS build explicit models, so that we can study exactly what our assumptions entail: On these assumptions, this sort of thing happens. When you alter the assumptions, that is what happens.
When you write explicit models you let others replicate your results. You can calibrate the model to historical cases, if there are data. You can test against current data to the extent that exists. And, importantly, you can incorporate the best medical expertise in a rigorous way.
With modern computing, the models, if need be, can be quite realistic spatially, behaviorally, biomedically, and in numerous other ways. You can execute a huge range of possible scenarios and containment strategies and do what we call sensitivity analysis to identify the most salient uncertainties. You know there are going to be uncertainties and you want to know how important they are. Which ones can you gauge? About which ones do you need to learn more?
Model Myths
There are some myths about explicit models that I want to refute immediately. Certainly in the policy sphere (if not in particle physics), such models do not replace judgments. They can make judgments better informed. They permit us to incorporate the best expertise and existing data in a rigorous way. But in making public health policy, there will be a central role for judgments, and models25 (at least at this stage of development) don’t change that.
Models, likewise, do not eliminate uncertainty. We are going to face uncertainty. If we could bound it, that would be useful. Sometimes models can help us do that, and help us identify those uncertainties that actually matter most. Not all uncertainties are equal. Models can help us rank them and set priorities and even figure out what data we need to collect. Without a model it is often not clear exactly what data are worth collecting.
On this point, non-modelers (and many modelers) often adopt a naive inductivism: “Science proceeds from observation, and then models are constructed to ‘account for’ the data.” Not always so. Maxwell’s theory predicted the existence of radio waves, which were only later sought, and observed. Further examples abound.26
While purely theoretical work is essential to basic scientific progress, in applied infectious disease modeling I think it is very important that modelers work closely with medical experts. This is one of the strengths of the MIDAS operation: when we set about trying to model pandemic flu, we actually had intensive consultations at CDC with the best flu experts we could convene, to thrash out what we should actually assume about a human-to-human variant of H5N1. Same for smallpox. We worked very closely with D.A. Henderson and others to arrive at detailed biomedical and behavioral assumptions for normal, modified (by prior immunity), and hemorrhagic smallpox before comparing intervention strategies (see below).
Just delivering a mathematical black box with lots of dials to twiddle—as we modelers are prone to do—is really not useful to decision makers. You have got to roll up your sleeves together with actual domain experts and grapple with everything, sort it out, and make your assumptions clear. It’s very useful that computers are such dumb, literal beasts. If you don’t make your assumptions crystal clear to the computer—and therefore to yourself—it just won’t run. The modeling enterprise itself forces this kind of explicitness upon you, and it may be as valuable as the final model.
From Ignorant Militance to Militant Ignorance
In particular, the enterprise of modeling—of squarely facing one’s imprecisions and uncertainties—engenders a healthy humility. At its core, the scientific habit of mind involves a kind of militant ignorance27; that’s right, an insistence on “I don’t know.” Much more common, I’m afraid, is an ignorant militance; a commitment to one’s preconceptions despite evidence.
A Rose Is Not a Rose
So, having convinced you, maybe, that modeling per se isn’t so bad, I want to say that there are profoundly different types of models. One type of model that has dominated the landscape until quite recently is the traditional so-called “low dimensional ordinary differential equation model.” These are very widely used
to project epidemic severity, to compare intervention strategies, and to estimate demand for vaccine, medical personnel, and so forth.
The problem with these models is that they typically assume a kind of perfect mixing in the population, what in physics would be called mass action kinetics. It is as though you took infectives and susceptibles and put them in a jar and shook the jar up with tremendous energy so that everybody smashes into everybody as if they were particles in a gas. In turn, the particles, if you will, are themselves homogeneous. Typically, it is just susceptibles and infectives. There is very little differentiation among the susceptibles or among the infectives in these models.
All of this makes for very elegant mathematics and has produced absolutely fundamental insights (e.g., herd immunity) and is entirely defensible in some domains. But in twenty-first-century urban industrial settings it can very seriously distort our estimates of severity and the policies we base on those estimates.
The real world is just a lot more complicated. It is very far from perfectly mixed. How do things unfold if smallpox or pandemic flu or some other bug is released on a modern metro system or at an international airport? In such cases, well-mixed models can be seriously misleading. Models are idealizations, and I am all for that, but they have to be productive and not misleading idealizations; to assume perfect mixing in processes of the sort we are worrying about here is really not productive. Indeed, I think it can do some damage in fact.
At the Brookings Center on Social and Economic Dynamics and in MIDAS, my colleagues and I are building models of a fundamentally different sort. We call them individual-based, or agent-based, models (ABM), and the core idea is this: Rather than write aggregate equations for the uniform mixing of entire homogeneous pools, in ABMs every single individual is represented. These are completely disaggregated models. Every individual is represented as a discrete software object, a little “cyberperson” in his or her own right. These agents (not to be confused with disease agents) can differ from one another in myriad ways. They can differ by age, by immunocompetence, by disease state. They can have actual itineraries, agendas, and activities that they execute in the computer. They may commute to work, go to school, work at the hospital, travel someplace, and adapt to conditions over time. Events unfold not in a well-mixed jar but on an explicit landscape of some sort, a town, a country, the globe. As I will show you, there are actual social networks governing who bumps into whom.
The Smallpox Model
The smallpox model was initiated by me and Donald Burke,28 then of the Johns Hopkins Bloomberg School, at the invitation of the National Academy of Sciences’ Committee on International Security and Arms Control (CISAC). At the time, the CISAC’s main concern was genetically modified variants, specifically
IL-4 variants. This was before 9/11 and the anthrax attacks. Subsequently, of course, issues of smallpox bioterror rose to the fore, and we joined the Smallpox Modeling Working Group of the Secretary of Health and Human Services’ Advisory Council on Public Health Preparedness. This working group was founded and chaired by D.A. Henderson, who also chaired the Advisory Council, to which we presented our final results. These are presented in detail in the articles attached with this lecture.
However, to reinforce my earlier point about the need for close collaboration between modelers and medical experts, the Working Group had intensive regular meetings to arrive at detailed assumptions about all the biomedical and critical behavioral aspects of this problem, and when I say “detailed assumptions,” I really mean it.
Figure 3-1 shows the natural history assumptions we arrived at for ordinary smallpox. We also developed the natural history assumptions for smallpox modified by prior immunity, and for hemorrhagic smallpox. It required the better part of two years of work, of really rolling up our sleeves—with experts directly engaged in the smallpox eradication—to converge on these assumptions and write them down explicitly and carefully. The results are published now in the International Journal of Infectious Diseases (Longini et al., 2006, and page 112). In addition to accommodating highly detailed inputs, agent-based models produce quite novel outputs.
Dendrograms
For example, because they track each individual (unlike homogeneous differential equations), agent-based models permit us to reconstruct exact transmission chains and thereby to address the question (which loomed large for SARS) of what makes someone a superspreader. Is it the person’s biology, his or her position in the social network, some foreseeable combination of factors? For the particular model realization depicted in Figure 3-2, hemorrhagics (red) die before they can transmit. But modified smallpox cases (green) —with less severe symptoms due to prior immunity—transmit very effectively, while the main transmitters are agents with ordinary smallpox (blue).
For a complete exposition of this model and, importantly, its calibration to historical data, please see the attached articles.
Let me emphasize again a practical advantage of agent-based models: Because they are rule-based rather than equation-based, they are accessible to non-modelers, which facilitates collaboration with medical experts. At the same time, there is no loss of rigor. The models can be run a large number of times under different assumptions and stochastic perturbations to produce a robust statistical portrait of the model’s behavior, which can then be compared to data by appropriate statistical means.
Regarding our work with D.A. Henderson on smallpox, I think it is fair to
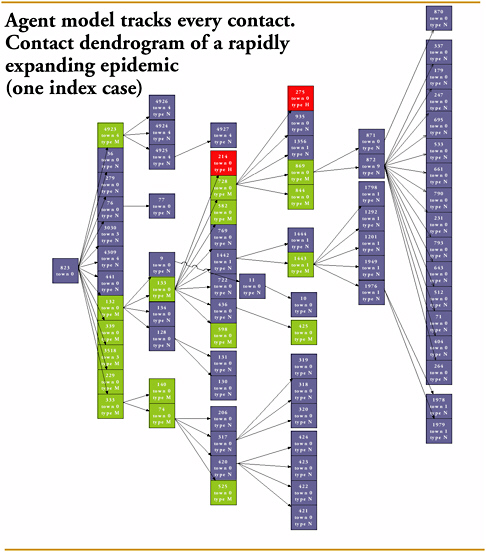
FIGURE 3-2 Contact dendrogram of a rapidly expanding epidemic (one index case).
SOURCE: Derived from Epstein et al. (2004).
say that, through engagement with domain experts, facilitated by a user-friendly agent-based approach, and incorporating all available data, we were able to develop novel and powerful approaches to containment; we met high scientific standards; and we enjoyed high policy credibility. Neither modeling in isolation nor expert opinion unsupported by models would have had the combined scientific and policy impact this collaboration achieved.
We aim to replicate this excellent experience on global pandemic flu within
MIDAS, and on a wide range of public health questions at the Brookings Center on Social and Economic Dynamics.
Concluding Points
To wrap up these brief informal remarks, I would say that explicit models are like Democracy. They are the worst imaginable system except for all the others, and in studying dynamics with the scale and complexity of global pandemic flu, I don’t think there is any alternative to explicit models. There is also no alternative to judgment, and modelers really need to work closely with medical professionals to make models that are maximally useful. As I say, delivering a black box with knobs to twiddle may not be very helpful. My own experience is that interdisciplinary teams comprised of modelers and medical experts are really the way to go. That is the way I have been going, and I certainly look forward to going further on pandemic flu and other emerging public health challenges.
In conclusion, to quote the great statistician, George Box, “All models are wrong, but some are useful.”
CONTAINING A LARGE BIOTERRORIST SMALLPOX ATTACK: A COMPUTER SIMULATION APPROACH29
Ira M. Longini, Jr., Ph.D.
Fred Hutchinson Cancer Research Center30
University of Washington31
M. Elizabeth Halloran, M.D., D.Sc., M.P.H.
Fred Hutchinson Cancer Research Center30
University of Washington31
Azhar Nizam, M.S.32
Emory University
Yang Yang33
Harvard University
Shufu Xu, M.S.30
Fred Hutchinson Cancer Research Center
Donald S. Burke, M.D.34
Johns Hopkins University
Derek A. T. Cummings, Ph.D.34
Johns Hopkins University
Joshua M. Epstein, Ph.D.35
The Brookings Institution
Introduction
The intentional release of smallpox remains a threat to the American population (Cohen and Enserink, 2002; Henderson et al., 1999). Our earlier work (Halloran et al., 2002b) showed that for a small attack involving around five initial infectives, post-release targeted vaccination of close contacts of identified infected people would be sufficient to control the epidemic. Our result is supported by other investigators using a simpler model (Eichner, 2003a) There is modeling evidence that a large attack may be difficult to contain (Kaplan et al., 2002). A stochastic model of a large smallpox attack indicates that targeted vaccination combined with early detection may be effective without resorting to mass vaccination (Eubank et al., 2004). Other work, not based on a dynamic epidemic model, suggests that given the small probability of a bioterrorist smallpox attack, preemptive mass vaccination is not a good strategy as opposed to reactive containment strategies (Bozzette et al., 2003).
Our earlier work also showed that preemptive voluntary vaccination to increase herd immunity could increase the effectiveness of a surveillance and containment control strategy, but further investigation would be needed for the case of a large attack. Currently there is virtually no effort to vaccinate the civilian population in the USA. The federal government’s goal to vaccinate 5–10 million first responders and hospital personnel preemptively by the summer of 2003 was not achieved (U.S. Census Bureau, 2000). Even the more modest plan to vaccinate 500,000 medical personnel has not been achieved (Enserink, 2003). As of October 31, 2005, about 40,000 people had been vaccinated (CDC, 2005c), and many states had paused their smallpox vaccination program pending further federal government guidance. Routine vaccination against smallpox in the USA was stopped in 1972, currently leaving at least 43 percent of the population of the USA completely susceptible. However, evidence suggests that substantial residual immunity remains in those previously vaccinated (Hammarlund et al.,
2003), and such immunity would give partial protection against severe disease and death given infection (Eichner, 2003b).
In this work, we address the question of whether post-release surveillance and containment, i.e., isolation of detected smallpox cases, and location and vaccination of their close contacts, would be sufficient to contain even a large smallpox release, given the current level of background immunity to smallpox in the population of the USA. We also examine the added benefit of prevaccination of hospital workers, reactive mass vaccination of the population after an attack has been detected, and reactive closing of the schools.
Materials and Methods
Many of the parameters and scenarios of our model were determined by the Smallpox Modeling Working Group, the Secretary’s Advisory Council on Public Health Preparedness, Department of Health and Human Services.36 Parameter values and modeling decisions made by the working group were based on the group’s collective knowledge of smallpox epidemiology and on information from Chapter 4 of Smallpox and its Eradication by Fenner et al. (1988). The simulation model developed here is a direct extension of our previous model (Halloran et al., 2002b), but for a larger population and potential attack. In addition, through the working group, we were able to derive a more accurate set of natural history parameters than for the previous model. The smallpox natural history and human behavior patterns that we give in the next section represent a blending of values from the literature and expert opinion that may be the most comprehensive description up to this time.
Natural History, Behavior, and Control Methods
We described the natural history of smallpox in terms of three timelines (Figure 3-3): (1) disease symptoms and recognition, (2) infectiousness, and (3) behavior of infected people. We also partitioned smallpox cases into three categories: (1) ordinary smallpox (Figure 3-3), (2) modified smallpox (Figure 3-4), and (3) hemorrhagic smallpox (Figure 3-5). For those who have never been vaccinated, we assumed that 95 percent would develop ordinary smallpox if infected, and the remaining 5 percent would develop hemorrhagic smallpox if infected. For those people over 32 years of age who were vaccinated before 1971, we assumed that 10 percent would be fully protected against smallpox infection,
30 percent would develop a less severe modified case of smallpox if infected, and the remaining 60 would develop non-modified smallpox if infected. Among that 60 percent, 95 percent of the cases would be ordinary smallpox and 5 percent hemorrhagic smallpox. About 57 percent of the population of the USA was born before 1971. We divided our simulated outbreaks into two periods. The first period is before recognition of smallpox, while the second period is after the first case of smallpox is recognized.
Figure 3-3 shows the natural history for ordinary smallpox. The incubation period distribution was assumed to vary from 7 to 17 days with a mean of 11.48 days. The incubation period was assumed to end with the onset of fever, followed by a macular rash on the 4th day of fever, with subsequent onset of papules and then vesicles. Before smallpox is known to be present, smallpox cases would not be recognized as such until the onset of vesicles, seven days after the onset of fever. After smallpox is known to be present, cases would be recognized at the onset of papules, six days after the onset of fever. Thirty percent of the cases would die 7–14 days after the onset of fever. People have varying degrees of transmission capabilities over the course of their infectious period, as shown in Figure 3-3. According to this pattern, 92 percent of an infected person’s infectiousness occurs after the onset of the macular rash, an assumption consistent with a recent statistical analysis of smallpox infectivity (Eichner and Dietz, 2003). Figure 3-3 shows that 47.5 percent of the cases would withdraw to the home at the end of the first day of fever, and 47.5 percent would go to the hospital at that time. The remaining 5 percent would continue to circulate but go to the hospital at the end of the third day of fever.
We modeled modified smallpox to have a similar incubation period to that of ordinary smallpox, but a milder course of disease with only a 10 percent case fatality rate (Figure 3-4). The infectiousness of people with modified smallpox would be 33 percent of that for people with ordinary smallpox. Hemorrhagic smallpox was modeled to have a shorter natural history and more severe disease progression than ordinary smallpox with a 100 percent case fatality rate (Figure 3-5). Infected people would begin internal bleeding four days after the onset of fever, and die on the seventh day after the onset of bleeding. Before smallpox is known to be present, we assumed that 50 percent of hemorrhagic smallpox cases would not be recognized and 50 percent would be recognized on the fifth day of fever. After smallpox is known to be present, all hemorrhagic cases would be recognized on the fourth day of fever. People with hemorrhagic smallpox would be five times more infectious than those with ordinary smallpox.
The Population
The model populations are based on a 50,000 person network of structured subpopulations of 2,000 people mixing in households, clusters of households, neighborhoods, preschool groups, schools, and the community at large. The age
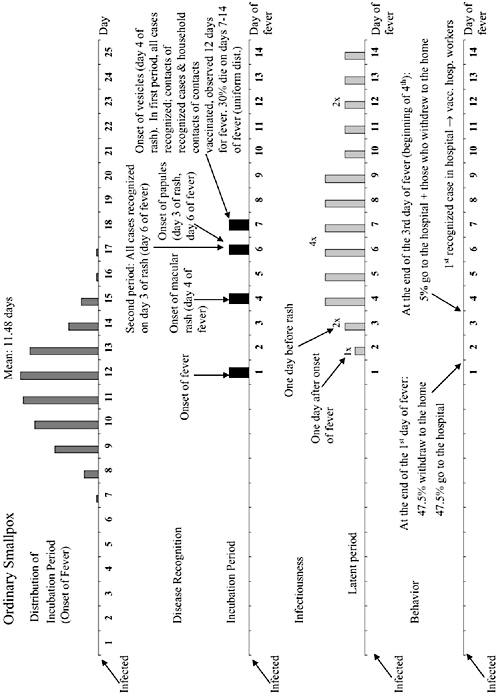
FIGURE 3-3 The natural history of ordinary smallpox in terms of time lines. Parameter values were determined through group consensus from the Smallpox Modeling Working Group and Chapter 4 of Fenner et al. (1988). The length of the incubation period follows the probability distribution shown in the top line. At the end of the incubation period, cases develop a fever, and then pass though a series of disease states. Before smallpox is recognized in the hospital (i.e., the first period), an ordinary case of smallpox would be recognized on the fourth day of rash. After this (i.e., the second period), smallpox is known to be present and all ordinary smallpox would be recognized in the hospital on the third day of rash. For infectiousness, the per contact transmission probability x (Table 3-4, see Annex 3-1), is set to 1x for the first day of fever, increased to 2x for the second day of fever, 4x at the onset of rash, etc., with an upper limit of 1.0. Thirty percent of ordinary smallpox cases would die between days 7 and 14, according to a uniform distribution. In the behavior time line, cases withdraw to the home or go to the hospital according to the pattern indicated. In surveillance and containment, close contacts of identified cases are vaccinated.
distribution and approximate household sizes were based on the U.S. Census 2000 (U.S. Census Bureau, 2000). The subpopulations are connected through adult workplaces and high schools, and the whole population through a hospital. We include one hospital since statistics show there is about one hospital per 50,000 people in the USA.37 The hospital has a total of 686 workers, 133 of whom can make close contact with smallpox cases until isolation measures in the hospital are instituted, based on a review of the numbers of employees having routine contact with patients.37 Each person in the population may visit the hospital with probability 0.001 each day. They mix with all infected people in the hospital in the first period before smallpox is recognized, but only with unisolated circulating cases during the second period after smallpox is recognized. Figure 3-6A shows a schematic of the configuration of a subpopulation of 2,000 people. Figure 3-6B shows how the subpopulations are connected through schools, workplaces, and a hospital to form the population of 50,000 people.
The Simulation Model
We developed a discrete-time, stochastic simulation model of smallpox spread within a structured population described above. As mentioned above, the model is an extension of our previous smallpox model (Halloran et al., 2002a), but for a larger population and with a more detailed disease natural history description. The model represents the number of close and casual contacts that a typical person makes in the course of a day. The basic person-to-person daily transmission probabilities, x, and mixing group sizes are given in Table 3-4 (see Annex 3-1). We define x as the probability that an infected person with ordinary smallpox, on the second day after the onset of fever, makes sufficient contact to infect an unvaccinated susceptible person in the mixing group being modeled. For example, if a child were infected with ordinary smallpox, the probability that this child would infect an unvaccinated adult in the household, one day after the onset of fever, would be 0.05. On the third day after the onset of fever, this probability would increase to 0.10 (see infectiousness timeline in Figure 3-3). The transmis-
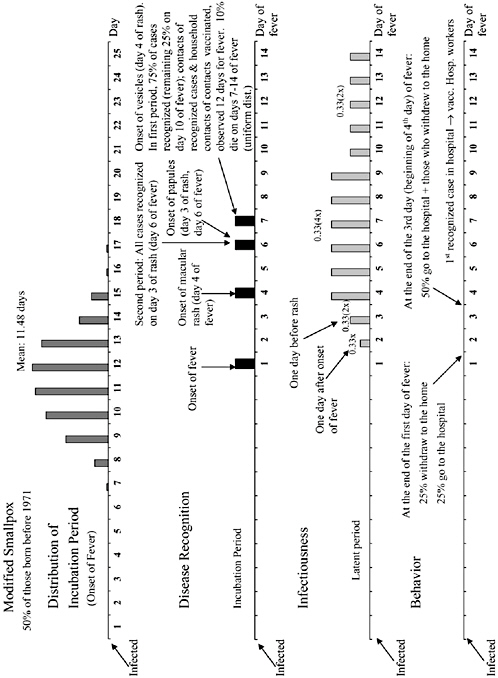
FIGURE 3-4 The natural history of modified smallpox in terms of time lines. Modified smallpox is assumed to have the same incubation period as ordinary smallpox, but to have a milder course of disease. The infectiousness of people with modified smallpox would be 33 percent of that for people with ordinary smallpox, with a case fatality rate of 10 percent. However, it would be harder to recognize modified smallpox and cases would be slower to withdraw to the home or go to the hospital than for ordinary smallpox. Before smallpox is recognized in the hospital (i.e., the first period), 75 percent of cases would be recognized on the fourth day of rash and the remaining 25 percent on the seventh day of rash. After this, the smallpox is known to be present (i.e., the second period), and all ordinary smallpox would be recognized in the hospital on the third day of rash.
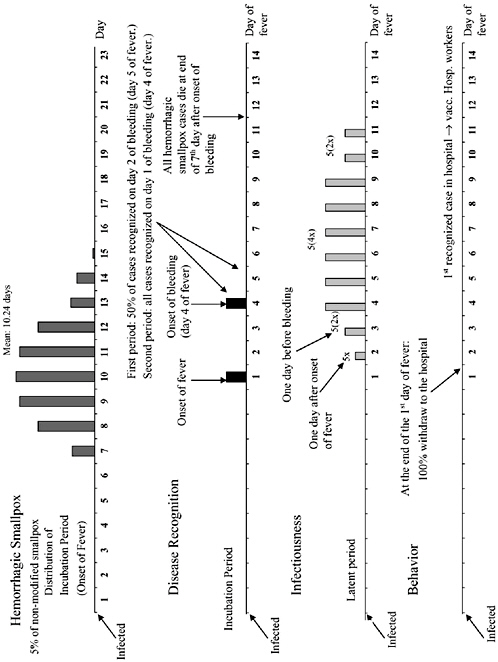
FIGURE 3-5 The natural history of hemorrhagic smallpox in terms of time lines. Hemorrhagic smallpox is assumed to have a shorter natural history and more severe disease progression than ordinary smallpox. Infected people would begin internal bleeding four days after the onset of fever, and 100 percent would die on the seventh day after the onset of bleeding. Before smallpox is recognized, we assumed that 50 percent of hemorrhagic smallpox cases would not be recognized and 50 percent would be recognized on the fifth day of fever. After smallpox is recognized, all hemorrhagic cases would be recognized on the fourth day of fever.
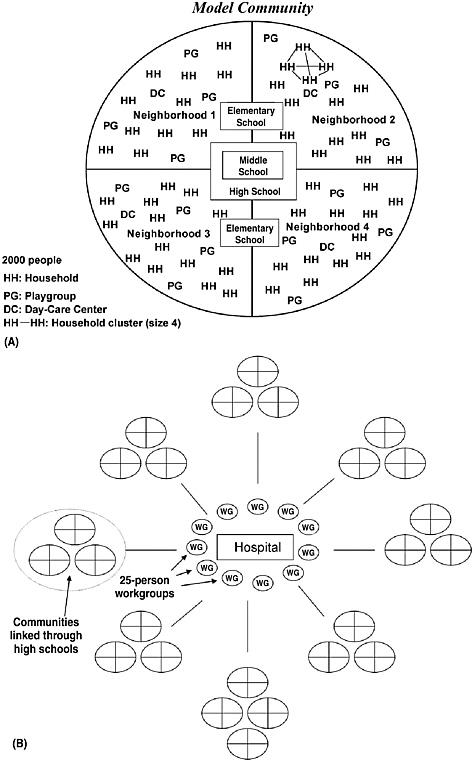
FIGURE 3-6 Structure of the populations. (A) The 2000 person subpopulations consist of households and household social clusters depicted by the connecting lines in neighborhood 2. Each subpopulation is partitioned into four neighborhoods. Small children mix in playgroups and daycare centers within their neighborhoods. The school mixing groups link neighborhoods as shown. (B) Clusters of the subpopulations are created by allowing ten percent of high school students in each of the clusters of subpopulations to mix with high schools in other subpopulations in the same cluster. All adults who work are randomly assigned to work in mixing groups of size 25 throughout the whole population. In addition, all people can attend a single hospital.
sion probability would be 0.20 for days 4–9, and it would drop back down to 0.10 for days 10–14. People who complete the full course of disease without dying are considered to be immune.
Each day, for each susceptible, the probability of becoming infected is calculated based on his vaccination status, who is infectious in his or her mixing groups, and his or her vaccination status, as well as the mixing group-specific transmission probabilities. As an example, consider the simplest case that no one is vaccinated and we ignore the complex natural history of smallpox for illustrative purposes. An elementary school child is exposed to the number of child and adult infectives in his household Ihc and Iha, his household cluster Ikc and Ika, his school Is, his neighborhood In, and the community Im with corresponding transmission probabilities for each contact of xhcc (child-to-child), xhac (adult-to-child) .… respectively. Then, symbolically, the probability P for that child to become infected on that day is:
This equation is evaluated term-by-term in order to identify the source of infection if an infection occurs. Once infected, a person passes through the natural history of the infection process (Figures 3-3 through 3-5). The length of the incubation period is randomly selected from the probability distributions. The rest of the disease progression follows deterministically as indicated in the Figures. Aspects of the infected person’s behavior, such as if and when he or she withdraws to the home or goes to the hospital, are simulated stochastically according to the probability distributions in Figures 3-3 through 3-5. The model assumes the same contact structure each day of the simulation with the exception of trips to the hospital.
We created a person-to-person graph of our population by constructing a contact structure proportional to the transmission probabilities given in Table 3-4 (see Annex 3-1). The resulting weighted graph has an average clustering coefficient of 0.48, much larger than the average clustering coefficient of 10−3 of an Erdös-Rényi random graph with the same number of vertices and average degree (Watts and Strogatz, 1998). The average shortest path was four people. This
large clustering coefficient and small average shortest path suggest that we have a small-world person-to-person contact graph (Watts and Strogatz, 1998; Watts, 1999). This indicates that the smallpox transmission will tend to infect close-knit groups such as households, daycare centers, and schools when introduced, and then remain confined to these groups for a few generations of transmission. After this, transmission will tend to jump to somewhat more socially distant groups in a sporadic fashion. This pattern of local clustering followed by larger jumps, makes smallpox susceptible to perifocal control efforts, such as surveillance and containment. This is in contrast to the rapid uniform transmission that would occur if the contact structure of the person-to-person graph was more like a random graph, i.e., random mixing. In this case, perifocal control measures would probably tend to fail (Kaplan et al., 2002).
Interventions
For those people who receive a fresh smallpox vaccination before they are infected, we assumed the vaccine efficacy is 0.97, and that response to vaccination is all-or-none (Halloran et al., 1997). For those who receive a fresh vaccination four days post-infection, we assumed that 90 percent would not develop disease and 10 percent would develop modified smallpox. For those vaccinated between 5–7 days post-infection, 60 percent would develop modified smallpox, 38 percent ordinary smallpox, and 2 percent hemorrhagic smallpox. Vaccination reduces the death rate of breakthrough infections, for old vaccinations or fresh vaccinations 4–7 days post-infection, to a very low level, i.e., 1 percent or less.
We evaluated a number of intervention strategies. The most basic for traditional smallpox control has been surveillance and containment, also referred to as targeted or ring vaccination, which is part of the Centers for Disease Control and Prevention response plan (CDC, 2002). For this control strategy, when the first case of smallpox is recognized, all hospital workers who deal with smallpox cases would be immediately vaccinated. Recognized cases of smallpox would be placed in hospital-based isolation, and their close contacts would be vaccinated and kept under observation. These close contacts would be those people in the recognized case’s household and, when appropriate, in the case’s household social cluster, daycare center, school group, or workplace. Contacts in the neighborhood or the community at large would not be considered to be close contacts and not be isolated. Children under one year of age are not vaccinated.
We considered mass reactive vaccination where vaccination would begin one day after recognition of the first case of smallpox, and would take seven days to complete to a particular level. Smallpox cases are not vaccinated. In addition, any person freshly vaccinated through contact tracing or pre-emptive vaccination in the hospital would not be revaccinated. The schools would serve as vaccination centers and be closed for that seven-day period. A further strategy that was considered was the prevaccination of different proportions of hospital workers.
We also considered reactive closing of the schools for ten days, starting one day after recognition of the first case of smallpox.
In accordance with the working group, we evaluated a range of control scenarios (Table 3-5). The baseline scenario involved people withdrawing to the home and others being placed in effective hospital isolation at the appropriate times, but no contact tracing or vaccination. Scenario 3 was surveillance and containment (with vaccination of close contacts) alone, and then scenarios 4–10 involved surveillance and containment plus various additional control measures including pre-emptive vaccination of hospital workers, reactive mass vaccination, and reactive school closings. Scenarios 1 and 2 involved no interventions and were used to help validate the simulations. For the attack scenario we assumed that 500 randomly selected people are initially infected. For each intervention scenario, 100 epidemics were stochastically simulated.
Results
Calibration of the model was based on historical data available on smallpox, including household secondary attack rates (Fenner et al., 1988), relative age-specific attack rates being higher in children (Thomas et al., 1971), and the distribution of secondary cases produced by an introductory case (Fenner et al., 1988; Mack, 1972). We roughly calibrated the transmission probabilities in households to observed household secondary attack rates from past smallpox epidemics. These ranged from 44 percent to 88 percent to unvaccinated people in a variety of populations in Africa and South Asia in the 1960s and 1970s (Fenner et al., 1988; Mack, 1972). For example, we set the child-to-adult household daily transmission probability x to 0.05. Using the information in Figure 3-3, if the infected child remained in the household over his entire infectious period, then the probability that he would infect the exposed adult would be 0.85 (i.e., household secondary attack rate of 85 percent). However, in reality the household secondary attack rate would be lower as the infected child would be placed in isolation when recognized as a smallpox case. Thus, 85 percent is the maximum household secondary attack rate. If the index infected child had modified smallpox, then the maximum secondary attack rate for child-to-adult transmission in the household would be 46 percent, and if the index case had hemorrhagic smallpox, then the maximum secondary attack rate would be 100 percent. These relationships are shown in Figure 3-7. The maximum secondary attack rate for other mixing groups is illustrated on this plot.
Figure 3-8A shows the first 60 days of one stochastically simulated smallpox epidemic with 500 randomly selected initially infected people from all age groups in the population for surveillance and containment (scenario 3), while Figure 3-8B shows the same for surveillance and containment plus preemptive hospital worker vaccination at 50 percent and reactive school closing and mass vaccination at 80 percent (scenario 9). Figures 3-8A and B show that the model
TABLE 3-5 Smallpox Simulation Scenarios
|
|
Scenario |
||||||||||
|
|
1 |
2 |
Baseline |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Background immunity |
|
+a |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Surveillance and containment |
|
|
Isolation but no vaccination |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Pre-emptive vaccination |
|
|
|
|
|
|
|
|
|
|
|
|
Pre-emptive vaccination (hospital only) |
|
|
|
|
10% |
50% |
10% |
50% |
10% |
50% |
10% |
|
Reactive school closure, 10 days |
|
|
|
|
|
|
+ |
+ |
+ |
+ |
+ |
|
Mass reactive vaccination |
|
|
|
|
|
|
40% |
40% |
80% |
80% |
|
|
aThe + indicates that the factor is present. |
|||||||||||
reproduces the characteristic epidemic waves of smallpox roughly every two weeks. Although an outbreak is not prevented, it is reduced to a low level.
Table 3-6 shows the number of cases, not counting the initial cases, when surveillance and containment, which includes vaccination of close contacts (scenario 3), is instituted. The total number of cases averages 828, with 50 percent of the cases from the hospital, 18 percent from the family or other close contacts, 19 percent from schools or the workplace, and 13 percent from the neighborhoods and community at large. This latter 13 percent of infecting contacts would be untraceable. These percentages are quite close to those observed for European smallpox epidemics for 1950–1971 (Table 3-7).
Table 3-8 gives the numbers of smallpox cases and deaths for the baseline and for scenarios 3–10. (Results for scenarios 1 and 2 are not in the Table 3-8 but are given below.) If the only action were the isolation of cases (baseline scenario), then the model predicts an average of 1,750 cases and 523 deaths. If we add vaccination and carry out surveillance and containment (scenario 3), then the average number of cases would be reduced to 828 and the number of deaths to 211. Figure 3-8A indicates that for surveillance and containment there would be a relatively large second wave of cases after the initial wave, and then a much smaller third
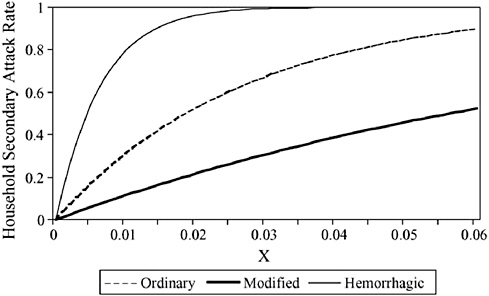
FIGURE 3-7 A plot showing the relationship between the transmission probability x during the second day of fever from an unvaccinated case of smallpox to an exposed unvaccinated person in a mixing group and the maximum household secondary attack (SAR) rate if he circulated in the mixing group for his entire infectious period. This relationship is based on the smallpox natural histories given in Figures 3-3 through 3-5.
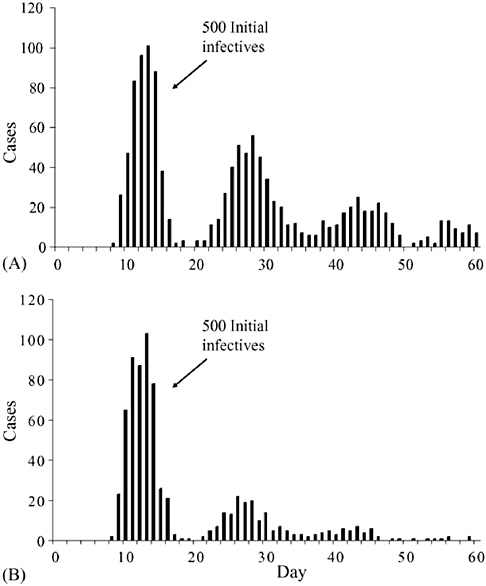
FIGURE 3-8 The first 60 days of one stochastically simulated smallpox epidemic with 500 randomly selected initially infected people from all age groups. (A) Epidemic surveillance and containment (scenario 3). This epidemic had a duration of 196 days, while the average duration of the epidemics under scenario 3 was 194 days. (B) Epidemic with surveillance and containment, 50 percent preemptive hospital vaccination and 80 percent reactive mass vaccination with reactive school closure for ten days (scenario 9). This epidemic had a duration of 91 days, while the average duration of epidemics under scenario 9 was 87 days.
TABLE 3-6 Distribution of Cases Excluding Initial Cases for Surveillance and Containment with Vaccination of Close Contacts (Scenario 3)a
|
|
Cases |
||
|
Source of cases |
Mean |
Q1b |
Q3b |
|
Household |
82 |
70 |
93 |
|
Neighborhood cluster |
62 |
50 |
72 |
|
Daycare |
6 |
3 |
8 |
|
Schools |
101 |
78 |
120 |
|
Workgroup |
60 |
19 |
87 |
|
Hospital (smallpox ward) |
413 |
362 |
463 |
|
General neighborhood |
52 |
44 |
60 |
|
Community |
54 |
46 |
63 |
|
Totalc |
828 |
694 |
935 |
|
aBased on 100 simulations. bQ1: first quartile; Q3: third quartile. cA small number of people may have been infected from more than one source. |
|||
TABLE 3-7 Average Distribution of the Sources of Infections for Smallpox Cases with Surveillance and Containment (Scenario 3), Compared to the Distribution Observed in European Epidemics, 1950-1971
|
Location |
Model |
European |
|
Hospital |
50% |
50% |
|
Family or other close contact |
18% |
22% |
|
Workplace or school |
19% |
14% |
|
Unknown source |
13% |
14% |
and fourth wave. Preemptive vaccination of 10 percent of hospital workers in addition to surveillance and containment (scenario 4) has a small effect on the average number of cases; however, preemptive vaccination of 50 percent of the hospital workers (scenario 5) has a relatively large effect on reducing the number of cases. Reactive mass vaccination of 40 percent of the susceptible population (scenarios 6 and 7) has a large additional effect. On average, 80 percent reactive mass vaccination (scenarios 8 and 9) is the most effective in reducing the outbreak to a minimal number of cases. By comparing scenarios 4 and 10, we see that reactive closing of the schools for ten days is not particularly effective.
Table 3-9 gives the numbers of fresh smallpox vaccinations for scenarios 3–10. Under surveillance and containment (scenario 3), an average of 7,501 fresh doses of vaccine would be used, far fewer than the ~25,500 doses that would be used under 40 percent reactive mass vaccination plus surveillance and containment and preemptive hospital vaccination (scenarios 6 and 7) or the
TABLE 3-8 Scenario Results, Excluding the 500 Initial Casesa
|
|
Cases |
Deaths |
||||
|
Scenario: action |
Mean |
Q1b |
Q3b |
Mean |
Q1 |
Q3 |
|
Baseline |
1,750 |
1,527 |
1,428 |
523 |
455 |
584 |
|
3:SCc |
828 |
694 |
935 |
211 |
173 |
239 |
|
4:SC + PHV10% |
768 |
653 |
872 |
197 |
168 |
231 |
|
5: SC + PHV50% |
678 |
595 |
750 |
180 |
156 |
206 |
|
6: SC + PHV10% + RSC + RMV40% |
439 |
390 |
474 |
96 |
84 |
107 |
|
7: SC + PHV50% + RSC + RMV40% |
367 |
341 |
394 |
83 |
73 |
91 |
|
8:SC + PHV10% + RSC + RMV80% |
253 |
218 |
276 |
38 |
732 |
44 |
|
9: SC + PHV50% + RSC + RMV80% |
203 |
185 |
219 |
33 |
29 |
38 |
|
10: SC + PHV10% + RSC |
712 |
152 |
798 |
182 |
152 |
206 |
|
PHV, pre-emptive hospital vaccination; RSC, reactive school closure; RMV, reactive mass vaccination. abased on 100 simulations. bQ1: first quartile; Q3: third quartile. cSC, surveillance and containment with vaccination of close contacts. |
||||||
~45,000 doses that would be used under 80 percent reactive mass vaccination plus surveillance and containment and preemptive hospital vaccination (scenarios 8 and 9). The average number of doses used with surveillance and containment decreases with increasing level of preemptive hospital worker vaccination, since the total number of vaccinations due to contact tracing is decreased due to fewer cases. This can be seen by comparing the number of vaccine doses needed for scenarios 3–5.
For orientation purposes, we ran the simulator assuming no prior immunity, no interventions, and that cases do not withdraw to the home or go to the hospital (scenario 1). Nearly the entire population is infected, an average of 49,500 cases. This result is expected since infected people are modeled to circulate in the community over their entire infectious period. The average number of deaths is 16,598 people. The addition of prior immunity (scenario 2) makes a small difference in the number of cases, averaging 46,643 people. Prior immunity makes a larger difference in the number of deaths, an average of 13,681. This decrease is mostly due to the increased number of modified smallpox cases among those people previously vaccinated. In addition, by comparing the baseline average of 1,750 cases to the average of 46,643 cases under scenario 2, we see the great effectiveness of people with early smallpox symptoms simply withdrawing to the home and entering hospital isolation.
Table 3-10 shows the results of a sensitivity analysis where we vary the time it takes to recognize a case and begin isolation of the case and vaccination of close contacts under the surveillance and containment scenario 3 (see case recognition days in Figures 3-3 through 3-5). This further delay could be the result
TABLE 3-9 Number of Vaccine Dosesa
|
|
Doses |
||
|
Scenario |
Mean |
Q1b |
Q3b |
|
3 |
7,501 |
6,825 |
7,966 |
|
4 |
7,221 |
6,542 |
7,772 |
|
5 |
6,725 |
6,231 |
7,185 |
|
6 |
25,677 |
25,481 |
25,856 |
|
7 |
25,472 |
25,267 |
25,667 |
|
8 |
45,246 |
45,203 |
45,284 |
|
9 |
45,214 |
45,178 |
45,262 |
|
10 |
6,888 |
6,336 |
7,357 |
|
aBased on 100 simulations. bQ1: first quartile; Q3: third quartile. |
|||
of some cases not being caught quickly, confusion about smallpox symptoms, or some other problem with the medical response. If we delay an additional day, the number of cases and deaths doubles. More than one day further delay would result in a further approximately 50 percent increase in the number of cases and deaths.
Discussion
This work suggests that the current federal government policy of post-release surveillance and containment, if effectively implemented, could be sufficient to contain either a small or large intentional release of smallpox. We have shown that reactive mass vaccination in addition to surveillance and containment during an attack results in fewer cases and deaths than surveillance and containment alone. However, many more people would need to be vaccinated for reactive mass vaccination than for surveillance and containment. Since the risk of vaccine-related illness is about 10−4 and vaccine related death is about 10−6 (Henderson et al., 1999), one would expect an average of 2.5–4.5 vaccine-related illnesses and a small probability that one person would die due to vaccination for the reactive mass vaccination strategies considered here. If logistically possible, implementation of reactive mass vaccination would make sense. Prevaccination of hospital workers results in somewhat smaller outbreaks in the event of an attack. However, since it is not known when or where an attack may occur, prevaccination strategies would require that large numbers of people be vaccinated throughout the entire country. This is true of any prevaccination program before an attack. Such programs either for hospital workers and first responders or for the general population may not be necessary given the effectiveness of surveillance and containment that could be carried out at the location of an attack. The benefits of such prevaccination need to be weighed against the potential harm that would
TABLE 3-10 Surveillance and Containment for Various Delays in Case Recognition, Excluding the 500 Initial Casesa
|
|
Cases |
Deaths |
||||
|
Additional delay in recognition (days) |
Mean |
Q1b |
Q3b |
Mean |
Q1 |
Q3 |
|
Current modelc (no additional delay) |
828 |
694 |
935 |
211 |
173 |
239 |
|
1 |
1,681 |
1,509 |
1,848 |
416 |
370 |
459 |
|
2 |
2,017 |
1,879 |
2,162 |
503 |
461 |
533 |
|
3 |
2,217 |
1,995 |
2,373 |
578 |
522 |
625 |
|
4 |
2,372 |
2,081 |
2,601 |
658 |
585 |
720 |
|
5 |
2,786 |
2,574 |
3,007 |
780 |
720 |
841 |
|
aBased on 100 simulations. bQ1: first quartile; Q3: third quartile. cModel default: smallpox cases are recognized in the hospital either seven days (ordinary and modified cases) or four days (hemorrhagic cases) after onset of fever. |
||||||
ensue due to vaccine-related injury. The quantitative validity of the above statements depends on the assumptions, parameter values, and model structure that we have used here. However, our general conclusions should be robust to this uncertainty.
Children under one year of age do not receive smallpox vaccine. However, in the absence of maternal antibodies, young children are at very high risk of serious disease and death if they contract smallpox. This makes the surveillance and containment policy very important for these children since the rapid vaccination of family members of index cases and of school children affords very young child indirect protection.
To assess the robustness of our conclusions about the effectiveness of control strategies modeled, we carried out a number of sensitivity analyses not given in the results. The total number of smallpox cases was found to be sensitive to variation in the transmission probabilities x in the different mixing groups. However, the relative effectiveness of the control strategies was not affected across the range from small to larger values of x. The most sensitive factor was timing of withdrawal to the home and isolation of cases. A delay in recognition of cases by one or more days beyond the hypothesized control strategy outlined in Figures 3-3 through 3-5 was found to result in poorly contained simulated epidemics (Table 3-10). The sensitivity analysis also reflects uncertainty about the exact onset of infectiousness relative to symptoms, since earlier than hypothesized onset of infectiousness would be equivalent to a delay in isolation. This result is consistent with a previous modeling exercise that showed logistical delays in fully implementing surveillance and containment could lead to a large outbreak (Kaplan et al., 2002).
We created a 50,000-person model population based on the U.S. census 2000 information and our conception of how a typical American population is
connected in terms of potential smallpox transmission. To assess whether we have the approximate connectivity of a typical U.S. population, we compared our person-to-person graph to the graph that was constructed from individual level daily travel and location visited survey data from Portland, Oregon, with a population of 1.6 million people (Eubank et al., 2004). The average clustering coefficient for both graphs is 0.48. This indicates that the degree to which the two populations are clustered into close mixing groups such as households, schools, and workplaces is similar. The mean shortest path for the Portland population was six, while it is four for our population. Thus, the links between clusters for our population are somewhat shorter than those in Portland. Both our graph and the one for Portland are small world with similar characteristics. Although our population is smaller than the Portland population, the connectivity of any person with others in the population is roughly similar for the two populations. Thus, we believe that our simulation population of 50,000 people is large enough to investigate the effectiveness of the various containment strategies against a large attack.
Our previous modeling work has shown that surveillance and containment would be effective in containing and sometimes preventing a smallpox outbreak for a small number of initial cases (Halloran, 2002b). In this work, using a model with different epidemiologic parameter values, we show that surveillance and containment could be effective in containing an outbreak with a large number of initial cases. This suggests that further prevaccination of the population of the USA would be counter-productive. However, a rapid and well-organized response to a smallpox bioterrorist attack would be needed to make containment efficient.
Acknowledgment
This research was partially funded by the Fogarty International Center, National Institute of Allergy and Infectious Disease grant R01AI32042, and the National Institute of General Medical Sciences MIDAS grant U01GM070749. Conflict of interest: No conflict of interest to declare.
INDIVIDUAL-BASED COMPUTATIONAL MODELING OF SMALLPOX EPIDEMIC CONTROL STRATEGIES38
Donald S. Burke, M.D.39
Johns Hopkins University
Joshua M. Epstein, Ph.D.40
The Brookings Institution
Derek A. T. Cummings, Ph.D.41
Johns Hopkins University
Jon I. Parker, B.S.
The Brookings Institution
Kenneth C. Cline, B.S.
Johns Hopkins University
Ramesh M. Singa, B.S.
Johns Hopkins University
Shubha Chakravarty, M.S.
The Brookings Institution
Agent-based modeling is a new scientific approach in the tradition of cellular automata made possible by recent advances in computing. In brief, an agent-based model or “artificial society” includes some population of “agents,” typically individual human beings, each implemented as a distinct object or data structure in a computer program. These agents interact locally with one another in the computer code. Over many iterations, these microinteractions can generate large-scale macroscopic phenomena of fundamental interest, specifically, the course of epidemics in space and time. When calibrated to actual epidemic data, these models become credible bases for policy analysis.
One distinguishing feature of individual-based models is that the individuals in the model (the people) are not aggregated into a few homogeneous pools (e.g., susceptibles, infectives, and removeds) (Longini et al., 2006). Rather, agent populations are highly heterogeneous; every single individual is explicitly modeled
and tracked. A second distinguishing feature of agent models is that events transpire on an explicit space. In the agent approach, people interact only with neighbors in the space, who change as agents move around, for example, coming and going to school or work in the model. Our simulation approach attempts to create a realistic depiction of local social contact dynamics in discrete and explicitly represented social units (the home, the hospital, and so on). In agent models where individual decision making is present, agents have bounded rationality and typically make use of simple rules based on local information (Berry et al., 2002).
All of this action can be depicted graphically in real time, as if looking down on the social space from above, watching agents move to and from the various social units (homes, schools, workplaces), changing colors as they progress through the phases of the disease. It is centrally important to note that, because of their explicit inclusion of physical space, local interactions, and individual heterogeneity, the agent models produce fundamentally different spatiotemporal epidemic dynamics than smoothed differential equation models (Epstein, 1999). When this highly visual mode of modeling produces a novel hypothesis, all the graphics can be turned off, and the model can be run stochastically for millions of cycles to explore the robustness of the finding. There is no sacrifice of rigor; indeed, we can generate extremely high volumes of clean data and analyze it statistically to yield a very high-fidelity characterization of model behavior and robust calibration to historical data.
The modeling approach taken derives directly from that previously developed by Epstein et al. (2004). This work was undertaken under the auspices of the Smallpox Modeling Working Group of the U.S. Department of Health and Human Services Secretary’s Advisory Council on Public Health Preparedness. The charge to members of the working group was to modify their existing smallpox epidemic models to incorporate agreed-on values for the natural history and transmission of the disease and then use the model to analyze epidemic outcomes under a variety of plausible attack and response scenarios.
Modeling
Assumptions and Parameters
This article describes an extended version of our basic agent-based smallpox model, distributed over a range of social architectures, population sizes, and assigned response scenarios (Epstein et al., 2004). Throughout this article, we use the detailed biomedical assumptions agreed on by the Smallpox Modeling Working Group.42 Values assigned included the distribution of ordinary, modified, and
hemorrhagic smallpox to be expected in the U.S. population and, for each form of the disease, the assumed distributions of incubation periods, time to disease recognition, infectiousness, and mobility effects of infection and disease (Longini, 2006). Other parameters, such as the probability of smallpox transmission per contact at various phases of the disease’s natural history, and contact rates per day in various social units (the home, school, workplace, and hospital) were estimated by calibration of the model to real epidemiologic data. A detailed description of all aspects of the model is included in the technical appendix.43
Simulated Social Structures
The basic social structure represented in the model was the town. Towns were composed of smaller social units representing households, workplaces, schools, and hospitals. The basic model unit of time was the “day,” which was parsed into two equal halves, a nighttime when all healthy individuals were at home and a daytime when healthy individuals were at work or school. No genders were assigned. Adults cycled between work and home, whereas children cycled between school and home.
The number of persons per household was distributed according to U.S. census figures (U.S. Census, 2000). For the “uniform” towns, all adults in a town went to one workplace, and all children went to one school. For the “hub-and-spoke” and “ring” towns (see following text), the town was divided into districts, each with its own local workplace and local school. Where the town architecture was composed of more than a single uniform district, 10 percent of workers “commuted” to the workplace of a contiguous district. Children attended school in the town in which they lived. For all towns, there was a single hospital, including 150 adult health-care workers who worked at the hospital rather than at the common workplace. During the daytime and nighttime, contacts were made with one of the eight possible physically neighboring individuals on the grid surface, wherever the individual was at that time (household, workplace, and so on). The proportion of contacts that were potential transmitting contacts in each social unit was assigned according to the calibration of the model to historical data (Mack, 1972).
In this study, we examined models for two sizes of total population: 6,000-person towns and 50,000-person towns. For the 6,000-person towns, we examined three social architectures: a single uniform town of 6,000 persons, a ring town
|
43 |
Available as a Data Supplement at http://www.aemj.org/cgi/content/full/j.aem.2006.07.017/DC1. |
of six districts of 1,000 persons each, and a hub-and-spoke town with a single central district of 2,000 persons surrounded by four districts of 1,000 persons (Figure 3-9A and Figure 3-9B). In each town there was a single hospital that served all districts but was staffed by persons from one district. Index cases were always seeded into one district, the district containing the hospital. The social architectures for 50,000-person towns were analogous but larger.
Calibration of the Model to Historical Data
The parameters governing the probability of smallpox transmission per contact and the contact rates in different social settings were chosen through a calibration of simulated epidemics with historical data. The historical data describe outbreaks resulting from 49 importations of a single case of smallpox into nonendemic Europe during the period from 1950 to 1971 (Mack, 1972). Two distributions from these real epidemic data were used for the calibration: 1) the distribution of the total number of cases resulting from each of these importations and 2) the distribution of the location where transmissions occurred (in a hospital setting, in a workplace or school setting, or in the home). A parameter sweep was performed in which the per-contact transmission probability and the contact rate in the hospital, the home, and the workplace or school were systematically varied. The resultant distributions of epidemic sizes and transmission locations from 1,000 calibrating simulation runs were compared with the known historical distributions. The model parameter settings for per-contact transmission and contact rates in each social setting were chosen that minimized the sum of squared deviations from the known historical distributions.
Baseline “No Response” Scenarios
We first conducted an evaluation of simulated epidemics in the unrealistic setting of a complete absence of public health response. Two base case ‘‘no response’’ scenarios were examined. These scenarios served as baselines for comparison of intervention strategies. Scenario 1 presupposed only a low level of immunity among adults due to vaccination 30 years ago or more. Scenario 2 was identical to scenario 1 except that transmission from hospitalized persons was set at zero to determine if the force of infection in the community alone was sufficient to sustain the simulated epidemics.
Evaluation of “Response” Scenarios
We then conducted an analysis of eight response scenarios specified by the working group. These scenarios involved contact tracing and vaccination of family, coworker, and hospital contacts, hospital isolation of all cases, preemptive vaccination of health-care workers, school closures, and mass reactive
vaccination. The complete spectrum of scenarios is summarized in Figure 3-10. For each of the three architectures of the 6,000-person town model, each of the eight response scenarios was run 35 different times, with a different random seed each time. Note that the model is stochastic; the use of a different random seed for each run ensures that particular realizations of the same model produce different random contact patterns in the population. The random seeds also ensure that model parameters drawn from set distributions (see Longini et al., 2006 and Figure 3-9) vary from individual to individual and run to run. For each combination of town architecture and response scenario, we report here the mean and the standard deviation (over the 35 simulated epidemic runs) for the following key epidemic outcome measurements: total number of cases, total number of deaths, total number of vaccinations, and total epidemic duration.
For the 50,000-person town model runs, the analysis format was similar to that for the 6,000-person towns, except that here 500 initial infected individuals were introduced into the population. Because these runs absorb substantially more computational resources than the comparable 6,000-person town simulations, we explored only two architectures: the single uniform large town of 50,000 and a ring of six districts of equal size. Instead of 35 simulated epidemic runs per scenarioarchitecture pair, we present the statistics for just ten stochastic realizations.
Results
Tabular Results
Cases, deaths, vaccinations, and epidemic durations for simulated epidemics under the two “no response” and the eight response scenarios are shown in Tables 3-11 and 3-12 (see Annex 3-1) for populations of 6,000 individuals and 50,000 individuals, respectively.
Simulated Epidemics in the Baseline “No Response” Scenario
Simulations under the highly unrealistic “no response” scenarios 1 and 2 gave rise to large and lengthy epidemics. Each index case, on average, initiated an epidemic chain of transmission that subsequently infected hundreds of other individuals.
Evaluation of Response Scenarios in 6,000-Person Towns
Response scenarios 3–10 were all examined in model populations with each of the three (single uniform, ring, and hub-and-spoke) town architectures, and 35 simulated epidemics were run for each scenario in each architecture. Results are displayed in Table 3-11 (see Annex 3-1). Although there are some minor differences in the impact of the different response scenarios in different town struc-
tures, the results for each response scenario show substantial concordance across all three town structures. Results are therefore presented in the text by scenario rather than by town structure.
In striking contrast to the “no response” scenarios 1 and 2, the interventions in scenario 3 alone are sufficient to limit the epidemic to a mean of fewer than 48 cases and a mean duration of less than 77 days. The addition of 10 percent or even 50 percent preemptive vaccination of hospital workers (scenarios 4 and 5) does not add appreciably to the protections afforded in scenario 3. Mass reactive vaccination of either 40 percent or 80 percent of the total population (scenarios 6–9) does provide some additional protection of the population, reduces the mean number of infected persons to fewer than 33, and shortens the mean epidemic duration to less than 60 days. The number of vaccinations given per infected person in scenarios 3, 4, and 5 was relatively low, averaging about 325 vaccinations per epidemic response. While reactive mass vaccination was effective in reducing the number of infections, the number of vaccinations per infected person was substantially greater under these scenarios (scenarios 6–9). School closure for ten days without mass vaccination (compare scenario 10 with scenario 4) appeared to provide little additional protection. The single uniform town tended to generate a higher mean total number of infected persons than did the more structured ring or hub-and-spoke town architectures, but this difference was not consistent across all scenarios.
Evaluation of Response Scenarios in 50,000-Person Towns
Response scenarios 3–10 were examined for 50,000-person towns with the single uniform and the ring architectures (but not the hub-and-spoke architecture); ten simulation runs were performed for each scenario for each town structure. Results of the epidemic simulations from the 50,000-person town are generally in close agreement with the results from the 6,000-person town presented previously. Specifically, under “no response” scenario 1, the epidemics run to near saturation with a large proportion of the population becoming infected. Epidemics under scenario 2 infect roughly half the population in both town sizes. The interventions in scenario 3 alone are sufficient to limit the epidemic to less than 10 percent of the population. Addition of 10 percent or 50 percent preemptive vaccination of hospital workers does not confer any appreciable additional protection. Mass reactive vaccination of either 40 percent or 80 percent of the population (scenarios 6–9) in the 50,000-person town model does provide some additional protection of the population, but the effect is less pronounced than in the 6,000-person town; this may reflect a higher proportion of persons initially infected in the 50,000-person town model (500, or 1 percent vs. 10, or 0.16 percent). School closure had no additional appreciable epidemic impact in the 50,000-person town model (scenario 10 vs. scenario 4).
Mass Vaccination
Four of the response scenarios examined in this project involved reactive mass vaccination, with population vaccine coverage of 40 percent (scenarios 6 and 7) or 80 percent (scenarios 8 and 9). Although these scenarios yielded smaller and shorter epidemics than response scenarios based on isolation, contact tracing, and targeted vaccination alone, the largest difference attributable to mass vaccination in the 6,000-person town was a reduction from 45.9 to 17.3 cases (scenario 4 [no mass vaccination] vs. scenario 9 [80 percent vaccine coverage]). By graphing the total epidemic size versus the number of vaccinations in each scenario, we calculate that the marginal ‘‘vaccine cost’’ to prevent one additional case is 172–213 vaccinations in the 6,000-person town/10-case attack model and 33–39 vaccinations in the 50,000-person town/500-case attack model.
Unique Features of the Model
To appreciate the unique features of this intrinsically stochastic agent-based modeling approach, a detailed analysis of data output from one scenario (scenario 3) in one population size (6,000-person town) with one town architecture (ring) is presented. Thirty-five epidemic simulation runs of this particular configuration were examined.
Epidemic size and duration. The size of epidemics ranged from a minimum of 12 cases (in addition to the ten attack cases) to a maximum of 83 cases, and epidemic durations ranged from a minimum of one epidemic generation beyond the attack (G0) cases to a maximum of six epidemic generations. The mean (±SD) simulated epidemic duration was 3.9 (±1.2) epidemic generations after the initial generation (G0) of 10 attack cases. On average, the 10-attack G0 cases represented 23 percent of the epidemic case total. The first generation (G1) wave of secondary cases alone accounted for 43 percent of the epidemic case totals; incidence thereafter declined rapidly with deployment of intervention strategies.
Epidemic reproductive rates. The epidemic reproductive rate (R) for each generation of cases (RGi→i+1) in each epidemic simulation run was calculated as the number of cases in each generation divided by the number of cases in the preceding generation (e.g., RG0→1 = cases G1/cases G0). This measure is not the same as a true R0 because in the scenarios evaluated here multiple cases were introduced into the population and epidemic control strategies were activated on diagnosis of the first attack (G0) case, thus minimizing transmission by G0 attack cases that clinically progressed more slowly and transmitted later. The mean measured for RG01 (across 35 simulated epidemics) was 1.88. Subsequent mean generational reproductive rates, while epidemic control interventions were deployed in the model, were measured as RG1→2 = G2/G1 = 0.46, RG2→3 = 0.43, RG3→4 = 0.42,
RG4→5 = 0.36, and RG5→6 = 0.35; none of the 35 simulated epidemics in the 6,000-person ring town scenario 3 lasted longer than six generations after the attack generation.
Clinical disease expression and transmission. In accordance with the values proposed by the working group expert advisors, cases were assigned one of three different clinical disease expressions: ordinary smallpox, modified smallpox, or hemorrhagic smallpox. Among all of the smallpox cases that occurred in these 35 simulated epidemic runs, 57 percent were ordinary, 40 percent were modified, and 3 percent were hemorrhagic cases. However, these proportions varied according to the epidemic generation (Figure 3-11A). In G0, the proportions were 76 percent ordinary, 20 percent modified, and 5 percent hemorrhagic. In G1 and subsequent generations, the proportions were 46 percent ordinary, 51 percent modified, and 3 percent hemorrhagic. These changes in clinical disease expression by epidemic generation reflect the effects of post-exposure vaccination of contacts, which rendered a number of cases to become modified that would otherwise have been ordinary cases (Fenner et al., 1988). We also calculated the epidemic reproductive rate for each clinical disease type for each epidemic generation. The initial disease-type epidemic reproductive rates, or RG(ordinary)0→1, RG(modified)0→1, and RG(hemorrhagic)0→1, were respectively measured to be 1.70, 1.57, and 6.19. The overall initial epidemic reproductive rate RG(all cases)0→1 value of 1.88 is a composite of these values. Subsequent epidemic generational values of R for ordinary, modified, and hemorrhagic smallpox were also calculated and are displayed in Figure 3-11B. After G0, epidemic generational values of RG for modified smallpox were consistently higher than for other types of smallpox at the same generation of the epidemic.
Sensitivity of results to day of withdrawal. We examined the sensitivity of our results to a number of our model assumptions. Most notably, we found that our results were very sensitive to the assumption of the period of time that infected individuals who did not go to the hospital or withdraw to their home on the second day of fever would circulate in the community. These individuals were a small proportion of cases that were not ill enough to withdraw from the community until later in their course of illness. The base model assumes that all individuals will have withdrawn from the community (to the hospital) on day 4 of fever. In our sensitivity analysis, we varied this day from the day fever begins to day 5 of fever. This model change is roughly equivalent to varying the proportion of transmission that occurs before and after symptoms begin, a factor that other investigators have suggested is very important for the controllability of an infectious disease (Fraser et al., 2004). The number of cases that resulted in our model of 6,000 persons under scenario 2 varied dramatically as a function of this parameter from a mean of 2,981 cases in our base model assumptions to a mean of 174 cases if these individuals withdrew from the community on the day their fever began.
FIGURE 3-11 Number of cases of each clinical disease expression type and epidemic reproductive rate attributable to each of these clinical disease types for each epidemic generation. Values shown are averages from 35 epidemic simulations for the 6,000-person ring town under response scenario 3. Generation 0 = index (attack) cases. Ordinary (open bars), modified (striped bars), and hemorrhagic (closed bars) smallpox cases are shown. (A) Cases of each clinical disease type by epidemic generation. (B) Epidemic reproductive rate for each clinical disease type at each epidemic generation.
Discussion
The objective of this modeling exercise was to evaluate the potential effectiveness of epidemic control strategies that might be deployed in response to a bioterrorist attack. Our main finding is that contact tracing and vaccination of household, workplace, and school contacts, along with effective isolation of diagnosed cases, can control epidemics of smallpox. In our 6,000-person town model, we found that in scenario 3 (the combination of interventions most closely parallel to current U.S. governmental policies) the expected total number of smallpox cases that would ensue from ten simultaneous introductions would be 25–40 additional cases (CDC, 2002). Our findings in the 50,000-person town model were consistent with these estimates; under scenario 3,500 introductions into a population of 50,000 would give rise to approximately 1,100 new cases of smallpox. In both size versions of the model, reactive mass vaccination at the town level had additional value in bringing an epidemic under control. We estimate the number of reactive mass vaccinations required to incrementally reduce the epidemic by one case to be about 190 vaccinations in the 6,000-person town/10-attack-case model versions and about 35 vaccinations in the more intense 50,000-person town/500-attack-case model version.
Although a good deal of variation in the size and other characteristics of the modeled epidemics is expected in a highly stochastic epidemic model, we were nonetheless surprised by some of our observations (Bailey, 1953; Whittle, 1955). In our epidemic simulation runs, 1) epidemics ranged dramatically in size and duration based on chance alone, 2) the epidemic impact of individual index (attack) cases ranged from no transmissions whatsoever to large and lengthy transmission chains, and 3) the epidemic reproductive rate varied substantially by clinical disease type and by epidemic generation and was dependent on the underlying social network configuration. These results suggest that the heterogeneity of our microscale, agent-based model has significantly impacted the resultant epidemics.
Limitations
It is possible that some important parameters may not have been considered in the development of this model. For example, age-specific differences in the pathogenicity and transmissibility of smallpox were not considered, other than as they relate to age older than 32 years and prior vaccination status as well as social contact processes (schools for children vs. workplace for adults). We did not explicitly include risks of smallpox vaccination as a source of adverse outcome in our model. The number of vaccinations used in each modeled response is given in the Results section and can be used to estimate adverse outcomes. Another potentially important biological variable unexamined in this exercise is the effect of seasonality on transmission of smallpox (Fenner et al., 1988).
Perhaps the most important model parameters incompletely considered in this work are the social networks and contact processes that dictate disease transmission patterns. Clearly, there is a trade-off between the inclusion of a large degree of detail and heterogeneity in the social structure in a model and the complexity of the resultant model (Ferguson et al., 2003). We have included the level of social detail that we believed necessary to capture the transmission dynamics of smallpox. Although we explicitly modeled person-to-person contacts in hospitals, households, schools, and workplaces, our representations of these social units were admittedly crude. Although we addressed a range of model parameterizations and model structures, a larger sensitivity analysis may reveal surprising results. In future work, we will continue to examine the sensitivity of our results to specific model parameters.
Another limitation of this work is not the model itself but its proper interpretation and use. We caution that the numbers of cases generated in various scenarios should not be taken as quantitative predictions, but instead as a basis for comparing and evaluating different intervention strategies. We also note that in this exercise we modeled only a single geographically confined attack on a relatively small discrete social unit (6,000- or 50,000-person town). In the event of a real smallpox attack, response strategies would have to consider larger social networks and possible repeated introductions over a wide geographic area.
Conclusions
Our simulation exercise revealed that contact tracing and vaccination of household, workplace, and school contacts, along with prompt reactive vaccination of hospital workers and isolation of diagnosed cases, could contain smallpox at both epidemic scales examined. Individual-based simulations of smallpox epidemics provide a valuable tool in crafting policy regarding outbreak response.
REFERENCES
Annas G. 2002. Bioterrorism, public health, and civil liberties. New England Journal of Medicine 346(17):1337-1342.
APHA (American Public Health Association). 1918. Influenza: A report of the American Public Health Association. Journal of the American Medical Association 71:2068.
Bailey NTJ. 1953. The total size of stochastic epidemic. Biometrika 40:177.
Bayer R, Fairchild A. 2002. The limits of privacy: Surveillance and the control of disease. Health Care Analysis 10(1):19-35.
Bell DM, World Health Organization Working Group on International and Community Transmission of SARS. 2004. Public health interventions and SARS spread. Emerging Infectious Diseases 10(11):1900-1906.
Benenson AS, Ed. 1995. Control of Communicable Diseases Manual. Washington, DC: American Public Health Association.
Berry BJL, Kiel LD, Elliott E. 2002. Adaptive agents, intelligence, and emergent human organization: Capturing complexity through agent-based modeling. Proceedings of the National Academy of Sciences 99(3):7187-7188.
Bozzette SA, Boer R, Bhatnagar V, Brower JL, Keeler EB, Morton SC, Stoto MA. 2003. A model for a smallpox-vaccination policy. New England Journal of Medicine 348(5):416-425.
Burke DS, Epstein JM, Cummings DT, Parker JI, Cline KC, Singa RM, Chakravarty S. 2006. Individual-based computational modeling of smallpox epidemic control strategies. Academic Emergency Medicine 13(11):1142-1149.
CDC (Centers for Disease Control and Prevention). 2002. Smallpox Response Plan and Guidelines (version 3.0). [Online]. Available: http://www.bt.cdc.gov/agent/smallpox/response-plan/ [accessed February 14, 2007].
CDC. 2005a. Public Health Guidance for Community-Level Preparedness and Response to Severe Acute Respiratory Syndrome (SARS). [Online]. Available: http://www.cdc.gov/ncidod/sars/guidance/I/index.htm [accessed January 26, 2007].
CDC. 2005b. Regulatory Impact Analysis of Proposed 42 C.F.R. Part 70 and 42 C.F.R. Part 71. [Online]. Available: http://www.cdc.gov/ncidod/dq/nprm/docs/draft_ria_final.pdf [accessed January 26, 2007].
CDC. 2005c. Smallpox Vaccination Program Status by State. [Online]. Available: http://www.cdc.gov/od/oc/media/pressrel/smallpox/spvaccin.htm [accessed February 15, 2007].
CDC. 2006. Questions and Answers on the Executive Order Adding Potentially Pandemic Influenza Viruses to the List of Quarantinable Diseases. [Online]. Available: http://www.cdc.gov/ncidod/dq/qa_influenza_amendment_to_eo_13295.htm [accessed April 12, 2007].
CDC. 2007. Ethical Guidelines in Pandemic Influenza. Advisory Committee to the Director, Ethics Subcommittee. [Online]. Available: http://www.cdc.gov/od/science/phec/panFlu_Ethic_Guidelines.pdf [accessed April 13, 2007].
Center for Law and the Public’s Health. 2001 (December 21). The Model State Emergency Health Powers Act. Prepared by the Center for Law and the Public’s Health at Georgetown and Johns Hopkins Universities, Washington, DC. [Online]. Available: http://www.publichealthlaw.net/MSEHPA/MSEHPA2.pdf; www.publichealthlawnet/msehpa2.pdf [accessed December 27, 2006].
Cetron M. 2006. Community-Wide Strategies in Pandemic Planning. Presentation delivered at Institute of Medicine workshop entitled “Modeling Community Containment of an Influenza Pandemic,” Washington, DC.
Cetron M, Landwirth J. 2005. Public health and ethical considerations in planning for quarantine. Yale Journal of Biology and Medicine 78(5):329-334. Also reprinted on page 99 of this report.
Cetron M, Simone P. 2004. Battling 21st-century scourges with a 14th-century toolbox. Emerging Infectious Diseases 10(11). [Online]. Available: http://www.cdc.gov/ncidod/eid/vol10no11/04-0797_12.htm [accessed December 27, 2006].
Chen H, Smith GJ, Li KS, Wang J, Fan XH, Rayner JM, Vijaykrishna D, Zhang JX, Zhang LJ, Guo CT, Cheung CL, Xu KM, Duan L, Huang K, Qin K, Leung YH, Wu WL, Lu HR, Chen Y, Xia NS, Naipospos TS, Yuen KY, Hassan SS, Bahri S, Nguyen TD, Webster RG, Peiris JS, Guan Y. 2006. Establishment of multiple sublineages of H5N1 influenza virus in Asia: Implications for pandemic control. Proceedings of the National Academy of Sciences 103(8):2845-2850.
Cohen J, Enserink M. 2002. Rough-and-tumble behind Bush’s smallpox policy. Science 298(5602):2312-2316.
Council on Ethical and Judicial Affairs. 2005 (January). The Use of Quarantine and Isolation in Public Health Interventions. Report of the Council on Ethical and Judicial Affairs. CEJA Report 1-I-05. [Online]. Available: http://www.ama-assn.org/ama1/pub/upload/mm/369/ceja_recs_1i05.pdf; www.amaassn.org/ama1/pub/upload/mm/31/quarantine15726.pdf [accessed December 27, 2006].
Eichner M. 2003a. Case isolation and contact tracing can prevent the spread of smallpox. American Journal of Epidemiology 158(2):118-128.
Eichner M. 2003b. Analysis of historical data suggests long-lasting protective effects of smallpox vaccination. American Journal of Epidemiology 158(8):717-723.
Eichner M, Dietz K. 2003. Transmission potential of smallpox: Estimates based on detailed data from an outbreak. American Journal of Epidemiology 158(2):110-117.
Enserink M. 2003. Infectious diseases. Smallpox vaccination campaign in the doldrums. Science 300(5621):880-881.
Epstein JM. 1999. Agent-based computational models and generative social science. Complexity 4(5):41-60.
Epstein JM, Cummings DAT, Chakravarty S, Singha RM, Burke DS. 2004. Toward a Containment Strategy for Smallpox Bioterror: An Individual-Based Computational Approach. Washington, DC: Brookings Institution Press.
Eubank S, Guclu H, Kumar VS, Marathe MV, Srinivasan A, Toroczkai Z, Wang N. 2004. Modelling disease outbreaks in realistic urban social networks. Nature 429(6988):180-184.
Fenner F, Henderson DA, Arita I, Jezek Z, Ladnyi ID. 1988. Smallpox and Its Eradication. Geneva, Switzerland: World Health Organization.
Ferguson NM, Keeling MJ, Edmunds WJ, Gani R, Grenfell BT, Anderson RM, Leach S. 2003. Planning for smallpox outbreaks. Nature 425(6959):681-685.
Fidler DP, Cetron MS. 2007. International Considerations. In Goodman RA, Hoffman RE, Lopez W, Matthews GW, Rothstein MA, Foster KL. 2007. Law in Public Health Practice, Second Edition. New York: Oxford University Press. Pp. 168-195.
Fraser C, Riley S, Anderson RM, Ferguson NM. 2004. Factors that make an infectious disease outbreak controllable. Proceedings of the National Academy of Sciences 101(16):6146-6151.
Garrett L. 2005 (July/August). The next pandemic? Foreign Affairs 84:3.
Germann TC, Kadau K, Longini IM Jr., Macken CA. 2006. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences 103(15):5935-5940.
Global Security. 2005. Flu Pandemic Mitigation: Quarantine and Isolation. [Online]. Available: www.globalsecurity.org/security/ops/hsc-scen-3_flu-pandemic-quarantine.htm [accessed January 26, 2007].
Global Security. 2006. Flu Pandemic Mitigation: Deaths. [Online]. Available: www.globalsecurity.org/security/ops/hsc-scen-3_flu-pandemic-deaths.htm [accessed January 26, 2007].
Goodman RA, Moulton AD, Matthews G, Shaw F, Kocher P, Mensah G, Zaza S, Besser R. 2006. Law and public health at CDC. Morbidity and Mortality Weekly Report 55(Sup02):29-33. [Online]. Available: http://www.cdc.gov/mmwr/preview/mmwrhtml/su5502a11.htm [accessed January 29, 2007].
Gostin LO. 2007. Public Health Law: Power, Duty, Restraint. Second Edition. New York and Berke-ley: Milbank Memorial Fund and University of California Press.
Gostin LO, Powers M. 2006. What does justice require for the public’s health? Public health ethics and policy imperatives of social justice. Health Affairs 25(4):1053-1060.
Gronvall GK, Borio LL. 2006. Removing barriers to global pandemic influenza vaccination. Biosecu-rity and Bioterrorism 4(2):168-175.
Halloran ME, Struchiner CJ, Longini IM. 1997. Study designs for evaluating different efficacy and effectiveness aspects of vaccines. American Journal of Epidemiology 146(10):789-803.
Halloran ME, Longini IM, Cowart DM, Nizam A. 2002a. Community trials of vaccination and the epidemic prevention potential. Vaccine 20(27):3254-3262.
Halloran ME, Longini IM, Nizam A, Yang Y. 2002b. Containing bioterrorist smallpox. Science 298(5597):1428-1432.
Hammarlund E, Lewis MW, Hansen SG, Strelow LI, Nelson JA, Sexton GJ, Hanifin JM, Slifka MK. 2003. Duration of antiviral immunity after smallpox vaccination. Nature Medicine 9(9):1131-1137.
Hawryluck L, Gold WL, Robinson S, Pogorski S, Galea S, Styra R. 2004. SARS control and psychological effects of quarantine. Emerging Infectious Diseases 10(7):1206-1212.
Henderson DA, Inglesby TV, Bartlett JG, Ascher MS, Eitzen E, Jahrling PB, Hauer J, Layton M, McDade J, Osterholm MT, O’Toole T, Parker G, Perl T, Russell PK, Tonat K. 1999. Smallpox as a biological weapon: Medical and public health management. Journal of the American Medical Association 281(22):2127-2137.
Heyman D. 2005. Model operational guidelines for disease exposure control. Center for Strategic and International Studies (CSIS). Pre-publication draft.
Heymann A, Chodick G, Reichman B, Kokia E, Laufer J. 2004. Influence of school closure on the incidence of viral respiratory diseases among children and on health care utilization. Pediatric Infectious Disease Journal 23(7):675-677.
HHS (Department of Health and Human Services). 2005a. HHS Pandemic Influenza Plan. [Online]. Available: http://www.hhs.gov/pandemicflu/plan/pdf/HHSPandemicInfluenzaPlan.pdf [accessed January 26, 2007].
HHS. 2005b. Control of Communicable Diseases (Proposed Rule). 42 C.F.R. Parts 70 and 71.
HHS. 2006a. HHS Pandemic Influenza Plan. Washington, DC: U.S. Department of Health and Human Services. [Online]. Available: http://www.hhs.gov/pandemicflu/plan [accessed December 27, 2006].
HHS. 2006b. HHS Pandemic Influenza Plan, Appendix 4. Principles of Modern Quarantine. Washington, DC: U.S. Department of Health and Human Services. [Online]. Available: http://www.hhs.gov/pandemicflu/plan/ [accessed December 27, 2006].
Iton AB. 2006. Rationing influenza vaccine: Legal strategies and considerations for local health officials. Journal of Public Health Management Practice 12(4):349-355.
IOM (Institute of Medicine). 2005. Quarantine Stations at Ports of Entry Protecting the Public’s Health. Washington, DC: The National Academies Press.
IOM. 2006. Modeling Community Containment for Pandemic Influenza: A Letter Report. Washington, DC: The National Academies Press.
Jackson MM, Lynch P. 1985. Isolation practices: A historical perspective. American Journal of Infection Control 13(1):21-31.
Johnson NP, Mueller J. 2002. Updating the accounts: Global mortality of the 1918-1920 “Spanish” influenza pandemic. Bulletin of the History of Medicine 76(1):105-115.
Kaplan EH, Craft DL, Wein LM. 2002. Emergency response to a smallpox attack: The case for mass vaccination. Proceedings of the National Academy of Sciences 99(16):10935-10940.
Kass NE. 2001. An ethics framework for public health. American Journal of Public Health 91(11):1776-1782. [Online]. Available: http://www.ajph.org/cgi/reprint/91/11/1776 [accessed December 27, 2006].
Kayman H, Oblorh-Odjidja A. 2006. Revisiting public health preparedness: Incorporating principles of social justice into pandemic preparedness planning for influenza. Journal of Public Health Management Practice 12(4):373-380.
Kobasa D, Jones SM, Shinya K, Kash JC, Copps J, Ebihara H, Hatta Y, Kim JH, Halfmann P, Hatta M, Feldmann F, Alimonti JB, Fernando L, Li Y, Katze MG, Feldmann H, Kawaoka Y. 2007. Aberrant innate immune response in lethal infection of macaques with the 1918 influenza virus. Nature 445(7125):319-323.
Kotalik J. 2005. Preparing for an influenza pandemic: Ethical issues. Bioethics 19(4):422-431.
Longini IM, Nizam A, Xu S, Unqchusak K, Hanshaoworakul W, Cummings DA, Halloran ME. 2005. Containing pandemic influenza at the source. Science 309(5737):1083-1087.
Longini IM, Halloran M.E. Nizam A, Yang Y, Xu S, Burke DS, Cummings DA, Epstein JM. 2006. Containing a large bioterrorist smallpox attack: A computer simulation approach. International Journal of Infectious Diseases 11(2):98-108.
Mack TM. 1972. Smallpox in Europe, 1950-1971. Journal of Infectious Diseases 125(2):161-169.
Mariner W. 2001. Bioterrorism Act: The wrong response. National Law Journal 24:A21.
Markel H, Stern AM, Navarro JA, Michalsen JR. 2006. A Historical Assessment of Nonpharmaceutical Disease Containment Strategies Employed by Selected U.S. Communities During the Second Wave of the 1918-1920 Influenza Pandemic. [Online]. Available: http://www.med.umich.edu/medschool/chm/influenza/assets/dtra_final_influenza_report.pdf [accessed on January 26, 2007].
Markovits D. 2005. Quarantines and distributive justice. Journal of Law, Medicine and Ethics 33(2):323-344.
Moulton AD, Gottfried RN, Goodman RA, Murphy AM, Rawson RD. 2003. What is public health legal preparedness? Journal of Law, Medicine, and Ethics 31(4):672-683. [Online]. Available: http://www2.cdc.gov/phlp/docs/moultonarticle.pdf [accessed January 29, 2007].
Murray CJ, Lopez AD, Chin B, Feehan D, Hill KH. 2006. Estimation of potential global pandemic influenza mortality on the basis of vital registry data from the 1918-20 pandemic: A quantitative analysis. Lancet 368(9554):2211-2218.
Normile D. 2006. Evidence points to migratory birds in H5N1 spread. Science 311(5765):1225.
Ontario Ministry of Health and Long-Term Care. 2005. Ontario Health Plan for an Influenza Pandemic. [Online]. Available: http://www.health.gov.on.ca/english/providers/program/emu/pan_flu/pan_flu_plan.html [accessed December 27, 2006].
Osterholm MT. 2005(July/August). Preparing for the next pandemic. Foreign Affairs 84:24-26.
Public Health Leadership Society. 2002. Principles of the Ethical Practice of Public Health. New Orleans: Public Health Leadership Society. [Online]. Available: http://www.apha.org/codeofethics/ethicsbrochure.pdf [accessed December 27, 2006].
Reich DS. 2003. Modernizing local responses to public health emergencies: Bioterrorism, epidemics, and the Model State Emergency Health Powers Act. Journal of Contemporary Health Law and Policy 19(2):379-414.
Rosenthal E. 2006 (April 15). Bird flu virus may be spread by smuggling. New York Times.
Rosling L, Rosling M. 2003. Pneumonia causes panic in Guangdong province. British Medical Journal 326(7386):416.
Rothstein M, Alcalde MG, Elster NR, Majumder MA, Palmer LI, Stone TH, Hoffman RE. 2003. Quarantine and Isolation: Lessons Learned from SARS. [Online]. Available: http://biotech.law.lsu.edu/blaw/cdc/SARS_REPORT.pdf [accessed January 26, 2007].
SARS Commission. 2006. vol. 1 and 2. Spring of Fear. [Online]. Available: http://www.sarscommission.ca/report/index.html [accessed January 26, 2007]. Shapiro v. Thompson. 1999. 394 US 618 (1969).
Smith CB, Battin MP, Jacobson JA, Francis LP, Botkin JR, Asplund EP, Domek GJ, Hawkins G. 2004. Are there characteristics of infectious diseases that raise special ethical issues? Developing World Bioethics 4(1):1-16. [Online]. Available: http://www.blackwell-synergy.com/doi/pdf/10.1111/j.1471- 8731.2004.00064.x?cookieSet=1 [accessed December 27, 2006].
Spotswood S. 2005. HHS flu plan aims to lift vaccine supply. U.S. Medicine. [Online]. Available: http://www.usmedicine.com/article.cfm?articleID=1210&issueID=82 [accessed January 26, 2007].
St. John RK, King RA, de Jong D, Bodie-Collins M, Squires SG, Tam TW. 2005. Border screening for SARS. Emerging Infectious Diseases 11(1):6-10.
Stern AM, Markel H. 2004. International efforts to control infectious diseases. 1851 to the present. Journal of the American Medical Association 292(12):1474-1479.
Stier DD, Goodman RA. In Press. Mutual aid agreements—essential tools for public health preparedness and response. American Journal of Public Health.
Stohr K, Esveld M. 2004. Will vaccines be available for the next influenza pandemic? Science 306(5705):2195-2196.
Sutton V. 2001 (Summer). Bioterrorism preparation and response legislation—the struggle to protect states’ sovereignty while preserving national security. The Georgetown Public Policy Review 93.
Taubenberger JK, Reid AH, Lourens RM, Wang R, Jin G, Fanning TG. 2005. Characterization of the 1918 influenza virus polymerase genes. Nature 437(7060):889-893.
Thomas DB, Arita I, McCormack WM, Khan MM, Islam S, Mack TM. 1971. Endemic smallpox in rural East Pakistan. II. Intravillage transmission and infectiousness. American Journal of Epidemiology 93(5):373-383.
Thomson AK, Faith K, Gibson JL, Upshur RE. 2006. Pandemic influenza preparedness: An ethical framework to guide decision-making. BCM Medical Ethics 7(1):E12.
Thorson AM, Petzold M, Nguyen TKC, Ekdahl K. 2006. Is exposure to sick or dead poultry associated with flulike illness? A population-based study from a rural area in Vietnam with outbreaks of highly pathogenic avian influenza. Archives of Internal Medicine 166(1):119-123.
Torda A. 2006. Ethical issues in pandemic planning. Medical Journal of Australia 185(10): S73-S76.
Tumpey TM, Basler CF, Aquilar PV, Zeng H, Solorzano A, Swayne DE, Cox NJ, Katz JM, Taubenberger JK, Palese P, Garcia-Sastre A. 2005. Characterization of the reconstructed 1918 Spanish influenza pandemic virus. Science 310(5745):77-80.
UN (United Nations). 1985. Annex. In International Covenant on Civil and Political Rights (E/CN.4/1985/4).
University of Toronto Joint Centre for Bioethics Pandemic Influenza Working Group. 2005. Stand on Guard for Thee: Ethical Considerations in Preparedness Planning for Pandemic Influenza. Toronto, Canada: University of Toronto Joint Centre for Bioethics. [Online]. Available: www.utoronto.ca/jcb/home/documents/pandemic.pdf [accessed December 27, 2006].
United Nations Economic and Social Council. 1985. Siracusa Principles on the Limitation and Derogation Provisions in the International Covenant on Civil and Political Rights.
Upshur RE. 2002. Principles for the justification of public health intervention. Canadian Journal of Public Health 93(2):101-103. [Online]. Available: http://www.fhs.mcmaster.ca/ceb/community_medicine_page/docs/upshur.pdf [accessed December 27, 2006].
Upshur RE. 2003. The ethics of quarantine. American Medical Association Journal of Ethics Virtual Mentor 5(11). [Online]. Available: www.ama-assn.org/ama/pub/category/11535.html [accessed December 27, 2006].
U.S. Congress. 1946. The Public Health Service Act. USC Title 42, Chapter 6A, Part G. U.S. Congressional Budget Office. 2006. A Potential Influenza Pandemic: An Update on Possible Macroeconomic Effects and Policy Issues. [Online]. Available: http://www.cbo.gov/ftpdocs/72xx/doc7214/05-22-Avian%20Flu.pdf [accessed January 26, 2007].
U.S. Census Bureau. 2000. Census 2000. [Online]. Age distribution was retrieved from www.census.gov/census2000/states/us.html, and household sizes were retrieved from http://factfinder.census.gov/servlet/DatasetMainPageServlet?_lang=en (see Census 2000 Summary File 1). [accessed October 29, 2002].
Watts DJ. 1999. Small Worlds: The Dynamics of Networks Between Order and Randomness. Princeton, NJ: Princeton University Press.
Watts DJ, Strogatz S. 1998. Collective dynamics of “small-world” networks. Nature 393(6684):440-442.
White House. 2005 (April 1). Executive Order: Amendment to E.O. 13295 Relating to Certain Influenza Viruses and Quarantinable Communicable Diseases. [Online]. Available: http://www.whitehouse.gov/news/releases/2005/04/20050401-6.html [accessed December 27, 2006].
White House Homeland Security Council. 2005. National Strategy for Pandemic Influenza. [Online]. Available: http://www.whitehouse.gov/homeland/nspi.pdf [accessed January 26, 2007].
Whittle P. 1955. The outcome of a stochastic epidemic. Biometrika 42:116-122.
WHO (World Health Organization). 2003. Hospital Infection Control Guidance for Severe Acute Respiratory Syndrome (SARS). [Online]. Available: http://www.who.int/csr/sars/infectioncontrol/en/ [accessed January 26, 2007].
WHO. 2004. WHO SARS Risk Assessment and Preparedness Framework. [Online]. Available: http://www.who.int/csr/resources/publications/CDS_CSR_ARO_2004_2.pdf [accessed January 26, 2007].
WHO. 2005a. WHO Checklist for Influenza Preparedness Planning. Sec 1.5.2. Geneva: World Health Organization. [Online]. Available: www.who.int/csr/resources/publications/influenza/FluCheck-6web.pdf [accessed December 27, 2006].
WHO. 2005b. Avian influenza A (H5N1) infection in humans. The Writing Committee of the World Health Organization Consultation on Human Influenza A/H5. New England Journal of Medicine 353(13):1374-1385.
WHO. 2005c. Avian Flu vs. Pandemic Flu. [Online]. Available: http://www.wvdhhr.org/healthprep/common/avian_vs_pandemic_flu.pdf [accessed January 26, 2007].
WHO. 2005d. Avian Influenza: Assessing the Pandemic Threat. [Online]. Available: http://www.who.int/csr/disease/influenza/H5N1-9reduit.pdf [accessed January 26, 2007].
WHO. 2006a. Avian Influenza—Spread of the Virus to New Countries. [Online]. Available: http://www.who.int/csr/don/2006_02_21b/en/index.html [accessed January 26, 2007].
WHO. 2006b. Avian Influenza: Significance of Mutations in the H5N1 Virus. [Online]. Available: http://www.who.int/csr/2006_02_20/en/index.html [accessed January 26, 2007].
WHO. 2007a. Situation Updates—Avian Influenza. [Online]. Available: http://www.who.int/csr/disease/avian_influenza/updates/en/index.html [accessed January 26, 2007].
WHO. 2007b. Cumulative Number of Confirmed Human Cases of Avian Influenza A/(H5N1) Reported to WHO. [Online]. Available: http://www.who.int/csr/disease/avian_influenza/country/cases_table_2007_05_16/en/index.html [accessed May 16, 2007].
Wong SS, Yuen KY. 2006. Avian influenza virus infections in humans. Chest 129(1):156-168.
World Health Assembly. 2005. Strengthening Pandemic Influenza Preparedness and Response. WHA 58:13.9. [Online]. Available: http://www.who.int/csr/disease/influenza/A58_13-en.pdf [accessed January 26, 2007].
World Health Organization Writing Group. 2006. Nonpharmaceutical interventions for pandemic influenza, international measures. Emerging Infectious Diseases 12(1):81-87. [Online]. Available: http://www.cdc.gov/ncidod/EID/vol12no01/05-1370.htm [accessed January 26, 2007].
ANNEX 3-1 follows
TABLE 3-4 Daily Transmission Probabilities, x,aAmong Children andAdults, by Mixing Group, and Group Sizes
TABLE 3-11 Summary of Results of Epidemic Simulation Runs Showing the Effects of “No Response” Scenarios 1 and 2 and Response Scenarios 3-10 on Epidemics Initiated by the Introduction of Ten Smallpox Cases into 6,000-Person Towns
|
Scenario |
Single Uniform Town |
Four Hub-and-Spoke Towns |
Ring of Six Towns |
|||||||||
|
Cases |
Deaths |
New Vaccina-tions |
Duration (days) |
Cases |
Deaths |
New Vaccina-tions |
Duration (days) |
Cases |
Deaths |
New Vaccina-tions |
Duration (days) |
|
|
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
|
|
No response |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5,231.6 (46.5) |
1,650.4 (34.7) |
NA (NA) |
649.7 (124.4) |
5,226.9 (58.3) |
1,638.9 (40.0) |
NA (NA) |
643.1 (146.1) |
5,240.2 (47.5) |
1638.7 (30.6) |
NA (NA) |
629.1 (115.0) |
|
2 |
2,981.3(623.2) |
935.0 (198.3) |
NA (NA) |
394.9 (82.2) |
2,521.2 (583.0) |
788.1 (181.5) |
NA (NA) |
470.9 (125.5) |
2,167.9 (996.3) |
676.4 (313.0) |
NA (NA) |
416.2 (125.3) |
|
Response |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
47.2(16.5) |
11.3 (5.1) |
355.7 (88.2) |
76.9 (17.7) |
35.5 (14.4) |
9.5 (4.9) |
295.0(78.4) |
69.2 (15.1) |
43.6 (14.8) |
11.4 (4.9) |
332.9 (68.8) |
75.6 (16.5) |
|
4 |
45.9(21.9) |
11.4 (5.8) |
351.6 (99.2) |
73.0 (17.7) |
39.9 (16.6) |
9.3 (4.2) |
309.7 (69.5) |
70.5 (16.5) |
34.8 (12.4) |
8.9 (4.2) |
306.8 (64.6) |
68.5 (16.1) |
|
5 |
35.9(12.7) |
9.8 (4.2) |
316.2 (62.0) |
66.9 (12.6) |
41.2 (11.8) |
11.0 (3.7) |
324.6 (60.2) |
71.4 (13.2) |
38.5 (17.7) |
10.3 (5.0) |
314.9 (75.9) |
65.6 (10.4) |
|
6 |
32.2(13.6) |
8.4 (4.5) |
2,373.1 (46.1) |
59.7 (12.7) |
28.9 (10.4) |
7.0 (3.1) |
2,359.8 (45.3) |
57.9 (11.1) |
24.2 (6.7) |
6.8 (3.0) |
2,357.9 (44.5) |
54.8 (10.6) |
|
7 |
25.1(8.6) |
7.0 (3.5) |
2,364.6 (49.7) |
58.3 (13.8) |
29.4 (8.9) |
7.5 (2.6) |
2,373.9 (42.4) |
60.0 (9.9) |
28.2 (10.70 |
7.8 (3.4) |
2,363.0 (51.9) |
58.3 (15.9) |
|
8 |
22.2(10.1) |
5.8 (2.9) |
4,502.7 (28.9) |
46.9 (6.4) |
19.8 (7.2) |
4.7 (2.6) |
4,492.5 (31.3) |
46.7 (10.2) |
17.5 (4.0) |
4.9 (1.9) |
4,505.0 (29.5) |
43.3 (7.4) |
|
9 |
17.3(4.7) |
4.3 (2.0) |
4,505.7 (38.4) |
45.2 (8.0) |
19.9 (5.6) |
5.9 (2.1) |
4,501.8 (38.0) |
46.7 (8.1) |
18.6 (5.8) |
5.1 (2.6) |
4,504.1 (29.80) |
45.2 (5.8) |
|
10 |
44.2(21.1) |
11.2 (5.5) |
334.9 (94.0) |
70.2 (18.3) |
42.5 (17.9) |
10.9 (5.3) |
323.5 (82.4) |
75.5 (19.5) |
32.5 (10.2) |
8.2 (3.9) |
282.9 (46.5) |
66.1 (10.0) |
|
Data from single uniform town, ring town, and hub-and-spoke town architectures are shown. For each scenario, the number of infected persons, number of deaths, number of vaccinations administered, and duration of the epidemic are shown.Totals include index generation (G0) cases along with subsequent cases. |
||||||||||||
TABLE 3-12 Summary of Results of Epidemic Simulation Runs Showing the Effects of “No Response” Scenarios 1 and 2 and Response Scenarios 3–10 on Epidemics Initiated by the Introduction of 500 Smallpox Cases into 50,000-Person Towns
|
Scenario |
Single Uniform Town |
Ring of Six Towns |
||||||
|
Cases |
Deaths |
NewVaccinations |
Duration (days) |
Cases |
Deaths |
New Vaccinations |
Duration (days) |
|
|
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
Mean (SD) |
|
|
No response |
|
|
|
|
|
|
|
|
|
1 |
46,474.6(109.3) |
14,641.7 (117.9) |
NA (NA) |
1,280.8 (159.6) |
46,463.7 (100.0) |
14,623.4 (66.2) |
NA (NA) |
1,204.5 (139.3) |
|
2 |
26,915.2(819.4) |
8,435.3 (288.6) |
NA (NA) |
453.2 (30.4) |
27,103.0 (784.3) |
8,476.0 (220.60 |
NA (NA) |
531.7 (77.2) |
|
Response |
|
|
|
|
|
|
|
|
|
3 |
1,609.5(90.2) |
415.6 (29.6) |
8,780.7 (445.2) |
104.3 (13.1) |
1,563.6 (95.4) |
406.8 (28.9) |
8,325.4 (407.7) |
105.1 (16.6) |
|
4 |
1,635.9(133.5) |
429.9 (35.0) |
8,945.1 (592.5) |
109.2 (18.6) |
1,500.2 (59.2) |
400.5 (16.1) |
8,114.5 (445.6) |
107.3 (10.1) |
|
5 |
1,657.3(88.0) |
429.6 (22.5) |
8,988.3 (371.2) |
112.5 (9.7) |
1,472.6 (126.7) |
392.1 (37.1) |
7,993.1 (618.2) |
101.9 (11.8) |
|
6 |
1,146.9(69.3) |
305.1 (21.1) |
22,023.1 (149.3) |
87.1 (6.5) |
1,101.2 (55.8) |
299.4 (13.7) |
21,723.2 (202.6) |
81.4 (6.3) |
|
7 |
1,160.2(52.5) |
310.6 (20.6) |
22,041.2 (206.0) |
86.8 (6.2) |
1,088.2 (43.2) |
295.1 (15.3) |
21,784.2 (202.6) |
90.5 (11.5) |
|
8 |
772.5(45.7) |
216.4 (14.0) |
37,516.9 (84.8) |
66.0 (8.9) |
775.0 (17.4) |
219.9 (11.6) |
37,529.3 (115.3) |
65.6 (10.3) |
|
9 |
780.5(25.6) |
211.7 (12.1) |
37,560.0 (59.6) |
63.6 (7.4) |
756.8 (32.1) |
214.8 (10.5) |
37,569.0 (117.8) |
60.3 (5.0) |
|
10 |
1,634.8(79.3) |
428.2 (21.6) |
8,928.2 (336.2) |
116.0 (14.9) |
1,512.6 (50.1) |
398.3 (20.2) |
8,018.1 (248.3) |
104.5 (11.1) |
|
Data from simulations on the single uniform town and ring town architectures are shown (simulations on the hub-and-spoke town architecture were not performed for the 50,000-person town). |
||||||||