2
Operations Research and Intelligence Analysis
Edward H. Kaplan1
This chapter presents an overview of the field of operations research (OR), with a glimpse toward its applicability to problems in intelligence analysis. I first define the field of operations research, and suggest the types of intelligence problems that it can and cannot best address. A brief review of the World War II origins of OR and subsequent developments follows. I then offer a selective tour of current OR applications to illustrate the range of activities in which operations research is used, and provide some evidence indicating the value gained from using OR in practice. I next suggest how operations researchers approach new problems, provide a brief survey of different OR modeling methods that have been developed over the years, and note that the use of these techniques is now facilitated by computerized spreadsheet programs. I then provide a few “back of the envelope” models more to illustrate the flavor of operations research reasoning than to highlight any particular discoveries. I close by suggesting some possible applications of these ideas to intelligence analysis, including the use of OR to study the intelligence production process.
WHAT IS OPERATIONS RESEARCH AND HOW IS IT USEFUL?
Massachusetts Institute of Technology (MIT) physicist, Philip Morse, defined operations research as the scientific study of operations (Morse, 1956). Operations are the physical means by which organizations “get
things done.” They are the organized, often repetitive activities and/or tasks carried out by firms, agencies, the military, or virtually any other organization in support of its mission. Examples include the steps involved in the production of manufactured goods, the servicing of customers in call centers (or restaurants or hospitals or online), the determination of routes and schedules for delivering parcels (e.g., FedEx) and/or people (e.g., the airlines), or the planning of terrorist attacks (and countermeasures to prevent such attacks).
As will be elaborated below, the scientific study of operations reflects the methods of physical science, which is not surprising because the founders of OR were physical scientists. Early studies focused on establishing the physical principles underlying the mainly military operations in question via the analysis of operational data, the formulation of (often simple) mathematical models from first principles, and the design and analysis of experiments to test the results of such models. Over time, however, the formulation and analysis of mathematical models became the hallmark of operations research studies, while the mathematics underlying such models developed to the point where today, the term “operations research” is as likely to refer to the mathematical methods involved as to field studies of actual operations.
The rationale for studying operations is not only to understand them (which is the usual goal of scientific investigation), but also to use such understanding to make better operational decisions. “Better” refers to improving matters in terms of the organization’s fundamental objectives: What decisions lead to higher (if not maximal) profits, lower (if not minimal) costs, increased numbers of infections averted, or reduced numbers of successful terror attacks? Thus, perhaps a more complete definition of OR is the scientific study of operations to make better decisions.
For intelligence analysts, operations research offers powerful tools for understanding and analyzing certain classes of problems. However, OR is by no means a “one-size-fits-all” approach to solving intelligence problem sets. Questions that address the operations, capabilities, or procedures underlying adversaries’ (or sometimes allies’) “systems of interest” can be studied using mainstream OR ideas, while operations research can assist in the study of questions that focus more on an adversary’s intentions by complementing other methods such as game theory (see Fingar, Chapter 1, and Bueno de Mesquita, Chapter 3, both in this volume).2 As an example,
although OR ideas are less helpful in answering whether Iran’s opposition leaders want to develop nuclear weapons, such ideas could be employed to estimate how long Iran would take to develop them. Although OR cannot tell us if Hezbollah intends to launch an attack on American soil, the methods of operations research could be used to estimate the number of operatives required to execute different types of terror attacks, or perhaps even estimate the number of Hezbollah operatives or sympathizers in the country. In applying OR to intelligence problems, the expectation is not that this approach will provide magic answers to otherwise unanswerable questions, but rather that the methods of OR can serve as powerful organizing devices for connecting different pieces of information, and suggest what unknown parameters for the system of interest are most important to ascertain.
THE ORIGINS OF OPERATIONS RESEARCH
Prior to the outbreak of World War II, Britain’s preparation for the anticipated conflict included experimental investigations into the deployment of newly developed radar technology to provide early warning and real-time tracking of German bomber attacks. By mid-1938, air-defense drills revealed that although it was technically feasible for the radar system to detect aircraft, “… its operational achievements fell far short of requirements” (Larnder, 1984, p. 471). The superintendent of the Bawdsey Research Station,3 A. P. Rowe, is credited with proposing that “… research into the operational—as opposed to the technical—aspects of the system should begin immediately” (Larnder, 1984, p. 471), and the term “operational research” was created to describe this new area of endeavor. Initial investigations included methods for managing fighters to counterattack bombers in both formation and individual combat. As the war progressed, staff of the then-formalized (in 1941) Royal Air Force Operational Research Section employed statistical analysis, deductive methods from the physical sciences, and common sense to analyze both offensive and defensive operations with an eye toward reducing their own casualties while inflicting maximal damage on the enemy (Dyson, 2006).
The leading British scientist associated with wartime OR is the Nobel Prize-winning physicist Patrick Blackett, who in 1940 was appointed as the Director of Naval Operational Research (Nobel Lectures, Physics 1942– 1962, 1964; McCloskey, 1987). He was involved in the early radar studies and is credited with leading the team that discovered the relationship between the size of merchant marine convoys and the number of merchant ships sunk in U-boat pack attacks. As detailed in Falconer (1976) and Morse
and Kimball (1951), the key finding was that the number of merchant vessels sunk per attack, while proportional to the number of attacking U-boats and inversely proportional to the number of naval escorts, was essentially independent of the number of merchant ships in a convoy. This led to the recommendation that merchant ships travel in larger convoys, which in turn greatly reduced shipping losses to the allied forces in the North Atlantic (see Kirby, 2003, for further details of the British origins of operational research).
Philip Morse (not incidentally Blackett’s friend and colleague), is regarded widely as the father of operations research in the United States. In 1942, Morse agreed to join the war effort by organizing a group of scientists to help the U.S. Navy study its antisubmarine operations (Morse, 1986). The different problems addressed and methods developed by Morse and his associates, originally contained in classified reports and memorandums, have been documented in Morse and Kimball’s Methods of Operations Research (1951), the first published text in the field. In addition to the merchant marine convoy problem discussed earlier, reported applications include finding the best search patterns to locate enemy ships and submarines, evaluating the trade-offs in the following situations:
-
Using planes as merchant marine escorts and having these same planes bomb U-boat docks;
-
Attacking enemy ships versus attacking the factories that produce ships;
-
Determining the required forces of different types to undertake various military operations;
-
Evaluating rapid maneuvering versus antiaircraft fire to defend warships against Kamikaze suicide plane attacks;
-
Developing countermeasures to enemy radar; and
-
Evaluating weapons effectiveness and determining the best methods for using them.
Basic physical reasoning (as captured in simple flow or differential equations), probability modeling, statistical analysis of both experimental and operational (i.e., field) data, and a good deal of (sophisticated!) common sense were used throughout the decision making. In later writing, Morse noted that for operations researchers, “Any field of mathematics, any technique of measurement that will bring results is used,” and that OR “… uses any and all of these techniques to study operations so that they may be understood, and thus understandingly controlled” (Morse, 1956, p. 6). Additional reflections on early OR methods and applications in the United States can be found in two Morse publications (Morse, 1948, 1952).
One additional development with military roots has had a profound impact on the field of OR. In 1946, mathematician George Dantzig was on
leave from his doctoral program at the University of California–Berkeley and working for the U.S. Air Force Office of Statistical Control. One challenge he faced was to help the Air Force mechanize the process by which it scheduled and deployed forces, equipment, training, and other functions. This challenge led Dantzig to the formulation of the linear programming problem, a technique with wide applicability to decision-making problems, and the simplex algorithm for solving linear programs (Gass, 2005; Dantzig, 1963). Linear programming and associated optimization techniques have since blossomed into one of the largest subfields of OR.
OR did not develop in isolation in the decades following World War II. At the intersection of the engineering, mathematical, social, and physical sciences, it shared methods, application areas, and personalities with other growing disciplines, especially economics, statistics, and computer science. For example, the OR technique of linear programming was crucial to the development of practical solution methods in game theory (McKinsey, 1952); game theory in turn has provided fundamental tools in economics and political science. A concise and entertaining account of such developments in operations research can be found in Gass and Assad (2005).
OR thus evolved as small groups of scientists worked to understand and improve military operations using whatever tools were available, or by developing new models if the situation so demanded. Only after World War II did operations researchers seek to organize professionally and in academia. In 1948, the Operational Research Club (later the Operational Research Society) was established in London, and the Operations Research Society of America (now the Institute for Operations Research and the Management Sciences) was founded in 1952. Morse initiated the Operations Research Center at MIT in 1953 and awarded its first Ph.D. to John D.C. Little in 1955 (Larson, 2007). Today, OR programs exist within engineering and/or management schools4 in major research universities around the world. The International Federation of Operational Research Societies boasts 48 active national member societies, and current applications beyond those found in the military abound in both the public and private sectors, as discussed next.
SELECTED CURRENT OPERATIONS RESEARCH APPLICATIONS
Manufacturing and Supply Chain Management
Returning to the definition of OR as the scientific study of operations for the purpose of making better decisions, manufacturing operations
provide a natural setting for study and application. Engineering the design of a product is one thing, but managing its production is another. How should the required production steps be scheduled to most efficiently use the available capacity of labor and machines? What is the “right” (i.e., profit maximizing) level of production over time? Given the need to assemble a myriad of parts and store partially finished and finished product (with attendant inventory holding costs) in the face of uncertain end-product demand, how much inventory (and what types) should be held over time, and when should orders for additional supply be placed? What are the best ways to measure quality levels and ensure the attainment of appropriate quality in production? How can one coordinate the activities of several different actors (or players)—such as suppliers, manufacturers, and retailers, each with their own incentives—to better coordinate entire supply chains? These questions and more fall within the subfield of manufacturing and supply chain management. OR methods for investigating such questions are a standard part of the curriculums found in schools of business/management and in industrial engineering programs (see Cachon and Terwiesch, 2008, and Hopp and Spearman, 2007, for introductory texts), while major manufacturing companies rely on such ideas in their daily activities.
Distribution and Logistics
Closely related to manufacturing and supply chain management is the area of distribution and logistics, which involves “ … the efficient transfer of goods from the source of supply through the place of manufacture to the point of consumption in a cost-effective way whilst providing an acceptable service to the customer” (Rushton et al., 2006, p. 6). To appreciate the problems and opportunities that arise in distribution management, one need only consider the success of companies such as United Parcel Service and FedEx, which have built entire businesses around efficient distribution systems (indeed, FedEx was identified by the Defense Science Board as a case study for learning how OR has been institutionalized successfully in the private sector; see Defense Science Board, 2009). The design and operation of such systems reflect some of the most famous problems in the study of network flows, including the transportation problem (what is the cheapest way to ship products from a set of supply nodes [or sources] to a set of demand nodes [or sinks]?), the shortest path problem (how can one find the shortest distance between any starting location and any set of destinations on a given transportation network?), the longest path problem (which in project management applications reveals the bottleneck activities capable of delaying completion time of the project in question), and the traveling salesperson problem (someone starting out from an origin point must visit a given set of locations before returning to the origin; what sequence of
visits minimizes the total travel distance?) (Ahuja et al., 1993). Distribution problems are not restricted to the shipment of discrete units; consider the flow (and pricing) of electricity, oil, natural gas, or electronic funds.
Private and Public Services
The key distinction between services and physical products is that services are usually produced and consumed at the same time. Customer satisfaction, often determined by the experience of waiting (Larson, 1987) along with the price of service, is a key objective in managing service operations (Wright and Race, 2004). Determining the appropriate service capacity (e.g., number of servers) is a problem common for services ranging from call centers (Aksin et al., 2007) to hospitals (Green, 2004); operations researchers typically apply queueing (or waiting line) theory to this type of problem (Gross et al., 2008). In the public sector, operations researchers have devoted considerable attention to the study and improvement of emergency services, including police (Larson, 1972), fire (Walker et al., 1979), and emergency medical services (Willemain and Larson, 1977). Additional public-sector applications include the criminal justice system, public transportation, energy, and the environment (Pollock et al., 1994). In the private sector, the real-time pricing of services, known as yield or revenue management, is another aspect of services management where OR has had a major impact. Revenue management methods are employed routinely in the airline, hotel, and car rental industries, among others (Talluri and van Ryzin, 2005).
Medicine and Public Health
Along with scholars and practitioners from many other academic disciplines, operations researchers have focused attention on different aspects of health care in recent years. Applications include clinical concerns such as optimizing radiation treatment for cancer, matching the supply and demand of transplantable organs, preparing for influenza or other pandemics, allocating resources for HIV prevention programs, and evaluating specific prevention and/or treatment interventions from the standpoint of program operations (see Brandeau et al., 2004, for numerous examples). The focus on the operations involved in delivering healthcare services is what distinguishes OR from other studies. Needle exchange programs provide an example of this perspective. These controversial programs enable drug injectors to exchange used needles and syringes for clean ones to prevent HIV transmission via needle sharing (National Research Council and Institute of Medicine, 1995). Although many studies focused on surveys of program clients to determine whether rates of needle sharing declined as a
result of such programs, an operations research study was what established the following principles: increased needle exchange rates reduce needle circulation times; the less time a needle spends circulating among drug injectors, the less likely it is to carry HIV (needles are shared by fewer people); and the lower the level of HIV among needles, the less likely drug injectors are to become infected with HIV. By systematically coding, tracking, and testing the needles in an exchange program for HIV infection over time, this study demonstrated that the predictions of this “circulation theory” were supported by the data, with the result that HIV transmission in this community was reduced substantially (Kaplan, 1995).
Homeland Security and Counterterrorism
Since the terrorist attacks of September 11, 2001, many operations researchers have turned their attention to problems related to terrorism. Examples include the defense of critical infrastructure such as electricity grids, pipelines, and transportation hubs, including airports and subway stations, chemical plants, nuclear reactors, and major ports. Models for these scenarios have been developed, and in many cases the recommended courses of action have been adopted (Brown et al., 2006). Other examples include the operational (as opposed to scientific) effectiveness of detectors of suicide bombers (Kaplan and Kress, 2005), evaluation and proposed improvements to US-VISIT (the Department of Homeland Security biometric identification program for immigration and border management at U.S. points of entry) (Wein and Baveja, 2005), and preparedness for potential bioterror attacks (Wein et al., 2003; Wein and Liu, 2005).
THE OPERATIONS RESEARCH VALUE PROPOSITION
In manufacturing and services applications, the monetary benefits that OR projects have generated, whether by increasing revenues or decreasing costs, have been documented in specific instances. Pringle (2000) reports several examples, including the following:
-
Working for Sears, Roebuck and Company, operations researchers designed a scheduling system that “ … generated a one-time cost reduction of $9 million as well as ongoing savings of $42 million per year” (p. 30);
-
Weyerhaeuser operations researchers solved the problem of “ … where to cut the stem into logs of what length and to what use should the resulting logs be allocated (export, lumber, plywood, paper) … resulting in savings well in excess of $100 million” (p. 30); and
-
Operations researchers at National Car Rental developed and implemented a revenue management system that improved revenue by $56 million in its first year of operation.
Horner (2000) relates the success of Sabre, the spin-off formed by American Airlines’ OR group that is widely credited with the creation of revenue management (by merging of real-time pricing with reservations and scheduling). Interviewing Thomas Cook, the former head of American’s operations research group, Horner reports that by 1998, “ … the revenue management system at American Airlines was generating nearly $1 billion in annual incremental revenue. To put that figure into perspective, consider that the airline’s total operating profit didn’t approach $1 billion until 1997” (p. 47).
Further examples of monetary benefits generated by industry OR groups appear in Bell et al. (2003), while Alden (2009) estimates conservatively that from 1972 through 2008, the total benefits generated by finalists for the Franz Edelman Award for achievement in operations research and the management sciences, the top award for applied operations research with about six finalists each year, exceed $160 billion. Clearly much can be gained by applying OR ideas in industry.
THE OPERATIONS RESEARCH APPROACH TO PROBLEM SOLVING
How do operations researchers get started with a new project? Leaving to the side purely mathematical studies meant to improve the quantitative methods of OR, the goal of an applied study is to improve decision making. Historically, this has placed OR groups in an advisory role in which responsible decision makers (e.g., military commanders, business executives, agency heads) request assistance to help improve matters in some regard. This does not imply that problems always arrive as well-posed questions; indeed, Morse and Kimball (1951, p. 5) wrote, “It often occurs that the major contribution of the operations research worker is to decide what is the real problem.” This latter statement applies equally well to independent operations researchers conducting research to achieve better outcomes in their area of interest.
Understanding the problem often requires understanding the environment and/or system in which the issue is embedded. For example, issues that might be addressed are the basic processes that characterize the flow of material in production processes; the transmission of infections in contagious outbreaks; the routing of Internet traffic; the movement of offenders through the criminal justice system; the generation and distribution of electricity; or the interdiction of terrorists en route to attack. What part of these processes represents cause for concern (e.g., excessive delays at
airports or hospitals) or alternatively presents an opportunity (e.g., differences in individuals’ willingness to pay for airline seats, hotel rooms, or cell phone minutes)? Basic understanding of the problem terrain enables decision makers and OR analysts to communicate more effectively about problems and/or opportunities in the environment.
Understanding the environment and/or system in question requires substantive expertise. Such expertise is often best gained via direct observation, which is why operations researchers have been known to ride around in police patrol cars, spend time on factory floors or in warehouses, or observe the formation and dissipation of lines at banks, on highways, in call centers, or at Disney World. Certainly the formative years of military OR saw analysts “living in the system,” able to witness new versions of “the problem” surface repeatedly over the course of World War II.
Another important part of getting started is figuring out just what the decision maker is trying to achieve. What are the objectives? If faced with two ways to implement the operation(s) in question, could the decision maker state which one is preferred and why? Getting decision makers to explicitly state their objectives in terms of performance measures represents a major step toward understanding the problem (see Fischhoff, this volume, Chapter 10). Possible objective/performance measure pairings include maximize profit, minimize cost, maximize lives saved, and minimize response time. With a common understanding of objectives and performance measures, problem identification becomes much easier.
The hallmark of an OR study is the creation of a mathematical model that represents the operations of the system under study, and the choices and alternatives available to the decision maker, and that situates both within the appropriate environment. Crafting a model is a creative act that is as much art as science. The relationship between observation and data collection on the one hand and model development on the other is bidirectional, in that the model can suggest new data to collect as easily as field observation can cause revision (or abandonment) of the model in question. Most OR students are familiar with mathematical problem sets meant to drill and further teach the nuances of the modeling methods under study. Modeling real applications is more like taking an operational situation into the real world, and decomposing it to the point where one can create problem set-like questions that address the system’s most important features and properties. For an empirical study of how operations modelers approach problems and formulate new models, see Willemain (1995).
THE SCOPE OF OPERATIONS RESEARCH METHODS
Although operations researchers employ many mathematical tools in their studies, and other quantitative disciplines apply many of these same
mathematical techniques, three sets of modeling approaches have become identified with OR: optimization, probability modeling (or stochastic processes), and decision analysis. All of these methods have and continue to be used in applications such as those outlined earlier. Although the interested reader can learn the basics of these methods from any good introductory textbook in operations research (e.g., Hillier and Lieberman, 2010), one should be aware that the methods themselves are active subjects of research among mathematical operations researchers, and new extensions and results for these techniques continue to be discovered.
Optimization problems involve the maximization or minimization of some objective function (e.g., maximize profit, minimize cost) of variables under the decision maker’s control (the decision variables), subject to resource or other constraints on the allowable values of these variables. The techniques used to solve optimization problems depend on the underlying mathematical specifics (e.g., whether the objective function is linear or nonlinear, whether the decision variables are continuous or integer valued), and include linear programming, nonlinear programming, integer programming, and dynamic programming, among others (Bradley et al., 1977). The solution to an optimization problem identifies the values of the decision variables that lead to the best outcome for the decision maker within the assumptions of the model, along with the value of that outcome (e.g., maximized profit or minimized cost), and also provides tools for examining the sensitivity of these results (values of the decision variables and the objective function) to changes in the assumptions made in constructing the model.
Probability modeling represents those operational situations where randomness and uncertainty dominate; these are known as stochastic processes. For example, queueing theory addresses problems where customers arrive at a service system according to some random process and the duration of service is uncertain. It provides answers to questions such as how long customers must wait for service, how many customers are in the system, and how busy service providers are; such models are fundamental to applications in service systems (Gross et al., 2008). Inventory theory provides additional models for understanding the flow and storage of intermediate and finished goods in production processes, blood/plasma supplies, and supply chains (Porteus, 2002). Reliability theory (also known as survival analysis) examines the probability of (and time to) failure of complicated systems such as nuclear power plants, space transport systems, or individuals suffering from disease by analyzing the interrelationships among components or subsystems that can give rise to total system failure or death in the case of the patient (Bazovský, 2004). For extremely complicated problems where a mathematical solution proves too difficult, simulation models are used to represent the operation of the system and generate data
of interest on a computer; the resulting data can then be analyzed statistically to infer relationships between system operations and performance measures of interest (Rubinstein and Kroese, 2007).
Decision analysis is a hybrid family of optimization and probability methods that has been developed to help decision makers evaluate alternative courses of action in the face of uncertain outcomes that evolve over time (Clemen and Reilly, 2001; Howard and Matheson, 1983; Raiffa, 1968). Helpful graphical tools such as decision trees and influence diagrams have been developed to represent the problem environment and further structure such problems. Decision analysis is where OR intersects most with psychology, where scholars of judgment and decision making have invested tremendous effort to study how individuals actually make decisions (with attendant biases) (see Fischhoff, Chapter 10; Arkes and Kajdasz, Chapter 7; and Spellman, Chapter 6, all in this volume). Another point of intersection is with rational choice and game theory models in economics and political science, which proceeds under the assumption that individuals behave as if they are experts at solving decision analysis problems and regularly do so in their strategic decision making (see Bueno de Mesquita, this volume, Chapter 3). The OR perspective is advisory; given a decision maker’s preferences, understanding of the alternative actions available, and valuation of the possible consequences associated with these alternatives, what is the best course of action? Decision analysis also provides methods for estimating the value of additional information that could be learned about the problem, in order to examine the sensitivity of recommended courses of action to the specific assumptions made when modeling the problem (as with optimization models) (see Fischhoff, this volume, Chapter 10).
OPERATIONS RESEARCH FOR THE MASSES
The theory underlying the mathematical methods described above is quite deep. For this reason, OR modeling work was limited to those with advanced mathematical training (and founders of the field, such as Blackett and Morse, certainly were gifted mathematicians). However, as with common statistical methods such as hypothesis testing and regression analysis, using OR properly in applied studies is possible without mastering all of the underlying mathematical theory. Indeed, over the past decade, OR methods have been computerized in easy-to-use spreadsheet packages such as Microsoft Excel, making it much easier to formulate and solve a variety of models (Winston and Albright, 2009). Also, often the analysis of seemingly complex models gives rise to insights that are shockingly elegant in their simplicity, as the examples of the next section are meant to demonstrate.
OPERATIONS RESEARCH ON THE BACK OF AN ENVELOPE
Go/No Go (Decision Analysis)
Many decisions can be represented as a choice between the “business as usual” status quo mode of operations (or no go), and changing to a risky alternative that might or might not succeed (go). Suppose that the risky alternative, if it succeeds, would deliver an incremental benefit of b units (e.g., additional profit, additional lives saved) relative to the status quo, while this same alternative, if it fails, would impose an incremental cost of c units relative to the status quo. Also, suppose the probability of the risky alternative succeeding is equal to p. This situation is depicted graphically in the decision tree in Figure 2-1; the square represents the decision between the status quo and the risky alternative that must be made, the circle represents the uncertain performance of the risky alternative (with the probabilities of success and failure indicated on the corresponding “branches” of the tree), and the incremental values associated with the various possible outcomes appear at the end of each branch.
The decision maker seeks to maximize the value expected from the consequences of this decision. Compared to the status quo (which has an expected incremental value of zero when compared to itself), the risky alternative is worth p × b – (1 – p) × c, which exceeds zero providing that p > c / (b + c). This model thus suggests a very simple rule. Note that knowing the precise value of the success probability p is unnecessary; one only needs to recognize whether this probability is above or below the threshold of c / (b + c). If the incremental penalty c greatly exceeds the incremental benefit b, one should only pursue the risky alternative if one is extremely certain it will succeed. On the other hand, if the incremental benefit is much larger than the incremental cost, unless one is quite certain that the risky alternative will fail, it appears advantageous to “go for it.”
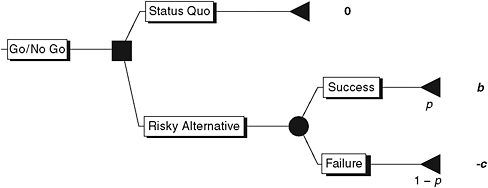
FIGURE 2-1 Go/no go decision tree.
Of course, decision analysis offers more complex methods than the simple example above. Perhaps of special relevance to intelligence analysts, decision analysis has developed tools that apply to decision makers who are risk averse (or conversely, risk prone). For example, given a coin toss that pays $0 if the coin lands tails, but $10 if the coin lands heads, a risk-averse decision maker would be willing to sell the rights to this lottery for, say, $4 even though the expected value of the gamble equals $5. Conversely, a risk-prone decision maker might not be willing to part with this gamble unless offered at least, say, $6. Decision analysis offers both methods for assessing whether a decision maker is risk averse or risk prone (or risk neutral for that matter), along with a methodology detailing how such decision makers should choose among their options (Clemen and Reilly, 2001; Howard and Matheson, 1983; Raiffa, 1968).
Little’s Theorem (Queueing)
Little’s Theorem is named after John D.C. Little, MIT’s first Ph.D. student in operations research. It states that the average number of customers in a queueing system (L) is equal to the product of the customer arrival rate (λ) and the mean time spent in the system (W), or simply L = λW (Little, 1961). The power of this simple formula stems from the nearly endless number of situations that can be construed as customers waiting for service. For example, if λ is the rate at which a new product enters a certain production stage, and W is the mean time spent per unit in that production stage, then L = λW is the mean work-in-process inventory for that production stage. If λ is the annual number of guns that illicitly enter circulation, and W is the mean time that an illicit gun remains in use, then L = λW is the average number of illicit guns in circulation available for use. If λ is the average number of airplanes that take off each day, and W is the mean time spent airborne per flight, then L = λW is the average number of airplanes in the sky. If λ is the average number of terror plots instigated each year, and W is the mean time spent from the time a new plot is hatched until it is either carried out successfully or abandoned/interdicted, then L = λW is the average number of terror plots currently in the “terror queue” (Kaplan, 2010). If λ is the average number of new intelligence reports initiated each year, and W is the mean time required to research and produce a report, then L = λW represents the expected number of reports currently being produced (or the intelligence work-in-process inventory). If λ is the annual rate of new HIV infections, and W is the mean time following infection during which a newly infected individual would present a result of “recently infected” on a test such as the BED5 assay that specifically tests for evidence
|
5 |
BED is a trademark of Calypte Biomedical Corporation. For more information see http://www.calypte.com/technologies-incidence-testing.asp [accessed October 2010]. |
of recent infection, then L = λW is the average number of persons who can be considered newly infected. Recent research estimating the annual rate of new HIV infections in the United States has turned this logic around by estimating L from samples of HIV-infected persons, and then estimating the HIV infection rate λ by inverting Little’s Theorem (Hall et al., 2008).
Waiting for the Bus (Probability)
Sometimes sampled information can look very different across observers simply because of differences in the physical processes by which data are collected. Imagine observing successive buses on an urban bus line as they arrive at and depart from the same bus stop. Suppose that 8 of 9 waits between successive buses are 1 minute (short gaps), but that 1 in 9 such intervals equals 10 minutes (long gaps). Now imagine a would-be passenger arriving at the bus stop exactly as a bus departs; our poor passenger literally has just missed the bus. What is the probability that this passenger faces a long wait of 10 minutes for the next bus? Clearly the answer equals 1/9, as by construction 1 in 9 of all intervals between buses equal 10 minutes. Now suppose that a second would-be passenger arrives at the same bus stop, but at a time that is random with respect to bus arrivals. What is the chance that this passenger faces a 10-minute gap? The answer is no longer equal to 1/9; the randomly arriving passenger has a 5 in 9 chance of landing in a long gap! The reason is that the chance of arriving in a gap of a given length is proportional both to the frequency with which such gaps occur and the gap duration. Thus, the chance of arriving in a long gap is proportional to (1/9) × 10, while the chance of arriving in a short gap is proportional to (8/9) × 1, yielding the probability of arriving during a long gap equal to (10/9)/(10/9 + 8/9) = 5/9 as claimed. The situation is even odder than this: The first passenger who just missed the bus must wait an average of 1 × 8/9 + 10 × 1/9 = 2 minutes for the next bus, while the second passenger on average waits (10/2) × 5/9 + (1/2) × 4/9 = 3 minutes; on average, a person who just misses the bus in this example faces a shorter wait for the next one than a person who arrives at a random time.
This is an example of what operations researchers call random incidence (or length-biased sampling in statistical parlance). It can explain how different people observing presumably the same phenomenon can see quite different things. For example, if one is interested in studying the progression of persons infected with a disease, one will obtain a different picture by following newly infected persons over time versus sampling ill patients with the same disease in the hospital and following them over time. Similarly, studies of the duration of unemployment spells will reveal quite different results for samples of newly unemployed persons as compared to random samples from persons currently receiving unemployment insurance.
Knapsack Problem (Optimization)
A common optimization problem is to allocate a budget across different activities. For example, given a fixed budget to spend on different healthcare programs, how much money should the government allocate to different care and prevention activities (Stinnett and Paltiel, 1996; Institute of Medicine, 2001)? One model for such problems that yields a practical allocation rule is the knapsack model. In this model, a number of possible activities (or programs) can receive funding. Let bi and ci respectively denote the unit benefits and costs of the ith activity (e.g., each unit could correspond to an incremental employee or facility), and suppose there is an upper limit to the number of units of activity i allowed (e.g., due to program capacity, or perhaps for political reasons that restrict the amount of funds any single program can receive). The goal is to maximize total benefits within a given budget, and the solution is particularly simple. First, rank the activities from the largest to smallest value of their “bang for the buck” ratios bi/ci. Then, allocate the largest amount of money possible to that activity with the highest such ratio (i.e., the smaller of the total budget and the maximum allowable amount). This activity produces the most benefit per dollar among all activities and is thus the most cost-effective means of generating benefits. Next, consider the budget that remains after subtracting the amount awarded to the most efficient program and move to the activity with the second highest bang for the buck ratio. Again, allocate the largest amount of money possible, update the budget, and move to the next most efficient activity. Continue in this manner until either all activities have been fully funded, or the remaining budget is exhausted while funding whatever activity currently ranks as the most efficient (in which case this activity will receive only partial funding). At the end of such an exercise, there will be a set of fully funded activities (those with the largest bang for the buck ratios), a set of activities that receive no funding, and potentially one activity that receives partial funding. Of course, it is possible that partial funding is not possible—constructing half a tank or two-thirds of a bridge, for example, probably has little value. In this case, more sophisticated optimization techniques are available to ensure that all funded activities are fully funded (e.g., integer or dynamic programming [Bradley et al., 1977]).
The most important aspect of this problem is the intuition behind the solution: Allocate resources in order of most to least efficient activities, that is, from the largest to smallest bang for the buck. In the HIV prevention example, this rule says that prevention programs should be funded in order of most to least infections prevented per dollar (Institute of Medicine, 2001). Although resource allocation problems typically are more complicated than the simple knapsack formulation, the principle of securing
funding for more efficient activities and programs before considering less efficient alternatives often provides a good heuristic.
Project Scheduling and the Critical Path (Optimization)
A common problem faced by project managers is to schedule the various activities that must be completed to finish a project. The term “project” can be interpreted quite broadly, with examples ranging from construction projects to fundraising campaigns to weapons development programs to terror attacks. One of the most important questions one can ask is, how long will completing the entire project take?
An easy approach for answering this question that can be implemented by hand for small problems (or with the aid of specialized computer programs such as Microsoft Project for larger ones) is as follows (for a spreadsheet implementation, see Winston and Albright, 2009): First, produce a list of all project tasks that must be completed along with estimates for the duration of each task. Second, for each task, note the “immediate predecessor” activities that must be completed immediately before the task in question can begin. Third, starting with those tasks for which there are no prerequisite activities (and hence can begin at “time zero” when the project starts), determine the earliest time that these activities can be completed. These are “first round” activities, and because their completion does not rely on other activities, their “early finish” times are simply the task durations. Fourth, for each remaining downstream task, the earliest time each task can begin is computed from the formula
Early Start Time = maximum {Early Finish Times}
where the maximum is taken over all the Early Finish Times of the immediate predecessors of the task in question. These Early Finish Times are computed as
Early Finish Time = Early Start Time + Task Duration
Note that the first round activities with no prerequisite activities all have Early Start Times of zero, while the second round of tasks that do have immediate predecessors will have Early Start Times determined from the first of the two formulas above. Applying these steps recursively until all tasks have been addressed yields the duration of the entire project.
This “critical path method” also identifies those activities that, if delayed, slow the completion of the entire project. For project managers, such critical activities are those that must be expedited. Alternatively, in an adversarial situation where one wishes to impede the progress of an enemy
project, delaying a critical activity in, for example, the planning of a terror attack can delay the entire project.
I have presented a highly simplified view of project scheduling that can be made more realistic. For example, task durations are unlikely to be known with certainty; more advanced models treat such durations as random variables, enabling one to compute the probability that a project is completed by a given date. Or, one could focus on cost/completion tradeoffs to examine how quickly one might complete a project given an expedition budget. In the next section, I discuss some applications of project management to intelligence problems.
OPERATIONS RESEARCH FOR INTELLIGENCE ANALYSIS
Operations research shares at least two common features with intelligence analysis. First, as stated in the Intelligence Community Directive (ICD 203) Analytic Standards, intelligence analysts are expected to “… perform their analytic and informational functions from an unbiased perspective” and “independent of political considerations” (Director of National Intelligence, 2007, p. 2). The intelligence analyst does not make decisions, but provides information in support of government (or military) executive decision makers. Operations researchers similarly play the advisory role of unbiased analysts in relation to executive decision makers. Writing about the separation of OR support and executive decision making, Morse and Kimball (1951, p. 2) state, “The requirement that the executive reach a decision concerning an operation is to some extent antagonistic to the requirement that he look at it scientifically and impersonally, as would be required in operations research” (emphasis added). The second shared concern is timeliness; the Analytic Standards directive states “Analytic products that arrive too late to support the work of the consumers weaken utility and impact. Analysts will strive to deliver their products in time for them to be actionable by customers” (Director of National Intelligence, 2007, p. 2). Writing more than half a century earlier, Morse and Kimball (1951, p. 10a) state, “An important difference between OR and other scientific work is the sense of urgency involved. In this field a preliminary analysis based on incomplete data may often be much more valuable than a more thorough study using adequate data, simply because the crucial decisions cannot wait on the slower study but must be based on the preliminary analysis. The big improvements often come from the first quick survey of a new field; later detailed study may only gain small additional factors.”
Given the military origins of OR and both the military and systems aspects of intelligence analysis, it should not prove surprising that operations research has been applied to intelligence analysis on occasion. For example, Caldwell et al. (1961) report on “A model for evaluating the
output of intelligence systems” where the object was to learn the relative contributions of different pieces of intelligence to the overall value of an intelligence assessment. Steele (1989) uses operations research models to illustrate the advantages and disadvantages posed by different communication protocols when the goal is to keep a secret. However, evidence for regular application of OR in intelligence analysis is hard to find. Heuer (1978, 1999), Schum (1987), Schum and Morris (2007), and Zlotnick (1967, 1972) all discuss the use of basic probability models, including Bayes’ Rule, with an eye toward assessing the likelihoods of various events or “states of affairs,” but there is no focus on operations in this otherwise engaging work. Operations ideas are almost entirely absent from intelligence analysis primers distributed by national intelligence agencies (Defense Intelligence Agency, 2008; U.S. Government, 2009). Indeed, in contrast to excellent military resources such as the operations research group at the Naval Postgraduate School6 and the Military Operations Research Society,7 with the exception of focused technical expertise in operations research such as that found at the National Security Agency,8 apparently few operations researchers work within the intelligence community (Defense Science Board, 2009).
Without suggesting that intelligence analysts should master OR, there are opportunities for improving intelligence analysis through appropriate application of operations research. Such opportunities present themselves when intelligence analysts focus on making inferences about adversarial supply chains, weapons development programs, the planning of terror attacks, the distribution of personnel or materiel, or any other operations of interest. Furthermore, as in the application of Little’s Theorem, issues that might not initially pose as operations can sometimes be construed as such. The following examples are meant to illustrate such opportunities for applying OR to intelligence problems.
Example: Producing Nuclear Weapons
The development of nuclear weapons provides an intriguing case study for applying operations research to intelligence questions. In asking whether or not a “proliferator” is pursuing a nuclear weapons program, it is important to understand the possible forms a project designed to produce such
|
6 |
http://www.nps.edu/Academics/Schools/GSOIS/Departments/OR/index.html [accessed October 2010]. |
|
7 |
http://www.mors.org [accessed October 2010]. |
|
8 |
The National Security Agency runs a summer program for operations research graduate students to work as apprentices to operations research and simulation modeling analysts; see http://www.nsa.gov/careers/opportunities_4_u/students/graduate/sport.shtml [accessed October 2010]. |
weapons could take. An OR approach to this problem focuses on identifying the infrastructure tasks necessary for weapons production in addition to the weapons production process itself, and paying careful attention to the necessary sequencing and timing of such tasks. Such project management and scheduling problems can be approached using more sophisticated versions of the critical path method described earlier. Harney et al. (2006) report precisely such a study. The basic scientific information required to design such weapons has been known and publicly available for quite some time (see Office of Technology Assessment, 1993, especially Chapter 4: Technical Aspects of Nuclear Proliferation). Working with this and other sources, Harney and colleagues were able to estimate that, depending on assumptions regarding resource availability (e.g., available budget, whether highly enriched uranium is produced or available immediately [i.e., stolen or purchased]), the time required to complete a first batch of six weapons would be 4 to 6.5 years. In a companion paper (Brown et al., 2009), the same researchers ask which tasks in the project network, if delayed, would maximally set back the weapons development project. Under many different scenarios, the authors identify two bottleneck tasks (“cascade loading” and “acquisition of pumps and piping”) that if interdicted can increase the duration of time to produce weapons by 37 percent if the proliferator is unaware of the interdiction effort (perfect covert action). Even if the proliferator is aware of the interdiction effort and modifies the production process accordingly (as modeled using game theory), interdicting these activities can still delay the overall project by 34 percent. Again, the idea is not that this model tells intelligence analysts the precise state of a proliferator’s nuclear weapons program, but it does suggest which production activities are crucial in the overall development project, and consequently what parameters might deserve a more focused intelligence effort.
Example: Detecting Terror Plots and Tracking Terror Operations
Estimating the size of hidden populations is a common problem across many fields of endeavor. Public health officials would like to know the number of persons newly infected with HIV (Hall et al., 2008), wildlife managers wish to know the size of various animal (Blower et al., 1981) or plant (Alexander et al., 1997) populations, and policy makers and professionals in law enforcement, drug treatment, and public health seek estimates of the number of drug injectors (Kaplan and Soloshatz, 1993; Rossi, 1999; Friedman et al., 2004). Similarly, the unknown number of undetected terrorists (or terror plots) is of great interest to counterterrorism, law enforcement, and homeland security decision makers. Although human intelligence from undercover agents or confidential informants has
been vital in interrupting specific plots (and the lack of such intelligence is an oft-mentioned failure leading up to 9/11), operations research offers an opportunity to estimate the number of undetected terror plots from undercover activity and utilization data. The relationships between the instigation and planning of terror attacks and the use of undercover intelligence agents can be characterized using queueing theory. Viewing terror plots as the “customers” and undercover agents as the “servers,” queueing theory allows one to estimate the number of waiting customers based on the servers’ utilization in a manner analogous to how one might estimate the number of waiting customers in a call center from the utilization of servers there (Kaplan, 2010). An important feature of the terrorist-detection process is that unlike the customers in most service systems, terrorists do not wish to be “served” and will leak false information to throw counter-terrorism investigators off track, while undercover agents and informants make “false positive” mistakes that lead to time wasted in pursuit of false leads (for more on assessing the credibility of human intelligence sources, see Schum and Morris, 2007). The hope is that the use of a model of the form proposed could provide an approach to making inferences about the overall level of terrorist activity from a body of intelligence reports that are otherwise studied only for information about specific individuals of interest. Additional applications that follow from this idea include determining the appropriate amount of resources to invest in undercover intelligence gathering, or evaluating the trade-off between investments in human sources versus improved detection technologies.
A different approach to tracking terror threats that developed recently builds on ideas from probability theory and project management. As reported by Godfrey and Mifflin (2009) and Godfrey et al. (2007), the various activities required to execute a terror attack can be organized in the form of a project network, with careful attention paid to the precedence relationships among tasks and the estimated probability distributions of the durations of each task. Given intelligence assessments regarding the status of different tasks, this TerrAlert model produces assessments of the time remaining until an attack takes place. It also suggests which project tasks to disrupt for maximum delay. To cite the authors, “For example, bombing a factory where we suspect a manufacturing task is being performed is most effective when that task is ongoing, less effective when the task is not yet started (raw materials can be rerouted to a different facility), and ineffective when the task is finished (final product has already been produced and distributed)” (Godrey et al., 2007, p. 354). TerrAlert has been installed at the Defense Threat Reduction Agency and the Office of Naval Intelligence’s Advanced Maritime Analysis Cell, though its current usage status is unknown.
Example: Connecting the Dots
Perhaps the most fundamental problem in intelligence analysis is that of “connecting the dots,” meaning “ … selecting and assembling disparate pieces of information to produce a general understanding of a threat …” (Hollywood et al., 2004, p. xv). Direct application of statistical tools such as data mining to large databases documenting travel or financial transactions invariably suffer from the false positive problem that follows from searching databases in which the base rate of individuals involved in terrorism is extremely low (Hollywood et al., 2009). Even systems oriented specifically for the tracking of terrorists suffer from this low base rate problem. For example, between July 2004 and November 2007, the Federal Bureau of Investigation’s (FBI’s) terrorist threat and suspicious incident tracking system (known as Guardian) received roughly 108,000 reports of potential terror threats and suspicious incidents, yet the FBI determined that the overwhelming majority of these were in no way connected to terrorism (U.S. Department of Justice, 2008). An operations research approach to this problem would begin by constructing deliberately oversimplified models of the current relationship between intelligence data collection and reporting on the one hand, and how seasoned intelligence analysts process such data to generate and test new hypotheses on the other, and evaluate (within the model) the success of this current approach. Only after understanding the current relationship could an attempt be made to employ OR methods to improve the results (to connect more dots within the same resource constraints currently faced). Hollywood et al. (2004) report a research proposal to resolve this issue.
Example: Modeling Intelligence Operations
The production of intelligence analysis can itself be viewed as a process characterized by oft-repeated operations of different types. For example, at the macro level, one can ask whether the “intelligence cycle”—requirements planning, data collection, data processing and exploitation, intelligence analysis and the production of intelligence reports, and product dissemination to government or military decision makers (the “consumers”)—is balanced in the sense that the overall intelligence budget has been divided appropriately among these different activities to maximize the value of intelligence produced by the entire system. For example, the Defense Science Board (2009, p. 31) considered the following potential operations research application with regard to expensive new biometric data collection capability to accompany Unmanned Aerial Systems (UAS): “OR techniques could be used to analyze the capability of the entire ISR9 system to effectively use the contemplated new collection capability and/or understand what additional costs would have
to be incurred. An obvious case in point would be whether or not appropriate investment has been made in the analytical resources (specific skills, recruitment, and training) and dissemination capability needed to handle the volume of new product that would be produced by a UAS investment.”
As another example, consider the allocation of intelligence analysts to different geographic regions of interest, or to different intelligence problem sets. The allocation of workers to tasks forms the basis for a classic OR model known as the assignment problem (Ahuja et al., 1993; Hillier and Lieberman, 2010). Rather than simply assigning a task to the best available analyst on an as-available basis, allocations based on the assignment model should result in better overall matches between intelligence coverage/expertise and analytical tasks. Both this and the prior example show that viewing the very creation of intelligence as a production process could itself prove to be a beneficial yet challenging application of operations research.
REFERENCES
Ahuja, R. K., T. L. Magnanti, and J. B. Orlin. 1993. Network flows: Theory, algorithms, and applications. Englewood Cliffs, NJ: Prentice-Hall.
Aksin, O. Z., M. Armony, and V. Mehrota. 2007. The modern call center: A multi-disciplinary perspective on operations management research. Production and Operations Management 16(6):665–688.
Alden, J. M. 2009. Operations research, the multi-billion dollar profit center. Edelman Awards Gala (pp. 14–16). Hanover, MD: Institute for Operations Research and the Management Sciences. Available: http://www.scienceofbetter.org/Edelman/09edelmanbook.pdf [accessed May 2010].
Alexander, H. M., N. A. Slade, and W. D. Kettle. 1997. Application of mark-recapture models to estimation of the population size of plants. Ecology 78(4):1230–1237.
Bazovský, I. 2004. Reliability theory and practice. New York: Courier Dover.
Bell, P. C., C. K. Anderson, and S. P. Kaiser. 2003. Strategic operations research and the Edelman Prize finalist applications 1989–1998. Operations Research 51(1):17–31.
Blower, J. G., L. M. Cook, and J. A. Bishop. 1981. Estimating the size of animal populations. London, UK: George Allen and Unwin.
Bradley, S. P., A. C. Hax, and T. L. Magnanti. 1977. Applied mathematical programming. Reading, MA: Addison-Wesley.
Brandeau, M. L., F. Sainfort, and W. P. Pierskalla, eds. 2004. Operations research and health care: A handbook of methods and applications. Boston, MA: Kluwer Academic.
Brown, G., M. Carlyle, J. Salmerón, and K. Wood. 2006. Defending critical infrastructure. Interfaces 36(6):530–544.
Brown, G. G., W. M. Carlyle, R. C. Harney, E. M. Skroch, and R. K. Wood. 2009. Interdicting a nuclear-weapons project. Operations Research 57(4):866–877.
Cachon, G., and C. Terwiesch. 2008. Matching supply with demand: An introduction to operations management. New York: McGraw-Hill/Irwin.
Caldwell, W. V., C. H. Coombs, R. M. Thrall, M. S. Schoeffler, and M. Hill. 1961. A model for evaluating the output of intelligence systems. Naval Research Logistics Quarterly 8(1):25–40.
Clemen, R. T., and T. Reilly. 2001. Making hard decisions. Pacific Grove, CA: Duxbury/Thomson Learning.
Dantzig, G. B. 1963. Linear programming and extensions. Princeton, NJ: Princeton University Press.
Defense Intelligence Agency. 2008. A tradecraft primer: Basic structured analytic techniques. Washington, DC: Directorate for Analysis, Defense Intelligence Agency.
Defense Science Board. 2009. Operations research applications for intelligence, surveillance and reconnaissance (ISR). Defense Science Board Advisory Group on Defense Intelligence. Washington, DC: Office of the Under Secretary of Defense for Acquisition, Technology, and Logistics.
Director of National Intelligence. 2007. Intelligence Community Directive (ICD) 203: Analytic Standards. June 21. Available: http://www.dni.gov/electronic_reading_room/ICD_203.pdf [accessed May 2010].
Dyson, F. 2006. A failure of intelligence. Technology Review 109(5):62–71.
Falconer, N. 1976. On the size of convoys: An example of the methodology of leading wartime OR scientists. Operational Research Quarterly 27(2):315–327.
Fisk, C. E. 1972. The Sino-Soviet border dispute: A comparison of the conventional and Bayesian methods for intelligence warning. Studies in Intelligence 16(2):53–62.
Friedman, S. R., B. Tempalski, H. Cooper, T. Perlis, M. Keem, R. Friedman, and P. L. Flom. 2004. Estimating numbers of injecting drug users in metropolitan areas for structural analyses of community vulnerability and for assessing relative degrees of service provision for injecting drug users. Journal of Urban Health 81(3):377–400.
Gass, S. I. 2005. The life and times of the father of linear programming. Operations Research/ Management Science Today 32(4):40–48.
Gass, S. I., and A. A. Assad. 2005. An annotated timeline of operations research: An informal history. New York: Kluwer Academic.
Godfrey, G. J., and T. Mifflin. 2009. Likelihood-based optimization of threat operation timeline estimation. 12th International Conference on Information Fusion, Seattle, WA, July 6–9.
Godfrey, G. A., J. Cunningham, and T. Tran. 2007. A Bayesian, nonlinear particle filtering approach for tracking the state of terrorist operations. Intelligence and Security Informatics, IEEE, May 23–24, pp. 350–355.
Golany, B., E. H. Kaplan, A. Marmur, and U. G. Rothblum. 2009. Nature plays with dice—terrorists do not: Allocating resources to counter strategic versus probabilistic risks. European Journal of Operational Research 192(1):198–208.
Green, L. V. 2004. Capacity planning and management in hospitals. In M. L. Brandeau, F. Sainfort, and W. P. Pierskalla, eds., Operations research and health care: A handbook of methods and applications (pp. 15–43). Boston, MA: Kluwer Academic.
Gross, D., J. F. Shortle, J. M. Thompson, and C. M. Harris. 2008. Fundamentals of queueing theory. Hoboken, NJ: John Wiley and Sons.
Hall, H. I., R. G. Song, P. Rhodes, J. Prejean, Q. An, L. M. Lee, J. Karon, R. Brookmeyer, E. H. Kaplan, M. T. McKenna, and R. S. Janssen. 2008. Estimation of HIV incidence in the United States. Journal of the American Medical Association 300(5):520–529.
Harney, R., G. Brown, M. Carlyle, E. Skroch, and K. Wood. 2006. Anatomy of a project to produce a first nuclear weapon. Science and Global Security 14(2–3):163–182.
Heuer, R. J., Jr., ed. 1978. Quantitative approaches to political intelligence: The CIA experience. Boulder, CO: Westview Press.
Heuer, R. J., Jr. 1999. Psychology of intelligence analysis. Washington, DC: Center for the Study of Intelligence, Central Intelligence Agency.
Hillier, F. S., and G. J. Lieberman. 2010. Introduction to operations research, 9th ed. New York: McGraw-Hill.
Hollywood, J., D. Snyder, K. McKay, and J. Boon. 2004. Out of the ordinary: Finding hidden threats by analyzing unusual behavior. Santa Monica, CA: RAND Corporation.
Hollywood, J., K. Strom, and M. Pope. 2009. Can data mining turn up terrorists? Operations Research/Management Science Today 36(1):20–27.
Hopp, W. J., and M. L. Spearman. 2007. Factory physics. New York: McGraw-Hill/Irwin.
Horner, P. 2000. The Sabre story. Operations Research/Management Science Today 27(3):46–47.
Howard, R. A., and J. Matheson, eds. 1983. The principles and applications of decision analysis (2 vols). Palo Alto, CA: Strategic Decisions Group.
Institute of Medicine. 2001. No time to lose: Getting more from HIV prevention. Committee on HIV Prevention Strategies in the United States. M. S. Ruiz, A. R. Gable, E. H. Kaplan, M. A. Stoto, H. V. Fineberg, and J. Trussell, eds. Division of Health Promotion and Disease Prevention. Washington, DC: National Academy Press.
Kaplan, E. H. 1995. Probability models of needle exchange. Operations Research 43(4):558–569.
Kaplan, E. H. 2010. Terror queues. Operations Research 58(4):773–784.
Kaplan, E. H., and M. Kress. 2005. Operational effectiveness of suicide-bomber–detector schemes: A best-case analysis. Proceedings of the National Academy of Sciences of the United States of America 102(29):10,399–10,404.
Kaplan, E. H., and D. Soloshatz. 1993. How many drug injectors are there in New Haven?: Answers from AIDS data. Mathematical and Computer Modelling 17(2):109–115.
Kirby, M. W. 2003. Operational research in war and peace: The British experience from the 1930s to 1970. London, UK: Imperial College Press.
Larnder, H. 1984. The origin of operational research. Operations Research 32(2):465–475.
Larson, I. Y., ed. 2007. The Operations Research Center at MIT. Hanover, MD: Institute for Operations Research and the Management Sciences.
Larson, R. C. 1972. Urban police patrol analysis. Cambridge, MA: MIT Press.
Larson, R. C. 1987. Perspectives on queues: Social justice and the psychology of queueing. Operations Research 35(6):895–905.
Little, J. D. C. 1961. A proof for the queueing formula L = λ W. Operations Research 9(3):383–387.
McCloskey, J. F. 1987. The beginnings of operations research: 1934–1941. Operations Research 35(1):143–152.
McKinsey, J. C. C. 1952. Introduction to the theory of games. New York: McGraw Hill.
Morse, P. M. 1948. Mathematical problems in operations research. Bulletin of the American Mathematical Society 54(12):602–621.
Morse, P. M. 1952. Operations research, what is it? Journal of Applied Physics 23(2):165–172.
Morse, P. M. 1956. Statistics and operations research. Operations Research 4(1):2–18.
Morse, P. M. 1986. The beginnings of operations research in the United States. Operations Research 34(1):10–17.
Morse, P. M., and G. E. Kimball. 1951. Methods of operations research. Cambridge, MA: MIT Press.
Nobel Lectures, Physics 1942–1962. 1964. Amsterdam, The Netherlands: Elsevier. Available: http://nobelprize.org/nobel_prizes/physics/laureates/1948/blackett-bio.html [accessed March 2010].
National Research Council and Institute of Medicine. 1995. Preventing HIV transmission: The role of sterile needles and bleach. J. Normand, D. Vlahov, and L. E. Moses, eds. Panel on Needle Exchange and Bleach Distribution Programs. Commission on Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Office of Technology Assessment. 1993. Technologies underlying weapons of mass destruction. U.S. Congress, Office of Technology Assessment Report OTA-BP-ISC-115. Washington, DC: U.S. Government Printing Office.
Pollock, S. M., M. H. Rothkopf, and A. Barnett, Eds. 1994. Operations research and the public sector. Amsterdam, The Netherlands: North-Holland.
Porteus, E. L. 2002. Foundations of stochastic inventory theory. Stanford, CA: Stanford University Press.
Pringle, L. 2000. Operations research: The productivity engine. Operations Research/Manage-ment Science Today 27(3):28–31.
Raiffa, H. 1968. Decision analysis: Introductory lectures on choices under uncertainty. Reading, MA: Addison-Wesley.
Rossi, C. 1999. Estimating the prevalence of injecting drug users on the basis of Markov models of the HIV/AIDS epidemic: Applications to Italian data. Health Care Management Science 2(3):173–179.
Rubinstein, R. Y., and D. P. Kroese. 2007. Simulation and the Monte Carlo Method. New York: John Wiley and Sons.
Rushton, A., P. Croucher, and P. Baker. 2006. The handbook of logistics and distribution management. London, UK: Kogan Page.
Schum, D. A. 1987. Evidence and inference for the intelligence analyst. New York: University Press of America.
Schum, D. A., and J. R. Morris. 2007. Assessing the competence and credibility of human sources of intelligence evidence: Contributions from law and probability. Law, Probability and Risk 6(1–4):247–274.
Steele, J. M. 1989. Models for managing secrets. Management Science 35(2):240–248.
Stinnett, A., and A. D. Paltiel. 1996. Mathematical programming for the efficient allocation of health care resources. Journal of Health Economics 15(5):641–653.
Talluri, K. Y., and G. van Ryzin. 2005. The theory and practice of revenue management. New York: Springer Science+Business Media.
U.S. Department of Justice. 2008. The Federal Bureau of Investigation’s terrorist threat and suspicious incident tracking system. Audit Report 09-02. Washington, DC: U.S. Department of Justice, Office of the Inspector General.
U.S. Government. 2009. A tradecraft primer: Structured analytic techniques for improving intelligence analysis. Available: https://www.cia.gov/library/center-for-the-study-of-intelligence/csi-publications/books-and-monographs/Tradecraft%20Primer-apr09.pdf [accessed March 2010].
Walker, W. E., J. M. Chaiken, and E. J. Ignall. 1979. Fire department deployment analysis. New York: Elsevier North Holland.
Wein, L. M., and M. Baveja. 2005. Using fingerprint image quality to improve the identification performance of the U.S. Visitor and Immigrant Status Indicator Technology Program. Proceedings of the National Academy of Sciences of the United States of America 102(21):7,772–7,775.
Wein, L. M., and Y. Liu. 2005. Analyzing a bioterror attack on the food supply: The case of botulinum toxin in milk. Proceedings of the National Academy of Sciences of the United States of America 102(28):9,984–9,989.
Wein, L. M., D. L. Craft, and E. H. Kaplan. 2003. Emergency response to an anthrax attack. Proceedings of the National Academy of Sciences of the United States of America 100(7):4,346–4,351.
Willemain, T. R. 1995. Model formulation: What experts think about and when. Operations Research 43(6):916–932.
Willemain, T. R., and R. C. Larson, eds. 1977. Emergency medical systems analysis. Lexington, MA: DC Heath and Company.
Winston, W. L., and S. C. Albright. 2009. Practical management science. Florence, KY: South-Western Cengage Learning.
Wright, J. N., and R. Race. 2004. The management of service operations. London, UK: Thomson Learning.
Zlotnick, J. 1967. A theorem for prediction. Studies in Intelligence 11(4):1–12.
Zlotnick, J. 1972. Bayes’ theorem for intelligence analysis. Studies in Intelligence 16(2):43–52.


























