2
Key Points Expressed by Presenters and Discussants
2.1 PERSPECTIVES ON COMPUTATIONAL THINKING AND COMPUTATIONAL THINKERS
Workshop participants extended the discussion started at the first workshop concerning the nature of computational thinking and computational thinkers. In offering one perspective, Peter Henderson, formerly chair of the Department of Computer Science and Software Engineering at Butler University, described computational thinking as generalized problem solving with constraints. He argued that almost every problem-solving activity involves computation of some kind. For Henderson, a toolsmith metaphor is a convenient means for characterizing the elements of computer science and also computational thinking—computer science offers sophisticated tools that strengthen problem solving. Henderson illustrated his point using an example from Thomas the Tank Engine—a series for preschool students. In one situation, Thomas is pulling two cars, one red and one green. They are on a track with a siding (connected on both sides), and the problem is to reverse the order of the two cars. This problem engages students in using a computational algorithm at a very early age.
Matthew Stone, a computational linguist at the Rutgers University’s Department of Computer Science and Center for Cognitive Science, argued that core ideas of computational thinking arise in many domains independent of computer technology. Stone pointed out the universality of computational thinking in the context of Jacquard looms that control the weaving of patterns, algorithmic approaches to choosing the grocery
checkout line with the shortest wait time, and representation of correspondences between symbols and the physical world such as between online banking and money.
Robert M. Panoff, founder and executive director of the Shodor Education Foundation, Inc., illustrated the generality of computational thinking by identifying three fundamental ideas that ground computational thinking:
• What you have now is what you had before plus what has changed. That is, Xnew = Xold + change in X.
• I am the average of my neighbors; that is, add up a bunch of numbers and divide by the number of numbers. This is the essence of solving Laplace’s equation.
• When two entities interact with each other, one of the entities acquires with some probability a property that the other entity already had. For example, if the two entities are people and the property is a wallet, there is some probability of a crime—an example found in criminology. If the entities are trees and the property is being on fire, there is some probability that the tree not on fire will become a tree that is on fire—an example from forest management. If the entities are particles and the property is momentum, there is some probability that one particle will acquire some of the momentum of the other particle—an example often found in physics.
Ursula Wolz, associate professor of computer science and interactive multimedia at the College of New Jersey, noted that concepts of computational thinking permeate journalism. The similarities stem from the reliance of both fields on language. Languages can be natural as found in journalism or formal as found in computer science. Both formal and informal languages involve access to information, aggregation of data, and synthesis of information. Concepts of reliability, privacy, accuracy, and logical consistency are essential to both formal and informal languages. Both involve knowledge representation (e.g., determining the appropriate granularity for reporting a story or taking data) and abstraction from cases.
2.2 ACTIVITIES OF COMPUTATIONAL THINKING
Workshop participants extended the discussion of activities associated with computational thinking that had been initiated at the first workshop. During the second workshop participants focused on educationally relevant activities.
Robert Tinker, founder of the Concord Consortium, argued that the
core of computational thinking is to break big problems into smaller problems that lend themselves to efficient, automated solutions. This approach can be implemented using realistic situations as well as visualizations. Tinker advocated introducing computational thinking in science for several reasons. Modern science regularly relies on computational models that are based on scientific principles and are illustrated using visualizations. For example, scientists explore visualizations of new proteins or of new theoretical accounts of tectonic plate movements.
Consulting scientist Walter Allan and outreach education coordinator Jeri Erickson, at ScienceWorks for ME of the Foundation for Blood Research, echoed this point. They argued that the ability to construct rules to specify the behavior of an agent is important to computational thinking. These rules might implement a scientific principle.
Tinker said that he favors exposing students to computational thinking in the context of scientific models and visualizations that depict phenomena in a realistic time sequence. Examples include visualizations of chemical interactions using software such as Molecular Workbench;1 of force and motion; and of plate tectonics. Students can interact with these visualizations, explore their behavior and limitations, and learn about the science represented in the model. This approach is consistent with the way scientists learn from visualizations and also resonates with the ways that scientists explore the natural world using the scientific method.
Mitch Resnick, professor of learning research at the MIT Media Lab, said that the ability to use computational media to create, build, and invent solutions to problems is central to computational thinking. He argued that computational thinkers can express themselves and their ideas in computational terms. He explained that meaningful expression requires developing both concepts and capacities. He pointed out that capacities for design and social cooperation are often neglected in school. Yet the capacity to design solutions has become more important as the world has increased in complexity. Students need the capacity to design solutions to personal problems such as determining energy-efficient home heating solutions. Students also have to be able to communicate their designs to others and to benefit from the expertise of multiple participants. As a result, students need a way to design solutions that are rich enough to cope with complexity and interactivity in a manner often associated with computational expression. And the design environment needs to support social cooperation in constructing meaningful expressions. Advances of these kinds are synergistic—computing technology itself opens up new possibilities for widespread cooperation.
_______________
1 The Molecular Workbench is available at “Molecular Workbench,” website, Concord Consortium, http://mw.concord.org/modeler/index.html. Last accessed February 7, 2011.
Supporting Resnick’s emphasis on social cooperation, Jill Denner—a developmental psychologist with Education, Training, Research (ETR) Associates—noted that students program differently in pairs than by themselves. She found that students in pairs spent more time doing programming and housekeeping tasks (e.g., saving and testing their code) than did individuals working alone. She observed that most students find programming in pairs highly motivating. When they collaborate students need to develop the ability to communicate concepts. Similarly, Idit Caperton, founder of the World Wide Workshop,2 described the supports in the Globaloria approach for collaboration and community. Globaloria participants develop original games and publish them on a community Wiki. Participants in the Globaloria community—teachers, students, staff, and teams—all maintain public blogs as design journals, share resources, and build on the products of their peers.
Danny Edelson, director of the National Geographic Society’s Geo-Literacy Program, argued that systems thinking is an essential activity of computational thinking. Edelson drew insight from his work in promoting geo-literacy. He noted that geo-literacy calls for a systems view of the world—an understanding of the world as a set of interconnected human social systems and physical environmental systems—and that computational thinking about complex problems calls for a similar understanding.
Jim Slotta, a professor at the University of Toronto’s Ontario Institute for Studies in Education, echoed the point that understanding complex systems requires computational thinking. He mentioned a Web-based Inquiry Science Environment (WISE)3 unit that uses scientific visualizations of global climate change to engage students in reasoning about how their own activities affect the accumulation of carbon dioxide. He noted that the visualizations were designed by Robert Tinker using NetLogo, a language created by Uri Wilensky.
2.3 CONTEXTS FOR COMPUTATIONAL THINKING
Most workshop participants echoed the notion articulated in the first workshop that the power of computational thinking is best realized in conjunction with some domain-specific content. Thus, to understand the human genome, individuals need to combine computational thinking and concepts in genetics. The diversity of possible contexts in which computational thinking applies illustrates its power. Computational thinking
___________________
2 Globaloria is available at “Globaloria,” website, World Wide Workshop, http://www.worldwideworkshop.org/programs/globaloria. Last accessed February 7, 2011.
3 “Web-based Inquiry Science Environment,” website, University of California, Berkeley, http://WISE.berkeley.edu. Last accessed February 7, 2011.
occurs in a vast array of domains. Developing expertise in computational thinking involves learning to recognize its application and use across domains.
Many participants provided examples of the use of computational thinking in everyday situations. Troubleshooting devices such as computers, cell phones, and digital cameras involves knowing how to return to a known state (typically by turning the device off and restarting) or test boundary conditions (such as interactions between two applications).
Joyce Malyn-Smith, strategic director of the Workforce and Human Development Program for the Education Development Center, Inc., noted that today’s youth carry their technological learning environment continuously in the form of cell phones, computers, and gaming devices. Schools are finding ways to engage students in using their devices to advance learning such as by having them take digital photos for science projects. After school, students bring their devices to community-based programs where they can engage in science inquiry and to museums where they play with exhibits. Taylor Martin, an associate professor of education at the University of Texas at Austin, supported this point, arguing that schools and after-school programs can exploit computational tools such as Facebook.
Lou Gross, at the University of Tennessee and also director of the National Institute for Mathematical and Biological Synthesis, emphasized the value of incorporating a computational worldview into the everyday experiences of students. To illustrate, Gross described an everyday problem—how to pick a checkout line at a grocery store. Gross asked participants to generate parameters that might affect one’s decision. Workshop participants suggested line length, the presence or absence of a bagger, someone writing a check, the number of items in a person’s cart, and whether the line is an express line. Gross pointed out that high school students often include the presence or absence of someone cute in the checkout line, thus illustrating the point that the criteria for decision making depend on the nature of the model involved and its purpose.
A number of participants described game playing and game development as activities well suited to developing computational thinking. They stressed the importance of games that involve domain-specific ideas such as simulations of political situations.
Jill Denner argued that the programming of computer games connects
to computational thinking in several ways. Computer games provide a context for the modeling of abstractions. For example, students might program a model of their make-believe world, create variables and new methods, and think at multiple levels of abstraction. They might consider how a player will interact with the game or conceptualize the goal of the game.
Idit Caperton argued that it is possible to learn any subject and to master complex topics or social issues by creating functional, representational, educational multimodal computer games in that domain. The Globaloria environment supports the collaborative development of games and also provides an opportunity for students to play each others’ games. For example, Globaloria provides a unit on game design, in which students design an original game about a complex topic (science, math, health, civics) and a social issue that matters to them. Students come up with an idea, assemble teams, and do research. Another Globaloria unit focuses on game development: students develop original game concepts, create prototypes, and produce a complete, playable interactive game. Each unit contains a structured set of learning topics, and each topic contains projects and assignments for students to complete. Assignments scaffold4 students to create critical parts of their own games.
Robert Tinker advocated the use of simple models of physical phenomena such as temperature, light, and force to teach computational thinking. He described activities in which students use temperature probes to capture data and use graphing programs to develop a model to explain their data. A student makes progress by manipulating and refining the model to reflect increasingly sophisticated understanding of the scientific concepts. The student learns both about the physics of the phenomena and about computational thinking.
John Jungck, at Beloit College and also founder of the BioQUEST Cur-
___________________
4 According to Susanne P. Lajoie, 2005, “Extending the Scaffolding Metaphor,” Instructional Science 33:541-557 (https://www.tlu.ee/~kpata/haridustehnoloogiaTLU/scaffoldinglajoie.pdf; last accessed May 20, 2011). “The term ‘scaffolding’ was used by Jerome Bruner (Wood et al., 1976) to describe the process in which a child or novice could be assisted to achieve a task that they may not be able to achieve if unassisted, until they are able to perform the task on their own. This definition was influenced by Vygotsky’s (1978) conception of the zone of proximal development which is ‘the distance between the actual developmental level as determined by independent problem solving and the level of potential development as determined through problem solving under adult guidance or in collaboration with more capable peers’ (p. 86). The implication is that individuals have learning potential that can be reached with scaffolding provided by tutors, parents, teachers, and peers.”
riculum Consortium, explained the interconnections between computational thinking and biology and described activities that engage students in linking the two. He pointed out that modern biology is essentially an information science. Today, biological data—environmental data and genomic data, for example—is multivariate, multidimensional, and multicausal, and it exists at multiple scales in enormous volume (increasing at terabytes of data per day). He noted that in BioQUEST,5 students pose original problems, iteratively apply computational thinking to solve those problems, and persuade their peers that their solution is useful and valid. For example, in one activity students pose problems about evolutionary similarities among genes. Using powerful databases they can align multiple sequences of the same gene from different organisms onto one three-dimensional structure. They iteratively refine their representation to illustrate evolutionary conservation across organisms. They use their representation to clarify the comparative biology of sequences in terms of structure, function, and phylogeny.
Walter Allan and Jeri Erickson described computational thinking in ecology and environmental science using a modeling approach. Using simulations to address topics found in the curriculum, they created activities to help students understand complex systems. For example, their Runaway Runoff simulation called for students to conduct experiments on phosphorus pollution using a simulated lake ecosystem.6 This simulation depicts a lake ecosystem, with fish, zooplankton, and algae that are visible to students as well as bacteria that are invisible to students. Students conduct experiments to develop a food web for the ecosystem. They examine the contents of the digestive tracts of the trout and zooplankton to see how changes in phosphorus affect the populations in the lake and the concentration of dissolved oxygen. They predict the impact of increasing levels of phosphorus on the different populations of fish and zooplankton.
Allan and Erickson explained that the activity scaffolds students to follow a cognitive pattern. This pattern features the same iterative refinement approach described by Jungck. Students start by making a prediction about how a system works. They use a simulation for testing, tinkering, and playing. They record their observations, refine their model of how the system works, and make further predictions. They summarize their findings in essays or posters that describe how runoff affects lake
___________________
5 BioQUEST Curriculum Consortium is available at “BioQUEST,” website, BioQUEST Curriculum Consortium, http://bioquest.org/. Last accessed February 7, 2011.
6 A sample student worksheet from the project can be seen at “Runaway Runoff Exercise 1: Who’s Who,” Worksheet, available at http://simbio.com/files/EBME_WSExamples/RunawayRunoff_WkSh1_example.pdf. Last accessed February 7, 2011.
ecology. These artifacts show that the students learn to make fairly sophisticated models of the lake ecosystem.
Allan and Erickson also described how they implemented this pattern in the “Program a Bunny” environment. In this environment, the bunny is an agent that the student programs to find and eat carrots in a field. The environment is probabilistic, so that carrots are not always located in the same places in the field. A program for a successful bunny must account for the randomness in the bunny’s environment. Students can test different programming strategies in a number of increasingly complex scenarios and refine their program. The initial “out of the box” solution is, by design, inadequate for bunny success. Thus, students must learn to modify the program. Modification of the program initiates a cognitive cycle similar to that of the Runaway Runoff simulation involving iterative refinement. The student observes the bunny’s success in finding carrots, develops a model of how the program works, and then thinks of another modification that is intended to further improve the bunny’s performance.
Lou Gross illustrated ways to use environmental science as a platform for computational thinking. Beginning with an aerial image of Washington, D.C., from Google Earth, students are asked, How would you describe this image? After listing typical topographic features such as buildings, roads, and trees, students eventually describe the image by saying how much of the image is this color or that color, how much is made up of buildings, how much of roads, and so on. Gross described these observations as the basis for describing the image as a vector where the components consist of the fraction of the image that is of each type. One interpretation of this vector is that it represents a probability distribution of the landscape for a discrete number of components. Students are scaffolded to realize that spatial aspects of the image are not included in the vector description. They explore how some large-scale temporal variations (such as the growth of cities) could be captured by a time-varying vector. This activity prepares students to use prepackaged software to take advantage of computational methods for looking at change across a landscape, e.g., coupling between an image, a dynamically changing vector, in this case a bar graph, and then an overall descriptor.
Danny Edelson showed how geography and earth science involve computational thinking. Edelson described some of the issues that arise for students learning to understand geographic data:
• Continuous versus discrete data sets. Students learn about the issues in transforming a map from a continuous representation to a map represented in discrete pixels or cells. They can articulate all the positive and negative implications of each representation and learn how the representation affects the results of their data analysis.
• Color representations of temperature. Students explore the implications of using color to represent temperature on a map. For example, although it makes physical sense to subtract two temperatures (e.g., January’s temperature from July’s temperature), it does not make much sense to subtract yellow from red. Color representations on the map cannot be manipulated in the same way as the underlying physical parameters. To resolve the paradox, students need to realize that temperature maps consist of regular arrays of numerical data. They can be transformed into colors, but their underlying mathematical character is maintained.
• Boolean operations. Boolean operations are key analytic tools for interpreting maps. Students gain insight into Boolean operations by testing and refining solutions to problems. For example, to analyze geographic data students might be asked to find counties in the United States whose African American population exceeds the Caucasian population.
• Spatial relationships as specifications of sets. In working with geographic data, a student might want to find the intersection of two regions on a map, where the regions are specified according to some nonspatial criteria. Managing such operations intellectually calls for thinking about them as combinations in one sense and as spatial entities in another sense.
• Satisfaction of multiple constraints in problem solving. Students might be asked to locate a power plant in areas that are both accessible to railroad transportation and close to large bodies of water. Students learn how to use logic tools to locate specific geographic features.
Robert Panoff advocated teaching computational thinking through computational science, in part because this approach develops metacognitive skills or the ability to monitor understanding of computational results. Panoff drew on quantitative reasoning and multiscale modeling to illustrate various anomalies in how people conceptualize quantity. Examples include:
• Inconsistent and faulty intuitions about numbers. Many people believe that two-fifths (2/5) is a small number, whereas 40 percent feels like a large number to them. Panoff noted that one metropolitan police department assigned more officers to patrols on Friday and Saturday night because a careful analysis of the data showed that just under 30 percent of car break-ins were on either a Friday or a Saturday night. Since 2/7 is 29 percent, the frequency of car break-ins was actually consistent across weekdays and weekends!
• Representations of numbers in computational media. In principle, the arithmetic expression given by 355/113 – 101/113 – 101/113 – 101/113 – 52/113 should equal zero. But when the expression is evaluated on most calculators, a non-zero result is obtained. Because most students realize
that “something’s not right” when they are confronted with this expression, such a realization can be the beginning of a serious exploration of how numbers are represented in a computer.
• Interpretation of orders of magnitude. Panoff noted that many people have difficulty recognizing the degree of precision necessary to make an inference. He illustrated the point by asking what a student needs to know in order to answer the question, How much bigger is Earth than Pluto? An obvious way to approach this problem is to perform Internet searches for the mass of Earth and the mass of Pluto. But an Internet search for the mass of Earth generates 20 or 30 different values, which have a spread of several percent. How does one know which value to use or how to proceed? Here context matters—why is one asking the question about relative sizes? If the question relates to how big an object has to be in order to be a planet, then in the absence of a formal definition of “planet,” one needs to know only that the ratio MEarth/MPluto is on the order of a few hundred—and a difference of “several percent” is simply irrelevant to knowing which value of MEarth to use.
Christine Cunningham, vice president at the Museum of Science, Boston, described engineering as a focus of computational thinking for elementary education. Echoing discussions from the first computational thinking workshop, she pointed to intellectual parallels between computational thinking and solving engineering problems. Cunningham stressed that understanding engineering habits of mind and mental processes is an important goal of elementary science. She illustrated how these habits of mind require important aspects of computational thinking. Cunningham identified 20 topics that are commonly covered in elementary science programs, paired each with an engineering specialty, and illustrated the pairing with a particular technological device or process. For example, environmental engineering can be introduced using water filtration devices to help students understand the human impacts on the water cycle. In another example, a solar cooker can illustrate principles of energy and connect to sustainable engineering.
Ursula Wolz described the use of the language arts and journalism as a vehicle for exploring computational thinking. She argued that insights into computational thinking can come from comparing the precision of computer languages to the challenges of precise communication in journalism using natural language. Journalism involves principled storytell-
ing and information dissemination. Journalism students are constructors of aggregated content (rather than just consumers). To produce a story, students must inquire, create, build, invent, iterate on the account, polish, and publish. Wolz emphasized that students iterate on defining the problem, researching it, drafting a solution, and testing it. They copy edit and fact check. In the end, they publish and get more feedback. All of these same notions arise in other instances of computational thinking.
2.3.6 Abstracting Problem Solving from Specific Contexts
Given the diversity of contexts discussed and even the diversity of problems within a single context, a number of workshop participants discussed the use of computational thinking across contexts or topics. For instance, several noted that individuals were likely to need different (though overlapping) sets of computational thinking skills. Thus, physicians need to learn how to use visualization tools, as do teachers. Joyce Mayln-Smith of the Education Development Center suggested that the computational thinking abilities needed by users of information technology tools and applications are different from those needed by producers or developers of such tools and applications. Consequently, the pedagogical approaches needed for developing these skills must be suited to the goal.
Michelle Williams, assistant professor of science education at Michigan State University, made a similar point, arguing for helping students and their teachers recognize that the computational thinking skills they use to make sense of representations of scientific knowledge work for multiple representations. Williams showed how a WISE project can scaffold students to use computational thinking skills as they engage with a number of computer-based representations. In her project students used simulations of mitosis to understand phases of cell division, and Punnett squares to determine the genotypes and phenotypes of different generations of plants, and they interacted with the Audrey’s Garden animation7 to make distinctions between inherited and acquired traits.
_____________________
7 See “Case of Audrey,” website, Exploring Younger Children’s Understanding of Heredity, http://education.msu.edu/research/projects/nsf-heredity/curriculum.html. Last accessed March 14, 2011.
2.4 PEDAGOGICAL ENVIRONMENTS FOR COMPUTATIONAL THINKING
2.4.1 Foci for Pedagogical Environments
Many presenters stressed that interactive visualizations or simulations are at the heart of computational thinking. This perspective cut across multiple disciplines. For example, John Jungck argued that the key to computational thinking in a biological context is in the power of visualization. Robert Tinker stressed the value of visualizations in simple models of scientific concepts such as temperature, light, and force to teach computational thinking. (See Figure 2.1.) Danny Edelson argued that Earth models are best understood in terms of dynamic and spatial models, and he illustrated the point using a NetLogo model for infiltration and runoff processes in a region in the presence of precipitation. Jim Slotta pointed to visualizations of global climate change. Michelle Williams emphasized visualizations in understanding genetic inheritance. Mike Clancy, senior lecturer in the Department of Computer Science at the University of California, Berkeley, suggested that the causal relationships depicted in models are similar to the causal relationships entailed in understanding what a computer program actually does in execution, so that, for example, a student needs to understand what causes a program bug or a program to perform in a certain way.
A second focus for pedagogical environments is the modeling and troubleshooting of data sets. For example, Robert Panoff noted the importance of understanding limitations in the underlying data. Danny Edelson noted that anomalous data often catch people’s attention and generate a teachable moment by motivating them to understand the cause of the anomaly. Panoff stated that even experts sometimes miss anomalies. Uri Wilensky of Northwestern University stressed the advantages seen when students collect data themselves and then use those data to try to fit models to those data, rather than using data provided by others. Christina Schwarz of Michigan State University illustrated how students benefit from iteratively refining their models of data they collect.
A third focus is searching for patterns in large data sets. John Jungck illustrated the forms of computational thinking students use to explore, analyze, interpret, and synthesize massive amounts of biological data. Similarly, Stephen Uzzo, vice president of technology at the New York Hall of Science, pointed out that e-science, which focuses on managing, modeling, and making discoveries in massive amounts of captured data, seeks patterns, dynamics, influences, and complex and emergent behav-
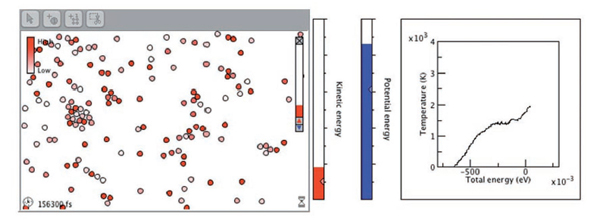
FIGURE 2.1 Molecular Workbench example—one step in integrating computational thinking into science. A learning progression for using computational thinking in science might start with learning that numbers are associated with physical properties like temperature, and end by having students create computational models of these properties. Along the way an important step is using computational models and seeing that these models are influenced by parameters. This figure is a snapshot from a Molecular Workbench (http://mw.concord.org/modeler) molecular dynamics model of phase change showing a liquid-gas mixture on the left that has been heated by adding kinetic energy until it is almost all gas. On the right, a graph of average per-atom kinetic energy against total energy shows a distinct plateau where all heating ended up increasing the potential energy, which resulted in pulling the atoms apart. Students can explore the effect on the liquid-gas transition temperature by changing the strength of attraction between atoms by using molecules and changing their number.
ior in whole systems.8 The computational thinking needed to engage in e-science addresses, among other things, complexity; data visualization; network science (that often results in theoretical generalizations); data interoperability, data sharing, and other collaboration skills; and the use of semantics for searching or creating more effective data structures.
2.4.2 Illustrative Pedagogical Environments
Workshop participants illustrated the potential of pedagogical environments for scaffolding learning, supporting iterative refinement, and enabling students to use visualizations or large data sets. Several alternative approaches were described.
• WISE (the Web-based Inquiry Science Environment). Jim Slotta described how WISE is designed to provide scaffolding for inquiry activities in science classrooms. WISE guides students to engage in computational thinking using scientific visualizations, simulations, models, complex data, or long-term projects. A typical WISE project might engage students in designing solutions to problems that require computational thinking (e.g., design a desert house that stays warm at night and cool during the day using simulations of the day/night cycle and other resources), debating contemporary science controversies using a variety of evidence (e.g., the causes of declining amphibian populations using systems thinking), critiquing scientific claims based on modeling (e.g., arguments for the occurrence of global climate change), or conducting virtual experiments (e.g., exploring a simulation of airbag deployment and studying factors such as velocity and driver height). Tools and interactive materials provided in the WISE environment support collaborative activities and cognitive guidance to promote reflection and critique.
• Scratch. Mitch Resnick described a computational environment called Scratch for facilitating individual expression. The MIT Media Lab developed Scratch as a companion to an online computational thinking community to help engage people in creative learning experiences and to facilitate creative thinking. A graphical programming language, Scratch gives its user the ability to build programs by snapping graphical blocks together. The blocks control the actions of different dynamic actors on a screen. This approach to program construction enables users to avoid issues of syntax and other details that often distract them from the critical processes of designing, creating, and inventing. Using Scratch, it is easy to engage in iterative refinement. Scratch also facilitates social cooperation
_____________________
8 See, for example, Defining e-science, website, U.K. National e-Science Centre, http://www.nesc.ac.uk/nesc/define.html. Last accessed February 7, 2011.
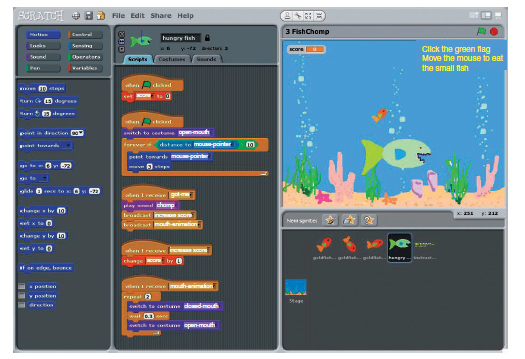
FIGURE 2.2 Scratch programming example—a screen-shot of a game made in Scratch. The goal of the game is to maneuver the big fish to eat the small fish. The programming scripts for the big fish are in the middle panel of the screen-shot. This program highlights several concepts, including the idea of an algorithm (e.g., iteratively point toward the mouse-pointer and take a few steps toward it); computational concepts like variables (shown in the “score” variable); and computational practices like modularization and abstraction (shown in the scripts for “increase-score” and “mouth-animation”). The graphical nature of the Scratch programming language makes it easier to focus on computational concepts and practices without worrying about syntax issues (which have no conceptual value). Also, the nature of the Scratch interface makes it easy to build up scripts in an incremental, iterative style aligned with modern software development practices.
by making it very easy for a user to share his or her design with others for comment and feedback. (See Figure 2.2.)
• Storytelling Alice. Storytelling Alice is a programming environment designed to motivate a broad spectrum of middle school students to learn to program computers through creating short three-dimensional animated movies.9 Jill Denner engages students with a use-modify-create approach. First, students play other students’ Alice games and work through three
___________________
9 Caitlin Kelleher, 2007, “Storytelling Alice,” website, Alice.org, http://www.alice.org/kelleher/storytelling/. Last accessed February 7, 2011.
tutorials that illustrate how to program with Alice. The goal of the “use” phase is for students to learn about the Storytelling Alice interface and the kinds of games that they might make. Second, students learn to modify an existing game through a series of graduated self-paced challenges. The goal of the “modify” phase is to understand the mechanisms that they will use to program a game. Third, a student creates an original game using the language. Students work with specific computational thinking concepts such as event handling, parallelism, additional methods, parameters, alternation, iteration, and conditional execution, and many of Denner’s students created their own methods and used parameters that illustrate the use of modeling and abstraction.
• Globaloria. Idit Caperton described Globaloria as a project-based learning environment for stimulating computational thinking, creativity, and inventiveness in youth and educators. Globaloria supports project-based, multidisciplinary, innovative and creative learning (of any subject) through software design and programming. Globaloria emphasizes six abilities, including the ability to program an educational game, wiki, or simulation; to use project management skills in developing programmable wiki systems in a Web 2.0 environment; to produce animated media and to program, publish, and distribute interactive purposeful digital media in social networks; to learn in a social constructionist manner and to participate actively in the exchange of ideas and artifacts; to undertake information-based learning, search, and exploration as they relate to the abilities above; and to surf websites and use web applications thoughtfully as they relate to the earlier abilities enumerated. (See Figure 2.3.)
Many presenters testified to the pedagogical value of features found in the environments described above. Panoff, Tinker, and Jungck, among others, stressed the importance of supporting iterative refinement. Denner, Caperton, Gross, Resnick, and others described sequences of activities that culminated in complex projects.
2.5 DEVELOPMENTAL CONSIDERATIONS AND COMPUTATIONAL THINKING
An important issue for many workshop participants was the development in novices of facility with computational thinking. Presenters offered varied perspectives on how computational thinking might develop and on what constraints should be considered. Those favoring project work generally argued that students working collaboratively on a compelling problem could use much more advanced forms of reasoning than teachers might expect. Others argued that young children have some impressive capabilities but also some very serious limitations.

FIGURE 2.3 Globaloria example—a depiction of the Globaloria learning environment, where students develop computational thinking skills through team design and creation of computer games. Students are tasked with using Web 2.0 tools and media in developing various games on topics such as health, civics, and science.
Robert Tinker noted that because students begin as concrete thinkers, it remains a challenge to identify the age or grade level at which children can handle abstraction. As an example, he said that second graders can hook up a probe to measure temperature and understand how the device works. Fourth graders can demonstrate reliable interpretations of heating and cooling curves and use the results to gain understanding of abstract principles. Even adults, however, often have difficulty with concepts such as thermal equilibrium or insulation. He reported on studies showing that even well-educated scientists were not sure about the value of wrapping a cold drink in a sweater to keep it cold.
The workshop participants argued that many theories of learning are relevant. Participants mentioned theories of multiple intelligences, knowledge integration, experience-based learning, how novices and experts learn, and how groups learn.
2.5.1 Development of Scientific Thinking in Children
Deanna Kuhn, a developmental psychologist at Columbia University, spoke about the evolution of young learners through different intellectual stages with respect to scientific thinking. She focused on how they use data and evidence and on their facility with scientific thinking.
For Kuhn, the first accomplishment of development involves accepting the possibility of false belief. The child must conceive of data as possibly not representing the complete reality. Very young students can recognize simple covariation in causal models; that is, Did A cause O? in simple cases. But they have difficulty with covariation in a multivariate context (e.g., Which A caused O?) or a negative antecedent and outcome (e.g., Not A and O). Such students often interpret data in isolation and do not look for large patterns.
Kuhn pointed out that although young children can do fundamental experimental design, they often close their inquiry prematurely. Premature closure sometimes occurs when children are presented with confirming evidence. Children often stop the inquiry at this point, not realizing that the inquiry remains unfinished and that confirming evidence is not sufficient to rule out competing hypotheses. Mitch Resnick noted that even adults identify one cause (of potentially many) and assume that a partial inquiry is completely explicative.
Although young children can successfully employ some of the intellectual skills of scientific thinking, they can have a hard time articulating how they know something. In particular, they do not understand the epistemological difference between claim and evidence. For example, looking at a photo of a boy standing on an award podium with a sign labeled with the number “1” and holding a trophy, a child is asked, “How do
you know that this boy won the race?” A child will often answer not with evidence of how she knows (e.g., “He is holding a trophy or the podium has a number 1 on it”) but with a theory of why the outcome makes sense (e.g., “His sneakers were fast”).
Students as old as 12 sometimes focus on evidence and data fragments that support their story, while ignoring or minimizing those that do not. For example, in explaining what causes an avalanche, a student may report that in case A, it was the slope angle that caused an avalanche. Yet the same student will claim that in case B, the slope angle did not make a difference because the slope angle was small and something else caused the avalanche. These students are having trouble distinguishing between a variable and a variable’s magnitude. The educational challenge at this level is to help the child see the data as evidence rather than as an example of a favored claim. Kuhn argues that when a child develops a sort of meta-awareness (control) over this sorting and attribution process, true scientific thinking can begin. Several participants noted that even graduate students sometimes ignore contradictory evidence and focus on supportive evidence.
Jill Denner reported on several lessons learned from her research. For example, she pointed out that individual differences matter a great deal, because individual students have different starting levels, willingness to fail, and motivations. Students are sometimes more comfortable, sometimes less, with the idea of following step-by-step instructions to carry out a task. Some students are more afraid than others to fail and thus are unwilling to tackle problems that entail the risk of failure (e.g., of using a concept incorrectly). Denner found it necessary to balance student engagement on a problem with motivating students to learn more complex or difficult concepts needed for their programs.
Denner also pointed out that students with poor reading skills face special challenges. Although the challenges of modifying programs are a good way to ease into game programming, understanding an existing program is a text-heavy exercise and thus is difficult for English-language learners and students who have reading difficulties.
As a preliminary point, a number of workshop participants felt that it is often possible to get students to use even advanced computational thinking without invoking the use of that term. For example, Robert Panoff argued that once students are thinking about a leaky bucket as a time and rate problem, they are in fact doing calculus. When they take the difference between two things and divide by the interval between those two things, they are taking derivatives. When they’re averaging,
they are doing integration. Panoff’s philosophy here is to help students break a big problem into smaller problems and let the computer do the small parts—a process that helps to empower students. Taylor Martin argued that educators could see this approach as being a “sneaky” way to get students to use computational reasoning. Once engaged, students continue to use computational thinking and even begin to see its applications across contexts.
As a point of departure for considering learning progressions, Joyce Malyn-Smith proposed a sequence:
• Grades K-4, to focus on computational thinking literacy, career awareness, and computational thinking skills for learning. An overarching theme in this time frame might be the lesson that learning is cumulative—a student can learn more by building on something he or she already knows.
• Grades 5-8, to continue to address computational thinking literacy but add career exploration and learning about computational thinking skills for various careers in science, technology, engineering, and mathematics (STEM). This exploratory phase would offer students an opportunity to test their interest in various careers.
• High school, a final preparatory phase, to prepare students to have the credentials to be able to keep doors open so that they can move into computing careers and careers in other STEM fields in which computational thinking will give them really strong opportunities.
Others, including Panoff, Allan and Erickson, and Denner, proposed looking at a learning progression for the development of computational thinking by applying the use-modify-create continuum over and over again. For example, a student first runs a model to see what happens. Then she may modify it by moving a slider bar, or two or three slider bars. And then she may change the number of slider bars. Finally, she writes a model that calls for the use of slider bars to change parameters. By iterating on this pattern, the student gains progressively more capabilities in the area of computational thinking.
Peter Henderson would start with computational thinking activities involving pattern recognition and naming in pre-K, although for the first several years, the term would not be introduced explicitly. Only later would the notion of computational thinking be explored as such. In this sequence, traditional mathematics, discrete mathematics, and logical reasoning are taught at all grade levels. This has important implications for high school, where an advanced placement (AP) course in discrete mathematics would replace the current AP course in computer science. A freshman discrete mathematics sequence would be introduced, similar to
that currently present for calculus. This approach would allow students to link mathematics and science following the traditional engineering educational model. This model emphasizes the connections across the science and math foundations of the disciplines (e.g., physics, chemistry, calculus). Clancy pointed out that this approach could also apply in college course sequences.
2.6 ASSESSMENTS FOR COMPUTATIONAL THINKING
Many workshop participants stressed the importance of student evaluation for pedagogical purposes. For example, Christine Cunningham pointed out that both teachers and students in the Museum of Science’s Engineering is Elementary project pay much more attention to material when student understanding of such material will be evaluated. She cautioned that narrow goals for evaluation are counterproductive. Students and teachers need to appreciate the links among topics, and goals for courses need to acknowledge these dependencies. If students and teachers know that an evaluation will involve student knowledge of, for example, looping, they proceed to learn and teach looping. However, if teachers and students realize that an evaluation will involve student knowledge of program design, and knowledge of looping helps students understand program design, both students and teachers are more likely to connect looping and program design.
To evaluate the connections and interdependencies in computational thinking in introductory programming courses, Mike Clancy uses a case study approach and lab-centric instruction. A case study is a worked-out solution accompanied by a narrative of how the solution was identified. The narrative discusses design tradeoffs, evidence for alternatives, methods for testing the solution, debugging, and other issues such as optimizing. Students respond to questions that require them to consider new alternatives, critique design choices, develop test suites, and interpret results of tests conducted by others.
Lab-centric instruction emphasizes hands-on lab hours supervised by a teaching assistant rather than lecture and discussion. But because there is more lab time than in most lecture/discussion courses, the course has room for a number of embedded assessment activities. Lab instructors can also monitor most of what the students are doing, and have a window into much of their thinking and not just their finished work. Thus lab instructors can notice confusion when it occurs and address it immediately to provide targeted tutoring. Clancy reported that students in lab-centric courses are less likely to drop the course, possibly because their confusions are caught before they become too burdensome.
2.7 TEACHERS AND COMPUTATIONAL THINKING
Teaching computational thinking requires both knowledge of the discipline and skill in teaching when students collaborate to solve complex problems (sometimes referred to as pedagogical content knowledge). John Jungck argued that the primary challenge for teachers of computational thinking is placing student interests at the center of problem posing. In courses where students pose and solve problems teachers lose much of the control they traditionally have over the learning process and may become uncomfortable. They need new skills to guide individual learners. Supporting students engaging in self-directed collaborative processes requires an ability to diagnose difficulties and give hints rather than supplying solutions. Designing effective assignments is also challenging, but many programs such as BioQUEST offer excellent options.
Michelle Williams stressed that to be effective, teachers have to understand where students are starting. Further, teachers need to determine the types of understandings that students must have to be successful and to design new ideas or computational activities to provoke students to engage in computational thinking.
Jungck noted that students in some cases may have more technical skills than their teachers in the area of using computers. Williams pointed out that teachers often find ways to make individual students class “experts” on troubleshooting the operating system or accessing online materials to take advantage of available technical skills. Williams also noted that teachers need professional development to become proficient in teaching computational thinking. In her work she found that teachers followed a learning progression, becoming more proficient over time in using technology and guiding students with inquiry questions. Thus teachers of computational thinking may well be called on to assume new and unfamiliar roles in the classroom and need support to become proficient in performing these roles.
Cunningham argued for the importance of building on what teachers know or feel comfortable doing. It is well known that many elementary school teachers are uncomfortable with science because of their limited preparation in this area. Cunningham argued that engineering (and presumably computational thinking) is even more terrifying. To build on what teachers know, Cunningham and colleagues begin their professional development by connecting exercises in literacy—an illustrated storybook for children—with engineering. The story has significant engineering content, but it is presented as a reading exercise so that teachers can use established skills to lead their classes. Students receive a very general introduction to engineering and to some computational thinking concepts from the book. The book provides context for the hands-on engineering activities that the kids will be doing in their classes.
2.7.1 Professional Development and Other Needs for Teacher Support
Participants described a number of alternative views concerning methods and models for professional development. Cunningham suggested starting small. Teachers tend to be more willing to invest a couple of class periods to experiment with a new concept, rather than an entire school semester or year. The success of one individual teacher with a particular concept or topic can catalyze others, as his or her students tell their friends about an interesting new experience in class. Other teachers also hear about such a program and often want to try it themselves. These efforts build grassroots support for change.
Jim Slotta agreed that teachers are more willing to use materials for a short period to see if their students benefit from a particular approach. He described the experience of the Technology-Enhanced Learning in Science (TELS) center, where teachers first used a 1-week unit featuring visualizations. He also noted that asking teachers to identify the topics for professional development was effective. Initially teachers asked for help with the technology. These issues were resolved, and the teachers then asked for guidance on using inquiry questions. Next teachers asked for help with using visualizations. Successful professional development involved making videos of varied teaching practices and conducting a dialog where teachers discussed the alternatives and identified a set of best practices.
Jill Denner reported a number of challenges in promoting computational thinking in middle school. These included mundane issues such as difficulties with hardware and software and with Internet access, consistent with the comments of Slotta. Taylor Martin emphasized that access to computers and provision of technical support are important, stressing that computers are the tool students will use in the workplace. Teaching computation without them is not really preparing students for the real world. Many schools lack access to computers or only have productivity tools like word processing rather than the computational environments mentioned in the workshop (e.g., WISE, Scratch, or Globaloria).
Several participants emphasized the importance of combining professional development with solid curricular materials. Because precollege teachers are often inexperienced with the subject matter of engineering, teaching materials have to be explicit and clear. Cunningham argued that when learning objectives drive the experiences embedded in curricular units, objectives need to be very explicit and specific rather than high-level and abstract. She argued that learning objectives should also be few in number and relatively narrow so that a high degree of student success is possible. She suggested that the materials provide ways of specifically assessing the scope and extent of student mastery and comprehension.
Cunningham and colleagues have found that hands-on experiences are particularly important for young learners. They have fielded many requests to replace physically manipulative experiences in handling objects with a click-and-drag interface on the computer that students can use to connect objects on the screen. But knowledge about the physical world that teachers take for granted cannot be assumed in students. For example, students don’t necessarily know that a fuzzy pompom will pick up pollen better than a smooth marble. In fact, that fact is engineering knowledge, and it’s “common sense” only if one has real-world experience with pompoms and marbles.
Experience with the physical world varies across populations. Cunningham reported that many students, including especially girls and underrepresented minorities, lack cultural experiences that illustrate the value of learning about engineering or the benefits of advances in engineering. She and her colleagues use hands-on materials as well as storybooks that bring these ideas to life.
Williams reported on her experience working with precollege teachers. She stressed the importance of engaging teachers in reviewing student work. She has found it valuable to have teachers use the scoring rubrics developed by the curriculum designers. She observed that teachers can make big gains in the sophistication of their teaching by making changes based on the gaps in their students’ knowledge.
2.7.2 Teachers and Career Awareness
Joyce Malyn-Smith pointed out that teachers can play an important role in helping students make connections between what they know and what they are learning. Teachers can encourage students to connect the new ideas to activities they would like to perform either in the present or in the future. Teachers can help students understand the connection between computational thinking and future earning power. Malyn-Smith said that students often have understanding of details about computational thinking from their areas of interest but lack the historical and cultural frameworks for placing such information in context. Teachers can help students to validate what they know and to understand how it is important and how it relates to what they are learning in class.
Williams added that instructional materials that connect to personally relevant problems can help teachers make connections between science and students’ ideas. Questions such as determining the origin of one’s eye color or distinguishing among possible ways to reduce the accumulation of greenhouse gases stimulate exciting conversations between students and teachers.
2.8 LEARNING CONTEXTS AND COMPUTATIONAL THINKING
Workshop participants contrasted formal, informal, and ubiquitous learning contexts. They noted that computational thinking may fit better in some contexts than others.
Several presenters stressed the challenges posed by a tightly packed curriculum that does not necessarily stress abstract thinking skills but that could provide a framework for integrating curricular content. Cunningham underscored the importance of integrating the new material—in this case, engineering—with what schools are already teaching. Successful integration can show how the new material contributes to understanding. Arguing for new material as a primary focus, however, is not likely to succeed because of preexisting curriculum demands.
Cunningham noted the importance of articulating how new content and skills in the Engineering is Elementary project connect to existing educational standards. Such connections could include, for example, core concepts of technology such as systems, processes, feedback, controls, and optimization; the design process as a purposeful method of planning practical solutions to problems; inclusion in the design process of such factors as the desired elements and features of a product or system or the limits that are placed on the design; and the need for troubleshooting.
Paulo Blikstein of Stanford University noted that often typical instruction is oriented toward declarative knowledge, whereas computational thinking is oriented toward procedural knowledge. In this view, declarative knowledge provides content (and is essential to particular fields or careers), whereas computational thinking is most useful for integrating and building connections in the midst of such knowledge. Those accustomed to thinking primarily in terms of declarative knowledge may find it difficult to appreciate educational themes oriented toward procedural knowledge.
Allan and Erikson reported that the development effort for the EcoScienceWorks10 project approached the use of programming instrumentally. Downplaying the use of programming was a response to the developers’ concern that some teachers might rebel because the Maine learning standards did not mention programming. They feared that they would have a hard time justifying spending scarce classroom time on program
___________________
10 EcoScienceWorks is available at “EcoScienceWorks: Exploring and Modeling Ecosystems Using Information Technology (IT),” website, Foundation for Blood Research, http://www.fbr.org/swksweb/esw.html. Last accessed March 14, 2011.
ming, even if focusing explicitly on programming might have significant educational value.
Robert Tinker observed that students involved in a very tightly packed K-12 curriculum do not have the time to master programming. His preferred approach is thus to use a programming environment such as NetLogo11 or AgentSheets12 that allows users to focus on the concepts represented rather than on the details of programming. Janet Kolodner of the Georgia Institute of Technology noted that another option is the use of powerful software suites in which the student can manipulate important parameters.
Several participants noted that learning about engineering or computational thinking may meet teacher goals that are not necessarily based in educational standards but are expected outcomes for students. For example, Cunningham observed that many elementary school teachers want to find ways to help their students work together in teams. Persuading students to work together, to respect each other, and to communicate what they’re doing is something that many teachers want to accomplish at the beginning of each year, because learning to work in groups is a skill elementary teachers are expected to develop in their young pupils. Educational activities that call for collaboration can often be an important part of such persuasion.
2.8.2 Out-of-School Computational Thinking
Given the issues relating to introducing computational thinking into schools, a number of workshop participants pointed to out-of-school venues as providing significant opportunities for exposure to computational thinking. In out-of-school venues, students have the time to engage in complex projects that are needed to nurture computational thinking. Malyn-Smith noted that learners need opportunities for thoughtful, reflective engagement with phenomena—not just a “drive-by” experience. Teachers in Malyn-Smith’s program are encouraged to think broadly about the knowledge base that students are developing in all of their activities, not just those provided in program settings. Teachers also engage in conversations with students about their interests and what they are learning in other settings, such as in museums, in watching television and listening to the radio, by playing games, and through what they’re doing with their friends.
___________________
11 NetLogo is available at “NetLogo.com,” website, Northwestern University, http://ccl.northwestern.edu/netlogo/. Last accessed March 14, 2011.
12 AgentSheets is available at “AgentSheets, Inc.,” website, AgentSheets, Inc., http://www.agentsheets.com/index.html. Last accessed March 14, 2011.
Out-of-school environments can provide curricular flexibility, appropriate staff capacity, infrastructure access, and access to effective programs, Malyn-Smith explained. This is especially valuable in rural areas. These interrelated challenges have constrained many previous educational innovations, and computational thinking is no different, she argued. For example, although nearly every middle school student learns from the textbook that trees help mitigate pollution, students in an after-school program can have a chance to go further, using modeling tools to map the trees in their school yard and to record relevant data on species, health, growing conditions, and the like.13 Students can use automated models to calculate the benefits of the trees in terms of pollution removal and runoff mitigation, and they can model alternative growth scenarios as they either “plant” new trees, let the existing trees continue to grow, or remove the trees for expanded parking. Re-running the model leverages the power of automation to quickly adjust the underlying parameters and see what the impacts are. This iterative process just doesn’t fit in a curriculum packed with hundreds of discrete topics that are connected loosely at best. Time allocations that allow for depth and complexity are possible in these programs. Schools have to provide this type of time allocation as part of the culture change needed for computational thinking to take root.
Stephen Uzzo promotes computational thinking as a way to help future scientists cope with the transformational effect of data-rich science. New York Hall of Science activities entail developing exhibits, implementing them, and then evaluating them for pedagogical efficacy in conveying the relevant concepts to students.
For example, Uzzo discussed a project developed cooperatively with the School of Library and Information Science (SLIS) at Indiana University. The SLIS macroscope helps to identify patterns, trends, and outliers in very-large-scale static or streaming data sets. The macroscope is an expandable and integrated set of applications that scientists can use to share scientific data sets and algorithms and to assemble them into workflows. Macroscopes continuously evolve as scientists add and upgrade existing plug-ins and remove obsolete ones to arrive at a set that is truly relevant for their work. This project requires little or no help from computer scientists.
Uzzo argued for a new generation of science students who know what it means to be an e-scientist, taking advantage of online data. He suggested that informal learning institutions may be in the best position
___________________
13This example is further elaborated in ITEST Small Group on Computational Thinking, 2010, Computational Thinking for Youth, Newton, Mass.: Education Development Center. Available at http://itestlrc.edc.org/resources/computational-thinking-youth-white-paper. Last accessed May 20, 2011.
to advance the cause of e-science. Specifically, he said that informal science institutions have an opportunity to integrate computational thinking in a broad range of science activities. These institutions are in a good position to conduct learning research on computational thinking and to integrate such research into professional development and curriculum development for K-12 formal education.
2.9 RESEARCH AND UNANSWERED QUESTIONS REGARDING COMPUTATIONAL THINKING
The first workshop report identified five open questions that at least some participants in that workshop believed were worth further exploration:
1. What is the structure of computational thinking?
2. How can a computational thinker be recognized?
3. What is the connection between technology and computational thinking?
4. What is the best pedagogy for promoting computational thinking?
5. What is the proper institutional role of the computer science community with respect to computational thinking?
Several of these questions were discussed in the second workshop: question 2 is related to the discussion of student assessment (Section 2.6); question 3 is addressed in Section 2.9.2; and responding to question 4 is implicitly the purpose of Sections 2.3 and 2.4. In addition, participants in the second workshop raised additional issues that are described below.
2.9.1 The Importance of a Process for Defining Computational Thinking
As noted above, the first workshop identified the structure of computational thinking as an important open question. A number of participants in this second workshop amplified this observation by pointing to the importance of a process for defining computational thinking.
For example, Joyce Malyn-Smith argued that the field needs a rigorous and valid way of bringing people together and figuring out what computational thinking is. It is necessary to have consistency because not everyone understands what computational thinking is about, or they see it only through their own lens. Absent a rigorous process for defining computational thinking, efforts to promulgate computational thinking in the curriculum will lack credibility. Whatever else it may be, computa-
tional thinking in the curriculum cannot be just a bunch of examples that are placed into the curriculum at the discretion of individual teachers.
Elaborating on the first workshop’s question regarding the connection between technology and computational thinking, Malyn-Smith identified two research questions. First, to what degree and in what ways does the technology expertise of youth contribute to their computational thinking? A related second question is, How and to what degree can the use of technological tools and systems and processes facilitate transfer of learning in STEM careers and in the sciences?
2.9.3 The Need for Interoperability
Al Aho noted that “the software world of today is largely a Tower of Babel, with lots of incompatible infrastructures and a lot of expense regarding who pays, who collects the data, who maintains the data, who maintains and evolves the software.” Stephen Uzzo said this was especially true in an e-science environment in which data is produced in prodigious quantities and there is a premium on making large data sets available to researchers reliably and promptly. In this view, computational thinking efforts would be facilitated by interoperability between applications used by researchers, and it must provide easy-to-use tools for processing, manipulating, and combining multiple data types.
Jim Slotta echoed these points when he observed that content from most platforms is not portable across platforms. Further, the environment of a given platform is generally unable to interact with other applications that are running on the machine. To address some of these limitations, Slotta and his team engaged with the computer science department to develop a new open-source architecture called SAIL (Scalable Architecture for Interactive Learning) for content display and manipulation that separates the various layers of the learning environment (and in particular the content and the user interface) wherever possible.
SAIL has been used in a number of other science education efforts as well. For example, SAIL is an integral element of the Science Created by You (SCY) project of the European Union.14 SCY is a large project that provides a flexible, open-ended learning environment for adolescents. Within this environment—called SCY Lab—students engage in personally
___________________
14This discussion of SCY includes material found at “Science Created by You,” website, http://www.scy-net.eu/. Last accessed February 7, 2011.
meaningful learning activities that can be completed through constructive and productive learning. Examples of such learning activities include browsing for information, generating a hypothesis, and distributing tasks.
Slotta has also developed a technology framework called SAIL SmartSpace (S3) to support a complex orchestration of people, materials, resources, groups, conditions, and so on. This framework can be regarded as a “smart classroom” infrastructure that facilitates cooperative learning in a milieu of physical and semantic spaces. From a technical standpoint, S3 supports aggregating, filtering, and representing information on various devices and displays (e.g., handheld devices, laptop computers); locational dependencies (i.e., allowing different things to happen depending on the physical location of a student); interactive learning objects; and an intelligent agent framework. The S3 environment is highly customizable and supports the coordination of people, activities, and materials with real-time sensitivity to inputs from students.
2.9.4 The Need for a Career Framework
Joyce Malyn-Smith contended that for computational thinking to get traction in the K-12 education community, it needs to be connected to frameworks and standards that are already implemented nationwide. An analysis of the Information Technology Career Cluster Initative’s model, for example, provides a way to organize a hierarchy of skills and knowledge that can be repurposed to support the integration of computational thinking in the K-12 arena. At the most basic level, this information technology skills framework calls for literacy and the ability to use common technology applications. Further up the hierarchy is fluency with information technology, which involves core knowledge and skill sets of technology-enabled workers employed in any industry sector. At the highest level of this model are the skill sets necessary for information technology producer or developer careers—those that involve the design, development, support, and management of hardware, software, multimedia, systems integration, and services. In short, individuals engaged in different activities are likely to need different (though overlapping) sets of technology skills.






























