Time-series studies of the effect of capital punishment on homicides study the statistical association of executions and homicides over time. As noted in the preceding chapter, panel studies also contain a time dimension, so the division between the two approaches is not perfect. Indeed, time-series studies can be thought of as a particular type of panel study, characterized by a small number of cross-sectional units, often only one or two. Some time-series studies analyze executions and homicides over a large number of periods; others examine the aftermath of single execution events. Whatever the length of the series, the intuition undergirding the analysis is that the presence of an effect of executions on homicide rates can be seen from the association of fluctuations of executions over time with fluctuations of homicides over time.
The time-series and panel studies we reviewed differ in several other important respects.
• First, the unit of time in time-series studies is usually months, weeks, or even days; in contrast, the unit of time in panel studies is usually a year. Thus, results from time-series studies are generally interpreted as measuring short-term effects of capital punishment.
• Second, time-series studies generally examine the association between execution events and homicides; panel studies generally measure the association of homicide rates with ratios that are intended to measure the probability of execution.
• Third, while most panel studies use very similar regression methods, time-series studies use a wide assortment of specialized time series methods.
• Fourth, the designs of time-series studies are more varied than are those of panel studies. Perhaps the most important difference among time-series studies is the number of execution events examined. Some time-series research focuses on the effect of a single execution event, and other studies combine data on many execution events and analyze their temporal association with homicide rates in a single statistical model.
The variation of research methods in the time-series studies makes it challenging to organize a cohesive discussion of the subject. It also is challenging to describe and critique the studies in a way that is understandable to audiences who do not have expertise in time-series methods. Methods for analysis of time-series data are specialized and often very technical. We address the second challenge by beginning this chapter with a nontechnical discussion of some relatively transparent problems of the studies. We then continue with further criticisms that of necessity are more technical.
Studies of single execution events attempt to identify whether a change in the homicide rate occurs in the immediate aftermath of a single execution. A decline is interpreted as evidence of deterrence; an increase is interpreted as evidence of a brutalization effect, whereby state-sanctioned executions “legitimate” homicide to some in the citizenry. If either such effect could be convincingly demonstrated, it would establish a threshold requirement for capital punishment to affect behavior, namely that “someone is seemingly listening.” However, as detailed below, the committee concluded that no existing study has successfully made such a demonstration and that the obstacles to success for a future study are formidable. As importantly, the committee concluded that a successful demonstration would have limited informational value.
Studies of a single execution event are subject to the same problem that bedevils most before-after studies. Because the execution is not conducted in the context of a carefully controlled experimental setting, other factors that affect the homicide rate may coincide with the execution event. Some event studies attempt to deal with this problem by examining changes over very short periods of time, days or a week. Although shortening the time window of observation may provide some protection from the effects of
other sources (but see discussion below), it opens other possible interpretations of the result. Even if a short-term effect could be established, it would be difficult to determine whether homicides were actually prevented or simply displaced in time. This possibility creates a fundamental conundrum: the study of short time frames increases the plausibility of the displacement in time interpretation, and the study of longer time frames increases the risk of confounding by other factors.
It is vital to understand that event studies do not speak to the question of whether and how a state’s sanction regime affects its homicide rate. The simplest illustration of this point involves the interpretation of a study that fails to find evidence that an execution event affects the homicide rate. Consider, for example, a study of the first execution after an extended moratorium. Suppose that the study convincingly demonstrated that the execution was not followed by any change in the homicide rate. One interpretation of this result is that capital punishment has no deterrent effect. However, another possibility is that the deterrent effect is large but that it was anticipated in advance of the execution due to the publicity given to the upcoming event. Both possibilities are logical and plausible, but they are not distinguishable by the event study methodology.
Alternatively, suppose that an event study found that homicides are reduced in the immediate aftermath of an execution and not just displaced in time. To generalize from this single execution requires consideration of the context in which the execution occurred. If it was the first execution after an extended moratorium, it is problematic to assume that such an effect would recur for subsequent executions. More generally, the effect of any given execution may depend on the proximity in time of that execution to other executions and to the frequency of executions more generally. For example, if an execution event study established convincingly that it averted one homicide that week, it does not follow that each additional execution would avert one more homicide. To complicate matters further, the effect of any one execution may depend on the identity of the person executed (e.g., an infamous serial killer or a person for whom there is some public sympathy) and the amount of publicity given to the execution.
The problem of generalizing from the findings of even a convincing event study is indicative of still another fundamental committee concern with all the time-series studies. The researchers who carry out such studies never clearly specify why potential murderers respond to execution events. Do potential murderers respond to the shock value of execution? If so, would the magnitude of the shock value change with each additional execution? One possibility is that the shock value might increase, perhaps because of reinforcement. Alternatively, it might decrease, perhaps because a potential murderer becomes inured to executions. Still another possibility is
that potential murderers respond to sanction risk probabilities and that execution events cause them to update their perceptions of those probabilities.
Studies of Deviations from Fitted Trends
This issue of why and how potential murderers react to executions is equally important to the interpretation of studies that combine data on executions and homicides over multiple time periods, deploying subtle time-series methods to analyze these data. Consider Figures 5-1 and 5-2, which plot executions and homicides, respectively, in Texas from 1990 to 2008. The most obvious way to examine the association of executions and homicides in Texas is to correlate these two time series. Over the period, this correlation is –0.68. However, there are innumerable obvious objections to interpreting this negative association as deterrence because many factors that influence the homicide rate were also changing over this time period. One manifestation of this observation can be seen in Figure 3-3 (in Chapter 3), which shows the close correspondence over time in the homi-
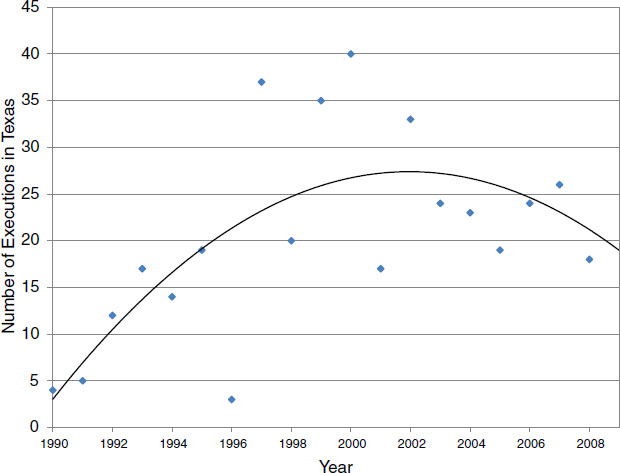
FIGURE 5-1 Executions in Texas from 1990 to 2008.
SOURCE: Data from Texas Department of Criminal Justice (2011).
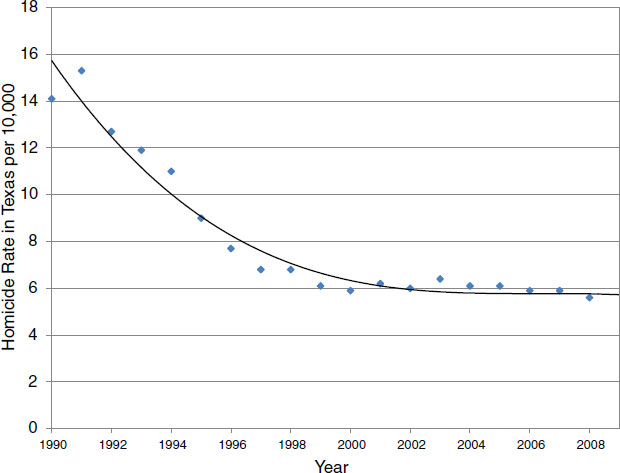
FIGURE 5-2 Texas homicide rate from 1990 to 2008.
SOURCES: Data from the Federal Bureau of Investigation (2011).
cide rates of three states with very different capital punishment sanction regimes—California, New York, and Texas.
Studies of executions and homicides over multiple time periods do not examine the raw time-series association between the homicide rate and number of executions. Instead they analyze the association between deviations from fitted statistical trend lines that summarize these two time series. One technical adjustment sometimes used to in these studies is that the data series be detrended. By “detrended” it is meant that the time series does not vary systematically with time (e.g., does not increase over time). As a consequence the time-series studies analyze the association between deviations from statistical trend lines that summarizes the execution time series and the homicide rate time series
As an illustration, consider again Figures 5-1 and 5-2. Superimposed on the raw time-series plots of executions and homicides are regression equations fit to the execution and homicide data. In the case of the execution time series, the regression uses a quadratic function of time to fit the raw
data. In the case of the homicide time series, the regression uses a cubic function of time to fit the data.
The time-series literature views the fitted regressions as “trends” that should be subtracted from the raw data prior to analysis. After that subtraction, researchers analyze the statistical association between deviations from the respective trends to draw inferences about the effect of executions on homicides. For example, in 1998, during the peak period of executions in Texas, the deviation of the actual number of executions from the fitted trend line is negative. A time-series researcher might examine the statistical association between this negative deviation and corresponding deviations of the homicide rate from its fitted trend line in 1999 and later years.
Unfortunately, the researchers who carry out these studies do not explicitly state their rationale for analyzing deviations in this fashion. They may believe that this form of analysis provides a basis for causal interpretation of findings that is more credible than analysis of raw data on homicides and executions. However, the committee concludes that analysis of deviations from fitted trends, at least as conducted in the published studies, does not provide a valid basis for inferring the effects of executions on homicides.
One reason for our conclusion is that the study of deviations from fitted trend lines, even with high frequency data, may not avoid the confounding problem that affects analyses of the raw correlation of executions and homicide rates over time. For example, the publicity given to executions may still be systematically related to deviations from an execution trend line. Indeed, one of the studies we reviewed (Stolzenberg and D’Alessio, 2004) reports that, even in deviation form, the execution and publicity time series were highly correlated.
A more fundamental concern is that execution event studies do not clearly specify why potential murderers respond to execution events. For potential murderers to react to a deviation from a fitted trend line requires that they recognize it as a deviation. To recognize it as a deviation requires that they be aware of the trend line from which deviations are measured. However, none of the studies discusses why potential murderers might be attentive to the trend lines fit by time-series researchers and, if so, how they might react to deviations from fitted trends. Indeed, the studies do not even ask whether potential murderers perceive the time-series evidence on executions in terms of a trend and deviations from the trend.
If potential murderers are attentive to the trend line, there would have to be a reason for giving it their attention. One possibility is that their behavior is affected by the trend line. For example, the escalation of executions in Texas during the 1990s might have been interpreted as an intensification of the state’s capital punishment sanction regime. Conventional deterrence theory would predict that such an escalation would reduce
homicides, assuming that intensification of the use of capital punishment did not alter other aspects of the sanction regime. But the brutalization theory might predict that this escalation increases murders. Yet neither of these predictions speaks to the question of how potential murderers react to deviations from the trend.
Consider, for example, the conventional economic model of criminal decision making. This model assumes that potential murderers respond to their perceptions of the probability of capture and punishment, which in this context is execution. Under this model, unless potential murderers perceive a deviation from trend as signaling a change in the probability of execution, they will not change their behavior even though their behavior is affected by the probability of execution. Thus, from the perspective of the economic conception of deterrence, a finding of no association between deviations from fitted execution and homicide trends is not indicative of a lack of deterrence.
In making this point, it is important to emphasize that the committee is not endorsing this deterrence-based model of behavior. We pose it to illustrate that the results of time-series analyses are not interpretable in the absence of a behavioral model.
Another possible behavioral model might build from the assumption that potential murderers react in fear to the shock value of executions and are thereby dissuaded from committing a murder. This assumption, however, does not suffice to interpret the results of time-series analyses of deviations from fitted trends. Why should deviations from a fitted trend have shock value separate from the trend itself? If there is no apparent shock value to a deviation from the trend line, does that mean that the trend line itself has no shock value?
The idea that potential murderers perceive and react to deviations from fitted execution time trends presupposes that they are attentive to trends and have mental models of how trends are formed. Moreover, their perceptions of trends must coincide with those of the researchers who fit trend lines to raw execution data. Otherwise, potential murderers would have no basis for recognizing deviations as such.
If time-series analysis finds that homicide rates are responsive to such deviations, the question is why? One possibility is that potential murderers interpret a deviation as new information about the intensity of the application of capital punishment—that is, that the deviation signals a change in the part of the sanction regime that relates to the application of capital punishment. If so, a deviation from the execution trend line may cause potential murderers to alter their perceptions of the future course of the trend line, which in turn may change their behavior.
Yet, even accepting this idea, a basic question persists. Why should the trend lines fit by researchers coincide with the perceptions of potential mur-
derers about trends in executions? If researchers and potential murderers do not perceive trends the same way, then time-series analyses do not correctly identify what potential murderers perceive as deviations. However, the published time-series studies do not ask whether and how potential murderers perceive trends. Moreover, no study performs an empirical analysis that tries to learn how potential murderers perceive the risk of sanctions. Hence, the committee has no basis for assessing whether the findings of time-series studies reflect a real effect of executions on homicides or are artifacts of models that incorrectly specify how deviations cause potential murderers to update their forecasts of the future course of executions.
Evidence Under Existing Criminal Sanction Regimes
One methodology used in time-series studies of deterrence is known as vector autoregressions (VARs). Research of this type estimates dynamic regressions that relate current homicide and execution rates to previous realizations of these two variables. The estimated relationships are then used to make inference about deterrence. Although this methodology has only recently been applied in studies of capital punishment and deterrence, it has been long used in studies of imprisonment and crime: see Durlauf and Nagin (2011) for a review. We extensively discuss its limitations as a source of information on deterrence because it is the methodological state of the art in time-series approaches to deterrence, and it seems poised to become widespread in capital punishment studies, despite the shortcomings we discuss.
VARs were originally developed by macroeconometricians to describe the time-series evolution of an economy (Granger, 1969; Sims, 1972, 1980; Sims, Goldfeld, and Sachs, 1982). The methodology was motivated by the idea that the evolution of an economy can usefully be represented as the superposition of short-run cyclical fluctuations on long-run trends. This idea suggests a three-step analysis. One first uses the raw time-series data on the economy to estimate the trends. One then “detrends” the raw data by subtracting the estimated trends. The detrending step also subtracts the means of each variable, to produce residuals that have no trend and zero mean. One finally estimates a VAR on the detrended and “demeaned” residual data to study the time-series properties of the short-run fluctuations.
VARs are commonly specified to be linear regressions. The use of linear regression is motivated by a statistical idea rather than a substantive one. That is, under relatively weak technical conditions, any stationary time-series can be represented as a dynamic linear relationship that is recoverable
from observation of the series.1 The detrending step of the VAR methodology is intended to render the residual time series stationary.
Some criminologists have used VARs to study deterrence. An immediate question is whether it makes sense to think of the time-series evolution of homicides and executions as the superposition of short-run cyclical fluctuations on long-run trends. The researchers have used various definitions of trends, assuming them to be either linear or nonlinear functions of time. The absence of a consensus approach to detrending reflects the absence of any persuasive theory of the generation of the purported trends. In any case, after detrending is somehow accomplished, VARs are estimated on the detrended residual data and used to describe short-run cyclical fluctuations in homicides and executions.
To illustrate the methodology, denote the detrended and demeaned homicide and execution rates in political unit i at time t as hi,t and ei,t, respectively, and suppose that there are multiple observations on these variables over time.2 The VAR representation of these rates is a two equation system of linear regressions
![]()
Thus, a VAR linearly relates current executions and homicides to previous executions and homicides, as well as to the current values of the random variables εi,t and ղi,t. The choice of how many lagged terms to use is made with the intention that εi,t and ղi,t be random variables that are uncorrelated across time. That is, these two random variables may be correlated at a point in time, but future and previous values cannot be correlated. Formally, εi,t and ղi,t are the one-period-ahead prediction errors for homicides and executions given that predictor variables are restricted to the linear histories of these variables.3 In the relatively simple case in which only finite lags appear in (1), the coefficients of the VAR may be estimated by ordinary least squares.
In studies of the deterrent effect of capital punishment, systems such as (5-1) have focused on the coefficients b1, b2,…, which relate lagged levels of execution rates to the time t homicide rate. If the bi coefficients are all equal to 0, then execution rates are said not to “Granger-cause” homicide rates. That term comes from econometrician Clive Granger, who proposed
__________________
1 This is known as the autoregression form of the Wold representation theorem: see Ash and Gardner (1975) for a fully rigorous treatment.
2 Some studies use levels rather than rates, but this distinction is not essential for understanding the methodology.
3 By linear, we refer to the fact that prediction of homicides and executions are not allowed to depend on more complicated functions of their joint histories than the additive structure in (1).
this statistical definition of causality as a way to summarize the dynamic relationships between time series. It is essential to understand that use of the word “cause” notwithstanding, a finding that the b1 coefficients are all equal to 0 is only a statement about the absence of a linear statistical relationship between current homicides and lagged executions, conditioning on lagged homicides. It is not a statement about causality as it is commonly understood in social science research that distinguishes statistical association from causation. The absence of Granger causality from execution rates to homicide rates only means that the best linear prediction of homicide rates, given the joint histories of homicide and execution rates, does not require knowledge of the history of execution rates; the history of homicides rates is sufficient. The absence of Granger causality does not imply that a counterfactual change in executions because of a change in the sanction regime facing potential murderers would fail to generate changes in homicides at later dates.
Despite the fact that Granger causality is only a statistical concept, findings on the statistical question of whether executions Granger-cause homicides have been used to make substantive claims about the deterrent effect of capital punishment. The absence of Granger causality has been interpreted by some researchers as evidence that capital punishment does not have a deterrent effect on homicides. In studies in which the estimates of the bi coefficients are negative, such findings have been alleged to be evidence of a deterrent effect, with higher execution rates in the past generating lower homicide rates in the future. In studies in which estimates of the bi coefficients are positive, those findings have been alleged to be evidence of a brutalization effect, with higher execution rates in the past generating higher homicide rates in the future.
In a study of the time-series relationships between homicides and executions, as well as the relationship between homicides and execution publicity in Houston, Stolzenberg and D’Alessio (2004) use this approach. The authors find that neither actual executions nor publicity about executions Granger-cause homicides and conclude that neither deterrence nor brutalization effects are present in the Houston data.
Land, Teske, and Zhang (2009) provide a particularly sophisticated analysis of this type, using data from Texas, by focusing directly on how a one-unit increase in ղi,t affects homicides at t + 1, t + 2, etc. In order to render this a well-posed question, it is necessary to address the contemporaneous correlation between ղi,t, the one-step-ahead prediction error to executions, and εi,t the one-step-ahead prediction error to homicides. In essence, Land, Teske, and Zhang resolve this contemporaneous correlation by assuming that εi,t = ρղi,t + vi,t such that εi,t and vi,t are contemporaneously uncorrelated, and so treat vi,t as the shock to homicides. Thus, the contemporaneous correlation between ղi,t and εi,t is resolved by assuming that
the shock to homicides is due to the shock to executions and some other unspecified factor. The researchers do not provide a model of the timing of executions, so it is difficult to assess this assumption.4 They find a negative association between executions and homicide and conclude that there is a net small deterrent effect from an additional execution. However, they also find that executions appear to displace homicides in time. Thus, the long-run deterrent effect is smaller than the short-run effect.
Taken on their own terms, Stolzenberg and D’Alessio (2004) and Land, Teske, and Zhang (2009) provide contradictory evidence on deterrence. Even though each paper uses monthly data from Texas, the papers reach opposite conclusions about the evidence of a deterrent effect. This does not mean that either paper contains errors, as the data sets used and the choice of VAR specification differ across the papers. Nonetheless, the papers’ contradictory findings illustrate that conclusions about a deterrent effect can be very sensitive to the choice of model and details as to how data are transformed prior to estimation. What might be thought to be relatively innocuous assumptions can matter greatly.
This observation leads to a broader critique of both papers. Neither asks what conclusions about deterrence can be drawn when one does not assume a particular time-series specification or when one allows for different deterrent effects in different time periods. Neither the time-series specification nor the appropriate data range are known a priori to a researcher. Although both papers engage in model selection exercises in order to generate specific VAR forms, this approach is inadequate for policy purposes. Model selection methods in essence assign a weight of 1 to the “best” model, given some criterion, but the data themselves do not necessarily assign such a weight. In other words, neither paper appropriately accounts for model uncertainty in providing deterrence estimates. The committee returns to this issue in Chapter 6.
A more basic question is whether evidence of the type presented in the Land, Teske, and Zhang (2009) and Stolzenberg and D’Alessio (2004) analyses actually speaks to the question of the deterrent effect of capital punishment. VARs only measure statistical associations in data. Thus, the fundamental question is the relationship between the statistical concept of Granger causality and the policy-relevant concept of causality as treatment response. The remainder of this section mainly discusses this basic issue. We then raise a second concern about criminological research that uses VARs.
__________________
4 One might plausibly argue that the assumption holds when time increments are short. However it may be that the judicial system’s willingness to grant stays of execution is affected by recent homicide activity, particularly when the homicides generate publicity.
Granger Causality and Causality as Treatment Response
The idea that Granger causality speaks to a deterrent effect of capital punishment is not a logical implication of social science theory. There may perhaps be theories of deterrence in which the presence of a deterrence effect would be equivalent to the statistical concept of Granger causality, but no such theory has yet been advanced. However, there already exist standard models of criminal behavior under which Granger causality tests are uninformative about deterrence.
For the sake of concreteness, we focus on the model of rational criminal behavior that has been the workhorse of much of the modern theory of deterrence, that of Becker (1968). This model, which assumes that the choice of whether to commit a crime (in this case, homicide) can be understood as a purposeful choice in which costs and benefits are compared, is controversial among some criminologists, sociologists, and economists. A particular concern has been the common assumption that potential criminals not only behave rationally, but also have so-called rational expectations; that is, that they correctly perceive the sanctions risk that they face. The discussion below should not be interpreted as a committee endorsement of this specific assumption or of the idea of rational criminal behavior more broadly. The discussion is meant to illustrate how this widely used theoretical formulation sharply delimits what can be learned from standard VAR estimates.
Put simply, the rational-criminal model places no restrictions on the presence or absence of Granger causality from executions to homicides. The reason the model does not imply such time-series restrictions on the relationship between executions and homicides is not a function of its specific rationality assumptions; rather, the central point is that the rational-criminal model supposes that individual beliefs about sanctions risks derive from their perception of the criminal sanction regime in which they live, not from the occurrence of executions per se.
The idea of a sanction regime is that a potential murderer faces a probability distribution of outcomes that will stem from the choice of committing murder. The first uncertain outcome is whether the murderer will be caught. Conditional on being caught, the potential murderer then faces a probability distribution of punishments. With some simplification of the way the criminal justice system works, the beliefs of a potential murderer about three probabilities matter: (1) the probability of not being caught, PNC, (2) the probability of being caught and serving a prison sentence, PP,5 and (3) the probability of being caught and being executed, PE. It is standard to regard PC = 1 – PNC as the certainty of punishment. The outcomes of imprisonment and execu-
__________________
5 In this example, we assume that there is a single prison sentence length for murder. In practice, there are many potential prison sentence lengths and a rational criminal will account for the probabilities of each of the sentences.
tion constitute the severity of punishment. The criminal sanction regime is defined by those probabilities and the two outcomes, sentence length if not executed and execution.
From the vantage of the rational-criminal model, short-run fluctuations in the occurrence of executions are irrelevant to murder decisions unless they cause individuals to revise their beliefs about the certainty and severity of punishment if a murder is committed. Although one can construct theories as to why the occurrence of executions would lead to revisions in beliefs (and one can find examples of such theories in the literature), tests of Granger causality as they have so far been used do not speak to the deterrence question. In particular, they ignore the distinction between the criminal sanction regime and the time-series realizations of one of the potential punishments under that regime, namely, executions. We emphasize that this point does not depend on the assumption that potential murderers rationally weigh the costs and benefits of murder. Rather, it rests on the much weaker assumption that potential murderers respond to their beliefs about sanction risks and not about execution events per se.
More specifically, a potential murderer makes the decision to commit a homicide against the background of a set of uncertain outcomes to that act. In a rational-criminal model, beliefs about sanction risk are not necessarily affected by the occurrence of a relatively high or low number of executions during the previous month or during any other time period. A potential murderer may simply interpret time-series fluctuations in the occurrence of executions as a reflection of time-series fluctuations in the number of people convicted of murder several years earlier, each execution taking place under a stationary sanction regime. Thus, execution events themselves need not alter perceptions of the sanction regime. It follows that an empirical finding of no Granger causality does not necessarily imply the absence of a deterrence effect to capital punishment.
Furthermore, if the candidate explanations for criminal behavior are either that criminals are not subject to deterrent effects or that potential murderers obey a rational model of criminal behavior, then Granger causality from executions to homicides does not necessarily provide support for the deterrence explanation. For example, suppose the rational choice theory of deterrence, which does not embody any explanation of the timing of executions, is correct. For the rational choice models under a stable sanction regime, Granger causality from fluctuations in executions to fluctuations in homicides tautologically occurs because of factors outside of changes in the sanction regime. Hence, Granger causality from executions to homicides cannot be attributed to the deterrence mechanism of the rational choice model. The upshot is that the validity of the claim of deterrence cannot alone be assessed by either the presence or the absence of Granger causal-
ity from executions to homicides. It must be assessed in the context of a behavioral model whether of the rational choice variety or not.
Under the rational-criminal model, one can potentially connect execution events to behavior if one discards the specific assumption of rational expectations and instead supposes that people use data on the occurrence of executions to update their subjective beliefs about the sanction regime in which they live. Suggestions of such updating appear in the some studies, but the committee is unaware of any formal model of beliefs and behavior that make tests of Granger causality that have interpretable implications for deterrence. Furthermore, as we emphasized earlier in the report, remarkably little is known about the perceptions of would-be murderers or about how their perceptions may change in response to executions.
Choice of Variables in VAR Studies
The use of vector autoregressions in the empirical studies of capital punishment and deterrence suffers from a second important limitation: insufficient attention to the choice of variables in the systems under study. The studies that use Granger causality to study deterrence have been almost exclusively focused on bivariate relations of the type described by equation (5-1). Although bivariate systems are relatively straightforward to analyze, especially when one is interested in the effects of shocks to one series on the behavior of another, they are not nearly as sophisticated as the form of vector autoregression analysis that is now conventionally used in macroeconomics, the field from which these methods are taken. In fact, the evolution of atheoretical models in macroeconomics has illustrated the importance of thinking about the time-series relationships among different collections of variables. Modern vector autoregression analysis works with far more complex systems than the bivariate ones found in studies of capital punishment.6
Without carefully specifying the set of relevant variables, findings from the VAR studies on deterrence and capital punishment may be an artifice of the choice of executions as the only variable that can affect homicides. For capital punishment, there is an obvious lacuna when focus is restricted to executions and homicides: entirely omitted are variables that measure the severity of punishment for murderers who are not executed. Virtually any behaviorally plausible formulation of deterrence would suggest that these variables are an essential part of the sanction regime relevant to a would-be murderer’s behavior.
The omission of time series of data that describe the noncapital pun-
__________________
6 For example, Leeper, Sims, and Zha (1996) analyze systems that use 13 and 18 distinct variables to study monetary policy and draw explicit contrasts with more parsimonious systems.
ishments meted out for homicides means that the bivariate systems omit critical variables necessary for complete description of a sanction regime. Therefore, even if people use observations of realized fluctuations in punishments to update their perceptions of sanction regimes, bivariate models cannot be interpreted as giving evidence of the deterrent effect of capital punishment per se. Fluctuations in the occurrence of executions may be correlated with fluctuations in the severity of the prison terms received by murderers who do not receive the death penalty, generating a classic problem of omitted variables. The omitted variables problem affects vector autoregressions just as it affects other types of regressions: spurious correlations may be produced and parameter estimates may be biased.
This argument can be generalized. Crime rates are well understood to vary with a host of demographic and socioeconomic variables. Land, Teske, and Zhang (2009) and Stolzenberg and D’Alessio (2004) omit such variables from their analyses. Findings of Granger causality or its absence depends on the set of variables under consideration. Therefore, by the standards of the modern use of vector autoregressions, neither of these studies considers a rich enough system of variables to justify interpreting their findings in terms of deterrence.
Inferences Under Alternative Sanction Regimes
The discussion above has concerned inference on deterrence under existing sanction regimes. A distinct question concerns the capacity of atheoretical time-series methods in general and Granger causality tests in particular to provide information on the deterrent effect of capital punishment under alternative sanction regimes from those that have existed and currently exist in the United States. As described elsewhere in this report, the historical capital punishment regime is one in which executions are very infrequent in comparison with the numbers of homicides. Furthermore, when a murderer is apprehended, execution typically does not occur even when the murderer receives the death penalty in trial. Liebman, Fagan, and West (2000) found that two-thirds of capital sentences are reversed on appeal. As we note elsewhere in the report, only 15 percent of capital sentences meted out between 1973 and 2009 have ended in an actual execution.
The alleged strength of atheoretical time-series methods—which is evinced in their reliance on the properties of the historical data as opposed to a priori assumptions on how people or groups behave—has the necessary consequence that these methods cannot speak to the deterrent effects of substantively different criminal sanction regimes. Alternative criminal sanction regimes would imply different coefficients for the vector autoregression system (5-1) if the individuals’ decision making or the process generating
executions was different under an alternative regime. In other words, the relationship between homicides and executions may depend on the criminal sanction regime. Hence, the historical relationships that are estimated when a system such as (5-1) is applied to data may change with the regime.
In macroeconomics, this dependence of statistical relationships on the underlying policy regime (in this case, the sanction regime for murder) is known as the Lucas critique (Lucas, 1976), although the idea goes back to Marschak (1953). In the case of capital punishment, the force of the Lucas-Marschak critique is self-evident. The available data on executions and homicides are generated in a context in which actual executions are quite unusual. As such, they are unlikely to provide useful information on hypothetical regimes under which capital sentences are regularly carried out.7
A second time-series approach used to study deterrence is what we will call the “event study” because it focuses on the association between homicide and a single execution or particular executions. This work takes seriously the idea that an execution is an unusual event and implicitly assumes that the event is of sufficient importance, considered relative to the background of other determinants of homicide, that it leaves a discernible footprint in the homicide time series.
This type of analysis was first performed by Phillips (1980), who identified 22 executions of “notorious murderers” in England in the period 1858-1921. For each execution, he studied the number of homicides in London in the weeks before and after the execution. He found a statistically significant difference between homicide rates in the week prior to an execution and the week after an execution. A more detailed analysis found that this reduction was subsequently reversed, so that homicides were displaced in time rather than reduced. In light of these results, Zeisel (1982) argued that Phillips’ evidence should be thought of as a delay rather than a deterrent effect. Phillips (1982) did not dispute this alternative interpretation in his rejoinder.
In our view, the Phillips study is not useful in assessing deterrence effects. One issue, raised by Zeisel, is that the narrow time horizon studied before and after the executions makes it hard to distinguish displacement from deterrence. Another serious problem is Phillips’ assumption that in the absence of a deterrent effect of execution, the process generating homicides
__________________
7 This distinction is well understood in the macroeconomic literature using vector autoregressions. Leeper and Zha (2003), for example, explicitly define criteria for “modest” policy interventions under which VARs may be used for policy evaluation. The explicit objective of their work is to identify vectors of shocks that occur with high enough probability that their effects may be evaluated under the assumption that the policy regime generating the shocks is unchanged.
is stationary over time. This assumption motivates his test of the null hypothesis that the homicide rate in the week before an execution is the same as in the week after it. There is little reason to believe this null hypothesis given that there are many potential sources of time variation in the determinants of homicides beyond the effects of executions. As a stark example of how Phillips’ approach can lead to spurious inferences, suppose that England experienced a long-run decline in homicide during the 1858-1921 period that Phillips studied. In that situation, the data would tend to show lower homicide rates in the week after executions than in the week before simply because the week after occurs later than the week before. Without a full specification of the properties of the total homicide process, one cannot understand the effects of individual executions.
Another limitation of Phillips’ analysis concerns external validity. It is not clear that the homicide process for England in 1858-1921 is the same as that for the modern United States. By analogy, one would not use data on the effects of changes in fiscal policy from 1858-1921 to evaluate current macroeconomic policy proposals.
A second example of this style of analysis is Cochran, Chamblin, and Seth (1994), which analyzed the effects of a particular execution on homicides in Oklahoma. The execution studied was that of Charles Troy Coleman. Coleman’s execution was the first in Oklahoma in 25 years. In addition to sharing the same limitations as those in Phillips’ study, the Oklahoma study has a fatal flaw in the research design. To see this, we describe some of the details of the model used.
The raw data for the study were weekly homicides in Oklahoma, which we denote as HOK,t. Prior to their analysis, the authors detrended and demeaned this time series. The researchers next regressed the residuals on lagged residuals. The result was a white-noise data series, εOK,t which represents the one-step-ahead forecast errors when HOK,t is regressed against its history, after any constant term and trends are removed. They then defined an intervention time series, It, which equals 0 prior to the execution and 1 afterward. Finally, they estimated the equation
![]()
where ξOK,t is a prediction error. They interpreted the coefficient α1 as measuring the effects of the execution. Different restrictions on this coefficient were considered. For example, if the α1 is required to sum to 0, this imposes the restriction that there can be no permanent effect of the execution on homicide rates, only a displacement effect.
The key conceptual problem with this approach is that it is logically impossible for a white-noise stochastic process to be correlated with an intervention series as it is defined here—there may be a correlation in a finite
data sample but not in the population. The reason is simple: the white-noise series has a mean of 0 and the intervention series does not. Hence, there is nothing that can be learned from the exercise involving specifications that do not impose the restriction that the long-run effect of the execution on homicides is zero. In terms of the underlying time-series mathematics, the “pre-whitening” described in the study assumes statistical properties for the homicide series that are inconsistent with equation 5-2 (see Charles and Durlauf, in press, for details). The authors argue the best specification for 5-2 is one that does not impose the requirement that the α1 coefficient sums to 0. In other words, the authors argue that the best specification for the effect of an execution on homicides is one that cannot in a population produce the result they assert holds in the finite sample.
A more persuasive example of an event study of deterrence is Hjalmarsson (2009). Methodologically, the approach in this paper originated in Grogger (1990), who proposed an appropriate statistical model for such an analysis, treating the homicide level as a count variable. We focus on the Hjalmarsson paper because it uses daily data and specifically focus on cities in which capital punishment is relatively common.
The analysis considered very short-run effects of executions in Dallas, Houston, and San Antonio, Texas. For the study, the daily counts of homicides in the cities were analyzed to see whether homicide rates varied in the days before and after an execution. Hjalmarsson found little evidence of a “local” (in time) deterrence effect. She was careful not to extrapolate her results to broader concepts of deterrence, recognizing that her limited time horizon does not allow one to distinguish between displacement and deterrence. As such, the analysis suffers from one of the same flaws as Phillips (1980), but her use of daily homicide counts may be useful to discern the immediate visceral effect of an execution.
We caution, however, that even this extremely short-run analysis may be susceptible to the problem that events relevant to homicide may co-occur with executions. To give one simple example, police departments may alter deployments of personnel in the periods immediately following executions that draw public attention. If so, one cannot interpret fluctuations in homicides immediately before and after an execution in terms of the deterrent effect of the execution.
Another strand of the literature estimates time-series regressions that relate homicide rates or levels to executions and other covariates. Although VARs are also time-series regressions, the work discussed in this section differs in several respects from the work discussed above. First, the regressions are estimated using raw homicide and execution data rather than detrended
and demeaned data. Second, lagged homicides are not included among the variables used to predict current homicides. Third, various other covariates than lags of executions and homicides are used among the predictor variables.
One example is the study by Bailey (1998), which considered the Coleman execution in Oklahoma, but it modifies some aspects of Cochran, Chamblin, and Seth (1994). In particular, this paper works with the time series of the level of homicides rather than a transformation of the time series into a white noise process, and it further includes various predictor variables in addition to the event of the execution to model the homicide level. Unfortunately, the paper does not report any equations, but the description it provides suggests that the analysis is based on the regression
![]()
In this regression, EUS,t is a measure of the number of executions in the United States. The idea is that the public may be aware of these executions through various channels. POK,t is a measure of the publicity given to executions throughout the country, as measured by days of newspaper coverage in the Oklahoman in a given week. This variable is intended to measure public information about executions; it is distinct from EUS,t in that it measures a particular information source. Xt is a vector of control variables, which include socioeconomic and demographic characteristics, as well as month-specific dummy variables; these dummies are included for ad hoc reasons. The study finds that the overall level of murders is positively associated with the publicity variables. When focus is limited to overall killings of strangers, as well as subsets of this category, the results are mixed, with some regressions finding a brutalization effect, others finding no effect, and some cases finding a deterrence effect.
Despite these mixed results, Bailey concludes that “No prior study has shown such strong support for the capital punishment and brutalization argument” (Bailey, 1998, p. 711). The author, in our view, overstates his findings by focusing on regressions with statistically significant coefficients. Other regressions, in which statistical significance fails, are not accounted for in the author’s strong conclusions. As noted in Chapter 4, a finding that an estimate is statistically insignificant does not imply that the true deterrent effect is zero or even that it is small. In other words, the study does not properly account for the dependence of the brutalization findings on particular regression specifications.
Beyond the specifics of Bailey’s study, this type of regression analysis, although still common in the social sciences, does not support causal claims. Regressions of this type are based on many arbitrary assumptions,
such as linearity of the effects of executions and other variables on homicides, as well as particular choice of control variables, without attention to the effects of alternative choices. Furthermore, despite the author’s claims, the execution of Coleman does not constitute a quasi-experiment. The timing of the execution is likely to be an endogenous outcome of the criminal justice system and should be modeled as such.
A different type of time-series regression analysis has been used by Cloninger (1992) and Cloninger and Marchesini (2001, 2006). These papers in essence estimate time-series regressions of the form
![]()
Here ΔHi,t denotes the change across years in the homicide rate in place I, and ΔHUS,t denotes the similar change in the United States as a whole. The researchers attempt to motivate this regression specification by analogy to the capital asset pricing model (CAPM) of finance.8 These studies, for periods with executions, evaluate deterrence by asking whether β, the average of ΔHi,t, and the average of εi,t is smaller in periods in which capital punishment either is possible or actually occurs. Taken as a whole, these studies find a deterrent effect for a capital punishment regime.
The committee concludes that the findings of these studies are not interpretable as providing evidence of a deterrent effect. The basic problem is that the analogy between a portfolio of assets and a portfolio of crimes is specious. The homicide model under study is constructed exclusively by analogy with finance. It pays no attention to the criminal justice system as an input in criminal decisions, time constraints on the part of criminals, differences in the reasons for crimes, etc. The various studies that use this methodology assert that all such factors are incorporated in the coefficient β, but there is no reason to believe that this is true. Because CAPM is predicated on investors’ optimally investing in financial instruments in the context of competitive markets for these products, for Cloninger’s specification to be sensible he would have to demonstrate that potential murderers engage in an analogous optimization problem that is aggregated to produce state-level homicide rates. No attempt is made to demonstrate this analogy.
Yet another time-series approach to measuring the deterrent effect of capital punishment is comparison of time series for homicides in two countries, one of which has capital punishment and the other of which does not,
__________________
8 The capital asset pricing model describes the relationship between risk and expected return for different assets. See Brennan (2008) for a description.
to see whether one can identify differences between the time series that may be plausibly attributed to capital punishment. In Chapter 3, for example, the committee displays homicide rates in, California, New York, and Texas, from 1974 through the early 1990s (see Figure 3-3) to illustrate the importance of accounting for variations, across time and place, in factors that influence murder rates other than the use of capital punishment. Donohue and Wolfers (2005) use this method and argue that the close tracking of the U.S. and Canadian homicide rates calls into question any deterrence effect to the death penalty, since this punishment only exists in the United States. Their argument is at best suggestive because they do not account for common trends in the two series, let alone common factors, such as the interdependence of the Canadian and American economies. It also does not take into account the de facto moratorium in the death penalty in the United States prior to the Furman decision. Thus, the fact that the U.S. and Canadian homicide series are highly correlated is not a legitimate basis for concluding that there is no deterrent effect of capital punishment in the United States.
In examining the cross-country differences in the homicide series in Singapore and Hong Kong, Zimring, Fagan, and Johnson (2010), to their credit, recognized that an informal comparison from two selected entities alone is not sufficient to draw inferences. Unfortunately, their more systematic efforts cannot address the data and modeling flaws in the study.
The basic idea of the Zimring, Fagan, and Johnson (2010) study is to see whether differences in the Singapore and Hong Kong homicide rates can be explained by execution rates in Singapore, none having occurred in Hong Kong over the time frame of the analysis. Letting hS,t denote the Singapore homicide rate in year t and hHK,t the Hong Kong homicide rate in year t, the paper examines whether hS,t – hHK,t, once trends are accounted for, is associated with either the execution rate for Singapore or the execution level in Singapore. Both contemporaneous and lagged effects of these execution variables are considered.
Singapore and Hong Kong were chosen on the basis that they are very similar polities, so that differences in the homicide rates between them cannot be attributed to differences in demographics or socioeconomic factors. The researchers further argue that the relative commonality of executions in Singapore in contrast with the United States makes the analysis of the two cities particularly informative. The study concludes that executions do not have predictive power for homicide differences between the two cities.
The committee concludes that this study fails to provide evidence on the deterrence question. One problem with the analysis has already been raised in our critical discussion above of the vector autoregression approach to deterrence: the failure to distinguish between the effects of a sanction regime on homicides and the effects of fluctuations in the rate of execu-
tions. The researchers argue that “Singapore is a best case for deterrence because a death sentence is mandatory for murder and because of celerity in the appeals process” (Zimring, Fagan, and Johnson, 2010, p. 2). In other words, Singapore, like Hong Kong, has a constant sanction regime over the sample. The authors (pp. 9-10) raise the idea that the execution rate matters for a potential murderer’s beliefs about the likelihood of being executed, but this assertion is rendered less plausible by their claims of regime stability for Singapore. If one thinks that deterrence depends on perceptions of the sanction regime, then the authors’ own argument about regime stability undermines a role for executions in learning. Such stability eliminates one channel by which executions might be informative about deterrence.
A distinct reason that this study is not informative about the deterrent effect of capital punishment is that the key assumption underlying the analysis—that any systematic or predictable component of the homicide rate difference, hHK,t – hS,t, can only be due to capital punishment—is not credible. The paper’s own regressions lead inevitably to this conclusion. In addition to studying the difference hHK,t – hS,t, the researchers also perform regressions of the Singapore homicide rate hS,t on the Hong Kong homicide rate hHK,t and their various execution measures. The logic of their thought experiment would require that hHK,t is a statistically significant predictor of hS,t, with a regression coefficient of 1. The validity of their analysis, in other words, is predicated on the assumption that the homicide rate in Hong Kong is a sufficient statistic for the homicide rate in Singapore, except for the presence of capital punishment in Singapore. In fact, the study found that the homicide rate in Hong Kong fails to predict the homicide rate in Singapore: the coefficient is far from 1 in value and far from statistical significance. Hence, the researchers’ own analysis indicates that the key assumption that justifies their analysis is not valid.
The study by Zimring, Fagan, and Johnson (2009) also suffers from first-order data problems. As the researchers note, the government of Singapore does not publish statistics on executions, and it routinely executes individuals convicted of a wide variety of crimes other than homicide. This leads the researchers to rely on constructed measures of executions and executions for murder. However, there are problems in the use of these constructed series. First, measurement error in independent variables produces biased estimates of coefficients; in the standard bivariate regression model, this bias reduces coefficient magnitude toward 0. Hence, their finding of a lack of evidence may be due to defects in their measure. The best the researchers can say about their estimated overall homicide series is that “we have developed a reliable minimum estimate of Singapore executions since 1981” (Zimring, Fagan, and Johnson, 2009, p. 7). This is uninformative as to what the degree of bias is in their estimates.
Second, the authors end up in an incoherent position in terms of map-
ping executions to the perceptions of potential murderers. In response to the lack of data on the split between executions for murder and executions for other crime, they argue that “But, of course, no data are available to the citizens of Singapore either, so the gross execution rate may be the appropriate risk for homicide to the extent that potential homicide offenders are aware of executions” (p. 6). The authors give no explanation as to how the potential murderers could possibly be aware of the overall execution rate but have no knowledge of the execution rate for particular offenses. Since the researchers conclude that data limitations prevent them from providing “stable and robust estimates of the unique effects of murder executions on murder” (p. 22), it is not clear why their negative findings on deterrence are informative about deterrence for murder.
The issue is not whether the authors did the best they could with the limited data, but whether the limited data allow one to draw inferences about deterrence. Note as well that given the researchers’ own description of capital punishment in Singapore—“The secret nature of both individual executions and aggregate murder statistics must be a deliberate choice of the highly centralized and statistically meticulous Singapore government” (p. 10)—there is no good reason to believe that any results from their study are informative about capital punishment in the United States, where information available to the public is of course completely different, leaving aside all other differences between the two countries.
The committee analysis of the different strategies for using time series to uncover deterrent effects for capital punishment has consistently found the inferential claims to be flawed, whether the study in question does or does not find evidence of a deterrence effect. A common theme in our critiques of individual studies is that the underlying “decision theory” of potential murderers is consistently un- or underspecified, so that the implications of the time-series relationships between executions and homicide rates is unclear. Why should actual executions, as opposed to the sanction regime, matter? As discussed above, following the logic of the strong form of the rational-criminal model that assumes rational expectations, there should be no effect from executions by themselves, since the sanction regime entirely determines the deterrence effect. This fact means that the time-series studies suffer from a common identification problem: the existence of plausible theories of the behavior of potential murderers for which the time-series relationships are uninformative about the presence or absence of a deterrence effect, let alone its magnitude.
Of course, it is possible that the correct behavioral model for potential murderers is one for which the time-series relationships are informative.
One possibility is that actual executions affect a potential murderer’s subjective probability of being executed if he commits the crime. If this is the rationale for the exercises, then Texas is not the ideal context for a study because executions are sufficiently routine in Texas that one would expect the informational content of a specific occurrence to be low. Yet because of the state’s high fraction of executions nationally, Texas data are frequently used for studies. Texas might have experienced changes in the execution sanction regime, which would be useful for identifying deterrent effects, but this perspective has not been systematically explored, despite some occasional references to regime shifts in Texas.9 In this respect, we think that the focus on Texas in the time-series literature may be misguided.
Another behavioral framework under which these exercises are informative is one in which an execution renders the possibility of the punishment more salient to a potential murderer. But such a framework would appear to imply that the effects of an execution will exhibit heterogeneity across types of potential murderers. For example, when murder is a crime of passion, one might argue that executive mental functioning is impaired. Hence, in this case salience comes into play because of a diminished capacity in thinking about consequences. Alternatively, one could argue that the impairment is such that the consequences of the action do not affect choice. This example illustrates that the implications of salience claims are far from obvious. Furthermore, we are unaware of any work that directly addresses salience as a source of deterrence and does so in a way that respects the fact that one needs a model of behavior, whether of the rational choice type or not, to interpret statistical findings.
Finally, we note that it is not even clear that executions per se are the source of salience. Is it obvious that actual executions are the main source of salience of the death penalty rather than, say, highly publicized death sentences? How do changes in the law or Supreme Court decisions affect salience? In the committee’s search of relevant studies, we did not find any in which the sources of salience were explored. Hence, although it is a perfectly logically coherent idea that executions make capital punishment salient and provides a deterrence effect for this reason, there is no empirical work to justify the claim. One of the recommendations in Chapter 6 will involve the collection of data on perceptions of sanction regime, which would facilitate such empirical work.
Another distinct problem with the time-series studies is that they do
__________________
9 Land, Teske, and Zheng (2009) should be commended for distinguishing between periods in Texas when the use of capital punishment appears to have been erratic and when it appears to have been systematic. But they fail to integrate this distinction into a coherently delineated behavioral model that incorporates sanctions regimes, salience, and deterrence. And, as explained above, their claims of evidence of deterrence in the systematic regime are flawed.
not provide a logical basis for linking the statistical findings back to a state’s capital punishment sanction regime. Suppose, for example, that an execution event study was conducted that provided credible evidence that the execution either increased or decreased homicides that are eligible for capital punishment. Such a study would not provide the basis for altering the sanction regime to either increase or decrease the number of executions because it would not be informative about what aspect of the regime caused the execution to have the effect identified by the study.
In summary, the committee finds that adequate justifications have not been provided to demonstrate that the various time-series-based studies of capital punishment speak to the deterrence question. It is thus immaterial whether the studies purport to find evidence in favor or against deterrence. They do not rise to the level of credible evidence on the deterrent effect of capital punishment as a determinant of aggregate homicide rates and are not useful in evaluating capital punishment as a public policy.
Ash, R.B., and Gardner, M.F. (1975). Topics in Stochastic Processes. New York: Academic Press.
Bailey, W.C. (1998). Deterrence, brutalization, and the death penalty: Another reexamination of Oklahoma’s return to capital punishment. Criminology, 36(4), 711-733.
Becker, G.S. (1968). Crime and punishment: An economic approach. Journal of Political Economy, 76(2), 169-217.
Brennan, M. (2008). Capital asset pricing model. In S.N. Durlauf and L. Blume (Eds.), The New Palgrave Dictionary of Economics (revised ed., vol. 1, pp. 641-648). London: Palgrave MacMillan.
Charles, K.K., and Durlauf, S. (in press). Pitfalls in the use of time series methods to study deterrence and capital punishment. Submitted to Journal of Quantitative Criminology, 28.
Cloninger, D.O. (1992). Capital punishment and deterrence: A portfolio approach. Applied Economics, 24(6), 635-645.
Cloninger, D.O., and Marchesini, R. (2001). Execution and deterrence: A quasi-controlled group experiment. Applied Economics, 33(5), 569-576.
Cloninger, D.O., and Marchesini, R. (2006). Execution moratoriums, commutations and deterrence: The case of Illinois. Applied Economics, 38(9), 967-973.
Cochran, J.K., Chamlin, M.B., and Seth, M. (1994). Deterrence or brutalization—An impact assessment of Oklahoma’s return to capital-punishment. Criminology, 32(1), 107-134.
Donohue, J.J., and Wolfers, J. (2005). Uses and abuses of empirical evidence in the death penalty debate. Stanford Law Review, 58(3), 791-845.
Durlauf, S., and Nagin, D. (2011). The deterrent effect of imprisonment. In P.J. Cook, J. Ludwig, and J. McCrary (Eds.), Controlling Crime: Strategies and Tradeoffs (pp. 43-94). Chicago: University of Chicago Press.
Federal Bureau of Investigation (2011). Uniform Crime Reports: Estimated Murder Rate in Texas 1960-2009. Available: http://www.ucrdatatools.gov [December 2011].
Granger, C.W.J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424-438.
Grogger, J. (1990). The deterrent effect of capital punishment: An analysis of daily homicide counts. Journal of the American Statistical Association, 85(410), 295-303.
Hjalmarsson, R. (2009). Does capital punishment have a “local” deterrent effect on homicides? American Law and Economics Review, 11(2), 310-334.
Land, K.C., Teske, R.H.C., and Zheng, H. (2009). The short-term effects of executions on homicides: Deterrence, displacement, or both? Criminology, 47(4), 1,009-1,043.
Leeper, E.M., and Zha, T. (2003). Modest policy interventions. Journal of Monetary Economics, 50(8), 1,673-1,700.
Leeper, E.M., Sims, C.A., and Zha, T. (1996). What does monetary policy do? Brookings Papers on Economic Activity, 1996(2), 1-78.
Liebman, J., Fagan, J., and West, V. (2000). Capital attrition: Error rates in capital cases, 1973-1995. Texas Law Review, 78, 1,839-1,861.
Lucas, R. (1976). Econometric policy evaluation: A critique. Carnegie-Rochester Conference Series on Public Policy, 1, 19-46.
Marschak, J. (1953). Economic measurements for policy and prediction. In W.C. Hood and T.C. Koopmans (Eds.), Studies in Econometric Method (pp. 1-26). New Haven: Yale University Press.
Phillips, D.P. (1980). The deterrent effect of capital punishment: New evidence on an old controversy. American Journal of Sociology, 86(1), 138-148.
Phillips, D.P. (1982). The fluctuation of homicides after publicized executions: Reply. American Journal of Sociology, 88(1), 165-167.
Sims, C.A. (1972). Money, income, and causality. American Economic Review, 62(4), 540-552.
Sims, C.A. (1980). Macroeconomics and reality. Econometrica, 48(1), 1-48.
Sims, C.A., Goldfeld, S.M., and Sachs, J.D. (1982). Policy analysis with econometric models. Brookings Papers on Economic Activity, 1982(1), 107-164.
Stolzenberg, L., and D’Alessio, S.J. (2004). Capital punishment, execution publicity, and murder in Houston, Texas. Journal of Criminal Law and Criminology, 94(2), 351-379.
Texas Department of Criminal Justice. (2011). Executed Offenders. Available: http://www.tdcj.state.tx.us/death_row/dr_executed_offenders.html [December 2011].
Zeisel, H. (1982). The deterrent effect of capital-punishment—Comment. American Journal of Sociology, 88(1), 167-169.
Zimring, F.E., Fagan, J., and Johnson, D.T. (2010). Executions, deterrence, and homicide: A tale of two cities. Journal of Empirical Legal Studies, 7(1), 1-29.


























