TABLE A-1
Stationary Population Process Model for Population Age j at Year i
|
Measure |
Formulation |
|
1. Population Size (N) |
For year i = 1: Nij = age – specific population size For year i > 1: Nij = Ni-1,j-1 – DWi-1,j-1 – CPi-1,j-1 |
|
2. Target Population (T) |
No Vaccine: Tij = Nij × Proportion Targetij where Proportion Targetij = 0 Vaccine Steady State for year i = 1: Tij = Nij × Proportion Targetij where Proportion Targetij = 1 Vaccine Introduced: Tij = Nij × Proportion Targetij with Proportion Targetij = Input (% of N)ij |
|
3. Vaccinated Immune (V) |
Vij = Tij × coverage rateij × effectivenessij |
|
4. Vaccinated Susceptible (VS) |
VSij = Tij × coverage rateij × (1 – effectivenessij) |
|
5. Not Vaccinated Immune (B) |
Bij = (Vij / herd immunityij) – Vij |
|
6. Not Vaccinated Susceptible (BS) |
BSij = Nij – Vij – VSij – Bij |
|
7. Total Cases (C) |
Cij = (VSij + BSij) × incidence rate |
|
8. Deaths by Disease (D) |
Dij = Cij × case fatality rate |
|
Measure |
Formulation |
|
9. Cases: Impairment (CP) |
CPij = (Cij – Dij) × proportion cases impaired |
|
10. Cases: Morbidity (CM) |
CMij = Cij – Dij – CPij |
|
11. Vaccine Complications (A) |
Aij = (Vij + VSij) × vaccine complications rate |
|
12. All Cause Deaths (DA) Including Disease |
No Vaccine: DAij = Nij × all cause mortality rate Vaccine Steady State: DAij = (Nij × all cause mortality rate) – Deaths averted by vaccine * Deaths averted by vaccine = Vaccine Steady State Dij – No Vaccine Dij Vaccine Introduced: DAij = (Nij × all cause mortality rate) – Deaths averted by vaccine * Deaths averted by vaccine = Vaccine Introduced Dij – No Vaccine Dij |
|
13. Cause Deleted Deaths (DE) Excluding Disease |
DEij = DAij – Dij |
TABLE A-2
Health and Economic Values for Population Age j at Year i
|
1. Premature Deaths Averted per Year |
|
|
2. Incident Cases Prevented per Year |
|
|
3. Quality-Adjusted Life Years (QALYs) Gained |
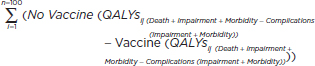 |
|
4. Disability-Adjusted Life Years (DALYs) Gainedaa |
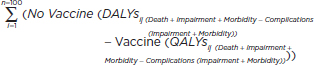 |
|
5. Net Direct Costs |
|
|
6. Delivery Costs |
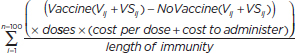 |
|
7. Health Care Costs (HC) Averted |
 |
|
8. Workforce Productivity (WP) Gained per Year |
 |
|
9. One-Time Costs |
Cost Research + Cost Licensure + Cost Start Up |
aFox-Rushby, J. A., and Hanson, K. 2001. Calculating and presenting disability-adjusted life years (DALYs) in cost-effectiveness analysis. Health Policy and Planning 16(3):326-331.
TABLE A-3
Detailed Expressions (in Reference to Table A-1 and Table A-2)
|
Measure |
Formulation |
|
|
All Cause Mortality Rate (Derived by Life Table Over Interval)a |
||
|
QALYsDeath |
||
|
QALYsImpairment by disease or complication |
||
|
QALYsMorbidity by disease or complication |
||
|
Disability-Adjusted Life Years (DALYs) Generalizationb |
Years of Life Lost (YLL) + Years of Life Lived with Disability (YLD) |
|
|
YLD or YLL (W = 1) |
||
|
DALYs Variables |
K = age weight modulation factor (0 = off, 1 = on) F = constant (0.1658) r = discount rate j = age of death (YLL) or age of onset of disability (YLD) G = parameter form the age weighting function (0.04) L = standard expectation of life at age a (YLL) or duration of disability (YLD) W = disability weight (YLD) |
|
|
DALYsDeath |
||
|
DALYsImpairment by disease or complication |
||
|
DALYsMorbidity by disease or complication |
||
|
Health Care Costs (HC)Death |
||
|
HCImpairments by disease or complication |
||
|
HCMorbidity by disease or complication |
 |
|
Measure |
Formulation |
|
|
Workforce Productivity (WP) Gained DeathDeath |
||
|
WPImpairment by disease or complication |
||
|
WPMorbidity by disease or complication |
aPreston, S., P. Heuveline, and M. Guillot. 2000. Demography: Measuring and modeling population processes. Chapter 3: The Life Table and Single Decrement Process. P. 46.
bFox-Rushby, J. A., and K. Hanson. 2001. Calculating and presenting disability adjusted life years (DALYs) in cost-effectiveness analysis. Health Policy and Planning 16(3):326–331.






