10
Seafloor Diagenetic Fluxes
W.R. MARTIN AND F.L. SAYLES
Woods Hole Oceanographic Institution
INTRODUCTION
Early diagenesis is an important contributor to the oceanic cycles of many components of seawater. In many cases, the flux across the sediment-water interface resulting from early diagenesis is comparable to input rates to the ocean from other sources. In the cases of many bioactive elements, the early diagenetic flux is considerably larger than, for instance, the riverine input to the ocean, as early diagenesis is intimately involved in the rapid cycling of these elements within the ocean. However, a general characteristic of early diagenetic fluxes, both for bioactive components of seawater and for the major seawater ions, is that they affect oceanic concentrations on long time scales, ranging from 104 to 107 years.
The study of early diagenesis is important to the study of ocean hisory, as early diagenetic reactions play an important role in fixing sediment composition. Diagenetic fluxes exceed burial rates for the major bioactive elements: about 90 percent of the organic carbon rain to the sea floor degrades during early diagenesis; over 60 percent of the biogenic silica, and about 80 percent of the CaCO3 reaching the sea floor dissolve. Thus, variations in diagenetic reaction rates can have disproportionately large effects on sedimentary concentrations and accumulation rates of these components.
It is important to recognize that, at the present time, any analysis of the role of early diagenesis in oceanic processes is data-limited. The spatial coverage of measurements is limited; more importantly, the interpretation of results often depends on the measurement technique used. For this reason, we begin our evaluation of early diagenetic fluxes with a review of measurement techniques and uncertainties. Then, we examine the ways in which early diagenesis affects the modern oceanic cycles of the major seawater ions, carbon, and silicon; and we examine its effects on the sedimentary record of ocean history as it is interpreted using organic carbon, CaCO3, and opal data.
THE MEASUREMENT OF BENTHIC FLUXES
The most sensitive indicators of early diagenetic reactions are the fluxes of dissolved reactants or products across the sediment-water interface. If the sedimentary system is in quasi-steady state over the time scale of the reaction of interest, the benthic fluxes of the reactants and/or products provide a measure of the reaction rate, integrated over the sediment column. Several considerations are essential to an evaluation of benthic flux measurements. Among the most important are the possibility of measurement artifacts, the resolution of the measurement method relative to the characteristic length or time of the
reaction being monitored, and the importance of model assumptions to the flux calculation.
Most benthic flux estimates made to date have been obtained by applying transport models to concentration versus depth profiles of pore water solutes. An important feature of these estimates is that they are only as accurate as the transport parameters needed to convert the concentration measurements into flux estimates. In pelagic sediments, the dominant transport process is molecular diffusion; here, accurate estimates of sediment diffusivity and porosity near the sediment-water interface are required. In continental margin sediments, solute transport is enhanced over that due to diffusion by biologically and physically driven irrigation, and models applied to pore water profiles must include independent estimates of the effects of these processes (Aller, 1980b; Christensen et al., 1984). Benthic flux estimates that are less dependent on transport models are obtained through the use of benthic flux chambers. In these experiments, sediments and a small volume of overlying water are enclosed for incubation periods of hours to about a month, and changes in concentration of diagenetic products or reactants in the overlying water are monitored. It appears that, with the possible exception of reactions with scale lengths on the order of a millimeter, the assumptions leading from these measurements to benthic flux estimates are reasonably robust (e.g., Bender et al., 1989). In the special case of rapid reactions occurring primarily within one or two millimeters of the sediment-water interface, neglect of the diffusive sublayer at the sediment-water interface may lead to erroneous flux estimates (Boudreau and Guinasso, 1982). Benthic flux estimates based on flux chamber experiments are probably preferable to pore water profile based estimates because, in most cases, the estimates are essentially model-independent.
A second consideration that is important to evaluating benthic flux estimates is the resolution of the method used. For pore water profile based estimates, accurate flux calculations depend on the relationship between the length scale over which the diagenetic reaction occurs in the sediments and the sampling length scale. Because many reactions occur on length scales of millimeters to one or two centimeters in many locations (Emerson and Bender, 1981; Bender and Heggie, 1984; Reimers, 1987; Bender et al., 1989), sampling resolution is an important limitation of many pore water based flux estimates. "Traditional" core sectioning and centrifuging/squeezing methods have been used with a resolution of 0.5 to 2 cm. In situ sampling methods based on "harpoon"-type samplers (Sayles et al., 1973b), while free of the artifacts associated with core recovery, have been limited to a sampling resolution of 2 to 5 cm. Recently, two methods capable of in situ measurement of several pore water components have begun to be used: electrode techniques for the measurement of dissolved oxygen and pH (Revsbech et al., 1980; Reimers
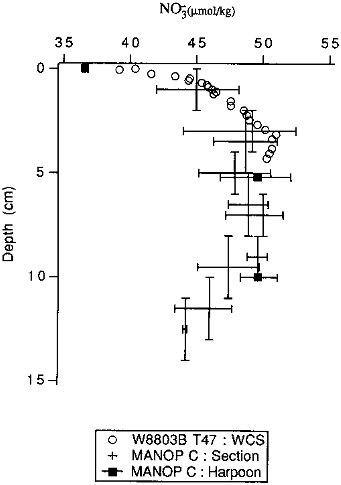
FIGURE 10.1 A comparison of the depth resolution of different pore water sampling techniques. Samples are from the eastern equatorial Pacific. The vertical bars on the section/centrifuge samples represent the sampling interval; the horizontal bars represent the range of values measured in the different cores samples. All MANOP data are from Jahnke et al. (1982b). The wholecore squeezer samples (open circles) are not strictly comparable to the section/centrifuge (crosses) or in situ (closed circles) samples; they were taken at the same latitude as the others but somewhat to the east of them and were taken several years later. Nonetheless, the concentrations are comparable, and the resolution comparison should be valid.
et al., 1986; Archer et al., 1989), and whole-core squeezers for measuring solutes whose concentration is not changed by disturbances of ion exchange equilibria on very short time scales (minutes) (Bender et al., 1987; Martin et al., 1988; Bender et al., 1989). Both of these methods are capable of millimeter-scale resolution. We compare the resolution of several of these techniques in Figure 10.1. For flux chamber based estimates, one must consider whether the experiment length is sufficient to produce a measurable concentration change in the solution component of
interest. Ultimately, experiment length is limited by the need to maintain incubation conditions close to those of the steady state sediment system. In most sediments, experiment length is limited by changes in the bottom water oxygen concentration or by the availability of labile organic matter in the closed system; these limitations make it difficult to measure fluxes of slowly reacting components of the system, particularly if they are present at high concentrations in bottom water. Thus, fluxes of major ions, and, to a lesser extent, ΣCO2, are difficult to measure using benthic flux chambers.
Because the changes in concentration that must be resolved to estimate benthic fluxes are often small, samples must be artifact-free. Artifacts introduced in the recovery of cores from the seafloor are known to significantly alter pore water concentrations for many of the major species of interest here. These artifacts occur as a result of warming during recovery and can strongly affect the major cations through ion exchange reactions (Mangelsdorf et al., 1969; Bischoff et al., 1970; Sayles et al., 1973a). De-pressurization during recovery of cores from the deep sea can also introduce artifacts through CaCO3 precipitation, substantially changing ΣCO2, alkalinity, and Ca2+ concentrations (Murray et al., 1980; Emerson et al., 1982). It is these problems that led to the development of in situ pore water sampling techniques (Barnes, 1973; Sayles et al., 1973b). Comparisons of profiles obtained by in situ and shipboard techniques have shown that shipboard techniques can be used for measuring dissolved oxygen, nitrate, and silicate; they do not appear to be suitable for phosphate measurement (Jahnke et al., 1982b). Because benthic flux chamber measurements are typically carried out in situ, they are free of artifacts due to shipboard separation of pore waters from the solid phases of sediments.
Sampling resolution, measurement artifacts, and transport model assumptions affect fluxes calculated from different measurement techniques to varying extents. There is another important class of model assumptions which affect all flux calculations equally. These assumptions result from our limited knowledge of diagenetically important chemical reactions. The outstanding example, one which will be important to our subsequent discussion, is the calculation of the rate of organic carbon degradation at the sea floor. Because of the difficulty of making artifact-free measurements of dissolved inorganic (and organic) carbon in pore waters, benthic organic carbon degradation rates are often estimated based on fluxes of nitrate and oxygen across the deep sea sediment-water interface, and on fluxes of sulfate in nearshore sediments. Translations of these measurements into organic carbon fluxes require assumptions about the oxidation/reduction stoichiometry of organic carbon degradation reactions (see Table 10.1). The oxidation states of C, N, and H in organic matter are
TABLE 10.1 Organic Matter Degradation Reactions
|

|
generally represented by assuming the elements are present as CH 2O and NH3. All of the the organic C is assumed to be oxidized to CO2; depending on the environmental redox potential, N is oxidized to NO3- (oxic degradation) or N2 (denitrification and Mn reduction), or released as NH3 (Fe reduction, sulfate reduction) (Froelich et al., 1979). Takahashi et al. (1985) have called into question the assumptions about the oxidation states of the reactants, par-
ticularly of organic H: using data taken on isopycnal surfaces in the upper water column, they have shown that the Redfield O2:C ratio may underestimate the true ratio (they estimate 172:122 ± 18 versus 138:106 in the Redfield scheme). In addition, several workers have measured substantial gradients of dissolved organic carbon and nitrogen across the sediment-water interface, both in continental margin and deep-sea sediments (Suess et al., 1980; Elderfield, 1981; Heggie et al., 1987): in several cases, DOC gradients an order of magnitude larger than the inorganic carbon gradients. Unfortunately, the diffusivity of DOC in marine sediments is unknown, and these gradients cannot be translated into fluxes. Existing estimates of the diffusivity of DOC indicate that it may be less than an order of magnitude smaller than that of dissolved inorganic carbon (Mackin, 1986); thus, it cannot be assumed that all organic C is oxidized to CO2 during degradation, and DOC cannot be ignored in the sedimentary carbon budget.
Assumptions about the C:N:P ratio in degrading organic matter are often made when a local, measurement-based estimate is not available. In fact, organic matter composition varies over significant ranges, and accurate calculation of carbon fluxes requires that this compositional variability be taken into account. C:N ratios of degrading organic matter have been estimated by measurements of solid phase elemental ratios (Table 10.2), yielding a range of about a factor of 2, from 6.6 to 12 (compared to the Redfield ratio of 6.6). Sediment trap measurements made by Honjo (1980) and by Martin et al. (1987) show that the C:N ratio at a site increases systematically with depth; Honjo's results also show that sedimentary organic matter has C:N systematically greater than that of the organic matter in deep sediment traps at the same locations (Table 10.2). Thus, organic matter appears to be fractionated during degradation, with N being recycled more rapidly than C (Suess and Muller, 1980; Martin et al., 1987). For that reason, C:N of the solid phase may not be the best measure of C:N of the degrading organic matter. Several workers have used ratios of pore water constituents, usually O2 and NO3- in oxic pelagic sediments, coupled with assumptions about redox stoichiometry, to derive C:N ratios (Berner, 1977). This procedure has yielded a range similar to that of the solid phase analyses, C:N ≈ 7 to 12 (Table 10.2). We conclude that carbon fluxes calculated from NO3- profiles will be systematically low if organic matter is assumed to have Redfield composition, and that an uncertainty of up to ± 50 percent may be introduced if the C:N ratio is not estimated at the measurement site.
In considering the sedimentary dissolution of CaCO3, we must also consider the stoichiometric relationship between organic carbon degradation and CaCO3 dissolution. Several lines of evidence indicate that, in the presence of CaCO3 in sediment, organic matter produced CO2 reacts essentially to completion and the stoichiometry as given in Table 10.1 is a reasonable representation of O2 oxidation
TABLE 10.2 C:N Ratios
|
Location |
C:N |
Sourcesa |
|
A. Solid Phase Analysis |
||
|
U.S. Atlantic Coast Continental Margin |
7.6 to 8.3 |
1 |
|
Hatteras Continental Rise |
8.6 ± 0.1, 8.4 ± 0.3 |
2 |
|
Hatteras Abyssal Plain |
7.0 ± 0.7, 5.4 ± 1.9, 6.6 ± 0.8 |
2 |
|
Bermuda Rise |
6.6 ± 0.8 |
2 |
|
Sargasso Sea |
5200 m trap: 7.4; sediment: 8.0 |
3 |
|
Equatorial Atlantic |
5000 m trap: 10.5; sediment: 12 |
3 |
|
Pacific Gyre |
5600 m trap: 9.6; sediment: 11 |
3 |
|
B. Pore Water ∆O2/∆NO3 – and -∆O2/∆ΣCO2 = 138:106 |
||
|
Central Equatorial Pacific |
8.1 ± 2.2 |
4 |
|
Eastern Equatorial Pacific |
7 |
5 |
|
Subtropical South Pacific |
12 |
6 |
|
Eastern Equatorial Pacific, |
|
|
|
10°S to 11°N |
7.6 ± 1.9 |
7 |
|
C. Nearshore sediments: SO42- reduction rate/NH4+, production rate and -∆ΣCO2/∆SO42- = 2 |
||
|
Long Island Sound |
5.5 to 10.7 |
8 |
|
a Sources (see references): 1—Premuzic et al. (1982); 2—Heggie et al. (1987); 3—Honjo (1980); 4—Grundmanis and Murray (1982); 5—Jahnke et al. (1982b); 6—Bender et al., 1985/1986); 7—Martin, Bender, Leinen, unpub. data; 8—Aller (1980a). |
||
and CaCO3 dissolution. Sayles (1981) and Emerson et al. (1982) both have shown that the observed relationship between Ca2+ and alkalinity is that predicted by the stoichiometry of Table 10.1. The ratio of ΣCO2 to alkalinity is similarly that which is predicted. Finally, the isotopic composition of the ΣCO2 added to the pore solutions requires a stoichiometry at least close to that predicted (McCorkle et al., 1985), although Sayles and Curry (1988) conclude that dissolution is perhaps 25 percent less than the predicted value. The relatively small departures from ideal stoichiometry reported by Sayles and Curry notwithstanding, it appears that the dissolution of CaCO3 can be calculated from ΣCO2 fluxes with reasonable accuracy.
It is clear that the calculation of early diagenetic fluxes depends to a significant degree on the measurement techniques used and on assumptions about the physical and chemical processes determining the fluxes. Any assessment of the importance of early diagenetic fluxes in surficial geochemical budgets must take the effects of experimental limitations and model assumptions into account. Because of the limited use of flux chambers and fine-resolution pore water sampling devices to date, most of the fluxes we discuss below were obtained with resolution-limited pore water sampling techniques. Fluxes of the major ions and estimates of calcium carbonate dissolution rates are based on in situ techniques, with a resolution of 2 to 5 cm, because of shipboard sampling artifacts for these components. For this reason, our flux estimates must be considered to be lower limits of the true fluxes.
EARLY DIAGENESIS AND MODERN OCEANIC CYCLES
Early diagenetic fluxes fulfill two roles in the modern oceanic cycles of the elements we are considering. For some, the reactions represent a primary input or removal term in the oceanic budget: they are a source of new dissolved material to seawater, or they remove solutes directly from seawater. Na, K, and Mg are affected in this way. For others, early diagenesis forms a part of the element's internal oceanic cycle: material that is fixed into the solid phase in the oceanic water column undergoes degradation during early diagenesis such that a significant portion is recycled back to the water column. The small fraction of the rain of these elements to the sea floor that survives degradation during early diagenesis represents a slow leak from the oceanic cycle. The bioactive elements fall into this category: C, Si, and Ca.
Na, K, and Mg
The early diagenesis of aluminosilicate minerals in oceanic sediments is characterized by the uptake of K+ and Mg2+ from seawater, and by the addition of Na+ and protons to seawater (Sayles, 1979). The reaction rate is slow enough that the resultant change in the composition of the sediments is not measurable; but the reaction rates can be determined by precise, artifact-free measurements of dissolved fluxes across the sediment-water interface. Sayles (1979; 1981) has estimated benthic fluxes from in situ sampled pore waters, using model fits to the pore water concentration versus depth data, at a large number of stations in the temperate north and south Atlantic, the Caribbean Sea, and the southern ocean between Africa and Antarctica. Representative data are shown in Figure 10.2. It is important to note that the first sample is at 5 cm below the sediment-water interface. The changes with depth of the Na+, K+, and Mg2+ concentrations appear to be slow enough for this relatively poor resolution not to affect the calculated fluxes greatly, but the fluxes will tend to represent lower limits on the early diagenetic reaction rates. The results of these studies are summarized in Table 10.3. The importance of these fluxes in the oceanic budgets of Na, K, and Mg can be estimated by integrating the fluxes, weighting global sediments crudely as 30 percent "margin" and 70 percent "central" (Table 10.4). In the case of Mg and K, early diagenetic reactions remove the elements from seawater at rates that are very nearly equal to their input rates from rivers; and Na is added to seawater at a rate comparable to its river input. There is little doubt that diagenetic fluxes are important to the oceanic cycles of these components of sea water. The time scale of changes in oceanic concentrations of these components that would result from changes in diagenetic processes is slow: the oceanic reservoir for each element is in excess of 1019 moles, giving them residence times with respect to diagenetic fluxes of millions of years.
C, Ca, and Si
Carbon, calcium, and silicon show broadly similar behavior in the oceans. Each is fixed into the solid phase by organisms living in the surface ocean: carbon by reduction during photosynthesis, calcium and silicon by precipitation to form the tests of planktonic organisms. The C, Ca, and Si rich particles degrade as they fall through the water column, and degrade further at the surface of the sediments. The result is that a slow input to the oceans, from rivers, and, to a lesser extent for Si and Ca, from seafloor hydrothermal activity, is balanced by a slow loss via burial in sediments; and rapid cycling between dissolved and particulate forms takes place within the oceans. Early diagenesis is an important part of the internal cycles of these elements.
We illustrate this behavior in Tables 10.5 and 10.6. The residence times of all of these elements are long
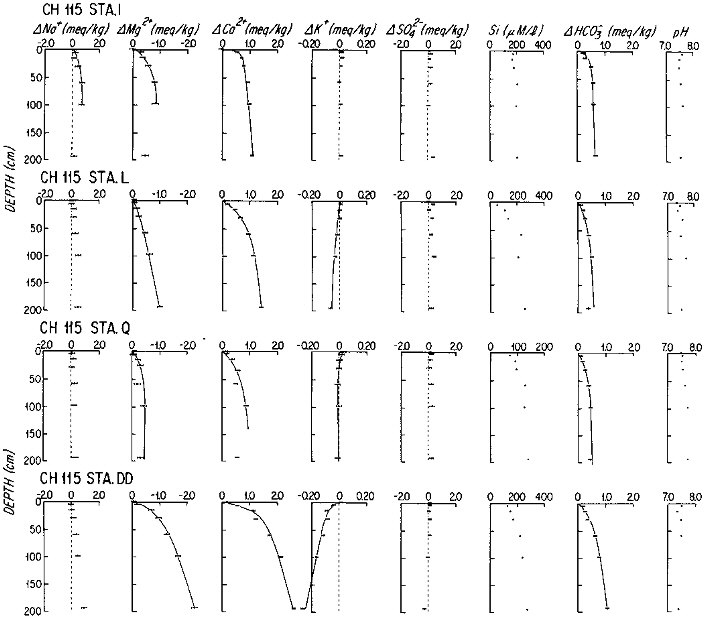
FIGURE 10.2 Profiles of the major components of seawater in the pore waters of marine sediments from subtropical South Atlantic. Stations I-Q are on the flanks of the Mid-Atlantic Ridge; Station DD is from the continental rise off Brazil. The solid lines are the analytical representation of the data from which fluxes were calculated.
relative to the ocean's mixing time of about 1000 years, ranging from 20,000 years for Si to 130,000 years for C and 106 years for Ca. They are fixed into particles in the surface ocean at a much faster rate: Ca at a rate 5 times faster than its input and burial rates, Si 25 times faster, and C 350 times faster. C, the most rapidly cycled of the three, is effectively remineralized in the surface ocean, and the fraction of primary production that reaches the sea floor is only about 2 percent in the deep sea (Smith and Hinga, 1983; Jahnke and Jackson, 1987), and 10 percent on the continental margins (Henrichs and Reeburgh, 1987). Si is the next most rapidly remineralized, as the surface ocean is highly undersaturated with respect to the solid phase present (Hurd, 1972): it has been estimated that about 55 percent of the biogenic silica precipitated in the surface ocean redissolves in the water column (e.g., Calvert, 1983), most of it in the surface ocean (Edmond, 1974). In contrast, the surface ocean is supersaturated with respect to the important CaCO3 minerals. While the deep ocean is undersaturated with respect to aragonite, large areas of the sea floor underlie water columns that are saturated with respect to calcite throughout their length. The proportion of the CaCO3 fixed in the surface ocean that reaches the sea floor is variable (e.g., Honjo, 1980; Dymond and Collier,
TABLE 10.3 Fluxes of Major Components of Seawater Across the Sediment-Water Inferface Estimated from In-Situ Sample Pore Water Profiles
|
|
Units of mEq/yr |
|
||||
|
|
Na |
Mg |
Ca |
K |
HCO3- |
Sourcesa |
|
Continental Margins Areas |
||||||
|
Northwest Atlantic (6)b |
3.5 |
-4.0c |
8.2 |
-0.2 |
10.3 |
2,3 |
|
Southwest Atlantic (4) |
0.7 |
-3.1 |
5.1 |
-0.7 |
3.8 |
1 |
|
Caribbean (7) |
2.1 |
-5.4 |
5.4 |
-0.1 |
5.8 |
1 |
|
South African (4) |
9.8 |
-10.0 |
13.0 |
-0.3 |
10.2 |
2 |
|
East Equatorial Pacific (2) |
— |
— |
9.9 |
— |
17.7 |
3 |
|
Average |
3.7 |
-5.6 |
7.8 |
-0.6 |
8.4 |
|
|
Central Areas |
||||||
|
Carbonate Rich (8) |
||||||
|
North Atlantic (6) |
4.0 |
-4.0 |
6.3 |
-0.2 |
8.4 |
2 |
|
South Atlantic (9) |
0.9 |
-1.5 |
2.8 |
-0.4 |
2.8 |
1 |
|
Average |
2.1 |
-2.5 |
3.4 |
-0.3 |
5.0 |
|
|
Biogenic SiO2 Rich |
||||||
|
Indian Ocean (7) |
1.2 |
1.5 |
1.8 |
-0.04 |
3.1 |
2 |
|
a Sources (see references): 1—Sayles (1979); 2—Sayles (1981); 3—Sayles and Curry (1988). b Number of stations used in average. c Negative numbers refer to a flux into the sediment from the overlying water. |
||||||
TABLE 10.4 Diagenetic Fluxes Between Sediment and the Oceans. Estimated from In-Situ Pore Water Profiles
|
|
Units of 1018 mEq/yr |
||||
|
|
Na |
Mg |
Ca |
K |
HCO3- |
|
"Margin" Areas |
3.6 |
-5.4 |
7.5 |
-5.8 |
8.1 |
|
Central Areas |
4.3 |
-5.2 |
6.9 |
-6.6 |
10.4 |
|
Total |
7.9 |
-10.6 |
14.4 |
-1.1 |
18.5 |
|
River Fluxa |
8.3 |
11.7 |
27.2 |
1.3 |
33.3 |
|
a Cation data from Martin and Meybeck (1979); HCO3- from Meybeck (1982). |
|||||
1988, Walsh et al., 1988), but CaCO3 is the most slowly cycled of the three biogenic sediment components.
The order of importance of early diagenesis to the internal cycles of the elements is, then, Ca > Si > C. We have estimated the involvement of early diagenesis by comparing its rate to the rate of formation of the solid phase in the surface ocean (Table 10.6). For carbon, we have calculated the early diagenetic flux as the difference between the rain rate to the sea floor and the burial rate, with the rain rate estimated from surface water productivity and compilations of benthic flux measurements for the deep sea (Smith and Hinga, 1983; Jahnke and Jackson, 1987), and a water column particle degradation model for coastal regions (Henrichs and Reeburgh, 1987). For Ca and Si, we show two estimates: in each case, the lower of the two is derived from compilations of pore water profile based benthic flux measurements, and the higher value is derived from steady-state ocean models. Both estimates are uncertain. Those based on benthic fluxes are lower limits, and are likely to be underestimates. This is especially true for Ca, since the pore water sampling was by coarse-resolution, in situ methods (Sayles, 1979, 1981), whereas the CaCO3 dissolution rate in surficial sediments is very rapid (Keir, 1983). Our estimates for the rate of benthic degradation of solid phase organic carbon, CaCO3, and SiO2 relative to the rates of formation of the solids: about 4 percent of the organic carbon formed annually degrades in the sediments, 5 to 40 percent of the SiO2, and 10 to 80 percent of the CaCO3. For the latter two, and especially for CaCO3, the lower estimate is probably unrealistic. Early diagenesis is a minor player in the cycling within the ocean of organic carbon, but is quantitatively significant both for CaCO3 and SiO2.
Early diagenetic reactions are clearly important determinants of the loss rates of all three elements from the oceans. Over 90 percent of the organic carbon rain to the sea floor degrades during early diagenesis, as do 30 to 80 percent of the CaCO3 rain and 50 to 90 percent of the SiO2 rain. Thus, the rates of early diagenetic reactions are generally larger than burial rates. If other parts of the oceanic cycles remain constant, changes in the rates of early diagenetic reactions must be reflected in changing burial rates.
TABLE 10.5 Oceanic Residence Times: C, Ca and Si
TABLE 10.6 Internal Oceanic and Early Diagenesis: Corg, CaCO3, and SiO2
|
|
Organic Carbon (1) |
||||
|
|
Open Ocean |
Coastal |
Total |
CaCo3 (2) |
SiO2 (3) |
|
Fixation in solid phase, Surface clean (moles/yr) |
3 x 1015 |
8 x 1014 |
3.8 x 1015 |
7 x 1013 |
1.7 x 1014 |
|
Flux to sediment/water Interface (moles/yr) |
7 x 1013 |
9 x 1013 |
1.6 x 1014 |
(>2.1 to <7) x 1013 |
(>1.5 to 8) x 1013 |
|
Burial (moles/yr) |
1 x 1012 |
9 x 1012 |
1 x 1013 |
1.4 x 1013 |
7 x 1012 |
|
Fraction of rain to the Seafloor that is recycled |
98% |
90% |
93% |
>30 to <80% |
>53 to 91% |
|
Early diagenetic flux/rate of fixation |
2.3% |
10% |
4% |
>10 to <80% |
>5 to 43% |
|
Sources: (1) Berner (1982), Smith and Hinga (1983), Jahnke and Jackson (1987), Martin et al. (1987); (2)Li et al. (1969), Forelich et al. (1982); (3) Calvert (1983), Ledford-Hoffman et al. (1986). |
|||||
Spatial Variability in Early Diagenetic Reaction Rates
There are significant spatial variations in the benthic degradation/dissolution rates of organic carbon, CaCO3, and SiO2. Quantitative evaluations of the spatial variability of benthic fluxes must take into account many factors affecting reactivity, which we will consider later. With the possible exception of CaCO3, however, there is an underlying correlation between the rain rate to the sea floor and the benthic flux (Reimers, 1989). For the major seawater ions involved in reactions of aluminosilicate minerals (Na, K, Mg), this correlation shows in the fact that the fluxes from sediments adjacent to continental sources of sediment are roughly twice as large as those from areas remote from land masses. The lowest fluxes are observed in sediments composed largely of biogenic silica, in the high latitude Indian Ocean (Table 10.3). For organic carbon, benthic degradation rates have been measured along transects moving away from the continental margins in the North Atlantic and North Pacific, and have been found to decrease systematically moving away from the continent, as does the surface water productivity (Smith and Hinga, 1983; Jahnke and Jackson, 1987). Benthic organic carbon degradation rates also have been measured across the equatorial high productivity zone in the Pacific, and they show a distinct maximum at the equator, where productivity is highest (Martin et al., 1988). Calvert (1983) has compared maps of the rate of extraction of Si from surface waters (Lisitzin et al., 1967) to maps of the asymptotic dissolved SiO2 concentration in sediment pore waters in the Atlantic Ocean. The latter quantity can be considered a rough indicator of benthic flux variations. There is a reasonable correlation, as values of both quantities increase moving toward the African coast in the equatorial Atlantic and moving northward north of about 35° N. Like the organic carbon degradation rate, the SiO2 dissolution rate shows a distinct maximum at the equator in the eastern Pacific (Martin et al., 1988).
The Oxidants for Organic Matter Degradation: O2, N, and S
There is another group of bioactive elements, the oxidants required for organic matter oxidation (O2, SO43-, and NO3-; see Table 10.1), which are removed directly from seawater by early diagenetic reactions. The net rate of loss of SO43- from seawater due to sulfate reduction during organic matter diagenesis is about 0.5 x 1012 moles/yr (Berner, 1982), a rate which is comparable to, but smaller than, the input rate of SO43- to the oceans by rivers and its removal by hydrothermal activity (Edmond et al., 1979). The residence time of S in the oceans with respect to these processes is long, on the order of 107 years. Oceanic dissolved O2 and fixed nitrogen levels may be affected on shorter time scales. Jahnke and Jackson (1987), for instance, used a compilation of benthic flux measurements to conclude that most of the oxygen consumption occurring below 3 km in the oceans is driven by sedimentary organic carbon degradation; and Emerson et al. (1987) inferred from determinations of the amount and lifetime of reactive organic carbon in pelagic sediments that increases in the sedimentary organic carbon degradation rate during the last glacial (due to increases in the sedimentary organic carbon concentration) could have had a significant influence on deep ocean apparent oxygen utilization rates. Sedimentary organic carbon degradation may also have important effects on the oceanic nitrogen cycle. In continental margin sediments, oxygen is often depleted during early diagenesis, and denitrification begins (Table 10.1). NO3- consumed during denitrification most likely is reduced to N2 (Bender et al., 1977; Froelich et al., 1979; Goloway and Bender, 1982; Jahnke et al., 1982a), and the N released from organic matter during denitrification and sulfate reduction also may ultimately be oxidized from NH3 to N2. Thus, organic matter degradation is a fixed nitrogen sink; in fact, some recent estimates of denitrification on continental shelves exceed estimates of inputs of fixed nitrogen to the ocean plus oceanic nitrogen fixation (Codispoti and Christensen, 1985; Christensen et al., 1987).
In this section, we have illustrated the roles of early diagenetic reactions in modern oceanic geochemical cycles. In the case of the elements affected by aluminosilicate mineral alteration reactions, early diagenesis is a primary source of the element to seawater (Na) or sink from seawater (K, Mg). For the bioactive elements, C, Ca, and Si, early diagenesis is an active player in the cycling of the elements within the ocean and an important determinant of loss rates from the ocean. For the major ions of seawater, the residence times of the elements with respect to input or loss due to early diagenesis are on the order of millions of years. The bioactive elements, C and Si, appear to have shorter residence times with respect to early diagenesis, about 104 years. The oxidants used during organic matter degradation are consumed during early diagenesis: for O2 and fixed nitrogen, the consumption rates may be rapid enough to affect oceanic distributions on thousand to ten thousand year time scales.
EARLY DIAGENETIC FLUXES AND THE SEDIMENTARY RECORD
Introduction
In the preceding section we showed that, as a general rule, diagenetic fluxes are small in the sense that changes in them affect oceanic geochemical cycles on time scales of tens of thousands of years. The significance of early diagenesis to the study of shorter-term processes (i.e., processes with time scales of hundreds to a few thousand years) lies in the fact that the history of past climatic change is an important source of information about the causes and effects of future change. Temporal variability in the concentrations and accumulation rates of the biogenic components of marine sediments are a key source of information on changes in oceanic and atmospheric conditions on the thousand to ten thousand year time scale of the events governing glacial-to-interglacial transitions. Because early diagenetic reactions at the surface of sediments may affect the relationship of observed concentrations and accumulation rates to oceanic and atmospheric conditions, correct interpretation of the sedimentary record requires an understanding of the relationships between rain rates to the sea floor, conditions at the surface of the sediments, and the ultimate concentrations and accumulation rates of sediment components.
The role of early diagenesis in fixing sediment accumulation rates can be viewed in terms of a simple mass balance model. In steady state, the rain rate of a sediment component to the sea floor (R) must equal the sum of its degradation/dissolution rate (F) and its burial rate (B). Then, defining the burial efficiency (E) as the fraction of the rain to the sea floor that is preserved,
If E is constant, or if burial rates are much larger than reaction rates, then early diagenetic reactions have little effect on burial rates, and the latter are easily translated into rain rates to the sea floor. We have shown already that this is not true for organic carbon, CaCO3, and SiO2 (Table 10.6): early diagenetic reaction rates are much greater than burial rates for organic carbon, and significantly larger for SiO2 and CaCO3. Burial rates are slow relative to reaction rates for these biogenic materials, and the relationship between
burial rates and rain rates is no longer simple. A numerical example illustrates the point. If 95 percent of the rain of, for instance, organic carbon is degraded during early diagenesis (F/R=0.95), then a 5 percent reduction in F due to a change in the sedimentary environment (F/R=0.9) will cause a doubling of the fraction of the rain that is preserved: the accumulation rate will double with no change in the rain rate. Although early diagenetic reactions affect oceanic concentrations of the chemical species of interest here only on long time scales, they cannot be ignored when sedimentary concentrations are considered: an understanding of early diagenetic reactions is essential to the interpretation of the sedimentary record.
Variations in Burial Efficiency in Marine Sediments: CaCO3, SiO2, and Organic Carbon
The simple mass balance of Eq. (10.1) hides the complexity of the relationships that determine burial efficiency for biogenic materials: relationships between solid phase reactivity, the chemical and biological environment of the sediments, and the transport processes that operate within the sediment column. The relationships can be demonstrated using simple diagenetic models, but application of the models to the problem of predicting spatial and temporal variability in burial efficiency, as well as to the more difficult problem of estimating burial efficiency variations through time from the sedimentary record, requires a wealth of data about early diagenesis. The data base does not yet exist. In the following paragraphs, we will review existing knowledge and present a framework for the examination of relevant sedimentary properties.
Measuring burial efficiencies is a difficult problem. It requires measurement of two of the three variables in Eq. (10.1), coupled with a steady-state assumption. All of the measurement uncertainties we mentioned previously—sampling resolution, stoichiometric uncertainties, possible sampling artifacts—apply to the benthic reaction rate determinations we will use. Additional uncertainties arise from the varying temporal resolution of the different measurements. Sediment trap based rain rate measurements typically average over a one or two year period. Because of the rate at which benthic organic carbon degradation and silica dissolution occur, benthic flux measurements of species involved in these reactions, and also in carbonate dissolution, are averaged over periods which may range from years to hundreds of years. The resolution of burial rate (accumulation rate) measurements is determined by sediment mixing, and can be limited to 103 to 104 years (Dymond and Lyle, 1985). Thus, comparisons of these different measurements must be interpreted with some caution. Where possible, we apply calculations from different pairs of measurements in order to compare results.
CaCO3
The simplest case among the three we examine is CaCO3. Sedimentary CaCO3 dissolves when the pore waters surrounding it are undersaturated with respect to the mineral phase (calcite or aragonite). By most accounts, resaturation is very rapid. Keir (1983), for example, estimated rate constants for dissolution of about 1000 percent/day. Recently, Archer et al. (1989) have estimated that the rate constant is 10 to 100 times slower; this is still rapid on the time scale of early diagenesis. The result of the rapidity of CaCO3 dissolution in undersaturated pore waters is that transport processes within the sediment column are of secondary importance in determining calcite burial efficiency.
Dissolution in sediments occurs for two reasons: because the sediments lie underneath undersaturated bottom water, and in response to acids released by the oxidation of organic matter by O2 (see the stoichiometry in Table 10.1). If only the first process is operating, dissolution will cease within a few millimeters of the sediment/water interface. The effects of the second process are to drive dissolution at water depths shallower than the CaCO3 saturation horizon and beneath the level in the sediments where the pore waters would reach saturation in the absence of organic carbon oxidation. Emerson and Bender (1981) used kinetic models of CaCO3 preservation and dissolution to suggest that it could lead to dissolution as much as 1000 m above the saturation horizon; Sayles (1981) used measurements of Ca2+ fluxes from sediments to demonstrate the occurrence of dissolution as much as 1500 m above saturation horizon in the North Atlantic. We will use calculations of the burial efficiency for CaCO3 to evaluate the importance of dissolution due to the introduction of acids from the oxidation of organic matter in the sediments and to demonstrate the variability in burial efficiency. The data are shown in Table 10.7, which lists burial efficiencies along with the carbonate content of the sediments and the method used for the calculation.
The stations in the Atlantic at which E is estimated all lie above the lysocline. Two stations lie on the continental margin, the rest in the deep Northwest Atlantic. All stations show dissolution of a significant fraction of the CaCO3 rain to the sea floor, with the largest fractional dissolution (50 to 74 percent) occurring in margin sediments. The average fractional dissolution for deep Atlantic stations is lower, 20 percent. However, these values were obtained by in situ sampling techniques with limited resolution near the sediment-water interface; as a result, the benthic Ca2+ flux, and therefore the CaCO3 dissolution rate, may be underestimated by more than a factor of two. Since all of these stations lie above the saturation horizon, all dissolution is due to the effects of organic matter oxidation, emphasizing the importance of this process.
TABLE 10.7 Fluxes of CaCO3
|
Location |
Water Depth (m) |
Depth Relative to Lysoclinea |
CaCO3 Rain (µM/cm2/yr) |
CaCO3 Dissolution Flux (µM/cm2/yr) |
Percent Dissolvedb |
Sedoiemt % CaCO3 |
Type of Data Used in Estimatesc |
|
Pacific Ocean |
|||||||
|
Site M |
3100 |
≤ |
6.6d |
6.2d |
94 |
3 to 5d |
1 |
|
|
|
|
|
11.8e |
180 |
|
2 |
|
Site H |
3600 |
> |
12.8d |
12.8d |
≈100 |
<1d |
1 |
|
|
|
|
|
11.9e |
93 |
|
2 |
|
Site C |
4450 |
> |
23f |
16g |
70 |
≈80 |
1 |
|
|
|
|
|
20h |
89 |
|
2 |
|
|
|
|
|
23i |
100 |
|
3 |
|
Site S |
4900 |
> |
7.3f |
7.3f |
100 |
<1 |
1 |
|
|
|
|
7.3f |
1.8h |
25 |
|
2 |
|
|
|
|
|
7i |
≈100 |
|
3 |
|
California borderland |
|||||||
|
San Pedro Basin |
|
> |
29j |
11k |
38 |
|
3 |
|
San Nicholas Basin |
|
> |
51j |
22k |
43 |
|
3 |
|
Atlantic Ocean |
|||||||
|
SEEP I (margin, U.S. East Coast) |
400 to 2750 |
< |
29l |
14l |
50 |
|
1 |
|
NW Atlantic margin |
|||||||
|
(41º30’N, 63º20’W) 3480 |
|
< |
6.8m |
5.0m |
74 |
43 |
4 |
|
NW Atlantic |
|||||||
|
(average 9 stations) <4200 |
|
< |
19n |
3.8o |
20 |
40 to 60º |
4 |
|
Notes: a <, ≤ and > represent water depths of less than, less than or equal to, and greater than the lysocline, respectively. b Percent of CaCO3 rain estimated to dissolve at or below the sediment-water interface. c Method used in calculating the Dissolution Flux; 1—particle rain, burial; 2—particle rain, diagenetic flux, (NO3-); 3—particle rain, diagenetic flux (O2); 4—diagenetic flux, burial (Ca+2) d Dymond and Lyle (1985); sediment trap data, 1-yr duration, burial rates from radioisotope dating. e Bender and Heggie (1984); estimates of TCO2 produced are from models of NO3 profiles in the pore water. f Dymond and Collier (1988); sediment trap, duration = 2 yrs at Site C, 1 yr at Site S. Site C values were 7 and 23 1 µM/cm2/yr in years 1 and 2, respectively. The first year was influenced by a strong ENSO event and the authors consider 23 µM/cm2/yr a more representative value. We have used this value in calculations. Since percent CaCO 3 ≈ 0 at Site S, total dissolution flux must equal rain. g Value calculated using burial flux of 7 µM/cm2/yr from Lyle et al. (1988). h Bender and Heggie (1984) report a range of fluxes for TCO2 derived from the oxidation of organic carbon estimated from NO3 profiles. i Emerson (1985) provides estimates of organic carbon oxidized from models of O2 microelectrode profiles in the pore water. The flux across the interface is assumed to be the integrated reaction rate, i.e., steady state. j Values for rain are the sum of estimates of the dissolution flux and burial flux. For stations where bottom waters are undersaturated, as the San Pedro and San Nichollas station, rain rate values are a minimum. The data are from Berelson et al. (1987). k Diagenetic flux is estimated from a model of CaCO3 dissolution that makes a number of assumptions regarding dissolution kinetics and depth in sediment to saturation; see Berelson et al. (1987) for details. The carbon oxidation rate is based on O2 consumption rates measured in situ with a benthic lander. l Average sediment-trap particle fluxes and CaCO3 accumulation in sediment from Biscaye et al. (1988). Transect is located south of Cape Code; water depths of 500 to 2750 m. m Diagenetic flux based upon Ca2+ flux of Sayles and Curry (1988) for two separate stations. Burial calculated from percent CaCO3 profile in sediments that exhibits sharp drop in CaCO3 (43 percent to 15 percent between 5 and 8 cm) typical of the interglacial-glacial transition in the north Atlantic. The transition at 11,000 yr is assumed to be at 6.5 cm, the porosity is 73 (±1) percent (unpublished data). n Calculated from a burial rate of 15 µM/cm2/yr recalculated from the data of Turekian (1965) and Bacon (1984) for cores in the general area of the pore water studies (12 below). o Average value of diagenetic flux for nine stations in the northwest Atlantic from Sayles (1981). Estimates based on Ca2+ fluxes determined by in situ water sampling. |
|||||||
The Pacific stations, with the exception of MANOP M, lie below the lysocline. It is immediately apparent that fractional dissolution at these sites, with the exception of the California borderland, is greater than at the Atlantic sites. Estimates range from 70 to 100 percent (except for one low estimate for MANOP S). The lower value at the California borderland site (Berelson et al., 1987) is surprising, and contrasts to the conclusion of Berger (1970), who found that 85 percent of foraminifera shells reaching the sediments there dissolved, even at depths as shallow as a few hundred meters on the slope of the Santa Barbara basin. The Pacific results argue for the importance of dissolution below the saturation horizon. The results tend to indicate that dissolution is occuring deep enough within the sediments to be measured by limited-resolution pore water profiles. At all the MANOP sites, estimates are based both on the particle rain/burial and particle rain/diagenetic flux pairs, and they agree well (again, the low estimate based on NO3- profiles at MANOP S is an exception). In addition, the pore water based estimates are calculated from organic matter oxidation stoichiometry, and so do not include dissolution as a result of undersaturated bottom waters. If the sediment trap based estimates of rain rates do not underestimate the true rain rate of CaCO3, then we must conclude that, even at these sites below the lysocline, dissolution due to metabolic acids is an important process.
SiO2
The driving force for biogenic silica dissolution in marine sediments is similar to that for CaCO3: pore waters are undersaturated with respect to the solid phase present. There are two important differences, however: seawater is universally undersaturated with respect to amorphous silica (Hurd, 1972), and pore waters rarely reach saturation; and the rate of dissolution is significantly slower for biogenic silica, occurring on a time scale of years to tens of years in sediments, compared to minutes to days for CaCO3. The result of these differences is that sediment mixing plays a more important role in determining silica preservation.
In laboratory experiments, it has been shown that the dissolution of opaline tests in seawater depends on the concentration of opal surface exposed to the seawater, on several details of surface characteristics, and on the degree of saturation of the water with respect to amorphous silica (Hurd and Theyer, 1975; Hurd, 1983). Marine pore waters rarely reach saturation with respect to amorphous silica (about 1000 µM at 3° C: Hurd and Theyer, 1975). However, pore waters do approach asymptotic dissolved silica concentrations in the upper 50 to 150 cm of the sediments. The values vary from little over 100 µM in sediments underlying unproductive surface waters (Bender et al.,
TABLE 10.8 Biogenic Silica Mass Balances: Percent Preservation
|
Location |
Percent Opal |
Percent Dissolved |
|
MANOP Ca |
15 |
91 |
|
MANOP Sb |
16 |
>85 |
|
Southern California borderlandc |
3.5 to 6.0 |
90 |
|
Antarctic continental shelfd |
||
|
Sulzberger Bay |
2 |
50 |
|
South central Ross Sea |
24 |
<25 |
|
a Lyle et al. (1988); Martin et al. (1988) b Dymond and Collier (1988); Martin et al. (1988) c Berelson et al. (1987) d Ledford-Hoffman et al. (1986) |
||
1985/86; Sayles, 1979), to values of up to 580 µM below the equatorial upwelling region in the eastern Pacific (Jahnke et al., 1982b), and to values in excess of 750 µM in the siliceous oozes of the southern ocean (Sayles, 1981). Schink et al. (1975) have explained this variability in asymptotic pore water values in terms of a kinetic model based on the rate law of Hurd (1972). According to this model, the asymptotic [SiO2] results from a balance between supply to the sediments and loss to overlying water. The balance depends on the rain rate of opal to the sea floor, the rate of opal dissolution, and the bioturbation mixing coefficient. Opal burial efficiency must also depend on these factors.
The data for calculating biogenic silica burial efficiencies are limited, but enough exist to illustrate its variability. In Table 10.8, we list calculations for five sites from the eastern equatorial Pacific, the California borderland, and the Antarctic continental shelf. Fractional dissolution varies substantially, from about 90 percent in eastern equatorial Pacific sediments to values as low as 25 percent on the Antarctic continental shelf. Clearly, the highest preservation rates occur on the Antarctic shelf (>50 percent of the rain is preserved). This is consistent with the fact that about 75 percent of the opal accumulation in marine sediments occurs in the deep ocean surrounding Antarctica and on the Antarctic continental shelf (Ledford-Hoffman et al., 1986).
Organic Carbon
The study of organic carbon diagenesis is complicated by the wide variety of compounds grouped under the heading. Its bulk reactivity varies with the source of the organic matter, as different compounds have differing susceptibilities to degradation in sediments (e.g., Emerson and Hedges, 1988); in addition, the composition of or-
ganic matter varies with its age, so that reactivity varies with depth below the sediment-water interface even at a given site (Middelberg, 1989). As a result of its varying composition and of the dependence of reactivity on environmental factors, organic carbon reactivity varies over several orders of magnitude. A compilation by Emerson and Hedges (1988) shows that the mean lifetime of the organic matter increases systematically with the age of the organic matter considered. They noted values of 0.1 years or less for fresh phytoplankton, years to tens of years for surficial sediments, hundreds of years for intermediate depth sediments (the upper 20 cm of the sediment column), and 106 years for very deep sediments.
Further complicating organic matter diagenesis is the existence of a suite of chemical reactions, with different thermodynamic driving forces, to accomplish organic matter degradation. They are shown in Table 10.1, in the order of their occurrence with increasing depth below the sediment-water interface. Although some details of the stoichiometry of the table are uncertain, the general validity of the model is well established. The suite of redox reactions leaves well-documented traces in pore waters. Oxic degradation is marked by oxygen consumption and NO3- production (with consumption indicated by positive curvature of the pore water profile, production by negative curvature: Berner, 1980), denitrification by NO3- consumption, Mn and Fe reduction by production of the dissolved reduced metal ion, and sulfate reduction by SO43- consumption and NH3 production. The reactions have been documented, through pore water profiles, benthic flux measurements, and sediment incubations, in pelagic (Froelich et al., 1979; Jahnke et al., 1982a), hemipelagic (Klinkhammer, 1980), and nearshore sediments (Elderfield et al., 1981).
The relative importance of the different electron acceptors depends on several factors: order of use, differing reactivities of organic matter exposed to the different electron acceptors, availability, and oxidizing capacity. The effect of these factors is that organic carbon degradation by dissolved oxygen accounts for about 90 percent of the organic carbon degradation in marine sediments (Henrichs and Reeburgh, 1987). In general, in pelagic and hemipelagic sediments of the eastern equatorial Pacific and the equatorial and northwest Atlantic, 90 to 99 percent of the organic carbon degradation is by O2, most of the rest being done by nitrate reduction (Jahnke et al., 1982a; Bender and Heggie, 1984; Sayles and Curry, 1988). Sulfate reduction occurs at rapid rates in shallow areas on the continental margins, but since these areas cover less than 10 percent of the sea floor, it is responsible for only a small fraction of the total organic carbon oxidized (Jorgensen, 1982). Jahnke et al. (1982b) and Henrichs and Reeburgh (1987) have pointed out that, although the secondary oxidants are responsible for only a small fraction of sedimentary organic carbon remineralization, they oxidize an amount of carbon approximately equal to that preserved in sediments. Thus, they may exert an important influence on the proportion of the organic carbon rain that is preserved. The importance of sulfate reduction lies in the fact that it occurs to a significant extent on continental margins, where the bulk of organic carbon burial in marine sediments takes place (Berner, 1982).
Organic carbon burial efficiency varies because of varying composition of the degrading organic matter pool, and also because of variations in electron acceptor availability. Although fresh organic matter appears to be degraded almost equally efficiently using either O2 or SO43- as an electron acceptor (Westrich and Berner, 1984), there is ample evidence to indicate that the concentration of dissolved oxygen in bottom water influences the extent of degradation of organic matter in marine sediments. The evidence takes the form of observations of enhanced burial efficiency in sediments underlying anoxic bottom waters (Canfield, 1989); an observation that the oxidation of organic carbon that had been deposited at depth by a turbidite flow is limited by the rate of diffusion of O2 into the sediments, despite the presence of other oxidants (Wilson et al., 1985); and predictions based on modeling studies and organic carbon preservation variations in the California borderlands (Emerson, 1985).
A further factor affecting organic carbon burial efficiency, which we examine below, is the relationship of transport away from the sediment-water interface by burial and mixing to degradation reactions. The result of the interactions of the various factors is that organic carbon burial efficiency varies over a wide range in marine sediments. One recent compilation (Henrichs and Reeburgh, 1987) shows a range of burial efficiencies from a few tenths of a percent in pelagic sediments of the eastern tropical Pacific to about 80 percent in coastal sediments at Cape Lookout Bight on the North Carolina coast. Henrichs and Reeburgh (1987) demonstrate a positive correlation between burial efficiency and bulk sedimentation rate, which results in the following pattern: burial efficiency generally increases from pelagic values of 0.6 to 16 percent, to values of 8 to 28 percent on the continental slopes, to 8 to 79 percent in shelf and estuarine sediments.
Discussion
Despite the uncertainties in the calculation of burial efficiencies, the first order result of measurements made to date is that the burial efficiency of organic carbon, CaCO3, and opal is highly variable. The implication of this result is that, in order to interpret temporal variations in burial rates of these three components in terms of rain rates to the sea floor
and variations in sedimentary environments, it is necessary to understand the causes of the burial efficiency variations. Perhaps the simplest case is CaCO3, because of the rapidity of the resaturation of pore waters with respect to the mineral phase. Even here, however, there is a complication: from the compilation presented here, we can conclude that reactions within the sediments account for 40 to 75 percent of CaCO3 dissolution at the sea floor, and a substantial fraction must be due to the acid introduced into pore waters by oxic degradation of organic matter. Thus, quantitative interpretations of CaCO3 preservation depend on an understanding of organic matter diagenesis. Opal diagenesis has been found to depend on a variety of factors, including rain rate variations, reactivity variations, and rates of sediment mixing (Schink et al., 1975). Organic carbon diagenesis depends on the same factors, but has added uncertainties due to the complexity of the material and the range of reactions responsible for its degradation. To enhance the accuracy and usefulness of paleoceanographic reconstructions based on concentrations and accumulation rates of biogenic sediment components, we must have adequate data on early diagenetic reactions and a framework for evaluating the data. We present such a framework in the next section.
A Model Including Transport and Reaction Effects: The Case of Organic Carbon
In steady state, the distribution of organic carbon with depth below the sediment-water interface is determined by a balance between transport processes, which tend to aid the preservation of organic carbon, and chemical reactions, which consume it. The relationships between the processes can be understood by considering a simple system in which organic carbon decays with a first-order rate constant, k, to a depth Xrxn below the sediment-water interface; is mixed, within a layer Xmix thick, by a quasi-Fickian diffusion process described by mixing coefficient, DB; and is buried at sedimentation rate, w. The mean lifetime of the organic carbon is 1/k. It takes a length of time, Xrxn/w, for a particle to be transported through the reaction zone by sedimentation; and a length of time that is proportional to Xrxn2/DB to be transported by mixing through the reaction zone. The competition between transport and reaction is clear: the thicker the reaction zone, and the slower the sedimentation and mixing rates, the longer a particle resides in the reaction zone, and the less likely it is to survive degradation. Preservation is enhanced by a thin reaction zone, rapid sedimentation and mixing, and low reactivity. A final factor is the thickness of the mixed layer. Mixing will clearly be most effective at sequestering organic carbon when Xmix exceeds Xrxn.
We formalize these arguments in the model described by Eq. (10.3). We assume that the sedimentary system is in steady state on the time scale of organic carbon degradation reactions; and take porosity and the sedimentation rate (w) to be constant. To enhance the model's generality, we allow both the organic carbon degradation rate constant (k) and the bioturbation mixing coefficient (DB) to decrease as the depth below the sediment-water interface increases:
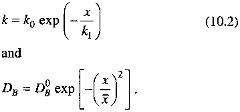
In this formulation, k1 corresponds roughly to Xrxn, ![]() to Xmix. In keeping with the findings of Berner (1980) and Boudreau and Westrich (1984), we assume that organic carbon degradation is first order with respect to the sedimentary organic carbon concentration. The decrease of k as depth below the sediment-water interface increases is consistent with the ''multi-G" model of Berner (Berner, 1980; Westrich and Berner, 1984; Emerson et al., 1987; Middelberg, 1989). Our representation of the depth dependence of the mixing coefficient follows the model of Christensen (1982). We apply a mass balance condition at the sediment-water interface (x=0), and specify that degradation reactions cease at some depth below the interface. In equation form (Berner, 1980), with C the sedimentary organic carbon concentration and R the organic carbon rain rate,
to Xmix. In keeping with the findings of Berner (1980) and Boudreau and Westrich (1984), we assume that organic carbon degradation is first order with respect to the sedimentary organic carbon concentration. The decrease of k as depth below the sediment-water interface increases is consistent with the ''multi-G" model of Berner (Berner, 1980; Westrich and Berner, 1984; Emerson et al., 1987; Middelberg, 1989). Our representation of the depth dependence of the mixing coefficient follows the model of Christensen (1982). We apply a mass balance condition at the sediment-water interface (x=0), and specify that degradation reactions cease at some depth below the interface. In equation form (Berner, 1980), with C the sedimentary organic carbon concentration and R the organic carbon rain rate,
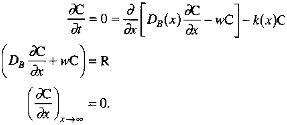
To examine the sensitivity of the organic carbon burial efficiency to model parameters, we transform the differential equation and boundary conditions into dimensionless variables (Table 10.9). The first, P1, measures the depths to which mixing and reaction are important: the larger is P1, the further organic carbon can be mixed below the layer in the sediments in which rapid degradation reactions occur. P2 is a dimensionless transport parameter: the larger it is, the more effective burial is, relative to mixing, at sequestering organic carbon below the reactive layer of the sediments. P3 is a dimensionless reaction parameter: as it increases, the degradation rate increases relative to the rate at which organic carbon is mixed through the
TABLE 10.9 Organic Preservation Model: Parameters
|
Parameter |
Explanation |
|
A. Input Parameters |
|
|
k0, k1 |
Describe the reaction rate of organic carbon, k(x) = k0e-x/k1. k0 in yr-1, k1 in centimeters |
|
DB0, x |
Describe the bioturbation mixing rate, DB = DB0exp(-x2/ |
|
w |
sedimentation rate, cm/yr |
|
B. Dimensionless Variables for Model Calculations |
|
|
P1 = x/k1 |
The ratio of the scale lengths describing the mixing coefficient and degradation rate profiles |
|
P2 = wk1/DB0 |
The dimensionless transport parameter. Interpreted as the ratio of the mean length of time for mixing through the reaction layer (k12/DB0) to the mean length of time for burial through that layer (k1/w) |
|
P3 = k0k12/DB0 |
The dimensionless reaction parameter. The ratio of the mean length of time for mixing through the reaction layer to the mean lifetime of the organic carbon with respect to degradation (1/k0) |
reactive layer. The output of the model is a dimensionless concentration parameter; when multiplied by the ratio, P2/P3, it is equal to the burial efficiency (E in the mass balance above).
We have applied the model to four oceanic sediments to test its ability to predict organic carbon burial efficiencies. The results are preliminary: the model requires that pore water nutrient, ΣCO2, and/or O2 data and solid phase organic carbon data be available for the determination of the degradation rate constant (pore water data to furnish the rate, solid phase data to convert the rate into a first-order degradation rate constant); and that sedimentation rate and bioturbation mixing rate data (we have used 210Pb measurements) be available. The needed information exists at only a few sites. The results are in Table 10.10. The trend in burial eficiencies is reproduced by the model, with the highest E at the southern California borderland site, a high value at the other continental margin site (Buzzards Bay, Massachusetts), and much lower values at the tropical Pacific (MANOP) sites, the lowest value occurring at the site that is farther from the equator. At the individual sites, the agreement between calculated and measured burial efficiencies is probably within the uncertainty in the data.
We examine the effects of the individual sedimentary parameters in the organic carbon burial efficiency contour map of Figure 10.3. The contours were calculated from an 11 x 11 grid of solutions to Eq. (10.3); the solutions had been obtained by varying P2 and P3 systematically, with P1 held constant at a value of 2.5. Contours are shown for two regions: those in the upper left are roughly representative of "pelagic" sedimentary environments, those in the middle and lower right correspond roughly to "continental margin" sediments. Within each region of the plot, successive contours represent a doubling of the burial efficiency. The effects of varying individual parameters are shown by the two clusters of arrows. Starting from the center of each cluster, each arrow shows the effect on E of doubling one model parameter. Varying the bioturbation mixing coefficient (DB0) has almost no effect at the high sedimentation rates characteristic of margin sediments: its arrow is almost parallel to the constant-E contours. At lower (pelagic) sedimentation rates (the cluster in the upper left), mixing has greater effect, with preservation increasing as the mixing rate increases. Doubling the sedimentation rate leads to a nearly proportional increase in burial efficiency. Both reaction parameters, k0, which represents the absolute degradation rate, and k1, which is related to the distance below the sediment-water interface over which organic carbon degradation reactions are important, significantly influence organic carbon preservation. Doubling either causes a proportionate decrease in E under continental margin conditions; their effects, especially that of the reaction scale length, are enhanced in pelagic sediments. The plot does not show the effect of varying the thickness of the mixing zone relative to the reaction zone, as parameter P1 is held constant. Variations in P1 have little effect at higher values of E; their effect at lower E can be seen by comparing the value plotted for MANOP C (''MC" in the figure), calculated using P1= 2.5, to the value obtained for the measured P1 (P1 = 7). The E value in the figure is low by about a factor of two: at low sedimentation rates, mixing is the most effective means of sequestering organic carbon, and increasing the depth below the interface to which mixing occurs causes corresponding increases in burial efficiency.
The model we have shown is a framework for the analysis of burial efficiencies of biogenic sediment components: it defines the sedimentary environment in terms of five measurable parameters. In order to be useful, it must be accompanied by information on the interrelationships between the parameters, and on how they are affected by changing oceanic conditions. One example of the application of the model is a comparison of the two equatorial Pacific sites included in our data set (MANOP C and MANOP S). The most important differences between the two sites are the higher sedimentation rate and reaction rate constant at MANOP C. If the only change were the increased sedimentation rate, burial efficiency would be ten times higher at site C than at site S. However, the reaction rate constant is also higher at site C, and as a
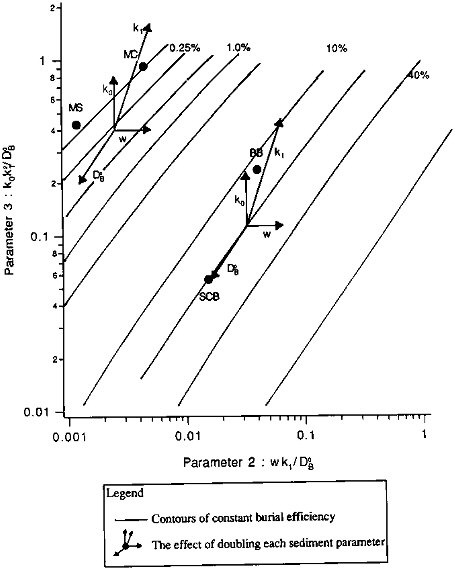
FIGURE 10.3 The sensitivity of organic carbon burial efficiency to changes in sediment parameters. Shown are contours of constant organic carbon burial efficiency, as a function of the model dimensionless transport parameter, Tm/Tb (parameter #2), and reaction parameter, Tm/Tr (parameter #3), with model parameter #1, x/k1, held constant at 2.5. Sites at which model calculations were compared to measured burial efficiencies (see Table 10.10) are shown by the closed circles. The two pelagic sediment sites are MANOP S (MS) and MANOP C (MC); the two continental margin sites are in Buzzards Bay, Massachusetts (BB), and in the San Clemente Basin (SCB) in the southern California borderland. The two clusters of vectors show the effects of organic carbon burial efficiency of varying the sediment parameters. Details are described in the text.
result, the net increase in E is only a factor of 2 to 3. This observation is in agreement with the correlations noted by Emerson (1985), using data from these sites and others: the rain rate of organic carbon to the sea floor increases with the bulk sedimentation rate, and the degradation rate constant varies with the rain rate. Thus, the model confirms the importance of variations in reactivity in determining the relationship between organic carbon burial efficiency and bulk sedimentation rate.
Our data set includes two continental margin sites, one in a shallow, coastal sediment (Buzzards Bay, Massachusetts), and a second in the California borderland, underlying poorly oxygenated bottom water (San Clemente Basin, with bottom water [O2] = 56 umol/kg). A comparison of these sites (Table 10.10) shows a lower burial efficiency in Buzzards Bay, despite its more rapid mixing and sedimentation rates. Changes in reaction rate constants are important: the rate constant at the sediment-water interface is about 50 percent higher at the Buzzards Bay site; more importantly, the rate constant decreases more slowly with depth there. Several factors could contribute to the differences. Oxygen penetrates to only about 5 mm below the sediment-water interface at the San Clemente Basin site (Reimers, 1987); in Buzzards Bay, Mn profiles show that oxygen diffusing across the sediment-water interface reaches similar depths (Martin, 1985), but irrigation is significant to depths of 20 cm in the warm months (Martin and Sayles, 1987), and it may supply O2 to regions well below the sediment-water interface. In addition, there is a larger supply of fresh organic matter to the sediments at the shallow Buzzards Bay site, making secondary oxidants more effective (Westrich and Berner, 1984; Emerson and
TABLE 10.10 Sample Calculations
|
|
Input Parameters |
|
Model Parameters |
|
Results |
|||||||
|
Site |
k0(yr-1) |
K1 (cm) |
w (cm/yr) |
DB0(cm2/yr) |
|
x (cm) |
P1 |
P2 |
|
P3 |
Ecalc (%) |
Emeas (%) |
|
Buzzards Bay |
0.073a |
4a |
0.05a |
5b |
|
10b |
2.5 |
0.040 |
|
0.234 |
12 |
7.4a |
|
SCB |
0.056c |
1c |
0.015d |
1d |
|
6d |
6 |
0.015 |
|
0.056 |
21 |
|
|
"MC" |
0.30e |
0.7e |
0.001f |
0.16g |
|
5g |
7.1 |
0.00438 |
|
0.919 |
0.3 |
1h |
|
"MS" |
0.03e |
1.2e |
0.0001f |
0.10g |
|
3g |
2.5 |
0.0012 |
|
0.43 |
0.1 |
0.5h |
|
Data Sources a McNichol et al. (1988) b Martin and Sayles (1987) c Bender et al. (1989) d R. Anderson, unpublished data e W. Martin, M. Bender, and M. Leinen, unpublished data (see Martin et al., 1988) f Emerson et al. (1987) g Cochran (1985) h Bender and Heggie (1984) |
||||||||||||
Hedges, 1988); the average temperature is higher in Buzzards Bay; and the "quality" of the organic matter may differ between the two sites. At these continental margin sites, as at the two equatorial Pacific sites, reactivity has an important influence on the burial efficiency versus sedimentation rate relationship.
Burial efficiencies are easy to model because the effects of transport processes are simple: increasing transport rates leads to increasing preservation rates. Unfortunately, accumulation rates (which are simply related to rain rates: see Eq. (10.1)) are difficult to measure, and sedimentary concentrations are often used in paleoceanographic models. The effects of transport processes on concentrations are complex: they tend to increase concentrations by enhancing preservation, but tend to decrease them by dilution (that is, the supply of, for instance, organic carbon to the sediments may be constant, but, because the organic carbon is buried or mixed more rapidly, it is spread through a thicker sediment layer). At low sedimentation rates, the preservation effect dominates, and increasing sedimentation tends to increase concentrations. At higher sedimentation rates, the dilution effect dominates, and increases tend to decrease concentrations. The concentration enhancement effect of increasing sedimentation rate is smaller, the more rapid the mixing coefficient and the thicker the mixed layer (Figure 10.4). Thus, in addition to the effects of varying reactivities, models relying on sedimentary concentrations to recreate rain rate variations to the sea floor must account for the complex effects of variable burial and mixing rates.
CONCLUSIONS
We have considered the roles played by early diagenetic reactions in the oceanic cycles of the major seawater ions, Na+, K+, Mg2+, Ca2+, and SO43-, and in the cycles of two additional major players in oceanic biological cycles, C and Si. The elements whose cycles are controlled by nonbiological reactions—Na, K, and Mg—are characterized by long oceanic residence times and diagenetic reactions that are slow in the sense that modest changes in their rates will affect oceanic cycles on time scales in excess of 106 years. Nonetheless, early diagenetic reactions are important, as they result in fluxes that are similar in magnitude to the other sources and sinks of the elements to and from seawater. Early diagenesis plays a larger role in the cycles of the biologically active elements, C, Ca, and Si. Diagenetic cycling rates are rapid with respect to the rates of riverine and hydrothermal input and burial in sediments. Residence times of the elements in seawater with respect to inputs resulting from early diagenesis are about 104 years for C and Si, nearly 106 years for Ca. Early diagenetic reaction rates are greater than burial rates: thus, they may exert important control over the rates of burial of the biogenic sediment components, organic carbon, calcite, and opal.
The burial efficiency of the biogenic sediment components—that is, the fraction of the rain to the sea floor that is preserved to become part of the sedimentary record—varies substantially in the oceans for each component. This last fact has two implications: early diagenesis must be understood to infer rain rates (hence, make paleoceanographic reconstructions) from sediment concentration and accumulation rate data; and early diagenesis must be understood to infer variations in diagenetic reaction rates from the sedimentary record. We have presented a framework for examining spatial, and ultimately temporal, variations in the early diagenesis of organic carbon. The framework needs to be extended to include the other biogenic sediment components, both individually and in an integrated early diagenetic model. There is a need for a greatly expanded data set to determine the interactions between the different parameters affecting diagenetic reaction rates: rain rates to the sea floor, reactivities, and sedimentation and sediment mixing rates.
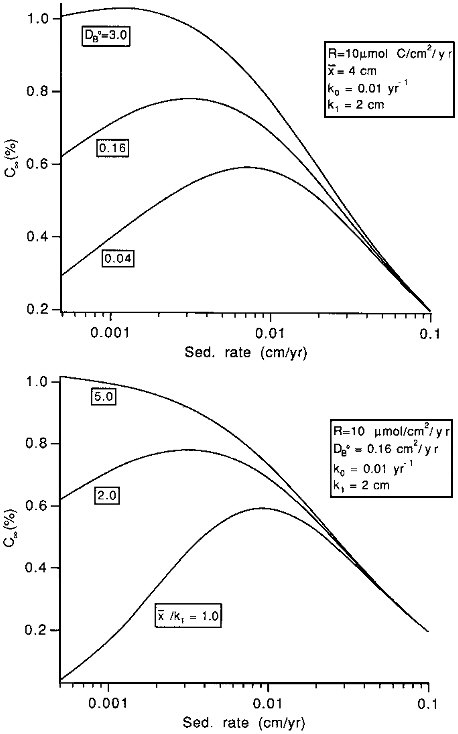
FIGURE 10.4 The effects of changes in the mixing rate parameters on the C∞ versus sedimentation rate w relationship. C∞ represents the organic carbon concentration in accumulating sediment, in percent on a dry weight basis. In the top figure, x/k1 is held constant at 2.0 and the mixing rate coefficient, DB0 is allowed to vary; in the bottom figure, DB0 is constant at 0.16, while x/k1 is varied. For both, the rain rate to the sediment-water interface is 10µmol C/cm 2/yr; the organic carbon degradation rate at x=0 (k0) is 0.01 per year, and k1 is 2 cm.
ACKNOWLEDGMENTS
The authors are grateful to R. Anderson, who provided unpublished data for model testing, and to D. McCorkle, A. McNichol, and C. Reimers, who read various drafts of the manuscript and provided critical comments. The work was supported by the National Science Foundation under grant No. OCE-87-11962. This is W.H.O.I Contribution No. 7297.
REFERENCES
Aller, R.C. (1980a). Diagenetic processes near the sediment-water interface of Long Island Sound. I. Decomposition and nutrient element geochemistry (S, N, P), in Estuarine Physics and Chemistry: Studies in Long Island Sound, B. Saltzman, ed., Academic Press, New York, pp. 237-349.
Aller, R.C. (1980b). Quantifying solute distributions in the bioturbated zone of marine sediments by defining an average microenvironment, Geochimica et Cosmochimica Acta 44, 1955-1965.
Archer, D., S. Emerson, and C.R. Smith (1989). Dissolution of calcite in deep-sea sediments: pH and O2 microelectrode results, Geochimica et Cosmochimica Acta 53(11), 2831.
Bacon, M.P. (1984). Glacial to interglacial changes in carbonate and clay sedimentation in the Atlantic Ocean estimated from Th-230 measurements, Isotope Geoscience 2, 97-111.
Barnes, R.O. (1973). An in situ interstitial water sampler for use in unconsolidated sediments, Deep-Sea Research 20, 1125-1128.
Bender, M.L., K.A. Fanning, P.N. Froelich, G.R. Heath, and V. Maynard (1977). Interstitial nitrate profiles and oxidation of sedimentary organic matter in the Eastern Equatorial Atlantic, Science 198, 605-609.
Bender, M.L., and D.T. Heggie (1984). Fate of organic carbon reaching the deep sea floor: A status report, Geochimica et Cosmochimica Acta 48, 977-986.
Bender, M.L., A. Hudson, D.W. Graham, R.O. Barnes, M. Leinen, and D. Kahn (1985/1986). Diagenesis and convection reflected in pore water chemistry on the western flank of the East Pacific Rise, 20° south , Earth and Planetary Science Letters 76, 71-83.
Bender, M., W. Martin, J. Hess, F. Sayles, L. Ball, and C. Lambert (1987). A whole-core squeezer for interstitial pore-water sampling, Limnology and Oceanography 32(6), 1214-1225.
Bender, M., R. Jahnke, R. Weiss, W. Martin, D. Heggie, J. Orchardo, and T. Sowers (1989). Organic carbon oxidation and benthic nitrogen and silica dynamics in San Clemente Basin, a continental borderland site, Geochimica et Cosmochimica Acta 53, 685-697.
Berelson, W.M., D.E. Hammond, and K.S. Johnson (1987). Benthic fluxes and the cycling of biogenic silica and carbon in two southern California borderland basins, Geochimica et Cosmochimica Acta 51, 1345-1363.
Berger, W.H. (1970). Planktonic foraminifera: selective solution and the lysocline, Marine Geology 8, 111-138.
Berner, R.A. (1977). Stoichiometric models for nutrient regeneration in anoxic sediments, Limnology and Oceanography 22(5), 781-786.
Berner, R.A. (1980). Early Diagenesis: A Theoretical Approach, Princeton University Press, Princeton, N.J.
Berner, R.A. (1982). Burial of organic carbon and pyrite sulfur in the modern ocean: Its geochemical and environmental significance, American Journal of Science 282, 451-573.
Biscaye, P.E., R.F. Anderson, and B.L. Deck (1988). Fluxes of particles and constituents to the eastern United States continental slope and rise: SEEP-1, Continental Shelf Research 8(5-7), 855-904.
Bischoff, J.L., R.E. Greer, and A.O. Luistro (1970). Composition of interstitial waters of marine sediments: Temperature of squeezing effect, Science 167, 1245-1246.
Boudreau, B.P., and N.L. Guinasso, Jr. (1982). The influence of a diffusive sublayer on accretion, dissolution, and diagenesis at the sea floor, in The Dynamic Environment of the Ocean Floor, K.A. Fanning and F.T. Manheim, eds., Lexington Books, Lexington, Mass., 502 pp.
Boudreau, B.P., and J.T. Westrich (1984). The dependence of bacterial sulfate reduction on sulfate concentration in marine sediments, Geochimica et Cosmochimica Acta 48, 2503-2516.
Broecker, W.S., and T.H. Peng (1982). Tracers in the Sea, Eldigio, New York, pp. 47-94.
Calvert, S.E. (1983). Sedimentary geochemistry of silicon, in Silicon Chemistry and Biogeochemistry, Academic Press, London, pp. 143-186.
Canfield, D.E. (1989). Sulfate reduction and oxic respiration in marine sediments: implications for organic carbon preservation in euxinic environments, Deep-Sea Research 36(1), 121-138.
Christensen, E.R. (1982). A model for radionuclides in sediments influenced by mixing and compaction, Journal of Geophysical Research 87(C1), 566-572.
Christensen, J.P., A.H. Devol, and W.M. Smethie, Jr. (1984). Biological enhancement of solute exchange between sediments and bottom water on the Washington continental shelf, Continental Shelf Research 3, 9-23.
Christensen, J.P., W.M. Smethie, and A.H. Devol (1987). Benthic nutrient regeneration and denitrification on the Washington continental shelf, Deep-Sea Research 34(5/6), 1027-1047.
Cochran, J.K. (1985). Particle mixing rates in sediments of the eastern equatorial Pacific: Evidence from 210Pb,239, 240Pu, and 137Cs distributions at MANOP sites, Geochimica et Cosmochimica Acta 49, 1195-1210.
Codispoti, L.A., and J.P. Christensen (1985). Nitrification, denitrification, and nitrous oxide cycling in the eastern tropical Pacific Ocean, Marine Chemistry 16, 277-300.
Dymond, J., and M. Lyle (1985). Flux comparisons between sediments and sediment traps in the eastern tropical Pacific: Implications for atmospheric CO2 variations during the Pleistocene, Limnology and Oceanography 30(4), 699-712.
Dymond, J., and R. Collier (1988). Biogenic particle fluxes in the equatorial Pacific: Evidence for both high and low productivity during the 1982-1983 El Niño, Global Biogeochemical Cycles 2(2), 129-137.
Edmond, J.M. (1974). On the dissolution of carbonate and silicate in the deep ocean, Deep-Sea Research 21, 455-480.
Edmond, J.M., C. Measures, R.E. McDuff, L.H. Chan, R. Collier, R., B. Grant, L.I. Gordon, and J.B. Corliss (1979). Ridge crest hydrothermal activity and the balances of the major and minor elements in the ocean: The Galapagos data, Earth and Planetary Science Letters 46, 1-18.
Elderfield, H. (1981). Metal-organic associations in interstitial waters of Narragansett Bay sediments, American Journal of Science 281, 1184-1196.
Elderfield, H., N. Luedtke, R.J. McCaffrey, and M. Bender (1981). Benthic studies in Narragansett Bay, American Journal of Science 281, 768-787.
Emerson, S. (1985). Organic carbon preservation in marine sediments, in The Carbon Cycle and Atmospheric CO2: Natural Variations Archean to Present, American Geophysical Union, Washington, D.C.
Emerson, S., and M.L. Bender (1981). Carbon fluxes at the sediment-water interface of the deep sea: Calcium carbonate preservation, Journal of Marine Research 39, 139-162.
Emerson, S., and J.I. Hedges (1988). Processes controlling the organic carbon content of open ocean sediments, Paleoceanography 3(5), 621-634.
Emerson, S., V. Grundmanis, and E. Graham (1982). Carbonate chemistry in marine pore waters: MANOP sites C and S, Earth and Planetary Science Letters 61, 220-232.
Emerson, S., C. Stump, P.M. Grootes, M. Stuiver, G.W. Farwell, and F.H. Schmidt (1987). Estimates of degradable organic carbon in deep-sea surface sediments from 14C concentrations, Nature 329, 51-53.
Froelich, P.N., G.P. Klinkhammer, M.L. Bender, N.A. Luedtke, G.R. Heath, D. Cullen, P. Dauphin. D. Hammond, B. Hartman, and V. Maynard (1979). Early oxidation of organic matter in pelagic sediments of the eastern equatorial Atlantic: Suboxic diagenesis, Geochimica et Cosmochimica Acta 43, 1075-1090.
Froelich, P.N., M.L. Bender, N.A. Luedtke, G.R. Heath, and T. DeVries (1982). The marine phosphorous cycle, American Journal of Science 282, 474-511.
Goloway, F., and M. Bender (1982). Diagenetic models of interstitial nitrate profiles in deep sea suboxic sediments, Limnology and Oceanography 27(4), 624-638.
Grundmanis, V., and J.W. Murray (1982). Stoichiometry of decomposing organic matter in aerobic marine sediments, Geochimica et Cosmochimica Acta 46, 1101-1121.
Heggie, D., C. Maris, A. Hudson, J. Dymond, R. Beach, and J. Cullen (1987). Organic carbon oxidation and preservation in NW Atlantic continental margin sediments, in Geology and Geochemistry of Abyssal Plains, pp. 215-236.
Henrichs, S.M., and W.S. Reeburgh (1987). Anaerobic mineralization of marine sediment organic matter: Rates and the role of anaerobic processes in the oceanic carbon economy, Geomicrobiology Journal 5(3/4), 191-237.
Honjo, S. (1980). Material fluxes and modes of sedimentation in the mesopelagic and bathypelagic zones, Journal of Marine Research 38(1), 53-97.
Hurd, D.C. (1972). Factors affecting solution rate of biogenic opal in seawater, Earth and Planetary Science Letters 15, 411-417.
Hurd, D.C. (1983). Physical and chemical properties of siliceous skeletons, in Silicon Chemistry and Biogeochemistry, Academic Press, London.
Hurd, D.C., and F. Theyer (1975). Changes in the physical and chemical properties of biogenic silica from the central equatorial Pacific, 1, Solubility, specific surface area, and solution rate constants of acid-cleaned samples, in Analytical Methods in Oceanography, American Chemical Society, Washington, D.C.
Jahnke, R.A., and G.A. Jackson (1987). Role of sea floor organisms in oxygen consumption in the deep North Pacific Ocean, Nature 329, 621-623.
Jahnke, R.S., R. Emerson, and J.W. Murray (1982a). A model of oxygen reduction, denitrification, and organic matter mineralization in marine sediments, Limnology and Oceanography 27, 610-623.
Jahnke, R.S., D. Heggie, S. Emerson, and D. Graham (1982b). Pore waters of the central Pacific Ocean: Nutrient results, Earth and Planetary Science Letters 61, 233-256.
Jorgensen, B.B. (1982). Mineralization of organic matter in the sea bed—the role of sulphate reduction, Nature 296, 643-645.
Keir, R.S. (1983). Variation in the carbonate reactivity of deep-sea sediments: Determination from flux experiments, Deep-Sea Research 30, 279-296.
Klinkhammer, G.P. (1980). Early diagenesis in sediments from the eastern equatorial Pacific, II, Pore water metal results, Earth and Planetary Science Letters 49, 81-101.
Ledford-Hoffman, P.A., D.J. DeMaster, and C.A. Nittrouer (1986). Biogenic silica accumulation in the Ross Sea and the importance of Antarctic continental-shelf deposits in the marine silica budget, Geochimica et Cosmochimica Acta 50, 2099-2110.
Li, Y-H., T. Takahashi, and W.S. Broecker (1969). Degree of saturation of CaCO3 in the oceans, Journal of Geophysical Research 74, 5507-5525.
Lisitzin, A.P., Y.A. Belyayev, Y.A. Bogdanov, and A.N. Bogoyavlensky (1967). Distribution, relationships and forms of silicon suspended in waters of the world ocean, International Geology Review 9, 604-623.
Lyle, M., D.W. Murray, B.P. Finney, J. Dymond, J.M. Robbins, and K. Brooksforce (1988). The record of late Pleistocene biogenic sedimentation in the eastern tropical Pacific Ocean, Paleoceanography 3, 39-59.
Mackin, J.E. (1986). The free-solution diffusion coefficient of boron: Influence of dissolved organic matter, Marine Chemistry 20, 131-140.
Mangelsdorf, P.C., Jr., T.R.S. Wilson, and B. Daniell (1969). Potassium enrichments in interstitial waters of recent marine sediments, Science 165, 171-174.
Martin, J.H., G.A. Knauer, D.M. Karl, and W.W. Broenkow (1987). VERTEX: Carbon cycling in the northeast Pacific, Deep-Sea Research 34(2), 267-285.
Martin, J.M., and M. Meybeck (1979). Elemental mass balance of material carried by major world rivers, Marine Chemistry 7, 173-206.
Martin, W.R. (1985). Transport of Trace Metals in Nearshore Sediments, PhD Thesis, M.I.T./W.H.O.I. Joint Program in Oceanography.
Martin, W.R., and F.L. Sayles (1987). Seasonal cycles of particle and solute transport processes in nearshore sediments: Rn-222/Ra-226 and Th-234/U-238 disequilibrium at a site in Buzzards Bay, MA., Geochimica et Cosmochimica Acta 51, 927-943.
Martin, W.R., and M.L. Bender (1988). The variability of benthic fluxes and sedimentary remineralization rates in response to seasonally variable organic carbon rain rates in the deep sea: A modeling study, American Journal of Science 288, 561-574.
Martin, W.R., M. Bender, M. Leinen, and J. Orchardo (1988). Benthic fluxes of NO3, SiO2, and O2 across the equatorial high productivity zone at 135° W, EOS 69(44), 1264.
McCorkle, D.C., S.R. Emerson, and P.D. Quay (1985). Stable carbon isotopes in marine pore waters, Earth and Planetary Science Letters 74, 13-26.
McNichol, A.P., C. Lee, and E.R.M. Druffel (1988). Carbon cycling in coastal sediments: 1. A quantitative estimate of the remineralization of organic carbon in the sediments of Buzzards Bay, MA., Geochimica et Cosmochimica Acta 52, 1531-1543.
Meybeck, M. (1982). Carbon, nitrogen, and phosphorous transport by world rivers, American Journal of Science 282, 401-450.
Middelberg, J.J. (1989). A simple rate model for organic matter decomposition in marine sediments, Geochimica et Cosmochimica Acta 53, 1577-1581.
Murray, J.W., S. Emerson, and R.A. Jahnke (1980). Pressure effect on the alkalinity of deep-sea interstitial water samples, Geochimica et Cosmochimica Acta 44, 963-972.
Premuzic, E.T., C.M. Benkovitz, J.S. Gaffney, and J.J. Walsh (1982). The nature and distribution of organic matter in the surface sediments of world oceans and seas, Organic Geochemistry 4, 63-77.
Reimers, C.E. (1987). An in situ microprofiling instrument for measuring interfacial pore water gradients: Methods and oxygen profiles from the North Pacific Ocean, Deep-Sea Research 34(12), 2019-2035.
Reimers, C.E. (1989). Control of benthic fluxes by particulate supply, in Productivity in the Ocean: Present and Past, W.H. Berger, V.S. Smetacek, and G. Wefer, eds., John Wiley and Sons, London, pp. 217-233.
Reimers, C.E., K.M. Fischer, R. Merewether, K.L. Smith, Jr., and R.A. Jahnke (1986). Oxygen microprofiles measured in situ in deep ocean sediments, Nature 320, 741-744.
Revsbech, N.P., J. Sorensen, T.H. Blackburn, and J.P. Lomholt (1980). Distribution of oxygen in marine sediments measured with microelectrodes, Limnology and Oceanography 25(3), 403-411.
Sayles, F.L. (1979). The composition and diagenesis of interstitial solutions—I. Fluxes across the seawater-sediment interface in the Atlantic Ocean, Geochimica et Cosmochimica Acta 43, 527-545.
Sayles, F.L. (1981). The composition and diagenesis of interstitial solutions—II. Fluxes and diagenesis at the water-sediment interface in the high latitude north and South Atlantic, Geochimica et Cosmochimica Acta 45, 1061-1086.
Sayles, F.L., and W.B. Curry (1988). δ13C, TCO2, and the metabolism of organic carbon in deep sea sediments, Geochimica et Cosmochimica Acta 52, 2963-2978.
Sayles, F.L., F.T. Manheim, and L.S. Waterman (1973a). Interstitial water studies on small core samples, Leg 15, in Initial Reports of the Deep Sea Drilling Project 15, B. Heezen et al., ed., U.S. Government Printing Office, Washington, D.C., pp. 33-54.
Sayles, F.L., T.R.S. Wilson, D.N. Hume, and P.C. Mangelsdorf (1973b). In situ sampler for marine sedimentary pore waters: Evidence for potassium depletion and calcium enrichment, Science 181, 154-156.
Schink, D.R., N.L. Guinasso, Jr., and K.A. Fanning (1975). Processes affecting the concentration of silica at the sedimentwater interface of the Atlantic Ocean, Journal of Geophysical Research 80(21), 3013-3031.
Smith, K.L., Jr., and K.R. Hinga (1983). Sediment community respiration in the deep sea, in The Sea, John Wiley & Sons, New York.
Suess, E., and P.J. Muller (1980). Productivity, sedimentation rate and sedimentary organic matter in the oceans, II. Elemental fractionation. Colloques Internationaux du C.N.R.S.—Biogeochemie de la Matiere Organique a l'Interface Eau-Sediment Marin 293, 17-26.
Suess, E., P.J. Muller, H.S. Powell, and C.E. Reimers (1980). A closer look at nitrification in pelagic sediments, Geochemical Journal 14, 129-137.
Takahashi, T., W.S. Broecker, and S. Langer (1985). Redfield ratio based on chemical data from isopycnal surfaces, Journal of Geophysical Research 90(C4), 6907-6924.
Turekian, K.K. (1965). Some aspects of the geochemistry of marine sediments, in Chemical Oceanography, J.P. Riley and G. Skirrow, eds., Academic Press, New York, pp. 81-126.
Walsh, I., J. Dymond, and R. Collier (1988). Rates of recycling of biogenic components of settling particles in the ocean derived from sediment trap experiments, Deep-Sea Research 35, 43-58.
Westrich, J.T., and R.A. Berner (1984). The role of sedimentary organic matter in bacterial sulfate reduction: The G model tested, Limnology and Oceanography 29(2), 236-249.
Williams, P.M., and R.R.M. Druffel (1987). Radiocarbon in dissolved organic matter in the central North Pacific Ocean, Nature 330, 246-248.
Wilson, T.R.S., J. Thomson, S. Colley, D.J. Hydes, N.C. Higgs, and J. Sorensen (1985). Early organic diagenesis: The significance of progressive subsurface oxidation fronts in pelagic sediments, Geochimica et Cosmochimica Acta 49, 811-822.






















