| ||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Copyright © 2009. National Academy of Sciences. All rights reserved. Terms of Use and Privacy Statement |
Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 121
A Reassessment of the Marine Salvage Posture of the United States
APPENDIX I
SALVAGE TUG REQUIREMENTS
GENERAL
The power required by a tug to tow a ship is a function of many variables. First, the size of the ship and its general characteristics influence the effect of the wind and wave forces acting upon it. Second, the size and characteristics of the tug as well as the type of propulsion are significant factors in determining not only the magnitude of the environmental forces acting on it but also its ability to operate in that environment. Last, but not least, the towline arrangement and the experience and expertise of the tug master and crew have a large bearing on the ability to tow in heavy weather.
When evaluating the ability of a tug to tow a vessel it is necessary to understand the dynamics of the situation. A tug towing a tanker can be represented for analysis purposes by three components:
A mass representing the ship, which is acted upon by time varying accelerations, damping, and spring coefficients.
A nonlinear spring representing the towline.
A mass representing the tug, which is also acted upon by time varying accelerations, damping, and spring coefficients.
This is a very complex system both from a theoretical point of view as well as in actual operation. The multiplicity of time varying forces and resulting motions combined with the nonlinearity of the towline can lead to extremely high dynamic loads on the system in heavy seas.
While one might prefer to think that any size vessel could be towed in any weather with a large enough tug, this is simply not the case. The limiting factor is a function of the relative motions between the two vessels and the ability of the towline and towing winch to allow for that relative motion without breaking, while still providing sufficient towing force to keep the vessel moving or at least to maintain its position. It was demonstrated—most dramatically in the case of the Amoco Cadiz—that even a world-class tug cannot tow a vessel under some conditions. The relative motions between the two vessels simply becomes too great for the towline's ability to stretch. Attaching a towline is a difficult and dangerous operation in storm conditions and may not be possible, again, due to relative motion between the vessels.
Tugs use several different methods to provide the stretch required in a towing system. First, an ocean towing winch may be designed to automatically pay out and heave line as the tension varies. This helps to reduce major shock loads. Next, the length and weight of the tow wire results in a catenary, which allows for some degree of relative motion between the tug and ship. Finally, the use of a doubled nylon hawser as a shock absorber within the towline adds stretch to the system.1,2 Together these allow substantial relative motion between the two vessels. While other methods are used to allow for relative motion between the vessels, the above are the most common.
OCR for page 122
A Reassessment of the Marine Salvage Posture of the United States
used to allow for relative motion between the vessels, the above are the most common. However, as the relative motion nears the limits of the winch, catenary, and hawser system capabilities, the towing arrangement will either become very stiff, with consequent large shock loads, or the winch will pay out more line than it can recover. In either case, the tug will be unable to continue towing.
Salvage Scenario
To estimate required tug horsepower, it is assumed that a vessel has lost all power upwind of a lee shore, and that the tug would be required to tow the vessel head into the wind and waves or at least maintain position relative to the lee shore.
Analysis Methodology
The calculations used in this study are based on published information relating to the behavior of tank vessels in various wind and sea conditions. A relatively simple procedure was used to analyze the size of tug required to tow various size tankers. This consisted of calculating the mean wind and wave forces on the tanker and tug and converting them into required bollard pull. This is a static analysis, not a dynamic analysis, and as such assumes that the towing system consisting of the towing winch, towline, and spring make adequate provision for relative motion between the two vessels. The calculation of the wind and wave forces is described below.
Wind and Wave Forces
In analyzing the forces on a large ship in storm conditions, it is necessary to estimate the actual sea state in terms of significant wave height and period, because wave drift forces acting on a vessel increase as the wave height increases and usually decrease as the wave period increases. Figure I-13 provides data on sea states relative to wind speed for fully developed seas. A fully developed sea is one in which the wind has been blowing long enough and far enough for the waves to develop to their maximum extent. Footnote a to this table notes that this rarely occurs for winds in excess of 50 knots. As shown in the table, a minimum duration of 69 hours and a fetch of 1,420 nautical miles would be required for a sea to become fully developed in 50-knot winds.
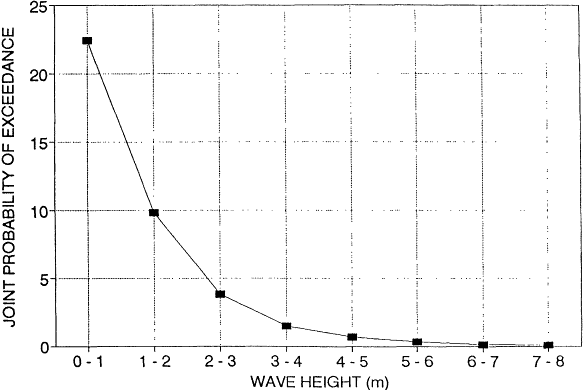
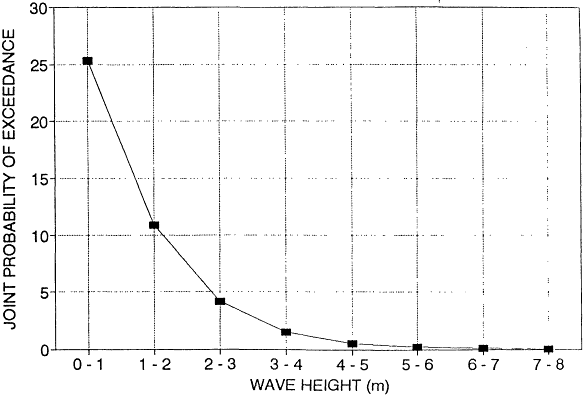
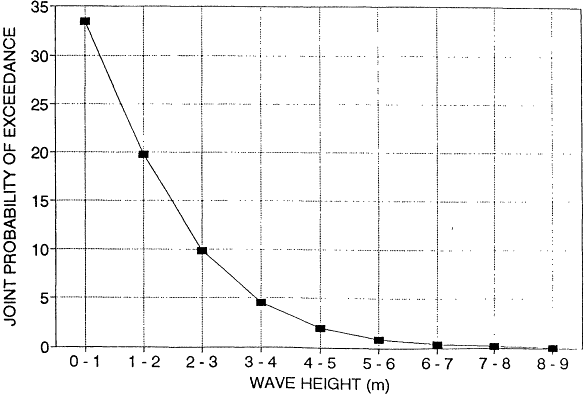
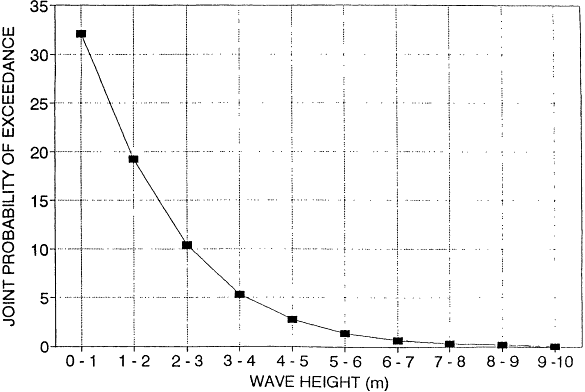
For this study, wave height and period statistics were taken from Global Wave Statistics by British Maritime Technology Limited.4 This book provides wave height and period probability distributions worldwide. These probability distributions are tied to specific areas of the world and specific wind directions. These data allow us to calculate the joint probability of various wave heights occurring at the same time as onshore winds for different regions of the United States. Graphs of the calculated joint probability are attached (Figures I-2 through I-6).
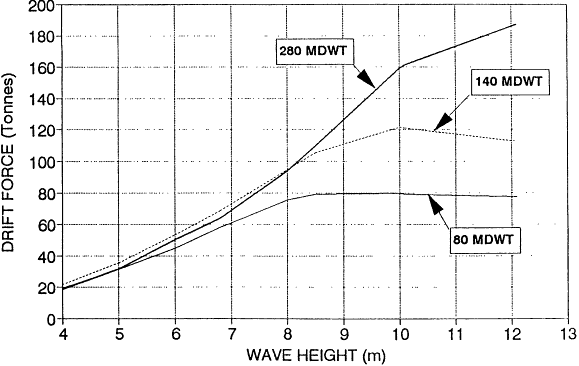
Based on a range of typical sea states, the mean wave drift forces were estimated using OCMOTA,5 ship motion and wave force prediction program developed by the Maritime Research Institute of the Netherlands (MARIN) for the Oil Companies International Marine Forum (OCIMF). To ensure that the probable range of wave heights and periods were fully covered, two different average wave periods were used for each wave height. This was done since wave drift forces are sensitive to wave period. The curves of wave drift force presented (Figure I-7) represent the mean of these two conditions. It should be noted that the wave energy spectrum used was a Jonswap spectrum with a peak enhancement factor of 3.3. This is representative of a building storm. The wave drift forces on a ship in a building storm are normally much higher than in a fully developed sea of the same height because of the shorter mean wave periods. Wind forces were calculated based on Prediction of Wind and
OCR for page 123
A Reassessment of the Marine Salvage Posture of the United States
Current Loads on VLCC's by OCIMF6 (Figure I-8). The sum of these forces together with the forces acting on the tug gives a reasonable estimate of the minimum bollard pull required to control a tanker in storm conditions.
Estimation of Required Tug Power
After calculating the wind and wave loads acting on the tankers, the tug/towwire resistance was added and an estimated loss of efficiency applied. This factor, which ranged from 20 to 28 percent, is an estimate of the loss of bollard pull resulting from the motions of the tug in waves. This is merely an estimate, but is in line with similar figures used by others.7
The conversion of bollard pull to horsepower must also be an estimate as it varies for each vessel. It depends greatly on the RPM and diameter of the propeller(s) and on whether the tug has Kort nozzle(s) around the propeller(s). For this paper, a factor of 75 horsepower per ton of bollard pull was used. This is typical of a twin screw tug in the 5,000- to 10,000-horsepower class with Kort nozzles.8 For a 7,000-horsepower tug, this equates to 93 tons of bollard pull.
RESULT AND CONCLUSION
The results of the analysis are displayed in Figures I-9 through I-11. In reviewing them, it is worthwhile to note the major trading routes for various size tankers:
VLCCs trade primarily to the U.S. Gulf with a smaller number trading ANS Crude from Alaska to the West Coast.
140-MDWT tankers trade primarily to the East Coast of the U.S. with a much smaller number trading in the U.S. Gulf and to the West Coast.
80-MDWT vessels trade primarily in the U.S. Gulf and on the East Coast with a smaller number trading on the West Coast.
This analysis shows that a tug of 7,000 horsepower is adequate for handling both a VLCC and a 140-MDWT tanker up to just short of a 20-foot (6-meter) sea state and for handling an 80-MDWT tanker up to a sea state of about 21.5 feet (6.5 meters). Beyond that point, a larger tug, or two tugs would be required. By referring to the joint probability curves (Figures I-1 through I-6) one can see that the probability of 6 to 6. 5 meter seas in combination with onshore winds is quite small. For each of the regions, the joint probability of having 16- to 20-foot (5- to 6-meter) waves in conjunction with onshore winds is:
East Coast
0.30%
Gulf Coast
0.05%
California
0.20%
Pacific NW
0.80%
Alaska
1.40%
These numbers represent the percentage of time in certain coastal waters when one would anticipate that a rescue tow or holding operation of a loaded VLCC would be beyond the capability of a single 7,000-BHP tug.
In 1978, DNV published Towing Operations Guidelines and Recommendations for Barge Transportation. This document was intended to provide guidance to the offshore industry on how large a tug would be required to transport major equipment offshore. These guidelines recommended using a tug capable of towing in 16.5-foot (5-meter) seas with 39-knot winds and up to a 2-knot current. This correlates very well
OCR for page 124
A Reassessment of the Marine Salvage Posture of the United States
with the conditions in which we would expect a 7,000-horsepower tug to be able to hold a large tanker.
It is important to note that the wave drift forces increase dramatically up to a 33-to 39-foot (10- to 12-meter) sea state. In these conditions the relative dynamic motions of the tug and tanker would preclude the tug from towing regardless of its horsepower. Even the largest oceangoing tugs cannot continue to tow in major storm conditions.
REFERENCES
1. OCIMF. 1981. OCIMF Recommendations on Equipment for the Towing of Disabled Tankers. London: Witherby and Company.
2. Hancox, David. 1987. Reed's Commercial Salvage Practice. Sunderland, England: Thomas Reed Publications Limited.
3. Noel, John V. 1977. Knight's Modern Seamanship, Sixteenth Edition. New York: Van Nostrand Reinhold Company.
4. Hogben, N. et al. 1986. Global Wave Statistics. England: Unwin Brothers Limited.
5. OCIMF. 1992. Users Guide OCMOTA. Maritime Research Institute Netherlands
6. OCIMF. 1977. Prediction of Wind and Current Loads on VLCCs. London: Witherby and Company.
7. Dai, Richard Y. T. et al. 1981. Offshore construction barge performance in towage operations. Proceedings 1981 Offshore Technology Conference. OTC 4164.
8. Blight, Graham J. et al. 1978. Resistance of offshore barges and required tug horsepower. Proceedings 1978 Offshore Technology Conference. OTC 3320.
OCR for page 125
A Reassessment of the Marine Salvage Posture of the United States
FIGURE I-1 Wind and sea scale for fully arisen sea.a
Wave Height-Feet
Wind Speed (knots)
Average
Significant Average 1/3 Highest
Average 1/10 Highest
Average Period
Average Wave Length
Minimum Fetch (nautical miles)
Minimum Duration (hours)
Average Wave Heightb (maximum)
0
0
0
0
-
-
-
-
-
2
0.05
0.08
0.10
0.5
10 in
5
18 min
5
0.18
0.29
0.37
1.4
6.7 ft
8
39 min
8.5
0.6
1.0
1.2
2.4
20
9.8
1.7 hrs
2(3)
10
0.88
1.4
1.8
2.9
27
10
2.4
13.5
1.8
2.9
3.7
3.9
52
24
4.8
31/2(5)
16
2.9
4.6
5.8
4.6
71
40
6.6
18
3.8
6.1
7.8
5.1
90
55
8.3
6(81/2)
19
4.3
6.9
8.7
5.4
99
65
9.2
20
5.0
8.0
10
5.7
111
75
10
22
6.4
10
13
6.3
134
100
12
91/2(13)
24.5
8.2
13
17
7.0
164
140
15
26
9.6
15
20
7.4
188
180
17
28
11
18
23
7.9
212
230
20
131/2(19)
30.5
14
23
29
8.7
258
290
24
32
16
26
33
9.1
285
340
27
34
19
30
38
9.7
322
420
30
18(25)
37
23
37
46.7
10.5
376
530
37
40
28
45
58
11.4
444
710
42
42
31
50
64
12.0
492
830
47
23(32)
44
36
58
73
12.5
534
960
52
46
40
64
81
13.1
590
1110
57
48
44
71
90
13.8
650
1250
63
29(41)
50
49
78
99
14.3
700
1420
69
51.5
52
83
106
14.7
736
1560
73
54
59
95
121
15.4
810
1800
81
56
64
103
130
16.3
910
2100
88
37(52)
59.5
73
116
148
17.0
985
2500
101
>64
>80
>128
>164
18
˜
˜
˜
45(-)
a To attain a fully arisen sea for a certain wind speed, the wind must blow at that speed over a minimum distance (fetch) for a minimum time (duration). When winds are 50 knots or more, the required fetch and duration for a fully arisen sea rarely occur. The wave heights shown in the last column, ''Average Wave Height'' represent what will be found on the average at given wind speeds.
Wave heights refer only to wind waves, and swells from distant or old storms are nearly always superimposed on the wind-wave pattern.
Practical Methods of Observing and Forecasting Ocean Waves, Pierson, Newuman, James, H.O. Pub. 603, 1955.
b H.O. 118A
OCR for page 126
A Reassessment of the Marine Salvage Posture of the United States
Figure I-2
East Coast onshore wave height probability distribution.
Figure I-3
U.S. Gulf Coast onshore wave height probability distribution.
OCR for page 127
A Reassessment of the Marine Salvage Posture of the United States
Figure I-4
California onshore wave height probability distribution.
Figure I-5
Pacific Northwest onshore wave height probability distribution.
OCR for page 128
A Reassessment of the Marine Salvage Posture of the United States
Figure I-6
Gulf of Alaska onshore wave height probability distribution.
OCR for page 129
A Reassessment of the Marine Salvage Posture of the United States
Figure I-7
80- to 280-MDWT tanker wave drift force.
Figure I-8
80- to 280-MDWT tanker wind force.
OCR for page 130
A Reassessment of the Marine Salvage Posture of the United States
FIGURE I-9
Tug power estimate required to hold 80-MDWT fully loaded tanker
Sig. Wave H
Wind Speed
Tanker Resistance
Tug Resist.
Minimum Bollard
Est. Loss of Efficiency
Required Bollard
Estimated Tug BHP
Wind
Wave
Total
meters
kn
tons
tons
tons
tons
tons
%
tons
HP
4
30
11
20
31
3
34
20
40
3000
5
35
14
31
45
4
49
22
60
4500
6
40
19
45
64
5
69
24
85
6400
7
45
24
76
100
7
107
26
135
10100
10
50
30
79
109
9
118
28
150
11300
Note: Loss of efficiency is estimate to show effect of motions on effective tug power.
FIGURE I-10
Tug power estimate required to hold 140-MDWT fully loaded tanker.
Sig. Wave H
Wind Speed
Tanker Resistance
Tug Resist.
Minimum Bollard
Est. Loss of Efficiency
Required Bollard
Estimated Tug BHP
Wind
Wave
Total
meters
kn
tons
tons
tons
tons
tons
%
tons
HP
4
30
14
22
36
3
39
20
46
3500
5
35
19
36
55
4
59
22
71
5400
6
40
24
54
78
5
83
24
103
7700
7
45
31
95
126
7
133
26
167
12500
10
50
38
121
159
9
168
28
215
16100
Note: Loss of efficiency is estimate to show effect of motions on effective tug power.
OCR for page 131
A Reassessment of the Marine Salvage Posture of the United States
FIGURE I-11
Tug power estimate required to hold 280-MDWT fully loaded VLCC.
Sig. Wave H
Wind Speed
Tanker Resistance
Tug Resist
Minimum Bollard
Est. Loss of Efficiency
Required Bollard
Estimated Tug BHP
Wind
Wave
Total
meters
kn
tons
tons
tons
tons
tons
%
tons
H P
4
30
16
19
35
3
38
20
46
3400
5
35
22
32
54
4
58
22
71
5300
6
40
29
50
79
5
84
24
104
7800
7
45
36
94
130
7
137
26
173
13000
10
50
45
159
204
9
213
28
272
20400
Note: Loss of efficiency is estimate to show effect of motions on effective tug power.
Representative terms from entire chapter:
wave height
Items in cart [1]
