came in, it was clear that the atmosphere supported a wave mode with very low frequencies but quite high propagation speed. After the turn of the century, radio wave techniques showed that there was an ionized component of this upper atmosphere. When Marconi propagated a wireless signal across the ocean, it was clear that some sort of reflecting mirror existed for radio waves. In an ideal situation the waves bounce between the Earth and this mirror, following the curvature of the Earth. Now the Earth is pretty smooth compared to the radio wavelengths used, but the upper atmosphere turns out to be not so smooth. Listening at night to distant baseball games broadcast by AM radio, one finds that the signal waxes and wanes, sometimes disappearing entirely. This was my own introduction, a frustrating one, to space weather. The radio wave mirror, called the ionosphere, is not very smooth. One of the goals of space weather forecasting is to predict the effects of the dynamic ionosphere on radio wave communications of all sorts, whether passing through or bouncing off the ionosphere.
Much of this ionospheric roughness is caused by internal gravity waves. In the developing field of radio science hundreds of papers have been written on traveling ionospheric disturbances (or TIDs) by scientists who study the reflected or refracted signals from the disturbed ionosphere. Man-made “Krakatau's,” called nuclear explosions, were found to create worldwide wave packets, as did large earthquakes.
Once, by pure chance, a wave launched by a major earthquake in the Kodiak Island region was captured by the current workhorse of upper atmospheric research, an incoherent scatter radar located in the Fairbanks area of Alaska (Kelley, 1985; see Figure 5 ). The disturbance lasted for nine hours as the atmosphere bobbed up and down with velocities exceeding 300 km per hour at heights of 400 km!
As we shall see later, Krakatau apparently also spawned the first observed clouds in the upper atmosphere. Within a few years after the volcano erupted, researchers began to report twilight clouds at the ridiculous height of 85 km where, it was thought, no atmosphere even existed. These are called noctilucent clouds since they can be seen by eye only when it is dark on the ground and the sun shines on them over the edge or limb of the Earth. Thus, the long summer twilights of Scandinavia are ideal conditions in which to see these clouds ( Figure 6 ). These clouds have a lot of structure and it is clear that there is wave activity at this height, just as clear in retrospect as the waves indicated by meteor contrails, which form at about the same height.
SOME THEORY DEALING WITH INTERNAL WAVES
Traveling ionospheric disturbances show that even at the farthest reaches of the atmosphere, wavelike activity occurs. In fact, the largest-amplitude waves seem to occur at the highest altitudes. This curious feature was illuminated by rocket experiments that deliberately left a trail of visible material in their wake. Using tracers much like barnstorming skywriters, these trails made by rocket scientists told a story of ubiquitous wave activity at high altitudes.
The structure of this trail is very similar to the sketches of meteor contrails made in 1866 (see Figure 4 ). In the man-made case, trimethyl aluminum (TMA) burns in oxygen, yielding a visible trail as shown in Figure 7 . Wave activity then distorts the trail with time. In the case of meteor contrails, some of the energy that ripped apart the meteor is stored and released over a long period, allowing the trail to be observed, if not fully understood, even today.
Colin Hines was among the first to recognize the implications of these observations and put together the first quantitative description of internal waves in a planetary atmosphere (Hines, 1960). The curious but undeniable result of his analysis is that wind and temperature fluctuations in any given wave packet should grow exponentially in strength as the wave propagates upward. No wonder such huge velocities are found in the highest reaches of the atmosphere above an earthquake, nuclear explosion, or thunderstorm.
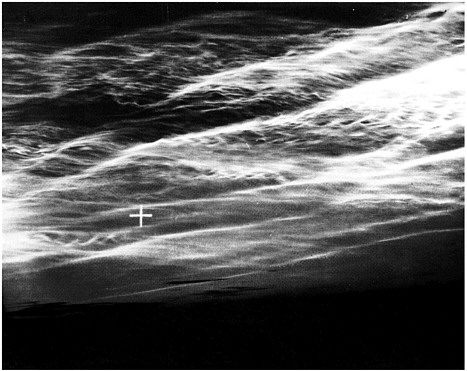
FIGURE 6 A noctilucent (night luminous) cloud photographed over Scandinavia. Reproduced from Witt (1957) with permission of Munksgaard International Publishers Ltd., Copenhagen, Denmark. Copyright 1957 by Munksgaard International Publishers Ltd.
Since all wave phenomena involve oscillatory behavior, it is illustrative to study a simple oscillation of the atmosphere before studying its wavelike behavior. Suppose we fill an imaginary, weightless balloon with air at a given height in the atmosphere. Since the balloon is weightless the parcel will stay where it is. Now suppose we gently displace it upward. Since atmospheric density decreases with height, the parcel will weigh more than the surrounding air and will sink back toward its original position. But it will overshoot the mark, only to be slowed down and eventually forced back up by buoyancy. The parcel will oscillate about its original spot with a frequency called the Brunt-Vaisalla frequency. In a more careful analysis, a real parcel of air will cool and expand as it goes upward and compress going downward, so this effect must be taken into account, but the result is changed only in detail. In the case of an atmosphere with a constant temperature, the oscillation period can be written in the form
where g is the gravitational constant for the Earth and H is the scale height of the atmosphere. In fact, H is the distance in which the air becomes thinner by about 30 percent, about 7 km near the surface. It is of some interest that the period of a pendulum is given by the expression
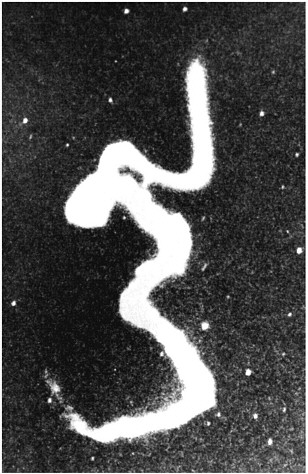
FIGURE 7 Highly distorted TMA trail released over Virginia from a sounding rocket. Reproduced from Kelley (1989) with permission of Academic Press, Inc.
where L is the length of the pendulum. Since H depends on the temperature, the period of (atmospheric) oscillation also depends on the temperature and on the rate at which it changes with height. The Brunt-Vaisalla period for the Earth's atmosphere varies as a function of height and solar cycle conditions, ranging from a few minutes to about 15 minutes (see Figure 8 ).
Such a purely vertical oscillation does not propagate and corresponds to what would happen directly above a volcanic eruption as hot gases push upward on the ambient atmosphere. Far away, however, like the effect of a pebble thrown into a pond, a set of waves is observed to propagate outward from the disturbance with frequencies less than the buoyancy frequency and longer periods. For example, the disturbances from an earthquake shown earlier had periods of the order of about an hour. In general, buoyancy waves have periods longer than the Brunt-Vaisalla period and sound waves have periods shorter than those of buoyancy waves.
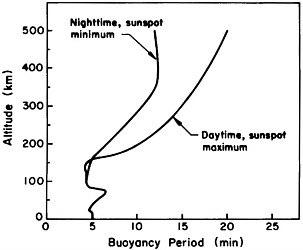
FIGURE 8 The free oscillation period of an atmospheric parcel as a function of height. Reproduced from Yeh and Liu (1974) with permission of the American Geophysical Union.
Hines provided a mathematical framework for the study of these waves by considering small changes in five quantities: pressure (p), temperature (T), density (ρ), horizontal velocity (v), and vertical velocity (w). Solving this problem thus requires five equations, which he accomplished by using two components of the momentum equation, the energy equation, the continuity equation, and the equation of state for the gas. The first four equations correspond, respectively, to the principles of momentum, energy, and mass conservation. Hines searched for solutions corresponding to a young physicist's best friend: a plane wave solution. In this formalism, kx = 2π/λx, kz = 2π/λz, and ω = 2π/P, where λx is the horizontal wavelength, λz is the vertical wavelength, and P is the period of the wave. In the small-amplitude approximation, all products of small quantities are ignored (small times small is really small) and a set of linearized equations results. By using the perfect gas law, one of the variables is quickly eliminated, leaving four equations with four unknowns:
where v and w are the components of the two-dimensional wind perturbation due to the wave; C0 is the speed of sound; and, p0 and ρ0 are the atmospheric pressure and density, respectively, at the height of
interest; the temperature variable has been eliminated by using the ideal gas law. The four-dimensional solution vector for the small perturbations is given by
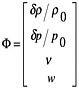
A tricky way to find the solution of four equations with four unknowns is to use matrix notation. Then either the vector F is zero (there is no wave at all) or the determinant of the matrix is zero. For the equation set above, the matrix equation is
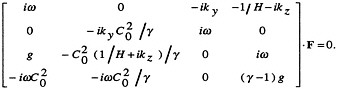
The solution after setting the determinant of the matrix equal to zero and after some algebra relates ω and k. For this set of equations, the result is
ω4 − ω2C20(k2y + k2z) + (γ − 1)g2k2y + iγgω2kz = 0.
In these equations, i is the imaginary number, ![]() one of the more valuable contributions of mathematics to science. Among the many interesting properties of the solution of these equations, two stand out:
one of the more valuable contributions of mathematics to science. Among the many interesting properties of the solution of these equations, two stand out:
-
The amplitudes of the pressure, density, temperature, and velocity all increase with altitude (just as the observational evidence suggested). But since the kinetic energy per unit volume is (1/2)ρ0(v2+ w2), how can the solution satisfy conservation of energy if v and w are increasing drastically with height? The answer to this riddle is that the kinetic energy of the wave is more precisely (1/2) ρ0(z)[v2(z) + w2(z)]; that is, both quantities change with height. Since ρ0 decreases exponentially with height in a planetary atmosphere, ( v2 + w2) must increase in order to conserve energy. So rather than defying this law, the increasing wave amplitude is necessary to satisfy it. In fact, all the perturbation quantities vary as
∼e+z/2H,
where e = 2.71... and H is the scale height of the atmosphere (H ~ 7 to 15 km below about 200 km and grows to 50 km at the top of the thermosphere). Thus, as the background density decreases by a factor of about 3, every scale height (v2 + w2) must increase by a factor of 3 just to compensate.
-
Another curious property of these waves is that as the energy propagates upward, the crests and troughs of the waves move downward (see Figure 9 ). Again, this was observed in the data and provided clear support of Hines' theory. To illustrate this feature provides a chance to once again showcase an important remote sensing tool—the incoherent scatter radar.
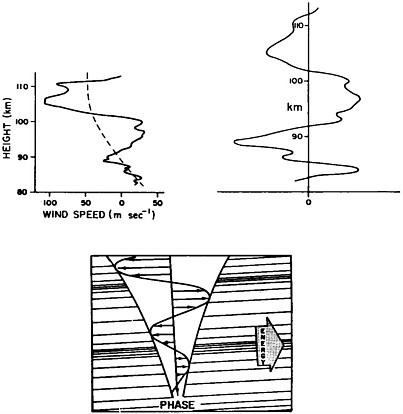
FIGURE 9 Real data and a cartoon showing the growth of atmospheric waves as they propagate upward (after Hines, 1974, as reprinted in Kelley, 1989, p. 228). Reproduced with permission of the American Geophysical Union.

FIGURE 10 The Arecibo Observatory dish, the largest contiguous radio wave collection surface ever built. Image reproduced courtesy of Charles Harrington/Cornell University Photography from the NAIC 1997 Summer Student Program Announcement. The Arecibo Observatory is part of the National Astronomy and Ionosphere Center, which is operated by Cornell University under a cooperative agreement with the National Science Foundation.
In the late 1950s, Bill Gordon, a professor at Cornell University, realized that a large enough radar could bounce a small signal from the ionosphere, even if the radio frequency was high enough to penetrate into space: that is, even though 99.99 percent of the radio wave signal would leave the Earth forever, some energy would “scatter back” incoherently. Each little electron—and I do mean little— would capture some of the energy and then radiate it back like a tiny antenna. Each electron's collection area is only 10−28 m2, so not much energy was going to be captured. Why not make up for this problem by building a huge collecting surface back on the Earth? The numbers looked good, and a few years later the Arecibo Observatory of the National Astronomy and Ionosphere Center (NAIC) was completed in Arecibo, Puerto Rico ( Figure 10 ). Thus, just about the time satellites were getting into space, so was remote sensing. With Arecibo, we could look through the ionospheric looking glass deep into space itself.
Being so tiny, electrons in the ionosphere can be pushed around easily by the wind. The ions are not so small, but electrical forces keep positive and negative charges together, and they all slosh back and forth like sand and small organisms in the surge of an ocean wave along the seafloor. This organization of the electrons makes the waves observable by radar as shown in the Arecibo data in Figure 11 . The downward slant of the oscillations is unmistakable (Djuth et al., 1997). The waves only seem to be coming down, since the energy is going upward just as Hines predicted.
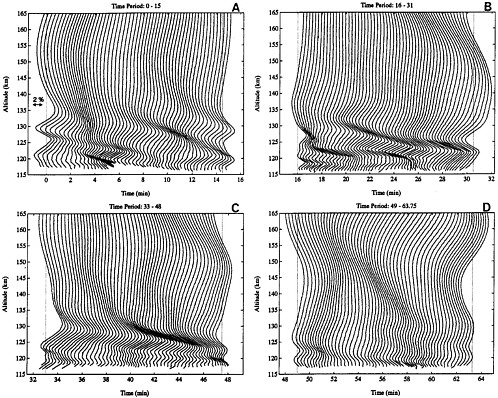
FIGURE 11 High-resolution profiles of ionospheric content versus time. Reproduced from Djuth et al. (1997) with permission of the American Geophysical Union.
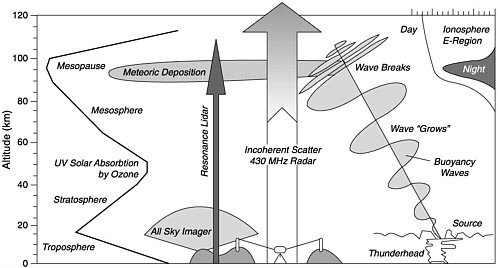
FIGURE 12 A cartoon showing some of the methods used to study the upper atmosphere over Arecibo, Puerto Rico. Courtesy of Paul Castleberg, Toyon Research Corporation, Goleta, California.
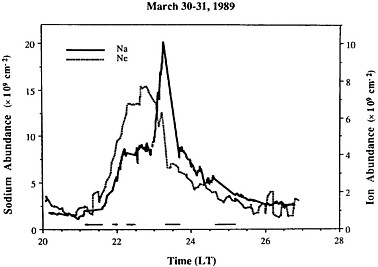
FIGURE 13 Sudden intense layers of meteoric atoms sometimes appear out of “nowhere” and can be illuminated by lasers from the ground. Here, the electron density of neon (Ne) was detected by the Arecibo radar and the sodium atoms (Na) by lidar. Reproduced from Mathews et al. (1993) with permission of the American Geophysical Union.








