B
Virtual Engineering: Toward a Theory for Modeling and Simulation of Complex Systems
John Doyle, California Institute of Technology
INTRODUCTION
This paper is a primer surveying a wide range of issues tied together loosely in a problem domain tentatively referred to as “virtual engineering ” (VE). This domain is concerned with modeling and simulation of uncertain, heterogeneous, complex, dynamical systems—the very kind of M&S on which much of the vision discussed in this study depends. Although the discussion is wide ranging and concerned primarily with topics distant from those usually discussed by the Department of the Navy and DOD modeling communities, understanding how those topics relate to one another is essential for appreciating both the potential and the enormous intellectual challenges associated with advanced modeling and simulation in the decades ahead.
Perhaps the most generic trend in technology is the creation of increasingly complex systems together with a greater reliance on simulation for their design and analysis. Large networks of computers with shared databases and high-speed communication are used in the design and manufacture of everything from microchips to vehicles such as the Boeing 777. Advances in technology
NOTE: This appendix benefited from material obtained from many people and sources: Gabriel Robins on software, VLSI, and the philosophy of modeling, Will O'Neil on CFD, and many colleagues and students.
have put us in the interesting position of being limited less by our inability to sense and actuate, to compute and communicate, and to fabricate and manufacture new materials, than by how well we understand, design, and control their interconnection and the resulting complexity. While component-level problems will continue to be important, systems-level problems will be even more so. Further, “components” (e.g., sensors) increasingly need to be viewed as complex systems in their own right. This “system of systems” view is coming to dominate technology at every level. It is, for example, a basic element of DOD's thinking in contexts involving the search for dominant battlefield awareness (DBA), dominant battlefield knowledge (DBK), and long-range precision strike.
At the same time, virtual reality (VR) interfaces, integrated databases, paperless and simulation-based design, virtual prototyping, distributed interactive simulation, synthetic environments, and simultaneous process/product design promise to take complex systems from concept to design. The potential of this still-nascent approach is well appreciated in the engineering and science communities, but what “it” is is not. For want of a better phrase, we refer to the general approach here as “virtual engineering” (VE). VE focuses on the role of M&S in uncertain, heterogeneous, complex, dynamical systems—as distinct from the more conventional applications of M&S. But VE, like M&S, should be viewed as a problem domain, not a solution method.
In this paper, we argue that the enormous potential of the VE vision will not be achieved without a sound theoretical and scientific basis that does not now exist. In considering how to construct such a base, we observe a unifying theme in VE: Complexity is a by-product of designing for reliable predictability in the presence of uncertainty and subject to resource limitations.
A familiar example is smart weapons, where sensors, actuators, and computers are added to counter uncertainties in atmospheric conditions, release conditions, and target movement. Thus, we add complexity (more components, each with increasing sophistication) to reduce uncertainties. But because the components must be built, tested, and then connected, we are introducing not only the potential for great benefits, but also the potential for catastrophic failures in programs and systems. Evaluating these complexity versus controllability tradeoffs is therefore very important, but also can become conceptually and computationally overwhelming.
Because of the critical role VE will play, this technology should be robust, and its strengths and limitations must be clearly understood. The goal of this paper is to discuss the basic technical issues underlying VE in a way accessible to diverse communities—ranging from scientists to policy makers and military commanders. The challenges in doing so are intrinsically difficult issues, intensely mathematical concepts, an incoherent theoretical base, and misleading popular expositions about “complexity.”
In this primer on VE, we concentrate on “physics-based” complex systems, but most of the issues apply to other M&S areas as well, including those involving “intelligent agents.” Our focus keeps us on a firmer theoretical and empirical basis and makes it easier to distinguish the effects of complexity and uncertainty from those of simple lack of knowledge. Our discussion also departs from the common tendency to discuss VE as though it were a mere extension of software engineering. Indeed, we argue that uncertainty management in the presence of resource limitations is the dominant technical issue in VE, that conventional methods for M&S and analysis will be inadequate for large complex systems, and that VE requires new mathematical and computational methods (VE theory, or VET). We need a more integrated and coherent theory of modeling, analysis, simulation, testing, and model identification from data, and we must address nonlinear, interconnected, heterogeneous systems with hierarchical, multi-resolution, variable-granularity models—both theoretically and with suitable software architectures and engineering environments.
Although the foundations of any VE theory will be intensely mathematical, we rely here on concrete examples to convey key ideas. We start with simple physical experiments that can be done easily with coins and paper to illustrate dynamical systems concepts such as sensitivity to initial conditions, bifurcation, and chaos. We also use these examples to introduce uncertainty modeling and management.
Having introduced key ideas, we then review major success stories of what could be called “proto-VE” in the computer-aided design (CAD) of the Boeing 777, computational fluid dynamics (CFD), and very large scale integrated circuits (VLSI). While these success stories are certainly encouraging, great caution should be used in extrapolating to more general situations. Indeed, we should all be sobered by the number of major failures that have already occurred in complex engineering systems such as the Titanic, Tacoma-Narrows bridge, Denver baggage-handling system, and Ariane booster. We argue that uncertainty management together with dynamics and interconnection is the key to understanding both these successes and failures and the future challenges.
We then discuss briefly significant lessons from software engineering and computational complexity theory. There are important generalizable lessons, but—as we point out repeatedly—software engineering is not a prototype for VE. Indeed, the emphasis on software engineering to the exclusion of other subjects has left us in a virtual “pre-Copernican” stage in important areas having more to do with the content of M&S for complex systems.
Against this background, we draw implications for VE. We go on to relate these implications to famous failures of complex engineering systems, thereby demonstrating that the issues we raise are not mere abstractions, and that achieving the potential of VE (and M&S) will be enormously challenging. We touch
briefly on current examples of complex systems (smart weapons and airbags) to relate discussion to the present. We then discuss what can be learned from control theory and its evolution as we move toward a theory of VE. At that point, we return briefly to the case studies to view them from the perspective of that emerging theory. Finally, we include a section on what we call “soft computing,” a domain that includes “complex-adaptive-systems research, ” fuzzy logic, and a number of other topics on which there has been considerable semi-popular exposition. Our purpose is to relate these topics to the broader subject of VE and to provide readers with some sense of what can be accomplished with “soft computing” and where other approaches will prove essential.
In summary before getting into our primer, we note that several trends in M&S of complex systems are widely appreciated, if not well understood. There is an increasing emphasis on moving problems and models from linear to nonlinear; from static to dynamic; and from isolated and homogeneous to heterogeneous, interconnected, hierarchical, and multi-resolution (or variable granularity and fidelity). What is poorly understood is the role of uncertainty, which we claim is actually the origin of all the other trends. Model uncertainty arises from the differences between the idealized behavior of conventional models and the reality they are intended to represent. The need to produce models that give reliable predictability of complex phenomena, and thus have limited uncertainty, leads to the explicit introduction of dynamics, nonlinearity, and hierarchical interconnections of heterogeneous components. Thus the focus of this paper is that uncertainty is the key to understanding complex systems.
A few simple thought experiments can illustrate the issues of uncertainty and predictability—as well as of nonlinearity, dynamics, heterogeneity, and ultimately complexity. Most of the experiments we discuss here can also be done with ordinary items like coins and paper.
Consider a coin-tossing mechanism that imparts a certain linear and angular velocity on a coin, which is then allowed to bounce on a large flat floor, as depicted in Figure B.1 . Without knowing much about the mechanism, we can reliably predict that the coin will come to rest on the floor. For most mechanisms, it will be impossible to predict whether it will be heads or tails. Indeed, heads or tails will be equally likely, and any sequence of heads or tails will be equally likely. Such specific predictions are as reliably unpredictable as the eventual stopping of the coin is predictable.
The reliable unpredictability of heads or tails is a simple consequence of the sensitivity to initial conditions that is almost inevitable in such a mechanism. The coin will bounce around on the floor in an apparently random and erratic manner

FIGURE B.1 Coin tossing experiment.
before eventually coming to rest on the floor. The coin's trajectory will be different in detail for each different toss, in spite of efforts to make the experiment repeatable. Extraordinary measures would be needed to ensure predictability (e.g., dropping the coin heads up a short distance onto a soft and sticky surface, so as always to produce heads).
Sensitivity to initial conditions (STIC) can occur even in simple settings such as a rigid coin in a vacuum with no external forces, not even gravity. With zero initial velocity, the coin will remain stationary, but the smallest initial non-zero velocity will cause the coin to drift away with distance proportional to time. The dynamics are linear and trivial. This points out that—in contrast with what is often asserted—sensitivity to initial conditions is very much a linear phenomenon. Moreover, even in nonlinear systems, the standard definition of sensitivity involves examining infinitesimal variations about a given trajectory and examining the resulting linear system. Thus even in nonlinear systems, sensitivity to initial conditions boils down to the behavior of linear systems. What nonlinearity contributes is making it more difficult to completely characterize the consequences of sensitivity to initial conditions.
Sensitivity to initial conditions is also a matter of degree; the coin-in-free-space example being on the boundary of systems that are sensitive to initial conditions. Errors in initial conditions of the coin lead to a drifting of the trajectories that grows linearly with time. In general, the growth can be exponential, which is more dramatic. If we add atmosphere, but no other external force, the coin will eventually come to rest no matter what the initial velocities, so this
is clearly less sensitive to initial conditions than the case with no atmosphere. A coin in a thick, sticky fluid like molasses is even less sensitive.
Not all features of our experiment are sensitive to initial conditions. The final vertical position is reliably predictable, the time at which the coin will come to rest is less so, the horizontal resting location even less so, and so on, with the heads or tails outcome perfectly unpredictable. It follows that any notion of complexity cannot be attributed to the system, but must include the property of it that is in question.
We can get a better understanding of sensitivity to initial conditions with some elementary mathematics. Suppose we have a model of the form x(t+1) = f(x(t)). This tells us what the state variable x is at time t+1 as a function of the state x at time t. This is called a difference equation, which is one way to describe a dynamical system—i.e., one that evolves with time. If we specify x(t) at some time, say t = 0, then the formula x(t+1) = f(x(t)) can be applied recursively to determine x(t) for all future times t = 1,2,3, . . . . This determines an orbit or trajectory of the dynamical system. This only gives x at discrete times, and x is undefined elsewhere. It is perhaps more natural to model the coin and other physical systems with differential equations that specify the state at all times, but difference equations are simpler to understand. For the coin, the state would include at least the positions and velocities of the coin, and possibly some variables to describe the time evolution of the air around the coin. If the coin were flexible, the state might include some description of the bending and its rate. And so on.
A scalar linear difference equation is of the form x(t+1) = ax(t), where a is a constant (the vector case is x(t+1) = Ax(t), where A is a matrix). If x(0) is given, the solution for all time is x(t) = atx(0). Thus, if a>1, nonzero solutions grow exponentially and the system is called unstable. Since the system is linear, any difference in initial conditions will also grow exponentially. (If a<1, then solutions decay exponentially to zero and the origin is a stable fixed point.)
Exponential growth appears in so many circumstances that it is worth dramatizing its consequences. If a = 10, then in each second x gets 10 times larger, and after 100 seconds it is 10100 larger. With this type of exponential growth, an error smaller than the nucleus of a hydrogen atom would be larger than the diameter of the known universe in less than 100 seconds. Of course, no physical system could have this as a reasonable model for long time periods. The point is that linear systems can exhibit very extreme sensitivity to initial conditions because of exponential growth. Of course, STIC is a matter of degree. The quantity ln(a) is one measure of the degree of STIC and is called the Lyapunov exponent.
Suppose we modify our scalar linear system slightly to make it the nonlinear system x(t+1) = 10x(t) mod10 and restrict the state to the interval [0,10]. This system can be thought of as taking the decimal expansion of x(t) and shifting the
decimal point to the right and then truncating the digit to the left of the units place. For example, if x(0) = p = 3.141592 ..., then x(1) = 1.41592 ... and x(2) = 4.1592 ... and so on. This still has, in the small, the same exponential growth as the linear system, but its orbits stay bounded. If x(0) is rational, then the x(t) will be periodic, and thus there are a countable number of periodic orbits (arbitrarily long periods). If x(0) is irrational, then the orbit will stay irrational and not be periodic, but it will appear exactly as random and irregular as the irrational initial condition. As is well-known, this system exhibits deterministic chaos. The Lyapunov exponent can also be generalized to nonlinear systems, and in this case would still be ln(a).
The several alternative mathematical definitions of chaos are all beyond the scope of this paper, but the essential features of chaotic systems are sensitivity to initial conditions (STIC), periodic orbits with arbitrarily long periods, and an uncountable set of bounded nonperiodic (and apparently random) orbits.
The STIC property and the large number of periodic orbits can occur in linear systems. But the “arbitrarily long periods” and “bounded, nonperiodic, apparently random ” features require some nonlinearity. Chaos has received much attention in the popular press, which often confuses nonlinearity and sensitivity to initial conditions in suggesting that the former in some way causes the latter, when in fact both are independent and necessary but not sufficient to create chaos. The formal mathematical definitions of chaos involve infinite time horizon orbits, so none of our examples so far would be, strictly speaking, chaotic. A simple way to get a system that is closer in spirit to chaos would be to put our coin in a box and then shake the box with some periodic motion. Even though the box had regular motion, under many circumstances the coin's motion in bouncing around the box would appear random and irregular.
A simple model with linear dynamics between collisions and a linear model for the collisions with the box would almost certainly be chaotic, although even this simple system is too complicated to prove the existence of chaos rigorously and it must be suggested via simulation. Very few dynamical systems have been proved chaotic, and most models of physical systems that appear to exhibit chaos are only suggested to be so by simulation. One-degree-of-freedom models of a ball in a cylinder with a closed top and a periodically moving piston have been proved chaotic. The ball typically bounces between the piston and the other end wall of the cylinder with the impact times being random, even though the dynamics are purely deterministic, and even piecewise linear.
To get a sense of the notion of bifurcation in dynamical systems, consider the following experiment. Drop a quarter in as close to a horizontal position and with as little initial velocity as possible. It will drop nearly straight down, and the air will have little effect at the speeds the coin will attain while it bounces around the floor. Now take a quarter-size piece of paper and repeat the experiment. The paper will begin fluttering rapidly and fall toward the floor at a large angle, landing far away from where a real quarter would have first hit the floor. This is
an example of a bifurcation, where a seemingly small change in properties creates a dramatic change in behavior. The heavy coin will reliably and predictably hit the floor beneath where it is dropped (at which point subsequent collisions may make what follows it quite unpredictable), whereas the paper coin will spin off in any direction and land far away, but then quickly settle down without bouncing. Thus one exhibits STIC, while the other does not.
A simple variant on this experiment illustrates a bifurcation more directly. Make two photocopies of the diagram in Figure B.2 (or just fold pieces of paper as follows), and cut out the squares along the solid line. The unfolded paper will flutter erratically when dropped, exhibiting STIC. Next, take one of the papers and fold it along one of the dashed lines to create a rectangularly shaped object. Turn the object so that the long side is vertical. Then make two triangular folds from the top left and bottom left corners along the dotted lines to produce a small funnel-shaped object. If this is dropped it will quickly settle into a nice steady fall at a terminal velocity with the point down. This is known as a relative equilibrium in that all the state variables are constant, except the vertical position, which is decreasing linearly. It is locally stable since small perturbations keep the trajectories close, and is also globally attracting in the sense that all initial conditions eventually lead to this steady falling.
If the folds are then smoothed out by flattening the paper more back to its prefolded shape, then only when the paper is dropped very carefully will it fail to flutter. This nearly flat paper has a relative equilibrium consisting of flat steady falling, but the basin of attraction of this equilibrium is very small. That is, the more folded the paper is, the larger the set of initial conditions that will lead to steady falling. If the folds are sharp enough and the distance to the floor great enough, then no matter how the paper is dropped it will eventually orient itself so the point is down, and then fall steadily.
This large change in qualitative behavior as a parameter of the system is changed (in this case, the degree of folding) is the subject of bifurcation analysis
FIGURE B.2 Proper folding diagram for bifurcation experiment.
within the theory of dynamical systems theory. In these examples, bifurcation analysis could be used to explore why a regular coin shows STIC only after the first collision, while the paper coin shows it only up to hitting the floor, as well as why the dynamics of the folded paper change with the degree of folding. Of course, bifurcation analysis applies to mathematical models, and developing such models for these examples is not trivial. To develop models that reproduce the qualitative behavior we see in these simple experiments requires advanced undergraduate level aerodynamics. These models will necessarily be nonlinear if they are to reproduce the fluttering motion, as this requires a nontrivial nonlinear model for the fluids.
Bifurcation is related to chaos in that bifurcation analysis has often been an effective tool to study how complex systems transition from regular behavior to chaotic behavior. While chaos per se may be overrated, the underlying concepts of sensitivity to initial conditions and bifurcation, and more generally the role of nonlinear phenomena, are critical to the understanding of complex systems. The bottom line is as follows:
-
We can make models from components that are simple, predictable, deterministic, symmetric, and homogeneous, and yet produce behavior that is complex, unpredictable, chaotic, asymmetric, and heterogeneous.
-
Of course, in engineering design we want to take components that may be complex, unpredictable, chaotic, asymmetric, and heterogeneous and interconnect them to produce simple, reliable, predictable behavior.
We believe that the deeper ideas of dynamical systems will be important ingredients in this effort.
It is tempting to view complexity in this context as something that arises in a mystical way between complete order (that the coin will come to rest) and complete randomness (heads or tails) and to settle on chaotic systems as prototypically complex. We prefer to view complexity in a different way. To make reliable predictions about, say, the final horizontal resting place, the distribution of horizontal resting positions, or the distribution of trajectories, we would need elaborate models about the experiment and measurements of properties of the mechanism, the coin, and the floor. We might also improve our prediction of, say, the horizontal resting location if we had a measurement of the positions and velocities of the coin at some instant after being tossed. This is because our suspicion would be that the greatest source of uncertainty is due to the tossing mechanism, and the uncertainty created by the air and the collisions with the floor will be less critical, but this would also have to be checked. The quality of the measurement would obviously greatly affect the quality of any resulting prediction, of course.
To produce a model that reliably predicted, say, the distribution of the trajectories could be an enormous undertaking, even for such a simple experiment. We would need to figure out the distributions of initial conditions imparted on the coin by the tossing mechanism, the dynamics of the trajectories of the coin in flight, and the dynamics of the collisions. The dynamics of the coin in the air is linear if the fluid/coin interaction is ignored or if a naive model of the fluid is assumed. If the coin is light, and perhaps flexible, then such assumptions may allow for too much uncertainty, and a nonlinear model with dynamics of the coin/ fluid interaction may be necessary (imagine a “coin” made from thin paper, or replace air by water as the fluid). If the coin flexibility interacts with the fluid sufficiently, we could quickly challenge the state of the art in computational fluid dynamics.
The collisions with the floor are also tricky, as they involve not only the elastic properties of the coin and floor, but the friction as well. This now takes us into the domain of friction modeling, and we could again soon be challenging the state of the art. Even for this simple experiment, if we want to describe detailed behavior we end up with nonlinear models with complex dynamics and the physics of the underlying phenomena is studied in separate domains. It will be difficult to connect the models of the various phenomena, such as fluid/coin interaction, and the interacting of elasticity of the floor and coin with frictional forces. It is the latter feature that we refer to as heterogeneity. Heterogeneity is mild in this example since the system is purely mechanical, and the collisions with the floor are relatively simple.
Our view of complexity, then, is that it arises as a direct consequence of the introduction of dynamics, nonlinearities, heterogeneity, and interconnectedness intended to reduce the uncertainty in our models so that reliable predictions can be made about some specific behavior of our system (or its unpredictability can be reliably confirmed in some specific sense, which amounts to the same thing). Complexity is not an intrinsic property of the system, or even of the question we are asking, but in addition is a function of the models we choose to use. We can see this in the coin tossing example, but a more thorough understanding of complexity will require the richer examples studied in the rest of this paper.
While this view of complexity has the seemingly unappealing feature of being entirely in the eye of the beholder, we believe this to be unavoidable and indeed desirable: Complexity cannot be separated from our viewpoint.
Up to this point, we have been rather vague about just what is meant by uncertainty, predictability, and complexity, but we can now give some more details. For our coin toss experiment, we would expect that repeated tosses would produce rather different trajectories, even when we set up the tossing mechanism identically each time to the extent we can measure. There would
presumably be factors beyond our control and beyond our measurement capability. Thus any model of the system that used only the knowledge available to us from what we could measure would be intrinsically limited in its ability to predict the exact trajectory by the inherent nonrepeatability of the experiment. The best we could hope for in a model would be to reliably predict the possible trajectories in some way, either as a set of possible trajectories or in terms of some probability distribution. Thus we ideally would like to explicitly represent this uncertainty in our model. Note that the uncertainty is in our model (and the data that goes with it). It is we—not nature—who are uncertain about each trajectory. 1 We now describe informally the mechanisms by which we would introduce uncertainty into our models.
A special and important form of uncertainty is parametric uncertainty, which arises in even the simplest models such as attempting to predict the detailed trajectory of a coin. Here the “parameters” include the coin's initial conditions and moments of inertia, and the floor's elasticity and friction. Parameters are associated with mechanisms that are modeled in detail but have highly structured uncertainty. Roughly speaking, all of the “inputs” to a simulation model are parameters in the sense we use the term here. 2
How do we deal with parametric uncertainty (see also Appendix D )?
-
Average case. If only average or typical behavior is of interest, this can be easily evaluated with a modest number of repeated Monte Carlo simulations with random initial conditions. In this case the presence of parametric uncertainty adds little difficulty beyond the cost of a single simulation. Also, in the average case the number of parameters does not make much difference, as estimates of probability distributions of outcomes do not depend on the number of parameters.
-
Linear models. If the parameters enter linearly in the model, the resulting uncertainty is often easy to analyze. To be sure, we can have extreme sensitivity to initial conditions, but the consequences are easily understood. Consider the linear dependence of the velocity and position of the first floor collision as a function of the initial velocities and positions of the coin. A set in the initial
1
Except in our discussion of VLSI later in this appendix, we ignore quantum mechanics and the intrinsically probabilistic behaviors associated with it. Quantum effects are only very rarely significant for the systems of interest here.
2
Some workers distinguish between “parameters” that can be changed interactively at run time, or in the course of a run, and “fixed data,” that can be changed only by recompiling the database. Both are parameters for the purposes of this paper.
-
condition space is easily mapped to a set of collision conditions. Both average and worse-case behavior can be evaluated analytically. For example, suppose we have some scalar function F(p), where p is some vector of n parameters. If F is linear, then evaluating its largest values over a convex set of parameters is straightforward, and in the case where each component of the parameters is in an interval, it is trivial.
-
Nonlinear/worst-case/rare event. If the parameters enter nonlinearly, then the analysis becomes more difficult—particularly if we are interested in worst-case behavior or rare events. For example, if F(p) is nonlinear and has no exploitable convexity properties, we may have to do a global and exhaustive search of p to determine, say, the maximum value of F. Such a search will grow exponentially with the dimension n of p. While this is an entirely different role of exponential growth than in sensitivity to initial conditions, the consequences are no less dramatic. If we only choose to examine a gridding of the space of parameters where we take 10 values of each element (this could be too coarse to find the worse case), then the number of functional evaluations will be 10n. No matter how quickly we do the functional evaluations, this exponential growth prohibits exploring more than a handful of parameters.
It does not take highly nonlinear dynamics to produce nonlinear dependence on parameters. A simplified model of coin flipping with a linear model for collisions and a linear model for flight between collisions is piecewise linear, but this is enough to produce complicated dependence on initial conditions. In a model with linear dynamics, the dependence of final conditions on initial conditions is linear, but parameters such as mass, moments of inertia, resistance, and so on, can enter the equations nonlinearly, thereby producing a nonlinear dependence of the trajectories on these parameters.
Evaluating worst-case or rare events can also be more difficult than the average case, because Monte Carlo requires an excessive number of trials or we have to exhaustively search all parameters for the worst case. This too can be computationally intractable, depending on the number of the parameters and the functional dependence on them. In some cases, exact calculation of probability density functions can be easier, and numerical methods for evaluating probability density functions by advanced global optimization methods is a current research topic.
Of course, we would always hope to discover some property of the parametric dependence that makes it possible to avoid this exponential growth in computation with the number of parameters. Unfortunately, it has been proved that evaluating, say, the stability of even the simplest possible nontrivial linear system depending on parameters is NP-hard, which implies that exponential growth is in a certain sense unavoidable. To explain the implications of this for evaluating parametric uncertainty will require several additional concepts, including obviously the meaning of NP-hard, and will be taken up in more detail later.
Not all uncertainty is naturally modeled as parametric. Suppose the fluid in which our coin is tossed cannot be neglected, as would be the case for a light paper coin in air, or a coin in water. The coin may exhibit erratic and apparently random motion as it falls. While we could in principle model the fluid dynamics of the atmosphere in detail, the error-complexity tradeoff is very unfavorable. Traditionally, noise is instead modeled as a stochastic process even when it is more appropriate to think of it as chaotic. That is easy to see in the case of wind gusts generated by fluid motions in the air. Just because the wind appears random and we do not want to model the fluid in detail does not mean that wind is naturally viewed as a random process. We model it as a stochastic process for convenience.
Other examples of phenomena that are often modeled as noise include arrival times for queues, thermal noise in circuits, and even the outcome of the process of coin flipping itself. In each case, the mechanism generating the noise is typically not modeled in detail, but some aggregate probabilistic or statistical model is used. Robust control has emphasized set descriptions for noise, in terms of statistics on the signals such as energy, autocorrelations, and sample spectra, without assuming an underlying probability distribution. Recently, the stochastic and robust viewpoints have been reconciled by the development of set descriptions that recover many of the characteristics and much of the convenience of stochastic models. Finally, Monte Carlo simulations adequately generate noise with pseudo-random number generators, which are neither truly chaotic nor random, but are periodic with very long periods. 3 Thus, it makes little sense to be dogmatic about insisting that models be stochastic, per se, but it is important that noise sources be explicitly modeled in some reasonable way. This may be accomplished in a number of ways:
-
Unmodeled dynamics. The use of constant parameters or noise to model aerodynamic forces generated by the fluid around our coin means not treating explicitly the complex, unsteady fluid flows that more accurately describe the physics. Even if we attempt to model the fluids in some detail, the forces and moments that the resulting model predicts will be “felt ” by the coin will be wrong, and the difference may depend on the coin's movements. It may be undesirable to then model these forces as noise, since that assumes that they do not depend on the coin 's movement. We may choose to model this type of uncertainty with a mechanism similar to noise above, but involving relationships between variables, such as coin velocities and forces. Like noise modeling, we
|
3 |
Some MC simulations have been done with genuinely random physical sources, such as decay of radioactive isotopes. |
-
use bounds and constraints, but now on the signals describing both the coin and the fluid. Similarly, rigid body models assume that forces directly generate rigid body motion, while models that included flexible effects allow for bending as well. Rather than modeling the flexibility in detail, we may choose to bound the error between forces and rigid body motions as constraints on signals. 4
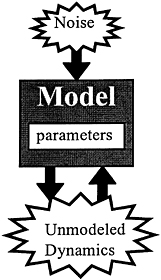
FIGURE B.3 Relationships of models and their parameters with noise and unmodeled dynamics. Noise excites model dynamics but not vice versa.
Noise, then, is similarly a special case of unmodeled dynamics where one assumes that the unmodeled dynamics excite the modeled dynamics but not vice versa (see Figure B.3 ). For example, modeling atmospheric gusts as noise assumes that the vehicle or coin motion has a negligible effect on the atmosphere compared to the fluid motions in the atmosphere generated by other sources. This is a reasonable assumption in many circumstances but might be unreasonable for, say, airplanes flying near large fixed objects such as the ground.
|
4 |
This issue of how to treat unmodeled dynamics comes up in quasi-steady aerodynamics of airplanes, which is a particular problem when considering the interactions of closely spaced vehicles whose flows affect each other, or when the vehicle is highly flexible. It is currently beyond the state of the art to do computational fluid dynamics (CFD) for a moving vehicle in a way that would allow the use of CFD codes in vehicle simulation. It is possible to put explicit uncertainty models into the coefficients and analyze their effects using methods from robust control. In fact, exactly this type of analysis for the Shuttle Orbiter during reentry and landing was among the first commercial successes of robust control, and the use of robustness analysis software is now standard in the Shuttle program. CFD, robust control, and the Shuttle reentry will be discussed in more detail later. |
-
Sensitivity to uncertainty. While we have discussed STIC with simple examples, models can be sensitive to all forms of uncertainty, not just initial conditions. This is a much more subtle notion and requires, unfortunately, deeper mathematics to explain. Indeed, as we will see from the engineering example later, sensitivity to unmodeled dynamics is a much greater problem generally than sensitivity to initial conditions.
To get some sense of the issues, here, suppose that we develop a model of the paper falling that assumes the paper is rigid and the flow is very simple, and that it seems to capture the qualitative dynamics of the experiment. Suppose we then try to use this model to predict, before doing any experiment, what would happen with tissue paper, where there is substantial flexibility. The behavior might be totally different, and no choices of parameters in our simpler model would capture the behavior of the falling tissue. One way to approach the tissue would be to try initially to bound the effects of flexibility in a rough way and check if this makes any difference to the outcome (assume for the moment we have some tools to do this). Presumably, this would reveal that the small flexibility makes little difference for the bifurcation analysis with regular paper, but makes a large difference with the tissue. The uncertain model of the tissue would suggest that we would be unable to reliably predict details of the trajectory as well as in the regular paper case without doing a more detailed model of the tissue flexibility. Thus, our initial model of the tissue would have been sensitive to unmodeled dynamics.
-
Games with hostile adversaries. This appendix deals largely with “hard” engineering examples, but before leaving the subject of uncertainty, it is worth noting a complication of particular importance in military applications—notably, the presence of a hostile adversary. It is a complication without direct parallel in normal science and engineering. Nature, while perhaps sometimes seeming to be capricious, does not consciously plan how to complicate our lives. In conflict, all the participants may have strategies that change in response to perceived actions of the other participants. These changes may seek to optimize some feature of events, or may merely be dictated by doctrine. They may be objectively “optimal” in some sense, or they may be idiosyncratic and risk-taking. Some adversaries may wish to optimize the likelihood of complete success, caring little about “expected value.” And all humans are subject to well-known cognitive biases that influence decisions.
Now, some of the methods discussed in this appendix might well be useful in modeling potential adversary behaviors. We could, for example, model all participants' options and reasoning, and then look at, say, minimax strategies. Indeed, robust control theory often models parameters, noise, and unmodeled dynamics in such a way that control design can be viewed as a differential game between the controller and “nature.” Such methods could be quite useful for designing robust strategies. We will not pursue this subject further here, except
to notice parenthetically that it is much easier to produce a computer program that plays grandmaster-level chess (which has been done) than it is to model accurately the actual play of a grandmaster (which might not be done in the foreseeable future). 5
The motivation for introducing uncertainty mechanisms into our models is to predict the range and distribution of possible outcomes of our experiments. What is somewhat misleading about coin tossing with respect to the broader VE area is the small scale of the experiment and its relative homogeneity. In VE modeling we must expect huge numbers of components with extremely diverse origins. We have discussed the features of a model that included nonlinearity, dynamics, interconnection of heterogeneous components, complexity, and uncertainty. Of these, only uncertainty is an intrinsic property of the modeling process, with the others introduced—perhaps reluctantly—to reduce the uncertainty in our models. This uncertainty management is the driving force behind complexity in models.
Conventional modeling in science and engineering is basically reductionist. Experiments are designed to be controlled and repeatable, usually with certain phenomena isolated. It is widely thought that if we model a system with sufficient accuracy, then we can reliably predict the behavior of that system. This standard modeling paradigm is poorly suited to VE. The phenomenon of deterministic chaos has shed some doubt on the conventional view, and it is now widely appreciated, even among the lay public, that quite simple models can produce apparently complex and unpredictable behavior. What is less well appreciated is an entirely different issue of how uncertainty in components interacts with the process of interconnection of components to produce uncertainty at the system level: There is simply no way of telling how accurately a component must be modeled without knowing how it is to be connected. Thus both the component uncertainty and the interconnection determine the impact of that uncertainty.
One reason that explicit uncertainty modeling is uncommon is that the typical “consumer” of a conventional model is another human sharing domain-specific expertise and an understanding of standard assumptions. Model uncertainty and the interpretation of assumptions are typically implicit and also part of the domain-specific expertise. Most scientific and engineering disciplines can almost be defined in terms of what they choose to both focus on and neglect about
|
5 |
Within the military domain, there are examples to illustrate all of these points. For example, RAND's SAGE algorithm, developed by Richard Hillestad, is used in theater-level models to “optimally” allocate and apportion air forces across sectors and missions. This not only establishes bounds on performance, but also reduces the number of variables, which makes it much easier to focus on tradeoffs among weapon systems and forces. This said, it is important to run cases in which the sides follow doctrine, because that behavior may be quite different and more realistic. |
the world. Within domains, the dominant assumptions and viewpoints are taken for granted and never mentioned explicitly. In the coin flipping experiment, terms such as inviscid flow might be mentioned, but not something like the assumption of chemical equilibrium.
Problems with conventional modeling arise in VE because the consumer of a model will be a larger model in a hierarchical, heterogeneous model, with possibly no intervention by human experts. We cannot rely on theory or software that is domain-specific, implicit, and requires human interpretation at every level. The more complex the system, the less critical individual components may become but the more critical the overall system design becomes. Furthermore, we are interested in modeling real-world behavior, not an idealized laboratory experiment.
The next question we address is, What constitutes a sensible notion of model error or fidelity? Again starting with a simple “naive” view, let us imagine that reality has some set of behaviors, that our model has some set of behaviors, and that we have some measure of the mismatch between these two sets. These may be heroic assumptions, but let us press forward for now.
Putting aside the cognitive preference for simplicity, we would perhaps obviously prefer high-fidelity models. The obstacles to model fidelity are the costs of modeling due to limited resources, mainly:
-
Computation,
-
Measurement, and
-
Understanding.
These limitations are ultimately connected to time and money. This suggests tradeoffs.
For the time being, we can think of computation cost naively as simply the cost of the computer resources to simulate our model, and measurement cost as the cost to do experiments, take data, and process those data to determine parameters in our model. It is obviously not so easy to formalize what we mean by understanding, but it is clear that we can have vastly different levels of understanding about different physical processes and this can greatly affect our ability to effectively model them.
Figure B.4 illustrates the tradeoff between fidelity and complexity, or more precisely the tradeoff between model error and resources. As we use more resources, we can reduce our error, but there are strong effects of diminishing returns. 6
|
6 |
Actually, errors could increase with cost if resources are used to build extra complexity to the point that the model begins to collapse under its own weight, but here we assume optimal use of the resources. |
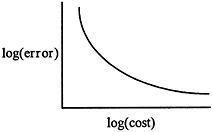
FIGURE B.4 Error-cost tradeoff.
A well-known example occurs in weather prediction. For standard computer simulations used in weather prediction, the error between the prediction and the actual weather grows with time due to sensitivity to initial conditions. Long-term predictability is viewed by experts as being impossible, and even massive improvements in computation and measurement will yield diminishing returns.
We can summarize the previous discussion as follows. No matter how sophisticated our models, there is always some difference between the model and the real world. Model uncertainty leads to unpredictability, which mirrors the unpredictability of real systems. This has two important aspects. One is that models can exhibit extreme sensitivity to variations in model assumptions, parameters, and initial conditions. The second, discussed below, is the combinatorial complexity of evaluating all the model combinations that arise from possible variations in assumptions, parameters, and initial conditions in all the subsystems, which makes a brute force enumeration prohibitively expensive. These are some of the fundamental limitations on the predictability of models, which will not be eliminated by advances in computational power, measurement technology, or scientific understanding. Thus in developing robust VE, there are certain “hard” limits on predictability, and it is important to understand and quantify the limits on the predictability of full system models in terms of the uncertainties in component models. Current VE enterprises generally do not have good strategies for dealing with these uncertainties, or for understanding how they propagate through the system model and ultimately affect the decision-making process they were intended to serve.
To make reliable predictions about the systems being modeled under uncertainty, we are often forced to add complexity in the form of nonlinearities, dynamics, and interconnections of heterogeneous components. Unlike uncertainty, none of these are intrinsic properties of our systems and models, but are added, perhaps reluctantly, to reduce uncertainty. It is tempting to say that all real systems are nonlinear, dynamic, and heterogeneous, but this is meaningless since
these are properties of models, not reality (although we will use the convenient shorthand of referring to some phenomena as, say, nonlinear when it might be more precise to say that high-fidelity models of the phenomena must be nonlinear). It would be more appropriate to say that modeling of physical systems leads naturally and inevitably to the introduction of such mathematical features. Complexity is due, in this view, simply to the presence of these features, and to the degree of their presence. This view of complexity will be a theme throughout, so let us consider a bit more detail on the meaning of dynamics, nonlinearity, and heterogeneity.
A dynamic model is simply one whose variables evolve with time, perhaps described by differential or difference equations, or perhaps more abstractly. For partial differential equations, the situation is even more complicated, since solutions can vary continuously with space as well as time. Thus, dynamical systems tend to be much more difficult to work with than static systems.
The importance of linear models is that they satisfy superposition, so that a linear function of a list of variables can be completely characterized by evaluating the function on one value of each variable taken one at time. In other words, the local behavior of a linear function completely determines its global behavior. Nonlinearity is the absence of this property, so that local information may say nothing about global behavior. What is critical in modeling uncertain systems is how the quantity that we want to predict depends on the uncertainty we are modeling. A linear dynamical system can depend nonlinearly on parameters in such a way as to make evaluation of the possible responses of the system very difficult. In turn, a nonlinear dynamical system may have outputs that depend only linearly on some parameters, and this may be easily evaluated. What is critical is the dependence on the uncertainty.
Again, nonlinearities are not responsible for sensitivity to initial conditions. It is when nonlinearities are combined with sensitivity to initial conditions that behavior can be a complex and unpredictable function of the initial conditions.
Heterogeneity in modeling arises from the presence in complex systems of component models dealing with material properties, structural dynamics, fluids, chemical reactions, electromagnetics, electronics, embedded computer systems, and so on, each represented by a separate and distinct engineering discipline. Often, modeling methods in one domain are incompatible with those in another.
Even when we can break the system into multiple levels with the lowest level containing only one modeling domain, the component models must be combined. Thus, a critical issue that must be dealt with in every aspect of modeling is how to combine heterogeneous component models.
A classical example of a mildly heterogeneous system occurs in the phenomenon of flutter, an instability created by the interaction of a fluid and an elastic solid, or more generally with a solid that has nontrivial dynamics. It is a critical limiting factor in the performance of many aircraft wings and jet engines, and a simple version of it could be seen in the “flutter” of the paper in the experiment above. There are two approaches to treating such heterogeneous systems. One is to do a fully integrated model of the system, which in this case is the domain of the field of aeroelasticity. The other is to make simplifying approximations about the boundary conditions between the heterogeneous components and then interconnect them. For flutter, this is typically done when assuming that the fluid is treated quasi-statistically, so forces and moments generated by the fluids do not depend on the dynamics of the solid material. This way, the dynamics of the fluid can be treated separately, approximated as a static map, and then simply connected with the dynamics of the solid. If this approximation is reasonable, as it is in our paper experiment, then simple models can predict the presence or absence of flutter.
Flutter is only a mildly heterogeneous system, because it involves continuum mechanical phenomena, but, for example, no chemistry, electromagnetics, or thermodynamics. In more profoundly heterogeneous systems, it is not possible to create huge new engineering domains to address the unique modeling problems associated with each possible combination of modeling problems. We must make suitable approximations of the boundary conditions between domains/components.
In simple situations it is often possible to use aggregated models that capture the system behavior without detailed treatment of the system's internal mechanisms. However, in developing detailed models of complex systems, it is common practice to break the system up into components, which are then modeled in detail. This can continue recursively at several levels to produce a hierarchical model, and the full system must then be built up from the component models.
This disaggregation approach is essentially the only way that complex system models can be developed, but it leads to a number of difficult problems, including the need to connect heterogeneous component models, and the need for multi-resolution or variable granularity models. Perhaps more importantly, this neo-reductionist approach to modeling may represent a reasonable scientific program for discovering fundamental mechanisms, provided one never wants to
reconstruct a model of the whole system. Applied naively, it simply does not work very well as a strategy for modeling complex systems.
There is need for multi-resolution or variable granularity models, because the process of component disaggregation can continue indefinitely to create an infinitely complex model (see also Appendix E ). It is possible, and even likely, that this process will not converge, as there can easily be extreme sensitivity to small component errors that are the consequence of interconnection and that can be evaluated only at the system level. For example, there might exist quite simple models for components and their uncertainty that interconnect to reliably predict system behavior, but it can be essentially impossible to discover these models by viewing the components in isolation. Thus one is in the paradoxical position of needing the full system to know what the component models should be, but having only the component models themselves as the route to creating a system model. Neither a purely top-down nor a bottom-up approach will suffice, and more subtle and iterative approaches are needed. Even the notion of what is a “component” is not necessarily clear a priori, as the decomposition is never unique and often the obvious thing to do is severely suboptimal.
The standard approach to developing variable error-complexity component models is to allow multi-resolution or variable granularity models. Simple examples of this include using adaptive meshes in finite element approximations of continuum phenomena, or multi-resolution wavelet representations for geometric objects in computer graphics. In hierarchical models, the problem of developing analogous variable resolution component models is quite subtle and will surely be an important research area for some time. Using these same examples, there are difficult problems associated with modeling continuum phenomena involving fluid and flexible structure interaction, as well as phase changes. Similarly, building aggregate multi-resolution models of interconnected geometric objects from multi-resolution component models is a current topic of research in computer graphics.
With this background of basic concepts, let us now consider some case studies to illustrate successful VE. Advocates of the power of modeling and simulation typically extrapolate from three shining examples, which could be thought of as “proto-VE” case studies: the computer-aided design (CAD) of the Boeing 777, computational fluid dynamics (CFD), and very large scale integrated circuits (VLSI). Each has made great use of computation and has challenged in various ways available hardware and software infrastructures. While these success stories are certainly encouraging, great caution should be used in extrapolating to more general situations, as a review of the state of the art will reveal. Indeed, each of these domains has serious limitations and faces major challenges. Examples of major failures of complex engineering systems (e.g., the Titanic, the

FIGURE B.5 The Boeing 777. SOURCE: Boeing Web site ( www.boeing.com/companyoffices/gallery/images/commercial/ ).
Tacoma Narrows bridge, the Denver baggage handling system, and the Ariane booster) should cause us all to be sobered. We will argue that uncertainty management together with dynamics and interconnection are the key to understanding both these successes and failures and the future challenges.
Boeing invested more than $1 billion (and insiders say much more) in CAD infrastructure for the design of the Boeing 777 (see Figure B.5 ), which is said to have been “100 digitally designed using three-dimensional solids technology. ” Boeing based its CAD system on CATIA (short for Computer-aided Three-dimensional Interactive Application) and ELFINI (Finite Element Analysis System), both developed by Dassault Systemes of France and licensed in the United States through IBM. Designers also used EPIC (Electronic Preassembly Integration on CATIA) and other digital preassembly applications developed by Boeing. Much of the same technology was used on the B-2 program.
While marketing hype has exaggerated aspects of the story, the reality nonetheless is that Boeing reaped huge benefits from design automation. The more
than 3 million parts were represented in an integrated database that allowed designers to do a complete 3D virtual mock-up of the vehicle. They could investigate assembly interfaces and maintainability using spatial visualizations of the aircraft components to develop integrated parts lists and detailed manufacturing process and layouts to support final assembly. The consequences were dramatic. In comparing with extrapolations from earlier aircraft designs such as those for the 757 and 767, Boeing achieved the following:
-
Elimination of >3,000 assembly interfaces, without any physical prototyping,
-
90 percent reduction in engineering change requests (6,000 to 600),
-
50 percent reduction in cycle time for engineering-change request,
-
90 percent reduction in material rework, and
-
50-fold improvement in assembly tolerances for the fuselage.
While the Boeing 777 experience is exciting for the VE enterprise, we should recognize just how limited the existing CAD tools are. They deal only with static solid modeling and static interconnection, and not—or at least not systematically—with dynamics, nonlinearities, or heterogeneity. The virtual parts in the CATIA system are simply three-dimensional solids with no dynamics and none of the dynamic attributes of the physical parts. For example, all the electronics and hydraulics had to be separately simulated, and while these too benefited from CAD tools, they were not integrated with the three-dimensional solid modeling tools. A complete working physical prototype of the internal dynamics of the vehicle was still constructed, a so-called “iron-bird” including essentially everything in the full 777.
While there was finite element modeling of static stresses and loads, all dynamical modeling of actual flight, including aerodynamics and structures, was done with “conventional” CFD and flight simulation, again with essentially no connection to the three-dimensional solid modeling. Thus while each of these separate modeling efforts benefited from the separate CAD tools available in their specialized domains, this is far from the highly integrated VE environment that is envisioned for the future, and is indeed far from even some of the popular images of the current practice. Thus while a deeper understanding of the 777 does nothing to reduce our respect for the enormous achievements in advancing VE technology or dampen enthusiasm for the trends the 777 represents, it does make clear the even greater challenges that lie ahead.
What are the next steps in CAD for projects like the 777? Broadly speaking, they involve much higher levels of integration of the design process, both laterally across the various subsystems, and longitudinally from preliminary design, through testing, manufacturing, and maintenance. They will require more systematic and sophisticated treatment of uncertainties, especially when dynamics
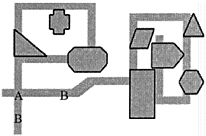
FIGURE B.6 Two multicomponent subassemblies in the 777 connecting only at point A.
are considered in a unified way. This will require introducing nonlinearities, heterogeneity, and variable resolution models.
Boeing engineers view these steps as enormous challenges that must be faced. Even something as simple-sounding as using the CATIA database describing the three-dimensional layout of the hydraulics and their interconnections as a basis for a dynamic simulation of the hydraulics remains an open research problem, let alone using CATIA as a basis for dynamic modeling and simulation of aerodynamics and structures. What is difficult to appreciate is how the sheer scale of keeping track of millions of components can be computationaily and conceptually overwhelming.
To illustrate some of the issues in the three-dimensional solid modeling for the 777, consider yet another simple experiment in two dimensions. Suppose that we have two two-dimensional subassemblies, each consisting of several components, that we wish to interconnect at point A as shown in Figure B.6 (the components shown have no meaning and are simply for illustration.) We want to be sure there are no unwanted intersections in the design, and it is clear from Figure B.6 that this assembly has no connections except at point A.
The 777 has millions of such parts. A virtual mock-up can be made from a parts and interconnection list so that designers can “fly through” the design to check for unwanted interconnections. The computer can also automatically check for such interferences so that these can be identified and redesigned before they are discovered (more dramatically and at much greater expense) during physical assembly. If there are n components, we can think of an n × n matrix of pairs of potential collisions, so 3,000,000 parts would have approximately n*(n -1)/2 = 4.5 × 1012 possible intersections to be checked. Although this grows only quadratically with the number of parts (not the exponential growth we are so concerned with elsewhere), the sheer number of parts makes brute force enumeration unattractive. Fortunately, there are standard ways to reduce the search.
FIGURE B.7 Simple bounding boxes with large intersection and not conclusively eliminating unwanted subassembly interconnection.
We could begin by putting large bounding boxes around the subassemblies, as shown in Figure B.7 . This could be used to eliminate potential intersections far away from these subassemblies (resulting in large sections of our interconnection matrix that would not need to be checked), but would not conclusively eliminate unwanted connections between the subassemblies. At this point, all the pairwise components of the subassemblies could be checked, or we could refine the bounding boxes, as shown in Figure B.8 . At this point, we would have eliminated all but 2 components, and they could be checked to see that the only intersection was at A. The bounding boxes in this case reduced the cost from computing 24 pairwise (4 × 6) intersections to computing 1 pairwise component and a few bounding boxes. The bounding boxes have simple geometries, so are more easily checked than the components, but need to be constructed. Clearly, there is a tradeoff, and one does not want to use too many or too few bounding boxes.
This is an example of a general technique for searching called divide and conquer, where the problem is broken up into smaller pieces using some heuris-
FIGURE B.8 Refined boxes show only intersection is at A.
FIGURE B.9 Refined boxes help find interferences.
tic. It is related to branch and bound, where, say, a function to be minimized is searched by successively breaking its domain into smaller pieces on which bounds of the function are computed. Suppose we want to compute the minimum distance between components that are not supposed to be connected (we want to make sure this function is bounded away from zero). A bounding box gives us upper and lower bounds on this function for the component combinations that are included in the bounding boxes. We can ignore pairs of boxes that are separated by more than the smallest upper bound we have, thus pruning the resulting tree of refined bounding boxes. This is illustrated in Figure B.9 , where the subassemblies are connected at point B, instead of A. The refined bounding boxes show how they can be used to focus the search for unwanted interconnections.
Note that if we introduce uncertainty in our description of the components, it can drastically increase the computation required to do pairwise checking and make the bounding box approach even more attractive. Actually, while the basics of solid modeling are well developed, there is no standard approach to uncertainty modeling even here and many open questions. Once we introduce uncertainty in a general way, then exponential growth in evaluating all the possibilities becomes a worry. Because three-dimensional solids inherently have limited dimensionality of contacts, it should be possible to avoid this. As we will see later, uncertainty in dynamical systems is even more challenging, and a version of the bounding box idea is quite useful in doing robustness analysis of uncertain dynamical systems as well.
It is interesting to note that the Boeing 777 used an advanced, though conventional, approach to modeling and simulation of the aerodynamics and flight. Aeromodeling is a convenient example because there is a long history of successful systematic modeling, yet substantial challenges remain. It also offers us a
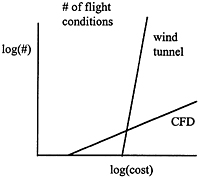
FIGURE B.10b Cost versus number of points at which aerocoefficients are obtained.
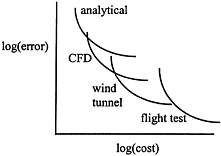
FIGURE B.10a Schematic of error-cost relationship of different approaches to obtaining aerocoefficients for flight modeling.
chance to discuss computational fluid dynamics (CFD) in a broader context that includes analytic tools, wind tunnels, and flight test. This is simply for illustration, but it will touch on broader issues in VE.
Standard rigid body airplane models typically consist of a generic form of the model as an ordinary differential equation (ODE) with vehicle-specific parameters for mass distributions, atmospheric conditions (dynamic pressure), and aerodynamic coefficients. This rigid body model determines what motion of the vehicle will result from applied forces due to propulsion and aerodynamics. Aerocoefficients are parameters that give the ratio of forces and moments generated on the vehicle to surface deflections and angular changes of the vehicle with respect to the ambient air flow. The standard quasi-steady assumption is that these aerocoefficients depend only on sideslip angle and angle of attack, and not on the history of the motion of the vehicle or the complex flow around it. Therefore the aerocoefficients are most compactly represented as a set of six functions, three forces and three moments, on the unit sphere (the two angles), plus additional functions for surface deflections. Obtaining these functions dominates standard aeromodeling and the use of CFD.
Aerocoefficients can be estimated analytically, computed using CFD, or measured in wind tunnels or flight tests. Figure B.10a shows schematically the error-costs associated with the various methods. Once the coefficients are obtained, they can be plugged into a dynamic model of the airplane, and the resulting nonlinear differential equations can be simulated. This figure is misleading in many ways, one of which is that the error-cost tradeoff between CFD and wind tunnel is oversimplified. Figure B.10b shows the cost to find the aerocoefficients at a certain number of points. Building a wind tunnel model is relatively expensive, but once it is available, the incremental time and cost to do an additional experiment are small. Research is being done to speed up both CFD and the
building of wind tunnel models, thus shifting both curves to the left. One of the most revolutionary developments currently going on in this area is the improvement in rapidly generating wind tunnel models from computer models. Researchers are currently working to change the traditional turnaround time from months to hours.
These figures do not address the fact that CFD and wind tunnels do not give exactly equivalent results. To a first approximation, wind tunnel tests can give lower overall modeling error by allowing the modeler to include additional factors, such as unsteady effects. On the other hand, CFD can provide detailed flow field information that is difficult to obtain experimentally and avoids experimental artifacts like wind-tunnel wall effects. Finally, flight tests give the most reliable predictions of aircraft behavior, although even here there are errors, since not all possible operational conditions can be tested or even necessarily anticipated. This is summarized in Figure B.10a , which shows the error versus complexity for various modeling methods, where, vaguely speaking, error is the difference between predicted operational behavior and actual operational behavior, and cost could be taken as the total dollar cost to achieve a given error with a specific method.
Note that the methods are complementary, each best for some particular error-cost level. They are also complementary in other ways, as the deeper nature of the errors is different as well. While the details may change with technology, the overall shape of this figure will not. One goal of VE is to reduce the error associated with simulation-based methods and thus reduce the need for wind tunnel and flight testing. If this is not done carefully, it is quite easy to simultaneously increase error and cost.
This discussion has taken a very superficial view of modeling and particularly of uncertainty, but has hopefully illustrated the tradeoff between error and cost that holds across both virtual and physical prototyping. One important point to note is that despite earlier euphoric visions of the role of CFD in aircraft design that suggested it would almost entirely replace wind tunnels, only a tiny fraction of the millions of aerodynamic simulations generated for a modern aircraft design are done using CFD. The remainder continue to be done with physical models in wind tunnels, and this is not expected to change in the foreseeable future. To get a slightly deeper picture of these issues, we need to examine CFD more closely.
Our second case history involves computational fluid dynamics (CFD). Fluid dynamics is a large and sophisticated technical discipline with both a long history of deep theoretical contributions and a more recent history of major technological
impact, so it is not surprising that it is poorly understood by outsiders. We focus on the aspects relevant to the broader VE enterprise.
Rather than following a particular group of molecules, fluid dynamical models adopt a continuum view of the fluid in terms of material elements or volume elements through which the material moves. Because of the simplicity of Newtonian fluids (those for which viscosity is constant, such as air flowing about an airplane), a fairly straightforward system of partial differential equations relate the dynamics of a fluid flow element to its local velocity, density, viscosity, and externally acting forces. These are the Navier-Stokes (N-S) equations, which have been known for more than a century and a half. They merely express conservation of mass and the other of momentum, but the three-dimensional case has 60 partial-derivative terms.
The N-S equations are thought to capture fluid phenomena well beyond the resolution of our measurement technology. Thus fluid dynamics holds a very important and extreme position in VE as an example of a domain where the resource limitation is due primarily to computation and measurement, rather than to ignorance about the phenomena (although this is not true for granular or chemically reacting flow). As one might expect, then, a major effort in fluid dynamics involves various numerical approximations to solving the N-S or related equations. Such numerical airflow simulations are the subject of computational fluid dynamics (CFD). The obvious approach is direct numerical solution (DNS) of a discrete approximation to the N-S equations. Unfortunately, turbulence makes this extremely difficult.
In effect, turbulence is a catch-all term for everything complicated and poorly understood in fluid flow. While there is no precise definition of turbulence, its general characteristics include unsteady and irregular flows that give something of the appearance of randomness; strong vorticity; stirring and diffusion of passive conserved quantities such as heat and solutes, and dissipation of energy by momentum exchange. Under typical aircraft flight conditions at high subsonic speeds, turbulence takes the form of a nested cascade of eddies of varying scale, ranging from on the order of meters to on the order of tens of micrometers; a span of 4 or more orders of magnitude. On average, the largest eddies take energy from the free flow and, through momentum exchange, feed it down, step by step in the cascade of eddies, to the smallest eddies, where it is dissipated as heat. However, it is also possible for energy to feed from smaller eddies to larger over limited times or regions, and these reverse energy flows can play a significant role. Turbulence is no more random than the trajectories of our coins, but its sensitivity to initial conditions is even more dramatic, since there are so many more degrees of freedom. Turbulence is considered one of the classic examples of chaotic dynamics, although this has not been proved.
To fully to capture the dynamics of the airflow in DNS, it is necessary to integrate numerically over a mesh fine enough to capture the smallest turbulent eddies but extensive enough to include the aircraft and a reasonable volume of air
about it. This is beyond current computational facilities. To overcome this, various approximations must then be made, that are at the heart of CFD. Here merely make a few observations. First, as was noted earlier, only a tiny fraction of the millions of aerodynamic simulations generated for a modern aircraft design are done using CFD. The remainder are still done with physical models in wind tunnels, and this is not expected to change soon. Second, CFD is used primarily to compute the static forces on objects that are fixed relative to the flow, and any dynamical vehicle motion combines these static forces with vehicle kinematics. Using CFD for computing dynamically the forces on objects that are themselves moving dynamically adds substantially to the computational complexity.
Finally, the various approaches to CFD result in widely varying computational requirements, yet there is no integrated “master” model other than the N-S equations themselves, and substantial domain-specific expertise is needed to create specific simulation models and interpret the results of simulations. Some approximations assume no viscosity and others large viscosity; some approximations focus on material elements and their motion (called Lagrangian formulations); others focus on volume elements through which material passes, and thus fluid velocities are the focus (called an Eulerian formulation); and still others try to track the movement of the larger-scale vortical structures in the fluid. The choices are dominated by the boundary conditions, as the fluid (air) being modeled in each case is identical, and even different approximations may be made in different parts of the same flow. For example, viscosity might be modeled only near a solid boundary, while the flow far from the boundary would be assumed to be inviscid. Thus, while the material itself is perfectly homogeneous, inhomogeneities arise in our necessary attempts to approximate the fluids.
What is particularly interesting for this appendix is the fact that, according to Paul Rubbert, 7 the chief aerodynamicist for Boeing, uncertainty management has become the dominant theme in practical applications like aircraft design. He claims that uncertainty management is replacing the old concept of “CFD validation.” He argues that both CFD and wind tunnels are “notorious liars,” yet modern aerodynamic designs are increasingly sensitive to small changes and error sources. Thus, better attention needs to be paid to modeling uncertainty and its consequences. CFD and wind tunnels are complementary, and the goal is to be able to reconcile the differences between their results and not to expect that they should give the same results. In this context, CFD users must be provided with the insight and understanding to allow them to manage the various sources
|
7 |
Private communication with John Doyle, California Institute of Technology, December 1996. |
of uncertainty that are present in their codes, and to understand how those uncertainties affect the specific aircraft behavior they are trying to predict.
In many respects, commercial aviation already is a remarkable feat in uncertainty management. We routinely get on airplanes and reliably arrive at our destination, and fortunately our airplanes crash much less frequently than our computers. Airplanes move in the very complex system of the earth's atmosphere and together with air traffic control constitute one enormously complex system delivering remarkably reliable transportation. At small time and large scales the atmosphere is also turbulent and chaotic, and occasional crashes due to atmospheric disturbances remind us that this is not a triviality.
Because of this turbulence in the atmosphere and near the vehicle, there is chaotic dynamics surrounding the vehicle at every scale from the microscopic to the global. Furthermore, most objects having the size and mass of a 777 and traveling at high subsonic speeds would exhibit extremely unpredictable trajectories, although eventually hitting the ground at high velocities would be a certainty. Almost any other connection of the millions of parts in a 777 would also fail to behave predictably, although the 777 itself is remarkably robust to a wide variety of component failures. Despite tremendous advances in computation and its application to CFD and CAD, no simulations are ever performed that come close to capturing all this complexity at all these scales. Yet in spite of all of this, these millions of components manage to successfully “fly in formation” such as to deriver reliable and predictable performance. Fortunately, this success is not a mystical process (that the current antiquated air traffic control works at all is fairly astonishing), but it does involve tremendous amounts of domain-specific expertise and hand-crafted solutions. We must be realistic and cautious about the way in which VE technology should interact with this process.
Our third case history involves very large scale integration (VLSI) —a technology that enables millions of transistors to be fabricated onto a silicon chip less than a square inch in size. Such a chip can function as a complete microprocessor system performing hundreds of millions of arithmetic operations per second. For example, today 's Intel's Pentium Pro microprocessor is faster than the most powerful supercomputers of the early 1980s, but costs 4 orders of magnitude less than those older machines. VLSI is an entirely different type of complex system than fluid dynamics, although both start with homogeneous materials: fluids and silicon/metal.
The number of transistors on a single chip, as well as the speed of microprocessors, has been roughly doubling every 18 months since the 1960s. This exponential-growth trend is known as “Moore's Law” (after Intel 's co-founder
Gordon Moore) and is expected to continue at least until the year 2010. VLSI feature size (i.e., minimum width of a wire on a chip) has recently dropped to below one fifth of a micron (one millionth of a meter, or about one hundredth of the width of a human hair) and continues to steadily shrink into the deep submicron range. The next decade will usher in single-chip microprocessors containing hundreds of millions of transistors and operating at multi-giga-FLOPS (billions of floating-point operations per second) speeds.
Until the early 1970s, VLSI design was primarily done manually; such a labor-intensive process was possible because of the low gate-count (typically in the hundreds to low thousands) of those early circuits. However, when VLSI permitted fabrication of circuits with hundreds of thousands of gates, hand-crafted design was no longer practical (nor in many cases even possible). The field of computer-aided design (CAD) of VLSI circuits matured into a discipline with multiple annual technical conferences, and by the mid-1980s, dozens of commercial VLSI CAD software systems became available (typically at six-figures per copy).
A commercial VLSI CAD system is typically structured as follows. First, the circuit design is specified abstractly, with “blocks” representing high-level functional units (e.g., adders, multipliers, and memories); the general connectivity among these modules is also specified at that stage. Next, the design is further synthesized and specified in greater detail, with modules being fleshed out from an available library of predesigned parts (and some from scratch if necessary). If the design is too large to fit on a single chip, a “partitioning ” step takes place, where the design is divided into several chip-sized modules (the typical optimization objective during partitioning is to minimize the wires that cross between modules, which in turn minimizes the number of wires that are forced to go offchip and onto the circuit board, thereby slowing down the overall circuit). Next, a general “floorplan” is developed to accommodate the various circuit components on the chip area. Once a good placement is obtained for the circuit elements, the detailed interconnections are routed among the modules. Placement and routing typically attempt to minimize the overall chip area, which in turn minimizes the fabrication costs and thus maximizes the chip vendor's profit margin. Placement and routing also tend to be the most complex and time-consuming of the various VLSI design phases, since these problems are computationally intractable.
Extensive verification and testing occur at each level, with subsequent iteration and modification. These tests ensure that the circuit, once fabricated, will meet the design specification, both in terms of logical functionality and in terms of operating speed; the overall speed of the proposed circuit is determined by running a massive finite-element-based simulation over the circuit, which simulates the exact physical behavior of the circuit (such timing simulations typically take place at micron scales and at picosecond time resolutions —they often require days or weeks to run to completion). Despite such extensive testing, gross
bugs can still slip, especially when the error occurs at the higher levels of the design process (e.g., at the specification level); naturally, the longer a bug goes undetected, the greater the incurred cost to the company (e.g., the infamous Pentium FDIV bug cost Intel almost $1 billion to fix).
Overall, the field of VLSI design has evolved in the footsteps of the field of software engineering. Thus, it is not surprising that VLSI CAD embraces the basic precepts of hierarchical structured top-down design, functional orthogonality, component libraries (i.e., subroutines), design reuse, beta-testing, and so on. Unfortunately, as discussed below, by following the software engineering paradigm, the VLSI design process also inherits the problems inherent in that area.
The key feature of VLSI design that has traditionally greatly simplified uncertainty management is that the logic level could be effectively decoupled from the physical level. That is, through the use of electrical thresholding and Boolean logic, the chip design is constrained so that uncertainty at the microscopic level does not propagate to the macrolevel. Other techniques for uncertainty management in VLSI design include component redundancy and fault-tolerance algorithms, which automatically compensate for manufacturing defects and unforeseen system transients. One major advantage of digital representations generally is that error-correction codes enable perfect reconstruction and reproduction of the digital signal, so that small uncertainties have exactly zero impact on the final output. This is in stark contrast with turbulence where uncertainty at the microscopic level can easily have macroscopic effects. Thus, VLSI has a special place in complex systems, and this feature of digital systems has been emulated and exploited in other domains as well.
The price paid for the complete isolation of component uncertainty in VLSI, and indeed the price paid for digital systems generally, is that system performance is sacrificed, sometimes enormously, in comparison with what would be possible if such an isolation were not maintained. This has been viewed as acceptable because it makes the design process manageable, and the evolution of fabrication technology allowed for both conservative design philosophies and dramatic progress in performance. Future trends in VLSI design may change this situation dramatically. The ever-shrinking feature size and growing gate counts of VLSI circuits are giving rise to a number of emerging trends and new fundamental problem areas.
First, thinner wires have a higher resistance, so interconnect delay now dominates the overall circuit speed (e.g., in current high-end designs, over three fourths of the clock period is due to signal propagation delays through wires). Moreover, wires take up most of the chip area, so VLSI physical design is now primarily a massive wiring-optimization problem (which is computationally intractable).
Typical problem instances are so large (and numerous), that even low-order polynomial-time algorithms are often much too slow in practical situations.
As feature sizes decrease into the ultra-submicron range, previously ignored phenomena become more significant, and indeed even begin to dominate the overall design. For example, parasitics such as capacitive-coupling between parallel wires (i.e., “cross-talk”) has recently become a major problem since it tends to substantially increase signal propagation delay, as well as cause spurious signals/switching in the circuit. Another problem is “electro-migration,” where the electrical current can randomly knock metal atoms out of the wires. This phenomenon tends to further “thin out ” already-thin wires, which in turn exacerbates the electro-migration problem (i.e., creating a positive feedback loop), until open faults occur (i.e., wires become disconnected), which can disrupt the functional correctness of the overall circuit.
As feature sizes shrink even further, quantum mechanical phenomena will begin to have significant effects on circuit performance (e.g., quantum uncertainty, particle tunneling, and quantization of mass and charge). As clock frequencies advance into the gigahertz range, wires begin to behave like transmission lines, and parasitic phenomena such as signal attenuation and antenna effects become major performance-limiting concerns. The physical and electrical properties of most materials are still not sufficiently well understood at such high frequencies and small scales (e.g., current timing simulation techniques break down and are still not reliably applicable to regimes with feature sizes below one tenth of a micron).
Finally, at these small-scale regimes, even the VLSI manufacturing process itself becomes quite problematic. The confluence of these trends suggests that fundamental physics considerations will become a dominant component of VLSI design, the distinction between digital and analog circuits will become increasingly blurred (certainly, analog considerations will migrate up well into the higher levels of the VLSI design process), and uncertainty management will become a much more difficult problem.
In this section we touch upon a number of computer-related subjects that bear on VE.
A commonly shared dream is that in a VE environment, an engineer (or decision maker, analyst, commander, and so on) with a sophisticated virtual reality (VR) interface is connected to networks of other engineers in various disciplines sharing a common database. Design changes automatically propagate
so other engineers can respond by evaluating the consequences including manufacturability and maintenance. Immersive visualization methods take data from experiments or tests on physical prototypes and facilitate the comparison of data with theory and simulation. Engineering design of the manufacturing process and its product, together with training for operation and maintenance, can proceed simultaneously and synergistically. Much of the future promise of VE is based on tools from computation, workstations, supercomputers, networks, and software engineering.
The hope is that future VE software environments, including VR features, will relieve design engineers from the tedious, repetitive, and routine tasks that still dominate much of engineering design and let them focus on the critical decisions involving uncertainty management in the face of cost constraints. The fear is that it will also give highly unqualified people the illusion that they can click a few menu items, run some multidisciplinary optimization, and design a new airplane or automobile that will actually work in the real world. Sophisticated VE environments will inevitably increase the gap between the best engineers and the average, facilitating both the possibility of much better engineering and also the likelihood of spectacular failures.
The entertainment industry will push VR for an increasingly realistic look and feel and an emphasis on fooling human senses, and the many challenges in further developing VR are already well funded and appreciated. Although there will be many similarities in software design, the paradigm of “realistic = looks good” should not dominate VE as well. Otherwise, engineers and programmers will ultimately design systems fine-tuned for VR that do not work in reality. Without a correct and fundamental mathematical structure, VE could fail spectacularly and the potential for abusing it could be tremendous.
Many aspects of these issues are already well understood in the DOD M&S community. For example, advanced distributed simulation (ADS) and high-level architecture (HLA) are motivated in part by the recognition that high-fidelity engineering applications may involve timing or other issues too fine for human perception, and thus training-based systems such as distributed interactive simulation (DIS) are inadequate. Furthermore, it is well understood that all forms of M&S are sensitive to modeling and testing assumptions, poorly understood physical phenomena, or even to well-understood phenomena that require excessive computation. Nevertheless, it is still safe to say that the computer science view dominates the current VE landscape.
Much of the current research in VE aims to make the design of complex systems more like the discipline of software engineering. To understand the implications of this, let us discuss briefly the history and basic trends in software engineering.
In the early days of computer science (1950s), computer hardware was expensive while computer software was free and quite primitive. By the mid-1960s, computer speed and memory capacity grew substantially, and along with computer performance grew the number of applications and user expectations. It was soon realized that building a large, complicated program is considerably more difficult than concatenating a series of smaller programs. “Programming in the large” often seemed to be an entirely new activity, exhibiting nonintuitive characteristics. To grapple with the growing complexity of software, more disciplined approaches to programming were explored; these included structured programming, strong type-checking, functional languages, program verification, software reuse, graphical user interfaces, and more recently, object-oriented design and programming, client-server applications, and network-based computing. However, none of these techniques proved to be a panacea, and each introduced new complexities and pitfalls.
Over the years, the problems associated with large software development efforts grew bigger and more pronounced. Some computer programs now contain over 15 million lines of code, and the programs for NASA 's proposed space station will have more than 80 million lines of code. Despite modern programming tools such as interactive debuggers and visual programming environments, the average productivity of professional software engineers working on large systems is only a couple of dozen lines of code per day. Expensive and sometimes catastrophic system failures have been due in part to software bugs (e.g., the recent Ariane rocket explosion, the Denver airport baggage system, and lost NASA space probes). Many large software systems diverge so much from their planned project timelines and budgets that they are abandoned altogether, sometimes at a loss of billions of dollars. Two recent examples include the failed attempt by the FAA to revamp its aging air traffic control system and the aborted plan by the IRS to upgrade its software system for tax collection.
Why is it so difficult to write reliable code? A number of factors contribute to the difficulties. First, the complexity of hardware is quite bounded (i.e., it is only expected to be able to execute a relatively small and simple set of machine instructions), while the complexity of software is unbounded (i.e., software is expected to do everything else).
Second, it is very difficult to define or characterize the set of all possible types of inputs and conditions under which a system is expected to operate. This is particularly true in “embedded systems, ” computer hardware and software operating as part of a larger system, such as an airplane or automobile as opposed to a PC or network of workstations. If the user of a word processor does something the software does not expect, it can simply refuse to accept the input and the impact is minimal. If the control system in a launch vehicle (e.g., Ariane 5) receives some data that are unexpected, simply shutting down will (and did) result in huge losses.
Software is also inherently fragile and removing a single line of code could
render a large program completely useless or even dangerous. Contrast such instabilities with the robustness of living organisms, where the removal or death of a cell (or even many cells) typically has little or no impact on the overall functionality of the organism. Similarly, most complex engineering systems are deliberately designed to degrade gracefully under component failures.
Third, there is an inherent lack of logical symmetry in verifying and validating computer code: although it is easy to establish that a piece of code is buggy by simply exhibiting the particular error in question, proving the absence of bugs is usually impossible. That is, negative results are much more difficult to come by in logic and mathematics than positive results, and it is usually much easier to give a counter-example than to prove the nonexistence of something.
Fourth, humans are not very good at keeping track of thousands (let alone millions) of interacting parts, be it lines of code, transistors on a chip, or gears, levers, and pulleys. Short-term memory can typically store seven (plus or minus two) items, and perhaps a few additional items by utilizing some simple aggregation techniques. It is therefore not surprising that even with the aid of mechanical tools (i.e., mathematics and other formalisms), complicated systems with millions of interacting parts typically quickly diverge beyond our ability to understand them.
Fifth, the synchronization of effort among large groups of people working on a single, tightly coupled system becomes a logistical nightmare after some parallelism threshold is reached, and the communications load among the workers grows superlinearly.
Finally, in most human endeavors, the difference between the best and the average performance is a relatively small factor. For example, most people can comfortably run a 10-minute mile; on the other hand, a gold-medalist Olympic athlete can only outperform this mediocre record by less than a factor of three (similar performance ratios hold for other common skills, such as swimming, biking, jumping, lifting, typing, and reading). In contrast, the best programmers can be over a factor of 100 more effective and productive than the average programmer. Most code is by definition written by average programmers, and programming will always be a very labor-intensive activity; it is therefore crucial to select software team leaders and chief architects carefully.
In summary, the difficulties we encounter in software engineering are not unique to computer programs, but rather are fundamental to many areas of science and engineering that are concerned with building large, complicated systems (and indeed result from the limits of our current technology and our own inherently limited capabilities). We should therefore not expect “silver bullet” solutions anytime soon to the software engineering problem. Indeed, the broader VE environment is likely to exaggerate and magnify the problems of software engineering.
Having said all this, we need to also keep in mind that the field of software engineering (and computer science in general) has also made great advances.
Personal computers are more user-friendly, with elementary school children now routinely using computers and “surfing” the World Wide Web. Typical PCs are now faster (and have more memory) than the Cray I supercomputer of the late 1970s, yet cost under $2,000. Portable laptop computers, weighing around 5 pounds or less, have become ubiquitous. Interactive run-time environments, sophisticated debuggers, and visual programming languages have made basic programming easy to learn and to teach. Electronic mail has greatly facilitated communication and data exchange among people and researchers around the world, and the World Wide Web has made vast amounts of valuable information easily accessible to everyone. Thus, despite the various difficulties, software engineering has made great strides and contributions over the years as well.
Since the beginning of the 20th century, a number of practical global optimization problems have been extensively studied. These problems include such classical formulations as Traveling Salesman, Boolean Satisfiability, Quadratic Programming, Hamiltonian Cycles, as well as a large variety of other partitioning, packing, placement, interconnection, routing, reachability, and approximation problems. Up until 1970, these problems had been attacked in isolation using ad hoc techniques, and in all cases researchers have failed to discover efficient (i.e., polynomial-time) algorithms for any of these problems. Nevertheless, no satisfying explanation existed as to why these problems all seem intractable, nor how these problems may be related to each other.
In the early 1970s, it was discovered that all of these problems are efficiently “reducible” to one another in a way that preserves solution quality (i.e., these algorithmic reductions map optimal solutions of any of these problems to optimal solutions of any other of these problems). This implies that if there existed an efficient algorithm for one of these problems, such an algorithm could be immediately (and mechanically) transformed into efficient algorithms for all of these problems. In other words, with respect to computational tractability, none of these problems is any more difficult than any of the other problems. Therefore, since none of these problems had been solved efficiently to that point, despite many decades of intense work by hundreds of good researchers, this unifying framework (technically referred to as “NP-completeness,” and more generally as “computational complexity theory”) provided the strongest evidence yet that all of these problems are computationally intractable. An NP-hard problem is classified as a problem that is at least as hard as the NP-complete class of problems.
These results provided a twofold contribution to the field of global optimization. First, once a computational problem is formally shown to be NP-hard, such a negative result saves much effort, since researchers need not bother to continue their search for an efficient algorithm to such a problem. Second, once we know that a problem is NP-hard, this gives us legitimate license to devise heuristic
approximate solutions, without having to worry that our work will be rendered obsolete any time soon by the discovery of an efficient exact algorithm. Today, these topics have become a mainstream subfield of computer science, with several yearly conferences being devoted to this subject.
Computational complexity theory is independent of what actual computers we use in practice and of our underlying computation model. This also means that speedups in VLSI technology or advances in parallel computing will not affect the class of problems that are “intractable. ” In short, computational complexity/intractability is fundamental, and cannot be overcome by “throwing silicon” at it.
Some problems are so intractable that there exist no algorithms whatsoever to solve them; such a problem is said to be “undecidable” (the topic of undecidability was pioneered by Alan Turing in the mid-1930s). Rather, it can be mathematically proved that for an undecidable problem, no algorithm exists whatsoever even in theory, no matter how complex or subtle a possible solution approach may be attempted (this is a much stronger negative result than the intractability/NP-completeness discussed above). Many undecidable problems are deceptively easy to state formally; for example, the problem of determining whether a given program runs forever (or halts eventually) over a given input is undecidable. In fact, any mathematical framework powerful enough to describe arbitrary programs (and this even includes simple arithmetic) is undecidable as well; such systems are said to be “computationally universal.” This has very strong implications for VE, and for dynamical systems in general, since most of these systems are computationally universal (i.e., they can simulate arbitrary computations or computer programs, and are therefore undecidable). Thus, many interesting questions about dynamical systems (such as long-term behavior, quiescence, and termination) are undecidable, and there exist no algorithms for the resolution of these problems in general (although particular classes of simple instances may be solved in ad hoc ways).
Both the history of software engineering and the theory of computational complexity have important implications for VE. While it is difficult to define or characterize the inputs to software, the uncertainty faced by complex systems is much greater than typically faced by most software. The inherent lack of logical symmetry in verifying computer code is even greater in more general complex systems. It is much easier to convincingly show that some design change will fail through simulation than it is to show that it will succeed. The former requires only one bad example, while the latter requires strong evidence of the complete absence of such examples. This is made even more severe in complex systems in uncertain environments.
As bad as we are at keeping track of million-line programs, and at working in
teams to write software, at least software is a highly homogeneous system and teams are usually composed of experts in at most two domains, software design and perhaps the application area that the software is targeted for. In VE we are faced with highly heterogeneous systems and teams. Also, the gap between the best and the average that shows up in software engineering is likely to be even greater in VE, and the consequences could be even more severe.
Paradoxically, many complex engineering systems work much more reliably than complex software systems. Thus, while we may expect VE to inherit many of the problems of software engineering, the constraints and discipline imposed by VE's connection with physical reality offer some differences with conventional software engineering that should not merely be overcome, but exploited. This underscores again the need for a theoretical foundation for VE that goes well beyond computer science.
Computational complexity theory also has a sobering message to deliver to a naively cheerful view of the future of VE. As we aim for cheaper, better, faster with complex systems for higher levels of performance, uncertainties in components and the environment will interact in new and unforeseen ways. Evaluating all the possibilities for failures due to these uncertainties is a computationally intractable problem, but one we cannot afford to ignore. A look back at famous failures of engineering systems will emphasize this point.
In this section we will briefly review case studies of famous failures of engineering systems: the Titanic, the Estonia Ferry sinking, the Tacoma Narrows Bridge collapse, subsynchronous resonance in power systems, telephone and power system outages, the Denver airport baggage handling system, and Ariane 5. While each of these failures was due partly or primarily to factors beyond engineering or technical considerations, we will concentrate on the technical issues. We have not included some of the most dramatic failures, such as Chernobyl, Challenger, or Bhopal, because these involve much more complicated interactions of engineering and human judgment, and they have received such extensive coverage.
We will argue later that there are unifying themes connecting these different disasters that are relevant to VE (dynamics, interconnection, and uncertainty management). We have suggested that complexity arises from the need to provide reliable predictability in the presence of uncertainty and that failures occur when uncertainties and interactions are not properly accounted for. These case studies will illustrate these issues and provide examples for a more extensive discussion in the next section.
In retrospect, for all of these failures, we can always identify a component that failed and do simple “back of the envelope” calculations with very simple models to explain the failure. It is essentially always possible to ignore, if we
choose, the system design issues that contributed to the failure. A deeper view also always reveals that there were system design flaws and that the apparent component failure was merely a symptom. Of course, the VE challenge is to create an environment where we are better at doing that before the failure occurs. 8
On April 14, 1912, the Titanic, the largest, most complex ship afloat, struck an iceberg and sank. It is generally agreed that the iceberg scraped along the starboard side of the ship, causing the plates to buckle and burst at the seams. Some investigators speculate that the ship was simply too large for the technology available; vibrations from its massive engines may have played some part in the buckling of the hull plates. The Titanic had a double-bottomed hull that was divided into 16 watertight compartments. Because four of these could be flooded without endangering the liner's buoyancy, it was considered unsinkable. Unfortunately, these compartments were not sealed off at the top, so water filled each compartment, tilting the ship, and then spilled over the top into the next one. Five compartments eventually flooded, slowly but surely sinking the ship. This is perhaps one of the all-time great failures to correctly model the interaction of uncertainty in the environment and the way it can couple with the dynamics of a system. A purely static view of the ship, one that ignored the dynamics of the water flow, would never have predicted the actual disaster.
It would seem unlikely that a mistake of the type that occurred in the Titanic would be repeated. However, a weak door lock was one of the main reasons for the 1994 Estonia ferry disaster that caused the deaths of more than 800 people. The ferry's bow visor, a huge top-hinged door at the front of the ferry that swung up to allow vehicles to be driven into and out of the ferry's car deck was secured by several locks. The lower lock, known as the Atlantic lock, was too weak to withstand extremely heavy pounding by rough seas. Stormy seas in the Baltic Sea on September 28 broke the lock between 30 minutes and 1 hour before the 157-meter (515-foot) ferry sank shortly after midnight. The noise of the loose bow visor slamming at the hull was heard by several survivors. The slamming set off a chain of events, including the breaking of other locks, that ended in the tragedy. Only 137 of the more than 900 people on board survived. The commission that investigated the incident said the shipbuilder did not have proper blue-prints for the lock when constructing the ferry in 1980. As a result, the commis
|
8 |
The following discussions abstract from many sources, written and verbal. |
sion says the shipbuilder apparently made its own calculations and underestimated how strong the lock should be. This particular failure would seem the one most likely to be caught with an integrated CAD system.
The Tacoma Narrows Bridge was the first suspension bridge across the Narrows of Puget Sound, connecting the Olympic Peninsula with the mainland of Washington, and a landmark failure in engineering history. Four months after its opening, on the morning of November 7, 1940, in a wind of about 42 miles (68 km) per hour, the 2,800-foot (853-meter) main span went into a series of torsional oscillations, the amplitude of which steadily increased until the convolutions tore several suspenders loose, and the span broke up. The bridge was designed to have acceptable horizontal displacement under the static pressure of a much larger wind, but was not designed to handle the dynamic instability caused by an interaction of the winds and the high degree of flexibility of the light, narrow, two-lane bridge. Modeling this type of fluid-structure interaction, a particularly simple type of flutter, was within the technical capability of engineers at the time, but was evidently not considered. A modern analysis would likely view the fluidstructure flutter as a bifurcation problem, and analyze the nature of the bifurcation as the wind speed increased. Immediately after the accident, numerous investigators were able to create both simple mathematical and scale physical models that exhibited the same failure as the actual bridge, and very simple models were able to predict the wind speed that would cause the collapse.
Series capacitors are often used in AC transmission systems to provide impedance compensation, particularly for long lines with high inductance, at the 60-Hz synchronous transmission frequency. Series capacitors are economical ways to increase load-carrying capacity and enhance transient stability, but the capacitors can combine with the line inductance to create oscillators with natural frequencies below 60 Hz. These electrical oscillators can interact with mechanical torsional vibrational modes of the generator turbine shaft, and in some circumstances can cause instabilities that snap the shaft. This happened dramatically at the Mohave Generating Station in Southern Nevada in 1971 when the turbine shaft broke twice before the condition was properly diagnosed. This is a classic example of uncertainty management gone awry. The capacitors were introduced to improve the stability on the electrical side and reduce the potential vulnerability to electrical side disturbances, but they had the unanticipated effect of destabilizing the mechanical side. The phenomenon is now reasonably well understood and is taken very seriously in design of power systems.
In recent years, there has been an increasing rash of large-scale breakdowns of both the telephone and the power systems, typically triggered by small events that lead to a cascade of failures that eventually bring down large portions of the network. The high complexity and interconnectedness of these networks are designed to improve their performance and robustness, but can lead to extreme and unexpected sensitivity to small disturbances. In both cases, highly interconnected nationwide networks allow load balancing to be achieved more economically, and the resulting system is, in principle and usually in practice, much more robust to large disturbances or variations in demand. The high degree of connectivity also makes it possible for small failures to propagate and lead to massive outages. The solution to these sensitivities is to add additional complexity in the form of more sophisticated control strategies. Without careful design, this trend to increasing complexity will not improve robustness.
The automated system was supposed to improve baggage handling by using a computer tracking system to direct baggage contained in unmanned carts that run on a track. Originally scheduled for completion in March 1994, the unfinished $234 million project helped postpone opening of the airport until February 1995. The delay reportedly cost the city roughly $1 million per day in operations costs and interest on bond issues, more than the direct cost of the project. Significant mechanical and software problems plagued the automated baggage handling system. In tests of the system, bags were misloaded, were misrouted, or fell out of telecarts, causing the system to jam. The baggage system continued to unload bags even though they were jammed on the conveyor belt, because the photo eye at this location could not detect the pile of bags on the belt and hence could not signal the system to stop. The baggage system also loaded bags into telecarts that were already full. Hence, some bags fell onto the tracks, again causing the telecarts to jam. This problem occurred because the system had lost track of which telecarts were loaded or unloaded during a previous jam. When the system came back online, it failed to show that the telecarts were loaded. The timing between the conveyor belts and the moving telecarts was not properly synchronized, causing bags to fall between the conveyor belt and the telecarts. The bags became wedged under the telecarts, which were bumping into each other near the load point.
The Ariane 5 was not flight tested because there was so much confidence in the M&S. The first flight carried $500 million of satellites and was destroyed about 40 seconds after liftoff. The error that ultimately led to the destruction of
the Ariane 5 launcher was clearly identified in the report of the investigating committee: a program segment for converting a floating point number, representing a measurement, to a signed 16 bit integer was executed with an input data value outside the range representable by a signed 16 bit integer. This run time error (out of range, overflow), which arose in both the active and the backup computers at about the same time, was detected, and both computers shut themselves down. This resulted in the total loss of attitude control. The Ariane 5 turned uncontrollably, and aerodynamic forces broke the vehicle apart. This breakup was detected by an on-board monitor, which ignited the explosive charges to destroy the vehicle in the air. The code in question was reused from an earlier vehicle where the measurement would not have become large enough to cause this failure.
It is tempting to simply dismiss this as a software bug that would be eliminated by better software engineering. It is obvious that the programmer should have checked that the measurement was small enough that the conversion could take place, and if it could not, have the control system take some appropriate action rather than simply shut down. In this case the appropriate action would have been to do nothing, because this measurement, ironically, was not even needed after liftoff. This may seem to make it a trivial issue, but the same code did work fine on the Ariane 4, although a control engineer would presumably have preferred it be done differently.
While the “software bug” view has some truth, it is misleading, because the failure was due to dynamics of the Ariane 5 that were different from those of the Ariane 4. It is the interaction of the software with the uncertainty in the environment and the dynamics of the vehicle that caused the failure. This is not a software issue, but a design flaw at a much deeper level. It is likely the programmers responsible had no idea how to determine if the Ariane 5 had dynamics such that under suitable environmental conditions the measurement would be too large. Presumably, they could have consulted appropriate experts in control and aerodynamics and anticipated the problem, but it would not have been a computer science issue at all.
We have argued that, on the one hand, complexity is generally undesirable. It makes our models difficult to work with, and the case studies above suggest that it can lead to unexpected and disastrous failures. Yet we see an accelerating trend to build increasingly complex systems because uncertainty management demands that we introduce complexity in our models. Let us illustrate this now with two simple and familiar current examples: smart weapons and airbags.
In smart weapons, sensors, actuators, and computers are added to counter uncertainties in atmospheric conditions, release conditions, and target movement. This yields reduced sensitivity to uncertainties in the environment, but at the price of increased sensitivity to a large number of new components. If a sensor or actuator component fails, the weapon may actually have much worse accuracy than a dumb weapon. If we are careful in our design, we can use this shift in vulnerability from uncertainty in the environment to uncertainty in our components to our great advantage by making sure that our critical components are sufficiently reliable. Interestingly, it could be argued that the most successful smart weapons so far have been the simplest, for example, Sidewinder and laserguided bombs.
Automobile airbags also reduce vulnerability to uncertainties in the environment. With an airbag you are safer in a high-speed collision with, say, a drunk driver who has crossed into your lane. Since you have no direct control of the other driver's behavior, an airbag is one of the most cost-effective control strategies you can take. Unfortunately, there is again increased vulnerability to component failures. Even without component failures, airbags can make certain circumstances more dangerous. For example, a low-speed collision may cause the air bag to deploy even though without the airbag there would be no danger of injury. Thus one could be injured by the airbag itself under normal operation even when the system functions properly. This is particularly serious with small passengers, who may be in more danger with an airbag than without. Overall there is a substantial net reduction in fatalities, but increased danger of injury and death in certain circumstances for all people, and possibly a net increase in danger to smaller people.
The awareness of the danger of airbags to children and small adults has provoked a flurry of research to make more advanced and more complex airbags. Proposed schemes include making the airbag deployment more adaptable to individual differences in size and body position by using infrared and ultrasonic sensors, together with weight sensors and capacitance sensors, which detect water in human bodies. Unfortunately, it is possible to fool these sensors as bags of groceries with a hot pizza sitting on a wet towel could presumably be mistaken for a person. Lower-technology solutions include simply setting the threshold for airbag deployment higher so they go off less frequently in slower-speed collisions. All these solutions again highlight that the design is driven by uncertainty management, and complexity is introduced as a by-product.
What these two examples illustrate is a kind of conservation principle that is at work in complex systems. Indeed, as we will discuss later, control theory has several such conservation principles that are critical to understanding complex
systems. Informally, when we introduce new components to reduce the effects of uncertainty in the environment, we inevitably create increased vulnerability either to these new components, or to other uncertainties in the environment. Since we control the design, if we are careful we can use this tradeoff to our advantage and shift our vulnerability from things that are more uncertain to things that are less, but explicit models of uncertainty are critical in achieving this. Unfortunately, with increasing complexity, evaluating these tradeoffs can be conceptually and computationally overwhelming.
The earlier section on software engineering discussed how large software development projects require a highly structured approach throughout, since interconnection management dominates component design. While this is now and always will be a challenging domain, it is still relatively homogeneous domain with limited uncertainty. Complex systems engineering has all of the challenges of software engineering plus heterogeneity (hardware and software plus chemical, electrical, mechanical, fluid, communications, and so on) and greater uncertainty (in environment and in system components). Complex systems remain even more poorly understood than large software systems.
Complex systems are poorly understood in part simply because nonlinear, heterogeneous, interconnected, complex dynamical systems are intrinsically difficult to model and understand. But more importantly, the role of uncertainty is critical, but very poorly understood. Furthermore, scaling of problem size can make the interaction of these issues overwhelming. As we will see, control theory addresses uncertainty management explicitly, but from a very narrow perspective. A deeper understanding of complex systems is emerging, but in separate and fragmented technical disciplines.
Finally, there is the “referee effect.” The referee effect comes from the observation that we notice referees only when they do a bad job. Similarly, we notice the details of our watches, televisions, phone systems, cars, planes, networks, and nuclear reactors only when they fail to provide reliable operation and shield us from the world's uncertainties. Basically, the product of a superior design process makes itself virtually invisible. Even when the design is flawed, it may appear to the user that the failure was due to some component, rather than an underlying design process. This is true in all the examples of failures above. Success or failure of components, including computer hardware and software, is relatively easily understood. The role of the system design process itself, deciding which components to use and how to interconnect them, remains a mystery outside of a narrow technical community. Thus complexity in engineering systems is very much in the eye of the beholder. A design engineer may deliberately introduce great complexity specifically for the purpose of providing the end user with an apparently simple and reliable system. The apparent complexity depends on the viewpoint, and traditionally the only global viewpoint is that of the control engineer.
Increasingly complex systems rely on advanced control systems, from cheap, fast computer disk drives to fly-by-wire aircraft to automobiles, integrated chemical production complexes, semiconductor manufacturing systems, and manned and unmanned space systems. Yet, ironically, control engineering and theory remain poorly understood outside of a narrow technical community. Traditionally, control engineers have been responsible for system integration because the control engineer adds the last component to a complex system, and does systemwide uncertainty management. Generally speaking, however, control theoreticians generally do not support this process. The situation is changing dramatically, and the trend is to more integration of system design and control design, but we need to accelerate this trend, and control theorists must expand their vision and make greater contact with other disciplines.
Although control theory by itself offers only a piece of a potential foundation for a theory of VE, it provides a very important complement to dynamical systems and computer science because uncertainty management is the central issue in automatic control systems. The experience and successes and failures of control theory provide important technical foundation and additional insight into the potential role of theory in complex systems. Ironically, until the last 10 years, control theory and practical control engineering have had a very distant relationship. The old story was that since controls were the most mathematical part of engineering it should not be surprising that it simply took decades for theory to get from academia to practice. While this certainly has some truth, another view is that much of the theory was basically irrelevant, and the reason for this irrelevance was inadequate treatment of uncertainty.
Tremendous progress has occurred in just the last decade in developing a mathematical theory of analysis of uncertain systems in the subfield of robust control. The new tools of structured uncertainty, integral quadratic constraints, linear matrix inequalities, operator theoretic methods, and so on, are well beyond the scope of this appendix, but a few observations can be made. The rate of transition from theory to practice has increased dramatically, and ironically, control theorists are doing theory that is both more mathematical and more relevant. Another important factor is that they are using modern software tools to get their theory into CAD design packages that are commercially available. Thus theory is now routinely used in industry before it has had time to get through the review and journal publication process. The former can take months, while the latter still takes years.
One of the most important messages from control theory is that there are fundamental conservation laws associated with uncertainty management in complex, interconnected systems. The informal notion suggested by the smart weapon and airbag examples that vulnerability to uncertainty could not be absolutely reduced but could only be moved around has theoretical expression in the math-
ematics of control theory. There are conservation laws where the “conserved quantities” are related to net system-level robustness with respect to component and environmental uncertainty. Interestingly, some of these conservation laws (e.g., Bode's integral formula) are based on results that are up to 50 years old, although they are getting modern extensions. They do require upper division undergraduate mathematics to express, however, and are beyond the scope of this review. Like energy conservation, they limit the performance of interconnected systems, but with proper understanding can be manipulated to our advantage. Also, like energy conservation, attempts to violate them are constantly being attempted, often with catastrophic results.
While control theory must play a central role in a theory of VE, current control theory has many inadequacies that must be addressed in this broader context. The first and most obvious is that control theorists take a very limited view of system interconnection, assuming that there is a fixed “plant” with a well-defined performance objective and a controller with adequate sensors, actuators, and computation to achieve the performance. The control design then amounts to solving for the “control laws” that yield the desired performance. This view of control is no longer relevant to even today's design environment where the systemwide control engineer's view of performance is needed at the earliest design stages. As cost-effective uncertainty management correctly takes its place as the dominant design issue, control engineers are forced to play a broader role, and control theory must catch up just to address the current needs, let alone the expanded needs of future VE.
Another weakness of control theory is that it tends to treat uncertainty and nonlinearity completely separately. This has traditionally been a remarkably effective strategy. To illustrate this, consider the problem of reentry of the Shuttle orbiter. Viewed as a whole, the dynamics are extremely nonlinear, and there are substantial uncertainties. The strategy has traditionally been to use a simplified nonlinear model with no uncertainty to develop an idealized global trajectory for reentry, and then use a local linearized model to design a feedback controller to keep the vehicle close to the trajectory in the presence of uncertainty. The sources of uncertainty included atmospheric disturbances, unmodeled vehicle dynamics due primarily to unsteady aerodynamic and structural effects, parametric uncertainty in the mass distribution and aerodynamic coefficients, and nonlinearities. The nonlinearities include both those that were in the simplified global model, which have been eliminated through linearization, and also higher-order nonlinearities that were not represented even in the global model. Both are treated as sources of uncertainty in the linearized model. This strategy works well because the idealized trajectory creates a relative equilibrium about which a linearization is quite reasonable, and the effects of nonlinearities do not dominate the local behavior about the trajectories. It is easy to imagine many circumstances where this clean separation is not effective, because there is so much uncertainty that either the idealized trajectory is not meaningful or the local
behavior cannot be kept close enough to the idealized trajectory to allow the nonlinearities to be treated as uncertainties.
Control theory also has other weaknesses that must be overcome. While mathematical sophistication is a strength of control theorists, they must overcome the natural distance this tends to create with other engineering disciplines. This is one reason why control theory has been applied to dynamical systems and computational complexity with some early successes, but has achieved less success in other areas. The limited connection with modeling and physics is even more troubling, as control theorists tend to view modeling as a mystical and unpleasant activity to be performed by others, hopefully far away.
While even a superficial exposition of the current state of the art in analysis of uncertain dynamical systems requires mathematics well beyond the scope of this paper, it is possible to suggest some of the ideas and difficulties with simple drawings. Recall the interference analysis. We can think of a three-dimensional solid component as being defined as a subset of real Euclidean 3-space. Thus, interference analysis is checking for any intersections of these subsets other than those that are specified. We can similarly think of components in a dynamical system as being defined as subsets of all the possible time trajectories that their state and boundary conditions can take. Thus, a circuit component can be thought of as specifying some set of currents and voltages, a mechanical component as specifying some set of velocities, positions, and forces, and so on. These sets are potentially very complicated as they are subsets of infinite dimensional spaces of time trajectories. Differential equations can be thought of as constraints that determine the set of behaviors.
An interconnection of components is equivalent to the intersection of the subsets that describe their behaviors. For example, two circuit elements connected at their terminals each constrains the signals between them, and an interconnection simply means that the constraints of both components are in effect. Engineering design may then be thought of as connecting components in such a way as to produce only a certain desired set of behaviors and no others. Undesirable behaviors are analogous to undesirable interferences in three-dimensional solids, in that they involve unwanted intersections of sets.
To make this point of view more concrete, recall the fluttering paper example, and assume we use a rigid body model of the paper in a case where the folds are fairly flat. The boundary conditions between the air and paper consist of the paper's position and orientation and their rates and the forces between the paper and the air. Both the paper and the air model put constraints on what these variables can be, and dropping the paper in air forces both sets of constraints to hold simultaneously. One solution consistent with the constraints is steady fall-
ing, but there are other fluttering motions that are also possible. The challenge in complex systems is discovering these extra solutions that may be undesirable.
If components are linear with no uncertainty, then their sets of behaviors are linear subspaces, and it is relatively easy to check globally for undesirable interconnections. This would be analogous to the three-dimensional solids all being just lines and planes. Uncertain or nonlinear components are more complicated to analyze. Very simple uncertain linear problems are NP hard, and simple nonlinear problems are undecidable. The strategy that has been exploited very successfully in robust control theory is a natural generalization of the bounding box idea to this setting of components of dynamical systems. Here the bounding boxes are in infinite dimensional spaces, and checking for their intersection requires sophisticated mathematical and computational machinery. So far, this is the only known method that successfully handles both parametric uncertainty and unmodeled dynamics and overcomes to some extent the intractability of these problems.
While the generalized bounding box methods (they are not called this in robust control theory, but are referred to with a variety of other, more technical terms) have been successful in control systems analysis and design (they are widely used throughout the world), their application outside of controls has been limited. What is particularly needed now is to put these methods more in the context of component interconnections, not just the plant-controller paradigm of standard control theory. Also, there remains a great need for methods to analyze uncertainty and nonlinearity together in some nontrivial way. Developing bifurcation analysis tools that allow for uncertainty would be a good initial step, and research in this direction is under way.
In robustness analysis of uncertain systems, it is usually much easier to find a failure if one exists than to guarantee that none exist when that is the case. This inherent asymmetry is present in three-dimensional interference analysis and software design and will be a major feature of VE. We must try to overcome this as much as possible, but recognize that a substantial asymmetry is unavoidable.
While we are far from having an integrated theory of VE, we can gather the various ideas we have discussed from dynamical systems, computer science, and control theory and briefly revisit the case studies. The success stories in the 777 solid modeling, in CFD, and in VLSI are encouraging, but extrapolation to the broader VE enterprise must be done with caution. Each success depends on very special features of the problem area, and there are substantial challenges within even these limited domains to extending the existing tools. None of these areas has faced up to uncertainty management in heterogeneous systems, though all are being increasingly faced with exactly that issue.
Among the failures considered, the Estonia Ferry disaster is the one most
FIGURE B.11 Other foundations for VE theory.
likely to have benefited from the use of three-dimensional solid CAD tools such as were used for the 777. The Titanic, Tacoma Narrows Bridge, subsynchronous resonance, and Ariane 5 failures can all be traced to specific unmodeled dynamics whose analysis, had it been considered, was well within the capability available at the time. Thus it is easy after the fact to view these as simple problems with simple solutions, but the deeper question is whether a disciplined and systematic approach to VE would help avoid such mishaps. The answer is not obvious because each of these failures involved heterogeneous interactions and dynamics that are unlike the success stories.
The telephone and power system failures and the Denver airport baggage handling system fiasco are more clearly examples where uncertainty management in complex systems went awry. These highly interconnected and automated systems are intended to improve performance and robustness and at the same time reduce cost, and they generally do so with respect to the uncertainties and objectives that are considered primary in these systems. Unfortunately, the very complexity introduced to handle uncertainties in some aspects of the system's environment lead to vulnerabilities elsewhere.
It is tempting to imagine that a design environment that stressed uncertainty management and explicit representation of uncertainty across discipline boundaries would have encouraged design engineers to be alerted in advance to the potential for these failures, but we will have to wait until we have a better picture of exactly what such an environment would consist of. The challenge will be to avoid believing too much in either virtual worlds, or our past experiences with real ones, as both can mislead us about future realities.
Figure B.11 is intended to convey the way in which some existing communities are addressing the various aspects of VE models: uncertainty, interconnec-
tion, dynamics, nonlinearity, and complexity. It is intended to suggest that all the issues are being addressed, but in a fragmented way. We touched briefly and informally on all these topics except statistics. CASE here means computer-aided software engineering, and complexity theory is computational complexity in theoretical computer science. There are other areas that should contribute to a VE theory, such as nonequilibrium physics, all aspects of scientific computing and numerical methods, optimization, and discrete-event and hybrid systems.
We have argued that while sophisticated hardware and software infrastructures are needed to form the substrate on which robust VE tools can be implemented, the infrastructure aspects of M&S are already emphasized to a high degree, and the issues focused on in this appendix need comparable attention. In doing so we have perhaps paid inadequate attention to the need for new and novel software and user-interface paradigms that would address unique needs of VE. We regret we have had neither the time nor the expertise to explore this further. An aspect of computing that we will briefly discuss, since it is so ubiquitous, is so-called “soft computing.”
Soft computing is usually taken to include fuzzy logic, neural-net computing, genetic algorithms, and so on, in contrast to the “hard computing techniques” of, say, numerical analysis, mathematical programming, structured and object-oriented programming, probability theory, differential equations, “hard” AI, and so on. According to its proponents, such as Lotfi Zadeh (see, e.g., Zadeh, 1994), “soft computing will revolutionize computing.” While it is certainly beyond the scope of this appendix to give a thorough discussion of this area, we can provide at least one perspective. There are two standard arguments made for soft computing. The first is that many problems do not lend themselves to hard computing solutions because the systems under consideration are dominated by what we would traditionally call “soft” issues, like economic and societal systems, and anything involving human decision making, common-sense reasoning, and natural language. Hard computing and hard AI have failed to achieve long-standing goals of making human-computer interactions more human-friendly precisely because they have failed to appreciate soft computing approaches. Soft computing, especially fuzzy logic, allows programming with natural language.
Indeed, Zadeh has characterized fuzzy logic as “computing with words.” The hope is that if you know a solution and you can simply and clearly articulate it in words, then you can program directly without translation to some programming language. There is substantial controversy regarding the degree to which fuzzy logic solves this problem, but the goal is certainly admirable, and there are cases in which fuzzy logic has been successful. On the other hand, many problems do not fit the fuzzy paradigm at all. In some cases, we can do a particular task well, but we cannot clearly articulate how we do it. Examples include chess
playing, vision, speech recognition, and almost all motor skills, such as those involved in sports or physical labor. Many of the tasks in which humans greatly outperform machines are also ones in which lower animals outperform humans. While biological systems do provide useful inspirations for machine automation, only humans typically articulate in words a detailed description of their own behavior. Perhaps more importantly, we often need the methods of mathematics, science, and engineering to help us find a solution. And in still other cases, using such methods permits us to find a better and more robust solution than possible with the simpler forms of fuzzy logic that have such intuitive appeal. By and large, we believe that the difficult problems of the VE enterprise are problems in which our naive intuition is likely to be dangerously wrong. In such cases, we should be cautious of seductive shortcuts.
The second argument for soft computing, and again fuzzy logic in particular, is that they more naturally exploit the tolerance for imprecision, uncertainty, partial truth, and approximation that characterize human reasoning.
In the context of VE, it is useful to distinguish two kinds of uncertainty:
-
The imprecision and ambiguities in our natural language, which parallels our sometimes limited ability to precisely specify what we want a system to do.
-
The uncertainty in our models of physical systems, as has been emphasized in this appendix.
While we have emphasized the latter, in the early stages in design of engineering systems the former can often dominate. If VE is successful in dealing effectively with type 2 uncertainty, then type 1 will be increasingly critical to overall system performance. It is here where fuzzy logic and soft computing hold the greatest promise. Advocates argue, though, that fuzzy logic is also ideally suited to handle uncertainty of type 2 as well. We disagree. Fuzzy logic is intended to capture properties of human language and simply does not address in any meaningful way many of the kinds of uncertainty we have discussed in this appendix and how uncertainty propagates with dynamics and interconnection. And, if one tried to use fuzzy logic to do so, it would quickly lose its comfortable “natural-language features.” Fuzzy logic may be useful in representing human decision making in a simulation environment, but we have not considered that issue here. It may also be useful in a variety of engineering contexts that are ultimately much simpler than those in VE.
Similar remarks apply to genetic algorithms. Optimization, and particular global search techniques, will play a critical role in present and future VE systems. Indeed, our proto-VE examples of aircraft design with CFD, VLSI, and CAD of the type used in the Boeing 777 are domains where global optimization is either already playing a huge role (VLSI) or a growing role. Statistical methods, advanced optimization theory, and even theoretical computer science (decidability, NP-hardness) are creating a foundation for this subject, both in academic research
and in industrial application. From this point of view, genetic algorithms are a very minor piece of the picture. Their popularity is due primarily to the ease with which people can use them (people who include not only deeply capable scientists, but also more ordinary people with no or little expertise in statistics, optimization, or complexity theory).
Genetic algorithms are often mentioned as a moderately effective way to do global search, especially on highly unstructured problems. Based on our experience, which tends to be in hard areas of engineering rather than, say, softer problems of military combat modeling, we remain skeptical. Despite the strong market demands for commercial software to assist in global search in such problems as VLSI design and analysis of uncertain dynamical systems, genetic algorithms have had almost no impact relative to more mathematical approaches such as branch and bound, and problem-specific heuristics. This is not to say, however, that genetic algorithms have no role to play in VE. The conceptual simplicity of the approach means that it can be used by domain experts who may not be familiar with more sophisticated optimization ideas or may not want to invest the time to program a better algorithm. Genetic algorithms can be used to explore global optimization in a new domain, and if it is successful, then there is clear encouragement for further investigation. If not, little investment has been made.
A term that often arises in conjunction with soft computing is “complex adaptive systems,” which can be considered to be a research area in its own right or a special case of what we have discussed here under the rubric of VE. It is not, however, a “new science,” nor is it a substitute for the work we have described. Instead, what it has accomplished so far is to provide a set of metaphors for taking new looks at difficult problems involving complex systems. While the celebration of chaos, nonlinearity, and emergent phenomena has perhaps been overdone, and while popularizers have sometimes given them a nearly mystical flavor that seems bizarre to those of us working in the VE domain that includes control, dynamical systems, nonequilibrium physics, and complexity theory, the metaphors and popularized discussions have greatly broadened the audience and are helping to open minds regarding the value of experimenting with methods quite different from the traditional ones.
In this sense, work on complex adaptive systems is helpful to the VE enterprise. The concern, of course, is that the simplifications of popularization— which sometimes include exaggerated promises and claims—will discredit those associated with complexity research when those exaggerations are better recognized. This is a common problem in science. For example, there were backlashes against artificial intelligence and expert systems because the more exaggerated claims were finally recognized as such. The backlashes were sometimes quite unfortunate, because the research in these areas has had profound effects. In any
case, as we have indicated from the very beginning of this appendix, dynamical systems concepts will necessarily be at the very heart of any useful theory of VE.
It is important that VE researchers develop the kind of nonlinear intuition that the subject encourages and also build on existing methods for analysis of nonlinear systems. Both the concept of chaos —that apparent complexity and randomness can arise from deep simplicity —and the concept of emergence—that apparent order and simplicity can arise from deep complexity —are of great importance. On the other hand, they are empty without the more technical concepts such as phase space, bifurcation, strange attractors, Poincare maps, Lyapunov exponents, Hamiltonians, Euler-Lagrange equations, symplectic maps, integrability, self-organized criticality, ergodicity, and entropy. Unfortunately, there is no easy access to this deeper work.
To end this discussion, we might tentatively propose a notion of “soft complexity” analogous to, and including, “soft computing,” in the same way that we might propose a notion of “hard complexity” that is analogous to and includes “hard computing.” The flavor of the distinction would be as follows: Soft complexity equals emergence, fractals, artificial life, complex adaptive systems, edge of chaos, control of chaos, . . . plus soft computing, fuzzy logic, neural nets, and genetic algorithms. Hard complexity equals information theory, algorithmic complexity, computational complexity, dynamical systems, control theory, CASE/CAD, nonequilibrium physics, statistics, numerical analysis, and so on. This appendix has clearly advocated the relative importance of “hard” over “soft” complexity in VE. Some of the more extreme advocates for soft complexity claim it will revolutionize analysis and design of complex systems and obviate the need for the “structured and mathematical approach” advocated here. While we obviously disagree with this assessment, it is likely that soft complexity can help make concepts of hard complexity accessible, albeit in a limited way, to a nontechnical audience. It is also likely that the soft complexity concepts will be quite valuable in communication and, probably, for certain types of initial exploration of concepts. In any case, popular expositions of soft complexity will continue to emerge and will have effects on decisions about investment. Our hope is that papers such as the current appendix will help maintain perspectives. 9
|
9 |
For differing perspectives, see a selection of papers by users of fuzzy logic, including engineers, in Proceedings of the IEEE, March 1995. See also the collections of Zadeh's papers (Yager et al., 1987). And, in this volume, see Appendix G for examples of fuzzy logic research. |























































