E
Multi-resolution Modeling and Integrated Families of Models
Paul K. Davis, RAND and the RAND Graduate School
Bernard Zeigler, University of Arizona
INTRODUCTION
This appendix discusses multi-resolution modeling (MRM) and the related subject of integrated families of models. 1 These have to do with changing resolution within a single model or connecting two or more models and—the key issue—doing so in a substantively valid way.
The reasons for wanting multi-resolution modeling are many, but they relate ultimately to the fact that we interact with the world at many different levels of resolution. We depend on low-resolution for (1) making initial cuts at problems, (2) “comprehending the whole ” without being lost in the trees, (3) reasoning about issues quickly, (4) analyzing choices in the presence of uncertainty, (5) using low-resolution information, and (6) helping to calibrate higher-resolution models.
We also need high-resolution models for many purposes, notably (1) to understand underlying phenomena, (2) to represent and reason about detailed knowledge, (3) to simulate “reality” and create virtual laboratories for studying
|
1 |
This appendix is largely based on work reported in Davis and Huber (1992), Davis (1993), and a review article discussing a related conference (Davis and Hillestad, 1993a,b). Some other material is adapted from presentations at a minisymposium, “Linking Simulations for Analysis, ” held by the Military Operations Research Society (MORS) in Albuquerque, N.Mex., February 25-26, 1997. The appendix also reflects discussions with Ben Wise, Paul F. Reynolds and students at the University of Virginia, Richard Hillestad of RAND, and Judith Dahmann of the Defense Modeling and Simulation Office (DMSO). |
phenomena that cannot be studied in any other way (e.g., a range of possible battles and wars), (4) to use high-resolution information, which is sometimes quite tangible (e.g., weapon performance), and (5) to help calibrate lower-resolution models.
This need for models at different levels of resolution will not change merely because computers become more capable. Thus, we also need to understand the relationships among phenomena at the different levels, which in practice means understanding how models at those levels should relate to each other.
It is also necessary to connect models of different resolution. Connections may be in software, so that one model takes data electronically from another, or “offline ” (by what is humorously known as “sneakerware”), where humans take data from one model and then feed it to another, often massaging it during the transfer.
If the only purposes were analytical, then it might be sufficient and desirable to work with model families—when good ones existed. From time to time, one would cross-calibrate the models to ensure consistency with all known information. Most of the time, however, one would use a specific model tailored to the problem.
With the advent of distributed simulation, however, much is changing. The need now exists to connect a variety of models, often with different resolutions, and to do so at run time. Further, as computing power has increased, some workers have become interested in doing analysis with models that normally operate at one level of resolution, but occasionally call higher-resolution subroutines.
There are many reasons for operating at multiple levels in an advanced distributed simulation (ADS) environment. One objective is to avoid high resolution except when needed with the purposes of (1) conserving network and CPU resources; (2) simplifying and accelerating scenario setup; (3) reducing the number of simulation operators; (4) speeding simulation execution; and (5) simplifying setup and execution of low-priority “context” segments of a simulation while allowing detailed and authoritative representation of high-priority segments. Another purpose is connecting legacy simulations written at different levels of resolution.
Table E.1 reminds us of the basic levels at which military issues must be studied. 2 Work at these levels requires different models, but a planner at one level (e.g., a joint task force (JTF) commander) cares whether his planning frame-
|
2 |
Adapted substantially from a briefing by Robert Lutz of Johns Hopkins University's Applied Physics Laboratory, a briefing given at the MORS minisymposium referred to in footnote 1. |
TABLE E.1 Levels of Campaign Models
|
Level of Model |
Scope |
Level of Detail |
Time Span |
Outputs |
Illustrative Uses |
Examples |
|
Theater/Campaign |
Joint and combined |
Highly aggregated |
Days to weeks |
Campaign dynamics (e.g., force drawdowns and movement) |
Evaluation of force structures, strategies, and balances; wargaming |
CEM, TACWAR, Thunder, JICM |
|
Mission/Battle |
Multiplatform, multitasking force package |
Moderate aggregation, with some entities |
Minutes to hours |
Mission effectiveness (e.g., exchange ratios) |
Evaluation of alternative force-employment concepts, forces, and systems; wargaming |
Eagle, Suppressor, EADSIM, NSS |
|
Engagement |
One to a few friendly entities |
Individual entities, some detailed subsystems |
Seconds to minutes |
System effectiveness (e.g., probability of kill) |
Evaluation of alternative tactics and systems; training. |
Janus, Brawler, ESAMS |
|
Engineering |
Single weapon systems and components |
Detailed, down to piece parts, plus physics |
Subseconds to seconds |
Measures of system performance |
Design and evaluation of systems and subsystems; test support |
Many, throughout R&D centers |
work and models are consistent with what he would obtain if he could do detailed analysis. So also, those who work at relatively high levels of detail are concerned about real-world contexts and constraints, which may be limiting factors in determining how systems are used and how they will perform (e.g., whether fighter aircraft will be permitted to engage at beyond visual range).
At any given level of activity, we need a model of how the world works that depends only on variables at that level of activity. For example, commanders maneuver forces and fires, and allocate other resources, defined doctrinally at their level. They must limit complexity if they are to operate effectively. They care deeply what goes on at higher levels of detail, but they can only check on such matters by exception. Instead, they must depend on doctrinal planning factors, aggregate models, and judgment with occasional high-resolution “calibrations.”
It is worth noting here that most analyses and exercises depend on being able to treat key phenomena in relatively higher detail than other, less-central phenomena. For example, in one campaign analysis, logistics may be represented by nothing more than supply and use rates (both in tons per day), while combat forces may be represented at the level of brigades, squadrons, and missile ships. In a logistics-oriented campaign study, this situation might be inverted, with combat being represented by a simple demand function, and logistics represented in some detail by airlift, entity-level sealift and logistics ships, and intra-theater distribution systems.
Assuming interest in having and linking models of different resolution, there are a number of related but distinct problems. These include the following:
-
Making selectable resolution feasible and sound within a distributed-simulation environment where there is need for repetitive aggregation and disaggregation.
-
Making selectable resolution feasible and sound within an analytical model where certain subroutines need to be at higher resolution than would be appropriate generally.
-
Developing sound mutually calibrated families of models so that, at each level, work reflects the full range of available knowledge.
For each, there is a distinction between working with existing models and designing new ones.
So far, our discussion has been abstract. Let us now provide more concrete examples.
Suppose one is assessing the potential value of a force posture dependent on naval and Air Force aircraft and on long-range missiles with precision weapons (e.g., missiles that might be launched from an arsenal ship). An operational analysis for a JTF commander might use models with factors such as the average number of aircraft sorties per day and the average number of armored vehicles killed per sortie. By contrast, a high-resolution simulation might consider variables such as the weapon configuration on each type of aircraft, the distance they must fly from aircraft carriers or bases, the tactics of maneuver (including concentration in time and dispersal of vehicles), and the capabilities of reconnaissance and surveillance systems. Both levels of resolution (and others in between) are respectable and important. However, estimates of, say, kills per sortie should be based on something more than conventional wisdom and Service claims. Too often, there is no documented basis. Further, there is no integrated family of models that would provide such a documented basis. Such a family is needed because the gap between test-range data and campaign effectiveness is too great for the connection to be drawn easily.
Multiple resolutions are needed even within individual simulations, especially in the distributed simulation environments central to the future of DOD's M&S. Some examples of why follow.
-
Different echelons. Some ground-warfare component simulations represent individual platforms as distinct entities, while others represent higher echelons as distinct entities. For example, semiautomated-forces models may represent tanks, while a corps-level combat model represents either companies or battalions. When these components are connected in the distributed simulation exercise, problems arise when a platform object needs to interact with an aggregate object. They also arise when aircraft entities need to interact with aggregate ground combat entities, or with naval entities. This cross-service issue makes it a greater concern for JSIMS.
-
Different levels of detail of entities. Even at a single echelon, entities may differ widely in the level of detail they represent. A basic aircraft simulation might represent only 3 degrees of freedom (DOF), such as X, Y, Z and their rates of change. A more detailed model might represent 6 DOF (X, Y, Z, yaw, pitch, roll, and their rates of change). Both support interactions with a simple range-only sensor model, but only the 6 DOF model supports a detailed sensor model that uses orientation to compute signature and detection probability.
-
Different processes within objects. Even if a simulation can always represent interactions between entities at the same level of resolution, the desirability
-
of simulating those interactions at all may vary over time. For example, a logistical base may simply use integer counters to model the cycling of equipment through various stages of readiness most of the time —but when the base comes under attack, it becomes important to represent those items of equipment as individual entities to be sensed and attacked. A C2 node in computer-generated forces may use simple decision logic when simulating noncritical parts of the battlefield, but use sophisticated decision logic when simulating critical parts— even though the same kinds of physical entities and physical interactions are supported everywhere.
The example above involved analysis, but there are also many problems that arise in distributed simulation intended for training and exercising forces and their commanders. Some are down-to-earth in character, but troublesome to simulationists who must do the best they can to construct a synthetic theater of war. Some of those problems are as follows: 3
-
Differing time steps. Suppose a semiautomated-forces model (e.g., ModSAF) runs with approximately 1-second updates for each entity, but is interfaced with a tactical-level model (e.g., AWSIM) that runs with approximately 1-minute time steps. What does ModSAF see between AWSIM updates, and how does AWSIM handle short-lived combat interactions?
-
Templating subobjects. When a battalion object encounters a collection of tank objects, where does the battalion place all its newly created vehicles as it deaggregates?
-
Duplication of C2processes. Do we need to write one computer-generated-forces (CGF) command-control rule set for a simulation when it is running battalion-level objects, and a whole separate CGF/C2 rule set when it is running entity-level objects? This would imply near-duplication of programming and knowledge-acquisition effort, multiplication of scenario setup effort, and exponentiation of VV &A effort.
-
Results correlation. If a combat process can be simulated at both high and low resolution, how can we guarantee consistency between the two results— even when the two processes start with the same scenario?
-
Consistency between repeated deaggregations. If one object changes resolution several times in a row, how can we ensure that the sequence of detailed views represents a coherence sequence? For example, as a battalion deaggregates, reaggregates, and deaggregates again, how can we make sure that the subordinate platoons (or even subordinate tanks) do not jump around in physically impossible
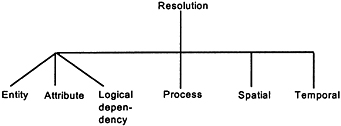
FIGURE E.1 Aspects of resolution.
-
ways? If the same logistical base is attacked several times in rapid succession, how can we ensure that the equipment on the base is properly placed? When do these issues matter?
-
Wide area sensors. When one wide area sensor, such as JSTARS or overhead assets, views the battlefield, must everything in the whole theater change resolution to support that one sensor?
Against this background of challenges, let us now discuss what is involved in multi-resolution modeling.
The difficulties in discussing variable resolution or multi-level resolution begin with the word “resolution,” since resolution is multifaceted as Figure E.1 suggests. To make matters worse, in comparing two typical military models, one often discovers that the first model has higher resolution in some respects and lower resolution in others.
Usually, people doing simulation think of higher resolution as associated with lower-level objects (e.g., with individual tanks rather than aggregate concepts such as battalions). However, a “high-resolution ” model representing individual vehicles might not distinguish among them, and it might assume they all moved in lockstep. Further, it might compute the attrition to vehicles by estimating a higher-level attrition (e.g., to battalions or even divisions) and then allocating that attrition among the vehicles. Such a model would have low resolution with respect to entity attributes, process, and so on. The point, then, is that “resolution” is a complex subject. This certainly applies to naval forces, because in some simulations a cruiser may be treated as a single object—in some respects analogous to a tank—whereas someone interested in the cruiser's armaments and sensors would see it as being a complex system with multiple levels of lower-level entities.
|
3 |
These problem examples were suggested by Ben Wise. |
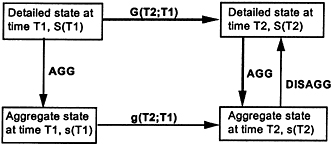
FIGURE E.2 Consistency diagram.
A primary concept in MRM is that of “consistency.” The recurring issue is whether two models—one of them having higher resolution than the other—are somehow “consistent.” This is not a straightforward concept because the answer depends on context. Figure E.2 depicts the issues graphically. If G and g are high-resolution and low-resolution models, which operate on initial states to generate subsequent states, then the first question of consistency is whether one can start at the top left corner with an initial detailed state and get the same aggregate state by aggregating the initial state and applying the aggregate model (down and right) or by applying the detailed model and then aggregating (right and down). That is, we might hope that the aggregate model gets the same aggregate result as the more detailed model.
A tougher criterion for consistency would be requiring that the same final detailed state could be generated by moving down, right, and up, or by moving right. This form of consistency is more difficult to achieve because information is discarded in the aggregation process. How, then, does one regenerate detailed state information at the end? The answer, in some cases, is that the final state of the real system does not in fact depend on the initial detailed state. For example, if a carrier battle group moves from one location to another and then takes up battle positions, the spatial distribution of ships may be independent of the original detailed state, and dependent only on a combination of local information and doctrine—information added as needed. More generally, however, we have to expect that the second type of consistency will not be achieved.
Even here there are subtleties, however. Should the aggregate model really generate the same final aggregate state, or would doing so be merely accidental? After all, the aggregation of the detailed state is an aggregation of only one case, whereas the aggregate model may be dealing with averages over many cases. To be less abstract here, one would not really expect a detailed theater model to generate precisely the same overall attrition and movement as an aggregate model. Instead, one might expect that a statistical average over cases of the detailed
model's overall attrition and movement for a given case might be consistent with the predictions of an aggregate model.
The difficulties in formulating consistency illustrate issues that a theory of modeling and simulation should address ( Appendix G ). Conceptual clarity and mathematical rigor can be gained by applying such concepts as morphism and experimental frame, which such a theory provides. The basic concept of morphism, called homomorphism, is illustrated in Figure E.3 . Two models are considered: S and S', where S may be bigger than S' in the sense of having more states. As in the consistency discussion above, when S' goes through a state sequence such as a,b,c,d, then S should go through a corresponding state sequence A,B,C,D. We do not assume that states of S and S' are identical—only that there is a predefined correspondence between them illustrated by the connecting lines in the figure. Now to establish that this correspondence is a homomorphism requires that whenever S' makes a transition, such as from state b to state c, then S actually makes the sequence of transitions involving corresponding states B and C.
Some points to notice in this definition are as follows:
-
The situation where S has many more states than S' occurs in two major contexts: in multi-resolution modeling when S is a high-resolution model and S' is a consistent (i.e., homomorphic) lower-resolution representation and in simulations where S is a simulation program and S' is the underlying model.
-
S may take a number of microstate transitions to make the macrostate transition from B to C. In the case of simulation, these are computation steps needed by the simulator to correctly execute the model state transition. In the multi-resolution case, both time and state are being aggregated in the lower-resolution model.
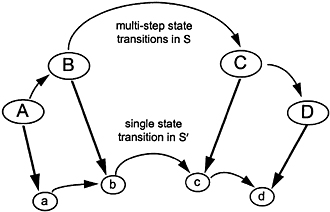
FIGURE E.3 State transitions in homomorphic models.
-
Sometimes, we require strict step-by-step correspondence—i.e., that the transition from a to b is mirrored by a one-step transition from A to B. This is the case where both models are required to operate in strict time synchrony, as might be necessary in a real-time application.
-
Typically, only a subset of the states in S correspond with those of S'. This subset is the operating region of the homomorphism. In the multi-resolution case, the operating region is the domain of the high-resolution model for which the low-resolution counterpart should be valid. For example, a high-resolution model of a fluid undergoing laminar flow may have a low-resolution representation, whereas its turbulent regimes may not. As discussed later in Appendix E, this is one place that the concept of experimental frame enters: an experimental frame specifies the operating region in which the low-resolution model must be a valid representation.
-
Also, to achieve tree abstraction, the correspondence between states must be many-to-one; that is, many states of S correspond to the same state in S'. For example, there may be many detailed states in the circle labeled B that are all represented by the same aggregated state b. In this case, the mapping from S to S' does not have an inverse. In other words, as mentioned above, where true abstraction is involved, disaggregation is not a unique operation.
-
A second important place where the concept of experimental frame helps bring clarity is in the relationship of the complete state of a model and its observable output. An experimental frame specifies the variables in which we are interested for some particular exercise. If a high-resolution model has the capability to compute such variables, it is indeed applicable to our frame of interest. However, the high-resolution model may do this in an “overkill” manner, and it may also compute a host of other variables that are not of interest in our frame. In this case, we may expect that a homomorphic low-resolution equivalent may exist.
Assuming we can define resolution and consistency in a context, a central challenge is developing integrated model families. How to develop these families is a frontier issue.
We may start by asking what we mean by “an integrated family of models.” First, we mean that depictions at different levels of resolution are appropriately consistent or morphic in one of the senses discussed above. We also mean that data can flow meaningfully from one model to another, either by connecting the models as software or by having humans turn outputs from one into inputs of another. The word “meaningfully” is significant because, in practice, it is often not evident how models purported to have a family relationship should be connected. The models have often been designed with different perspectives on how the world works, as well as with different meanings for the same word or phrase
(e.g., “force ratio”). Or, it may be that the models were constructed with different operating regions of validity.
Yet another characteristic of integrated models would be that the variable names and function names would be conceived within the same global view, from top to bottom, thereby making it much easier to understand what a given variable means and how it relates to variables above and below it.
Note here that the goal of integration is not to create “seamlessness” (impossible), but rather—as suggested to us by John Doyle—to create “good seams,” so that moving across levels of resolution maintains a clear and consistent sense of the system.
Integration of models has always been desirable, but analysts working in a single small organization have often been able to work around problems by studying the various models in detail and developing “good-enough” procedures. They have taken shortcuts and sometimes made errors, but at least the situation was to some extent under control. By contrast, consider the situation with distributed simulation. Here workers in different organizations are using data from each other's models and hoping that they are doing so sensibly, but without having full familiarity with all the pieces—and without even knowing the individuals who created the pieces. This makes the needs even greater than ever before.
Having discussed some of the most fundamental issues, let us now review briefly some of the conclusions available from previous work. We highlight some that bear on common misunderstandings.
-
Just building a good high-resolution model is not the answer, even with fast computers. To many people, it seems as though the answer is simply to “do it right” with a high-resolution model and, as necessary, to generate aggregate displays. That, however, is wrongheaded. First, we do not have the knowledge necessary to build the requisitely comprehensive high-resolution wide-scope models (e.g., the knowledge to represent human behaviors well). Second, even if we did, we would not have the necessary data. Indeed, many of the critical data are unknowable in advance. Third, even if we somehow had the model and all the necessary data, we could often not do analysis without aggregating and smoothing. 4 And, to do that, we would need to know how to do the aggregation
|
4 |
As one example here, the exploratory analysis emphasized in Appendix D is not feasible without abstraction (aggregation) because the curse of dimensionality is overwhelming even with massive computer power. With multi-resolution designs, however, exploration can first be accomplished with relatively abstract intermediate variables, and then refined by “zooming in” on those subordinate high-resolution variables of most importance. |
-
and smoothing. Fourth, even if we could do all that, we would not know whether to believe the results or how to understand them, because the “explanation” would be at the level of bullets and trees. That is, we might have to construct aggregate models to comprehend and explain.
In summary, the problem here is not with computer speed, but with matters more fundamental. 5
-
Pure bottom-up approaches fail. For related reasons, efforts to build complex system models strictly from bottom-up details have generally failed— collapsing under the weight of data requirements and shear complexity. Despite heroic efforts, they have often not been able to generate macroscopic behavior (recall Clausewitz's discussion of friction in war). By contrast, approaches that freely mix top-down and bottom-up approaches have a better track record (e.g., approaches that build in command and control structures from the top down). Further, recent work suggests that it is useful to think also about minimizing some details at the bottom of the bottom-up effort. Sometimes, it appears that only a few key features of entity-level behavior really matter to macroscopic behavior. The point here is that past experience, as well as theory, indicates that “purist approaches” based on strictly bottom-up (or, for that matter, strictly top-down) attitudes should be resisted. To represent complex systems well, one must use information from all levels, and welcome doing so rather than regarding some of it as the application of fudge factors. It is also important to be open to the need for iteration, because which entities make sense is sometimes not apparent until one has considerable experience, including experience observing so-called emergent phenomena. 6
-
Object-oriented programming will not solve the problem. Object-oriented programming is excellent for describing hierarchies of natural objects (e.g., the carrier battle group that breaks down into component ships). However, the hard part of variable-resolution modeling or developing integrated families of models lies not in the object description, but in the description of how processes
5
It is significant that physicists do not explain the skidding of an automobile in terms of Schrodinger's equation. They work with engineering-level equations and concepts such as the coefficient of friction, which they measure. Similarly, much of our best knowledge of military operations comes from aggregate-level observations and is expressed in the concepts of aggregate models. The commonly held notion that the best information resides only at high resolution is wrong.
6
We base our comments here on our experience, our sense of the literature, and very helpful discussions with fellow panelist John Doyle and with Chris Barrett and Darryl Morgeson of Los Alamos National Laboratories (specifically about their experiences with the TRANSIM modeling effort to represent automobile traffic in large cities, with both detailed bottom-up modeling and a more agent-based approach using cellular automata). For an excellent semi-popular description of agent-based modeling and emergent phenomena by one of the pioneers in the study of complex-adaptive systems, see Holland (1995). For a recent survey of related work and its potential relevance to military problems, see Ilachinski (1996a,b). For a good entry to the important work on complexity of the Sante Fe Institute, see its Web page ( www.santefe.edu ).
-
at different levels interact. To use the example we started with, how does aggregate-level air-to-ground effectiveness relate to entity-level factors such as single-shot kill probabilities for precision weapons launched from 10-km altitude on a foggy day against a tank in the open? Relating these is analogous to relating thermodynamic relationships to the relationships of molecular physics and chemistry. Actually, it is harder, because in physics averaging in the process of aggregation does not have to contend with living, thinking, competitive warriors who are attempting to avoid things “averaging out” (e.g., by concentrating forces).
The point here is that we need humility in taking on the challenges of aggregation and disaggregation. Remarkably, modelers often display more hubris than humility in this regard. “Designing on the fly” at the computer terminal, they do violence to the underlying phenomena as they assume aggregate relationships that ignore complications and assume, implicitly or explicitly, circumstances such as uniform distributions, independent events, and constant remixing. Similarly, high-resolution modelers sometimes ignore frictional processes and give only short shrift to the all-important issues of higher-level command and control decisions. Whether one programs with an object-oriented language is irrelevant when the real difficulties are phenomenological.
One possible solution to design challenges is called integrated hierarchical variable-resolution modeling (IHVR) (Davis, 1993). When feasible, it simplifies and clarifies the problems associated with crossing levels of resolution, either within a single model or within an integrated family. The basic idea is to design the models so that a given key high-level variable is expressed as a function of lower-level (higher resolution) variables, each of which is in turn a function of lower-level variables, recursively down to the lowest level. Ideally, this generates perfect hierarchical trees in which a given variable relates to variables above it and below it in the same tree or subtree, but never to variables in another tree or subtree. There is no cross-talk.
Figure E.4 illustrates the basic concept with a simplified representation of the ship-defense problem. 7 Suppose one is concerned about the probability that a particular ship (e.g., an Aegis cruiser) survives an attack by enemy ballistic or cruise missiles. In some war games, one might just specify that probability as a parameter, varying its value to see the consequences (Level 1 modeling). More
|
7 |
The discussion here assumes, for simplicity only, that the incoming missiles can be treated independently. This is not true in practice, and a more serious treatment would require considering salvo tactics, saturation effects, and so on. The result would be a blurring of the levels and a blurring of the concept of leakage. As one possible outcome, a “correct” aggregation—or at least a good approximation—might involve a leakage that was a function of the number of attacking missiles and their “type tactics.” |
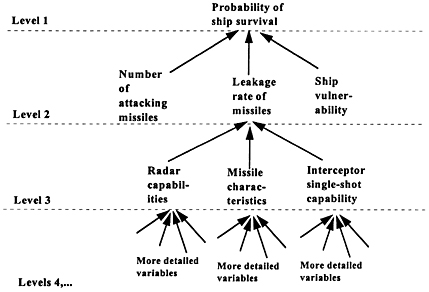
FIGURE E.4 An illustrative model hierarchy.
typically, one might have a model that calculates the probability of ship survival as a function of the number of attacking missiles, the leakage rate of those missiles, and the ship's vulnerability (i.e., the likelihood of being disabled as a function of the number of missiles that strike it). This would be Level 2 analysis, with leakage rate specified as a parameter, and perhaps varied. But leakage rate could be calculated from more detailed factors if the information were available. It could be calculated as a function of radar characteristics, missile characteristics, and the single-shot kill capability of its interceptors. And so on, down to more and more levels of detail. Now, the hope would be that the estimates of ship survival would be “consistent” regardless of how the calculation was made. This would be possible if the probability distribution of leakage rates assumed at Level 2 was generated from Level 3 analysis—averaged appropriately over all the relevant operational circumstances. In some cases, it might be adequate at Level 2 to use a “best estimate leakage” and an uncertainty range, without the embellishment of a probability distribution.
If one has this type of design, then it is easy in principle to proceed. One can run the model starting at any level of the tree, treating the lowest-level variables at that level as parameters. The values of these parameters should then be made consistent with an appropriate context-specific statistical average (or probability distribution) over results of running the model at the next lower level (higher resolution). This consistency should be obtained by adjusting models and data at all levels in the tree to represent “hard” information at whatever level of resolution it is found. For example, the reliability of a complex weapon system may be
based not on laboratory experiments, but on the experience of dozens of military units over time.
Another benefit of this approach is that it is straightforward to define and give names to variables without getting them confused. For example, there may be a half-dozen different force ratios in a ground combat model, but each would have the necessary adjective to distinguish it.
Unfortunately, there are three basic problems in trying to achieve this ideal of IHVR. First, aggregation and disaggregation are conceptually difficult and often quite subtle—not only in military modeling, but also more generally. Consider here the efforts that have gone into deriving respectable mathematical expressions for thermodynamic-level characteristics of nature from the molecular laws of physics and statistical mechanics. These problems have been considered hard even for equilibrium systems and a Mother Nature who is not trying to complicate things.
The second problem is that there typically are many complex interactions in a realistic simulation model, interactions that violate the image of pure and independent hierarchical trees. In military affairs, for example, one might think that one could treat Army, Navy, Air Force, and Marine forces as having their own hierarchical processes. However, an accurate depiction would show a good deal of cross-talk, even more as joint operations become the rule rather than the exception.
A third problem is that analysts commonly take different “perspectives” of the same problem depending on precisely what problem they are working. Attempts to impose a single perspective would make no sense. However, different perspectives imply different hierarchical depictions. For example, Navy and Marine officers often conceive command-control systems differently for air campaigns. So also, in some cases Marines might model their air forces as providing a kind of force multiplier rather than as destroying enemy vehicles at a certain rate per sortie. This might reflect a particular view of how the air forces would be employed (e.g., for suppression and as directed fire akin to artillery). That perspective would not “fit” well with Air Force models affecting ground combat, but it would arguably be just as valid. The conclusion here is that we should not assume that a given set of hierarchical relationships would always be “right.” Analysts understand this viscerally, but simulation modelers sometimes tend to think of their preferred representations as being uniquely correct.
Past militarily relevant work has contributed to a better understanding of the conditions under which various idealized aggregate models are or are not consistent with higher-resolution idealized depictions. Such work has only a limited potential, however, because it depends on toy problems such as problems de-
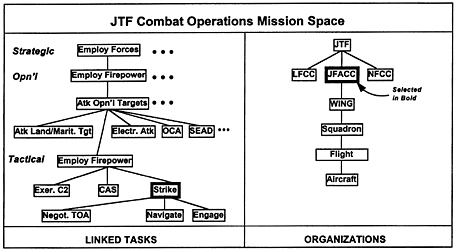
FIGURE E.5 A slice from a CMMS. SOURCE: Jefferson, DMSO (1996).
scribable precisely by Lanchester-square laws. What is most needed in the next phase of work is development of good decompositions and approximations. The world, after all, is to a large extent described by “partially decomposable hierarchical systems” (Simon, 1996). What are the right decompositions for military work? The answer is unclear, but the following are reasonable hypotheses.
Although workers in different aspects of DOD work will continue to have differing perspectives about how to characterize systems, there can be considerable convergence—to a small set of alternative structures rather than an unbounded set. Further, there can be agreement on the names to be used for commonly recognized entities and relationships, or at least on “standard” names and translations. Such developments would be quite valuable in efforts to build variable-resolution or multi-level resolution models. 8 Thus, the efforts of OSD's Defense Modeling and Simulation Office to encourage common models of the mission space (CMMS) should be supported. A good development here is agreement of the JWARS and JSIMS program offices to work on CMMS jointly. Figure E.5 (DMSO, 1996c), taken from DMSO materials, illustrates what is at issue. It is not exotic; rather, it is communicating concretely a vision of how the real world works. It shows breakdowns of tasks and organizations for a joint task force (JTF).
|
8 |
Simple, worked-out examples illustrating these issues are given in Davis (1993). |
A second hypothesis is that great strides will be made in MRM only by exploiting natural temporal and spatial scales, some of which need to be identified and defined. As noted above, real-world processes are often interconnected, making hierarchical modeling and MRM very difficult. However, if one breaks the simulation into appropriate temporal and spatial chunks, it is likely that simplifications can be made that will create approximate hierarchies. With luck and hard theoretical work, it may be possible to deal with the errors so created by making occasional adjustments in coefficients—much as is done currently as models adjust coefficients when forces maneuver from one type of terrain to another over a period of hours.
Finding the appropriate scales and ways to exploit them will not necessarily be easy because warfare operations have become quite complex as maneuver of forces has begun to give way to maneuver of fire, as lethality has increased, and as a relatively small number of C4ISR systems have come to play an increasingly critical role. It is also plausible that aggregate models will sometimes not be as useful as in earlier days because the decisive events may be fewer in number and more highly correlated. None of this is clear, however, and in-depth research is badly needed (as discussed in Chapter 6 ).
Fortunately, it is sometimes possible for even a modest amount of theoretical work to shed light on confusing multi-resolution issues. As one example, a recent study used analytical expressions to show how the advantages gained from operational-level concentration depend on the relative time scales for C4ISR, maneuver, and duration of battle (Davis, 1995). The work demonstrated that quite different aggregate-level laws would apply, depending on the relationship among time scales. Although the work used a highly simplified model assuming Lanchester equations, the basic principles demonstrated were more generally valid and the points made had not been well understood over the years.
Many insights can be gained by conducting simulations conceived as computational experiments. This is especially true when several groups approach the same problem, even with allegedly equivalent tools. These often produce surprises, even for experts. Further, they can guide development of better approximate models at lower levels of resolution (Hillestad, Owen, and Blumenthal, 1992; Hillestad and Juncosa, 1993).
With modern computer technology it is also possible to design huge sets of computational experiments in an effort to “explore” the space of possibilities and gain an appreciation for what matters and when, especially in the presence of large uncertainties.
A different tack will often be critical in dealing with MRM issues. Rather than putting substantial effort into developing sound MRM relationships that can be used within simulations, it may sometimes be wise to adopt standards for distributed simulations designed to avoid the need to move back and forth among levels of aggregation. It may also be possible to design the entities of M&S to have a mix of high- and low-resolution attributes, with the entities “carrying along” just that subset of high-resolution information most needed for the interactions of the particular simulation. Ideas along this line have been proposed and pursued by both Paul Reynolds and his collaborators at the University of Virginia (Natrajan and Tuong, 1995) and Ben Wise of Science Applications International Corporation.
Modular design is essential and is facilitated by object-oriented methods. Given a sufficient library of modules, it may be possible to change representations (perspectives) from one application to another without too much special-purpose tailoring to adjust the relevant hierarchies. It seems unlikely that a hardwired family of models will prove nearly as valuable as one that allows analysts with different problems to tailor the models suitably without great difficulty. Perhaps most of the alternative representations with real value can be conceived in advance, but it is doubtful. On the other hand, with appropriate configuration control and documentation, each well-conceived tailoring would produce a new option that others could use in the future. Thus, the broader notions of model modularity and repositories to facilitate reuse are also consistent with needs for MRM.
A basic problem in both the design and the use of model families is that most workers do not really understand what is involved in crossing levels of resolution. As examples of what workers need, and as an opportunity to reinforce points made earlier, consider the following. Often, workers seem to believe that all they need to improve results are some high-resolution subroutines to be called as needed in the course of running their more aggregate simulation. Suppose that such subroutines exist, however. They must be initialized with high-resolution input parameters, which are nonuniquely determined by the lower-resolution state variables. Which disaggregation should one use? Or should one instead run a large number of the high-resolution cases using different input parameter values, and then somehow average the results statistically? If so, what statistical approach would be suitable for the problem at hand?
More generally, how “should” one calibrate values of input parameters at different levels of a model family? The answer is not at all straightforward. As above, there are complex issues of statistical averaging, made more difficult by the fact that the humans in military operations are, as mentioned earlier, trying to avoid the circumstances in which everything averages out. Also, there are many different sources of information, some of it at high resolution (e.g., the number of weapons of a given type carried by a given aircraft on a given day's sorties) and some of it at low resolution (e.g., the typical frictionally caused delays in various command and control processes). How can all this information best be used? Aggregate-level data may have important implications for high-resolution models (e.g., the implication that unmodeled frictions slow processes up), and vice versa (e.g., a serious mismatch between the effective shooting ranges of the adversaries may mean that aggregate models based on Lanchester equations or anything remotely comparable will fail catastrophically under some circumstances, as happened in Desert Storm—in part due to poor practices by the Iraqi ground forces (Biddle, 1996)).
Currently, there are few relevant primers, especially in military work, but even in the community more generally. Such primers are needed.
Although the current problems are due more to intellectual shortcomings such as the lack of good theories than to technology, technology can also help a great deal. It seems very unlikely, for example, that workers will go about their calibrations without fast running models and appropriate tools to define cases and accomplish the relevant statistical manipulations.
Fortunately, the theory and tools supporting integrated families of models have been making steady but slow progress, although the advances are not well known to the majority of military simulationists. Early work in aggregation theory for economic systems dates back to the early sixties (Simon and Ando, 1971). Cale (1995) gives a recent survey of results of aggregation theory in the ecosystems simulation context. The theory states conditions under which error may or may not be expected as a result of aggregation. Since it is generically stated, it may apply to many military situations. Indeed, it bears some resemblance to the work discussed in Davis and Huber (1992) and Hillestad and Juncosa (1993). The underlying homomorphism mappings and hierarchical, modular construction techniques have provided the basic tools to construct families of models in both ecological (Zeigler, 1979a) and generic contexts (Zeigler, 1978, 1979b, 1993). Fishwick developed a software system to demonstrate the feasibility of a hierarchical multi-resolution approach to wire frame animation of human
body motion (Fishwick, 1986, 1989). A contemporaneous conference, “Enabling Technology for Simulation Science” organized by Alex Sisti of Rome Labs ( www.rl.af.mil/Lab/IR/IRXtra/confpro.html ) features a review of recent work on model abstraction and its latest developments.
The next generation of military models needs to be designed so as to produce integrated families that cross levels of resolution. This will require a good deal of theoretical effort involving mathematics, software engineering, and—perhaps most important—a deep understanding of the phenomenology coupled with an appreciation for how models of different resolution should and should not be used. Currently, the field lacks ability to apply the necessary theory, tools, and primers. However, there are insights in the literature that provide a foundation. What is needed is both further development of this and use of it in implementing actual simulation systems.




















