Progress Toward Understanding How Waves Break
M.S.Longuet-Higgins (University of California at San Diego, USA)
Abstract. This paper reviews a number of investigations into the dynamics of breaking waves. The simplest time-dependent model of gravity-wave breaking is the lowest superharmonic instability of a steep Stokes wave. Recent calculations for both deep-water waves and for solitary waves in shallow water show that as the wave steepness increases, the region of instability is increasingly confined to the wave crest, and takes the limiting form of a “crest instability”. The nonlinear development of the instability depends crucially on the sign of the initial disturbance. Positive perturbations lead to overturning of the crest, negative perturbations lead to a transition to a periodic wave of lower amplitude, then to a quasi-periodic recurrence.
At wavelengths up to 2m surface tension and viscous effects are found to be drastically important. An improved linear theory has been given for the generation of ripples ahead of the wave crest (parasitic capillaries). When these ripples become nonlinear, a “capillary jump ” is sometimes formed, which can be described in terms of two half-solitary capillary waves. Shedding of mean vorticity by the highly-damped ripples leads to an unstable shear-flow, which may separate from the leading edge of the jump. Instabilities of the shear flow in the form of “vortex waves” may account for the “Type 2” capillary waves seen crestwards of the leading edge by Duncan et al. [1].
The onset of breaking in modulated groups of waves occurs at lower wave steepnesses than do crest instabilities. Some examples are discussed, but a satisfactory theory is still lacking.
1.
Introduction
Since the early 1970's increasing attention has been given by oceanographers to the influence of breaking waves on the transfer of heat and momentum between atmosphere and ocean, the production of aerosols and spray, the generation of the underwater sound field, and the evolution of the wave spectrum itself. On the other hand, naval hydrodynamicists are interested especially with the action of breaking waves on moving or stationary structures—the influence of bow waves on wave resistance, turbulent wakes and noise production, wave loading on oil rigs and coastal defenses, not to mention the capsizing of ships in heavy seas.
My personal interest was rekindled recently by the striking photographs taken by Professor Duncan and his collaborators at the University of Maryland; see Duncan et al. (1994) [1]. These are illuminated cross-sections, taken at intervals of 0.01s, of gentle breaking produced by focussing wave energy with a controlled wavemaker —a technique for studying wave breaking demonstrated at an earlier Symposium on Naval Hydrodynamics (Longuet-Higgins 1974) [2]. The most remarkable feature is that the crest of the wave eventually collapses into turbulence without the surface ever having overturned on itself.
There are several problems raised by these photographs (see Figure 1):
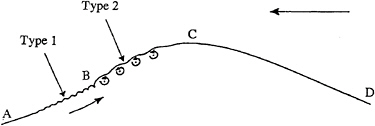
Figure 1. Schematic diagram of a gently breaking wave as observed by Duncan et al. [1].
-
Why does the wave crest become asymmetrical, with a bulge on the forward face?
-
Why do short (Type 1) capillary waves appear below the forward edge, or toe of the bulge?
-
Why do longer (Type 2) capillaries appear above the forward edge?
-
Why do the Type 2 capillaries grow and collapse?
-
How are these phenomena related to other types of wave breaking?
A few days after Jim Duncan made these observations in 1992, I happened to be visiting his laboratory and had with me a copy of a 1982 thesis by my student Philip Cleaver [3] which treated what we now call “crest instabilities”, that is the instabilities of the flow near the crest of an almost-highest Stokes wave. It appeared that these calculations might be relevant to the phenomena recorded by Duncan. As it turns out, the initial bulge in Duncan's experiments cannot be interpreted directly as a crest instability. Nevertheless the incentive to carry out further investigations has led to a deeper understanding of how crest instabilities are related to other instabilities of steep waves, in both deep and shallow water. Furthermore, the presence of ripples, both Type 1 and Type 2, suggests that capillary, and also viscous, effects are in some ways important, even for gravity waves of length l m or more. Subsequent investigations have shown these suppositions to be correct, in a way that I hope to explain in this lecture.
One of the simplest approaches to wave breaking is to model the initial flow as an instability of a uniform train of steep, irrotational gravity waves. Here progress has recently been made by studying the basic superharmonic instabilities of a progressive wave, namely those having the same space periodicity as the unperturbed wave. Some recent numerical calculations extending to very steep waves are summarised in Section 4 below. It is found that these instabilities become localised near the wave crests. To interpret the results and to introduce a proper scaling, it is convenient first to summarise the theory of the “ almost-highest wave,” which describes the asymptotic form of the flow in the crest of a steep Stokes wave of less than maximum steepness; see Section 2. The instabilities of this crest flow have been recalculated in three recent papers, as described in Section 3, and in Section 4 it is shown that these “crest instabilities” do indeed correspond to limiting forms of the superharmonic instabilities. Similar results for solitary waves in shallow water are described in Section 5.
To follow the development of the crest instabilities beyond the linear, infinitesimal stage, boundary-integral techniques can be used, as described in Section 6. This method reveals some surprising differences in the subsequent time-histories of the flow, depending upon the sign of the initial disturbance. The flow may either develop as a plunging breaker or make a recurrent transition to a wave of lower amplitude.
For waves up to 2m in length the effects of surface tension can be important. An improved linear theory for the production of parasitic capillary waves in described in Section 7. A descriptive theory is also given for the nonlinear features known as “capillary jumps;” see Section 8. The effect of surface tension on crest instabilities is described in Section 9. New work on viscous effects, including the generation of shearing currents and the production of turbulence, is described in Section 10. Lastly, in Section 11 we discuss one of the main unsolved problems to do with breaking waves: the incidence of breaking in modulated groups of waves. Section 12 is a brief summary of the conclusions.
As is customary in modelling the very rapid late stages of wave breaking, the direct action of the wind on the water surface will be ignored; the pressure there is assumed to be constant. For simplicity it is also assumed that the motion is essentially two-dimensional. Until the onset of the viscous effects discussed in Section 10, the flow is assumed to be irrotational.
Among many other investigations which it will not be possible to discuss in detail we may mention two: Jenkins' [4] calculation of a steady-state plunging wave crest—in this review we shall be concerned rather with the time-dependent problem of how such a flow comes into existence—and the dynamical theory by Shrira et al. [5] for the three-dimensional structures known as “horse-shoe” waves.
2.
The near-limiting form of steep Stokes waves
When steady, irrotational gravity-waves (Stokes waves) approach their limiting steepness, conventional methods of calculation, e.g. by Fourier series or integral equations tend to lose accuracy. On the other hand the profile of the limiting wave in deep water, with a 120° rest angle, was determined many years ago by Michell (1893) [6]; a modern calculation by Williams (1981) [7] is accurate to at least 7 decimal places. So why not work downwards, from the steepest wave? In the wave of limiting steepness (ak)max=0.4432 the radius of
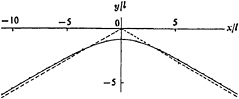
Figure 2. Form of the wave crest in a near-limiting progressive gravity wave. Full line: surface profile. Broken line: 30° asymptotes. From Longuet-Higgins and Fox [8].
curvature R at the crest is zero, and the particle velocity q at the crest vanishes, in a reference frame moving with the wave speed. Longuet-Higgins and Fox [8, 9] proposed that in general the flow near the crest be characterised by an inner length-scale
(2.1)
where g denotes gravity (see Figure 2). As x/l and y/l go to infinity the flow tends asymptotically to the Stokes corner-flow. At the crest itself (x/l, y/l)=(0,−1). The free surface is uniquely determined and the radius of curvature at the crest is found to be
R=5.15l (2.2)
see [8]. In deep water this crest-flow can be matched to the flow in the rest of the wave by defining a small parameter
(2.3)
where c0=(g/k)1/2 denotes the speed of linear gravity waves of length L=2π/k, and by identifying three regions of the wave as in Figure 3. In region I whose width is of order ![]() 2L, the flow is given by the asymptotic flow just described, to lowest order; and the length-scales are of order
2L, the flow is given by the asymptotic flow just described, to lowest order; and the length-scales are of order ![]() 2L. In region III the flow is that in the limiting Stokes wave to lowest order. Between these is a matching zone II, whose width is of order
2L. In region III the flow is that in the limiting Stokes wave to lowest order. Between these is a matching zone II, whose width is of order ![]() L. The process of matching, described in [9], leads
L. The process of matching, described in [9], leads
Figure 3. Sketch showing the three zones involved in the matching process. From Longuet-Higgins and Fox [9].
to the result that the parameter ![]() is related to the wave steepness ak by the simple formula
is related to the wave steepness ak by the simple formula
(2.4)
The lowest-order correction to the inner flow (that in Zone I) is of order ![]() 3(α−1), where α is the lowest positive root of the transcendental equation
3(α−1), where α is the lowest positive root of the transcendental equation
(2.5)
that is
α=1.8027. (2.6)
In other words, the theory predicts that in near-limiting waves, quantities will typically differ from their limiting values by amounts of order ![]() 2.4081, approximately.
2.4081, approximately.
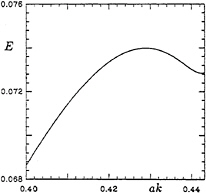
Figure 4. The energy density E in a steep progressive wave, as a function of the wave steepness ak.
A third prediction of the theory, relevant to what will follow, is that the energy density E of a steep Stokes wave of a given wavelength is not always an increasing function of the wave steepness ak, but goes through a sequence of maxima and minima before the maximum steepness (ak=0.4432); see Figure 4. The first maximum in E occurs when ak=0.4292.
3.
Crest instabilities
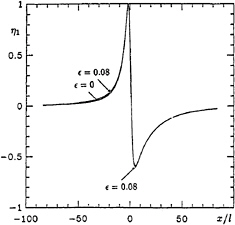
The normal-mode instabilities of the crest flow, that is to say those growing initially like eβt, where Re(β)>0, have been investigated by Longuet-Higgins and Cleaver (1994) [ 10], Longuet-Higgins, Cleaver and Fox (1994) [11] and Longuet-Higgins and Dommermuth (1996) [12]. The form of the lowest mode is shown in Figure 5. It has a peak elevation on the forward face of the crest, and a peak depression on the rear face. Because the perturbations are linearised, the displacement is normalised so as to make the maximum elevation equal to unity.
How are these crest instabilities related to the known instabilities of a steep Stokes wave in deep water?
4.
Superharmonic instabilities: deep water
Two kinds of normal-mode perturbations of steep Stokes waves can be distinguished, those that; are superharmonic, having the same space periodicity as the initial wave train, and those that are subharmonic, i.e. with a longer space periodicity. We pay attention first to the simplest superharmonic perturbations. It was first shown numerically by Tanaka (1983) [13] and confirmed theoretically by Saffman (1985) [14] that the simplest superharmonic normal modes of a deep-water Stokes wave became unstable at a wave steepness ak corresponding to the first maximum of the energy density E (see Section 2). Thus the square of the eigenfrequency σ=iβ passes from positive to negative values at this value of the wave steepness ak. It was shown by Longuet-Higgins, Cleaver and Fox [11] that the values of β1 for crest instabilities were asymptotic to the rates of growth calculated by Tanaka [13]. No data for the eigenfunctions were published by Tanaka, but the calculations have been carried to higher values of ak and the corresponding eigenfunctions computed in a more recent paper [15].
To verify the accuracy of the unperturbed surface profiles, we show in Figure 6 the radius of curvature R at the crest of steep waves. The length l being defined by equation (2.1), it will be seen that the values of R/l lie practically on a straight line,
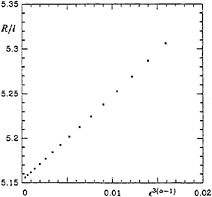
Figure 6. The scaled radius of curvature R of a steep Stokes wave, plotted against ![]() 3(α−1). From Longuet-Higgins and Tanaka [15].
3(α−1). From Longuet-Higgins and Tanaka [15].
whose equation is
R/l=5.1525+9.5 ![]() 3(α−1). (4.1)
3(α−1). (4.1)
In Figure 7a we see profiles of the lowest unstable mode at three different values of the parameter ω=1−qc/qt, where qc and qt are the particle speeds at the crest and the trough respectively. The range of ω is from 0 to 1, with ω=1 corresponding to the steepest wave. (The three values ω=0.84, 0.88 and 0.92 correspond to ak=0.4331, 0.4375 and 0.4405 respectively). As the wave steepness increases the perturbations become narrower. When, however, the profiles are plotted with the scaled coordinate x/![]() 2 as in Figure 7b, they appear to converge to the same asymptotic form as shown in Figure 5. This earns them the name “crest instabilities.”
2 as in Figure 7b, they appear to converge to the same asymptotic form as shown in Figure 5. This earns them the name “crest instabilities.”
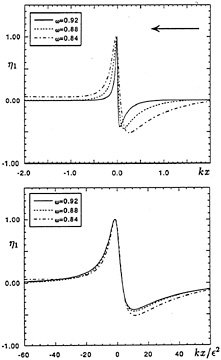
Figure 7. Profiles of the lowest superharmonic instability η1 in a progressive deep-water wave at three wave steepness ak=0.4331, 0.4375 and 0.4405. (a) Unscaled, and (b) scaled horizontally by l=q2/g. From Longuet-Higgins and Tanaka [15].
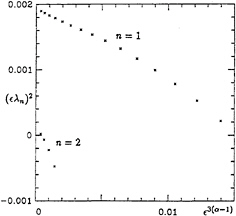
Figure 8. Squared rates of growth of the two lowest normal-mode instabilities of deep-water waves. From Longuet-Higgins and Tanaka [15].
The squared growth-rates ![]() are shown in Figure 8, scaled by factor
are shown in Figure 8, scaled by factor ![]() 2. For the smallest values of
2. For the smallest values of ![]() , where the asymptotic theory applies, the squared frequencies do indeed depend linearly on
, where the asymptotic theory applies, the squared frequencies do indeed depend linearly on ![]() 3(α−1).
3(α−1).
At larger values of ![]() the squared grown-rate diminishes, and passes through zero at the steepness ak corresponding to the first maximum of E. At this point the form of the perturbation tends towards a pure phase-shift; see Section 5.
the squared grown-rate diminishes, and passes through zero at the steepness ak corresponding to the first maximum of E. At this point the form of the perturbation tends towards a pure phase-shift; see Section 5.
5.
Instabilities in solitary waves
Historically there has been some interplay between studies of solitary waves in shallow water and waves in deep water. Moreover, the corresponding calculations for solitary waves can often be carried to greater accuracy, yielding new or stronger conclusions.
Early calculations of the highest solitary wave have been summarised in a review paper by Miles (1980, Section 4) [16]. Probably the most accurate calculation was later performed by Williams [7] whose numerical results have been confirmed to at last five decimal places by Evans and Dorr [17].
The most interesting theoretical results, however, concern the behaviour of solitary waves whose height is somewhat less than the maximum. In 1974 it was discovered that many integral properties of solitary waves, including their speed and total energy, attain maxima at heights less than the limiting wave height (Longuet-Higgins and Fenton) [ 18]. These authors used a series expansion with convergence accelerated by Padé approximants. Their conclusion was later confirmed by Byatt-Smith and Longuet-Higgins [19] using an integral equation method. The latter also gave a physical explanation. As with periodic waves in deep water, all the calculations experienced difficulties for waves approaching the maximum height.
An advance came with the introduction of a theory for the almost-highest wave [8, 9]. Besides the application to deep-water waves, Fox [20] in his Ph.D. thesis applied it also to solitary waves with similar results, namely that the speed c, height H, mass M, momentum (or impulse) I, and the potential and kinetic energies V and T, were all found to satisfy relations of the type
F=F1+A![]() ′3 cos (2.143 ln
′3 cos (2.143 ln ![]() ′–B)+0(
′–B)+0(![]() ′4) (5.1)
′4) (5.1)
where a suffix 1 denotes the value for the highest wave and ![]() ′ is a small parameter defined by
′ is a small parameter defined by
(5.2)
similar to (2.3) except that here c0 denotes the linear phase-speed (gh)1/2 of waves in shallow water of depth h. Note that owing to the term ln ![]() ′, which tends to −∞ as the limiting wave is approached, the right-hand side of (5.1) is oscillatory in
′, which tends to −∞ as the limiting wave is approached, the right-hand side of (5.1) is oscillatory in ![]() ′. In fact, we can write
′. In fact, we can write
(F–F1)=![]() ′3A cos(θ–B) (5.3)
′3A cos(θ–B) (5.3)
where θ=2.143 ln![]() and A and B are amplitude and phase constants. In Fox [20] the constants A and B were evaluated, in general, to only one significant figure, and the results were not published at that time. A more accurate computation of the integral quantities, described by Longuet-Higgins and Tanaka [15], has allowed the constant in (5.3) to be calculated to at least two significant figures (Longuet-Higgins and Fox) [21]. The results are summarised in Figure 9. Here the vectors are shown
and A and B are amplitude and phase constants. In Fox [20] the constants A and B were evaluated, in general, to only one significant figure, and the results were not published at that time. A more accurate computation of the integral quantities, described by Longuet-Higgins and Tanaka [15], has allowed the constant in (5.3) to be calculated to at least two significant figures (Longuet-Higgins and Fox) [21]. The results are summarised in Figure 9. Here the vectors are shown
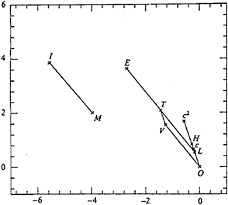
Figure 9. A plot of Δc, ΔH, ΔM, ΔI, ΔV, ΔT, ΔE and ΔL for a solitary wave (see equations (5.1) to (5.4)). From Longuet-Higgins and Fox [21].
ΔF=AeiB (5.4)
graphically for each of the quantities F= c, H, M, I, V and T; also the total energy E=V+T and the Lagrangian density L= T–V. It will be noticed that there are certain (exact) collineations. In particular L and H lie on the line Oc through the origin O. IM is not parallel to ET.
For many years it had been thought, on the basis of the approximate KortewegdeVries equation, that all solitary waves were essentially stable to small perturbations. But Tanaka [22] showed numerically that the lowest-order perturbation of a solitary wave becomes unstable at the wave height for which the total energy E is a maximum—just as for waves in deep water. More recently (Longuet-Higgins and Tanaka [15]) the calculations have been carried to even steeper waves, and it has been shown that the second mode also becomes unstable at the next stationary value of E, the first positive minimum. The same is no doubt true of the higher modes. The eigenfunctions of the two lowest modes are also calculated accurately. Figure 10 shows the lowest mode plotted against the scaled coordinate x/![]() ′2 at four successive wave heights approaching the limiting height. The profiles appear to be converging to the same limiting
′2 at four successive wave heights approaching the limiting height. The profiles appear to be converging to the same limiting
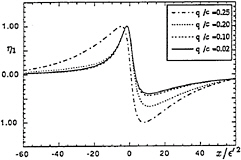
Figure 10. Scaled profiles of the lowest mode of instability η1 of the solitary wave, at four different wave heights. From Longuet-Higgins and Tanaka [15].
form as for the deep-water wave (Figure 6b).
When on the other hand (![]() ′λ1)2 approaches zero, which is at the first stationary value of E, the eigenfunction tends to a pure phase-shift. This is illustrated by Figure 11 which shows the first mode η1 when q/c=0.25, corresponding to
′λ1)2 approaches zero, which is at the first stationary value of E, the eigenfunction tends to a pure phase-shift. This is illustrated by Figure 11 which shows the first mode η1 when q/c=0.25, corresponding to ![]() ′=0.2287 or H/d=0.7842, only marginally above the critical wave steepness. This is compared to a pure phase-shift of the same solitary wave (which is just proportional to the gradient of the surface profile).
′=0.2287 or H/d=0.7842, only marginally above the critical wave steepness. This is compared to a pure phase-shift of the same solitary wave (which is just proportional to the gradient of the surface profile).
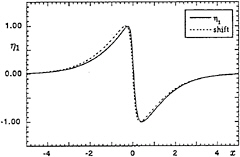
Figure 11. Comparison of the lowest mode of instability of the solitary wave at a wave height close to the first energy maximum, compared to a pure phase-shift. From Longuet-Higgins and Tanaka [15].
The form of the second mode is shown in Figure 12, scaled similarly. Here
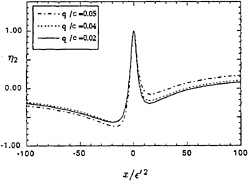
Figure 12. Scaled profiles of the second mode of instability η2 for solitary waves at three different wave heights. From Longuet-Higgins and Tanaka [15].
also there appears to be convergence as q/c → 0. Figure 13 shows the behaviour of the growth rates λ1 and λ2. As predicted, when plotted against ![]() ′[3(α–1)] the scaled quantities
′[3(α–1)] the scaled quantities ![]() ′λ1 and
′λ1 and ![]() ′λ2, and their squares, behave linearly as
′λ2, and their squares, behave linearly as ![]() ′ → 0. Further data and comparisons with deep water waves and with the asymptotic theory will be found in Longuet-Higgins and Tanaka [15].
′ → 0. Further data and comparisons with deep water waves and with the asymptotic theory will be found in Longuet-Higgins and Tanaka [15].
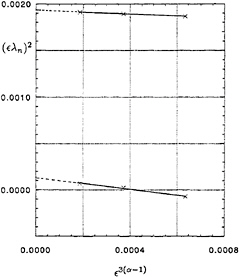
Figure 13. Squared growth-rates, scaled, for the two lowest instabilities of the solitary wave. From Longuet-Higgins and Tanaka [15].
6.
Finite-amplitude development of crest instabilities
We have so far described only the initial, infinitesimal stage of a crest instability. Because of the rapid rate of growth of the lowest mode, this instability soon becomes nonlinear. The later stage of development can however be followed by a boundary-integral, time-stepping technique, as was first done for solitary waves by Tanaka et al. [23]. However, the nonlinear development was found to depend crucially on the sign of the initial disturbance. The same perturbation, if reversed in sign, led not to wave breaking but to a smooth transition of the original wave to a lower solitary wave having almost the same total energy. This is possible because of the energy maximum occurring at an intermediate wave height. The speed and momentum of the final wave were slightly different from their original values, the difference being made up by a slight disturbance trailing the main wave.
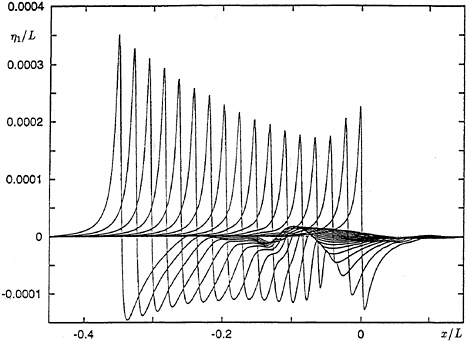
Similar calculations have been performed for deep-water waves by Longuet-Higgins and Dommermuth [12] following a less complete study by Jillians [24]. Here the initial perturbation was that given by the asymptotic theory of Section 3, which approximates the actual normal-mode instability. Figure 14 shows the growth of the lowest mode, for a “positive” initial perturbation, that is to say one with a maximum on the forward face, and Figure 15 shows overturning of the surface profile, as expected. The growth-rates of the “positive” and “negative” perturbations are compared with the linear theory in Figure 16.
The profile resulting from the “negative” initial disturbance developed as in Figure 17, with a transition to a wave of lower amplitude and almost the same total energy. Unlike the solitary wave, however, the wave profile then returned almost to its original form, in a kind of nonlinear recurrence; see Figure 18 where the crest-to-trough wave height is plotted as a function of the time t. One might say that this recurrence phenomenon resembles that displayed by the solitary wave, except that with the solitary wave the period of recurrence is infinite.
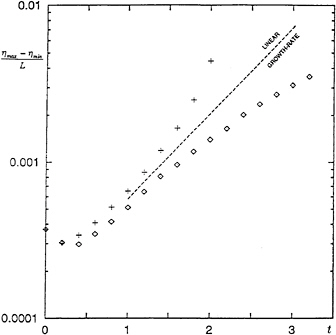
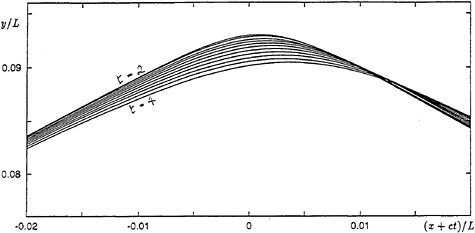
Figure 17. Nonlinear development of the surface profile resulting from a negative perturbation. From Longuet-Higgins and Dommermuth [12].
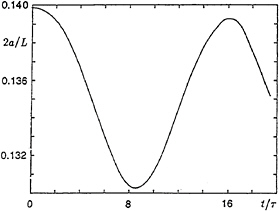
Figure 18. The crest to trough wave amplitude of a deep-water wave as a function of the time t following a negative perturbation. From Longuet-Higgins and Dommermuth [12].
7.
Wave-generated ripples
We now discuss some of the unexpectedly important effects of surface tension on gravity waves having wavelengths even as great as 2m.
A typical photograph of short gravity waves (Figure 19a) shows a train of ripples riding just ahead of the wave crests. How are these “parasitic capillary waves” generated? An early theory [25] suggested that they were due to surface-tension
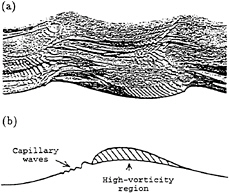
Figure 19. (a) Photograph of short gravity waves showing wave-generated ripples (b) sketch of turbulent zone beneath the wave crest. After Ebuchi et al. [26].
forces acting near the crest of a steep gravity wave, where the surface curvature is localised. As seen in a reference frame moving with the phase-speed c, the waves appear as a steady current in the opposite direction—the localised pressure near the crest then produces ripples upstream of the crest, that is on the forward face of the wave.
A modern form of the theory, which includes accurate calculations of the gravity-wave profile, has recently been given Longuet-Higgins [27]. Figure 20, from that paper, shows the curvature κ in steep Stokes wave as a function of the distance s from a wave crest, measured along the surface. Clearly κ is concentrated near the crests. In the troughs, κ is smaller and almost uniform; the profile is roughly a circular arc.
The influence of gravity on the ripples, which affects their speed, enters through the effective gravitational acceleration g*. This includes not only the component of gravity normal to the surface but also the centrifugal acceleration arising from the speed q of the current and the curvature κ of the surface, that is
g*=g cos θ–κq2 (7.1)
where θ is the surface inclination. Figure 21 shows that g* may vary from as little as 0.63g at the wave crests to 1.3g in the troughs. Ripples will be generated, accord-
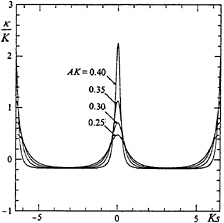
Figure 20. The surface curvature κ in steep gravity waves, as a function of the distance s from the wave crest, measured along the free surface. From [27].
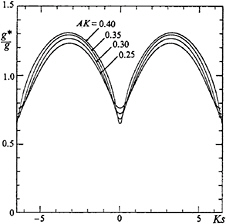
Figure 21. The effective gravity of g* for a particle at the surface of a deep-water gravity wave, as a function of distance s along the profile. From [27].
ing to the linear theory, only when the local current-speed q exceeds the minimum phase-speed cmin of capillary-gravity waves, given by
cmin=(4g*T)1/4 (7.2)
where T denotes surface tension (the density being unity). For low (subcritical) gravity waves it is always true that q>cmin, but for steep (supercritical) gravity waves there
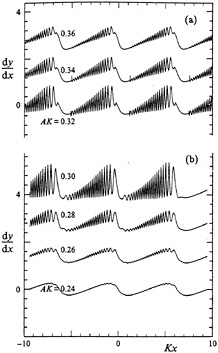
Figure 22. The calculated surface slope dy/dx in a wave of length 8.0 cm (b) Subcritical wave steepness, (b) supercritical. From [27].
is a region near the crest where q<cmin. This part of the wave profile is non-resonant or “hard”. It is bounded by two caustics, at which q=cmin. The rest of the wave profile, where ripples can be generated is resonant or “soft”. Figure 22 shows the calculated surface slope dy/dx of a typical wave of length L=8.0 cm, at difference steepnesses AK of the gravity wave. The wave travels to the left and the crests are at Kx=–2π, 0 and 2π, where K=2π/L. Viscous damping is included in the calculation. The ripples appear mainly on the forward face of the wave, as expected. The critical wave steepness is AK=0.32. In Figure 22a, all the waves are subcritical, and the ripple steepness clearly increases with AK. In Figure 22b the gravity waves are supercritical and the ripple steepness diminishes with AK. Thus the ripple steepness is a maximum when AK=(AK)crit.

Figure 23 shows a comparison between the calculated surface slopes in a gravity wave of period 0.20s (wavelength L=6.5 cm) and the slopes measured by Cox [28] at a fixed point in his laboratory tank (without wind). There is generally good agreement. Some differences may be due to the fact that the waves were not perfectly steady, as can be seen from Figure 23a.
Figure 24 shows a similar calculation for the 10 cm waves in Figure 19. The waves are subcritical. The wavelengths of the ripples in the main train correspond very

well. However, there is some discrepancy in the surface profiles immediately ahead of the crest, which is due to nonlinearity, as we shall now see.
8.
Capillary jumps
The theory in Section 7 was based on the assumption that the parasitic capillaries were small perturbations superposed on nonlinear gravity waves, and that the slopes relative to the unperturbed gravity wave were small. Observations suggest that the assumption is not always justified. There is one feature near the crest, however, which may be understood in terms of a type of nonlinear capillary-gravity wave discovered recently, namely a solitary wave on deep water (Longuet-Higgins [29,30]; Vanden-Broeck and Dias [31]).
Figure 25 shows a one-parameter family of solitary waves each determined uniquely by its maximum surface slope αmax or by the depth H of the central trough relative to the level at infinity. As H decreases towards zero the tails develop more oscillations, and the whole wave train resembles a packet of infinitesimal waves with phase and group velocity equal to cmin; see Longuet-Higgins [32]. Figure 26 shows that as H increases from zero the speed c of the solitary wave is a decreasing function of H, being generally less than cmin.
Imagine then a non-uniform surface current U as in Figure 27, where U decreases towards the right. If U is everywhere slightly less than Cmin, it may be possible for a steady wave to be superposed on the current such that on the left it has the character of a solitary wave of speed c1=|U1|, and on the right it is like a solitary wave
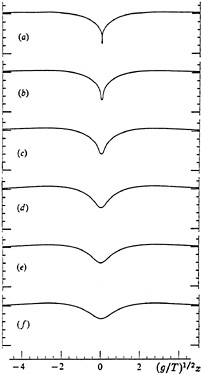
Figure 25. A family of capillary-gravity solitary waves. From Longuet-Higgins [28].
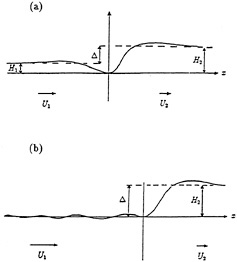
Figure 27. Sketch of a capillary jump on a non-uniform stream U (a) A trapping jump, (b) a leaky jump. From Longuet-Higgins [33].
of slower speed c2=|U2| and therefore of greater height H2. Assuming the two halves can be joined smoothly at the trough near x=0, then the difference in level between the two sides at large distances from the origin will be
Δ=H2–H1. (8.1)
In an extreme case the solitary wave on the right may have the limiting form shown in Figure 25a, and then
H2=1.49 (T/g)1/2. (8.2)
This represents the maximum value of Δ. Provided the current-speed U1 on the left is also less than cmin, the energy will be trapped near x=0 as in Figure 25c, giving a “trapping jump”. If on the other hand U1≤cmin we may expect an unlimited train of waves on the left, giving a “leaky jump”. A common situation in which to find a velocity gradient such as described is on the forward face of a progressive gravity wave; see Figure 27c. For steep Stokes waves,
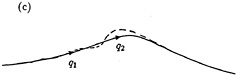
Figure 27c. Sketch of a capillary jump on a Stokes wave.
dq/ds is typically a minimum not far from the wave crest. Therefore we may expect to find a capillary jump in such a situation. Even though the wave is supercritical in the sense of Section 7 and the crest is “hard” to infinitesimal waves, nevertheless a half-solitary wave may occur which, in the case of a leaky jump, can produce a train of parasitic capillary waves.
9.
Effect of surface tension on crest instabilities
We are now in a position to understand the influence of surface tension on the crest instabilities described in Sections 2 to 6.
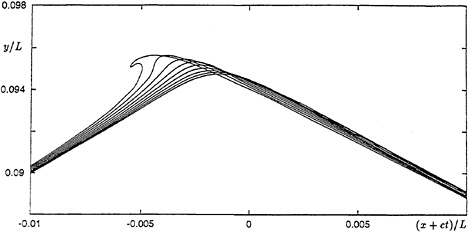
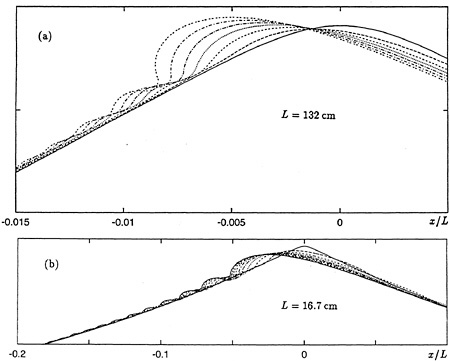
If surface tension is applied artificially to the unstable wave in Figure 15 at time t=0 and if the wavelength L is 132 cm, the wave develops not as in Figure 15 but as in Figure 28a. The crest does not overturn, but instead forms a capillary jump, with a few ripples or parasitic capillaries “upstream”. Figure 28b shows a similar result when L=16.7 cm. Surface tension dominates the motion. It makes little difference when the initial perturbation is absent altogether; in each case the capillary jump develops in a similar way, though at a somewhat lower rate.
fOur conclusion is that the crest instability is a comparatively weak instability, at these short gravity wavelengths. An example of surface tension acting on a fast-growing gravity-wave instability will be given in Section 11.
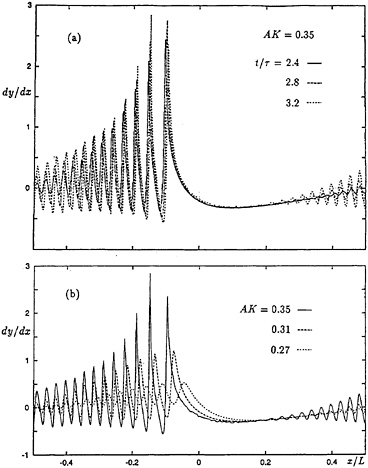
Figure 29. Computed surface slopes of an 8.0 cm gravity wave when surface tension is applied at time t=0. (a) AK=0.35, t/τ=2.4, 2.8 and 3.0 (τ=wave period); (b) AK =0.27, 0.31 and 0.35, t/τ=3.2. From Longuet-Higgins and Dommermuth [34].
With the same time-stepping technique we are able to carry out a fully nonlinear calculation of the growth of parasitic capillary waves on a regular, periodic train of Stokes waves. For example we show in Figure 29 the surface slope dy/dx corresponding to a Stokes wave of length L=8.0 cm, when surface tension is applied at time t=0. Compare Figure 22. For the nonlinear calculation there is no need to use a WKB approximation as in the linear theory. The two kinds of calculations are compared in Figure 30, where the maximum ripple slope s has been plotted against the initial gravity-wave steepness ak. It can be seen that whereas in the linear theory s has a maximum at the critical value of ak, in the nonlinear theory s increases monotonically with ak throughout the whole range.
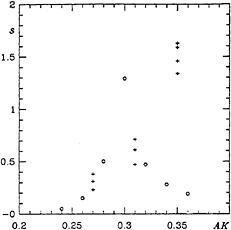
Figure 30. Maximum slope s of capillary waves on an 8.0 cm gravity wave as a function of ak. Comparison of linear theory (○) and nonlinear computation (+).
A numerical simulation of Duncan et al.'s experiment has been carried out by Yao et al. (1996) [45] using a boundary-integral technique embodied in their routine LONGTANK. The initial conditions at the wave-maker are those of Duncan et al. [1]. Without surface tension, the focussed wave overturns and breaks, as in a plunging breaker. If a realistic value T=74 dyne/cm is applied then the surface does not overturn but the profiles of Figures 1a and 1b of Duncan et al. [1] are accurately reproduced.
10.
Viscous effects
Capillary waves will, because of their high rate of damping, produce a strong, rectified, shearing current at the free surface, as proved in Longuet-Higgins [35]. The vorticity in this shear will be convected back towards the crest, and the current so produced may become unstable (Longuet-Higgins 1994) [36]. Alternatively the flow can separate at the toe of the jump, producing a strong free shear layer which is unstable. This seems to be the explanation for the Type 2 ripples above the toe of the bulge in Figure 1 above. As shown in Longuet-Higgins [36] the ripples represent “vortex waves,” which soon break up into turbulence (c.f. Duncan et al. [1]). Thus the wave can effectively break without the free surface ever overturning. It is also possible that some spilling breakers may be initiated in this way.
In [36] only two-dimensional instabilities of a simple shear flow were considered. It is very likely that the surface current is unstable to three-dimensional disturbances also, and that these will eventually dominate. This would tend to explain the “streamwise vortices” that Ebuchi et al. [26] have observed in the crests of 10 cm waves.
On larger scales, vorticity may be injected by an overturning wave, simply as a result of the difference in horizontal velocity between the forwards jet and the forward face of the wave onto which it falls. This way of initiating a spilling breaker is qualitatively similar to that described above.
Lin and Rockwell [37] have carried out careful experiments on the evolution of breaking waves forced by a submerged aerofoil. They have found that, with one experimental configuration, the dominance of capillary wave effects which is exemplified in Duncan et al.'s photographs [1] may be limited to a certain range of Froude numbers (based on the chord of the aerofoil). Even within this range the surface profile and velocity field are extremely sensitive to small changes in the Froude number. It should be commented that the Weber number must also be highly relevant to the flow.
11.
Breaking in modulated wave trains
On a scale larger than 2m, the capillary and viscous effects that were discussed in Section 7 to 8 become less important. The problem then is, how to give a rational account of breaking in a random field of gravity waves in an ideal fluid, and without the immediate influence of the wind.
In random seas there are two interesting limiting cases. The first is when the spectrum is broad, containing energetic short waves superposed on the dominant waves. In such a case the shorter waves can be shown theoretically [38] and experimen-
tally [39] to steepen and break on the crests of the dominant waves. A statistical model of whitecaps has been constructed on this basis [40, 41].
The second important limiting case is when the wave spectrum is sufficiently
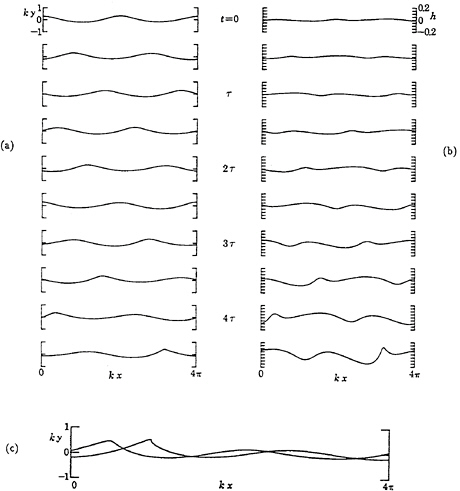
Figure 31. The nonlinear development of a subharmonic instability in a deep-water wave of initial steepness ak=0.25. (a) Surface profiles, (b) the perturbation, enlarged×20, (c) final stage of wave breaking. From Longuet-Higgins and Cokelet (1978) [42].
narrow that the surface can be thought of as a more or less slowly modulated wave train. The best-known example, in two dimensions, is the subharmonic Benjamin-Feir instability, in which the modulation of the waves gradually increases and may lead to breaking. Figure 31 shows the nonlinear development of a wave group containing just two waves, studied numerically by Longuet-Higgins and Cokelet (1978) [42]. Starting with a nearly uniform wavetrain of steepness ak=0.25, the modulation gradually grows until after about 4.5 wave periods one of the waves suddenly develops a local instability, increases in height and overturns, all in about one-sixth of a wave period. The fluctuation in steepness of the individual waves is shown in Figure 32, as a function of time.
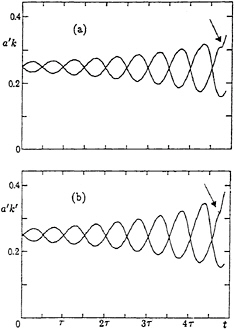
It is important to distinguish between the initial wave steepness
(ak)IN=0.25, (11.1)
the steepness at the onset of breaking
(ak)ON=0.32 (11.2)
and the wave steepness at overturning
(ak)OV=0.38. (11.3)
Similar results have been found in laboratory experiments by Bonmarin [43]. It is notable that the abrupt change in the character of the flow at the onset of breaking occurs at a much lower steepness than any of the superharmonic or crest instabilities discussed earlier which can occur only above the energy maximum at ak=0.429. Nevertheless the shapes are very similar.
An interesting unsolved question is: what determines the onset of breaking?
Recently Yao et al. [44] have presented data on the inception of wave breaking in random seas, obtained with their numerical program LONGTANK. A summary is in Figure 5 of Yao et al. [45], which suggests that in water of arbitrary uniform depth breaking tends to begin when the horizontal particle velocity q is about equal to the local group-velocity cg.
Here some caution must be exercised, since for nonlinear waves the concept of group-velocity is not well-defined. A discussion of various definitions is given by Peregrine and Thomas (1979) [46]. Their Figure 8 shows that when ak>0.3 the various possibilities differ significantly from one another (and from the linear group-velocity) especially in deep water.
We may note that for solitary waves, where the group-velocity must presumably be defined as equal to the phase-speed c, the onset of crest instabilities actually occurs in waves of less than the limiting height (see Section 5). Hence the relation q=cg does not hold exactly.
It may also be noted that in order for the particle velocity in a deep-water wave to exceed one-half the phase-speed c, we find by calculation that the wave steepness ak must exceed 0.3490, not 0.32 as in Figure 32. This might be attributed to a nonlinear increase in the group velocity, if one adopted a suitable definition of cg. However, we see from Figure 32 that the wave immediately preceding the wave that breaks does not itself break, although it attains a steepness of 0.343. Hence it seems that the apparent relation of the horizontal particle speed to the group velocity can be true only approximately, or else in a statistical sense. Nevertheless the question of how and why waves break in a modulated group remains one of the most important unsolved problems.
What is the effect of surface tension on the breaking of a modulated wave train? We can repeat the calculation by Longuet-Higgins and Cokelet [42] of a two-wave subharmonic instability but now including surface tension. If we assume a wavelength L=66 cm, for example, (the horizontal periodicity being 2L) then at an initial steepness ak=0.25 capillarity has a negligible effect, at first. But in the final stage of overturning, seen in Figure 33, the form of the jet
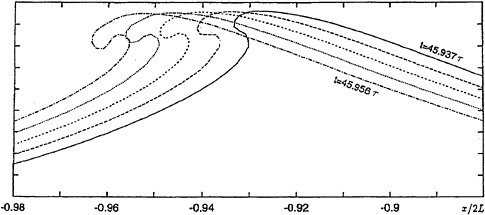
is considerably modified by surface tension. Unlike the crest instabilities and the gentle breaker seen in Duncan's experiments, here the jet is sufficiently energetic that capillarity is unable to prevent overturning of the surface, even when the wavelength L is smaller.
12.
Conclusions
-
The crests of steep periodic gravity waves conform accurately to the asymptotic theory for the almost-highest wave, having a radius of curvature R given by equation (2.7) with l=q2/2g.
-
The simplest superharmonic perturbations of Stokes waves, which become unstable at steepnesses ak corresponding to the first energy maximum, at first are simple phase-shifts of the whole wave. As ak increases the instabilities become more and more concentrated near the crest. Their length-scale is proportional to q2/2g, and their form and rate of growth is in agreement with the lowest instability of the almost-highest wave. They may appropriately be called “crest instabilities”.
-
Similar results hold, with greater accuracy, for solitary waves in shallow water. Here the crest instabilities are the only normal-mode instabilities of the wave as a whole.
-
The nonlinear development of a crest instability depends crucially upon the sign of the initial, infinitesimal disturbance. Positive perturbations lead to overturning and plunging breakers, negative perturbations lead to a transition to a lower wave of almost the same energy, then to a periodic recurrence—in deep-water. In shallow water the period of the recurrence is infinite.
-
Surface tension has a drastic effect on steep gravity waves with lengths L up to 1.5m or more. Parasitic capillary waves appear on the forward face of the wave. A linear theory shows that the source of these ripples is the region of sharp curvature near the wave crest. For very steep (supercritical) gravity waves the waves are trapped between two caustics in the wave trough.
-
A nonlinear theory for parasitic capillary waves shows that a “capillary jump” can occur near the crest of a steep gravity wave. This can be thought of as the joining of two deep-water solitary capillary-gravity waves, of different height. The jump may be either trapping or leaky.
-
Viscous damping of the parasitic capillaries leads to the generation of a shearing current, which convects vorticity into the crest of the gravity wave, producing shear instability and turbulence. In short gravity waves this is called a “capillary roller”. In the experiments of Duncan
-
et al., the Type 2 capillaries seen above the edge of the jump before turbulent collapse can be interpreted as shear instabilities, or “vortex waves”.
-
Breaking in modulated wave trains (wave groups) occurs generally at lower wave steepnesses than in a uniform wave train. In a periodic group containing two waves (Figure 31) the onset of breaking occurred in a wave for which ak=0.32. Final overturning was at ak=0.38. There is no unique relation between the group velocity and the horizontal particle velocity at the onset of breaking.
-
Contrary to earlier conclusions, the initial crest bulge in the experiments of Duncan et al. is not a crest instability, since it occurs at a lower wave steepness, but resembles more the instability that occurs in a wave group. However the final form of a breaking wave is remarkably invariant, whether it arises from a crest instability or from a wave group. To find a rational theory for the onset of breaking waves in a group is a main unsolved problem.
Acknowledgements
The author's work has been supported by the Office of Naval Research under Contracts N00014–91–1582 and N00014– 91–1–0008.
References
1. Duncan, J.H., Philomin, V., Qiao, H. and Kimmel, J. 1994 The formation of a spilling breaker Phys. Fluids 6, S2.
2. Longuet-Higgins, M.S. 1974 Breaking waves—in deep and shallow water. Proc. 10th Symp. on Naval Hydrodynamics ( Cambridge, Mass.) U.S. Govt. Printing Off., pp. 597–605.
3. Cleaver, R.P. 1992 Instabilities of surface gravity waves. Ph.D. thesis, University of Cambridge, 224 pp.
4. Jenkins, A.D. 1994 A stationary potential-flow approximation for a breaking-wave crest J. Fluid Mech. 280, 335–347.
5. Shrira, V.I., Badulin, S.I. and Kharif, C. 1996 A model of water-wave “horse-shoe” patterns. J. Fluid Mech. 318, 375–405.
6. Michell, J.H. 1893 On the highest gravity waves on deep water. Phil. Mag. (5) 36, 430.
7. Williams, J.M. 1981 Limiting gravity waves in water of finite depth. Phil. Trans. R. Soc. Lond. A 302, 139–188.
8. Longuet-Higgins, M.S. and Fox, M.J.H. 1977 Theory of the almost-highest wave: The inner solution. em J. Fluid Mech. 80, 721–741.
9. Longuet-Higgins, M.S. and Fox, M.J.H. 1978 Theory of the almost-highest wave. II. Matching and analytic extension J. Fluid Mech. 85, 769–786.
10. Longuet-Higgins, M.S. and Cleaver, R.P. 1994 Crest instabilities of gravity waves. Part 1. The almost-highest wave. J. Fluid Mech. 258, 115–129.
11. Longuet-Higgins, M.S., Cleaver, R.P. and Fox, M.J.H. 1994 Crest instabilities of gravity waves. Part 2. Matching and asymptotic analysis. J. Fluid Mech. 259, 333–344.
12. Longuet-Higgins, M.S. and Dommermuth, D.G. 1996 Crest instabilities of gravity waves. Part 3. Nonlinear development and breaking. J. Fluid Mech. (in press).
13. Tanaka, M. 1983 The stability of steep gravity waves. J. Phys. Soc. Japan 52, 3047–3055.
14. Saffman, P.G. 1985 The superharmonic instability of finite-amplitude water waves. J. Fluid Mech. 159, 169–174.
15. Longuet-Higgins, M.S. and Tanaka, M. 1996 On the crest instabilities of steep surface waves. J. Fluid Mech. (in press).
16. Miles, J.W. 1980 Solitary waves. Ann. Rev. Fluid Mech. 13, 11–43.
17. Evans, W.A.B. and Dörr, U. 1991 New minima in solitary water wave properties close to the maximum wave. Rep. Phys. Lab., Univ. of Kent, Canterbury, U.K., 22 pp.
18. Longuet-Higgins, M.S. and Fenton, J.D. 1974 On the mass, momentum, energy and circulation of a solitary wave. II. Proc. R. Soc. Lond. A 340, 471– 493.
19. Byatt-Smith, J.G.B. and Longuet-Higgins, M.S. 1976 On the speed and profile of steep solitary waves. Proc. R. Soc. Lond. A 305, 175–189.
20. Fox, M.J.H. 1977 Nonlinear effects in surface gravity waves. Ph.D. thesis, Univ. of Cambridge, Sept. 1977, 90 pp.
21. Longuet-Higgins, M.S. and Fox, M.J.H. 1996 Asymptotic theory for the almost-highest wave. J. Fluid Mech. 317, 1– 19.
22. Tanaka, M. 1986 The stability of solitary waves. Phys. Fluids 29, 650– 655.
23. Tanaka, M., Dold, J.W., Lewy, M. and Peregrine, D.H. 1987 Instability and breaking of a solitary wave. J. Fluid Mech. 185 235–248.
24. Jillians, W.J. 1989 The superharmonic instability of Stokes waves in deep water. J. Fluid Mech. 204, 563–579.
25. Longuet-Higgins, M.S. 1963 The generation of capillary waves by steep gravity waves. J. Fluid Mech. 16, 138–159.
26. Ebuchi, N., Kawamura, H. and Toba, Y. 1987 Fine structure of laboratory wind-wave surfaces using an optical method. Boundary-Layer Met. 39, 133–151.
27. Longuet-Higgins, M.S. 1995 Parasitic capillary waves: a direct calculation. J. Fluid Mech. 301, 79–107.
28. Cox, C.S. 1958 Measurements of slopes of high-frequency wind waves. J. Mar. Res. 16, 199–225.
29. Longuet-Higgins, M.S. 1988 Limiting forms for capillary-gravity waves. J. Fluid Mech. 194, 351–375.
30. Longuet-Higgins, M.S. 1989 Capillary-gravity waves of solitary type on deep water. J. Fluid Mech. 200, 451–470.
31. Vanden-Broeck, J.-M. and Dias, F. 1992 Gravity-capillary solitary waves in water of infinite depth and related free-surface flows. J. Fluid Mech. 240, 549– 557.
32. Longuet-Higgins, M.S. 1993 Capillary-gravity waves of solitary type and envelope solitons on deep water. J. Fluid Mech. 252, 703–711.
33. Longuet-Higgins, M.S. 1996 Capillary jumps on deep water. J. Phys. Oceanogr. (in press).
34. Longuet-Higgins, M.S. and Dommermuth, D.G. 1996 Effects of surface tension on breaking waves, (submitted).
35. Longuet-Higgins, M.S. 1992 Capillary rollers and bores. J. Fluid Mech. 240, 659–679.
36. Longuet-Higgins, M.S. 1994 Shear instability in spilling breakers. Proc. R. Soc. Lond. A 446, 399–409.
37. Lin, J.C., and Rockwell, D. 1995 Evolution of a quasi-steady breaking wave. J. Fluid Mech. 302, 29–44.
38. Longuet-Higgins, M.S. 1987 The propagation of short surface waves on longer gravity waves. J. Fluid Mech. 177, 293–306.
39. Longuet-Higgins, M.S. 1990 Mechanisms of wave breaking in deep water, pp. 1–30 in Sea Surface Sound, ed. B.R.Kerman. Dordrecht, D.Reidel Publ. Co., 639 pp.
40. Longuet-Higgins, M.S. 1987 A stochastic model for sea surface roughness. I. Wave crests. Proc. R. Soc. Lond. A 410, 19–34.
41. Longuet-Higgins, M.S. 1991 A stochastic model of sea-surface roughness. II. Proc. R. Soc. Lond. A 435, 405–422.
42. Longuet-Higgins, M.S. and Cokelet, E.D. 1978 The deformation of steep surface waves on water. II. Growth of normal-mode instabilities. Proc. R. Soc. Lond. A 364, 1–28.
43. Bonmarin, P. 1989 Geometric properties of deep-water breaking waves. J. Fluid. Mech. 209, 405–433.
44. Yao, Y., Wang, P. and Tulin, M.P. 1994 Wave groups, wave-wave interaction and wave breaking: results of numerical experiments. Proc. 20th Symp. on Naval Hydrodynamics ( Santa Barbara, Calif.) 16 pp.
45. Yao, Y., Wang, P. and Tulin, M.P. 1996 Surface tension effects on breaking waves—LONGTANK simulation. Univ. of Calif. Santa Barbara, Ocean Eng. Lab., Tech. Rep. 95–132.
46. Peregrine, D.H. and Thomas, G.P. 1979 Finite-amplitude deep-water waves on currents. Phil. Trans. R. Soc. Lond. A 292, 371–409.