The Flow Field in Steady Breaking Waves
D.Coakley (David Taylor Model Basin, USA), J.Duncan (University of Maryland, USA)
Abstract
An experimental investigation of steady breaking waves produced by towing fully submerged two-dimensional hydrofoils at constant depth (d), speed (U) and angle of attack is presented. Measurements include the temporal evolution of streamwise and cross-stream profiles of the breakers and flow fields, obtained by particle image velocimetry, in the turbulent zone that rides on the forward face of the wave. (This zone is called the breaking region.) Disturbances on the streamwise profiles propagate downstream at a speed of roughly 0.65 times the speed of the breaker, while disturbances on the cross-stream profiles do not appear to propagate. The wavenumbers, frequencies, phase speeds and amplitudes of the dominant disturbances in the cross-stream profiles increase as the breaker strength is increased (by decreasing the depth of the foil below the free surface). In order to explore the effect of scale on the above results, experiments are performed with three foils with chords of 15, 20 and 30 cm at the same values of Froude number (where ![]() g is the acceleration of gravity) and d/c. When the results are nondimensionalized using the time scale 2πU/g and the length scale 2πU2/g, it is found that as the scale is increased the frequencies and wavenumbers decrease and the disturbance amplitude increases. The phase speed of these disturbances nondimensionalized by the foil speed does not change with scale. One instantaneous flow field and one mean flow field obtained by averaging 10 instantaneous flow fields are presented for a breaker generated by the 15-cm foil. The development of a shear layer between the nearly stagnant fluid in the breaking region and the fast-moving underlying fluid is clearly seen in the average flow field. This shear layer grows in thickness with distance from the leading edge of the breaking region and significant downstream flow appears at the free surface upstream of the wave crest.
g is the acceleration of gravity) and d/c. When the results are nondimensionalized using the time scale 2πU/g and the length scale 2πU2/g, it is found that as the scale is increased the frequencies and wavenumbers decrease and the disturbance amplitude increases. The phase speed of these disturbances nondimensionalized by the foil speed does not change with scale. One instantaneous flow field and one mean flow field obtained by averaging 10 instantaneous flow fields are presented for a breaker generated by the 15-cm foil. The development of a shear layer between the nearly stagnant fluid in the breaking region and the fast-moving underlying fluid is clearly seen in the average flow field. This shear layer grows in thickness with distance from the leading edge of the breaking region and significant downstream flow appears at the free surface upstream of the wave crest.
1
Introduction
A number of authors have investigated steady two-dimensional breaking waves produced by hydrofoils moving at constant depth, speed and angle of attack. Battjes and Sakai [1] performed LDV measurements of the flow fields of two such breakers. They found the wake to behave like the momentum-deficient wake of a two-dimensional body in an infinite fluid. Duncan [2, 3, 4] measured the mean breaker shape and the mean flow field in the wake for a number of experimental conditions. The turbulent region of fluid riding on the forward face of the wave was defined as the breaking region. It was found that the drag associated with the breaking process correlated with the downslope component of the weight of the breaking region. The magnitude of the drag due to breaking was found to range from about 1.0 to 3.0 times the maximum drag that could be associated with a nonbreaking wavetrain. Cointe and Tulin [5] performed a theoretical analysis of these waves. The theory was based on a mixing-zone model of the breaker and used some of the experimental data of Duncan to determine the constants of the model. The results were consistent with Duncan's data and explained a number of dynamical effects. The first flow field measurements in the breaking region of these waves was presented by Lin and Rockwell [6, 7]. From analysis of several instantaneous flow fields obtained by particle image velocimetry, they were able to verify that the flow in the breaking region was nearly stagnant as was assumed by other investigators.
Surface ripples generated by these breaking waves have also been investigated previously. Banner and Fooks [8] used two wire-type wave-height gauges to obtain two-point statistics both upstream and downstream of the wave crests. Two breaking waves were studied (wavelengths of 0.2m and 0.33m). Radar returns from these waves were also obtained. It was found that the frequency spec
tra at all spatial locations showed the same peak frequency in a given wave and that this frequency decreased with the wavelength of the breaker. The wavelength of these fluctuations increased with the wavelength of the breaker. These disturbances were found to propagate downstream. More recently, Walker, Lyzenga, Ericson and Lund [9] studied surface ripples on waves generated with a submerged hydrofoil in a recirculating water channel. They used a single flow speed of 108 cm/sec and studied three waves of different breaking strengths by varying the angle of attack of the foil. Surface shape measurements in the breaking region and in the wake were made photographically with a laser light sheet (aligned with the flow direction) and a video camera. The temporal sampling rate of this system was 30 images per second. Radar returns from these breakers were also measured. It was found that the variance in surface height fluctuations was largest at the breaking region and decreased rapidly with distance behind the breaking wave crest. The temporal frequency of these fluctuations was low at the toe of the breaker and about 8 Hz further back on the breaker. This frequency remained constant with distance downstream in the wake. The variation of these frequencies with breaker strength was not reported, presumably because of the rather low temporal sampling frequency used in this work. It was also found that the wavenumber of the ripples decreased with distance downstream. The fact that the frequency was constant with distance downstream while the amplitude and wavenumber decreased lead the authors to speculate that the ripples were behaving like surface waves propagating on a spatially varying current, which has speeds of 0 at the breaking region and 108 cm/sec in the far wake.
In the present work, both the surface ripples and flow fields in steady, hydrofoil-produced breaking waves are investigated. The waves are generated by three NACA 0012 hydrofoils with chords (c) of 15, 20 and 30 cm. Waves were generated with with one towing speed (U) and three depths of submergence (d) for each foil. The conditions were chosen with a single Froude number ![]() and three values of d/c that were used for all the experiments. In this way, the effect of experimental scale was investigated. The surface ripple measurements were taken from high-speed movies of the breakers. Both streamwise and cross-stream profiles were taken. The flow field in the breaking region was measured with particle image velocimetry for the weaker breaking conditions. Unlike the studies of Lin and Rockwell [6, 7] many realizations of the flow field were measured in order to obtain average statistics of the flow fields. In addition, the flow field in the wake of the breakers was also measured to obtain the drag due to breaking. At the time of this writing the analysis of the data is incomplete. In the following the data presented is primarily from the experiments with the 15- and 20-cm foils and is centered on results from streamwise profiles. Some data from cross-stream profiles and limited PIV measurements in the breaking region is also presented.
and three values of d/c that were used for all the experiments. In this way, the effect of experimental scale was investigated. The surface ripple measurements were taken from high-speed movies of the breakers. Both streamwise and cross-stream profiles were taken. The flow field in the breaking region was measured with particle image velocimetry for the weaker breaking conditions. Unlike the studies of Lin and Rockwell [6, 7] many realizations of the flow field were measured in order to obtain average statistics of the flow fields. In addition, the flow field in the wake of the breakers was also measured to obtain the drag due to breaking. At the time of this writing the analysis of the data is incomplete. In the following the data presented is primarily from the experiments with the 15- and 20-cm foils and is centered on results from streamwise profiles. Some data from cross-stream profiles and limited PIV measurements in the breaking region is also presented.
In the following the details of the experimental methods are presented in Section 2. This is followed in Section 3 by the results and discussion. Finally, the conclusions are given Section 4.
2
Experimental Details
2.1
Tank and hydrofoils
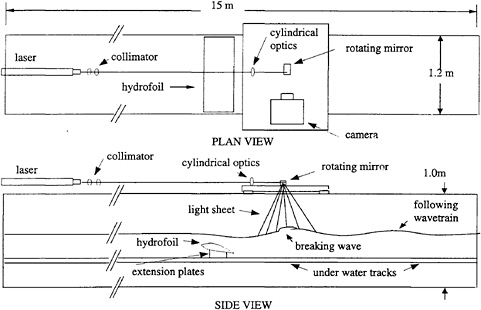
The experiments were performed in a tank that is 15 m long, 1 m deep, and 1.2 m wide, see Fig. 1. For visualization purposes, the side walls of the tank are composed of tempered glass. The tank includes an underwater towing system for the hydrofoils and an above-surface instrument carriage that moves with the breaking wave. The tracks for the subsurface towing system are 14 meters long and are made of 3.8 cm stainless steel angle. These tracks are positioned at a nominal distance of 48 cm from the tank bottom. Measurements showed that the rail depth variation did not exceed ±0.75 mm in the center 8 m of the tank where the wave measurements were taken. The force for moving the foil through the water is supplied by a cable and pulley towing system that is powered by an electric motor and gear box located below the tank at one end (see Figure 1). The foil can be towed at speeds up to 1.2 m/s. The same motor that tows the hydrofoils also tows the above-surface instrument carriage. The carriage travels on two precision tracks, one on each side of the tank, and is supported by hydrostatic oil-film bearings. These bearings result in a very low vibration level for the carriage which serves as a platform for the camera and optical equipment. Reproducibility checks on the towing speed speed, made by timing the foil and carriage over a 4-m distance, showed less than 1% error in speed from run to run.
Three hydrofoils were used in the present study. Each hydrofoil has a NACA 0012 shape and is made of anodized aluminum. This foil shape is symmetric
about the chord (c) with the maximum thickness (0.12c) occurring at 0.3c from the nose. The three hydrofoils have chords of 15.0, 20.0 and 30 cm. All foils have a span of 1.191 m (a little smaller than the width of the tank). The hydrofoils ride on the stainless steel tracks described above via two delrin guides. The guides are attached to the hydrofoils via thin extension plates which are aligned with the flow and are located 2.87 cm from each end of the foil. The breaking waves produced by these hydrofoils appeared to be two-dimensional in the center 0.6 m of the tank. Thus, all measurements were conducted in this region.
2.2
Measurement techniques
The measurements reported herein include surface profile histories of the breaking waves, water surface height versus time at a fixed location in the tank as the wave passes by, and velocity field measurements in the breaking region. The above measurement techniques are described in the following sections.
2.2.1
Surface profile measurements
The breaker surface profile measurement apparatus is shown in Figure 2. The measurement technique is photographic and uses a 5-W Argon-Ion laser mounted at one end of the tank for a light source. The laser beam was collimated by two spherical lenses mounted near the laser. This collimated beam was directed along the center of the tank, at a distance of 0.8 m above the water surface. Upon reaching the instrument carriage, a 12-facet mirror rotating at 25,000 rpm reflected the beam downward and spread it into a light sheet exceeding 50 cm in width. The thickness of the light sheet was adjusted by a pair of cylindrical lenses also mounted on the carriage. The thickness was set to 1 mm for all the experiments. Fluorescein dye was mixed with the water at a concentration of 2 ppm. Thus, the water illuminated by the laser light sheet emitted greenish-yellow light. A 16-mm high-speed camera mounted on top of the carriage, and set to 400 frames per second viewed the measurement area with the aid of two front-surface mirrors. A high-pass optical filter was placed in front of the camera lens to block out any light coming directly from the laser due to specular reflections from the water surface. Lenses and object distances were chosen so that the field of view was nominally equal to the chord of the foil. To minimize regions where the intersection of the light sheet and the water surface was hidden by local peaks of the water surface between the camera and the light sheet (called dropouts) while allowing reasonably height sensitivity, a look-down angle of nominally 40 degrees was used. The above system produced high-speed movies of the intersection of the light sheet with the water surface. Profile histories were taken with the light sheet and camera oriented as shown in Figure 2 to obtain streamwise profiles of the breaker and with the camera and light sheet turned 90 degrees about a vertical axis to obtain cross-stream profiles with the camera looking downstream.
In order to obtain the surface profile history from the high-speed movies, each frame was digitized with a resolution of 130 pixels/mm and the surface profiles were obtained using a numerical technique with a threshold-based edge finder. To provide reference points in each frame, light-emitting diodes were mounted on the carriage in a manner such that they appeared in the upper left and right corners of all images. Calibration of this system was achieved by photographing several stationary targets including a flat water surface at various heights. Thin lens theory rectification equations including perspective distortion according to Rosenfeld and Kak [10] were implemented. The difference between the actual positions and the predicted positions was minimized using the Powell optimization routine [11] by allowing the lookdown angle to vary. Using this method gives an error of 0.12 cm or less at t95 uncertainty for any point in any wave profile. It is estimated that the precision accuracy of this measurement system is 1% for length measurements. (Unless otherwise specified, all precision errors will be based on the student t test to the 95 percent level [12].) The bias error of the data is estimated at 3.0% for length measurements.
Profiles of surface height versus time as the waves passed by a fixed location in the tank were also measured. These measurements were made for both nonbreaking (for calibration purposes) and breaking waves in order to obtain the profile of the entire surface deformation pattern. For these measurements, the instrument carriage was disconnected from the towing cables and held at a fixed position in the tank. The high-speed movie camera was replaced by a ccd line-scan camera (EG&G Reticon) with a 105–210 mm lens. The single line of 2048 light sensitive elements in the camera was oriented vertically so that the top pixels imaged the air where the illumination was low and the bottom pixels imaged the water which was bright due to
the fluorescing dye illuminated by the laser. The surface height was taken as the boundary between the dark and light pixels. The sampling frequency of the camera was set to 200 Hz. To increase the light available to the camera, the wide light sheet generated with the rotating prism was replaced by a narrow light sheet generated with two cylindrical lenses.
2.2.2
Particle image velocimetry
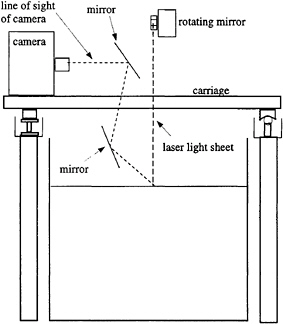
The flow field was measured in the breaking region of the wave with particle image velocimetry (PIV). The light source for these measurements was a dual NdYAG laser system. The laser system provided two sequential light pulses at up to 200 mJ in energy and 10 ns duration at precise time separations. In all cases reported here, the time separation between pulses was 0.5 ms or shorter, and was measured by two calibrated oscilloscopes to be within 1% of its set value. The two laser beams were collimated into a single beam which then formed a light sheet as it passed through a set of cylindrical lenses before entering the side of the tank with a horizontal trajectory, see Figure 3. An underwater mirror arrangement deflected the spreading light sheet so that it was vertical and aligned with the direction of wave travel. The light sheet thickness was focused near the still water surface. The light sheet thickness was chosen to be either 1 mm, 2 mm or 4 mm depending on the measurement condition.
The flow was seeded with either 12-micron silver-coated hollow glass spheres or 1.4-micron Titanium-Dioxide particles. The light sheet thickness and particle density were such that about 12 particles were present per square millimeter of measurement area. The images of the particles were captured with a Nikon F3 35-mm camera and a 200-mm, f/2.8, fixed-focal-length lens and recorded on Kodak Tmax ASA 400 black-and-white film. A rotating mirror was placed in the optical path of the camera to provide a bias velocity to the images of the particles. The camera and rotating mirror were mounted in a sturdy housing which maintained the close geometrical alignment needed for the experiments, see Figure 3. The camera pointed in a direction parallel to the length of the tank. The mount also allowed rotation of the camera and mirror about the center line of the camera lens so that the camera could look up toward the water surface with an angle of up to 20 degrees from the horizontal. The in-air optical distance from film plane to the measurement volume was approximately 0.9 m resulting in a field of view of about 12 cm at the light sheet. The bias velocities provided by the rotating mirror were typically equivalent to, but sometimes faster than, twice the wave phase speed and in the direction opposite to the wave propagation.
Timing of the lasers, camera and mirror rotation was accomplished with a specially constructed timing circuit. Between experimental runs, the timing circuit fired the laser system continuously with a 30 Hz repetition rate. During each run, upon the closing of a stationary limit switch actuated by the passing of a spindle attached to the tow cables, the timing box interrupted the laser firing cycle so that the lasers fired a known time later, triggered the camera whose shutter remained open for 1/30 of a second, and started the mirror rotation. The relative position of the foil and the camera at the time the lasers fired was repeatable to less than 1 mm with this system. The magnitude of this error was governed by the interaction of the spindle with the limit switch.
In the breaking region, the turbulence intensity is high, the local velocities range approximately from 0 up to the wave phase speed, and the free surface is very rough. Therefore, a look-up angle of 17 degrees was used for the camera and a second camera was used to view the water surface from above with a 30 degree look-down angle, see Figure 3. The combination of the two camera views allowed the surface to be located with an accuracy of about 1 mm in most regions of the images despite the large local peaks and valleys of the surface. To achieve adequate quality of the images of the particles in the underwater images, the lens aperture was set to f/16 or f/22 and the camera was modified by the inclusion of a wedge-shaped lens mount which tilted the film plane with respect to the centerline of the lens. This tilting was such that it shortened the optical path for particles in the top of image and increased it for particles in the bottom of the image, thus offsetting the difference in optical path caused by the large look-up angle.
The PIV images were digitized with a Nikon 3510AF, eight-bit film scanner at a spatial resolution of 125 pixels per millimeter (4000 by 2500 pixels per negative). Images with no flow (stationary hydrofoil) were analyzed to obtain the bias velocity induced by the mirror. Velocities were obtained using two-dimensional correlation techniques. The correlation functions were computed directly and with Fourier transform methods using window sizes
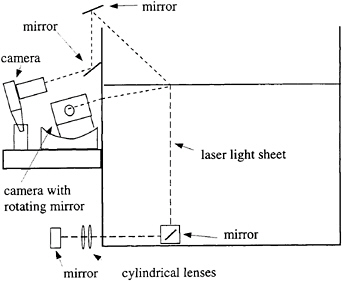
Figure 3: Schematic showing end view of PIV setup.
of 80 by 80 pixels. The resulting velocities are accurate to better than 5% of the 11 pixel displacement corresponding to the wave phase velocity. (Based on laboratory-scale velocity, with velocities of almost twice the phase velocity, the accuracy is 3%). The correlation techniques give obviously bad results in areas of high shear. Techniques to deal with this problem are presently under investigation. In the present, preliminary results, bad vectors (a bad vector being defined as a vector exceeding a thresh old standard deviation from its nearest neighbors), were replaced by the average of their nearest neighbors. Since the PIV results are used only for descriptive purposes in the present paper, the above techniques are considered adequate.
2.3
Experimental conditions
A set of Froude-scaled experimental conditions was chosen in order to aid in scaling the laboratory results up to full scale. The largest towing speed practical in the present tank, 100cm/s, was chosen for the largest foil. At the present time, preliminary results are available only for the two smaller foils and the corresponding experimental conditions are given in Table 1 ![]()
Table 1: Experimental conditions.
|
c(cm) |
U(cm/s) |
d(cm) |
d/c |
Fr |
|
15 |
69.28 |
12.0 |
0.8 |
0.571 |
|
15 |
69.28 |
15.3 |
1.02 |
0.571 |
|
15 |
69.28 |
16.5 |
1.10 |
0.571 |
|
20 |
80.0 |
16.0 |
0.8 |
0.571 |
|
20 |
80.0 |
20.4 |
1.02 |
0.571 |
|
20 |
80.0 |
22.0 |
1.10 |
0.571 |
|
30 |
97.98 |
24.0 |
0.8 |
0.571 |
3
Results and Discussion
In the following, the data is presented nondimensionally with lengths and times scaled with the wavelengths (λ0) and periods (T0) obtained from the deepwater dispersion relation:
(1)
and
(2)
When mass units are required the value of the density of fresh water at 20C, 0.9982 gm/cm2 is used. For the cases considered in this paper, λ0=30.77, 41.02 and 61.55 cm and f0=2.25, 1.95 and 1.59 Hz
for the breakers produced by the 15-cm, 20-cm and 30-cm foils, respectively. Throughout this paper, the breakers will be referred to by the speed which produced them, e.g. the 69-cm/s breaker refers to the breaker produced by the 15-cm foil.
3.1
Surface profile measurements
The parts of the surface profiles upstream of the breaker, where the flow is laminar and the surface curvatures are small, should not be affected significantly by surface tension and viscous effects. Thus, if the flow conditions are successfully Froude scaled, surface profiles upstream of the breaker for tests with the two hydrofoils and the same values of d/c should be identical when nondimensionalized by λ0. The surface profiles were measured with the optical wave-height gauge placed at a fixed position in the tank. Figure 4 shows the results of averaging a small number of runs (between 3 and 8) of each of the 6 cases (the 15 and 20-cm foils with d=0.8c, 1.02c, and 1.1c). An important measure contained in these figures is the vertical distance from the mean water level to the trough immediately behind the foil. This height was found not to vary by more than 3% between the two foil scales for a given value of d/c. It is believed that this variation is due to a slight change in angle of attack between the two foils. This inaccuracy in angle of attack is estimated at 0.24 degrees and is considered unavoidable with the present experimental setup.
Surface profile histories of the breaking regions were obtained from the high-speed movies (taken at 400 frames/s) as described in the previous section. Every other frame of each movie (a sampling rate of 200 Hz) was digitized and the surface profiles were obtained with a threshold-based edge detector that allowed multi-valued surface heights at any streamwise position. This process typically resulted in about 400 profiles from a single experimental run. In order to perform the spectral analysis described in the following, the surface profiles were then conditioned to remove the multi-valued surfaces, taking the highest value in such cases. The data was then averaged and the average was subtracted from each of the conditioned profiles. The resulting data from both streamwise and cross-stream profiles for both hydrofoils and d/c=1.02 is given in Figure 5. All profiles are plotted in non-dimensional coordinates. The streamwise profiles show an area near the leading edge of the breaking region where the surface fluctuations oscillate upstream and downstream. However, over most of the breaking region it is apparent that the surface height fluctuations propagate downstream and that the wavelength of these fluctuations increases with downstream distance. Similar results for a single flow speed and several depths of submergence where reported by Walker et al. (1996) with a sampling frequency of 30 Hz. In the cross-stream profiles, the surface height fluctuations do not appear to propagate. It is evident from the comparison of the streamwise and cross-stream profile histories that there is a strong two-dimensional component to the surface ripples which is aligned parallel to the wave crest. Since the distances and times in Figure 5 are scaled with λ0 and T0, respectively, the profile histories would be identical in a statistical sense if surface tension and viscosity did not play a role. The difference between the sets of profiles from the larger and smaller scale experiments is primarily that there is more small-scale structure in the larger scale experiment.
Further examination of the differences between the surface-height fluctuations at the two experimental scales was performed through spectral analysis of data like that shown in Figure 5. Figure 6 shows the resulting spectra for the streamwise profile histories and Table 2 contains the nondimensional frequencies (f/f0) and wavenumber (k/k0) of the spectral peaks. The dimensionless phase speed, c/c0 where c=ω/k and c0=ω0/k0, is also given in the table. All three dimensionless quantities decrease as the breaker becomes more intense (smaller d/c) for both hydrofoils. The dimensionless frequencies and wavenumbers decrease as the scale is increased from the 69-cm/s breaker to the 80-cm/s breaker while the phase speeds remain nearly the same. The smallest changes in frequency and wavenumber with scale occur for the cases with d/c=1.02. It is expected that processing additional experimental runs will give more consistent results between the different experimental conditions.
Wavenumber-frequency spectra calculated from the cross-stream surface profile histories for d/c= 1.02 are shown in Figure 7. The corresponding wavenumber-frequency spectra calculated from the streamwise surface profile histories were presented in the center row of Figure 6. Cross-stream profiles for the other experimental conditions (d/c=0.8 and 1.10) are currently being reduced. The cross-stream spectra are dominated by energy at zero wavenumber. This result can be anticipated from the profile history data in Figure 5 in that the data is dominated by two-dimensional structure
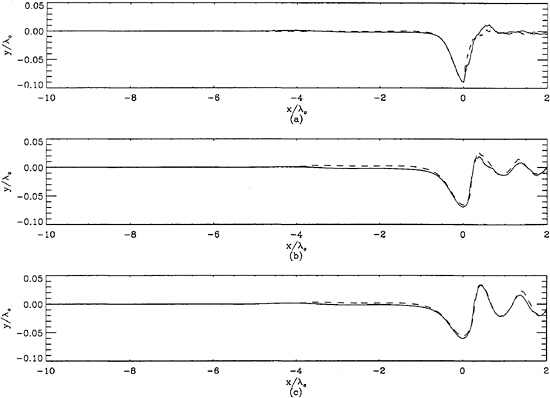
Figure 4: Comparison of the nondimemsional average wave profiles for the 15-cm and 20-cm hydrofoils. This data was taken with the stationary optical wave-height gauge. (a) 0.8c depth; (b) 1.02c depth; (c) 1.10c depth. The solid lines are the 15-cm foil cases, and the dashed lines are the 20 cm foil cases.
Table 2: Spectral peaks, dominant disturbance, presented as reciprocal wavenumber (length/cycle) nondimensionalized by the wavelength, frequency, nondimensionalized by the deep water wave frequency, and characteristic velocity.
|
69-cm/s wave |
80-cm/s wave |
|||||||
|
d/c |
k/k0 |
f/f0 |
c/c0 |
k/k0 |
f/f0 |
c/c0 |
||
|
0.8 |
6.7 |
4.0 |
0.60 |
6.91 |
5.4 |
3.2 |
0.59 |
10.7 |
|
1.02 |
7.2 |
5.0 |
0.69 |
3.72 |
6.8 |
4.9 |
0.72 |
5.69 |
|
1.10 |
8.8 |
6.6 |
0.75 |
1.47 |
7.6 |
6.0 |
0.79 |
2.12 |
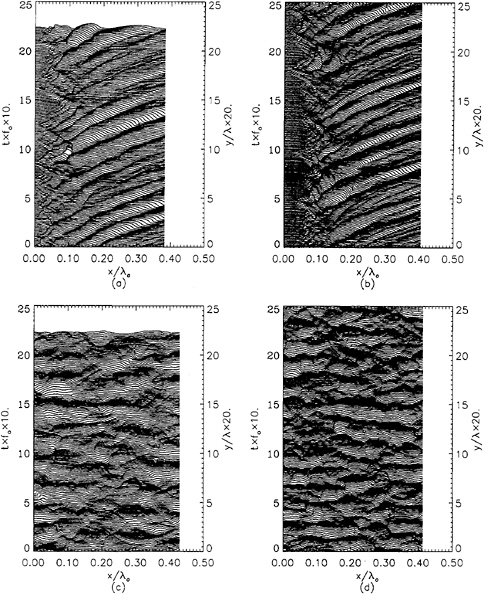
Figure 5: Breaking region profile histories for d/c=1.02. Each curve is a profile of dimensionless surface height versus dimensionless horizontal distance. The profiles at successive times are displaced vertically upward in the plots for clarity of the presentation. (a) 15-cm foil, streamwise profiles; (b) 20-cm foil streamwise profiles; (c) 15-cm cross-stream profiles; (d) 20-cm foil cross-stream profiles.
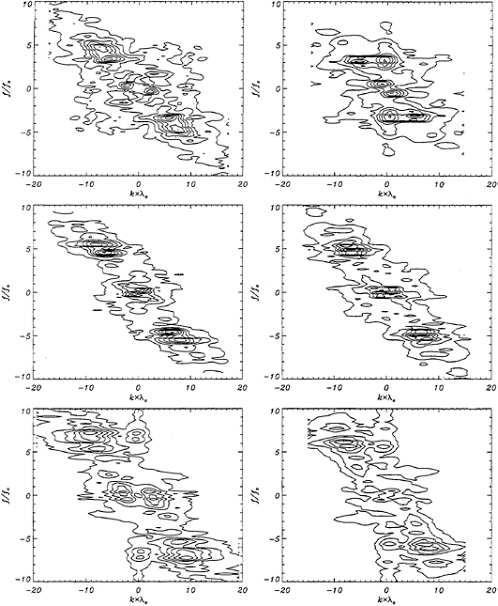
Figure 6: Wavenumber-frequency spectra from streamwise profile histories for the six Froude-scaled conditions. The three left-hand graphs are the 69-cm/s cases, and the right-hand graphs are the 80-cm/s cases. In both columns, the depths of submergence are 0.8c (top), 1.02c (middle) and 1.10c (bottom).
that is aligned cross-stream and propagates downstream. Thus, the cross-stream profiles show high-frequency structure that rides on a mean level that moves up and down as the two-dimensional structures move through the measuring station.
Another interesting parameter describing the surface-height fluctuations is the variance. The variances were calculated from the streamwise profile histories for each of the six experimental conditions and are given in Table 2 nondimensionalized by ![]() As can be seen from the data, the variance increases with both breaker intensity and wave scale. The difference in variance between the breakers produced by the two foils appear to increase with the intensity of the breaker. The change in variance between the 69-cm/s breakers and the 80-cm/s breakers is approximately a factor of 1.2 for the weakest breakers and 1.5 for the strongest breakers.
As can be seen from the data, the variance increases with both breaker intensity and wave scale. The difference in variance between the breakers produced by the two foils appear to increase with the intensity of the breaker. The change in variance between the 69-cm/s breakers and the 80-cm/s breakers is approximately a factor of 1.2 for the weakest breakers and 1.5 for the strongest breakers.
The above results indicate a significant departure from Froude scaling for the wavenumbers, frequencies and amplitudes of the surface ripple statistics. Duncan and Dimas [13] compared experimental ripple measurements to the results of an inviscid, linear, free-surface shear-flow instability model without surface tension. It was found that the dominant frequencies and wavenumbers of the surface-height fluctuations correspond to the the most unstable waves on a shear layer that is produced between the flow in the breaking region, which was assumed to be a weak recirculation region, and the fast-moving underlying flow. Using this model of ripple generation one can think of two causes for the lack of Froude scaling of the present surface ripple data. First, at the two experimental scales, the scaled shear layer maybe significantly different and this would then affect the most unstable wavenumbers and frequencies. Second, if the shear layers do Froude scale, the most unstable waves might be changed because of the varying influence of surface tension and viscosity. The flow field measurements presented in the following section are aimed at exploring these effects. Only preliminary results for one experimental condition are available at the present time.
3.2
Flow field measurements
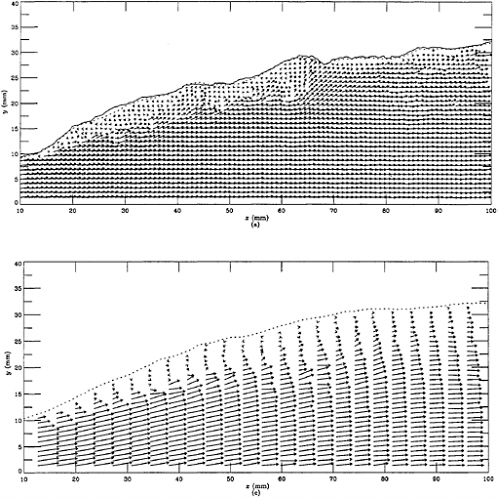
To gain a measure of understanding of the flow field beneath the breakers, particle image velocimetry (PIV) was conducted for three of the nine cases studied as part of this work. Approximately 400 images have been taken but, to date only data from 10 images taken of the 69-cm/s breakers with d/c=1.02 have been partially analyzed. Figure 8 shows a single realization of flow field of this breaking wave and an average flow field obtained 10 similar instantaneous flow fields. The reference frame chosen is that of the breaking wave crest. The instantaneous flow field shows a nearly stagnant region on the forward face of the wave with a thin shear layer separating it from the underlying flow. This is similar to the findings of Lin and Rockwell (1995 and 1996). Downstream of x=65 mm the flow in the breaking region is slow but primarily downstream while upstream of this point the flow close to the free surface is directed upstream. The average flow field shows some spatial fluctuations that indicate that a larger number of samples is needed to obtain a good average. However, it does begin to show the characteristics of a mixing-layer flow. The mean shear layer is thin at the toe of the breaking region and increases in thickness with distance downstream. Upstream of about x=75 mm the flow at the surface is nearly stagnant as can be seen by the small magnitude and nearly random orientation of the velocity vectors. Downstream of x=75 mm the shear layer has grown significantly in thickness and the flow at the surface is consistently downstream. A mixing layer model with a stagnation point at the crest was used in the work of Cointe and Tulin [5].
3.3
Jet formation
Drops are sometimes formed from the surface of the breaking region. This process can be initiated by jets which emerge from the surface due to strong turbulent motions which overcome gravitational and surface tension forces. A sequence of streamwise wave profiles showing the formation of two jets is presented in Figure 9. This sequence is from an experimental run with the 30-cm foil at d/c=0.8. The sequence on the left shows 0.86 seconds of data, with the time between profiles of 0.025 s. The two jets are formed near the toe of the breaker during this sequence, one at a time of 0.2 s and one at 0.55 s. Both jets have at least some forward component of velocity over their entire lifetime. The center plot in Figure 9 shows the first jet in more detail. The underside of the jet is somewhat ragged and changes from frame to frame because of the image digitization. The second jet, shown in the right-hand plot, appears after the remnants of the first jet are overtaken by a forward moving disturbance which falls ahead of the toe. As this second disturbance is overtaken by the
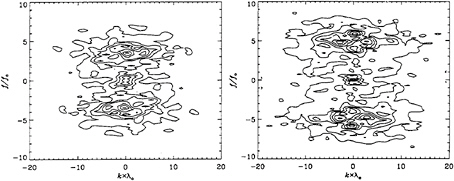
Figure 7: Wavenumber-frequency spectra from cross-stream profile histories for two Froude-scaled conditions with d/c=1.02. The left-hand graph is for U=69 cm/s, and the right-hand graph is for U=80 cm/s.
rest of the wave, a third forward moving disturbance interacts with it, producing the jet. The jet characteristic speed is on the order of 100 cm/s, the characteristic acceleration is 10 m/s2, and the length of the jet is about 1 cm. The high-speed movies indicate that drops are formed after the jet falls into the water surface. These are not picked up by the surface following algorithm and are therefore not visible in the figure.
3.4
Full-scale observations
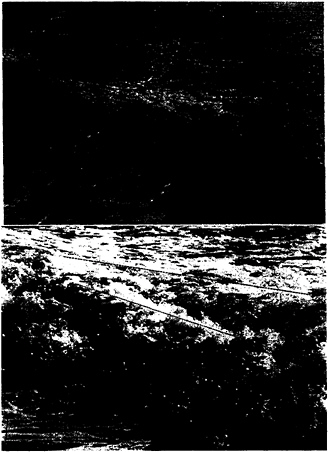
The present experiments cover a range of flow speeds from about 70 to 100 cm/s. Full scale ship speeds might be as high as 1500 cm/s, but because it is primarily the divergent waves that are breaking and the crest angle of these waves is at about 19° from the ship's path, the actual phase speed of these waves is at most about 1500 cos(90–19°) ≈ 500 cm/s. This indicates that the wave phase speed at full scale can be as much as 5 times the wave phase speeds in the present experiments. Thus, it is relevant to ask whether the surface disturbances found in the laboratory will be seen in the breakers around full-scale ships. To this end, Figure 10 is presented which shows two photographs of the stern waves generated by the Brittany, a 60-ft long personnel transport vessel/work boat. Both photographs were taken in the summer of 1995, off Eleuthera Island, Bahamas. The top photograph shows the diverging transom wave at a steady speed of 11 knots. The camera was pointed in a direction slightly starboard of astern. The field of view is 8 to 10 m at the center of the photograph. The wave crest is shown as a dashed line. The local peaks ahead of the crest appear similar to the ones in the present experiments as shown in the streamwise profiles in Figure 5. The bottom photograph shows a diverging transom wave at a steady speed of 8 knots. The camera is pointed in a direction slightly aft of midway between the starboard and stern quarters. The wave crest is shown as a dashed line. The dotted line is the peak of a dominant disturbance which is in the process of traveling up and to the left (towards the wave crest). This disturbance is so large that it might be mistaken for the wave crest itself. Six to 8 m of the crest is visible. Many of the approximately 150 photographs taken during the voyage display similar large disturbances. These disturbances are thought to be large-scale versions of the disturbances observed in the laboratory. It is also interesting to note that in the bottom photograph many droplets can be seen as well as many jet-like projections from the surface. These projections are similar to those shown in Figure 9. Many of the droplets appear to be formed from the jet-like projections
4
Conclusion
Surface profile and flow field measurements from a Froude-scaled steady breaking wave experiment have been presented. The streamwise profile measurements show significant effects of scale with the dimensionless wavenumber and frequency of the surface disturbances decreasing, the dimensionless phase speed remaining nearly constant and the dimensionless amplitude increasing with scale. At the larger scales, the formation of surface jets that tend to eject droplets into the air are observed. Preliminary particle-image-velocimetry measurements
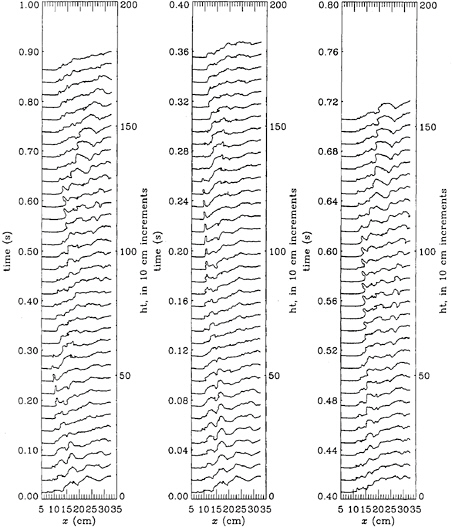
Figure 9: Sequence of jet formation, 30-cm foil, d/c=0.8: (left) 1-second time sequence with 0.025 seconds between frames; (center) closeup of first jet formation in the left sequence, 0.01 seconds between frames; (right) closeup of second jet formation in the left sequence, 0.01 seconds between frames.
in the breaking region were presented. A flow field obtained by averaging 10 instantaneous flow fields clearly shows the evolution of a shear layer between the nearly stagnant fluid in the breaking region and the fast-moving underlying flow. From this preliminary data, it appears that the flow at the free surface near the crest is directed downstream.
Acknowledgments
This work was supported by the Office of Naval Research under contract N00014–90-J-1977 and the David Taylor Model Basin (DTMB). The authors acknowledge a number of helpful discussions with D.Rockwell and J.Katz on PIV techniques. Haibing Qiao assisted in the data acquisition of the breaker region PIV experiments, construction of the PIV equipment, and in writing some of the PIV analysis software. John Hamilton of DTMB engineered and built a timing device that was used in the PIV measurements. Alexandra Wenz developed most of the high-speed films used during these experiments. Arno Miessner and Sebastian Muncher helped to analyze some of the early high-speed movie films. Sven Eisen helped to construct some of the tank apparatus. Bruce Webster of DTMB is gratefully acknowledged for his patience in allowing a flexible work schedule for Mr. Coakley.
References
[1] Battjes, J.A. and Sakai, T. 1981 Velocity field in a steady breaker. J. Fluid Mech. 111, 421–437.
[2] Duncan, J.H. 1981 An experimental investigation of breaking waves generated by a towed hydrofoil. Proc. R. Soc. Lond. A 377, 331–348.
[3] Duncan, J.H. 1983a The breaking and nonbreaking wave resistance of a two-dimensional hydrofoil. J. Fluid Mech. 126, 507–520.
[4] Duncan, J.H. 1983b A note on the evaluation of the wave resistance of two-dimensional bodies from measurements of the downstream profile. J. Ship Res. 27, No. 2, 90–92.
[5] Cointe, R. and Tulin, M.P. 1994 A Theory of Steady Breakers. J. Fluid Mech. 276, 1–20.
[6] Lin, J.-C. and Rockwell, D. 1994 Instantaneous Structure of a Breaking Wave. Physics of Fluids 6, 2877–2879.
[7] Lin, J.-C. and Rockwell, D. 1996 Evolution of a Quasi-Steady Breaking Wave. J. Fluid Mech. (in press).
[8] Banner, M.L. and Fooks, E.H. 1985. On the microwave reflectivity of small-scale breaking water waves . Proc. R. Soc. London Ser. A 399, 93–109.
[9] Walker, D.T., Lyzenga, D.R., Ericson, E.A. and Lund, D.E. 1996 Radar Backscatter and Surface Roughness Measurements for Stationary Breaking Waves. Proc. R. Soc. Lond. A (in press).
[10] Rosenfeld, A. and Kak, A. 1982 Digital Picture Processing, Academic Press.
[11] Press, W., Flannery, B., Teukolsky, S. and Vetterling, W. 1986 Numerical Recipes, Cambridge University Press, Cambridge, U.K.
[12] Coleman, H.W. and Steele, W.G. 1989 Experimentation and Uncertainty Analysis for Engineers, John Wiley and Sons, New York.
[13] Duncan, J.H. and Dimas, A.A. 1996 Ripples Generated by Steady Breaking Waves, submitted to the J. Fluid Mech.