Divergent Bow Waves
M.Tulin, M.Wu (University of California at Santa Barbara, USA)
Abstract
Divergent waves are studied utilizing a high resolution 2D+T simulation. The effects of changes in speed, beam, and draft are studied and discussed for Wigley-like hulls. A satisfactory comparison is made with fully non-linear 3-D calculations by Hoyte Raven with RAPID. The present simulations confirm the non-linear characteristics of the bow waves, earlier observed by W.Froude, Inui, and Miyata. An explanation is offered here for these observations in terms of the narrow wave spectra arising from interference between the two sides of the hull at the location of the splash peak. For normal ship slenderness (B/L=0.1–0.2) the divergent bow wave crests tend to be straight due to the narrow spectrum, and the wave crests are very steep, resembling Stokes limiting waves, and/or breaking. Strong breaking has a similarity to the breaking of two dimensional progressive waves: an energetic plunging jet forms. Further simulations and measurements are recommended.
1.
Introduction
The flow at the bow of ships takes a variety of forms, depending mainly on the shape of the bow. For sufficiently blunt shapes, breaking occurs ahead of the bow. For sufficiently fine bows, a thin splash is created on the side of the hull which rises and eventually falls, and oblique waves appear moving away on either side. For a long time the study of both of these bow flows had been neglected. Finally, however, the blunt bow came under scrutiny through: experimental studies of full tankers, Baba(1969); suggestions about the morphology of the free surface before blunt bodies, Tulin(1970); an analysis of the inviscid free surface stability before the bow, and detailed two-dimensional calculations at both low(smooth) and high(jet) Froude numbers, Dagan and Tulin(1973); exact two-dimensional calculations of the “smooth” flow before the bow, vanden Broeck and Tuck(1977); an asymptotic analytical theory of blunt bow flow before three dimensional shallow water ships, Fernandez(1981); studies of the necklace vortex and of viscous free surface stability, Mori(1985); exact unsteady free surface calculations of evolving bow waves, Grosenbough and Yeung(1989), Yeung(1991); and through exact analytical modeling of jet flows at the bow, Dias and vanden Broeck(1993); and others.
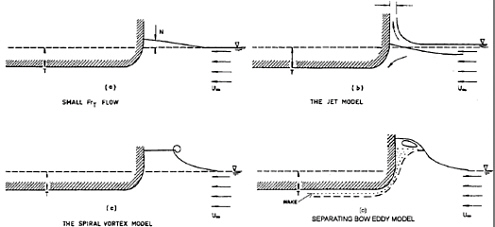
The flow is decelerated in front of the blunt bow and the free surface rises a distance which scales with the square of the draft Froude number, Fd. In this process, the free surface is seen to be disrupted for small draft Froude numbers, Fd=O(1). It is not yet known whether a smooth undisrupted rise is possible even for very small Fd, while for larger speeds, a jet sheet runs up at the bow before falling over forward. The earliest schematic guess as to these flow regimes is shown as Figure 1 (a)–(c) from Tulin(1970). To these we should add Figure 1 (d), showing a low speed turbulent eddy sitting on the dividing stream line; the later is our present view as to what happens for Fd=O(1); this situation is somewhat similar to a breaker above a hydrofoil, Cointe and Tulin (1994).
Between blunt and fine ships, a sequence of events may occur in the transition between bow breaking and divergent wave systems. We do not know very much about this transition, but it certainly deserves to be explored systematically.
For fine ships with a sharp stem, the free surface flow is not much decelerated before the stem, but upon reaching it, is diverted sharply upwards and then rises on the hull at a constant upward velocity first, but then in almost ballistic trajectory, eventually to level off and fall down.
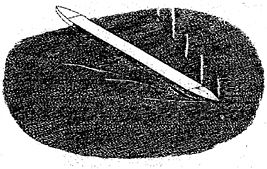
An entire thin sheet is formed in this process and appears as a splash or spray on either side of the hull, Figure 2. This spray as viewed in successive vertical sections aft of the stem, resembles the rise or jet formation which occurs during two dimensional water entry; indeed the mechanism of water entry and of the fine bow flow are closely related.
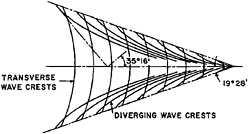
In Michell's thin ship theory, this splash appears as a result of the calculation so that it is not entirely of nonlinear origin. Following the splash, an oblique wave then appears on each side of the hull, often followed by others. These waves were observed by Froude, who called them “divergent” waves, Figure 3, and described them in the context of the entire wave system, including the broad crested transverse waves. Subsequently, Lord Kelvin, who knew about Froude's observations deduced the wave pattern behind an infinitesimal disturbance. A set of nested divergent waves appeared, Figure 4. Since that time, actual divergent bow waves have with little exception been linked with the Kelvin wave pattern, and simply considered part of it. In fact, the waves drawn by Froude, Figure 3, differ substantially and in a basic way from Kelvin's picture, Figure 4; we will account for this difference later. We owe to Inui(1970) and his colleagues in Tokyo, Inui, et at(1979), Miyata(1981), the earliest attention to little understood aspects of divergent bow waves. Miyata claimed, following experimental studies that these waves were non-dispersive and non-linear; he called them “surface shock waves”. After their work, the subject rested until now, perhaps because for conventional Froude numbers the divergent waves do not contribute in a major way to the wave resistance. Of course, at higher speeds, they are important and eventually merge with spray. Recently, there has arisen an interest in the very long narrow wake behind ships which can be observed remotely. For naval combatant ships, photographs show substantial wakes created abeam the ship by the extensive breaking of divergent bow and stern waves; the same can be observed in early photographs in the Tokyo tank using aluminum powder on the surface, see Figure 5. This has created an interest in divergent waves for their own sake.
How to predict these waves? The numerical computation of ship wave resistance and patterns has evolved through Michell, Guilloton, Neuman-Kelvin, and Dawson techniques to fully non-linear codes [Daube, Raven(1993)]. No doubt, the best of these latter codes can provide useful information on the divergent waves, provided they can resolve the thin bow splash and steep waves which sometimes appear. Very often bow waves are seen to break, sometimes strongly, and the 3-dimensional codes may then have trouble. For sufficiently fine ships, we know that the divergent wave pattern, both at the bow and stern, emerges from numerical calculations made on the basis of nonlinear slender body theory, Tulin and Wu(1994). The calculation is carried out in two dimensions, vertical and transverse, and successively in time (2D+T). It has the advantage of high resolution, sufficient to define breaking, and even to trace out overturning jets. At the same time, it neglects certain three dimensional effects which become increasingly important as the ship becomes full. For instance, it does not allow upstream influence, so it can not predict breaking before the bow. However, it has much to recommend it for fine ships like combatants, and especially for the higher Froude numbers where massive breaking of divergent waves is observed. Furthermore, the theory can be applied to divergent stern waves, about which we know little.
There is much to understand about divergent waves, both bow and stern: their source or origin; the shapes they take and the patterns they make; the influence of the beam, draft, and the speed on their strength and propagation, the onset and type of breaking, and even their post breaking behavior.
Our principal purpose here is to report and comment on the calculations of some nonlinear 2D+T numerical studies of divergent waves and to illuminate their basic mechanics. We begin with a discussion of some past ideas.
2.
The inadequacy of ray theory; the splash as a high speed inner flow
For fine ships without sharp corners except at the bow and stern, at normal Froude numbers, the Michell theory shows that the ship 's wave pattern is equivalent to two Kelvin patterns originating at the bow and stern. The ray theory according to Keller(1974,1979) also concludes that all the rays must originate at discontinuities in the waterline shape, which normally occur only at the bow and stern.
After originating at the bow (and stern), the trajectory of the rays depends upon and may be calculated in terms of the “displacement” flow about the hull. The deformation by the displacement flow of the ray propagating waves, with amplitudes calculated according to linear theory, was studied by Inui and Kajitani(1977) and later, in the same spirit, by Yim(1981). Subsequently, Tulin(1985) produced a general ray analysis of the generation and propagation of waves around a ship of finite beam.
In Keller ray theory it was proposed to base the displacement flow on a naive Froude number expansion. Tulin showed that the calculation of the amplitude of waves propagating on rays is dependent on the pressure gradient at the stagnation point in the low Froude number flow, and the theory gives rise to unbounded amplitudes for wedge bows. Then he raised the question, “is the naive Froude number expansion even applicable (uniformly convergent) in the neighborhood of the point of the bow?” He continued, “there exists a good chance that it is not. I say that because in nature it is normal on wedge models, see Standing (1974), to find the highest point on the free surface at some distance aft of the point of the bow (as Michell's theory predicts!); is it possible that this behavior is reflected at all Froude numbers on a scale near the bow which increases with speed, perhaps as U2, creating an inner flow at the point of bow for which the naive Froude number expansion is an outer flow.”
The simulation results presented here clearly show that the side splash on the hull is crucial for the generation of divergent waves. Furthermore, we shall show that it scales exactly as the “high speed ” inner flow suggested by Tulin. Our calculations indicate that the relaxation of the splash is the prime source of divergent waves. One of the consequences of this discovery is that conventional ray theory, which is conceived as asymptotic to zero Froude number, cannot predict the generation of divergent waves. Whether it is relevant to wave propagation is another question.
Eventually we conclude that neither ray theory nor linear theory is relevant to the understanding of bow divergent waves. The key to their understanding lies in the spectral wave number content in the splash, which for typical ships is governed by the ship's beam. This is a non-linear effect. Furthermore the waves are typically very steep and sometimes breaking.
3.
The wedge flow
The free surface flow about the inclined wedge, for which a length scale is absent, offers an important opportunity for understanding the morphology of bow waves produced by fine ships. Its consideration leads immediately to understanding of the inner flow (side splash) and to essential scaling relations. These, in turn, allow us to understand some of the effects of speed on the divergent waves, particularly, their spatial pattern.
For an inclined wedge (wedge angle α, stem angle β) at speed U, the wave height η, at any longitudinal location ![]() measured from the wedge-still water intersection, must on dimensional grounds obey the scaling law:
measured from the wedge-still water intersection, must on dimensional grounds obey the scaling law:
(1)
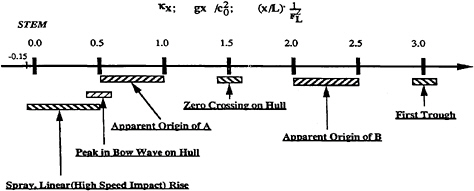
This means that the flow speed U simply serves(through κ) as a factor scaling both η and the actual position ![]() on the free surface where certain flow features appear. Therefore high speed features such as the origination of splash, appear closer and closer to the bow as the speed decreases; equivalently low speed features (like disappearance of waves) will always appear if we look far enough behind the wedge. And in between the splash at the bow and the wave free field to the rear, we can expect to find observable waves. These are the divergent waves. A chronology of events near the bow can be constructed, based on the scaling of eq. (1) and using other results, see Figure 6.
on the free surface where certain flow features appear. Therefore high speed features such as the origination of splash, appear closer and closer to the bow as the speed decreases; equivalently low speed features (like disappearance of waves) will always appear if we look far enough behind the wedge. And in between the splash at the bow and the wave free field to the rear, we can expect to find observable waves. These are the divergent waves. A chronology of events near the bow can be constructed, based on the scaling of eq. (1) and using other results, see Figure 6.
The flow near the bow begins as a spatially self similar spray, just as in gravity-free water entry, and every line originating at ![]() and lying on the free surface is a straight line, since in the absence of κ;
and lying on the free surface is a straight line, since in the absence of κ;
(2)
This is confirmed in the 2D+T calculations, which then show that for sufficiently large values of ![]() along the wedge, the spray sheet is maintained at high levels by the continually expanding wedge, and does not fall. However, divergent waves do originate in the sheet and propagate outwards, Figure 7. We note that the
along the wedge, the spray sheet is maintained at high levels by the continually expanding wedge, and does not fall. However, divergent waves do originate in the sheet and propagate outwards, Figure 7. We note that the
area in a vertical cross section of any wedge, A(x), increases as the square of the distance aft (A~x2) and this growth seems sufficient to maintain the splash and prevent its fall. Meanwhile, the water displaced by the growing wedge is partially carried off in the transversely propagating wave. In the case of a ship like the Wigley hull, the vertical section area grows at first like A~x, and the splash is then not maintained, but reaches a peak and falls; the growth after the bow region actually decreases and eventually falls to zero midships. This slow growth no doubt accounts for the difference between the wedge and conventional hulls. Another major difference is that the hull has a characteristic length, the beam B, while the wedge does not.
Wedge Bow Resistance The wedge flow possibly sheds light on the wave resistance originating at the bow. From dimensional considerations, it must be that the wedge resistance, Rb, is:
Rb~ CD·ρU6/g2 (3)
where CD is a non-dimensional number depending only on α, β. Since we have neglected the transverse waves in our considerations, this can be regarded as the wedge wave resistance arising from the inner flow at the bow, and which we associate with the divergent wave system.
The Water Entry and Wavemaker Analysis. The wedge flow corresponds to the vertical water entry of a two dimensional wedge in a vertical cross section. In the 2D+T view, the fine bow corresponds to an expanding section in the vertical plane, more like a wavemaker action. In each successive section the underwater area of the wedge or ship increases and the water displacement appears generally above the mean water line. This is the basic reason for the appearance of the splash. In this process, the water acquires potential and kinematic energy which must correspond to work done by the downward moving wedge or by the expanding hull. In the case of the ship, this splash relaxes, and its energy is transformed into a wave propagating to each side. This wave lies mainly above the mean water level.
For typical FL, the splash collapses before midship; there may be additional water rise further along the hull, however, to accumulate additional displaced water due to the growth in ship sectional area.
In accord with the scaling of eq.(1), as the speed and/or beam increases, the splash height, area and energy grow. The area and energy do not grow as the same way, as area is linear with increase in height, and energy is quadratic. This seems to lead to divergent waves which for typical ships are strongly non-linear in their 2D+T simulations.
Very little is understood about these non-linear positive waves, which are, furthermore, propagating in the presence of the hull. Our simulations show them often to be very sharp and/or breaking. One of our main purposes here is to learn more about them in their 2D+T simulation.
4.
The 2D+T approximation
Linear slender body theory has, of course, been applied to the ship wave problem, and is known to lead to results similar to Michell 's theory. It is, however, restricted to small wave elevation and cannot predict non-linear wave behavior. We will show later, that divergent waves for typical ship slenderness, behave very differently than predicted by Michell theory.
The theory we will use here is a so called non-linear cross flow theory. It was first developed at the OEL of UCSB by H.Maruo (1990) (see also Song and Maruo(1993), Maruo and Song (1994)) for the prediction of ship deck wetness, and therefore allows for the motion of ships in oncoming waves. The application here to steady ship motion is a special and simple case. The great advantage of this theory is that it allows free surface elevations around the hull of the same order as the ship draft. The theory does this by reducing the 3-D problem to a continuous sequence of unsteady 2-D problems in vertical sections. Since the 2-D free surface problem can be solved with high resolution by the BEM, it is possible to compute the shape of the free surface with high resolution, including overturning jets. This is another advantage of the method.
The 2D+T approximation was introduced into aerodynamics by M.Munk for the prediction of loads on inclined slender bodies of revolution and low aspect ratio wings. It has
been extended to compressible flow and is known to be very useful for bodies of beam/length of O(10–1) or smaller. These aerodynamic cases correspond, in a certain way, to the flow about ships at sufficiently high FL(O(1) or greater), and the 2D+T method has been used for the analysis of the performance of high speed, low aspect ratio planing boats, Tulin(1956), and for the study of the resistance of high speed, slender displacement hulls, Tulin and Hsu(1986); in both cases, gravity is completely neglected.
All 2D+T methods are asymptotic to the regime: (B/L)2<<1. As a result, the continuity equation, ![]() 2Φ=0, is approximated by:
2Φ=0, is approximated by:
(4)
where x, y, z are the streamwise, transverse, and vertical coordinates respectively; B, d, L are beam, draft, and ship length. This approximation fails, even for slender bodies, in the vicinity of hull stagnation points and other corners, where the flow is highly accelerated in the streamwise direction. The method would not apply, for example, to blunt bows, even for small (B/L). For fine bows, however, the stagnation point is weak, and does not exist on the free surface.
As a consequence of (4), the flow is two dimensional and each section is unaware of the hull in any downstream section. The absence of upstream influence has the consequence that the water rises abruptly at the stem of the ship; actual observations are in accord with this for fine ships, where the rise is observed to begin only a small distance, see Figure 8, ahead of the stem.
In the small slenderness regime, (B/L)2<<1, the free surface condition is also approximated by,
(5)
and is satisfied on the actual free surface; the motion is steady in ship co-ordinates. In fixed co-ordinates, the motion becomes unsteady and,
U∂/∂x=∂/∂t (6)
so that on the free surface, (5) becomes the exact two dimensional condition in a fixed vertical section through which the ship moves,
(7)
As the water first encounters the ship bow, η has not had time to grow very much, and I and II dominate. This is the region described by eq.(2) in the case of the wedge. When η is fully developed and of O(d), I and III are of the same order, and, ![]() For typical ship speeds, Fd=O(1), so all of the terms in (7) are important for normal speeds in the vicinity of the bow.
For typical ship speeds, Fd=O(1), so all of the terms in (7) are important for normal speeds in the vicinity of the bow.
Away from the hull, the divergent crest lines are fairly straight and steep, see Figure 3; eq.(7) is capable of dealing with propagating divergent waves of very high steepness because of the inclusion of II. Although eq.(7) is also capable of describing transverse waves, eq.(4) can not. Therefore transverse waves do not arise in this approximation. This is, it seems, the principal deficiency of the 2D+T approximation. However, the transverse waves may be adequately described by other methods, and, it seems possible to marry the two systems. This possibility is, however, beyond the present scope.
The Computations. The general scheme of the BEM computation has been described in Song and Maruo (1993). In the present calculations, time steps and grid size were chosen to provide convergence. Most of the calculations were made with Δt·U/L=0.0007 and Δy/L=0.0017, and were carried out on supercomputer CRAY C90. For a typical computation, one hour CPU time is required for one ship length.
5.
Wave patterns for the Wigley like hulls
For ease of computation and in order to do parametric studies, the Wigley hull was used as a basis. The stem was slightly raked (5° usually), as required by the program. Many calculations have been made and only a sampling can be presented here.
The calculation of splash requires very high resolution in both time step and free surface. In Figure 8 we show a prediction compared with measurements from Tokyo. The effect of the rise before the hull has been captured by moving the calculation forward by a small distance; then the comparison is excellent.
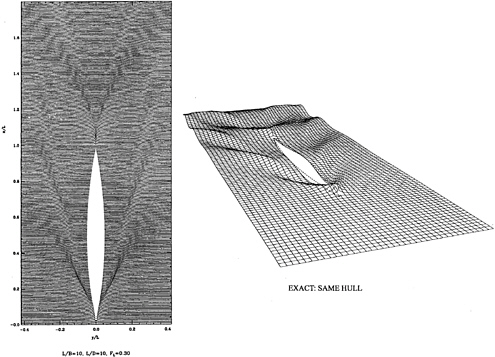
Adequate measurements of Wigley wave patterns away from the hull are not available for a general comparison with calculations. We are, however, able to compare a specific calculation with the 3-D fully non-linear calculation made at MARIN by Hoyte Raven using RAPID. The comparison of the wave pattern for our parent ship (L/B=L/d=10) is shown as Figure 9. The same individual divergent waves, bow and stern, can be seen in each calculation, and their origins and extent match well. Notice the prominent “rooster trail” behind the stern and the resulting diverging waves. There are differences. The 2D+T waves are sharper and less dispersive, and transverse waves are absent. Much remains for the future in terms of understanding the roles of differences in the two methods: transverse waves; grid sizes, etc. It is hoped that in future we may also make comparison with experiments of other hull shapes (Series 60, for example). Meanwhile the present comparison with Raven's calculation gives some confidence in the general patterns predicted in our calculations.
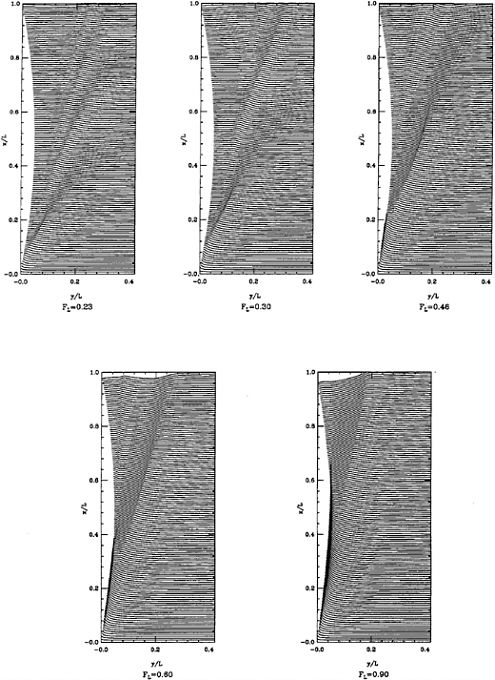
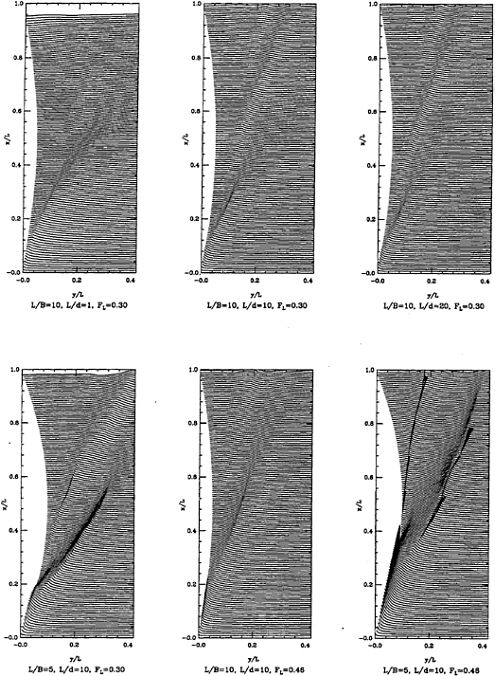
Speed Effects. The effect of speed is shown in a series of calculations for the parent ship for FL=0.23–0.90, Figure 10. The forward wave, (A), is always the steepest and most prominent crest is very sharp over extensive regions for the FL shown up to 0.46, but it doesn't quite break. The splash becomes higher, and moves aft with increase and it seems to originate from the center of the bow splash. Its in speed. For the highest speed, the splash is dominant and is beginning roughly to resemble the spray thrown off by planing craft; wave (A) in this case seems weaker than at lower speeds, perhaps due to the reduction in hull cross sectional area past midships. In all cases the crest lines are much straighter than Kelvin's pattern suggests, and their angle to the flow decreases with increasing speed, as noted by Miyata.
Bottom Effects What is the effect of the ship bottom on these divergent waves? This is illustrated in Figure 11 (top) where the draft is systematically varied. Most striking, for the largest draft, L/d=1, the crest lines are not straight, but are continuously concave, as in the Kelvin pattern. On the other hand, for the shallowest draft, L/d=20, the wave crests are straight and sharper (close to breaking) and even show a slightly convex tendency where they are strongest. The bottom is therefore playing an important role.
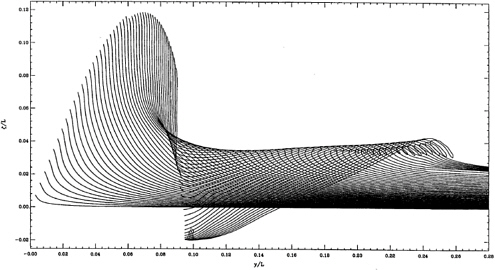
Beam Effects and Breaking The marked effect of beam is shown in Figure 11 (bottom). A decrease in beam provides dispersive-type bow waves, but as might be expected, an increase in beam leads to breaking. This takes the form of an overturning jet, as shown in Figure 12. To continue the calculations aft, the jets are cut and the calculation resumed. This accounts for the sawtooth appearance of the jet locus in Figure 11 (bottom right). As can be seen, the breaking can be very prolonged. In nature the plunging jets will impact the water and in plunging into undisturbed water throw up a splash of its own. This kind of behavior can be observed in pictures of strongly breaking ship waves, Figure 2, and plunging waves in tanks and the ocean. The calculation of these effects is beyond our scope, although hope exists for inviscid modeling. The details of the initiation and development of a strong wave (A) at the bow is shown in figure 12. Notice particularly that the outgoing wave originates in the collapse of the splash. Its propagation is similar in many ways to waves breaking in wave groups: in the rise of the crest, the steepening of the front, and in the jet's formation and growth.
Overturning Splash For other hull shapes than Wigley, the hull splash itself may overturn and merge with a breaking wave, (A). A comparison is made here of a portion of the bow splash for a naval frigate (calculated) and a similar ship under way (photo), see Figure 13. The comparison is striking, and gives confidence to the 2D+T modeling. This example serves to demonstrate that the shape of the bow is essential for the details of the splash formation; perhaps the bow flare has accentuated the breakdown of the splash. Since we believe that divergent bow waves are produced, at least in part, by the bow splash, it could be a test of 3-D codes to reproduce the flow at the bow of this frigate in reasonable detail.
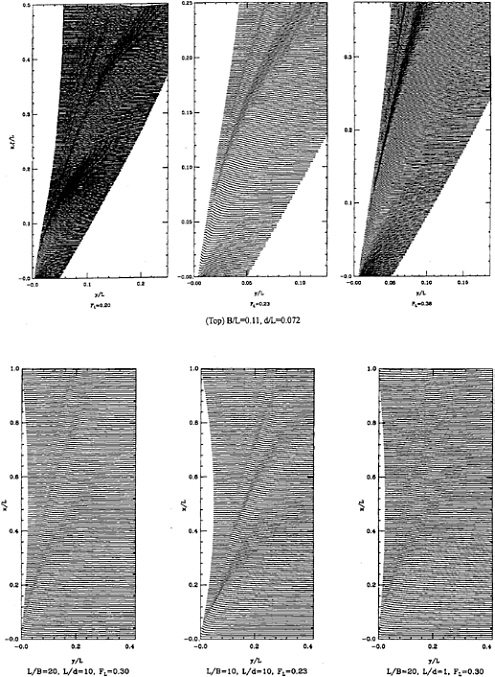
Non-linear Effects vs. Michell Theory We have computed the divergent wave field for the hulls based on Michell theory and applied it by offsetting transversely the center line in the Michell theory to the edge of the hull for each distance aft; a somewhat distorted Kelvin-like pattern appears, which is not at all surprising.
For the parent hull, this Kelvin pattern has hardly any resemblance to the calculation. Moreover, when the beam is reduced by half, to L/B=20, maintaining the draft at L/d=10, a resemblance begins to emerge, see Figure 14. We may therefore conclude that the slenderness of the hull, B/L, is a dominant factor in determining not only the steepness, but also the wave patterns of divergent waves. In particular, an increase in B/L to about 0.1 produces waves (A) and (B) with straight or almost straight crest lines. This is an indication of a narrow spectrum for the divergent waves with a concentration of energy at a particular wave number corresponding to the speed of the waves with straight crests. This is a different situation than predicted by Michell theory, where the spectrum is continuous.
6.
The narrow divergent wave spectrum
Since the bow divergent waves seem to arise from the relaxation of the bow splash, the spectral wave number content of the free waves in the divergent system must be found in a transverse cut through the splash at its maximum. It is crucial, however, to consider both sides of the hull, since the opposing sides can communicate under the hull for normal drafts; this results in interference between the two sides. Then it can be seen that the transverse spacing, B', between the two splashes is the dominant length in the spectrum, at least when this distance is much larger than the width of the splash itself. This spacing, B', scales with the beam, B, and may be roughly approximated as B. However, for the lowest speeds, B'<B, since the splash moves forward and the hull narrows, and at the highest speed where the splash has moved in the vicinity of the maximum beam, B'>B, since the effective transverse spacing, B', must also include the actual width of the splash.
As a consequence of this narrow spectrum around wave length B, the normal spacing between successive straight divergent waves, when they occur, will be close to B. This is the case for the parent hull at FL=0.30.
The key to understanding the bow wave system is Figure 3, the Froude sketch. The individual straight and parallel waves require for their existence a narrow wave spectrum. The normal spacing between the crests seems close to the beam, confirming that the dominant spectral length is B. The angle through the groups (dashed) is about half of the inclination of the separate wave crests to the ship direction. This confirms the propagation of the wave energy at the group velocity, Cg=C/2. And this proves that the bow system is thoroughly dispersive, despite the straightness of the crests, whose explanation, given above, lies in the narrow wave spectrum. The disappearance of the crests outside (roughly) the Kelvin angle may also be observed and requires a dispersive mechanism; in fact, it is due to destructive interference with other waves. Shock waves created at the bow of airfoils, it may be noted, would propagate long distances without such effects.
This explanation of the narrow spectrum, that it is due to the dominance of the transverse separation of the two side splashes on either side of the hull, is completely consistent with the reported effect of the draft and beam on the crest lines. When the draft is abnormally large, as the case L/d=1, the water on opposite sides of the hull cannot effectively communicate, and the splash acts if it is on a single deep wall. In this case, the distributed spectral content in a single splash by itself will result in a dispersive type bow wave, This effect was illustrated in figure 11 (top). The same effect occurs as the beam is decreased, as shown in Figure 11 (bottom). However, a reduction in draft from the parent form, L/d=10 to L/d=20, results, as might be expected, in even straighter crests. All of these remarks apply to wave (A), and sometimes to (B), although the speeds of the latter are sometimes slightly lower.
The Wave Angles According to the ideas just put forth, the velocity of the divergent wave normal to itself, CN, is approximated by the linear dispersion relationship in the form:
(8)
The inclination, δ, of the straight crests is:
δ=sin–1CN/U (9)
or, using (8):
(10)
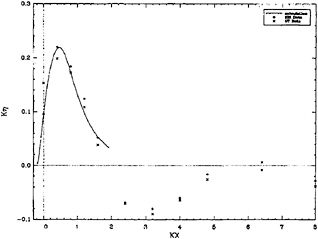
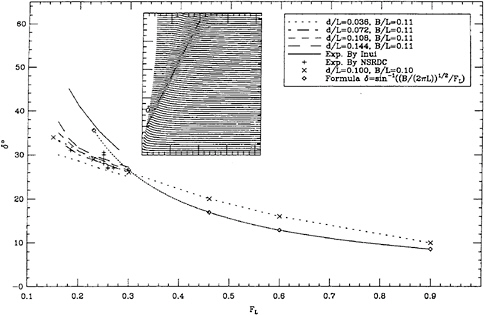
In Figure 15, comparisons are made between the inclination of bow wave (A) and: our 2D+T
calculations for various Wigley hulls; NSRDC measurement; Tokyo measurements; and equation (10). The comparison between present estimates and the NSRDC measurement, Ratcliffe and Lindenmuth(1990), are excellent. The Tokyo measurements are high at low speeds, and this may be due to the presence of surface tension effects. The approximation, eq. (10), is surprisingly good, considering its simplicity. Certainly the correlation with calculations is sufficient to justify the ideas behind it: that the width of the hull, B' ≈ B, in the neighborhood of the splash determines the location of the energy in the divergent wave spectrum, and that the length and speed of the divergent wave (A) is closely related to B'.
7.
The steepness of divergent waves; the Stokes limiting wave
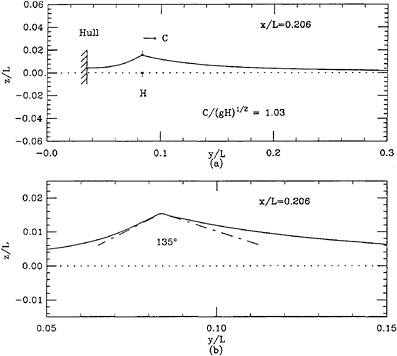
The divergent bow waves for typical ship parameters are steep. This is illustrated in Figure 16 where we show the shape of a divergent, nonbreaking bow wave in a vertical cross section at X/L=0.206 for the parent hull at FL=0.3. the crest is almost, but not quite pointed and the included angle is only 10% larger than for Stokes limiting wave. The height of the wave in the transverse plane is also somewhat larger than that of the Stokes limiting wave (k=g/C2):
(11)
This is clearly quantitative evidence as to the non-linearity of the wave. The calculation of waves of this steepness may pose a difficult challenge for 3-D computation methods.
Eventually as the waves propagate outward, in every case the waves lose height and at the same time the crest broadens and the wave form rapidly subsides. This seems to occur rapidly, and is no doubt due to destructive interference effects, as in the Kelvin kinematical theory.
8.
Summary and conclusion
-
New understanding of the divergent waves produced by normal fine ship bows is reached, based largely on high resolution numerical simulations in 2D+T.
-
The 2D+T simulations have been carried out from the bow into the region behind the ships and reproduce the bow splash waves, the rooster tail, and stern waves.
-
These simulations have the advantage of high resolution, sufficient to define both breaking and post breaking. The evolution and growth of plunging breakers (jets) has been calculated.
-
A comparison has been made for a typical Wigley hull (B/L=d/L=0.1; FL=0.3) with the exact fully non-linear 3-D calculation of Raven at MARIN, Figure 9. The general appearance of the multi-wave system is identical in each simulation (splash, three bow divergent waves, rooster tail, two stern divergent waves on each side of the hull). The origins of each feature and general extent are closely similar. However, the crests of the 2D+T waves are much sharper.
-
For typical fine ship slenderness (B/L=0.1), the crests of the divergent bow waves tend to be straight and their inclination decreases with increasing Froude number.
-
The divergent bow waves have their origin in the bow splash which appears on either side of the bow and the spectral content of the waves originates in the spectral content in the splash cross section taken where the splash reaches its maximum height.
-
For ships of normal beam and draft, the wave spectral content is dominated by the width of the bow at the maximum of the splash due to interference between the two sides. When this width is approximated by B, a good estimate of the wave inclination and its variation with speed can be made.
-
For a slender (B/L=0.1) Wigley hull, the steepness of the divergent bow wave is close to that of a Stokes limiting wave. When the beam is increased to B/L=0.2, massive breaking (plunging) of the divergent waves occurs.
-
The deformation of a breaking bow wave when observed in a vertical cross section has strong similarities to that of breaking two dimensional progressive waves.
-
There remains much yet to learn about divergent waves and the 2D+T method seems a highly useful tool. Although it fails to produce transverse waves, it offers the high resolution necessary to study very steep and breaking waves.
-
Some subjects for future 2D+T simulation studies are: other ship hulls (Series 60; naval frigate); bow modifications to reduce breaking;
-
transom flows; the rooster tail; stern wave breaking and its reduction.
-
It is strongly recommended that a data base be provided of detailed measurements and photographs of divergent waves and stern flows for a suitably broad family of hulls.
Acknowledgement
The authors are grateful for the support from the Office of Naval Research, Computational Ship Hydrodynamics Program, directed by Dr. Edwin P.Rood; and to Hoyte Raven for providing RAPID calculations for comparison purposes.
References
Baba, E. 1969 A study on free surface flow around bow of slowly moving hull forms . J. Soc. Naval Arch. Japan 137.
Cointe, R. and Tulin, M.P. 1994 A theory of steady breakers. J. Fluid Mech. 276.
Dagan, G. and Tulin, M.P. 1972 Two dimensional free surface past blunt bodies. J. Fluid Mech. 51.
Dias, F. and vanden Broeck, J.-M. 1993 Nonlinear bow flows with spray. J. Fluid Mech. 255.
Fernandez, G. 1981 Nonlinearity of the three-dimensional flow past a flat blunt ship . J. Fluid Mech. 108.
Grosenbough, M.A. and Yeung, R.W. 1989 Nonlinear free-surface flow at a two dimensional bow. J. Fluid Mech. 209.
Inui, T. 1970 Wave patterns and hull forms of ships. JUBILEE Memorial, NSMB.
Inui, T. and Kajitani, 1977 H. A study on local nonlinear free surface effects in ship waves and wave resistance. Schifftechnik, Band 24 Heft 118.
Inui, T., Kajitani, H and Miyata, H. 1979 Experimental investigation of the wave making in the near field of ships. J. Soc. Naval Arch. Japan 173.
Keller, J.B. 1974 Wave patterns of non-thin or full-bodied ships. Proc. 10th Symp. Naval Hydrodynamics, Cambridge, MA.
Keller, J.B. 1979 The ray theory of ship waves and the class of streamlined ships. J. Fluid Mech. 91.
Maruo, H. 1990 Prediction of deck wetness: A theoretical development. Technical Report 90– 53, OEL, UCSB.
Miyata, H. 1980 Characteristics of nonlinear waves in the near field of ships and their effects on resistance. Proc. 13th Symp. Naval Hydrodynamics, Tokyo, Japan .
Mori, K. 1985 Necklace vortex and bow wave around blunt bodies. Proc. of 15th Symp. Naval Hydrodynamics, Hamburg, Germany.
Ratcliffe, T.J., Lindenmuth, W.T. 1990 Kelvin wake measurements obtained on five surface ship models. DTRC-89/038.
Raven, H. 1993 Nonlinear ship wave calculations using the RAPID method. Proc. 6th Int. Conf. on Num. Ship Hydrodynamics. Iowa City, USA.
Song, W and Maruo, H. 1993 Bow impact and deck wetness: simulations based on nonlinear slender body theory. Proc. ISOPE, Singapore.
Standing, R. 1974 Phase and amplitude discrepancies in the surface wave due to a wedge-ended hull form. J. Fluid Mech. 62.
Tulin, M.P. 1956 Theory of slender surface planing at high speeds. Schiffstechnik, 14.
Tulin, M.P. 1970 Cavity flows and breaking waves. JUBILEE Memorial, NSMB.
Tulin, M.P. 1985 Surface waves from the ray point of view. Proc. of 15th Symp. Naval Hydrodynamics, Hamburg, Germany.
Tulin, M.P. and Hsu, C.C. 1986 Theory of high speed displacement ships with transom sterns. J.S.R., 21–1.
Tulin, M.P. and Wu, M 1994 Bow waves on fine ships—nonlinear numerical studies. In Proc. 9th Int. Workshop on Water Waves and Floating Structures. Kyushu, Japan.
vanden Broeck, J.-M. and Tuck, E.O. 1977 Proc. 2nd Int. Conf. Num. Ship Hydrodynamics, Berkeley.
Yeung, R.W. 1991 Nonlinear bow and stern waves-inviscid and viscous solutions. Mathematical Approaches in Hydrodynamics, SIAM press.
Yim, B. 1981 A ray theory for nonlinear ship waves and wave resistance. Proc. 3rd Int. Conf. on Num. Ship Hydrodynamics, Paris.