Examination of the Flow Near the Leading Edge and Closure of Stable Attached Cavitation
A.Leger, P.-W.Yu, K.Laberteaux, S.Ceccio (University of Michigan, USA)
Abstract: The flow near both the cavity detachment and closure region of attached cavitation is investigated. Cavity detachment from a ventilated sphere is examined, and the relationship between the location of cavity detachment and flow separation is related to the geometry of the cavity near detachment. The flow field near the closure of a natural partial cavity is investigated with Particle Imaging Velocimetry (PIV), and preliminary results are provided.
Introduction: The inception and dynamics of sheet cavitation is of considerable interest to designers of ship propellers. Sheet cavitation can cause a loss of performance, pressure pulsations, and cavitation erosion. Ideally, designers of these devices would have analytical tools which could be used to predict the occurrence of sheet cavitation, its potential for instability, and its potential for erosion. Today, however, the current design tools can only predict the general location of sheet cavitation inception, and this is usually done by examining the fully wetted potential flow around blade surfaces of the propeller.
Inception is predicted when the pressure on the lifting surfaces falls below the liquid vapor pressure (e.g. the CP.MIN=σ criteria). This method often cannot provide critical information about the detailed nature of the cavity sheet such as the topology of the sheet, the extent of the sheet, the erosiveness of the sheet, or its potential to become unstable and form cloud cavitation. In addition, models of attached cavitation often require a priori information about the cavitating flow. Constraints which have been used in predicting inception include the location of cavity detachment and length of the cavity. Models of the closure region of the cavity must be used for the case of partial cavitation. These models often do not capture the detailed flows in that region.
In the present study, we are examining the flow fields near the inception and the closure of stable attached cavities, and our goal is to provide new insights into the physical processes of cavity formation and closure. Two parallel experimental research programs are described below. First, we are examining the process of cavity detachment on a bluff object. Second, we are examining the closure region of a closed partial cavity. The experimental techniques employed in each study are described, and current results are presented and discussed.
Experimental Methods: The experiments described here were conducted in the Cavitation and Multiphase Flow Laboratory at the University of Michigan Department of Mechanical Engineering and Applied Mechanics.
Measurements were made in the Blow Down Water Tunnel (BDWT), and a description of this facility is provided in Tassin et al. (1995). In brief, the BDWT consists of two 1.5 m3 tanks connected via a contraction, a test section and a diffuser. Controlled application of pressure and vacuum to the two tanks are employed to produce the desired flow in the test section, which is 76.2 mm square and approximately
260 mm long. Between 10 and 20 seconds of steady flow can be produced with velocities in the range of 5 to 25 m/s (in the empty test section). The test section velocity is determined by measuring the pressure difference between the test section entrance and the pressure near the entrance of the contraction. This pressure difference was related to the test section velocity using LDV measurements of the average flow velocity in the center of the empty test section. The free and dissolved air content of the BDWT can be qualitatively controlled through deaeration and by allowing free gas bubbles to reach the free surfaces in the two tanks.
In the study of the detachment region of an attached cavity, results are presented here for the cavity flow over a 25.4 mm diameter brass sphere which was mounted on a sting within the BDWT test section. The surface of the sphere was either highly polished or roughened. The sting was plumbed to permit injection of air into the cavity, and a separate pressure tap was used to measure the difference between the cavity pressure and the static pressure of the flow upstream of the model. Five 203 µm diameter holes were placed in the sphere at an angular location of 22.5 degrees measured from the stagnation point, and fluorescein dye was injected

Figure 1: The 25.4 mm diameter sphere mounted on a sting in the BDWT test section. A ventilated cavity flow behind the sphere was created to study the region of cavity separation.
through these holes to permit visualization of the flow near the surface of the sphere. Flash photography and high speed video imaging were used to capture images of the dye streak as it flowed over the sphere. This setup is shown in Figure 1.
The flow streamlines near the surface of the sphere were recorded using particle tracers. The flow was illuminated with a continuous light sheet produced with an Argon-Ion laser, and silvered hollow glass spheres of nominally 10 µm diameter were added to the flow as tracers. Photographic images of the streamlines near the cavity were produced by time exposing the image of the flowing particles.
A wedge was used to produce a partial cavity in the study of the closure of partial cavitation. The wedge had an angle of 26.5 degrees and a step height of 19 mm, and was mounted to the wall of the test section. Partial cavities formed on the vertex of this wedge. An image of this setup is shown in Figure 2. Double pulsed Particle Imaging Velocimetry (PIV) was used to investigate the flow field in the closure region of the cavity. The details of the PIV experimental setup is provided in Tassin et al. (1995) and Yu (1995). Two frequency-doubled Nd-YAG lasers were used to produce a pulsed light sheet, and the flow was seeded with fluorescent latex particles with an average

Figure 2: A wedge mounted on the wall of the BDWT test section. A natural cavity separates from the vertex of the wedge.
diameter of 30 µm. The light sheet had an average thickness of 1 mm and was positioned parallel to the mean flow direction with maximum intensity near the closure region of the cavity. Two cameras were placed on opposite sides of the sheet to record images of the light sheet. One camera recorded all the scattered light from the bubbles and particles within the sheet, and the second camera was equipped with a filter to block the scattered laser light while recording the fluorescent return of the particles. Thus, it was possible to detect only the motion of the particle tracers as they flowed in the bubbly region behind the cavity. The double pulsed images recorded on the photographs were digitized and processed to determine particle pairs.
Flow Field Near the Leading Edge of a Ventilated Cavity: Developed attached cavitation results from the detachment of the flow from either a smooth surface or at a discontinuity of the slope on the surface. It is often not clear where a cavity will separate from a smooth surface simply from examination of the fully wetted flow. Brennen (1969a and 1969b) examined the fully developed cavity flows over a sphere and cylinder, and Arakeri and Acosta (1973) and Arakeri (1975) studied flows over a variety of headforms. These studies revealed that the viscous flow near the surface strongly influences the inception and location of cavity detachment.
Arakeri (1975) studied the relationship between laminar boundary layer separation and cavity detachment. Cavities were shown to be preceded by laminar boundary layer separation in the non-cavitating flow, yet the location of the cavity detachment was not necessarily near the non-cavitating separation point. Figure 3 shows a schematic drawing of the cavity detachment for a nominally two dimensional cavity, as presented by Arakeri. The boundary layer is observed to separate upstream of the cavity detachment, and the cavity interface is observed to curve into the solid surface. Arakeri offered correlations to predict the location of boundary layer separation upstream of the cavity and the distance between the boundary layer separation and the cavity detachment, λ. The position of boundary layer separation was found to be a weak function of Reynolds number and a strong function of cavitation number. λ was related to the Taylor-Saffman number, µUo/T (where µ is the dynamic viscosity of the fluid, T is the surface tension, and Uo is the freestream velocity), and to the momentum thickness of the non-cavitating boundary layer near the point of boundary layer separation.
Franc and Michel (1985) also significantly expanded the work of Arakeri with examination of the flow over a series of bodies, including hydrofoils. Franc and Michel also recognized the relationship between the presence of non-cavitating laminar boundary layer separation and the formation of attached cavitation, and they proposed a method to predict the location of cavity detachment on smooth surfaces. Their method recognizes that the presence of a cavity will alter the pressure distribution around the cavitating object, and this will modify the growth of the boundary layer upstream of the point of cavity detachment. It was shown that a cavity will detach if the modified boundary layer separates upstream of the cavity.
Franc and Michel point out the “cavity detachment paradox.” A cavity must be preceded by laminar boundary layer separation. However, the cavity pressure may be the lowest pressure of the flow, and this would result in a favorable pressure gradient just upstream of the cavity. Thus, laminar separation would not be expected to occur. Need the region upstream of the cavity be in tension (or have pressure lower than the cavity pressure, in the case of a
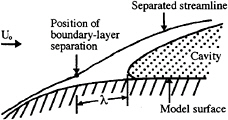
Figure 3: Schematic drawing of the cavity detachment region (after Arakeri, 1975).
ventilated cavity)? Moreover, the laminar separation streamline and the cavity free streamline enclose a region of fluid bounded by two stagnation points, and this would suggest that there is a fluid sink downstream of the cavity without a corresponding source. Thus, the flow may recirculate or be three-dimensional in the region upstream of cavity separation.
With these questions in mind, we have initiated our study of this flow by examining the detachment of a ventilated cavity flow behind a sphere. This is a well-characterized flow (both cavitating and non-cavitating), and we can use previous results for comparison and validation. First, we examined the non-cavitating flow around the sphere to determine whether blockage effects were significant and to determine the accuracy with which we can determine boundary layer separation with dye injection. Figure 4 presents the angle of flow separation measured from the front stagnation point as a function of Reynolds number, Re=U0D/v, where D is the diameter of the sphere and v is the liquid kinematic viscosity. Data from the present study is
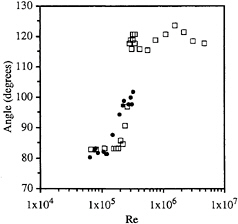
Figure 4: Angle of flow separation on the non-cavitating sphere for varying Reynolds number (•). The angle is measured from the front stagnation point. The data of Achenbach (1975) is shown for comparison (□).
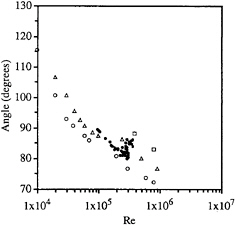
Figure 5: Angle of cavity detachment as a function of Reynolds number for 0.3 <σ< 0.5 (•). The data of Arakeri (1975) is presented for comparison for σ=0.1 (○),; σ=0.25 (☐), and σ=0.5 (Δ).
compared to that of Achenbach (1972), and the agreement is good.
The freestream pressure was reduced, and air was injected into the wake of the sphere forming a fully developed cavity. Figure 5 shows the angle of cavity detachment versus Reynolds number for a small range of cavitation numbers ![]() where P0 is the freestream static pressure, PC is the cavity pressure, and ρ is the fluid density. Data presented by Arakeri (1975) is also shown for cavitation on 6.35 and 12.7 mm diameter spheres, and the trends in the data are similar. The position of cavity detachment in these tests is upstream of the non-cavitating laminar separation point in the first set of tests, and this result also has been observed for developed cavity flows behind cylinders and hydrofoils (Arakeri and Acosta, 1973;, Arakeri, 1975; and Franc and Michel, 1985).
where P0 is the freestream static pressure, PC is the cavity pressure, and ρ is the fluid density. Data presented by Arakeri (1975) is also shown for cavitation on 6.35 and 12.7 mm diameter spheres, and the trends in the data are similar. The position of cavity detachment in these tests is upstream of the non-cavitating laminar separation point in the first set of tests, and this result also has been observed for developed cavity flows behind cylinders and hydrofoils (Arakeri and Acosta, 1973;, Arakeri, 1975; and Franc and Michel, 1985).
Figure 6 presents a close-up side view of the cavity detachment region with associated dye visualization. The surface of the cavity forms a sharp curve as it detaches from the solid surface, and this implies a hydrophilic surface. Figure 7 shows a similar flow visualized with particle streaks, and the
separation streamline appears to intersect the cavity free streamline. Figure 8 is a close-up view of the detachment region, again employing particle streak visualization. These time exposed images reveal slowly moving particles recirculating in the separation region bounded by the cavity interface and the separation streamline.
The cavity has a finite thickness near the point of detachment which forms a forward facing step. The “step height”, h, is a function of both the Reynolds number and the cavitation number, as shown in Figure 9. Interfacial tension between the liquid and cavity gas will result in a pressure difference across the interface in this region of steep curvature. The pressure jump across the cavity at the point of detachment, PD–PC, is approximated by ![]() Here,
Here, ![]() is roughly
is roughly
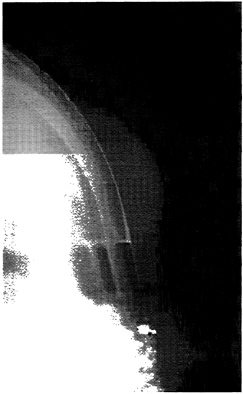
Figure 6: A close-up side view of the cavity detachment region. Re=1.8×105 and σ=0.5

Figure 7: The flow near the cavity detachment region visualized by particle streaks. Re=1.2×105 and σ=0.2

Figure 8: Close-up particle streak images of the recirculating region ahead of the cavity detachment. Re=1.1×105 and σ=0.1
0.01, leading to only a small modification of the local cavitation number. Thus, it is expected that the gas/liquid interfacial tension will not play a significant role in the process of cavity detachment. However, the solid-liquid interfacial tension may play a more significant role.
In general, as the Reynolds number increases, h decreases. Also, as the cavitation number is reduced, h increases. Arakeri (1975) suggested that the momentum thickness of the boundary layer just upstream of cavity detachment strongly influences the region of cavity detachment. We do see that h is dependent on the Reynolds number, but the dependence is approximately linear, while the momentum thickness will vary as Re1/2 for laminar boundary layers. The distance between boundary layer separation and cavity detachment, λ, can be related to the cavity thickness at cavity detachment. Figure 10 suggests such a relationship. A linear fit of the data reveals that λ ≈ 3h.
The cavity thickness begins to increase for Re>2.6×105, and this is due to the increasing three-dimensionality of the flow near the point of cavity detachment. For Re<1×105, a smooth streamsurface
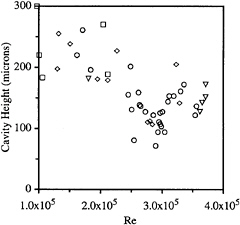
Figure 9: The cavity “step height”, h, as a function of Reynolds number for varying cavitation numbers. σ=0.33–0.38 (☐), σ= 0.39–0.43 (◇), σ=0.44–0.46 (○), σ= 0.47–0.52 (∇).
separates from the sphere. But, as the Reynolds number increases, streamwise indentations begin to form near the point of cavity detachment. Figure 11 shows three images of the cavity with varying numbers of these features, which we will refer to as “divots”. High speed video images show that a divot forms when a disturbance locally indents a region of the cavity interface, and this disturbance rapidly evolves into a single thin fluid-filled channel. A divot may persist for long periods of time, and it can remain stationary, oscillate, or travel in the circumferential direction. Some divots would merge together, and others would be destroyed by flow disturbances.
Increasing the Reynolds number increased the formation of these divots, but it appears that they do not form as the result of a periodic instability of the cavity interface. Brennen (1969b) examined these structures as they formed on the interface of spheres and cylinders in polymeric solutions, and it was found that a circumferential disturbance near the point of cavity detachment would grow in amplitude and frequency with increasing Reynolds number. In the present study, however, we did not observe this mechanism of divot formation. Instead,
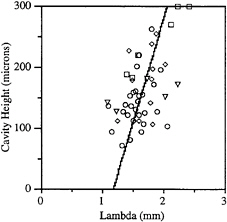
Figure 10: The cavity step height, h, as a function of separation distance, λ, for varying cavitation numbers. σ=0.33–0.38 (□), σ= 0.39–0.43 (◇), σ=0.44–0.46 (○), σ= 0.47–0.52 (∇). The line represents a least-squares fit.
divots were formed at random locations on the sphere circumference, and, if the water in
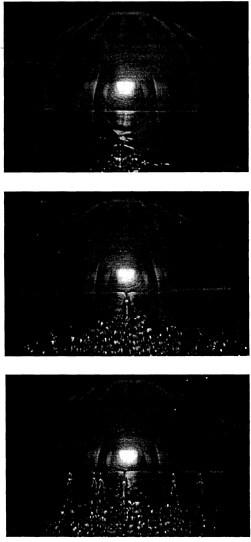
Figure 11: Three images of the cavity with varying number of divots. (a) Re=1.2×105 and σ=0.53 (b) Re=1.9×105 and σ= 0.44 (c) Re=2.0×105 and σ=0.47.
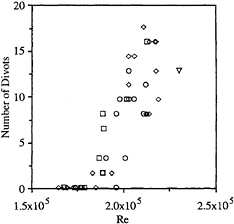
Figure 12: The average number of divots as a function of Reynolds number for varying cavitation numbers. The data represents flows in which re-entrant jets did not disturb the cavity detachment region. σ=0.33–0.38 (☐), σ=0.39–0.43 (◇), σ=0.44–0.46 (○), σ=0.47–0.52 (∇). The field of view covered 1/8th of the sphere circumference.
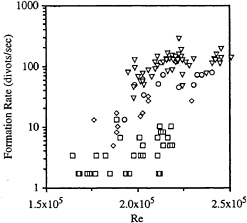
Figure 13: The rate of divot formation as a function of Reynolds number. Data is divided into four groups, ranging from flows with no re-entrant jet (☐) and with approximately 2 (◇), 6 (○) and >6 (∇) jets per second in the field of view which covered 1/8th of the sphere circumference.
the BDWT was allowed to settle for long time periods before an experiment, the number of divots created would be substantially reduced. The non-Newtonian nature of Brennen's flows may be responsible for the observed differences.
Divots were also created and destroyed by the action of a re-entrant flow which originated downstream of the cavity separation zone. Figure 12 presents the average number of divots as a function of Reynolds number for cavity flows where re-entrant jets were not observed to impinge on the cavity detachment region. Figure 13 shows the frequency of divot formation as a function of Reynolds number and the frequency of re-entrant jet formation. As the Reynolds number increases, the likelihood that a divot will form and persist increases.
A sphere was roughened to artificially trip the boundary layer upstream of cavity separation, and it was found that there was very little difference between the tripped and untripped flows, and this suggests that a strong favorable pressure gradient upstream of the cavity separation may lead to re-laminarization of the boundary layer.
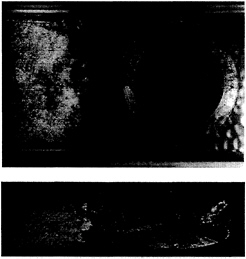
Figure 14: Plan and oblique view of a partial cavity which has formed at the vertex of the wedge. Uo=10 m/s, σ=1.2, and the cavity length is approximately 50 cm.
Flow Field in the Closure Region of a Stable Partial Cavity: The dynamics of partial cavitation has been examined by several investigators. The formation of cloud cavitation via the re-entrant jet is discussed by Knapp et al. (1970) and Furness and Hutton (1975). Recent experimental work has been conducted by Avellan et al. (1988), Kubota et al. (1989), Yamaguchi et al. (1990), and Le et al. (1993a and 1993b). In these studies, the details of the flow surrounding both steady and unsteady attached cavitation have been examined using a variety of experimental techniques. Avellan et al. (1988) and Kubota et al. (1989) employed LDV to determine the mean and phase averaged flow field around partial cavities, and Le et. al. (1993a and 1993b) employed mean and dynamic pressure measurements. Detailed measurements near attached cavities are made difficult by the large range of flow scales, the presence of two phases, and the unsteadiness of the cavity surface and closure region.
We are currently examining the flow field near the closure region of partial cavities using Particle Imaging Velocimetry (PIV). A wedge is used to produce a partial cavity. By varying the angle of the wedge, it is possible to create both open and closed partial cavities. The images presented here are for closed cavities. A view of the cavitating wedge is shown in Figure 14, and Figures 15 and 16 present typical PIV images and the measured vector fields in a region close to the cavity closure. Shown in the figures are the filtered and unfiltered double-pulsed images and the vectors field reconstructed from the filtered images. These images are relatively lightly seeded, and particle tracking was used to identify individual velocity vectors of the flow. Comparison of the filtered and unfiltered images reveal the utility of fluorescent flow tracers. While bubbles may mask some of the particles, it is still possible to discern individual particle pairs quite close to the cavity closure.
Discussion: Our study of the detachment and closure region of attached cavitation is continuing; however, the results presented here reveal some new insights and will guide our studies.

Figure 15: Three images of the closure region of a partial cavity- (a) unfiltered double-pulsed PIV image, (b) the filtered image, and (c) the velocity vectors recovered from the filtered image. Scales are shown.

Figure 16: Three images of the closure region of a partial cavity- (a) unfiltered double-pulsed PIV image, (b) the filtered image, and (c) the velocity vectors recovered from the filtered image. Scales are shown.
Detailed examination of the cavity detachment region has revealed that the local geometry of the cavity can be related to the position of boundary layer separation upstream of the cavity. The cavity forms a “forward facing step” with a step height which is 2 to 3 times larger than the boundary layer thickness. It is expected that such a geometry would lead to an upstream boundary layer separation. However, it is unclear how the location of flow separation is influenced by the local cavity geometry.
There is a recirculating region upstream of the cavity, and the flow in this region may be either two or three-dimensional. At higher Reynolds numbers, the interface develops small depressions or “divots. ” These divots are created and destroyed by disturbances in the flow such as freestream turbulence or the impingement of a re-entrant jet into the detachment region. As the Reynolds number increases, the overall number of divots also increases. These structures form when there is a local breakdown in the two-dimensional flow near the cavity detachment, resulting in a complex three-dimensional flow. It is unclear at present if a laminar separation is still present upstream of the cavity in these cases.
Lastly, we have developed techniques to examine the flow field in the closure region of a partial cavity. By employing fluorescent flow tracers, it is possible to detect Lagrangian flow tracers in the bubbly region just downstream of the cavity closure. We currently are employing particle tracking to analyze the PIV images, and we are striving to increase the density of vectors which can be measured. With PIV, we will be able to determine how the flow field closes behind the cavity and the momentum deficit in the cavity wake.
Acknowledgments: We would like to thank Prof. Joseph Katz for making available to us the fluorescent particles used in the PIV. This work is being supported under the Office of Naval Research contract number N00014 –96–1–0076, Dr. E.P.Rood, technical monitor.
References:
Achenbach, E. 1972. Experiments on the flow past spheres at very high Reynolds numbers . J. Fluid. Mech. 54, pp. 565–575.
Arakeri, V.H. 1975. Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid. Mech. 68, pp. 779–799.
Arakeri, V.H. and Acosta, A.J. 1973. Viscous effects in the inception of cavitation on axisymmetric bodies . Trans. ASME I: J. Fluids Eng.. 95, pp. 519–527.
Avellan, F.; Dupont, Ph.; and Rhyming, I. L. 1988. Generation mechanism and dynamics of cavitation vortex downstream of a fixed leading edge cavity, Proc. 17th Symp. on Naval Hydrodyn., The Hague
Brennen, C.E. 1969a. The dynamic balances of dissolved gas and heat in natural cavity flows. J. Fluid. Mech. 37, pp. 115–127.
Brennen, C.E. 1969b. A numerical solution of axisymmetric cavity flows. J. Fluid. Mech. 37, pp. 671–688.
Franc, J.P. and Michel, J.M. 1985. Attached cavitation and the boundary layer: experimental investigation and numerical treatment. J. Fluid. Mech. 154, pp. 63–90.
Furness, R.A. and Hutton, S.P. 1975 Experimental and technical studies of two-dimensional fixed-type cavities. J. Fluids Eng., 97, pp 515–522.
Knapp, R.T.; Daily, J.W.; and Hammit, F. G. 1970. Cavitation, McGraw-Hill.
Kubota, A.; Kato, H.; Yamaguchi, H.; and Maeda, M. 1989. Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling techniques. J. Fluids Eng.., 111, pp 204–210.
Le, Q.; Franc, J.P.; and Michel, J.M. 1993. Partial Cavities: Global Behavior and Mean Pressure Distribution , J. Fluids Eng.., 115, pp 243–248.
Le, Q., Franc, J.P., and Michel, J.M. 1993. Partial Cavities: Pressure Pulse Distribution Around the Cavity J. Fluids Eng.., 115, pp 249–254.
Tassin, A.L.; Li, C.-Y; Ceccio, S.L.; and Bernal, L.P. 1995. Velocity field measurements of cavitating flows. Exp. in Fluids, 20, pp. 125–130.
Yu, P.-W. 1995. Experimental and numerical investigation of cavitating flows. Doctoral Thesis, University of Michigan











