Appendix D Future Directions for Low Power Electronics
For nearly four decades, low power silicon microelectronics have improved exponentially in both performance and productivity. The switching energy, or power-delay product, of a binary transition has been reduced by about five orders of magnitude, and the number of transistors per chip has increased by about eight orders of magnitude. At the same time, the price range of chips has remained almost constant. The National Technology Roadmap for Semiconductors (NTRS) projects a 64-billion-bit dynamic random access memory (DRAM) chip by 2010 (Semiconductor Industry Association, 1994). Perhaps the most compelling questions confronting the surging $150 billion worldwide semiconductor industry are how much further the laws of physics (and economics) will enable this progress to continue and what the critical limits most likely to determine how many billions of transistors we will manufacture in future commercially viable low power silicon chips are. Several focused efforts to address this question have been reported in the last two decades (Keyes, 1975a, 1979; Meindl, 1983, 1995).
The central thesis of this appendix is that early twenty-first century opportunities for low power gigascale integration (GSI) will be governed by an ordered progression or hierarchy of theoretical and practical limits, whose five levels can be classed as fundamental limits; material limits; limits on device; limits on circuit; and limits on systems (Meindl 1983, 1995). The following section reviews recent enhancements of this hierarchy and identifies the critical limits that present the most formidable challenges to continued progress toward low power GSI.
THEORETICAL LIMITS
Energy transfer per binary transition is a very useful metric for comparing the performance of switching operations at all levels of the hierarchy of limits on low power GSI. Using logarithmic coordinates in the power-delay plane, where the ordinate is the average power transfer during a binary transition, P, and the abscissa is the delay time of the transition, td, results in a diagonal constant switching energy locus, E = Ptd. Interconnect performance can also be illustrated at all levels of the hierarchy in a logarithmic plot of "reciprocal length squared,"
L-2, versus response time, t, where L is the distance traversed by an interconnect that joins two nodes on a chip and t is the response time of the interconnect circuit. Using logarithmic coordinates in the L-2 vs. t plane results in a diagonal constant distributed resistance, rrint, capacitance, ccint, locus L-2t = rintcint, for an interconnect. For continued improvements in low power electronics, both the E = Ptd and L-2t = rintcint loci must migrate toward the lower left corners of their displays.
Fundamental Limits
At the first level of the hierarchy are three fundamental limits on low power electronics (Meindl, 1995). Derived from thermodynamics, the first of these is a result of the random thermal motion of carriers in solids. This limit imposes a minimum switching energy, E, on a binary transition of approximately 2 to 4 kT or 0.05 to 0.1 eV at room temperature, where kT is the familiar thermal energy. Quantum mechanics, and more specifically the Heisenberg uncertainty principle, defines the second fundamental limit, which requires a switching energy E > h/td, where h is Planck's constant and td is the transition time, for td = 1.0 ps, E > 0.004 eV. The propagation velocity of an electromagnetic wave traveling in free space (co = 3 × 1010 cm/sec) determines the third fundamental limit.
Within these fundamental limits, the switching energy required to overcome the thermal energy of an electron, as well as the energy uncertainty resulting from its wavelike behavior, are orders of magnitude smaller than projected system limits on switching energy. (A fundamental opportunity for further reducing energy dissipation in binary switching operations, derived from the second law of thermodynamics, is based on conserving or recycling switching energy by maintaining constant entropy in a computing engine. This approach is practical for a limited range of applications). Nevertheless, the propagation velocity of a high-speed pulse traveling on an effectively lossless global interconnect now approaches 50 percent of the velocity of light in free space. Consequently, it appears that the most binding fundamental limit is currently determined by the velocity of light.
Material Limits
There are four material limits at the second level of the hierarchy. Three are imposed by semiconductor materials and the fourth by interconnect materials (Meindl, 1995). A switching energy limit is defined by the amount of energy that must be stored in a cube of semiconductor material to produce a binary transition voltage of 1 V. ( The selection of a 1 V transition is justified in the following discussion of circuit limits). This energy—about 10 eV—is approximately 20 percent larger for silicon (Si) than for gallium arsenide (GaAs), an insignificant difference.
A transit time limit is determined by the interval required for an electron to be transported through the cube. For Si, this interval is about 0.33 ps, assuming that the material operates at its breakdown field strength and carrier saturation velocity. This transit time limit is 33 percent larger for Si than for GaAs, again an insignificant difference.
The third key material limit is defined as the intrinsic switching delay per unit of heat removal of a generic device located at the top surface of a chip whose bottom surface is in contact with an ideal heat sink. This heat-conduction-limited delay is about three times as large for GaAs as for Si, because GaAs has three times the thermal resistivity of Si. In this instance, Si offers a significant advantage.
The fourth material limit is the propagation velocity of an electromagnetic wave in a uniform dielectric material whose relative permittivity is greater than unity. For a typical dielectric, such as SiO2, the value of this limiting velocity is roughly 50 percent of the corresponding fundamental limit for virtually lossless interconnects. (For lossy interconnects, the relaxation time, τ = ρε, where ρ is the conductor resistivity and ε the dielectric permittivity, represents the key material limit.)
The implications of the three semiconductor material limits are that switching energy and transit time constraints imposed by semiconductor materials per se are well below those projected for the system level, and that Si is indeed the semiconductor material of the future for low power GSI. The interconnect materials of the future are unclear but, as at the fundamental level, the time-of-flight of an electromagnetic wave appears to be the most binding material limit for virtually lossless interconnects.
Performance Limits on Devices
Proceeding to the third level of the hierarchy, the key limits on low power electronics are imposed by the switching energy and delay of a metal-oxide-semiconductor field effect transistor (MOSFET) and the response time of an interconnect (Meindl, 1995). Both MOSFET limits are defined largely by its minimum allowable effective channel length, Lmin, at an assumed drain voltage of 1.0 V. Analytical and numerical calculations as well as recent experimental data show that Lmin for a bulk MOSFET with a uniform channel doping profile is about 100 nm, assuming a 3.0 nm gate oxide thickness in order to avoid tunneling current, a maximum drain voltage of 1.5 V, and a threshold voltage of 0.35 V. The corresponding switching energy is approximately 104 eV. For an abrupt retrograde channel doping profile, Lmin drops to about 50 nm. For a symmetrical dual-gate silicon-on-insulator (SOI) MOSFET, a device that we do not yet know how to manufacture, the projected Lmin is approximately 25 nm. Postulating a bulk MOSFET with a yet-to-be-demonstrated high-permittivity gate dielectric stack, an Lmin in the range of 25 nm can be projected. Finally, an additional opportunity for achieving a sub-25 nm channel length is based on reducing gate oxide thickness
below the 3.0 nm tunneling limit to the 1.5 to 2.0 nm range, which is still sufficiently large that MOSFET gate current would be small compared to the average current drain of a typical logic circuit.
The strong message conveyed by the foregoing discussion of MOSFET scaling limits is that we have more than 20 years of device scaling in the offing—if the historic level of inventiveness is maintained. This 20 year projection assumes that the current rate of scaling minimum feature size will persist at least through the 125 nm generation of technology and thereafter will not fall below one-half its current rate, as noted in the following discussion of practical limits.
Although MOSFET scaling richly benefits both performance and productivity, the impact of scaling interconnect dimensions is markedly different. A critical device level limit is defined by the response time of an interconnect. Using a canonical distributed resistance-capacitance network as a model, response time is given by t = rintcintL2, as described in the opening paragraph of this discussion of theoretical limits. For example, assuming a 1.0 mm technology, the minimal 10 ps switching delay of a MOSFET is 10 times as large as the response time of a 1.0 mm long interconnect implemented with Al and SiO2. But, for 0.1 mm technology, the 100 ps response time of a 1.0 mm interconnect is at least ten times larger than the switching delay of a MOSFET. Moreover, for 0.1 mm technology, the switching energy of a 1.0 mm interconnect is greater, by a factor of approximately 1,200, than the switching energy of a minimum size MOSFET. This simplified example clearly suggests that the most binding device performance limits on low power GSI will be imposed by interconnects and not by MOSFETs—unless current circuit and system configurations are significantly altered to avoid the use of long interconnects.
As the number of interconnects multiplies, innovative techniques and technologies will be required to reduce wire capacitance. Integrating memory with logic by use of emerging integrated memory technology will allow interconnect lengths to be kept short by eliminating the need for high-capacitance external memory access. Significant advances have also been made in the area of low-swing drivers and in techniques ranging from adding regulators on-chip to energy recovery approaches.
Limits on Circuits
At the fourth level of the hierarchy, there are four generic circuit limits on low power electronics imposed by the static transfer characteristic of a logic gate, by the power-delay product or switching energy of the gate, by its propagation delay time, and finally by the response time of a global interconnect circuit (Meindl, 1995). To maintain the quintessential capability to restore binary "zero" and "one" levels virtually without error throughout a large digital system, the transfer characteristic of a complementary metal-oxide semiconductor (CMOS) logic gate must have a slope with an absolute magnitude of at least unity at the transition point where input and output signals are equal.
Imposing this quantizing constraint on the transfer characteristic of a CMOS inverter circuit reveals that the minimum allowable supply voltage of CMOS circuits is approximately 2 to 4 kT/q or 50 to 100 mV at room temperature. Then, one may ask, why not immediately reduce supply voltage from the 3.0 V range now commonly used to the 50 to 100 mV range and thereby reduce the energy per switching transition by three orders of magnitude? To do so without sacrificing performance would require scaling down threshold voltage, Vt, roughly in proportion to the reduction in supply voltage, Vdd. Because MOSFET subthreshold current increases exponentially as threshold voltage is reduced, the result of such drastic scaling of supply and threshold voltage would be an unacceptably large static current drain in a CMOS logic circuit.
A more interesting question to ask, therefore is, what the optimal value of supply voltage that minimizes the total energy is or what the average power dissipation per clock cycle of a typical gate circuit in a complex logic network is. Note that the total energy consists of the sum of the dynamic (or switching) energy and the static (or standby) energy drain during a clock period whose value is determined by performance requirements. A simplified expression for this optimal supply voltage (Bhavnagarwala et al., 1996) indicates its dependence on: S, MOSFET subthreshold swing ;µ, subthreshold channel carrier mobility; ncp, the number of gates in the critical path of the logic network; a, the network activity factor or probability that a gate will switch during a given clock cycle; b, the fraction of a clock cycle available for logic operations or the clock skew factor; vsat, the channel carrier saturation velocity; L, the effective channel length; and Vdd/Vt, the ratio of supply voltage to threshold voltage determined by performance requirements.
Clearly, each MOSFET technology and each logic network configuration defines its own optimal supply voltage for low power operation. Computing values of Vdd (opt) for a wide range of device and logic network parameters indicates that Vdd (opt) = 1.0 V is a midrange value that is broadly advantageous. Consequently, a 1.0 V supply voltage is used to compute limits at the material, device, circuit, and system levels of the hierarchy of limits on low power electronics.
For a specified supply voltage, Vdd, and total circuit load capacitance, Cc, the switching energy limit E = (1/2) Cc (Vdd)2 has a value of about 4x104 eV for 100 nm technology. The corresponding propagation delay limit, td, is approximately 0.01 ns (Meindl, 1995). The fourth circuit limit is the response time of a global interconnect circuit consisting of the interconnect itself and a driver stage, whose output resistance is matched to the characteristic impedance, Zo, of the global interconnect. The response time limit is given approximately by t = 2.3(L/v) where L is the length and v is the velocity of wave propagation of the interconnect (Meindl, 1995).
Which of the four key circuit limits appears to be the most formidable barrier to the progress of low power GSI? Assuming lightly loaded gate circuits, more like those found in a ring oscillator than in a fully loaded system
environment, a representative circuit level propagation delay limit for 100 nm technology will be taken as 0.01 ns. For a global interconnect length of L = 3.0 cm, a representative value of the circuit response time is t = 0.46 ns, which assumes the use of "fat" conductors (Sai-Halasz, 1995) with a 1.5 × 1.5 µm cross section and neglects skin effect. The fat conductors reduce total interconnect DC resistance to less than 2.3 times the driver transistor output resistance. Once again, it appears that limits associated more closely with interconnects than with MOSFETs impose the dominant circuit level constraints on the performance of low power GSI. This observation tends to hold true for both "RC-limited" minimum-geometry local interconnects as well as for "LC or time-of-flight-limited" fat global interconnects.
Limits on Systems
System limits are by far the most numerous and nebulous limits in the hierarchy. At the same time, they are also the most restrictive, and we are therefore compelled to pay close attention to them. Among the virtually countless system limits are five generic constraints that apparently cannot be avoided. These limits are imposed by the architecture of a chip; by the switching energy of its semiconductor technology; by the energy storage capacity of low power portable systems or the heat removal capacity of the packaging technology of desk-top systems; by operating cycle time; and finally, by the size of the chip containing the low power system (Meindl, 1995). To exploit the advantages of sub-100 nm MOSFETs and preclude the negative effects of relatively long (and therefore slow) local and global interconnects, radically new chip architectures must be engaged. The period of avoiding this problem is over.
Historic shifts in architectural style in order to exploit fully the strengths of available implementation technologies have occurred in the past. Prior to the advent of integrated circuits, discrete transistors were expensive, and passive parts were economical, prompting ancient design styles that minimized the use of transistors. The extremely limited menu of resistors, capacitors, and inductors offered by monolithic semiconductor technology quickly brought forward design styles that virtually excluded all passive components, with the notable exceptions of small capacitors in DRAMs and poor resistors in static random access memory (SRAMs). To reiterate, in order to continue to capture the benefits of MOSFET reductions in scale in low power systems, we simply must have architectural innovations that preclude, or at least drastically reduce, the need for long local and global interconnects. Systolic arrays exemplify such architectures (Kung, 1982).
The system level switching energy limit closely parallels the corresponding circuit level limit, with the distinction that capacitive loading is much greater because of the longer interconnects. The need for early but reliable estimates of capacitive loading of random logic networks is acute, in order to estimate chip size, power dissipation, performance, and cost. Recently, a new derivation of a complete stochastic frequency distribution of chip wiring, including local,
semiglobal, and global interconnects, was reported (Davis, et al., 1996). Figure D-1 illustrates a comparison of the predictions of this distribution with actual data. A valuable result of the distribution is an improved capability to project the switching energy limit and power dissipation for a given system on a chip. This projection must be based on critical path models, including both a chain of random logic gates and a global interconnect circuit (Meindl, 1995).
For low power portable systems, the third generic system limit simply requires that the total power dissipation of a chip, Ps, be less than Eb/Tb, where Eb is the allotted battery energy for the chip and Tb is the operating interval between battery rechargings. For desk-top systems, this limit requires that Ps < QAs, where Q is the package cooling coefficient (dimensionally W/cm2) and As is the chip area. To satisfy timing constraints, the fourth generic system limit imposes the requirement that the total cycle time, Tc, must be less than the maximum value of clock skew, Tcs, plus the critical logic path delay, Tcp, which consists of both a random logic portion and a global interconnect portion. The global interconnect response time depends on the size of the chip and thus engages the final system limit.
A rather complicated looking, but piece wise simple, composite plot illustrating the entire hierarchy of theoretical limits on low power GSI in the power versus delay plane is presented in Figure D-2. The curves are labeled as follows: (1) fundamental limit from thermodynamics, (2) fundamental limit from quantum mechanics, (3) material limit on switching energy, (4) material limit on transit time, (5) material limit on thermal conduction capacity, (6) device limit on switching energy, (7) device limit on transit time, (8) circuit limit on switching energy, (9) circuit limit on propagation delay time, (10) system limit on switching energy, (11) system limit on heat removal, and (12) system limits on cycle time and chip size.
The system limits apply to a one billion gate system organized as a 32 × 32 systolic array of "random-logic-like" macrocells; implemented with 100 nm CMOS technology in a 4.54 × 4.54 cm die; enclosed in a package with a 50 W/cm2 cooling capacity; and operating at a 1.0 GHz clock frequency. The allowable design space for the target system is the small triangle whose vertices are labeled tdmin, corresponding to the maximum performance system (and therefore minimum propagation delay time) that 100 nm semiconductor technology in a 50 W/cm2 package can provide; Pmin, corresponding to the minimum power dissipation (per switching transition) that the system can accommodate for 1.0 GHz operation; and Pmax, corresponding to the maximum power dissipation (per switching transition) and therefore the largest minimum feature size and presumably the most mature and lowest cost technology that can provide 1.0 GHz performance in a 50 W/cm2 package.
The system parameters for this example were selected to illustrate the very limited design window that will exist for one billion gate, 100 nm, 1.0 GHz GSI technology. Power dissipation can be reduced drastically simply by derating
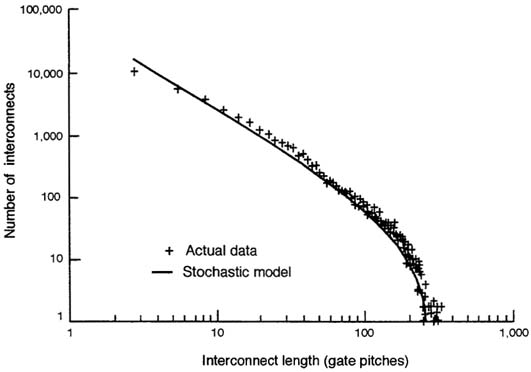
FIGURE D-1 Interconnect length distribution density function: interconnect length distribution density versus interconnect length.
performance, which in effect moves the right boundary of the design triangle to the right, corresponding to larger propagation delay times (i.e., values of tdmin) at the system level.
Practical Limits
Practical limits on low power GSI must, of course, be in compliance with the theoretical constraints but must also take into account manufacturing costs and markets, which are governed by the laws of economics. In light of our understanding of the key physical limits on the performance of low power GSI, the paramount question to be addressed is how many transistors we can expect to manufacture in a single Si chip that will prove to be commercially viable at some specified future time. Therefore, our focus is shifting from performance limits to productivity limits. The number of transistors per chip, Ntr, can be expressed rather elegantly in terms of three macrovariables that measure our rate of progress toward GSI. This expression is Ntr = F-2x D2x (PE)tr, where F is the minimum feature size, D is the square root of die area and (PE)tr is the packing efficiency of transistors in units of transistors per minimum feature square (Meindl, 1995).
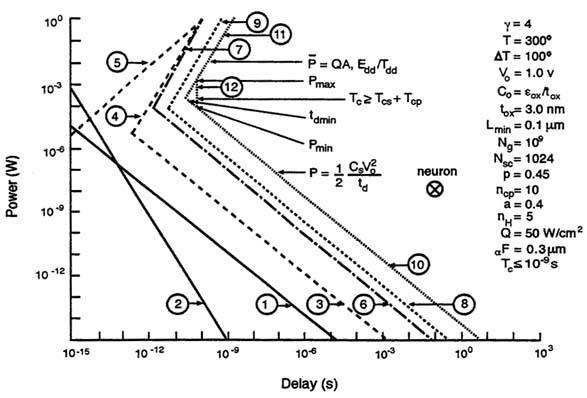
FIGURE D-2 Average power transfer per binary switching transition, P, versus transition time, td. Source: Chandrakasan and Brodersen. 1995.
Both retrospectively and prospectively, scaling down minimum feature size is the single most potent contributor to improvements in both the performance and productivity of low power microelectronics. Small scale integration in 1960 began with average values of F = 25 µm. By 1980, F had been reduced to approximately 2.5 mm and, if the historic rate of scaling persists as expected for the remainder of this decade, F will reach an average value of 0.25 µm for state of the art commercial chips by the turn of the century. Beyond 2000, minimum feature size is expected to continue to scale down at approximately its historic rate of 50 percent every six years until we arrive at the 0.125 mm generation of chips about a decade from now. At that juncture, a break point in the F versus year, Y, curve is expected, owing to a combination of technological and economic factors (which have proven to be highly unpredictable in the past!).
One, and only one, of many possible scenarios that may follow is that optical lithography will finally, as at some point it must, reach its practical limits—at the 0.125 µm generation of chips (or shortly thereafter). When this occurs, possible alternatives include extreme ultraviolet (EUV) or soft x-ray lithography. The relatively short wavelengths of this alternative apparently will require new photon sources, new masking techniques, new resist materials and processes, and new metrologies. The challenges that these prospective advances present appear to be disproportionately more difficult than those that the semiconductor community has met successfully throughout its history.
The same conclusion may well be warranted regarding virtually all of the associated ultra clean sub-0.125 µm fabrication processes, such as ion implantation, rapid thermal processing, and plasma enhanced chemical vapor deposition, which must accompany a new pace-setting suboptical lithography technology in a manufacturing environment (Ohmi, 1994). Consequently, a break point in the F versus Y curve in the near vicinity of the 0.125 µm generation of chips appears to be a plausible scenario on the basis of the technological challenges to be met. Briefly referring to economic issues, a forceful argument that supports this forecast is that the rapidly escalating costs of the entire suite of sub-0.125 µm manufacturing technologies will require more than a three year period between successive generations of products in order to recover costs and operate profitably.
Assuming this breakpoint scenario, what is likely to follow? In the past, one salient change in the rate of advance of microelectronics technology occurred about 1972, when the rate of increase of die size, D, and the rate of increase of transistor packing efficiency, (PE)tr, abruptly declined, causing the time interval for doubling the number of transistors per chip to increase from 12 to 18 months (Meindl, 1995). In general, technological historians have often observed that many commercial technologies, such as structural materials, automobiles, aircraft, and lighting, consistently tend to follow a characteristic ''S-shape," or sigmoidal, pattern of development when the state of the art is plotted against calendar year (Meindl, 1983). Initially, during a post-discovery or invention phase, the rate of advance is slow, mainly due to resource limitations. This period is followed by an intermediate period of rapid progress due to large investments in competing commercial operations. A concluding phase is marked by only incremental improvements, due to approaching physical limits, causing saturation of a mature technology.
The general occurrence of this pattern prompts speculation that the approximate time interval to reduce F by 50 percent will increase from 6 to 12 years following the 0.125 mm generation. At this reduced rate, scaling should be expected to continue through the later years of the second decade of the next century. Then, scaling of bulk MOSFETs is projected to terminate due to a soft collision with their limiting allowable dimensions in the 0.0625 to 0.050 µm range. Beyond that point, however, lie further opportunities for scaling through reduction of gate oxide thickness below the 3.0 nm tunneling limit and through SOI MOSFETs, so that at this point we do not yet see the saturation of a mature MOSFET scaling technology imposed by physical limits.
Projections of trends in minimum feature size depend on understanding theoretical limits, based on relatively well understood principles of physics. Unfortunately, this is not the case for scaling chip dimension, D, or transistor packing efficiency, (PE)tr. However, two variables that have consistently been rather closely related to chip dimension are minimum feature size and wafer diameter. Throughout the past two decades, both F and D have maintained constant rates of scaling, and no changes in these rates are projected for about the
next decade (Meindl, 1995). Beyond the 0.125 mm generation of chips, the simplifying assumption is made that the time interval of a 50 percent reduction of F is equal to the interval of a 50 percent increase of D. Maximum wafer diameter is projected to reach 300 mm by 2000 and 400 mm by 2010 (Semiconductor Industries Association, 1994). Transistor packing efficiency, (PE)tr, has improved at a steady rate for more than two decades, and no change in this value is projected, which implies the rather startling forecast of about one MOSFET per minimum feature square by 2010. This achievement is not imaginable without multiple levels of thin-film transistors, stacked transistors, and side wall transistors, such as we are beginning to see in high density SRAM and DRAM chips. Moreover, today common use of multiple levels of interconnections prompts the projection of multiple levels of transistors.
Following individual projections of the three macrovariables, F, D, and (PE)tr, a more confident forecast of the composite curve of the number of transistors per chip versus calendar year can be generated. Figure D-3 unambiguously forecasts a one billion transistor chip by 2000, a projection articulated initially in 1983 (Meindl, 1983). According to the scenario detailed in the preceding discussion and indicated by segment G in Figure D-3, in which the rates of scaling of both minimum feature size and square root of die area are reduced by 50 percent after the 0.125 µm generation, a one trillion transistor chip will be manufactured before 2020. An unusual extension of Figure D-3 can be calculated on the basis of the new complete stochastic frequency distribution for a
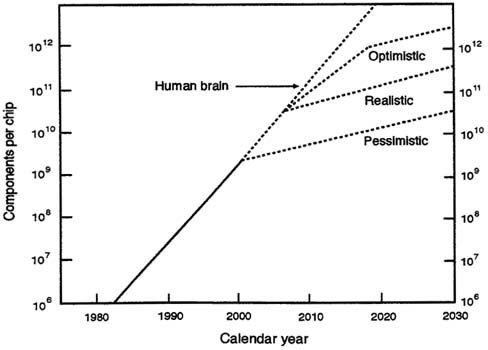
FIGURE D-3 Number of transistors per chip, Ntr, versus calendar year, Y.
wiring network, described earlier in the discussion of theoretical system limits. The number of interconnect elements per chip can be expressed as
Nint = Lint / F = FO . R . (nf / ntr) . Ntr (1)
where Lint is the total length of interconnect per chip, FO is the average fan-out per gate, R is the average interconnect length in gate pitches, nF is the number of minimum feature lengths per gate pitch, and ntr is the average number of transistors per gate. In this expression, FO, nF, are relatively constant, R varies slowly with Ntr, and, clearly, Ntr varies rapidly with calendar year.
A graph of Nint versus year is illustrated in Figure D-4 for microprocessor chips. This plot introduces a new metric for GSI, which indicates that the number of interconnect elements per chip for microprocessors and logic now exceeds one billion and is expected to rise to approximately one trillion elements per chip before 2010. A rough rule of thumb at the moment is that the number of interconnect elements per chip is about 50 to 100 times greater than the number of transistors per chip for microprocessor and logic chips.
A remarkable contrast exists between the preceding treatments of theoretical and practical limits on low power GSI. Projections of theoretical limits are based rather solidly on a foundation provided by the laws of physics, as applied to particular materials, devices, circuits, and systems resulting from
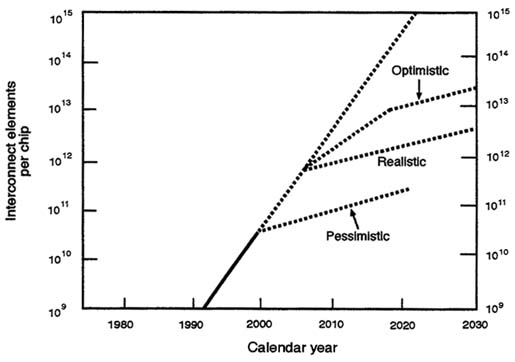
FIGURE D-4 Number of interconnect elements per chip, Nint, versus calendar year, Y.
technological innovations and inventions. Consequently, we must anticipate changes in theoretical limits in response to innovations and inventions. But we should also expect accurate forecasts of limits based on assumptions that are reasonable at the time of their engagement. In contrast, practical limits are based largely on empirical experience that cannot be as neatly codified and interpreted as the laws of physics. Although this fact is unlikely to change, it is desirable to seek some way to engage the laws of physics more directly toward improving understanding of practical limits. This is precisely the objective of the following discussion of practical limits that are "intrinsic" to GSI. We seek to define intrinsic or built-in practical limits that are quintessential to the nature of GSI.
It is difficult to imagine another property of GSI that is as intrinsic as the capacity for batch fabrication of billions of transistors and interconnect elements per chip and hundreds of chips per wafer. This capacity for simultaneous manufacturing is the sine qua non of microelectronics. Therefore, the singular intrinsic limit that we might choose to be able to define is the number of transistors per chip that is economically viable. The foregoing discussion of practical limits, summarized in Equation (1), clearly implies the myriad of complex factors that combine to determine a viable value for the number of transistors per chip.
What is needed is an approach that somehow reaches beyond this myriad and addresses the intrinsic nature of the problem. This leads to the quest to determine a limit on Ntr based on random placement of dopant atoms in a silicon lattice (Keyes, 1975b; De et al., 1996). As a result of both the simultaneous fabrication of many billions of transistors that is inherent to GSI, as well as the presence of many millions of Si lattice sites in the active region of each transistor, the opportunity to designate the placement of a dopant atom at a particular lattice site within each transistor is utterly beyond reach. Consequently, an intrinsic limit on the number of transistors per chip is set by the effects of random placement of dopant atoms in the active channel region of a MOSFET.
The binomial frequency distribution describes the probability of locating a specific number of dopant atoms within a given volume of Si. For a large number of lattice sites, n, within the active region of a MOSFET, and a small probability, p, of site occupancy by a dopant, the average number of dopant atoms per n-sites is given by µ = np, and the standard deviation from this number is s = (np)1/2. Assume a MOSFET scaling factor S > 1. Calculating the ratio s/µ = 1/np, it becomes clear that—because the number of lattice sites, n, decreases as S-5/2 due to scaling down MOSFET dimensions, while the probability of occupancy, p, increases as S due to scaling up doping concentration—the standard deviation relative to the average number of dopant atoms increases as S3/2. The result is a larger standard deviation in the distribution of MOSFET parameters, such as threshold voltage and saturation current, as device dimensions scale down. Simultaneously, the number of MOSFETs per chip scales upward. The result of these two abetting increases is a rapidly escalating maximum deviation of MOSFET parameter values for the ensemble of devices within a given chip. At
some value of maximum deviation of a MOSFET parameter, for example of Vt, logic circuits will cease to operate without errors.
The approximately ±90-percent maximum deviations in Vt predicted for the NTRS (National Technology Roadmap for Semiconductors) 2010 generation of chips, assuming MOSFETs with uniform channel doping profiles (De et al., 1996), is a rather alarming projection. It indicates strongly that new device structures departing markedly from those that have been the vehicles of scaling over the past two decades must be invented and developed in order to reach the 2010 generation of chips! This is a remarkable insight derived from projecting intrinsic practical limits.
CONCLUSION
What are the critical limits most likely to determine how many billions of transistors we should expect to manufacture in a commercially viable silicon chip? We began with that question. Have we answered it? No—and yes. No, we do not believe that the saturation level of GSI is yet in sight from the perspective of approaching physical limits. Yes, we can look ahead with confidence to another decade of scaling minimum feature size, switching energy, and number of transistors per chip at the exponential rates of the past two decades. From then on, the greatest uncertainty that confronts us is what course microlithography will follow.
The committee believes that a viable new suboptical microlithography technology will be developed, for two principle reasons. First, the principles of physics are not at all discouraging. Second, the economic incentives for doing so are virtually irresistible. The prospects of scaling future species of MOSFETs to 25 nm minimum feature sizes (and perhaps beyond) are promising. Furthermore, between the 25 nm MOSFET and the 0.118 nm tetrahedral radius of a Si atom lie still another two decades of opportunity to scale dimensions, about as much as we have "consumed" so far. Discounting any sub-25 nm breakthroughs, between the 125 nm and the 25 nm generations of chips we can forecast four or five intermediate generations, which should carry us to the trillion transistor chip or terascale integration (TSI).
Therefore, following our anticipated achievement of the 125 nm generation in about a decade, at a rate of three to six years per succeeding generation, we should expect scaling to continue into the 2020 to 2030 time frame. As long as minimum feature size and the number of transistors per chip continue to scale, the advance of low power microelectronics will continue, assuming long interconnects can be largely avoided through new system architectures.
REFERENCES
Bhavnagarwala, A.J., V.K. De, B.L. Austin, and J.D. Meindl. 1996. Circuit techniques for low power CMOS GSI. Pp. 193–196 in Digest of Technical Papers, IEEE International Symposium on Low Power Electronics and Design, Monterey, California, August 11–14. Castine, Maine: John H. Wuorinen.
Chandrakasan, A.P., and R.W. Brodersen. 1995b. Low Power Digital CMOS Design. Norwell, Mass.: Kluwer Academic Publishers.
Davis, J.A., V.K. De, and J.D. Meindl. 1996. Optimum low power interconnect networks. Pp. 78—79 in Digest of Technical Papers, IEEE International Symposium on VLSI Technology, Honolulu, Hawaii, June 10—14. Castine, Maine: John H. Wourinen.
De, V.K., X. Tang, and J.D. Meindl. 1996. Random MOSFET parameter fluctuation limits to gigascale integration. Pp. 198—199 in Digest of Technical Papers, IEEE International Symposium on VLSI Technology, Honolulu, Hawaii, June 10—14. Castine, Maine: John H. Wuorinen.
Keyes, R.W. 1975a. Physical limits in digital electronics. Proceedings of the IEEE 63(5): 740—767.
Keyes, R.W. 1975b. The effect of randomness in the distribution of impurity atoms on FET thresholds . Applied Physics 8: 251—259.
Keyes, R.W. 1979. The evolution of digital electronics towards VLSI. IEEE Journal of Solid State Circuits 14(2): 193—201.
Kung, H.T. 1982. Why systolic architectures?. IEEE Computer 15(1): 37—47.
Meindl, J.D. 1983. Theoretical, practical and analogical limits in ULSI. Pp. 8—13 in Digest of Technical Papers, IEEE International Electronic Devices Meeting, December. Castine, Maine: John H. Wourinen.
Meindl, J.D. 1995. Low power microelectronics: Retrospect and prospect. Proceedings of the IEEE 83(4): 619—635.
Meindl, J.D. 1996. Gigascale integration: is the sky the limit?. IEEE Circuits and Devices 12(November): 19—24, 32.
Ohmi, T. 1994. Scientific semiconductor manufacturing based on ultra clean processing concept. Pp. 3—22 in Proceedings of the International Conference on Advanced Microelectronic Devices and Processing, Sendai, Japan, February 28–March 4. Sendai: Tohoku University.
Sai-Halasz, G.A. 1995. Performance trends in high-end processors. Proceedings of the IEEE 83(1): 20—36.
SIA (Semiconductor Industry Association). 1994. The National Technology Roadmap for Semiconductors. San Jose, Calif.: Semiconductor Industry Association. Updated version to be published in fall 1997.















