This paper was presented at a colloquium entitled “Genetics and the Origin of Species,” organized by Francisco J.Ayala (Co-chair) and Walter M.Fitch (Co-chair), held January 30–February 1, 1997, at the National Academy of Sciences Beckman Center in Irvine, CA.
Origin of Genes
(intron/exon/module/evolution)
WALTER GILBERT*, SANDRO J.DE SOUZA, AND MANYUAN LONG
Department of Molecular and Cellular Biology, Biological Laboratories, Harvard University, 16 Divinity Avenue, Cambridge, MA 02138
ABSTRACT We discuss two tests of the hypothesis that the first genes were assembled from exons. The hypothesis of exon shuffling in the progenote predicts that intron phases will be correlated so that exons will be an integer number of codons and predicts that the exons will be correlated with compact regions of polypeptide chain. These predictions have been tested on ancient conserved proteins (proteins without introns in prokaryotes but with introns in eukaryotes) and hold with high statistical significance. We conclude that introns are correlated with compact features of proteins 15-, 22-, or 30-amino acid residues long, as was predicted by “The Exon Theory of Genes.”
The role of introns and exons in the history of genes has been the subject of debate between two extreme positions. One side holds that introns were used to assemble the first genes, an “introns-early” view (1, 2), and the other side maintains that introns were added during evolution to break up previously continuous genes, an “introns-late” view (3, 4). This discussion has a significant impact on our conceptions about the way genes were constructed in the first cells. Unfortunately, the two sides make opposing judgments about each piece of evidence, and no decisive evidence has yet been agreed upon.
For example, in the context of phytogenies, that bacteria have no introns whereas vertebrates have many introns is interpreted differently by the two sides. One view is that introns were there originally and were simply lost; the alternative view is that they were gained. In homologous genes, one often finds introns in similar but not identical positions between genes separated by great evolutionary distances. The early-intronists say that these positions represent the same original intron, possibly moved slightly in position (intron drift or sliding). The late-intronists say that it is obvious that introns could not have existed in such closely neighboring positions in a single original gene and that, because introns could not have moved, these near coincidences must be evidence of insertion.
There have been efforts to correlate introns with the three-dimensional, structure of proteins. The introns-late view denies that there are any such correlations and asserts that introns behave as though they were inserted randomly into the structure of genes (5). Alternatively, the early-intron position generally affirms such a connection but, up to now, has not been able to muster any strong statistical evidence. Recently, however, we have defined such a correlation in a way that yields strong statistical support (6).
There are three possible scenarios for the evolutionary history of introns. One is that there were introns at the very beginning of evolution and that during evolution they were lost or, possibly, mostly lost and some added. This complex of ideas is “The Exon Theory of Genes” (2). The extreme alternative view is that introns were added very late in evolution, even in the last few million years, and thus have nothing to do with the rearrangement of pieces of genes. There is no exon shuffling on this picture. A third, intermediate view, popular in its own right, is that the introns arose at the initiation of multicellularity. In this picture, the Cambrian explosion used introns to create exon shuffling and a profusion of new genes. The idea of exon shuffling is that introns are as hot spots for genetic recombination, which is a property that introns would have solely because of their length. Introns affect the rate of homologous recombination between exons in a way that scales with length, but, more importantly, they affect nonhomologous recombination as the square of their length. Consider a new gene made by a new combination of regions of earlier genes by an unequal crossing-over event, a rare event at the DNA level, that matches small, similar sequences between two DNAs. To make a new protein that contains the first part of one protein with the second part of another requires such a rare, and in frame, event. However, if the regions that encode parts of the protein are separated by 1,000–10,000-base-long introns along the DNA, a process of unequal crossing-over occurring anywhere within that intron between the exons will create a new combination of exons. There is a combinatorial number of ways to find the matching of short sequences to initiate the unequal crossing over, and thus the recombination process will go a million to a hundred million times faster in the presence of an intron. This is a great enhancement of the rate of creation of new genes.
The Exon Theory of Genes (2) is a specific statement of the idea that the first genes were made of small pieces. The crucial elements of that theory are that the very first genes and exons represented small polypeptide chains ˜15–20 amino acids long, that the basic method used by evolution to make new genes was to shuffle the exons, and that a major trend of evolution was then to lose introns and to fuse small exons together to make complicated exons. (The first enzymes probably were aggregates of such short gene products, but these ur-exons were soon tied together by an intron/exon system so that the proteins would have a covalently connected backbone.)
The dominant evolutionary processes are thus to be recombination within introns, the sliding and drift of introns to change amino acid sequence around their borders, and the loss of introns, which can change the gene structure but does not affect protein structure. The strength of this concept is its argument that one searches sequence space not by amino acids and point mutations but by larger elements. We might compare a protein to a sentence. It is easier to understand the sentence as made up of words rather than simply as a string of letters.
© 1997 by The National Academy of Sciences 0027–8424/97/947698–6$2.00/0 PNAS is available online at http://www.pnas.org.
How are introns lost? The most direct way is retroposition. A spliced RNA transcript of a gene with an intron/exon structure is copied back into cDNA by a reverse transcriptase, and that DNA is inserted into the chromosome within an intron of a previously existing gene. Splicing can now make that element serve as a complex exon in a new gene. (This process makes pseudogenes, if the reinsertion does not fall under a promoter.) A clear example of this process was worked out in the jingwei gene system in Drosophila (7).
The argument that the first exons were 15–20 amino acids long does not have direct support in today’s exon distribution, which peaks at lengths of 35–40-amino acid residues (8). In terms of exon fusion, we expect that there has been, on average, two or three acts of fusion in going from the original 15–20-amino acid long exons to the pieces that are being shuffled today.
That protein evolution begins with 15–20-residue polypeptides, essentially small ORFs, whose products are just long enough to have some shape in solution (or as an aggregate) provides an answer to the classic problem of how long proteins evolved. Although it is impossible to find one of (20)200 sequences by a random process (there is not enough carbon in the universe), all short fragments 15–20-residues long can be found in a few mols of material.
Although we have described the Exon Theory of Genes as involving DNA-based introns and exons, the theory flows naturally out of an RNA world view (9) that (i) pictures RNA genetic material, creating (by splicing) RNA enzymes to do all of the biochemistry, (ii) introduces then activated amino acids, one by one, to build up oligopeptides to support ribozyme function, and, finally, (iii) uses 20 amino acids, short exons, and mRNA splicing to create protein enzymes. This RNA world picture is supported by the ribosome’s RNA-based peptide-bond catalysis, by the spliceosome’s RNA enzyme-based splicing mechanism, and by the essential RNA involvement in DNA synthesis and the biosynthesis of the DNA precursors (10).
How can one devise any proofs or disproofs of these attitudes about the origin of genes? The polar views make different predictions, which can be tested (8, 11). The theory that introns are present today because there was exon shuffling in the original genes makes certain predictions about intron position and phase whereas theories that the introns were added to DNA sequence by a random process make different predictions. One example of such an introns-added theory is the hypothesis of a transposable element that bears splicing signals on its ends. If such an element were to insert into a gene, its RNA transcript would be spliced out, and the gene product would be unaffected. An element of this kind could spread through the genome as selfish DNA and put introns everywhere.
Intron Phase Predictions
The first set of predictions involves intron phase, the position of the intron within a codon. Even though there is no signature on the message after an intron has been spliced out, the intron position along the DNA can be referenced to the ultimate protein sequence. An intron can lie either between the codons, phase 0, after the first base, phase 1, or after the second base, phase 2. This is an evolutionarily conserved property if the intron remains present in the gene. If the introns had been inserted into the DNA, there would be no “phase” preference at the point of insertion. That insertion, as a DNA process, could take note of DNA sequence but not protein sequence. If, on the other hand, the exons had been shuffled and exchanged, the simplest model would have all introns in the same phase so that every combination between exons would work. Thus, introns-early predicts phase bias, and introns-late predicts (in its simplest form) equal numbers in each phase.
A second property is phase correlation. Consider an exon bounded by introns. If the two introns had been inserted into a continuous gene, there could be no necessary relation between the phases of the intron that lies before and the intron that lies after the exon. The two events of insertion, and hence the phases, should be uncorrelated. On the other hand, if the exon had been inserted into a previously existing intron, then the phases of the intron on either side should be the same so that the reading frame will continue across it. That is, exon shuffling suggests that exons should be multiples of three bases. Intron addition makes no such commitment.
How might one test these predictions? We constructed a database of exons by going to GenBank, identifying all genes with introns, purging that set to remove related genes, and getting a set of quasi-independent genes: 1636 genes with 9192 internal exons from GenBank 84 (8). We then looked at a special subset of those eukaryotic genes: those that have homologous sequences in the prokaryotes. In our database, there were 296 such genes with 1496 introns (8). These genes have the following essential, property: They are prokaryotic genes that are colinear with a region of an eukaryotic gene. The prokaryotic gene has no introns; the region of eukaryotic gene has introns. Any introns-late model requires that all of these introns be inserted because there cannot have been exon shuffling for these sequences. Although one might argue in general, for eukaryotic sequences, that they could have been made by exon shuffling, these particular parts of eukaryotic sequence cannot be so made because they are orthologous and thus derive from, the cenancestor. In an introns-late picture, all the introns in these homologous regions must be derived. They must have been inserted, and so they should show no phase bias and no phase correlations. According to the introns-early model, there should be such correlations because some or all of these introns originated in the progenote where these genes were assembled by exon shuffling.
In fact, this subset of introns in ancient, conserved regions does show a phase bias; 55% are in phase 0, 24% are in phase 1, and 21% are in phase 2. (The alternative model predicts 33%, 33%, and 33%.) Still more interesting, from a biological viewpoint, there is an excess of symmetric exons, symmetric pairs of exons, triples, and quadruples of exons. Table 1 shows these data (8). All of these sets show an excess of multiples of three, significant at about the 1% level. This is the first strong argument for the existence of ancient introns. The excess of symmetric exons in these ancient conserved regions is predicted in a simple way by the idea that the introns were used to assemble the first gene, but it is not predicted by an insertional model without special biochemical pleadings that forces this result to happen. (One might, in principle, argue that introns inserted into special sequences on the DNA, like AG|GT, and that these sequences might show a bias relative to amino acid sequence to generate a phase bias. To this one might then add the ad hoc assumption that the splicing mechanism sees both ends of the exon and likes it to be a
Table 1. Intron correlations in ancient conserved regions
multiple of three.) A simpler interpretation is that there was exon shuffling in the formation of the first genes.
Introns Correlate with Protein Structure
If genes had been put together from small shuffled pieces, proteins should be made up of repeated small elements, possibly elements of folding, although the evolutionary argument only requires elements that can be subject to natural selection. Evolution requires only function; it does not require biochemical structure. The prediction of the Exon Theory of Genes is that there should be such elements that evolution has selected, which we call modules, and that they should be coextensive to exons.
By module, we mean a region of polypeptide chain that can be circumscribed in space by a maximum diameter. If one traces the Cα positions along the backbone of the polypeptide chain in space and requires that all of the pairwise distances be less than some maximum value, then this region of the chain must fold back and forth in space. Putting a maximum length over the Cα distances, roughly speaking, means that as that region of chain travels through space, it can be circumscribed by a sphere of that diameter.
How might one define the boundaries of such modules? The module notion was first introduced by Mitiko Go in the early 1980s and was used to predict the existence of novel introns. She used it (12) to suggest that there should be a novel intron in globin and that the intron was later discovered in the leghemoglobin of plants. We used that same idea to predict the existence of positions in which one might find introns in triosephosphate isomerase (13, 14). One difficulty with this notion, and a challenge that the introns-late supporters have made, is that this concept of compactness does not provide a sharp view of where the boundaries are to be. The “spheres” overlap, and one does not have a clean definition of where one module stops and the next begins. We have converted this difficulty into a virtue (6) by suggesting that one should take the overlap regions between the spheres that surround the folded portions and, rather than asking for a single intron to be added at a precise position, define these overlaps as “boundary regions” within which introns might lie. Such boundary regions are designed such that, if one put an intron into each of those regions along the gene, the gene product would be dissected into modules less than the specified diameter. This notion is well defined, and one can now write a computer program to define those regions.
Fig. 1 shows this definition of the boundary regions for globin. By constructing a distance plot, a Go plot, of all pairwise distances between Cα positions along the protein and marking all distances >28 Å in black, one can easily see that the five large triangles along the diagonal identify the longest segments of polypeptide chain that lie in 28-Å modules and that the four small overlap triangles define the boundary regions. The gene thus is divided into two portions, one that corresponds to modules and another that corresponds to boundary regions.
This yields a very simple statistical test. The boundary regions are approximately one-third of a gene: Do introns lie preferentially in these regions, or are their positions random? Again, we considered ancient conserved regions, choosing ones that correspond to three-dimensional structures homologous to bacterial genes without introns and to eukaryotic sequences with introns, to ask: Do those intron positions in the eukaryotic homologs tend to lie in the boundary regions or do they not? The two theories predict quite opposite effects. These are all derived introns on the introns-late model, they were added to the preexisting gene, and their positions should be random. The early-intron model predicts that these positions should fall in the boundary regions.
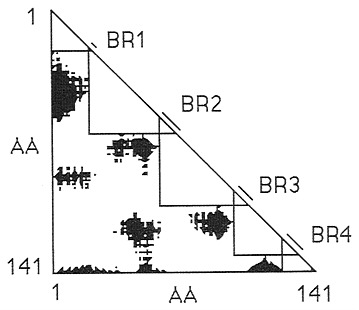
FIG. 1. Go plot for horse hemoglobin. The black spots represent pairs of amino acids whose α-carbons are separated by 28 Å or more. The five large triangles correspond to modules. Boundary regions (BR) are defined by the overlap of these triangles.
Using 28 Å to define the modules, a size that was used before to define modules for triosephosphate isomerase or globin, we examined a set of 32 ancient proteins and a corresponding set of 570 intron positions. The random expectation was to find 182.5 introns in the boundary regions, but we found 214. That is a 17% excess, not a big number, but there are so many positions that the χ2 is 8 and the P value is less than 0.005.
One might wonder if there could be some other reason, rather than ancient introns, that introns might lie within the boundary regions. One possibility might be the existence of some special sequences in the boundary regions, or some sequence biases, that could serve as targets for insertion. We have examined the sequences in the boundary regions and do not find any particular sequence or compositional bias at the amino acid level or the DNA level. Occasionally, people conjecture that introns might have targeted sequences like AGG or AGGT, “proto-splicing” sequences, but there is no excess of those sequences in the boundary regions. Craik and his coworkers once suggested that introns might lie on the surface of proteins (15), thus one might think that the boundary regions perhaps are on the surface of the proteins and that is why introns are in those regions. However, in this set of proteins, neither the boundary regions nor the introns are biased toward the surface (6).
So far, we have not been able to identify any bias-dependent model that would put introns into the boundary regions. The hypothesis we are testing, the Exon Theory of Genes, says that intron positions should lie within these boundary regions. Even though some introns may have been added in the course of evolution, even though some introns may have been lost, even though some introns may have moved, and even though the protein structure may have altered since it was put together, one can still, see an excess there.
A further argument that the excess of intron positions in the boundary regions is due to intron antiquity is found in the examination of an “ancient” subset of the intron positions. We examined those introns that have the same, or similar, positions in three of the four groups: plants, vertebrates, invertebrates, and fungi. Of the 20 introns in this subset, 13 lie in the boundary regions whereas only 6.5 are expected. That is a 100% excess, as opposed to the 17% excess overall. Thus, in a group that is selected to be ancient, we found a higher bias. (That bias was significantly different from the 17%; the χ2 for the difference between 100% and 17% was 6.5, a P value ≈ 0.01.) This finding is further support for the idea that the
underlying signal is due to ancient introns. If the pattern is simply one of biased insertion, then any subset should simply have a value ranging around the 17% excess.
The 28 Å size was purely arbitrary, a particular one that we had used historically. It worked, and we had chosen that size before we knew that this analysis would work, but there was no profound reason for that size. Because we have a computer program that can take any diameter and decompose the protein into modules corresponding to that diameter, we can ask: Is there some optimal decomposition? Fig. 2 shows the results of varying the module diameters from 6 Å, which is one amino acid apart along the chain, out to 50 Å and plotting the χ2 values for the significance of the excess of introns within the boundary regions. Fig. 2 shows three peaks of significance: one peak corresponding to an ≈21-Å diameter, one of an ≈28-Å diameter, and one of an ≈33-Å diameter. The peaks rise to probabilities ≈0.001. This is a strong statistical argument that there are three differently sized structural elements in these proteins that are correlated with intron positions. (One might worry that the curve shows a statistical calculation repeated a thousand times; if the phenomenon had been purely random, at least one of the points should have yielded a P value of 0.001. If one examines the underlying distribution of the excess of intron positions, one sees that it is robust: Smooth peaks appear in the excess of the observed intron positions over the expectations.)
Thus, we conclude that intron positions are correlated with modules of three different diameters: 21 Å, 28 Å, and 33 Å. Can we understand these modules in a more informative way? We can ask about the average length of the polypeptide chain contained within each of these modules, which is equivalent to asking for the average length of the hypothetical exons predicted by the computer program. Fig. 3 shows that the 21-Å modules have an average length of 15 amino acid residues; the 28-Å modules have an average length of 22 residues; and the
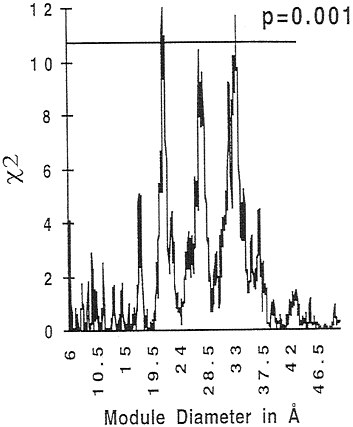
FIG. 2. χ2 distribution for the matching of intron positions to the boundary regions of 32 ancient proteins as a function of module diameter. The 570 intron positions were drawn from version 90 of GenBank. There are three major peaks of significance around module diameters of 21, 28, and 33 Å.
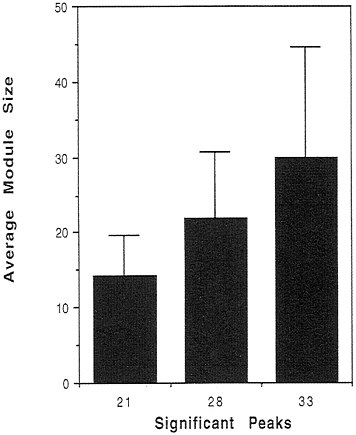
FIG. 3. Lengths of predicted modules for the peaks of significance around 21, 28, and 33 Å. The three peaks correspond to distributions centered around 15, 22, and 30 amino acid residues in length.
33-Å modules have an average length of 30 residues (with a considerable spread). We have given a very strong statistical argument, with P values ≈0.001, that introns define elements of protein structure with sizes of 15, 22, and 30 residues. This feature is exactly what the Exon Theory of Genes suggested back in 1987.
Recently, we went back to the database. Since the calculation was first done, there are 90 more introns, 662 in total, so we can redo the calculation to see if it is better or worse. Most of the novel intron positions have come in through the Caenorhabditis elegans project, so they represent great evolutionary distances from many that were in the database before. With the new data, the peaks improve in statistical significance. Fig. 4 shows that the peak at 21 Å rises to a χ2 ≈ 19, and both it and the peak at 28 Å rise to a P value less than 0.0001.
Currently, we are analyzing the shapes that make up these peaks. The peak at 21 Å, for the set of 32 proteins, arises from a set of 822 modules. Because we know the structures of the proteins, we know the three-dimensional structures of each of these modules, and we can search for signs of exon shuffling. The hypothesis that we are testing not only says that there should be correlations of ancient introns with these modules but also that there should be a pattern of reuse of these elements. What we expect to find is that some 21-Å regions, some 28-Å regions, and some 33-Å regions will have been used over and over again. Once we have a classification of shapes that are reused, we will ask for further evidence that those shapes correspond to shuffled exons. Such evidence would be that those modules that have been reused are ones correlated with introns or that those modules that have been reused show sequence similarities that would suggest a divergent evolution. At this time, we know these patterns only very crudely. The most common module is an α-helix followed by a turn and a strand; ≈8–10% of all shapes at 21 Å are of that form. Then there are strand-turn-helix shapes, helix-turn-helix, and strand-turn-strand shapes repeating in the 21 Å peak. The other peaks contain more complicated shapes.
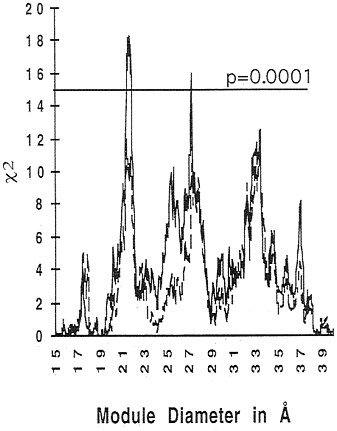
FIG. 4. The same analysis shown in Fig. 2 (dashed line) was repeated using a database of intron positions based on GenBank version 96 (662 intron positions, continuous line). The peaks around 21, 28, and 33 Å now reach χ2 values around 19, 15, and 13, respectively.
DISCUSSION
We have reviewed here two strong, statistical arguments that there were ancient introns used to shuffle exons in the first genes. Both arguments detect a signal of the presence of ancient introns in today’s intron spectrum, over a background that could be due to new introns, to moved introns, or to mutation and change of the protein structures. Both arguments, intron phase correlations and intron correlation to modules, were applied to ancient conserved regions of gene sequence. These are regions of sequence conserved between prokaryotes and eukaryotes; thus, these genes, on any theory, came into existence early in evolution, possibly in the progenote, certainly in the cenancestor, the last common ancestor. These regions are colinear between the prokaryotic forms and their eukaryotic homologs.
It is for these ancient conserved regions especially that the two theories make the most divergent predictions. All forms of introns-late theories assert that these genes came into existence before there were spliceosomal introns. Hence, all of the introns in their eukaryotic counterparts had to be inserted during the course of evolution; they must be derived characters because the prokaryotic form, on those theories, was created as a continuous whole. No exon shuffling can have intervened for these eukaryotic counterparts because they are colinear to the prokaryotic forms. Conversely, all introns-early theories predict that these proteins actually were assembled from exons in the progenote or later by exon shuffling. During the evolution of the prokaryotes, these theories predict that all of the introns were lost. Only in the eukaryotic forms did (some of) these introns survive.
Thus, for these introns, one theory says all were added, and thus should, obey random statistics, and the other theory predicts that the current introns will show correlations due to their ancient origin. The databases of gene sequences have so increased in size that one can show that these traces of ancient introns have sharp statistical significance. As the databases continue to increase in the future, these tests will become even more convincing.
Issues of Selection and Adaptation
Are the introns under selection? In general, we argue that they are not. The hypothesis that the role of introns was to speed up evolution by increasing the recombination between exons is not based on the idea that they therefore were selected for that use. Such an idea would be a wrong teleological view, i.e., that they are present because they aid future selection. Rather, our view is that they are present because the easy path in the past that lead to the creation of a gene used them and that they have not yet been removed by selective pressure. Although the introns are not under any selective pressure in general, where there has been pressure on DNA size there would have been loss of introns, such as in prokaryotes, Arabidopsis, or other small genome organisms. Drosophila, for example, recently has been shown to have a high deletion frequency for unneeded DNA (16) associated with genome slimming, which suggests that many current introns in Drosophila may be adaptive and be maintained by such features as enhancers or gene expression timing. Many introns in Drosophila are very small, which may reflect the deletion pressure for loss of sequence that still does not go to completion because of the difficulty of removing the intron exactly. Gerald Fink (17) suggested that, in S. cerevisae, a special mechanism (in that case a runaway reverse transcriptase) led to the loss of introns as a result of bombarding the genome with cDNA copies of spliced messengers.
Could natural selection on added introns create the observed correlation between introns and protein features? Such models fail because, for these ancient conserved genes, they involve selection for a future purpose. One such model, for example, hypothesizes that, as introns are being added to these ancient (continuous) genes, a well formed exon is shuffled off for use in some other gene and hence selected for. In reality, selection could fix that novel exon in the new gene in the population, but that selection would fail to fix the correct ancestral (donor) form of the gene in the population. (If the organisms had sex, then the donor form is unlinked and hence not fixed. If the organism, had only one linkage group, so that the donor form would be fixed by piggybacking, so too would all of the wrongly inserted introns everywhere in the genome.)
CONCLUSION
We have examined a large set of introns in ancient conserved regions. All of these introns should have been derived, late features if the first genes had been continuous. We found, however, that these introns show patterns of correlation to the gene sequence and to the protein structure of the gene products that are consistent with the predictions of The Exon Theory of Genes.
We thank the National Institutes of Health for support (Grant GM 37997). S.J.d.S. was supported by Fundacao de Amparo a Pesquisa do Estado de Sao Paulo and the PEW-Latin American Fellows Program.
1. Doolittle, W.F. (1978) Nature (London) 272, 581–582.
2. Gilbert, W. (1987) Cold Spring Harbor Symp. Quant. Biol. 52, 901–905.
3. Palmer, J.D. & London, J.M.J. (1991) Curr. Opin. Genet. Dev. 1, 470–477.
4. Cavalier-Smith, C.C.F. (1978) J. Cell Sci.
5. Stoltzfus, A., Spencer, D.F., Zuker, M., Logsdon, J.M.J. & Doolittle, W.F. (1994) Science 265, 202–207.
6. de Souza, S.J., Long, M., Schoenbach, L., Roy, S.W. & Gilbert, W. (1996) Proc. Natl. Acad. Sci. USA 93, 14632–14636.
7. Long, M. & Langley, C. (1993) Science 260, 91–95.
8. Long, M., Rosenberg, C. & Gilbert, W. (1995) Proc. Natl. Acad. Sci. USA 92, 12495–12499.
9. Gilbert, W. (1986) Nature (London) 319, 618.
10. Gesteland, R.F. & Atkins, J.F., eds. (1993) The RNA World, (Cold Spring Harbor Lab. Press, Plainview, NY).
11. Long, M., de Souza, S.J. & Gilbert, W. (1995) Curr. Opin. Genet. Dev. 5, 774–778.
12. Go, M. (1981) Nature (London) 291, 90–93.
13. Straus, D. & Gilbert, W. (1985) Mol. Cell. Biol. 5, 3497–3506.
14. Gilbert, W., Marchionni, M. & McKnight, G. (1986) Cell 46, 151–154.
15. Craik C.S., Sprang, S., Fletterick, R. & Rutter, W.J. (1982) Nature (London) 299, 180–182.
16. Petrov, D.A., Lozovskaya, E.R. & Hartl, D.L. (1996) Nature (London) 384, 346–349.
17. Fink, G.R. (1987) Cell 49, 5–6.






