5
Streamflow Prediction: Capabilities, Opportunities, and Challenges
Stephen J. Burges
Department of Civil Engineering
University of Washington
Introduction
The annual Wolman Lecture of the National Research Council's (NRC) Water Science and Technology Board is in honor of one of the great scientist-engineers of the century. This colloquium, which expands the scope of the annual lecture, is a fitting way to discuss some of the developments that resulted from the Eagleson committee's report Opportunities in the Hydrologic Sciences (NRC, 1991a). Peter Eagleson provided the intellectual drive and force for that committee. The report followed an earlier one by a committee chaired by Walter Langbein (Ad Hoc Committee on Hydrology, 1962). The Langbein committee's report followed an incisive assessment of "The Field, Scope, and Status of the Science of Hydrology," by Robert Horton (Horton, 1931). It is fitting that there are vignettes of Abel Wolman, Walter Langbein, and Robert Horton on pages 29, 44, and 41, respectively, of the 1991 NRC report.
The conclusions from the Eagleson committee's report included: "To meet emerging challenges to our environment we must devote more attention to the hydrologic science underlying water's geophysical and biogeochemical role in supporting life on earth. The needed understanding will be built from long-term, large-scale coordinated data sets and, in a departure from current practices, it will be founded on a multidisciplinary education emphasizing the basic sciences. The supporting educational and research infrastructure must be put in place" (NRC, 1991 a, p. 11).
Sixty years earlier Robert Horton noted that
A complete list of the problems of hydrology is impossible. It would be nearly co-terminous with a list of the applications of hydrology in both pure and ap-
plied science and in addition would involve much that is fundamental to the science itself. . . . As in physics and other sciences, an advance towards the solution of one problem uncovers others. The central problem is that of determining the physical processes and principles and the quantitative relations involved in the hydrologic cycle—or less comprehensively, as put by Ed. Imbeaux, the solution of the runoff problem. This problem serves also as an illustration of the fact that, in general, science can only progress as fast as the necessary quantitative data become available (Horton, 1931, p. 199)
We will see Horton's "uncovering of problems" demonstrated in several of the illustrations in this paper.
The chosen theme of this paper involves hydrologic applications to societally important issues associated with "runoff." All applications discussed depend on skills culled from many disciplines and are rooted in the basic sciences. The issues are concerned with effecting the water budget for catchments of various scales, with emphasis on floods and droughts. A comprehensive coverage of the hydroclimatology related to floods and droughts, flood forecasting and drought prediction, water supply forecasting, and flood and drought management, is given in Paulson et al. (1991). The challenges we face in predicting the streamflow for floods and droughts are exciting and daunting and will push us to the limits of intellectual and technological capabilities. The concerns that Horton had about availability of suitable data are equally relevant today.
Streamflow Prediction
The most important input to the land surface for hydrologic predictions is precipitation. Inability to forecast, measure, or model the spatial and temporal amounts and form of precipitation will limit any analysis, interpretation of data, or attempts to model the hydrologic response to that precipitation. Hoyt et al. (1936) demonstrated the importance of determining areal rainfall accurately for flood estimation using unit hydrographs. Dawdy and Bergman (1969) provided one of the earliest comprehensive model demonstrations of the importance of rainfall variability and uncertainty for streamflow hydrograph predictions. In catchments where snowfall constitutes a major part of the incident precipitation, accurate depiction of the spatial coverage and depth of snow is essential to streamflow prediction. Many have investigated aspects of this problem. An illustration of the nature of the problem for complex terrain and possibilities for using spatially distributed modeling is given by Wigmosta et al. (1994). They used digital elevation data (180-m grid) to illustrate potential applications for a spatially distributed hydrology vegetation model that they developed to estimate water yield from the Middle Fork Flathead River in northwestern Montana. Satellite observations of snow cover were used to test the model's spatial predictive capabilities. Their work represents the state of the art in spatial modeling and
emphasizes the need for more complete and informative spatial data for model inputs and environmental decision making.
Time and Spatial Scales—Droughts
There are several time and spatial scales of concern in drought prediction. Much depends on the definition of drought. If ''agricultural drought" is the major issue, prediction of the spatial and temporal patterns of precipitation over relatively large areas is needed. The prediction time scales range from a month or so before scheduled planting, during the growing season, and near the end of the growing season. The timeliness of the prediction as well as its accuracy is of crucial economic importance to agribusiness. The early-season forecasts must be sufficiently accurate to influence seed planting and other farming decisions.
A second time scale involves multiple year below-critical precipitation patterns. This requires semiquantitative forecasts of large-scale atmospheric circulation patterns and associated hydroclimatological balances at the mesoscale to estimate the state of water distribution in the soil column throughout the area. The associated issue of precipitation recycling through regional reprecipitation of some of the evaporated water puts additional demands on the need to couple hydrological and meteorological models suitable for making hydroclimatic forecasts. Eltahir and Bras (1996) have provided a comprehensive review of the significance of precipitation recycling at continental and regional scales.
For much of the world where water is stored in reservoirs for later redistribution for societal needs, additional hydroclimatological forecasting is needed, particularly concerning streamflow. Good estimates are needed of the time patterns of streamflow to each reservoir as well as estimates of the release schedules necessary to meet societal contracts and environmental laws. The quality and timeliness required of the forecast depend on the size of the reservoir, the seasonal pattern of streamflow inputs, and the relative amount of water that is to be released to some schedule for societal and ecological purposes. For small reservoirs (capacity is a small fraction of the mean annual flow volume of the river and releases are also relatively small), short-term forecasts (on the order of weeks to several months) are all that are needed. The most important forecasts are for anticipated seasonal flow patterns.
Over-year storage is provided when the reservoir is on the order of the mean annual flow volume or larger and the annual release schedule is on the order of 50 percent or larger of the mean annual inflow volume. For much of the United States the combined demands placed on release schedules for reservoir systems put them into the over-year category. When reservoirs are relatively full, accurate short-term forecasts are needed for operational management purposes. When reservoir levels are lower, accurate long-term forecasts are essential. Some relief can be achieved with interties in complex systems. There is no relief, however, for complex systems that all experience the same broad regional climate and
areally extensive shortage of streamflow. It is such forecasts that are hardest to make and of growing importance to society.
Time and Spatial Scales—Floods
The issue of floods poses a different set of requirements. There are multiple time and spatial scales. Burges (1989) addressed the issue of trends in forecasting and hydrologic modeling of hazardous floods. He addressed principally the issue of real-time flooding. There is another issue of clustering of major floods (Barros and Evans, 1997) that tend to occur over relatively short periods. Predicting such vulnerability is important when implementing engineering works in flood-prone areas. Clearly, if we had fair knowledge that a period of clustered major flooding was anticipated, work could be postponed or increased construction risk management measures would need to be taken. The usual assumption of quasi-stationarity of floods used in risk assessment for the design of temporary works to keep work areas dry during construction would invalidate standard economic risk decisions. An additional issue involves riverine navigation. If superflood clusters were predicted, alternative transportation plans could be considered, although the reallocation might be marginal if the principal mode of transportation is riverine (e.g., in the Mississippi River Basin).
If we restrict the discussion to riverine flooding (and do not concern ourselves here with major issues of coastal, estuarine, and lake shore flooding), real-time or relatively short lead-time forecasts of river flow rates and inundation levels can have different degrees of usefulness and precision. Forecasts can be made with greatest precision when the lead time is short or when an upstream stream gage measures the hydrograph that, after propagation downstream, creates the flood hazard. We are best able to estimate the changes in a hydrograph as it propagates downstream with little local inflow between an upstream location and the downstream location of concern. We have much poorer skills in attempting to estimate what the hydrograph will be at an upstream location when we have only an estimate of rain to be expected at some future time. Even when we have measured rain, our best predictions are associated with main channel flood flow routing. In short, most skill is associated with "how to route," and least skill is associated with "what or how much to route."
Riverine flooding can be generated by one or several concurrent mechanisms. Depending on the time of year and geographic location, riverine flooding may be caused by rainfall, snowmelt, rainfall and snowmelt combined, catchment thawing, or ice breakup, movement, damming, and ice dam breaching. Riverine flooding can also be caused by movement of hyperconcentrated sediment-laden flood waters. When engineered facilities are involved, the impact of naturally generated streamflow may be mitigated by storage in dams, containment by levees, diversion through floodways, or by inundating locations that have been made flood proof or designated for sacrificial flooding.
In almost all forecasting situations, estimates or measurements of precipitation are needed for input to some appropriate model. In most cases this means measurement and processing of spatial rainfall at time t and predicting spatial rainfall over the catchment at time t + Δt. Georgakakos and Kavvas (1987) provide an extensive review of all aspects of precipitation modeling, analysis, and prediction as well as several suggestions for research that should lead to improved prediction. They have hopes for stochastic precipitation extrapolation where precipitation models are coupled with remote (radar) and ground sensors. Schaake (1989) has demonstrated how quantitative stochastic precipitation forecasts for 4 x 4 km grids with time steps of about 15 minutes and up to 3 hours lead time, coupled with catchment geomorphology (representation of spatial locations of first-order basins and dominant channel links), are important for flash flood warning schemes where hydrologic response times are short. Foufoula-Georgiou and Krajewski (1995) report on developments since the earlier assessment of Georgakakos and Kavvas. Much work remains to be done on approaches for including forecasts of spatial precipitation patterns into appropriate hydrologic models and flood warning systems.
The Art and Science of Flood Forecasting
There is still art and science involved in making precipitation forecasts and in estimating spatial rainfall from modern radar measurements. Krzysztofowicz (1995) provided an extensive review and assessment of advances associated with flood forecast and warning systems. Krzysztofowicz' assessment is that only a small amount of information is added over the predictive skill for rainfall spatial coverage and depth using storm dynamics models (on the order of one hour of lead time for convective rain) beyond what can be achieved by estimating the storm trajectory based on radar scans alone.
We depend heavily on radar (and ground measured rain) for rainfall estimates for real-time flood forecasting. Krzysztofowicz (1995) brought to the attention of the community and summarized the report of a case study by Amburn and Fortin (1993), who reported on the June 5, 1991, storm over Osage County in Oklahoma. This case study emphasized the importance of human judgment in issuing a flood warning for convective storms. Two rain gages in the basin of interest and nine nearby gages were used to estimate basin average rainfall (1.44 in.), which, when combined with a rainfall runoff model, indicated that the maximum river stage would be below the bank full-level and would not pose a flood threat. Modern radar (WSR-88D) estimates suggest a basin average rain depth of about 5.2 in. This radar estimated that rainfall depth for the storm would cause the hydrologic model to predict a major flood. The rain gages in the basin did not represent the rain depth adequately, and the radar reflectivities were increased by the presence of hail. Subjective inputs and reports from field observers were used to estimate basin average rainfall of 2.8 in. This latter estimate, used with a
model, predicted a flood, and a timely warning was issued 2.5 hours before flood stage was reached.
This example is important in several ways. A relatively simple hydrologic model was used rather than a more complex spatial model. The inputs to the model were "best subjective and objective" estimates. The purpose of timely warning was achieved. Much remains to be done to sharpen radar estimates of rainfall depth. The spatial coverage of storm patterns, however, is helpful for spatial models, and we need to be working toward implementing them. The critical caveat is that the process is far from automation.
Extreme Storms and Floods
One major hydrometeorological issue is assessing the adequacy of existing emergency spillways or hydrological design of emergency spillways. Critical inputs include complete spatial and temporal descriptions of extreme storms and the associated complete flood hydrograph. Few data for these extreme situations are available. An opportunity for studying an extreme storm and the associated basin response occurred with an extraordinary flood in the Rapidan River (drainage area of 295 km2) on June 27, 1995. The peak flood flow rate of 3,000 m3s-1 (or 10.2 m3s-1km-2) fell on the envelope curve of maximum flood discharge per unit area in the United States for rivers east of the Mississippi River. Radar reflectivity for the storm was recorded by the WSR-88D radar at Sterling, Virginia, located at an ideal distance of 80 to 100 km from the basin boundaries (Smith et al., 1996a). Smith et al. (1996b) have provided an extensive analysis of the storm and its temporal movement. The highest estimated rainfall depth within the basin exceeded 600 mm in 6 hours.
Smith et al. (1996b) used considerable skill to reconstruct the likely rainfall history for the basin. Forensic hydrometeorology was needed for the reconstruction activities. There were no operational standard rain gages located in the basin, and the stream gage recording equipment was destroyed when the river reached high stage. Fortunately, however, diligent hydrologists from the Virginia Department of Environmental Quality were present at the stream gage location, and they recorded the stage variation with a video camera. The hydrograph was reconstructed from the visual record.
The standard 4 × 4 km radar precipitation estimates provided by the National Weather Service (NWS) indicated a total rainfall over the catchment that was one-third of the measured runoff. Smith et al. (1996b) give a detailed explanation for this gross underestimation. One of the causes was the use of a standard, but inappropriate, U.S.-wide (Z-R) relationship (derived for completely different raindrop distribution circumstances) between radar reflectivity (Z) and rainfall rate (R). Nonstandard rain gages provided approximate point estimates of total rainfall at five locations. These data, together with the limits imposed by the measured hydrograph, provided a basis for deriving a more realistic Z-R relationship.
In addition to this calibration of the radar reflectivities, Smith et al. (1996b) developed additional rainfall rate products at 6-minute intervals at the scale of 1 × 1 km to take advantage of all radar information. They also made extensive use of the radar volume scans to determine an atmospheric mass balance for purposes of estimating storm efficiency. The atmospheric sounding at Sterling, Virginia, provided additional crucial information for the analysis.
Some of the key findings from Smith et al. (1996b) are displayed here in Figures 1, 2, and 3. Figure 1 shows the reconstructed (estimated) discharge hydrograph and the radar-estimated rainfall input rate over the entire catchment. Figure 2 shows the centroid of the storm track. The dominant precipitation hugged the topographic ridges, demonstrating the considerable influence of local orography on storm movement and rainfall delivery. Figure 3 shows a map of radar-estimated total storm depth.
Smith et al. (1996b, p. 3105) observed that "a striking feature of the Rapidan storm was its small size and long duration. Rain area ranged from a minimum of approximately 50 km2 to a maximum area of approximately 350 km2." Three basins, "South," "Conway," and ''Rapidan'' are shown in Figure 2. The maximum aggregated discharge per unit area of all three subbasins (295 km2) was 10.17 m3s-1km-2. The discharge rates in the higher rainfall Conway and main stem Rapidan basins (Figure 3) would likely have been higher. How much higher is untestable.
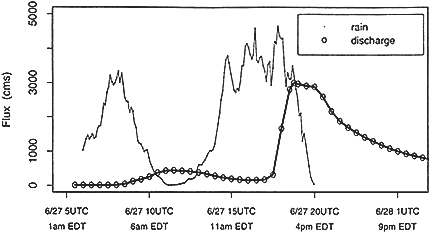
Figure 1 Estimated discharge hydrograph for the Rapidan River at Ruckersville, Virginia, and 6-minute time series of basin-averaged rainfall rate for the Rapidan River upstream of Ruckersville for June 27, 1995. Source: Reprinted, with permis-sion, from Smith et al. (1996b, Fig. 3). © 1996 from the American Geophysical Union.
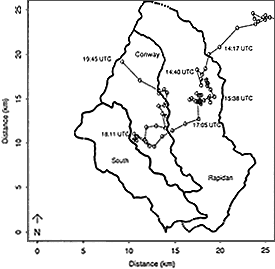
Figure 2 Track of the Rapidan storm as represented in surface rainfall centroid locations. Source: Reprinted, with permission, from Smith et al. (1996b, Fig. 9). © 1996 from the American Geophysical Union.
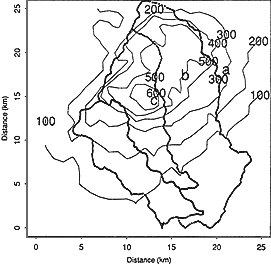
Figure 3 Map of storm total rainfall accumulations (in millimeters), June 27, 0000-2000 UTC (Universial Time Coordinates) at 1 km grid scale derived from Sterling (radar) volume scan reflectivity observations. Source: Reprinted, with permission, from Smith et al. (1996b, Fig. 10). © 1996 from the American Geophysical Union.
This was an extreme storm. When the final analysis was completed, Smith et al. (1996b) estimated that the average rainfall over the 295-km2 basin was 0.344 in and that runoff depth was 0.296 m. They also pointed out the critical importance of the Doppler velocity observations for estimating the atmospheric water budget for this storm. Their final observation has significant implications for engineering design:
The influence of small-scale topographic features on Rapidan rainfall suggests that probabilities of catastrophic rainfall are locally variable and may be guided by the spatial characteristics of the watershed itself. This in turn implies that probabilities of mass wasting and flood impacts may be site-specific, even within a small area that otherwise appears to be climatically homogeneous. . . .
The influence of topographic features on Rapidan rainfall has significant implications for engineering hydrometeorology procedures used for design of high hazard structures, in particular Probable Maximum Precipitation (PMP) procedures. A cornerstone of PMP analysis is the storm transposition procedure. Transposition of the Rapidan storm to any other location is implausible. This brings into question the practice of transposing storms like the August 19–20, 1969 Virginia storm that exhibited strong links to topographic features but for which details of storm structure and evolution are not available (Smith et al., 1996b, p. 3112).
Rapidan Basin—Possibilities for Spatial Modeling of Runoff Production?
There are several questions concerning possibilities for spatial precipitation runoff modeling for situations similar to the Rapidan River basin. The basin has high relief and should be amenable to distributed spatial hillslope hydrologic modeling using models similar to that of Wigmosta et al. (1994). There was considerable mass wasting in the upper basins, so the assumed geometry and soil properties at the start of the storm changed appreciably during the storm. It is unclear how to model the hydrologic response of such a basin during extreme rainfall. The normal problem is determining the supply of water to the channels ("what" or "how much" to route). In the case of the Rapidan the available water would be difficult to determine in space and time. A large fraction became streamflow, so the larger questions in this setting would be "how to route water across and through changing hillslopes'' and "how to route water, sediment, and other debris" through the changing channel system.
Policy Issues—Extreme Storm Data
There are significant policy issues related to the Rapidan storm. Smith et al. (1996b) have demonstrated the considerable utility of the full Doppler information obtainable from the U.S. NWS's WSR-88D radar reflectivity information. It is evident that effort needs to be placed by NWS personnel on developing accu-
rate rainfall rate and storm rainfall depth products at scales useful to the hydrometeorology community. This suggests shorter time and smaller spatial increments being developed and archived for use. The need for early and accurate calibration of radars is obvious. The importance of atmospheric sounding data is clear. More of such data is needed rather than less. Finally, the issue of how to calibrate radars must be addressed. Much has been written about the inadequacy of point rainfall for hydrologic modeling. It is clear to this observer that there is a critical need for a network of ground-based rainfall-measuring devices as well as disdrometer information if we are to make best use of the capability of radars. The kind of measurements needed is addressed below. There is also need for ground-based gages to supplement radar measurements where the radars miss the rain production parts of clouds.
Issues in Radar and Rain Gage Calibration
There are few locations where the rate and depth of rainfall reaching the ground can be estimated and measured by radar, a standard tipping bucket rain gage, and an electromechanical device for measuring drop-size distribution (disdrometer). Steiner et al. (1997) report on such measurements and estimation of rainfall at a climatological station located in Goodwin Creek near Oxford, Mississippi. The Goodwin Creek equipment is maintained by staff members of the National Sedimentation Laboratory of the U.S. Department of Agriculture's Agricultural Research Service (USDA-ARS). The tipping bucket gage is calibrated regularly; the ground-level disdrometer has been in place since April 1996 and is located approximately 2 m from the tipping bucket gage. The WSR-88D radar used to estimate rainfall over the Goodwin Creek site is located in Memphis, Tennessee, 121.2 km from the site. This is close to the optimum distance for radar rainfall estimation reported by Smith et al. (1996a). The ground-based instrumentation is to provide information suitable for calibrating the radar for use in estimating rainfall rate, rainfall amount, and rainfall kinetic energy. The objective is to provide detailed spatial and temporal patterns of rainfall kinetic energy for use with modern erosion estimation models.
The accumulated rainfall depths from eight storms were presented by Steiner et al. (1997). The recorded depth in the disdrometer and the corresponding percentage recorded by the standard tipping bucket gage ranged from a low of 61 percent to a high of 94 percent. Storm depths (mm) and the associated percentage caught by the tipping bucket gage from three representative storms were 16.9 and 71 percent, 5.8 and 61 percent, and 30.9 and 94 percent. There is no apparent simple correction scheme that can be implemented to adjust the tipping bucket rainfall rate record to reflect actual rainfall reaching the ground.
Figure 4 presents information for the storm of June 9, 1996, to emphasize variations in precipitation rate and accumulated depth as estimated from radar reflectivities or as measured directly. The instantaneous rainfall rate (averaged
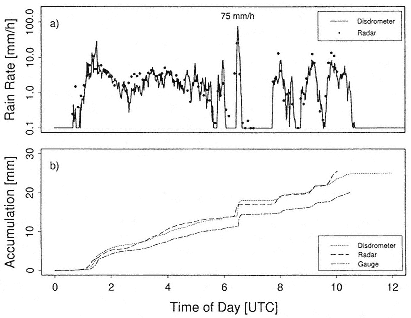
Figure 4 Time series of instantaneous rainfall rate determined from radar reflectivity and ground-based disdrometer and accumulated rainfall determined from radar reflectivity, disdrometer accumulations, and a tipping bucket rain gage, Goodwin Creek, Mississippi, June 9, 1996. Source: Reprinted, with permission, from Steiner et al. (1997). © 1997 from the University of Mississippi.
over 5 to 6 minutes) was estimated for a radar pixel of plan dimension 1 × 2.1 km (1° azimuth at a distance of 121 km) corresponding to the lowest radar sweep at an angle of 0.5°. The disdrometer measurements are recorded at 1-minute increments. Steiner et al. (1997) reported details of this storm as follows:
Rainfall was continuous from 0100 to 0600 UTC. Afterwards more of a cellular pattern was exhibited until rain stopped around 1100 UTC. Accompanied with a five-degree temperature drop from 21° to 16° Celsius within the hour following 0100 UTC, the relative humidity increased from around 90 percent to saturation. Wind speeds (10m elevation) were in the range of 3 to 5 m/s with a gust reaching 7 m/s. The following 10 hours, however, were very stationary with winds from the WNW blowing generally less than 3 m/s, the temperature remained at about 16° Celsius (though after 0800 UTC it decreased by another degree), and the relative humidity stayed around 100 percent.
The accumulated rainfall measured by the disdrometer was 25.1 mm. The corresponding amount measured by the tipping bucket gage was 20.1 mm, which
was 80.4 percent of the calibrated ground-level disdrometer value. The peak (1-minute) rainfall rate recorded by the disdrometer was about 75 mm/hour. Figure 4a shows the time series of the radar-estimated rainfall rate and the rainfall rate measured with the disdrometer on a logarithmic scale. Figure 4b shows the accumulated rainfall depth on a linear scale. For this storm the radar-estimated rainfall and the disdrometer-measured rainfall rates and accumulated amounts are in close agreement. The accumulated catches from the disdrometer and the tipping bucket rain gage (there was no wind shield for the latter) diverged up to about 0006 UTC. There were catch differences associated with each rainfall spike for the remainder of the storm.
Policy Issues—Rain Gage and Radar Calibration
The different estimates of precipitation for the June 9, 1996, storm shown here highlight the need for much more rigorous analysis of precipitation as it reaches the ground than we have done in the past. The network of installed rain gages is likely to be used to help calibrate the NEXRAD network of radars in the United States. Steiner et al. (1997) have shown that careful examination of rainfall data recorded by the existing network of gages will be required before the data can be used to determine appropriate radar reflectivity-rainfall relationships. Disdrometer measurements as well as readings from rate-recording rain gages that are recessed such that their rims are at ground level ("buried gages") will be needed to help calibrate the network of radars. This will provide an opportunity for a comprehensive new ground-level rain-measuring network to be established.
Catchment Mass Balance at a Range of Scales
The fundamental problem of hydrology is determining the water balance for a specified time and region. The balance can be effected by using sufficient measurements of precipitation, runoff, ground water discharge, changes in soil water storage, and evaporation flux, if they are available. Usually a combination of measured data and model-interpolated or-estimated fluxes or states, typically for evaporation, soil moisture storage states, and ground water flow and storage, are used. Evaporation from land surfaces averages about 60 percent of precipitation (Brutsaert, 1986). While few direct measurements are made of evaporation, considerable work has been done in the past decade to describe and quantify turbulent transfer mechanisms in the atmospheric boundary layer to improve methods for parameterizing evaporation and transpiration at catchment and regional scales. Much of that work has been along the lines described by Brutsaert (1986); an excellent summary is given by Parlange et al. (1995).
The difficulty in effecting the water balance is knowing the spatial and temporal distributions of precipitation inputs and whether the precipitation is in
liquid or solid form, as well as the spatial and temporal patterns of evaporation and transpiration. An added complication is associated with determining movement of water to the ground water zone and thereafter the movement of ground water at scales ranging from a few tens of meters of travel to a channel to hundreds of kilometers as regional ground water movement. Few measurement systems are established that track ground water movement adequately enough to permit a complete and accurate description of the water balance.
At relatively small scales (a few hectares), it ought to be possible to represent the relevant processes fairly accurately. Modeling and measurement efforts at small scale for two situations are discussed below to indicate some of the issues that are involved in improving streamflow prediction. The first illustration is for combining modeling and monitoring to represent the hydrology of small humid-zone catchments before and after land use change. The second is for representing the hydrology at small scale in a semiarid catchment where Horton (infiltration limited) overland flow is the primary mechanism by which water from the hillslope reaches the stream channel system. There are many other examples that could be used, but the two chosen demonstrate the range of issues of interest.
Small-Scale Catchment Hydrology—Humid Mediterranean-Marine Climate
Wigmosta and Burges (1997) have presented an adaptive hydrologic monitoring and modeling approach designed to describe the surface hydrology of forested catchments in the humid Pacific Northwest. The objective was to use the minimum monitoring consistent with a spatially distributed model of the dominant hydrologic processes (1) to describe the spatial wetting and drying patterns throughout a catchment during the year, (2) to predict the surface outflow, and (3) to estimate evapotranspiration and recharge to underlying aquifers. The model needed sufficient spatial resolution to be useful in describing the same features after the land had been converted to suburban use.
Figure 5 shows schematically the processes that are represented. Evaporation and transpiration are represented as physical water transport rather than as energy fluxes. Any desired degree of spatial disaggregation can be used for precipitation input and representation of hillslope and channel hydrologic processes. The acronyms HOF and SOF correspond to Horton Overland Flow and Saturated Overland Flow, respectively. Modeling and measurement are done continuously in time. Several years of continuous in-time (typically at a time increment of 15 minutes) concurrent modeling and measurement are needed to calibrate the model. Two example applications were reported, one involving a 37-ha forested catchment where monitored data for two wet seasons were used to calibrate the model, and a 16.7-ha suburban catchment where data for one water year were used for calibration. In both cases the model was used to estimate
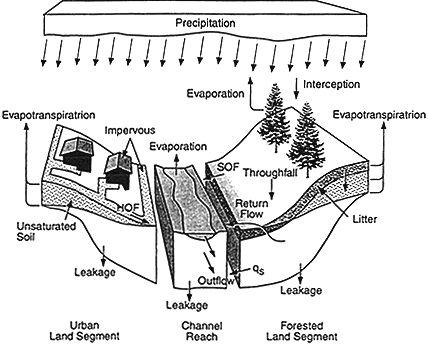
Figure 5 Model representation of urban and forest hillslope elements draining to a channel reach. Each hillslope element is modeled as a vertical two-dimensional section aligned with the dominant downhill flow path. Source: Reprinted, with permission, from Wigmosta and Burges (1997, Fig. 1). © 1997 from the American Geophysical Union.
catchment areally averaged evapotranspiration and leakage through the underlying till layer (aquifer recharge). A single rain gage was used in both situations to represent precipitation input.
Annual summary information for the four water years for the forested catchment are shown to illustrate aspects of the catchment mass balance. Figure 6 shows the principal wet and dry season distributions of water for the 37-ha forested catchment. All quantities are expressed as depth of water averaged over the catchment. The forest soil thickness ranged from about 0.8 to 1 m and was underlain by dense till. Precipitation and runoff depths were measured and evapotranspiration (ET) and till recharge were estimated by the model. There are several key observations. Precipitation is distinctly seasonal. The wet (October 1 to April 30) and dry (May 1 to September 30) season classifications are arbitrary but correspond to the dominant rain and lesser rain periods. If we think of the catchment (37 ha or about 91 football fields) as a pixel in a larger-scale
situation, we could represent the inputs and outputs as part of a distributed representation of the hydrology of the landscape.
Flow production from the catchment is small to negligible in the dry season, but more than 50 percent of the evapotranspiration occurs then. The two years where wet and dry season evapotranspiration rates were almost equal correspond to low wet season rainfall with increased evaporation occurring during the wet season. The till leakage provides recharge to a deeper aquifer that provides sustained water supply to down-basin streams. ET is not known accurately, so a small change in the real ET could significantly alter the actual recharge. The need for accurate estimation of the residual leakage for aquifer health and stream ecology is obvious. It is equally obvious that it is a nontrivial exercise and that hydroclimatic data need to be recorded for a range of weather patterns to provide guidance for effecting the relevant water budget using a combination of modeling and hydrologic measurements. At a minimum, some shallow piezometers (about
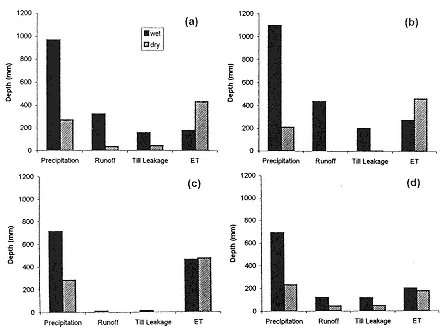
Figure 6 Wet (October 1 to April 30) and dry (May 1 to September 30) season measured precipitation and runoff and calculated till leakage and evapotranspiration for water years (a) 1990, (b) 1991, (c) 1992, and (d) 1993, for a 37-ha forested catchment. Source: Reprinted, with permission, from Burges et al. (1998, Fig. 7). © 1998 from the American Society of Civil Engineers.
1 m deep) are needed to provide critical information about variations in soil water storage.
The implications for land use change when the forest soil is removed and compacted for urban development ought to be obvious. Most municipality stormwater managers are concerned with the runoff part of the balance. With a thinner soil there will be less recharge in this setting and a change in ET and runoff patterns. The ecological importance of recharge is often overlooked.
The illustration presented above is for a situation where continuous measurement and modeling are required to effect the water balance. In the following example, Horton runoff production from individual storms is the principal hydrologic issue of concern.
Small-Scale Catchment Hydrology—Semiarid Monsoon Climate
Goodrich et al. (1995) conducted careful measurements of convective rainfall on an intensively monitored experimental catchment, Lucky Hills—104, which is a part of the USDA-ARS Walnut Gulch Experimental Watershed. The measurements were made during the summer monsoon season (July–September) of 1990. Lucky Hills—104 catchment has an area of 4.4 ha (about nine football fields). The hope when representing the hydrology of such a relatively small catchment with low topographic relief is that a single rain gage would be suitable for effecting the hydrologic balance.
Figure 7 shows the contours of total rainfall for the storm of August 12, 1990. Measurements at 48 nonrecording (cumulative) rain gages were used to construct the rain contour map; the maximum contour shows a depth of 55 mm. While the rainfall cumulative total is relatively uniform, a single tipping bucket recording rain gage is inadequate to capture all the features of the spatial rainfall pattern that are needed to predict flow production and delivery to the channel.
Figure 8 shows the modeled and measured hydrologic responses for the 4.4-ha catchment for the short-duration storm of August 3, 1990. The average rainfall depth was approximately 12.7 mm, and the measured runoff volume was 3.5 mm peak were insensitive to Manning's n on averaged over the catchment. This figure shows the end result of using the state-of-the-art distributed Horton runoff model of the USDA-ARS-KINEROSR, the research version of KINEROS (Woolhiser et al., 1990). The best-modeled hydrographs are shown when using five combinations of one, two, three, and four recording rain gages to estimate the spatial rainfall coverage of this 4.4-ha catchment. This figure emphasizes the need for more than one rain gage in an extremely small catchment and the importance of the spatial locations of those gages if the response to convective rainfall is to be modeled accurately. (The finest-resolution radar rainfall pixel is 1 × 1 km, which is 22.7 times larger than the Lucky Hills—104 experimental catchment.) This gives pause when considering forecasting flood response from convective storms in larger catchments in semiarid areas.
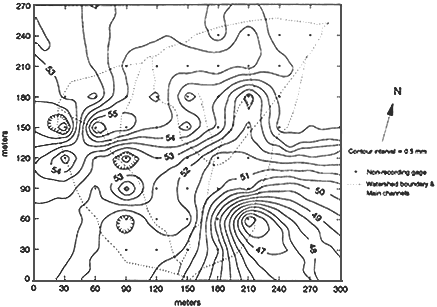
Figure 7 Contour map of the rainfall depth for the storm of August 12, 1990, at Lucky Hills (interpolation by isotropic Kriging). Source: Reprinted, with permis-sion, from Goodrich et al. (1995, Fig. 5). © 1995 from Elsevier Science.
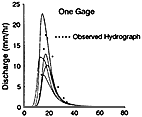
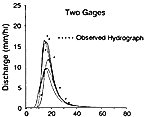
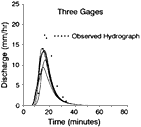
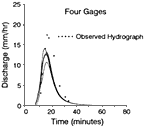
Figure 8 Modeled hydrographs for five combinations of one, two, three, and four recording rain gages in Watershed LH-104 (August 3, 1990). Source: Reprinted, with permission, from Faures et al. (1995, Fig. 2). © 1995 from Elsevier Science.
Woolhiser (1996) presents a comprehensive discussion of physically based rainfall-runoff models used to estimate hydrographs in principally Hortonian runoff production situations and their strengths, weaknesses, and potential. He emphasizes the importance of knowledge of spatial and temporal rain patterns:
One cannot disagree with the fact that it is difficult or impossible to calibrate models with many interacting parameters. . . . The works of Goodrich (1990) and Michaud and Sorooshian (1994) give us valuable insight into problems of calibration for watersheds when Hortonian runoff is the primary runoff generation mechanism, and where infiltration into the channels becomes more important with increasing basin scale. It is especially revealing that parameter sensitivities change dramatically with both basin scale and the magnitude of the rainfall input. For example, Goodrich (1990) found that runoff volume, peak rate, and time to peak were insensitive to Manning's n on both planes and channels for watershed LH-106 (0.36 ha), while Michaud and Sorooshian (1994) found that runoff characteristics were very sensitive to Manning's n in channels . . . for WG-1 (150,000 ha). . . . The importance of spatial and temporal resolution of rainfall data cannot be overemphasized (Woolhiser, 1996 p. 126).
Large-Scale Catchment Hydrology
The two small catchment examples that have been given are for the situation where the control volume is the watershed and the inputs are defined by measured (or spatially estimated) precipitation at the ground surface. As the area of interest increases, it is important to couple hydrology with atmospheric water and energy balances. In principle, if the control volume were extended above the watershed to include the complete airshed and all water and energy fluxes across both boundaries were measured, it would be effective to do approximate major catchment plan view pixel hydrologic modeling using the moisture accounting models developed 30 years ago. The need to model surface energy fluxes as well as hydrologic fluxes and water storage states, at whatever pixel size is being used, has necessitated the development of models that do both energy and moisture accounting. A model that contains essential subsurface hillslope representation of appropriate flow physics, evaporation, transpiration, snow accumulation, melt, and ablation has been developed and demonstrated by Wigmosta et al. (1994). The model is intended primarily for use in complex terrain, and its use was demonstrated at a pixel scale of 180 m. In principle, it should be able to be coupled with a mesoscale meteorology (MM) model, which in turn should be nested within a general circulation model (GCM). The application demonstrated by Wigmosta et al. (1994) did not included this coupling. This is an area for cooperative multidisciplinary research and application.
Simpler conceptual vertical water storage models that release water laterally to streams and vertically to the atmosphere (and in some case to ground water
recharge) have been developed for use at relatively large pixel scales in continental river-basin-scale hydrologic modeling compatible with the scale of GCMs. Liang et al. (1994) developed a two-layer variable infiltration capacity model (VIC-2L) that conceptualizes statistically the spatial distribution of soil moisture and runoff production zones within a catchment. The model has been tested against moisture and sensible and latent heat flux data collected during the First SLSCP Field Experiment (FIFE) experiment in Kansas. The model has been applied by Abdulla (1995) and Abdulla and Lettenmaier (1997) to the Arkansas-White-Red River Basin using a 1° × 1° (approximately 10,000 km2) land surface grid size. The VIC-2L model was calibrated to catchments ranging in size from 100 to 10,000 km2 to permit application to the basin using regionally estimated parameters.
This form of modeling effort has pushed the limit of data handling and has required use of relatively coarse-scale data sets of soil classification, vegetation cover, etc. The work has shown a direction that is needed for the future. It represents what is needed for the GEWEX Continential-Scale International Project (GCIP) component of Global Energy and Water Cycle Experiment (GEWEX). Abdulla's work and that of workers who are continuing his efforts point to the need for more coordinated data sets of regional streamflow time series and more complete attempts to define basin precipitation coverage.
The bulk of the work to date involving hydrology at the continental river basin scale has focused on coupling hydrology with GCM and mesoscale meteorology representations of the surface water and energy fluxes and corresponding river flow. The enormously complicated issue of determining the (residual) recharge of aquifers and the importance of regional-scale groundwater movement has received limited attention. While the pioneering efforts of the early part of the GCIP program are commendable, much more remains to be done in the context of the complete water balance.
Issues in Longer-Term Streamflow Prediction
So far this discussion has been concerned with relatively short-term forecasts of flood flow given estimates of precipitation patterns and issues of effecting the water balance starting with measured precipitation. There are many issues, principally the influence that spatial and temporal patterns of water have on society, where predictions of future water availability are extremely important. All of these predictions are concerned with climatic variability, whether it will be generally wetter or drier than usual for time spans on the order of months to seasons to years to many years. The important hydrologic challenge is how to convert broad and uncertain predictions of climatic variability into corresponding patterns of channel flow, and spatial patterns of evaporation and transpiration, soil moisture states, and ground water recharge. In an ideal setting the predictions would be done using coupled GCMs, MMs, and hydrologic models to ensure that
the climatic predictions are compatible with precipitation recycling and ground surface (and vegetation) thermal fluxes.
We are aware of the forms of climatic variability from studies of historical information. A "drought atlas" is available on CD-ROM for the conterminous United States (Teqnical Services Inc., 1997) that has summaries of precipitation and streamflow probabilities for individual stations and adjacent regions. It can be used to get a sense of the risk to drought that the society in a given region faces. Probabilities are provided, starting in any given month, for the likelihood that rainfall will be above particular depths for time increments up to five years. Similar information is available for streamflow at specific locations. This product is available to the community largely through the efforts of James R. Wallis, a former member of the Water Science and Technology Board.
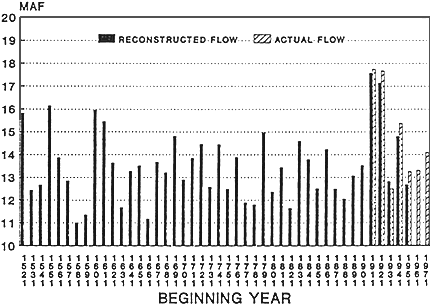
Analysis of longer-term streamflow records and paleosurrogates of streamflow volumes, most notably tree ring growth indices, has shown that sustained periods of above-and below-"normal" patterns are not uncommon. Figure 9 shows decadal average reconstructed streamflow volumes for the Colorado River at Lee's Ferry. This figure shows clearly that there are decadal periods of substantially above-and below-average river flow volume.
Figure 10 shows systemwide river flow volume for the Salt-Verde River Basin in Arizona. There is a significant range in the annual inflow volume as well as distinct long-term patterns of substantially below-average flow volume.
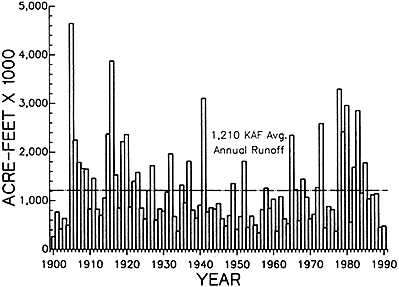
Figure 10 Annual runoff in the Salt, Tonto, and Verde river watersheds between 1900 and 1990. Source: NRC (1991b).
In this instance water supply is managed by increased pumping from aquifer reservoirs in dry years and recharging during wet years. Conditional probabilistic information, given the current states of river flow and reservoir storage, concerning the likelihood of low-, medium-, or high-flow conditions during the next several years, would be beneficial for developing operation strategies for such systems.
The historical record gives us other information that suggests actions that are needed for extended climatic variability prediction. Figure 11 shows an apparent relationship between the grouping of superfloods in the Upper Mississippi and Missouri river basins and aspects of the Southern Oscillation Index (SOI) between 1955 and 1985. A superflood was defined as a flood from a basin having an area greater than 10,000 km2 whose peak response was thought to exceed the "100-year" magnitude. Figure 11 suggests a close link to the negative phase of SOI during El Niño events. El Niño events last on the order of two to seven years. Relatively long lead forecasts of the nature and extent of El Niño events would provide important hydroclimatic policy information for the region.
Predictability of "Low-Frequency" Climatic Variability
Superflood groupings and spatially and temporally extensive low-flow conditions are associated with broad features of global atmospheric circulation. Barros and Evans (1997) indicate that the spatial distributions of sea surface temperatures (SSTs), the cryosphere, and atmospheric aerosols influence the dominant atmospheric moisture circulation patterns and the resulting climatologies, weather patterns, and corresponding hydrology. The Holy Grail of the field is to couple complete ocean thermodynamics with the atmosphere and hydrosphere. Eagleson (1986) provides a clarion call to the community with his paper "The Emergence of Global-Scale Hydrology" in which he stresses the importance of global-scale modeling of the coupled ocean-atmosphere-land surface to address issues of hydrologic persistence. Much work has been done since then and much remains to be done. In a recent report, Gu and Philander (1997) show how interdecadal climate fluctuations depend on oceanic exchange between the tropics and extratropics. This emphasizes the importance of pursuing in various ways the Holy Grail. So far, GCMs have been operated with SST patterns placed in known locations and also with varying assumptions concerning the state and spatial and temporal patterns of the cryosphere. The field is at an early stage of development.
Most-low frequency relationships between broad continental U.S. climate and weather patterns have been tied in some way or another to El Niño-Southern Oscillation (ENSO) anomalies. Considerable efforts have been expended to determine related forecast skill, with particular interest in estimating the spatial and temporal patterns of SST anomalies. Ropelewski and Halpert (1996) have attempted to quantify measured Southern Oscillation precipitation relationships
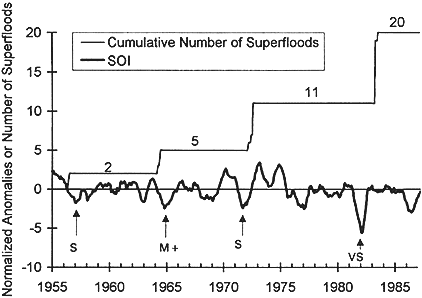
Figure 11 Monthly anomalies of Southern Oscillation Index and number of superfloods for the Upper Mississippi and Missouri river basin. Arrows indicate strength of El Niño-Southern Oscillation Events as defined by Quinn et al. (1987). VS = very strong, S = strong, M+ = moderate/strong. Source: Reprinted, with permission, adapted from Barros and Evans (1997, Fig. 1). © 1997 from the American Society of Civil Engineers.
principally in tropical areas. The objective was to provide long-range forecasters with quantitative guidance when making seasonal and multiseasonal predictions. They note, however, that there is considerable variation in the spatial variations of patterns in precipitation percentiles in some regions. Cane et al. (1997) report on trends in the twentieth-century SST patterns and suggest causes that include global warming. Ji et al. (1996) report on the state of the art of forecasting skill of the National Centers for Environmental Prediction (NCEP) coupled general circulation models. Numerous measures of forecast skill could be used. Based on Ji et al.'s Figure 11 (model CMP 10), anomaly correlations indicate that for the ENSOs in the 1982–1992 period the model had valuable forecast skill for about 6 months and some useful skill for up to 12 months beyond. For the 1992 to 1995 period the skill level dropped to about 4 months. Even with these limitations, using historical weather patterns in a "fuzzy" forecasting mode might have some use. What is not clear is whether CMP10 predictions would be useful for predicting superflood conditions sufficiently far in advance to be of broad benefit to society.
While the search for physical cause-effect relationships for making long lead-time forecasts of broad atmospheric patterns is important and may offer the best hope for future directions, pragmatic forecasts are still needed and a variety of approaches are in use. One approach that appears to have useful forecasting skill has been developed by Lall and Mann (1995) and Lall et al. (1996). Lall and Mann (1995) used Singular Spectral Analysis and Multitaper Spectral Analysis to identify high fractional variance bands in the time series of climatic variables in the Great Salt Lake region as well as volume changes for the lake. The frequency bands of interest were 15 to 18, 10 to 12, 3 to 7, and 2 years. The interannual variations were consistent with ENSO signals and suggested that there may be forecasting predictability for this relatively large-scale closed basin.
Lall et al. (1996) treat the biweekly Great Salt Lake volume time series (1847 to 1992) as the output from a finite-dimensional nonlinear dynamical system and used nonlinear regression to discern the apparent dynamics. The resulting models (Multivariate Adaptive Regression Spline—MARS) were used for forecasting and showed substantial success. The ability to make forecasts for periods between 1.2 to 4.16 years ahead was demonstrated for the period 1984 to 1994. Figure 12 demonstrates this apparent forecast success. Given the observations of Ji et al. (1996), it is not known how well the scheme would have worked for the shorter-duration ENSOs after 1992. Lall et al. (1996, Figure 6) also shows successful four-years-ahead forecasts. The closed Great Salt Lake Basin is a highly persistent long-memory hydrologic system. The apparent success that Lall et al. (1996) have had suggests that there may be benefits from trying the approach in other highly persistent systems, particularly those that are correlated in some way to persistent ENSO-like signals.
Probabilistic Forecast and Extended Streamflow Prediction
Krzysztofowicz (1995) describes the various Quantitative Precipitation Forecast (QPF) products that were being produced by the then Techniques Development Laboratory and the National Meteorological Center (now NCEP) of the U.S. National Weather Service. More recently, a National Research Council committee (NRC, 1996) has emphasized the need for a closer connection between QPFs and how they will be used in hydrologic models for hydrologic prediction, particularly short-term flood warning. The report provides guidance for the modernization efforts of the NWS. In recommendation 3–10 of the report, the committee recommended that "the Office of Hydrology . . . should consider spatially distributed, continuous simulation hydrology models to replace/augment spatially lumped and parametric models. . . . "
An important part of the NWS modernization is the work of the Advanced Hydrologic Prediction System (AHPS) for water resources management. The Water Resources Forecasting System (WARFS) has development of long lead-time forecasts of streamflow as a key goal. It is clear that this is an important
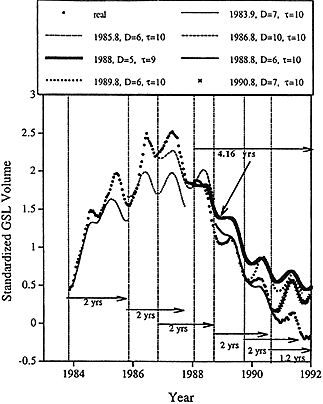
Figure 12 Forecasts of 1.2 to 4.16 years from different starting points during the 1983 to 1992 rise and fall of the Great Salt Lake, Utah. Source: Reprinted, with permission, from Lall et at. (1996, Fig. 8). © 1996 from the American Geophysical Union.
national priority, reiterated in recommendation 3–18 (NRC, 1996): "Field personnel and users of products and services should have a greater involvement in the further definition and development of the WARFS and other components of AHPS." AHPS will be undergoing a demonstration testing starting in March 1997 (Carlowicz, 1996) using the Des Moines River in Iowa as a test case. The target is to provide 25, 50, and 75 percent exceedance flow rate forecasts for days, to weeks, to multiple months ahead.
The potential benefits from spatial modeling and implementation of the WARFS program highlighted here are important. Resource prioritization is likely to be an issue with reductions in federal government funding. If a priority had to be established, work toward spatial representation of hydrologic processes (spa-
tial modeling) to take advantage of the spatially variable precipitation input (provided by radar and rain gage networks) in regions subject to flash floods is appropriate and timely. An all-pervasive need is long lead-time forecasts of water supply in locations of the country where resource use is already high.
A related issue is the information needs and contributions of GEWEX. Cahine (1997) makes the case for additional effort to explore skill capabilities in seasonal and interannual climate prediction. This will require more rather than less effort from the modernized NWS. Atlas (1997) summarizes the state of the modernization program and emphasizes successes that have been achieved. Gains in 6-to 12-months-ahead forecasts depend on the full implementation of the Automated Weather Information Processing System. Much remains to be done to realize the full potential of modernization of the NWS.
We are in the relatively early stages of making hydrologic use of probabilistic QPFs. Few hydrologists have determined how to make use of them, which suggests a greater need for those making the forecasts and those using them to work closely. The older extended streamflow predictions issued by river forecast centers of the NWS have been used by water resource managers. Crowley (1993) has reported on a modeling scheme to provide probabilistic forecasts of basin runoff, over-take precipitation, lake evaporation, net basin supply, and over-take air temperature for the Great Lakes Basin. He illustrates the approach with a 6-months-ahead probabilistic forecast of five broad classes of net basin supply for Lake Superior. The range of potential conditions could readily be put into context with the experience for the previous autumn-winter period. Crowley (1996) describes an approach that uses all existing historical information as well as the long lead-time probabilistic QPF. This permits building a large set of possible future hydrologic spatial time series from which outlook probabilities and other parameters can be estimated. An example shows the probabilistic net basin supply forecasts by month for one year ahead. Crowley's work is indicative of how the work of atmospheric scientists and hydrologists can be combined to yield societally useful products for resource management decision making.
A Final Grand Challenge
Figure 13 shows the time series of May to April water year cumulative inflow volume to the surface reservoirs that serve the southwestern region of western Australia, including the Perth metropolitan area, for the period from 1911 to 1994. The annual inflow volume is expressed in billions of liters (giga liters, or GL). A giga liter can be visualized as the volume occupied by a 1-m depth of water covering a square kilometer. There are many notable features of this figure.
First, the range of inflow volume from year to year is large, with three years exceeding 800 GL and four years less than 100 GL. The reservoirs currently are targeted to supply approximately 180 GL. The average inflow volume for the
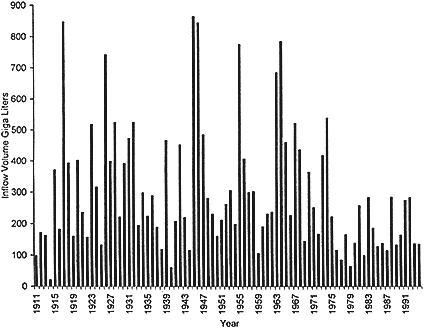
Figure 13 Total annual inflow to Perth, western Australia, water supply dams for May to April water years 1911 to 1994.
entire period is approximately 320 GL. For the period 1975 to 1994 it is 187 GL. The desired supply fraction to the mean inflow level for these two periods is 56 and 96 percent, respectively. The reservoirs are of sufficient size and the nature of the inflow variability for the entire record is such that they are adequate for supplying 56 percent of the long-term mean annual flow. They are considerably undersized to supply 96 percent of the recent mean annual flow for the last 20 years of the record.
The region of interest extends approximately 120 km north-south and 60 km east-west. The catchments are all located east of the Darling scarp, which is approximately 20 km inland from the coastline. There is a general reduction of rainfall and streamflow from the south to the north. The uncertainty of inflow volumes to the multiple reservoir system is a major cause of concern for the society. The population served is approximately 1.2 million. The population to be supplied by the system of surface and ground water sources is anticipated to grow to 1.7 million by the year 2011.
Determining if the recent 20 years is a likely guide to the future is a nontrivial task. To illustrate the demands that this situation places on hydrologic
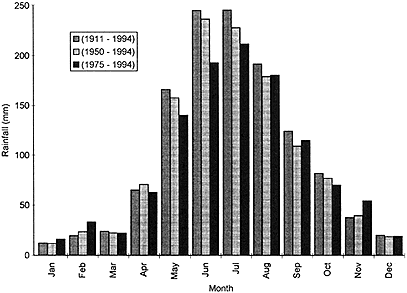
Figure 14 Monthly rainfall (mm) near Serpentine Dam, a part of Perth, western Australia, water supply system.
science, consider summary features of the seasonal rain supply and associated inflow to one of the reservoirs, Serpentine Dam, in the southeastern part of the supply area. The monthly average rainfall near Serpentine Dam is shown in Figure 14. (The annual average rainfall is 1,232 mm, and the average for the 1975–1994 period is 1,061 mm.) The bulk of the rain falls in five months during the winter. There has been a reduction in the mean monthly rainfall for May, June, and July in the past 20 years relative to the complete record. The corresponding reduction in inflow is dramatic and is shown in Figure 15. June and July inflow are each about one-half of the long-term average; there are noticeable reductions in August, September, and October. The reduction in rainfall and inflow to Helena Reservoir, approximately 45 km to the north, is more noticeable. The average annual rainfall is 1,045 mm and for the 1975–1994 period 865 mm. The reductions in inflow were dramatic. Inflow in June and July was about a third of the long-term average; in August, September, and October it was about 40 percent of the long-term average.
The rain that falls on the Perth water supply catchments infiltrates readily into the highly permeable lateritic soils. If a substantial storm follows closely a series of antecedent storms that have made the soil column relatively wet, subsurface flow is delivered to the channels. For storms with short interarrival times
there is more surface flow generated than for storms having longer interarrival times, all other conditions being equal. Consequently, aggregated measured (or estimated) monthly rainfall depth information that does not contain complete information about the individual storms (depth, duration, and time between storms) has extremely limited value for streamflow prediction. Most longer-term estimation schemes do not yet contain this necessary detail.
Water supply systems operators and planners need multiyear forecasts of rainfall amounts for planning and operating their systems. Long-term forecasts are needed for the capacity expansion problem to determine the most dependable mix of supply between ground water, which requires expensive treatment, and water from surface reservoirs. Surface reservoirs fill in years of large positive excursions in the inflow volume from the long-term mean. This means it is important to be able to estimate the relative frequency of years when inflow will be larger than normal.
Figure 15 shows the relative deficit of large excursions in the past 20 years. Larger inflow volumes are associated with larger than usual wet season rainfall. Prediction of likely increased wet season rainfall should be a target. For wet
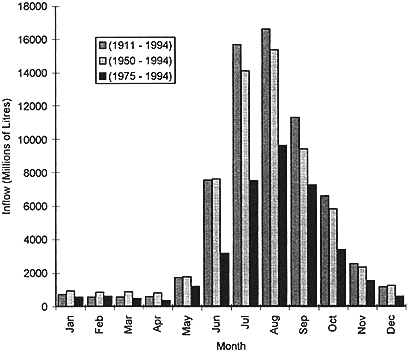
Figure 15 Monthly inflow in millions of liters to Serpentine Dam, Perth water supply system.
season rainfall closer to the average or lower than average, prediction of likely temporal storm patterns is necessary, particularly concerning the timing for large storms following other large storms. This poses a ''grand challenge'' for coupled ocean and climate models, particularly for nested mesoscale meteorology models. Refined prediction of inflows to surface reservoirs will place heavy demands on improved rainfall-runoff models that can track accurately the apportionment of water between recharge to ground water and movement to streams by predominantly subsurface flow paths.
Burges (1996) summarized the findings of research needs identified by research scientists and engineers who participated in a workshop that was held in Perth in 1996 to address the critical water supply issue for the growing Perth region. The summary calls for pushing the scientific limits of coupled ocean, atmospheric, and hydrologic models particularly the limits of prediction of likely precipitation over decade-long periods.
Summary and Recommendations
The examples presented emphasize the need for hydrologists to have a broad-based education and to be able to work closely with, and pose critical questions to, colleagues in ocean and atmospheric sciences, civil and environmental engineering, ecology, water systems management, and emergency preparedness personnel. There is a need for both generalists and specialists. The problems involved are multidisciplinary. All the examples involve various aspects of the water balance for a catchment. Two issues come to the fore. The first is the need to predict precipitation inputs in space and time for time horizons ranging from minutes to multiple years. We must learn to make use of even fuzzy long-term predictions for environmental management and associated societal decision making. The second issue concerns the need to improve the measurement or estimation of precipitation at a range of spatial scales. Calibration of weather radars should be given high priority. The hopes that accurate spatial precipitation coverage and depth will be provided in the near future, mainly by radar measurement, are perhaps optimistic.
There is considerable need for a new network of accurate ground-based measuring systems to augment what will be provided from radar coverage. This is evident from recent work by Kuligowski and Barros (1996) and the above-cited works by Smith et al. (1996b), Krzysztofowicz (1995), Goodrich et al. (1995), and Steiner et al. (1997). Much is likely to be achieved from modernization of the NWS. We all must work cooperatively to ensure that the NWS takes a leadership role in developing techniques and delivering products that are beneficial to society. There is a great deal to be gained by the NWS supporting external research groups and individuals to help achieve its modernization goals.
Much remains to be done in hillslope hydrology, as indicated by the work of Goodrich et al. (1995) and Burges et al. (1998). Renewed effort is required to
develop hydroclimatology schemes that are compatible with features of spatially distributed hydrologic models and associated measurement systems. Measurement systems will combine ground-based measurement and radar estimation of precipitation, features of boundary layer water and energy transport, and remotely sensed atmospheric and ground-level hydrologic states and fluxes.
In all that is attempted there are many intellectual and developmental challenges. The "grand challenge" is working toward connecting ocean, atmosphere, and hydrosphere interactions into a coherent approach that will yield hydrologically useful information at the hillslope, catchment, and continental river basin scale for time scales up to the order of a decade. Mesoscale meteorology models and associated supporting measurements will provide the needed information at time scales on the order of minutes, hours, or several days. The need for longer-term information will require greater coordination and championing of the cause of research scientists and practitioners from hydrology, meteorology, and oceanography than has been done.
Scientific and managerial leadership, and coordination between programs in various agencies, has been provided by the founding program director for hydrologic sciences at the National Science Foundation, L. Douglas James, as he has worked to implement the findings of the Eagleson committee's report. Increased coordination is needed for the integration of hydrologic science with the atmospheric and ocean sciences to approach the many practical issues of the water budget and how it influences society and how society influences it. The Water Science and Technology Board has done a commendable job in covering the spectrum of water issues. The time appears to be ripe to establish a new NRC board to focus on hydrologic science, in its broadest context, including human-influenced ecosystems and societal infrastructure. Such a board would be charged with the development and nurturing of hydrologic science, particularly as it relates to water and society, and have as its primary charge to attend to all aspects of science associated with the hydrologic cycle.
The Eagleson committee's report was visionary and echoed leadership from an earlier era. Horton concluded his 1931 paper by saying that "the most immediate needs for the advance of the science are (a) the collection of additional basic data along various lines, (b) correlative research and coordination of existing results, and (c) research to provide connective tissue between related problems" (p. 202).
It is up to our generation to ensure that the leadership provided initially by the WSTB and the Eagleson committee is continued and that Robert Horton's clarity of vision is not lost. Horton's "connective tissue" is more important than ever.
Epilogue
We are clearly behind the times considering hydroclimatology and the timing of major climatic and storm features. Lerner and Loewe in Camelot reported on the state of meteorology and climatology at the time of King Arthur at Camelot:
ARTHUR: It's true! It's true! The crown has made it clear.
The climate must be perfect all the year. A law was made a distant moon ago here: July and August cannot be too hot. And there's a legal limit to the snow here In Camelot. The winter is forbidden till December And exits March the second on the dot. By order, summer lingers through September In Camelot. Camelot! Camelot! I know it sounds a bit bizarre, But in Camelot, Camelot That's how conditions are. The rain may never fall till after sundown. By eight, the morning fog must disappear. In short, there's simply not A more congenial spot For happily-ever-aftering than here In Camelot.
Boring as it would be to live in such a climate, a critical component is missing: the information is not quantitative!
Acknowledgment
The work reported here was supported in part with funds from the National Science Foundation under grant EAR-9506391.
References
Abdulla, F. 1995. Regionalization of a Macroscale Hydrological Model. Water Resources Series, Technical Report #134. Department of Civil Engineering, University of Washington.
Abdulla, F., and D. P. Lettenmaier. 1997. Application of regional parameter estimation schemes to simulate the water balance of a large continental river. J. Hydrol. 197:258–285.
Ad Hoc Panel on Hydrology. 1962. Scientific Hydrology. Washington, D.C.: U.S. Federal Council for Science and Technology.
Amburn, S. A., and S. Fortin. 1993. Use of WSR-88D and Surface Rain Gage Network in Issuing Flash Flood Warnings and Main Stem Flood Forecasts Over Osage County, Oklahoma, June 5, 1991. Pp. 321–330 in NOAA Technical Memorandum NWS ER-87, Post-print Volume, Third National Heavy Precipitation Workshop. Washington, D.C.: U.S. Department of Commerce.
Atlas, D. 1997. Budgetary foul weather. Science 275:1719.
Barros, A. P., and J. L. Evans. 1997. Designing for climate variability. J. Prof. Issues Eng. Educ. Practice 123(2):62–65.
Brutsaert, W. 1986. Catchment-scale evaporation and the atmospheric boundary layer. Water Resour. Res. 22(9):39S–45S.
Burges, S. J. 1989. Hazardous floods: Trends in forecasting and hydrologic modeling. Pp. 210–228 in Proceedings of the Pacific International Seminar on Water Resources Systems, Tomamu, Japan.
Burges, S. J. 1996. Climate variability and water resources in the south-west of western Australia: Research needs and priorities. Pp. 21–23 in Climate Variability and Water Resources Workshop, Water and Rivers Commission (WA). J. K. Ruprecht, B. C. Bates, and R. A. Stokes, eds. Water Resources Technical Report Series No. WRT5. Pp. 21–23.
Burges, S. J., M. S. Wigmosta, and J. M. Meena. 1998. Hydrologic effects of land-use change in a zero-order catchment. J. Hydrol. Eng. 3(2):86–91.
Cahine, M. T. 1997. The success of seasonal-to-interannual climate prediction requires GEWEX. Global Energy and Water Cycle Experiment, World Climate Research Programme News 7(1):2.
Cane, M. A., A. C. Clement, A. Kaplan, Y. Kushnir, D. Pozdnyakov, R. Seager, S. E. Zebiak, and R. Murtugudde. 1997. Twentieth-century sea surface temperature trends. Science 275:957–960.
Carlowicz, M. 1996. NWS hydrologists predict better river forecasts. EOS Tran. Am. Geophys. Union 77(52):529–530.
Crowley II, T.E. 1993. Probabilistic great lakes hydrology outlooks. Water Resour. Bull. 29(5):741–753.
Crowley II, T.E. 1996. Using NOAA's new climate outlooks in operational hydrology. J. Hydrol. Eng. 1(3):93–102.
Dawdy, D. R., and J. M. Bergman. 1969. Effect of rainfall variability on streamflow simulation. Water Resour. Res. 5(5):958–966.
Eagleson, P. S. 1986. The emergence of global-scale hydrology. Water Resour. Res. 22(9):6S–14S.
Eltahir, E. A. B., and R. L. Bras. 1996. Precipitation recycling. Rev. Geophys. 34(3):367–378.
Faures, J.-M., D. C. Goodrich, D. A. Woolhiser, and S. Sorooshian. 1995. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 173:309–326.
Foufoula-Georgiou, E., and W. Krajewski. 1995. Recent advances in rainfall modeling, estimation, and forecasting. Pp. 1125–1137 in U.S. National Report to International Union of Geodesy and Geophysics 1991–1994, Reviews of Geophysics, Supplement. Washington, D.C.: American Geophysical Union.
Georgakakos, K. P., and M. L. Kavvas. 1987. Precipitation analysis, modeling, and prediction in hydrology. Rev. Geophys. 25(2):163–178.
Goodrich, D. C. 1990. Geometric Simplification of a Distributed Rainfall-Runoff Model over a Range of Basin Scales . Ph.D. dissertation, Department of Hydrology and Water Resources, Tucson, University of Arizona. Tucson.
Goodrich, D. C., J.-M. Faures, D. A. Woolhiser, L. J. Lane, and S. Sorooshian. 1995. Measurement and analysis of small-scale convective storm rainfall variability. J. Hydrol. 173:283–308.
Gu, D., and S. G. H. Philander. 1997. Interdecadal climate fluctuations that depend on exchanges between the tropics and extratropics. Science 275:805–807.
Horton, R. E. 1931. The field, scope, and status of the science of hydrology. Trans. Am. Geophys. Union. Pp. 189–202.
Hoyt, W. G. 1936. Studies of Relations of Rainfall and Run-off in the United States. U.S. Geological Survey Water Supply Paper 772. Washington, D.C.: U.S. Government Printing Office.
Ji, M., A. Leetma, and V. E. Kousky. 1996. Coupled model prediction of ENSO during the 1980s and 1990s at the National Centers for Environmental Prediction. J. Climate 9(12):3105–3120.
Krzysztofowicz, R. 1995. Recent advances associated with flood forecast and warning systems. Pp. 1139–1147 U.S. National Report to International Union of Geodesy and Geophysics 1991–1994, Reviews of Geophysics, Supplement. Washington, D. C.: American Geophysical Union.
Kuligowski, R. J., and A. P. Barros. 1996. Evidence of orographic precipitation effects in the Appalachian Mountains. EOS Trans. Am. Geophys. Union 77(17):S112.
Lall, U., and M. Mann. 1995. The Great Salt Lake: A barometer of low-frequency climatic variability. Water Resour. Res. 31(10):2503–2515.
Lall, U., T. Sangoyomi, and H. D. I. Abarbanel. 1996. Nonlinear dynamics of the Great Salt Lake: Nonparametric short-term forecasting. Water Resour. Res. 32(4):975–985.
Liang, X., D. P. Lettenmaier, E. F. Wood, and S. J. Burges. 1994. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 99(D7):14,415–14,428.
Michaud, J., and S. Sorooshian. 1994. Comparison of simple versus complex distributed runoff models on a midsized semiarid watershed. Water Resour. Res. 30(3):593–605.
National Research Council. 1991a. Opportunities in the Hydrologic Sciences . Washington, D.C.: National Academy Press.
National Research Council. 1991b. Managing Water Resources in the West Under Conditions of Climate Uncertainty: A Proceedings. Washington, D.C. National Academy Press.
National Research Council. 1996. Assessment of Hydrologic and Hydrometeorological Operations and Services. Washington, D.C.: National Academy Press.
Parlange, M, B., W. E. Eichinger, and J. D. Albertson. 1995. Regional scale evaporation and the atmospheric boundary layer. Rev. Geophys. 33(1):99–124.
Paulson, R. W., E. B. Chase, R. S. Roberts, and D. W. Moody (Compilers), 1991. National Water Summary 1988–1989—Hydrologic Floods and Droughts. Water Supply Paper 2374. U.S. Geological Survey, Denver, Co.
Quinn, W. H., V. T. Neal, and S. E. A. Mayolo. 1987. El Niño occurrences over the past four and a half centuries. J.Geophys. Res. 92(C13):14449–14461.
Ropelewski, C. F., and M. S. Halpert. 1996. Quantifying southern oscillation—precipitation relationships. J. Climate 9(5):1043–1059.
Schaake, J. C. 1989. Linking hydrologic and meteorologic components to form an operational flash flood forecast system (abstract). EOS Trans. Am. Geophys. Union 70(15):341.
Smith, J. A., D. J. Seo, M. L. Baeck, and M. D. Hudlow. 1996a. An intercomparison study of NEXRAD precipitation estimates. Water Resour. Res. 32(7):2035–2045.
Smith, J. A., M. L. Baeck, M. Steiner, and A. J. Miller. 1996b. Catastrophic rainfall from an upslope thunderstorm in the Central Appalachians: The Rapidan storm of June 27, 1995. Water Resour. Res. 32(10):3099–3113.
Steiner, M., J. A. Smith, S. J. Burges, and C. V. Alonso. 1997. Use of RADAR for remote monitoring of rainfall rate and rainfall kinetic energy on a variety of scales. Pp. 831–839 in Management of Landscapes Disturbed by Channel Incision. S. S. Y. Wang, E. J. Langendoen, and F. D. Shields, Jr., eds. University, Miss.:University of Mississippi.
Teqnical Services, Inc. 1997. National Electronic Drought Atlas Users Guide. Web site: www.teqservices.com.
Wigmosta, M. S., and S. J. Burges. 1997. An adaptive modeling and monitoring approach to describe the hydrologic behavior of small catchments. J. Hydrol. 202(1–4):48–77.
Wigmosta, M. S., L. W. Vail, and D. P. Lettenmaier. 1994. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res, 30(6):1665–1679.
Woolhiser, D. A. 1996. Search for physically based runoff model—A Hydrologic El Dorado. J. Hydr. Eng. 122(3):122–129.
Woolhiser, D. A., R. E. Smith, and D. C. Goodrich. 1990. KINEROS, A Kinematic Runoff and Erosion Model. Documentation and User Manual, Publication ARS-77. Agricultural Research Service, U.S. Department of Agriculture. Washington, D.C.: U.S. Government Printing Office.