6
Symmetry Tests in Nuclear Physics
Introduction: Priorities and Challenges
The realization that symmetries are the key to understanding and classifying the structure of matter and the fundamental forces is among the deepest theoretical insights of this century. The seminal work is identified with the Nobel Prizewinning nuclear theorist, Eugene Wigner, whose ideas have influenced every area of modern physics. The structure and behavior of nuclei reflect the symmetries of the basic building blocks and their interactions. Nuclei can also be laboratories for studying the symmetries of the fundamental processes themselves.
High-energy particle physics grew out of early nuclear physics, so it is not surprising that there are similarities between some of the scientific goals of the two fields. Each field brings its own arsenal of experimental and theoretical techniques. Understanding the fundamental forces, the main focus of particle physics, is an essential step toward a deep understanding of the nucleus. But the nucleus can be a powerful tool for studying fundamental forces themselves. To exploit the nucleus as a research tool, experimentalists capitalize on the understanding of the structure of specific nuclei accumulated over the last sixty years. Successful nuclear models are the instruction manuals for understanding this nuclear laboratory. There has been enormous progress in the last two decades, and amazing experimental feats have been accomplished: nuclear physicists have measured neutrino scattering from specific nuclear states, observed the incredibly weak process of double beta decay, and detected neutrinos coming from the Sun despite the feeble strength of the basic interactions of neutrinos at
low energies. There are a number of challenging questions for nuclear physicists at the particle physics boundary:
- Do neutrinos have mass? Are the leptons from different generations mixed together by the weak interaction?
- Is the pattern of symmetry violations found experimentally at low energies consistent with the Standard Model description? Can a direct manifestation of a violation of time-reversal symmetry be discovered at low energies?
- What is the significance of the mixing of quarks from different generations? Will more precise experiments show that mixing parameters satisfies the quantum mechanical laws of probability within the context of three generations of quarks and leptons?
The Standard Model
The first hint of the existence of the fundamental weak force was the discovery of radioactivity about a century ago. It has taken most of the last hundred years to establish the Standard Model, a surprisingly complete description of the fundamental particles and their interactions. The most important clues came from elegant experiments that studied weak-interaction phenomena. The Standard Model describes the electromagnetic, weak, and strong interactions; gravity is the only known interaction missing. While there are occasional hints of the need for revision, no confirmed experiment contradicts the Standard Model. Nevertheless, despite the successes, most physicists are convinced that a more complete theory of nature will eventually replace it. The Standard Model has a disturbingly large number of parameters whose numerical values are not explained; many aspects of the model seem unnatural.
Since the early 1970s, experimentalists have mounted a two-pronged assault on the Standard Model attempting to discover its limitations: trying to verify its quantitative predictions to the highest possible precision, and searching for new, unexpected, and inconsistent phenomena. The top priority of high-energy physics is to discover direct evidence for the Higgs boson, the particle responsible for all finite particle masses according to the Standard Model. If there is no Higgs boson, then the Standard Model must be revised. The prudent search for the Higgs is at the highest available energy. Searches for specific extensions to the Standard Model (for example, a class of attractive theories classified as grand unified supersymmetric models) are often, but not always, carried out at high energies. Nevertheless, it may turn out that testing the Standard Model precisely at low energies is the most economical way to find new physics. Low-energy experiments often have unique discovery potential.
The best-established part of the Standard Model is its description of the electromagnetic interaction. Called quantum electrodynamics (QED), it developed well before the weak and strong interaction were incorporated into the
modern Standard Model. QED is the theoretical prototype of the entire Standard Model. Confidence in QED comes mostly from atomic physics tests. Although no longer a major thrust, precision tests of QED continue with nuclear physicists participating in important areas. One aspect of the most interesting modern work involves a simple but exotic atom, muonium, consisting of an antimuon (the antiparticle of the muon) and a bound electron. Elegant muonium experiments have been done by nuclear and atomic physicists who exploit medium-energy nuclear physics accelerators, which are muon sources. Nuclear physicists are working with particle and atomic physicists on major new experiments to determine precisely the magnetic moment of the muon (to be precise, the quantity g – 2). The muon's g – 2 is a measure of the QED corrections to the quantitative relationship between the muon's spin and its magnetic moment. In principle, theory can predict g – 2 exactly, but calculating the value to better and better precision is a formidable theoretical task. For decades, newly developed experimental and theoretical techniques have challenged each other, searching for a discrepancy that might indicate that the underlying theory is wrong. Modern experiments rely on sophisticated accelerator technologies, and muon, which have a lifetime of only two-millionths of a second, are confined in specially constructed storage rings. These experiments have the unique capability of testing particular Standard Model predictions. But the main thrust of the nuclear physics assault on the Standard Model focuses on the fundamental weak interaction. An active area of research involves detailed studies of the phenomena of nuclear beta decay, the process responsible for natural radioactivity.
The elementary particles of the Standard Model are summarized in Figure 6.1. The fundamental constituents of matter are the structureless quarks and leptons and the forces between them that arise from the "exchange" of particles called gauge bosons. Photons, gluons, and the W and Z bosons are the gauge bosons for the electromagnetic, strong, and weak forces, respectively. The interactions are characterized by special kinds of symmetry classified as gauge symmetries. In a quantum theory, a symmetry is a specific change of variables that leaves all the physical predictions unchanged. Each symmetry implies an associated conservation law obeyed by the interaction. The correct theory of nature must account for the conservation laws that are verified experimentally. For example, one symmetry of electrodynamics implies that the photon has no mass and that electric charge is conserved. No experiment has ever found a violation of electric-charge conservation or a nonzero photon mass, and this symmetry is well established. The fact that photons themselves do not have electric charge makes QED rather simple. The strong force described by quantum chromodynamics (QCD) is mediated by massless gluons, but they are self-interacting; consequently, QCD is much more complicated than QED. One important implication of self-interacting gluons is that under normal conditions, quarks are confined. The basic building blocks of all hadrons and ultimately the atomic nucleus, the quarks, apparently cannot exist in isolation. In particular, no experiment has

FIGURE 6.1
The few basic building blocks (quarks and leptons) and the exchange particles (gauge bosons) of the Standard Model are economically displayed in a chart much smaller than the periodic table of the elements.
succeeded in isolating a quark. While it is believed that quark confinement is fully consistent with the Standard Model, a rigorous theoretical demonstration has not been made because of the complications of dealing with a nonlinear theory.
Beta decay is a process in which a nucleus emits an electron and a neutrino and results from the exchange of a particle, in this case a massive W boson. In beta decay, one of the quarks transforms into a quark of a different type (a different flavor) and at the same time a W boson is emitted, which quickly decays into an electron and a neutrino (electrons, muons, tauons, and neutrinos are the elementary particles that are classified as leptons). The character of the particular interaction is determined by the properties of the exchanged particles; the range of the interaction depends on their mass. The weak interaction is a weak force with a short range because the W and Z gauge bosons are rather heavy, about 90 times heavier than the proton.
The Standard Model has already stood up against decades of intense experimental scrutiny. Why, then, is it not regarded as the best possible theory of nature, "the ultimate theory"? In spite of its successes, the Standard Model has about 19 parameters that are apparently arbitrary—numbers whose origins are not understood. Moreover, some of the parameters have values that are hard to understand. For example, in the present Standard Model, neutrino masses are all set to zero (in fact, the model would not require a big change to incorporate finite neutrino mass). The situation is much different from that of the massless photon, because there is no obvious symmetry in the Standard Model that accounts for massless neutrinos. In general, the particle masses are modified by interactions. Keeping physical neutrino masses zero seems to require a conspiracy: the magnitude of the bare neutrino masses and the strength of the interactions must be almost exactly tuned to give zero in the end. Physicists have come to regard theories that must be finely tuned as unnatural and unsatisfactory.
All the quarks are assigned a one-third unit of baryon number. So far, baryon number is absolutely conserved according to experiment. But, as with the zero neutrino masses, no underlying symmetry explains baryon-number conservation. If there were a symmetry, baryon number should be associated with a force, like electric charge, but experiments have found no force that couples to baryon numbers. A similar problem occurs for leptons: experiments seem to require conserved lepton numbers (lepton number discriminates between leptons from different generations) in the absence of an underlying symmetry. With no good reasons for these conservation laws, searches for violations of baryon and particularly lepton number continue to be actively pursued by nuclear physicists.
The unsatisfactory features of the Standard Model suggest specific areas for experiments to probe. For example, looking for conclusive evidence of nonzero neutrino mass is a major goal of nuclear physics.
Testing Symmetries
Understanding the symmetries relevant to the behavior of the physical world, even approximate symmetries, organizes the underlying physics. The connection between symmetries and conservation laws is the key link in this understanding. Conservation laws for energy and momentum are understood as a consequence of underlying symmetries with respect to translations in time and space. If the laws of nature are the same everywhere in the universe and do not change in time, then energy and momentum must be conserved absolutely. The conservation laws for energy and momentum are so well tested and so well established that it is almost inconceivable that a violation will ever show up.
As experimental and theoretical tools grew more sophisticated, symmetries other than those of space-time were introduced in physics. These go under the name of internal symmetries. Electric-charge conservation is one example. Some related internal symmetries first studied in nuclear physics include charge independence
and charge symmetry. Neutrons, being neutral particles, are not affected much by the electromagnetic force. On the other hand, protons, being charged, feel a much larger electrical force. Charge symmetry is a statement about the strong force: the nuclear force between two neutrons is the same as the nuclear force between two protons. Charge independence is a bigger symmetry, relating a proton-neutron system to a proton-proton or neutron-neutron system: the nuclear force between any two nucleons (be they protons, neutrons, or a combination) is the same, apart from the electroweak contributions. The ideas of charge symmetry and charge independence in nuclear physics led to the marvelous concept of isospin. Isospin is an abstract way of describing the symmetry between neutrons and protons. The theoretical description of isospin is mathematically similar to angular momentum and spin, but isospin is in a completely abstract space in which the axes have something to do with the type of particle or the flavor. This revolutionary theoretical idea is the prototype of techniques for describing all internal symmetries. Charge symmetry and charge independence are not exact symmetries in nuclear systems, and accounting for the observed deviations tests our understanding of the limits of this symmetry. Isospin symmetry is broken by the electromagnetic interaction and because each type of quark has a definite mass. Understanding broken symmetries better is an ongoing goal of modern nuclear physics; the particulars of symmetry breaking are studied with careful measurement of polarization effects in reactions with light nuclear systems at medium-energy nuclear physics accelerators. One recent experiment (shown in Figure 6.2) employed sophisticated methods of polarizing liquid hydrogen targets and highly polarized proton beams.
For a long time, it was assumed that the laws of nature are unchanged by mirror reflection: a process seen in a mirror should be completely consistent with its theoretical description. Experiments had already established that other spatial transformations—translations and rotations—are indeed symmetries obeyed by the laws of physics; furthermore, no evidence for inversion symmetry breaking was evident in the structure of atoms or nuclei, so it was assumed that all physical laws obey mirror symmetry. It came as a tremendous surprise in 1956 when it was discovered that the weak interaction violates mirror symmetry. The associated quantum number, parity, is not conserved in certain fundamental processes. The first clear experimental demonstration was done by a group of nuclear physicists. They studied the beta decay of 60Co that had been diffused into a paramagnetic salt and spin-polarized in a high magnetic field at low temperatures. It was found that electrons emitted in this decay are emitted preferentially in the direction of the nuclear spin. But when viewed in a mirror, the relative orientation of the electron momentum to the nuclear spin reverses, as shown schematically in Figure 6.3. The observed asymmetry in the 60Co beta decay means that we would be able to tell whether we were viewing the process directly or in a mirror! The observation of parity violation caused physicists to question whether or not other discrete transformations—conjugation of charges (exchanging particles for antiparticles)

FIGURE 6.2
The apparatus used at the Indiana University Cyclotron Facility (IUCF) to measure small violations of charge symmetry in nuclear forces. The experiment was a high-precision study of the scattering of a spin-polarized neutron beam by a spin-polarized proton target. The scattered neutrons and protons were detected in the counters shown. (Courtesy Indiana University Cyclotron Facility.)
and reversal of time (the process evolving in reverse)—are symmetries of nature. It was quickly realized that charge-conjugation symmetry is violated as badly as reflection symmetry.
Spatial Reflection Symmetry
Experiments suggest that reflection symmetry is broken as badly as it could be in processes like beta decay. This observation is incorporated into the Standard Model, but what is the reason for maximal parity violation? There are alternative models to the Standard Model—for example, attractive left-right symmetric models that contain an extra set of intermediate-vector bosons with the other sense of parity violation. Consistency with low-energy experiments is obtained if the extra bosons have masses sufficiently large not to have an effect. Nuclear physicists are instrumental in testing this plausible class of Standard Model extensions. Precise measurements of basic parity-violating effects in the

FIGURE 6.3
Schematic diagram of the principle of the first experiment to discover that reflection symmetry is violated by the weak interaction. A 60Co nucleus has many of the properties of a spinning top. If the electron from the beta decay of 60Co were to be emitted along one sense of the axis of the spinning nucleus, then the situation would be just the opposite in a mirror. Nuclear physics experiments have clearly demonstrated that reflection symmetry is not obeyed by the weak interaction.
ordinary beta decay of muons and nuclei are compared to the exact Standard Model predictions. Nuclear physicists have invented novel techniques for polarizing nuclei and measuring the positron helicities to accomplish these tests. The neutron is also an excellent system for study, because it is possible to achieve a high degree of neutron polarization and the neutron is simple and more easily understood theoretically than are more complex nuclei. Presently, the most precise experiments exploit muon beta decay and ordinary nuclear beta decay. The muon experiments have significant prospects for improvement because of new initiatives for intense low-energy muon sources at meson factories. For nuclear beta decay, the rates are usually high; improving the sensitivity is a matter of eliminating systematic uncertainties. The latest experiments attempt to study the beta decay of radioactive atoms in the extremely clean environments of optical traps. Optical trapping is a way of confining atoms to a small region of space by using the radiation pressure of laser light. These experiments promise enormous improvements, but the level of precision of existing experiments is good enough to rule out theories with extra exchange gauge particles as heavy as several
hundred GeV compared to the 90-GeV W and Z particles of the Standard Model. Currently, the limits from low-energy experiments are often beyond those from direct searches at high-energy accelerators.
Time-Reversal Symmetry
Reversal of time is the only discrete transformation of space-time that has not been demonstrated to be broken. A violation of time-reversal symmetry means that nature favors the course of a fundamental process to proceed with a particular direction of time. If nature were symmetric under time reversal, we could not determine if a movie of a fundamental process were running forward or backward. It is natural to have a sense of the direction of time. For example, people age, beaches erode, and crops grow; the reverse is unnatural. These kinds of time-symmetry violation are understood as the natural tendency of complicated systems to evolve toward a more and more disordered state, but at the level of the fundamental interactions, the significance of an arrow of time is much more important. A deeper understanding of time-reversal invariance may hold the key to understanding the origin of the universe. It is convincingly argued that time-symmetry breaking is an essential ingredient for creating a universe that is primarily matter instead of equal mixtures of matter and antimatter. Nuclear physicists probe this question with experiments searching for the electric-dipole moments (EDMs) of neutrons and atoms. Static EDMs are forbidden in the absence of time-symmetry violation. In the case of atoms, an EDM can arise if the electron has an electric-dipole moment or if there is a time-symmetry-violating interaction within the nucleus. The most recent experiment to search for the electric-dipole moment of the neutron is shown in Figure 6.4. The limits on the existence of atomic and neutron EDMs provides some of the best constraints on some of the most plausible extensions to the Standard Model. One class of possible extension is called supersymmetric theories, which predict the existence of a large number of new and as yet undiscovered particles. Important constraint on many of these new theories comes from searches for Standard Model-forbidden rare decays of muons. The most precise limits on rare muon decay comes from experiments carried out at the Los Alamos Meson Physics Facility (LAMPF) during the last two decades. Other constraints come from low-energy experiments searching for EDMs of electrons and nucleons.
It is also possible that time-reversal-symmetry breaking might show up in the decay of an unstable system. Modern experiments search for T-violating correlations in the beta decay of neutrons, mesons, and particular nuclei. A new search for a T-violation effect in neutron beta decay is now under way at the National Institute of Standards and Technology (NIST) reactor in Gaithersburg, Maryland, shown in Figure 6.5. Another precise limit on T-violation comes from the beta decay of 19Ne. The experiment uses the atomic beam technique applied to radioactive atoms produced online at a cyclotron. A related transformation,
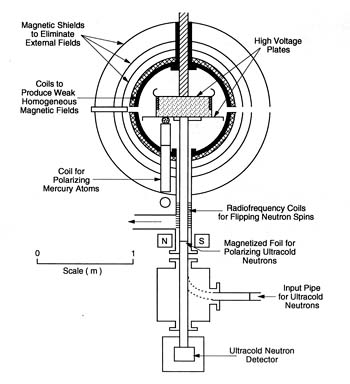
FIGURE 6.4
Schematic diagram of the experiment to search for a neutron electric-dipole moment at the Laue-Langevin Institute (ILL) in Grenoble, France. The experiment exploits the unusual properties of ultracold neutrons. Ultracold neutrons can be confined in material bottles and polarized with thin magnetized foils. This experiments searches for a change in the neutrons' precession frequency caused by an imposed electric field. The neutrons' precession is directly compared to the precession of an isotope of mercury, which should show no effect. The effect of an electric field on the neutrons' precession would indicate an electric-dipole moment and a violation of time-reversal symmetry. (Courtesy of Laue-Langevin Institute.)
called CP, is obtained by combining mirror reflection with the exchange of particles with antiparticles; CP was discovered to be a broken symmetry at high-energy accelerators during the 1960s. The effect is small, showing up in particular decay modes of the neutral K-mesons. Theory makes a strong case that CP violation implies T-violation, but so far no explicit T-violation has been observed. The answer to this puzzle will be a major advance in the quest for a better

FIGURE 6.5
An experiment to study how well time-reversal symmetry is obeyed in the beta decay of the free neutron. A beam of cold neutrons enters the detector region form the upper right. The detector is situated in a carefully designed magnetic guide field. Some of the detector elements for measuring the decay electrons and residual protons from neutron beta decay are visible to just downstream of the experimentalists shown in the photograph.
theoretical description of nature. The Standard Model incorporates T-violation in a set of parameters that are taken from kaon-decay experiments, but the size of any direct T-violation effects is predicted to be too small to measure with present experimental techniques. If T-violation were found at the level of sensitivity of present experiments, it would already be evidence for a breakdown in the Standard Model.
Precision Measurements of Standard Model Parameters
Precisely measuring the Standard Model parameters is essential, as one of the best ways of establishing the consistency (or inconsistency) of the theory. All experiments, independent of the energy of the process involved, must yield exactly the same value of the particular parameter. Nuclear physics experiments play an important role in this program by establishing consistency at low energies.
For reasons still unknown, the weak interaction mixes quarks together (in the sense of quantum mechanics) in peculiar ways. Four Standard Model parameters characterize this mixing. One parameter is measured in ordinary nuclear beta decay and others in the beta decays of particles containing strange and bottom quarks. The determination of the weak vector coupling constant from nuclear beta decay is crucial. The experiments involve measurements of masses, decay energies, and branching ratios, among the most precise measurements in nuclear physics. This work exploits the most sophisticated nuclear physics devices available; for example, a recent experiment exploited the Gammasphere, one of the world's best tools for elucidating the nuclear structure of nuclei with large angular momentum. Small corrections from the effect of the electromagnetic interactions within the nucleus must be made with extremely good precision, using the most sophisticated shell-model representations of the nucleus. At the level of present experiments a tantalizing hint of a discrepancy with the Standard Model is emerging, but better precision is required before a firm conclusion is possible. Studies of neutron beta decay can also shed light on this issue, but the precision is not quite up to the level of the experiments using nuclear decays. These same neutron-decay experiments are presently the best way to measure the nucleon axial vector coupling, which should eventually be predicted with precision by QCD. Neutron-decay experiments are expected to improve with the availability of more intense sources of cold and ultracold neutrons being planned at future neutron-spallation facilities. Meanwhile, particle and nuclear physicists have collaborated to mount an experiment to improve the precision of the mixing parameter that comes from strangeness-changing beta decay by measuring the lifetime for a kaon to beta decay into a pion. In Europe, a U.S.-led group is studying the beta decay of the pion at a large nuclear physics cyclotron in Switzerland. From the theoretical standpoint, pion decay is perhaps the cleanest way to study this particular Standard Model parameter, but the experiment is extraordinarily difficult because of the small probability that a pion decays in the required way.
Beta-decay experiments can be designed to search for unexpected forces, and it is likely that the old process of nuclear beta decay will remain a valuable tool for a long time. Techniques for storing neutrons, atoms, and ions in traps hold the promise of experimental breakthroughs. New intense sources of cold and ultracold neutrons and intense sources of exotic radioactive nuclei at future exotic-beam facilities will make this an even more active research area in the coming years. Figure 6.6 shows about 50,000 radioactive 21Na atoms being used to study reflection symmetry. This experiment should help answer the puzzle of whether or not parity is violated as badly as it could be in processes like beta decay. This technique will have even more applications at future exotic-beam facilities capable of producing even larger quantities of short-lived radioactive atoms.

FIGURE 6.6
The monitor in this photograph is displaying about 50,000 atoms of radioactive 21Na that are confined in a specially designed atom trap on the right. The isotope 21Na has a half-life of only 22 seconds so the atoms must be continuously produced with a cyclotron accelerator. Collecting radioactive atoms and studying their decays is an excellent method of testing the symmetries implied by the Standard Model.
One of the best ways to measure the mixing between the weak and electromagnetic interactions, the Weinberg angle, is to study the parity-violating interaction between electrons and the nuclei of particular atoms. Parity mixing has been seen in several atomic systems; the best measurement at present is done with 133Cs atoms. Nuclear physicists are exploring the possibility of measuring this effect in atomic francium, where the parity-mixing effect should be about 18 times larger. Since there are no stable isotopes of francium, the experiment must be carried out with a small number of radioactive atoms. Recently, nuclear physicists have managed to collect francium in a magneto-optic trap. Studying parity mixing in a series of isotopes of the same atom is an attractive method of making the determination of the Weinberg angle at low energy more reliable. One way to carry out such a program is to do these experiments with radioactive atoms.
The Search for Neutrino Mass
Nuclear physics played a key role in establishing the existence of the mysterious neutrino that was originally proposed to explain the apparent lack of energy conservation in nuclear beta decay. Unique among all the elementary constituents of the Standard Model, the neutrino interacts exclusively by the weak interaction, making its direct detection extremely difficult. It was first observed directly by experimentalists who used a nuclear reactor as a neutrino source. From the beginning, the neutrino was expected to be very light. Enrico Fermi was first to point out that neutrino mass could be determined from systematic studies of electrons from nuclear beta decay. The masses of neutrinos are taken to be zero in the Standard Model but, as was noted above, there is no natural explanation for zero-mass neutrinos. Finding out whether or not neutrinos have mass is among the most important issues in modern physics. Finite neutrino mass would require a modification of the current Standard Model, and present a number of intriguing cosmological implications.
Nuclear physicists have refined the method of measuring neutrino mass from the beta decay of tritium, Fermi's original suggestion. The conclusion of a half-dozen experiments in the last decade has been that the electron neutrino has a mass no larger than 10 eV, or less than 1/50,000 of the electron's mass. These experiments have reached a level of accuracy at which subtleties of atomic and molecular physics are important systematic uncertainties. A better understanding of the molecular and atomic physics involved is needed before the existing data can be used to put more stringent limits on the neutrino mass. Figure 6.7 is a photograph of one of the large spectrometers built to study the mass of the neutrino on the basis of tritium beta decay. At present, a half-dozen direct searches for neutrino mass from the decay of tritium have found no evidence for finite neutrino mass. However, the high-precision data are not completely understood, and all the experiments indicate a systematic deviation from the normal theory of beta decay. The origin of the deviation may have a simple explanation; for example, an unappreciated complication of the molecular physics of the radioactive tritium source, or it may be a clue that will lead to new physics. Efforts to resolve this issue are continuing.
A fascinating process that would cause neutrinos of one type to change into another is at the heart of what is evolving into a major scientific advance. The possibility that neutrinos of different types might transform into one another is allowed by the quantum nature of neutrinos. Such neutrino oscillations would occur if at least one of the neutrino types had mass and if neutrinos were to mix in a way similar to the quarks. Thus, neutrino oscillations offer another way to look for finite neutrino mass. In the absence of definite predictions about the likely masses and mixings of neutrinos, and in view of the solar neutrino results already discussed above, a number of experiments with different sensitivities are going on at high-energy accelerators, lower-energy nuclear-physics accelerators,

FIGURE 6.7
A large beta spectrometer (7 feet in diameter) designed especially to measure the energies of electrons emitted from the beta decay of radioactive tritium, an isotope of hydrogen with two neutrons and one proton. The photograph shows the enormous magnetic field coils in this toroidal spectrometer. By carefully studying the spectrum of electrons from tritium decay, it is possible to detect whether or not the neutrinos, also emitted in the beta-decay process, have a mass that is different from zero. (Courtesy of Lawrence Livermore National Laboratory.)
and reactors. Other important experiments use natural sources of neutrinos either from the Sun or from the collisions of cosmic-ray particles in the upper atmosphere. There are exciting results from a number of these experiments. The evidence of neutrino mass from atmospheric neutrinos and solar neutrinos seems particularly convincing, but there are also positive indications from an accelerator experiment.
An experiment using neutrinos produced in the beam stop of the LAMPF proton linac seems to show evidence of muon antineutrinos oscillating into electron antineutrinos, but other experiments have not reproduced this evidence yet. A photograph of the inside of the 100-ton liquid scintillator detector used in this experiment at LAMPF is shown in Figure 6.8. The neutrino mass hinted at, if this result were correct, is rather large and tantalizing because there could be cosmological and astrophysical implications. A sufficiently large neutrino mass might help explain the puzzling astrophysical evidence that much of the matter in the universe is not ordinary hadronic matter. Fortunately, a similar oscillation experiment in England may provide confirming evidence in the next few years. Experiments proposed at higher-energy accelerators should be capable of seeing the same effect with even better sensitivity. The other indications of neutrino mass using natural neutrino sources suggest smaller mass scales; while this does not directly contradict the LAMPF result, a fairly drastic modification of the Standard Model is necessary in order to accommodate all the positive indications.
The earliest neutrino oscillation experiments were carried out by nuclear physicists at reactors. With reactor sources one searches for the disappearance of electron neutrinos into any of the other types. Experiments have steadily improved over the years. The evidence is strong that neutrino oscillations have not been observed from reactor sources. These negative findings do not contradict the positive indications; instead, they help pin down the magnitude of the masses and mixings that could explain all the experiments. Sensitive, long-baseline reactor experiments are under way in Europe, Japan, and the United States.
Neutrino oscillations are the most natural explanation for the solar neutrino puzzle described above. Several consistent experiments go into establishing the conclusion that too few electron neutrinos are coming from the Sun. The favored theoretical solution involves the exciting possibility that otherwise subtle effects of neutrino oscillations get amplified as neutrinos pass though the dense matter in the Sun. The evidence is strong, but the SNO experiments can confirm it conclusively by simultaneously measuring the oscillations of the electron neutrino and the total flux of all neutrino types. Using the Sun as a source for studying neutrino properties is a beautiful example of cross-disciplinary physics. Years of experimental and theoretical work to understand the nuclear-reaction power sources within the Sun and the thermodynamics and mechanical processes of the burning process provide the essential foundation for interpreting these results.
A recent experiment using the SuperKamiokande experiment in Japan is providing perhaps the strongest evidence for neutrino oscillations. For some

FIGURE 6.8
The interior of a large neutrino detector used at LAMPF to study whether or not neutrino oscillations occur. The active detector is a large tank of scintillating liquid viewed by about 1,000 large light-detecting photomultiplier tubes. This experiment provides evidence that could indicate that neutrinos do in fact have finite mass. (Courtesy of Los Alamos Meson Physics Facility.)
time, several large underground detectors indicated that the ratio of muon- and electron-type neutrinos detected underground was inconsistent with expectations based on a seemingly reliable estimate. The SuperKamiokande experiment has dramatically demonstrated that the anomaly can be traced to a difference in the number of upward going and downward going muon-type neutrinos that are detected. The conclusion is that muon-type neutrinos seem to be oscillating on their way to the detector, but that electron neutrinos do not oscillate by a detectable amount in that distance. That the electron-type neutrinos do not show evidence for oscillations here would be completely consistent with the conclusions from CHOOZ, the most recent and most sensitive long-baseline reactor experiment, and also with the solar results, indicating a rich structure of neutrino masses and mixing parameters in satisfying analogy to what is seen for the quarks. Many questions remain. Why are the neutrinos so light? Are neutrinos the same type of fermions as the charged leptons? Or, in the jargon of the field, Are they Majorana or Dirac particles?
Neutrinos with mass could have a dramatic effect on the extremely rare process of double beta decays. Double beta decay, with the emission of two electrons and two neutrinos, is simply the rare coincidence of two simultaneous beta decays. Two-neutrino double beta decay is expected to occur, even with massless neutrinos. Double beta decay was predicted early in the century, but it was directly observed only during the last decade. The first direct observation of this process was an experimental milestone made possible by some of the most advanced modern techniques of low background counting, invented specifically for this research. The observed double-beta-decay lifetimes are many trillions of times longer than the age of the universe. By now, two-neutrino double beta decay has been seen in about a dozen different isotopes. Double beta decays without neutrinos are also possible, if neutrinos have mass and are of the Majorana type, meaning that they are their own antiparticles. In this case, a neutrino emitted by one neutron can be absorbed by another, leaving two electrons that share all the decay energy. Double beta decay, with or without neutrinos, can be the dominant mode of decay for certain nuclear systems that are energetically forbidden to decay by ordinary beta decay. Neutrinoless double beta decay has not yet been observed, and whether or not neutrinos are of the Majorana type is still an open question, the answer to which will have profound implications. The current upper limit on the electron neutrino Majorana mass, derived from limits on neutrinoless double beta decay, is less than about 0.5 eV, and, thereby, experiments have already eliminated a number of previously proposed Standard Model extensions. The most sensitive experiment used several kilograms of isotopically enriched 76Ge, which decays by the double-beta process. In this experiment, the 76Ge itself was made into a detector capable of measuring the energy of decay electrons with excellent resolution. To avoid backgrounds, the experiment was done in an underground laboratory. Despite the great difficulties (the double-beta-decay process was observed only ten years ago for the first time), there has
been tremendous progress in this field. There are now numerous observations in different systems. Experiments are being proposed that could improve existing limits on the neutrinoless process by orders of magnitude. Interpreting the limits in terms of fundamental neutrino parameters requires a close collaboration between the experimentalists and nuclear theorists.
The Weak Interaction Within the Nuclear Environment
The nuclear interior provides a unique environment for studying the weak interaction between hadrons, with no leptons involved. The weak force is exceedingly feeble compared to the strong nuclear force, but parity violation provides us with the necessary clue for recognizing its effects. While the weak force can mostly be ignored in describing the structure of nuclear systems, it still introduces a small violation of mirror-reflection symmetry. The weak interaction in its purest form has too short a range to act directly; instead, it organizes itself as a perturbation to the various meson exchange forces between the nucleons. Much has been learned about the weak hadronic interaction, but significant puzzles remain to be solved. Sensitive experiments combined with sophisticated theory are still inadequate to provide a completely consistent picture of the structure of the weak force within the nucleus. Investigations of the weak-interaction-induced parity mixing of nuclear levels in well-chosen systems can discriminate between the charged current (arising from W exchange) and neutral current (arising from Z exchange) components of the nucleon-nucleon weak force. The effect of the charged currents is consistent with expectations, but there is no clear evidence of the expected neutral current effect in nuclei. However, recent evidence of a nuclear anapole moment (basically a doughnut-shaped or toroidal nuclear magnetic field configuration within a nucleus) from studies of atomic parity mixing is consistent with the expected size of the nucleon-nucleon neutral current. New experiments are clearly called for. Although the effects are extremely small and hard to observe in the nucleon-nucleon system, they have been seen directly in proton-proton scattering. A new experiment is planned to measure the effect of parity violation on the gamma rays following the capture of polarized neutrons on protons. This experiment could solve the puzzle about the missing effect of the Z in nuclei, because it is free from the theoretical uncertainties that are required to interpret finite nuclei. However, the experiment is exceedingly difficult, because the size of the expected effect is only at the part in 100 million level.
The weak force should also affect the outcome of neutron-nucleus elastic-scattering experiments. These experiments are sensitive to the interference of low-energy neutron capture resonances with angular momenta of zero and one. The method is exquisitely sensitive to a small parity-breaking force, because the nucleus acts as an amplifier. In experiments with polarized neutron beams from
spallation sources, parity-mixing effects as large as several percent have been observed. Analyzing the observed effects in nuclei is an example of the interplay between nuclear structure and the fundamental interactions. Statistical models of the nuclear state distributions are used to extract the mean values of the parity-mixing matrix elements. Figure 6.9 shows some of the data from a measurement of parity-violating neutron scattering on thorium. The size of the parity-violating effects indicates dramatically how the nucleus can be used to amplify small features of the fundamental forces.
Exotic Particle Searches, Rare Decays, and Nuclear Physics
Nuclear systems are often exploited in attempts to verify speculations about hypothetical new particles. For example, nuclear experiments were instrumental in studying the possible existence of a particle called the axion, proposed several
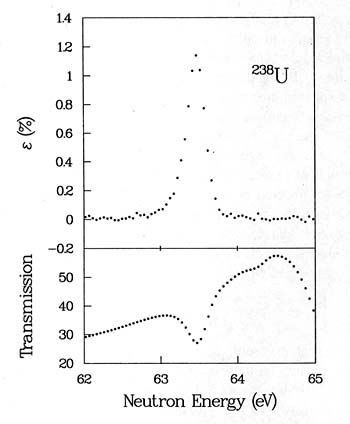
FIGURE 6.9
Data from an experiment measuring the transmission of polarized neutrons through a target of 238U. The difference in transmission for the two neutron polarization states demonstrates parity violation in the nuclear force. The enormous effect, larger than a percent, is a consequence of the nucleus's ability to amplify an exceedingly small intrinsic parity violation from the weak interaction.
years ago as a consequence of a new symmetry introduced to explain the observed CP symmetry of the strong interaction. As first proposed, the axion would decay to two photons or positron-electron pairs. Over the course of several years, this possibility was ruled out by a series of searches, primarily using nuclei. Unfortunately, the mass of the axion and its interaction strengths are not completely specified by theory, so experiments have not yet excluded them completely. An ongoing experiment searches for very light axions. This experiment exploits the predictions that axions couple to photons and that very light ones should have an effect on a finely tuned electromagnetic resonance cavity.
Nuclear techniques have been applied to searches for free quarks, very light scalar particles, and several other possible particles suggested by various theories. Nuclear physicists have been quick to apply their sizable arsenal of experimental techniques to discovering whether or not particular proposals concerning new particles correspond to what actually exists in nature.
Decay mechanisms that are forbidden within the context of the Standard Model might otherwise be expected. For example, the proton should be stable in the Standard Model, but it is expected to have a decay mode in various grand unified models, which extend the Standard Model by including quarks and leptons in more democratic multiplets. Proton-decay experiments have mostly been undertaken by high-energy physicists, with some participation from the nuclear physics community. These experiments are being steadily improved, and the upper limit on the proton lifetime is now longer than about 1032 years. A related process of neutron-antineutron oscillations was also an active area of investigation during the last decade. Again, no effects were seen, but useful limits were obtained from experiment. Observing forbidden decays of mesons and leptons might also be signals of physics beyond the Standard Model. One possibility that has received much attention is the search for the decay of the muon into an electron and a gamma ray. Several attempts to find this process have been made at medium-energy accelerators around the world. These limits, like the limits on the neutron and electron electric-dipole moment, provide some of the best constraints on supersymmetric extensions to the Standard Model.
Outlook
This area of research is motivated by a desire to gain new insights into the most fundamental aspects of the structure that underlies nuclear physics. It has remained a vital subfield of nuclear physics because the issues are fundamental and because a constant flow of new experimental opportunities has been made possible by capitalizing on advances in experimental physics. Advancements in the fundamental experimental tools of nuclear physics—the newest accelerators and the most advanced detector systems—are essential for the future health of this research. Ironically this research area also relies on some of the oldest accelerator facilities of nuclear physics. Much of the work is carried out at small
accelerators at national laboratories and universities, small tandem accelerators, and cyclotrons. Access to small facilities with specific capabilities for particular experiments is also an important priority for this subfield. This area enriches the field of nuclear physics by sharing frontiers with other fields of physics, overlapping and enhancing work in atomic physics, high-energy particle physics, and astrophysics.
Although nearly all new facilities for nuclear physics will be exploited for testing the Standard Model, some future facilities have obvious utility that make them a high priority for the field. The new generation of intense sources of cold and ultracold neutrons hold the potential of allowing the Standard Model's version of the weak interaction to be better tested in a simple hadronic system. Precision studies of neutron beta decay and better searches for a neutron electric-dipole moment require access to the most intense research reactors and spallation sources available. Access to more intense neutron sources that become available in the next decade has a high probability of leading to a major discovery in this area of research.
The venerable area of nuclear beta decay has a new life because of the advent of new techniques of atom manipulation, new methods of polarizing nuclei, sophisticated online isotope separators, and new radiation detection methods. Ion or atom traps offer new opportunities for reducing the systematic uncertainties that now limit this research, but these techniques make more stringent demands on the production of particular radioactive species. A high-intensity exotic-beam accelerator would also be the source of radioactive atoms required for this research, and an exotic-beam facility is a high priority for this area of research.
In the next five years the newest solar neutrino experiments should finally resolve the question of whether or not the neutrino and its interactions are the cause of the solar neutrino problem. The discovery of neutrino masses and mixing could lead to the next scientific revolution, leading to the first significant change in the Standard Model two-and-a-half decades after it was established. Currently there are two other experimental indications that neutrinos may have mass. The signal from atmospheric neutrinos should be elucidated in a series of planned, long-baseline experiments at accelerators. The second indication appeared in a medium-energy nuclear physics accelerator experiment. Nuclear physicists will continue to participate in the follow-up experiments that should resolve these issues in the coming years.






















