2
The Structure of the Nuclear Building Blocks
Introduction
It is a remarkable fact of nature that the average distance between protons and neutrons inside an atomic nucleus is only half again as large as the individual protons and neutrons themselves. This was first revealed by applying the same experimental technique—the scattering of electrons—to probe the distribution of electric charge within both nuclei and protons, using electron beams of higher energy to resolve the finer spatial details inside protons. Because of this close packing, the internal structure of protons and neutrons (collectively called nucleons) plays an important role in nuclear physics: it influences, and can in turn be modified by, the distribution, motion, and interactions of nucleons inside nuclear matter. This mutual influence grows in importance when, in comparison with conditions in ordinary nuclei, the nucleons are squeezed even closer together (as they are in neutron stars) or are heated to even faster motion (as in the early universe).
There are some parallels between the structures of nuclei and nucleons. Both are systems of many smaller particles undergoing strong and highly complex interactions. However, a unique feature of the structure of nucleons introduces problems unlike any faced previously by scientists studying how solids, molecules, atoms, or nuclei are constructed: the particles—quarks and gluons—that appear to be the ultimate constituents of neutrons and protons have never been found in isolation from other quarks and gluons, and thus cannot be examined in their free state. A successful theory of nucleon structure must build in interactions among the quarks and gluons that are strong enough to keep them confined
within neutrons, protons, or other strongly interacting particles built from quarks and gluons. All these particles, as a class, are called hadrons.
In the theory of quantum chromodynamics (QCD), where quarks interact by exchanging gluons, confinement arises because the gluons interact with other gluons, as well as with quarks. As a result, two quarks interact more and more strongly as they are pulled further apart, as if they were connected by a rubber band. This behavior is in dramatic contrast to the rapidly weakening electromagnetic force that binds electrons to nuclei in atoms, and to the even more rapidly weakening force that binds protons and neutrons to each other in the nucleus. While the mechanism of confinement within QCD is understood qualitatively, its very strength makes a quantitative treatment extremely difficult. Obtaining a quantitative understanding of the confinement of quarks and gluons inside hadrons remains one of the greatest intellectual challenges facing physicists.
While studies of the issues surrounding confinement have traditionally been done at the interface with particle physics, nuclear physicists are playing an increasingly vital role in addressing this challenge, through experiments and theory. They seek answers to three basic questions:
- What is the structure of nucleons?
- Can QCD account quantitatively for the confinement of quarks and gluons inside hadrons?
- Is the structure of hadrons modified inside nuclear matter?
Major efforts in nuclear theory are devoted to developing techniques for performing at least approximate QCD calculations, and for demonstrating how the conventional treatments of nuclei—as assemblies of nucleons exchanging mesons—can be viewed as an effective low-energy limit of QCD. Successful theoretical approaches must explain the structure not only of nucleons, but of other hadrons as well.
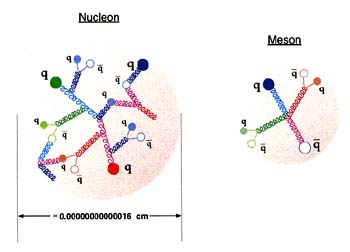
FIGURE 2.1
Schematic illustration of the substructure of a proton or neutron (left) and of a meson (right), according to the theory of quantum chromodynamics (QCD). Among the constituents confined within the nucleon are three point-like valence quarks, shown here as heavy colored dots, which interact by exchanging gluons shown as spring-like lines. Instead of three quarks, the meson has one quark and one antiquark (dot with white center) as valence constituents. The strong interactions induce additional gluons and a "sea" of virtual quark-antiquark pairs, shown as smaller, fainter dots. Quarks are labeled "q" and antiquarks "¯q". The colors of the constituents represent their intrinsic strong charges, the source of their participation in QCD interactions. Note that quarks appear only in groups of three (with different colors) or in quark-antiquark pairs. The nature of the strong interactions inside a nucleon and the relative contributions of various types of valence and sea quarks, as well as gluons, to the nucleon's overall properties have become major topics of research in nuclear physics.
The Internal Structure of Protons and Neutrons
The strength of the QCD confining interactions leads to the picture of a nucleon, illustrated in Figure 2.1, as a seething ensemble of a large and ever-changing number of constituents. A major aim of nuclear experiments through the next decade is to take detailed "snapshots" of this structure at various levels of resolution. The highest resolution is provided by highly energetic projectiles, which interact with individual quarks, antiquarks, and gluons inside a proton or neutron. These interactions, being sensitive to the motion of the struck particle,
can map the probability for finding the various constituents as a function of the fraction they carry of the nucleon's overall momentum. Such detailed maps provide crucial tests for QCD calculations of the nucleon structure; a number of basic features have yet to be delineated or understood. At the same time, less-energetic projectiles must be used to obtain a lower-resolution, but more global. view of the nucleon's properties. These include its overall size and shape, distributions of charge and magnetism, and its deformability when subjected to external electric or magnetic fields. These lower-energy spatial maps serve as essential assembly drawings in understanding how the nucleon is actually put together.
First Steps
The earliest spatial maps of nucleons revealed that both protons and neutrons have sizes on the order of one ten-trillionth of a centimeter (a distance named 1 fermi, in honor of Enrico Fermi. one of the greatest of nuclear physicists). These maps were made by scattering electrons elastically from hydrogen or deuterium targets, at sufficiently high energies that the electrons could resolve structures smaller than 1 fermi. Deuterium (whose nucleus comprises only one proton and one neutron) was needed to provide a neutron target because free neutrons are radioactively unstable, decaying with a lifetime of about 15 minutes. Electron scattering probes the distribution of electric charge and magnetism within the target; the early experiments had already provided a hint that smaller, electrically charged constituents resided inside the uncharged neutron.
It took a different kind of experiment, deep inelastic scattering, to provide the first definitive evidence for the quark substructure. In this process, as illustrated in Figure 2.2, an incident high-energy electron transfers not only momentum to the target nucleon (as in elastic scattering as well) but also a large quantity of energy. The energy lost by the electron is transformed into additional particles (mostly mesons) produced in the scattering. Even though these extra particles were not detected in the early experiments, new information was gained by noting that the dependences of the scattering probability on energy transfer and on momentum transfer were strongly correlated. The observed correlation suggested that the electron had actually scattered from a very small, charged object (quark) within the proton.
Technological Advances
The techniques used in the early explorations of nucleon structure recently have been revitalized by technological advances in nuclear physics. These advances permit physicists to address more sophisticated scientific issues by allowing more detailed snapshots of the internal state of protons and neutrons. In addition, these methods have been supplemented by techniques with complementary sensitivities, using beams of high-energy hadrons.
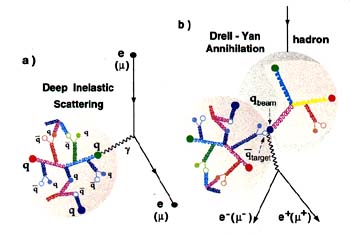
FIGURE 2.2
Two ways of probing the distribution of quarks and antiquarks inside nucleons. In (a), an electron (or a muon, a heavier cousin of the electron) scatters from a single quark (or antiquark) and transfers a large fraction of its energy and momentum to the quark via an intermediary photon (shown as a squiggly line). Such deep-inelastic-scattering measurements have provided important general information on how a proton's overall momentum is shared among its quarks. The technique has recently advanced to allow the separation of contributions from different types of quarks—for example, from strange quarks in the induced sea around the valence quarks.
In (b) (the Drell-Yan process), the induced antiquarks in the sea of the target nucleon are probed more directly when a quark inside an incident hadron has enough energy to annihilate with one of these antiquarks. The energy released by annihilation produces a “virtual" photon, which then materializes as an electron-positron pair at very high relative energy (or as an analogous pair of muons). By detecting this pair, one can probe the antiquark and quark structure of the hadrons.
Nuclear physicists have extended both these techniques to study quarks and antiquarks inside nuclei, as well as nucleons, and to probe the sharing of the nucleon's overall spin about its direction of motion, as well as of its momentum, among the quarks and antiquarks.
Among the most dramatic technical improvements relevant to experiments in this field are:
- advances in the production of spin-polarized beams and targets, and
- new electron accelerators and detector systems that allow the many particles produced in scattering processes to be detected in time coincidence.
Spin polarization refers to the preferential orientation, along some chosen direction in space, of the intrinsic spins of the particles that make up a beam or a target. With techniques now available, the spins can be aligned in the same direction for as many as 90 percent of the electrons in a beam or the protons in a target. Furthermore, polarized neutrons can be prepared inside polarized deuterium or 3He nuclei, for use as targets, as indicated in Figure 2.3. The polarization is a powerful tool; it allows one to separate the effects of small but important processes that depend strongly on the polarization direction of the beam and/or target from more dominant contributions to the scattering that depend differently, or not at all, on the polarizations. For example, polarization measurements allow, for the first time, high-precision maps of the small but nonzero electric-charge distribution within the uncharged neutron, without being overwhelmed by the effects of the much stronger interactions of the electron beam with the magnetism of the neutron or with the charge of the partner proton inside a deuterium target nucleus. The new technology also provides access to new structural features, such as the spin substructure of the nucleon: deep-inelastic-scattering experiments carried out with polarized beams and polarized targets have begun to reveal how the spins and orbital motions of quarks and gluons combine to produce the overall angular momentum of a proton or a neutron.
One of the inherent difficulties in obtaining new information on hadron structure is that high energies are required to probe small objects. At these high energies, many new particles can be produced in reactions with nucleons. New structure properties can be determined if these particles can be analyzed and identified as coming from the interaction of a single beam particle with a single target particle. Thus, detectors that can track many particles simultaneously, over broad ranges of angle and energy, are required. Suitable systems, such as that pictured in Figure 2.4, are being commissioned and shortly will allow a new class of electron-scattering experiments to be performed. It is also crucial to use accelerators that deliver the electron beam continuously to the target, rather than in short time bursts, in order to attain practical counting rates for the events of interest while minimizing the rate of "accidental" coincidences among particles arising from two or more unrelated interactions in the target. CEBAF—the most powerful continuous-beam electron accelerator ever built—provides a micro-scope of unprecedented capabilities for studies of nucleon structure.
Electromagnetic interactions, such as deep inelastic scattering, are sensitive to the charge and magnetism of quarks, but not to other quark properties, and not sensitive at all to the uncharged gluons that bind the quarks together. To obtain a more complete picture of the nucleon substructure, it is important to complement these sensitivities with measurements of quite different processes induced by beams of high-energy hadrons. One example, illustrated in Figure 2.2. is known as Drell-Yan annihilation, where a quark from a hadron projectile undergoes matter-antimatter annihilation with an antiquark from the target (or vice versa). Studies of this process have allowed separation of structure features
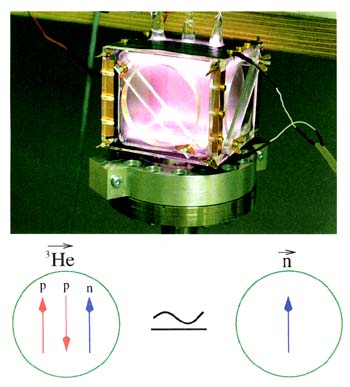
FIGURE 2.3
Among recent technological advances that facilitate dramatic improvements in measurements of neutron substructure is the development of spin-polarized 3He targets of usable density. The photograph shows a cell filled with 3He gas, which is exposed to laser light of appropriate frequency to "pump" most of the gas atoms into a state with the desired orientation of the nuclear spin. The purple glow is from light emitted by excited 3He atoms. This particular target has been used in a deep inelastic scattering experiment to measure the contributions of quarks and antiquarks to the overall spin of a neutron.
The lower frame illustrates why a spin-polarized. 3He nucleus can serve as an effective surrogate for a target neutron of known spin orientation. The nucleus comprises two protons, which spend nearly all of their time with opposite spin orientations, plus a single neutron, which nearly always shares the spin preference with which the 3He nucleus is prepared. To good approximation, it is only the quarks and antiquarks inside the neutron that contribute to changes in the scattering probability when the 3He spin is reversed.

FIGURE 2.4
Parts of the CEBAF Large Acceptance Spectrometer. This system allows one to detect, identify, and measure the momenta of multiple particles resulting from the interaction of energetic electron beams with nucleons and nuclei. At its core is a novel superconducting magnet that produces a toroidal field capable of bending the trajectories of the emerging particles without perturbing a spin-polarized target mounted along the spectrometer's axis. Three (out of a total of six) "slices" of the superconducting coils for this magnet are shown in the photograph on the left. Detectors fit in between and beyond the coils, including the inner "drift chambers" shown on the right, which measure precisely the position where charged particle tracks cross them. When coupled with the continuous beam available from the accelerator, this spectrometer will facilitate experiments of unprecedented thoroughness to probe the structure of nucleons and their many excited states. (Courtesy of the Thomas Jefferson National Accelerator Facility.)
associated with the primary (valence) quarks versus the induced "sea" of quark-antiquark pairs. Other processes can produce gluon maps of very fast colliding nucleons, by measuring the probability to create new particles, or high-energy gamma rays, in whose formation the gluons in one or both participants play the decisive role. Experiments using such hadron probes will benefit greatly from recent technological advances. For example, at RHIC the contributions of gluons and sea quarks to the proton's spin will be discerned from the results when two very high-energy beams of spin-polarized protons collide.
Experimental Opportunities
According to the Standard Model of particle physics, quarks and antiquarks come in six different varieties, or "flavors," characterized by different masses. Only the two lightest varieties, called up quarks and down quarks, participate as valence quarks in nucleons. Indeed, in the original, simplified picture of a proton's substructure, all its properties were thought to arise from combining two up quarks and one down quark in a state with no relative orbital motion. Although this picture provides a deceptively successful account for some properties, such as the overall magnetism of the proton and neutron, it is clearly an incomplete representation of the complex quark-gluon dynamics. Experiments planned for the coming decade should yield a far more realistic picture of what goes on inside the nucleon, including the roles of sea quarks of various flavors, of gluons, and of the orbital motion of all these constituents.
The induced sea of quarks and antiquarks inside a nucleon is a fascinating manifestation of the strong confining forces that nuclear physicists seek to understand. Electrically charged particles, which interact via the much weaker electromagnetic force, have a small probability to liberate virtual electron-positron pairs from the surrounding vacuum. These particles are called virtual because they exist only fleetingly, soon to be swallowed up by the vacuum once again. These electron-positron pairs have subtle, but measurable, effects on the structure of atoms—effects whose study led to crucial early successes of the field theory known as quantum electrodynamics. In contrast, the analogous pairs of virtual quarks and antiquarks in a nucleon are excited with high probability and profoundly influence the nucleon's properties. It is a critical goal of experiments on nucleon structure to probe the relative probabilities for finding quarks of different flavors in the sea.
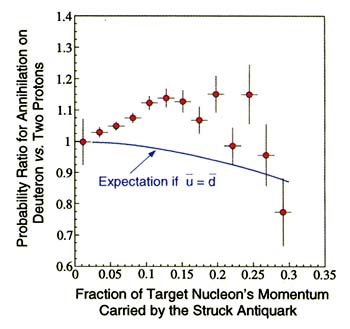
For example (see Box 2.1 for details), recent measurements of both deep inelastic scattering and Drell-Yan annihilation processes have refuted the naive expectation that anti-up and anti-down quarks might be found with equal probability in the proton's sea. A most intriguing implication of this discovery is that the essence of the sea may be captured in a picture where the virtual quark-antiquark pairs are thought of as mesons, which they resemble (as can be seen in Figure 2.1). In particular, the observed preference for anti-down quarks is consistent
|
BOX 2.1 Sampling the Proton's Flavors How, exactly, are protons and neutrons made? Nature has guarded her secret recipes as vigilantly as the Coca-Cola Company, even to the extent of forbidding the ingredients from ever being used alone. Nonetheless, nuclear physicists are uncovering the proton's secrets little by little, exploiting ever more selective techniques to isolate individual "flavors" in the complex mélange. Physicists have discovered six flavors, or varieties, of quarks—the tiny constituents of protons, neutrons, and all their heavier cousins. The different flavors have been given the metaphorically confused names: up, down, strange, charmed, bottom, and top. Until recently, only the two lightest types, up and down, were known with certainty to reside in a proton. Indeed, many of the proton's distinguishing features can be understood as emerging from a combination of three primary—two up and one down—quarks. Surprisingly, though, physicists believe that these primary (or valence) quarks account for only a small fraction of the proton's mass. Some of the remaining mass is associated with a "sea" of quark-antiquark pairs induced by the presence of the valence quarks. Though individual pairs appear and vanish, they are found with high probability, much as the flickering lights in a dense swarm of fireflies. The transient quarks and antiquarks in this sea can be of the up or down variety or, in principle, of any other flavor. The flavor composition of the quark sea, which gives the proton and the neutron much of their complexity and richness, is the focus of a number of ongoing experiments. Physicists' initial naive expectation was that nature would mix different flavors in the sea in proportions depending only on the quark mass associated with each flavor. Since up and down quarks have nearly equal masses, they should then appear with nearly equal probability in both protons and neutrons. That expectation is refuted by recent results, shown in Figure 2.1.1, from an experiment at the Fermi National Accelerator Laboratory. These results imply a strong preference for down over up antiquarks in the proton's sea. Why should nature prefer such a flavor imbalance? One possible explanation is that the proton spends some of its time as a neutron surrounded by a positively charged pi meson. But this description uses the language of conventional nuclear theory, dealing with protons, neutrons and mesons, rather than with quarks directly. One of the primary goals of nuclear physics is to understand the relations between these two languages, and the conditions under which one or the other provides the more efficient description of matter. The result of the Fermilab experiment suggests that the theoretical framework that works best for treating the structure of nuclei may also be unexpectedly useful in treating the internal structure of protons and neutrons. Quark flavors other than up or down can appear in a proton only as part of the sea. At present, there is particular interest in the strangeness flavor, which corresponds to the next lightest quark mass after up and down quarks. Hints from several different experiments have suggested that strange quarks and antiquarks have a greater role in the proton than would be expected on the basis of their mass alone. A series of ongoing and planned experiments at several laboratories (an example is shown in Figure 2.1.2) seeks to distinguish strange quarks by their contribution to the weak interaction between electrons and protons. This interaction will be unmasked from the normally dominant electromagnetic interaction by searching for a characteristic violation of mirror symmetry. The violation can be |
with the effect of the proton occasionally emitting, then reabsorbing, a virtual pi meson. The conventional view of nuclei, in terms of nucleons and mesons rather than quarks and gluons, may thus even provide a relevant approximation to QCD in treatments of nucleon structure. It will be interesting to see if such treatments also remain useful in addressing the presence of heavier quarks and antiquarks, such as those with the "strangeness" flavor, in the nucleon's sea. As discussed in Box 2.1, a series of experiments at CEBAF and other accelerators is
aimed at determining the contributions of strange sea quarks to nucleon properties.
A particular nucleon property in which strange quarks may play a significant role is the spin substructure. The intrinsic spin and the associated magnetism of a proton are among its defining characteristics. They are, for example, essential in accounting for radiation observed from the heavens and in allowing magnetic resonance imaging. Measuring and understanding the relative contributions to
the proton's spin from its various constituents is a major goal of nuclear physicists. The first information has been provided by recent, polarized, deep-inelastic-scattering experiments. The results, shown in Figure 2.5, suggest that the intrinsic spins of all the quarks and antiquarks combined account for only a fraction (less than about 30 percent) of the nucleon's overall spin. In particular, the net contribution from up and down quarks seems to be partially canceled by that from the strange quarks, which appear to line up opposite to the overall spin direction. However, this interpretation relies on arguments based on quite different measured properties of hadrons, and it must be confirmed by future experiments that can separate the spin contributions from valence and sea quarks, and from quarks of different flavors.
The next generation of experiments on the spin substructure will study reactions induced by both polarized lepton (electron, positron, and muon) beams and polarized proton beams on polarized protons. The results will also provide the first information on the contribution from the spin of gluons to the proton spin, a contribution that recent theoretical work suggests may be large. Experiments with colliding beams of polarized protons at RHIC will be especially well suited to probe this gluonic role. If the quark and gluon spins together do not account for the nucleon spin, the only remaining source available to "balance the books" (as indicated in Figure 2.5) is the relative orbital motion of the quarks and gluons. Thus, early in the next century, these experiments on the spin substructure may indirectly lead us beyond our current, still rudimentary understanding of quark motion inside a nucleon.
One of the major advances of the past five years was the first measurement of the spin substructure of a polarized neutron, made possible by innovative developments in spin-polarized deuterium and 3He targets. These experiments permitted a quantitative test of a rigorous QCD prediction, the Bjorken sum rule, for the net difference between the quark spin distributions in a proton and a neutron. The recent data agree with the sum rule value, demonstrating that our maturing picture of the nucleon's substructure remains consistent with QCD.
In parallel with these probes of the "trees" inside the nucleon "forest," nuclear physics experiments are improving the quality of the global view of the forest itself, by applying modern technology to study the electromagnetic interactions of nucleons at lower energies. One example, illustrated in Figure 2.6, is the vastly improved precision expected from ongoing polarization experiments mapping the neutron's electric charge distribution, which is related to the overall spatial layout of valence and sea quarks. A second example is provided by recent measurements of the distortions induced in a nucleon's charge and magnetization distributions when it is exposed to external electric and magnetic fields. These properties have been measured by scattering beams of photons—the quantum carriers of the electric and magnetic fields—from nucleons. Greater flexibility in the nature of these stimulating fields can be obtained, and hence a number of new features of the nucleon's response can be measured, in future experiments in
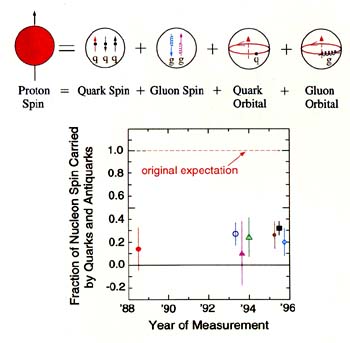
FIGURE 2.5
How do the proton's various constituents contribute to its overall spin? As illustrated by the upper diagram, the quarks, antiquarks, and gluons are all believed to have their own intrinsic spins, and these must contribute. But so also must the relative orbital motions of the quarks and gluons inside the proton. Measuring and understanding the relative contributions from these different sources is a major goal of nuclear physicists.
The first measurements of the proton's spin substructure have been made recently, employing the technique of deep inelastic scattering with spin-polarized beams bombarding spin-polarized targets. By combining these measurements with constraints from other data, one can infer the fraction of the proton's spin carried by the intrinsic spin of quarks (and antiquarks) of different flavors. The results of experiments performed at CERN, SLAC, and DESY, summarized in the graph, point to an unexpected outcome: all the quarks and antiquarks together account for no more than one-third of the total spin. More direct probes of the spin alignment of different flavors of quarks, separation of the contributions from quarks and antiquarks, and extraction of information on the gluon spin contributions are goals of ongoing and planned second-generation experiments.
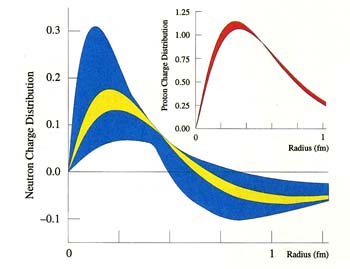
FIGURE 2.6
Although the neutron and proton are equally important in building nuclei, the quality of experimental information available about their internal structure has been vastly different, because one cannot make a target of free neutrons. For example, the graphs here compare what we know from electron-scattering experiments about the amount of electric charge per unit radial distance from the center of a neutron (on the left) versus a proton. The width of the blue band for the neutron and of the curve for the proton indicate the approximate level of uncertainty in the currently available experimental information. The crude data for the neutron suggest that smaller charged particles do indeed reside inside, with positive charges preponderant near the center and negative charges near the periphery, but provide little additional constraint on nucleon structure calculations. Our knowledge of the neutron will be brought closer to a par with the proton (as suggested by the yellow band on the left) by a new series of experiments, made possible by the advent of continuous-beam electron accelerators and by advances in the technology for measurements of spin polarization.
which the real photon beams are replaced by virtual photons, emitted and absorbed when an electron interacts inelastically with a target nucleon.
The proton and neutron represent the lowest energy states of a family of hadrons that can be constructed from up and down valence quarks taken in combinations of three. The energies of the higher-lying states, and the probability that a nucleon may be elevated into one or another of them by exposure to photon or electron beams, carry additional information about the quark substructure. The new advances in accelerators and detectors, particularly at CEBAF
with the apparatus pictured in Figure 2.4, will, over the next several years, allow a dramatic increase in detailed information on the properties of these excited states. These states are referred to as resonances, rather than as particles, because they exist for only a tiny fraction of a second; one detects their excitation by looking at the particles emitted when the resonances decay or de-excite. The study of these resonances is complicated by the fact that their spectrum is no longer really discrete: their very short lifetimes imply (by the Heisenberg uncertainty principle) that each of them can be produced over a broad range of excitation energies, and the energies overlap for different resonances. Spin-polarized beams and targets will be essential in disentangling the effects of individual resonances and measuring their structure.
In summary, the coming generation of experiments will assemble a rather detailed, multifaceted empirical picture of the internal structure of protons and neutrons. If QCD is a valid theory for the confinement of quarks inside hadrons, then, eventually, one or more of the techniques developed for solving QCD (see the following subsection) must reproduce this empirical picture. In the meantime, the experimental results serve as an invaluable guide in the construction of structure models, which seek to bridge the gap between the nucleon-meson and quark-gluon descriptions of hadronic matter. The evolving empirical picture of the nucleon's substructure provides a necessary baseline against which to compare the measured properties of nucleons when they are embedded inside nuclear matter.
Accounting for Confinement: from QCD to Nuclear Theory
The best-established calculational technique for quantum field theories works when the fundamental interaction is quite weak. This is true in QCD only when two quarks have a separation very much smaller than the size of a hadron. Indeed, the theory is quite successful in this regime in accounting for hard collisions between hadrons at very high energy. However, new theoretical approaches are required for QCD to confront its most important manifestation in the matter around us: the phenomenon of quark confinement. Two approaches are being actively pursued. In one, full numerical solutions to the field theory are obtained, using the most powerful existing computers, but even this requires artificially restricting the hadron's constituents to exist at certain discrete points in space and time. The second approach concentrates on “effective" theories, which retain the crucial symmetries of QCD but relegate other details to parameters that must be adjusted to reproduce several key experimental results. These effective theories hold the promise to establish a clear connection between QCD and the more phenomenological treatments developed over decades to account for observations of nuclear structure and reactions. Measurements of hadron properties provide critical guidance in selecting appropriate crucial QCD features, in determining
parameter values, and in testing the self-consistency of these calculations. In particular, experimental searches for new mesons and for new excited states of the proton and neutron have the potential to unveil predicted missing links, to reveal elusive quark-gluon properties omitted from model calculations, or to suggest unforeseen symmetries in the complex QCD interactions inside hadrons.
Working with Quarks and Gluons
The masses of atoms and nuclei are nearly equal to the sums of the masses of all their constituents; the interactions among the nucleus and the electrons in an atom, or among the many nucleons inside a nucleus, cause only slight changes in the overall mass. The situation in a hadron is radically different! The bare masses of the three valence quarks in a nucleon are believed to contribute no more than a few percent to the overall nucleon mass. Instead, the nucleon mass—and therefore the mass of our visible world—is dominated by the strong confining interactions, as manifested in the high probability for finding virtual quark-antiquark pairs or gluons inside the nucleon, in addition to the valence quarks. The strength of these interactions makes it at once essential and exceedingly difficult to calculate the effect of the interactions reliably, in order to interpret measurements of hadron properties.
The difficulty in QCD calculations of hadron structure is epitomized by the fate of a basic symmetry property of QCD, chiral symmetry. Chiral symmetry considerably simplifies the interactions of quarks in the limit in which their masses are considered as negligibly small, by forbidding gluon-exchange from reversing the "handedness" (or chirality) of quarks (i.e., from flipping one that spins clockwise when viewed along the direction of its motion, like a right-handed screw, into one spinning in the opposite direction, analogous to a left-handed screw). All of the "excess baggage" accompanying the valence quarks inside a hadron makes them appear much heavier than they really are, and thereby causes a violation of this symmetry. A major goal of approximations to QCD is to understand quantitatively the extent of this violation, together with its dependence on the density and temperature of the nuclear matter in which the hadrons are placed.
The most promising approach to approximating quark confinement and chiral symmetry breaking in hadrons is to solve QCD numerically on a computer. The approach is approximate because it reduces the problem to one involving only a finite (and small) number of bodies. This is done artificially, by restricting each constituent to occupy one of a discrete set of points, distributed on a regularly spaced lattice in space and time. The extraction of reliable physical predictions hinges on demonstrating that the results of such calculations converge to unique answers as the lattice spacing is reduced toward zero and the lattice volume is increased. Both of these changes are severely limited in extent by available computing power. Much of the ongoing theoretical development of this
approach is devoted to finding more efficient ways of formulating the QCD problem, to ease the computing crunch. Nuclear theorists are deeply involved in these developments.
Already, however, lattice QCD calculations have achieved considerable success in reproducing some basic observed properties, such as mass ratios, sizes, and decay characteristics for various hadrons. Such calculations have led to quantitative estimates of the extent of chiral symmetry breaking, by predicting the probability of finding virtual quark-antiquark pairs and gluons inside hadrons. More importantly, they have quantified QCD predictions of two entirely new phenomena, which nuclear physicists will be subjecting to experimental tests throughout the next decade. One is a predicted phase transition, in which quarks will shed their excess baggage and chiral symmetry will be restored, in strongly interacting matter at sufficiently high temperature. The search for this new phase of matter in collisions of relativistic nuclei at RHIC is described in Chapter 4. The second prediction is for the existence of a new class of mesons, which do not have a valence quark and antiquark, as do typical mesons, but rather consist of gluons alone (gluonium). The experimental search for gluonium is described in Box 2.2. If these predictions are not confirmed by experiments, the mechanism of confinement postulated in QCD will have to be questioned.
In addition to particles composed of pure glue, QCD also predicts the existence of hybrid hadrons that contain more complicated valence configurations than three quarks or a single quark-antiquark pair. Discovery of the corresponding particles is an important goal of nuclear physics. Indeed, in contrast to this rich array of possibilities, nearly all of the hadrons known to date seem to be explainable in terms of the simplest quark configurations. Their measured properties can be reproduced surprisingly well if one considers the constituents to be massive pseudo-quarks, which somehow combine features of valence quarks, sea quarks, and gluons. Theoretical models based on these effective building blocks can provide qualitative insight into hadron structure that complements attempts to solve QCD numerically. But a true breakthrough in insight awaits a more detailed understanding of the relationship of the pseudo-quarks to the real fundamental particles of QCD.
Working with Nucleons and Mesons
The computational barriers are too high to imagine applying lattice QCD calculations any time soon to predict the interactions among two or more hadrons, despite their obvious importance for understanding nuclei. Indeed, these interactions appear quite complex within the framework of QCD: quarks and gluons interact by virtue of their intrinsic "color charge," but hadrons are constrained by the confinement mechanism to have no net color charge. The force between nucleons, for example, must reflect the sort of indirect effect suggested in Figure 2.7, wherein two or more momentary leakages of color between the
|
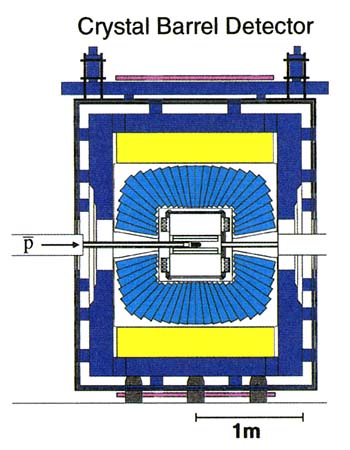
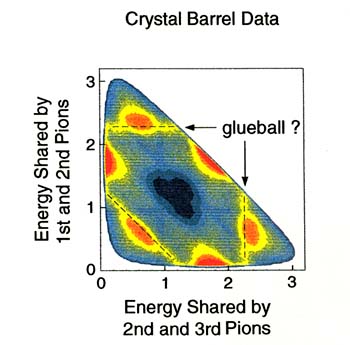
BOX 2.2 Where's the Glue? Nuclear physicists study matter whose behavior is governed by the strongest of nature's forces. The smallest observed particles that feel and are capable of exerting this force are called hadrons, and an entire zoo of them has been discovered. And the search is on for even more hadrons, but now for a new, exotic species that holds the key to understanding all the rest. The hardon zoo includes not only the protons and neutrons that build nuclei and the pi mesons that are exchanged between protons and neutrons when they interact, out also many heavier cousins of both of these types of particle. It was to introduce some order that physicists invented the concept of quarks as the building blocks of hadrons. But quarks alone were not enough. The Heisenberg uncertainty principle dictates that particles confined to a volume as small as the interior of a hadron must be moving very fast, so there must be some "glue" to hold them together. No problem: physicists invented another new particle, the gluon, whose exchange between quarks was postulated to provide this binding force, in somewhat the same way that the exchange of photons between nuclei and electrons provides the electric force that binds atoms. Now there is clear experimental evidence that high-energy particles interact with individual quark-like particles inside a proton. But the fact that no one has ever succeeded in isolating a free quark or gluon adds intrigue to the story. This fact suggests a binding force so strong that it is effectively impossible to overcome. The remarkable success of quantum chromodynamics (QCD) is that it is the only viable field theory proposed for the strong interaction in which this confinement of quarks and gluons within hadrons arises naturally. The important remaining question is this: Is QCD the correct theory of hadron structure? What testable predictions does it make that arise inevitably from its mechanism for confinement? Confinement arises in QCD from a simple, but radical, postulate: the gluons themselves carry a strong interaction charge, in contrast to photons, which carry no electric charge. QCD then predicts that gluons can interact among themselves, and can even assemble to form exotic quarkless mesons. Such hadrons, referred to as glueballs or gluonium, must exist if the confinement mechanism in QCD correctly describes reality. And so, the search for them is on, with high priority. How does one try experimentally to distinguish a glueball from conventional mesons, whose primary constituents are a single quark plus a single antiquark? The glueballs must be electrically neutral, and they may take on masses unexpected for conventional mesons, or quantum properties forbidden to them. Since gluons can produce quark-antiquark pairs, the glueballs can decay to conventional mesons, but they should do so "democratically," with little regard for the flavor of the daughter mesons they spawn. And glueballs should be produced preferentially in relatively quark-free environments, such as the aftermath of matter-antimatter annihilation. Sophisticated detectors (Figure 2.2.1) have been built to sift through the debris of collisions where the quarks in a proton and the corresponding antiquarks in an antiproton extinguish one another, in search of decay daughters or granddaughters of potential glueballs. Elaborate sleuthing methods have been developed for the necessary multistep reconstructions of the "scene of the decay." They involve energy-sharing diagrams, such as the colorful one shown in Figure 2.2.2), where the ultimate progenitors appear as enhanced lines at characteristic energies. |
nucleons compensate for one another. How can this view be joined with the different picture that has so successfully accounted for the scattering of nucleons and for nuclear structure at low energies? In that picture, the strong interaction between low-energy nucleons is mediated primarily by the exchange of pi mesons (called pions for short) between them. A crucial step along the path from quarks and gluons to nuclei—a path being scouted by many nuclear theorists—is to understand why the pion is "chosen" as such a dominant manifestation of QCD interactions at low energies.
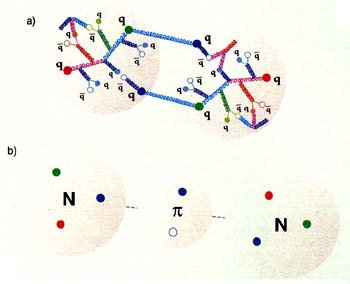
FIGURE 2.7
The simplest contributions to the force between nucleons, as viewed from (a) QCD and (b) conventional nuclear theory. In (a), the exchange of two colored gluons causes two quarks in each nucleon to change their colors (blue changes to green and vice versa in the case illustrated). This process produces a force without violating the overall color neutrality of the nucleons. The strength of the force depends on the separation of the different quark colors within each nucleon. On the other hand, low-energy nuclear physics measurements show clearly that the longest-range part of the force arises from the exchange of a single pi meson between two nucleons, as in (b). In this low-energy view, the internal structure of each nucleon is generally attributed to three pseudo-quarks, which somehow combine the properties of the valence quarks, sea quarks, and gluons predicted by QCD. Nuclear physicists are seeking to understand how these and other contributions combine to give the overall nuclear force.
The special role of the pion within QCD is that of primary agent for the breaking of chiral symmetry in nucleons and nuclei. An up or down quark can change from left-handed to right-handed (or vice versa), violating chiral symmetry, if it emits or absorbs a pion rather than a gluon. If the pion had zero mass—a so-called Goldstone boson—the symmetry would still be preserved in nuclear interactions as long as pions as well as quarks were included within the system considered. It is thus the pion's unusually low mass, in comparison with all other mesons, that keeps the symmetry at least approximately satisfied in nature. As
near-Goldstone bosons, pions interact with one another, and with nucleons, fairly weakly when they have low momentum. This observation suggests that the more traditional methods for solving quantum field theories when the interactions are weak may be applicable to QCD at low energies, if the theory can be expressed in terms of nucleons and pions as the main players, rather than quarks and gluons. Developing and testing such an effective field theory, known as chiral perturbation theory, is an important theme in contemporary nuclear physics. The forms of the allowed interactions among pions and nucleons are restricted by the symmetries of QCD, but experiments must be used to determine their precise strengths, which are still too hard to calculate directly. Once the strengths are fixed, chiral perturbation theory can predict as yet unmeasured properties of pion interactions.
Experimental tests of these predictions, and hence of the self-consistency of the effective theory, evaluate the ability of QCD to deal with chiral symmetry breaking at low energies. Important ongoing tests involve the study of decay modes of heavier mesons to pions and photons, the probability of producing pions in photon-proton collisions, and the interaction of two pions when they have essentially no relative momentum. The most unambiguous way to measure this last interaction calls for forming an exotic cousin of the hydrogen atom in the laboratory, one in which the proton is replaced by a positively charged pion and the electron by a negative one, orbiting each other under the influence of their mutual electric attraction. Experimental attempts to study this system combine atomic, nuclear, and particle physics techniques to shed light on QCD and its connections to conventional nuclear theory.
Hadrons in Nuclear Matter
Nucleons and mesons are the building blocks of ordinary nuclear matter, but there is no guarantee that these building blocks have properties in nuclei identical to those of the isolated hadrons we study in the laboratory. According to QCD, the properties of hadrons are strongly influenced by the induced sea of quark-antiquark pairs and by the gluons produced in the confining interactions. But the conditions for achieving the most favorable overall energy balance, and hence the probability for exciting these virtual particles, may well be different in a group of closely spaced nucleons than inside an isolated nucleon. Indeed, there are theoretical predictions that the probability of finding virtual quark-antiquark pairs decreases systematically (thereby partially restoring the chiral symmetry of QCD) as the density of surrounding nuclear matter is increased; at very high densities this probability vanishes. If such changes can be definitively observed in experiments planned for the coming decade, it will have a profound influence on our understanding of quark confinement, of nuclear matter, and of the densest stars.
If the quark-antiquark pair probability decreases inside nuclear matter, so should the masses of most hadrons, and their sizes and interactions may change
correspondingly. It is an important goal of future experiments to search for direct evidence of such modifications of hadron properties. Several techniques have been applied in searches to date. Measurements sensitive to the internal spatial structure of nucleons have been made by scattering beams of electrons and neutrinos from individual nucleons inside nuclei. Attempts have been made to determine the masses of mesons produced in nuclear matter by studying their decay, especially to such daughter products as leptons (electrons, positrons, and muons), which are not themselves significantly affected by passage through the surrounding matter. No generally accepted evidence has yet been observed for significant modifications at normal nuclear densities. Indirect hints of appreciable changes are afforded by systematic differences observed in the spin-dependent interactions of nucleons with other nucleons inside versus outside nuclei. The best hope for definitive tests of the predicted variations may lie with measurements of the properties of mesons produced in rather high-density matter formed in the collisions of energetic heavy nuclei.
A complementary approach to searching for changes in nucleon structure inside nuclear matter is to probe the distribution of quarks and gluons in nuclei, using high-energy beams of leptons or hadrons, via the deep-inelastic-scattering and Drell-Yan annihilation processes. When the nucleus is viewed under such a powerful microscope, one loses sight of specific hadrons; the struck quark or gluon may reside in any of the nucleons or mesons present in the nucleus. The deep-inelastic-scattering measurements shown in Figure 2.8 have already demonstrated that the quarks share the overall momentum of a nucleus in a manner clearly, but mildly, different from what one would expect for an ensemble of free nucleons. The interpretation of these differences must take account of relatively mundane effects, such as the binding of the nucleons and the presence of virtual mesons being exchanged between them, along with any systematic effect of nuclear matter on the internal structure of the nucleons. Calculations suggest that the mundane effects are not sufficient to account for all of the deviations seen in Figure 2.8. The residual effects are consistent, for example, with models in which the size of a nucleon changes slightly, but systematically, in nuclear matter.
The interpretation of the deep-inelastic-scattering experiments is aided by comparison to results from Drell-Yan annihilation, which, unlike the former process, can be used selectively to probe the antiquarks in the nucleus, yielding greater sensitivity to the presence of mesons. Surprisingly, Drell-Yan data show no evidence of the surplus of antiquarks predicted to arise from pions being exchanged between nucleons. This result is confirmed by nuclear reaction measurements, which have searched for the characteristic change in a proton's spin orientation when it absorbs a pion from the nucleus. The failure to observe the expected pion excess—a basic manifestation of nuclear forces—may itself reflect changes in hadron properties (e.g., in the size of nucleons) inside nuclear matter. Such a systematic change in nucleon size would show up clearly in the gluons'
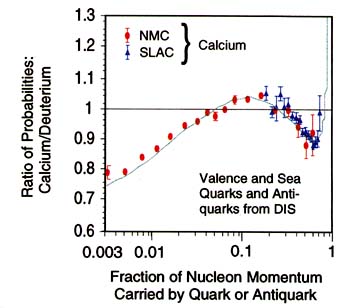
FIGURE 2.8
Results of deep-inelastic-scattering experiments carried out at CERN and SLAC that probe the distribution of quarks and antiquarks in nuclei. The results are plotted as the ratio of the probabilities for finding quarks and antiquarks with a given fraction of the average nucleon's momentum in a medium-mass nucleus versus deuterium. The sizable deviations of this ratio from unity demonstrate that the quark environment inside nuclear matter is different from that inside a free nucleon. Important nuclear effects are observed at both small momentum fractions, where induced sea quarks are expected to dominate, and at larger values, in the realm populated primarily by valence quarks. Such measurements provide one window on possible changes in hadron substructure inside nuclear matter. For example, in the green model calculation that reproduces the data, it is assumed that bound neutrons and protons have systematically different sizes than their free counterparts.
share of the nuclear momentum, which will first be measured in proton-nucleus collisions at RHIC.
Even more dramatic changes in structure, offering unique opportunities to test QCD, can occur for very fast hadrons passing through nuclear matter. During their short traversal time, quantum mechanics allows these particles to exist not just as any one of the known free hadrons, but as some combination of many of
them (e.g., a combination of a proton and its various excited states, which may have a much smaller size than a free proton). Experimental searches for effects of such shrunken, transitory hadrons are of special interest, because QCD predicts that they will survive passage through nuclear matter much more readily than hadrons of ordinary size. Their survival is enhanced, according to QCD, because the various color charges are closer together inside a small hadron, and interactions with surrounding nucleons grow weaker with decreasing separation of these internal colors. This QCD prediction—that a nucleus will act as a sort of hadron “strainer"—will be tested in the coming decade by experiments that attempt to produce such shrunken hadrons in hard, high-energy collisions of electron, proton, or heavy-ion beams with nucleons in nuclei. If the prediction is confirmed, then nuclei may be used as filters to study the transition from the simplest QCD interactions to the complicated ones that dominate in the more permanent world of nucleons and nuclei. Full exploitation of such filtering possibilities is likely to require a new accelerator, capable of delivering continuous electron beams, of substantially higher energy than are available at CEBAF, or colliding beams of electrons and protons.
It is equally important to study how the interactions of lower-energy hadrons change when they are embedded in nuclear matter. The effects of the nuclear medium on nucleon-nucleon and pion-nucleon forces have been investigated intensively for many years. There is now renewed interest in the interactions of hadrons containing a strange valence quark, because they may play an important role in the high-density matter present in neutron stars, as detailed in Chapter 5. The lightest mesons that contain a strange valence quark or antiquark are called kaons. Kaons can be produced in the laboratory—and collected to form a beam—or can be implanted in nuclei by nuclear reactions that substitute a strange quark for an up or down quark. Experiments at CEBAF and other laboratories will provide information on the interaction of implanted, negatively charged kaons with the surrounding nucleons in a nucleus. It has been predicted that the partial restoration of chiral symmetry in nuclear matter, discussed above, will change this interaction at very low energy from being slightly repulsive in the free case to attractive in nuclei. If this prediction is borne out by future experiments, it could have a strong bearing on the possibility that large numbers of kaons "condense" into a single quantum state in neutron stars.
Outlook
Nucleons are built from quarks and gluons. Yet nearly all of their mass—hence, the total mass of which we and our surroundings are made—appears to arise not from intrinsic quark and gluon masses, but rather from the excess baggage the quarks carry by virtue of their confinement within the nucleon. It is crucial for understanding the structure of matter to test the validity of QCD as a
theory of quark confinement within hadrons. The next decade should bring enormous progress toward a meaningful confrontation of theory and experiment.
The new facilities at CEBAF and RHIC, together with continuing opportunities for selected experiments at high-energy laboratories, will dramatically improve empirical knowledge of nucleon structure. Ongoing investigations of the meson spectrum should confirm or disprove the discovery of hadrons whose primary constituents are gluons, thereby testing a prediction directly tied to the confinement mechanism of QCD. Measurements of pion interaction probabilities at low energies will reveal whether QCD leads to a self-consistent treatment of the observed violations of one of the theory's basic symmetries. This experimental progress will exploit a wide variety of accelerator facilities and state-of-the-art instrumentation. Still, the quest for ultimate understanding of the excess baggage carried by quarks within nucleons is likely to require upgrades to currently available facilities. For example, continuous electron beams of higher energy or a spin-polarized, electron-proton collider may be needed to probe correlated behavior among pairs of quarks, or spin contributions from the abundant gluons, which each carry less than a few percent of the nucleon's momentum.
In parallel with experimental progress, advances in computer performance and in theoretical techniques will fuel more quantitatively credible numerical solutions of QCD on a space-time lattice. Direct comparisons of experimental results to quantitative QCD predictions for aspects of meson and nucleon structure will have to form one of the primary testing grounds for the theory, just as the validity of quantum electrodynamics has been established in good part by quantitative accounts for observed details of atomic energy levels. On the other hand, it is unlikely that numerical solutions of QCD will be viable within a decade for systems containing more than a single nucleon. Further development of more phenomenological approaches, inspired by QCD but also guided by experimental results, will be needed to establish more firmly the QCD basis for the force between nucleons, or the structure of hadrons in dense nuclear matter.
Investigations of the evolution of hadron structure with the density and temperature of surrounding nuclear matter are just beginning. Resolution of some of the relevant issues, such as QCD effects on the passage of fast hadrons through nuclear matter, may well require accelerator facilities with beam energies and characteristics beyond those now available. Other questions, such as the occurrence of pion or kaon condensation or of a transition from nuclear to quark matter at very high densities, may only be settled by combining substantial extrapolations from laboratory experiments with successful models of stellar behavior, constrained by astronomical observations. In addressing these issues, nuclear physicists are attempting to build an essential bridge, linking the fundamental theory of nature's strongest force to the makeup of the densest objects in the cosmos, and spanning the microscopic structure of the atomic nuclei that constitute nearly all of the mass we observe around us.