Kinematic Positioning with DGPS: Expanding Frontiers in Aerogeophysics
Robin Bell
Lamont-Doherty Earth Observatory
INTRODUCTION
In 1995, the National Research Council published a report on “Airborne Geophysics and Precise Positioning” (National Research Council, 1995) Much of the material presented here is summarized from that report, although this discussion focuses on the differential GPS applications exclusively.
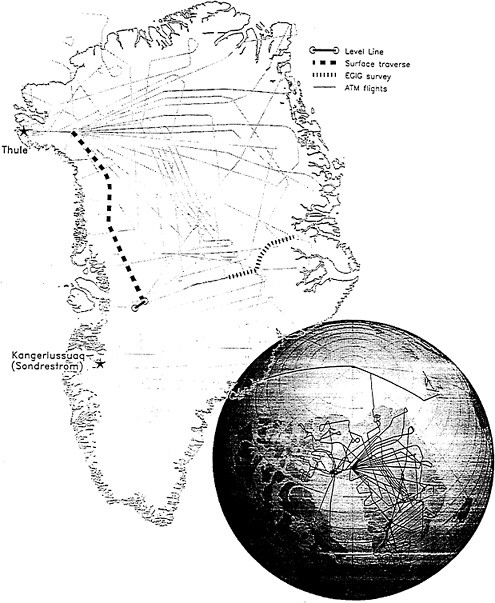
Airborne geophysics has long been used for regional studies of remote and inaccessible areas. Recent developments in precise positioning of aircraft with the Global Positioning System (GPS) have greatly expanded the range of previously intractable science problems which now can be addressed with airborne techniques (i.e. Brozena et al, 1992). Differential GPS techniques for modern aerogeophysical studies include both real-time navigation of the aircraft and post-mission recovery of the precise positions for data reduction. Major science problems which have been addressed recently with aerogeophysics include deciphering the dynamics of the world's major ice sheets, imaging surface displacements due to earthquakes and decoding the structure of the continental lithosphere. Airborne studies often recover higher resolution data than can be retrieved with satellite technology. Subsequently the aircraft based approach fills a unique niche where land and ship based operations are expensive, difficult or even impossible (Figure 1 and Figure 2).
Broad spectrum instrumented aircraft have demonstrated the capacity both to pursue process-oriented science questions and to survey unexplored regions. An example of an application of such airborne technology is identification of active volcanism beneath the West Antarctic ice sheet (Blankenship et al, 1992). The presence of this volcano has important ramifications for the stability and dynamic processes which govern the ice sheet (Figure 3). This feature was undetected before the application of high resolution airborne surveys, despite the imaging of this area by satellites and the traversing of this region by surface vehicles. Expanding high resolution airborne technology to recover even shorter wavelength signals will have important applications in the resource and environmental industries. Accurate navigation and precision position are critical to the recovery of these shorter wavelengths.
Aerogeophysics today are being used for several major research strategies, for long wavelength reconnaissance studies of unknown areas high resolution studies of detailed processes and for precise monitoring studies. Differential GPS continues to play a major role in the development of all these research strategies. The precise positioning and accurate navigation permit the acquisition of high resolution systematic data sets especially in inaccessible areas such as regions characterized by rugged terrain, dense vegetation or surface hazards which can range from political instabilities to glacial crevasses.
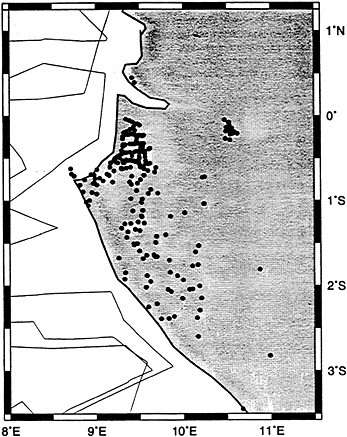
FIGURE 1 Land gravity measurements (dots) and marine gravity surveys (lines) of coastal Gabon. The land measurements were made principally on roads close to major cities. (Data from Watts et al., 1985).
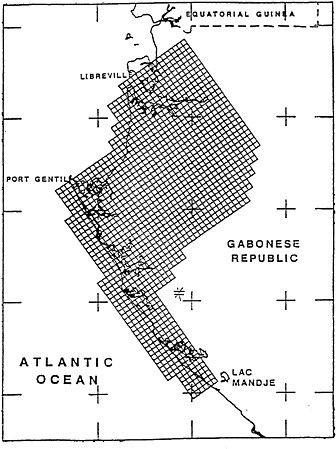
FIGURE 2 Airborne gravity survey (lines) flown over Gabon in 6 x 6 km grid. The sampling strategy is not limited by access to roads. (Figure courtesy of W. Gumert, Carson Geophysical).
The scientific motivation for enhanced use of DGPS technology in aerogeophysics is driven by a broad constituency from researchers interested in global change to mineral companies attempting to identify new major prospects to environmental scientists constraining the extent of contamination from a safe, remote distance. Aerogeophysics provides unique access to regions and results in systematic data sets otherwise impossible to acquire.
Interdisciplinary earth science problems can be addressed with research strategies which integrate aerogeophysics and differential GPS. An example of a global change issue addressed with aerogeophysics is ice sheet mass balance where real time differential techniques are necessary to accurately locate the experiment and precise positioning in three dimensions is critical to the analysis of the ice surface. Erosion processes and landform evolution can also be studied with an accurately navigated aerogeophysical platform used to trace region changes in topography. Similarly aerogeophysics can be used to trace emerging hot spots in hydrologic studies by enabling the simultaneous acquisition of geologic imaging and measurements of developing salt water intrusions (Babu et al, 1991).
Natural hazards, an emerging priority at both the national and international science communities, can be studied with aerogeophysics combined with DGPS. Specific examples include recovering eruption volumes using precise topographic mapping tools (Garvin, 1993) and recovering the regional distribution of motion from an earthquake using repeat airborne SAR interferometry (Massonnet et al, 1993).
Commercial motivations for high resolution aerogeophysics emerge from both the mineral and petroleum industries. The mineral industry uses high resolution aeromagnetics extensively to trace geologic structures in order to identify potential ore bodies. Petroleum explorationist use aerogeophysics, both gravity and magnetics, to examine structure beneath thick salt sheets which cannot be imaged with seismic techniques, to identify faults which bound sedimentary basins and to image oil bearing sedimentary sequences. Airborne gravity gradiometry is an emerging priority target of these industries. (Boddard et al, 1991 and Bell et al, 1995).
Aerogeophysics with precise GPS support can also be used for site characterization. Site characterization is of use for nuclear verification when used to monitor small changes in surface topography associated with an underground explosion (Houser, 1970). For environmental site characterization, aerogeophysics can be used to identify disturbed soil (Doll et al, 1993 and Phillips, 1993), often indicative of contaminated sites, as well as outlines of buried containers (Figure 4 and Figure 5).
Several type of aerogeophysical measurements can be used to address these scientific motivations. The suite of aerogeophysical measurements which require high resolution differential GPS include: gravity field measurements, gravity gradiometry, electromagnetic measurements, measurements of the earth's magnetic field, precise topography recovery via direct range measurements, recovery of precise topography from Synthetic Aperture Radar (SAR) and ice penetrating radar.
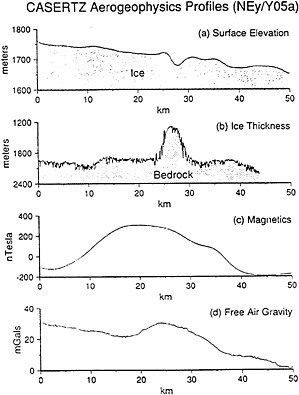
FIGURE 3 Evidence for active volcanism beneath the West Antarctic Ice Sheet from precise surface altimetry measurements and other airborne geophysical observations. The measurements were made as part of a major study of the stability mechanisms of the West Antarctic ice sheet and were collected along a north-south profile. (a) Surface elevations from a GPS-positioned laser altimeter reveals an anomalous depression in the ice surface located at 28 km. (b) Depth to bedrock (Ice thickness) from ice penetrating radar observations. The prominent feature at 26.5 km is centered in a shallow rimmed caldera. (c) Total magnetic field observations reveal a large anomaly between 0 and 40 km that is strongly correlated with the caldera and central edifice. (d) Free air gravity anomaly of 7 mGal is associated with the central edifice at 24 km. (Figure modified from Blankenship et al., 1993).
Two primary uses of differential GPS are employed for high resolution aerogeophysical applications today including navigation and precise positioning. The navigation application ensures that the fundamental measurements acquired during an experiment are acquired in the proper location. The second application is for precise positioning which requires the post processing of the carrier phase GPS data from the aircraft and the fixed base station. For aerogeophysical DGPS navigation the differential correction is broadcast to the aircraft in real time at a high data rate. In remote areas a dedicated broadcast system may be required. In North America it may be possible to make use of the government or commercially broadcast corrections. For the precise positioning for high resolution aerogeophysics, the aircraft position must be recovered to better than 50 cm in post-mission processing. This positioning is recovered by post-mission reduction of the carrier phase data acquired from a fixed base station and a GPS system mounted aboard the aircraft. This data must be recorded at 1 Hz data rate at both the dual frequency receivers. Installing and maintaining sufficient ground GPS receivers can be a significant logistical impact on an aerogeophysical project.
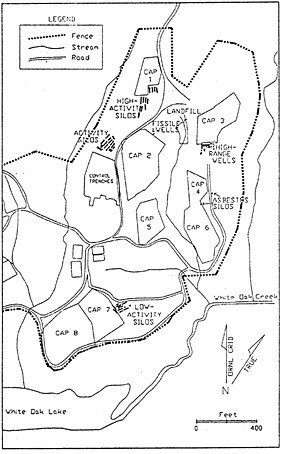
FIGURE 4 Map showing waste sites and buildings in the survey area, Oak Ridge National Laboratory. (Figure modified from Doll et al., 1993).
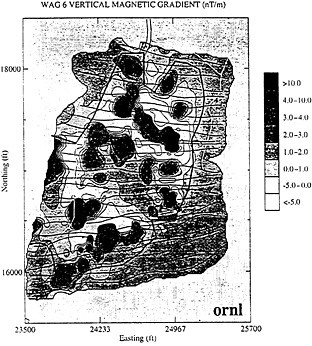
FIGURE 5 Short-wavelength magnetic anomalies (vertical component) measured from a GPS-navigated helicopter are associated with high-and low- activity silos, surface pipes (labeled “high range wells ”), high-and low-activity materials disposal trenches (capped areas 1, 2, 4, 7, and Control Trenches), biological disposal trenches (capped areas 5 and 8), and asbestos disposal trenches (capped area 6). (Figure modified from Doll et al., 1993).
The aerogeophysical requirements for DGPS include use of dual frequency receivers recording carrier phase data at a high data rate (1 Hz). Ancillary data which can be useful include base magnetometer measurements to identify periods of high ionospheric activity. Orbits are required for the positioning applications but not for the real time navigation.
Differential GPS is being increasingly integrated into high resolution aerogeophysical applications. For optimal usage, several coordination issues need to be addressed. First, an increased awareness of Federal and commercial DGPS systems must to be integrated into both commercial and academic aerogeophysical planning. The increased awareness will have the impact the quality of the navigation used for aerogeophysical surveys. The awareness of available continuously operating GPS site may have result in reduced costs to the commercial and academic applications.
Outstanding issues in kinematic GPS is the robustness of algorithms for reduction of the GPS data for precise positions. Efforts to enhance these algorithms will provide improved resolution and scientific results.
Babu, H.V.R., N.K. Rao, and V.V. Kumar, 1991, Bedrock topography from magnetic anomalies: An aid for groundwater exploration in hard-rock terrains. Geophysics, v. 56, p. 1051-1054.
Bell, R.E., R. Anderson and L. Pratson, 1997, Gravity gradiometry resurfaces. The Leading Edge, January, p. 55-59.
Blankenship, D.D., R.E. Bell, S.M. Hodge, J.M. Brozena, J.C. Behrendt, and C.A. Finn, 1993, Active volcanism beneath the West Antarctic ice sheet and implications for ice-sheet stability. Nature, v. 361, p. 526-529.
Bodard, J.M., J.G. Creer, and M.W. Asten, 1993, Next generation high resolution airborne gravity reconnaissance in oil field exploration. Energy Exploration and Exploitation, August Special Issue, p. 198-234.
Brozena, J., M. Chaloma, R. Forsberg, and G. Mader, 1992, The Greenland Aerogeophysics Project. EOS, Transactions of the American Geophysical Union, v. 73, p. 130.
Doll, W.E., J.E. Nyquist, J.S. Holladay, V.F. Labson, and L. Pellerin, 1993, Preliminary results of a helicopter electromagnetic and magnetic survey of the Oak Ridge Reservation, Tennessee for environmental and geologic site characterization. In Bell, R.S., and C.M. Lepper, eds., Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems, p. 281-295.
Garvin, J.B., 1993, Mapping new and old worlds with later altimetry. Photonics Spectra, v. 27, p. 89-94.
Houser, F.N., 1970, A summary of information and ideas regarding sinks and collapse, Nevada Test Site. U.S. Geological Survey Open File Report 474-41 (NTS-216).
Massonnet, D., M. Rossi, C. Carmona, F. Adragna, G. Peltzer, K. Feigl, and T. Rabaute, 1993, The displacement field of the Landers earthquake mapped by radar interferometry. Nature, v. 364, p. 138-142.
William Krabill
Laboratory for Hydrospheric Processes, NASA Wallops Flight Facility
Chreston Martin
EG&G Washington Analytical Services Center, Inc.
There is currently considerable uncertainty as to whether the ice sheets of Greenland (and Antarctica) are growing larger or smaller [Drewry and Morris, 1993; Hubrechts, 1994; Warrick and Oerlemans; 1990; Van der Veen, 1991; Douglas, et al., 1990]. The traditional technique for such an assessment is to infer mass-balance by comparing total snow accumulation with total ice loss. Since both of these numbers are very large and have significant errors in their measurement, their difference has large percentage uncertainty. As a result, traditional measurements are only capable of telling us that ice sheet mass balance may be responsible for a sea level rise, or fall, of as much as 2 mm per year.
Mass balance can also be estimated by comparing repeat, precise measurements of surface-elevation profiles across the ice sheets, provided the elevation profiles cover most of the continent. Elevation profiles can be obtained by satellite radar-altimetry, but with high accuracy only over relatively smooth surfaces with slopes of less than about one degree due to the large beam-limited radar footprint. Additional uncertainties are introduced due to radar penetration into the snow, which is a relatively poorly understood effect. These problems can be overcome by using a laser altimeter, and the Geoscience Laser Altimetry System (GLAS) is presently being developed for precise elevation mapping of polar regions and is scheduled for launch on the Earth Observation System Land Ice Altimetry (EOS ALT-L) mission around 2002.
Precise elevation measurements can also be made from an aircraft borne laser altimeter when the aircraft is positioned by differential GPS, with overall elevation accuracies in the 10-20 cm range. Such measurements have been made by NASA, starting in 1991, the first year in which the GPS constellation was adequate to support the 6-8 hour missions necessary to gather elevation measurements over ~ 1000 km profiles. Differential GPS measurements for aircraft positioning used base stations at Sondrestrom Air Force Base in 1991-1994 and at Thule Air Force Base in 1994-1995. These base sites are shown on Figure 1, along with the flight profiles which have been flown over Greenland.
The basic concept of airborne laser monitoring of ice terrain is shown in Figure 2. The aircraft laser scans a 100-150 meter wide swath underneath the aircraft in order to allow for navigation inaccuracies when the flight line is reflown. The aircraft itself is navigated using real-time GPS positioning, which may be in error by 50 meters or so, due in large part to the use of Selective Availability in the transmitted GPS ephemeris and code data. The swath width, however, is sufficiently wide to accommodate navigation errors on any pair of flights designed to follow great circle paths between specified way points. The monitoring of elevation changes then amounts to differencing elevations on the overlap portions of flight lines from different time periods, normally one or more years apart.
The scanning laser is only one of the instruments which were carried on the Greenland ice mapping missions of 1991-1995. The aircraft itself was a P-3 on all missions (although two different P-3 aircraft have been used) flying at a height of 400-600 meters above the surface at a speed of approximately 120 m/s. Instrumentation flown included:
-
A scanning lidar (10-15 degrees off nadir, 800-2000 pulses/s);
-
A profiling lidar;
-
Ku-Band Radar (University of Massachusetts) for ice penetration studies;
-
VLF Radar (University of Kansas) for deep ice penetration measurements;
-
GPS Receivers (Ashtechs, Turborogues);
-
GPS coupled to P-3 Autopilot;
-
Inertial Navigation Units for heading, pitch and roll measurements.
It should be noted that the instrumentation configuration has changed slightly from year to year and not all instruments have been flown on all missions. In particular, the 1992 mission made only profiling measurements over Greenland.
For various reasons, the primary GPS receiver on all missions was some model Ashtech, in particular the P-12 receiver in 1993 and the Z-12 in 1994-1995. For
Two types of calibrations are necessary for the terrain mapping system. The first is for the laser itself, which is a leading edge tracker and thus must be calibrated for both bias and range walk. This is done on the ground, using ranging to a target board, both pre-mission and post-mission, and for a variety of return signal strengths. The post-mission calibration is generally considered the most appropriate for application to mission data, since instrument temperatures are closer to those during the actual mission. Variations in calibration of only a few centimeters are observed from day to day, although the calibration may also show slight long term drifts.
The other type of calibration is for the scanning laser (now referred to as the Airborne Terrain Mapper or ATM, although the earlier system used was referred to by its original name of Airborne Oceanographic Lidar or AOL) whose platform is mounted such as to be near horizontal for normal in-flight attitude. However, the scanner platform orientation relative to the inertial navigation system (INS) reference system must be determined to somewhat better than 0.1 degree since, for an aircraft altitude of 400 meters, a 0.1 degree mounting error would introduce a height error of 19 cm for an off-nadir angle of 15 degrees, and a height error of 12 cm for an off-nadir angle of 10 degrees. The relative orientation between the ATM platform and the INS reference can be estimated by flying over either a flat surface or surface of known orientation, and comparing the observed ranges with those computed on the basis of the GPS position estimate of the aircraft GPS antenna, the measured position of the scanner mirror relative to the GPS antenna in the aircraft (INS) coordinate system, the INS attitude measurements (heading, pitch and roll), and a model of the scanner measurement system.
Prior to the 1994 missions, the preferred flat surface was water, supplemented by flights over surveyed airport runways at various altitudes (helpful in validating range biases and the estimation of off-nadir mounting angle and other parameters in the scanner measurement model). However, over-water data is frequently degraded by low return signal levels, surface waves, and volume backscatter. In 1994, open water was difficult to find around Thule, so data was taken over sea ice instead. This turned out to be very fortuitous, since such data has a very low noise level and insignificant volume backscatter. Sea ice has thus become the preferred flat surface, and sea ice data is now used, when available, to complement the runway data for ATM mounting bias estimates. It may be noted that these bias estimates are relatively stable from day to day and will include variations in INS pitch and roll errors. For the 1995 mission, the mounting bias estimates were sufficiently stable that a single set of numbers were used for the entire mission.
Because of their use for positioning the laser spot on the surface, INS pitch and roll errors are a source of concern, particularly at high latitudes. The observed variations in “mounting biases” show, however, that the variations seldom reach a level of 0.1 deg and are within 0.05 deg most of the time. Attempts have been made to monitor the variations in INS errors through the use of GPS attitude estimates using several GPS antennas on board the aircraft. In general, these attitude estimates are less accurate that the INS estimates, due to measurement noise, multipath effects, and structural deflections of the aircraft. It is also possible to monitor the long term pitch error variation of the INS through the comparisons of scanner forward scan elevation measurements with backward scan elevation measurements. The comparison of forward scan elevations with backward scan elevations is, in practice, simplified if there are simultaneous elevation measurements by a profiling laser, as has frequently been the case. The simultaneous profiling measurements also allows the overall elevation measurements to be monitored for systematic variations, such as inflight bias stability. Profiling measurements have been used to check scanner elevations, but their systematic use for pitch monitoring has not yet been done, partly because the procedure cannot account for roll errors, and partly because data averaging will greatly reduce the effects of pitch errors.
Figure 1 shows the trajectories which NASA has flown across Greenland in 1993, 1994, and 1995. There were 11 missions flown in 1993, 14 in 1994, and 4 in 1995. Not shown are the 7 trajectories flown in 1991 and the 3 (profiling only) trajectories flown in 1992. In assessing the accuracy of the elevation profiles (or swaths) obtained, the major error sources can be divided into the following categories:
-
The aircraft trajectory as determined from differential GPS;
-
Aircraft pitch and roll as provided by the aircraft INS;
-
Laser bias, either constant or slowly varying;
-
Laser measurement noise.
GPS trajectory errors can arise from several sources, including improper accounting for cycle slips,
tropospheric modeling errors, satellite ephemeris errors, and GPS receiver difficulty in following rapidly varying ionospheric conditions. The relative importance of these error sources has varied from year to year. Ephemeris accuracy and receiver performance have generally improved from year to year, except for a setback in 1994 with the first full-time application of Anti-Spoofing. The current error source of greatest concern is tropospheric modeling. To minimize this problem, the 1995 missions carried instrumentation for measuring and recording atmospheric temperature and pressure aboard the P-3. Even with this data and recorded meteorological data near the ground receiver, it has been found desirable to estimate scale factor parameters to obtain optimum trajectory accuracy.
A number of tests have been performed to validate data accuracy. The results of one such validation are shown in Table 1 which shows the mean agreement of surface elevations determined by the ATM system with a surveyed ramp at Thule Air Force Base during May 1995.
TABLE 1 Comparison of Surface Elevations of Thule Ramp Overflights with GPS Truck Survey
|
Date |
Mean Diff. (cm) |
Sigma (cm) |
|
950519 |
−8.57 |
5.90 |
|
950520 |
−3.46 |
6.18 |
|
950520 |
11.21 |
5.51 |
|
950522 |
−4.73 |
7.35 |
|
950522 |
7.70 |
6.69 |
|
950523 |
−5.95 |
6.13 |
|
950523 |
−2.95 |
5.79 |
|
950524 |
2.28 |
6.08 |
|
950524 |
1.17 |
5.59 |
|
950526 |
−3.79 |
6.79 |
|
950527 |
3.67 |
6.36 |
|
950527 |
−10.40 |
7.00 |
|
950530 |
−3.28 |
5.60 |
|
950530 |
−3.99 |
6.46 |
The primary error source which should not be significant in the differences shown is GPS positioning error which should have negligible contributions from satellite ephemeris and tropospheric propagation errors, due to the fact that the reference station is only a few kilometers from the runway. Effects of phase noise and multi-path will, however, still be present. INS pitch and roll errors will also be included since the ramp width was less than the scanner swath width, leading in some cases to tracking only on one side of the aircraft so that roll errors would propagate into the differences shown with little reduction from averaging. For the 14 ramp passes shown in the table, the overall mean agreement is −1.5 cm and the rss agreement is 6.0 cm. Since the ramp surface is a slightly poorer reflector than snow, the noise levels to be expected over ice should be slightly lower than the 6 cm shown in Table 1 for the ramp passes.
For missions in 1993, all missions left Sondrestrom and flew east along an approximately 10 km long corridor. In 1994, all passes left Thule and flew along the approximately 25 km long Thule - Camp Century corridor. Passes along these corridors should show agreement similar to the ramp passes, since trajectory errors should have been comparable because of the short distances to the reference station. Table 2 shows the comparisons about a mean surface made along this corridor for both years. Again, the peak differences are about 10 cm and the rms is around 5 cm.
For elevation measurements made throughout the missions, elevation differences have been computed at crossovers of missions with themselves and with other missions flown in the same year. To some extent, all trajectories may have common systematic error sources, such as tropospheric propagation modeling errors and satellite ephemeris errors. However, there are significant PDOP changes for a trajectory during a mission, so crossover differences even for the same mission can be meaningful. For 1994, the differences show the following characteristics:
|
Differences |
Percent |
|
0 cm - 5 cm |
29.0 |
|
5 cm - 10 cm |
18.7 |
|
10 cm - 15 cm |
15.9 |
|
15 cm - 20 cm |
16.8 |
|
20 cm - 25 cm |
5.6 |
|
25 cm - 30 cm |
6.5 |
|
30 cm - 35 cm |
3.7 |
|
35 cm - 40 cm |
1.9 |
|
40 cm - 45 cm |
1.9 |
|
>45 cm |
0.0 |
These crossover differences are heavily influenced by trajectory errors, although attempts to improve some of the larger crossovers with various improvements in the trajectories have not been very successful. Nevertheless, some 64% of the crossovers are less than 20 cm. It should also be pointed out that 1994 was a relatively difficult year for trajectory determination and that the crossovers for 1995 missions are significantly better. Elevation measurements that have been made in-situ on the Greenland ice sheet can be used to make absolute checks on ATM elevations. These checks are presently being made.
TABLE 2 Comparison of Elevation Measurements Made along Corridors with Multiple Passes in 1993 and 1994
|
Flight Segment |
Mean Difference |
|
|
Date |
Direction |
(cm) |
|
930624 |
E-W |
−2.3 |
|
930628 |
W-E |
1.1 |
|
930701 |
W-E |
0.3 |
|
930701 |
E-W |
0.9 |
|
930708 |
W-E |
5.6 |
|
930709 |
E-W |
−5.4 |
|
940523 |
E-W |
4.5 |
|
940526 |
W-E |
2.1 |
|
940526 |
E-W |
2.0 |
|
940528 |
E-W |
−6.4 |
|
940531 |
W-E |
6.3 |
|
940531 |
E-W |
1.8 |
|
940601 |
E-W |
3.5 |
|
940606 |
W-E |
−3.5 |
|
940606 |
E-W |
−1.1 |
|
940607 |
W-E |
4.3 |
|
940607 |
E-W |
7.5 |
|
940608 |
W-E |
−8.0 |
|
940608 |
E-W |
0.7 |
|
940609 |
E-W |
−2.7 |
|
940614 |
W-E |
−10.5 |
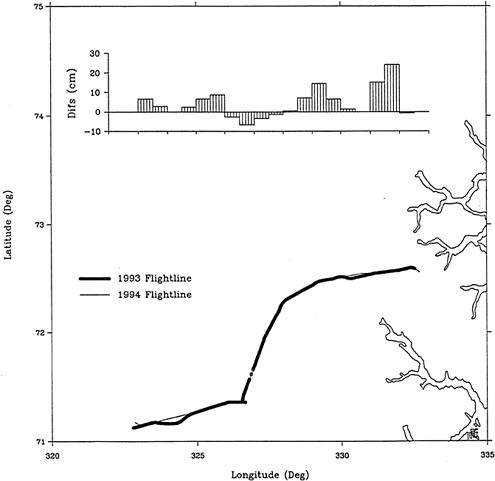
We now would like to show several of year to year comparisons of elevation profiles which demonstrate the capability of aircraft laser altimetry with differential GPS positioning to measure changes in ice surface elevation. Figure 3 shows a comparison of elevation measurements from different years along the 40 km flight line labeled “Level Line” in Figure 1. This figure shows raw elevation measurements from 1995 differenced from data taken in 1994, 1993, 1992 and 1991. The 1992 data was taken using a profiling laser, while all the other data was taken using the scanning laser discussed above. The profiling data comparisons show a relatively clear change at around the decimeter level from year to year. The profiling data is not really inconsistent but its noisier characteristics have not yet been explained.
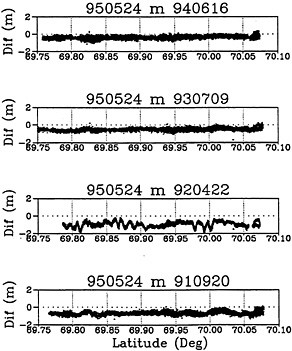
FIGURE 3 Comparison of elevation measurements made in different years along “level line.”
The second elevation comparison is along the “Surface Traverse” line shown in Figure 1. Figure 4 shows the 1995 elevations differenced from the 1994 elevations. This comparison is also at the raw data rate, but the changes are quite clear and relatively smooth. The elevation changes exceed 50 cm at around 72 degrees latitude and, as in Figure 3, show a decreasing elevation with time.
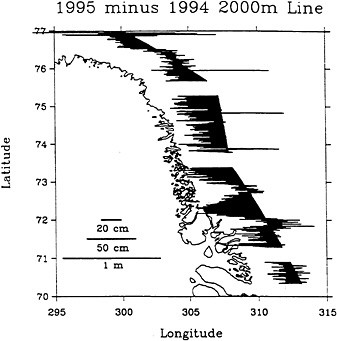
FIGURE 4 Differences between elevation measurements made along “surface traverse” line between 1995 and 1994.
The final comparison is shown in Figure 5 and gives the comparison between elevations along the EGIG line of Figure 1 from 1993 and 1994. These differences have been smoothed and show differences which change significantly along the flight line and which do not exceed 20 cm. We infer that elevation changes along this flight line are quite stable. We do not yet have sufficient confidence in the GPS trajectories and elevation measurements to state that the differences shown are geophysical changes. However, it is clear that the aircraft borne lidar system is indeed capable of making elevation measurements at the sub 20 cm accuracy level expected.
Douglas, B.C., R.F. Cheney, L. Miller, and W.S. Agreen, Greenland ice sheet: is it growing or shrinking? Science, 248, 288-289, 1990.
Drewry, D.J, and E.M. Morris, The Response of large ice sheets to climate change. Phil. Trans. R. Soc. London B, 338, 235-242, 1992.
Huybrechts, P., The present evolution of the Greenland ice sheet: an assessment by modelling. Global and Planetary Change, 9, 39-51, 1994.
Van der Veen, C.J., State of balance of the cryosphere, Rev. Geophys. 29, 433-455, 1991.
Warrick, R., and J. Oerlemans, Sea Level Rise. in J.T.Houghton, G.J. Jenkins, and J.E. Ephraums (Eds), Climate Change, the IPCC Scientific Assessment. Cambridge University Press, 257-282, 1990.
George Born and Kevin Key
Colorado Center for Astrodynamics Research, University of Colorado-Boulder
In addition to precise orbit determination, another GPS application for satellite altimetry is calibration/validation (cal/val) of the altimeter range bias and bias drift. This quantity must be monitored in order to use the altimeter data to measure accurately any change in global sea level and to provide a basis for relating altimeter measurements from one mission to the next. The GPS receiver provides the data necessary to relate the altimeter range measurement to the range measurement inferred from the tide gauge and orbit determination data.
In the case of single frequency altimeters such as Geosat Follow-On (GFO) and ERS 1&2, GPS provides critical information on the total electron content (TEC) in the altimeter nadir column from which a correction for path delay can be made. Lack of an accurate ionospheric correction is the major error source in generating accurate sea surface topography maps from these missions. This is especially true for mesoscale and gyre scale features. Hence, an accurate means of correction for ionospheric refraction would provide a significant enhancement to single frequency altimeter data.
INTRODUCTION
On the TOPEX/Poseidon mission the cal/val activity was carried out at the Texaco offshore platform, Harvest (Born, 1995). A dual frequency codeless GPS receiver was deployed at the platform and used to monitor platform elevation with time. Tide gauges were deployed at the platform to monitor sea level which was related to the GPS antenna phase center through a survey of the platform. During each repeat cycle the satellite ground track passed directly over the platform and the altimeter measurement was compared to that inferred from the in situ measurements (Christensen et al., 1994).
An alternative method for calibrating the altimeter is to deploy a GPS equipped buoy beneath the ground track of the satellite and measure sea height relative to a fiducial GPS site nearby (Rocken et al., 1990, Kelecy et al., 1992, Kelecy et al., 1994). Results of a GPS buoy experiment demonstrate that this technique has comparable accuracy to the platform cal/val configuration and can be done anywhere a fiducial site located near the open ocean is available (Born et al., 1994).
In the case of single frequency altimeters such as GFO and ERS 1&2, an alternate means of correcting for the ionospheric path delay must be used. Studies have shown that this is best accomplished by assimilating TEC data from the GPS constellation and a set of globally distributed ground stations into a model of the ionosphere. Several models are available for this task; the PRISM model (Daniell and Brown, 1995) has been used extensively in tests for this application (Schreiner et al., 1996). IRI is another model which could be used for this purpose (Bilitza et el., 1993). During the latter part of 1996, a workshop will be sponsored by NASA to recommend a technique for ionospheric correction for single frequency altimeter missions.
Several experiments with GPS buoys demonstrating the ability to accurately measure sea level and significant wave height have been carried out (Rocken et al., 1990, Kelecy et al., 1992, Kelecy et al., 1994, and Born et al., 1994). A recent experiment, described here, has been carried out to demonstrate the capability of a GPS buoy or a constellation of buoys to map sea level in a geographic area of interest.
On the days of May 22 and 24, 1995, a wave rider style buoy was deployed by the University of Colorado off the California coast near the Texaco oil platform, Harvest (Figure 1). The buoy, shown schematically in Figure 2, was equipped with a GPS antenna attached to a dual-frequency carrier phase tracking receiver, in order to provide an accurate measurement of the sea surface height as a function of time, latitude, and longitude. The purpose of this deployment was three fold: 1) to demonstrate the ability of the buoy to calibrate the height measurement of the T/P satellite altimeter; 2) to
demonstrate the ability of buoy to map the ocean's surface in the across-track direction of the T/P overpass; and 3) to demonstrate the ability of the buoy to accurately measure the sea state.
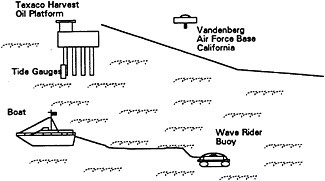
FIGURE 1 Pictorial representation of the experiment. The buoy is a platform for a TurboRogue Antenna and is connected to a boat which stores a TurboRogue receiver. Meanwhile at Vandenberg Air Force base a second TurboRogue receiver and antenna are recording data at the same time. Additionally, tide gauge data is recorded at the Texaco oil platform Harvest for comparison with the buoy derived sea surface heights.
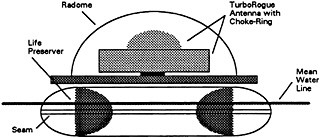
FIGURE 2 Schematic of the wave rider buoy. The mean water line was measured relative to a seam running around the middle of the life preserver as indicated above.
As shown in Fig. 3, experiment results indicate that around the time of the T/P overflight, the measured sea surface height differs by less than ±1.5 cm from the tide gauge measurements. The capability for high accuracy determination of sea level at a point has been previously reported in Born et al., 1994. The major new objective of this experiment was to map the sea height in the vicinity of the Harvest Platform.
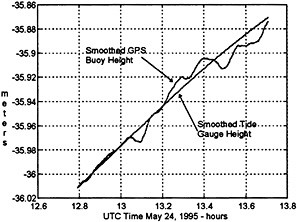
FIGURE 3 A comparison of the GPS buoy derived sea surface height and the NOAA acoustic tide gauge sea surface height. The buoy was located 1.1 Km south-east of the tide gauges; thus, the measured height has been corrected by 0.0022 meters as determined by OSUMSS95. Both heights are mapped to the TOPEX ellipsoid (Ae = 6378136.3 and 1/f= 298.257).
Before and after the overflight of the T/P spacecraft, the buoy was deployed at several locations around the Harvest platform for the estimation of a sea surface map. A paraboloid was fit to the ocean height as a function of position from the Harvest platform with a root mean square error of 2.4 cm relative to the Ohio State University Mean Sea Surface (OSUMSS95, Yi, 1995) values in a five Km circle about the Harvest platform. The differences may be explained by oceanographic features at the time of the experiment or by error sources in the either the GPS derived sea surface height or the OSUMSS95. This experiment showed that detailed mapping of ocean topography is feasible and could be used to obtain useful information on the geoid and circulation features in areas of limited geographic extent.
Finally, wave spectra were calculated from buoy sea surface height time series such as that shown in Figure 4. Figure 5 illustrates the power spectral density of the sea state at various times during this experiment. The power spectral density can be used to compute significant wave height, H1/3. This experiment demonstrates that a simple buoy design can give comparable results to that obtained from more complex configurations such as the Harvest Platform.
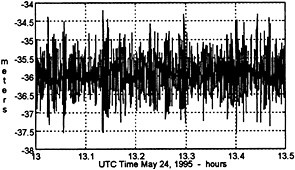
FIGURE 4 A typical sea surface height time history. This figure shows the sea surface including wave heights as a function of time.
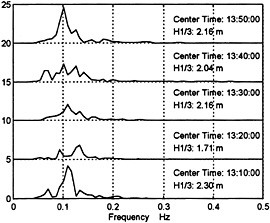
FIGURE 5 Spectral power densities of the sea state near the Harvest platform. The plots are derived from the buoy measured sea surface heights on May 24, 1995 during the hours of 13:00:00 - 14:00:00 UTC. The spectra were generated using an FFT with 4.3 minutes (256 observations) of data centered at the times indicated. Also included are H1/3 values for each of the data sets.
A number of satellite altimeters missions both current and planned will fly single frequency altimeters and thus have no direct measure of ionospheric path delay. These include the GFO mission and ERS 1&2. Consequently, sea surface topography from these single frequency altimeters is corrupted by signals introduced by the ionosphere, primarily at gyre and basin scales. For example, based on comparisons between T/P data and ionospheric model results, we often see TEC errors that result in five to ten centimeter topography errors with length scales of one or two thousand km in the vicinity of the equatorial currents. These scales are important for measuring mean circulation and monitoring circulation variability in the oceans. Ionospheric errors limit our ability to combine data from these altimeters with the more accurate T/P data.
One possible source of columnar TEC for ionospheric correction is an ionospheric model. Unfortunately, without assimilation of data which is temporally and spatially near to the point of interest, these models are not of sufficient accuracy for this purpose. This is especially true in the equatorial and mid latitude regions. Another solution is the direct use of GPS derived TEC data which has been interpolated to gridded maps. In this case the major problem is the lack of tracking stations on islands and in coastal areas. Consequently, use of a model with assimilation of direct measurements of TEC data seems the most promising.
Several studies of assimilating GPS TEC data into ionospheric model have been performed. The model most frequently used for this application is PRISM (Daniell et al., 1995). These studies generally have shown that assimilation of TEC data into a model works well if the point of interest was within 500 Km of the ground site from which the TEC data was measured and was within two hours in time (Schreiner et al., 1996). The TEC data for these studies was obtained from the Jet Propulsion Laboratory in the form of raw line of sight data and gridded data (Mannucci et al., 1995).
As stated before, the major problem with using GPS TEC data for oceanographic applications is the lack of stations in ocean areas and in the southern hemisphere. Consequently, any augmentation of the global GPS network with dual frequency receivers on islands or in coastal areas would be of benefit to oceanographic applications of satellite altimetry. Another partial solution to this problem could be to outfit ships of opportunity with GPS receivers. This data could be returned via satellite links and processed by JPL, for example, as part of their ongoing activity to produce global TEC maps.
Another potential source of TEC data is a constellation of satellites flying GPS receivers and measuring electron density profiles during occultation with the GPS satellite constellation. GPS-Met is the prototype for such a system. The advantage here is that no ground station is required and the majority of the data would be over the oceans.
This paper has addressed the question of using GPS in the cal/val of satellite radar altimeters, and in the correction of the data for ionospheric path delay. For the cal/val requirements there are no significant new demands on the GPS ground system or receivers. This activity requires a fiducial site within a few tens of kilometers of the calibration site. It would be of interest to carry out additional experiments to measure ocean surface topography in a limited geographic area using an array of GPS receivers to further explore the potential of GPS for fine scale mapping of ocean topography.
Ionospheric path delay correction for single frequency altimeter missions requires additional ground sites equipped with dual frequency GPS receivers, especially in ocean areas and in the southern hemisphere. A possible alternative to more ground sites would be the use of ships of opportunity to carry dual-frequency GPS receivers across ocean basins. Another possibility would be the use of occultation data from an array of GPS receivers on orbit. These alternatives should be explored.
Bilitza, D., K. Rawer, T. Gulyaeva. 1993. International Reference Ionosphere - Past, Present, and Future, Advances in Space Research, Vol. 13, No. 3, 1993.
Born, G.H. 1995. Guest Editor, Marine Geodesy, Special Issue: TOPEX/POSEIDON Calibration/Validation, Vol. 18, No. 1-2, Jan-June, 1995.
Born, G.H., M.E. Parke, P. Axelrad, K.L. Gold, J. Johnson, K.W. Key and D.G. Kubitschek. 1995. Calibration of the TOPEX altimeter using a GPS buoy, Journal of Geophysical Research, Vol. 99, pp. 24,517-24,526, December 15, 1995.
Christensen E. J., et al. 1994. Calibration of TOPEX/POSEIDON at Platform Harvest, Journal of Geophysical Research, Vol. 99, No. C12, DEC 15, 1994.
Daniell, R. E.,Jr., and L. D. Brown. 1995. PRISM: A Parameterized Real-Time Ionospheric Specification Model, Version 1.5, Phillips Laboratory Technical Report, May, 1995.
Kelecy, T.M., G.H. Born, and C. Rocken. 1992. GPS Buoy and Pressure Transducer Results from the August 1990 Texaco Harvest Oil Platform Experiment, Marine Geodesy, Vol. 15, pp. 225-243, 1992.
Kelecy, T.M., M.E. Parke, G.H. Born and C. Rocken. 1994. Precise Sea Level Measurements Using the Global Positioning System Journal of Geophysical Research, Vol. 99, No. C4, pp. 7951-7959, April 1994.
Mannucci, A., B. Wilson, and D. N. Yuan. 1995. An Improved Ionospheric Correction Method for Wide-Area Augmentation Systems, ION GPS - 95, Palm Springs, CA, Sept. 12-15, 1995.
Rocken, C., T.M. Kelecy, G.H. Born, L.E. Young, G.H. Purcell, and S.K. Wolf. 1990. Measuring Precise Sea Level From a Buoy Using The Global Positioning System, Geophysical Research Letters, Vol. 17, No. 12, pp. 2145-2148, November 1990.
Schreiner, W.S., R.E. Markin, and G.H. Born. In press. Correction of Single Frequency Altimeter Measurements for Ionospheric Delay, IEEE Trans. on Geoscience and Remote Sensing, in press.
Yi, Y. 1995. Determination of Gridded Mean Sea Surface from Altimeter Data of TOPEX, ERS-1, and GEOSAT. Ph. D. Thesis. Department of Geodetic Science and Surveying, The Ohio State University, Columbus, Ohio, 1995.
Robert Schutz
Center for Space Research, University of Texas at Austin
INTRODUCTION
Satellites in low Earth orbit (LEO) have requirements for position determination accuracy that encompasses the centimeter-level to the kilometer-level, depending on the application. Traditional approaches to this problem, usually referred to as “orbit determination,” have relied on ground-based ranges (measured with radar or laser), range-rate (measured from doppler shift) or angles (measured from photographic plates with respect to stars). With these ground-based measurements, the orbit determination problem was solved by determining the satellite position and velocity at some epoch that produced a solution to the equations of motion that “best-fit” these measurements. The classical “best-fit” criteria was based on “least-squares,” an orbit determination technique established by Gauss (1809). In current terminology, this technique is referred to as a “dynamical” technique since it relies on the solution of the equations of motion which are based on Newton's Second Law.
In recent years, the flexibility offered by the Global Positioning System (GPS) has become increasingly evident. In fact, GPS can meet the centimeter-level requirements as well as the kilometer-level needs. The basic design of GPS, including the effects of Selective Availability (SA) and Anti-spoofing (AS), offers a straightforward position determination at the 100 meter accuracy level. Furthermore, this determination can be made in real-time without reliance on the equations of motion describing the LEO satellite dynamics, a “kinematic ” technique. Differential techniques, such as those described by Hofmann-Wellenhof (1992), enable orbit determination at the centimeter-level to meter-level. The emphasis in this paper is directed to the centimeter-level LEO satellite applications.
The most well-known satellites with centimeter-level orbit determination requirements are those carrying altimeters. The first altimeter satellite with a GPS receiver was TOPEX/POSEIDON (T/P), launched in August 1992 with a Motorola GPS receiver, a doppler beacon known as DORIS and a satellite laser ranging (SLR) reflector. The GPS receiver was a dual frequency P-code receiver, able to simultaneously track up to six GPS satellites. With the cooperation of the Department of Defense, AS was “off” during extended periods in 1992 and 1993. During these periods, comparisons were made between the orbit determined with GPS and the orbit determined with DORIS and SLR. Furthermore, the GPS data were independently analyzed with different approaches and software. The comparison between the independently determined orbits led to the conclusion that the T/P orbit accuracy was 2-3 cm radial and <10 cm horizontal (along-track and cross-track). The results have been described by Melbourne et al. (1994), Yunck et al. (1994) and Schutz et al. (1994). During periods when AS was “on”, the T/P receiver tracks L1 only, but ionosphere errors degrade the orbit determination accuracy to the 5-6 cm level in the radial component.
Future altimeter satellites slated to carry GPS receivers to fulfill the science objectives include the Navy Geosat Follow-On (launch: 1996) with a radar altimeter, and the Geoscience Laser Altimeter (launch: 2002). Since the altitude of both satellites is lower than T/P, the mission objectives cannot be achieved without a dual frequency GPS receiver because of greater ionosphere effects than experienced at the higher T/P altitude.
Dual frequency GPS receivers which do not carry the AS-decryption keys have been developed and demonstrated in orbit. The MicroLab I was launched into a 750 km altitude orbit in April 1995 with a flight version of the widely used TurboRogue receiver marketed by Allan Osborne Associates based on JPL designs. The flight version, known as the TurboStar, uses a cross-correlation technique between the L1 and L2 frequencies to obtain L2 measurements, while the L1 pseudorange and carrier phase is obtained from the C/A-code. The primary disadvantage of the cross-correlation determination of L2 compared to P-code determination, for example, is a weaker signal to noise ratio. The MicroLab I receiver, known as the GPS/MET receiver, is designed to provide atmospheric temperature profiles by tracking the GPS signals through the atmosphere (e.g., Ware, et al., 1994).
The GPS/MET backup receiver was flown on the Wake Shield, a free-flyer deployed and retrieved by the Space Shuttle in September 1995 (Schutz, et al., 1995; Schroeder, et al., 1996). This flight took place at an altitude of 400 km. Analysis of the GPS data has revealed the magnitude of gravity and atmospheric drag
error at this altitude. Furthermore, the data will be used to improve these models.
Centimeter-level orbit determination of a LEO satellite requires dual frequency carrier phase measurements, which have a precision of a few millimeters, as well as pseudorange measurements, which have a precision of a few decimeters. The primary disadvantage of the phase measurement is the resolution of the ambiguity term, but various estimation approaches exist to compensate for this term.
Although errors exist in the models that describe the forces acting on a LEO satellite, the force environment is significantly more benign than the aircraft case. Thus, even though kinematic approaches are essential for high precision positioning of an aircraft, the dynamical approaches have produced more accurate results for the LEO satellite [Yunck, 1994; Davis, 1996].
The dynamical approaches are fundamentally based on the solution to the equations of satellite motion, which are derived from Newton 's Laws. Philosophical differences exist in the treatment of some forces and in the level of fidelity imposed for the representation of the equations of motion. The treatment of unmodeled and mismodeled forces may use a stochastic representation or an empirical model based on the periodic nature of the effect of the forces on the orbit.
All precision orbit determination (POD) approaches use GPS carrier phase measurements as the primary data. With a network of ground stations, one technique is based on the explicit formation of “double-differences ” (DD) as described by Hoffmann-Wellenhof (1992). The DD is formed by differencing the phase measurements as follows:
-
form single difference (SD) from receiver 1 (R1) and two satellites (SV1 and SV2) as SD = Phase (SV1) - Phase (SV2) for R1
-
form SD from receiver 2 (R2) using the same two satellites in Step 1
-
form the DD by differencing the SD obtained in Steps 1 and 2
In this example, R1 could be the satellite-borne receiver and R2 could be a ground-based receiver. The resulting DD removes common errors, particularly satellite clocks and receiver clocks, as well as Selective Availability. If the DD is based on carrier phase measurements, it will exhibit a term based on the sum of the ambiguity terms from each individual carrier phase. If the DD is based on pseudorange, there will be no ambiguities unless the receivers have not been calibrated.
Alternate approaches form a range-like carrier phase, which will be influenced by clocks. In this case, terms that represent the clock variations are included in the set of parameters to be estimated in the orbit determination process.
Davis [1996], using a high fidelity simulation of the 700 km GLAS orbit, compared the orbit results obtained from the explicit formation of double differenced phase and from the stochastic treatment of clocks, as well as the kinematic solution. In all cases, the methods that modeled the satellite dynamics performed better than the kinematic, and the results of evaluating different processing strategies in the dynamic mode yielded comparable accuracies (1-2 cm radial and <10 cm horizontal).
In spite of expectations that SA may be “turned off” in the future, the prudent analysis approach for future space missions retains the ability to eliminate SA effects. The approaches described here essentially remove or accommodate SA and will, furthermore, function in the presence of SA as well as without SA.
Some LEO satellites, particularly those carrying altimeters, require the orbit to be known with centimeter-level accuracy in the radial component. Some of these satellites have horizontal accuracy requirements also (along-track and cross-track) at the decimeter-level. For the altimeter satellites, the orbit accuracy requirements are further stated within the context of a stable reference frame. In these applications, the evolution of the reference frame used over a series of satellites, perhaps spanning a decade or more, must be known to correlate results obtained with one satellite to those obtained with a follow-on satellite. The reference frame requirements are presently being met by the International Rotation Service (IERS) through the IERS Terrestrial Reference Frame (ITRF), as described by Boucher et al. (1994). The long term operational stability of the reference frame with complete geodetic monitoring is an essential part of altimetric missions that use multiple satellites and will span 10-20 year periods.
A global network of GPS receivers is required to support centimeter-level POD. The network currently organized under the International GPS Service for Geodynamics (IGS) includes approximately 100 sites. Of these sites, approximately 30-40 well-distributed sites are required to support GPS POD for a LEO satellite. Additional network requirements include high stability for the ground receiver antenna, common antennas with
well-determined characteristics, and low site multipath. For some LEO applications, the ground receiver data should be available within 24-36 hours.
Two frequency receivers are required for both ground receivers and the LEO satellite for removal of ionosphere effects. Furthermore, the receivers must measure both pseudorange and carrier phase on both frequencies. A further receiver requirement is the ability to track at least eight GPS satellites simultaneously, although the ability to track 12 satellites is desired.
The TurboStar receiver used on MicroLab I and WakeShield (WSF-02) is a dual frequency receiver that uses a cross-correlation technique to obtain the L2 measurements. Although the technique has been demonstrated to provide high precision measurements, the technique produces a noisier measurement under AS conditions compared to P-code tracking. At low elevations, the better signal-to-noise ratio offered by P-code tracking is preferred. With these considerations, it is desirable that AS be deactivated, except in periods of national emergency.
Although the techniques described previously remove the effects of SA to a high level of accuracy, deactivation of SA, except in periods of national emergency, is desirable because of the improvement for real time positioning. From the user equipment view, this is the simplest and least expensive solution to obtain 10 meter level positioning in real time. The meter level positioning offered by differential corrections complicates the hardware and software for the LEO satellite, but deactivation of SA would enable 10 meter level positioning with no change in hardware. The high precision (centimeter-level) applications do not, at present, have real-time requirements at this level. Those application requirements are met with delays of 24-36 hours or longer.
Real-time operations that require positions from GPS can be conducted with the GPS ephemeris information broadcast by the satellites. The centimeter-level requirements will use the GPS orbits produced by the IGS Analysis Centers, but the T/P experience showed that the most accurate results were obtained when the GPS orbits were determined simultaneously with the orbit of the LEO satellite. In some applications, there may be requirements for the production of the LEO satellite ephemeris to support other data products.
The T/P GPS demonstration experiment provided data for study of issues related to the development of techniques and procedures to achieve centimeter-level positioning accuracy on future satellites, especially altimeter satellites. Techniques have been developed that enable determination of the orbit of a LEO satellite to the centimeter-level in the radial component and better than 10 cm in the horizontal components. These techniques remove the effects of SA to achieve this level of accuracy without access to classified information. Furthermore, the global network of IGS stations and the reference frame developments conducted within the IERS should, in principle, support the future needs for centimeter-level POD.
A variety of techniques have demonstrated the ability to meet the requirements. Studies have shown that dynamical techniques provide greater accuracy than kinematical techniques; however, force model improvements are usually required to support the dynamical approaches. Depending on the LEO satellite characteristics and its orbit, an adjustment of the gravity field and nongravitational parameters may be required. Such adjustments, however, have been shown by analysis of T/P data and simulations to be the preferred approach.
The centimeter-level accuracy requires use of dual frequency GPS receivers for removal of the ionosphere, even for the LEO satellite. Additional requirements include measurement of pseudorange and carrier phase, with the latter measured to a precision of a few millimeters. These measurements should be simultaneously collected from at least eight GPS satellites. Current techniques for making measurements on the L2 frequency are acceptable; however, deactivation of Anti-Spoofing is preferred to provide a more robust signal at low elevations.
Although the analysis techniques remove the effects of SA, deactivation of SA is desired to support real-time activities at minimal cost. For example, the precision pointing of an instrument requires knowledge of both satellite position and spatial orientation. Improved positioning at the 10 meter level would stimulate new developments in such areas.
Boucher, C., Z. Altamimi, L. Duhem. 1994. Results and analysis of the ITRF-93, IERS Tech. Note 18, Observatoire de Paris, Paris.
Davis, G. 1996. GPS-based precision orbit determination for low altitude geodetic satellites, Ph.D. dissertation, The University of Texas at Austin, May 1996.
Hofmann-Wellenhof, B., H. Lichtenegger, J. Collins. 1992. GPS Theory and Practice, Springer-Verlag, Wien-New York, 1992.
Melbourne, W., E. Davis, T. Yunck, B. Tapley. 1994. The GPS flight experiment on TOPEX/POSEIDON, Geophys. Res. Letters, Vol. 21, No. 19, 2171-2174, Sept. 15, 1994.
Schroeder, C., B. Schutz, P. Abusali. 1996. STS-69 relative positioning GPS experiment, to appear in the Proceedings of the AAS/AIAA Astrodynamics Meeting, Austin, TX. (Conference Paper AAS 96-180).
Schutz, B., P. Abusali, C. Schroeder, B. Tapley, M. Exner, R. McCloskey, R. Carpenter, M. Cooke, S. McDonald, N. Combs, C. Duncan, C. Dunn, T. Meehan. 1995. GPS tracking experiment of a free-flyer deployed from space shuttle, Proccedings of ION GPS-95, Vol. I, 229-235, September 1995.
Schutz, B., B. Tapley, P. Abusali, H. Rim, 1994. Dynamic orbit determination using GPS measurements from TOPEX/POSEIDON , Geophys. Res. Letters, Vol. 21, No. 19, 2179-2182, Sept. 15, 1994.
Ware, R., M. Exner. 1995. GPS sounding of the atmosphere from low Earth orbit: preliminary results, submitted to Bulletin of the American Meteorological Society, 1995.
Yunck, T., W. Bertiger, S. Wu, Y. Bar-Sever, E. Christensen, B. Haines, S. Lichten, R. Muellerschoen, Y. Vigue, and P. Willis. 1994. First assessment of GPS-based reduced dynamic orbit determination on TOPEX/POSEIDON, Geophys. Res. Letters, Vol. 21, 541-544, April 1994.
Kevin Leaman
Division of Meteorology and Physical Oceanography
Rosenstiel School of Marine and Atmospheric Science, University of Miami
INTRODUCTION
The use of, and requirements for DGPS in oceanography are strongly conditioned by the type of observations being made and by the scale of phenomena under investigation. Under the general heading of oceanographic observations we may include physical, chemical, biological and geological/ geophysical data; however, the author's own back-ground will inevitably slant the discussion toward ocean physics.
For much of its history sea-going physical oceanography has consisted mainly of obtaining hydro-graphic station data at various locations in ocean basins, from which circulation patterns and relative (geostrophic) velocities and transports could be inferred. The latter requires a knowledge of station positions to an accuracy which depends on the scales observed, and on geographic location. For example, a large-scale WOCE (World Ocean Circulation Experiment) hydrographic grid in the North Atlantic Ocean, whose stations may be separated by hundreds of kilometers, need not in absolute terms be positioned as accurately as a small-scale hydrographic grid over some tens of kilometers to study so-called “spin-off eddies” from the Gulf Stream. Also, the effect of station position errors on computed geostrophic velocities is magnified near the equator due to the smallness of the Coriolis parameter.
One of the earliest applications of (non-Differential) GPS in physical oceanography was to improve position accuracy of stations made in, for example, the Somali Current of the Indian Ocean, where other means of continuous electronic navigation such as LORAN-C were unavailable and where dead-reckoning between satellite fixes could be quite inaccurate. The availability of accurate GPS navigation has also clearly been of use in tasks such as returning to fixed locations to recover current meter moorings anchored to the bottom. However, here too it is simply necessary to get within one kilometer or so of the true location; from that point the ship can (usually) easily find the mooring using acoustic tracking and listening for the mooring's acoustic pinger. In other words, standard GPS data (with no differential corrections) were adequate.
Over the past one to two decades considerably more effort in physical oceanography has been devoted to measuring absolute, as opposed to relative geostrophic, horizontal ocean currents. A major reason for this is that earlier assumptions (such as a “level of no motion”) used to reference relative geostrophic currents could cause large errors in the computed transports (of mass, and thereby of other even more important quantities such as heat) of ocean currents. For example, a systematic offset of 1 cm/s in the southward flow of the Deep Western Boundary Current east of the Bahamas, which extends over 4 km depth and offshore for roughly 100 km, would produce a 4x106 m3/s error in transport, an amount which is more than 10% of the northward transport of the Florida Current at that latitude. As described briefly below, different devices have been developed to make these observations, including acoustic Doppler current profilers (ADCP's) and acoustically tracked current probes (e.g. oceanic “weather balloons”) such as PEGASUS (Spain et al, 1981). Regardless of the device used, the goal of measuring absolute horizontal ocean currents to an accuracy of order 1 cm/s or better imposes navigational requirements which can only be met by GPS or, increasingly, DGPS. In fact, with a few exceptions (e.g. Dzieciuch and Munk, 1992) virtually all applications of GPS or DGPS in physical oceanography have been in pursuit of this goal.
ADCP's have been mounted to subsurface moorings (shooting up to the surface), to ship hulls (Griffiths, 1994), to towed bodies (Münchow et al, 1995) and to conductivity/temperature/pressure (CTD) probes lowered from vessels (Firing and Gordon, 1990). Regardless of the configuration, all ADCP's use multiple acoustic beams to measure Doppler shifts in the acoustic signal induced by ocean current flow past the transducer faces. By combining results from the different beams and gating return signals to different ranges from the transducer faces it is possible to generate an ocean current profile relative to the transducers over ranges of several hundred meters, depending on the volume of
backscatterers in the water. Clearly, to obtain absolute velocities the transducers themselves must be navigated, which is now typically being done by GPS in the case of Lowered (by cable) ADCP's (or LADCP 's; Fischer and Visbeck, 1993; Hacker et al, 1996; Wilson, 1994). There remain a number of open questions regarding the accuracy of this approach, particularly since it is really the attending research vessel and not the LADCP instrument package (which may be suspended from the vessel by several kilometers of cable) that is being navigated by GPS. In general, DGPS has not been used in these applications. Although the reasons for this are not clear they no doubt stem in part from the difficulty in obtaining DGPS corrections at sea, although some work using DGPS with ADCP's deployed from towed bodies behind a vessel has been done (Münchow et al, 1995).
“Local” (that is, attitude sensing) DGPS has also been used to track ship headings to provide direction for water speeds measured by hull-mounted ADCP's (Griffiths, 1994). Although in principle the 3DF GPS (Ashtech) used by that author could also provide information on pitch and roll, in practice the internal pitch and roll sensors in the ADCP are used instead.
Over about the past 15 years acoustically tracked probes which follow the current as they fall to a pre-determined depth or the bottom (where they release ballast weights) and then make a return ascent through the water column have been developed to measure absolute ocean currents (Spain et al, 1981). These devices have been deployed in a wide range of experiments (see, for example, Leaman et al, 1987). Earlier versions of these systems used at least two acoustic transponders which were deployed to the ocean bottom and whose positions were accurately determined by the attending research vessel. The geometry of the transponder array, along with the pressure measured by the probe as it “pings” on the transponders while descending or ascending allow one to track the probe and thereby generate a vertical profile of absolute horizontal ocean currents. This method can meet the ~1 cm/s accuracy stipulated above. However, the method suffers from several drawbacks, among which are: a) once deployed, stations cannot be moved; b) a considerable investment of expensive ship time is needed to survey the transponder locations; and c) the most expensive part of the system --the acoustic probe -- is at the greatest risk of being lost.
With these considerations in mind we began several years ago a project in collaboration with the Colorado Center for Astrodynamics Research (CCAR) to develop a GPS-based acoustic current profiler (dubbed “Fast PEGASUS” or “Polaris”). In this system the bottommounted acoustic transponders are replaced with two surface buoys (one of which can actually be the research vessel) that listen for and range on an actively pinging acoustic probe as it falls through the water column (Leaman, 1991). The whole system is “dynamic” in the sense that both the probe and the tracking buoys are in motion relative to a coordinate system fixed to the Earth (Fig. 1).
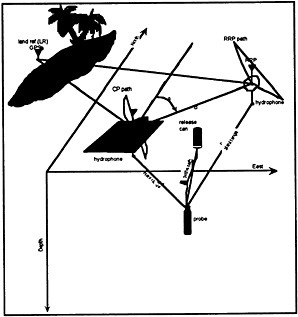
FIGURE 1 Arrangement of Fast PEGASUS land reference GPS station and two “roving” GPS receivers which form the acoustic baseline for the observation site at sea..
To obtain absolute velocity profiles the probe is tracked acoustically relative to the surface-drifting buoys and the buoys themselves are tracked using internally mounted GPS/DGPS receivers. These buoys are designed as modified spars with an acoustic receiver (hydrophone) at the bottom and GPS and data telemetry antennas at the top (Fig. 2).
The accuracy requirement stipulated above dictated that the buoy positions would have to be tracked at least in relative terms to at least a 1m rms position accuracy over the duration of the profile and that relatively frequent (e.g. once every two seconds) position samples would have to be obtained. This latter requirement in turn dictated that we would have to establish our own land reference station at the Rosenstiel School of Marine and Atmospheric Science (which was done) since the 30-second sampling rate of the Continuously Operated Reference Stations (CORS) was not rapid enough.
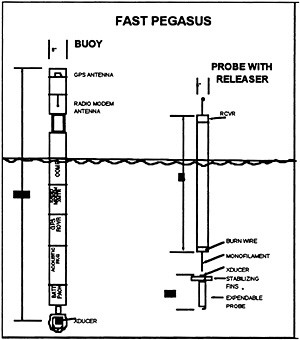
FIGURE 2 Construction of the drifting acoustics/GPS buoy and the acoustic probe. The probe is released from the surface remotely by a radio signal from the research vessel.
The magnitude of the contributions to the apparent measured velocities caused by certain effects such as changes in ionospheric propagation delays was at first unclear. Therefore, initial tests were carried out using highly accurate Trimble SSE receivers at both buoys and at the land reference station (Leaman and Rocken, 1994; Leaman et al, 1995). These are dual frequency p-code receivers capable of storing carrier phase information as well; however, in addition to their high cost they are not particularly well suited to deployment from sea-going buoys, in part because of their size. The SSE can also do cross-correlations to preserve delay information in the presence of Anti-Spoofing (A/S). It was judged that the capabilities of these receivers along with the use of a land reference station to provide DGPS capability -- primarily to remove the “dithering” of position introduced by the “Selective Availability” policy (S/A) of the Dept. of Defense -- would be more than sufficient to provide our required level of accuracy.
This turned out in fact to be the case, and absolute velocity profiles were successfully obtained in the Florida Current east of Miami ( Fig. 3; Leaman et al, 1995). It should be noted in Fig. 3 that the variability seen between the up and down portions of the profile is typical of this location. Because of the high vertical and lateral current shears found in this region the probe never “sees” the same water parcel on the way down as on the way up (note also the change in scale between the u and v components). In fact, as a result of these measurements it was found to be unnecessary to use the carrier phase information. Although these trials were successful, questions still remained as to what extent the GPS component could be “pared down” to make use of less expensive (and less complex) receivers. In particular, the following questions arose:
-
Could a C/A code receiver with carrier phase data (which at the time of the initial trials did not exist on the market) approach the accuracy of the p-code receiver in our particular application?
-
How large are apparent velocities induced by changes in ionospheric propagation, and can these effects be removed or reduced when using a single-frequency receiver?
-
Do we need a land reference station?
-
Can we achieve the desired level of accuracy using 30-second DGPS corrections (we had assumed earlier that this was the case; however, we had not actually tested this)?
To answer these questions a series of experiments was carried out at the Rosenstiel School, University of Miami in the summer and fall of 1995 (Key et al, 1996). Based on this work, the answers to these questions can be briefly stated.
-
Yes. The more recently available NovAtel single frequency receivers with carrier phase data appear to be adequate.
-
These apparent velocities are quite small (significantly less than 1 cm/s) and their relative contribution can be removed or reduced using the “Differenced Range Versus Integrated Doppler” (DRVID) algorithm (Key et al, 1996).
-
Yes. In particular, such stations will be needed as long as S/A is implemented. However, even after such time as S/A may be removed, use of a land reference station will probably be advisable in order to insure the quality of the measured velocities since, for example, any “common mode” GPS errors (between buoys for example), whether they arise from S/A or from other causes, can be removed.
-
No. It appears that too much variability is present in the 2-30 second period range. However, since at
-
least some of this variability arises from the presence of S/A in the signal, this question should probably be re-visited (S/A was on when these tests were conducted).
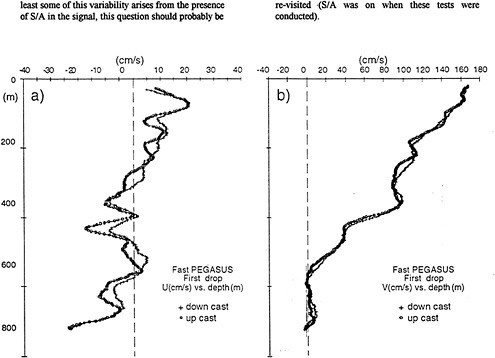
FIGURE 3 Example of absolute velocity data (u=east; v=north) obtained in the Florida Current by the POLARIS acoustics/GPS velocity profiler. Most of the differences between the up and down profiles are caused by natural variability in the current structure (see text).
We are in the process of refining the design of this system with the expectation that it will be used in upcoming oceanographic field experiments such as North Atlantic WOCE. This mainly involves installing a better data acquisition computer (PC-104 type) on board the buoys and feeding the acoustic range data into the GPS data stream. We anticipate that this step will allow us to generate effectively “real-time” velocity profiles, in particular if a standard grid of land reference stations can provide DGPS data to the ship in a timely manner and at a sufficiently high data rate when needed. It should be noted that these reference sites do not have to be particularly close to the locations where we are making the profiles. Since we are concerned only with velocity information and are relatively unconcerned about any bias introduced by long baselines (as long as that bias does not change appreciably over the duration of a drop), our range from the land reference is limited mainly by the common visibility of the satellite constellation (which should contain enough common satellites at ranges less than, say, 2000 km). However, any DGPS support framework should be able to respond rapidly to shipboard
data requirements; that is, it should be flexible enough to respond to requests for, for example, higher sampling rates during a period when a ship is actively involved in making observations which require those higher rates. Clearly, in some areas of the world we will for the foreseeable future be required to do our own referencing, since in those areas there are no networks of land-based GPS sites.
We are also investigating other possible applications of this combined acoustic/DGPS navigation and tracking system beyond its use with velocity probes. As one example, the multi-channel acoustic receivers used on the buoys (currently there are four frequencies, but this is expandable) could be used to track small clusters of neutrally buoyant floats. (Sometimes called RAFOS floats, these are subsurface drifters designed to sink to a pre-set depth and then drift with the currents at that depth). Such arrays would be of value for example in small-scale turbulent dispersion experiments.
Dzieciuch, M. and W. Munk, 1992. Interpretation of GPS offsets from a steady course, J. Atmos. Oceanic Technol., 9, 862-866.
Firing, E. and R. L. Gordon, 1990. Deep ocean acoustic Doppler current profiling, Proc. Fourth IEEE Working Conference on Current Measure-ments, Clinton, MD, Current Measurement Technology Committee of the Ocean Engineer-ing Society 192-201.
Fischer, J. and M. Visbeck, 1993. Deep velocity profiling with self-contained ADCPs, J. Atmos. Oceanic Technol., 10, 764-773.
Griffiths, G., 1994. Using 3DF GPS heading for improved underway ADCP data, J. Atmos. Oceanic Technol., 11, 1135-1143.
Hacker, P., E. Firing, W. Wilson and R. Molinari, 1996. Direct observations of the current structure east of the Bahamas, to appear in Geophys. Res. Letters.
Key, K., S. Anderson, P. Axelrad, P. MacDoran and G. Born, 1996. Analysis of Fast PEGASUS GPS equipment and algorithms, Colorado Center for Astrodynamics Research, Univ. of Colorado, CCAR Rep. No. 96-031, 27 pp.
Leaman, K.D., 1991. The use of electronic aids to navigation (GPS) to improve absolute and relative vertical current profiler measurements from ships. In: Proceedings International Sym-posium on Marine Positioning, INSMAP 90, Symposium held at the University of Miami, PIP Printing, 460-471.
Leaman, K.D., R.L. Molinari and P. Vertes, 1987. Structure and variability of the Florida Current at 27 deg N: April 1982 - July 1984, J. Phys. Oceanogr., 17(5), 565-583.
Leaman, K.D. and C. Rocken, 1994. Fast PEGASUS: An ocean current profiler using combined GPS and acoustic navigation- results of a feasibility study, EOS Trans., 75(3), 41.
Leaman, K.D., P.S. Vertes and C. Rocken, 1995. Polaris: A GPS-navigated ocean acoustic current profiler, J. Atmos. Oceanic Technol., 12(3), 541-549.
Münchow, A., C. Coughran, M. Hendershott and C. Winant, 1995. Performance and calibration of an acoustic Doppler current profiler towed below the surface, J. Atmos. Oceanic Technol., 12, 435-444.
Spain, P.F., D.L. Dorson and H.T. Rossby, 1981. Pegasus: A simple, acoustically tracked velocity profiler, Deep-Sea Res., 28A, 1553-1567.
Wilson, W.D., 1994. Deep ocean current profiling with a lowered broadband acoustic Doppler current profiler, OCEANS '94: Proceedings, Institute of Electrical and Electronics Engineers New York, 660-665.
Paul Montgomery and Bradford Parkinson
Department of Aeronautics and Astronautics, Stanford University
Biography Paul Montgomery is a Ph.D. candidate in Aeronautics and Astronautics at Stanford. He received a M.S. from Stanford in 1992 and a B.E. in mechanical engineering from the University of Melbourne in 1986. Brad Parkinson is the Edward C. Wells Professor of Aeronautics and Astronautics at Stanford. Director of GPS program. Director and co-principal investigator of Gravity Probe B at Stanford University.
Using the carrier phase of the GPS signal, one is able to resolve relative displacements in space to the centimeter level. This paper describes the use of carrier differential techniques to determine the position, velocity, attitude and angular velocity of an autonomous aircraft in real time. The full state GPS estimates are used in linear quadratic (LQ) feedback control to automate the flight of the aircraft from takeoff thru landing. We present flight data from recent flight tests. In addition to GPS, the aircraft is instrumented with a variety of inexpensive conventional sensors including alpha and beta vanes, and a dynamic pressure sensor (pitot). These provide an independent measurement of the aircraft velocity relative to the air. This independent measurement enables estimation of the the absolute wind vector, which is used in waypoint tracking. 1
INTRODUCTION
While it is possible to stabilize an aircraft with less than full state information, using GPS allows the use of linear quadratic control techniques directly, furthermore it provides the accuracy necessary to attempt a fully automatic precision landing. We used state estimates derived from carrier differential GPS measurements from onboard GPS sensors and a pitot (dynamic pressure) sensor to fly a 12 foot aircraft autonomously from take-off to landing. This was an exercise in systems integration, GPS sensing and automatic control. The current configuration uses the GPS constellation unaugmented by additional ranging sources such as pseudolites. Section 1 discusses the aircraft, aircraft modeling and the hardware configuration of our system. Section 2 briefly discusses the GPS signal processing. Section 3 discusses the estimation of the ambient wind. Section 4 discusses the control hierarchy and supervisory level of control. Section 5 presents flight data and results to date. Section 6 presents conclusions and discusses ongoing work related to the project.
The aircraft is a high wing design of balsa and plywood construction. It is powered by a 22 inch propeller driven by a 3.7 cubic inch 2 stroke ignition engine. The aircraft has conventional controls including flaps and steerable tricycle landing gear. Takeoff weight is 65 lbs. Four GPS antennae are mounted on the aircraft, located at the nose, on top of the vertical tail and on each wing tip. The aircraft flies at a nominal airspeed of 19m/s and stalls at approximately 13m/s. A schematic of the entire system, showing flight and ground hardware is shown in figure 1. The ground segment consists of the reference GPS receiver attached to a radio modem and the ground-station computer. The computer displays real time telemetry from the flight hardware, a summary of the uplinked reference phase data, and provides the ability to uplink flight commands or control laws to the aircraft. A critical item of the ground hardware is the radio control (RC) transmitter, which allows a human pilot to override the flight computer and assume manual control if necessary. This feature was used routinely during system development and debugging. The air hardware consists of two GPS receivers, a 486 single board computer (SBC), a 68332 based microcomputer and two radio modems. The GPS receivers are signal processor boards from Trimble TANS units
|
1 |
Presented at Institute of Navigation. National Technical Meeting. January 1996, Santa Monica Ca. |
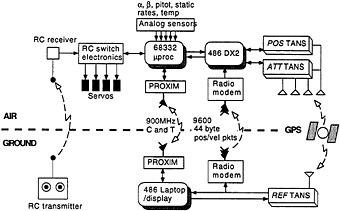
FIGURE 1 System schematic.
with customized embedded software. One GPS receiver is dedicated to generating raw phase data for position and velocity, the other for attitude and angular velocity. The raw phase data from each unit is packetized and serially transmitted to the 486 at 10 Hz. Each phase packet from the attitude TANS is processed to generate an attitude and angular velocity datum. Each phase packet from the position TANS must be combined with reference phase data with a matching time stamp from the reference station receiver to generate a position and velocity datum. The reference station data are received over the radio modem that is serially connected to the 486. The 68332 microprocessor is used to interface to the analog electronics for alpha, beta and pitot measurements. It presents these data serially to the 486 along with RC commands read from the RC receiver. The 68332 also transmits a summary of the analog and processed GPS data to the groundstation at 5 Hz over the second radio modem link. The 486 assembles the raw GPS data and processes it to estimate the position, velocity, attitude and angular velocity of the aircraft. Using the GPS and pitot data a feedback control law is calculated. The feedback control vector is output to the servos via the 68332 if the RC pilot has enabled computer control. Actual output to the servos is a sum of the RC pilot inputs with the computer generated control. This allows the pilot to exert some authority at all times if only to perturb the system momentarily, and simplifies such details as establishing trim. During flight, the raw GPS, analog and RC data is stored in onboard RAM for subsequent download. Replaying this data in post-flight processing allows the earlier flight to be reconstructed in detail.
Aircraft modeling A linearized math model of the aircraft was used for the control synthesis. This model was generated analytically rather than from system or parameter identification. Non-dimensional aerodynamic stability derivatives were estimated using a vortex panel model of the aerodynamic surfaces at nominal airspeed and angle of attack. Non-dimensional thrust characteristics of the propeller were similarly modeled. Engine/propeller experiments were performed at the nominal airspeed to determine engine rpm as a function of throttle setting. Mass and inertia properties were experimentally determined to within 10 percent. The gain of the servos from input (ms) to output (control surface motion in deg) was experimentally characterized for each control surface. The flight control surfaces are mechanically actuated by short pushrod linkages which are mechanically arranged for best linearity, servo authority and minimum deadband, while providing adequate control surface motion. The throttle servo uses linkage nonlinearity to advantage to approximately re-linearize the non-linear engine rpm response to throttle near idle. The resulting gain of the engine from throttle input (ms) to rpm has been generated experimentally during flight.
The above data were used to generate a perturbation model for the lateral and longitudinal modes, which decouple to first order. The longitudinal state may be conveniently represented as [u w q θ]T representing perturbations from nominal in forward airspeed, downward airspeed, pitch rate and pitch angle respectively. The lateral state may be similarly represented as [v r p ϕ]T, representing perturbations from nominal in sideslip (lateral airspeed), yaw-rate roll-rate and roll angle. The resulting linearized model reveals the well known aircraft modes [2]. Both phugoid and dutch roll are lightly damped oscillatory and require stability augmentation. Phugoid has a period of approximately ten seconds and dutch roll a period of approximately three seconds. The longitudinal short period (weathervane) mode has a period of approximately one second and is well damped. The spiral divergence mode is slow and marginally stable but also in need of stability augmentation.
In all differential carrier techniques, one is measuring the distance between a pair of GPS antennae. The beauty of this technique is that the GPS carrier provides a suitably short ‘yardstick' to allow subcentimeter precision in the measurement, and due to its differential nature, common mode error sources cancel exactly. With GPS carrier differential positioning, two separate receivers are necessary, requiring the solution of their relative clock offset in addition to the three components of their cartesian displacement. These four unknowns require a minimum of four measurements for solution. This in turn dictates that a minimum of four satellites be simultaneously tracked by both the air and ground receivers. The six-channel TANS receivers al-
low upto six satellites be simultaneously tracked. This provides a potentially overdetermined set of position equations which may be solved in a least squares sense. With GPS attitude, the locality of all antennae allows the use of a common clock. In this case the relative clock bias is zero by design, allowing its elimination from the solution vector entirely. The three remaining degrees of freedom in attitude are solved in a least squares sense. The body-fixed vectors between one antenna (designated master) and each of the other antennae are called ‘baselines'. The raw attitude measurements are the observed differential phases across each baseline for each satellite in track. With three baselines and a six channel receiver there are upto eighteen measurements to resolve the three degrees of attitude freedom [1].
The common problem in all carrier differential techniques is the determination of the so called ‘integer cycle ambiguities'. The raw measurement available from the receiver is the fractional portion of the carrier phase between two antennae, projected onto the line-of-sight to the observed satellite. The (generally time invariant) integer portion of this inner product is unknown and must be determined in some manner before the GPS data can be used for position or attitude calculation. This is called the integer cycle ambiguity problem.
For our determination of position, the integers are not found, but rather defined by placing the air and reference antennae in a known (pre-surveyed) relative position prior to takeoff. The clock bias difference is taken from the pseudo-range clock bias estimates at each receiver. Once these integers are known, our problem becomes one of maintaining carrier lock on satellites during flight.
The attitude integer resolution problem is somewhat more difficult due to the greater number of integers to be found, one for each satellite/baseline combination. Once again, it is possible to find these integers by placing the antenna array in a known orientation and solving for them explicitly. In practice, our aircraft is about the largest array where this is easy, requiring orientation accuracy within ±5 degrees about each axis for a worst case relative satellite orientation. Given that the true attitude at initialization is approximately known, this difficulty may be somewhat reduced by using the phase sensitivity to perturbations about the initialization state. This allows acquisition of the least sensitive integers first, and subsequent refinement of the initial guess. This method is suitable for integer determination prior to takeoff. To determine the attitude integers in flight requires a more sophisticated motion based technique. An elegant motion based technique described in [1] is not suitable in our case due to a nearly planar baseline array. We make use of an integer resolution technique developed at Stanford which works for planar arrays and in cases of severe antenna occlusion [9]. With this technique we have been successful in achieving reliable integer resolution during flight and even in cases where an entire baseline has been removed.
With a known position or attitude, it is possible to solve for the integers of new satellites as they come into view during flight by using the solution equations in reverse. This process, called ‘patching ', presents a number of problems which can cause the position integrity to degrade over time.
-
At least 4 common satellites must be visible at all times to both the air and reference receivers in order to retain position integrity. During banking turns, the probability that low elevation satellites will be occluded at the flight receiver is high. At best, this will reduce the geometric strength of the position solution.
-
In solving for the cycle integer of a newly acquired satellite, the projection of the position error along the line-of-sight to the new satellite must be less than one half cycle of the GPS carrier. If this is not the case then the patched integer will be rounded to an incorrect and inconsistent integral value. This will result in a position error which grows with time, proportional to the initial error. This error will tend to propagate into the other integers over time, particularly if patching is frequent.
-
With correct integers, the position solution is good to approximately 1cm multiplied by PDOP. In cases where the geometry is weak and PDOP is large, this effect alone may account for a half cycle (10 cm) position error.
In practice, these problems are obstacles to the robustness of our positioning technique. Since the focus of our work is GPS as a sensor for automatic control rather than robustness, our current solution is to fly at times when there are 4 or more satellites above 25 degrees of elevation and to constrain banking during turns to less than 25 degrees. We have had success with this approach, but a more robust solution would be to augment the system with at least one pseudolite seen continuously by both air and ground receivers. Such an addition would also aid the geometric dilution of precision in the vertical direction. Unfortunately, adding a pseudolite also adds to the complexity of setup and surveying required, as well as introducing non-linearity and near-far issues. Another approach would be to use a roving antenna which always has view of the sky.
Position is calculated relative to the reference receiver antenna in a differential manner. One has two antennae, typically one on the ground (the reference station)
and one on the object being sensed. Each antenna looks at several common satellites. There will be a phase difference in the signal measured between the antennae. This phase difference will come partially from the distance between the two antennae in the direction of the satellite (si· Δx) and partially from the time offset in the local clocks. In matrix form and ignoring noise, one has the following equation:
where ΔΦi is the difference between the measured phase at the air receiver and the reference receiver and Oi is the determined integer cycle ambiguity. By observing n satellites, one gets several of these equations, and may build a (possibly over-determined) matrix equation which an be solved in a least-squares sense to find Δx and τ provided n ≥ 4:
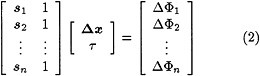
In practice, timing errors make this process a little more complex [6], but equation 2 illustrates the essence of the method.
With carrier differential GPS, the fundamental observable is the phase of the GPS carrier, beat against the receiver local oscillator. This may be processed as shown above to yield a measurement of position. To extract a velocity measurement one must effectively differentiate this (noisy) phase or position signal.
Velocity and angular velocity solutions are calculated using phase-rate measurements strobed from the receiver's phase tracking loops at 10 Hz. The differentiation is achieved at the lowest signal processing level within the receiver by filtering the fundamental beatphase measurements against a steady state Kalman filter. The Kalman filter is based on an assumed second order kinematic model, and has bandwidth set to accommodate the expected vehicle dynamics. The phaserate measurements are output quantized in units of 6mm/s (0.03 Hz). In practice, using the current tracking loops within the TANS, the noise in the velocity solution is comparable with that which would be achieved by a first difference of the position solution, however avoids the delay associated with a first difference. To minimize the noise in this measurement, the tracking loop bandwidth of the reference receiver should be limited to that necessary to track the reference signal. The noise in the position and velocity solution may also be reduced by modifying the low level estimator in the flight receiver to more accurately reflect known vehicle dynamics.
Differentiating equation 2 with respect to time, gives
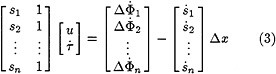
Where the (constant) integer ambiguity term has vanished and ![]() is the result of differencing the phase-rate measurements from the air and reference receivers. The matrix on the left hand side of the equation has not changed since the position calculation. Its derivative on the right hand side contributes only a very small correction term which may be readily calculated by interpolating the line of sight vectors. Once again, timing errors, omitted here, make the analysis a little more complex but add little conceptually.
is the result of differencing the phase-rate measurements from the air and reference receivers. The matrix on the left hand side of the equation has not changed since the position calculation. Its derivative on the right hand side contributes only a very small correction term which may be readily calculated by interpolating the line of sight vectors. Once again, timing errors, omitted here, make the analysis a little more complex but add little conceptually.
The attitude and angular velocity calculations are simpler in that the time bias term exits the equations entirely due to the use of a common oscillator. The signals actually measured (after accounting for the differences in antenna cable lengths) are given, ignoring noise, by the equation
Øij= bi· A · sj− kij (4)
Here bi is the vector distance between the master antenna and slave antenna i as measured in the body basis (called baseline i). sj is a line-of-sight unit vector to satellite j expressed in the reference frame (East-North-Up in this application), kij are the cycle integers, which we will here assume to be known, and A is a rotation matrix that maps vectors between the East-North-Up reference frame and the body frame in which the baseline vectors bi are known. Note that a vector dot-product notation is used rather than a matrix-multiplication notation, making it clear that a scalar is being produced.
The task is to determine the rotation matrix A which uniquely specifies the attitude. Updating attitude at 10 Hz, the difference in attitude from one timestep to the next is small, and the local linearize and (linear least squares) solve approach proposed by [1] works well in practice. During operational attitude, we also solve for wing flexure by augmenting the solution vector with an additional wing flexure state. This is important since wing flexure upto 0.25 cycles has been observed in flight tests. An estimate of the body referenced attitude error covariance is available as a by-product of the least-squares or weighted least squares solution.
Differentiating the above equation, and making use of the fact
A = −[ω×] A (5)
where [ω×] is the skew-symmetric cross product matrix formed from the (baseline array) angular velocity vector. Ignoring the ṡ term as negligible, one has the scalar equation for the baseline array angular velocity
Øij= −sj·AT[bi×] · ω (6)
There may be upto #baselines × #channels such scalar equations. These are stacked to form an overdetermined set of linear equations in ω which is then readily solved in a linear least squares or weighted least squares sense. The angular velocity solution is unbiased and has an RMS noise that scales with baseline length [8]. With our baselines, experimental results with a stationary array indicate an RMS additive noise of less than 0.3 deg/s about each axis. The angular velocity solution is dependent on the attitude solution, and in our code is calculated subsequent to it, making use of the significant matrix factorization (cholesky decomposition) already completed. Where structural flexure is significant as it is in the aircraft, one should also account for the flexure rate. It may be shown the symmetric mode flex-rate is observable, but anti-symmetric mode is not.
With current software, a new attitude and angular velocity solution is calculated every 100ms, as soon as new phase becomes available from the attitude receiver. Due to uplink latency of approximately 50ms, position and velocity solutions are calculated subsequent to the attitude/angular velocity calculation, as soon as timestamps from the local and reference position receivers can be matched. The aircraft position and velocity vectors, originally calculated in ENU, are subsequently expressed in runway relative and body relative bases respectively, using the known runway azimuth and the current attitude estimate. The aircraft position and velocity are finally corrected (using the attitude and angular velocity) for terms due to the moment arm between the tail mounted position antenna and the aircraft CG. Control is recalculated immediately each time a new attitude solution becomes available.
The use of alpha and beta vanes in addition to GPS enables estimation of the absolute wind vector. GPS provides a measurement of the aircraft attitude and absolute velocity in the ENU basis. The pitot alpha and beta measurements measure the aircraft's air-relative velocity in the aircraft body basis. Using the known attitude, this air-relative velocity may be expressed in the ENU basis. The difference between the two velocity vectors in ENU is attributable, ignoring noise to the ambient air movement. We use the above technique to estimate the ambient wind at the GPS update rate. In using the alpha and beta vanes, one desires to measure
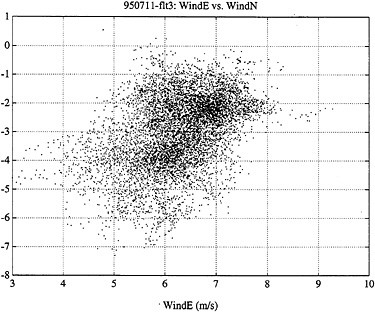
FIGURE 2 Unfiltered wind data from a 10 minute flight.
the free stream incidence angles, it is important therefore to remove the effect of the aircraft itself on the flow field at the point of measurement. A smaller correction is due the velocity at the vanes induced by the angular velocity of the aircraft. A scatter plot of East and North components of unfiltered flight data taken over a ten minutes is shown in figure 2. As would be expected, the wind shows variation about a nominal direction and strength. It is also instructive to plot the average wind vector as a function of altitude. In many of our flights, this revealed significant wind-shear in the first 500m of altitude. Any aircraft instrumented as described above becomes a probe, able to record the wind profile of the atmosphere it flies thru. This sort of data would certainly be of value to air traffic controllers if it could be collected and transmitted by aircraft on approach or departure. Since downbursts are characterized by a recognizable wind shift profile, such data could provide information important for a downburst detection or early warning system.
The aircraft linearized state model described in section 2 was augmented with altitude, heading and localizer states and discretized for a sample rate of 10 Hz, corresponding to the control update period of the GPS system. This sampling rate is adequate to handle the aircraft dynamics with a comfortable oversampling margin.
Control laws were designed using LQ synthesis [2] for the following primitives:
longitudinal
-
airspeed hold
-
altitude hold
-
glideslope hold
-
flare
lateral
-
bank angle hold
-
heading hold
-
localizer hold
-
runway centerline hold for ground tracking
These control laws use the the full state information derived from GPS, and airspeed from the pitot sensor. A general control law of the form
u = −C * (x − Nxr) − Cixi + Nu * r (7)
was used, allowing state feedback (C), command feedforward (Nx & Nu) and integral error feedback (Ci). u is the resulting control vector. Command inputs r were injected using either command feedforward or by introducing the commands as offsets in the integral error states. Airspeed hold is achieved by fixing the throttle to be either maximum (for climb) or minimum (for descent), and using elevator to control airspeed. Altitude/airspeed hold is achieved by regulating integral errors on altitude and airspeed using throttle and elevator. Glideslope hold uses the same control law as altitude hold, but regulates to an altitude that is a function of the approach geometry. Flare is achieved by switching to a mode where the aircraft attempts to regulate the integral error from a commanded altitude trajectory using only elevator. Throttle is set to minimum. Since the aircraft cannot hold altitude without throttle, integrator windup causes the aircraft to flare just prior to touchdown and ultimately stall. For landing, the desired trajectory is a quadratic flare which transitions from glideslope to touchdown.
Bank angle hold is achieved by command feedforward and state feedback to aileron and rudder. A constant bank angle is commanded while regulating the sideslip velocity to zero. The yaw rate commensurate with the commanded bank angle of 25 degrees is approximately 10 deg/s. Heading hold is achieved by regulating the integral error from the commanded heading to zero while commanding a zero bank angle. Localizer hold is achieved by regulating the integral tracking error to zero, while commanding a zero bank angle. This forces the aircraft to crab into the wind to counter any crosswind component. Runway centerline tracking is similar to the localizer hold, but uses a steerable nosewheel rather than the lateral aerodynamic surfaces. The control modes together represent the primitives that are used in a hierarchy to perform the commands presented by a supervisory level of control. An example of the lateral control hierarchy is a turn to track on a new heading. After being instructed to track a new heading, first a bank angle hold is used to turn toward the desired heading. When within a tolerance band about this heading, the heading hold mode is entered. While in heading mode, a heading command is chosen to ensure the aircraft will converge with the specified tracking path, accounting for the ambient wind. Finally, when in proximity to the specified track, the tracking mode is entered. A similar hierarchy exists for the longitudinal control. When switching between modes, to avoid the potential problem of limit cycle behaviour, a simple hysteresis scheme was used. This hysteresis makes it more difficult to re-enter a lower level in the hierarchy once a higher level has been achieved. Another potential problem results from the use of integral states. When switching control modes, the physical interpretation of the integral states may alter. For example, what was an integral state on heading error may become an integral state on tracking error. The new integral states can be initialized to any value. One reasonable choice is to initialize the new integral states to achieve continuity of the controls across the mode switch. Other choices can excite transients and result in less desirable behavior.
A waypoint architecture is used to parameterize the desired flightpath of the aircraft. A number of waypoints forming a closed path are specified, originating and terminating at the known runway initialization point. The waypoints are specified runway relative, and then rotated or reflected according to run-way azimuth and the active traffic pattern direction. Figure 3 illustrates the flightpath that was specified for the auto-takeoff to landing experiments. It consists of two rectangles aligned on their common edge with the runway. The smaller circuit was navigated after takeoff and prior to landing to keep the aircraft close enough to enable manual recovery in case of an engine failure. The runway azimuth is 120 degrees from true North, and right traffic is employed. The small circles in the plot represent waypoints that were preprogrammed into the flight computer. In addition to a runway relative location, the heading from the preceding waypoint and altitude, each waypoint has associated with it a “turninit' value. The turninit value specifies the distance from the waypoint when the aircraft should commence a turn towards the following waypoint if there is no wind. The turninit value assumes a circular arc between adjacent flightpaths. The radius of the turn is kinematically related (assuming a co-ordinated turn) to the commanded bank angle and airspeed. After a turn is commenced the lateral control hierarchy is used to steer the aircraft onto the new heading and track. First a bank angle hold autopilot is engaged, then (if necessary) a convergent heading
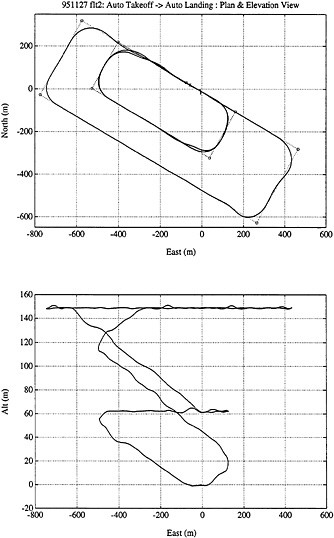
FIGURE 3 Waypoints and flight trajectory.
hold and finally the tracking hold autopilot. The turn to new leg is open loop, and wind may result in the aircraft being off-track when the turn is complete. A first order correction is used to remove the effect of the average wind during the turn. The delta heading and commanded yaw-rate are used to estimate the time required to complete the turn. During this time the aircraft will be blown off track by a distance equal to the wind velocity perpendicular to the new leg multiplied by the time taken for the turn. To correct for this effect, the waypoint logic adjusts the turninit value accordingly. The aircraft will then commence the turn to a new leg either earlier or later depending on the average wind.
The primitives for flying a pre-programmed course are now in place save for the transition from takeoff roll to flight. The aircraft was intentionally designed with a nose down runway attitude. This design allows the aircraft to maintain ground contact until the computer registers sufficient airspeed for flight. During takeoff roll, bank angle is damped by ailerons and heading error is regulated by feedback to the nosewheel steering and rudder. Elevator is set to neutral and throttle to maximum. When airspeed is sufficient for flight, the airspeed integral state is initialized to give a positive elevator pulse and the airspeed regulation mode is entered. The elevator pulse is sufficient to raise the nose and cause a clean transition from rolling to flight. Airspeed regulation at full throttle regulates the aircraft to a steady climb. At liftoff, the lateral control mode switches from runway heading hold to flight tracking mode, tracking along the upwind line toward the first waypoint.
We have succeeded in achieving the objective of flying from takeoff to landing using only GPS and a pitot on six flights from eight attempts. The attempts were made on two separate mornings in late November and early December 1995. Figure 4 shows aggregate plots of landing data from four landings plotted against distance alongtrack. The glideslope aim point intersects the ground at 0m alongtrack, with touchdown occurring at approximately +35m. The altitude is measured relative to the reference antenna, so the true ground is at approximately −1m. The dotted line depicts the commanded glideslope and flare trajectory. At touchdown, airspeed is approximately 14m/s, or about 1m/s above stall speed. The remaining plots depict aggregate pitch, elevator and cross track error thru touchdown. The two .failed attempts are attributable to loss of position integrity due to the satellite occlusion during banking turns as discussed in section 3. During flight, full state information from GPS was used directly as the sensor for automatic control. The control
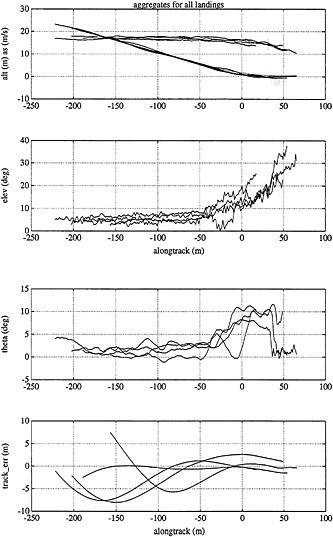
FIGURE 4 Aggregate results from 4 automatic landings.
was unaided by inertial instruments of any kind. The GPS measurement was augmented only by the pitot to measure airspeed. Alpha and beta measurements were not used in control laws directly, however a wind estimate derived from the alpha and beta vanes was used at a supervisory level to correct for the wind in predicting turn commencement for waypoint tracking. This is distinct from earlier flight tests on commercial aircraft, where GPS was used in auto-coupled approaches [4]. In these earlier flight tests, the IBLS system developed at Stanford was used to emulate traditional ILS signals. In effect, GPS and the aircraft inertial reference unit were used together by the aircraft's flight control system to execute the automatic approach and landing.
One is interested in the navigation sensor error (NSE), which is a measure of how well the navigation sensor performed in measuring truth, and the flight technical error (FTE), which is a measure of how well the control system, did in regulating to the sensor. These together comprise the total system error. Work by [3] indicates that when the cycle ambiguities for position are correctly known, the position error lies within the volume of a baseball. In our case, the same confidence cannot be assumed. Over time, particularly when PDOP is large, our patching process introduces errors which grow with time. Since our flights are relatively short, usually less than fifteen minutes, this process has been adequate for our purposes when the satellite geometry is favorable. It is difficult to do flight comparisons with benchmark systems. Such experiments have been performed by [5] comparing carrier differential position results with those from laser ranging. These experiments have shown that the GPS results agree with the laser ranging results to within the accuracy specification of the laser system. We have not attempted such a comparison, but have performed end-around checks on the sanity of the GPS position data. In such tests, the position integers are initialized from a surveyed point. After flying from takeoff to landing and returning to the same point, a comparison is made between the pre and post flight measurements. Figure 5 shows the difference between pre and post flight measurements of the same location for a successful automatic flight. (0,0) is the integer initialization point. This data was selected because satellite elevation and geometry was marginal for our purposes on this flight and much patching was required. It was a successful flight and is included in the aggregate flight data. Figure 6 shows the number of satellites common to both the air and reference receivers, the position residual in carrier cycles2 (lower plot) and the 0.5* the vertical component of dilution of precision (DOP) over the same flight. As the aircraft navigated the traffic pattern course, signals from low elevation satellites were repeatedly lost and re-acquired. The number of measurements varied between 4 and 6, and the DOP varied accordingly. The residual is seen to grow with
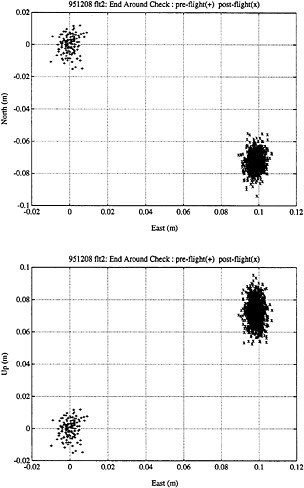
FIGURE 5 Pre and post flight measurements of same location. Integer initialization point is at (0,0).
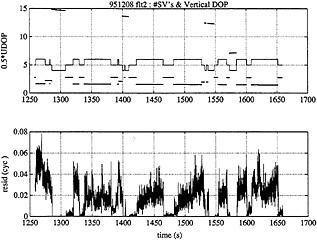
FIGURE 6 number of common satellites, 0.5* vertical component of DOP (upper plot) & residual over flight (lower plot).
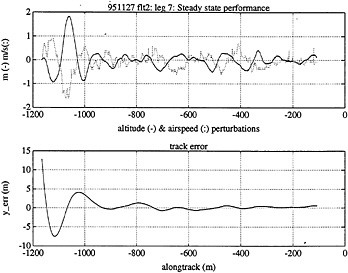
FIGURE 7 Steady state performance over downwind leg in figure 3.
time when 5 or more measurements are held for a long enough period to discern a trend. Such data are typical of results when one (or more) of the cycle integers is incorrect. The overall result (see fig 5) indicates that a 15cm error has accumulated over the period of the flight. The assumption that the error at any time between the pre and post flight checks is less than 15cm is unproven but seems reasonable. Errors larger than a meter would certainly be evident since the aircraft would be landing visibly off course. The total accumulated error is approximately the diameter of the main gear Wheels and is not large enough to be problematic in the flare or landing. As a further check, video of the landings was compared with the GPS data at touchdown. In all cases, these visual checks were consistent with the GPS data to an observational accuracy of approximately 1m. Figure 7 shows details of the long downwind leg from the flight plotted in figure 3. At steady state, the RMS cross track, altitude and airspeed errors were measured to be 0.44m 0.23m and 0.21m/s respectively. This flight was made in the early morning before substantial thermal activity was evident and there was a smooth crosswind of approximately 5 m/s at the test altitude. These results give an indication of the control system FTE in smooth air.
We have demonstrated that GPS can be used to generate real time position, velocity, attitude and angular velocity signals that have utility for automatic control. We have used these signals to achieve autonomous takeoff to landing of a real airplane for the first time. We
have also integrated alpha and beta sensors to infer the ambient wind vector in real time. The velocity and angular velocity solutions are inferred from phase rate (doppler) signals extracted from the phase locked loop within the receiver. Phase is the fundamental observable, and the phase rate signal is necessarily more noisy. This in turn leads to velocity and angular velocity solutions that are equivalently more noisy than the analogous position or attitude solution. The noise in all measurements may be reduced at the expense of tracking performance by reducing the bandwidth of the phase state estimator. The mobile receiver must have adequate bandwidth to track the dynamics of the vehicle but a stationary reference receiver can and should be filtered more heavily. The aircraft we controlled requires stability augmentation for phugoid, dutch roll and spiral divergence modes. Dutch roll and phugoid are both lightly damped with periods of approximately 3s and 10s respectively. The fastest mode is short period, which is naturally well damped at a frequency of 1 Hz. We set the phase state estimator bandwidth to 2 Hz. This gives adequate bandwidth to track the aircraft dynamics, while admitting a minimum of noise. In our experience the attitude and angular velocity solution is much more robust than the position solution. The principal reason is that there are many more measurements available. With our 6 channel receivers, there are upto 18 measurements to determine the 3 attitude unknowns versus a maximum of 6 to determine the 4 unknowns required for a position solution. To add robustness in the position solution one may consider using additional ranging signals such as pseudolites. Generally this will require having a receiver with more than 6 channels. It also complicates the surveying and setup and adds non-linearity and near/far issues. An alternative is to use a number of antennae and switch between them to keep the sky in continuous view. These are areas of ongoing research.
ACKNOWLEDGEMENTS
The authors would like to thank the FAA for ongoing funding of this project and Trimble Navigation for discount hardware and access to their receiver code. Particular thanks must go to Dr Andrew Conway of the ARL at Stanford for his collaborative effort in developing software used in this project [6]. We would also like to thank Dr Andreas Nowatzyk for his great help in solving the many radio interference problems that plagued us during systems integration.
[1] Clark Emerson Cohen. Attitude Determination Using GPS. PhD thesis, Stanford University, Department of Aeronautics and Astronautics, December 1992.
[2] A. E. Bryson. Control of Spacecraft and Aircraft. AA271B Class Notes, Department of Aeronautics and Astronautics 1992, Stanford University.
[3] B Pervan C Cohen and B Parkinson. Integrity Monitoring for Precision Approach using Kinematic GPS and a Ground-Based Pseudolite. Navigation, Volume 41 No.2 Summer 1994.
[4] C E Cohen et al. Preliminary Results of Cat. III Precision Landing with 110 Automatic Landings of a United Boeing 737 Using GNSS Integrity Beacons. ION National Technical Meeting, Anaheim, California, January 1995.
[5] C Cohen B Pervan D Lawrence S Cobb D Powell B Parkinson. Real-Time Flight Testing Using Integrity Beacons for GPS Category III Precision Landing. Navigation, Vol 41 No.2 Summer 1994.
[6] A Conway. Autonomous Control of a model Helicopter using carrier phase GPS. PhD thesis, Stanford University, Department of Electrical Engineering, February 1995.
[7] P Montgomery H Uematsu B Parkinson. Full state estimation and control of a large model aircraft using carrier differential GPS. Proceedings: DSNS April 1995. Norway.
[8] P Montgomery, H Uematsu and B Parkinson. Analysis of angular velocity determination using GPS. Proceedings: ION GPS-94 Sept 1994. Salt Lake City.
[9] A Conway P Montgomery S Rock R Cannon and B Parkinson. A new motion based algorithm for GPS attitude integer resolution. in review: contact paulm@relgyro.stanford.edu