3
Application of Statistical Science to Testing and Evaluating Software Intensive Systems
Jesse H. Poore, University of Tennessee; and Carmen J. Trammell, CTI PET Systems, Inc.
1. Introduction
Any large, complex, expensive process with myriad ways to do most activities, as is the case with software development, can have its cost-benefit profile dramatically improved by the use of statistical science. Statistics provides a structure for collecting data and transforming it into information that can improve decision making under uncertainty. The term ''statistical testing'' as typically used in the software engineering literature has the narrow reference to randomly generated test cases. The term should be understood, however, as the comprehensive application of statistical science, including operations research methods, to solving the problems posed by industrial software testing. Statistical testing enables efficient collection of empirical data that will remove uncertainty about the behavior of the software intensive system and support economic decisions regarding further testing, deployment, maintenance and evolution. The operational usage model is a formalism that enables the application of many statistical principles to software testing and forms the basis for efficient testing in support of decision making.
The software testing problem is complex because of the astronomical number of scenarios of use and states of use. The domain of testing is large and complex beyond human intuition. Because the software testing problem is so complex, statistical principles should be used to guide testing strategy. In general, the concept of "testing in quality" is costly and ineffectual; software quality is achieved in the requirements, architecture, specification, design and coding activities. Although not within the scope of this essay, verification or reading techniques (Basili et al., 1996) are of critical importance to achieving quality software and may efficiently and effectively displace some testing. The problem of doing just enough testing to
remove uncertainty regarding critical performance issues, and to support a decision that the system is of requisite quality for its mission, environment or market, is a problem amenable to solution by statistical science. The question is not whether to test, but when to test, what to test and how much to test.
Testing can be justified at many different stages in the life cycle of a software intensive system. There is, for example, testing at various stages in development, testing of reusable components, testing associated with product enhancements or repairs, testing of a product ported from one hardware system to another, and "customer testing" (i.e., field experience). Service in the field is the very best "testing" information, because it is real use, often extensive, and free except for the cost of data collection. The usage model can be the framework, the common denominator, for combining test and usage experience across different software engineering methods and life cycle phases so that maximum use can be made of all available testing and field-use information.
A statistical principle of fundamental importance is that a population to be studied must first be characterized, and that characterization must include the infrequent and exceptional as well as the common and typical. It must be possible to represent all questions of interest and all decisions to be made in terms of this characterization. All experimental design methods require such a characterization and representation, in one form or another, at a suitable level of abstraction. When applied to software testing, the population is the set of all possible scenarios of use with each accurately represented as to frequency of occurrence.
One such method of characterization and representation is the operational usage model. The states-of-use of the system and the allowable transitions among those states are identified, and the probability of making each allowable transition is determined. These models are then represented in the form of one or more highly structured Markov chains (a type of statistical model, see e.g. Kemeny and Snell, 1960), and the result is called a usage model (Whittaker and Poore, 1993; Whittaker and Thomason, 1994).
From a statistical point of view, all of the topics in this paper follow sound problem solving principles and are direct applications of well-established theory and methodology. From a software testing point of view, the applications of statistical science discussed below are not in
widespread use, nor is the full process presented here in routine use. Many methods and segments of the process are used in isolated pockets of industry, on both experimental and routine bases. This paper is a composite of what is in hand and within reasonable reach in the application of statistical science to software testing.
Statistical testing based on usage models can be applied to large and complex systems because the modeling can be done at various levels of abstraction and because the models effectively allow analysis and simulation of use of the application rather than the application itself.
Many of the methods that follow are well within the capability of most test organizations, with a modest amount of training and tool support. Some of the ideas are more advanced and would require the services of a statistician the first few times they are used, or until packaged in specialized tool support. Some of the advanced methods would require a resident analyst. However, the methods lend themselves to small and simple beginnings with big payoff, and to systematic advancement in small steps with continued good return on the investment.
2. Failures in the Field
Failures in the field, and the cost (social as well as monetary) of failures in the field, are the motivation behind statistical testing. The collection, classification and analysis of field failure reports on software products has been standard practice for decades for many organizations and is now routine for most software systems and software intensive systems regardless of the maturity of the organization. Field data is analyzed for a variety of reasons, among them the ability to budget support for the next release, to compare with past performance, to compare with competitive systems, and to improve the development process.
Field failure data is unassailable as evidence of need for process improvement. The operational front line is the source of the most compelling statistics. The opportunities to compel process changes move upstream from the field, through system testing, code development, specification writing, and into stating requirements. Historically, the further one moves
upstream, the more difficult it has been to effect a statistically based impact on the software development process that is designed to reduce failures in the field. Progress has been made, however, in applying statistical science to prevention of field failures: given an operational usage model, it is possible to have a statistically reasoned and economically beneficial impact on all aspects of the software life cycle.
3. Understanding the Software Intensive System and Its Use
A usage model characterizes the population of usage scenarios for a software intensive system. Usage models are constructed from specifications, user guides, or even existing systems. The "user" might be a human, a hardware device, another software system, or some combination. More than one model might be constructed for a single system if there is more than one environment of interest.
For example, a cruise control system for tracks has both human and hardware users since it exchanges information with both. The usage model would be based on the states of use of the system—system off, system on and accelerating, system on and coasting, etc.—and the allowable transitions among the states. The model could be constructed without regard to whether the supplier will be Delco or Bosch. It will be irrelevant that one uses a processor made by Motorola and the other by Siemens and that they have very different internal states, that one is programmed in C and the other in Ada. It is conceivable that the system would be tested in two environments of use—operation as a single vehicle and operation in a convoy with vehicle-to-vehicle communication.
First Principles
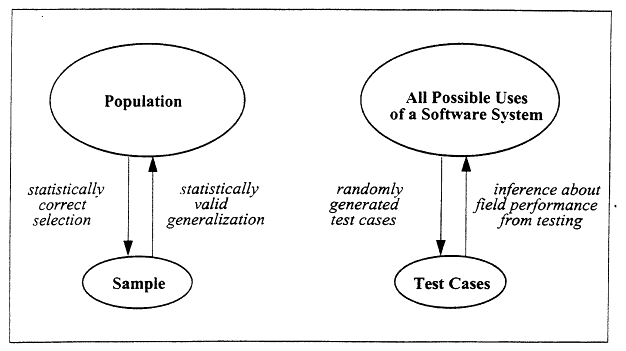
When a population is too large for exhaustive study, as is usually the case for all possible uses of a software system, a statistically correct sample must be drawn as a basis for inferences
about the population. Figure 1 shows the parallel between a classical statistical design and statistical software testing. Under a statistical protocol, the environment of use can be modeled, and statistically valid statements can be made about a number of matters, including the expected operational performance of the software based on its test performance.
Statistical Testing Process
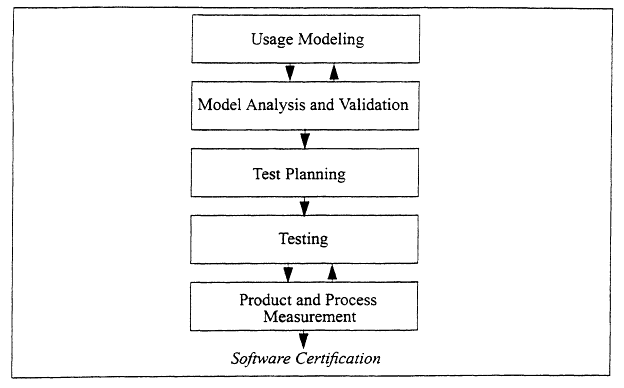
Statistical testing can be initiated at any point in the life cycle of a system, and all of the work products developed along the way become valuable assets that may be used throughout the life of the system. The statistical testing process involves the six steps depicted in Figure 2.
Building Usage Models
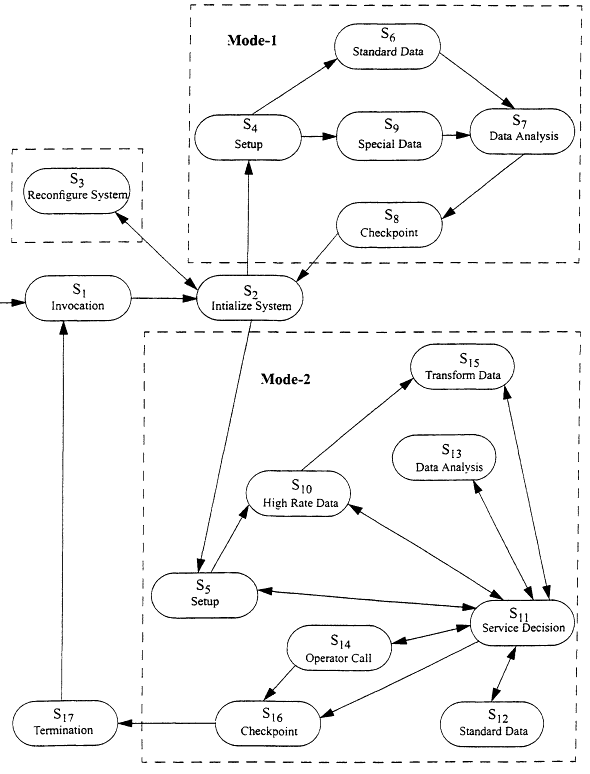
An operational usage model is a formal statistical representation of all possible uses of a system. A usage model may be represented in the familiar form of a state transition graph, where the nodes represent states of system use and the arcs represent possible transitions between states (see Figure 3). If the graph has any loops or cycles (as is usually the case), then there is an infinite number of finite sequences through the model, thus an infinite population of usage scenarios. In such graphical form, usage models are easily understood by customers and users, who may participate in model development and validation. As a statistical formalism, a usage model lends itself to statistical analysis that yields quantitative information about system properties.
The basic task in model building (Walton, Poore, and Trammell, 1995) is to identify the states-of-use of the system and the possible transitions among states-of-use. Every possible scenario of use, at the chosen level of abstraction, must be represented by the model. Thus, every possible scenario of use is represented in the analysis, traceable on the model, and potentially generated from the model as a test case.
There are both informal and formal methods of discovering the states and transitions. Informal methods such as those associated with "use cases" in object-oriented methods may be used. A formal process has been developed (Prowell, 1996; Prowell and Poore, 1998) that drives the discovery of usage states and transitions. The process is based on the systematic enumeration of sequences of inputs and leads to a complete, consistent, correct and traceable usage specification.
Usage models are finite state, discrete parameter, time homogeneous, recurrent Markov chains. Inherent in this type of model is the property that the states have no memory; some transitions in an application naturally do not depend on history, whereas others must be made independent of history by state-splitting, making the states sufficiently detailed to reflect the relevant history. This leads to growth in the number of states, which must be managed. A usage model is developed in two phases—a structural phase and a statistical phase. The structural phase concerns possible use, and the statistical phase, expected use. The structure of a model is defined by a set of states and an associated set of directed arcs that define state transitions. When represented as a stochastic matrix, the 0 entries represent the absence of arcs (impossible transitions), the 1 represents the certain transitions, and all other cells have transition probabilities of 0 < x < 1 (see Table 1). This is the structure of the usage model.
The statistical phase is the determination of the transition probabilities, i. e., the x's in the structure. There are two basic approaches to this phase, one based on direct assignment of probabilities and the other on deriving the values by analytical methods.
Models should be designed in a standard form consisting of connected sub-models with a single-entry and single-exit. States and arcs can be expanded like macros. Sub-models of canonical form can be collapsed to states or arcs. This permits model validation, specification analysis, test planning, and test case generation to occur on various levels of abstraction. The structure of the usage models should be reviewed with the specification writers, real or prospective users, the developers, and the testers. Users and specification writers are essential to represent the application domain and the workflow of the application. Developers get an early opportunity to see how the system will be used, and look ahead to implementation strategies that take account of use and workflow. Testers, who are often the model builders, get an early
opportunity to define and automate the test environment.
Software Architecture
The architecture of the software intensive system is an important source of information in building usage models. If the model reflects the architecture of the system, then it will be easier to evolve the usage model as the system evolves. The architecture can be used to directly identify how models should be constructed and how testing should proceed.
A product line based on a common set of objects used through a graphical user interface might have a model for each object as well as a model for the user interface. Each object could be certified independently and the object interactions as permitted by the user interface would be certified with the interface. A new feature might be added later by developing a new object and a modification to the interface; this would require a new model for the new object and an updating of the model for the interface. Importance sampling might be used to emphasize testing of the changed aspects of the interface.
Protocols and other standards established by the architecture can also be factors in usage model development. For example, a usage model for the SCSI protocol has been developed and used in constructing models of several systems that use the SCSI protocol.
Assigning Transition Probabilities
Transition probabilities among states in a usage model come from historical or projected usage data for the application. Because transition probabilities represent classes of users, environments of use, or special usage situations, there may be several sets of probabilities for a single model structure. Moreover, as the system progresses through the life cycle the probability set may change several times, based on maturation of system use and availability of more information.
When extensive field data for similar or predecessor systems exists, a probability value may be known for every arc of the model (i.e., for every nonzero cell of the stochastic matrix of transition probabilities, as in column 4 of Table 2). For new systems, one might stipulate expected practice based on user interviews, user guides, and training programs. This is a reasonable starting point, but should be open to revision as new information becomes available.
When complete information about system usage is not available, it is advisable to take an analytical approach to generating the transition probabilities, as will be presented in section 5. In order to establish defensible plans, it is important that the model builder not overstate what is known about usage or guess at values.
In the absence of compelling information to the contrary, the mathematically neutral position is to assign uniform probabilities to transitions in the usage model. Table 2 column 3 represents a model based on Figure 3 with uniform transition probabilities across the exit arcs of each state.
4. Model Validation with Customer and User
A usage model is a readily understandable representation of the system specification that may be reviewed with the customer and users. The following statistics are assured to be available by the mathematical structure of the models and are routinely calculated.
- Long run probability. This is the long-run occupancy rate of each state, or the usage profile as a percentage of time spent in each state. These are additive, and sums over certain states might be easier to check for reasonableness than the individual values (for example, Model in Figure 3).
- Probability of occurrence in a single sequence. This is the probability of occurrence of each state in a random use of the software.
- Expected number of occurrences in a single sequence. This is the expected number of times each state will appear in a single random use or test case.
- Expected number of transitions until the first occurrence. For each state, this is the expected number of randomly generated transitions (events of use) before the state will first occur, given that the sequence begins with Invocation. This will show the impracticality of visiting some states in random testing without partitioning and stratification.
- Expected sequence length. This is the expected number of state transitions in a random use of the system and may be considered the average length of a use case or test case. (Using this value and transitions until first occurrence, one may estimate the number of test cases until first occurrence.)
These statistics should be reviewed for reasonableness in terms of what is known or believed about the application domain and the environment of use. Given the model, these statistics are derived without further assumptions, and if they do not correspond with reality then the model must be changed. These and other statistics describe the behavior that can be expected in the "long ran," i.e., in ongoing field use of the software. It may be impractical for enough testing to be done for all aspects of the process to exhibit long run effects; exceptions can be addressed through special testing situations (as discussed below).
Operational Profiles
Operational profiles (Lyu, 1995) describe field use. Testing based on an operational profile ensures that the most frequently used features will be tested most thoroughly. When testing schedules and budgets are tightly constrained, profile-based testing yields the highest practical reliability; if failures are seen they would be the high frequency failures and consequent engineering changes would be those yielding the greatest increase in reliability. (Note that critical but infrequently used features must receive special attention.)
One approach to statistical testing is to estimate the operational profiles first and then create random test cases based on them. The usage model approach is to first build a model of system use (describe the stochastic process) based on many decisions as to states of use,
allowable transitions and the probability of those transitions, and then calculate the operational profile as the long run behavior of the stochastic process so described.
Operational Realism
A usage model can be designed to simulate any operational condition of interest, such as normal use, nonroutine use, hazardous use, or malicious use. Analytical results are studied during model validation, and surprises are not uncommon. Parts of systems thought to be unimportant might get surprisingly heavy use while parts that consume a large amount of the development budget might see little use. Since a usage model is based on the software specification rather than the code, the model can be constructed early in the life cycle to inform the development process as well as for testing and certification of the code.
Source Entropy
Entropy is defined for a probability distribution or stochastic source (Ash, 1965) as the quantification of uncertainty. The greater the entropy, the more uncertain the outcome or behavior. As new information is incorporated into the source, the behavior of the source generally becomes more predictable, and less uncertain. One interpretation of entropy is the minimum average number of "yes or no" questions required to determine the result of one outcome or observation of the random event or process (Ash, 1965).
Each state of a usage model has a probability distribution across its exit arcs to describe the transitions to other states, which appears as a row of the transition matrix. State entropy gives a measure of the uncertainty in the transition from that state.
Source entropy is by definition the probability-weighted average of the state entropies. Source entropy is an important reference value because the greater the source entropy, the greater the number of sequences (test cases) that it would be necessary to generate from the usage model,
on average, to obtain a sample that is representative of usage as defined by the model.
Specification Complexity
Some systems are untestable in any meaningful sense. Some systems have such a large number of significant paths of use and such high cost of testing per path, that there is not sufficient time and budget to perform an adequate amount of testing by any criteria, even with the leverage of statistical sampling. This situation can be recognized early enough through usage modeling to be substantially mitigated.
A usage model represents the capability of the system in an environment of use. All usage steps are probability weighted. Any model with a loop or cycle (other than the one from Termination to Invocation) has an infinite number of paths; however, only a finite number have a probability of occurring that is large enough to consider them. The complexity of a model can be viewed as the number of statistically typical paths (to be thought of as ''paths worth considering''). Note that this concept of complexity has nothing to do with the technical challenge posed by the requirements, nor with the intricacies of the ultimate software implementation. It is simply a measure of how many ways the system might be used (how broadly the probability mass is spread over sequences) and, therefore, a measure of the size of the testing problem.
Complexity analysis can be used to assess the extent to which modification of the specification (and usage model) would reduce the size of the testing problem. By excluding states and arcs from the model, such what-if calculations can be made. For example, mode-less display systems that allow the user to switch from any task to any other task are far more expensive to test than modal displays that restrict tasks to categories. It is possible, also, to compare the differences in complexity associated with different environments of use (represented by different sets of transition probabilities, as in Tables 3 and 4). Complexity analysis can be used to assess the impact on testing of changes in the requirements and system implementation. Because the usage model is based on the specification, the model can be developed, validated,
and analyzed before code is written. An analysis of the complexity of the model might lead to simplification of the specification in various ways, before code development begins.
When the system cannot be changed to reduce complexity and the test budgets cannot be made adequate, usage models can help to focus the budgets on the most important states, arcs and paths. Certain usage states might be critical to achieve (or to avoid) and the number of pathways by which one might achieve (or avoid) these states could be very important. In a slightly more complex situation, there may be two or more states among which passage should be quick and easy (or virtually impossible). Trajectory entropy provides a measure of the uncertainty in selecting a path from a set of paths. A variation on the techniques of Ekroot and Cover (1993) produces the measure of specification complexity (Walton, 1995). Trajectory entropy is the sum of the uncertainty of the first step in the path plus the conditional uncertainty of the rest of the path, given the first step. This value is the ratio of the source entropy to the stationary probability of the invocation state and is used as an index of specification complexity, the minimum average number of yes-no questions one would have to ask to identify the path taken. When 2 is raised to this power, an estimate of the number of paths worth considering is obtained. Many well-posed questions involving states, arcs and paths can be expressed in a mathematical model with a closed form solution.
Simulation
All the analyses mentioned above have closed form solutions and are applicable to all usage models because of their mathematical structure. However, questions do arise for which the analytical expressions or solutions might not exist or might be difficult to formulate. In some of these cases an effective bound on the solution is available, in other cases not.
For example, the expected number of sequences before each state first appears in random testing is computed analytically as shown in Table 3 and 4. However, the expected number of sequences before all the states in an arbitrary subset of model states appear at least once in random testing is a harder question and the answer depends upon the arrangement of the states in
the graph, as well as the probabilities. While this solution can be bounded analytically, a simulation is easily constructed to get an estimate of the answer to the question.
Moreover, many questions that depend strictly on the structure of the graph will not have a general solution. In these cases simulations can usually be constructed to approximate an answer. Since there can be a great deal of variation among the realizations of a model, the simulations might have to run for millions of sequences, but the cost of such simulations is generally not prohibitive. Not all aspects of the sequences will reach asymptotics at the same rate, so some simulations may resolve quickly while others might require analysis of a great many sequences.
It is an extremely valuable aspect of the usage model that simulations are readily available when analytical solutions do not exist or are very difficult to work out.
Model Revision and Revalidation
As mentioned above, these statistics and analyses flow from the usage model without further assumptions. If the structure of the model represents the capability of the system and if the probabilities represent the environment of use, then the conclusions are inescapable. If they do not agree with what is known or believed about the application, then the model must be changed.
Even small models embody a great deal of variation. Consequently, it is not always obvious how to change a model in order to change its statistics. Moreover, small changes in the probabilities can have large and unanticipated side effects. An alternative to the cycle of setting probabilities, analyzing statistics and revising probabilities is to analytically generate models with stochastic matrices guaranteed to have certain statistics, as described in the next section.
5. Representing Usage Models with Constraints
An alternative to the direct assignment of transition probabilities discussed in section 3 is generation of transition probabilities with the aid of mathematical programming (specifically, convex programming) (Walton, 1995). Usage models can be represented by a system of constraints and the matrix of transition probabilities can be generated as the solution to an optimization problem. In general, three forms of constraints are used to define a model: structural, usage, and test management constraints.
Structural Constraints
Structural constraints are so named because they define model structure: the states themselves and both possible and impossible transitions among the usage states.
Structural constraints are of four types:
- Pi,j = 0 defines an impossible transition between usage state i and usage state j.
- Pi,j = 1 defines a certain transition between usage state i and usage state j.
- 0 < Pi,j < 1 defines probabilistic transition between usage state i and usage state j.
- Each row of P must sum to one.
Usage Constraints
If one has no information about the expected usage of the system, one should generate uniform probabilities for the possible transitions from each state. As new information arises, it is recorded in the form of constraints:
- Pi,j = c may be used for known usage probabilities, i.e., probability values that are exactly known on the basis of historical experience or designed controls.
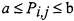 defines estimated usage probabilities as a range of values. Defining an estimate as being within a range allows information to be given without being overstated.
defines estimated usage probabilities as a range of values. Defining an estimate as being within a range allows information to be given without being overstated.- Pi,j = Pk,m defines equivalent usage probabilities, values that should be the same whether or not one knows what the value should be.
- Pi,j = d Pk,m defines proportional usage probabilities, where one value is a multiple of another.
Probability values can be related to each other by a function to represent what is known about the relationship, without overstating the data and knowledge. More complex constraints may be expressed as:
- Pi,j = f(Pk,m), where one value is a function of another.
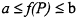 , where the value of a function of the matrix P is bounded, for example, to constrain the average test case length to a certain range.
, where the value of a function of the matrix P is bounded, for example, to constrain the average test case length to a certain range.
Most usage models can be defined with very simple constraints.
Test Management Constraints
Finally, constraints may be used to represent test management controls. Management constraints are of the same forms as usage constraints. A limitation on revisiting previously tested functionality, for example, may be represented in the form of a known usage probability in the section above—a constant that limits the percentage of test cases entering a certain section of the model.
Objective Functions
Mathematical programming is a technique for determining the values of a finite set of decision variables which optimize an objective function subject to a specified set of mathematical constraints. The general problem of optimizing any function subject to a set of unrestricted constraints can be analytically or computationally intractable. The problem is tractable when it is restricted to convex programming, the minimization of a convex objective function subject to a finite set of convex constraints.
When mathematical programming is used to generate transition probabilities, the solution generated is optimized for some objective function while satisfying all structural, usage and management constraints. Theoretically, one could construct a system of constraints for which there is no solution. In practice, if one does not overstate data and knowledge, this is unlikely.
Analysis of a usage model invariably leads to modification of the transition probabilities in order to incorporate new information, or to change focus at different phases of the process. With complex usage models, individual changes in transition probabilities may result in unintended, poorly understood and unwanted side effects. Better control and understanding is maintained if models are amended through revised or additional constraints and regenerated relative to an optimization objective, rather than by estimation of individual transition probabilities.
Objective functions can be formulated, for example, to minimize cost of testing or to maximize value of testing. Also, entropy measures can be used in objective functions in order to minimize or maximize the uncertainty or variability in the model and, consequently, in the sequences randomly generated from the model.
There are, in general, many sets of transition probabilities that collectively satisfy a system of constraints. Even when the usage profile (stationary distribution) is fully prescribed, many sets of transition probabilities are possible for the usage model which have the same usage profile. Consequently, the certification strategy must be based on a carefully reasoned choice among them that produces the desired overall effects. Mathematical programming can be used to make that choice.
6. The Benefits of Usage Modeling
As early as possible in the life cycle, one or more usage models is developed (both the structure and the transition probabilities), and the model is validated. To the best ability of the model developers, with the information available to them, the model represents the operational capability of the system at the desired level of abstraction, and the statistics agree with what is known or believed about the intended environment of use. The following is a summary of the many beneficial uses of the model in planning, managing and conducting testing.
Testing Scripts
A script is associated with each arc of the usage model. This script constitutes the instructions for testing the transition from one state of use to another as represented by the arc. Scripts should be developed by experienced testers and should be validated. The scripts are a significant factor in assuring experimental control during testing.
In the case of testing performed by humans, the script can tell the tester what to do, what inputs to give the system, and what to look for in deciding that the transition was made correctly or not. Testing can be a tedious activity which degenerates in effectiveness unless specific measures are taken to keep the testers focused on what to do and what to look for. Furthermore, testing effectiveness can vary greatly from one person to another unless steps are taken to assure uniformly effective testing. Every test is a traversal of a series of arcs through the model; if the scripts are granular and are followed, they will assure uniform testing.
In the case of automated testing, the scripts will be commands to testing software or equipment and in some cases will contain the information needed to verify correct performance. Lines of code have been used as scripts in such a way that the test case literally becomes a
program to be compiled and executed by the automated test facility.
Recording Testing Experience
The usage model provides a method of recording testing experience that can be used in assessing test sufficiency and other aspects of the software development process.
A testing chain is a representation of testing experience. A testing chain is started by using just the structure of states and arcs (no transition probabilities) for the usage model. As test sequences are executed, each arc successfully traversed (no failure) is marked and the relative frequencies across the exit arcs of each state are calculated. Given enough random sequences, these relative frequencies will converge to the probabilities of the usage model. The measure of similarity between the weights on the usage model (expected traffic) and the weights on the testing chain (tested traffic) is discussed later as a stopping criterion for testing.
Two types of failures are possible. The first type does not impair or distort the functioning of the system, and the transition to the next state can be made. For example, a spelling error might appear in a message on the screen, or a window might be in the wrong location. In such cases, a new state is created to represent the failure and two new arcs are created, one from the departure state to the failure state and one from the failure state to the destination state, and each of the two new arcs gets a mark. Any time in the future that the same failure appears from the same departure state, these two arcs will each be marked again.
A second type of failure is one in which it makes no sense to continue the test case. For example, if the system crashes and it is impossible to continue, or if the failure renders further steps meaningless as in the case of a destroyed file. In such cases, a new state is created to represent the failure and two new arcs are created, one from the departure state to the failure state and one from the failure state to the termination state, and each of the two new arcs gets a mark. Any time in the future that the same failure appears from the same departure state, these two arcs will each be marked again.
Several testing chains can be maintained. One testing chain could be maintained from the
beginning of all testing and another might be maintained for each version of the system, with a new testing chain started each time the code is changed. The cumulative data may be used for process analysis and the data on each version for product analysis. The testing chain can represent all testing experience, special cases as well as random testing, or it can represent just random testing. It is possible to instrument code to maintain a "testing chain" based on actual field experience as well.
Support for Experimental Design
Design of statistical experiments is being used increasingly in testing software intensive systems (Nair et al., 1998). Although the use of experimental design in software testing is not widespread, the variety of applicable techniques has great potential to transform the testing field.
Designed experiments tell in advance how much testing and what kind of testing will be required to achieve desired results. Indeed, with most of these methods it is possible to influence product design decisions in order to make such testing feasible and more economical. Some characterization of the population under study is necessary for any application of experimental design. The usage model can be of value in all cases.
- Combinatorial design. A class of statistical experimental design methods known as combinatorial designs is used to generate test sets that cover the n-way combinations of inputs (Cohen, 1997). For certain types of applications, including data entry screens, this approach has been used to minimize the amount of testing required to satisfy use-coverage goals. Combinatorial design deals with test factors, levels within factors, and treatments (combinations of factor levels) but leaves other issues unaddressed; for example, one must chose among many different test cases that cover all pairs of factor levels. Given a usage model, the treatments will appear as visitation of states of use in specific sequences and the likelihood of these sequences arising in use may be taken into account. Both combinatorial design and operational profiles may be used to plan testing.
- Partition testing. Partitioning is a standard statistical technique for increasing the efficiency of random sampling. It is applicable to increasing the efficiency of random testing as well. Partitions can be identified and defined in terms of the usage model. For example, based on Figure 3 test cases might be partitioned into those that include system reconfiguration (state 3) and those that do not; those that include visiting states in Mode-1 and those that do not. The reliability model of Miller et al. (1992) can be used since the probability mass of each block of the partition can be calculated from the model, as can the probability mass of test cases run in each block.
- Rare events and accelerated rate testing. Some testing must address infrequent but highly critical situations in order to remove uncertainty or estimate reliability that takes rare events into account. Experimental design has been used to determine the most efficient approach to testing combinations of factors associated with rare events and reliability models have been developed for these situations (Alam et al., 1997; Ehrlich et al., 1997). Usage models can be built from many different perspectives, including process flow. Critical states, transitions, and sub-paths that would have low likelihood of arising in field use (or in a random sample) can be identified from the usage model. The probability of reaching any given state or transition can be calculated directly from the model, as can the traversal of any sub-path. For example, in Figure 3 one might look for unlikely system configurations (state 3) in combination with high rate data (state 10).
- Sequential testing. In some cases each test is so expensive to run or to evaluate that it is important to decide based on the outcome of each test whether or not additional testing is justified. The degree to which the variety and extent of testing is representative of the variety and extent of use expected in the field can be calculated directly from the usage model and the testing record.
- Economic testing criteria. Different forms or modes of failures in the field can result in different operational economic loss. Usage models together with mathematical programming methods can be used to design testing to minimize the potential of economic loss from field failure (Sherer, 1996).
- Economic stopping criteria. Mathematically optimal rules have been developed for
supporting decisions to stop testing, based on the known cost of continued testing versus the expected cost of failure in the field (Dalal and Mallows, 1988). Quantitative analysis of the usage model can assist in assessing the cost of continued testing and the risk of failure in the field.
Guiding Special Test Situations
Application of statistical science includes creating special, non-random, test cases. Such testing can remove uncertainty about how the system will perform in specific circumstances of interest, aid in understanding the sources of variation in the population, and contribute to effectiveness and control over all testing. In all instances, however, the usage model is the road map for planning where testing should go and recording where testing has been. A few of the many special situations that can be represented in terms of the usage model are as follows.
- Model coverage tests. Using just the structure of the model, a graph-theoretic algorithm generates the minimal sequence of test events (least cost sequence) to cover all arcs (and therefore all states) (Gibbons, 1985). If it is practical to conduct this test, it is a good first step in that it will confirm that the testers know how to conduct testing and evaluate the results for every state of use and every possible transition. For large models, even this compelling testing strategy may not be affordable!
- Mandatory tests. Any specific test sequences that are required on contractual, policy, moral, or ethical grounds can be mapped onto the model and rim.
- (Non-random) regression tests. Existing regression test suites can be mapped to the model. This is an effective way to discover the redundancy in the test suite and assess its omissions. One can calculate the probability mass accounted for by the test suite. Of course, one may use the model to create or enhance a regression test set.
- Most likely use. The most likely test scenarios can be generated in rank order to some number of scenarios, or to some cumulative probability mass.
Some balance must be reached between the amount of test time and money that will be spent in special testing and the amount that will be reserved for testing based on random sampling. Only random testing supports inferences about expected operational performance.
Generating Random Samples of Test Cases
Random test cases can be automatically generated from the usage model, constituting a random sample of uses as the basis for statistical estimation about the population. Each test case is a ''random walk'' through the stochastic matrix, from the initial state to the terminal state. The script associated with each arc of the model is generated at each step of the random walk. Test cases are generated as scripts for human testers or as input sequences for automated testing. One may generate as large a set of test cases as the budget and schedule will bear and establish bounds on test outcomes before incurring the cost of performing the tests.
A random sample of test cases is still a random sample when used multiple times. Thus, it is legitimate to rerun the test set after code changes (regression testing) and to use the results in statistical analysis, provided the code was not changed to specifically execute correctly on the test set. It is not uncommon to see situations where the code always works on the test set, but does not work in the field; developers in some organizations literally learn what the testers are testing. Bias in evaluation must also be avoided. Testers may expect correct results because they have always been correct in the past; testers may learn the test set as well. If testing and the random test sets are independent of the developers and maintenance workers, reuse of the random test sets is a valid statistical testing strategy that can facilitate automated testing and substantial reductions in the time and cost of testing.
Importance Sampling
As was mentioned above, it is generally the case that many sets of transition probabilities exist that satisfy all known constraints on usage. In other words, there are many usage models (same structure, different transition probabilities) that are consistent with what is known about the environment of use.
Objective functions are used to choose the model that satisfies all constraints and is optimal relative to some criterion. By a combination of additional management constraints and objective functions the resulting model can emphasize aspects of the system or of the testing process that are important to testers. The following are among the controls that are possible:
- costs can be associated with each arc, and one can minimize cost;
- value can be associated with each arc, and one can maximize value;
- probabilities associated with exiting arcs that control critical flow can be manipulated;
- certain long run effects can be regulated by constraints;
- some entropy measures can be maximized to increase uncertainty and increase variability in the sequences;
- some entropy measures can be minimized to reduce variability.
One must always be wary of constructing an overly complex model that might be ill-conditioned relative to the numerical methods used in calculating the solution. Too many constraints that are functions of long run behavior are not advised. (Source entropy of a Markov chain is not a convex function. It becomes convex if the stationary distribution or operational profile is fixed.) A statistical analyst must be involved in this kind of modeling.
Recent theoretical developments (Gutjahr, 1997) hold promise for dynamic revision of probabilities as testing progresses in order to optimize sampling relative to an importance objective.
Test Automation
Usage models have led to increased test automation in almost every situation in which they have been used. Test automation is attractive because it vastly increases the number of tests that can be run and greatly reduces the unit cost of testing. Test automation is more cost effectively done when planned as a companion to the system development, but can also be cost effective for existing systems for which long-term evolution is anticipated.
Test automation depends upon three things: (1) generation of test cases in quantity in a form suitable for automated test runners, (2) an oracle or means of confirming that the system executes the test case correctly, and (3) a test runner that can initiate testing and report results.
The usage model is an excellent means of controlled generation of test cases in any desired quantity. Control is achieved by setting probabilities in order to implement importance sampling. Test cases are produced by walking the graph with a random number generator.
The oracle is the means by which one confirms that each step of the test case does what it is supposed to do (sufficient correctness) and nothing more (complete correctness). This is generally the difficult issue. Some systems have natural and easy oracles much like double inversion of a matrix or squaring a square root; for example, a disk drive control unit might be tested by writing a file to disk and then reading it back. Sometimes a predecessor system can be used because the behavior of the new system is to be identical to the behavior of the old system. Sometimes the testing will be manual the first time as the correct behavior is recorded and then automated on subsequent runs of the test suite.
There are several test runners on the market to which scripts can be sent and which will return information for constructing the testing chain.
Testing
Testing is expensive; industry data indicates that about half the software budget is spent on testing. Testing costs are best attacked in the development process, by clarifying and simplifying requirements, providing for testability and test automation, and verifying code against specifications. When high quality software reaches the test organization, there are two
goals: (1) provide the development organization with the most useful information possible as quickly as possible in order to shorten the overall development cycle, and (2) certify the system as quickly and inexpensively as possible. Just "more testing" will certainly add cost, but will not necessarily add new information or significantly improve reliability estimates.
- Resource and schedule estimation. Calculations on a usage model provide data for effort, schedule, and cost projections for such goals as coveting all states and transitions in the model or demonstrating a target reliability. Estimating the time and cost required to conduct the test associated with each arc of the usage model can lead to estimates for sequences; average sequence lengths can be used to estimate the time and cost of executing test sets.
- Reliability analysis, with failures. The testing chain provides the basis for a data-driven estimation of reliability. In the presence of failures, reliability can be assessed without additional mathematical assumptions (in contrast to reliability growth models). The failure states of the testing chain are made absorbing and the reliability of the system is defined to be the probability of going from the invocation state to the termination state without being absorbed in a failure state. The failure states in a testing chain can be ranked with respect to their impact on reliability, which is used to help decide the order in which to work on code corrections.
- Reliability analysis, no failures. In the absence of failures, reliability models based on the binomial are sometimes used (Parnas, 1990). Alternatively, the reliability models of Miller et al. (1992), which are based on partitioning the sample space, can be used to take advantage of the structure of the model in order to improve the confidence in the reliability estimate.
- Test sufficiency analysis. A stopping criterion can be calculated directly from the statistical properties of the usage model and testing chain. The log likelihood ratio (Kullback, 1958) (Kullback discriminant) can be calculated for these Markov chains and provides evidence for or against the hypothesis that the two stochastic processes are equivalent. The Kullback discriminant is a measure of the difference between expected field usage (usage model) and actual experience in testing (testing chain) that can be monitored during testing because the testing chain is changing with each test event (transition). A graph of the discriminant will have a terrace-like appearance of declines and plateaus as failure-free testing proceeds; when a failure
occurs it will step up. This is an information theoretic comparison of the usage and testing chains to assess the degree to which the testing experience has become representative of expected field use. As the testing chain converges to the usage model, it becomes less likely that new information will be gained by further testing generated from the usage model.
Simulation
Testing can be simulated by generating the test cases and marking the testing chain as if the test cases has been rim. Simulated testing is an inexpensive way to answer important questions. For example:
- which specific states, arcs, paths will be covered in the course of executing a random test set, and which should be covered by special test cases?
- how many additional random sequences would have to be run without a new failure in order to reach the reliability goal?
- if a failure occurs in a given transition, what will be the impact on the estimated reliability?
- how much will the measured reliability, discriminant, state coverage, arc coverage, etc., improve if a certain number of additional sequences are run?
By analysis and simulation, one can be assured that a test plan has the potential to answer the questions and address the issues of interest to test management. Similarly, one has the information to know at any stage if the failures encountered have rendered the testing goals (quality demonstration) unattainable.
7. Product and Process Improvement
Certification
The certification process involves ongoing evaluation of the merits of continued testing. Stopping criteria are based on reliability, confidence, and uncertainty remaining. Decisions to continue testing are based on an assessment that the goals of testing can still be realized within the schedule and budget remaining.
In most cases users of statistical testing methods release a version of the software in which no failures have been observed in testing. Reliability estimates such as those in Miller et al. (1992) are recommended in this case.
Software is sometimes released with known faults. If the test data includes failures, then reliability and confidence may be calculated from the testing chain. The reliability measure computed in this manner reflects all aspects of the sequences tested, including the probability weighting defined by the usage model.
Certification is always relative to a protocol, and the protocol includes the entire testing process and all work products. An independent audit of testing must be possible to confirm correctness of reports. An independent repetition of the protocol should produce the same conclusions, to within acceptable statistical variation.
Incremental Development
The Cleanroom software engineering process (Poore and Trammell, 1996) uses the testing approach described in this paper. Cleanroom produces software in a stream of increments to be tested. An increment may be "accepted," indicating that the development process is working well, by different (less stringent) criteria than will be used to certify the final product. If increment certification goals are not met, review of experience may show that changes are needed in the process itself, for example, better verification, changes to the usage model, improved record keeping, more frequent analysis of test data, or rethinking of the entire increment plan. If certification goals are met, the process moves ahead with the next increment
or system acceptance.
The historical testing chain and related statistics will reflect consequences of all failures seen and fixed from the very beginning of testing through all versions of the system to the one released. The historical chain may be used to review the development and testing processes across increments. The historical testing chain and the collection of testing chains from version to version can be used to assess reliability growth.
Reliability Growth Modeling
Many reliability growth models exist in the literature (Lyu, 1995). In each case the model developer sets out a list of basic beliefs about the phenomenon of improving software reliability in a failure-repair cycle. A mathematical model is devised that embodies the basic beliefs as its assumptions. The model is applied to the stream of field failure data, and statistical techniques are used to predict the future failure profile based on the trend of past data. If the software maintenance organization and the user base become sufficiently stable and repetitive, however good or bad, a suitable model for which the assumptions are materially met can be identified by statistical methods. Reliability growth can be measured to support post-deployment decisions.
Reliability growth can also be measured during system test and used to support deployment decisions. When the predicted level of failures is within acceptable intensity, duration and cost, the product can be released. Moreover, one can compare actual field experience with predicted field experience to assess the suitability of the reliability growth model being used.
Reliability growth modeling is being applied successfully to products that permit software changes in the field, and for which there is a degree of tolerance for failures, such as in central office telephone switches, computer operating systems and the like. Its use is problematic once the code is embedded in a system and inaccessible for change; in these cases the goal of testing is to demonstrate that the version of the software that is to be embedded in the system is
of sufficiently high reliability to render a recall sufficiently unlikely.
Combining Testing Information
There are many situations in the life cycle of a software intensive system where it would be beneficial to use existing testing and field use information to identify and minimize the additional testing that is needed to support a decision regarding the system. These situations can be generally classified as development, reengineering, maintenance, reuse and porting. Effective configuration control over the software and correct association of the testing records with code or system versions is required to use such information in a statistically valid way. Furthermore, a common basis for describing the testing done and for interpreting the data is necessary. Usage models have the potential to be the common denominator for test planning and evaluation of results in all testing situations in the system life cycle. The specific statistical models for combining information have not been worked out for every situation, but some progress has been made and work continues in this effort to unify testing. The theoretical path seems clear in all cases.
Development
The incremental development cycle of the Cleanroom software engineering process concludes each cycle with statistical testing to support the decision to move forward with development of the next increment. In the case of the final increment the decision is to deploy or accept the system. The testing protocol for incremental development is based on a comprehensive usage model in which one section is opened to generate test cases in the first increment; a second section is opened additionally for the second increment, etc. In each increment some testing is done in the previous section, but most is in the new section. The statistics associated with each increment of testing have the same usage model as a basis for
combining test information.
An evolutionary procurement of a defense system is based on the concept of a series of fielded systems with past performance, new requirements and new technology coming together for each successive version of the system. Previous testing records and field data are available after the first version. The usage model for the fielded version would be a subset of the model for the new version and the starting point for testing the new development. The field experience from various environments of use could be expressed in terms of the usage model and, together with planned revisions and changes, form the basis for testing.
Reuse
Many systems involve reuse of existing systems or system components, with or without reengineering. Object oriented reuse ranges from pattern instantiation, to framework integration, to class-subclass hierarchy extensions with polymorphic methods. If a component is to be reused without change, then the usage model originally used to certify the component can be used to assess the testing necessary for the new use. One would have the original usage model and testing records (testing chains and statistics), plus field use summarized as an estimate of sequences actually run. A set of transition probabilities would describe the new use. It is straightforward to compare the new use against the records of previous testing and use to determine whether or not further testing is required for the new use.
Reengineering
Reengineering typically involves changing the technology from which the system is made, for example, one or more of the hardware processor, memory units, power supplies or even the programming language and data structures, but generally preserves the way the system is used (otherwise, it would be new development or maintenance rather than reengineering).
Usage specifications usually survive, with varying degrees of change. The original usage model might change in structure. Usage states and arcs can be associated with underlying changes in the technology. Usage models might be used to assess the extent of change and to guide testing; the greater the change, the harder the testing problem.
Maintenance
Maintenance is usually associated with small change to an operational system. Thus, the developmental testing and field use records are available. Field experience indicates that good understanding of both the usage model (states and arcs) and the architecture and implementation of the system are required in order to map maintenance changes to relevant parts of the usage model. Testing after maintenance must address both known impact areas and the possibility of unanticipated impacts, and be planned using records of prior model-based testing and field use.
Porting
Porting is the process of moving a system to new or additional "platforms," usually meaning different operating systems for the same hardware, new hardware running the same operating system, or the hardware and operating system of a different vendor. Given a good software architecture and design that anticipated the porting, the changes to the system will be minimal but the services provided by the hardware and operating systems can be significantly different. Given multiple platforms on which the system must rim, what is the optimal amount of testing to be done on each platform in order to support a decision to deploy each? Generating test cases and recording test results based on a common usage model and a common set of statistics makes this a tractable problem.
A common framework for planning and recording all testing and field use in the life cycle of a system can lead to substantial cost savings in testing and much better information to support
decisions.
Conclusion
Most usage modeling experience to date is with embedded real-time systems (Oshana, 1997), application program interfaces (APIs) and graphical user interfaces (GUIs). Models as small as 20 states and 100 arcs have proven very useful. Typical models are on the order of 500 states and 2,000 arcs; large models of more than 2,000 states and 20,000 arcs are in use. Even the largest models developed to date are small in comparison to similar mathematical models used in industrial operations research, and are manageable with available tool support. Large models must be accepted as appropriate to many software systems and to the testing problem they pose. The size is not to be lamented, because the larger and more complex the testing problem, the greater the need for the assistance that modeling and simulation afford.
Since 1992, the IBM Storage Systems Division has developed and applied Markov chain usage models for certification of tape drives, tape controllers, tape libraries, disk drives and disk controllers. Some products are tested based on up to five different usage models, including models of customer use, a data communication protocol model, a model keyed to the injection of hardware and media failures, and a stress model. Many of these models are reused from product to product because only the technology of the product changes and not the architecture of the product, the way it is used or the standards to which it is built. Transition probabilities have been determined by using instrumentation measurements collected during internal use combined with external customer command traces originally collected for performance analysis of previous products. The test facility is highly automated and employs compiler writing technology to automatically compile executable test cases from abstract arc labels, which permits testing a large number of scripts. Stopping criteria are based on both high reliability estimates and substantial agreement between testing experience and expected field experience. Use of this technology has significantly reduced the testing effort and improved field reliability.
Special tools are available for integration into existing testing environments that support
those activities of testing based on usage models that have settled into ''standard practice,'' namely:
- systematic enumeration of input sequences to drive the discovery of behavior and identification of states and allowable transitions,
- usage model editing,
- generating uniform probabilities when specific values are not given,
- generating a standard set of statistics for model validation,
- generating the minimum cost state and arc coverage scripts,
- generating test cases with scripts,
- automatic construction of testing chains based on sequences generated and feedback of testing results,
- sorting failures according to the impact of repair on expected reliability,
- monitoring reliability, the discriminant and coverage measures as testing proceeds.
General tools must be used for aspects in which there has been insufficient experience to identify and justify specialized tools; for example, constraint-based generation of transition probabilities and related optimization problems must be solved using general purpose convex programming solvers. General purpose graph editors must be used for graphical model editing. Also, simulations must be programmed in a general purpose language.
Some activities of statistical testing are computationally intensive, with run-time for analyses a function of the number of states or the number of arcs in a usage model. While the computations would seem routine to an operations research analyst, they might seem prohibitive to some software engineers. Ironically, software engineering environments tend to be computationally starved. Computation times do not become an issue in work flow until the models reach about 2,000 states. In general, all the time and effort spent in modeling, analysis, and simulation will be recouped with dividends in the avoidance of uninformative testing.
Usage models facilitate the application of many aspects of statistical science to software testing, because (1) they offer a formalism in which to represent the statistical issues of interest
and (2) they have the ability to generate test cases and record the results of testing. They facilitate test planning as a part of the product or system requirements definition, which in turn makes it possible to optimize the amount of testing done at each stage of system development. Usage models set the stage for getting the best information from testing for the least cost. The economics of software failures in the field and the cost of testing complex systems make the use of statistical science imperative to software testing.
TABLE 1
Example of a Usage Model Structure, Transition Matrix Format
|
To State |
||||||||||||||||||
|
From State |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
1 |
0 |
l |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
2 |
0 |
0 |
x |
x |
x |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
4 |
0 |
0 |
0 |
0 |
0 |
x |
0 |
0 |
x |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
x |
x |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
8 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
x |
0 |
0 |
0 |
x |
0 |
0 |
|
|
11 |
0 |
0 |
0 |
0 |
x |
0 |
0 |
0 |
0 |
x |
0 |
x |
x |
x |
x |
x |
0 |
|
|
12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
x |
0 |
0 |
0 |
0 |
x |
0 |
|
|
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
17 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
TABLE 2
Example Usage Models, One Structure, Two Matrices of Transition Probabilities
|
From-State |
To-State |
Uniform Probabilities |
Specific Environment |
|
(1) Invocation |
(2) Initialize System |
1 |
1 |
|
(2) Initialize System |
(3) Reconfigure System |
1/3 |
1/12 |
|
(2) Initialize System |
(4) Mode-1 Setup |
1/3 |
8/12 |
|
(2) Initialize System |
(5) Mode-2 Setup |
1/3 |
3/12 |
|
(3) Reconfigure System |
(2) Initialize System |
1 |
1 |
|
(4) Mode-1 Setup |
(6) Mode-1 Standard Data |
1/2 |
3/4 |
|
(4) Mode-1 Setup |
(9) Mode-1 Special Data |
1/2 |
1/4 |
|
(5) Mode-2 Setup |
(10) Mode-2 High Rate Data |
1/2 |
1/12 |
|
(5) Mode-2 Setup |
(11) Mode-2 Service Decision |
1/2 |
11/12 |
|
(6) Mode-1 Standard Data |
(7) Mode-1 Data Analysis |
1 |
1 |
|
(7) Mode-1 Data Analysis |
(8) Mode-1 Checkpoint |
1 |
1 |
|
(8) Mode-1 Checkpoint |
(2) Initialize System |
1 |
1 |
|
(9) Mode-1 Special Data |
(7) Mode-1 Data Analysis |
1 |
1 |
|
(10) Mode-2 High Rate Data |
(11) Mode-2 Service Decision |
1/2 |
3/4 |
|
(10) Mode-2 High Rate Data |
(15) Mode-2 Transform Data |
1/2 |
1/4 |
|
(11) Mode-2 Service Decision |
(5) Mode-2 Setup |
1/7 |
2/16 |
|
(11) Mode-2 Service Decision |
(10) Mode-2 High Rate Data |
1/7 |
1/16 |
|
(11) Mode-2 Service Decision |
(12) Mode-2 Standard Data |
1/7 |
4/16 |
|
(11) Mode-2 Service Decision |
(13) Mode-2 Data Analysis |
1/7 |
4/16 |
|
(11) Mode-2 Service Decision |
(14) Mode-2 Operator Call |
1/7 |
1/16 |
|
(11) Mode-2 Service Decision |
(15) Mode-2 Transform Data |
1/7 |
3/16 |
TABLE 2
Example Usage Models, One Structure, Two Matrices of Transition Probabilities
|
(11) Mode-2 Service Decision |
(16) Mode-2 Checkpoint |
1/7 |
1/16 |
|
(12) Mode-2 Standard Data |
(11) Mode-2 Service Decision |
1 |
1 |
|
(13) Mode-2 Data Analysis |
(11) Mode-2 Service Decision |
1 |
1 |
|
(14) Mode-2 Operator Call |
(11) Mode-2 Service Decision |
1/2 |
1/2 |
|
(14) Mode-2 Operator Call |
(16) Mode-2 Checkpoint |
1/2 |
2/2 |
|
(15) Mode-2 Transform Data |
(11) Mode-2 Service Decision |
1 |
1 |
|
(16) Mode-2 Checkpoint |
(17) Termination |
1 |
1 |
|
(17) Termination |
(1) Invocation |
1 |
1 |
TABLE 3
Usage Statistics for the Model with Uniform Probabilities on the Exit Arcs
|
State Identification Number |
Long Run Probabilities |
Prob. of Occurrence in a Single Sequence |
Expected Number of Occurrences in a Single Sequence |
Expected Number of Transitions Until Occurrence |
Expected Number of Sequences Until Occurrence |
|
1 |
0.0449 |
1.0000 |
1.00 |
22.25 |
1 |
|
2 |
0.1348 |
1.0000 |
3.00 |
1.00 |
1 |
|
3 |
0.0449 |
0.5000 |
1.00 |
22.25 |
1 |
|
4 |
0.0449 |
0.5000 |
1.00 |
19.25 |
1 |
|
5 |
0.0749 |
1.0000 |
1.67 |
9.00 |
1 |
|
6 |
0.0225 |
0.3333 |
0.50 |
42.50 |
2 |
|
7 |
0.0449 |
0.5000 |
1.00 |
21.25 |
1 |
|
8 |
0.0449 |
0.5000 |
1.00 |
22.25 |
1 |
|
9 |
0.0225 |
0.3333 |
0.50 |
42.50 |
2 |
|
10 |
0.0674 |
0.7500 |
1.50 |
16.67 |
1 |
|
11 |
0.2097 |
1.0000 |
4.67 |
10.75 |
1 |
|
12 |
0.0300 |
0.4000 |
0.67 |
43.12 |
2 |
|
13 |
0.0300 |
0.4000 |
0.67 |
43.12 |
2 |
|
14 |
0.0300 |
0.5000 |
0.67 |
36.75 |
2 |
|
15 |
0.0637 |
0.6538 |
1.42 |
21.53 |
1 |
|
16 |
0.0449 |
1.0000 |
1.00 |
20.25 |
1 |
|
17 |
0.0449 |
1.0000 |
1.00 |
21.25 |
1 |
Number of arcs is 28.
Expected sequence length is approximately 23 states.
Expected number of sequences to cover the least likely state is approximately 3.
Expected number of sequences to cover the least likely arc is approximately 7.
The log base 2 source entropy is approximately 1.0197.
The specification complexity index is approximately 22.71 (or 6,861,000 sequences).
TABLE 4
Usage Statistics of Model for Specific Environment
|
State Identification Number |
Long Run Probabilities |
Prob. of Occurrence in a Single Sequence |
Expected Number of Occurrences in a Single Sequence |
Expected Number of Transitions Until Occurrence |
Expected Number of Sequences Until Occurrence |
|
1 |
0.0250 |
1.0000 |
1.00 |
40.08 |
1 |
|
2 |
0.0998 |
1.0000 |
4.00 |
1.00 |
1 |
|
3 |
0.0083 |
0.2499 |
0.33 |
120.28 |
3 |
|
4 |
0.0665 |
0.7273 |
2.67 |
12.03 |
1 |
|
5 |
0.0582 |
1.0000 |
2.33 |
16.00 |
1 |
|
6 |
0.0499 |
0.6667 |
2.00 |
18.04 |
1 |
|
7 |
0.0665 |
0.7273 |
2.67 |
14.03 |
1 |
|
8 |
0.0665 |
0.7273 |
2.67 |
15.03 |
1 |
|
9 |
0.0166 |
0.4000 |
0.67 |
58.11 |
2 |
|
10 |
0.0215 |
0.4843 |
0.86 |
58.52 |
2 |
|
11 |
0.2662 |
1.0000 |
10.67 |
17.10 |
1 |
|
12 |
0.0665 |
0.7273 |
2.67 |
31.13 |
1 |
|
13 |
0.0665 |
0.7273 |
2.67 |
31.13 |
1 |
|
14 |
0.0166 |
0.5000 |
0.67 |
66.67 |
2 |
|
15 |
0.0553 |
0.6935 |
2.22 |
33.82 |
1 |
|
16 |
0.0250 |
1.0000 |
1.00 |
38.08 |
1 |
|
17 |
0.0250 |
1.0000 |
1.00 |
39.08 |
1 |
Number of arcs is 28.
Expected sequence length is approximately 40 states.
Expected number of sequences to cover the least likely state is approximately 4.
Expected number of sequences to cover the least likely arc is approximately 16.
The log base 2 source entropy is approximately 0.9169.
The specification complexity index is approximately 36.68 (or 1.1 × 1011 sequences).
References
Alam, M.S., et al. 1997 Assessing software reliability performance under highly critical but infrequent event occurrences. In review.
Ash, R. 1965 Information Theory. New York: Wiley.
Basili, V., et al. 1996 The empirical investigation of perspective-based reading. Empirical Software Engineering 1:133-164.
Cohen, D.M. 1997 The AETG system: An approach to testing based on combinatorial design. IEEE Transactions on Software Engineering 23(7):437-444.
Dalal, S., and C. Mallows 1988 When should one stop testing software? Journal of the American Statistical Association 83(403).
Ehrlich, W., et al. 1997 Application of accelerated testing methods for software reliability assessment. In review.
Ekroot, L., and T.M. Cover 1993 The entropy of Markov trajectories. IEEE Transactions on Information Theory 39(4):1418-1421.
Gibbons, A.M. 1985 Algorithmic Graph Theory. Cambridge, U.K.: Cambridge University Press.
Gill, P.E., W. Murray, and M.H. Wright 1981 Practical Optimization. New York: Academic Press.
Gutjahr, W.J. 1997 Importance sampling of test cases in Markovian software usage models. Probability in the Engineering and Informational Sciences 11:19-36.
Kemeny, J.G., and J.L. Snell 1960 Finite Markov Chains. D. Van Nostrand Company, Inc.
Kullback, S. 1958 Information Theory and Statistics. New York: John Wiley and Sons.
Lyu, M.R. 1995 Handbook of Software Reliability Engineering. New York: McGraw-Hill.
Miller, K., et al. 1992 Estimating the probability of failure when testing reveals no failures. IEEE Transactions on Software Engineering. January.
Nair, V.N., D. James, W. Ehrlich, and J. Zevallos 1998 A statistical assessment of some software testing strategies and applications of experimental design techniques. Statistica Sinica 8:165-184.
Oshana, R. 1997 Software testing with statistical usage based models. Embedded Systems Programming 10(1):40-55.
Parnas, D. 1990 An evaluation of safety critical software. CACM. 23(6):636-648.
Poore, J.H., and C.J. Trammell 1996 Cleanroom Software Engineering: A Reader. Oxford, United Kingdom: Blackwell Publishers.
Prowell, S.J. 1996 Sequence-Based Software Specification. Ph.D. Dissertation, University of Tennessee, Knoxville, Tenn.
Prowell, S.J., and J.H. Poore 1998 Sequence-based specification of deterministic systems. Software—Practice & Experience 28(3 ):329-44.
Sherer, S.A. 1996 Statistical software testing using economic exposure assessments. Software Engineering Journal September:293-297.
Walton, G.H., J.H. Poore, and C.J. Trammell 1995 Statistical testing of software based on a usage model. Software—Practice & Experience 25(1):97-108.
Walton, G.H. 1995 Generating Transition Probabilities for Markov Chain Usage Models. Ph.D. Dissertation, University of Tennessee, Knoxville, Tenn.
Whittaker, J.A., and J.H. Poore 1993 Markov analysis of software specifications. ACM Transactions on Software Engineering and Methodology 2(1):93-106.
Whittaker, J.A., and M.G. Thomason 1994 A Markov chain model for statistical software testing. IEEE Transactions on Software Engineering 30(10):812-824.