2
On the Performance of Weibull Life Tests Based on Exponential Life Testing Designs
Francisco J. Samaniego and Yun Sam Chong, University of California, Davis
1. Exponential Life Testing
Applications abound in which investigators seek to make inferences about the lifetime characteristics of a ''system'' of interest from data on the failure times of prototypical systems placed on test. There are a good many different experimental designs that might be considered in planning a given life testing application; often, some form of data censoring (aimed at bounding the experiment's duration) or some sequential procedure (aimed at possibly resolving the test based on early failures) are part of the test plan. The analysis of life testing data is usually preceded by the setting of assumptions regarding the underlying probability distribution of system lifetimes. Among the most studied parametric life testing models are the exponential, gamma, Weibull, Pareto and lognormal families (see Lawless, 1982); nonparametric analyses under various assumptions on the distribution's hazard function or residual lifetime characteristics have also been developed (see Barlow and Proschan, 1975; Hollander and Proschan, 1984).
By far, the most comprehensive development of exact statistical procedures in life testing has occurred under the assumption of exponentiality. For virtually all other assumed models, the analysis of failure time data involves extensive use of numerical optimization methods and asymptotic approximations. The exact performance of tests and estimates developed under nonexponential assumptions has, for the most part, resisted analytical treatment, and has thus been studied mostly via simulation. The temptation to use exponential life testing methods is no doubt due, in part, to the marked lack of success in dealing with the theoretical properties of nonexponential life testing in a definitive way. The ease with which relevant distribution theory
(especially that involving ordered failure times) can be produced, and the occasional "conservatism" of the exponential assumption, have also contributed to its popularity, in spite of its notorious nonrobustness. It is important to acknowledge that the exponential assumption is very special and highly restrictive, so that its use should be discouraged except in circumstances in which there is good physical, empirical and practical support for the model. In due course, we will review the basics of exponential life testing, both to make the present paper self-contained and to set the stage for the various comparisons we wish to make with alternative analyses. First, however, we will describe the type of problem—a sort of statistical hybrid—on which the present investigation is focused.
Suppose a statistician is faced with an application in which two hypotheses concerning the mean life µ of a new system are to be tested. He wishes to resolve the test of H0: µ = µ0 against the alternative H1 : µ = µ1, where µ1 < µ0 are fixed and known, with certain predetermined probabilities α and β for type I and type II errors (also often called the producer's and consumer's risks). Having no pressing reason to doubt exponentiality in the application at hand, the statistician determines (using the Department of Defense's Handbook H108, for example; U.S. Department of Defense, 1960) that these goals can be accomplished with an experimental design calling for some specific number of observed failures (say r), rejecting H0 in favor of H1 if the total time on test Tat the time of the rth failure is less than the threshold T0. Among the advantages afforded by an exponential life test plan is the fact the the resources required to perform the test (that is, the number of systems that must be placed on test and the maximum amount of testing time needed to resolve the rest) may be calculated in advance. The fact that the duration of the test, in real time, can be controlled and made suitably small by placing n > r systems on test while still resolving the test upon the rth failure is also an important advantage.
Consider, now, the analysis stage of this life testing experiment. Suppose that when the data have been collected, their characteristics suggest that they are definitely not exponential. It then falls upon the statistician to analyze the available data under some alternative model or, perhaps, nonparametrically. Let us suppose, as will be tacitly assumed in the sequel, that the two-parameter Weibull distribution is taken as an appropriate underlying model for the
experiment in question. It is then incumbent upon the statistician to test the means µ0 vs µ1 under the Weibull assumption. The goal of this paper is to examine the consequences of this paradigm shift. We will study the resultant error probabilities associated with the Weibull test, and will explore the potential that exists for resource savings (smaller sample sizes, less testing time) when the Weibull model is entertained during the design stage rather than only at the analysis stage of the experiment. Our study has enabled us to identify the circumstances under which rather substantial resource savings are possible. For a study which examines similar questions in the contrast of interval estimation, see Woods (1996).
We now turn to a brief description of the mechanics of exponential life testing. Let us first suppose that a sample X1...,Xr of system lifetimes is available for observation, and that these data are independent and identically distributed according to the exponential distribution Exp(θ) with density function
For short, we will write ![]() . The statistic
. The statistic ![]() , which may be described as the "total time on test" for the r systems taken together, is a sufficient statistic for θ and is distributed according to the gamma distribution Γ (r,θ) with density function
, which may be described as the "total time on test" for the r systems taken together, is a sufficient statistic for θ and is distributed according to the gamma distribution Γ (r,θ) with density function
We use the subscript r : r to reflect the fact that the experimental design calls for sampling r failure times out of a random sample of size r. The standard estimate of θ based on Tr:r is the sample mean
which is both the maximum likelihood estimate and the minimum variance unbiased estimate of θ. For any fixed α ![]() (0,1), the best test of size α for testing H0 : θ = θ0 vs H1 : θ = θ 1 < θ0 is the test which rejects H0 if and only if
(0,1), the best test of size α for testing H0 : θ = θ0 vs H1 : θ = θ 1 < θ0 is the test which rejects H0 if and only if ![]() , where c is determined by the equation
, where c is determined by the equation
Since, given θ = θ0, 2T/θ0 is distributed as ![]() variable, it is clear that the threshold for rejection is given by
variable, it is clear that the threshold for rejection is given by ![]() , where
, where ![]() is such that
is such that ![]() when
when ![]() . The test which rejects H0 when
. The test which rejects H0 when
is, in fact, uniformly most powerful for testing against H1 : θ < θ0, and, in particular, maximizes the power (or minimizes the "consumer's risk" β) at the alternative θ = θ1. If we assume that the levels of α and β are fixed and determined in advance, then it remains to find the sample size r for which these levels obtain. Since r must satisfy the equation
it follows that the required sample size is the smallest integer r = r0 for which
The fact that the required sample size r0 is completely determined by the values of α, β and the "discrimination ratio" θ1/θ0 is a special feature of exponential life testing that facilitates the automated application of this methodology. Once a sample size r = r0 is obtained through (1.7), the rejection threshold c in (1.4) may be represented as
The constant c/θ, which is independent of model parameters, will appear in several of our tabulations as the multiplier which, together with the θ0 of interest, determines the rejection threshold of the desired test.
Execution of the exponential life test above is perhaps most easily described in terms of the "total time on test" (TTT) function. If X(1) <,...,< X(r) are the ordered failure times in our sample of size r, then the TTT function may be written, for ![]() as
as
where ![]() and j = 0, 1,...,r -1. The TTT function keeps track of the total amount of test time logged by working systems up to a fixed time t. Clearly
and j = 0, 1,...,r -1. The TTT function keeps track of the total amount of test time logged by working systems up to a fixed time t. Clearly
The TTT function is itself a useful tool in reliability modeling. Plots involving a rescaled version of this function will be discussed in the next section.
Returning to the problem of testing H0: θ = θ0 vs H1 : θ = θ1, we note that the test may be resolved as follows: if the rth failure occurs before the total time on test exceeds the threshold r0c, that is, if Tr:r(X(r)) < r0c, then H0 is rejected in favor of H1; otherwise, H0 is accepted. In the latter case, the experiment is completed at time t0, where
while in the former case, the experiment is terminated at time t = X(r) < t0. Thus the threshold r0c, with c given in (1.8), represents the maximum total test time that could be required to resolve the test, that is, to be able to accept or reject H0 on the basis of the data. Together, r0 and c describe the total resources that must be committed to guarantee successful completion of the life test.
Extension of the above discussion to type II censored data is immediate. If ![]() , and if the experiment is terminated upon the occurrence of the rth failure, then the statistic
, and if the experiment is terminated upon the occurrence of the rth failure, then the statistic
is sufficient for θ. Moreover, since Tr:n has precisely the same distribution as Tr:r, that is, since
the best test of H0 : θ = θ0 vs H1 : θ = θ1 has the same form as before, that is, rejects H0 if
where
is the MLE (and UMVUE) of θ.
Similarly, the sample size required to resolve this test, given set values for α, β and θ1/θ0, is r0 derived via (1.7), and the maximum total testing time needed is again the constant r0c, where c is given in (1.8). The number n of systems on test influences test performance only with regard to the test's duration. Let us expand the definition of the total time on test function to accommodate the case of type II censoring; for ![]() , define
, define
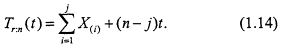
Then, under type II censoring, the experiment is terminated at time t = X(r) if ![]() or, otherwise, at time t = t0, where t0 satisfies the equation
or, otherwise, at time t = t0, where t0 satisfies the equation
It is easy to see that the random time min(X(r0), t0 (X)) at which the experiment is terminated is bounded above by the factor r0c/(n-r 0). Thus, the waiting time until the test is completed can be made suitably small for any fixed r0 by choosing the sample size n sufficiently large. This strategy of course is based on a tacit assumption of the correctness of the exponential model in the application of interest; when exponentiality fails, this practice can yield highly misleading results.
There are a host of other experimental designs for exponential life testing, including type I censoring (that is, censoring at a fixed time t), random record designs (that is, observing only record breaking failure times) and sequential designs. The type of study which will be pursued in this paper can be carried out analogously for other designs, but we have chosen to focus exclusively on complete and type II censored data. This choice is motivated by the fact that these two designs are frequently encountered in practice and also by our belief that the general lessons learned from analyzing these particular designs will hold more broadly. For example, the distribution theory developed in Samaniego and Whittaker (1986) shows that inverse sampling from an exponential distribution until the occurrence of the rth record value (that is, successive minimum) yields a test statistic (again, the total time on test) that has properties identical to those of the designs mentioned above. In particular, the resources required to resolve testing problems for predetermined values of α, β θ0 are again given by the pair (r0, c) of (1.7) and (1.8).
Instead of pursuing greater breadth in the designs considered, we will direct our efforts at examining two particular designs (complete samples and type II censoring) in depth.
As a guide for military applications of exponential life testing, DoD Handbook H108 provides tabled values of the required sample size r0 and the constant c/θ0 through which the total test time required by a particular application can be computed. An excerpt from Table 2B-5 of that Handbook, showing the five tabled values given corresponding to error probabilities α =. 1 and β = 1, appears in Table 1. If, for instance, one wishes to test H0: θ = 1,000 hrs vs H1: θ = 500 hrs, and one sets α = .1 = β, then Table 1 indicates that 15 or more systems should be put on test, and that a total test time required to ensure resolution of the test is 15(.687)(1,000) = 10,305 hrs.
Before proceeding with our study of alternatives to exponential life tests, we briefly review what is known about their lack of robustness. Of special interest to us is the behavior of exponential life tests when the underlying distribution is a nonexponential Weibull, since it is then that the procedures we investigate in the sequel stand to provide improved performance. We thus restrict ourselves to this particular circumstance and describe the findings of Zelen and Dannemiller (1961), who studied the performance of exponential life tests for Weibull data in exhaustive detail. In that paper, four specific life testing designs were studied: complete samples, type II censored samples, truncated type II censored samples, and samples obtained sequentially. We quote from Zelen and Dannemiller's discussion section:
None of the four life testing procedures studied in this paper is robust with respect to Weibull alternatives. In particular, the censored life test and the truncated nonreplacement test are strikingly non-robust. It is obvious from the graphs of the O.C. curves that lots having low mean failure time have a high probability of acceptance when the failure times follow a Weibull distribution with shape parameter p > 1. This tendency is increased as p increases.... We have tried to show that dogmatic use of life testing procedures without a careful verification of the assumption that failure times follow the exponential distribution may result in a high probability of accepting "poor quality" equipment.
In the case of complete and type II censored samples, the operating characteristics plotted by Zelen and Dannemiller indicate the extent to which the risk of a high probability of acceptance of a hypothesized mean of 1,000 occurs at mean values less than 1,000.
The performance of the exponential test of H0: θ = 1,000 vs H1: θ = 500 at the nominal values α = .1 = β is shown there to deteriorate as the Weibull shape parameter increases from 1 to 3. It is interesting to note that at θ = 500 and θ = 1,000, the probabilities α and β of error actually decrease in the complete sample setting; this is a manifestation of the conservative nature of these tests. Since Weibull distributions with shape parameter greater than I are lighter tailed than the exponential, these distributions are more tightly concentrated about the mean, rendering it easier to distinguish between two candidate mean values on the basis of a Weibull sample. For complete samples, the nonrobustness of which Zelen and Dannemiller write becomes evident as the mean value at which the probability of accepting H0 is being computed moves toward the null value 1,000 from the alternative value of 500. At θ = 750, for example, the probability of accepting H0: θ = 1,000 goes from .615 under exponentiality to .837 under a Weibull distribution with shape parameter equal to 3. In spite of this type of inflation, it is clear that exponential life tests carried out with complete samples offer reasonable performance in that even under rather severe departures of the Weibull type, they deliver error probabilities at selected key parameter values θ0 and θ1 that are smaller than those set at the planning stage. The question that will interest us as we proceed is: since the achieved α and β levels are both lower than planned for or required, what savings might be possible with a test that is calibrated to achieve the nominal values of α and β when the data are Weibull?
The case of censored samples is markedly different from the above. In an example involving n = 28 systems on test with censoring at the 14th failure, Zelen and Dannemiller note that the probability of acceptance of H0: θ = 1,000 is exceedingly high for all potential mean values between the alternative 500 and the null 1,000. Remarkably, the probability of accepting the null hypothesis of mean 1,000 when the true mean is 500 is .985 when the sample is drawn
from a Weibull distribution with shape parameter 3. Even when the shape parameter is 1.5, this probability is unduly high (.463).
The lessons to be learned from the phenomena documented above include (1) exponential life testing based on complete samples works fairly well in a Weibull environment, but there should be opportunities for saving resources when that environment is recognized in advance; and (2) exponential life testing based on censored samples works very poorly in a Weibull environment, and alternative procedures should be considered when the exponential assumption is suspect. The sequel is largely devoted to the study of ways of addressing these two issues.
Before proceeding, let us make special mention of the scope of this paper, and its attendant limitations. We have begun by discussing exponential life testing based on complete or type II censored samples. In sections 3 and 4, we will develop a comparable analysis under the assumption that the underlying distribution of the observable failure time data is, instead, a nonexponential Weibull. Both analyses assume that it is a random sample of items simultaneously and independently placed on test. Because of the memoryless property of the exponential distribution, exponential life testing methods can be validly applied (assuming the model is appropriate) to data on time between failures of repairable systems by treating time between failures as independent exponential observations. Such an extension will not generally be valid under Weibull assumptions. In the latter case, the alternative analysis developed in this paper would be applicable only when each repair following an observed failure could reasonably be considered "perfect" in the sense of restoring the item to its condition when new. When such an assumption cannot be justified, the appropriate reanalysis of data should be based on a more elaborate modeling of the failure process, perhaps as a nonhomogeneous Poisson process. Nonparametric alternatives in this setting have been developed by Nelson (1995) and by Lawless and Nadeau (1995) and have been shown to work very well in a variety of applications (without the restrictive NHPP and independence assumptions). Such analyses lie beyond the scope of the present paper.
Other issues not covered in the present report include the treatment of systems with multiple failure modes and the treatment of accelerated life testing data. Parallel developments
in those areas, where Weibull alternatives to exponentiality assumptions are developed, would certainly be worthwhile.
2. Weibull Considerations
The Weibull distribution is arguably the most popular parametric alternative to the exponential distribution in reliability applications. Like the gamma model, it contains the exponential distribution as a special case, so that the adoption of a Weibull assumption represents a broadening from the exponential model rather than a rejection of it. Often, statistical extreme value theory forms the basis for the applicability of the Weibull model; when system failure can be attributed to the failure of the weakest of its many components, the Weibull model will tend to describe failure data quite well. The parametrization we will employ for the Weibull is as follows: X has a Weibull distribution with parameters A > 0, B > 0 (henceforth denoted as X~ W(A,B)) if X has distribution function
and density function
where A is the "shape" parameter and B1/A the scale parameter of the distribution. The mean and variance of X ~ W(A,B) can be written as:
and
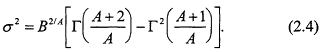
The coefficient of variation cv = σ/µ is independent of the parameter B and may be written as
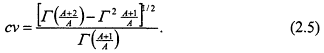
It is apparent from (2.2) that the W(1,B) distribution is simply the exponential distribution Exp(B). A more interesting and valuable connection between the Weibull and exponential models is the fact that if X ~ W(A,B), then XA ~ Exp(B).
There is a rather substantial literature on modeling and inference involving the Weibull distribution. A keyword search of the Current Index to Statistics, volumes 1-19 (American Statistical Association, 1975 to 1995), shows that there were 647 articles published in statistics journals between 1975 and 1993 on Weibull-related topics. Much of this literature deals with estimation issues, with goodness of fit questions, with separate families tests (for example, testing Gamma vs Weibull) or with robustness issues. Good overviews on estimation and testing procedures may be found in the recent books by Lawless (1982), Sinha (1987) and Bain and Engelhardt (1991). Other references with extensive discussion of inference for the Weibull distribution include Mann, Shafer and Singpurwalla (1972), Sinha and Kale (1979) and Nelson (1982 and 1990).
Of particular interest to us are testing procedures which seek to distinguish between two mutually exclusive collections of Weibull models. In the sequel, we will examine and compare various approaches to testing competing hypotheses about a Weibull mean. The literature on this latter problem is rather sparse. When the shape parameter is assumed known, the test of interest can be executed easily after transforming the data into exponential variables. With the scale parameter known, Bain and Weeks (1965) developed tests and confidence intervals for the unknown shape parameter. For the general problem, when both A and B are unknown, there is rather limited guidance on how to proceed. Thoman, Bain and Antle (1969) have developed MLE-based confidence intervals for each parameter when the other parameter is unspecified. However, it is known that large sample methods based on the asymptotic behavior of maximum likelihood estimates behave rather poorly for small and moderate samples (see Lawless, 1975). Likelihood ratio tests for
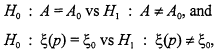
where ξ(p) is the pth quantile of the underlying probability distribution, are discussed in Lawless (1982) and recommended as preferable to tests based on the large sample distributions of MLEs. Lawless (1982:195-197) discusses Weibull life test plans briefly, stating that ''life test plans under the Weibull model have not been thoroughly investigated it is almost always impossible to determine exact small-sample properties or to make effective comparisons of plans, except by simulation.... Therefore, little formal discussion of the merits of different plans has taken place Further development of test plans under a Weibull model would be useful.'' It is our hope that the discussion of Weibull life testing in this paper will contribute to a better understanding of the possible advantages and risks these methods involve.
As we have described the problem of interest in the introductory section, the statistician, after collecting data under an exponential life test plan, takes the opportunity to reconsider his distributional assumptions. "Physics of failure" considerations might, in certain cases, point to an alternative model. In the case that Weibull alternatives to the exponential are considered sufficiently broad, one can carry out a formal test of the hypothesis H0 : A = 1 (that is, X is exponential) vs ![]() (that is, X is nonexponential Weibull). Such a test is outlined in Thoman et al. (1969). More generally, there is a variety of existing goodness of fit tests through which an alternative model, Weibull or otherwise, might be identified. Attractive and usually quite effective alternatives to formal or analytical procedures are two widely used graphical methods: total time on test (TTT) plots and plots of transformed failure times on suitably chosen probability paper. We discuss these two methods below as possible tools in determining the viability of exponential assumptions against Weibull alternatives.
(that is, X is nonexponential Weibull). Such a test is outlined in Thoman et al. (1969). More generally, there is a variety of existing goodness of fit tests through which an alternative model, Weibull or otherwise, might be identified. Attractive and usually quite effective alternatives to formal or analytical procedures are two widely used graphical methods: total time on test (TTT) plots and plots of transformed failure times on suitably chosen probability paper. We discuss these two methods below as possible tools in determining the viability of exponential assumptions against Weibull alternatives.
Total time on test plots were introduced by Barlow, Bartholomew, Bremner and Brunk (1972), and their properties have been studied further by Barlow and Campo (1975), Barlow (1979), Chandra and Singpurwalla (1981) and Neath and Samaniego (1992). Barlow, Toland and Freeman (1988) employ TTT plots in a large scale accelerated life testing experiment as a guide to appropriate modeling. Such plots are widely used as goodness of fit indicators for the
exponential distribution. In what follows, we will restrict attention to the total time on test function in (1.14) since the complete sample version in (1.9) is subsumed by (1.14) when n = r. We note that the TTT function in (1.14) has domain [0,X(r)] and range  . To render TTT plots both manageable and comparable, a rescaled version of the function is generally used. For an arbitrary positive random variable X with distribution F and finite mean µ, the total time on test transform τ is defined as
. To render TTT plots both manageable and comparable, a rescaled version of the function is generally used. For an arbitrary positive random variable X with distribution F and finite mean µ, the total time on test transform τ is defined as
where ![]() , and the survival function
, and the survival function ![]() . As is well known, τ(1) = µ. The empirical counterpart τn of τ is obtained by replacing F in (2.6) by the empirical cdf Fn. If n items are placed on test, and the ordered lifetimes {X(1), X(2),...} are observed, then τn may be evaluated at x = j/n as
. As is well known, τ(1) = µ. The empirical counterpart τn of τ is obtained by replacing F in (2.6) by the empirical cdf Fn. If n items are placed on test, and the ordered lifetimes {X(1), X(2),...} are observed, then τn may be evaluated at x = j/n as
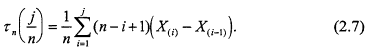
Thus, nτn(r/n) is precisely the cumulative survival time of all tested items at the time of the rth failure. The transform τn is continuous arid is linear for ![]() for each j. For complete samples, the function
for each j. For complete samples, the function
is plotted for ![]() , while for type II censored data, the function
, while for type II censored data, the function
is plotted for ![]() . In both cases, the plots lie in the unit square. It is easy to verify that the TTT transform τ of the exponential distribution is linear, and that the rescaled transform of the exponential is the diagonal line in the unit square.
. In both cases, the plots lie in the unit square. It is easy to verify that the TTT transform τ of the exponential distribution is linear, and that the rescaled transform of the exponential is the diagonal line in the unit square.
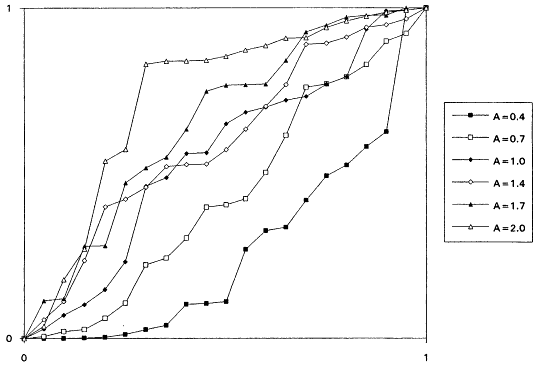
The failure rate of a distribution is defined as f(t)/F(t). The failure rate of the Weibull distribution W(A,B) is given by
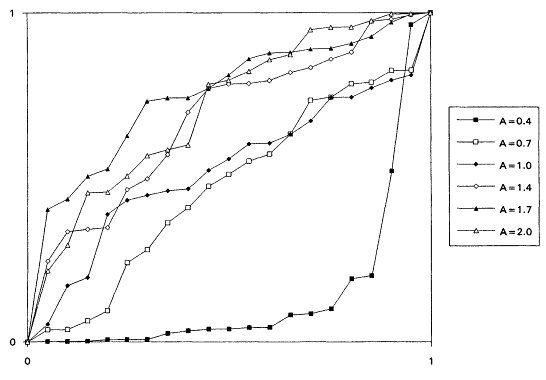
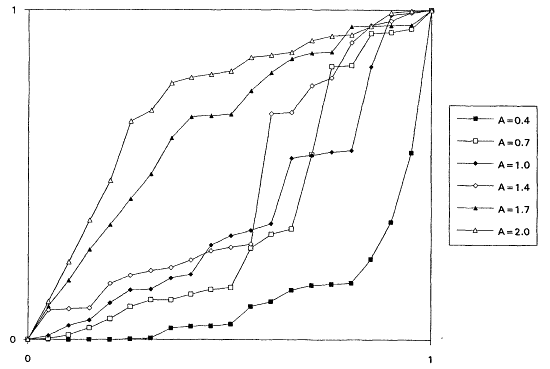
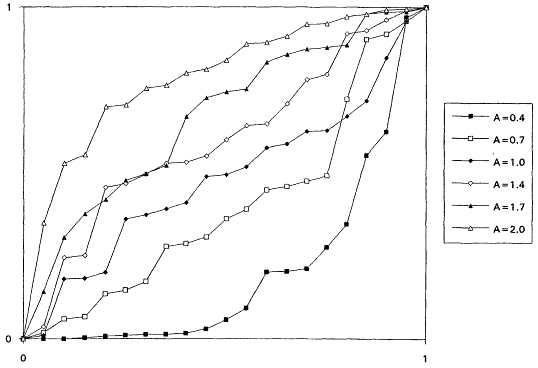
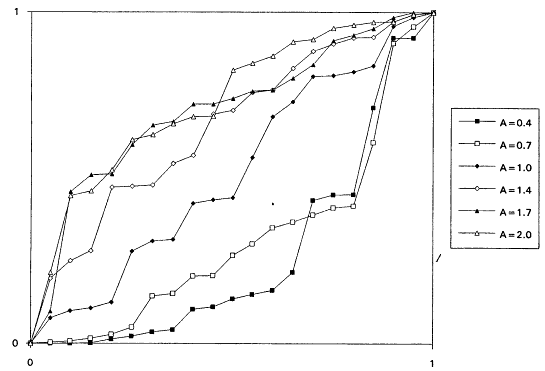
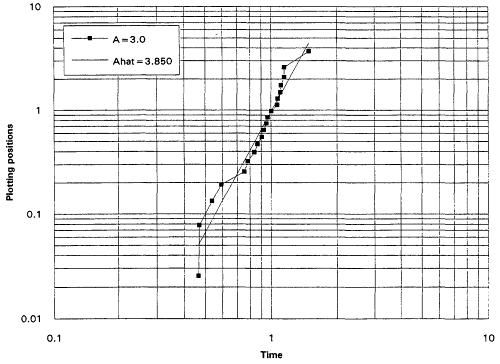
which is decreasing for A < 1 and increasing for A > 1. It is known that the rescaled TTT transform of a distribution with increasing failure rate (IFR) is concave and that for a distribution with decreasing failure rate (DFR) is convex. Thus, the TTT plot based on a sample from a nonexponential Weibull might be expected to exhibit some nonlinearity—concavity when A > 1 and convexity when A < 1. Plotting a scaled TTT transform for data collected according to an exponential life testing plan is an excellent way to detect possible departures from exponentiality. In Figures 1 to 6, we display the TTT plots from six consecutive simulated Weibull experiments, each featuring complete samples of size 20 from eight Weibull distributions with varying shape parameters. These figures give a feeling for the variability in TTT plots for a fixed value of A, and for the general character of the plots as A varies from 0.3 to 3.0.
From the TTT plots above, it should be evident that detecting departures from an exponentiality assumption is not an exact science. For example, five of the six simulated TTT plots of data drawn from the W(3.0, 1.0) distribution show convincing IFR behavior, while one, from the second simulation, is much less definitive. While a TTT plot may not be conclusive, it will often be quite suggestive of possible nonexponentiability; as such, it seems reasonable to suggest that such graphical investigations be a standard part of the analysis of life test data. For formal tests for exponentiality based on the TTT transform, see Barlow and Proschan (1969) and Klefsjö (1980).
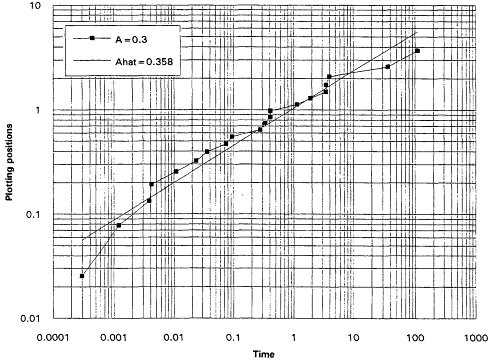
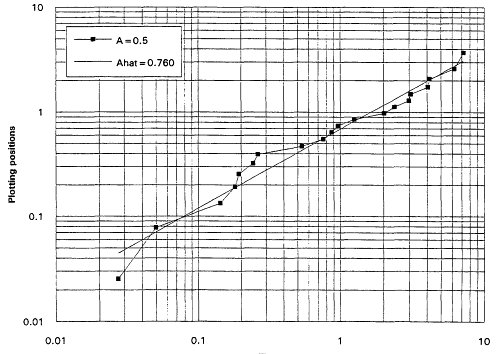
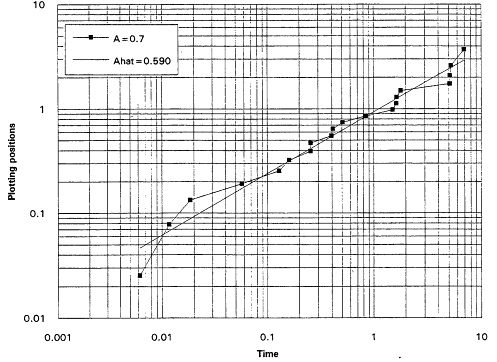
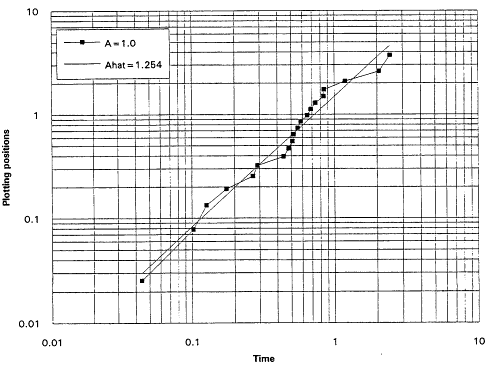
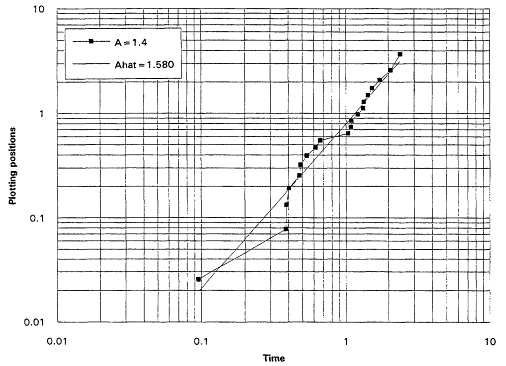
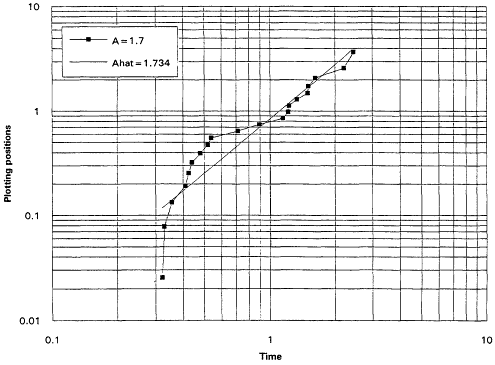
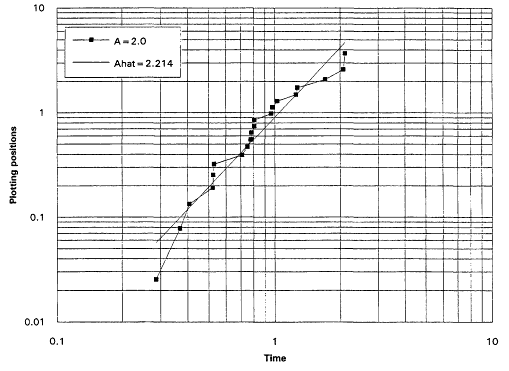
It is, of course, true that a TTT plot does not point directly toward a Weibull alternative when it casts doubt upon the exponential assumption. Detecting IFRness or DFRness is a good start, but the checking for Weibullness requires more. Nelson (1990) and others advocate plotting life testing data on Weibull probability paper. A strong linear trend in such plots is indicative of an underlying Weibull distribution. These plots are based on the following considerations: The Weibull survival function is
and thus
Equation (2.10) is the basis for the expected linearity in a Weibull plot. The plot itself is simply a scatter diagram consisting of the points ![]() for i = 1,...,r. The parameters
for i = 1,...,r. The parameters ![]() and A are generally estimated by the intercept and slope of the least squares line fitted to these points. The figures that follow show Weibull plots for eight simulated samples of size 20 from Weibull distributions with varying shape parameters. These plots (Figures 7 to 14) appear as scatter diagrams of the points
and A are generally estimated by the intercept and slope of the least squares line fitted to these points. The figures that follow show Weibull plots for eight simulated samples of size 20 from Weibull distributions with varying shape parameters. These plots (Figures 7 to 14) appear as scatter diagrams of the points ![]() on log-log paper.
on log-log paper.
Through use of the graphical methods described above, or otherwise, assume that the statistician, after gathering data according to an exponential life test plan, determines that the data are more appropriately modeled as a nonexponential Weibull. It will then be necessary to proceed with an analysis appropriate for these broadened assumptions. The next two sections are dedicated to an examination of various ways of carrying out a Weibull life test.
3. Weibull Life Testing—Part I
The classical theory of hypothesis testing yields its strongest results in problems in which the null and alternative hypotheses are simple, that is, specify the underlying probability model completely. In that circumstance, it is possible to construct tests that will minimize the consumer's risk β among tests with producer's risk less than or equal to some fixed level α. When one or both of the hypotheses of interest are composite rather than simple, optimal testing procedures exist only in rather special circumstances. The problem of interest here is of this latter type, and no "optimal" tests have been devised for solving this problem. Specifically, we are interested in tests which compare two prespecified values of the population mean based on an available sample (be it complete or censored) drawn from a Weibull distribution. When the basic observable lifetime is distributed according to W(A,B), then the null hypothesis H0 : µ = θ0 actually represents the complex composite hypothesis that the parameter pair (A,B) satisfies the equation

Thus, testing H0 : µ = θ0 vs H1 : µ = θ1 forces one to consider whether the parameter pairs (A,B) consistent with H0 provide an adequate explanation of the data by comparison to the explanation provided by (A,B) pairs satisfying H1. We will eventually examine three specific ways of testing θ0 vs θ1 in the context above. We first treat a simpler problem for which an exact and optimal solution is available. Our purpose is to construct a "gold standard" against which solutions to the original problem can be compared.
Let us, then, assume that a random sample X1,...,Xr is available from what was originally thought to be an exponential distribution, and that the sample size r was determined on the basis of an exponential life test plan for testing H0 : µ = θ0 vs H1 : µ = θ1, where θ0 > θ1, at fixed predetermined values of the error probabilities α and β. Assume further that, once the data was collected, the assumption
was adopted. Finally, let us suppose that the shape parameter A is known precisely. Then we may transform the data to
and test H0: µ = θ0 vs H1 : µ = θ1 on that basis. We note, however, that the discrimination ratio θ1/θ0 in the original problem is affected by the transformation in (3.3). Specifically, the original hypotheses may now be rewritten as
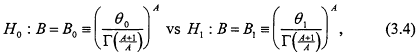
to be tested on the basis of data from Exp(B). The discrimination ratio in this latter problem is

which is a decreasing function of A. This change is significant in that the performance characteristics of exponential life tests depend very strongly on this parameter. The
discrimination ratio is a measure of the distance between the null and alternative hypotheses. If that ratio is reduced sharply, the new testing problem can be resolved with much greater power. In particular, given the same sample size, the α, β values that can be realized in the transformed environment will be much smaller than the nominal levels with respect to which the test was planned. Alternatively, the same nominal α, β values could have been achieved with a substantially smaller sample size. The flip side of these outcomes must also be mentioned. In the DFR case, we see that the discrimination ratio increases under a power transformation. It will then be generally true that error probabilities are larger than their nominal values when the sample size is held constant, and it may take a substantially larger sample size to achieve the nominal levels of α and β. Thus, life testing in a Weibull environment is not necessarily advantageous to the tester. Fortunately, in many engineering applications of the Weibull distribution, the shape parameter A turns out to be substantially larger than 1, and the opportunity exists for the execution of tests with smaller error probabilities or tests requiring less in the way of resources for their implementation. When infant mortality (and an initial decreasing failure rate) is present, the institution of a bum-in phase, in which key defects are detected early and removed, will tend to result in burned-in systems whose lifetimes are well modelled by an IFR distribution.
One of the main goals of the present study is to characterize the magnitude of the gains or losses attributable to a shift from the exponential to the Weibull paradigm. In order to do this, it is necessary to have tables like our Table 1 (that is, Table 2B-5 in DoD Handbook H108) in much more extensive form. As mentioned in the discussion following Table 1, an exponential life test for testing H0 : θ = 1,000 hrs vs H1 : θ = 500 hrs with α = β =.1 requires that at least 15 systems be placed on test, and requires a total time on test of up to 10,305 hrs. Now, suppose it is determined that the Weibull distribution W(2,B) is the appropriate model under which the data from this experiment should be analyzed. In this particular Weibull environment, after squaring each observed failure time, we are testing the hypotheses H0 : B = 1,273,231 hrs2 vs H1: B = 318,208 hrs2 based on data from the exponential distribution Exp(B). Since the discrimination ratio in this new problem is 1/4, we'd now like to determine, for comparison purposes, the test resources that would be required to carry out the latter test at α = β =.1. Two
difficulties arise in trying to do this. First, the discrimination ratio 1/4 does not appear in Table 1, so that the values of the required sample size r0 and critical threshold c/θ0 can only be roughly determined by interpolation. Second, the critical threshold in the new problem relates to a function other than total test time—in general, it is a threshold which provides a bound for the statistic ![]() rather than for the total time on test
rather than for the total time on test ![]() . We will now consider each of these matters carefully.
. We will now consider each of these matters carefully.
In order to be able to examine the impact of an arbitrary power transformation from W(A,B) to Exp(B), we need to have a table comparable to Table 1, but containing values of r0 and c/θ0 for any value of the discrimination ratio between 0 and 1. The computations involved are conceptually simple—we need to find, for fixed values of α, β and the ratio θ1/θ0, the smallest integer r0 satisfying inequality (1.7) and the associated value of c in (1.8). In developing our tabulations, we have utilized the Peizer-Pratt approximation (see Alfers and Dinges, 1984) for X2 tail probabilities for degrees of freedom θ, and an approximation based on the Central Limit Theorem for degrees of freedom >100. Normal tail probabilities were approximated using an "error function" which is a special case of the incomplete gamma function (see Press et al., 1992:220). Whenever the inverse of the normal or X2 distribution was needed, we employed numerical approximations for the quantiles of interest based on Newton-Raphson iterations. For computations involving the gamma function, we used table of Γ( x) for x = 1.0(.01)2.0 found in Abramowitz and Stegun (1964), with linear interpolation as needed. We note that stable, highly accurate algorithms for the functions above are available in various popular software packages (NAG, IMSL, S+, netlib). In the first four columns of each page in Tables 2, 3, 4 and 5, we have recorded the discrimination ratio, the required number r0 of systems on test, the critical threshold c/θ0, where c is computed via equation (1.8), and the realized value of β when the exponential life test is executed at the indicated nominal significance level α.
Our expansion of DoD Handbook H108's Table 2B-5 is restricted to four typical choices of α, β: α = β = .01 (Table 2), α = β = .05 (Table 3), α = β = .10 (Table 4) and α = β = .25 (Table 5). In each of these four tables, we record, for different values of the shape parameter A
of the underlying Weibull parameter (for A = .1 (.1)3), the values of four measures of the impact of carrying out a Weibull life test: SSR (for "sample size ratio"), TTTR (for "total time on test ratio") BR (for the ratio of error probabilities β of the Weibull test and the planned exponential test at the same fixed values of α and r) and r/n (for the censoring fraction at which the Weibull analysis approximately achieves the nominal error probabilities in the exponential test plan). We now turn to a description of the reasoning and computations involved in producing these four measures.
As the discrimination ratio changes from θ1/θ0 to (θ1θ0 )A in the course of shifting from exponential to Weibull assumptions, so do the sample size requirements for any fixed α and β. In general, the smallest integer r0 satisfying (1.7) is an increasing function of the discrimination ratio, so that, when A > 1, the sample size needed to resolve the Weibull test will be smaller than that called for in the original test plan (and, conversely, will be larger when A < 1). The ratio of these two sample sizes is recorded as SSR. If, for example, for α = β = .1, and the original discrimination ratio is .5, then r0= 15 for the exponential test plan. If A = 2, then the new discrimination ratio is .25, and the new required sample size is r0 = 4. In the column labeled SSR under A = 2.0, and in the row for θ1/θ0 = .5, one finds the tabulated value SSR = .267 which, of course, is equal to 4/15.
Determining the maximal total time on test that might be required in the Weibull environment is a little trickier. Indeed, it cannot be determined exactly, though useful (indeed, sharp) upper and lower bounds can be obtained. In the case of complete samples from W(A,B ), we know that the Weibull life test will stop as soon as
where c may be obtained from Table 4 through the use of the value of c/θ0 corresponding to the discrimination ratio (θ1θ0 )A and the formula

The question then arises: what are the possible values of the total time on test ![]() under the constraint in (3.6)? That question is answered by the following result:
under the constraint in (3.6)? That question is answered by the following result:
Lemma 1: Let X be the set of all vectors ![]() of nonnegative real numbers such that
of nonnegative real numbers such that
Then, if A > 1,
and if A < 1,
Moreover, these bounds are sharp.
Proof: The upper bound in (3.9) and the lower bound in (3.10) may be obtained quite readily by Lagrangian optimization. The other two bounds may be obtained by variational and/or geometric arguments. We eschew these approaches in favor of a simple argument based on majorization ideas (see Marshall and Olkin, 1979). If x, y are vectors in ![]() , then x is majorized by y
, then x is majorized by y ![]() if
if ![]() and the ordered vectors, with
and the ordered vectors, with ![]() and
and ![]() satisfy the inequalities
satisfy the inequalities
A real valued function ϕ is Schur convex if ![]() whenever
whenever ![]() , and Schur concave if
, and Schur concave if ![]() whenever
whenever ![]() . It is clear from these definitions that a Schur convex function is maximized, among vectors
. It is clear from these definitions that a Schur convex function is maximized, among vectors ![]() with nonnegative components and a fixed sum S, by the vector x that majorizes all the rest, namely
with nonnegative components and a fixed sum S, by the vector x that majorizes all the rest, namely
and is minimized, within this same class of vectors, by the vector x majorized by all the rest, namely
Similarly, among the class of vectors of interest, a Schur concave function will be maximized by xm and minimized by xM. It remains to show that these ideas provide a solution to the problem posed by the Lemma.
It is well known (see Hardy, Littlewood and Pólya, 1929) that if g(x) is a real valued convex function, then the function
is Schur convex, and if g is concave, ϕ in (3.14) is Schur concave. Now, since the function
is convex for ![]() when p > 1 and is concave for
when p > 1 and is concave for ![]() when 0 < p < 1, we have that
when 0 < p < 1, we have that
is Schur convex on ![]() for p > 1 and is Schur concave on
for p > 1 and is Schur concave on ![]() for 0 < p < 1. Now, consider the functions of x given in (3.8) and (3.9). By defining
for 0 < p < 1. Now, consider the functions of x given in (3.8) and (3.9). By defining ![]() , we may rewrite the problem at hand as: minimize and maximize
, we may rewrite the problem at hand as: minimize and maximize
among ![]() Since ϕ* in (3.17) is Schur concave when A > 1, we have that
Since ϕ* in (3.17) is Schur concave when A > 1, we have that
Transforming back from y to x yields (3.9). It follows, similarly, by the Schur convexity of ϕ* when A < 1, that, in this case,
Replacing yi by ![]()
![]() in (3.19) yields (3.10).
in (3.19) yields (3.10).
The lemma above allows us to bound the total time on test required in a Weibull environment to achieve the nominal α and β levels. We will use these bounds differently, depending on whether A > 1 or A < 1. If A > 1, then the total time on test required to resolve the Weibull test based on the transformed data will generally be smaller than the maximal TTT called for in the exponential life test plan. In this case, the upper bound in (3.9), with K = r*c*, where r* and c* correspond to the sample size and critical threshold for the transformed discrimination ratio, serves as an indicator of the potential savings in TTT in the new environment. It is, of course, an upper bound; the true savings may be substantially greater! The total time on test ratio (TTTR) tabulated for each combination of discrimination ratio and shape parameter, is the ratio of the maximal (that is, upper bound) TTT in the Weibull environment to the planned-for TTT in the original exponential environment. For example, for α= β = .1 and discrimination ratio is .5, the TTT required to guarantee resolution of the exponential life test is, as we have seen, 10,305 hrs. If one then assumes a W(2,B) environment, the new discrimination ratio is .25, requiring, to achieve the same α and β levels, that r = 4 observations be placed on test and that a maximum value for ![]() of K = 4(.436)(1,273,239) = 2,220,529 hrs2. Thus, the upper bound on the total time on test is
of K = 4(.436)(1,273,239) = 2,220,529 hrs2. Thus, the upper bound on the total time on test is ![]() hrs. From this, we find that TTTR = 2,980.3/10,305 = .289, as recorded in Table 4 in the TTTR column under A = 2.0 and across from θ1/θ0 = .5. It is possible to give a closed form expression for TTTR as a function of A, α, and the sample sizes r0 and r1 in the exponential and Weibull environments:
hrs. From this, we find that TTTR = 2,980.3/10,305 = .289, as recorded in Table 4 in the TTTR column under A = 2.0 and across from θ1/θ0 = .5. It is possible to give a closed form expression for TTTR as a function of A, α, and the sample sizes r0 and r1 in the exponential and Weibull environments:
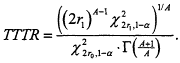
We will define TTTR differently when A < 1. In these cases, the TTT required to resolve the test in the Weibull environment will tend to be larger than that required in the original exponential test plan. We are thus interested in determining a bound which the TTT will exceed with certainty. In doing so, we employ the lower bound in (3.10). For A < 1, our tabled values of TTTR represent the ratios of the smallest possible value of the required total test time in the
Weibull environment to the required TTT in the exponential test plan. As an example, consider the computation of TTTR in testing the hypotheses H0 : µ = 1,000 vs H1 : µ = 250 at α = β = .1. Assume that the true distribution is W(1/2,B). Since the discrimination ratio is .25, the exponential life test plan calls for setting 4 systems on test, and the TTT required to ensure the resolution of the test is 4(.436)(1,000)= 1,744 hrs. To achieve α= β = .1 in the W(1/2,B) environment, given that the new discrimination ratio is .5, one needs to place 15 systems on test and require a TTT commensurate with the equation
From (3.10), it follows that
Thus, a lower bound on the ratio of the total time on test in the Weibull vs exponential environments is given by TTTR = 3,539.8/1,744 = 2.03. This latter value, or more precisely, the value 2.027, is recorded in Table 4 in the TTTR column under A = 0.5 and across from θ1/θ0 = .25. As an aside, we note that the upper bound provided in (3.10) indicates that the total time on test might be as much as 30.4 times as large as that required by an exponential life test plan; thus, while 1,744 hrs of testing are required by the original plan, the TTT in the Weibull environment with A = 1/2 will fall between 3,540 and 53,018 hrs.
The BR column in Tables 2 to 5 is more or less self-explanatory. The exponential test plan corresponding to a fixed discrimination ratio stipulates a certain sample size r as necessary to achieve fixed, nominal α and β values. If the data is actually drawn from W(A,B) with A known, and if the same sample size r is used in executing the Weibull test at significance level α, then a new level of α is attained—all it β. We define BR as the ratio β/β. An asterisk in the BR column means BR < .0005.
We now turn to the subject of censoring and, in particular, to the interpretation of the column labeled r/n in Tables 2 to 5. While type II censoring does not alter the power function of an exponential life test, but only serves to accelerate the completion of the test, its impact in
Weibull life testing is quite different. In particular, the behavior of the total time on test statistic in Weibull life testing is strongly influenced by the number of systems on test; indeed, we demonstrate below that the upper bound on TTT in Weibull environment with A > 1, tends to infinity as n grows in r-out-of-n life tests. Thus, while one can increase n with impunity in exponential life tests, one must be very careful in using censored life test designs when the underlying distribution is Weibull. We will motivate below a guideline for identifying what might be considered a reasonable upper bound for the amount of censoring one should entertain in a particular application. The tabled ratio r/n identifies this bound. If r/n = 4, for example, then the number n of systems on test should not exceed n = r/4 = 2.5r. We will return to our r/n computation momentarily. First, we extend Lemma 1 to a result which applies to type II censored samples and provides the bounds utilized in that computation.
Lemma 2: Let X be the set of all vectors ![]() of nonnegative real numbers such that
of nonnegative real numbers such that
where ![]() are positive weights. Then for A > 1,
are positive weights. Then for A > 1,
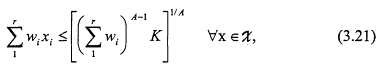
and for A < 1,
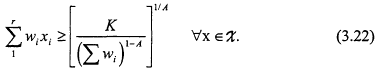
Proof: We show, by Lagrangian methods, that the bounds in (3.21) and (3.22) are the values associated with the unique critical points of the function ![]() in each case. Then, an easy geometric argument involving hyperplanes above or below the surface in (3.20) will demonstrate that these values are extrema. Let
in each case. Then, an easy geometric argument involving hyperplanes above or below the surface in (3.20) will demonstrate that these values are extrema. Let
To find critical points of the function ![]() under the constraint (3.20), we solve the equations
under the constraint (3.20), we solve the equations
and
It is evident from the above that there is a single critical point of f, namely
where λ is chosen so that
This results in the values
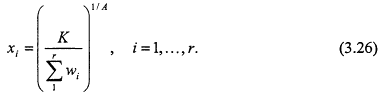
The value of the function ![]() at this critical point is
at this critical point is
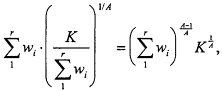
which is equivalent to the upper bound in (3.21) when A > 1 and to the lower bound in (3.22) when A < 1.
We can now introduce the r/n column in Tables 2 to 5. The TTTR computation in these tables is based on the assumption that complete (that is, uncensored) samples of size r are available. If, however, the life test plan calls for type II censoring, and is terminated, at the latest, when the rth failure occurs among the n systems on test, then the TTT statistic becomes
![]() , which is of the form
, which is of the form ![]() with unequal, positive weights. From Lemma 2, we see that, when A > 1, the maximum total time on test under the exponential test plan constraint
with unequal, positive weights. From Lemma 2, we see that, when A > 1, the maximum total time on test under the exponential test plan constraint ![]() is given by
is given by
A worrisome feature of this value is that it is unbounded in n, when A > 1, as assumed above. For the complete sample design based on r observed failures,
the constraint on ![]() being the same as in the censored case, given that the transformed problem is based on an underlying exponential distribution. Now the ratio we have called TTTR measures (conservatively) the extent to which TTT could have been reduced if an appropriate Weibull life test had been conducted. Suppose we take particular values of the discrimination ratio, α, β and A > 1 as fixed and given. We could then ask the question: what sample size n would yield a censored sampling plan in the Weibull environment that has (at worst) an equivalent TTT requirement as that of the original exponential test plan? The answer is the following: the value of n yielding a maximum TTT no larger than the required TTT in the exponential test plan is the solution to the equation
being the same as in the censored case, given that the transformed problem is based on an underlying exponential distribution. Now the ratio we have called TTTR measures (conservatively) the extent to which TTT could have been reduced if an appropriate Weibull life test had been conducted. Suppose we take particular values of the discrimination ratio, α, β and A > 1 as fixed and given. We could then ask the question: what sample size n would yield a censored sampling plan in the Weibull environment that has (at worst) an equivalent TTT requirement as that of the original exponential test plan? The answer is the following: the value of n yielding a maximum TTT no larger than the required TTT in the exponential test plan is the solution to the equation

that is,
or, as we will record it,
The formula for r/n in (3.31) is derived in the same way for A < 1, and will be applied in Tables 2 to 5 for arbitrary A. However, since TTTR has different interpretations for A > 1 and A < 1, so
too does the fraction r/n. As stated above, when A > 1, r/n represents the censoring ratio that yields a test in the Weibull environment for which the required total time on test is no greater than the TTT specified in the exponential test plan. For A < 1, r/n represents the censoring ratio for which the minimum possible TTT in the Weibull environment is approximately equal to the TTT specified in the exponential test plan. The actual TTT experienced in executing the Weibull life test can, of course, be much larger than that minimum. Thus, caution must be exercised in interpreting an r/n ratio when A < 1. Further, it is possible, when A < 1, for r/n to exceed 1. Such an outcome simply points to the fact that the minimum possible TTT in the Weibull environment will be less than or equal to the required TTT in the exponential test plan when one reduces the sample size from r to the value of n for which r/n is the tabulated value.
As an example of the computation of r/n, suppose θ1/θ0 = .5, A = 2.0 and α= β = 0.1. From Table 4, we find that TTTR = .289, so that r/n = (.289)2 = .0835, which is recorded as r/n-.084 in Table 4. From this, we deduce that a test plan which places 48 systems on test and resolves the test upon the 4th failure would have a total test time no larger than 10,305 hrs, the test time associated with the exponential test plan based on 15 observed failures.
Given the definitions of SSR, TTTR, BR and r/n in the preceding paragraphs, we now present the tables in which these measures appear.
While Tables 2 to 5 largely speak for themselves, a few comments on them seem warranted at this point. In general, these tables confirm that there are potential resource savings available when one recognizes an IFR Weibull environment and carries out a Weibull life test instead of an exponential one. Similarly, more resources are required in carrying on Weibull life tests when the DFR Weibull analysis is carried out instead of an exponential life test. Since IFR Weibull distributions arise with some frequency in life testing applications, the magnitude of the measure SSR, TTTR, BR and r/n when the shape parameter is large is of special interest. Contour plots showing level curves of each of these measures are especially revealing.
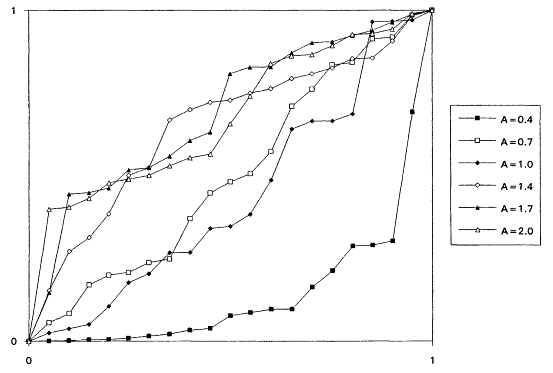
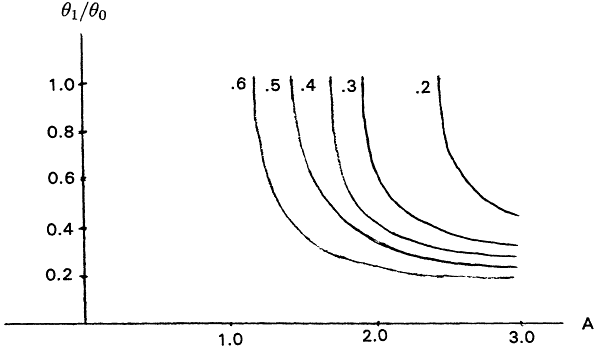
As an example, a rough sketch of the level curves of TTTR as a function of the discrimination ratio θ1/θ0 and the value of the shape parameter A is shown in Figure 15 for the case α = β = .1. These plots are only approximate, of course, since the discreteness of sample
size selection causes the computed values of TTTR (and the other measures as well) to be a rather choppy function of the discrimination ratio for each fixed value of A.
From Figure 15, one may infer that the most substantial savings in TTT are made in situations in which both the discrimination ratio and the Weibull shape parameter are high. In applications, the costs associated with life tests when the discrimination ratio is high (say, greater than .7) are generally prohibitive; thus, even though the resource savings afforded by a Weibull life test might be substantial, the cost of the alternative analysis is still likely to be prohibitive. If the discrimination ratio is .9, for example, an exponential life test plan for, say, H0 : θ = 1,000 vs H1 : θ = 900 at α = β = .1 would require at least r = 593 systems on test and a total test time of 561,571 hrs. If A = 2.5, say, the Weibull test with the same error probabilities could be accomplished with r = 96 systems on test and a total test time no greater than 102,206 hrs. While these savings are striking, the experiment may still be too costly to perform. It appears that the kind of problems in which recognizing a Weibull environment and performing a Weibull life test will be both feasible and economically attractive will be those in which ![]() and
and ![]() .
.
We will return to our discussion of Tables 2 to 5 in the concluding section. It is perhaps worth noting here that the measure BR shows quite dramatically the power of Weibull life tests when the shape parameter A is reasonably large; for fixed values of A, BR appears to vary inversely with the discrimination ratio. We also note that, for fixed A > 1, the amount of censoring that can be accommodated per the r/n computation is an increasing function of the total time on test ratio, which in turn tends to increase as a function of the discrimination ratio.
4. Weibull Life Testing—Part 2
In section 3, we studied the performance characteristics of Weibull life tests under the simplifying assumption that the Weibull shape parameter A was known. The assumption is not totally whimsical, since engineering experience with a particular type of application might make such an assumption quite reasonable. The exponential assumption is, after all, nothing more than
the assumption that the Weibull shape parameter is known to be equal to one. One might consider the results of section 3 to apply to the situation in which the statistician guesses (or estimates) the value of the Weibull shape parameter, and happens to guess it correctly. It is, of course, necessary to move beyond this first step, and to engage seriously the question of how to execute a Weibull analysis in the general, two-parameter problem. This section is devoted to examining three specific possibilities in that regard.
Suppose ![]() , where A > 0, B > 0 are unknown, and we wish to test to hypotheses
, where A > 0, B > 0 are unknown, and we wish to test to hypotheses ![]() vs
vs ![]() . The approach of section 3 immediately suggests a possible approach to this testing problem: estimate A from data, and carry out a Weibull test, as in the preceding section, with the estimate  taken as the known value of A. The performance of the resulting test procedure is, naturally, dependent upon the quality of the estimate Â. This ''plug-in'' method has a history. In an estimation framework, Gong and Samaniego (1981) described the large sample behavior of the solutions of a reduced system of likelihood equations when certain (nuisance) parameters were replaced by
. The approach of section 3 immediately suggests a possible approach to this testing problem: estimate A from data, and carry out a Weibull test, as in the preceding section, with the estimate  taken as the known value of A. The performance of the resulting test procedure is, naturally, dependent upon the quality of the estimate Â. This ''plug-in'' method has a history. In an estimation framework, Gong and Samaniego (1981) described the large sample behavior of the solutions of a reduced system of likelihood equations when certain (nuisance) parameters were replaced by ![]() estimators. In the context of testing composite hypotheses, Neyman (1959) gave conditions under which tests utilizing
estimators. In the context of testing composite hypotheses, Neyman (1959) gave conditions under which tests utilizing ![]() estimators of the nuisance parameters have a certain type of asymptotical optimality. More specifically, Neyman showed that, under fairly standard regularity conditions, test statistics which were uncorrelated with the logarithmic derivative of the likelihood with respect to the nuisance parameters (under a null hypothesis specifying a fixed value of a given parameter) were "locally asymptotically most powerful" in testing that null hypothesis against its compliment. Such tests were named C(α) tests by Neyman, in deference to the similarity of his regularity conditions to those posited by Cramér (1946) in his work on the large sample theory of maximum likelihood estimators.
estimators of the nuisance parameters have a certain type of asymptotical optimality. More specifically, Neyman showed that, under fairly standard regularity conditions, test statistics which were uncorrelated with the logarithmic derivative of the likelihood with respect to the nuisance parameters (under a null hypothesis specifying a fixed value of a given parameter) were "locally asymptotically most powerful" in testing that null hypothesis against its compliment. Such tests were named C(α) tests by Neyman, in deference to the similarity of his regularity conditions to those posited by Cramér (1946) in his work on the large sample theory of maximum likelihood estimators.
The essence of a C(α) test is the substitution of one or more unknown parameters by ![]() estimators, and the testing of hypotheses concerning a lower dimensional parameter space. We will examine two tests based on such an approach. The first of these is based on the fact that the coefficient of variation of the Weibull distribution, given in (2.5), depends only on
estimators, and the testing of hypotheses concerning a lower dimensional parameter space. We will examine two tests based on such an approach. The first of these is based on the fact that the coefficient of variation of the Weibull distribution, given in (2.5), depends only on
the shape parameter of the distribution and is independent of the second parameter B. A ![]() estimator of the parameter cv is readily available; a natural estimate is the sample cv, or
estimator of the parameter cv is readily available; a natural estimate is the sample cv, or
where ![]() and s are the sample mean and standard deviation, respectively. Now the relationship between cv and A in (2.5) is not easily inverted; we will therefore deal with that inversion numerically. In spite of that slight complication, the inversion which expresses A as a function of cv will, by virtue of the continuity and differentiability of the functional relationship, provides us with a
and s are the sample mean and standard deviation, respectively. Now the relationship between cv and A in (2.5) is not easily inverted; we will therefore deal with that inversion numerically. In spite of that slight complication, the inversion which expresses A as a function of cv will, by virtue of the continuity and differentiability of the functional relationship, provides us with a ![]() estimator of A. Table 6 represents a numerical compilation from which one can obtain an estimated shape parameter from an estimated cv. We have relied upon this table for obtaining
estimator of A. Table 6 represents a numerical compilation from which one can obtain an estimated shape parameter from an estimated cv. We have relied upon this table for obtaining ![]() when
when ![]() , since interpolation in these cases provides acceptable accuracy. When
, since interpolation in these cases provides acceptable accuracy. When ![]() , the bisection method was used to calculate Â, pivoting on the expression in (2.5) until sufficient accuracy in  was attained.
, the bisection method was used to calculate Â, pivoting on the expression in (2.5) until sufficient accuracy in  was attained.
The testing method for which results are recorded under the "cv" column in Tables 7 to 9 is the C(α)-type test with A estimated by the appropriate function  of the sample coefficient of variation. Once A is set equal to Â, the test is carried out as in section 3, leading to rejection of the hypothesis ![]() in favor of
in favor of ![]() if the statistic
if the statistic ![]() is sufficiently small.
is sufficiently small.
The second testing procedure we study here is the likelihood ratio test of the hypotheses ![]() vs
vs ![]() based on a Weibull sample. Execution of such a test requires the maximization of the Weibull likelihood L, given by
based on a Weibull sample. Execution of such a test requires the maximization of the Weibull likelihood L, given by
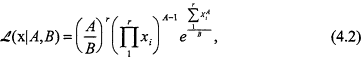
over ![]() and over
and over ![]() . The likelihood ratio statistic we compute is
. The likelihood ratio statistic we compute is

Standard theory implies that, for sufficiently large r, the statistic ![]() is approximately distributed as a
is approximately distributed as a ![]() random variable. To compute
random variable. To compute ![]() in (4.3), we employed two-dimensional Newton-Raphson iterations in the unrestricted maximization required by the denominator of
in (4.3), we employed two-dimensional Newton-Raphson iterations in the unrestricted maximization required by the denominator of ![]() , and carried out the (essentially) one-dimensional search required by the numerator of
, and carried out the (essentially) one-dimensional search required by the numerator of ![]() using the "golden-section" search algorithm as described by Luenberger (1989:199). Given that we were interested in a one-sided test, we defined the rejection region of the test based on the likelihood ratio as follows: if the unrestricted maximization of L in (4.2) results in MLEs  and
using the "golden-section" search algorithm as described by Luenberger (1989:199). Given that we were interested in a one-sided test, we defined the rejection region of the test based on the likelihood ratio as follows: if the unrestricted maximization of L in (4.2) results in MLEs  and ![]() for which
for which ![]() accept H0. Otherwise, compute the likelihood ratio statistic
accept H0. Otherwise, compute the likelihood ratio statistic ![]() , and reject H0 if
, and reject H0 if
Since ![]() is expected to be large under departures from µ = µ0 in either of two directions, we doubled the nominal tall probability of the χ2 distribution and reject only when the data is indicative of a mean value smaller than µ0. For sufficiently large r, this procedure should have a significance level close to α. In Tables 7 to 9, the performance of this test is recorded in the columns labeled "
is expected to be large under departures from µ = µ0 in either of two directions, we doubled the nominal tall probability of the χ2 distribution and reject only when the data is indicative of a mean value smaller than µ0. For sufficiently large r, this procedure should have a significance level close to α. In Tables 7 to 9, the performance of this test is recorded in the columns labeled " ![]() ."
."
We might mention, at this point, the fact that an additional possibility exists for constructing a C(α)-type test: one could estimate the shape parameter A by the maximum likelihood estimate Â, and carry out the test in section 3 with A replaced by that estimate. We have confirmed, via simulation, that the performance of that test, in small and moderate samples, is essentially indistinquishable from the likelihood ratio procedure described above. We have therefore excluded the MLE-driven C(α)-type test from the simulation results reported here.
Finally, we will investigate the performance of a third approach to tests involving Weibull means. As discussed in section 2, it is possible to examine the Weibull assumption through appropriate plots on Weibull probability paper. Formal estimation and hypothesis tests may be developed from these fitting procedures. Chernoff and Lieberman (1956) gave
conditions under which certain plots were optimal for estimating particular parameters. Nair (1984) has studied the large sample behavior of estimators of model parameters derived from probability plots and, in particular, showed that, under suitable regularity conditions, estimates obtained via ordinary least squares are ![]() and asymptotically normal. This latter work suggests that one might test hypotheses concerning Weibull means by first estimating the shape parameter from the least squares fit to data plotted on Weibull probability paper, and then carrying out the appropriate exponential test based on the transformed data
and asymptotically normal. This latter work suggests that one might test hypotheses concerning Weibull means by first estimating the shape parameter from the least squares fit to data plotted on Weibull probability paper, and then carrying out the appropriate exponential test based on the transformed data ![]() as if A = Â is the true shape parameter. The hypothesis
as if A = Â is the true shape parameter. The hypothesis ![]() is rejected when
is rejected when ![]() is smaller than an appropriate threshold. The performance of the test based on an least squares estimator of the Weibull shape parameter from a Weibull probability plot is recorded in Tables 7 to 9 in the column labeled "
is smaller than an appropriate threshold. The performance of the test based on an least squares estimator of the Weibull shape parameter from a Weibull probability plot is recorded in Tables 7 to 9 in the column labeled "![]() ."
."
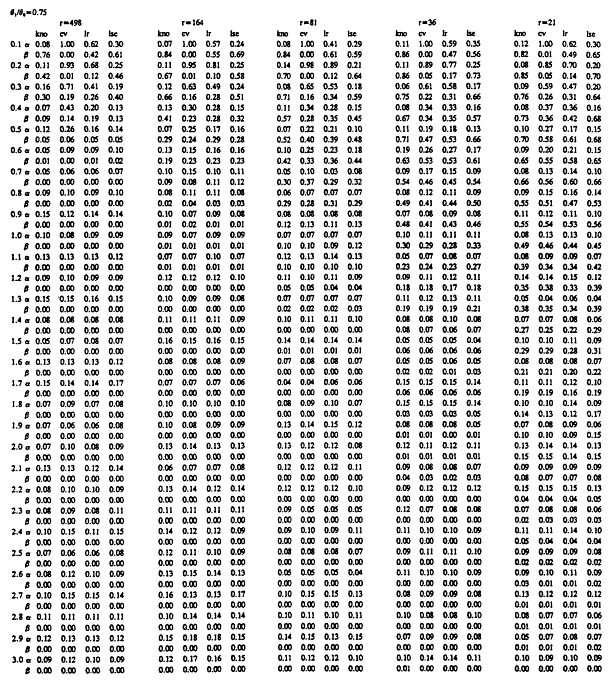
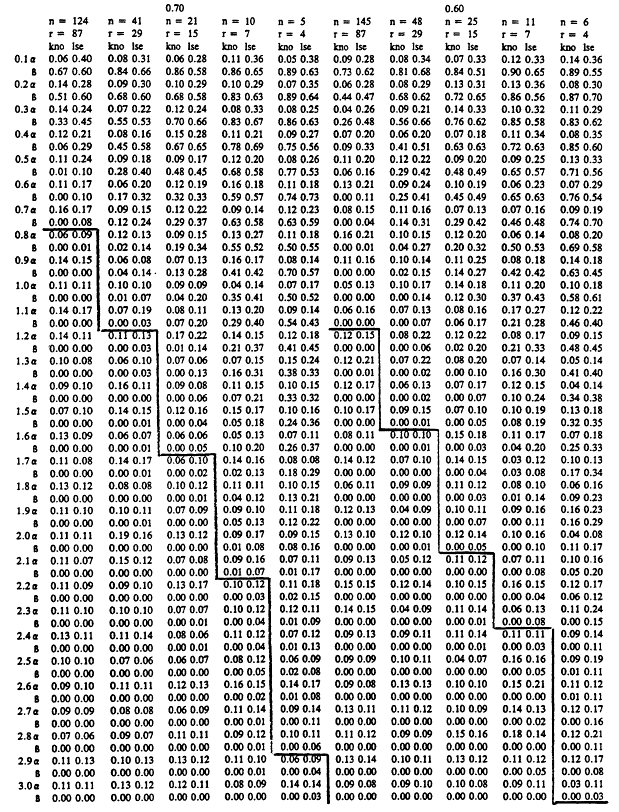
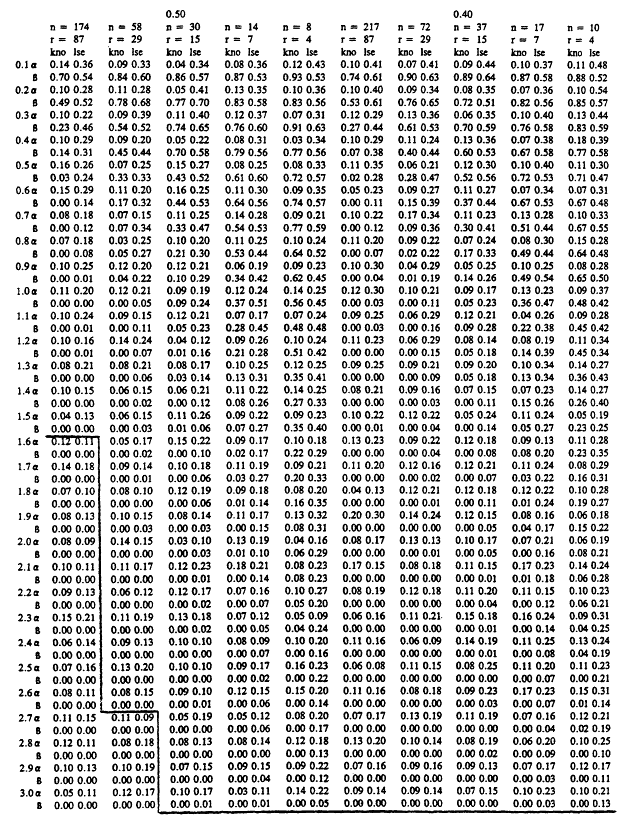
We are now in a position to describe the contents of Tables 7 to 9. Each table summarizes a simulation study for a fixed value of the discrimination ratio' Table ![]() , Table
, Table ![]() , and Table
, and Table ![]() . In all three studies, simulations were carried out for assumed Weibull samples with five possible sample sizes, and with Weibull shape parameters ranging from 0.1 to 3.0 in increments of 0.1. The median sample size among the five used for each table was set to be equal to the sample size required by an exponential test plan with the set value of θ 1/θ0 for that table and the error probabilities set to α= β = .1. For example, when θ1/θ0 = .25, the exponential test plan calls for a minimum of r = 4 systems on test (r = 15 when θ1/θ0 = .5 and r = 81 when θ1/θ0 = .75). For a particular sample size, the error probabilities α and β realized in 100 repetitions of each of four tests are recorded. The first column, labeled "kno," records the α and β achieved by the test in section 3, where the true value of the shape parameter A of the underlying Weibull distribution is taken as known and is used in testing for mean life. In the column labeled "cv," the error probabilities β and β are given for a test which treats the estimate  based on the sample coefficient of variation as if it were the true value of the shape parameter A. In the column labeled "
. In all three studies, simulations were carried out for assumed Weibull samples with five possible sample sizes, and with Weibull shape parameters ranging from 0.1 to 3.0 in increments of 0.1. The median sample size among the five used for each table was set to be equal to the sample size required by an exponential test plan with the set value of θ 1/θ0 for that table and the error probabilities set to α= β = .1. For example, when θ1/θ0 = .25, the exponential test plan calls for a minimum of r = 4 systems on test (r = 15 when θ1/θ0 = .5 and r = 81 when θ1/θ0 = .75). For a particular sample size, the error probabilities α and β realized in 100 repetitions of each of four tests are recorded. The first column, labeled "kno," records the α and β achieved by the test in section 3, where the true value of the shape parameter A of the underlying Weibull distribution is taken as known and is used in testing for mean life. In the column labeled "cv," the error probabilities β and β are given for a test which treats the estimate  based on the sample coefficient of variation as if it were the true value of the shape parameter A. In the column labeled "![]() ,'' α and β are recorded for the version of the likelihood ratio test discussed above. Finally, in the column labeled "
,'' α and β are recorded for the version of the likelihood ratio test discussed above. Finally, in the column labeled "![]() ,'' α and β are given for the test in
,'' α and β are given for the test in
which the least squares estimator  from a Weibull probability plot is used as if it were the true value of the shape parameter. The first and third tests were carried out so as to achieve a significance level of 0.1. The rejection region of the second and fourth tests were chosen to yield significance level 0.1 under the assumption that A = Â. The results of our simulations appear below.
Tables 7 to 9 have some rather striking features. It will be clear from these tables that when the underlying Weibull distribution is strongly DFR, that is, when A is quite near zero, testing hypotheses concerning the mean value is an extremely difficult proposition. Even tests which substitute the correct true value of the shape parameter into the density have very low power at the alternative hypothesis, even for relatively large sample sizes. The exact, best test of vs µ1 has suitably small α and β values if A is not too small, and requires a somewhat larger value A to ensure such behavior when the sample sizes are small. For sample sizes equal to the required sample size for exponential life tests with α = β = .1, the test with known A performs very well, with α and β hovering at or below 0.1 for all A > 1. Fortunately, in practice, the recurrence of A near zero is not at all common.
The most surprising and encouraging aspect of Tables 7 to 9 is the fact that the three procedures for testing means in the general two parameter problem each performs nearly as well as the best test when A is known. The appropriate ground for comparison purposes is the collection of tests in which the true parameter A exceeds 1.0. This is the domain of primary interest in applications, and is the domain in which the "gold standard", that is, the test based on known A, achieves acceptable error probabilities. Inspection of Tables 7 to 9 reveals that all three general tests perform well in these settings. The values A0 for which ![]() for
for ![]() are roughly estimated in Table 10 as a function of the ordered sample sizes
are roughly estimated in Table 10 as a function of the ordered sample sizes ![]() . (So the r(1) through r(5) of Table 10 represent 2,3,4,8, and 22 for Table 7; 4,7,15,29, and 87 for Table 8; and 21, 36, 81, 164, and 498 for Table 9.)
. (So the r(1) through r(5) of Table 10 represent 2,3,4,8, and 22 for Table 7; 4,7,15,29, and 87 for Table 8; and 21, 36, 81, 164, and 498 for Table 9.)
As an example of the surprising competitiveness of a two parameter Weibull life test, consider testing ![]() vs
vs ![]() at α = .1. Suppose 15 systems are placed on test, as prescribed by an exponential life test plan with α = β =. 1. If the data happens to be
at α = .1. Suppose 15 systems are placed on test, as prescribed by an exponential life test plan with α = β =. 1. If the data happens to be
governed by a Weibull distribution with shape parameter A = 1.2, and the fact that A = 1.2 is somehow revealed to the experimentor, the best test of H0 vs H1 of size α= 0.1 can be executed after appropriately transforming the data to ![]() . Table 8 shows this test as having error probabilities α = .11 and β = .02 in our simulation. We expect β to be less than 0.1 here since a shape parameter of 1.2 has served to decrease the effective discrimination ratio, so that 15 observations is more than actually required to achieve α = β =. 1 in the life test based on transformed data. For the tests which did not benefit from knowledge of the true A, we find that the cv-based test had α = .11, β = .02, the likelihood ratio test had α = .13, β= .02, and the least-squares-based test had α = .09, β = .03. The performance of all three procedures are clearly indistinguishable from that of the best test in this instance. A general perusal of Tables 7 to 9 shows that this example is not an isolated instance of this type of performance.
. Table 8 shows this test as having error probabilities α = .11 and β = .02 in our simulation. We expect β to be less than 0.1 here since a shape parameter of 1.2 has served to decrease the effective discrimination ratio, so that 15 observations is more than actually required to achieve α = β =. 1 in the life test based on transformed data. For the tests which did not benefit from knowledge of the true A, we find that the cv-based test had α = .11, β = .02, the likelihood ratio test had α = .13, β= .02, and the least-squares-based test had α = .09, β = .03. The performance of all three procedures are clearly indistinguishable from that of the best test in this instance. A general perusal of Tables 7 to 9 shows that this example is not an isolated instance of this type of performance.
We interpret the excellent performance of all four tests we have studied (including the C(α)-type test based on the maximum likelihood estimate of A) as constituting compelling evidence that Weibull life testing is both feasible and efficient. The lack of sensitivity of C(α)-type tests to the precision of the estimated shape parameter, and the ability of such tests to achieve error probabilities comparable to those of the best possible test when A is known, provides strong support for using such tests in practice. Among the four tests we've studied, we would favor the MLE-based C(α)-type test, since it has exhibited competitive small sample behavior, and is, of course, defensible asymptotically as well.
As we have seen, Weibull life testing does not enjoy the immunity from the effects of censoring that characterizes exponential life testing. It is thus important to extend the investigation above to the censored data case. In what follows, we examine the performance of a particular procedure for testing two hypothesized Weibull means in the general two parameter problem under a type II censoring design. More specifically, we have selected for study the censored data version of the " " test based on the least squares fitting of transformed censored data with a straight line of the form (2.10). The execution of this test, that is, the development of a Weibull probability plot under censoring, involves no increased complexity. The fundamental question of interest will be whether the estimated shape parameter  obtained from such a plot
" test based on the least squares fitting of transformed censored data with a straight line of the form (2.10). The execution of this test, that is, the development of a Weibull probability plot under censoring, involves no increased complexity. The fundamental question of interest will be whether the estimated shape parameter  obtained from such a plot
has sufficient accuracy and precision to provide reasonable performance in the associated C(α)-type test in samples of small or moderate size. Our simulations will address this question. Before describing our findings in this regard, we pause to discuss briefly the other two procedures we've studied in the complete sample case.
![]()
An extension of the cv test has not been pursued for lack of a reliable estimate of the Weibull coefficient of variation from censored data. The problem does not appear to have been treated in the literature; various ad hoc estimates with which we experimented proved unsatisfactory. We had greater success in extending the ![]() test to censored data. Conceputally, the latter problem can be dealt with adequately. Programs have been written to obtain the required likelihood ratio statistic from censored data. However, as of this writing, we have not satisfactorily resolved the attendant numerical issues. For these and other reasons, we have not to date completed a simulation study on censored data cv or
test to censored data. Conceputally, the latter problem can be dealt with adequately. Programs have been written to obtain the required likelihood ratio statistic from censored data. However, as of this writing, we have not satisfactorily resolved the attendant numerical issues. For these and other reasons, we have not to date completed a simulation study on censored data cv or ![]() tests comparable to the study on which we report below. Since our primary purpose in examining the censored data case is to determine whether tests exist which provide satisfactory (that is, nearly optimal) performance in cases of practical interest (that is, moderate sample sizes, shape parameter moderately large), the simulation we have done will suffice and provides an affirmative answer to this question.
tests comparable to the study on which we report below. Since our primary purpose in examining the censored data case is to determine whether tests exist which provide satisfactory (that is, nearly optimal) performance in cases of practical interest (that is, moderate sample sizes, shape parameter moderately large), the simulation we have done will suffice and provides an affirmative answer to this question.
In Table 11, we record the realized error probabilities for two tests, the first being the optimal test (kno) when the Weibull shape parameter A is fixed and known and the second being the ![]() test in which A has been estimated from the Weibull probability plot. The six sections of this table provide α and β for censored Weibull samples with A = .1(.1)3.0 and for censoring fraction
test in which A has been estimated from the Weibull probability plot. The six sections of this table provide α and β for censored Weibull samples with A = .1(.1)3.0 and for censoring fraction ![]() and .4 in succession. For each lower bound on the censoring fraction, we have estimated α and β for five different possible sample sizes n. The jagged lines drawn across the table represent, roughly, the lower boundary for the shape parameter A for which the
and .4 in succession. For each lower bound on the censoring fraction, we have estimated α and β for five different possible sample sizes n. The jagged lines drawn across the table represent, roughly, the lower boundary for the shape parameter A for which the ![]() test is, for practical purposes, comparable to the optimal test.
test is, for practical purposes, comparable to the optimal test.
Several conclusions may be reliably drawn from Table 11. The performance of the ![]() based on censored data improves as A increases, as r/n increases and as n increases (while holding the other two of these parameters fixed). Our simulation gives strong support to
based on censored data improves as A increases, as r/n increases and as n increases (while holding the other two of these parameters fixed). Our simulation gives strong support to
the claim that under moderate censoring (say ![]() a Weibull environment with sufficiently large shape parameter (say A > 1.5), and large enough n (say n > 20), Weibull life testing using the
a Weibull environment with sufficiently large shape parameter (say A > 1.5), and large enough n (say n > 20), Weibull life testing using the ![]() procedure provides excellent performance, with error probabilities α and β quite close to the best possible values.
procedure provides excellent performance, with error probabilities α and β quite close to the best possible values.
5. Discussion
In the fall of 1992, the Committee on National Statistics of the National Research Council hosted a workshop, co-sponsored by the Department of Defense, on statistical issues in defense analysis and testing (see Samaniego, 1993; and Rolph and Steffey, 1994). Much discussion during that workshop was centered around the intriguing question "how much testing is enough?" The question was considered more than just interesting. Efficient use of the resources available for testing in the DoD acquisitions programs is always of interest, but is especially pressing in the face of declining budget allocations for operational testing and evaluation. At least part of the motivation for the present study is drawn from the workshop's (and subsequent) discussion of resource-related issues. A second source of motivation for this study is the apparent overuse of exponential life testing methodology in both military and civilian applications. It seems that a careful study on the cost-saving potential of alternative treatments of life testing data might have rather broad utility.
This paper begins with a review of exponential life testing methods, and discusses basic properties of the Weibull distribution and how that distribution might be identified as an appropriate model for life testing data. Of particular interest to us has been the mechanics of Weibull life testing and the statistical performance, and cost, of this alternative approach. The results of section 3 show quite graphically that Weibull life tests can, in certain circumstances, provide substantially greater statistical power than exponential life tests based on the same sample size, and can offer substantial savings in both sample size and testing time when the goal is to match the statistical power of a planned exponential life test. While Tables 2 to 5 ostensibly offer guidance only for the very special case in which the Weibull shape parameter A is known,
and while these tables were constructed, primarily, to compare exponential and Weibull life testing for complete samples, they are more widely applicable. We will elaborate on this shortly. Yet even in the narrowest domain of applicability (that is, complete samples, A known), these tables provide important insights. First, they show quite emphatically that exponential life testing can be especially misleading when the underlying distribution is a DFR Weibull; it is clear that a much larger sample size and much greater testing time are needed to achieve any given nominal error probabilities than what an exponential life test plan would prescribe. The good news carried by Tables 2 to 5 is that, when the underlying distribution is an IFR Weibull, considerable savings are possible. Our results confirm and expand upon some of the findings in Anderson's (1994) thesis. From Tables 2 to 5, one can see that a 20-30% reduction in needed test resources is typical when the shape parameter A = 1.2, a 60-70% reduction is typical when A = 2.0 and a 70-90% reduction is typical when A = 3.0. Potential cost savings of such magnitudes should certainly provide a strong incentive for life testing practitioners to try to detect an IFR Weibull environment when it is present, and to utilize Weibull life testing methods when Weibull modeling is deemed appropriate.
The results reported in Tables 7 to 9 of section 4 carry important practical implications. There tabulations show, in general, that the three approaches we've considered for real-life Weibull life testing (that is, when both Weibull parameters are unknown) perform nearly as well, in IFR Weibull environments, as the optimal test with the shape parameter assumed known. This suggests that the savings available in the idealized setting of section 3 can also be realized in real, practical life testing scenarios. Especially interesting to us is the fact that the general tests, particularly the cv- and ![]() -based tests, are competitive with the ideal test even for small sample sizes. This is clear by inspection of the columns of achieved α and β levels of the four tests for sample size
-based tests, are competitive with the ideal test even for small sample sizes. This is clear by inspection of the columns of achieved α and β levels of the four tests for sample size ![]() in Table 7, for sample size
in Table 7, for sample size ![]() in Table 8 and for sample size
in Table 8 and for sample size ![]() in Table 9. The general tests perform adequately when the Weibull shape parameter A > 1, and perform exceptionally well when A > 2. In the testing problems we have examined, it is clear that the estimation of the shape parameter prior to executing a formal test has only a second-order, and quite modest, effect on test performance. Thus, even with relatively unstable estimators of A, like those obtained from Weibull probability plots based on small or moderate samples, one can
in Table 9. The general tests perform adequately when the Weibull shape parameter A > 1, and perform exceptionally well when A > 2. In the testing problems we have examined, it is clear that the estimation of the shape parameter prior to executing a formal test has only a second-order, and quite modest, effect on test performance. Thus, even with relatively unstable estimators of A, like those obtained from Weibull probability plots based on small or moderate samples, one can
still test hypotheses concerning Weibull means quite reliably, provided the censoring fraction is reasonably small.
Let us now consider how one might use the tabulations in sections 3 and 4 in a practical problem. For now, we'll restrict our attention to the case of complete samples, that is, r = n. In many engineering applications in which Weibull models are routinely entertained, the investigators involved have a good feel for the range of Weibull shape parameters that tend to arise. Some sort of IFR behavior is a common occurrence, and it is possible, even likely, that reasonable bounds can be placed a priori on the anticipated value of the shape parameter A. All that's really needed to employ Tables 2 to 5 with profit is a reliable lower bound on A. Suppose, for example, that one wishes to test H0 : µ = 1,000 vs H1 : µ = 500 at α = β = .05. From Table 3, we see that an exponential life test plan requires that at least r = 23 systems be placed on test, and that a total testing time of 15,709 hrs be planned for. Assume that the experiment is judged to be well modeled by a Weibull distribution, and assume that the experimentors can assert with some confidence that the shape parameter A is bounded below by, say, 1.5. Now note that a Weibull life test for known A = 1.5 can achieve α = β = .05 with a sample size of r = 23(.478) = 11 and a maximum testing time of 15,709(.527) = 8,279 hrs. If A > 1.5, further savings would be possible. For example, if A is known to be 2.5, the test can be accomplished with a sample of size r = 5 and a total test time no greater than 3,880 hrs.
It should be emphasized that Weibull life tests having characteristics such as those above require knowledge of the value of the shape parameter. Recall, however, that under precisely the circumstances with which we are dealing, the general Weibull tests of section 4 may be employed with confidence. Our recommendation would therefore be: carry out a Weibull (cv-or ![]() -based) test with a sample of r = 11 systems, terminating the test on the basis of the value of the statistic
-based) test with a sample of r = 11 systems, terminating the test on the basis of the value of the statistic ![]() . Provided that the underlying model is indeed Weibull with shape parameter >1.5, this procedure should secure savings of 50% or more in sample size and total testing time while maintaining error probabilities in the neighborhood of the nominal levels used in the design of the experiment.
. Provided that the underlying model is indeed Weibull with shape parameter >1.5, this procedure should secure savings of 50% or more in sample size and total testing time while maintaining error probabilities in the neighborhood of the nominal levels used in the design of the experiment.
It is natural to ask how the above generalizes to censored-data designs. We can give at least a partial answer to this question. We should first note that in the Weibull test of section 3, based on a data transformation depending on the known true value of the Weibull shape parameter A, the statistic
has the distribution Γ (r,B) irrespective of the number of systems n on test, so that the realized values of α and β, and the reported value of SSR, hold for these tests under type II censoring. As we have noted previously, however, the maximal total time on test associated with a fixed value of T in (5.1) does depend on n and grows without bound as ![]() . Thus, in order to identify a value T0 such that the test is sure to be resolved with TTT no greater than T0, one would need to bound the value of n. It should be recognized that this upper bound on TTT may be considerably larger than the realized TTT in actual Weibull life testing, especially since that upper bound is achieved only when all observed failure times are identical and satisfy a constraint of the form of (3.20). In any case, the influence of type II censoring on the tables in. section 3 is exclusively through the total time on test ratio. The measure TTTR is increasing as a function of n, and reaches the value 1 (corresponding to the circumstance in which the TTT in exponential and Weibull tests have the same maximal value) when n is equal to r times the reciprocal of the recorded value of r/n.
. Thus, in order to identify a value T0 such that the test is sure to be resolved with TTT no greater than T0, one would need to bound the value of n. It should be recognized that this upper bound on TTT may be considerably larger than the realized TTT in actual Weibull life testing, especially since that upper bound is achieved only when all observed failure times are identical and satisfy a constraint of the form of (3.20). In any case, the influence of type II censoring on the tables in. section 3 is exclusively through the total time on test ratio. The measure TTTR is increasing as a function of n, and reaches the value 1 (corresponding to the circumstance in which the TTT in exponential and Weibull tests have the same maximal value) when n is equal to r times the reciprocal of the recorded value of r/n.
Our investigations regarding Weibull life testing in the censored data case, while not as comprehensive as we'd like, support the general conclusion that it is possible to test competing Weibull means reliably in the presence of censoring. In applications of that type, our simulations indicate that extreme censoring can be dangerous, that is, can lead to quite inflated error probabilities unless the shape parameter A is very large. In standard applications of the Weibull model, where the shape parameter ![]() , Weibull life testing based on moderate sample sizes
, Weibull life testing based on moderate sample sizes ![]() and modest censoring
and modest censoring ![]() provides excellent performance. Our conclusions are based on our study of the performance of the
provides excellent performance. Our conclusions are based on our study of the performance of the ![]() procedure. We conjecture that an appropriately implemented cv or
procedure. We conjecture that an appropriately implemented cv or ![]() procedure will have similar performance characteristics.
procedure will have similar performance characteristics.
One might rightly seek an intuitive explanation of the phenomena that have been observed in this paper. Why would one expect to be able to test hypotheses concerning means more efficiently under an IFR Weibull model than under an exponential one? The best explanation may be in terms of the variance of observed lifetimes under the two models. For a model with a given mean, an IFR Weibull has smaller variance than an exponential, making it possible to detect departures from a hypothesized value of the mean more economically when IFR Weibull assumptions hold. This fact suggests that the resource-saving potential of life testing in an IFR Weibull environment is likely to arise as well for certain gamma and lognormal models as well.
There are a number of unresolved issues that must be left to future studies. Studies of alternative life testing designs, including type I censoring and sequential designs, would be of interest. Even within the framework of the present study, extension of our results and findings to various cases in which ![]() would be useful, as would expansion of our tables to larger values of the shape parameter, including, at a minimum,
would be useful, as would expansion of our tables to larger values of the shape parameter, including, at a minimum, ![]() . Also, similar studies for other models, especially for the gamma family, would provide useful guides to alternative life testing methodology. In the context of the hybrid statistical problem discussed in the introductory section—where an alternative model is selected after data has been gathered according to an exponential life test plan—it would be important, in practice, to be able to carry out an appropriate analysis for the model identified as most suitable, be it the Weibull or some other failure-time model deemed to be applicable to the life testing experiment of interest.
. Also, similar studies for other models, especially for the gamma family, would provide useful guides to alternative life testing methodology. In the context of the hybrid statistical problem discussed in the introductory section—where an alternative model is selected after data has been gathered according to an exponential life test plan—it would be important, in practice, to be able to carry out an appropriate analysis for the model identified as most suitable, be it the Weibull or some other failure-time model deemed to be applicable to the life testing experiment of interest.
TABLE 6
Shape Parameter A Corresponding to the Coefficient of Variation cv
|
cv |
A |
cv |
A |
cv |
A |
|
428.8314 |
0.10 |
0.7238 |
1.40 |
0.3994 |
2.70 |
|
47.0366 |
0.15 |
0.7006 |
1.45 |
0.3929 |
2.75 |
|
15.8430 |
0.20 |
0.6790 |
1.50 |
0.3866 |
2.80 |
|
8.3066 |
0.25 |
0.6588 |
1.55 |
0.3805 |
2.85 |
|
5.4077 |
0.30 |
0.6399 |
1.60 |
0.3747 |
2.90 |
|
3.9721 |
0.35 |
0.6222 |
1.65 |
0.3690 |
2.95 |
|
3.1409 |
0.40 |
0.6055 |
1.70 |
0.3634 |
3.00 |
|
2.6064 |
0.45 |
0.5897 |
1.75 |
0.3581 |
3.05 |
|
2.2361 |
0.50 |
0.5749 |
1.80 |
0.3529 |
3.10 |
|
1.9650 |
0.55 |
0.5608 |
1.85 |
0.3479 |
3.15 |
|
1.7581 |
0.60 |
0.5474 |
1.90 |
0.3430 |
3.20 |
|
1.5948 |
0.65 |
0.5348 |
1.95 |
0.3383 |
3.25 |
|
1.4624 |
0.70 |
0.5227 |
2.00 |
0.3336 |
3.30 |
|
1.3529 |
0.75 |
0.5112 |
2.05 |
0.3292 |
3.35 |
|
1.2605 |
0.80 |
0.5003 |
2.10 |
0.3248 |
3.40 |
|
1.1815 |
0.85 |
0.4898 |
2.15 |
0.3206 |
3.45 |
|
1.1130 |
0.90 |
0.4798 |
2.20 |
0.3165 |
3.50 |
|
1.0530 |
0.95 |
0.4703 |
2.25 |
0.3124 |
3.55 |
|
1.0000 |
1.00 |
0.4611 |
2.30 |
0.3085 |
3.60 |
|
0.9527 |
1.05 |
0.4523 |
2.35 |
0.3047 |
3.65 |
|
0.9102 |
1.10 |
0.4438 |
2.40 |
0.3010 |
3.70 |
|
0.8718 |
1.15 |
0.4341 |
2.45 |
0.2974 |
3.75 |
|
0.8369 |
1.20 |
0.4279 |
2.50 |
0.2938 |
3.80 |
References
Abramowitz, M. and Stegun, I.A. (eds.) 1964 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Wiley and Sons.
Alfers, D., and Dinges, H. 1984 A normal approximation for beta and gamma tail probabilities. Zeit. Wahr. 65:399-419.
American Statistical Association 1975 Current Index to Statistics: Volumes 1-19. Alexandria, Va.: American Statistical -93 Association.
Anderson, T.P. 1994 Current Issues Concerning Reliability Estimation in Operations Test and Evaluation Unpublished Master's Thesis, Naval Postgraduate School, Monterey, Calif.
Bain, L.J., and M. Engelhardt 1991 Statistical Analysis of Reliability and Life Testing Models, Theory and Methods. Second edition. New York: Dekker.
Bain, L.J., and D.L. Weeks 1965 Tolerance limits for the generalized gamma distribution. Journal of the American Statistical Association 60:1142-1152.
Barlow, R.E. 1979 Geometry of the total time on test transformation. Naval Research Logistics Quarterly 26:393-402.
Barlow, R.E., D. Bartholomew, J. Bremner, and H. Brunk 1972 Statistical Inference Under Order Restrictions. New York: John Wiley and Sons.
Barlow, R.E., and R. Campo 1975 Total time on test processes and applications to failure data analysis. Pp. 451-481 in R.E. Barlow, R. Fussell, and N.D. Singpurwalla, eds., Reliability and Fault Tree Analysis. Philadelphia, Pa.: SIAM.
Barlow, R.E., and F. Proschan 1969 A note on tests for monotone failure rate based on incomplete data. Annals of Mathematical Statistics 40:595-600.
1975 Statistical Theory of Reliability and Life Testing. New York: Holt, Reinhart and Winston.
Barlow, R.E., R.H. Toland, and T. Freeman 1988 A Bayesian analysis of the stress-rupture life of Kevlar/Eposy spherical pressure vessels. In C. Clarotti and D. Lindley, eds., Accelerated Life Testing and Experts' Opinions in Reliability. Lindley, Amsterdam: North-Holland.
Chandra, M., and N.D. Singpurwalla 1981 Relationships between some notions which are common to reliability theory and economics. Math. Operational Research 6:113-121.
Chernoff, H., and G. Lieberman 1956 The use of generalized probability paper for continuous distributions. Annals of Mathematical Statistics 27:806-818.
Cramér, H. 1946 Mathematical Methods of Statistics. Princeton: Princeton University Press.
Gong, G., and F.J. Samaniego 1981 Pseudo maximum likelihood estimation: Theory and methods. Annals of Statistics 9:861-869.
Hardy, G., J. Littlewood, and G. Pólya 1929 Some simple inequalities satisfied by convex functions. Messenger Mathematics 58:145-152.
Hollander, M., and F. Proschan 1984 Nonparametric concepts and methods in reliability. Pp. 613-655 in P.R. Krishniah, and P.K. Sen, eds., Handbook of Statistics, Volume 4: Nonparametric Methods. Amsterdam: North-Holland.
Klefsjö, B. 1980 Some tests against aging based on the total time on test transform. Statist. Res. Report No. 1979-4, University of Umeå (Umeå, Sweden).
Lawless, J.F. 1975 Construction of tolerance bounds for the extreme value and Weibull distributions. Technometrics 17:255-261.
1982 Statistical Models and Methods for Lifetime Data. New York: John Wiley and Sons.
Lawless, J.F., and C. Nadeau 1995 Some simple robust methods for the analysis of recurrent events. Technometrics 37:158-168.
Luenberger, D. 1989 Linear and Nonlinear Programming. Second edition. Reading, Mass.: Addison Wesley.
Mann, N.R., R.E. Schafer, and N.D. Singpurwalla 1974 Methods for Statistical Analysis of Reliability and Lifetime Data. New York: John Wiley and Sons.
Marshall, A., and I. Olkin 1979 Inequalities: The Theory of Majorization and Its Applications . New York: Academic Press.
Nair, V. 1984 On the behavior of some estimators from probability plots. Journal of the American Statistical Association 79:823-831.
Neath, A., and F. Samaniego 1992 On the total time on test transforms of an IFRA distribution. Statistics and Probability Letters 14:289-291.
Nelson, W. 1982 Applied Data Analysis. New York: John Wiley and Sons.
1990 Accelerated Testing: Statistical Models, Test Plans and Data Analyses. New York: John Wiley and Sons.
1995 Confidence limits for recurrence data—Applied to cost a number of product repairs. Technometrics 37:147-157.
Neyman, J. 1959 Optimal asymptotic tests of composite statistical hypotheses. In U. Grenander, ed., Probability and Statistics, the Harold Cramér Volume. New York: John Wiley and Sons.
Press, W., S. Teukalsky, W. Vetterling, and B. Flannery 1992 Numerical Recipes in C: The Art of Scientific Computing. Second edition. Cambridge, U.K.: Cambridge University Press.
Rolph, John E. and Duane L. Steffey, eds. 1994 Statistical Issues in Defense Analysis and Testing: Summary of a Workshop. Committee on National Statistics and Committee on Applied and Theoretical Statistics, National Research Council. Washington, D.C.: National Academy Press.
Samaniego, F.J. 1993 On the Needs of the DoD Testing Community and the Expertise in the Statistical Research Community: A Look at the Interface. Technical Report #286, Division of Statistics, University of California, Davis, Calif.
Samaniego, F.J., and L.R. Whittaker 1986 On estimating population characteristics from record-breaking observations: I. parametric results. Naval Research Logistics Quarterly 33:531-543.
Sinha, S.K. 1987 Reliability and Life Testing. New York: John Wiley and Sons.
Sinha, S.K., and B.K. Kale 1979 Life Testing and Reliability Estimation. New Delhi: Wiley Eastern Limited. Thoman, D.R., L.J. Bain, and C.E. Antle
1969 Inferences on the parameters of the Weibull distribution. Technometrics 11:445-460.
U.S. Department of Defense 1960 Handbook H108: Sampling Procedures and Tables for Life and Reliability Testing (Based on the Exponential Distribution). Washington, D.C.: U.S. Department of Defense.
Woods, W.M. 1996 Using wearout information to reduce reliability demonstration test time, Proceedings of the First Annual U.S. Army Conference on Applied Statistics, Army Research Laboratory, Adelphi, MD, Publication QRL-SR-43.
Zelen, M., and M. Dannemiller 1961 The robustness of life testing procedures derived from the exponential distribution. Technometrics 3:29-49.