Page 32
6—
Surface Temperature Observations
Summary of Trends
Globally averaged surface temperatures have been rising over the last century, but at an uneven rate. Temperatures increased from 1900 to the 1940s, and then leveled off or even decreased until the mid- to late- 1970s. Since that time, globally averaged surface temperatures have increased again. Sea surface temperatures (SST) and land surface air temperatures both show these same features, although the magnitude of the century-scale changes and year-to-year variability of the land air temperatures are greater than those of SST (see Figure 6.1). The fact that a centennial-scale warming trend with similar decadal-scale features exists in both independently collected data sets serves as a useful check on the reality of the surface temperature trend. Long-term warming, as well as warming over the past two decades, has occurred in both hemispheres and in all seasons (Jones et al., 1999). Although not all regions have warmed, the warming trend since 1976 has been very widespread, as indicated in Figure 6.2. Another widespread feature of the global surface temperature signal is that, at least over the last half century—the period for which we have the most data—the mean daily minimum land, air temperature has been increasing at approximately twice the rate of the mean daily maximum temperature (see Figure 9.4) (Karl et al, 1993; Easterling et al., 1997).break
Page 33
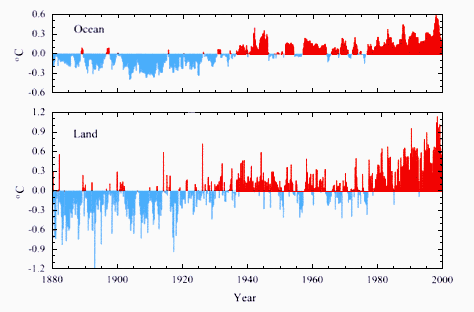
Figure 6.1.
Time series of seasonally averaged temperature anomalies (1880–1999).
The upper figure shows globally averaged sea surface temperature. The
lower figure shows globally averaged surface air temperature over land.
The anomalies are computed as differences from the 1880–1998 mean.
The first season is December 1879–February 1880, and the last season
is June–August 1999. The data are based on the Quayle et al. 1999) data set.
The exact magnitude of the temperature trend depends on how the observations are globally averaged. Very different global averaging techniques have been used in various studies. Quayle et al. (1999) created separate globally averaged land and ocean time series using only those grid boxes containing data, and then combined the two series with a 30%/70% weighting, proportional to the global area of land and ocean surfaces. The data used in this approach include satellite-derived sea surface temperatures. Jones et al. (1999) employed a different approach, combining land and ocean in situ data in the same gridded data set, with interpolation into blank grid boxes with at least four neighbors, and then areally averaging the grid boxes into a single time series. In a third approach, Hansen and Lebedeff (1987) produced a global time seriescontinue
Page 34
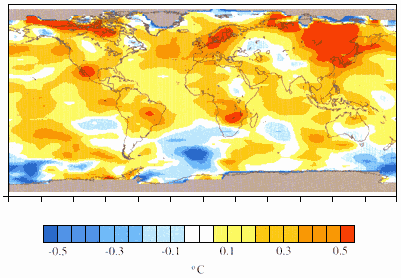
Figure 6.2.
Global surface temperature trends (°C/decade) for the 20-year period 1979– 98
computed using the method of ordinary least squares. The data have been interpolated
to a 5°x5° grid by Jones et al. (1999). The gridded data have been subjected to a slight
additional smoothing to simplify the pattern.
from only land data by using a given station to represent temperature change to distances suggested by correlation studies. The resulting time series has been shown to be representative of combined land and ocean temperature (Peterson et al., 1998a). This approach has recently been updated to include urban adjustment and an increased number of stations (Hansen et al., 1999). All three of these very different approaches yield quite similar results (see Figure 6.3).
The exact value of the trend in globally averaged temperatures depends not only on which of these methods are used to globally average the data, but also on the time period assessed, as well as on the technique that is used to determine the linear trend. In fact, the method used to determine the linear trend can have a greater impact on the result than the method of creating globally averaged temperatures (Peterson et al., 1998a). The most common method for determining trends—least squared deviations—indicates linear trends from the time series of +0.053,continue
Page 35
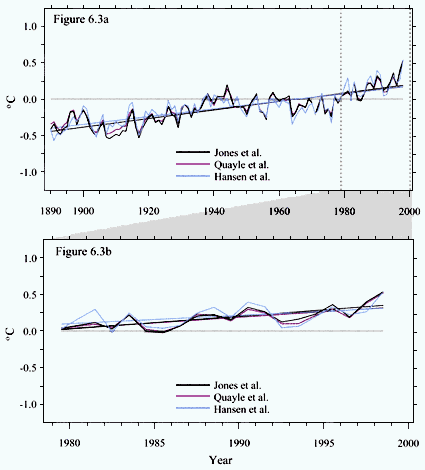
Figure 6.3.
Comparison of global-mean annually averaged surface temperature time series, illustrating
the similarity of results from three different analyses. The series, displayed as anomalies from
their 1961–1990 means, are from (a)1890–1998 and (b) 1979–98, and include least squares
linear regression lines for each. The purple line represents the Quayle et at. (1999) data set; the
black line represents the Jones et al. (1999) data set; and the aqua line represents the Hansen et
al. (1999) data set.
Page 36
+0.059, and +0.053 °C/decade for the period 1890–1998 and +0.17, +0.19, and +0.13 °C/decade for 1979–9811 for Quayle et al. (1999), Jones et al. (1999), and Hansen et al. (1999), respectively (Figure 6.3).
As revealed in Figure 6.3, the increase in the global temperature time series is not linear, nor is there any physical basis for expecting it to be linear. Figure 6.3 also shows that 1998 is by far the warmest year on record, with 1997 the next warmest. In addition, the past ten years (1989–98) have been the warmest decade on record.
Considerable corroborating evidence exists to support the analyses indicating that global surface temperature has risen during this period of historical instrumental record. For example, Oerlemans (1994) recorded a general retreat of glaciers around the world over the past 100 years. De la Mare's (1997) analysis of whaling records indicates that a 25% decrease in Antarctic sea ice occurred between the mid-1950s and the early 1970s. There are indications that in the past 20 years, the extent of Antarctic sea ice may have increased slightly, while the extent of Arctic sea ice has decreased (Parkinson et al., 1999; Vinnikov et al., 1999). In addition, measurements from submarines indicate that the average thickness of sea ice across the open Arctic Ocean has declined by 1.3 meters, or 40 percent, from 1958 to the 1990s (Rothrock et al., 1999). Borehole temperatures can also provide an independent instrumental validation of surface measurements. Pollack et al.'s (1998) analysis of underground temperature measurements from four continents indicates that the average surface temperature of the earth has increased by about 0.5 °C in the twentieth century. Warming of surface temperature should also cause a rise in sea level as a result of thermal expansion of the ocean and melting of glaciers. There is considerable evidence that global-mean sea level has in fact risen 10–25 cm over the past 100 years (Warrick et al., 1996).
Sources of Uncertainly in Trend Estimates
Surface temperature is primarily observed by several thousands of individual thermometers. While the technology for building accurate, reliable thermometers for in situ environmental measurements has beencontinue
11 To further illustrate the sensitivity of a two decade-long time series to the endpoints, if 1976 instead of 1979 is used as the starting date, the trend is approximately 0.02 °C/ decade greater.
Page 37
in existence for over 150 years, there are many problems with the data from these instruments. The data can be erroneous due to instrument problems (e.g., a bubble in the liquid-in-glass thermometers), or contain errors caused by faulty transcription, digitization, or transmission of the data. Such quality control problems add noise to the data, but are not likely to add a bias to the results because of the large number and variety of sites monitored.
However, homogeneity and spatial coverage problems could potentially add a bias to the results. A surface temperature time series is considered homogeneous if variations are caused only by variations in weather and climate (Conrad and Pollak, 1950). Unfortunately, most long-term climatological time series have been affected by a number of non-climatic factors that make these data unrepresentative of the actual climatic variation occurring over time. These factors include changes in: instruments, observing practices (e.g., depth of the water intake for SST measurements), station locations, formulae used to calculate means, and station environment (e.g., urbanization) (Jones et al., 1985; Karl and Williams, 1987; Gullett et al., 1990; Heino, 1994). They occur in measurements of land air temperature, marine air temperature, and sea surface temperature (Folland and Parker, 1995; Peterson et al., 1998b). Some changes cause sharp data discontinuities, while other changes, particularly change in the environment around the station, can cause gradual biases. All of these inhomogeneities can bias a time series and lead to misinterpretations of the studied climate unless they are accounted for by adjusting or ''correcting" the data.
One of the largest sources of uncertainty in global surface temperature analyses is due to incomplete sampling (see Figure 2.7 for data coverage). Large portions of the earth have few in situ observations. This is particularly true of polar regions, uninhabited deserts, and oceanic regions away from the usual shipping and fishing areas. To make matters worse, the locations of observations frequently change with time, and there has not always been a steady improvement in data coverage. For example, starting only in 1978, a limited number of drifting buoys have been placed in the tropical and southern oceans where whaling fleets once took observations. While surface station coverage increased during the nineteenth and most of the twentieth centuries, the difficulties in near-real time international data exchange and the success of many retrospective data gathering efforts (e.g., Bradley et al., 1985; Petersoncontinue
Page 38
and Griffiths, 1997) means that we have fewer land surface in situ observations available in the 1990s than in the 1970s or 1980s.
Using the Comprehensive Ocean/Atmosphere Data Set (COADS; Woodruff et al., 1998), Trenberth et al. (1992) analyzed sources of errors for in situ SSTs. By assessing the variability within 2° longitude by 2° latitude boxes within each month for 1979, they found that individual SST measurements are representative of the monthly mean to within a standard error of ±1.0 °C in the tropics and ±1.2 to 1.4 °C outside the tropics. The standard error is larger in the North Pacific than in the North Atlantic and it is much larger in regions of strong SST gradient, such as in the vicinity of the Gulf Stream, because both within-month temporal variability and the within-2° box spatial variability are enhanced. The total standard error of the monthly mean in each box decreases proportionately to the square root of the number of observations available. The overall noise in SSTs ranges from less than 0.1 °C over the North Atlantic to greater than 0.5 °C over the oceans south of about 35 °S.
In addition to the problems of in situ data, satellite-derived SSTs add another source of uncertainty. While Reynolds and Smith (1994) use optimal interpolation to blend satellite-derived and in situ SSTs, there are biases, particularly in areas with sparse in situ data, that can still occur due to volcanic aerosols (Reynolds and Smith, 1994) and differences between satellite-observed ocean skin temperature compared to in situ observed bulk temperature (Reynolds and Marsico, 1993). The incomplete adjustment of satellite data could decrease the linear trend of globally averaged surface temperature between 1979 and 1999 by up to 0.05 °C/decade (Hurrell and Trenberth, 1999). Also, there are large uncertainties in the location of the sea ice margins in regions of sparse data (Hurrell and Trenberth, 1999).
Efforts to Correct the Problems
Efforts to address these problems started over a century ago. The First International Maritime Conference, held in Brussels in 1853, agreed on the need for international cooperation and adopted a standard set of observational instructions and ship weather-log forms (WMO, 1994). Such efforts have continued through to the present international effort to create the Global Climate Observing System Surface Network (Petersoncontinue
Page 39
et al., 1997). At the same time, historical sea surface temperature data continue to be digitized to fill in gaps in the available in situ data (e.g., Woodruff et al., 1998). While new approaches to derive surface temperature over land using satellite data are under development (e.g., Basist et al., 1998), the satellite data these approaches require may only go back to 1987.
The possibility, indeed probability, of erroneous data is addressed by every major data set compiler as part of the quality control effort (e.g., Jones et al., 1999; Peterson et al., 1998c). While all erroneous data points cannot be removed from a data set without the risk of removing a great deal of good data as well, biases due to large isolated errors can be eliminated. Biases due to discontinuities in the observing network are a much more difficult problem to resolve. However, a great deal of work on homogeneity problems has been done over the past decade or more, as summarized in a recent review of homogeneity research (Peterson et al., 1998b). This work attempts to estimate the magnitude of the bias caused by random station moves, installation of new instrumentation, and changes in observing practices such as changing the time of observation of maximum/minimum thermometers from late afternoon to early morning. Once the magnitude of the bias is determined, the data can be adjusted to account for these inhomogeneities.
A more difficult problem is assessing the impact of small, gradual changes in the observing network. Urbanization (and land-use changes in general) and the resultant urban warming is the most commonly cited example of this type of problem. Recent efforts to assess this bias focus on identifying which stations are rural and which are urban, using map-based metadata12 (Peterson and Vose, 1997) or night-lights derived metadata (Owen et al., 1998). Long-term global temperature trends calculated both from the full land surface network, and from rural stations only, turn out to be very similar (differing by about 0.05 °C per 100 years), despite some differences in regions sampled (e.g., India has few long-term rural stations) (Peterson et al., 1999).
The uneven spatial distribution of in situ data, and the change in their distribution over time, can also potentially create biases. Some of the approaches to addressing this problem are: (a) acquiring more data through digitization of historical records, (b) improving internationalcontinue
12 Metadata (or data about data), in this context, is information that describes the environment in which a measurement is made and/or the methods and/or tools used to make the measurement.
Page 40
exchanges, (c) reconstructing full global grids using the spatial and temporal covariance of the field (e.g., Smith et al., 1998), and (d) developing new space-based observing systems. However, global coverage of in situ data can never be achieved, particularly historically. Therefore, inventive area averaging techniques have been developed to provide robust estimates of global temperatures. These techniques include grid-box averaging of climate anomalies (e.g., Jones, 1994), or averaging of the interannual change in temperature (Peterson et al., 1998a). A more complex approach that interpolates anomalies adjusted to regional reference stations produces information for each grid box (Hansen and Lebedeff, 1987). Smith et al. (1998) also fill in the full grid using the spatial and temporal covariance of the sea surface temperature field together with the available data. Within this latter approach is the assumption that the covariance pattern developed in the satellite era is an appropriate guide for interpolating data in earlier eras.
Several efforts have been made to put error bars on global surface temperature time series, primarily by focusing on the impact of inadequate spatial sampling and using model simulations of global climate. Jones et al. (1997) estimated that the typical standard errors for annual data on the interannual time scale since 1951 are about ±0.06 °C.13 Errors associated with century-scale surface temperature trends are probably an order of magnitude smaller than the observed warming of about 0.5 °C per 100 years since the late nineteenth century (Karl et al., 1994).break
13 Unless stated otherwise, the quantitative error estimates given in this report represent 95% confidence intervals.









