International Benchmarking of US Mathematics Research
Panel Members
PETER D. LAX (Chair), Professor of Mathematics and Director, Courant Mathematics and Computing Laboratory, New York University, New York, NY
MICHAEL F. ATIYAH, Master, Trinity College, Cambridge, England
SPENCER J. BLOCH, Professor, Department of Mathematics, University of Chicago, Chicago, IL
JOSEPH B. KELLER, Professor, Departments of Mathematics and Mechanical Engineering, Stanford University, Stanford, CA
JACQUES-LOUIS LIONS, President, French Academy of Sciences and Professor, College de France, Paris, France
YURI I. MANIN, Director, Max Planck Institut fur Mathematik, Bonn, Germany
RUDOLPH A. MARCUS, A.A. Noyes Professor of Chemistry, California Institute of Technology, Pasadena, CA
GARY C. McDONALD, Head, Operations Research Department, GM Research and Development Center, Warren, MI
CATHLEEN S. MORAWETZ, Professor Emeritus, Courant Institute of Mathematical Sciences, New York University, New York, NY
PETER SARNAK, Chair, Department of Mathematics, Princeton University, Princeton, NJ
I.M. SINGER, Institute Professor, Massachusetts Institute of Technology, Cambridge, MA
MARGARET H. WRIGHT, Distinguished Member of Technical Staff, Bell Laboratories, Lucent Technologies, Murray Hill, NJ
Project Staff
DEBORAH D. STINE, Study Director
PATRICK P. SEVCIK, Research Associate
JOHN R. TUCKER, Senior Program Officer
NORMAN GROSSBLATT, Editor
Mathematics Benchmarking Guidance Group
MARYE ANNE FOX (Chair), Vice President for Research, University of Texas at Austin, Austin TX
PHILLIP A. GRIFFITHS, Director, Institute for Advanced Study, Princeton, NJ
DANIEL KLEPPNER, Professor of Physics, Massachusetts Institute of Technology, Cambridge, MA
AVNER FRIEDMAN, Director, Institute for Mathematics and its Applications, University of Minnesota, Minneapolis, MN
SAMUEL WINOGRAD, IBM Fellow, International Business Machines Corporation, Thomas J. Watson Research Center, Yorktown Heights, NY
ROBERT MacPHERSON, Professor, School of Mathematics, Institute for Advanced Study, Princeton, NJ
Staff:
LAWRENCE E. McCRAY, Executive Director, COSEPUP
DEBORAH D. STINE, Associate Director, COSEPUP
JOHN R. TUCKER, Director, Board on Mathematical Sciences
NORMAN METZGER, Executive Director, Commission on Physical Sciences, Mathematics, and Applications
Figures and Tables
Report
|
Figure 1: |
Percentage of Mathematics-Research Papers Published by US Authors |
|||
|
Figure 2: |
Percentage Unemployment Among New US PhDs in Mathematics, Autumn of Year Shown |
|||
|
Figure 3: |
Number of PhDs Produced by US Mathematics Departments, Spring of Year Shown |
|||
|
Figure 4: |
Employment Status of PhD Mathematicians in the US |
|||
|
Figure 5: |
Doctoral Recipients: Total Number and US and Non-US Citizens |
|||
|
Figure 6: |
Percentage of Foreign Natural-Sciences Doctoral Students in Various Countries |
|||
|
Figure 7: |
Stay Rates—Percentages of Foreign Doctoral Students Who plan to Remain in the United States, Averaged Over 1988-1992 |
|||
|
Figure 8: |
Total Full-Time PhD Students in Mathematical Sciences |
|||
|
Table 1: |
Decrease in Applications to PhD Programs in Mathematics, 1994 to 1996 |
|||
|
Figure 9: |
Median Salaries in 1993 of US PhDs Who Received Their Degrees in 1985-1990, by Field |
|
Figure 10: |
Percentages of Academic Scientists with Federal Support, 1993 |
|||
|
Figure 11: |
Percentage Increase in Federal R&D Expenditures at Universities and Colleges, by Field |
|||
|
Appendix B |
|
|||
|
Figure B-1: |
Number of US Institutions Awarding PhDs in Mathematics, 1920-1995 |
|||
|
Figure B-2: |
Number of PhDs Awarded in Mathematics in the United States, 1920-1995 |
|||
|
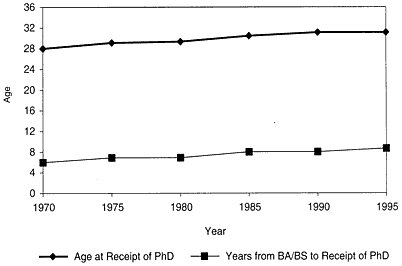
Figure B-3: |
Median Time to PhD and Age at Receipt of PhD in Mathematics in the United States |
|||
|
Figure B-4: |
Doctoral Recipients: Total Number of US and Non-US Citizens |
|||
|
Figure B-5: |
Number of First Degrees in Mathematics and Computer Science |
|||
|
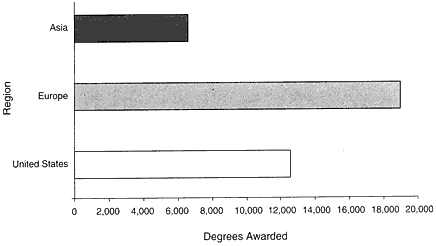
Figure B-6: |
Doctoral Degrees in Natural-Sciences, 1992 |
|||
|
Figure B-7: |
Number of PhD Mathematicians Employed in the United States |
|||
|
Table B-1: |
Employment Status of PhD Mathematicians in the United States |
|||
|
Table B-2: |
Occupation Status of PhD Mathematicians in the United States |
|||
|
Figure B-8: |
Median Salaries in 1993 of US PhDs Who Received Their Degree in 1985-1990, by Field |
|||
|
Figure B-9: |
Citizenship of Full-Time Mathematics Faculty with PhDs Hired During 1991-1992 in the United States |
|||
|
Figure B-10: |
Source of PhDs of Full-Time Mathematics Faculty Hired During 1991-1992 in the United States |
|||
|
Figure B-11: |
Percentage of Unemployed New US Mathematics PhDs |
|||
|
Figure B-12: |
Median Nine-and Twelve-Month Salaries of New US PhDs for Teaching or Teaching and Research in 1995 Dollars |
|||
|
Table B-3: |
Federal Support for the Mathematical Sciences, Fiscal Year 1995-1998, in Millions, Current Dollars; and in Millions, Constant 1992 Dollars |
|||
|
Figure B-13: |
Percentages of US Academic Scientists with Federal Support, 1993 |
|||
|
Figure B-14a: |
Federal Funding of US Mathematical Research—Academic, 1993-1995 Average |
|||
|
Figure B-14b: |
Federal Funding of US Mathematical Research—All R&D |
|||
|
Figure B-15: |
Percentage of Mathematical Research Papers Published by US authors |
|||
|
Figure B-16: |
Number of Mathematical Research Papers by US and EC Authors, 1981-1996 |
EXECUTIVE SUMMARY
The United States is clearly preeminent in mathematics today. The field is thriving in terms of both quality and opportunities. Not only are there stellar researchers in all fields at American institutions, but they are backed by a broad and active research community. Mathematical research in the United States has many links with science, engineering, and technology and is broadening its contacts with education at all levels. But this position of eminence is fragile. Increasing demands are placing a strain on the mathematics community.
In making judgments about mathematics, the International Benchmarking of US Mathematics Research Panel kept these points in mind:
-
Mathematics is the language and tool of most of the sciences.
-
Mathematical results often have a long life.
-
Mathematical research is conducted on a very broad front, and seemingly disjointed branches often turn out to be intimately related.
-
Ideas of abstract mathematics often are crucial ingredients in practical applications.
-
Mathematics is one of the pillars of education in kindergarten, elementary school, high-school, and college.
The present strength in US mathematics is due to:
-
Continued attractiveness of the United States to talented people around the world.
-
A strong system of graduate education.
-
Diversity and flexibility of the US research enterprise.
-
Sustained funding for research from universities and the federal government.
The United States continues to attract some of the best graduate students and postdoctoral fellows from all over the world; a substantial portion of active research mathematicians now in the United States come from outside the United States. But we are in danger of losing our preeminent position if we do not face some critical issues and challenges. Some critical issues and challenges must be faced:
-
US leadership in mathematics rests on the health of research universities, which today are experiencing severe financial pressure and conflicting demands.
-
The United States is not taking sufficient advantage of its native mathematical talent: while graduate enrollment from abroad thrives, the number of American students applying to graduate school in mathematics is diminishing.
-
Serious thought is needed about how to make better connections between mathematics and other fields, because mathematics is crucial in much interdisciplinary research.
-
US industry has reduced its commitment to long-range research in mathematics.
1
BACKGROUND
In 1993, the Committee on Science, Engineering, and Public Policy (COSEPUP) of the National Academy of Sciences, the National Academy of Engineering, and the Institute of Medicine issued the report Science, Technology, and the Federal Government: National Goals for a New Era. This report recommended that the United States be among the world leaders in all major fields of science and maintain clear leadership in selected fields. A similar recommendation was made in a later National Research Council (NRC) report, Allocating Federal Funds for Science and Technology, published in 1995—that the United States ''strive for clear leadership in the most promising areas of science and technology and those deemed most important to our national goals."
Both reports stated that quantitative measures, such as dollars spent and number of scientists supported, were inadequate indicators of leadership and that policy decisions about programmatic issues or resource allocation would be better informed by comparative international assessments. Independent field-specific panels were suggested as the best means for obtaining such evaluations. Each panel would consist of researchers in the particular field, researchers in closely related fields, and research users who follow the field, and each panel would include researchers from outside the United States.
In late 1996, COSEPUP began an experimental study of the effectiveness and outcome of such panels. The present report—an evaluation of US research in mathematics—was prepared by the first panel and will be followed by studies in materials science and immunology. Each panel has been asked to address the following questions:
-
What is the position of the United States in research in the field relative to that in other regions or countries?
-
What key factors influence relative US performance in the field?
-
On the basis of current trends in the United States and abroad, what will be the relative US position in the near term and the longer term?
2
SCOPE AND NATURE OF THE PANEL'S EVALUATION
Mathematics is the most formal and rigorous of the sciences, but there is no universally accepted definition of mathematics (and the panel has not attempted to formulate one). In this report, to conform with the 1992 report Educating Mathematical Scientists: Doctoral Study and the Postdoctoral Experience in the United States, published by the NRC Board on Mathematical Sciences, mathematics broadly includes pure mathematics, applied mathematics, statistics and probability, operations research, and scientific computing.
Mathematics has several properties that complicate its assessment:
-
Mathematical research generally has a particularly long "shelf life": large parts of it do not become obsolete. Not infrequently, a much earlier result or insight—even from a previous century—is suddenly the key to solving a modern problem.
-
Seemingly diverse subfields of mathematics often form unexpected links.
-
Throughout science and engineering, mathematics provides a universal language, tools for analysis, abstractions to guide understanding, and methods for solving problems. Consequently, mathematical research has a tightly coupled, two-way connection with other fields: mathematical discoveries influence research in other fields, and developments in other fields provide new problems for mathematicians to study. However, the contributions of mathematical research are often not labeled explicitly as such.
-
Mathematical training is a central part of the education of all US citizens, from kindergarten through high school and college.
Because of the first two properties, we have not defined and separately assessed subfields of mathematics, but rather have focused on mathematics as a whole. Because of the third and fourth properties, our evaluation reaches beyond mathematics to fields and activities where mathematics research has a direct and visible impact. We also recognize that important mathematical research is conducted by people whose affiliations and titles do not explicitly identify them as mathematicians; some of the difficulties associated with this phenomenon are described in SIAM (1995).
US mathematics research was defined by the panel as research in the mathematical sciences conducted by residents of the United States working in US institutions.
The panel would like to mention 5 key caveats with respect to its analysis. First, following its charge from COSEPUP, this report is based on the qualitative judgments of the panel members informed by both their own knowledge and the sparse quantitative data available. The panel has attempted to be as fair and impartial as possible, balancing the points of view of US academic mathematical researchers with views of leading mathematicians from outside the United States, nonmathematical US researchers, and industrial researchers. In addition, the panel was specifically charged not to make recommendations. With more time and effort, additional opinions and data could have been collected, but such efforts would have been expensive relative to the additional guidance obtained.
Second, given the diversity of mathematical sciences, no panel could represent all the subfields of mathematics. The panel has done its best to review all subfields, but some are undoubtedly better analyzed than others. The findings and conclusions here do not apply uniformly to all areas of the mathematical sciences. For example, statistics has enjoyed much stronger employment prospects than most other areas. Thus, some variation in interpretation of these results is required when focusing on specific areas.
Third, many statements in this report are not based on numerical data, mainly because of the paucity of statistics that allow meaningful comparisons among countries. For example, undergraduate and PhD degrees in the United States are not directly comparable with all similarly labeled degrees in other industrialized countries. Even when quantitative information is available, sometimes it contains so many ambiguities that we were reluctant to rely on it. To understand the position in other countries when suitable data were unavailable or unclear, the panel relied on the informed judgments of panel members and colleagues from outside the United States.
Fourth, a substantial amount of mathematics is carried out by people bearing other labels: physicists, chemists, electrical engineers,
economists, computer scientists, and statisticians. Some Nobel prizes in these fields have been awarded for mathematical work.
Fifth, had this report been written 7 years ago, the Soviet Union would have loomed large as a competitor of the United States. The collapse of the Soviet Union changed that; Russia is in disarray on all fronts, infrastructure is collapsing, and many of the best former Soviet mathematicians have found employment abroad, particularly in the United States. At present, mathematics in Russia and Ukraine is a shadow of its former self.
3
RELATIVE POSITION OF US RESEARCH IN MATHEMATICS
3.1 The Discipline
3.1.1 Leadership
Our first means of evaluation was an ad hoc survey. The panel divided the mathematical sciences into 19 subfields corresponding roughly to the classification used by the International Mathematical Union, and each panel member was assigned a set of subfields in which he or she was knowledgeable. For every subfield, the assigned panel members identified a reasonable number (between 5 and 10) of internationally recognized leaders in several countries. These experts were asked to draw up a list of about 10 speakers (10 is the average number of speakers on a given subfield at an international congress on mathematics), without regard to nationality, for a hypothetical international mathematics congress. Speakers were to be selected because their research was at the leading edge and driving the subfield. Our intent was not to identify the most-famous or best-established people, but rather those whose research was the most important at the time. The demographic results of this informal process were remarkably uniform in each subfield and across subfields. In 17 of the 19 subfields, at least half those named are citizens or permanent residents of the United States. In the other two, about 40% of those named work in the United States.
A second means of evaluating research leadership was to examine the lists of winners of major prizes in mathematics. This measure can be criticized on several grounds: far fewer prizes are awarded in mathematics than in many other sciences, prizes do not uniformly cover all subfields of mathematics, and prizes awarded on an international basis
are invariably subject to (unstated) requirements that they not be dominated by a single country. Nonetheless, the panel felt that the clear leadership of US mathematics was demonstrated by looking at two of the most prestigious prizes in mathematics: the Fields medal and the Wolf prize. The Fields medal is presented every 4 years at the International Congress of Mathematicians (ICM) and is by tradition given to mathematicians younger than 40. Of the 38 Fields medals awarded so far, 14 (about 37%) went to people in the United States; more than 40% of Fields medal winners are now working in the United States. The Wolf prizes have been given annually since 1978 for outstanding achievement in physics, chemistry, medicine, agriculture, the arts, and mathematics. More than half (15 of 28) of the recipients of the Wolf prize in mathematics, which is not restricted by age of the recipient, now live in the United States. Moreover, although there is no Nobel prize in mathematics, the 1994 Nobel prize in economics was shared by a US mathematician, John F. Nash.
A third indicator is the US representation among the plenary speakers at two large and prestigious international mathematics meetings. The ICM is typically attended by about 4,000 mathematical researchers. ICM speakers are chosen by distinguished committees with some attention to balanced geographic distribution among the speakers. At the last ICM, in 1994, 8 of 16 (50%) of the 1-hour plenary speakers were from the United States. In 1990 (Kyoto), 9 of 15 (60%) were American, and in 1986 (Berkeley), 8 of 16 (50%). For the International Congress on Industrial and Applied Mathematics (ICIAM), attended by about 2,500 mathematical researchers, plenary speakers are chosen by a committee representing mathematics societies from 12 countries or regions, and substantial attention is paid to balancing the plenary speakers among those countries. In the 1995 ICIAM, 7 of 20 (35%) of the invited plenary speakers were from the United States, and in 1991, 6 of 20 (30%).
3.1.2 Depth
The three indicators just described reflect clear US leadership based on the accomplishments of a relatively small number of stellar mathematicians. We felt that we should also assess the more-robust measure of depth in research leadership; US leadership would be fragile if it depended on the location of a few individuals. We believe that the United States has substantial depth in all subfields of mathematics, on the basis of the following observations:
-
In the United States, 183 institutions award PhDs in the mathematical sciences. The 20 or so top-ranked mathematics departments in this group are comparable in research excellence with those at the best universities anywhere in the world.
-
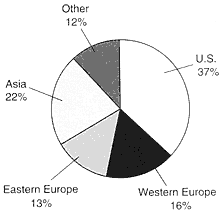
As shown in figure 1, US mathematicians consistently produced about 40% of the total research publications in mathematics from 1981 to 1993.
-
The American Mathematical Society (AMS), an organization of researchers in the mathematical sciences, has 30,000 members, including 22,000 US members. Non-US citizens join AMS through reciprocity agreements. The Society for Industrial and Applied Mathematics (SIAM), an organization of researchers in applied mathematics and scientific computing, has 6,400 US members in a total membership of 9,000. Annual attendance by US residents at the joint research conferences held by AMS and the Mathematical Association of America (MAA) is about 3,500. Annual attendance by US residents at SIAM research conferences is about 2,300. The meetings and publications of these societies play a major role in disseminating mathematical ideas. Membership in the societies is a rough measure of sustained interest.
3.2 Mathematics in a Broader Context
As mentioned in section 2, the quality of mathematical research can partly be measured by its effects on closely related activities. We consider four: scientific and engineering research, industry, government, and education. It is difficult to carry out this analysis, because it is hard to document which mathematics-related activities are conducted by mathematicians and which by people trained in other scientific and engineering fields.
3.2.1 Science and Engineering
Numerous studies have documented in great detail the strong connections of mathematical sciences research with the physical,
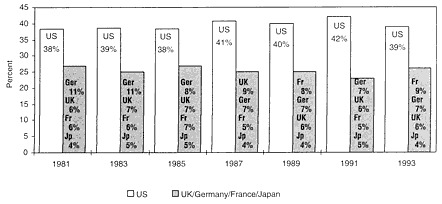
FIGURE 1 Percentage of mathematics-research papers published by US authors. Source: NSB 1996, appendix table 5-31.
biologic, and social sciences, engineering, and medicine. We list a small subset of diverse recent instances in which US mathematical research is closely linked with other fields. That a broad spectrum of mathematics contributed to these examples emphasizes the unity of the mathematical sciences (see section 2).
-
Physics has been the science closest to mathematics for the longest time, and their closeness continues today. Many of history's most famous scientists worked in both physics and mathematics (from Newton, Euler, Gauss, Lagrange, Poisson, Kelvin, Maxwell, Poincaré, and Rayleigh to Einstein, Weyl, von Neumann, and Witten). Mathematical physics is extremely active in the United States; many questions of common interest in mathematics and physics arise from quantum mechanics and field theory, general relativity, fluid and multiphase flow, electromagnetic theory, and materials science. Semiconductor modeling, thin films, and signal transmission in optical fibers are three special areas of high mathematical content (see, for example, NRC 1993).
-
Biology, physiology, and theoretical and computational chemistry are adopting mathematical approaches, and some eminent US researchers in these fields actively collaborate with mathematicians (NRC 1995a, b). Mathematical Challenges from Theoretical/Computational Chemistry (NRC 1995a) describes recent successes, such as the development of commercial products from quantitative structure-activity relationships and the insights into molecular structure gained from group theory and topology. Materials scientists and mathematicians have increasingly been forming research partnerships. A 1995 Minerals, Metals, and Materials Society-SIAM workshop on modeling microstructural evolution (Chen and others 1996) produced 70 papers by US mathematician, physicist, and materials scientist coauthors. A joint 1996 initiative of the National Science Foundation (NSF) and the Defense Advanced Research Projects Agency (DARPA) in materials science attracted numerous proposals involving research from all subfields of mathematics.
-
Computer science traditionally relies on particular branches of mathematics, certainly logic but also combinatorics and number theory. Recently, the astonishing growth of traffic on the Internet has led to new applications in queuing theory, discrete mathematics, combinatorial optimization, and protocol verification. The report Cryptography's Role in Securing the Information Society (NRC 1996a) discusses the need for mathematical research in, for example, number theory and logic to develop and analyze cryptographic techniques guaranteed to remain secure when faced with continuing gains in raw computing power.
-
Imaging has relied on and inspired new mathematics for over 20 years. The basis of the CAT-Scan, the Radon transform, was first described nearly 80 years ago. Mathematical research today in, for
-
example, deblurring and real-time detection of anomalies links directly with medical applications. The report Mathematics and Physics of Emerging Biomedical Imaging (NRC 1996b) states that "many of the envisioned innovations in medical imaging are fundamentally dependent on the mathematical sciences." The mathematics of imaging is also important in astronomy, biology, geosciences, weather, and cartography.
-
Engineering, in all its fields, uses sophisticated mathematics to formulate, analyze, and solve problems, particularly those in which early prototyping and experimentation are too expensive or too risky. The 1995 symposium on "Frontiers of Engineering" held at the National Academy of Engineering highlighted four topics of research in engineering—biotechnology, design and manufacturing, environmental engineering, and information technology; US mathematicians have been active contributors to all four (NAE 1996; SIAM 1995).
-
In meteorology, biotechnology, and other "grand-challenge" problems, mathematicians and scientists in other fields have had major successes. The nature of such interdisciplinary collaborations is discussed in two studies—1 by COSEPUP (1996) and the other by the National Academy of Public Administration (NAPA 1995).
That list demonstrates the success of US mathematics research in taking part in research in science, engineering, and medicine. Much of it has been achieved through computing, both locally and through supercomputer centers. There was no feasible way for the panel to determine the interactions of mathematics with science and engineering in other countries. Panel members from outside the United States and our sampling of reports from other countries confirm that all industrialized nations are vigorously encouraging interdisciplinary research in which mathematics plays a part (see section 5.2).
3.2.2 Industry
Many large companies in the United States that rely on technical innovation support research and development laboratories that employ PhD mathematicians. In 1995, 21% of doctoral mathematical scientists in the US workforce were employed in private industry—a proportion that has steadily increased over the years (see table B-1). In 1975, 11% of PhD mathematicians worked for industry; in 1985, 19%. That trend might indicate that the flexibility of mathematics PhD programs is increasing. A few US industrial research laboratories—Bell Labs, IBM Research, and General Electric—have been world-famous for their research in mathematics and in other sciences. Major US companies, such as AT&T, Boeing, and General Motors, have maintained active, high-quality groups of research mathematicians. However, it is often
difficult to identify mathematical research in medium-or small-scale industrial settings because the organizational structures are cross-disciplinary.
In many widely publicized instances, mathematical research has made substantial contributions to US industry successes. The aerodynamic design of the Boeing 777 was accomplished by computing airflow, pressure, temperature in the exterior of the proposed design; research on numerical methods, adaptive grid generation, and optimization was crucial. The visualization system allowed thousands of scientists, engineers, and customers to work together (Council on Competitiveness 1996). Mathematics was also central to the remarkable animation in the 1995 Disney film Toy Story (SIAM 1996). Another example is the soliton, discovered around 1965 by the mathematicians N.J. Kruskal and M.D. Zabusky, that is now poised to play a key role in the transmission of signals in optical fibers. The mathematical concept of wavelets is an increasingly important tool for the storage and recovery of information, for instance, fingerprints.
Mathematical research has played well-documented roles in many other fields of industry that have strengthened the economic position of the United States, particularly in the automotive, pharmaceutical, communication, and computer industries (NRC 1991). Within the last few years, there has been a great deal of interest by banks and investment houses in employing mathematicians to use mathematical techniques to model and analyze financial trends (COSEPUP 1995); financial mathematics depends on a number of recent discoveries and techniques found in mathematics. Attempts to assess precisely the contributions of mathematical research to industrial problems are hindered by the blurring of disciplinary boundaries throughout most of industry (SIAM 1995).
Especially since the 1980s, US academic mathematicians have created programs and organizations, partially funded by industry, that are designed to involve mathematics research with industrial problems. Examples include the Institute for Mathematics and its Applications at the University of Minnesota and several programs at public and private universities.
Outside the United States, strong connections exist between research mathematics and industry. In France, a rapid development immediately followed World War II in the fields of applied mathematics and scientific computing; many strong researchers took jobs in industry. In Germany, recently created institutes combine academic and industrial partners, for example, in aerospace and automotive manufacturing. Several institutions in the UK support research interactions between mathematicians and industry. Examples are the Rolls-Royce Readership in Computational Fluid Dynamics at Oxford, the Newton Institute at Cambridge, and the Basic Research Institute in the Mathematical
Sciences at Bristol (founded with partial funding from the UK branch of Hewlett-Packard).
3.2.3 Government Laboratories and Agencies
During and after World War II, the US government established laboratories in which research in mathematics (and many other disciplines) was supported. In 1993, government laboratories employed 4.5% of the mathematical-sciences PhDs in the United States (NSF 1996a, table 20). Even with the cuts in defense spending that began in the early 1990s, US government labs have maintained substantial investments in mathematical research. Mathematical research is an integral part of the mission of federal laboratories, such as those of the Department of Energy at Los Alamos, Livermore, Berkeley, Argonne, and Oak Ridge; several Department of Defense laboratories; of the National Security Agency; of the National Institute of Standards and Technology; of the National Center for Atmospheric Research; of the National Aeronautics and Space Administration; of the National Oceanic and Atmospheric Administration; and other agencies such as the Bureau of the Census of the Department of Commerce.
The position of mathematics research conducted in government laboratories varies in other industrialized countries. In the United Kingdom, for example, until the 1980s, the missions of several government laboratories (such as the National Physical Laboratory and AERE Harwell) included basic research, but this has now been de-emphasized or eliminated. There apparently remain a large number of research mathematicians in the Defense Research Agency, but their numbers are classified. Major decreases in defense spending in the UK have led to concomitant reductions in mathematical research in the associated laboratories. Nonmilitary research in government laboratories has been cut; several nondefense laboratories that employed research mathematicians have been privatized and have moved toward commercial, short-term activities, rather than long-term research.
In France, government research laboratories were established in 1939, and mathematics plays a prominent role in several of them (for example, Institut National de Recherche en Informatique et en Automatique (INRIA) and Institute de Hauts Etudes (IHES)). We found no data specifically about mathematics; national laboratories account for 22% of all research in France, and half of French scientists work full-time on research in laboratories run by government agencies. About 20% of all scientists and engineers work in government laboratories (NSF 1996c, p. 36).
International comparisons are difficult because of differences in organizational structures; for example, many government laboratories in France are integrated within universities.
3.2.4 Mathematics Education
Of all the sciences, mathematics is most closely scrutinized for its function in education, largely because mathematical skills are seen as a key indicator of the scientific and technologic development of the citizenry. The panel stresses the need for a healthy relationship between mathematical research and mathematics education. To bring modern, simpler ways of looking at material and to incorporate appropriate recent research into graduate and undergraduate education in mathematics and other fields, the role of active researchers is crucial. Research experiences that encourage mathematical skills and innovation are a growing part of US undergraduate mathematics education.
Research mathematicians from all sectors of the US higher-education system, including the most-prestigious mathematics departments, are increasingly involved in improving the teaching of mathematics, at every level of education, to both specialists and nonspecialists. ''Service teaching" of undergraduate mathematics to nonmajors is the responsibility of mathematics departments in all US universities, and many leading US academic mathematicians regularly teach elementary courses for mathematics nonmajors. There have always been divided views on this. There was a period when many nonmathematics departments taught these courses; however, when research universities expanded, these departments were happy to shift this responsibility to mathematics departments. Now the reverse is occurring due to the general shrinking of research universities. The best solution appears to be better teaching by mathematicians operating in full cooperation with the departments concerned. New methods based on that idea have led to major improvements in calculus teaching.
Policy-making and professional organizations of US research mathematicians are deeply involved in education. The NRC Board on Mathematical Sciences, the NRC Mathematical Sciences Education Board, AMS, MAA, and SIAM regularly initiate studies and publish reports about various aspects of mathematics education. Collaboration between high schools and research mathematicians is rare but increasing. However, despite the increased efforts of many mathematicians, we have a long way to go, compared to many other countries, in teaching mathematics effectively in kindergarten through high school, as illustrated in the recent evaluation of 8th-grade mathematics instruction in the Third International Mathematics and Science Study (TIMSS) (ED 1996).
It is beyond the scope of this report to discuss the enormous task of improving the mathematical level of the general population. The contribution of research mathematics to this task in only a small though essential part. However, the level of mathematics education at the K-12 level affects the research community in two ways:
-
Inadequate high-school education makes it more difficult for college and university instructors to maintain standards and create an intellectually challenging curriculum.
-
Because of the lack of interesting exposure to mathematics, fewer students are interested in studying mathematics or pursuing mathematics as a career.
Mathematics education is a major concern in all other countries of which the panel is aware, but we have only anecdotal data about how research mathematicians elsewhere are involved in education. There is a general concern in Europe (except in France) that the quality of education is going down. Japan, according to a recent report, has an outstanding mathematics curriculum (Askey 1993).
The early recognition and training of the mathematically talented is traditional in Russia, France, Hungary, Romania, and Poland. We are happy to report that this tradition is gaining ground also in the United States, through special high schools, special publications for the young, correspondence courses, statewide contests, national and international olympiads, intense summer programs, and so on.
4
FACTORS THAT INFLUENCED PAST US PERFORMANCE IN MATHEMATICS
We have identified four leading influences on the success of US mathematical research: attractiveness to foreign talent, quality and structure of graduate education, diversity of the mathematical research enterprise, and financial support for research and infrastructure.
4.1 Attractiveness to Talent from Outside the United States
A policy of welcoming distinguished scientists as citizens or permanent residents has enabled the United States to attract from abroad many of the world's best senior mathematicians and promising young mathematicians. Leading scientists, including mathematicians, fled to the United States from the Nazis during 1933-1945 and were followed by a second flood after World War II, from 1945-1955. This concentration of immigrants raised the level of US mathematics to the top. Substantial increases in the number of outstanding mathematicians immigrating to the United States—for example, from China and the former Soviet Union—have also occurred more recently. The pattern of assimilating top talent from all nations outside the United States has been consistent and striking.
America has long been viewed as the "promised land" of freedom, wealth, and opportunity. In addition, mathematicians were drawn to the United States for several practical reasons, discussed below—more and better jobs, high salaries, funding for research, and greater mobility than in any other country. On the last issue, for example, European professors tend not to move once they secure a chair. In France, professors
migrate toward Paris. In contrast, it is not uncommon for many of the best US professors to change jobs repeatedly.
4.2 Quality and Structure of Graduate Education in Mathematics
Because the brightest students want to study with the best people, the presence, described above, of leading mathematicians at universities throughout the United States has been a major factor in the visibility and appeal of US graduate education since the end of World War II, when the "GI Bill" enabled poor but talented students to take advantage of educational opportunities.
US graduate education in the sciences, mathematics, and engineering has been concurrently boosted by two other influences. After the launch of Sputnik in 1957, the United States adopted various national policies that strongly encouraged the study of mathematics, science, and engineering from elementary through graduate school. The large number of "baby boom" undergraduates entering colleges and universities in the 1960s and 1970s led to substantial expansion in mathematics departments and graduate programs throughout the United States.
One structural aspect of US graduate education in mathematics stands out in comparison with other countries: the much lower level of specialization required to enter a graduate program. For example, it is possible to enter a US PhD program in mathematics without an undergraduate degree in mathematics; such late shifts of major are extremely rare in other countries. This "late start" feature increases flexibility and choice for prospective students. By the time US students begin their dissertation research, they are typically as well prepared as their counterparts elsewhere, but possibly older.
Strong US graduate programs in mathematics have been able to attract top-quality students not only in the United States but also from abroad, showing again the great appeal of the US mathematics environment to foreign talent. A well-known example is the enrollment in the 1980s of a large number of brilliant graduate students from China, Taiwan, Hong Kong, and the USSR. Many of them then remained in the United States after receiving the PhD, and some outstanding mathematicians in the United States today belong to this group.
4.3 Diversity of the US Research Enterprise
Before World War II, only a handful of US research universities were distinguished in mathematics; today, at least 2 dozen have uniformly high-quality faculty across most subfields of mathematics, and many more have stellar researchers in particular subfields. Rather than being dominated by a few institutions or individuals, this diffuse struc-
ture allows a wide range of mathematicians from across the entire country—and with their institutions—to excel. The diffusion of talent is strengthened by a level of professional mobility that is unmatched elsewhere.
Four independent research institutes in the mathematical sciences contribute to the quality of US mathematics. The Institute for Advanced Study, founded in the 1930s, has long been a major force in pure mathematics, drawing talented people from around the world. The Center for Discrete Mathematics and Theoretical Computer Science at Rutgers, the Mathematical Sciences Research Institute at the University of California, Berkeley and the Institute for Mathematics and its Applications at Minneapolis—all funded largely by the National Science Foundation (NSF)—have been created since 1980. A somewhat different model is the Courant Institute which is integrated with the mathematics and computer science departments at New York University. Those four and the National Institute of Statistical Sciences have increased awareness of research accomplishments, brought leading and junior researchers together, provided support for postdoctoral students, and created ties between different subfields of mathematics—for example, geometry and mathematical physics—and between mathematics and industry. There are many analogous institutes abroad (for example, the Max Planck Sonderforschung and the Oberwolfach in Germany, the Euler Institute in Russia, the Mittag-Leffler Institute in Sweden, the Newton Institute at Cambridge, and the IHES in France).
Since World War II, mathematics in US universities has branched out and expanded into new fields. The invention and development of electronic computers provided a stimulus for mathematics throughout the world. The United States pioneered in the use of computers, thanks partly to the leadership of von Neumann, and to the success of the semiconductor, software, and computer industry. Computing in England began during the war, primarily from the work of Alan Turing. The rest of the industrial world is catching up, but the United States still dominates.
The field of computer science was spawned jointly by mathematics and electrical engineering, and many parts of computer science remain closely linked with mathematics. Consistent and dramatic increases in computing power have encouraged mathematicians to tackle longstanding problems, formulate and solve new problems, devise new numerical methods, and produce software. Graduate programs that combine mathematics with various scientific fields have been initiated. Thus, the growing roles of mathematics in science, engineering, and medicine are formally recognized and encouraged in many places, as discussed in section 3.2.1. The emerging role of mathematics in business, finance, and modern management has also been spawned by new mathematical methods and greater computer power.
4.4 Adequate Funding
The three factors already mentioned explicitly rely on sustained funding for mathematical research, which comes from various sources, both public and private. Funding for individual faculty members gives them time to concentrate on research, and it supports graduate students; funding for conferences, workshops, summer schools, and other infrastructure facilitates interactions that are central to a thriving mathematical research community. These have greatly increased the exchange of information through personal discussion in mathematical research over the last two decades.
The predominant element in funding of United States mathematics research has been the strong commitment to intellectual excellence by private and public universities. To preserve and build research quality, universities have been willing to expend financial resources to hire and support the world's best mathematicians, as noted above in the discussion of the diversity of US mathematical research. That has occurred since World War II. Before then, mathematics professors were expected to focus on teaching, and research was considered an attractive sideline except at a few elite institutions, such as Harvard, Yale, Princeton, and Berkeley. Today, many institutions still focus on teaching, but almost 50 focus on research as well.
The second-most important element is support by the federal government. Federal funding for mathematics began during World War II when the United States Office of Scientific Research and Development recruited mathematicians and other scientists to work on applied problems of military significance. Soon after the war, the US government established the Office of Naval Research, the NSF, and other agencies to support scientific research. At the same time, existing government research laboratories were enlarged, and new ones were created. Today, the leading agencies supporting basic research in mathematics are NSF, the Department of Defense, the Department of Energy, and the National Security Agency. In the decentralized American system, federal funds have played a vital role in promoting communication and enabling institutions to maintain world-class research by individual faculty and small research groups.
In addition, faculty at state universities receive research funding from the states, and some private universities offer extra research support for faculty who do not receive federal funding. Several private foundations—such as Sloan, Guggenheim, Ford, and Packard—offer awards for junior faculty, senior-faculty sabbaticals, and special projects.
5
CURRENT TRENDS
It is obvious. but should nonetheless be emphasized, that broad economic and political trends in the United States affect mathematics research. This report cannot possibly address all the complex and controversial issues concerning, for example, optimal mechanisms for federal and industrial support of research, the proper role of research universities, and the pressures of international competition. Many reports on these topics have been produced during the last few years by COSEPUP, the Office of Science and Technology Policy, the National Science Board (NSB), the Industrial Research Institute, the Council on Competitiveness, and others.
With specific reference to mathematics, the US preeminence in mathematical research, described in section 3. has been attained in large part because of the factors listed in section 4. However, unemployment among recent PhDs has created tremendous stress on US mathematics during the 1990s. In this section, we identify a variety of current trends—positive and negative—that are affecting or are likely to affect the relative position of US mathematical research in scientific accomplishments and development of the knowledge base.
5.1 Vitality of the Mathematical Sciences
The panel wishes to emphasize that US mathematical research is thriving in both quality and opportunities. Many new subfields of mathematics have been developed, and some major long-standing problems have been solved, thereby opening new avenues for solving other problems (as did Wiles's proof of Fermat's last theorem). New
methods of solution have been introduced, new connections between different fields have been discovered, and new ways to apply mathematics in science and engineering have been found. Computing has transformed, and will continue to transform, all subfields of mathematics. Mathematicians worldwide express a similar level of enthusiasm for their field.
5.2 Interdisciplinary Research
Although most people agree that interdisciplinary science should be encouraged, there is no universally accepted strategy for doing so. The relative effectiveness of different approaches will be understood only after more experience is gained. In the meantime, US research mathematicians are continuing to play active—in many instances, leading—roles in interdisciplinary research. To name just one topic of current interest, mathematical research will be crucial in making sense of massive data sets (NRC 1996c), particularly when data-gathering happens adaptively in real time; lack of progress in this arena is a recognized impediment to progress in biology, medicine, astronomy, physics, and geosciences.
US universities and federal funding agencies are trying to create programs that encourage mathematicians in all subfields to create links with other disciplines. In times of tight budgets, however, it is difficult to justify moving money away from already-squeezed disciplinary research programs that have consistently produced outstanding results. Anecdotal evidence suggests that interdisciplinary programs, especially those perceived as "risky," are struggling to adapt within existing structures.
The United States is not alone in attempting to devise policies that support interdisciplinary science and engineering despite budget pressures. The European Union and other Europe-wide programs explicitly seek to improve scientific cooperation among the countries of the region. To prepare scientists for international work, increasing mobility of faculty and students is being encouraged. Thus, the mobility of scientists in Europe might soon rival that of scientists in the United States, previously one of the strongest qualities of the US research enterprise (see section 4.1).
Individual European countries are spending considerable sums to support interdisciplinary research. For example, the German government has begun experimental programs to increase interdisciplinary training and prepare scientists for nonacademic employment (NSF 1996c, p. 28). In France, megaprojects "grands programmes" with multiyear funding have been financed by the government in fields of scientific priority, and the National Committee for Scientific Research is vigorously supporting collaborative projects in materials science, nanotechnology, and the environment (NSF 1996c, p. 36).
5.3 Employment Prospects for New PhDs
5.3.1 Academic Jobs
Many US universities have experienced severe financial crises during the 1990s for a variety of reasons, such as the general "downsizing" trend in the US economy and lower-than-expected undergraduate enrollments. The consequent unfavorable job market for recent PhDs in science has been discussed in detail in several reports (for example, NSF 1996b, COSEPUP 1995), but no consensus has emerged about ways to solve or even alleviate the unemployment and underemployment of PhDs.
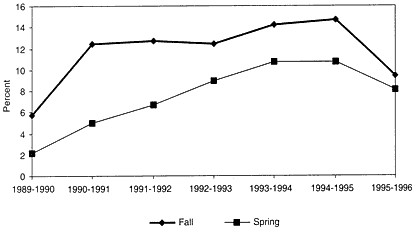
These developments have, not surprisingly, affected mathematics, inasmuch as higher education is the largest US sector that employs mathematics PhDs. (In 1993, jobs in universities and 4-year colleges accounted for 65.2% of all employed US doctoral recipients in the mathematical sciences, followed by 24.8% in private industry and 4.5% in government) (NSF 1996c, table 20). Figure 2 depicts the unemployment rate among new PhDs in mathematics from 1989 to 1995.
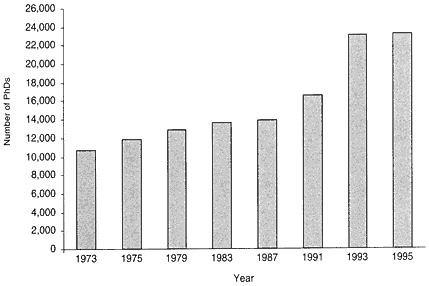
The most-prominent reason for the sudden worsening of the job market in 1990 is obvious: an oversupply of new PhDs relative to the availability of tenure-track positions in colleges and universities. The number of PhDs produced by US mathematics departments began to increase in the middle 1980s, rose during the early 1990s, and has shown signs of instability recently, as shown in figure 3 (see section 5.5).
During the same period, the number of academic positions open to new PhDs in mathematics has been shrinking. From 1989 to 1994, the
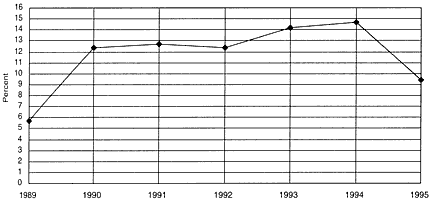
FIGURE 2 Percentage unemployment among new US PhDs in mathematics, autumn of year shown. Source: AMS 1996.
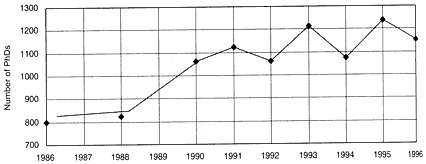
FIGURE 3 Number of PhDs produced by US mathematics departments, spring of year shown. Source: AMS 1997c.
number of positions offered in US mathematics departments to new PhDs fell by 33%; from 1995 to 1996, there was a 6% drop in the number of new PhDs employed by US academic institutions (Davis 1997). During 1994-1995, there were 240 tenure-track positions for new doctoral recipients in US doctorate-granting departments in the mathematical sciences and 184 non-tenure-track positions.
Beyond the diminishing number of academic jobs for new PhDs lies a phenomenon that seems particularly prevalent in US mathematics: a growth in nonpermanent positions. In 1994-95, temporary positions accounted for 50% of the openings for new PhDs in doctorate-granting departments of mathematics. In the autumn of 1996, 64% of the 256 new PhDs who found jobs in academic institutions were in non-tenure-track positions; of those employed in doctorate-granting departments, 84.2% were in non-tenure-track jobs. Overall, the number of full-time US faculty not eligible for tenure rose by 29% from 1991 to 1995.
The existence of an underclass of PhDs who continue to work from year to year at low wages in nonpermanent jobs has led to frustration among recent PhDs (Davis 1997). There has been some recent growth in the number of postdoctoral positions, alleviating unemployment and at the same time providing much further training for fresh PhDs. The law abolishing retirement at a fixed age, which recently began affecting those in academic positions, might further diminish the number of job openings. Most other countries have a fixed retirement age. The pressure on the concept of tenure is likely to increase. Data on the employment situation in other countries are unavailable, but anecdotal information indicates that the problems experienced here in the academic job market are also occurring in other countries.
5.3.2 Industrial Jobs
The industrial employment market presents a mixed picture. As shown in figure 4, industrial employment of mathematicians has been increasing. But general trends in industrial research indicate a decrease in spending. Since 1988, industrial spending on research and development in the United States has not increased substantially in constant dollars. In addition, less and less is spent on longer-term research; basic research constituted 6% of industrial expenditures for research and development in 1988 and 2% in 1993 (Council on Competitiveness 1996). Industry's expenditures on basic research declined at an annual average constant-dollar rate of 4.6% from 1991 to 1995 (NSB 1996). In contrast, it is interesting to note, mathematics is expected to grow at both AT&T and Bell Laboratories.
The industrial-research funding picture is more optimistic outside the United States. Many European governments are actively encouraging nondefense industrial research and development; details about these
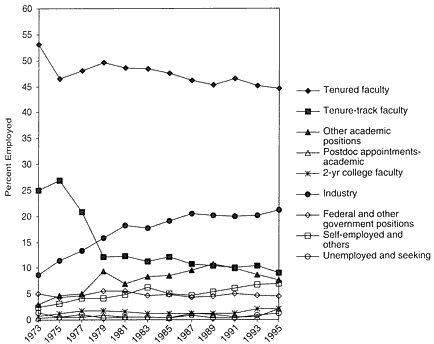
FIGURE 4 Employment status of PhD mathematicians in the US. Source: Analysis conducted by the National Research Council Office of Scientific and Engineering Personnel for this study.
trends can be found in a recent NSF report (1996c). The United States has trailed, for some time, Germany and Japan in civilian research and development as a percentage of GDP; industrial R&D expenditures have been relatively flat in the United States while growing in competitor countries (Council on Competitiveness 1996).
5.4 Foreign Graduate Students
The overall implications of foreign graduate students for US science are discussed in several recent reports, for example, by COSEPUP (1995). Detailed recent data are given by NSB (1996).
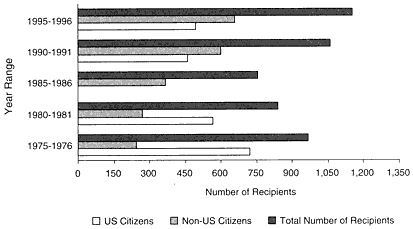
During the 1990s, mathematics has been one of the scientific fields most affected by growth in the number and proportion of US PhDs received by non-US students. As figure 5 shows, the number of non-US PhD recipients increased by 78% from 1985 to 1995. Furthermore, in every year since 1990, foreign students have received more than half the PhDs awarded in mathematics in the United States.
That phenomenon occurs elsewhere, and high proportions of foreign students in the sciences are relatively common in other industrialized countries, especially those with former colonial ties. The percentages of foreign natural-science doctoral students in several countries are depicted in figure 6. The large increase shown for Japan is due to Japan's strategy to attract and train foreign students.
A closely related issue is the number of foreign-born PhD recipients who remain permanently in the United States. The panel found no data on how many foreign students receiving mathematics PhDs intend to
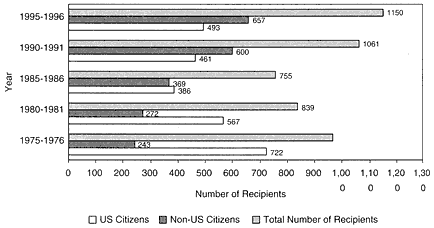
FIGURE 5 Doctoral recipients: total number and US and non-US citizens. Source: AMS 1996.
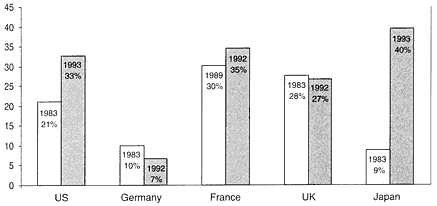
FIGURE 6 Percentage of foreign natural-science doctoral students in various countries. Source: NSB 1996, appendix table 2-33.
remain in the United States after receiving their degrees. However, the overall picture of ''stay rates" for foreign students in all science and engineering fields, as shown in figure 7, suggests that such intentions are widespread and confirms the attractiveness of the United States to foreign talent mentioned in section 4.1.
To explore the question further, the panel conducted its own informal survey of 10 highly rated US mathematics departments. Of 397
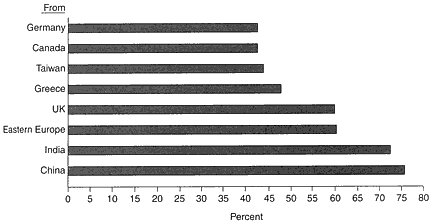
FIGURE 7 Stay rates-percentages of foreign doctoral students who plan to remain in the United States, averaged over 1988-1992. Source: NSB 1996, table 2-15.
tenured faculty, 21% received their undergraduate degree outside the United States; for 107 tenure-track faculty, this statistic was 58%. Thus, the number of faculty in US mathematics departments with undergraduate degrees from outside the United States can be expected to increase.
Stay rates in other countries were found only for France, where 56% of non-French people who received mathematics PhDs in 1992 remained in France (NSF 1996c).
5.5 Graduate Education
As discussed in section 5.3.1, the number of PhDs produced by US universities grew substantially from the middle 1980s through the 1990s. However, the trend has recently changed as doctorate-granting institutions have begun to reduce the size of their graduate programs. In particular, in the autumn of 1996, the projected size of the new class of PhD students in mathematics at US universities was 2,384 compared with 2,546 in the autumn of 1994. Figure 8 shows the total population of full-time doctoral students in mathematics for 1980, 1985, and the 1990s. Since a high in 1992, the number of full-time PhD students in mathematics has steadily decreased.
An online NSF data brief of February 1997 (NSF 1997a) reveals that, among all US doctoral students in the sciences, the largest percentage from 1994 to 1995 occurred in the mathematical sciences and physics, each of which experienced a 6% reduction.
The decreases in applications by both US and non-US students are dramatic, although it is unknown whether they signal the beginning of a trend. Interest in obtaining a PhD in mathematics appears to have been affected by the employment prospects described in section 5.3 for both US and non-US students. A very recent set of data (AMS 1997a, b)
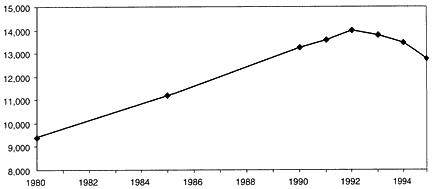
FIGURE 8 Total full-time PhD students in mathematical sciences. Source: NSF 1995.
TABLE 1 Decrease in applications to PhD programs in mathematics, 1994 to 1996
collected in mid-1996 shows that there has been a uniform drop in applications to mathematics graduate schools from 1994. Table 1 shows data on the 48 top-ranked mathematics departments and on all doctoral programs in mathematics. Other reasons for the decline might be competition from computer science, biologic science, and medicine and poor preparation in high school and college.
Another issue is the degree to which women and members of minority groups are pursuing graduate degrees in mathematics. From 1983 to 1993, the percentage of new PhDs who were women grew from 16.1% to 23%; this is slightly greater than the percentage for all the physical sciences and computer science. The percentage of minority-group members receiving mathematics PhDs is much smaller. For example, only 8 of some 583 mathematics PhDs awarded to Americans went to blacks in 1993, and this number has remained roughly constant over the last decade. The situation for Hispanic Americans is a bit different: 16 received degrees (NSF 1996b).
No data were found on the size of graduate mathematics programs in other countries.
5.6 Support
In section 4.4. we stated that an important underpinning for US success in mathematical research has been sustained support and
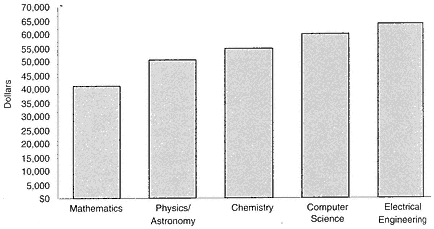
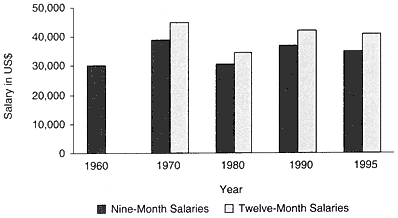
FIGURE 9 Median salaries in 1993 of US PhDs who received their degrees in 1985-1990, by field. Source: NSF 1996a, appendix table 5-27.
funding. Before choosing to obtain a PhD in mathematics, the most-talented people are likely to consider not simply their expected salary, but also their likelihood of receiving support for the time and resources needed to carry out their research.
Figure 9 compares the 1993 median salaries of US PhDs who received their degrees in 1985-1990 in mathematics, computer science, chemistry, physics/astronomy, and electrical engineering. One might reasonably conclude that mathematics PhDs have less-favorable salary prospects than other science PhDs. We have no comparable data for other countries.
It is difficult to make international comparisons with respect to salaries and federal support because university researchers in other countries do not typically receive summer salary support from individual government grants. In the UK and Canada, for example, academic salaries are paid entirely by universities.
As to federal research support, figure 10 shows that a lower percentage of academic mathematicians received US federal support in 1993 than any other category of doctoral scientists except social scientists.
Finally, the mathematical sciences have not fared well, compared with other sciences, in overall federal support in recent years (see figure 11). For example, in 1994-1995, overall federal support for academic research and development grew by 5%, but support for the mathematical sciences dropped relative to that for other sciences. Mathematics had the lowest rate of growth (1%) in federal funding for research and was
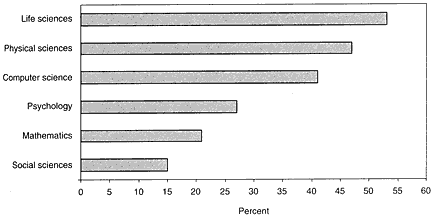
FIGURE 10 Percentages of academic scientists with federal support, 1993. Source: NSB 1996, appendix table 5-27.
the only science whose support grew at a rate lower than that of inflation, which was 1.8% (NSF 1997b).
The details of the picture vary by agency. On the basis of current dollars in the actual FY1996 and estimated FY1997 budgets, the Divi
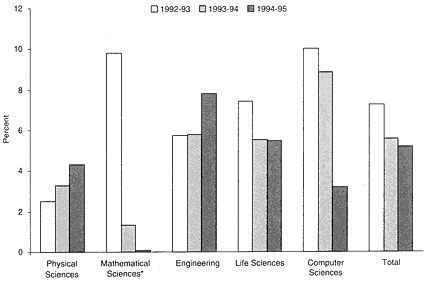
FIGURE 11 Percentage increase in federal R&D expenditures at universities and colleges, by field. Source: NSF 1997b, table 1 and discussions with NSF staff.
6
LIKELY FUTURE RELATIVE POSITION OF US MATHEMATICS
The current trends described in section 5 are obviously mixed. This section summarizes our best estimate about the future relative position of US mathematical research.1
6.1 Intellectual Quality
As already stressed in section 5.1., the field is full of new results, new methods, new points of view, and new problems. Because the United States is preeminent, mathematics in the United States is likely in the near term to retain its dominant position in the world. In the long term, however, some of this momentum might be lost, depending on how we rise to new challenges and potentially damaging developments described below.
6.2 Interdisciplinary Research
Notable successes in interdisciplinary research (see sections3.2.1. and 3.2.2.) have made this aspect of US mathematical research of preeminent importance today—although not uniformly throughout the United States. As recognition of the importance of mathematics in interdisciplinary research grows, opportunities will expand for collaborations that enrich other sciences and mathematics. The panel believes that the future relative position of the United States in interdisciplinary mathematical research depends in large part on the effectiveness with which these opportunities are realized. As observed in sections 5.2 and
5.3.2, governments, universities, and industry in other countries are actively supporting mechanisms that encourage interdisciplinary research. The United States must pay serious attention to this issue.
6.3 US Graduate Education in Mathematics
The panel is especially concerned about the potential erosion of the US research base because of a decrease in the number of graduate students at leading universities. The trends discussed in section 5.4 imply that the future position of US mathematics is likely to depend increasingly on graduate students and postdoctoral fellows from other countries; this makes our preeminence precarious if jobs in their countries of origin become more attractive to foreign students or if changes in immigration laws close the United States doors to non-native mathematicians. In addition, there is a dearth of minority-group members in mathematics. The panel believes that the United States must cultivate its own mathematical talent to retain its leading stature in mathematical research. A key factor in this cultivation is the quality of mathematics education in K-12 and college.
6.4 Support for Mathematical Research
The most important safeguard of US preeminence in mathematical research—and in all the sciences—is the flourishing of both private and state research universities. Some of the stresses faced today by US research universities are described by the Council on Competitiveness as "facing a funding squeeze and growing, often contradictory, demands" (Council on Competitiveness 1996, p. 21). The research universities respond to this squeeze in part by reducing staff size. This situation affects mathematics because research universities provide a stable base, both financial and professional (see section 4.4). The current trend toward hiring temporary faculty discussed in section 5.3.1 is a prime indication that US universities might provide much less of that support in the future.
Today the research universities are the major instruments in the United States for research and development that fuel high technologies, an extremely important part of the US economy. Mathematics has prospered in part because it plays an important role in this research. But the research enterprise is at risk if the support for research universities continues to decline.
7
REFERENCES
ABIE (Australian Bureau of Industry Economics). Australian Science: Performance from Published Papers. Report 96/3. Canberra, Australia: Australian Government Publishing Service, 1996.
AMS (American Mathematical Society). "AMS Task Force on Employment, Report to the Mathematical Community Part I: Academic Hiring Survey, 1991-1992", Notices of the AMS, April 1992.
AMS (American Mathematical Society). "1996 Annual AMS-IMS-MAA Survey (First Report)", Notices of the AMS, December 1996.
AMS (American Mathematical Society). "Recent Trends in Graduate Admissions in Mathematics Departments", Notices of the AMS, February 1997a.
AMS (American Mathematical Society). "A Survey of Four-Year and University Mathematics in Fall 1995: A Hiatus in Both Enrollment and Faculty Increases", Notices of the AMS, September 1997b.
AMS (American Mathematical Society). "1996 Annual AMS-IMS-MAA Survey (Second Report)", Notices of the AMS, September 1997c.
Askey, Richard. "The Japanese University Entrance Examinations in Mathematics", FOCUS Newsletter, Mathematics Association of America, vol. 13, no. 1, 1993.
Chen, L.Q., B. Fultz, J.W. Cahn, J.R. Manning, J.E. Morral, J. Simmons, eds. Mathematics of Microstructure Evolution. The Minerals, Metals, and Materials Society, Warrendale, PA, and Society for Industrial and Applied Mathematics, Philadelphia, PA, 1996.
COSEPUP (Committee on Science, Engineering, and Public Policy). Science, Technology, and the Federal Government: National Goals for a New Era. Washington, D.C.: National Academy Press, 1993.
COSEPUP (Committee on Science, Engineering, and Public Policy). Reshaping the Graduate Education of Scientists and Engineers. Washington, D.C.: National Academy Press, 1995.
COSEPUP (Committee on Science, Engineering, and Public Policy). An Assessment of the National Science Foundation's Science and Technology Program. Washington, D.C.: National Academy Press, 1996.
Council on Competitiveness. Endless Frontier, Limited Resources. Washington, D.C.: Council on Competitiveness, 1996.
Davis, Geoff. "Mathematicians and the Market", March 30, 1997. http://www.cs.dartmouth.edu/~gdavis/policy/papers.html.
ED (U.S. Department of Education). Pursuing Excellence, NCES 97-198. National Center for Education Statistics. Washington, D.C.: U.S. Government Printing Office, 1996.
NAE (National Academy of Engineering). Frontiers of Engineering. Washington, D.C.: National Academy Press, 1996.
NAPA (National Academy of Public Administration). National Science Foundation's Science and Technology Centers: Building an Interdisciplinary Research Paradigm. Washington D.C.: National Academy of Public Administration, 1995.
NRC (National Research Council). Mathematical Sciences, Technology, and Economic Competitiveness. Washington, D.C.: National Academy Press, 1991.
NRC (National Research Council). Mathematical Research in Materials Science. Washington, D.C.: National Academy Press, 1993.
NRC (National Research Council). Mathematical Challenges from Theoretical/Computational Chemistry. Washington, D.C.: National Academy Press, 1995a.
NRC (National Research Council). Calculating the Secrets of Life: Applications of the Mathematical Sciences to Molecular Biology. Washington, D.C.: National Academy Press, 1995b.
NRC (National Research Council). Allocating Federal Funds for Science and Technology. Washington, D.C.: National Academy Press, 1995c.
NRC (National Research Council). Research-Doctorate Programs in the United States: Continuity and Change. Washington, D.C.: National Academy Press, 1995d.
NRC (National Research Council). Cryptography's Role in Securing the Information Society. Washington, D.C.: National Academy Press, 1996a.
NRC (National Research Council). Mathematics and Physics of Emerging Biomedical Imaging. Washington, D.C.: National Academy Press, 1996b.
NRC (National Research Council). Massive Data Sets: Proceedings of a Workshop. Washington, D.C.: National Academy Press, 1996c.
NRC (National Research Council). Preserving Strength While Meeting Challenges: Summary Report of a Workshop on Actions for the Mathematical Sciences. Washington, D.C. National Academy Press, 1997.
NSB (National Science Board). Science and Engineering Indicators -1996. Arlington, VA: National Science Foundation, 1996.
NSF (National Science Foundation). Characteristics of Doctoral Scientists and Engineers in the United States, 1993. NSF 96-302. Arlington, VA: National Science Foundation, 1996a.
NSF (National Science Foundation). Women, Minorities, and Persons with Disabilities in Science and Engineering: 1996. NSF 96-311. Arlington VA : National Science Foundation, 1996b.
NSF (National Science Foundation). Human Resources for Science & Technology: The European Region. NSF 96-316. Arlington, VA: National Science Foundation, 1996c.
NSF (National Science Foundation). Data Brief. 97-303. Arlington, VA: National Science Foundation, February 7, 1997a.
NSF (National Science Foundation). Data Brief. 97-304. Arlington, VA: National Science Foundation, March 7, 1997b.
NSF (National Science Foundation). Knowledge and Distributed Intelligence. See World Wide Web documents at http://www.nsf.gov.
NSF (National Science Foundation). 1995 Graduate Student Survey. Available at http://www.nsf.gov.
SIAM (Society for Industrial and Applied Mathematics). Mathematics in Industry. Philadelphia: SIAM, 1995.
SIAM (Society for Industrial and Applied Mathematics). "Mathematics meets film animation in Kansas City community lecture", SIAM News, vol. 29, no. 7, 1996.
United Kingdom Office of Science and Technology. The Quality of the UK Science Base. London, UK: Department of Trade and Industry, March 1997.
APPENDIX A
PANEL AND STAFF BIOGRAPHICAL INFORMATION
Panel
Peter D. Lax [NAS*] (Chair) is professor of mathematics and director of the Courant Mathematics and Computer Lab at New York University. Before taking his current positions, he was director of the Courant Institute of Mathematical Sciences (1972-1980) and director of the AEC Computing and Applied Mathematics Center (1964-1972), both at NYU. He is a National Medal of Science awardee, former president of the American Mathematical Society (AMS), and a former National Science Board member. He has extensive experience as a lecturer overseas, particularly in Germany, France, and the United Kingdom as well as being a foreign member of the French, Chinese, Hungarian, and Russian academies of sciences. He is a member of the American Philosophical Society. Dr. Lax has received many honorary degrees, the Wolf Prize (1987), the National Academy of Sciences Prize in Applied Mathematics (1983), the Norbert Wiener Prize of AMS and the Society for Industrial and Applied Mathematics (1975), the Chauvenet Prize of the Mathematical Association of America (1974), and the Steele Prize of AMS (1992).
Michael F. Atiyah [NAS-F] is director of the Isaac Newton Institute for Mathematical Sciences in Cambridge, England, and president of the Royal Society (1990-1995). He has recently retired as master of Trinity College, Cambridge. Before this, he was a Royal Society research professor and fellow of St. Catherine's College, Oxford (1973-1990). He has served as professor of mathematics at the Institute for Advanced
Study in the United States (1969-1972) and Savilian Professor of Geometry at University of Oxford (1963-1969). He attended Victoria College in Cairo and received his BA (1952) and PhD (1955) from the University of Cambridge. Sir Michael is a member of many academies of sciences. He holds many honorary doctorates and several honorary fellowships. Sir Michael has been a member of the Executive Committee of the International Mathematical Union (1966-1974), president of the London Mathematical Society (1975-1977), president of the Mathematical Association (1981-1982), member of the Science and Engineering Research Council (1984-1989), member of the Council of the Royal Society (1973-1974), vice-president of the Royal Society (1984-1985), and chairman of the European Mathematical Council (1978-1990). He received the Fields Medal in 1966.
Spencer J. Bloch [NAS] is professor of mathematics at the University of Chicago. He was an instructor, lecturer, and assistant professor at Princeton (1971-1974) and an associate professor at the University of Michigan (1974-1976). Dr. Bloch has done pioneering work in the application of higher algebraic K theory to algebraic geometry, particularly in problems related to algebraic cycles, and is regarded as the world's leader in this field. His work has firmly established higher K theory as a fundamental tool in algebraic geometry. Dr. Bloch received his BA at Harvard (1966) and his PhD from Columbia (1971).
Joseph B. Keller [NAS] is professor of mathematics and mechanical engineering (emeritus) at Stanford University. Before this, he was at Courant Institute of Mathematical Sciences, New York University (1948-1979), where he received his PhD in mathematics (1948). He is a foreign member of the Royal Society and was honorary professor of mathematical sciences at the University of Cambridge. He is a recipient of the Wolf Prize (1997), the Frederick E. Nemmers Prize (1996), the National Academy of Sciences Award in Applied Mathematics and Numerical Analysis (1995), the National Medal of Science (1988), the Timoshenko Medal (1984), the Eringen Medal (1981), and the von Karman Prize (1979). He was von Neumann Lecturer (1983) and Gibbs Lecturer of the American Mathematical Society (1977).
Jacques-Louis Lions [NAS-F] is professor at the College de France in Paris and president of the French Academy of Sciences. He has contributed fundamental research in nonlinear partial differential equations, including homogenization and control. He has trained an entire generation of modern applied mathematicians in France. He has pioneered industrial and applied mathematics cooperation in France as cofounder of Institut National de Recherche en Informatique et en Automatique (INRIA) and as president of the French Space Agency. In addition, he is
a former president and secretary of the International Mathematical Union.
Yuri I. Manin is a member (since 1993) and director (since 1995) of the Max Planck Institute for Mathematics. He is also leading researcher of the Steklov Mathematical Institute of the Russian Academy of Sciences (since 1960, now in absentia.) In 1965-1992, he was professor of algebra at Moscow University and held various visiting professorships, in particular at Harvard University, Columbia University, and the Massachusetts Institute of Technology. He is a member of the Academy of Sciences, Russia, the Royal Society of Sciences of the Netherlands, the Academia Europaea, the Max-Planck-Gesellschaft, the Gottingen Academy of Sciences Class of Physics and Mathematics, and the Pontificia Academia Scientiarum. He won the Lenin Prize for work in algebraic geometry (1967), the international Frederic Esser Nemmers Prize in Mathematics of Northwestern University (1994) and the Brouwer Golden Medal of the Royal Society and Mathematical Society of the Netherlands for work in number theory (1987).
Rudolph A. Marcus [NAS] is A.A. Noyes Professor of Chemistry at the California Institute of Technology. He is also an honorary professor at Fudan University in Shanghai, China, and at the Institute of Chemistry in the Chinese Academy of Sciences in Beijing. Dr. Marcus holds an honorary fellowship at University College of the University of Oxford and was Linnett Visiting Professor of Chemistry at the University of Cambridge. He previously held positions at the University of North Carolina, the Polytechnic Institute of Brooklyn, the Courant Institute of Mathematical Sciences of New York University, the University of Illinois, the University of Oxford, and the California Institute of Technology. Dr. Marcus received his BSc (1943) and PhD (1946) in chemistry from McGill University in Montreal, Canada. He is a fellow of the National Academy of Sciences, the American Academy of Arts and Sciences, the Royal Society of Chemistry, and the Royal Society of Canada, and he is a member of the Royal Society, the International Academy of Quantum Molecular Science, the American Philosophical Society, the American Association for the Advancement of Science, the American Chemical Society, and the American Physical Society. Dr. Marcus received the Nobel prize in chemistry in 1992.
Gary C. McDonald is head of the Operations Research Department at the General Motors Research and Development Center. Before this, he was head of the mathematics department at the center (1983-1992). He is also adjunct professor of mathematics at Oakland University. Dr. McDonald started as associate senior research mathematician at General Motors in 1969 and has held the positions of senior research
mathematician (1972-1976) and assistant department head (1976-1983). He received his BA (1964) from St. Mary's College and his MS (1966) PhD (1969) from Purdue University. He is a fellow of the Institute of Mathematical Statistics, the American Statistical Association, and the American Association for the Advancement of Science.
Cathleen S. Morawetz [NAS] is professor emeritus at the Courant Institute of Mathematical Sciences of New York University. She has been with the institute since starting as a research associate (1952). She held positions as assistant professor (1957-1960), associate professor (1960-1965), professor (1965-present), and chairman (1981-84) Department of Mathematics, associate director (1978-1981), deputy director (1981-1984), and director (1984-1988). Dr. Morawetz was a trustee of the Alfred P. Sloan Foundation (1980-1984) and a member of the National Research Council's Board on Mathematical Sciences. She was president of the American Mathematical Society during 1995-1996 and is a member of the Mathematical Association of America, and the Society for Industrial and Applied Mathematics and a fellow of the American Association for the Advancement of Science. She received her BA (1945) from the University of Toronto, her MS (1946) from the Massachusetts Institute of Technology, and her PhD (1951) from New York University.
Peter Sarnak is chairman of the Department of Mathematics at Princeton University. Before this, he was the H. Fine Professor (1995-1996). He has also been professor at Stanford University (1987-1991), the Sherman Fairchild Distinguished Scholar at the California Institute of Technology (1989), a fellow at the Institute of Advanced Studies at Hebrew University (1987-1988), and assistant and associate professor at the Courant Institute of Mathematical Sciences of New York University (1980-1983). Dr. Sarnak received his BSc (1974) from the University of Witwatersrand in South Africa and his PhD (1980) from Stanford University. He is a member of the American Academy of Arts and Sciences and was a Sloan fellow (1983-1985) and presidential young investigator (1985-1990).
I.M. Singer [NAS] is Institute Professor at the Massachusetts Institute of Technology (MIT). His research has been in the fields of index theory/manifold invariants/elliptic analysis, differential geometry, functional analysis, and operator theory. He has been teaching calculus intermittently between 1949 and 1997. He received the AMS Bocher Memorial Prize (1969), the National Medal of Science (1983), the Wigner Medal (1988), and the AMS Award for Public Service (1993). He was chairman of the National Academy of Sciences Committee on Science and Public Policy (1973-1978) and was with the White House Science Council from
1982 to 1988. Dr. Singer received his BS (1944) from the University of Michigan and his MS (1948) and PhD (1950) in mathematics from the University of Chicago. He is a member of the Council of the National Academy of Sciences, the Governing Board of the National Research Council, the American Academy of Arts and Sciences, the American Mathematical Society (vice president, 1970-1972), the American Physical Society, and the American Philosophical Society.
Margaret H. Wright [NAE] is a Distinguished Member of Technical Staff at Bell Laboratories, Lucent Technologies. Before joining Bell Laboratories she worked in the Department of Operations Research at Stanford University (1976-1988). Dr. Wright holds a BS in mathematics, and MS and PhD degrees in computer science, from Stanford University. She served as president of the Society for Industrial and Applied Mathematics during 1995-1996. Her research involves theory and algorithms for optimization and linear algebra, scientific computing, and solution of real-world optimization problems.
Staff
Deborah D. Stine is the study director and associate director of the Committee on Science, Engineering, and Public Policy (COSEPUP). She has been working on various projects throughout the National Academy of Sciences complex since 1989. She received a National Research Council group award for her first study for COSEPUP on policy implications of greenhouse warming and a Commission on Life Sciences staff citation for her work in risk assessment and management. Other studies have addressed graduate education, responsible conduct of research, careers in science and engineering, environmental remediation, the national biological survey, and corporate environmental stewardship. She holds a bachelor's degree in mechanical and environmental engineering from the University of California, Irvine; a master's degree in business administration; and a PhD in public administration, specializing in policy analysis, from the American University. Before coming to the Academy, she was a mathematician for the Air Force, an air-pollution engineer for the state of Texas, and an air-issues manager for the Chemical Manufacturers Association.
John R. Tucker has been director of the Board on Mathematical Sciences (BMS) since 1994. He earned degrees in mathematics at Washington College (BA) and George Washington University (Mphil and PhD). He has worked as a researcher with Chi Associates, Inc., and an assistant professor of mathematics at Virginia Commonwealth University and Mary Washington College. He joined the National Research Council in 1989 as program officer for the BMS and advanced to senior program officer in 1993. His interests include nonlinear dynamics, order
and disorder, mixing processes, and mathematical developments in biology and medicine.
Lawrence E. McCray is executive director of the Committee on Science, Engineering, and Public Policy (COSEPUP). He held positions in the Environmental Protection Agency, the US Regulatory Council, and the Office of Management and Budget before coming to the National Academy of Sciences in 1981. He has directed Academy studies in carcinogenic risk assessment, export controls, nuclear winter, and federal science budgeting. A Fulbright scholar in 1968, he received the Schattschneider award in 1972 from the American Political Science Association for the best dissertation in American government and politics. In 1987, he received the National Research Council staff award. He joined COSEPUP in 1988 as executive director and since 1994 has served concurrently as the director of the NRC Policy Division.
Patrick P. Sevcik is research associate with the Committee on Science, Engineering, and Public Policy (COSEPUP). He works on a variety of projects for COSEPUP, the Policy Division (PD), and the PD Office of Special Projects, assisting Deborah Stine and Lawrence McCray. Before coming to the National Research Council in 1993, he was an assistant program officer with the International Republican Institute from 1990 to 1993, working on democracy development, primarily in central and eastern Europe. He has held positions at the White House in the Office of Political Affairs (1989-1990) and on Capitol Hill (1987-1988) in the office of Representative John DioGuardi (R-NY). During that time, he also held concurrent positions in several Slovak-American organizations. He holds a BA in international affairs, with an emphasis on Soviet and Eastern European studies, from the George Washington University. He has also studied Russian language and culture at the Leningrad Polytechnic Institute in Leningrad.
APPENDIX B
STATISTICAL DATA ON THE FIELD OF MATHEMATICS
This appendix is a collection of some of the data that various members of the panel reviewed before developing conclusions. It provides the available data on education, employment, funding, and papers and citations. Most of the information is available only for the United States, but non-US data, when available, are included.
Education
Figure B-1 shows how the number of institutions in the United States awarding PhDs in mathematics has grown since 1920. Figure B-2 provides the number of PhDs that these institutions awarded during the same period. The drastic increase in PhDs in the 1960s was probably due to the draft exemption during the Vietnam War. The big increase in degrees granted in the 1980s probably occurred when computer science came into vogue.
Figure B-3 shows how long it took students to attain their degrees and provides the age at which they received their doctorate. Figure B-4 shows how many of those students were foreign citizens, and table 1 in section 5.5 shows the decrease in applications to US PhD programs in mathematics by US and non-US citizens.
Figure B-5 compares the number of first degrees (equivalent to a BS in the United States) in mathematics and computer science in the United States and western Europe. The data were available only for mathematics and computer science combined, and computer science grew rapidly during the period covered, especially in western Europe.
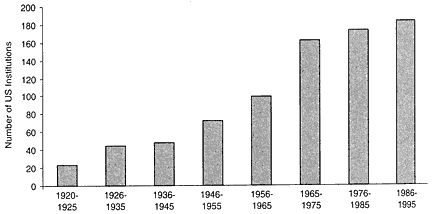
FIGURE B-1 Number of US institutions awarding PhDs in mathematics, 1920-1995. Source: Analysis conducted by the National Research Council's Office of Scientific and Engineering Personnel for this study.
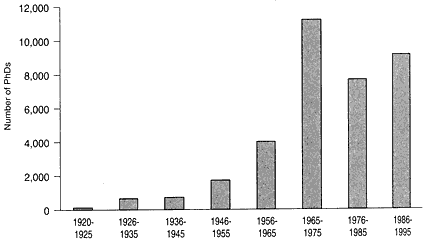
FIGURE B-2 Number of PhDs awarded in mathematics in the United States, 1920-1995. Source: Analysis conducted by the National Research Council's Office of Scientific and Engineering Personnel for this study.
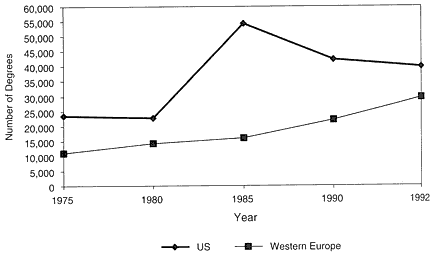
FIGURE B-5 Number of first degrees in mathematics and computer science. Source: NSF 1996c, p. 34.
Figure B-6 shows the number of doctoral degrees awarded in natural sciences in Asia, Europe, and the United States in 1992. Mathematics cannot be separated out from these data.
Employment
Figure B-7 shows the number of PhD mathematicians employed in the United States from 1973 to 1991. Where they are employed is shown in table B-1, and the type of work they are doing is shown in table B-2.
The data are from the Survey of Doctorate Recipients (SDR). The SDR is a biennial longitudinal survey, dating back to 1973, of research doctorates working in the United States. The survey questionnaire is sent in the spring to a sample of about 50,000. These people are asked a series of demographic and employment-characteristics questions. The response rate for the survey has varied over the years; in the late 1980s it was about 60%. That has been improved during the last 2 survey cycles through the use of second-wave mailings and telephone interviews; in 1995, it was about 85%.
The sample is stratified across 3 variables: field of degree, sex, and a combination variable that includes degree field, sex, handicap status, ethnic group, and nationality of birth. The results of the survey are statistically analyzed to translate the data into weighted numbers for the entire population. From these data, the doctorate workforce in science and engineering can be analyzed across different dimensions by looking
TABLE B-1 Employment Status of PhD Mathematicians in the United States
|
|
1973 |
1975 |
1977 |
1979 |
1981 |
1983 |
1985 |
1987 |
1989 |
1991 |
1993 |
1995 |
|
Tenured and tenure-track faculty |
9,238 |
10,332 |
10,690 |
10,341 |
10,936 |
11,233 |
11,887 |
11,627 |
12,057 |
12,209 |
12,779 |
12,437 |
|
Tenured faculty |
6,280 |
6,546 |
7,458 |
8,303 |
8,715 |
9,124 |
9,469 |
9,438 |
9,801 |
10,039 |
10,386 |
10,338 |
|
Tenure-track faculty |
2,958 |
3,786 |
3,232 |
2,038 |
2,221 |
2,109 |
2,418 |
2,189 |
2,256 |
2,170 |
2,393 |
2,099 |
|
Other academic positions |
343 |
666 |
779 |
1,582 |
1,266 |
1,592 |
1,693 |
1,950 |
2,313 |
2,133 |
1,994 |
1,788 |
|
Postdoctoral appointments—academic |
41 |
73 |
93 |
146 |
102 |
102 |
83 |
264 |
210 |
99 |
105 |
484 |
|
2-yr college faculty |
87 |
183 |
284 |
290 |
275 |
233 |
233 |
245 |
252 |
257 |
454 |
466 |
|
Industry |
1,027 |
1,622 |
2,064 |
2,635 |
3,274 |
3,350 |
3,795 |
4,179 |
4,355 |
4,295 |
4,658 |
4,886 |
|
Federal and other government positions |
586 |
601 |
719 |
918 |
988 |
887 |
958 |
871 |
965 |
1,076 |
1,083 |
1,045 |
|
Self-employed and others |
280 |
448 |
634 |
686 |
855 |
1,195 |
989 |
940 |
1,177 |
1,292 |
1,550 |
1,597 |
|
Postdoctoral appointments—other |
31 |
35 |
31 |
30 |
87 |
33 |
47 |
25 |
45 |
19 |
50 |
27 |
|
Unemployed and seeking employment |
161 |
79 |
168 |
66 |
102 |
105 |
86 |
169 |
91 |
62 |
211 |
301 |
|
Elementary-and high school teachers |
22 |
35 |
49 |
52 |
102 |
172 |
130 |
196 |
172 |
192 |
123 |
155 |
|
TOTAL |
11,816 |
14,074 |
15,511 |
16,746 |
17,987 |
18,902 |
19,901 |
20,466 |
21,637 |
21,634 |
23,007 |
23,186 |
|
Tenured and tenure-track faculty |
78.2% |
73.4% |
68.9% |
61.8% |
60.8% |
59.4% |
59.7% |
56.8% |
55.7% |
56.4% |
55.5% |
53.6% |
|
Tenured faculty |
53.1% |
46.5% |
48.1% |
49.6% |
48.5% |
48.3% |
47.6% |
46.1% |
45.3% |
46.4% |
45.1% |
44.6% |
|
Tenure-track faculty |
25.0% |
26.9% |
20.8% |
12.2% |
12.3% |
11.2% |
12.2% |
10.7% |
10.4% |
10.0% |
10.4% |
9.1% |
|
Other academic positions |
2.9% |
4.7% |
5.0% |
9.4% |
7.0% |
8.4% |
8.5% |
9.5% |
10.7% |
9.9% |
8.7% |
7.7% |
|
2-yr college faculty |
0.7% |
1.3% |
1.8% |
1.7% |
1.5% |
1.2% |
1.2% |
1.2% |
1.2% |
1.2% |
2.0% |
2.0% |
|
Industry |
8.7% |
11.5% |
13.3% |
15.7% |
18.2% |
17.7% |
19.1% |
20.4% |
20.1% |
19.9% |
20.2% |
21.1% |
|
Federal and other government positions |
5.0% |
4.3% |
4.6% |
5.5% |
5.5% |
4.7% |
4.8% |
4.3% |
4.5% |
5.0% |
4.7% |
4.5% |
|
Self-employed and others |
2.4% |
3.2% |
4.1% |
4.1% |
4.8% |
6.3% |
5.0% |
4.6% |
5.4% |
6.0% |
6.7% |
6.9% |
|
Postdoctoral appointments—other |
0.3% |
0.2% |
0.2% |
0.2% |
0.5% |
0.2% |
0.2% |
0.1% |
0.2% |
0.1% |
0.2% |
0.1% |
|
Unemployed and seeking employment |
1.4% |
0.6% |
1.1% |
0.4% |
0.6% |
0.6% |
0.4% |
0.8% |
0.4% |
0.3% |
0.9% |
1.3% |
|
Elementary-and high school teachers |
0.2% |
0.2% |
0.3% |
0.3% |
0.6% |
0.9% |
0.7% |
1.0% |
0.8% |
0.9% |
0.5% |
0.7% |
|
Source: Analysis conducted by the National Research Council's Office of Scientific and Engineering Personnel for this study. |
||||||||||||
TABLE B-2 Occupation Status of PhD Mathematicians in the United States
|
|
1973 |
1975 |
1977 |
1979 |
1981 |
1983 |
1985 |
1987 |
1989 |
1991 |
1993 |
1995 |
|
Research |
2,605 |
3,100 |
3,637 |
4,272 |
4,483 |
4,620 |
5,411 |
5,409 |
5,958 |
6,005 |
5,848 |
5,902 |
|
Basic research |
1,510 |
1,490 |
1,662 |
2,017 |
1,878 |
1,924 |
2,746 |
3,025 |
3,270 |
2,984 |
2,797 |
2,836 |
|
Applied research |
799 |
919 |
1,222 |
1,321 |
1,588 |
1,335 |
1,444 |
1,799 |
1,921 |
2,299 |
2,676 |
2,660 |
|
Development |
296 |
691 |
753 |
934 |
1,017 |
1,361 |
1,221 |
585 |
767 |
722 |
375 |
406 |
|
Research management |
521 |
631 |
593 |
1,160 |
824 |
1,059 |
1,135 |
1,077 |
1,156 |
771 |
2,300 |
1,861 |
|
Management—other |
665 |
932 |
1,265 |
1,357 |
1,230 |
1,164 |
1,660 |
1,360 |
1,398 |
1,438 |
|
|
|
Teaching |
7,454 |
8,622 |
8,603 |
8,601 |
9,311 |
9,590 |
9,460 |
9,484 |
9,794 |
9,161 |
10,239 |
10,108 |
|
Professional services |
37 |
74 |
106 |
136 |
365 |
212 |
226 |
44 |
71 |
169 |
562 |
520 |
|
Consulting |
177 |
222 |
232 |
406 |
648 |
763 |
611 |
448 |
629 |
|
|
|
|
Computing |
|
|
|
|
|
|
|
|
|
794 |
2,322 |
2,587 |
|
Other work activities, no response |
299 |
414 |
907 |
748 |
927 |
1,389 |
1,312 |
2,547 |
2,542 |
2,571 |
1,525 |
1,907 |
|
Federal support |
3,879 |
3,680 |
4,000 |
4,716 |
4,533 |
5,853 |
5,009 |
7,293 |
8,189 |
7,911 |
4,656 |
5,507 |
|
No federal support, no response |
8,015 |
10,315 |
11,343 |
11,964 |
13,352 |
12,944 |
14,806 |
13,004 |
13,359 |
13,661 |
18,143 |
17,378 |
|
TOTAL |
23,652 |
27,990 |
30,686 |
33,360 |
35,673 |
37,594 |
39,630 |
40,666 |
43,096 |
42,481 |
45,592 |
45,770 |
|
Research |
11.0% |
11.1% |
11.9% |
12.8% |
12.6% |
12.3% |
13.7% |
13.3% |
13.8% |
14.1% |
12.8% |
12.9% |
|
Basic research |
6.4% |
5.3% |
5.4% |
6.0% |
5.3% |
5.1% |
6.9% |
7.4% |
7.6% |
7.0% |
6.1% |
6.2% |
|
Applied research |
3.4% |
3.3% |
4.0% |
4.0% |
4.5% |
3.6% |
3.6% |
4.4% |
4.5% |
5.4% |
5.9% |
5.8% |
|
Development |
1.3% |
2.5% |
2.5% |
2.8% |
2.9% |
3.6% |
3.1% |
1.4% |
1.8% |
1.7% |
0.8% |
0.9% |
|
Research management |
2.2% |
2.3% |
1.9% |
3.5% |
2.3% |
2.8% |
2.9% |
2.6% |
2.7% |
1.8% |
5.0% |
4.1% |
|
Management—other |
2.8% |
3.3% |
4.1% |
4.1% |
3.4% |
3.1% |
4.2% |
3.3% |
3.2% |
3.4% |
0.0% |
0.0% |
|
Teaching |
31.5% |
30.8% |
28.0% |
25.8% |
26.1% |
25.5% |
23.9% |
23.3% |
22.7% |
21.6% |
22.5% |
22.1% |
|
Professional services |
0.2% |
0.3% |
0.3% |
0.4% |
1.0% |
0.6% |
0.6% |
0.1% |
0.2% |
0.4% |
1.2% |
1.1% |
|
Consulting |
0.7% |
0.8% |
0.8% |
1.2% |
1.8% |
2.0% |
1.5% |
1.1% |
1.5% |
|
|
|
|
Computing |
|
|
|
|
|
|
|
|
|
1.9% |
5.1% |
5.7% |
|
Other work activities, no response |
1.3% |
1.5% |
3.0% |
2.2% |
2.6% |
3.7% |
3.3% |
6.3% |
5.9% |
6.1% |
3.3% |
4.2% |
|
Federal support |
16.4% |
13.1% |
13.0% |
14.1% |
12.7% |
15.6% |
12.6% |
17.9% |
19.0% |
18.6% |
10.2% |
12.0% |
|
No federal support, no response |
33.9% |
36.9% |
37.0% |
35.9% |
37.4% |
34.4% |
37.4% |
32.0% |
31.0% |
32.2% |
39.8% |
38.0% |
|
Source: Analysis conducted by the National Research Council's Office of Scientific and Engineering Personnel for this study. |
||||||||||||
at different demographic and employment characteristics and by taking different cohorts. This provides for both longitudinal and time-series analyses, as shown here.
Of course, differentiating between research and teaching in determining the type of work for faculty is difficult. However it is fruitful to think about the nonresearch and teaching positions that mathematicians are obtaining and how they are changed over time.
Figure 4 in section 5.3.2 shows some of this information graphically. Note how the percentage of mathematicians employed as tenured and tenure-track faculty has declined while the percentage of mathematicians employed in industry has increased. The percentage in government employment has remained stable.
Figure B-8 shows the median salaries for PhD mathematicians and PhD holders in several related fields.
Figure B-9 shows the citizenship of faculty hired in 1991-1992 and figure B-10 the source of their PhDs.
Of particular concern is the unemployment status of new PhDs. Figure B-11 shows the change in unemployment rate for new mathematics PhDs from 1989 to 1996. The salaries of the new PhDs who attained academic employment are shown in figure B-12; the 9-month salaries included data on 102 men and 38 women, and the 12-month salaries included data on 20 men and 7 women.
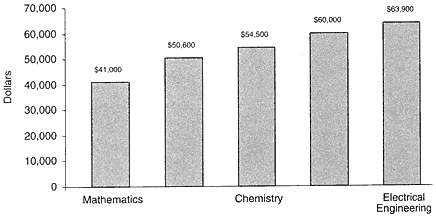
FIGURE B-8 Median salaries in 1993 of US PhDs who received their degree in 1985-1990, by field. Source: NSF 1996a, appendix table 5-27.
Funding
The information provided in this section, unless otherwise indicated, is from an analysis conducted by the Joint Policy Board for Mathematics for the American Association for the Advancement of Science. It produces an annual analysis of federal budget data on the field of mathematics.
There are 7 dedicated programs in mathematical sciences at 3 agencies: the Department of Defense (DOD), the Department of Energy (DOE), and the National Science Foundation (NSF). NSF focuses on fundamental research and its vitality, DOD looks on mathematical sciences as a problem-solving technology that can reduce costs in the development and deployment of hardware and software, and DOE and other agencies—such as the Department of Transportation, the Environmental Protection Agency, the National Aeronautics and Space Administration, the National Institutes of Health, and the National Institute of Standards and Technology—maintain mostly-applied mathematics and statistics activities to enable progress in fields related to their missions. All other agencies use applied mathematics and statistics.
Table B-3 shows federal support for academic mathematical-sciences research. Figure B-13 compares the percentage of academic mathematical scientists who have federal support to the percentages in other fields. Federal support for all mathematical research (basic, applied, and development) is shown in figure B-14.
The NSF Department of Mathematical Sciences (DMS) supports development of mathematical and statistical ideas and techniques, encourages the integration of mathematics with other disciplines, and encourages the diffusion of mathematics into technology. Grants are provided to individual investigators, research institutes, and centers for shared computing equipment, postdoctoral fellowships, research conferences, and undergraduate programs such as curriculum development.
NSF supports three mathematics institutes—the Institute for Mathematics and its Applications (IMA) at the University of Minneapolis was supported at $1,900,000 and the Mathematical Sciences Research Institute (MSRI) at the University of California, Berkeley was supported at $3,110,000 in FY1996. The IMA nearly matches the NSF support with funds from industry, sponsoring institutions, other agencies, and the University of Minnesota. The MSRI has limited additional support outside the NSF award. In 1998, there will be a recompetition for the location of the institutes in the mathematical sciences. The MSRI and the IMA are under review for ''bridging" awards until the new national institutes are established as a result of the recompetition. Since its inception in 1989, the Center for Discrete Mathematics and Theoretical Computer Science (DIMACS) at Rutgers University and its staff have received a total of $74 million in science and technology center (STC)
TABLE B-3 Federal Support for the Mathematical Sciences, Fiscal Year 1995-1998, in Millions, Current Dollars
|
|
Actual FY 95 |
Actual FY 96 |
Estimate FY 97 |
Percent Changea FY 96-97 |
Budget Request FY 98 |
Percent Change FY 97-98 |
|
National Science Foundation |
87.69 |
91.70 |
98.22 |
7.11% |
102.00 |
3.8% |
|
DMS* |
85.29 |
87.70 |
93.22 |
6.29% |
97.00 |
4.1% |
|
Other MPS |
2.40 |
4.00 |
5.00 |
25.00% |
5.00 |
0.0% |
|
Department of Defenseb |
77.40 |
77.30 |
67.80 |
–14.01% |
73.60 |
8.5% |
|
AFOSR |
17.50 |
16.70 |
17.10 |
2.39% |
17.10 |
0.0% |
|
ARO |
15.00 |
15.00 |
13.00 |
–15.38% |
15.00 |
15.4% |
|
DARPA |
21.00 |
22.90 |
19.50 |
–17.43% |
22.40 |
14.8% |
|
NSA |
2.50 |
2.50 |
2.10 |
–19.05% |
2.10 |
0.0% |
|
ONR |
21.40 |
20.20 |
16.10 |
–25.47% |
17.00 |
5.6% |
|
Department of Energy |
15.70 |
16.00 |
16.00 |
0.00% |
16.00 |
0.0% |
|
University support |
6.20 |
5.50 |
5.00 |
–10.00% |
5.00 |
0.0% |
|
National laboratories |
9.50 |
10.50 |
11.00 |
4.76% |
11.00 |
0.0% |
|
TOTAL, All Agencies |
180.79 |
185.00 |
182.02 |
–1.61% |
191.60 |
5.3% |
|
Federal Support for the Mathematical Sciences, Fiscal year 1995-1998, in Millions, Constant 1992 Dollars |
||||||
|
|
Actual FY 95 |
Actual FY 96 |
Estimate FY 97 |
Percent Changea FY 96-97 |
Budget Request FY 98 |
Percent Change FY 97-98 |
|
National Science Foundation |
81.48 |
83.44 |
87.20 |
4.51% |
88.26 |
1.2% |
|
DMS* |
79.25 |
79.80 |
82.76 |
3.71% |
83.93 |
1.4% |
|
Other MPS |
2.23 |
3.64 |
4.44 |
1.99% |
4.33 |
–2.5% |
|
Department of Defenseb |
71.92 |
70.34 |
60.19 |
–16.86% |
63.68 |
5.8% |
|
AFOSR |
16.26 |
15.20 |
15.18 |
–0.13% |
14.80 |
–2.5% |
|
ARO |
13.94 |
13.65 |
11.54 |
–18.28% |
12.98 |
12.5% |
|
DARPA |
19.51 |
20.84 |
17.31 |
–20.39% |
19.38 |
12.0% |
|
NSA |
2.32 |
2.27 |
1.86 |
–22.04% |
1.82 |
–2.5% |
|
ONR |
19.88 |
18.38 |
14.29 |
–28.62% |
14.00 |
2.9% |
|
Department of Energy |
14.59 |
14.56 |
14.20 |
–2.54% |
13.84 |
–2.5% |
|
University support |
5.76 |
5.00 |
4.44 |
–12.61% |
4.33 |
–2.5% |
|
National laboratories |
8.83 |
9.55 |
9.77 |
2.30% |
9.52 |
–2.5% |
|
TOTAL, All Agencies |
167.99 |
168.34 |
161.59 |
–4.18% |
165.78 |
2.6% |
|
a Column added by authors of this report. b The FY1998 budgets for DOD's mathematical programs are estimates based on DOD's overall budget request for basic research. * MPS = Directorate for Math and Physical Sciences. Source: AAAS Report XII: Research and Development, FY 1998, Chapter 20 |
||||||
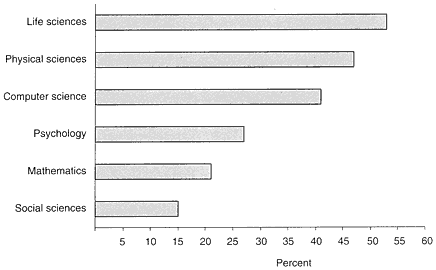
FIGURE B-13 Percentages of US academic scientists with federal support, 1993. Source: NSB 1996, appendix table 5-27.
and individual-investigator grants, of which NSF support has accounted for 50%. In 1995, total funding was $9.9 million. The STC program is nearing its end, and DIMACS will need to decide soon whether it will recompete for NSF STC funds. Other large projects supported by NSF include the Institute for Advanced Studies at $1,333,000 and the National Institute for Statistical Science at $1,068,000 in FY1996.
In DOD, the Air Force Office of Scientific Research supports research in subjects such as optimization, signal-processing, probability and statistics, computational mathematics, and dynamics and control. The Army Research Office focuses on the mathematics of materials science, high-performance computing, stochastic methods in image analysis, and mathematical and computational issues in intelligent manufacturing. The Office of Naval Research supports research in the mathematical subfields of applied analysis, discrete mathematics, numerical analysis, operations research, and probability and statistics. The Defense Advanced Research Projects Agency supports research that facilitates the development of technologies needed to meet future military needs. Of particular interest recently have been mathematical aspects of signal-and image-processing, electromagnetics, modeling and simulation of manufacturing processes, and optimized portable application libraries.
The National Security Agency is the nation's largest employer of mathematical scientists. It has a competitive grants program that
FIGURE B-14a Federal funding of US mathematical research—academic, 1993-1995 average.
FIGURE B-14b Federal funding of US mathematical research—all R&D. Key: NSF = National Science Foundation; DOD = Department of Defense; DOE = Department of Energy; HHS = Department of Health and Human Services; NASA = National Aeronautics and Space Administration; USDA = Department of Agriculture; DOC = Department of Commerce; DOT = Department of Transportation; DOI = Department of the Interior. Source: NSB 1996.
supports unclassified academic research in discrete mathematics, algebra, number theory, probability, statistics, and cryptology.
The DOE focuses its R&D support on applied computer and computational mathematics, science and technology.
Papers and Citations
Two recent reports—one from Australia and the other from the United Kingdom—have analyzed scientific performance on a comparative basis using research-paper production and citation data. As noted in the Australian Bureau of Industry Economics report Australian Science: Performance from Published Papers (1996), there are a number of problems in using such data, including a bias toward roman script and English-language journals; the greater attention paid to papers by renowned authors than to high-quality papers by less-known authors, technical papers, review articles, and recipes with little frontier science; and self-citation and citation circles.
Other problems occur because journal prestige and variation among disciplines is not considered. Time lag is a problem. There can be differential counting or miscounting due to multiple authorship, multiple field allocation, limits on the number of citations by journal, and changes in the number of journals in the field over time. And authors might use the same material with slight elaborations or break up a major article into several minor ones.
Papers "ahead of their time" and research communicated in nonjournal form (such as working papers, scientific equipment, computer programs, and seminar papers) might not be cited. Other outputs (such as teaching, advice to government, commercial research, and scientific services) are not included in bibliometric analyses.
Thus, citation rates measure visibility but not inaccessible work and not necessarily quality.
Figure B-15 shows the percentage of mathematical-research papers published by US authors relative to authors in 4 other countries that have strong mathematics programs. Figure B-16 compares the number of papers produced by US mathematicians with those produced in the European Community.
The UK report The Quality of the UK Science Base (1997) identifies the following as the top countries according to share of world's citations in mathematics:
-
United States.
-
United Kingdom.
-
Germany.
-
France.
-
Japan.
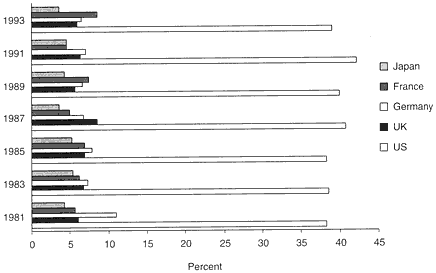
FIGURE B-15 Percentage of mathematical-research papers published by US authors. Source: NSB 1996, appendix table 5-31.
FIGURE B-16 Number of mathematical-research papers by US and EC authors, 1981-1996. Source: Institute for Scientific Information, National Science Indicators on Diskette, 1981-1996. Philadelphia, PA.
Another measure that was used in the UK report is the relative citation impact. The relative citation impact for a country in a particular field is defined as the country's share of the world's citations in the field divided by its share of world publications in the field. It can be thought of as a comparison of a country's citation rate for a particular field with the world's citation rate for the field. A relative citation impact (or rate) higher than 1 shows that the country's citation for the field is higher than the world's. According to the UK report, it is a measure of both the impact and the visibility of a country's research (as disseminated through publications) and gives some indication of the quality of the average paper.
The top countries in mathematics according to the relative citation impact index are:
-
Denmark.
-
Norway.
-
UK.
-
US.
-
Netherlands.