8
DEVELOPING MATHEMATICAL PROFICIENCY BEYOND NUMBER
In this chapter, we go beyond number to examine other domains of school mathematics in grades pre-K to 8. Because a great deal of the curriculum dealing with number leads naturally to algebra and because whether and how to teach algebra to all children is a hotly debated topic in many schools, we devote the bulk of the chapter to issues of beginning algebra. The first section is organized according to the algebraic activities of representing, transforming, and generalizing and justifying, which allows us to survey the literature relevant to learning algebra in grades pre-K to 8. We close the chapter with two briefer sections: one on measurement and geometry, the other on statistics and probability. As we noted in Chapters 1 and 3, these domains are intimately related to number. Measurement is one of the most common uses of number, and the geometry studied in elementary and middle school uses lengths, areas, and volumes usually expressed as numerical quantities. Statistics and probability involve the quantification of phenomena dealing with data and chance. Throughout the last two sections we emphasize the strands of conceptual understanding and adaptive reasoning because these have been the focus of much recent research and because traditional instruction has tended to emphasize the development of procedural fluency instead.
Beginning Algebra
For most students, school algebra—with its symbolism, equation solving, and emphasis on relationships among quantities—seems in many ways to signal a break with number and arithmetic. In fact, algebra builds on the proficiency that students have been developing in arithmetic and develops it
Algebra builds on the proficiency that students have been developing in arithmetic and develops it further.
further. In particular, the place-value numeration system used for arithmetic implicitly incorporates some of the basic concepts of algebra, and the algorithms of arithmetic rely heavily on the “laws of algebra.” Nevertheless, for many students, learning algebra is an entirely different experience from learning arithmetic, and they find the transition difficult.
The difficulties associated with the transition from the activities typically associated with school arithmetic to those typically associated with school algebra have been extensively studied.1 In this chapter, we review in some detail the research that examines these difficulties and describe new lines of research and development on ways that concepts and symbol use in elementary school mathematics can be made to support the development of algebraic reasoning. These recent efforts have been prompted in part by the difficulties exposed by prior research and in part by widespread dissatisfaction with student learning of mathematics in secondary school and beyond. The efforts attempt to avoid the difficulties many students now experience and to lay the foundation for a deeper set of mathematical experiences in secondary school. Before reviewing the research, we first describe and illustrate the main activities of school algebra.
Previous chapters have shown how the five strands of conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition are interwoven in achieving mathematical proficiency with number and its operations. These components of proficiency are equally important and similarly entwined in successful approaches to school algebra.
The Main Activities of Algebra
What is school algebra? Various authors have given different definitions, including, with “tongue in cheek, the study of the 24th letter of the alphabet [x].”2 To understand more fully the connections between elementary school mathematics and algebra, it is useful to distinguish two aspects of algebra that underlie all others: (a) algebra as a systematic way of expressing generality and abstraction, including algebra as generalized arithmetic; and (b) algebra as syntactically guided transformations of symbols.3 These two main aspects of algebra have led to various activities in school algebra, including representational activities, transformational (rule-based) activities, and generalizing and justifying activities.4
The representational activities of algebra involve translating verbal information into symbolic expressions and equations that often, but not always, involve functions. Typical examples include generating (a) equations that represent quantitative problem situations in which one or more of the quan-
tities are unknown, (b) functions describing geometric patterns or numerical sequences, and (c) expressions of the rules governing numerical relationships (see Box 8–1 for an example of each).
Proficiency with representational activities involves conceptual understanding of the mathematical concepts, operations, and relations expressed in the verbal information, and it involves strategic competence to formulate and represent that information with algebraic equations and expressions. Hence, facility with generating expressions and equations combines two of the strands of mathematics proficiency.
The second kind of algebraic activities—the transformational or rule-based activities—includes, for instance, collecting like terms, factoring, expanding, substituting, solving equations, and simplifying expressions. These activities are largely concerned with changing the form of an expression or equation to an equivalent one using the rules for manipulating algebraic symbols. For example, in solving the equation 4(x+3)=2x+19, you can replace the expression 4(x+3) by the equivalent expression 4x+12. Subsequently, by subtracting 2x and then 12 from both sides, the equation 4x+12=2x+19 can be replaced by the equivalent equation 2x=7; finally, dividing both sides by
|
Box 8–1 Representational Activities of Algebra
SOURCES: Bell, 1995, p. 61; Lee and Wheeler, 1987, p. 160; Mason, 1996, p. 84. Used by permission of Elsevier Science and of Kluwer Academic Publishers. |
2 yields the solution ![]() Facility with symbolic computation in algebra has an obvious parallel with, and indeed draws upon, procedural fluency in the domain of number. Just as in arithmetic, aspects of conceptual understanding and strategic competence interact with each other and with procedural fluency in transformational activities in algebra.
Facility with symbolic computation in algebra has an obvious parallel with, and indeed draws upon, procedural fluency in the domain of number. Just as in arithmetic, aspects of conceptual understanding and strategic competence interact with each other and with procedural fluency in transformational activities in algebra.
Lastly, there are the generalizing and justifying activities. These include problem solving, modeling, noting structure, justifying, proving, and predicting. These activities are not exclusive to algebra, but they often use its language and tools. For example, the consecutive numbers problem (show that the sum of two consecutive numbers is always an odd number) illustrates how algebra is used to generalize and justify.5 Arithmetic can be used to generate many instances to show that the sum of two consecutive numbers is odd: 3+4=7, 12+13=25, and so on. But the representational and transformational aspects of algebra make it possible to justify that the sum is always odd. The sum of two consecutive integers can be represented with algebra as x+(x+1), where the key is the recognition that x represents any whole number. This expression can be transformed into the equivalent expression 2x+1, which is the general form of any odd number. This example illustrates the power of algebra, as against arithmetic, as a tool for making generalizations and providing justifications, at least for those learners who understand how statements using variables express generality.
Generalizing and justifying activities typically involve examining and interpreting representations that have previously been generated or manipulated. Such activities can provide insight into, for example, the underlying mathematical structure of a situation, or they can yield answers to specific questions or conjectures. They encourage students to develop an awareness of the role that algebra can play in mathematical thinking. All of the strands of algebraic proficiency come together in these activities, especially adaptive reasoning.
One of the great strengths of algebra is that, for experts, a great deal of its transformational activity can be carried out in what appears to be a rather automated manner. Once a student makes the transformation rules his or her own, the algorithms of algebra can be executed, in a sense, without thinking. The student needs to be thinking, for example, not of what the letters in the expressions refer to or of the operations he or she is carrying out, but only that the actions on the symbolic objects are allowable. In fact, once an expression or equation has been generated (or provided) and the goal is known, it seems to be treated in an almost mindless fashion. But is that possible?
Every algebraic manipulation involves an anticipatory element, a sense of the direction in which you want to be going and of what the desired expression will look like once you get there.6 The development of this sense of anticipation provides an alternative to the “blind” manipulation that is so often performed by beginning algebra students.7 Research suggests, however, that such anticipatory thinking is not acquired without effort. Even students with extensive algebra experience can make poor strategic decisions that leave them “going round in circles” because they cannot seem to “see” the right thing in algebraic expressions.8
The transformational aspects of algebra have traditionally been emphasized in U.S. textbooks, which have tended to pay more attention to the rules to be followed in manipulating symbolic expressions and equations than to the concepts that support those rules or give meaning to the expressions or equations being manipulated. Although few experimental comparisons have been conducted, research has shown that rule-based instructional approaches that do not give students opportunities to create meaning for the rules or to learn when to use them can lead to forgetting,9 unsystematic errors,10 reliance on visual clues,11 and poor strategic decisions.12 For example, experienced algebra students were found to choose inappropriate strategies when deciding what to do next in the simplification of an algebraic expression and would often end up with an expression that was more difficult to deal with, even though they had performed legal transformations.13 Beginning algebra students were found to be quite haphazard in their approach; they might simplify 4(6x–3y)+5x as 4(6x–3y–5x) on one occasion and do something else on another.14 When the consecutive numbers problem was given to 113 high school students who had studied algebra, only 8 worked the problem correctly.15 The rest made a variety of errors, including substituting a few values for x to show the sum’s “oddness,” using different letters for each number (x and y), representing the consecutive numbers as 1x and 2x, and setting the expression x+(x+1) equal to a fixed odd number and then solving for x. In one of the few experimental studies of rule-based instruction, students who were taught an estimate-and-test sense-making strategy performed better in solving systems of equalities and inequalities than students taught rule-based equation solving.16
Data from the National Assessment of Educational Progress (NAEP) further reveal the shortcomings of traditional school algebra. For example, one of the NAEP tasks from the second mathematics assessment involved completing the table shown in Box 8–2. Most of the students with one or two years of algebra could recognize the pattern—adding 7—from the given nu-
|
Box 8-2 Table Completion Task from NAEP Give the values of y when x=3 and when x=n. SOURCE: Carpenter, Corbitt, Kepner, Lindquist, and Reys, 1981. Used by permission of the National Council of Teachers of Mathematics. |
merical values and use it when x=3 (with success rates of 69% and 81% for the two groups of students, respectively). They were less successful, however, when asked to derive from the same table the value of y when x=n (correct response: y=n+7; success rates: 41% and 58%, respectively).
The next three sections of the chapter present representative findings from the large body of research on algebra learning and teaching for the three types of algebraic activity sketched above. Since much of this research has been carried out with students making the transition from arithmetic to algebra, it casts light on the kinds of thinking that students bring with them to algebra from the traditional arithmetic curriculum centered on algorithmic computation that has been predominant in U.S. schools.17 Indeed, many studies have been oriented toward either developing approaches to teaching algebra that take this arithmetic thinking into account or, more recently, developing approaches to elementary school mathematics that build foundations of algebraic reasoning earlier.
Much research also has focused on linear relations and linear functions, perhaps because these are considered the easiest and are the first ones encountered by students making the transition from arithmetic to algebra. Although the domain of algebra is far richer than linear relations, much of the research at the cusp of arithmetic and algebra focuses on them.18 Some of the newer curriculum programs, however, introduce nonlinear relations along with linear relations in the middle grades. In particular, exponential growth relations (e.g., doubling) have been shown to be an accessible topic for middle school students.19
Several of the teaching approaches discussed in the following sections have profitably used computer technologies, especially graphics, as a means of making algebraic symbolism more meaningful. These studies provide evidence of the positive role that computer-supported approaches can play in the learning of algebra, as well as suggesting that technology can be a means for making algebra accessible to all students, including those who, for whatever reason, lack skill in pencil-and-paper computation.20 Thus, these examples suggest that some version of “algebra for all” may be viable.
The Representational Activities of Algebra
What the Number-Proficient Student Brings
Traditional representational activities of algebra center on the formation of algebraic expressions and equations. Creating these expressions and equations involves understanding the mathematical operations and relations and representing them through the use of letters and—for equations—the equal sign. It also requires thinking that proceeds in rather different ways from the thinking that develops in traditional arithmetic.
In the transition from arithmetic to algebra, students need to make many adjustments, even those students who are quite proficient in arithmetic. At present, for example, elementary school arithmetic tends to be heavily answer oriented and does not focus on the representation of relations.21 Students beginning algebra, for whom a sum such as 8+5 is a signal to compute, will typically want to evaluate it and then, for example, write 13 for the box in the equation 8+5=□+9 instead of the correct value of 4. When an equal sign is present, they treat it as a separator between the problem and the solution, taking it as a signal to write the result of performing the operations indicated to the left of the sign.22 Or, when doing a sequence of computations, students often treat the equal sign as a left-to-right directional signal. For example, consider the following problem:
Daniel went to visit his grandmother, who gave him $1.50. Then he bought a book for $3.20. If he has $2.30 left, how much money did he have before visiting his grandmother?
In solving this problem, sixth graders will often write 2.30+3.20=5.50–1.50 =4.00, tacking the second computation onto the result of the first.23 Since 2.30+3.20 equals 5.50, not 5.50–1.50, the string of equations they have written violates the definition of equality. To modify their interpretation of the equality sign in algebra, students must come to respect the true meaning
of equality as a statement that the two sides of an equation are equal to each other.
Students oriented toward computation are also perplexed by an expression such as x+3; they think they should be able to do something with it, but are unsure as to what that might be. They are not disposed to think about the expression itself as being the subject of attention. Similarly, they need to rethink their approach to problems. In solving a problem such as “When 3 is added to 5 times a certain number, the sum is 38; find the number,” students emerging from arithmetic will subtract 3 from 38 and then divide by 5— undoing in reverse order, as they have been taught, the operations stated in the problem text. In contrast, they will be taught in algebra classes first to represent the relationships in the situation by using those operations and not reversing them: 3+5x=38.
Although most students beginning algebra have had some experience with the use of letters in arithmetic, such as finding the number n such that n+12=37, rarely have they worked with more general problem situations in which the letter can take on any of an infinite set of values. In a third-grade class,24 the students were presented with the problem, “Who can make up a number sentence that equals 10 but has more than two numbers adding up to 10?” Most students started with examples like 5+2+3=10 and 8+1+1=10, but the class went on to generate a variety of equations, including 200–200+10=10 and 1,000,000–1,000,000+10=10. With the teacher’s help, they soon were able to formulate the equation x–x+10=10, for any number x. This use of a letter as variable, where the letter can take on a range of values, is seldom seen in typical elementary school mathematics. More often, the letter, or some placeholder, represents an unknown, and only one numerical value will make the equation true. In algebra, both of these conceptions of literal terms (or letters) are important.
A number of recent intervention studies have shown how selected modifications of elementary school mathematics might support the development of algebraic reasoning. One approach infuses elementary mathematics with a systematic use of problems requiring students to generalize, to determine values of a literal term that satisfy quantitative constraints (with or without equations), or to treat numbers in algebraic ways. For example, students might be asked to determine how many ways the number 4 can be written using a given number of 1s and the four basic operations. Since each expression must equal 4, students must distinguish among the different possibilities on the basis of their symbolic form rather than their value when evaluated.25
Another approach is to assist elementary school teachers in modifying their instructional materials and classroom practices to emphasize generalizing and expressing generality in elementary mathematics, particularly using patterns, functions, and the notions of variable. Third graders whose teachers were given such assistance showed substantial increases in their understanding of variable and equality compared with traditionally instructed students in the same grade and school. Further, these third graders outperformed fourth graders on items testing number sense from a mandated statewide assessment.26
A third approach to modifying elementary school mathematics focuses on helping teachers understand their students’ thinking when the students are asked to generalize operations and properties from arithmetic. In one combination first-and-second-grade class, the teacher focused on number sentences twice a week during the school year. Instruction started with true and false number sentences and progressed to increasingly complex forms of open sentences. Number sentences were also used to help the children articulate and represent conjectures about properties of numbers and operations. By the end of the year most of the students (13 of 17) developed a relational concept of equality and operations, along with an ability to form and express general relations among number sentences.27 In particular, the majority of these students no longer made mistakes like writing 13 for the box in 8+5=□+9.
Much of the difficulty that students experience when they first encounter algebra is symptomatic of the cognitive challenges inherent in moving from one mode of thinking to another, from arithmetic reasoning to algebraic reasoning. Research on algebra learning has sought to uncover the ways in which beginning algebra students think, thus helping ease their transition into algebra. In the examples cited above of research on more algebraic approaches to elementary school mathematics that are intended to avoid transition problems, the approaches are in their early stages. Although the long-term impact of these approaches is still unknown, they offer considerable promise for avoiding the difficulties many students now experience.
Developing Meaning
Much of the algebra research in the 1970s and early 1980s yielded evidence that incoming algebra students have trouble interpreting letters as variables.28 Building on these findings, recent work has focused on how students learn to use algebraic letters to represent a range of values.
One investigator studied an approach designed to address students’ difficulties with thinking about and symbolizing algebraic expressions.29 Students were asked to give instructions to an “idealized mathematics machine”: for example, “I want the machine to add 5 to any number I give it; how will I write the instructions?” or “I want the machine to add any two numbers I give it” or “Have the machine find the area of any square, given a side.” The students easily made sense of the idea of employing letters to write rules that would enable the machine to solve whole classes of problems. In the examples above, the rules would be expressed using (x+5), (x+y), and x2, respectively. This approach addresses two issues related to the introduction of algebra: the usefulness or purpose of learning algebra, and the difficulty of new algebraic concepts. The investigator emphasized that “children who are not persuaded on the former point will make little effort to try and come to terms with the latter” and added that “certainly the evidence…clearly indicated this to be the case.”30 The majority of the students in the study made significant gains in thinking about the letters in algebraic expressions as taking on multiple values (from 23% correct on the pretest to 85% correct on the delayed posttest) and in improving their attitude toward algebra (at the beginning of the study, they “hated algebra, didn’t understand it” and complained that “letters are stupid; they don’t mean anything”).31 Later research in which students used actual computers confirmed these results, both with respect to increasing the students’ motivation and developing their understanding of algebraic expressions as general computational procedures.32
Representational activities of algebra can interact with well-established natural-language-based habits.
Representational activities of algebra can interact with well-established natural-language-based habits. These interactions are particularly clear in the well-studied class of tasks exemplified by the so-called students-and-professors problem:33
At a certain university, there are six times as many students as professors. Using S for the number of students and P for the number of professors, write an equation that gives the relation between the number of students and the number of professors.
A robust reversal error is committed by a majority of students, ranging from first-year algebra students to college freshmen, who write “6S=P” and treat the “6” as an adjective modifying the “S” as if it were a noun.34 This error occurs across different versions of the problem and is resistant to easy correction.35 The error, while of intrinsic interest, has an especially important connection to the instruction that students receive prior to studying algebra. In particular, detailed correlational analyses have shown that the error’s robust-
ness is strongly associated with students’ understanding of rates and ratios— the worse their understanding, the more robust the error.36 Such findings could signal the connections between building proficiency in using algebra as a representational tool and building conceptual understanding of number ideas—in this case, multiplicative ideas. Interestingly, related findings show that a procedural perspective that treats the variables in the equation as input-output pairs leads to improved equation-writing performance,37 which is consistent with the results described above using the idealized machine and the computer.
A series of teaching experiments conducted over three years during the late 1980s in Mexico and the United Kingdom demonstrated the potential of computer spreadsheets to help students grasp the meaning of variables and algebraic expressions, including students who had been having difficulty with traditional approaches to algebraic symbolism.38 Further, spreadsheets can provide a vehicle for introducing students to formal symbolism.39 For an example of how a student can profit from the use of a spreadsheet, see Box 8–3. This student was a tenth grader in a low mathematics track of a school in England who had little previous experience with algebra.
Experimental studies involving spreadsheets have also shown enhanced student learning relative to traditional instruction.40 Studies of the use of spreadsheets have found that it is relatively easy for students to pass from a mixture of spreadsheet and algebraic notation to traditional algebraic symbolism.41 It should be noted that the spreadsheet approach involves creating a range of values for the expressions that represent the various relationships in the problem statement. Thus, a spreadsheet column of the values that are generated provides an explicit representation of sample values of each variable. Moreover, the particular value of X that solves the problem is often found in one line of the spreadsheet array (if the situation is linear). In the spreadsheet approach, therefore, the unknown is viewed simply as that particular value that satisfies the constraints of the problem.
In general, the use of spreadsheets has been found to be an effective way to develop several notions involved in the representational activities of algebra. It encourages discussion of the role of a letter as both a variable and an unknown; it provides meaningful experience in creating algebraic expressions; and it puts the focus squarely on the representation of quantitative relationships. Research from both small-group instruction42 and broad-based implementations involving several schools43 provides support for these claims.
Closely related to spreadsheets are intelligent tutors in which students label spreadsheet-like worksheets and fill in calculated results for specific
|
Box 8–3 Building on Spreadsheet Experiences Jo, like several of her 14- and 15-year-old peers, had some previous experience with algebra. But she disliked mathematics and had performed very poorly on the algebra test given at the beginning of the study. She viewed algebraic symbols as no more than letters of the alphabet whose numerical values corresponded to their position in the alphabet. During a four-month study (with one lesson per week), Jo learned how to use a spreadsheet to solve various kinds of word problems. At the end of the study, she was given the following problem to solve (with no computer available): One hundred chocolates were distributed to three groups of children. The second group received four times as many chocolates as the first group. The third group received 10 chocolates more than the second group. How many chocolates did the first, second, and third groups receive? Jo drew a spreadsheet on paper and showed in her written solution how the spreadsheet code was beginning to play a role in her thinking processes. Interviewed subsequently, she was asked, “If we call this cell x, what could you write down for the number of chocolates in the other groups?” She wrote the following, which shows that she was now able to represent the problem using the literal symbols of algebra (note that the syntax of many spreadsheets requires the entry of an equal sign before the algebraic expression):
SOURCE: Sutherland, 1993, p. 22. Used by permission of Micromath. |
values of the variable.44 For example, given the situation that a plumbing company charges $42 per hour plus $35 for the service call, students are asked to find the cost of a 3-hour service call and of a 4.5-hour service call. This inductive-support strategy has students provide an arithmetic representation for the problem before being asked to give the algebraic representation. Such an intelligent tutor has been made part of an experimental ninth-grade algebra curriculum that focuses on the mathematical analysis of realistic situations.
When the curriculum was tested in three urban schools, students in the experimental classes significantly outperformed students in comparison classes on standardized tests (42% correct vs. 37% correct) and on tests targeting the curriculum’s objectives (38% correct vs. 18% correct).45
Recent research in algebra learning also has examined coordinate graphs as a means of representing the relationships of problem situations and providing visual support for symbolic expressions. This use of graphs has usually been done with families of functions; that is, linear functions, quadratic functions, exponential functions, and so on. The wide assortment of computer graphing packages on the market that not only generate coordinate graphs but also link operations on them to updated tabular and symbolic representations have made it feasible for mathematics teachers to use innovative approaches involving these representations.46
One research group that has worked extensively with multirepresentational approaches to the teaching of elementary algebra has developed a computer-intensive, function-based algebra curriculum focused on problem solving that has been tested in first-year algebra classes, as well as college algebra classes.47 The curriculum uses several kinds of software to “develop students’ understanding of algebra concepts and their ability to solve problems requiring algebra, before they master symbol manipulation techniques.”48 An adaptation of a sample problem from the curriculum is presented in Box 8–4.
Even though this curriculum was not intended as an alternative curriculum to be compared to a traditional one, members of the research team carried out a few such evaluations. Interviews and tests of one cohort of students at the end of their first year of algebra showed that the experimental group did significantly better than their counterparts from conventional classes in improving their problem-solving abilities and in comprehending the notion of variable. For example, in constructing mathematical representations, the success rates were 48% versus 21%; in interpreting mathematical representations, 78% versus 28%; and in planning solutions and solving problems, 77% versus 66%, respectively.49
A similar approach to teaching algebra that involves graphing calculators has been implemented in a three-year high school mathematics curriculum used in several states.50 When students from three schools at the end of their third year in this curriculum were compared with students nearing the end of their high school algebra experience in advanced algebra classes in three other schools, the students in the new curriculum did better than the comparison group on algebraic tasks that were embedded in applied problem contexts when graphing calculators were available (43% correct for the project group
|
Box 8–4 Weather Balloon Problem Situation. Summer weather in Maryland and Pennsylvania brings heavy clouds and thunderstorms on many late afternoons. As warm, moist air rises, it cools. When the air has cooled to the condensation temperature, it forms water drops. These data were recorded by a weather balloon sent up on a warm day. Data
t(a)=__.
SOURCE: Heid, 1990, p. 195. A later version of this problem appears in Fey, Heid, et al., 1999, p. 171. Used by permission of the National Council of Teachers of Mathematics. |
vs. 34% for the comparison group). On transformation tasks involving equation solving and expression simplification without any context and for which calculators were not permitted, however, the comparison group scored higher (38% correct vs. 29%). This finding did not surprise the researchers because the new curriculum had not emphasized symbolic manipulation with paper and pencil, whereas the curriculum for the comparison group had consisted almost exclusively of such manipulation. In fact, when the equation-solving tasks were presented in a contextualized form, such as the example shown in Box 8–5, the students in the new curriculum were more successful than the comparison students (61% correct vs. 45%).51
The ways that graphing calculator use can produce improved student performance were examined more deeply in a recent study.52 The study used a three-condition pretest-posttest design to study the impact of prolonged use of the graphing calculator throughout the entire school year for all topics of the mathematics curriculum (i.e., functions and graphs, change, exponential and periodic functions). Three experimental classes used the graphing calculator throughout the year; a second set of five experimental classes used the graphing calculator with only one topic for six weeks; and four classes, which served as the control group, covered the same subject matter throughout the year but without the graphing calculator. The students who used the calculator throughout the year had enriched solution reper
|
Box 8–5 Water Business Problem The Turtle Mountain Springs Company made plans for growth in its share of the water business. They predicted that annual income from the sale of its bottled water B and filters F would change over time according to the following formulas. Time, t, is in years since 1990, and income is in millions of dollars per year. Bottled Water Income: B=20+5t Filtering Devices Income: F=28+3t Question: When does the Turtle Mountain Springs Company expect the two water products to give the same annual income? SOURCE: Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000, p. 347. Used by permission of the author. |
toires and a better understanding of functions. The students who used the graphing calculator for only a short period of time did no better on the posttest than the students in the control group. They merely replaced their algebraic and guess-and-test procedures with graphing methods. Unlike the students who spent more time using the graphing calculator, they were not able to enrich their conceptual understanding of functions.
The widespread availability of computer and graphing-calculator technologies has dramatically affected the kinds of representational activities that have been developed and studied since the 1980s. Today’s graphing programs, curve fitters, spreadsheets, and spreadsheet-like generators of tables of values and so on have been found to provide more effective environments than pencil and paper for introducing students to variables, algebraic expressions, and equations in a problem-solving context. Research has documented that the visual and numerical supports provided for symbolic expressions by digital representations of graphs and tables help students create meaning for expressions and equations in ways difficult to manage in learning environments not supported by computers or calculators. More research is needed into the ways that computers and graphing calculators are being used and can be used effectively in the early grades.
The Transformational Activities of Algebra
What the Number-Proficient Child Brings
In the previous section, we discussed some of the perspectives brought to the study of algebra by students emerging from traditional elementary school arithmetic. These perspectives included the following:
-
An orientation to execute operations rather than to use them to represent relationships; which leads to
-
Use of the equal sign to announce a result rather than signify an equality;
-
Use of inverse or undoing operations to solve a problem and the corresponding absence of a notion of describing a situation with the stated operations of a problem; and
-
A perception of letters as representing unknowns but not variables.
In this section, we discuss additional features of arithmetic thinking that must be addressed when students encounter the transformational activities of algebra.
Students who are proficient with arithmetic are generally assumed to have facility with the arithmetic operations of addition and multiplication and their inverses (subtraction and division), with computations written in a horizontal form, and with the equivalence of numerical expressions. These notions, however, are not always as well cultivated in elementary school mathematics as they should be if they are to serve as a basis for algebraic reasoning.
Students emerging from six or seven years of elementary school mathematics are ordinarily aware of the close relationship between addition and subtraction. After all, they check subtraction written vertically by adding the answer (the difference) to the number above it (the subtrahend) to see if it gives the number in the top line of the subtraction (the minuend). But they seem less comfortable with moving among the written forms of this relationship—for example, from an addition statement written horizontally to its equivalent subtraction (e.g., writing 35+42=77 as 35=77–42). Thus, these students seem somewhat bewildered when asked in initial algebra instruction to express, say, x+42=77 as x=77–42. The same confusion over the written notation for the inverse relationship between addition and subtraction is seen in the errors students make in solving equations53 when they judge, say, x+37=150 to be equivalent to x=37+150 and x+37=150 to be equivalent to x+37–10=150+10.
Solving equations and simplifying expressions require the ability to reason about operations as expressions of quantitative relationships rather than just procedures. Researchers have found that sixth graders lack adequate experience in developing this ability. Students were asked to judge the equivalence (without computing the totals) of three-term arithmetic expressions with a subtraction and an addition operation;54 for example, 685–492+947, 947+492–685, 947–685+492, and 947–492+685. The typical answer was that you needed to calculate to decide whether the expressions were equivalent. Similar results were found in another study55 when students of the same age were presented with the task of stating the value of □ in the expression (235+□)+(679–122)=235+679. Findings such as these illustrate that traditionally instructed students who are proficient with numbers need to shift from thinking about “finding the answer” to thinking about the “numerical relationships” underlying the calculations they perform and the nature of the methods they use.
Traditionally instructed students who are proficient with numbers need to shift from thinking about “finding the answer” to thinking about the “numerical relationships” underlying the calculations they perform and the nature of the methods they use.
Students’ experience with equivalence in earlier grades is often restricted to their study of equivalent fractions. For example, ![]() is equivalent to
is equivalent to ![]() which is equivalent to
which is equivalent to ![]() and so on. But this equivalence is one of numbers, not of operations or expressions. There are few opportunities in the present
and so on. But this equivalence is one of numbers, not of operations or expressions. There are few opportunities in the present
elementary school number curriculum for students to gain experience with these more abstract forms of equivalence. It would be helpful, for example, if the curriculum included perimeter problems in which students were asked to calculate the perimeter of a 7-by-4 rectangle in three ways that yield equivalent expressions: 2(7+4), (2×7)+(2×4), and 7+7+4+4. Such situations are ideal for initiating discussions of the equivalence of arithmetic expressions and of the properties underlying that equivalence. Because such occasions are currently quite rare in the part of the curriculum dealing with number, however, notions of equivalence generally have to be further developed when arithmetic is extended to algebra.
Developing Meaning
Students’ notions of equality and equivalence, as well as their deepening understanding of the relationship between operations and their inverses, are developed through the transformational activities of algebra, especially those related to simplifying expressions and solving equations. A great deal of research has been carried out on this sphere of algebraic activity.
Performing the same operation on both sides of the equation is an important formal equation-solving procedure. This method, however, is often not the first one taught to students. Trial-and-error substitution of values for the unknown and other informal techniques such as the cover-up method and working backwards (undoing) are used to introduce equation solving (see Box 8–6).
In one comparison of the cover-up method with the formal procedure of performing the same operation on both sides of the equation in six seventh-grade classes, the students who learned to solve equations by means of the cover-up method performed better than those who learned both methods in close proximity.56 The students who learned to solve equations using only the formal method performed worse than those who learned both methods. These findings suggest that students learning formal methods of equation solving may benefit from well-timed prior instruction in the informal technique of “cover up.”
Another study found that students who were entering their first algebra course showed one of two preferences when solving simple linear equations in which there was only one operation: Some used trial-and-error substitution; the others used undoing.57 For two-step equations involving two operations such as 2x—5=11, the latter group of students spontaneously extended their right-to-left undoing technique: Take 11, add 5 to it, then divide by 2.
|
Box 8–6 Two Methods for Solving Equations
|
||||||||||||||||
For equations involving multiple operations, such as 3x+4–2x=8, they erroneously generalized their method and simply undid each operation as they came to it. For example, they would take 8, divide it by 2, add 4, and then subtract 3. (They had to ignore the last operation of multiplication because they had run out of operands.) A preference for the undoing method of equation solving seemed to work against the students when they were later taught the procedure of performing the same operation on both sides of an equation. The students who preferred the undoing method were, in general, unable to make sense of “performing the same operation on both sides.” The instruction seemed to have its greatest impact on those students who had an initial preference for the informal method of substitution and who viewed the equation as a balance between left and right sides. This observation suggests that learning to operate on the structure of a linear equation by performing the same operation on both sides may be easier for students who already view equations as entities with symmetric balance and not as statements about a calculation on the left side and the answer on the right.
Despite the considerable body of research on creating meaning for the transformational activities of algebra, few researchers have been able to shed light on the long-term acquisition and retention of transformational fluency. In one study, students were able to produce a meaningful justification for
equivalence transformations, but soon afterwards most remembered only the rules, and some did not even remember that much.58 According to another study, recency of experience seems to account best for students’ ability to carry out certain transformational activities.59 Regardless of the teaching approach used, whether reform-based or traditional (i.e., oriented toward symbol manipulation), students’ ability to carry out successfully the transformational activities of algebra by the end of their high school career appears to be severely limited. This result has been found repeatedly, even in recent studies: “Few students [can] do the kinds of basic symbolic calculation that are common fare on college-admission and placement tests.”60
The Role of Technology
Transformational activities of algebra have benefited substantially less than representational activities from the use of computer technology to help develop meaning and skill. Nevertheless, a few researchers have used graphing technology as a means of providing a foundation for simplifying expressions and solving equations.61 This research is based on the idea that an important aspect of students’ mathematical development is their ability to support the symbolic transformations of algebraic objects by means of visual representations. For instance, the graphs of two functions can be added geometrically to arrive at a third graph whose expression is their algebraic sum. Equations also can be solved by graphing the functional expressions on each side of an equation on a computer or graphing calculator, zooming in on the point of intersection, and finding the approximate value of x for which the two functions are equal.
In one study the students had become so skilled at graphing linear functions by focusing on the y-intercept and slope that they could do it mentally (see Box 8–7). Although most teachers of algebra would be happy if a student could solve equations mentally by visualizing graphs, they would not be satisfied with solutions found by such informal methods. The issue is not, however, simply being able to produce a more accurate solution than one obtained by examining a graph. If it were, computer software and calculators that can do symbol manipulation could be called on to generate solutions that are as accurate as desired. The issue is the role the process plays in learning:
When symbol manipulators become widely available, we will probably take the same view with equation solving that we do with graphing. That is, we will continue to teach students paper-and-pencil means for solving linear equations because the idea is important and the process
|
Box 8–7 Mentally Graphing to Find the Solution to an Equation Toward the end of a study of equation solving by means of a graphical representation, a seventh grader was asked to solve the equation 7x+4=5x+8 (an equation whose solution is x=2). Rather than graph the two expressions, the student took a “shortcut.” Interviewer: Can you solve 7x+ 4=5x+8? Jer: Well, you could, see, it would be like start at 4 and 8, this one would go up by 7, hold on, 8, 8 and 7, hold on, no, 4 and 7, 4 and 7 is 11. They’d be equal, like, 2 or 3 or something like that. Interviewer: How are you getting that 2 or 3? Jer: I’m just like graphing it in my head. SOURCE: Kieran and Sfard, 1999, p. 15. Used by permission of the author. |
is generalizable, but we will also teach how to use symbol manipulators to solve these and more-complicated equations [emphasis added].62
Thus, most teachers—for the time being, at least—remain insistent that students learn to do by hand the various algebraic transformations of expressions and equations. In 1989 one mathematics educator noted that “the unanswered question standing in the way of reducing the manipulative skills agenda of secondary school algebra is whether students can learn to plan and interpret manipulations of symbolic forms without being themselves proficient in the execution of those transformations.”63 Very little research has been conducted since then to help resolve the question; however, the research that has been done is quite telling. A recent study investigated the impact on algebra achievement of a three-year integrated mathematics curriculum in which technology was used to perform symbolic manipulations as well as to link various representations of problem situations.64 In this study, which involved over 300 high school students in 12 schools, some support was found for the notion that learning how to interpret results of algebraic calculations is not highly dependent on the ability to perform the calculations themselves.
Furthermore, skill in algebraic symbol manipulation was not a prerequisite for the students’ success in problem solving, and as the researchers emphasized, “when those students had access to the kind of technological tools that are becoming standard mathematical tools, they could overcome limited personal calculation skills.”65
Although researchers have made notable advances in finding ways to make representing and interpreting algebraic expressions and equations more meaningful for students with the help of computer and calculator technology, similar efforts in the realm of transforming expressions and equations have been less abundant. As inexpensive symbol manipulators continue to become available for the algebra classroom, it may be feasible to develop and evaluate programs that incorporate their use. At present, despite the occasional use of calculator- and computer-supported approaches to the transformational activities of algebra, the traditional rule-based methods for developing manipulative skills tend to dominate. However, few people at any level in education are satisfied that the traditional approach leads to sufficient proficiency in algebra for most students.
Generalizing and Justifying Activities of Algebra
In this section, we consider activities such as solving problems, modeling situations, noting mathematical structure, justifying, proving, and predicting. None of these activities is exclusive to algebra, but in all of them algebra is often used as a tool. Several of these activities require a certain level of skill in representing and transforming algebraic expressions, as well as in adaptive reasoning. Two problems from the research literature help illustrate the issues (see Box 8–8).
Justifying Generalizations
Students given Problem A in Box 8–8 tended to give a strictly numerical justification in Part 1. The explicit demand of Part 2 to use algebra, however, requires translating the nonspecific number and the sequence of operations into algebraic notation and then manipulating that notation to obtain an expression that can be interpreted in terms of the problem’s conditions. If x is the number, that translation yields
(5x+12–x)/4⇒(4x+12)/4
⇒4(x+3)/4
⇒x+3.
|
Box 8–8 Problems That Involve Generalizing and Justifying Activities Problem A Part 1. A girl multiplies a number by 5 and then adds 12. She then subtracts the original number and divides the result by 4. She notices that the answer she gets is 3 more than the number she started with. She says, “I think that would happen, whatever number I started with.” Part 2. Using algebra, show that she is right. Problem B Triangular numbers can be built with dots as shown below. The first four triangular numbers are 1, 3, 6, and 10. Part 1. Predict the number of dots in the 20th triangle. Part 2. Give a rule for predicting the number of dots in any triangle. 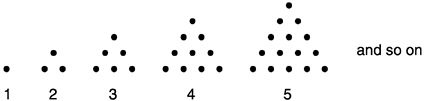 SOURCES: Arzarello, 1992; Lee and Wheeler, 1987. Used by permission of Springer-Verlag and by the authors. |
More specifically, the major conceptual demands of Problem A are the following: (a) translating from a verbal representation to a symbolic representation through the use of a letter as a variable to represent “any number,” (b) manipulating the algebraic expression to yield simpler equivalent expressions with the underlying aim of arriving at an expression indicating “3 more than the number she started with,” and (c) being aware that the algebraic result—the expression x+3—constitutes a proof or justification of the result that one obtains empirically by trying several particular numbers. Note that
the only conceptual demand that is somewhat independent of the context is manipulating the algebraic expression to yield simpler algebraic expressions. That activity is very important, however, since it allows the student to see at a glance why the result for the above problem is always x+3, whatever the value of x. The evolving sequence of simplified algebraic expressions can permit a perception of “x+3-ness” in a way that is not so readily available from simply reading the problem. Thus, the algebraic representation can induce an awareness of structure that is much more difficult, if not impossible, to achieve using everyday language.
One hundred eighteen algebra students who had already taken algebra for a year were given Problem A. Only nine set up the expression (5x+12–x)/4 and then reduced it algebraically to x+3. Four of them went on to “demonstrate further” by substituting a couple of numerical values for x. Thirty-four others set up the equation (5x+12–x)/4=x+3 and then proceeded to simplify the left side, yet they did not base their conclusions on their algebraic work. Instead, they worked numerical examples and drew conclusions from them.
For the great majority of students, therefore, this task posed enormous problems both in representing a general statement and in using that statement to justify numerical arguments. According to the researchers, these students seemed completely lost when asked to use algebra. “Formulating the algebraic generalization was not a major problem for the [few] students who chose to do so; using it and appreciating it as a general statement was where these students failed.”66 Therefore, for the students who responded to the request to use algebra, their difficulties were related not to the simplification of the expression but to the third of the conceptual demands outlined above: being aware that the algebraic result constitutes a proof or justification of the arithmetical result that one obtains empirically by trying several numbers. This research also suggests that even when students are successfully taught symbolic manipulation, they may fail to see the power of algebra as a tool for representing the general structure of a situation. Without some skill with symbolic manipulations, however, students are unlikely to use algebra to justify generalizations.
Even when students are successfully taught symbolic manipulation, they may fail to see the power of algebra as a tool for representing the general structure of a situation.
Predicting Patterns
Tasks involving geometric and numerical patterns are a frequent means of introducing students to the use of algebra for predicting. Problem B in Box 8–8 is typical. To help students find a pattern in the arrangement of dots
in the problem, they might be asked to use a table of values in which the first column points to a position in the sequence and the second column gives the corresponding number of dots.67
|
Sequential position (x) of the triangular number |
Number of dots (y) in the triangular number |
|
1 |
1 |
|
2 |
3 |
|
3 |
6 |
|
4 |
10 |
|
· |
· |
|
· |
· |
|
· |
· |
Two kinds of rules describe this table. One, the recursive rule, is based on an analysis of the growth occurring in the right-hand column. For the nth triangle, add n dots to the number of dots in the previous triangle. But this right-hand regularity, which is not too difficult to detect, is easier to say in words than to symbolize algebraically. The other kind of rule, the closed form, requires analyzing both columns together to try to determine a relationship between a member of the left-hand column and the corresponding member in the right-hand column. Algebra students have more difficulty deriving the latter rule, y=x(x+1)/2, than the former.68
The use of computer technology can enable students to engage in activities like those above without having to generate or transform algebraic equations on their own.69 But students have to learn how to use the equations produced by the technology to make predictions, even if they do not actually generate them by hand.
Through an emphasis on generalization, justification, and prediction, students can learn to use and appreciate algebraic expressions as general statements. More research is needed on how students develop such awareness. At the same time, more attention needs to be paid to including activities in the curriculum on identifying structure and justifying. Their absence is an obstacle to developing the “symbol sense”70 that constitutes the power of algebra.
Algebra for All
Because of advancements in the use of technology and its prevalence today, a greater understanding of the fundamentals of algebra and algebraic reasoning is viewed as necessary for all members of society, including those
who are low achieving or underserved.71 The U.S. eighth-grade curriculum is not as advanced as those of other countries. In the Third International Mathematics and Science (TIMSS) Video Study, for example, whereas 40% of U.S. eighth-grade lessons included topics from arithmetic, German and Japanese eighth-grade lessons were more likely to cover algebra and geometry.72 Over the past decade, however, more and more U.S. schools have started to offer first-year algebra in the eighth grade. According to data collected by NAEP, 25% of eighth-grade students were enrolled in algebra in 1996 compared with 16% in 1990.73 Further, all but 3% of the twelfth-grade students reported that they had taken first-year algebra, the majority in grade 9. Although the goal of “algebra for all” has essentially been achieved by the time students reach the end of high school, many of these students experience difficulties in their first course in algebra.
The study of algebra need not begin with a formal course in the subject. Recent research and development efforts have been encouraging. By focusing on ways to use the elementary and middle school curriculum to support the development of algebraic reasoning, these efforts attempt to avoid the difficulties many students now experience and to lay a better foundation for secondary school mathematics.74 From the earliest grades of elementary school, students can be acquiring the rudiments of algebra, particularly its representational aspects. They can observe that over time and across different circumstances, numerical quantities may vary in principled ways—the essence of the concept of variable. They can learn about functions by studying how a change in one variable is reflected in the behavior of another. As students encounter algebraic ideas, they discover the value of precise language and of working with clear definitions.
Once students are familiar with the laws of arithmetic, they can learn to see them as a convenient summary of arithmetic practice and as a valuable guide to methods that work. Students can learn to express the laws algebraically and can use them to support their reasoning and to justify their claims about numbers. It is important that they become aware of the role played by general statements expressed in algebraic symbols when justifying numerical arguments or discussing classes of situations. Little is known, however, about the relative effectiveness of strategies for helping students learn to justify their claims. With the development of new approaches to algebra and the infusion of the rudiments of algebra in the elementary and middle grades, an algebra-proficient population might become a reality.
Measurement and Geometry
In elementary and middle school mathematics, the closely related domains of measurement and geometry are often referred to as measure and space. Geometry, as its Greek origin as “earth measure” indicates, is a route for developing an understanding of two- and three-dimensional space. Measurement, too, is a process that links mathematics with the world, and with science in particular. Measure is a diverse topic, built on the need to quantify particular attributes of an object or phenomenon. By learning about how length, area, and volume are measured, students mentally structure and revise their construction of space, both large-scale and small-scale. When they study science, they need to know about other measures, such as time, density, and speed, and they need to know about choosing a measurement scale and considering the precision of their measurements. Although measurement and the theory behind it can be treated as distinct from geometry, there is much pedagogical value in returning geometry to its roots in spatial measure. Our discussion focuses on the measurement of length, area, and volume, three measures that are the basis for the connection between geometry and number, as shown in chapter 3 through the geometric interpretations of the operations of addition and multiplication.
There is much pedagogical value in returning geometry to its roots in spatial measure.
Acquiring Measure Concepts
The early work of Piaget and his collaborators75 focused on showing that understanding measure entails successive mental restructurings of space. The idea of a unit of measure is fundamental, as is the notion that measurement involves the organized accumulation of standard units. Further, conservation of length, area, and volume (understanding that these quantities do not change under transformations such as reflection or other rigid motion) was considered both a hallmark of, and a constraint on, children’s development in each domain of spatial measure. Studies conducted in the last two decades, however, have generally failed to support the contention that there is a tight coupling between understanding a spatial measure and knowing when it is conserved.76
Length Measure
Length needs to be understood from several perspectives: for example, as magnitude, as a span, as the distance traveled, or as motion.77 Proficiency in the measurement of length requires the learner to restructure space so that
he or she “sees” a count of n adjacent unit lengths as representing a distance of n units. Children need to recognize the need for identical units, and they need to understand that a unit can be partitioned into smaller units.78
Children’s first understanding of length measure involves the direct comparison of objects.79 They observe that two congruent objects can be put side by side and shown to have the same length. As early as first grade, children typically understand that the lengths of two objects can be compared by representing them with a string or paper strip. First graders can also use given units to find the length of different objects, and they associate higher counts with longer objects.80 This apparent ease of counting, however, need not imply understanding of length measure as a distance. First and second graders, for example, often fail to see the point of having identical units of length measure. They freely mix units such as inches and centimeters, counting them all to “measure” a length.81
Given a measuring device such as a ruler, very few young children understand that any point on the scale can serve as the starting point or origin, and even many older children (e.g., fifth graders) respond to measurement with a nonzero origin by simply reading off whatever number on a ruler aligns with the other end of the object.82 These difficulties young children have in understanding length indicate that teachers cannot assume that their students understand various aspects of the number line. When the number line is used as a pedagogical tool, efforts must be made to be sure that students understand that they are counting lengths, not the endpoints where the numbers are. In a recent teaching experiment on measuring length, children used computer tools that provided them experience with a unit and the repetition of units to get a measurement. The tools helped the children mentally restructure lengths into units.83 In other studies, researchers have placed a premium on transitions from active forms of length measure, like pacing, to recording and symbolizing these forms as “foot strips” and other kinds of measurement tools.84 Tools like foot strips help children reason about the mathematically important components of activity (e.g., pacing) so that invariants like unit are represented physically and then mentally.85 Although constructing and using tools have a long tradition in teaching practice, recent teaching experiments have shown ways in which these practices can contribute to conceptual change.86
Area Measure
The basic idea of measuring area is that of coverings region by units that “just fît” (an idea that is sometimes called tiling). In many ways the development of area measure parallels that of length, but it lags behind. First and second graders often treat length measure as a surrogate for area measure. For example, some children will measure the area of a square by measuring the length of one side, moving the ruler parallel to itself a bit and measuring the length again, and so on, treating length as a space-filling attribute.87 When provided with geometric manipulatives (squares, right triangles, circles, and rectangles) for use in finding the area measure of a variety of shapes, most students in grades 1 to 3 freely mix units and then report the total count of those units.
As they progress through the elementary grades, students usually begin to differentiate area measure from length measure, and the space-filling (tiling) requirement of the unit becomes more apparent to most of them. Other aspects of area measure, however, remain problematic. Students find it very difficult to decompose and then recompose shapes or even to see one shape as a composition of others, an idea that is fundamental to conservation.88 For example, students in grades 1 to 3 often cannot think of a rectangle as an array of units.89
By the end of the elementary grades, students typically understand core concepts like using identical units and covering the object for length measure but not for area measure. Younger children often employ resemblance as the prime criterion for selecting a unit of area measure, suggesting the need for attention to the qualities of a unit that make it suitable for measuring area. The common instructional practice of declaring that the square is the unit of area measure may lead to procedural competence but may violate students’ preconceptions about what makes a unit suitable.
Teaching experiments with area measure have revealed that second graders could develop a comprehensive understanding of area measure when they began by solving problems involving partitioning and redistributing areas without measuring.90 It is worth emphasizing that this approach makes conservation of area a fundamental construct rather than an afterthought. Later, when the children explored the suitability of different units (e.g., beans) for finding the areas of irregular shapes like handprints, they found that units like squares had desirable properties of space filling and identity. By the end of the school year, these children had little difficulty creating two-dimensional arrays of units for rectangles and even for irregular (nonpolygonal) shapes.
Volume Measure
The measurement of volume presents some additional complexities for reasoning about the structure of space, primarily because the units of measure must be defined and coordinated in three dimensions. Although the evolution of children’s conceptions of units of volume measure is not well understood, an emerging body of work addresses strategies that children use to measure a volume when given a unit.91
In one study, fifth graders who had a wide range of experience with representations of volume and its measurement typically organized space into three-dimensional arrays, and most could conceive of volume as a product of area and height.92 Thus, traditional notions about how volume concepts develop may need to be revised in light of the results from recent teaching experiments.
Developing Geometric Reasoning
Early work on geometric reasoning suggested that proficiency in geometry develops in a sequence of stages associated with age93 and that children can be assisted, through appropriate activities, to move to more advanced levels of reasoning.94 Recent work has confirmed the effectiveness of appropriate activities even as it has called into question the notion of a stage-like sequence.95
Reasoning About Shape and Form
Children enter school with a great deal of knowledge about shapes. They can identify circles quite accurately and squares fairly well as early as age four.96 They are less accurate at recognizing triangles (about 60% correct) and rectangles (about 50% correct). Given conventional instruction, which tends to elicit and verify this prior knowledge, children generally fail to make much improvement in their knowledge of shapes from preschool through the elementary grades.97
Instruction needs to build on students’ informal knowledge and move beyond it. For example, in one experiment, first graders were given a 10-day instructional sequence to help them identify specific classes of quadrilaterals and understand the relationships among the classes.98 They learned to arrange the figures from the most to the least general members of the class (e.g., from quadrilaterals to squares), to embed hierarchies in the names they gave to shapes (e.g., “square-rectangles”), and to examine characteristics of the figures.
Encouraged to reflect on and articulate their developing knowledge, the children subsequently demonstrated levels of reasoning well beyond their earlier performance, both in their precision of language and in their use of arguments based on the properties of shapes rather than on visual comparison to some prototypical shape.
In another study, fourth graders were encouraged to reflect on and articulate their ideas about concepts such as angle and line and also about relational concepts, such as class inclusion among quadrilaterals. One group of 16 students received instruction with Logo, a computer programming language with a feature called Turtle Geometry that allows children to instruct a turtle on the screen to move, tracing a geometric path as it goes. A second group of 16 students used traditional tools like protractors and rulers. On a set of geometry items from NAEP,99 the performance of both groups well exceeded the performance by the high school students in NAEP. Moreover, on measures of abstracting and applying geometric properties for reasoning, the fourth graders who had used Logo as a construction tool significantly outperformed their contemporaries.100
Although previous work had suggested that children’s reasoning about geometric figures is based on global appearances, primary school children in one study101 routinely used a variety of attributes of shape and form to describe how two shapes, in either two or three dimensions, were alike yet different from a third shape. Their judgments about shape and form revealed distinctions that appeared to involve several distinct forms of mental operation, ranging from simple feature detection (“it has four sides”), to comparison to known prototypes (“it’s squarish”), to mental representation of the action-based embodiment of transforming one form into another (“if you push the top of this one [a parallelogram] to the side, it makes a rectangle”). Mixture across levels of reasoning was the rule, not the exception.
Concepts about shapes begin forming in the preschool years and stabilize as early as age 6.102 Hence, if preschool provides sufficient opportunities for children to learn about geometric figures, by the end of second grade they should be able to “identify a wide range of examples and non-examples of a wide range of geometric figures; classify, describe, draw, and visualize shapes; and describe and compare shapes based on their attributes.”103
Although they have considerable experience with three-dimensional objects, students are less proficient with three-dimensional geometric shapes than they are with two-dimensional ones. Even intermediate-grade students have difficulty naming solids, using names of plane figures instead.104 In reasoning about solids, they refer to a variety of characteristics, such as
“pointyness” or slenderness.105 Studying only plane figures in the early grades may be responsible for some of the difficulty students have in discriminating between the terms for two- and three-dimensional figures. Construction activities involving foldout shapes of solids may help students make such discriminations.106 Other promising activities need to be developed and investigated.
An important and difficult geometric figure for students to understand and be able to use is the angle. In the course of schooling, students need to encounter multiple mathematical conceptions of angle,107 including: (a) angle as movement, as in rotation or sweep; (b) angle as a geometric shape, a delineation of space by two intersecting lines; and (c) angle as a measure, a perspective that encompasses the other two.108 Although as preschoolers, they encounter and use angles intuitively in their play, children have many misconceptions about angles. They typically believe that angle measures are influenced by the lengths of the intersecting lines or by the angle’s orientation in space.109 The latter conception decreases with age, but the former is robust at every age.110 Some researchers have suggested that students in the elementary grades should develop separate mental models of angle as movement and angle as shape.111
There is some research on instructional approaches that attempt to develop the two models of angles. With appropriate instruction, Logo’s Turtle Geometry can support the development of measures of rotations.112 The students, however, rarely connected these rotations to models of the space in the interior of figures traced by the turtle.113 Simple modifications to Logo helped students perceive the relationship between turns and traces (the path made by Logo’s turtle), and the students could then use turns to measure static intersections of lines.114 Another approach used multiple concrete analogies such as turns, slopes, meetings, bends, directions, corners, and openings to help children develop general angle concepts by recognizing common features of these situations.115 Other research took as the starting point children’s experience with physical rotations, especially rotations of their own bodies.116 In time, students were able to assign numbers to certain turns and integrate turn-as-body-motion with turn-as-number.
An understanding of angle requires novel forms of mental structuring, the coordination of several potential models, and an integration of those models. The long developmental process is best begun in the early grades. Common admonitions to teach angles as turns run the risk of students developing only one concept of angle since they rarely spontaneously relate situations involving rotations to those involving shape and form.
In several studies of instruction in space and geometry,117 teachers have posed challenging tasks (e.g., design a playground), engaged students in mathematical explanation and justification, and provided computer tools (e.g., Sketchpad,118 Logo) and related means (e.g., Polydrons119) for reasoning about space. The emerging portrait of mathematical reasoning in these contexts suggests that children’s conceptions of shape and form can encompass fairly sophisticated mathematical understanding.
Reasoning About More Advanced Concepts
During the last decade, studies of geometry learning have focused less exclusively on shape and form, although conceptions of form are still a prominent topic. Related ideas like congruence, symmetry, similarity, and transformation have received more systematic attention in recent studies. Beginning as early as age 4, children can create and use strategies for judging whether two figures are the same size and shape.120 By about first grade they can develop sophisticated and accurate mathematical procedures for determining congruence.
Children also have intuitive notions of symmetry from a very early age, preferring symmetric figures over asymmetrical ones.121 Vertical bilateral symmetry, in particular, seems to be easier for children to identify than horizontal symmetry.122 Young children can identify similar shapes in certain situations. They can verify their identifications using an overhead projector,123 and they can use computers to create similar figures.124
The findings are mixed regarding children’s ability with geometric motions. In one study, second graders could perform transformations manually but not mentally.125 In contrast, other researchers found that children do learn something about these motions and appear to internalize them.126 Slides appear to be the easiest motion, followed by flips and turns, although the difficulty depends on the specific task.127 Computer environments can be particularly useful in helping students develop proficiency with congruence, similarity, symmetry, and transformations.128
Several researchers have looked at the effects of introducing children to ideas about modeling space. In these studies, middle school students made significant progress in developing their conceptions of proportion and scale when they used a computer-assisted-drawing (CAD) tool to map their classroom129 or designed a playground and its equipment.130 Modeling of space can be done by primary grade children as well. For example, first graders learned about properties of shapes as they searched for a configuration of
players (ultimately a circle) that would be “fair” (equidistant) in a classroom game of tag.131
Some research has focused on relationships between spatial models and learning about science. For example, middle school students’ understanding of area and volume measure was found to make a significant contribution to their understanding of concepts like buoyancy,132 and the idea of similarity in substance helped in developing their understanding of similarity of shapes.133 Engineering problems involving stability have also been employed to help middle school students understand the relationship between geometry and the success or failure of architectural structures.134
Collectively, research on geometry points the way to a significant expansion of what is meant by the study of shape and form in school mathematics. Children enter school with much informal knowledge of geometry that can be developed throughout the grades. Given children’s affinity toward, knowledge of, and ability to gain geometric knowledge, it is important that this domain of mathematics not be neglected. Instruction in geometry needs to complement the study of number and operation in grades pre-K to 8.
Statistics and Probability
In the elementary and middle grades, the domains of statistics and probability are often referred to as the study of data and chance. Research in these two domains is less extensive than that in number and operation, in algebra, or in measurement and geometry. But like measurement and geometry, many of the central conceptual structures of statistics and probability have been identified, especially with respect to school mathematics in grades pre-K to 8.135
Learning to Use Data
Although the graphing of data is a common activity in grades pre-K to 8 and has been the focus of some investigations, recent research into students’ statistical thinking at the elementary and middle school grades has adopted a broader perspective. Four key processes have been studied: describing, organizing, representing, and analyzing data.136 We consider research on each of these processes in turn, starting with a definition of the process.
Describing Data
Describing data involves reading displays of data (e.g., tables, lists, graphs); that is, finding information explicitly stated in the display, recognizing graphical conventions, and making direct connections between the original data and the display. The process is essentially what has been called reading the data,137 and researchers have found that the majority of students in the elementary and middle school grades can read data displays accurately.138 Although children in the primary grades often give idiosyncratic descriptions of data, explorations with categorical and numerical data in instruction that incorporates technology produce more focused and less idiosyncratic descriptions.139
Organizing Data
The process of organizing, and reducing, data incorporates mental actions such as ordering, grouping, and summarizing.140 Data reduction also includes the use of representative measures of center (often termed measures of central tendency) such as mean, mode, or median, and measures of spread such as range or standard deviation. Research on organizing data at grades pre-K to 8 is quite limited.
Most of the available research on data reduction by elementary school students has focused on their understanding of measures of center, particularly the mean. The most familiar measure of center is the mean, which is computed by adding up all the data values and dividing by the number of values. The median is the middle value when the data are sorted (or the mean of the two middle values). The mode is the most common data value. All of these measures of center are called “averages” for some kinds of data. With housing prices and incomes, for example, the preferred average is the median because the mean is easily skewed by a few very high incomes, giving a false impression of income for an “average” or typical family. With clothing sizes, the preferred average is the mode because it gives the best impression of the typical buyer.
First and second graders have informal conceptions of mode and median as measures of center, and they also have some conception of spread.141 Most elementary school students understand that the mean is located between extreme values.142 Nearly all realize that the mean is influenced by values in the data set and that the mean does not necessarily equal one of the actual data values. In a study of fourth, sixth, and eighth graders’ concept of average, the younger students interpreted the average as the mode.143 Although
the researchers claimed that these students did not see the data set as an entity that can be represented by a single value, an alternative interpretation is that the students used the mode because it is so easily identified in a graph.144 Some students consider the average to be a data point roughly centered within the data, that is, they conceptualize average as median.145 Students in the primary grades seem not to have the idea of center as a mathematical point of balance, a vital characteristic of the mean. They cannot use an algorithmic procedure to find the mean, let alone create a data set given the mean.146 Different measures of center appear to be important for different students; all need eventually to understand the different measures and their purposes.
Representing Data
Representing data in visual displays requires the generation of different organizations of data according to certain conventions. Many elementary students have difficulty creating visual displays of data.147 First and second graders’ knowledge of how to represent data appears to be constrained by difficulties in sorting and organizing data, and technology has been found to be helpful in overcoming those difficulties.148
Studies of middle school students have revealed substantial gaps in their abilities to construct graphs from given data.149 Processes like organizing data and conventions like labeling and scaling are crucial to data representation and are strongly connected to the concepts and processes of measurement. Given the difficulties students experience, instruction might need to differentiate these processes and conventions more sharply and utilize the potential of technology to make them more accessible to students.
Analyzing Data
The process of analyzing, and interpreting, data incorporates recognizing patterns and trends in data and making inferences and predictions from the data. It includes what has been referred to as reading between the data and reading beyond the data.150 Reading between the data requires students to compare quantities and use mathematical operations to combine and integrate data and to identify mathematical relationships expressed in the data or in visual representations of the data. Reading beyond the data requires students to make predictions or inferences from the data that are neither explicitly nor implicitly stated in the visual representation.
Elementary school students have difficulty analyzing and interpreting data. In one study, 80% of the first and second graders interviewed gave idiosyncratic or incomplete responses when they attempted to analyze data from a line plot and a bar graph.151 In another study, almost all the fourth and sixth graders could describe bar graphs, but fewer could interpret them, and many fewer still could use the graphs to predict.152
Learning About Chance
Although there has been substantial research on students’ probabilistic thinking over the past 50 years by both psychologists153 and mathematics educators,154 only recently has students’ learning about chance been examined with a view toward informing instruction. In this section, we examine what is known about students’ probabilistic thinking about five key concepts: sample space, probability of an event, probability comparisons, conditional probability, and independence.155
Sample Space
Students exhibit an understanding of sample space when they are able to identify the complete set of possible outcomes in a random experiment, an experiment in which the actual outcome cannot be determined ahead of time even though the set of possible outcomes can be determined. When two coins are flipped, for example, the possible outcomes may be represented as HH, HT, TH, and TT.
Several studies have addressed children’s thinking about sample space.156 Recent research has concluded that a substantial number of students in grades 1 through 3 are not able to list the outcomes of a one-dimensional experiment (such as rolling a single die) even after instruction.157 The students in these studies adopted a deterministic posture, maintaining that it was “always” possible to predict a particular outcome. The situation with respect to two-dimensional experiments (such as rolling two dice) is also problematic. Although some children as young as seven years can use efficient procedures for listing all outcomes,158 other children in grades 4 through 6 are reluctant or unable to list them all.159
Probability of an Event
Although probability tasks used in research with elementary and middle school students have typically involved equally likely outcomes, a number of
researchers have investigated children’s probabilistic thinking about unequally likely events.160 In comparing event probabilities, students commit themselves to one of three strategies: (a) a numerator strategy in which they only examine the part that corresponds to the event; (b) an “incomplete” denominator strategy in which they examine the part that corresponds to the complement of the event; and (c) an integrating strategy in which they recognize the moderating effect that each part has on the other.161 In a recent study that incorporated instruction, the kind of reasoning that third graders used was fundamental to their quantifying probability situations in a meaningful way.162 Overall, comparisons of event probabilities are difficult for students and seem to be linked to their proficiency with rational numbers.
Comparisons of event probabilities are difficult for students and seem to be linked to their proficiency with rational numbers.
Probability Comparisons Across Sample Spaces
Students’ understanding of probability comparisons is measured by their ability to determine and justify which of two probability situations is more likely to generate the target event in a random draw. For example, given a bag with 2 red and 2 blue bears and another with 3 red and 4 blue, they might be asked, “Which bag would give the better chance of getting a red bear?” Researchers have found that elementary and middle school students use both intuitive and informal quantitative strategies for comparing the probabilities of the target event.163 In one seminal study the three incorrect strategies used by students in grades 1 through 5 involved choosing the probability situation with: (a) more instances corresponding to the target event; (b) fewer instances corresponding to the nontarget event; and (c) a greater difference (as opposed to greater ratio) of instances favoring the target event.164
Conditional Probability
A number of studies have addressed elementary and middle school students’ thinking in conditional probability situations—their ability to recognize when the probability of an event is or is not changed by the occurrence of another event.165 For example, the conditional probability of drawing a white ball, given that you have already drawn and not replaced a white ball from a bag containing three white balls and three red balls, is 0.4, not 0.5. When fifth, sixth, and seventh graders were asked to determine conditional probabilities, the performance of the sixth and seventh graders was dramatically lower when the tasks involved selection without replacement compared with selection with replacement.166 Similar results were found in a study167 with students in grades 6 through 8. In a study with third graders, several
levels of thinking in conditional probability were identified, with few children being able to recognize that the probabilities changed in situations of selection without replacement. Following instruction, 51% were able to recognize that conditional probabilities changed in these situations.168 Children have difficulty determining the conditioning event and may be confused about the context of a conditional probability problem.
Independence
Students’ intuitive understanding of independence is measured by their ability to recognize and justify when the occurrence of one event has no influence on the occurrence of another. In one study, students in grades 4 through 8 were asked to determine which event was more likely: obtaining 3 heads by tossing one coin 3 times, or by tossing 3 coins simultaneously.169 Some 38% of fourth and fifth graders and 30% of seventh and eighth graders with no prior instruction in probability responded that the probabilities were not equal. Follow-up interviews revealed that these students harbored the pervasive misconception that the outcomes of a coin toss can be controlled. Similar misconceptions were evident in other studies of middle school students.170 Misconceptions of the kind illustrated above have been characterized more generally as representativeness—a belief that a sample or sequence of outcomes should reflect the whole population.171
From Arithmetic to Mathematics
As children move from number to other domains of mathematics, they both use their proficiency with number and develop it further. The school mathematics curriculum, although separated into domains for the purposes of this report, needs to be experienced by the learner as a unified whole.
In general, the arithmetic thinking of number-proficient students emerging from the typical elementary school mathematics program is different from the thinking that is central to algebra. Some of the conceptual understanding of the arithmetic thinker requires an adjustment when the student engages in the main types of activities in algebra. Whereas arithmetic focuses on number and numerical answers, school algebra focuses on relations. Algebra remains, however, a natural extension of arithmetic. Students’ numerical thinking can therefore continue to grow and develop into algebraic thinking, but their numerical thinking habits must be taken into account.
Just as current research has influenced conceptions of algebra in the early grades, the nature of school algebra in higher grades has likewise been evolv-
ing. Over the past two decades, computational tools have increasingly influenced the kinds of transformations that are important to learn, the kinds of representations, especially graphical ones, that are readily accessible, and the kinds of applications of mathematics that are appropriate to address. One of the biggest shifts has been to emphasize the ideas of pattern, function, and variation.172 This new focus is particularly amenable to approaches that begin in the elementary grades and continue through middle school, and a sizable body of instructional materials has been developed that reflects this emphasis.173 But the long-term impact of these materials is as yet unknown.
Recent research on measurement and geometry suggests that children’s development of geometric reasoning can be greatly enhanced in instructional environments that are specifically designed to promote such understanding and that children’s thinking may fluctuate across stages identified by earlier researchers. Furthermore, computer technologies offer the promise of being able to support developing understanding in ways not available before.
Unlike the domains of measurement and geometry, research on the development of concepts of statistics and probability indicates that, especially for probability, very young children are capable of less than developmental theories might predict. Fundamental concepts in both domains, such as the conventions of scaling in graphs and the makeup of the sample space, need more careful attention in initial instruction. As in the areas of measurement and geometry, technology offers promise for helping to support and link students’ developing conceptions of data and chance. It is still an open question when and how many of the central conceptual structures of probability and statistics should be introduced in the elementary and middle grades.
Notes
|
|
symbols. Other students who gave the same incorrect answer drew a diagram showing six students and one professor and seemed to think of S and P as units of measure rather than variables. They thought it just as sensible to write 6S=P as to write 12 in.=1 ft. |
|
35. |
Rosnick and Clement, 1980. |
|
36. |
Kaput and Sims-Knight, 1983. |
|
37. |
Soloway, Lochhead, and Clement, 1982. |
|
38. |
Sutherland and Rojano, 1993. |
|
39. |
Sutherland, 1993. |
|
40. |
Kalchman, Moss, and Cass, 2001; Koedinger, Anderson, Hadley, and Mark, 1997. |
|
41. |
Sutherland, 1993. |
|
42. |
For example, Davis and Pobjoy, 1995; Sutherland, Jinich, Mochón, Molyneux, and Rojano, 1996. |
|
43. |
Koedinger, Anderson, Hadley, and Mark, 1997; Moreno, Rojano, Bonilla, and Perrusquia, 1999; Rojano, 1999. |
|
44. |
Koedinger and Anderson, 1998. |
|
45. |
Koedinger, Anderson, Hadley, and Mark, 1997. |
|
46. |
For example, Borba and Confrey, 1996. |
|
47. |
Fey, 1989b; Heid, 1988; Heid, Sheets, Matras, and Menasian, 1988; O’Callaghan, 1998. |
|
48. |
Heid, Sheets, Matras, and Menasian, 1988, p. 2. |
|
49. |
Heid, 1988. |
|
50. |
Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000. |
|
51. |
Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000. |
|
52. |
Streun, Harskamp, and Suhre, 2000. |
|
53. |
Kieran, 1982, 1984. |
|
54. |
Chaiklin and Lesgold, 1984. |
|
55. |
Collis, 1975. |
|
56. |
Whitman, 1976. |
|
57. |
Kieran, 1988. |
|
58. |
Kieran and Sfard, 1999. |
|
59. |
Linchevski and Vinner, 1990. |
|
60. |
Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000, p. 357. |
|
61. |
Kieran and Sfard, 1999; Thompson and Thompson, 1987. |
|
62. |
Usiskin, 1998, pp. 17–18. |
|
63. |
Fey, 1989a, pp. 206–207. |
|
64. |
Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000. |
|
65. |
Huntley, Rasmussen, Villarubi, Sangtong, and Fey, 2000, p. 357. |
|
66. |
Lee and Wheeler, 1987, p. 149. |
|
67. |
See “Building Blocks” in Chapter 3 for several other approaches to this problem. |
|
68. |
Arzarello, 1992; Swafford and Langrall, 2000. |
|
69. |
See, for example, Heid, Sheets, Matras, and Menasian, 1988. |
|
70. |
Arcavi, 1994. |
|
71. |
Edwards, 1990. |
|
171. |
Tversky and Kahneman, 1974. See Shaughnessy, 1992, pp. 470–473, for a discussion. |
|
172. |
Fey, 1989a, 1989b. |
|
173. |
See, for example, Phillips, Gardella, Kelly, and Stewart, 1994. |
References
Acredolo, C., O’Connor, J., Banks, L., & Horobin, K. (1989). Students’ ability to make probability estimates: Skills revealed through application of Anderson’s functional measurement methodology. Student Development, 60, 933–945.
Amir, G.S., & Williams, J.S. (1999). Cultural influences on children’s probabilistic thinking. Journal of Mathematical Behavior, 18, 85–107.
Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14(3), 24–35.
Arzarello, F. (1992). Pre-algebraic problem solving. In J.P.Ponte, J.F.Matos, J.M. Matos, & D.Fernandes (Eds.), Mathematical problem solving and new information technologies (NATO ASI Series, vol. 89, pp. 155–166). Berlin: Springer-Verlag.
Ball, D.L., & Bass, H. (1999, June). What counts as an explanation in math class? Interdisciplinary analysis of teaching. Paper presented at the mathematics education seminar series of the Weizmann Institute of Science, Rehovot, Israel.
Ball, D.L., & Bass, H. (2001). What mathematical knowledge is entailed in teaching children to reason mathematically? In National Research Council, Knowing and learning mathematics for teaching: Proceedings of a workshop (pp. 26–34). Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/10050.html. [July 10, 2001].
Battista, M.T. (1999). Fifth graders’ enumeration of cubes in 3D arrays: Conceptual progress in an inquiry classroom. Journal for Research in Mathematics Education, 30, 417–448.
Battista, M.T., & Clements, D.H. (1998). Students’ understanding of three-dimensional cube arrays: Findings from a research and curriculum development project. In R. Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 227–248). Mahwah, NJ: Erlbaum.
Battista, M.T., Clements, D.H., Arnoff, J., Battista, K., & Van Auken Borrow, C. (1998). Students’ spatial structuring of 2D arrays of squares. Journal for Research in Mathematics Education, 29, 503–532.
Beaton, A.E., Mullis, I.V.S., Martin, M.O., Gonzalez, E.J., Kelly, D.L., & Smith, T.A. (1996). Mathematics achievement in the middle school years: IEA’s Third International Mathematics and Science Study (TIMSS). Chestnut Hill, MA: Boston College, Center for the Study of Testing, Evaluation, and Educational Policy. Available: http:// www.timss.org/timss1995i/MathB.html. [July 10, 2001].
Bednarz, N., Radford, L., & Janvier, B. (1995). Algebra as a problem-solving tool: One unknown or several unknowns? In L.Meira & D.Carraher (Eds.), Proceedings of the nineteenth international conference for the Psychology of Mathematics Education (vol. 3, pp. 160–167). Recife, Brazil: Federal University of Pernambuco. (ERIC Document Reproduction Service No. ED 411 136).
Behr, M., Erlwanger, S., & Nichols, E. (1980). How children view the equal sign. Mathematics Teaching, 92, 13–15.
Bell, A. (1995). Purpose in school algebra. In C.Kieran (Ed.), New perspectives on school algebra: Papers and discussions of the ICME-7 Algebra Working Group [Special issue]. Journal of Mathematical Behavior, 14, 41–73.
Berg, C.A., & Phillips, D.G. (1994). An investigation of the relationship between logical thinking structures and the ability to construct and interpret line graphs. Journal of Research in Science Teaching, 31, 323–344.
Blanton, M., & Kaput, J. (2000). Characterizing generative and self-sustaining teacher change in a classroom practice that promotes students’ algebraic thinking. In T. Nakahara & M.Koyama (Eds.), Proceedings of the Twenty-fourth International Conference for the Psychology of Mathematics Education (vol. 1, p. 144). Hiroshima, Japan: PME Program Committee.
Bochner, S. (1966). The role of mathematics in the rise of science. Princeton, NJ: Princeton University Press.
Boero, P. (1993). About the transformation function of the algebraic code. In R.Sutherland (Ed.), Algebraic processes and the role of symbolism (pp. 55–62). London: University of London, Institute of Education.
Booth, L.R. (1984). Algebra: Children’s strategies and errors. Windsor, UK: NFER-Nelson.
Borba, M.C., & Confrey, J. (1996). A student’s construction of transformations of functions in a multiple representational environment. Educational Studies in Mathematics, 31, 319–337.
Borovcnik, M.G., & Bentz, H.J. (1991). Empirical research in understanding probability. In R.Kapadia & M.Borovcnik (Eds.), Chance encounters: Probability in education (pp. 73–105). Dordrecht, The Netherlands: Kluwer.
Bright, G.W., & Friel, S.N. (1998). Graphical representations: Helping students interpret data. In S.P.Lajoie (Ed.), Reflections on statistics: Learning, teaching, and assessment in grades K-12 (pp. 63–88). Mahwah, NJ: Erlbaum.
Brown, C.A., Carpenter, T.P., Kouba, V.L., Lindquist, M.M., Silver, E.A., & Swafford, J. O. (1988). Secondary school results for the fourth NAEP mathematics assessment: Discrete mathematics, data organization and interpretation, measurement, number and operations. Mathematics Teacher, 81, 241–248.
Burger, W., & Shaughnessy, M. (1986). Characterizing the van Hiele levels of development in geometry. Journal for Research in Mathematics Education, 17, 31–48.
Carpenter, T.P. (1975). Measurement concepts of first- and second-grade students. Journal for Research in Mathematics Education, 6, 3–13.
Carpenter, T.P., Coburn, T., Reys, R., & Wilson, J. (1976). Notes from National Assessment: Recognizing and naming solids. Arithmetic Teacher, 23, 62–66.
Carpenter, T.P., Corbitt, M.K., Kepner, H.S., Jr., Lindquist, M.M., & Reys, R.E. (1981). Results from the second mathematics assessment of the National Assessment of Educational Progress. Reston, VA: National Council of Teachers of Mathematics.
Carpenter, T.P., & Levi, L. (1999, April). Developing conceptions of algebraic reasoning in the primary grades. Paper presented at the meeting of the American Educational Research Association, Montreal.
Carpenter, T.P., & Lewis, R. (1976). The development of the concept of a standard unit of measure in young children. Journal for Research in Mathematics Education, 7, 53–64.
Carraher, D., Brizuela, B., & Schliemann, A. (2000). Bringing out the algebraic character of arithmetic: Instantiating variables in addition and subtraction. In T.Nakahara &
M.Koyama (Eds.), Proceedings of the Twenty-fourth International Conference for the Psychology of Mathematics Education (vol. 2, pp. 145–152). Hiroshima, Japan: PME Program Committee.
Carry, L.R., Lewis, C., & Bernard, J. (1980). Psychology of equation solving: An information processing study (Final Technical Report). Austin: University of Texas at Austin, Department of Curriculum and Instruction. (ERIC Document Reproduction Service No. ED 186 243).
Chaiklin, S., & Lesgold, S. (1984, April). Prealgebra students’ knowledge of algebraic tasks with arithmetic expressions. Paper presented at the meeting of the American Educational Research Association, New Orleans. (ERIC Document Reproduction Service No. ED 247 147).
Clement, J. (1982). Algebra word problem solutions: Thought processes underlying a common misconception. Journal for Research in Mathematics Education, 13, 16–30.
Clement, J., Lochhead, J., & Monk, G. (1981). Translation difficulties in learning mathematics. American Mathematical Monthly, 88, 286–290.
Clements, D.H. (2000). Geometric and spatial thinking in early childhood education. Paper presented at the meeting of the National Council of Teachers of Mathematics, San Francisco.
Clements, D.H., & Battista, M.T. (in press). Logo and geometry (Journal for Research in Mathematics Education Monograph Series). Reston, VA: National Council of Teachers of Mathematics.
Clements, D.H, & Battista, M.T. (1990). The effects of Logo on children’s conceptualizations of angle and polygons. Journal for Research in Mathematics Education, 21, 356–371.
Clements, D.H., & Battista, M.T. (1989). Learning of geometric concepts in a Logo environment. Journal for Research in Mathematics Education, 20, 450–467.
Clements, D.H., Battista, M.T., & Sarama, J. (1998). Development of geometric and measurement ideas. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 201–225). Mahwah, NJ: Erlbaum.
Clements, D.H., Battista, M.T., Sarama, J., & Swaminathan, S. (1996). Development of turn and turn measurement concepts in a computer-based instructional unit. Educational Studies in Mathematics, 30, 313–337.
Clements, D.H., Battista, M.T., Sarama, J., & Swaminathan, S. (1997). Development of students’ spatial thinking in a unit on geometric motions and area. Elementary School Journal, 98, 171–186.
Clements, D.H., Swaminathan, S., Hannibal, M.A.Z., & Sarama, J. (1999). Young children’s concepts of shape. Journal for Research in Mathematics Education, 30, 192– 212.
Collis, K.F. (1975). The development of formal reasoning. Newcastle, Australia: University of Newcastle.
Confrey, J. (1992, April). First graders’ understanding of similarity. Paper presented at the meeting of the American Educational Research Association, San Francisco.
Confrey, J. (1994). Splitting, similarity, and the rate of change: New approaches to multiplication and exponential functions. In G.Harel & J.Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 291–330). Albany: State University of New York Press.
Confrey, J., & Smith, E. (1994). Exponential functions, rates of change, and the multiplicative unit. Educational Studies in Mathematics, 26, 135–164.
Confrey, J., & Smith, E. (1995). Splitting, covariation, and their role in the development of exponential functions. Journal for Research in Mathematics Education, 26, 66–86.
Crosby, A.W. (1997). The measure of reality. Cambridge: Cambridge University Press.
Curcio, F.R. (1987). Comprehension of mathematical relationships expressed in graphs. Journal for Research in Mathematics Education, 18, 382–393.
Curcio, F.R. (1989). Developing graph comprehension. Reston, VA: National Council of Teachers of Mathematics.
Davis, G.E., & Pobjoy, M. (1995). Spreadsheets as constructivist tools for the learning and teaching of mathematics. In O.P.Ahuja (Ed.), Quality mathematics education in developing countries (pp. 25–56). New Delhi: UBSPD.
Del Grande, J.J. (1987). Can grade two children’s spatial perception be improved by inserting a transformation geometry component into their mathematics program? (Doctoral dissertation, University of Toronto, 1986). Dissertation Abstracts International, 47(10), 3689A.
Edwards, E.L., Jr. (Ed.). (1990). Algebra for everyone. Reston, VA: National Council of Teachers of Mathematics.
Ellis, S., Siegler, R.S., & Van Voorhis, F.E. (in preparation). Developmental changes in children’s understanding of measurement procedures and principles.
English, L.D. (1991). Young children’s combinatoric strategies. Educational Studies in Mathematics, 22, 451–474.
English, L.D. (1993). Children’s strategies for solving two- and three-stage combinatorial problems. Journal for Research in Mathematics Education, 24, 255–273.
Falk, R. (1983). Children’s choice behaviour in probabilistic situations. In D.R.Grey, P. Holmes, V.Barnett, & G.M.Constable (Eds.), Proceedings of the First International Conference on Teaching Statistics (vol. 2, pp. 714–716). Sheffield, UK: University of Sheffield. (ERIC Document Reproduction Service No. ED 262 977).
Fey, J. (1989a). Technology and mathematics education: A survey of recent developments and important problems. Educational Studies in Mathematics, 20, 237–272.
Fey, J.T. (1989b). School algebra for the year 2000. In S.Wagner & C.Kieran (Eds.), Research issues in the learning and teaching of algebra (pp. 199–213). Reston, VA: National Council of Teachers of Mathematics; Hillsdale, NJ: Erlbaum.
Fey, J.T., Heid, M.K., with Good, R.A., Sheets, C., Blume, G.W., & Zbiek, R.M. (1999). Concepts in algebra: A technological approach. Chicago: Everyday Learning.
Fischbein, E., & Gazit, A. (1984). Does the teaching of probability improve probabilistic intuitions? Educational Studies in Mathematics, 15, 1–24.
Fischbein, E., & Schnarch, D. (1997). The evolution with age of probabilistic intuitively based misconceptions . Journal for Research in Mathematics Education, 28, 96–105.
Fischbein, E., Barbat, I., & Minzat, I. (1971). Intuitions primaires et intuitions secondaires dans l’initiation aux probabilities [Primary and secondary intuitions in introductory probability]. Educational Studies in Mathematics, 4, 264–280.
Fischbein, E., Nello, M.S., & Marino, M.S. (1991). Factors affecting probabilistic judgments in students and adolescents. Educational Studies in Mathematics, 22, 523– 549.
Fisher, K.M. (1988). The students and professors problem revisited. Journal for Research in Mathematics Education, 19, 260–262.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht, The Netherlands: Reidel.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, The Netherlands: Reidel.
Friel, S.N., Bright, G.W., Frierson, D., & Kader, G. (1997). A framework for assessing knowledge and learning in statistics (K-8). In I.Gal & J B.Garfield (Eds.), The assessment challenge in statistics education (pp. 55–64). Amsterdam, The Netherlands: International Statistical Institute.
Fuys, D., Geddes, D., & Tischler, R. (1988). The van Hiele model of thinking in geometry among adolescents (Journal for Research in Mathematics Education Monograph No. 3). Reston, VA: National Council of Teachers of Mathematics.
Gagatsis, A., & Patronis, T. (1990). Using geometrical models in a process of reflective thinking in learning and teaching mathematics. Educational Studies in Mathematics, 21, 29–54.
Genkins, E.F. (1975). The concept of bilateral symmetry in young children. In M.F. Rosskopf (Ed.), Children’s mathematical concepts: Six Piagetian studies in mathematics education (pp 5–43). New York: Teachers College Press.
Gravemeijer, K.P. (1998). From a different perspective: Building on students’ informal knowledge. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 45–66). Mahwah, NJ: Erlbaum.
Green, D.R. (1983). A survey of probability concepts in 3000 pupils aged 11–16 years. In D.R.Grey, P.Holmes, V.Barnett, & G.M.Constable (Eds.), Proceedings of the First International Conference on Teaching Statistics (vol. 2, pp. 766–783). Sheffield, UK: University of Sheffield. (ERIC Document Reproduction Service No. ED 262 977).
Greeno, J.G. (1982, March). A cognitive learning analysis of algebra. Paper presented at the meeting of the American Educational Research Association, Boston.
Gutiérrez, A., Jaime, A., & Fortuny, J.M. (1991). An alternative paradigm to evaluate the acquisition of the van Hiele levels. Journal for Research in Mathematics Education, 22, 237–251.
Heid, M.K. (1988). “Algebra with Computers”: A description and an evaluation of student performance and attitudes (Report submitted to the State College Area School District Board of Education). State College: Pennsylvania State University.
Heid, M.K. (1990). Uses of technology in prealgebra and beginning algebra. Mathematics Teacher, 83, 194–198.
Heid, M.K., Sheets, C., Matras, M.A., & Menasian, J. (1988, April). Classroom and computer lab interaction in a computer-intensive algebra curriculum. Paper presented at the meeting of the American Educational Research Association, New Orleans.
Henderson, D.W. (1996). Experiencing geometry on plane and sphere. Upper Saddle River, NJ: Prentice Hall.
Hiebert, J. (1981a). Cognitive development and learning linear measurement. Journal for Research in Mathematics Education, 12, 197–211.
Hiebert, J. (1981b). Units of measure: Results and implications from national assessment. Arithmetic Teacher, 28, 38–43.
Hiebert, J. (1984). Why do some children have trouble learning measurement concepts? Arithmetic Teacher, 31, 19–24.
Huntley, M.A., Rasmussen, C.L., Villarubi, R.S., Sangtong, J., & Fey, J.T. (2000). Effects of standards-based mathematics education: A study of the Core-Plus Mathematics Project algebra and functions strand. Journal for Research in Mathematics Education, 31, 328–361.
Jacobson, C., & Lehrer, R. (2000). Teacher appropriation and student learning of geometry through design. Journal for Research in Mathematics Education, 31, 71–88.
Jones, G.A. (1975). The performances of first, second, and third grade children on five concepts of probability and the effects of grade, I.Q., and embodiments on their performances (Doctoral dissertation, Indiana University, 1974). Dissertation Abstracts International, 35(07), 4272A–4273A.
Jones, G.A., Langrall, C.W., Thornton, C.A., & Mogill, A.T. (1997). A framework for assessing and nurturing young children’s thinking in probability. Educational Studies in Mathematics, 32, 101–125.
Jones, G.A., Langrall, C.W., Thornton, C.A., & Mogill, A.T. (1999). Students’ probabilistic thinking in instruction. Journal for Research in Mathematics Education, 30, 487–519.
Jones, G.A., Thornton, C.A., Langrall, C.W., & Tarr, J.E. (1999). Understanding students’ probability reasoning. In L.V.Stiff & F.R.Curcio (Eds.), Developing mathematical reasoning in grades K-12 (1999 Yearbook of the National Council of Teachers of Mathematics, pp. 146–155). Reston, VA: NCTM.
Jones, G.A., Thornton, C.A., Langrall, C.W., Mooney, E.S., Perry, B., & Putt, I.J. (2000). A framework for characterizing children’s statistical thinking. Mathematical Thinking and Learning, 2, 269–307.
Jones, G.A., Thornton, C.A., Langrall, C.W., Mooney, E.S., Wares, A., Perry, B., & Putt, I.A. (1999). Using students’ statistical thinking to inform instruction. Paper presented at the research presession of the meeting of the National Council of Teachers of Mathematics, San Francisco.
Kalchman, N., Moss, J., & Case, R. (2001). Psychological models for the development of mathematical understanding: Rational numbers and functions. In S.Carver & D. Klahr (Eds.), Cognition and instruction: Twenty-five years of progress (pp. 1–38). Mahwah, NJ: Erlbaum.
Kaput, J.J. (1994). Democratizing access to calculus: New roads to old roots. In A.H. Schoenfeld (Ed.), Mathematical thinking and problem solving (pp. 77–156). Hillsdale, NJ: Erlbaum.
Kaput, J.J. (1995). A research base supporting long term algebra reform? In D.T.Owens, M.K.Reed, & G.M.Millsaps (Eds.), Proceedings of the Seventeenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 71–94). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 389 539).
Kaput, J., & Sims-Knight, J. (1983). Errors in translations to algebraic equations: Roots and implications. Focus on Learning Problems in Mathematics, 5(3), 63–78.
Kay, C.S. (1987). Is a square a rectangle? The development of first-grade students’ understanding of quadrilaterals with implications for the Van Hiele theory of the
development of geometric thought (Doctoral dissertation, University of Georgia, 1986). Dissertation Abstracts International, 47(08), 2934A.
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12, 317–326.
Kieran, C. (1982, March). The learning of algebra: A teaching experiment. Paper presented at the meeting of the American Educational Research Association, New York. (ERIC Document Reproduction Service No. ED 216 884).
Kieran, C. (1983). Relationships between novices’ views of algebraic letters and their use of symmetric and asymmetric equation-solving procedures. In J.C.Bergeron & N. Herscovics (Eds.), Proceedings of the Fifth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 161– 168). Montreal: University of Montreal. (ERIC Document Reproduction Service No. ED 289 688).
Kieran, C. (1984). A comparison between novice and more-expert algebra students on tasks dealing with the equivalence of equations. In J.M.Moser (Ed.), Proceedings of the Sixth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 83–91). Madison: University of Wisconsin. (ERIC Document Reproduction Service No. ED 253 432).
Kieran, C. (1988). Two different approaches among algebra learners. In A.F.Coxford (Ed.), The ideas of algebra, K-12 (1988 Yearbook of the National Council of Teachers of Mathematics, pp. 91–96). Reston, VA: NCTM.
Kieran, C. (1992). The learning and teaching of school algebra. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 390–419). New York: Macmillan.
Kieran, C. (1996). The changing face of school algebra. In C.Alsina, J.Alvarez, B.Hodgson, C.Laborde, & A.Pérez (Eds.), Eighth International Congress on Mathematical Education: Selected lectures (pp. 271–290). Seville: S.A.E.M.Thales.
Kieran, C., & Sfard, A. (1999). Seeing through symbols: The case of equivalent expressions. Focus on Learning Problems in Mathematics, 21(1), 1–17.
Kirshner, D. (1989). The visual syntax of algebra. Journal for Research in Mathematics Education, 20, 274–287.
Kirshner, D., & Awtry, T. (in press). The visual salience of algebra transformational rules.
Koedinger, K.R., & Anderson, J.R. (1998). Illustrating principled design: The early evolution of a cognitive tutor for algebra symbolization. Interactive Learning Environments, 5, 161–180.
Koedinger, K.R., Anderson, J.R., Hadley, W.H., & Mark, M.A. (1997). Intelligent tutoring goes to school in the big city. International Journal of Artificial Intelligence in Education , 8, 30–43.
Küchemann, D. (1978). Children’s understanding of numerical variables. Mathematics in School, 7(4), 23–26.
Küchemann, D. (1981). Algebra. In K.M.Hart (Ed.), Children’s understanding of mathematics: 11–16 (pp. 102–119). London: John Murray.
Lee, L., & Wheeler, D. (1987). Algebraic thinking in high school students: Their conceptions of generalisation and justification (Research report). Montreal: Concordia University, Mathematics Department.
Lehrer, R., & Chazan, D. (Eds.). (1998). Designing learning environments for developing understanding of geometry and space. Mahwah, NJ: Erlbaum.
Lehrer, R., Jacobson, C., Kemeny, V., & Strom, D. (1999). Building on children’s intuitions to develop mathematical understanding of space. In E.Fennema & T.R.Romberg (Eds.), Classrooms that promote understanding (pp. 63–87). Mahwah, NJ: Erlbaum.
Lehrer, R., Jacobson, C., Thoyre, G., Demeny, V., Strom, D., Horvath, J., Gance, S., & Koehler, M. (1998). Developing understanding of geometry and space in the primary grades. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 169–200). Mahwah, NJ: Erlbaum.
Lehrer, R., Jenkins, M., & Osana, H. (1998). Longitudinal study of children’s reasoning about space and geometry. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 137–167). Mahwah, NJ: Erlbaum.
Lehrer, R., Randle, L., & Sancilio, L. (1989). Learning pre-proof geometry with Logo. Cognition and Instruction, 6, 159–184.
Lehrer, R., & Schauble, L. (2000a). Inventing data structures for representational purposes: Elementary grade students’ classification models. Mathematical Thinking and Learning, 2, 49–72.
Lehrer, R., & Schauble, L. (2000b). Modeling in mathematics and science. In R.Glaser (Ed.), Advances in instructional psychology (vol. 5, pp. 101–159). Mahwah, NJ: Erlbaum.
Lehrer, R., & Schauble, L. (2000c). The development of model-based reasoning. Journal of Applied Developmental Psychology, 21(1), 39–48.
Lehrer, R., Schauble, L., Strom, D., & Pligge, M. (2001). Similarity of form and substance: Modeling material kind. In S.Carver & D.Klahr (Eds.), Cognition and instruction: Twenty-five years of progress (pp. 39–74). Mahwah, NJ: Erlbaum.
Linchevski, L., & Vinner, S. (1990). Embedded figures and the structures of algebraic expressions. In G.Booker, P.Cobb, & T.N.de Mendicuti (Eds.), Proceedings of the Fourteenth International Conference for the Psychology of Mathematics Education (vol. 2, pp. 85–92). Oaxtepec, Mexico: PME Program Committee. (ERIC Document Reproduction Service No. ED 411 138).
Lindquist, M. (1989). The measurement standards. Arithmetic Teacher, 37, 22–26.
Lochhead, J. (1980). Faculty interpretations of simple algebraic statements: The professor’s side of the equation. Journal of Mathematical Behavior, 3, 29–37.
MacGregor, M., & Stacey, K. (1993). Cognitive models underlying students’ formulation of simple linear equations. Journal for Research in Mathematics Education, 24, 217–232.
Mason, J. (1996). Expressing generality and roots of algebra. In N.Bednarz, C.Kieran, & L.Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 65–86). Dordrecht, The Netherlands: Kluwer.
Mason, J., Graham, A., Pimm, D., & Gowar, N. (1985). Routes to/roots of algebra. Milton Keynes, UK: Open University Press.
Matos, J.M.L.de. (1999). Cognitive models for the concept of angle (Unpublished doctoral dissertation, University of Georgia, 1999). Dissertation Abstracts International, 60(05), 1491A. Abstract available: http://wwwlib.umi.com/dissertations/fullcit/9928965. [July 10, 2001].
McClain, K., Cobb, P., Gravemeijer, K., & Estes, B. (1999). Developing mathematical reasoning within the context of measurement. In L.V.Stiff & F.R.Curcio (Eds.),
Developing mathematical reasoning in grades K-12 (1999 Yearbook of the National Council of Teachers of Mathematics, pp. 93–106). Reston, VA: NCTM.
Metz, K.E. (1997). Dimensions in the assessment of students’ understanding and application of chance. In I.Gal & J.B.Garfield (Eds.), The assessment challenge in statistics education (pp. 223–238). Amsterdam, The Netherlands: International Statistical Institute.
Metz, K.E. (1998). Emergent ideas of chance and probability in primary grade children. In S.P.Lajoie (Ed.) Reflections on statistics: Learning, teaching, and assessment in grades K-12 (pp. 149–174). Mahwah, NJ: Erlbaum.
Mevarech, Z.R., & Kramarsky, B. (1997). From verbal descriptions to graphic representations: Stability and change in students’ alternative conceptions. Educational Studies in Mathematics, 32, 229–263.
Middleton, J., & Corbett, R. (1998). Sixth-grade students’ conceptions of stability in engineering contexts. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 249–265). Mahwah, NJ: Erlbaum.
Miller, K.F., & Baillargeon, R. (1990). Length and distance: Do preschoolers think that occlusion brings things together? Developmental Psychology, 26, 103–114.
Mitchell, J.H., Hawkins, E.F., Jakwerth, P.M., Stancavage, R.B., & Dossey, J.A. (1999). Student work and teacher practices in mathematics (NCES 1999–453). Washington, DC: National Center for Education Statistics. Available: http://nces.ed.gov/spider/webspider/1999453.shtml. [July 10, 2001].
Mitchelmore, M.C. (1993). The development of pre-angle concepts. In A.Baturo & L. Harris (Eds.), New directions in geometry education: Proceedings of the third annual conference on Mathematics Teaching and Learning (pp. 87–93). Brisbane, Australia: Centre for Mathematics and Science Education, Queensland University of Technology.
Mitchelmore, M.C. (1998). Young students’ concepts of turning and angle. Cognition and Instruction, 16, 265–284.
Mitchelmore, M.C., & White, P. (2000). Development of angle concepts by progressive abstraction and generalisation. Educational Studies in Mathematics, 41, 209–238.
Mokros, J., & Russell, S.J. (1995). Children’s concepts of average and representativeness. Journal for Research in Mathematics Education, 26, 20–39.
Mooney, E.S. (1992). Development of a middle school statistical thinking framework (Doctoral dissertation, Illinois State University, 1992). Dissertation Abstracts International, 60(04), 1056A.
Moore, D.S. (1997). Statistics: Concepts and controversies (4th ed.). New York: Freeman.
Moreno, L., Rojano, T., Bonilla, E., & Perrusquia, E. (1999). The incorporation of new technologies to school culture: The teaching of mathematics in secondary school. In F.Hitt & M.Santos (Eds.), Proceedings of the Twenty-first Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 2, pp. 827–832). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 433 998)
Mullis, I.V. S., Martin, M.O., Beaton, A.E., Gonzalez, E.J., Kelly, D.L., & Smith, T.A. (1997). Mathematics achievement in the primary school years: IEA’s Third International Mathematics and Science Study (TIMSS). Chestnut Hill, MA: Boston College. Available: http://www.timss.org/timss1995i/Achievement.html. [July 10, 2001].
National Council of Teachers of Mathematics. (1997). A framework for constructing a vision of algebra: A discussion document. Reston, VA: National Council of Teachers of Mathematics.
Nhouyvanisvong, A. (2001). Enhancing mathematical competence and understanding: Using open-ended problems and informal strategies (Unpublished doctoral dissertation, Carnegie Mellon University, 1999). Dissertation Abstracts International, 61, 5010B.
Nieuwoudt, H.D., & van Niekerk, R. (1997, March). The spatial competence of young children through the development of solids. Paper presented at the meeting of the American Educational Research Association, Chicago.
Noss, R., Hoyles, C., & Healy, L. (1997). The construction of mathematical meanings: Connecting the visual with the symbolic. Educational Studies in Mathematics, 33, 203– 233.
O’Callaghan, B.R. (1998). Computer-intensive algebra and students’ conceptual knowledge of functions. Journal for Research in Mathematics Education, 29, 21–40.
Peak, L. (1996). Pursuing excellence: A study of U.S. eighth-grade mathematics and science teaching, learning, curriculum, and achievement in an international context. Washington, DC: National Center for Educational Statistics. Available: http://nces.ed.gov/spider/webspider/97198.shtml. [July 10, 2001].
Penner, E., & Lehrer, R. (2000). The shape of fairness. Teaching Children Mathematics, 7, 210–214.
Pereira-Mendoza, L., & Mellor, J. (1991). Students’ concepts of bar graphs: Some preliminary findings. In D.Vere-Jones (Ed.), Proceedings of the Third International Conference on Teaching Statistics (vol. 1, pp. 150–157). Amsterdam, The Netherlands: International Statistical Institute.
Perham, F. (1978). An investigation into the effect of instruction on the acquisition of transformation geometry concepts in first grade children and subsequent transfer to general spatial ability . In R.Lesh & D.Mierkiewicz (Eds.), Concerning the development of spatial and geometric concepts (pp. 229–241). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 159 062).
Perner, J. (1979). Discrepant results in experimental studies of young children’s understanding of probability. Child Development, 50, 1121–1127.
Phillips, E., with Gardella, T., Kelly, C., & Stewart, J. (1994). Patterns and functions (Curriculum and Evaluation Standards for School Mathematics Addenda Series, Grades 5–8, F.R.Curcio, Series Ed.). Reston, VA: National Council of Teachers of Mathematics.
Phillips, E.A., Smith, J.P., III, Star, J., & Herbel-Eisenmann, B. (1998). Algebra in the middle grades. New England Mathematics Journal, 30(2), 48–60.
Piaget, J., & Inhelder, B. (1956). The child’s conception of space. London: Routledge & Kegan Paul. (Original work published 1948).
Piaget, J., & Inhelder, B. (1975). The origin of the idea of chance in the child. London: Routledge & Kegan Paul. (Original work published 1951).
Piaget, J., Inhelder, B., & Szeminska, A. (1960). The child’s conception of geometry. New York: Basic Books.
Pimm, D. (1995). Symbols and meanings in school mathematics. London: Routledge.
Putt, I.J., Jones, G.A., Thornton, C.A., Perry, B., Langrall, C.W., & Mooney, E.S. (1999). Young students’ informal statistical knowledge. Teaching Statistics, 21, 74–77.
Radford, L. (1994). Moving through systems of mathematical knowledge: From algebra with a single unknown to algebra with two unknowns. In J.P.da Ponte & J.F.Matos (Eds.), Proceedings of the eighteenth international conference for the Psychology of Mathematics Education (vol. 4, pp.73–80). Lisbon, Portugal: PME Program Committee. (ERIC Document Reproduction Service No. ED 383 537).
Raghavan, K., Sartoris, M.L., & Glaser, R. (1998). Interconnecting science and mathematics concepts. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 267–295). Mahwah, NJ: Erlbaum.
Rojano, T. (1996). Developing algebraic aspects of problem solving within a spreadsheet environment. In N.Bednarz, C.Kieran, & L.Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 137–145). Dordrecht, The Netherlands: Kluwer.
Rojano, T. (1999, April). The potential of spreadsheets in the learning of algebra. Paper presented at the meeting of the American Educational Research Association, Montreal.
Rosnick, P. (1981). Some misconceptions concerning the concept of variable. Mathematics Teacher, 74, 418–420.
Rosnick, P., & Clement, J. (1980). Learning without understanding: The effect of tutoring strategies on algebra misconceptions. Journal of Mathematical Behavior, 3, 3–27.
Rosser, R.A., Ensing, S.S., Glider, P.J., & Lane, S. (1984). An information-processing analysis of children’s accuracy in predicting the appearance of rotated stimuli. Child Psychology Monographs, 110, 21–41.
Saenz-Ludlow, A., & Walgamuth, C. (1998). Third graders’ interpretations of equality and the equal symbol. Educational Studies in Mathematics, 35, 153–187.
Schliemann, A.D., Carraher, D.W., & Brizuela, B. (2000, April). From quantities to ratio, functions, and algebraic relations. Paper presented at the meeting of the American Educational Research Association, New Orleans.
Schroeder, T.L. (1988). Elementary school children’s use of strategy in playing microcomputer probability games. In R.Davidson & J.Swift (Eds.), Proceedings of the Second International Conference on Teaching Statistics (pp. 51–56). Victoria, BC: University of Victoria.
Schultz, K.A., & Austin, J.D. (1983). Directional effects in transformational tasks. Journal for Research in Mathematics Education, 14, 95–101.
Shaughnessy, J.M. (1992). Research in probability and statistics: Reflections and directions. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 465–494). New York: Macmillan.
Sims-Knight, J., & Kaput, J.J. (1983). Exploring difficulties in transformations between natural language and image-based representations and abstract symbols systems of mathematics. In D.Rogers & J.Sloboda (Eds.), The acquisition of symbolic skills (pp. 561–569). New York: Plenum.
Soloway, E., Lochhead, J., & Clement, J. 1982). Does computer programming enhance problem solving ability? Some positive evidence on algebra word problems. In R.J. Seidel , R.E.Anderson, & B.Hunter (Eds.), Computer literacy (pp. 171–185). New York: Academic Press.
Sophian, C., & Crosby, M.E. (1998, August). Ratios that even young children understand: The case of spatial proportions. Paper presented at the meeting of the Cognitive Science Society of Ireland, Dublin, Ireland.
Strauss, S., & Bichler, E. (1988). The development of children’s concepts of the arithmetic average. Journal for Research in Mathematics Education, 19, 64–80.
Streun, A.V., Harskamp, E., & Suhre, C. (2000). The effect of the graphic calculator on students’ solution approaches: A secondary analysis. Hiroshima Journal of Mathematics Education, 8, 27–10.
Sutherland, R. (1993). Symbolising through spreadsheets. Micromath, 10(1), 20–22.
Sutherland, R., & Rojano, T. (1993). A spreadsheet approach to solving algebra problems. Journal of Mathematical Behavior, 12, 353–383.
Sutherland, R., Jinich, E., Mochón, S., Molyneux, S., & Rojano, T. (1996). Mexican/British project on the role of spreadsheets within school-based mathematical practices (Final report to the Spencer Foundation, Grant No. B-1493). Chicago: Spencer Foundation.
Swafford, J.O., & Langrall, C. (2000). Grade-six students’ preinstructional use of equations to describe and represent problem situations. Journal for Research in Mathematics Educational, 31, 89–112.
Tarr, J.E., & Jones, G.A. (1997). A framework for assessing middle school students’ thinking in conditional probability and independence. Mathematics Education Research Journal, 9, 39–59.
Thompson, A.G., Philipp, R.A., Thompson, P.W., & Boyd, B.A. (1994). Calculational and conceptual orientations in teaching mathematics. In D.B.Aichele & A.F.Coxford (Eds.), Professional development of teachers of mathematics (1994 Yearbook of the National Council of Teachers of Mathematics, pp. 79–92). Reston, VA: NCTM.
Thompson, P., & Thompson, A. (1987). Computer presentations of structure in algebra. In J.C.Bergeron, N.Herscovics, & C.Kieran (Eds.), Proceedings of the Eleventh International Conference for the Psychology of Mathematics Education (vol. 1, pp. 248–254). Montreal: University of Montreal. (ERIC Document Reproduction Service No. ED 383 532 ).
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185, 1124–1131.
Usiskin, Z. (1988). Conceptions of school algebra and uses of variable. In A.F.Coxford & A.P. Shulte (Eds.) The ideas of algebra, K-12 (1988 Yearbook of the National Council of Teachers of Mathematics, pp. 8–19). Reston, VA: NCTM.
Usiskin, Z. (1998). Paper-and-pencil algorithms in a calculator-and-computer age. In L. J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 7–20). Reston, VA: NCTM.
Van Hiele, P.M. (1984a). A child’s thought and geometry. In D.Fuys, D.Geddes, & R. Tischler, English translation of selected writings of Dina van Hiele-Geldof and P.M.van Hiele (pp 243–252). Brooklyn: Brooklyn College. (Original work published 1959).
Van Hiele, P.M. (1984b). The problem of insight in connection with school children’s insight into the subject matter of geometry. In D.Fuys, D.Geddes, & R.Tischler, English translation of selected writings of Dina van Hiele-Geldof and P.M.van Hiele (pp. 237–241 ). Brooklyn: Brooklyn College. (Original work published 1957).
Van Hiele-Geldof, D. (1984). The didactics of geometry in the lowest class of secondary school. In D.Fuys, D.Geddes, & R.Tischler, English translation of selected writings of Dina Van Hiele-Geldof and P.M.Van Hiele (pp. 1–214). Brooklyn: Brooklyn College. (Original work published 1957).
Vergnaud, G., Benhadj, J., & Dussouet, A. (1979). La coordination de l’enseignement des mathématiques entre le cours moyen 2e année et la classe de sixième [The coordination of the teaching of mathematics between the fifth and sixth grades]. Paris: Institut National de Recherche Pédagogique.
Vurpillot, E. (1976). The visual world of the child. New York: International Universities Press.
Wagner, S., Rachlin, S.L., & Jensen, R.J. (1984). Algebra Learning Project: Final report. Athens: University of Georgia, Department of Mathematics Education.
Watson, J.M. (1997). Assessing statistical thinking using the media. In I.Gal & J.B. Garfield (Eds.), The assessment challenge in statistics education (pp. 123–138). Amsterdam, The Netherlands: International Statistical Institute.
Watson, J.M., Collis, K.F., & Moritz, J.B. (1997). The development of chance measurement. Mathematics Education Research Journal, 9, 60–82.
Watt, D.L. (1998). Mapping the classroom using a CAD program: Geometry as applied mathematics. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 419–438). Mahwah, NJ: Erlbaum.
Wenger, R.H. (1987). Cognitive science and algebra learning. In A.H.Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 217–251). Hillsdale: NJ: Erlbaum.
Wertsch, J.V. (1998). Mind as action. New York: Oxford University Press.
Whitman, B.S. (1976). Intuitive equation solving skills and the effects on them of formal techniques of equation solving (Doctoral dissertation, Florida State University, 1975). Dissertation Abstracts International, 36(08), 5180A. (University Microfilms No. 76–2720)
Williford, H.J. (1972). A study of transformational geometry instruction in the primary grades. Journal for Research in Mathematics Education, 3, 260–271.
Zawojewski, J.S., & Heckman, D.S. (1997). What do students know about data analysis, statistics, and probability? In P.A.Kenney & E.A.Silver (Eds.), Results from the sixth mathematics assessment of the National Assessment of Educational Progress (pp. 195–223). Reston, VA: National Council of Teachers of Mathematics.
Zech, L., Vye, N.J., Bransford, J., Goldman, S., Barron, B.J., Schwartz, D.L., Kisst-Hackett, R., Mayfield-Stewart, C., & the Cognition and Technology Group. (1998). An introduction to geometry through anchored instruction. In R.Lehrer & D.Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 439–463). Mahwah, NJ: Erlbaum.



























































