9
TEACHING FOR MATHEMATICAL PROFICIENCY
Previous chapters have described mathematical proficiency as the integrated attainment of conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition. Effective forms of instruction attend to all these strands of mathematical proficiency. In this chapter we turn from considering what there is to learn and what is known about learning to an examination of teaching that promotes learning over time so that it yields mathematical proficiency.
Instruction as Interaction
Our examination of teaching focuses not just on what teachers do but also on the interactions among teachers and students around content.1 Rather than considering only the teacher and what the teacher does as a source of teaching and learning, we view the teaching and learning of mathematics as the product of interactions among the teacher, the students, and the mathematics in an instructional triangle (see Box 9–1).
We view the teaching and learning of mathematics as the product of interactions among the teacher, the students, and the mathematics.
Certainly the knowledge, beliefs, decisions, and actions of teachers affect what is taught and ultimately learned. But students’ expectations, knowledge, interests, and responses also play a crucial role in shaping what is taught and learned. For instruction to be effective, students must have, perceive, and use their opportunities to learn. The particular mathematical content and its representation in instructional tasks and curriculum materials also matter for teachers’ and students’ work, but teachers and students vary in their interpretations and uses of the same content and of the same curricular resources. Students interpret and respond differently to the same mathemati-
|
Box 9–1 The Instructional Triangle: instruction as the interaction Among Teachers, Students, and Mathematics, in Contexts 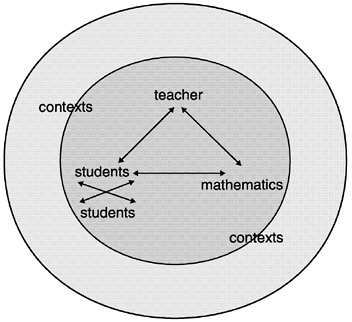 SOURCE: Adapted from Cohen and Ball, 1999, 2000, in press. |
cal task, ask different questions, and complete the work in different ways. Their interpretations and actions affect what becomes the enacted lesson. Teachers’ attention and responses to students further shape the course of instruction. Some teachers may not notice how students are interpreting the content, others may notice but not investigate further, and still others may notice and respond by reiterating their own interpretation.
Moreover, instruction takes place in contexts. By contexts we mean the wide range of environmental and situational elements that bear on instruction—for instance, educational policies, assessments of students and teachers,
school organizational structures, school leadership characteristics, the nature and organization of teachers’ work, and the social matrix in which the school is embedded. These matter principally as they permeate instruction—that is, whether and how they enter into the interactions among teachers, students, and content.2 Hence, what goes on in classrooms to promote the development of mathematical proficiency is best understood through an examination of how these elements—teachers, students, content—interact in contexts to produce teaching and learning.
Much debate centers on forms and approaches to teaching: “direct instruction” versus “inquiry,” “teacher centered” versus “student centered,” “traditional” versus “reform.” These labels make rhetorical distinctions that often miss the point regarding the quality of instruction. Our review of the research makes plain that the effectiveness of mathematics teaching and learning does not rest in simple labels. Rather, the quality of instruction is a function of teachers’ knowledge and use of mathematical content, teachers’ attention to and handling of students, and students’ engagement in and use of mathematical tasks. Moreover, effective teaching—teaching that fosters the development of mathematical proficiency over time—can take a variety of forms. To highlight this point, we use excerpts from four classroom lessons and analyze what we see going on in them in light of what we know from research on teaching.
Four Classroom Vignettes
The pedagogical challenge for teachers is to manage instruction in ways that help particular students develop mathematical proficiency. High-quality instruction, in whatever form it comes, focuses on important mathematical content, represented and developed with integrity. It takes sensitive account of students’ current knowledge and ways of thinking as well as ways in which those develop. Such instruction is effective with a range of students and over time develops the knowledge, skills, abilities, and inclinations that we term mathematical proficiency.
The four classroom vignettes we present below offer four distinct images of what mathematics instruction can look like. Each vignette configures differently the mathematical content and the roles and work of teachers and students in contexts; hence, each produces different opportunities for mathematics teaching and learning. Two points are important to interpreting and using these vignettes. First, to provide a close view, each vignette zooms in on an individual lesson. Effective instruction, however, depends on the
coherent connection over time among lessons designed collectively to achieve important mathematical goals. For example, some of these teachers may be attempting to develop students’ productive disposition toward mathematics and as mathematics learners, but it is difficult to pinpoint isolated attempts in a single lesson since that development takes place gradually—over months rather than minutes. Second, rather than seeking to argue that one of these lessons is “right,” our analysis probes the possibilities and the risks each affords. The instructional challenge in any approach to teaching and learning is to capitalize on its opportunities and ward off its pitfalls.
The first example (Box 9–2) is typical of much teaching that many American adults remember from their own experience in mathematics classes.3 Note how the teacher, Mr. Angelo, constructs the lesson in a way that structures the students’ path through the mathematics by tightly constraining both the content and his students’ encounters with it. The approach used by Mr. Angelo structures and focuses students’ attention on a specific aspect of the topic: multiplying by powers of 10. He has distilled the content into an integrated “rule” that his students can use for all instances of multiplication by powers of 10.
|
Box 9-2 Mr. Angelo— Teaching Eighth Graders About Multiplying by Powers of 10 After a conducting a short warm-up activity and checking a homework assignment that focused on multiplying by 10, Mr. Angelo announces that the class is going to work on multiplying by powers of 10. He is concerned that students tend to perform poorly on this topic on the spring tests given by the school district, and he wants to make sure that his students know what to do. He reviews briefly the idea of powers of 10 by showing that 100 equals 102, 1000 equals 103, and soon. Going to the overhead projector, he writes the following:
“Who knows the first one?” Mr. Angelo asks. “Luis?” “Forty,” replies Luis. Nodding, Mr. Angelo points to the second, “And this one?” Sonja near the front offers, “Forty-five hundred.” “That’s right—forty-five hundred,” affirms Mr. Angelo, and he writes the number on the overhead transparency. “And what about the last one?” he asks. “Forty-five thousand,” call out several students. |
|
Writing “45,000,” Mr. Angelo says, “Good, you are all seeing the trick. What is it? Who can say it?” Several hands shoot into the air. Ethel says, “You just add the same number of zeros as are all together in the number and in the number you are multiplying by. Easy.” “Right,” says Mr. Angelo. “Let’s try some more and see if you are getting it.” He writes three more examples:
“So who can do these?” he asks, looking over the students. “What’s the first one?” “Three hundred!” announces Robert, confidently. Mr. Angelo pauses and looks at the other students. “Who can tell Robert what he did wrong?” There is a moment of silence and then Susan raises her hand, a bit hesitantly. “I think it should be twenty-one hundred,” she says. “You have to multiply both the 3 and the 7, too, in ones like this. So 3 times 7 is 21, and then add two zeros—one from the 30 and one from the 70.” “Good!” replies Mr. Angelo. “Susan reminded us of something important for our trick. It’s not just about adding the right number of zeros. You also have to look to see whether the number you are multiplying by begins with something other than a 1, and if it does, you have to multiply by that number first and then add the zeros.” He writes 2100 after the equals sign and continues with the remaining examples. Mr. Angelo writes another three examples on the overhead:
“I wonder whether I can fool you. Now we are going to multiply by decimals that are also powers of 10: one tenth, one hundredth, one thousandth, and so on. We’ll do easy ones to start.” Who knows the first one?” he asks. “Luis?” “Point four five,” replies Luis. Nodding, Mr. Angelo rephrases Luis’s answer: “Forty-five hundredths.” He then points to the second, “How about this one?” Nadya responds, “Point zero four five,” almost inaudibly. “That’s right. Forty-five thousandths,” Mr. Angelo affirms, and he writes the number on the overhead. “And what about the last one?” “Point zero zero forty-five,” responds the girl near the front again. Mr. Angelo writes “0.0045” and says, “Good, does anyone see the rule. Who can say it?” After a long pause, one hand in the back goes up. “You just move the decimal point.” |
|
“Right,” says Mr. Angelo. “You move the decimal point to the left as many places as there are in the multiplier.* But think now. What did we decide happens to the product when we multiply a decimal by 10, 100, or 1,000? These are the powers of 10 that are greater than one, right?” This time several hands go up. “You just add the same number of zeros to the end of the number as are in the number you are multiplying by.” “Okay, that is what we said. But now we are ready for a better rule now that we have looked at some powers of 10 that are less than one. They are numbers like one tenth, one hundredth, one thousandth, and so on. Instead of having two completely different rules, it is better to have one good rule. And here it is. Listen carefully: “When you multiply by a power of 10 that is greater than one, you move the decimal point to the right as many places as the number of zeros in the multiplier. When you multiply by a power of 10 that is less than one, you move the decimal point to the left as many places as there are in the multiplier.” Mr. Angelo illustrates the movement of the decimal point with a colored pen. He explains, “You can remember which way to move the decimal point if you remember that multiplying by a number greater than one makes the product bigger and multiplying by a number less than one makes the product smaller. Right makes bigger, left makes smaller.” “Let’s practice this a bit now and get it under our belts.” Mr. Angelo passes out a worksheet with 40 exercises that resemble what was done in class. He goes over the first exercise to make sure his students remember what to do. While the students work, Mr. Angelo circulates around the room, answering questions and giving hints. The students make a variety of computational errors, but most seem able to use the rule correctly. Mr. Angelo is pleased with the outcome of his lesson. |
This lesson focuses on mathematical procedures for multiplying by powers of 10. Mr. Angelo designs the work to progress from simple examples (multiplying by 10, 100, and 1,000), to more complex ones (multiplying by multiples of powers of 10), to multiplying by powers of 10 less than one.4 He stages the examples so that the procedure he is trying to teach covers more and more cases, thus leading to a more general rule usable for multiplication by any power of 10 other than 10°=1.
Mr. Angelo asks brief questions to engage students in the steps he is taking. By giving the students a rule, he simplifies their learning, heading off frustration and making getting the right answer the point—and likely to be attained. Concerned about the spring testing, he attempts to ensure that his students develop a solid grasp of the procedure and can use it reliably. He is careful to connect what are often two disjointed fragments: a rule for adding zeros when multiplying by powers of 10 greater than one and a different rule for moving the decimal point when multiplying by powers of 10 less than one.
Although Mr. Angelo integrates these two “rules,” he does not work in the underlying conceptual territory. He does not, for example, explain why, for problems such as 30×70=?, students multiply the 3 and the 7. He might have shown them that 30×70=3×10×7×10 and that, using associativity and commutativity, one can multiply 3 by 7 and then multiply that product by 10 times 10, or 100. Instead, he skips this opportunity to help the procedure make sense and instead adds an extra twist to the rule. He also does not show his students what they are doing when they “move the decimal point.” In fact, of course, one does not “move” the decimal point. Instead, when a number is multiplied by a power of 10 other than one, each digit can be thought of as shifting into a new decimal place. For example, since .05 is one tenth times .5, in .5×10–1=?, the 5 can be thought of as shifting one place to the right—to the hundredths place, which is one tenth of one tenth. If a 5 is in the tens place, then multiplying by 10 shifts it to the left one place, to the hundreds place: What was 50 is now 500. Describing these changes in terms of “adding zeros” or “moving the decimal point” stays at the surface level of changes in written symbols and does not go beneath to the numbers themselves and what it means to multiply them. Students miss an opportunity to see and use the power of place-value notation: that the placement of digits in a numeral determines their value. A 5 in the tens place equals 50; in the hundredths place, 0.05; and in the ones place, 5. Mr. Angelo offers his students an effective and mathematically justifiable rule, but he does so without exploring its conceptual underpinnings.
In lessons such as Mr. Angelo’s, mathematics entails following rules and practicing procedures, often with little attention to the underlying concepts.5 Procedural fluency is given central attention. Adaptive reasoning is not Mr. Angelo’s goal: He does not offer a justification for the rule he is teaching, nor does he engage students in reasoning about the structure of the place-value notation system that is its foundation. He focuses instead on ensuring that they can use it correctly. Other aspects of mathematical proficiency are also not on his agenda. Instead, Mr. Angelo has a clear purpose for the lesson, and to accomplish that purpose he controls its pace and content. Students speak only in response to closed questions calling for a short answer, and students do not interact with one another. When a student gets an answer wrong, Mr. Angelo signals that immediately and asks someone else to provide the correct answer. The lesson is paced quickly.
We turn now to our second teacher, Ms. Lawrence, who is working with her fifth graders on adding fractions (Box 9–3). Ms. Lawrence’s goals are different from Mr. Angelo’s. Although she also structures the lesson to accomplish her goals, unlike Mr. Angelo, she emphasizes explanation and reasoning along with procedures. The pace of the lesson is carefully controlled to allow students time to think but with enough momentum to engage and maintain their interest.
|
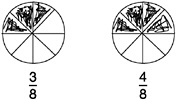
Box 9–3 Ms. Lawrence— Teaching Fifth Graders About Adding Fractions After a few minutes in which the class does mental computation to warm up, Ms. Lawrence reviews equivalent fractions by asking the students to provide other names for She asks the students how to find the sum. One student, Betsy, volunteers that you just add the numerators and write the sum over the denominator. “Why does this work?” Ms. Lawrence asks. She asks Betsy to go to the board and explain. Confidently, Betsy draws two pie diagrams, one for each fraction, and explains that the denominator tells the size of the pieces and the numerators how many pieces all together: |
 In response, Ms. Lawrence poses another problem, this time involving unlike denominators: Ms. Lawrence then asks how you could find the exact sum. Jim raises his hand and offers 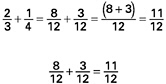 She asks Jim why he chose 12 as the common denominator. “Twelve is the smallest number that both 3 and 4 go into,” replies Jim. “How did you come up with that?” Ms. Lawrence asks. “By multiplying 3 and 4,” he answers. Ms. Lawrence turns to the class. “Let’s take a closer look. Jim got the equivalent fractions by multiplying the numerator and denominator of each fraction by the denominator of the other fraction. So if we show all the steps, it looks like this.” She then reworks the problem to make her point, justifying each step by giving a property of the rational numbers: Ms. Lawrence stops and looks at the students. “How do we know that what Jim did makes sense? How do we know that he is adding the same fractions as in the original problem: |
|
“Oh!” exclaims Lucia. “I know! Two thirds is equivalent to eight twelfths. We could show that with a picture like what Betsy drew for three eighths and four eighths. If we draw two thirds on a pie that has three pieces, those two pieces will actually make eight pieces on that same pie if it’s divided into 12. But the eight pieces, eight twelfths, will equal the same total amount of pie as two pieces that are each one third of the pie.” She pauses, and beams, looking at Ms. Lawrence expectantly. “Is that right?” “Yes, you explained it well,” says Ms. Lawrence. “Can someone come up and make pictures to show what Lucia just said?” Several hands go up, and Ms. Lawrence picks Nicole, who comes to the board and represents accurately what Lucia said. Ms. Lawrence makes a few additional remarks to make sure that all the students understand. Ms. Lawrence continues with three more examples, showing all the steps in each. She then asks the students to generalize the process by writing “a rule that would work for any two fractions.” Several students volunteer a verbal rule. “Let’s try this out on a couple of less obvious examples,” she says, writing on the overhead projector: Ms. Lawrence asks the students to work on these problems in pairs. As the students work, she walks around, listening, observing, and answering questions. Satisfied that the students seem to understand and are able to carry out the procedure, she assigns a page from their textbook for practice. The assignment contains a mixture of problems in adding fractions, including some fractions that already have like denominators and many that do not, and in adding whole numbers as well as several word problems. Ms. Lawrence wants the practice that she provides to require the students to think and not merely follow the algorithm blindly. She believes that this way of working will equip them well for the standardized test her district administers in April and the basic skills test they have to take at the beginning of sixth grade. She expects the students to remember the procedure because they have had opportunities to learn why it makes sense. She knows that this approach is understandable to her students’ parents, while at the same time she is stretching them beyond what some have been demanding—a solid focus on basic skills. She feels comfortable with the balance she has struck on these issues. SOURCE: This vignette was constructed to embody the principles from Good, Grouws, and Ebmeier, 1983. |
In this lesson, Ms. Lawrence is trying to develop her students’ ability to add fractions with like or unlike denominators. She wants them to understand how to convert fractions to fractions with the same denominator and add them, and to have a reliable procedure for doing so. She also wants them to understand why the procedure works. Her lesson is designed to engage the students actively in the conceptual and procedural development of the topic. She begins by reviewing equivalent fractions, a concept both familiar and necessary for the new work. She poses a variety of questions and expects the students to explain their reasoning. She does not stop with well-articulated statements of the procedure but demands explanation and connection to the underlying meaning. She seeks to make the procedure make sense by asking for and providing explanations.
In this lesson, time is spent in a variety of ways to address Ms. Lawrence’s goals: The students spend time practicing mental computation, developing a general rule for adding fractions, explaining and making sense of others’ explanations, and working with a partner to practice on more complex examples of what they were learning. The lesson proceeds at a steady pace, but one that affords time for developing the ideas. Ms. Lawrence checks to see whether the students are understanding before she assigns them independent work, and the assignment mixes familiar and extension problems to help strengthen students’ proficient command of the content. Although the focus of the lesson is not on strategic competence, when she asks students to estimate the sum of two fractions, she is helping them become sensitive to strategies they might use.
Our third teacher, Mr. Hernandez, is working on making and linking different representations of rational numbers (Box 9–4). He works hard to engage all his students in active work on the mathematics. Toward that end, he asks challenging questions that allow for a variety of solutions, and he expects the students to push themselves. He is conscious of the district and state basic skills assessments, but he has concluded that if he invests in this sort of work with his students, it pays off in their preparedness for the test. Occasionally, he finds that the approach is not working for some of his students, and he seeks ways to build their skills more solidly. He worries a bit, since the parents have been quite vocal in his school, with much pressure about getting students to algebra in eighth grade. He takes a strong stand on the importance of developing a solid foundation with number and representation, particularly with rational numbers.
This lesson is different from either Mr. Angelo’s or Ms. Lawrence’s. Mr. Hernandez has selected a task that draws on students’ past experience
|
Box 9–4 Mr. Hernandez— Teaching Seventh Graders About Representations of Rational Numbers Mr. Hernandez presents his seventh graders with a set of rectangular grids of various sizes. He lists specified portions of these areas—as a percentage of the total, a fraction of the total, a decimal fraction of the total, or a specific number of squares— and the students are to shade that portion. For each region shaded, he asks them to give a fraction, a decimal, or a percent to represent the shaded part of the total area. After working on the problems alone, the students are expected to be able to explain their strategies to the rest of the class. After the students have had a chance to work on the task for about 15 minutes, Mr. Hernandez calls on Michelle to do the first problem at the overhead projector: Shade .725 of the area of an 8-by-10 grid Drawing a grid on the transparency, Michelle incorrectly shades 72.5 of the 80 squares. Mr. Hernandez asks her to explain her thinking. “I’m not sure,” she admits. He then asks her to reread the problem. He asks the class to think about what would happen if they tried to distribute 100% across the 80 squares. “Each square would represent more than 1%,” responds Michelle, a glimmer of understanding on her face. “Wouldn’t each square represent 1.25%?” asks Eric. Michelle thinks for a minute and then explains that after allocating 1 percent to each square there would be 20 left over and that 20 divided among 80 would give one quarter more for each square or 0.25. “Oh, I see!” exclaims Michelle excitedly, doing some calculations off to the side of the transparency. “Fifty-eight squares should be shaded for 72.5% of 80, because 58 times 1.25 equals 72.5! Is that it?” In the discussion that follows, Louis says that he multiplied 0.725 by 80 to get 58 and explains that he obtained a fraction Throughout the lesson, Mr. Hernandez presses the students to make their reasoning explicit and to explain their solution processes. He requires them to say what the symbols and representations mean in the context of the problems they are solving. When the students arrive at a numerical answer, he asks questions such as “Can you explain what that number refers to?” |
|
To wrap things up for today, Mr. Hernandez summarizes the different strategies presented. He then assigns a similar set of problems for homework and asks the students to experiment with the various strategies they had seen in class with an eye toward determining the one they thought “best.” “What does it mean for a strategy to be ‘best’?” asks Laura. “Good question!” says Mr. Hernandez. “That’s part of what I want you to think about. What criteria would you use to decide whether one strategy was better than others?” Several hands shoot up, but he waves them down. “We’ll discuss that tomorrow. I want everyone to work on this first.” SOURCE: Adapted from Henningsen and Stein, 1997. |
with decimals, percents, and fractions—all of which they have modeled using multiple representations prior to this lesson—while also setting them up to extend their proficiency in this domain. He has used this same task many times and has discussed it with other teachers who have also used it with their students. He knows what students are likely to do and where they might stumble. He has prepared questions to help move the work firmly toward the mathematical goal. He is able to take advantage of students’ questions as they arise. He appraises the mathematical value of their questions and makes careful decisions, on the spot, as to which are worth taking up in class, which might be better simply answered, and which merit individual work but do not seem worth bringing up in class for everyone’s consideration.
The students have had considerable experience representing areas other than the usual 10×10 grid. At the same time, the task Mr. Hernandez presents is not yet routine for the students and is open to a variety of solution strategies. He does not tell them what to do; instead, he uses the task as the medium for the lesson development. Mr. Hernandez has given the discussion of multiple solution strategies a great deal of thought before making it part of the lesson, for he is aware that explicitly examining the correspondences among alternative representations is crucial. If students merely see different representations without explicit attention to their correspondences, the lesson he is teaching will not produce the learning that he is striving for. The discussion of multiple solution strategies at the overhead projector provides an opportunity for Mr. Hernandez and several of the students to model
adaptive reasoning and conceptual understanding. He also knows how much he has to do to make sure that the productive work the students are doing comes together at the end. He has found this way of working valuable. He is sensitive to the critical role that he plays during the lesson, even though it seems that the students are doing a large amount of the talking and the work.
We have been looking at upper elementary and middle school classrooms. In the last sample lesson (Box 9–5), a fourth teacher, Ms. Kaye, is attempting to develop her first-grade students’ understanding of subtraction as it is used to compare quantities. She wants the students to find and consider their own ways of making comparisons of two-digit whole numbers in which the larger number has the smaller digit in the ones place.
|
Box 9–5 Ms. Kaye—Teaching First Graders About Comparing Prices Ms. Kaye gives her first-grade class a problem that involves comparing prices on a menu. She reads the following problem several times and writes the numbers on the overhead projector: At Wu’s Dairy a single ice cream cone costs 59¢. A double costs 85¢. How much more does a double dip cost than a single dip? The children eagerly set to work on the problem at their desks. A number of tools— including counters of various kinds, plastic coins, and base-10 blocks—are available in the corner of the room. While the children work, Ms. Kaye talks with individual children about their solutions. Ms. Kaye stops at Kurt’s desk and asks him what he is doing. He explains that he is trying to find out how much more 85 is than 59 and proceeds to make 59 with base-10 blocks. Ms. Kaye asks him what he is going to do next. Without answering, Kurt makes 85, again with the blocks. Once more Ms. Kaye asks him what he is going to do next. Staring at the blocks, Kurt does not respond. Ms. Kaye asks what he is trying to figure out. “How much bigger 85 is than 59,” he murmurs. He does not seem know how to proceed. Ms. Kaye focuses his attention on the base-10 blocks and asks whether they could help him figure it out. Saying that he wants find out how much more there is in the 85 set of blocks than the 59 set, Kurt proceeds to match the two sets, pairing block for block. He trades in a rod (a 10) from the 85 set for 10 ones to make possible the matching of the 5 ones and the 9 ones. After the matching is complete, Kurt counts the blocks left unmatched and gets |
|
two rods (tens) and six units (ones). “That’s 26 more,” he announces, looking up and smiling at his accomplishment. This interaction with Kurt takes about five minutes. Continuing to circulate around the class, Ms. Kaye works with five more students in a similar fashion, asking questions, watching, listening carefully, and guiding where needed. After about 15 minutes of individual work by the students, Ms. Kaye gathers the class together for a discussion of the problem. Some of the students are asked to share their solutions with the rest of the class. As they do, Ms. Kaye asks them to explain what they are doing and why. She asks the children to compare solutions: “How is Mina’s solution like the one Brian showed? How is it like Liona’s? Are there differences?” Five children present their solutions. Two have counted up from 59 to 85, although using different approaches. Another counts with money from 59¢ to 85¢. One has subtracted 59 from 85, another 59¢ from 85¢. One child has 34¢ for an answer, and Ms. Kaye gently guides her to see where she made an error, which she corrects. After each child finishes, Ms. Kaye tries to make sure that the presented solution is clear. She also keeps asking the class to compare the different strategies. Ms. Kaye presents a new problem, and the work begins again, following the same pattern as before. Again, she works with individual students. Over the course of the class period, she is able to work individually with almost half the class; the next day, while working on the next set of problems, she will try to get to the rest. At the end of the lesson, Ms. Kaye asks the children to summarize what they did in class by writing in their math journals. She reads over their shoulders and notes how much more articulate they are becoming in speaking and in writing. She passes out a sheet of paper with a problem for homework, asks them to put the sheet in their backpacks, and sends them out for recess. SOURCE: Adapted from Carpenter, Fennema, Fuson, Hiebert, Human, Murray, Olivier, and Wearne, 1999. |
In this lesson, students work on contextualized problems—problems set in a realistic context—that are designed to develop their ability to model situations and use arithmetic operations to solve questions about comparing quantities. Developing the students’ representational ability and adaptive reasoning is an explicit goal. In particular, Ms. Kaye is trying to develop in
her students the inclination and skill to compare alternative representations for a problem situation and their solutions to the problem. She has been impressed by their developing capacity to work sensibly with numbers larger than she would have expected several years ago. Ms. Kaye is also deliberately working on helping the students develop language as a tool for doing mathematics: to pose and respond to questions, to give explanations, to reflect on their work. The lesson is structured in a way that enables Ms. Kaye, when the class is working independently, to deal individually with students, guiding their work in particular ways while remaining attuned to each student’s efforts and progress.
The approach Ms. Kaye is using takes considerable planning: The task that the students are doing must be mathematically productive of the next step in the curriculum, and it must also be engaging and appropriately difficult for all the children, so that they are able to work without constant supervision. It also takes developing norms in the class whereby the teacher can work individually with students and be able to attend closely to the mathematical knowledge and ways of reasoning being used by each child. This approach is worth developing, Ms. Kaye believes, for it continually provides her with accurate information about what the students are learning, information she uses to shape how she continues the lesson. The lesson also provides students with time to work alone, uninterrupted by others’ thinking, as well as with time to share and compare ideas, methods, and results. Ms. Kaye is aware of risks she runs with this approach. For example, when students share different methods, they may become confused. Students may end up wondering what the right answer to the problem is. However, she has seen the benefits of this approach and is committed to continuing to work on developing her skills in working with students in these ways. She knows that some parents are pleased and others worried about what she is doing. She works hard to keep the parents informed and frequently invites them in to observe and later talk with her about what she and the children are doing. She finds that this investment in parents’ awareness and support has paid off in terms of her students’ learning, as well as in communication between home and school.
Comparing the Lessons
The four classroom vignettes provide snapshots of different ways in which students, teachers, and content interact to produce different opportunities for student learning, teaching practice, and curriculum content to be mani-
fested. With respect to developing the mathematical proficiency of the students in the class, each approach affords possibilities, and each holds risks.
Consider first the mathematical content and how each teacher selects, shapes, and represents it for learning. Mr. Angelo, for example, constrains the content topic of multiplying by powers of 10 in ways that make it likely that all students will be able to produce correct answers, at least as long as they remember the rule. He provides them with a single rule that consolidates two separate rules, adding zeros and moving decimal points. His role is to demonstrate, provide practice, and check on their progress. The focus of this lesson is not to explore different methods for solving problems or probe the underlying meanings. Rather, he is deeply concerned with helping every student in his class learn to multiply by powers of 10 efficiently and accurately.
With respect to developing the mathematical proficiency of the students in the class, each approach affords possibilities, and each holds risks.
Mr. Angelo recognizes that one risk he faces is that students will develop competence with the procedure and yet lack understanding of what they are doing or why. Should they forget the procedure, they would have no conceptual basis for reconstructing it. However, he has seen that when they learn rules solidly, they are able to demonstrate procedural fluency with routine mathematical procedures. One way in which he has tried to avoid that risk is to make sure that the rules his students do learn are not mere fragments (add zeros, move decimal points). More general rules have greater power; he knows that and works to avoid giving the students lots of bits and pieces. He also designs his work with them to stage the development of the procedure in a way that he thinks will help build a better platform for their capacity to multiply numbers by powers of 10.
Ms. Lawrence organizes her students’ mathematical work to bring them to a general process for adding fractions, including an indication of its natural origins and why it works. She asks questions designed to take the lesson where she wants it to go; the students are expected to participate in that venture, answering questions and following the development of the ideas. What she makes mathematically central—a procedure for adding fractions together with its justification—melds conceptual understanding, procedural fluency, and adaptive reasoning. How she engages students requires active participation on their part, following closely her design for the lesson. Her students rarely produce unexpected ideas or solutions, for she tightly plans her lessons to anticipate what students will do and say, and their contributions typically fit her plan.
Again, Mr. Hernandez’s lesson about different representations of rational numbers is different from either Mr. Angelo’s or Ms. Lawrence’s. Mr. Hernandez’s approach involves less control of students’ work as he seeks
to develop their understanding and skill. He takes rational number—a topic often treated piecemeal in school mathematics—and works explicitly on connections: How do different representations of the same rational number map onto one another? The problems he offers students are not as straightforward as those provided by any of the other teachers: That is, the mathematical work is designed to challenge the students’ thinking and to elicit specific variations in their strategies and solutions. The tasks and the ways in which Mr. Hernandez uses them are not designed to lead students directly to obvious conclusions. Instead, they set the stage for the work he intends. Students’ solutions and explanations provide raw material for the lesson, and Mr. Hernandez expects the students to work on one another’s solutions during the class discussion. He has seen that students will not automatically be able to engage in discussions of complex mathematical problems, especially in classrooms as diverse as his. Consequently, he has been working hard over the last few years to develop his own skills at getting all students involved, including challenging different students appropriately.
In Ms. Kaye’s first-grade lesson on whole numbers, the students are not taught a procedure for solving comparison problems (e.g., When you see “how many more?” it means you should subtract). In fact, a major mathematical goal of her lesson goes well beyond comparison of two quantities. It is to generate and uncover different solution strategies, including modeling situations and using representations, to explore and justify those strategies, and then to find similarities and differences between different solutions. She wants to build on her students’ mathematical understanding.
Ms. Kaye’s lesson also illustrates that how the development of the mathematical content in instruction can rest on the teacher engaging students in solving mathematical problems. In her class the students’ ideas and methods generate significant portions of the lesson’s substance, and the students are expected to play a major role in the development of the lesson—sharing their solutions, providing explanations, analyzing options. Ms. Kaye’s forays around the room give her detailed information about individual students’ progress that she uses in directing their mathematical work toward her goals.
Because Ms. Kaye has designed a lesson that opens up space for a variety of student ideas and methods, her approach risks generating multiplicity without clarity, connection, or closure. Although it is not Ms. Kaye’s intention, the students may conclude that mathematics is a subject in which everyone can devise his or her own equally valid concepts and methods. The students may fail to appreciate the need for analysis, comparison, and evaluation—for common knowledge—or may continue to use their own safe procedures rather
than developing more sophisticated ones. These are serious risks, ones she has seen emerge both in her own teaching before she was as aware of this problem as she is now and in the classrooms and accounts of many of her colleagues. Consequently, she is now much more careful to see to it that the lesson is pulled together at the conclusion, so that the mathematical points are made plain for students. Ms. Kaye keeps a close eye on all the district’s learning goals for first grade as she uses problems like the one in the lesson, being careful that she covers the curriculum for the year.
While Ms. Kaye poses a problem that invites a wide range of solution methods appropriate for students at different places in their understanding, Mr. Hernandez gives a problem strategically designed to elicit specific approaches, material to be used to advance students’ understanding of the correspondences among representations of rational numbers. In both Mr. Hernandez’s and Ms. Kaye’s classes, the students hear, use, and interact with other students’ ideas. In Mr. Angelo’s and Ms. Lawrence’s classes, the teacher is the source of the lesson substance, and the students engage less with one another as a source and medium of mathematical work.
These vignettes help to show that the mathematical content and how it is framed and formulated into instructional tasks make a difference for the learning opportunities provided in a lesson. How the teacher interprets and uses such tasks to develop a lesson also fundamentally shapes instruction. Moreover, the ways in which the students make sense of and engage with the tasks and the teacher significantly affect how the lesson proceeds. All teachers face the challenge of engaging students in the mathematical work, maintaining their focused involvement in it, and helping them take advantage of instruction to learn. Each of our four teachers manages this challenge differently, which has different consequences for students’ opportunities to learn. Mr. Angelo constrains the mathematical content in ways that focus students’ attention on the specific learning goals of the lesson, making divergence of method or result unlikely. Ms. Lawrence musters students’ engagement by asking them to explain and justify what they are saying. Mr. Hernandez’s approach relies on setting challenging tasks and using anticipated students’ solutions—errors as well as correct solutions—as part of the lesson material. Ms. Kaye engages the students through thought-provoking, carefully chosen tasks that invite multiple representations and strategies, and then she works intensively with individual students. Whereas Mr. Angelo runs the risk of his students forgetting the procedure since they lack the conceptual foundation, Ms. Kaye risks confusing her students with a blizzard of solution methods. Ms. Lawrence maintains a tight focus and hence reduces the ambiguity for
her students—ambiguity that in Mr. Hernandez’s lesson may be leading to frustration or disengagement for his students.
Teachers vary in how they manage the content and the incentives for students to engage in and succeed with it, and their choices present different advantages and risks for learning. Although it may not seem obvious, teachers who teach in ways like Mr. Hernandez and Ms. Kaye must prepare in detail for class; many observers of teaching fail to appreciate the significance of design and preparation in making these sorts of lessons more effective in helping students learn. Teachers like Mr. Angelo and Ms. Lawrence, however, need to work hard to figure out what their students are actually taking from instruction and what that implies for their approach to teaching common mathematical procedures.
The four lessons make plain that instruction does not occur in a vacuum. Parents, administrators, policies, the expectations of other teachers all may affect teachers’ conceptions and practices. Teachers are differentially sensitive to particular features of their environments and respond in different ways. Mr. Angelo is concerned about the pressures exerted by testing and tailors his approach to target the focus of these tests. Mr. Hernandez, in contrast, is sure that approaching the topic more conceptually and with more complexity will equip his students to do well even on relatively routine, skill-based tests. Just as teachers’ perceptions of their environments affect instruction, so too do students’ perceptions. For example, if students hear criticism at home or if parents are puzzled and concerned about the mathematics program, students’ resulting unease will affect their interactions with their teachers.
These snapshots of four classrooms are no more than glimpses into a complex set of interactions happening over time. They are segments from single lessons and, as such, provide a nearsighted view of school mathematics instruction. Instruction is not self-contained in serial lessons but draws on what happened yesterday, last week, last fall. Ideas about decimal notation that were taken up in a previous unit are used as Mr. Hernandez’s students grapple with correspondences among different ways to represent rational numbers. Ms. Kaye’s work with her first graders early in the year, helping them learn to express mathematical ideas in speech and in writing, equips them to write better now. Later learning builds on earlier successful accomplishment; new ideas are constructed using those already known. For example, a teacher could not effectively define a prime number if her students did not already possess some understanding of factoring. That understanding might have been developed in a variety of ways, but without it teaching the concept of a prime number would require simultaneously teaching about factors.
Neither in one lesson nor over a year does any one of the core elements of instruction—mathematical content, teacher, students—alone determine what happens. Instead, it is in enactment—in their mutual and interdependent interaction—that instruction unfolds. The quality of instruction does not inhere in any single element, whether challenging, exemplary curriculum material; competent, enthusiastic teachers; or capable, eager students. What makes curriculum exemplary, teachers competent, and students capable is their skilled use of one another to produce teaching and learning. How well they can take advantage of the possibilities afforded by the lesson and how well they can avoid the pitfalls determine how well students are able to use instruction to learn and how well teachers are able to guide that learning.
We turn next to what research on teaching has to say about shaping the nature and quality of instructional interaction. Given the possibilities that are paramount in each of the episodes described above and the potential risks of each approach, what is known about how to take advantage of the possibilities and avoid the pitfalls?
Findings from Research on Teaching
The interactive perspective on instruction6 that we take in this chapter shapes our discussion of the studies we review. Using the instructional triangle depiction of instruction in Box 9–1, we ask what is known about the impact on student learning of how teachers select and use content (the teacher-content side of the triangle), how teacher and students interact (the teacher-student side), and how students interact with content (the student-content side). Although we discuss each side of the instructional triangle separately, instruction is not about one side alone but is about the trilateral interaction among teacher, students, and content.
Teachers and Content
What is learned depends on what is taught. Choosing the content, deciding how to present it, and determining how much time to allocate to it are ways in which learning is affected by how the teacher interacts with the content. Furthermore, some decisions about the content are made not at the classroom level but at the school, district, or even state levels.
Opportunity to Learn
The circumstances that allow students to engage in and spend time on academic tasks such as working on problems, exploring situations and gather-
ing data, listening to explanations, reading texts, or conjecturing and justifying have been labeled opportunity to learn. As might be expected, students’ opportunity to learn affects their achievement. In fact, opportunity to learn is widely considered the single most important predictor of student achievement.7 Opportunity to learn can be influenced by individual students, their teachers, their schools or school districts, or even the country’s educational system.
Research at the local and national levels has identified the curriculum as a potent force in students’ opportunity to learn. Students in different curriculum tracks receive differential opportunities to learn mathematics, which is then reflected in their achievement.8 Some studies show that when students believed to be less capable academically are given an opportunity to learn, they can in fact do so.9
Many curriculum decisions are made at the school or district level and lie outside the province of the classroom teacher. Nevertheless, teachers still have considerable control over their students’ opportunity to learn. U.S. elementary school teachers vary widely, for example, in how much instructional time they allocate to various school subjects. In one study of second-grade classes, the average time allocated to mathematics ranged dramatically from a low of 24 to a high of 61 minutes a day for different teachers.10 In another study some “teachers spent as much as 40 percent of their time teaching mathematics; several others never taught mathematics in the twenty randomly chosen hours when our observers visited each classroom.”11 That sort of variation is not unusual across classrooms and even within an individual teacher’s practice. Teachers also vary in how they manage the time they have, sometimes focusing on one strand of proficiency and ignoring others. For example, two fourth-grade teachers ostensibly following the same mathematics textbook were found to spend their time quite differently: One teacher focused on concepts, and the other emphasized drill and practice of computational skills.12 Even when the amount of time and the textbook are uniform, therefore, students can encounter different content and have different opportunities to learn it.
Consider the lessons of Mr. Angelo and Ms. Lawrence in the vignettes presented above. These two teachers use about the same amount of instructional time. The crucial differences lie in how they use that time. Mr. Angelo works on developing fluency with the procedures without a focus on their underlying meanings or justification. Ms. Lawrence, in contrast, spends most of her time developing understanding of a procedure through structured
interactions with her students. Mr. Angelo gives 40 practice problems, whereas Ms. Lawrence uses only four.
Task Selection and Use
Researchers have recently taken a closer look at instruction by investigating the choice and use of academic tasks. Tasks are central to students’ learning, shaping not only their opportunity to learn but also their view of the subject matter. The cognitive demand of tasks can vary significantly. Moreover, the tasks typically assigned to students in many classrooms make only minimal demands on their thinking, relying primarily on memorization or use of procedures without connections to concepts. There is growing evidence that students learn best when they are presented with academically challenging work that focuses on sense making and problem solving as well as skill building.13 Take a couple of the tasks from our lesson vignettes. The task presented by Mr. Hernandez, shading 0.725 of an 8×10 grid, is a cognitively demanding task for seventh graders. His students have had prior experience with decimals, percents, and fractions, all of which they have modeled using multiple representations. But they have not had to coordinate the three, a mathematical problem of considerably more sophistication. The task presented by Mr. Angelo is less cognitively demanding, for all that students have to do is recall the steps of the procedure and answer questions about them. Still, whatever task a teacher poses, its cognitive demand is shaped by the way students use it. In fact, tasks that are set up to engage students in cognitively demanding activities often degenerate into less demanding activities as teachers and students work together to help the student “understand.”14
Several factors have been identified as influencing the decline in cognitive demand from task setup to task enactment. Chief among them is that the task is made routine in one of two ways: The students may start pressing the teacher to reduce the challenge by specifying explicit procedures or steps for them to perform, or the teacher may take over the demanding aspects of the task when the students encounter difficulty by either telling them or demonstrating what to do.
Similarly, factors have been identified that help to maintain student engagement at a high level.15 One is choosing tasks that build on students’ prior knowledge. In our vignettes both Ms. Lawrence and Ms. Kaye use students’ prior knowledge to engage them in demanding cognitive tasks. Ms. Lawrence links what students already know about adding fractions to
the new topic of adding fractions with unlike denominators. Rather than merely presenting the process, she guides them in formulating the process themselves, building on their existing knowledge. Ms. Kaye uses students’ informal knowledge about numbers, money, and operations to pose a demanding two-digit subtraction problem to her first graders. She also provides so-called scaffolding to help Kurt stay engaged in the task without showing him how to do it.
The use of scaffolding is another factor that helps to maintain student engagement at a high level. By offering a subtle hint, posing a similar problem, or asking for ideas from other students, Mr. Hernandez provides some scaffolding to assist his students as they reason through the grid problems. He does so without reducing the complexity of the task at hand or specifying exactly how to proceed. He allows substantial time for discussion of the problem, thus affording the students an opportunity to learn by considering and discussing multiple solution strategies.
Allocating neither too much nor too little time for the task is another factor associated with keeping engagement and cognitive demand high. Recall how Ms. Lawrence steps back to give her students a chance to think. Had she not provided that opportunity, Jim might not have come up with his solution. Mr. Hernandez also allows ample time for discussing the problems, thus affording his students an opportunity to learn by considering and discussing multiple solution strategies. The discussion of multiple solution strategies at the overhead projector provides an opportunity for Mr. Hernandez as well as several students to model a high level of performance—another factor that helps maintain engagement in cognitively demanding tasks. Ms. Lawrence also models a high level of performance by justifying each step in the general procedure for adding fractions with unlike denominators.
A final factor in maintaining high levels of student engagement with demanding tasks is sustained pressure from the teacher on explanation and the development of meaning. Throughout their lesson, Ms. Lawrence and Mr. Hernandez press students to explain their solution processes and to attach meaning to the symbols they are using. Ms. Kaye does likewise, both as she talks with individual students and as she responds to individual students presenting their solutions to the class. Teachers must not only select and successfully launch a high-level mathematical task but must also actively and consistently support students’ cognitive activity without reducing the complexity and cognitive demands of the task. In the classroom the teacher, the students, and the task clearly interact in a dynamic way to shape students’ learning.
Planning
Given that the learning of mathematics develops interactively over time, effective teachers understand that teaching requires considerable effort at design. Such design is often termed planning, which many teachers think of as a core routine of teaching.
Studies of how U.S. teachers plan show that they tend to focus on the activities in which students will be engaged and how those activities will be organized.16 Teachers’ plans seldom elaborate the content that the students are to learn through their engagement with the proposed activities.17 Other research suggests that teachers who make detailed plans can sometimes be relatively inflexible when students encounter difficulties or raise thoughtful questions. These teachers are committed to their plans and have difficulty making midcourse adjustments.
Some teacher educators have made planning a central objective of their teacher preparation programs. Most programs provide prospective teachers with model plans or rubrics to scaffold their planning. Derived from teacher educators’ ideas about what would constitute helpful approaches to preparing lessons, these frameworks do not necessarily reflect what good teachers do.
Researchers have rarely explored what it might mean to prepare for teaching in ways that would elaborate content goals and simultaneously equip the teacher with good maps of the paths they might take to reach desired destinations. Because many curriculum materials seek to do this sort of preparation for teachers, an important area for research is how teachers use the highly elaborated teachers’ guides often held up by educators as positive examples. What do teachers read when planning, how do they interpret and use what they read, and how do those uses affect their teaching?
Recent studies of Japanese professional development programs have revealed a practice termed lesson study that involves groups of teachers working together on single lessons, elaborating goals, investigating pupils’ thinking and difficulties with particular content, and exploring different representations and tasks. The teachers make repeated trials of these lessons, improving them in light of their collective study of the effectiveness of the lesson designs. We discuss this approach to professional development in chapter 10. Here we highlight the idea of designing lessons to combine a significant elaboration of one’s content goals with a dedicated and thorough anticipation of and preparation for a range of likely student responses. Planning can profitably be seen as a detailed form of instructional design aimed at reducing the uncertainties of one’s practice, centered on the continual adjustment and
improvement of instruction, and informed by a close scrutiny of what happens as the lesson unfolds.
Teachers and Students
Teacher Expectations
Teachers’ selections of tasks and their interactions with students during instruction are guided by their beliefs about what students need to learn and are capable of learning.18 Low expectations can lead a teacher to interact with certain students in ways that fail to support their development of mathematical proficiency. For example, in comparison with their treatment of high achievers, some teachers consistently wait less time for low achievers to answer a question before calling on someone else. They tend to give these students the answer rather than helping them improve their responses by rephrasing questions, they criticize them more frequently for failure and praise them less frequently for success, they call on them less often, and they give them less cognitively demanding questions and tasks.19 Mr. Hernandez might easily have succumbed to such a temptation in responding to Michelle’s wrong answer. Instead, he asked her to reread the problem and think about what would happen if 100% were to be distributed across the 80 squares. That is, he expected Michelle to be able to solve the problem if she persisted in working on it—and on her own and with assistance from her classmates, she did.
Successful teachers not only expect their students to succeed but also see themselves as capable of motivating and instructing students effectively.
Closely related to teachers’ expectations is their sense of efficacy, the feeling that they are effective in helping students learn. Successful teachers not only expect their students to succeed but also see themselves as capable of motivating and instructing students effectively. Less successful teachers lack confidence either in themselves as instructors (e.g., “I don’t know the mathematics well enough to teach it effectively”; “I know what I want to teach, but I don’t know how to give my students what they need to be able to learn it”) or in their students’ learning potential (e.g., “No teacher could be effective with these students because they lack ability, motivation, supportive home environments, and so on”). Studies have identified consistent relationships among teachers’ sense of efficacy, the patterns of teacher-student interactions that occur in their classrooms, and their students’ achievement. For example, teachers with a high sense of efficacy tend to appear more confident in the classroom, to be more positive and less critical with their students, to be better classroom managers, to be more accepting and effective in responding to challenges from students (e.g., “Why are we learning this?”), and to be more effective in supporting growth and achievement.20
These findings on teachers’ sense of efficacy underscore the importance of preparing teachers so they possess sufficient knowledge to teach with confidence and effectiveness. They need to know the mathematics they will teach, their students’ current mathematical thinking, and strategies for representing mathematics and meeting their students’ learning needs. Helping teachers become proficient in understanding their students’ reasoning, in choosing a good follow-up question, and otherwise providing scaffolding for their students can be particularly challenging because such techniques require high levels of all three types of knowledge and are different from the techniques emphasized in most teachers’ prior experience.21
Motivation
To make consistent progress toward proficiency, students need to be motivated to engage productively in mathematics lessons and the learning activities in those lessons. Motivation for school mathematics learning depends primarily on the interaction of students with teachers and of students with mathematical tasks.22 Traditional approaches to motivation typically either attempt to make learning fun or to rely on grades and other extrinsic rewards and punishments to pressure students to put forth the necessary effort. Recent research on students’ motivation has moved well beyond these traditional conceptions to establish a richer, more balanced depiction of motivation, allowing the identification of effective motivational strategies that apply to the teaching of all subjects, including mathematics.23
Students’ motivation depends on both expectation and value.24 That is, students are motivated to engage in a learning task to the extent that they expert to be able to perform the task successfully if they apply themselves and the degree to which they value the task or the rewards that performing it successfully will bring. Therefore, teachers can motivate students to strive for mathematical proficiency both by supporting their expectations for achieving success through a reasonable investment of effort and by helping them appreciate the value of what they are learning.
Maintaining an expectation of success. To make steady progress toward proficiency, students need continued confidence that they can meet the challenges of school mathematics. The most basic strategy for supporting students’ expectations of success (and their related perceptions and beliefs, such as a sense of efficacy) involves two basic elements. The first is to design for success by assigning tasks on which students can succeed if they invest reasonable effort. The second is to provide whatever scaffold-
ing may be needed to help students acquire and apply concepts, skills, and abilities as they work on assignments. This strategy involves building on students’ current knowledge, which in turn requires understanding what they already know and where they are headed.
Other strategies include helping students to commit themselves to goals that are near at hand, specific, and challenging and then following up by helping them assess their performance in terms of their progress toward those goals rather than by comparing their performance to that of their classmates. In modeling their own mathematical thinking, in communicating expectations to students, and in socializing students’ attitudes and beliefs, teachers should continually emphasize that mathematical proficiency is built up through experiences in learning and applying what has been learned (and are not innately given and limited). They need to emphasize that students can meet daily challenges successfully and move toward higher levels of proficiency if they consistently put forth reasonable effort and that such effort results in a gradual but productive deepening of understanding and refinement of skill.25
Valuing learning activities. To be optimally motivated, students need not only confidence that they can achieve success but belief that what they are learning is worth learning. Traditional approaches to the value aspect of motivation have attempted not to help students see value in learning activities but instead to link their performance on these activities to something else that they do value, such as the prospect of earning rewards. Rewards can be useful, but they need to be handled carefully because they can undermine intrinsic motivation and distract students’ attention from learning goals if they are overemphasized. Rewards can also have undesirable side effects if they are tied to competitions that create winners and losers.
Alternative strategies for addressing the value aspect of motivation involve taking advantage of students’ existing intrinsic motivation by emphasizing topics they find interesting and tasks they find enjoyable. For example, students usually enjoy responding actively rather than merely listening; opportunities to interact with their peers; situations that invite thought by posing divergent questions; and activities with game-like features, such as puzzles and brainteasers.26 These strategies for intrinsic motivation can be helpful, although teachers may find that their opportunities to use such strategies are limited by constraints of time and curriculum.
Moreover, although use of these strategies may increase students’ enjoyment of a lesson, it does not directly stimulate their motivation to learn what the lesson is designed to teach. Motivation to learn includes the students’
tendency to find mathematical activities meaningful and worthwhile, to try to get intended learning benefits by attempting to make sense of the activities, to relate the new knowledge or skills they are developing to their prior knowledge or skills, and to think about how they can apply the mathematics they are learning. Teachers create motivation to learn by modeling it in their own classroom discourse, communicating their expectations for success, assuming that their students are already motivated to learn, and molding their class into a coherent learning community. When teaching particular lessons or providing learning activities, teachers can spur students’ motivation to learn by communicating enthusiasm for the content, stimulating curiosity or suspense, personalizing the content to make it more concrete or familiar, introducing it in ways that stimulate interest or an appreciation for its value, engaging the students in authentic applications of the content, and helping them to remain goal oriented and attuned to strategies as they work on applications.27
The lessons taught by our four teachers illustrate some of these principles. These teachers provide environments that support learning. Their students participate actively by answering questions, offering solutions, or providing explanations. Ms. Lawrence, Mr. Hernandez, and Ms. Kaye focus on students’ understanding and sense making, and they try to connect the lesson to students’ prior knowledge. Mr. Angelo gives his rule for multiplying by powers of 10 and relates it to the earlier “add zeros” rule for multiplying by powers of 10 greater than one. His approach of giving explicit rules to follow helps to assure success on the tasks, provided that students can remember the rule. Mr. Angelo relies for motivation on the personal engagement he shows with his students and on the extrinsic pressures built into the grading system. Rather than motivate students through interest or intrinsic aspects of the intellectual work, he inspires confidence because the goal seems attainable.
Teaching Students with Special Needs
Although existing research does not provide clear guidelines for teaching mathematics to children with severe learning difficulties, existing evidence and experience suggest that the same teaching and learning principles apply to all children, including special-needs children. It has long been assumed that children with moderate, mild, and borderline mental retardation or learning disabilities are not capable of meaningful or conceptual mathematical learning and, thus, unlike other children, have to be taught by rote. Researchers
have found, however, that it useful not to prejudge them or to assume that they learn by means of different “laws of learning.” Instead, it is in the best interest of special-needs children to assume that the following principles apply to all children: (a) learning with understanding involves connecting and organizing knowledge; (b) learning builds on what children already know; and (c) formal school instruction should take advantage of children’s informal everyday knowledge of mathematics.28
Learning difficulties among special-needs children stem largely from instruction that violates one or more of these principles. Common mistakes in their instruction include (a) not assessing, fostering, or building on their informal knowledge; (b) overly abstract instruction that proceeds too quickly; and (c) instruction that relies on memorizing mathematics by rote. In other words, the learning difficulties of special-needs children and children in general are the same.
When special-needs children are taught mathematics in accordance with the above principles, many show significant improvement in learning concepts and skills and can exhibit considerable proficiency.29 Furthermore, even within what are presumed to be homogeneous groups of children, there are significant individual differences in their readiness and capacity to learn particular mathematical skills and concepts. Together, these findings imply that many, if not all, special-needs children can benefit from meaningful instruction that addresses the development of all five strands of proficiency and that gives attention to both the students’ thinking and the mathematics.
Note that it does not follow from the above principles that special children should be treated identically to their same-age peers. For children with mental retardation, for example, it may take several years to help them construct the number or arithmetic concepts that other children do in a much shorter span of time. Moreover, applying these principles to teaching special-needs children may require creative adaptations. With children who are blind, for example, computer-based instruction may not be helpful or may need to be adapted in imaginative ways. Likewise, for children with communication disorders, creative solutions may be required to enable them to benefit from small-group work.30 Again, good instruction of special-needs children will depend on reflective, knowledgeable, and flexible teachers.
Special-needs children can benefit from careful and thoughtful use of both mainstreaming and segregated instruction. Mainstreaming is an instructional tool that can be used wisely or not. Currently, it is all too often used inflexibly and ineffectively. Consider the case of Ann, a Down syndrome child, who is placed in a regular eighth-grade mathematics class along with
children the same chronological age. Ann sits through class after class with little or no comprehension of the instruction. The assigned aide tries to discuss the instruction afterward, but with little success. The aide also provides simplified or watered-down worksheets (e.g., asking Ann what half of various amounts are instead of worksheets on operations on fractions). In brief, Ann’s integration into the class is in name only and does almost nothing to foster her mathematical proficiency or even rote learning of mathematics.
It is worth noting that Alfred Binet devised the IQ test and advocated segregated instruction for low-ability students for the most humane of reasons. As the case of Ann illustrates, he saw that such children were often utterly lost in regular classrooms and suffered terribly there. Because segregated instruction was implemented poorly or abused, it has now largely been abandoned. Now educators advocate mainstreaming for the most humane of reasons. Unfortunately, this approach is all too frequently being implemented poorly. In the end there is no substitute for providing adequate support for all children. This support includes providing sufficient staff who are both well trained and caring. Real improvement in the education of special-needs children will also require moving past dogmatic positions and taking a reflective approach that takes into account the best interests of each child.
Interactions with Different Students
In the mathematics class the teacher naturally interacts differently with different students. Sometimes, however, differential interactions are associated not with differences in mathematical ability or accomplishment but with differences in students’ social class, ethnicity, language, or gender. For example, studies have shown that boys have a larger number of academic interactions with teachers in mathematics class than girls do. Not only is the quantity of interactions different, but the quality differs also. Studies have documented that girls often receive simpler, more routine questions than boys, who then receive more difficult and challenging questions.31 As noted earlier, some teachers interact differently with lower achieving students than higher achieving students, giving them less time to respond, asking them less demanding questions, criticizing them more often, and calling on them less. And lower achieving students are disproportionately children of color, from poverty, or from households without native speakers of English. Not only is there substantial evidence that teachers interact differently with students, but students from marginalized groups are also more vulnerable than other students are to self-fulfilling prophecies of low expectations.32
Interactions between teacher and student need to be appropriate to the student and the content, regardless of the student’s social class, ethnicity, language, or gender. Effective teachers often make use of their students’ interests to engage them in academic tasks. Effective teachers of urban African American students do so by making use of the culture of their students. They demonstrate an understanding of their students’ backgrounds and experiences, link classroom content to those experiences, use familiar cultural patterns, and focus on the child.33 High expectations for all students without regard to their social class, ethnicity, or gender can also pay high dividends. For example, low-achieving minority students can do as well as other students when placed in more demanding programs.34 Also, in a study of teachers in schools serving children of poverty, higher achievement results were obtained when teachers placed more emphasis on meaning in their mathematics classrooms.35 Because the quality of the interaction of teacher and student around the content is so critical to the success of instruction, the most successful teachers are not merely sensitive to the cultural diversity of their students but use that diversity to enrich the learning experiences they provide to the class as a whole.36
Communities of Learners
Creating classrooms that function as communities of learners has been the focus of much recent research and scholarship in mathematics education.37 In the research on teaching and learning mathematics with understanding, four features of the social culture of the classroom have been identified.38 The first is that ideas and methods are valued. Ideas expressed by any student warrant respect and response and have the potential to contribute to everyone’s learning.
A second feature of a classroom community of learners is that students have autonomy in choosing and sharing their methods of solving problems. Students recognize that many strategies are likely to exist for solving a problem, they respect the methods used by others and that others need to understand their own methods, and they are given the freedom to explore alternatives and to share their thinking with the rest of the class. Notice how Mr. Hernandez has three other students besides Michelle share their solutions to the grid problem. Ms. Kaye has five students present their solution methods. She also engages the class in a discussion of the similarities and differences between the various methods. In contrast, Ms. Lawrence and Mr. Angelo, although they call on students to answer questions, are more
interested in presenting a correct solution method than in soliciting multiple methods.
A third feature of classrooms that function as communities of learners is an appreciation of the value of mistakes as sites of learning for everyone. Mistakes are not covered up; rather, they are used as opportunities to examine reasoning and to deepen everyone’s analysis. The appreciation of mistakes is a fundamental aspect of mathematical work outside the classroom; inside, it helps build the community. When Michelle makes a mistake on the grid problem, Mr. Hernandez does not tell her it is wrong and then call on someone else. He uses it instead to push her thinking.
Finally, a core feature of these classrooms is the recognition that the authority for whether something is both correct and sensible lies in the logic and structure of the subject rather than the status of the teacher or the popularity of the person making the argument. The resolution of disagreements resides in mathematical argument. Both Mr. Hernandez and Ms. Kaye have their students justify their solution strategies. Although Ms. Lawrence frequently asks her students to justify their work, when she presents the procedure for adding fractions with unlike denominators, she provides the justification. She does use mathematical properties to explain the procedure, however, rather than simply present the rule as Mr. Angelo did. Hence, in addition to selecting tasks with goals in mind and sharing essential information, the teacher’s primary role is to establish a classroom culture that supports learning with understanding, thereby serving to motivate students to learn.
Managing Discourse
An important part of classroom instruction is to manage the discourse around the mathematical tasks in which teachers and students engage. Teachers must make judgments about when to tell, when to question, and when to correct. They must decide when to guide with prompting and when to let students grapple with a mathematical issue. Their decisions do not simply rest with the mathematical task at issue. They also need to decide who should get the floor in whole-group discussions and how turns should be allocated. Teachers have responsibility for moving the mathematics along while affording students opportunities to offer solutions, make claims, answer questions, and provide explanations to their colleagues. The point of classroom discourse is to develop students’ understanding of key ideas. But it also provides opportunities to emphasize and model mathematical reasoning
and problem solving and to enhance students’ disposition toward mathematics. Therefore, discourse needs to be planned with these goals in mind, not merely as a “checking for understanding” form of recitation.
Teachers are often inclined to call on students who have the correct or desired solutions. This practice makes managing the discourse less complex, since less complicated or confusing ideas get the floor. It also shapes both the task and students’ opportunities to learn from it.
Our four teachers manage the discourse in their classrooms in very different ways. In Mr. Angelo’s lesson, for instance, he does virtually all the talking, opening only a few constrained entry points for students to offer their answers. Ms. Kaye, in contrast, deliberately elicits five disparate solutions from a range of students. The group discussion forms the content of the lesson, so individual students’ ideas contribute directly to the enacted curriculum of the class. Ms. Lawrence controls students’ contributions to the lesson but proffers complex questions so that the discourse requires substantial work from students. She manages by planning strategic questions to move the lesson to its goal. Mr. Hernandez incorporates students’ ideas into his design, deliberately sowing questions that will get particular issues and ideas on the table for the class to hear and learn from. Managing the discourse is both one of the most complex tasks of teaching and the least thoroughly studied. Research needs to make visible teachers’ considerations as they handle classroom discourse and the consequences of their moves for students’ learning.
Grouping
Students are sometimes grouped for instruction either by curriculum path or achievement level. Grouping by curriculum, often called tracking, is more common in high school, where different curriculum tracks exist for students with different goals for the future: college, business, or trades. Grouping by achievement level is more common in elementary and middle schools. At those grades, homogeneously grouped classes are usually taught essentially the same content, but the higher the level, the greater the depth and breadth of mathematical ideas and the more rapid the pace.
Grouping by achievement level is especially relevant in grades pre-K to 8. We make two points about such grouping. First, it is in fact grouping by achievement and not ability grouping, as it is so often called. The test scores (and in some cases school grades) that provide the basis for such grouping are measures of mathematical knowledge and skills that students have accumu-
lated to date; they are not measures of some underlying (presumably fixed, stable, and possibly innate) substrate of mathematical ability. What is known about neural capacity and brain functioning with respect to mathematical abilities is limited and largely speculative. The evidence does not support any practice of grouping pre-K to grade 8 students according to their supposed mathematical abilities. Meanwhile, data from international comparisons (especially studies of Asian countries) support proceeding on the assumption that all students can achieve important mathematical learning goals and working within heterogeneously grouped classes to see that students do.
In the United States, interest in grouping students by achievement for mathematics instruction has waxed and waned over the years. Proponents of homogeneous grouping claim that reducing the range of achievement levels within a class or group enables the teacher to meet that group’s needs more consistently. Opponents of such grouping claim that the advantages to high achievers are overstated. Instead of providing low achievers with ideal instruction that helps them make rapid gains in proficiency, homogenous grouping typically results in low achievers being taught a barren curriculum by less capable teachers in classes that lack strong peer role models. Any gains that might accrue to the high achievers are more than offset by losses to the low achievers and by the resultant perpetuation of social class, racial, and ethnic inequities in schooling.39
This controversy highlights a second point about grouping: Many studies on grouping have been conducted over the years (including studies on grouping for mathematics instruction), but the results concerning effects on achievement have been both weak and mixed.40 The findings indicate that overall mathematical achievement is likely to be similar whether students are grouped homogeneously or heterogeneously, especially if the same curriculum is provided to all groups. When the curriculum is altered, tracking appears to benefit students in high-track classes.41 At the same time, there is evidence that heterogeneous classes may help students whose earlier performance was low, with little effect on other students’ performance.42 An analysis of data from the National Education Longitudinal Study (NELS), however, found that the estimated achievement of average and high-achieving students would be depressed in heterogeneous eighth-grade mathematics classes.43 If one were to look only at these achievement data, one might conclude that it makes little difference whether students are grouped homogeneously or heterogeneously. However, concerns raised about undesirable side effects of homogeneous grouping in grades pre-K-8 in the United States, as well as international comparison data indicating that some countries with the most impressive
mathematical achievement scores practice heterogeneous grouping, suggest that heterogeneous grouping is the wiser course in the elementary and middle school grades.
Significant improvements in students’ mathematical achievement are more likely to result from adjustments in curriculum and instruction than from adjustments in how students are assigned to classes. The snapshot of Ms. Kaye’s class illustrates how a teacher can work effectively with a heterogeneous group of students. All of her first graders are given the same problem, but she encourages the use of different solution strategies depending on the level of the student. Mr. Hernandez provides another example. He allows students to present both more and less sophisticated procedures, provided the students can explain them. In each case the key is the interaction of the teacher and the students around a challenging problem, rather than some particular instructional organization.
Cooperative Groups
Cooperative grouping of students in a class is a teaching practice that has become popular in recent years. Because it has also been a target of concern and criticism, we devote specific attention to it and to the warrants for and conditions of its use. First, important to realize is that there is no single practice or structure that can be identified as “cooperative groups.” Cooperative groups are usually groups of three, four, or five students who have been given a task to work on together, with some effort by the teacher to specify the role each child is to play in the group’s work. The several different models for organizing and conducting cooperative groups generally share common goals. One goal is to specify the social processes of the groups so as to accommodate students’ lack of experience with collective work and to provide them with support. A second is a commitment to distributing classroom talk more widely, encouraging all students to talk, to share their ideas, and to become more actively engaged intellectually. A third is to help students develop their social and collaborative skills and not just support their learning of content. Like most such techniques and tools, whether cooperative groups contribute to the development of mathematical proficiency depends primarily on how they are used.
Several models of cooperative grouping have been extensively studied. The research indicates that these cooperative group methods are likely to have positive effects on achievement and on other social and psychological characteristics.44 The effects on achievement appear to be related to the use
of specific rewards for a group based on its members’ performance rather than on the particular cooperative method used. Ensuring the accountability of individual group members for the collective work can prevent one or two students from doing it all while the others simply copy or sit passively. The most effective methods combine group goals with individual accountability.
Effects of such grouping on outcomes other than achievement are more impressive. Cooperative grouping arrangements promote friendship and positive social interaction among students who differ in achievement, gender, race, or ethnicity, and they promote acceptance of handicapped students who have been placed in regular classes. Although there may be disadvantages to using cooperative groups, their judicious use may have potential nonacademic benefits.
For cooperative groups to be effective, students need to be taught how to work in this mode. Simply telling students to push their desks together and work on a task together does not ensure cooperative learning. Skills for working cooperatively have to be taught directly, and students need to be prepared for both the social and the cognitive demands of such work. Further, there is evidence that children’s collaborative interactions vary across social and cultural groups.45 For teachers to use cooperative groups effectively, they also need to select, organize, and present tasks that are well suited both to collaborative work and to the curriculum.
Cooperative grouping is one of many instructional practices that teachers may choose to use at times. It is neither a wholesale replacement for wholeclass instruction nor a disastrous technique to be avoided at all costs. Further, the cooperative methods that have been found to produce positive learning outcomes take knowledge and skill to implement. Like any practice, cooperative groups can be used effectively or not.
Assessment
Information about students is crucial to a teacher’s ability to calibrate tasks and lessons to students’ current understanding and skills. Mr. Hernandez and Ms. Kaye have each designed the lesson to afford them critical information about their students’ progress. The tasks they frame create a strategic space for students’ work and for gaining insight into students’ thinking. Ms. Lawrence gets some of the same sort of information from her probing of Jim’s solution. Although Mr. Angelo and Ms. Lawrence get some idea of how students are doing by circulating around the room, they use the questions they ask during class as their primary mode of assessment during the lesson.
In addition to tasks that reveal what students know and can do, the quality of instruction depends on how teachers interpret and use that information. Teachers’ understanding of their students’ work and the progress they are making relies on the teachers’ own understanding of the mathematics and their ability to use that understanding to make sense of what the students are doing. Moreover, after interpreting students’ work, teachers need to be able to use their interpretations productively in making specific instructional decisions: what questions to ask, tasks to pose, homework to assign. Studies show that when teachers learn to see and hear students’ work during a lesson and to use that information to shape their instruction, their instruction becomes clearer, more focused, and more effective.46
More formal sources of assessment information can also help improve the quality of instruction, including homework, project reports, notebooks, journals, quizzes, tests, and examinations. The more precise and detailed the information and the better coordinated it is with curricular goals, the better a resource it is for instruction. Teachers’ ability to interpret and make judicious strategic use of assessment information from many sources is a critical factor in their instructional effectiveness.
Students and Content
Students and Tasks
How well a mathematical task works to support students’ learning is a function both of its quality—that is, of its potential for stimulating mathematics learning—and of the ways students interpret and use it. The tasks Mr. Hernandez designed offer sufficient complexity to be challenging because he has varied the grid from the familiar 10×10 to other configurations. His students can make sense of these tasks and are able to work on them, coming up with solutions that open opportunities for instruction. Had the tasks been either too difficult or too trivial for these students, the tasks might not have worked. One important consideration in designing mathematical tasks, therefore, is that they must take account of what the students already know and must maximize the possibility for the students to make progress in learning the content. This process entails judgments about design so that the tasks anticipate students’ responses and are built on appropriate-sized mathematical steps. All four of our teachers were able to choose and pose problems that engaged their students in addressing the mathematical goals for the lesson. Where the lessons differed was in the mathematical significance of the tasks and in the challenge they posed to students’ thinking and learning.
Practice
Role of practice. To many students, practice is as much a part of studying mathematics as of playing a sport or a musical instrument. The role of practice in mathematics, as in sports or music, is to be able to execute procedures automatically without conscious thought. That is, a procedure is practiced over and over until so-called automaticity is attained.47
The role of practice in mathematics, as in sports or music, is to be able to execute procedures automatically without conscious thought.
There are cognitive benefits to automatization. The more automatically a procedure can be executed, the less mental effort is required. Since each person has a limited amount of mental effort that he or she can expend at any one time, more complex tasks can be done well only when some of the subtasks are automatic.48 Hence, the automatization of mathematical procedures is justifiable when those procedures are regularly required to complete other tasks. For example, basic multiplication combinations such as 4×6=24 and 6×7=42 are needed for estimation, multidigit multiplication, single-digit division, multidigit division, and addition and multiplication of fractions, to name a few. Therefore, multiplication combinations need to be practiced until they can be produced quickly and effortlessly. The availability of calculators and computers raises the question of which mathematical procedures today need to be practiced to the point of automatization. Single-digit whole number addition, subtraction, multiplication, and division certainly need to be automatic, since they are used in almost all other numerical procedures. Opinions vary, however, as to which other procedures should be made automatic.
Kinds of practice. Textbook and worksheet exercises offer the most common kinds of practice used in U.S. mathematics classrooms. Such exercises are used to provide students frequent and repeated opportunities to practice what they have learned. Often the practice is directly associated with the topic of the lesson, with the teacher or other students providing assistance until the student can perform independently. Another approach distributes the practice over a longer period: On any one day, only a few of the exercises assigned might address the lesson topic, and the rest would address topics studied earlier in the year. Such distributed practice is based on the principle that mastery is achieved gradually and once achieved is maintained through regular practice. A number of studies of the U.S. curriculum have concluded that it is too repetitive.49 These criticisms are about topics being retaught year after year, not about students practicing learned concepts and procedures throughout the year to improve efficiency and retention. Ms. Lawrence’s assignment of a mixture of problems is presumably no acci-
dent. Notice that she has even included problems on whole-number addition to help her students maintain their skill with that operation.
Sites for practice that often go unrecognized are problem solving and the learning of new content.50 When a group of primary teachers in several studies shifted their emphasis from skills to problem solving, for example, there was no overall change in their students’ computational performance.51 Their students were still getting ample opportunity to practice computations. Ms. Kaye’s lesson is an example of how practice can be embedded in problem-solving activity. Students can also practice previously learned skills while they are learning new material. Consider how much practice students get with single-digit addition while learning how to add multidigit numbers.
Homework
Homework is widely viewed as a useful supplement to classroom instruction. Little is known, however, about how much or what kinds of homework to assign for learning to be optimal. The limited research on homework has been confined to investigations of the relation between the quantity of homework assigned and students’ achievement test scores. Neither the quality nor the function of homework has been considered.52 In fact, even the definition of homework—done in school or not and with what assistance, if any— has not always been clear. Several useful purposes that homework can serve have been identified, including providing practice, preparing students for the next class, fostering traits such as responsibility and independence, and communicating with the home. Assigning homework for punishment, however, is always inappropriate.53
As a site for practice, homework can be used to increase procedural fluency and to maintain skill. Homework can provide for both focused and distributed practice. When used for practice, homework assignments should be realistic in length and difficulty if students are to complete them independently and successfully. Students, however, need to be able to perform procedures correctly before they undertake practice without supervision. Otherwise, the practice can automatize incorrect procedures, which are then difficult to correct. Further, homework must be monitored and followed up if it is to have instructional value.54 In making her homework assignment, Ms. Lawrence first determines that the students understand the new procedure and can perform it correctly. The next day she will follow up on the assignment by asking the students to check one another’s work on selected problems.
Students can be assigned tasks for homework that might be used to launch the next day’s lesson or to engage the class in an enrichment activity. For example, Mr. Angelo uses the homework to introduce the rule for multiplying by powers of 10. In Mr. Hernandez’s class, students are asked to try the various strategies that have been presented and to think about which one they thought was “best” in preparation for the next day’s discussion.
Homework also provides a means to communicate with parents about the importance of schoolwork and learning. Many opportunities exist to send home assignments that call for relatively little parental involvement. They may require no specialized knowledge, or relatively simple guidelines may be provided. For example, parents or other caregivers can supervise practice on the basic number combinations. Homework support needs to be provided, however, when home environments may make doing homework difficult.
Manipulatives
The use of concrete materials, sometimes termed manipulatives, for teaching mathematics is widely accepted, particularly in the elementary grades. Manipulatives should always be seen as a means and not an end in themselves. They require careful use over sufficient time to allow students to build meaning and make connections. Beginning in the 1960s, manipulatives gained popularity in U.S. elementary school mathematics with the introduction of a variety of concrete materials, including base-10 blocks, Cuisenaire rods, chips for trading, logic blocks, fraction pieces, and Unifix cubes, to name a few.
Manipulatives have had their advocates and critics. Both sides agree, however, that simply putting concrete materials on desks or suggesting to students that they might use manipulatives is not enough to guarantee that students will learn appropriate mathematics from them. The relationship between learning and the use of manipulatives is far more complex than many mathematics educators have thought. Recent research has explored how students interact with manipulatives. Students may not look at these objects the same way adults do, and it can be a challenge for students to see mathematical ideas in them. When students use a manipulative, they need to be helped to see its relevant aspects and to link those aspects to appropriate symbolism and mathematical concepts and operations.55 Observational studies have documented cases in which students were taught to use manipulatives in a prescribed way to perform “wooden algorithms.”56 If students do not see the connections among object, symbol, language, and idea, using a manipula-
tive becomes just one more thing to learn rather than a process leading to a larger mathematical learning goal.57
When used well, manipulatives can enhance student understanding. They can, for example, enable teachers and students to have a conversation that is grounded in a common referential medium, and they can provide material on which students can act productively provided they reflect on their actions in relation to the mathematics being taught.58 The base-10 blocks that Kurt is using in Ms. Kaye’s class provide both student and teacher with a way to discuss the problem that would have been more difficult without the blocks. Research on four successful projects aimed at teaching multidigit number concepts and operations through a problem-solving approach found that, although different in approach, the projects treated the use of conceptual supports, whether manipulatives or diagrams, in similar ways.59 Each project provided sustained opportunities for students to construct connections between the conceptual support, the written symbols, and the number words and to use the object-word-symbol triad in solving multidigit addition and subtraction problems. Manipulatives also help students correct their own errors.60 The evidence indicates, in short, that manipulatives can provide valuable support for student learning when teachers interact over time with the students to help them build links between the object, the symbol, and the mathematical idea both represent.
Calculators
Although calculators are used more frequently than manipulatives in grades 4 and 8, the use of calculators is more controversial in mathematics lessons in grades pre-K-8 than are manipulatives, particularly in the elementary grades. Although mathematics educators have advocated the appropriate use of calculators since the 1970s, persistent concerns have been expressed that an extensive use of calculators in mathematics instruction interferes with students’ mastery of basic skills and the understanding they need for more advanced mathematics.61
A large number of empirical studies of calculator use, including long-term studies,62 have generally shown that the use of calculators does not threaten the development of basic skills and that it can enhance conceptual understanding, strategic competence, and disposition toward mathematics. A meta-analysis of 79 research studies on the effects of calculator was conducted in 1986 and extended in 1992 with nine additional studies.63 This analysis found that with the exception of the fourth grade, students at all
grade levels who used calculators together with traditional instruction maintained their computational skills. For average-ability students, a small negative effect at fourth grade suggested that sustained use of calculators at that grade might hamper the acquisition of basic skills. On the other hand, use of calculators enhanced basic skills acquisition by average-ability students at all other grade levels, so the negative effect at fourth grade might have been an artifact of conditions specific to those studies that included fourth graders. For all ability groups at all grades, problem solving was improved by the use of calculators. The positive effects were found when calculator use was permitted in testing; the effects were weak or absent, but never negative, when testing was conducted without calculators. Students using calculators were also found to possess a better attitude toward mathematics and a better self-concept in mathematics. This meta-analysis of calculator use has been widely cited to support efforts to introduce calculators into mathematics instruction in grades K to 8. Meta-analysis as a procedure for synthesizing research results, however, has not been without its critics.64 Studies included in such metaanalyses often vary in quality and use a variety of different treatments labeled with a single term, in this case “calculator use.”
Long-term studies of calculator use, however, support the findings of the meta-analysis. A study in Sweden found that students in grades 4–6 who used calculators improved in conceptual understanding, the ability to choose the correct operation, and proficiency with estimation and mental arithmetic but did not lose skill in pencil-and-paper calculations when compared with students in traditional classes.65 The students in the experimental classes continued to study algorithms, but they spent relatively less time on algorithms and more on problem solving than students in the traditional classes. In an Australian project involving over 60 teachers and 1,000 students, students who had been given unrestricted access to a calculator beginning in kindergarten were familiar with a wider range of numbers, were better with mental calculations and estimation, and were better able to tackle real-world problems than students who had not had access to calculators. Their pattern of use of standard algorithms, left-to-right algorithms, and invented methods did not vary greatly from that of the children who did not have access to calculators. Further, they did not become reliant on calculators at the expense of other methods of calculations. In sum, no detrimental effects of calculator use were observed.66 These findings are consistent with those from England in which six-year-olds in a calculator awareness project, compared with children in a regular program, demonstrated knowledge of a wider range of numbers, including decimals and negative numbers. Project children also performed
better than traditionally taught children with respect to understanding and mental computations and were more enthusiastic and persistent.67
Calculator use has been increasing in the United States since 1980. In the 1996 NAEP, teachers of 80% of both fourth graders and eighth graders reported that their students had access to calculators at school. Only 33% of the fourth graders were reported to use calculators as frequently as once a week, whereas 76% of the eighth graders reportedly used calculators daily or weekly. These percentages were up from 16% and 56%, respectively, in 1992. Concomitantly, the percentage of students who never or hardly ever used calculators in class was down from 51% to 26% at the fourth grade and from 24% to 9% at the eighth grade.68 On TIMSS similar percentages for calculator use were reported by U.S. teachers. In some countries, including some high-achieving countries (such as Japan and Korea) as well as in some low-achieving countries, mathematics teachers rarely had students use calculators.69 Internationally, there does not appear to be a correlation between calculator use and achievement in mathematics.
The question, therefore, is not whether but how calculators should be used. There is very little empirical research, however, on the effectiveness of various uses of calculators. Issues just beginning to be investigated include when calculators should be introduced, how young children should use them, and how much time needs to be spent on written algorithms when calculators are available. In the experimental projects described above, calculator use was accompanied by instruction on number combinations and traditional written algorithms and by an emphasis on mental calculations. These projects also demonstrate how instructional emphasis in a calculator-inclusive environment can shift from computational procedures to problem solving and mental arithmetic. Although there is substantial support for the use of calculators in school mathematics, their role and place remain open to debate and experimentation.
Issues in Improving Instruction
Research on teaching mathematics offers useful direction for developing instructional practices that lead to mathematical proficiency. The studies we have cited, as well as others too numerous to include, offer a set of recurrent findings worthy of attention. Although these findings are presented in broad strokes, they matter for the finer-grained questions of concern to practitioners and policy makers, parents, and the public. Unless these findings are understood, efforts to improve instructional quality and consequent learning are likely to founder.
First, no instructional practice, commodity, or material exists independently of context and participants as a durable and reliable resource for developing mathematical proficiency. How teachers and students interpret, value, and use such matters as time, curriculum, books, tasks, and calculators shapes whether and how these affect instruction.
Second, effectiveness depends on enactment. The effectiveness of a curriculum, for example, depends not only on its mathematical integrity and organizational design, but also on how usefully it guides instruction. Although analyses of the content of instructional materials are crucial, so too are analyses of how those materials actually play out in lessons day by day across units of instruction: what is taught, in what ways, and what students learn. The same can be said of tools and techniques such as manipulatives, calculators, small-group work, and homework.
Third, teachers and students’ interactions about mathematics iteratively shape the effectiveness of their instructional work. Teachers’ expectations of students can shape the nature of the tasks the teachers pose, what they ask, how long they wait, how and how much encouragement they provide— elements that together compose students’ opportunities to learn as well as their motivation and confidence to learn. The students’ responses, in turn, affect teachers’ estimates of their capacity and progress, shaping their next moves with students.
Although much is known about effective instruction, many questions merit close study if teachers and researchers are to develop the kind of knowledge needed to improve instruction. We conclude with some core issues crucial to building the knowledge base on teaching and learning for mathematical proficiency.
The first issues center on our myopia in examining the research. The research on teaching that we reviewed was almost entirely U.S. based. Closer probes of practice in other social, political, and cultural settings may challenge many current assumptions about effective instruction in mathematics. Despite an intense and appropriate interest in practices in other countries, Americans know too little about instruction or its effects in other systems. The interactive framework in this chapter offers a perspective that could be used to design studies to look across systems. Comparative research that affords opportunities to learn about key elements of teaching and learning, as well as examining both practice and the environments that shape it, would be enormously helpful in developing a greater knowledge of teaching and learning for mathematical proficiency. Researchers need to address not just what the curriculum is but how it is used and what teachers and students do with
it, not just how much time is allocated for mathematics but how that time is spent. They need to investigate not just whether calculators or other resources are used, but how they are used.70 Research that looks across countries can provide a sharper picture of what matters in instruction aimed at developing proficiency.
A second set of issues concerns instruction over time. Although learning is fundamentally temporal, too little research has addressed the ways in which instruction develops over time. Many studies are restricted to isolated fragments of teaching and learning, providing little understanding of how the interactions of teachers, students, and content emerge over time, and how earlier interactions shape later ones. How do ideas developed in class affect later work, and what affects teachers’ and students’ ability and inclination to make such links, as well as their use of such connections over time? How is time used, and how does its use by teachers and students affect the quality of instruction?
A third arena concerns students and how their diversity affects instruction. Too little research offers insight into the experience of students and how the instruction offered, together with their responses to it, affects their learning. Still more important, there are too few well-designed studies that would offer insight into how instruction might be developed to work effectively for all students. Too often, research on classroom teaching and learning either studies faceless, colorless students and teachers out of context, or it is situated in particular contexts but lacks a design that permits analyses that could provide the knowledge needed for effective instruction in mathematics.
Fourth, too little research has addressed what it takes for students to learn mathematics in class. What do students need to do, and know how to do, in order to profit from the instruction offered by each of our four teachers? A cursory glance at any mathematics class makes plain that the skills, abilities, knowledge, and dispositions displayed by students are not the same, and yet teachers and researchers rarely attend to what students need to know and be able to do in order to use instruction effectively. People seem to assume implicitly that instruction acts on students and that opportunities to learn are actually moments of learning. Research that examined both what students have to know and do in mathematics instruction and what teachers can do to enable all students to make use of that instruction would add significantly to the knowledge base on teaching and learning mathematics.
A fifth set of issues has to do with reconnecting research on teacher knowledge with instructional effectiveness. Although most people believe that teachers’ knowledge of mathematics and of students makes a difference for
the quality of teaching, little empirical confirmation of this belief can be found. Moreover, too little is known about the mathematical knowledge that teachers need and how it is used in instruction. We discuss this point more in chapter 10, but it is important to the discussion in this chapter, too. Every time we reiterate that how teachers use texts, manipulatives, and calculators makes the difference, we are hovering around questions concerning what teachers know and how they make use of that knowledge in teaching.
Finally, too little of the extant research probes the work of teaching at a sufficiently fine grain to contribute to the development of a conceptual and practical language of practice. Much of the interactive work in instruction remains unexamined, which leaves to teachers the unnecessary challenge of reinventing their practice from scratch, armed with only general advice. Suggestions that a class “discuss the solutions to a problem” provides little specificity about what constitutes a productive discussion and runs the risk of a free-for-all session that resembles sharing more than instruction. Research needs to be designed to illuminate what is entailed in a “discussion” and to probe the specific moves that teachers and students engage in that lead to productive rather than an unproductive discussions.
Instruction that develops mathematical proficiency is neither simple, common, nor well understood. It comes in many forms and can follow a variety of paths. As this chapter demonstrates, such instruction offers numerous fertile sites for research that could make a profound difference in teachers’ practice and their students’ learning.
Notes
References
Argys, L.M., Rees, D.I., & Brewer, D.J. (1996). Detracking America’s schools: Equity at zero cost? Journal of Policy Analysis and Management, 15, 623–645.
Ball, D.L. (1992a). Constructing new forms of teaching: Subject matter knowledge in inservice teacher education. Journal of Teacher Education, 43, 347–356.
Ball, D.L. (1992b). Magical hopes: Manipulatives and the reform of math education. American Educator, 14, 46–47.
Ball, D.L., & Bass, H. (2000). Making believe: The collective construction of public mathematical knowledge in the elementary classroom. In D.Phillips (Ed.), Constructivism in education (Ninety-ninth Yearbook of the National Society for the Study of Education , Part 1, pp. 193–224). Chicago: University of Chicago Press.
Bandura, A. (1997). Self-efficacy: The exercise of control. New York: Freeman.
Bandura, A., & Schunk, D. (1981). Cultivating competence, self-efficacy, and intrinsic interest through proximal self-motivation. Journal of Personality and Social Psychology, 41, 586–598.
Baroody, A.J. (1987). Children’s mathematical thinking: A developmental framework for preschool, primary, and special education teachers. New York: Teachers College Press.
Baroody, A.J. (1996). An investigative approach to teaching children labeled learning disabled. In D.K.Reid, W.P.Hresko, & H.L.Swanson (Eds.), Cognitive approaches to learning disabilities (3rd ed., pp. 545–615). Austin, TX: Pro-Ed.
Baroody, A.J. (1999). The development of basic number and arithmetic knowledge among children classified as mentally retarded. In L.M.Glidden (Ed.), International review of research in mental retardation (vol. 22, pp. 51–103). New York: Academic Press.
Becker, J. (1981). Differential treatment of females and males in mathematics class. Journal for Research in Mathematics Education, 12, 40–53.
Berliner, D. (1979). Tempus educare. In P.Peterson & H.Walberg (Eds.), Research on teaching: Concepts, findings, and implications. Berkeley, CA: McCutchan.
Berliner, D., & Biddle, B. (1995). The manufactured crisis: Myth, fraud, and the attack on America’s public schools. New York: Addison-Wesley.
Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex and setting. Buckingham, UK: Open University Press.
Brolin, H., & Björk, L-E. (1992). Introducing calculators in Swedish schools. In J.T.Fey and C.R.Hirsch (Eds.), Calculators in mathematics education (1992 Yearbook of the National Council of Teachers of Mathematics, pp. 226–232). Reston, VA: NCTM.
Brophy, J. (1998). Motivating students to learn. Boston: McGraw-Hill.
Brophy, J., & Kher, N. (1986). Teacher socialization as a mechanism for developing student motivation to learn. In R.Feldman (Ed.), Social psychology applied to education (pp. 256–288). New York: Cambridge University Press.
Campbell, P.F. (1996). Empowering children and teachers in the elementary mathematics classrooms of urban schools . Urban Education, 30, 449–475.
Case, R. (1985). Intellectual development: Birth to adulthood. New York: Academic Press.
Carpenter, T.P., Fennema, E., Fuson, K., Hiebert, J.Human, P., Murray, H., Olivier, A., & Wearne, D. (1999). Learning basic number concepts and skills as problem solving. In E.Fennema & T.A.Romberg, Mathematics classrooms that promote understanding (pp. 45–61). Mahwah, NJ: Erlbaum.
Carpenter, T.P., Fennema, E., Peterson, P.L., Chiang, C.P., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26, 499–531.
Cawley, J.F. (1985). Cognition and the learning disabled. In J.F.Cawley (Ed.), Cognitive strategies and mathematics for the learning disabled (pp. 1–32). Rockville, MD: Aspen.
Clark, C., & Yinger, R. (1979). Teachers’ thinking. In P.L.Peterson & H.J.Walberg (Eds.), Research on teaching: Concepts, findings, and implications (pp. 231–263). Berkeley, CA: McCutchan.
Cobb, P., Boufi, A., McClain, K., & Whitenack, J. (1997). Reflective discourse and collective reflection. Journal for Research in Mathematics Education, 28, 258–277.
Cobb, P., Wood, T., Yackel, E., Nicholls, J., Wheatley, G., Trigatti, B., & Perlwitz, M. (1991). Assessment of a problem-centered second-grade mathematics project. Journal for Research in Mathematics Education, 22, 3–29.
Cohen, D.K. (1990). Revolution in one classroom: The case of Mrs. Oublier. Education Evaluation and Policy Analysis, 12, 311–329.
Cohen, D.K., & Ball, D.L. (1999). Instruction, capacity, and improvement (CPRE Research Report No. RR-043). Philadelphia: University of Pennsylvania, Consortium for Policy Research in Education. Available: http://www.gse.upenn.edu/cpre/docs/pubs/rr43.pdf. [July 10, 2001].
Cohen, D.K., & Ball, D.L. (2000, April). Instructional innovation: Reconsidering the story. Paper presented at the meeting of the American Educational Research Association, New Orleans.
Cohen, D.K., & Ball, D.L. (in press). Making change: Instruction and its improvement. Phi Delta Kappan.
Cooper, H. (1989). Homework. New York: Longman.
Donlan, C. (1998). Number without language? Studies of children with specific language impairments. In C.Donlan (Ed.), The development of mathematical skills (pp. 255–274). East Sussex, UK: Psychology Press.
Doyle, W. (1983). Academic work. Review of Educational Research, 53, 159–199.
Doyle, W. (1988). Work in mathematics classes: The context of students’ thinking during instruction. Educational Psychologist, 23, 167–180.
Druckman, D., & Bjork, R.A. (Eds). (1994). Learning, remembering, believing: Enhancing human performance. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/2303.html. [July 10, 2001].
Dweck, C., & Elliott, E. (1983). Achievement motivation. In E.M.Heatherington (Ed.), P.H.Mussen (Series Ed.), Handbook of child psychology: Vol. 4. Socialization, personality, and social development (4th ed., pp. 643–691). New York: Wiley.
Ellis, S.A., & Gauvain, M. (1992). Social cultural influences on children’s collaborative interactions. In L.T.Winegar & J.Valsiner (Eds.), Children’s development within social context (pp. 155–180). Hillsdale, NJ: Erlbaum.
Epstein, J. (1988). Homework practices, achievements, and behaviors of elementary school students (Report No. 26). Baltimore: Johns Hopkins University, Center for Research on Elementary and Middle Schools. (ERIC Document Reproduction Service No. ED 301 322).
Epstein, J. (1998, April). Interactive homework: Effective strategies to connect home and school. Paper presented at the meeting of the American Educational Research Association, San Diego, CA.
Feather, N. (Ed.). (1982). Expectations and actions. Hillsdale, NJ: Erlbaum.
Fennema, E., Carpenter, T.P., Franke, M.L., Levi, L., Jacobs, V.R., & Empson, S.B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27, 403–434.
Fey, J.T. (1979). Mathematics teaching today: Perspectives from three national surveys. Mathematics Teacher, 72, 490–504.
Fey, J.T. (1989). Technology and mathematics education: A survey of recent developments and important problems. Educational Studies in Mathematics, 20, 237–272.
Flanders, J.R. (1987, September). How much of the content in mathematics textbooks is new? Arithmetic Teacher, 35, 1, 18–23.
Foster, M. (1995). African American teachers and culturally relevant pedagogy. In J.A. Banks & C.M.Banks (Eds.), Handbook of research on multicultural education (pp. 570– 581). New York: Macmillan.
Freeman, D., & Porter, A. (1989). Do textbooks dictate the content of mathematics instruction in elementary schools? American Educational Research Journal, 26, 403– 421.
Fuson, K.C. (1986). Roles of representation and verbalization in the teaching of multidigit addition and subtraction. European Journal of Psychology of Education, 1, 35–56.
Fuson, K.C., Wearne, D., Hiebert, J.C., Murray, H.G., Human, P.G., Olivier, A.I, Carpenter, T.P., & Fennema E. (1997). Children’s conceptual structures for multidigit numbers and methods of multidigit addition and subtraction. Journal for Research in Mathematics Education, 28, 130–162.
Fuson, K.C., & Briars, D.J. (1990). Using a base-ten block learning/teaching approach for first and second grade place-value and multidigit addition and subtraction. Journal for Research in Mathematics Education 21, 180–206.
Geary, D.C. (1993). Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin, 114, 345–362.
Geary, D.C. (1994). Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association.
Good, T.L., & Brophy, J.E. (2000). Looking in classrooms (8th ed.). New York: Longman.
Good, T.L., Grouws, D.A., & Ebmeier, H. (1983). Active teaching. New York: Longman.
Groves, S. (1993). The effect of calculator use on third graders’ solutions of real world division and multiplication problems. In I.Hirabayashi, N.Nodha, K.Shigematsu, & F.L.Lin (Eds.), Proceedings of the Seventeenth International Conference for the Psychology of Mathematics Education, (vol. 2, pp. 9–16). Tsukuba, Japan: PME Program Committee. (ERIC Document Reproduction Service No. ED 383 536).
Groves, S. (1994a). Calculators: A learning environment to promote number sense. Paper presented at the meeting of the American Educational Research Association, New Orleans. (ERIC Document Reproduction Service No. ED 373 969).
Groves, S. (1994b). The effect of calculator use on third and fourth graders’ computation and choice of calculating device. In J.da Ponte & J.F.Matos (Eds.), Proceedings of the Eighteenth International Conference for the Psychology of Mathematics Education (vol. 3, pp. 33–40). Lisbon, Portugal: PME Program Committee. (ERIC Document Reproduction Service No. ED 383 537).
Hatano, G. (1988). Social and motivational bases for mathematical understanding. In G. B.Saxe & M.Gearhart (Eds.), Children’s mathematics (pp. 55–70). San Francisco: Jossey-Bass.
Hart, K. (1996). What responsibility do researchers have to mathematics teachers and children? In C.Alsina, J.M.Alvarez, B.Hodgson, C.Laborde, & A.Perez (Eds.), 8th International Congress on Mathematics Education: Selected lectures (pp. 251–256). Seville, Spain: S.A.E.M.Thales.
Hembree, R., & Dessart, D.J. (1986). Effects of hand-held calculators in precollege mathematics education: A meta-analysis. Journal for Research in Mathematics Education, 17, 83–99.
Hembree R., & Dessart, D.J. (1992). Research on calculators in mathematics education. In J.Fey & C.Hirsch (Eds.), Calculators in mathematics education (pp. 23–32). Reston, VA: National Council of Teachers of Mathematics.
Henningsen, M., & Stein, M.K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28, 524–549.
Hiebert, J. (1990). The role of routine procedures in the development of mathematical competence. In T.J.Cooney & C.R.Hirsch (Eds.), Teaching and learning mathematics in the 1990s (1990 Yearbook of the National Council of Teachers of Mathematics, pp. 31–40). Reston, VA: NCTM.
Hiebert, J., & Wearne, D. (1993). Instructional tasks, classroom discourse, and student learning in second grade. American Educational Research Journal, 30, 393–425.
Hiebert, J., Carpenter, T.P., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Husén, T. (Ed.). (1967). International study of achievement in mathematics: A comparative study of twelve countries (vol. 2). New York: Wiley.
Johnson, D., Johnson, R., & Maruyama, G. (1983). Interdependence and interpersonal attraction among heterogeneous and homogeneous individuals: A theoretical formulation and a meta-analysis of the research. Review of Educational Research, 53, 5– 54.
Knapp M.S., Shields, P.M., Turnbull, B.J. (1995). Academic challenge in high-poverty classrooms. Phi Delta Kappan, 76, 770–776.
Knapp, M.S. (1995). Teaching for meaning in high poverty classrooms. New York: Teachers College Press.
Kulik, J.A. (1992). An analysis of the research on ability grouping: Historical and contemporary perspectives (Ability Grouping Research-Based Decision Making Series, No. 9204). Ann Arbor: University of Michigan.
Ladson-Billings, G. (1999). Mathematics for all? Perspectives on the mathematics achievement gap. Unpublished paper prepared for the National Research Council, Washington, DC.
Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American Educational Research Journal, 27, 29–63.
Leder, G.C. (1987). Teacher student interaction: A case study. Educational Studies in Mathematics, 18, 255–271.
Leder, G.C. (1992). Mathematics and gender: Changing perspectives. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 597–622). New York: Macmillan.
Linchevski, L., & Kutscher, F. (1998). Tell me with whom you’re learning, and I’ll tell you how much you’ve learned: Mixed-ability versus same-ability grouping in mathematics. Journal for Research in Mathematics Education, 29, 533–554.
Loveless, T. (1998). The tracking and ability grouping debate. Fordham Report, 2(8), 1– 27. Available: http://www.edexcellence.net/library/track.html. [July 10, 2001].
Mason, D.A., & Good, T.L. (1993). Effects of two-group and whole-class teaching on regrouped elementary students’ mathematics achievement. American Educational Research Journal, 30, 328–360.
Mason, D., Schroeter, D., Combs, R., & Washington, K. (1992). Assigning average achieving eighth graders to advanced mathematics classes in an urban junior high. Elementary School Journal, 92, 587–599.
McKnight, C.C., Crosswhite, F.J., Dossey, J.A., Kifer, E., Swafford, J.O., Travers, K.J., & Cooney, T.J. (1987). The underachieving curriculum: Assessing U.S. schools mathematics from an international perspective. Champaign, IL: Stipes.
Mitchell, J.H., Hawkins, E.F., Jakwerth, P.M,. Stancavage, F.B., & Dossey, J.A. (1999). Student work and teacher practices in mathematics (NCES 1999–453). Washington, DC: National Center for Educational Statistics. Available: http://nces.ed.gov/spider/webspider/1999453.shtml. [July 10, 2001].
Miller, D., & Kelley, M. (1991). Interventions for improving homework performance: A critical review. School Psychology Quarterly, 6, 174–185.
Mosteller, F., Light, R.J., & Sachs, J.A. (1996). Sustained inquiry in education: Lessons from skill grouping and class size. Harvard Educational Review, 66, 797–842.
National Council of Teachers of Mathematics. (1974, December). NCTM Board approves policy statement on the use of minicalculators in the mathematics classroom. NCTM Newsletter, 11, 3.
National Research Council. (1999a). Global perspectives for local action: Using TIMSS to improve U.S. mathematics and science education. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/9605.html. [July 10, 2001].
National Research Council. (1999b). Improving student learning: A strategic plan for education research and its utilization. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/6488.html. [July 10, 2001].
Nunes, T., & Moreno, C. (1998). Is hearing impairment a cause of difficulties in learning mathematics? In C.Donlan (Ed.), The development of mathematical skills (pp. 227–254). East Sussex, UK: Psychology Press.
Oakes, J. (1985). Keeping track: How schools structure inequality. New Haven: Yale University Press.
Oakes, J., Gamoran, A., & Page, R.N. (1992). Curriculum differentiation: Opportunities, outcomes, and meanings. In P.W.Jackson (Ed.), Handbook of research on curriculum (pp. 570–608). New York: Macmillan.
Porter, A. (1993). School delivery standards. Educational Research, 22, 24–30.
Resnick, L., & Omanson, S. (1987). Learning to understand arithmetic. In R.Glaser (Ed.), Advances in instructional psychology (vol. 3, pp. 41–95). Hillsdale, NJ: Erlbaum.
Ruthven, K. (1996). Calculators in mathematics curriculum: The scope of personal computational technology. In A.J.Bishop, K Clements, C.Keitel, J.Kilpatrick, & C. Laborde (Eds.), International handbook of mathematics education (pp. 435–468). Dordrecht, The Netherlands: Kluwer.
Ruthven, K. (1998). The use of mental, written and calculator strategies of numerical computation by upper primary pupils within a “calculator-aware” curriculum. British Educational Research Journal, 24, 21–42.
Schmidt, W.H., McKnight, C.C., & Raizen, S.A. (1997). A splintered vision: An investigation of U.S. science and mathematics education. Dordrecht, The Netherlands: Kluwer.
Sharan S. (1980). Cooperative learning in small groups: Recent methods and effects on achievement, attitudes, and ethnic relations. Review of Education Research, 50, 241– 271.
Shavelson, R.J., & Stern, P. (1981). Research on teachers’ pedagogical thoughts, judgments, decisions, and behavior. Review of Educational Research, 51, 455–498.
Shuard, H. (1992). CAN: Calculator use in the primary grades in England and Wales. In J.T.Fey and C.R.Hirsch (Eds.), Calculators in mathematics education (1992 Yearbook of the National Council of Teachers of Mathematics, pp. 33–45). Reston, VA: NCTM.
Siegler, R.S., & Stern, E. (in press). Conscious and unconscious strategy discoveries: A microgenetic analysis. Journal of Experimental Psychology: General.
Silver, E.A., & Stein, M. (1996). The QUASAR Project: The “revolution of the possible” in mathematics instructional reform in urban middle schools. Urban Education, 30, 476–521.
Slavin, R.E. (1980). Cooperative learning. Review of Educational Research, 50, 315–342.
Slavin, R.E. (1983). Cooperative learning. New York: Longman.
Slavin, R.E. (1987). Ability grouping and student achievement in elementary schools: A best-evidence synthesis. Review of Educational Research, 57, 293–336.
Slavin, R.E. (1993). Ability grouping in the middle grades: Achievement effects and alternatives. Elementary School Journal, 93, 535–552.
Slavin, R.E. (1995). Cooperative learning: Theory, research, and practice (2nd ed.). Boston: Allyn & Bacon.
Smith, J.P., III. (1996). Efficacy and teaching mathematics by telling: A challenge for reform. Journal for Research in Mathematics Education, 27, 387–402.
Sophian, C. (1997). Beyond competence: The significance of performance for conceptual development. Cognitive Development, 12, 281–303.
Steele, C. (1992, April). Race and the schooling of black Americans. Atlantic Monthly, pp. 68–78.
Stein, M.K., Grover, B.W., & Henningsen, M. (1996). Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. American Educational Research Journal, 33, 455–488.
Stevenson, H.W., & Stigler, J.W. (1992). The learning gap: Why our schools are failing and what we can learn from Japanese and Chinese education. New York: Simon & Schuster.
Stigler, J.W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York: Free Press.
Thompson, A.G., & Briars, D.J. (1989). Assessing students’ learning to inform teaching: The message in NCTM’s Evaluation Standards. Arithmetic Teacher, 37 (4), 22–26.
Thompson, P.W., & Lambdin, D. (1994). Research into practice: Concrete materials and teaching for mathematical understanding. Arithmetic Teacher, 41, 556–558.
Thornton, C.A., & Bley, N.S. (1994). Windows of opportunity: Mathematics for students with special needs. Reston, VA: National Council of Teachers of Mathematics.
Wood, T. (1999). Creating a context for argument in mathematics class. Journal for Research in Mathematics Education, 30, 171–191.
Wearne, D., & Hiebert, J. (1988). A cognitive approach to meaningful mathematics instruction: Testing a local theory using decimal numbers. Journal for Research in Mathematics Education, 19, 371–384.
























































