6
The Design of Learning Environments
In this chapter we discuss implications of new knowledge about learning for the design of learning environments, especially schools. Learning theory does not provide a simple recipe for designing effective learning environments; similarly, physics constrains but does not dictate how to build a bridge (e.g., Simon, 1969). Nevertheless, new developments in the science of learning raise important questions about the design of learning environments—questions that suggest the value of rethinking what is taught, how it is taught, and how it is assessed. The focus in this chapter is on general characteristics of learning environments that need to be examined in light of new developments in the science of learning; Chapter 7 provides specific examples of instruction in the areas of mathematics, science, and history—examples that make the arguments in the present chapter more concrete.
We begin our discussion of learning environments by revisiting a point made in Chapter 1—that the learning goals for schools have undergone major changes during the past century. Everyone expects much more from today’s schools than was expected 100 years ago. A fundamental tenet of modern learning theory is that different kinds of learning goals require different approaches to instruction (Chapter 3); new goals for education require changes in opportunities to learn. After discussing changes in goals, we explore the design of learning environments from four perspectives that appear to be particularly important given current data about human learning, namely, the degree to which learning environments are learner centered, knowledge centered, assessment centered, and community centered. Later, we define these perspectives and explain how they relate to the preceding discussions in Chapters 1–4.
CHANGES IN EDUCATIONAL GOALS
As discussed in Chapter 1, educational goals for the twenty-first century are very different from the goals of earlier times. This shift is important to keep in mind when considering claims that schools are “getting worse.” In
many cases, schools seem to be functioning as well as ever, but the challenges and expectations have changed quite dramatically (e.g., Bruer, 1993; Resnick, 1987).
Consider the goals of schooling in the early 1800s. Instruction in writing focused on the mechanics of making notation as dictated by the teacher, transforming oral messages into written ones. It was not until the mid to late 1800s that writing began to be taught on a mass level in most European countries, and school children began to be asked to compose their own written texts. Even then, writing instruction was largely aimed at giving children the capacity to closely imitate very simple text forms. It was not until the 1930s that the idea emerged of primary school students expressing themselves in writing (Alcorta, 1994; Schneuwly, 1994). As in writing, it was not until relatively recently that analysis and interpretation of what is read became an expectation of skilled reading by all school children. Overall, the definition of functional literacy changed from being able to sign one’s name to word decoding to reading for new information (Resnick and Resnick, 1977); see Box 6.1.
In the early 1900s, the challenge of providing mass education was seen by many as analogous to mass production in factories. School administrators were eager to make use of the “scientific” organization of factories to structure efficient classrooms. Children were regarded as raw materials to be efficiently processed by technical workers (the teachers) to reach the end product (Bennett and LeCompte, 1990; Callahan, 1962; Kliebard, 1975). This approach attempted to sort the raw materials (the children) so that they could be treated somewhat as an assembly line. Teachers were viewed as workers whose job was to carry out directives from their superiors—the efficiency experts of schooling (administrators and researchers).
The emulation of factory efficiency fostered the development of standardized tests for measurement of the “product,” of clerical work by teachers to keep records of costs and progress (often at the expense of teaching), and of “management” of teaching by central district authorities who had little knowledge of educational practice or philosophy (Callahan, 1962). In short, the factory model affected the design of curriculum, instruction, and assessment in schools.
Today, students need to understand the current state of their knowledge and to build on it, improve it, and make decisions in the face of uncertainty (Talbert and McLaughlin, 1993). These two notions of knowledge were identified by John Dewey (1916) as “records” of previous cultural accomplishments and engagement in active processes as represented by the phrase “to do.” For example, doing mathematics involves solving problems, abstracting, inventing, proving (see, e.g., Romberg, 1983). Doing history involves the construction and evaluation of historical documents (see, e.g., Wineberg, 1996). Doing science includes such activities as testing theories
|
BOX 6.1 Literacy: Then and Now Colonists were literate enough if they could sign their name, or even an X, on deeds. When immigrants arrived in large numbers in the 1800s, educators urged schools to deliver “recitation literacy” to the foreign children who filled the schoolrooms. That literacy was the ability to hold a book and reel off memorized portions of basic American texts such as the opening paragraph of the Declaration of Independence, a part of the Gettysburg address, or some Bryant or Longfellow. With the coming of World War I, and the prospect of large numbers of men handling new equipment in foreign countries, Army testers redefined reading. Suddenly, to the dismay of men used to reading familiar passages, passing the army reading test meant being able to make sense, on the spot, of never-before-seen text. Currently, that kind of “extraction literacy,” revolutionary in 1914, looks meager. Finding out who, what, when, where or how simply does not yield the inferences, questions, or ideas we now think of as defining full or “higher literacy.” The idea of a classroom where young women, poor and minority students, and learning disabled students all read (not recite) and write about (not copy) Shakespeare or Steinbeck is a radical and hopeful departure from the long-running conception of literacy as serviceable skills for the many and generative, reflective reading and writing for the few (Wolf, 1988:1). |
through experimentation and observation (e.g., Lehrer and Schauble, 1996a, b; Linn, 1992, 1994; Schwab, 1978). Society envisions graduates of school systems who can identify and solve problems and make contributions to society throughout their lifetime—who display the qualities of “adaptive expertise” discussed in Chapter 3. To achieve this vision requires rethinking what is taught, how teachers teach, and how what students learn is assessed.
The remainder of this chapter is organized around Figure 6.1, which illustrates four perspectives on learning environments that seem particularly important given the principles of learning discussed in earlier chapters. Although we discuss these perspectives separately, they need to be conceptualized as a system of interconnected components that mutually support one another (e.g., Brown and Campione, 1996); we first discuss each perspective separately and then describe how they interrelate.
LEARNER-CENTERED ENVIRONMENTS
We use the term “learner centered” to refer to environments that pay careful attention to the knowledge, skills, attitudes, and beliefs that learners bring to the educational setting. This term includes teaching practices that
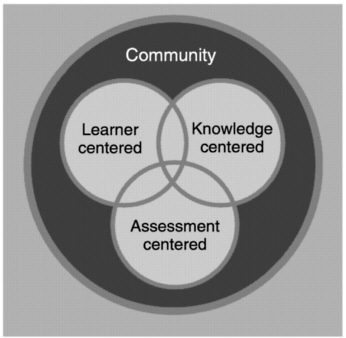
FIGURE 6.1 Perspectives on learning environments. SOURCE: Bransford et al. (1998).
have been called “culturally responsive,” “culturally appropriate,” “culturally compatible,” and “culturally relevant” (Ladson-Billings, 1995). The term also fits the concept of “diagnostic teaching” (Bell et al., 1980): attempting to discover what students think in relation to the problems on hand, discussing their misconceptions sensitively, and giving them situations to go on thinking about which will enable them to readjust their ideas (Bell, 1982a:7). Teachers who are learner centered recognize the importance of building on the conceptual and cultural knowledge that students bring with them to the classroom (see Chapters 3 and 4).
Diagnostic teaching provides an example of starting from the structure of a child’s knowledge. The information on which to base a diagnosis may be acquired through observation, questioning and conversation, and reflection on the products of student activity. A key strategy is to prompt children to explain and develop their knowledge structures by asking them to make predictions about various situations and explain the reasons for their predictions. By selecting critical tasks that embody known misconceptions, teachers can help students test their thinking and see how and why various ideas might need to change (Bell, 1982a, b, 1985; Bell et al., 1986; Bell and Purdy, 1985). The model is one of engaging students in cognitive conflict and then having discussions about conflicting viewpoints (see Piaget, 1973; Festinger, 1957). “To promote learning, it is important to focus on controlled changes
of structure in a fixed context…or on deliberate transfer of a structure from one context to another” (Bell, 1985:72; see Chapter 7).
Learner-centered instruction also includes a sensitivity to the cultural practices of students and the effect of those practices on classroom learning. In a study of the Kamehameha School in Hawaii, teachers were deliberate in learning about students’ home and community cultural practices and language use and incorporated them in classroom literacy instruction (Au and Jordan, 1981). After using the native Hawaiian “talk-story” (jointly produced student narratives), shifting the focus of instruction from decoding to comprehending, and including students’ home experiences as a part of the discussion of reading materials, students demonstrated significant improvement in standardized test performance in reading.
Learner-centered teachers also respect the language practices of their students because they provide a basis for further learning. In science, one standard way of talking in both school and professional science is impersonal and expository, without any reference to personal or social intentions or experiences (Lemke, 1990; Wertsch, 1991). This way, which predominates in schools, privileges middle-class, mainstream ways of knowing and constitutes a barrier for students from other backgrounds who do not come to school already practiced in “school talk” (Heath, 1983). Everyday and scientific discourses need to be coordinated to assist students’ scientific understanding.
In science discourse as it develops in most classrooms, students’ talk frequently expresses multiple intentions or voices (see Ballenger, 1997; Bakhtin, 1984; Warren and Rosebery, 1996; Wertsch, 1991). In their narratives and arguments, students express both scientific and social intentions: scientific in that the students present evidence in support of a scientific argument; social in that they also talk about themselves as certain types of people (e.g., virtuous, honest, trustworthy). If the responses of other students and the teacher to these multivoiced narratives are always keyed to the scientific point, it helps to shape the meaning that is taken from them and relates them back to the context of the unfolding scientific argument (Ballenger, 1997). In standard science lessons, the scientific point in the talk of many students, particularly those whose discourse is not mainstream, is often missed, and the social intention is often devalued (Lemke, 1990; Michaels and Bruce, 1989; Wertsch, 1991; see Chapter 7).
In another example of connecting everyday talk and school talk, African American high school students were shown that many of their forms of everyday speech were examples of a very high form of literacy that was taught in school, but never before connected with their everyday experience (Lee, 1991, 1992). Like Proust who discovered he had been speaking prose all of his life, the students discovered that they were fluent in a set of competencies that were considered academically advanced.
Overall, learner-centered environments include teachers who are aware that learners construct their own meanings, beginning with the beliefs, understandings, and cultural practices they bring to the classroom. If teaching is conceived as constructing a bridge between the subject matter and the student, learner-centered teachers keep a constant eye on both ends of the bridge. The teachers attempt to get a sense of what students know and can do as well as their interests and passions—what each student knows, cares about, is able to do, and wants to do. Accomplished teachers “give learners reason,” by respecting and understanding learners’ prior experiences and understandings, assuming that these can serve as a foundation on which to build bridges to new understandings (Duckworth, 1987). Chapter 7 illustrates how these bridges can be built.
KNOWLEDGE-CENTERED ENVIRONMENTS
Environments that are solely learner centered would not necessarily help students acquire the knowledge and skills necessary to function effectively in society. As noted in Chapter 2, the ability of experts to think and solve problems is not simply due to a generic set of “thinking skills” or strategies but, instead, requires well-organized bodies of knowledge that support planning and strategic thinking. Knowledge-centered environments take seriously the need to help students become knowledgeable (Bruner, 1981) by learning in ways that lead to understanding and subsequent transfer. Current knowledge on learning and transfer (Chapter 3) and development (Chapter 4) provide important guidelines for achieving these goals. Standards in areas such as mathematics and science help define the knowledge and competencies that students need to acquire (e.g., American Association for the Advancement of Science, 1989; National Council of Teachers of Mathematics, 1989; National Research Council, 1996).
Knowledge-centered environments intersect with learner-centered environments when instruction begins with a concern for students’ initial preconceptions about the subject matter. The story Fish Is Fish (Chapter 1) illustrates how people construct new knowledge based on their current knowledge. Without carefully considering the knowledge that students’ bring to the learning situation, it is difficult to predict what they will understand about new information that is presented to them (see Chapters 3 and 4).
Knowledge-centered environments also focus on the kinds of information and activities that help students develop an understanding of disciplines (e.g., Prawat et al., 1992). This focus requires a critical examination of existing curricula. In history, a widely used history text on the American Revolution left out crucial information necessary to understand rather than merely memorize (Beck et al., 1989, 1991). In science, existing curricula tend to overemphasize facts and underemphasize “doing science” to ex-
plore and test big ideas (American Association for the Advancement of Science, 1989; National Research Council, 1996). As noted in Chapter 2, the Third International Mathematics and Science Study (Schmidt et al., 1997) characterized American curricula in mathematics and science as being “a mile wide and an inch deep.” (Examples of teaching for depth rather than breadth are illustrated in Chapter 7.)
As discussed in the first part of this book, knowledge-centered environments also include an emphasis on sense-making—on helping students become metacognitive by expecting new information to make sense and asking for clarification when it doesn’t (e.g., Palincsar and Brown, 1984; Schoenfeld, 1983, 1985, 1991). A concern with sense-making raises questions about many existing curricula. For example, it has been argued that many mathematics curricula emphasize
…not so much a form of thinking as a substitute for thinking. The process of calculation or computation only involves the deployment of a set routine with no room for ingenuity or flair, no place for guess work or surprise, no chance for discovery, no need for the human being, in fact (Scheffler, 1975:184).
The argument here is not that students should never learn to compute, but that they should also learn other things about mathematics, especially the fact that it is possible for them to make sense of mathematics and to think mathematically (e.g., Cobb et al., 1992).
There are interesting new approaches to the development of curricula that support learning with understanding and encourage sense making. One is “progressive formalization,” which begins with the informal ideas that students bring to school and gradually helps them see how these ideas can be transformed and formalized. Instructional units encourage students to build on their informal ideas in a gradual but structured manner so that they acquire the concepts and procedures of a discipline.
The idea of progressive formalization is exemplified by the algebra strand for middle school students using Mathematics in Context (National Center for Research in Mathematical Sciences Education and Freudenthal Institute, 1997). It begins by having students use their own words, pictures, or diagrams to describe mathematical situations to organize their own knowledge and work and to explain their strategies. In later units, students gradually begin to use symbols to describe situations, organize their mathematical work, or express their strategies. At this level, students devise their own symbols or learn some nonconventional notation. Their representations of problem situations and explanations of their work are a mixture of words and symbols. Later, students learn and use standard conventional algebraic notation for writing expressions and equations, for manipulating algebraic expressions and solving equations, and for graphing equations. Movement along this continuum is not necessarily smooth, nor all in one direction.
Although students are actually doing algebra less formally in the earlier grades, they are not forced to generalize their knowledge to a more formal level, nor to operate at a more formal level, before they have had sufficient experience with the underlying concepts. Thus, students may move back and forth among levels of formality depending on the problem situation or on the mathematics involved.
Central to curriculum frameworks such as “progressive formalization” are questions about what is developmentally appropriate to teach at various ages. Such questions represent another example of overlap between learnercentered and knowledge-centered perspectives. Older views that young children are incapable of complex reasoning have been replaced by evidence that children are capable of sophisticated levels of thinking and reasoning when they have the knowledge necessary to support these activities (see Chapter 4). An impressive body of research shows the potential benefit of early access by students to important conceptual ideas. In classrooms using a form of “cognitively guided” instruction in geometry, second-grade children’s skills for representing and visualizing three-dimensional forms exceeded those of comparison groups of undergraduate students at a leading university (Lehrer and Chazan, 1998). Young children have also demonstrated powerful forms of early algebraic generalization (Lehrer and Chazan, 1998). Forms of generalization in science, such as experimentation, can be introduced before the secondary school years through a developmental approach to important mathematical and scientific ideas (Schauble et al., 1995; Warren and Rosebery, 1996). Such an approach entails becoming cognizant of the early origins of students’ thinking and then identifying how those ideas can be fostered and elaborated (Brown and Campione, 1994).
Attempts to create environments that are knowledge centered also raise important questions about how to foster an integrated understanding of a discipline. Many models of curriculum design seem to produce knowledge and skills that are disconnected rather than organized into coherent wholes. The National Research Council (1990:4) notes that “To the Romans, a curriculum was a rutted course that guided the path of two-wheeled chariots.” This rutted path metaphor is an appropriate description of the curriculum for many school subjects:
Vast numbers of learning objectives, each associated with pedagogical strategies, serve as mile posts along the trail mapped by texts from kindergarten to twelfth grade…. Problems are solved not by observing and responding to the natural landscape through which the mathematics curriculum passes, but by mastering time tested routines, conveniently placed along the path (National Research Council, 1990:4).
An alternative to a “rutted path” curriculum is one of “learning the landscape” (Greeno, 1991). In this metaphor, learning is analogous to learning
to live in an environment: learning your way around, learning what resources are available, and learning how to use those resources in conducting your activities productively and enjoyably (Greeno, 1991:175). The progressive formalization framework discussed above is consistent with this metaphor. Knowing where one is in a landscape requires a network of connections that link one’s present location to the larger space.
Traditional curricula often fail to help students “learn their way around” a discipline. The curricula include the familiar scope and sequence charts that specify procedural objectives to be mastered by students at each grade: though an individual objective might be reasonable, it is not seen as part of a larger network. Yet it is the network, the connections among objectives, that is important. This is the kind of knowledge that characterizes expertise (see Chapter 2). Stress on isolated parts can train students in a series of routines without educating them to understand an overall picture that will ensure the development of integrated knowledge structures and information about conditions of applicability.
An alternative to simply progressing through a series of exercises that derive from a scope and sequence chart is to expose students to the major features of a subject domain as they arise naturally in problem situations. Activities can be structured so that students are able to explore, explain, extend, and evaluate their progress. Ideas are best introduced when students see a need or a reason for their use—this helps them see relevant uses of knowledge to make sense of what they are learning. Problem situations used to engage students may include the historic reasons for the development of the domain, the relationship of that domain to other domains, or the uses of ideas in that domain (see Webb and Romberg, 1992). In Chapter 7 we present examples from history, science, and mathematics instruction that emphasize the importance of introducing ideas and concepts in ways that promote deep understanding.
A challenge for the design of knowledge-centered environments is to strike the appropriate balance between activities designed to promote understanding and those designed to promote the automaticity of skills necessary to function effectively without being overwhelmed by attentional requirements. Students for whom it is effortful to read, write, and calculate can encounter serious difficulties learning. The importance of automaticity has been demonstrated in a number of areas (e.g., Beck et al., 1989, 1991; Hasselbring et al., 1987; LaBerge and Samuels, 1974; see Chapter 2).
ASSESSMENT-CENTERED ENVIRONMENTS
In addition to being learner centered and knowledge centered, effectively designed learning environments must also be assessment centered. The key principles of assessment are that they should provide opportunities
for feedback and revision and that what is assessed must be congruent with one’s learning goals.
It is important to distinguish between two major uses of assessment. The first, formative assessment, involves the use of assessments (usually administered in the context of the classroom) as sources of feedback to improve teaching and learning. The second, summative assessment, measures what students have learned at the end of some set of learning activities. Examples of formative assessments include teachers’ comments on work in progress, such as drafts of papers or preparations for presentations. Examples of summative assessments include teacher-made tests given at the end of a unit of study and state and national achievement tests that students take at the end of a year. Ideally, teachers’ formative and summative assessments are aligned with the state and national assessments that students take at the end of the year; often, however, this is not the case. Issues of summative assessment for purposes of national, state, and district accountability are beyond the scope of this volume; our discussion focuses on classroom-based formative and summative assessments.
Formative Assessments and Feedback
Studies of adaptive expertise, learning, transfer, and early development show that feedback is extremely important (see Chapters 2, 3, and 4). Students’ thinking must be made visible (through discussions, papers, or tests), and feedback must be provided. Given the goal of learning with understanding, assessments and feedback must focus on understanding, and not only on memory for procedures or facts (although these can be valuable, too). Assessments that emphasize understanding do not necessarily require elaborate or complicated assessment procedures. Even multiple-choice tests can be organized in ways that assess understanding (see below).
Opportunities for feedback should occur continuously, but not intrusively, as a part of instruction. Effective teachers continually attempt to learn about their students’ thinking and understanding. They do a great deal of on-line monitoring of both group work and individual performances, and they attempt to assess students’ abilities to link their current activities to other parts of the curriculum and their lives. The feedback they give to students can be formal or informal. Effective teachers also help students build skills of self-assessment. Students learn to assess their own work, as well as the work of their peers, in order to help everyone learn more effectively (see, e.g., Vye et al., 1998a, b). Such self-assessment is an important part of the metacognitive approach to instruction (discussed in Chapters 3, 4, and 7).
In many classrooms, opportunities for feedback appear to occur relatively infrequently. Most teacher feedback—grades on tests, papers,
worksheets, homework, and on report cards—represent summative assessments that are intended to measure the results of learning. After receiving grades, students typically move on to a new topic and work for another set of grades. Feedback is most valuable when students have the opportunity to use it to revise their thinking as they are working on a unit or project. The addition of opportunities for formative assessment increases students’ learning and transfer, and they learn to value opportunities to revise (Barron et al., 1998; Black and William, 1998; Vye et al., 1998b). Opportunities to work collaboratively in groups can also increase the quality of the feedback available to students (Barron, 1991; Bereiter and Scardamalia, 1989; Fuchs et al., 1992; Johnson and Johnson, 1975; Slavin, 1987; Vye et al., 1998a), although many students must be helped to learn how to work collaboratively. New technologies provide opportunities to increase feedback by allowing students, teachers, and content experts to interact both synchronously and asynchronously (see Chapter 9).
A challenge of implementing good assessment practices involves the need to change many teachers’, parents’, and students’ models of what effective learning looks like. Many assessments developed by teachers overly emphasize memory for procedures and facts (Porter et al., 1993). In addition, many standardized tests that are used for accountability still overemphasize memory for isolated facts and procedures, yet teachers are often judged by how well their students do on such tests. One mathematics teacher consistently produced students who scored high on statewide examinations by helping students memorize a number of mathematical procedures (e.g., proofs) that typically appeared on the examinations, but the students did not really understand what they were doing, and often could not answer questions that required an understanding of mathematics (Schoenfeld, 1988).
Appropriately designed assessments can help teachers realize the need to rethink their teaching practices. Many physics teachers have been surprised at their students’ inabilities to answer seemingly obvious (to the expert) questions that assessed their students’ understanding, and this outcome has motivated them to revise their instructional practices (Redish, 1996). Similarly, visually based assessments of “number sense” (see Case and Moss, 1996) have helped teachers discover the need to help their students develop important aspects of mathematical understanding (Bransford et al., 1998). Innovative assessments that reveal students’ understanding of important concepts in science and mathematics have also been developed (Lehrer and Schauble, 1996a, b).
Formats for Assessing Understanding
Teachers have limited time to assess students’ performances and provide feedback, but new advances in technology can help solve this problem (see Chapter 9). Even without technology, however, advances have been made in devising simple assessments that measure understanding rather than memorization. In the area of physics, assessments like those used in Chapter 2 to compare experts and novices have been revised for use in classrooms. One task presents students with two problems and asks them to state whether both would be solved using a similar approach and state the reason for the decision:
-
A 2.5-kilogram ball with a radius of 4 centimeters is traveling at 7 meters/second on a rough horizontal surface, but not spinning. At some later time, the ball is rolling without slipping 5 meters/second. How much work was done by friction?
-
A 0.5-kilogram ball with a radius of 15 centimeters is initially sliding at 10 meters/second without spinning. The ball travels on a horizontal surface and eventually rolls without slipping. Find the ball’s final velocity.
Novices typically state that these two problems are solved similarly because they match on surface features—both involve a ball sliding and rolling on a horizontal surface. Students who are learning with understanding state that the problems are solved differently: the first can be solved by applying the work-energy theorem; the second can be solved by applying conservation of angular momentum (Hardiman et al., 1989); see Box 6.2. These kinds of assessment items can be used during the course of instruction to monitor the depth of conceptual understanding.
Portfolio assessments are another method of formative assessment. They provide a format for keeping records of students’ work as they progress throughout the year and, most importantly, for allowing students to discuss their achievements and difficulties with their teachers, parents, and fellow students (e.g., Wiske, 1997; Wolf, 1988). They take time to implement and they are often implemented poorly—portfolios often become simply another place to store student work but no discussion of the work takes place— but used properly, they provide students and others with valuable information about their learning progress over time.
Theoretical Frameworks for Assessment
A challenge for the learning sciences is to provide a theoretical framework that links assessment practices to learning theory. An important step in this direction is represented by the work of Baxter and Glaser (1997), who
|
BOX 6.2 How Do You Know? A 1-kilogram stick that is 2 meters long is placed on a frictionless surface and is free to rotate about a vertical pivot through one end. A 50-gram lump of putty is attached 80 centimeters from the pivot. Which of the following principles would allow you to determine the magnitude of the net force between the stick and the putty when the angular velocity of the system is 3 radians/second?
Performance on this item was near random for students finishing an introductory calculus-based physics course. The temptation is to match the “rotation” surface feature of the problem with “angular momentum,” when in fact the problem is solved by a simple application of Newton’s second law. Data such as these are important for helping teachers guide students toward the development of fluid, transferable knowledge (Leonard et al., 1996). |
provide a framework for integrating cognition and context in assessing achievement in science. In their report, performance is described in terms of the content and process task demands of the subject matter and the nature and extent of cognitive activity likely to be observed in a particular assessment situation. The framework provides a basis for examining how developers’ intentions are realized in performance assessments that purport to measure reasoning, understanding, and complex problem solving.
Characterizing assessments in terms of components of competence and the content-process demands of the subject matter brings specificity to generic assessment objectives such as “higher level thinking and deep understanding.” Characterizing student performance in terms of cognitive activities focuses attention on the differences in competence and subject-matter achievement that can be observed in learning and assessment situations. The kind and quality of cognitive activities in an assessment is a function of the content and process demands of the task involved. For example, consider the content-process framework for science assessment shown in Figure 6.2 (Baxter and Glaser, 1997). In this figure, task demands for content
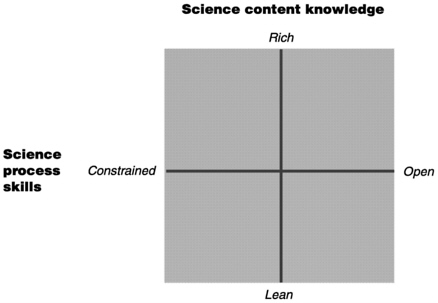
FIGURE 6.2 Content-process space of science assessments.
knowledge are conceptualized on a continuum from rich to lean (y axis). At one extreme are knowledge-rich tasks, tasks that require in-depth understanding of subject matter for their completion. At the other extreme are tasks that are not dependent on prior knowledge or related experiences; rather, performance is primarily dependent on the information given in the assessment situation. The task demands for process skills are conceptualized as a continuum from constrained to open (x axis). In open situations, explicit directions are minimized; students are expected to generate and carry out appropriate process skills for problem solution. In process-constrained situations, directions can be of two types: step-by-step, subject-specific procedures given as part of the task, or directions to explain the process skills that are necessary for task completion. In this situation, students are asked to generate explanations, an activity that does not require using the process skills. Assessment tasks can involve many possible combinations of content knowledge and process skills; Table 6.1 illustrates the relationship between the structure of knowledge and the organized cognitive activities.
COMMUNITY-CENTERED ENVIRONMENTS
New developments in the science of learning suggest that the degree to which environments are community centered is also important for learning. Especially important are norms for people learning from one another and continually attempting to improve. We use the term community centered to refer to several aspects of community, including the classroom as a commu-
TABLE 6.1 Cognitive Activity and Structure of Knowledge
|
|
Structure of Knowledge |
|
|
Organized Cognitive Activity |
Fragmented |
Meaningful |
|
Problem Representation |
Surface features and shallow understanding |
Underlying principles and relevant concepts |
|
Strategy Use |
Undirected trial-and-error problem solving |
Efficient, informative, and goal oriented |
|
Self-Monitoring |
Minimal and sporadic |
Ongoing and flexible |
|
Explanation |
Single statement of fact of description of superficial factors |
Principled and coherent |
nity, the school as a community, and the degree to which students, teachers, and administers feel connected to the larger community of homes, businesses, states, the nation, and even the world.
Classroom and School Communities
At the level of classrooms and schools, learning seems to be enhanced by social norms that value the search for understanding and allow students (and teachers) the freedom to make mistakes in order to learn (e.g., Brown and Campione, 1994; Cobb et al., 1992). Different classrooms and schools reflect different sets of norms and expectations. For example, an unwritten norm that operates in some classrooms is never to get caught making a mistake or not knowing an answer (see, e.g., Holt, 1964). This norm can hinder students’ willingness to ask questions when they do not understand the material or to explore new questions and hypotheses. Some norms and expectations are more subject specific. For example, the norms in a mathematics class may be that mathematics is knowing how to compute answers; a much better norm would be that the goal of inquiry is mathematical understanding. Different norms and practices have major effects on what is taught and how it is assessed (e.g., Cobb et al., 1992). Sometimes there are different sets of expectations for different students. Teachers may convey expectations for school success to some students and expectations for school failure to others (MacCorquodale, 1988). For example, girls are sometimes discouraged from participating in higher level mathematics and science. Students, too, may share and convey cultural expectations that proscribe the participation of girls in some classes (Schofield et al., 1990).
|
BOX 6.3 Talking in Class A speech-language pathologist working in an Inuit school (in northern Canada) asked a principal—who was not an Inuit—to compile a list of children who had speech and language problems in the school. The list contained a third of the students in the school, and next to several names the principal wrote, “Does not talk in class.” The speech-language pathologist consulted a local Inuit teacher for help determining how each child functioned in his or her native language. She looked at the names and said, “Well raised Inuit children should not talk in class. They should be learning by looking When the speech-language pathologist asked that teacher about one toddler she was studying who was very talkative and seemed to the non-Inuit researcher to be very bright, the teacher said: “Do you think he might have a learning problem? Some of these children who don’t have such high intelligence have trouble stopping themselves. They don’t know when to stop talking” (Crago, 1988:219). |
Classroom norms can also encourage modes of participation that may be unfamiliar to some students. For example, some groups rely on learning by observation and listening and then becoming involved in ongoing activities; school-like forms of talking may be unfamiliar for the children whose community has only recently included schools (Rogoff et al., 1993); see Box 6.3.
The sense of community in classrooms is also affected by grading practices, and these can have positive or negative effects depending on the students. For example, Navajo high school students do not treat tests and grades as competitive events the way that Anglo students do (Deyhle and Margonis, 1995). An Anglo high school counselor reported that Navajo parents complained about their children being singled out when the counselor started a “high achiever” bulletin board and wanted to put up the pictures of students with B averages or better. The counselor “compromised” by putting up happy stickers with the students’ names on them. A Navajo student, staring at the board, said “The board embarrasses us, to be stuck out like that” (Deyhle and Margonis, 1995:28).
More broadly, competition among students for teacher attention, approval, and grades is a commonly used motivator in U.S. schools. And in some situations, competition may create situations that impede learning. This is especially so if individual competition is at odds with a community ethic of individuals’ contributing their strengths to the community (Suina and Smolkin, 1994).
An emphasis on community is also imortant when attempting to borrow successful educational practices from other countries. For example, Japanese teachers spend considerable time working with the whole class, and they frequently ask students who have made errors to share their thinking with the rest of the class. This can be very valuable because it leads to discussions that deepen the understanding of everyone in the class. However, this practice works only because Japanese teachers have developed a classroom culture in which students are skilled at learning from one another and respect the fact that an analysis of errors is fruitful for learning (Hatano and Inagaki, 1996). Japanese students value listening, so they learn from large class discussions even if they do not have many chances to participate. The culture of American classrooms is often very different—many emphasize the importance of being right and contributing by talking. Teaching and learning must be viewed from the perspective of the overall culture of the society and its relationship to the norms of the classrooms. To simply attempt to import one or two Japanese teaching techniques into American classrooms may not produce the desired results.
The sense of community in a school also appears to be strongly affected by the adults who work in that environment. As Barth (1988) states:
The relationship among adults who live in a school has more to do with the character and quality of the school and with the accomplishments of the students than any other factor.
Studies by Bray (1998) and Talbert and McLaughlin (1993) emphasize the importance of teacher learning communities. We say more about this in Chapter 8.
Connections to the Broader Community
An analysis of learning environments from the perspective of community also includes a concern for connections between the school environment and the broader community, including homes, community centers, after-school programs, and businesses. Chapters 3, 4, and 5 showed that learning takes time; ideally, what is learned in school can be connected to out-of-school learning and vice versa. Often, however, this ideal is not reached. As John Dewey (1916) noted long ago:
From the standpoint of the child, the great waste in school comes from his inability to utilize the experience he gets outside…while on the other hand, he is unable to apply in daily life what he is learning in school. That is the isolation of the school—its isolation from life.
The importance of connecting the school with outside learning activities can be appreciated by considering Figure 6.3, which shows the percentage of time during a typical school year that students spend in school, sleeping,
and engaged in other activities (see Bransford et al., 2000). The percentage of time spent in school is comparatively small. If students spend one-third of their nonsleeping time outside of school watching television, this means that they spend more time watching television in a year than they spend in school. (We say more about television and learning in the next section.)
A key environment for learning is the family. Even when family members do not focus consciously on instructional roles, they provide resources for children’s learning, activities in which learning occurs, and connections to community (Moll, 1986a, b, 1990). Children also learn from the attitudes of family members toward skills and values of schooling.
The success of the family as a learning environment, especially in children’s early years (see Chapter 4), has provided inspiration and guidance for some of the changes recommended in schools. The phenomenal development of children from birth to age 4 or 5 is generally supported by family interactions in which children learn by engaging with and observing others in shared endeavors. Conversations and other interactions that occur around events of interest with trusted and skilled adult and child companions are especially powerful environments for children’s learning. Many of the recommendations for changes in schools can be seen as extensions of the learning activities that occur within families. In addition, recommendations
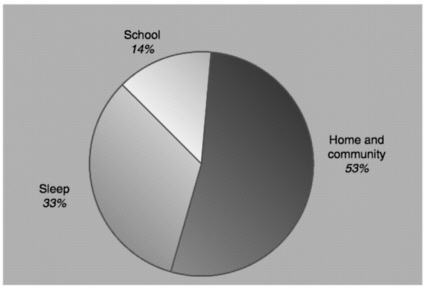
FIGURES 6.3 Comparison of time spent in school, home and community, and sleep. Percentages were calculated using 180 school days each year, and each school day was estimated to be 6.5 hours in length.
to include families in classroom activities and planning hold promise of bringing together two powerful systems for supporting children’s learning.
Children participate in many other institutions outside their homes that can foster learning. Some of these institutions have learning as part of their goals, including many after-school programs, organizations such as Boy and Girl Scouts and 4-H Clubs, museums, and religious groups. Others make learning more incidental, but learning takes place nevertheless (see McLaughlin, 1990, on youth clubs; Griffin and Cole, 1984, on the Fifth Dimension Program).
Connections to experts outside of school can also have a positive influence on in-school learning because they provide opportunities for students to interact with parents and other people who take an interest in what students are doing. It can be very motivating both to students and teachers to have opportunities to share their work with others. Opportunities to prepare for these events helps teachers raise standards because the consequences go beyond mere scores on a test (e.g., Brown and Campione, 1994, 1996; Cognition and Technology Group at Vanderbilt, in press b).
The idea of outside audiences who present challenges (complete with deadlines) has been incorporated into a number of instructional programs (e.g., Cognition and Technology Group at Vanderbilt, 1997; Wiske, 1997). Working to prepare for outsiders provides motivation that helps teachers maintain student interest. In addition, teachers and students develop a better sense of community as they prepare to face a common challenge. Students are also motivated to prepare for outside audiences who do not come to the classroom but will see their projects. Preparing exhibits for museums represents an excellent example (see Collins et al., 1991). New technologies that enhance the ability to connect classrooms to others in the school, to parents, business leaders, college students, content area experts, and others around the world are discussed in Chapter 9.
TELEVISION
For better or for worse, most children spent a considerable amount of time watching television; it has played an increasingly prominent role in children’s development over the past 50 years. Children watch a great deal of television before entering school, and television viewing continues throughout life. In fact, many students spend more hours watching television than attending school. Parents want their children to learn from television; at the same time they are concerned about what they are learning from the programs they watch (Greenfield, 1984).
Watching Different Kinds of Programs
Television programming for children ranges from educational to purely entertaining (see Wright and Huston, 1995). And there are different ways of watching programs—a child may watch in isolation or with an adult. Furthermore, just as in domains like chess, physics, or teaching (see Chapter 2), people’s existing knowledge and beliefs affect what they notice, understand, and remember from viewing television (Newcomb and Collins, 1979). The same program can have different effects depending on who is watching and whether the viewing is a solo activity or part of an interactive group. An important distinction is whether the program is intended to be educational or not.
One group of preschoolers aged 2–4 and first-grade students aged 6–7 watched about 7–8 hours of noneducational programming per week; the preschool children also watched an average of 2 hours of educational programming per week, and the older students watched 1 hour. Despite the low ratio of educational to noneducational viewing, the educational programs seemed to have positive benefits. The 2- to 4-year-old preschoolers performed better than non-viewers of educational programs on tests of school readiness, reading, mathematics, and vocabulary as much as 3 years later (Wright and Huston, 1995). Specifically, viewing educational programs was a positive predictor of letter-word knowledge, vocabulary size, and school readiness on standardized achievement tests. For the older students, the viewing of educational programs was related to better performance on tests of reading comprehension and teachers’ judgments of school adjustment in first and second grades, compared with children who were infrequent viewers. Overall, the effects of television viewing were not as widespread for the older students, and there were fewer significant effects for the older children than for the preschoolers. It is important to note that the effects of watching educational programs were evident “even when initial language skills, family education, income, and the quality of the home environment are taken into account” (Wright and Huston, 1995:22).
Effects on Beliefs and Attitudes
Television also provides images and role models that can affect how children view themselves, how they see others, attitudes about what academic subjects they should be interested in, and other topics related to person perception. These images can have both positive and negative effects. For example, when 8- to 14-year-olds watched programs designed to show positive attributes of children around the world, they were less likely to say that children from their own country were more interesting or more intelligent (O’Brien, 1981), and they began to see more similarities among
people around the world (Greenfield, 1984). And children who watched episodes of Sesame Street featuring handicapped children had more positive feelings toward children with disabilities.
However, children can also misinterpret programs about people from different cultures, depending on what they already know (Newcomb and Collins, 1979). Stereotyping represents a powerful effect of watching television that is potentially negative. Children bring sex role stereotypes with them to school that derive from television programs and commercials (Dorr, 1982).
As a powerful visual medium, television creates stereotypes even when there is no intent to sell an image. But experimental studies indicate that such stereotyping effects decrease with children as young as 5 if adults offer critiques of the stereotypic portrayals as the children watch programs (Dorr, 1982). Thus, entertainment programs can educate in positive ways and learned information can be extended through adult guidance and commentary.
In sum, television has an impact on children’s learning that must be taken seriously. But the medium is neither inherently beneficial nor harmful. The content that students watch, and how they watch it, has important effects on what they learn. Especially significant is the fact that informative or educational programming has been shown to have beneficial effects on school achievement and that a preponderance of non-educational, entertainment viewing can have negative effects. Furthermore, the benefits of informative viewing occur despite the fact that the ratio of young children’s viewing tends to be 7:1 in favor of entertainment television. These findings support the wisdom of continued attempts to develop and study television programs that can help students acquire the kinds of knowledge, skills, and attitudes that support their learning in school.
THE IMPORTANCE OF ALIGNMENT
In the beginning of this chapter we noted that the four perspectives on learning environments (the degree to which they are learner, knowledge, assessment, and community centered) would be discussed separately but ultimately needed to be aligned in ways that mutually support one another. Alignment is as important for schools as for organizations in general (e.g., Covey, 1990). A key aspect of task analysis (see Chapter 2) is the idea of aligning goals for learning with what is taught, how it is taught, and how it is assessed (both formatively and summatively). Without this alignment, it is difficult to know what is being learned. Students may be learning valuable information, but one cannot tell unless there is alignment between what they are learning and the assessment of that learning. Similarly, students may be learning things that others don’t value unless curricula and assess-
ments are aligned with the broad learning goals of communities (Lehrer and Shumow, 1997).
A systems approach to promote coordination among activities is needed to design effective learning environments (Brown and Campione, 1996). Many schools have checklists of innovative practices, such as the use of collaborative learning, teaching for understanding and problem solving, and using formative assessment. Often, however, these activities are not coordinated with one another. Teaching for understanding and problem solving may be “what we do on Fridays”; collaborative learning may be used to promote memorization of fact-based tests; and formative assessments may focus on skills that are totally disconnected from the rest of the students’ curriculum. In addition, students may be given opportunities to study collaboratively for tests yet be graded on a curve so that they compete with one another rather than trying to meet particular performance standards. In these situations, activities in the classroom are not aligned.
Activities within a particular classroom may be aligned yet fail to fit with the rest of the school. And a school as a whole needs to have a consistent alignment. Some schools communicate a consistent policy about norms and expectations for conduct and achievement. Others send mixed messages. For example, teachers may send behavior problems to the principal, who may inadvertently undermine the teacher by making light of the students’ behavior. Similarly, schedules may or may not be made flexible in order to accommodate in-depth inquiry, and schools may or may not be adjusted to minimize disruptions, including nonacademic “pullout” programs and even the number of classroom interruptions made by a principal’s overzealous use of the classroom intercom. Overall, different activities within a school may or may not compete with one another and impede overall progress. When principals and teachers work together to define a common vision for their entire school, learning can improve (e.g., Barth, 1988, 1991; Peterson et al., 1995).
Activities within schools must also be aligned with the goals and assessment practices of the community. Ideally, teachers’ goals for learning fit with the curriculum they teach and the school’s goals, which in turn fit the goals implicit in the tests of accountability used by the school system. Often these factors are out of alignment. Effective change requires a simultaneous consideration of all these factors (e.g., Bransford et al., 1998). The new scientific findings about learning provide a framework for guiding systemic change.
CONCLUSION
The goals and expectations for schooling have changed quite dramatically during the past century, and new goals suggest the need to rethink
such questions as what is taught, how it is taught, and how students are assessed. We emphasized that research on learning does not provide a recipe for designing effective learning environments, but it does support the value of asking certain kinds of questions about the design of learning environments.
Four perspectives on the design of learning environments—the degree to which they are student centered, knowledge centered, assessment centered, and community centered—are important in designing these environments.
A focus on the degree to which environments are learner centered is consistent with the strong body of evidence suggesting that learners’ use their current knowledge to construct new knowledge and that what they know and believe at the moment affects how they interpret new information. Sometimes learners’ current knowledge supports new learning, sometimes it hampers learning: effective instruction begins with what learners bring to the setting; this includes cultural practices and beliefs as well as knowledge of academic content.
Learner-centered environments attempt to help students make connections between their previous knowledge and their current academic tasks. Parents are especially good at helping their children make connections. Teachers have a harder time because they do not share the life experiences of each of their students. Nevertheless, there are ways to systematically become familiar with each student’s special interests and strengths.
Effective environments must also be knowledge centered. It is not sufficient only to attempt to teach general problem solving and thinking skills; the ability to think and solve problems requires well-organized knowledge that is accessible in appropriate contexts. An emphasis on being knowledge centered raises a number of questions, such as the degree to which instruction begins with students’ current knowledge and skills, rather than simply presents new facts about the subject matter. While young students are capable of grasping more complex concepts than was believed previously, those concepts must be presented in ways that are developmentally appropriate. A knowledge-centered perspective on learning environments also highlights the importance of thinking about designs for curricula. To what extent do they help students learn with understanding versus promote the acquisition of disconnected sets of facts and skills? Curricula that emphasize an excessively broad range of subjects run the risk of developing disconnected rather than connected knowledge; they fit well with the idea of a curriculum as being a well-worn path in a road. An alternative metaphor for curriculum is to help students develop interconnected pathways within a discipline so that they “learn their away around in it” and not lose sight of where they are.
Issues of assessment also represent an important perspective for viewing the design of learning environments. Feedback is fundamental to learning, but opportunities to receive it are often scarce in classrooms. Students may receive grades on tests and essays, but these are summative assessments that occur at the end of projects; also needed are formative assessments that provide students opportunities to revise and hence improve the quality of their thinking and learning. Assessments must reflect the learning goals that define various environments. If the goal is to enhance understanding, it is not sufficient to provide assessments that focus primarily on memory for facts and formulas. Many instructors have changed their approach to teaching after seeing how their students failed to understand seemingly obvious (to the expert) ideas.
The fourth perspective on learning environments involves the degree to which they promote a sense of community. Ideally, students, teachers, and other interested participants share norms that value learning and high standards. Norms such as these increase people’s opportunities to interact, receive feedback, and learn. There are several aspects of community, including the community of the classroom, the school, and the connections between the school and the larger community, including the home. The importance of connected communities becomes clear when one examines the relatively small amount of time spent in school compared to other settings. Activities in homes, community centers, and after-school clubs can have important effects on students’ academic achievement.
Finally, there needs to be alignment among the four perspectives of learning environments. They all have the potential to overlap and mutually influence one another. Issues of alignment appear to be very important for accelerating learning both within and outside of schools.
























