7
Effective Teaching: Examples in History, Mathematics, and Science
The preceding chapter explored implications of research on learning for general issues relevant to the design of effective learning environments. We now move to a more detailed exploration of teaching and learning in three disciplines: history, mathematics, and science. We chose these three areas in order to focus on the similarities and differences of disciplines that use different methods of inquiry and analysis. A major goal of our discussion is to explore the knowledge required to teach effectively in a diversity of disciplines.
We noted in Chapter 2 that expertise in particular areas involves more than a set of general problem-solving skills; it also requires well-organized knowledge of concepts and inquiry procedures. Different disciplines are organized differently and have different approaches to inquiry. For example, the evidence needed to support a set of historical claims is different from the evidence needed to prove a mathematical conjecture, and both of these differ from the evidence needed to test a scientific theory. Discussion in Chapter 2 also differentiated between expertise in a discipline and the ability to help others learn about that discipline. To use Shulman’s (1987) language, effective teachers need pedagogical content knowledge (knowledge about how to teach in particular disciplines) rather than only knowledge of a particular subject matter.
Pedagogical content knowledge is different from knowledge of general teaching methods. Expert teachers know the structure of their disciplines, and this knowledge provides them with cognitive roadmaps that guide the assignments they give students, the assessments they use to gauge students’ progress, and the questions they ask in the give and take of classroom life. In short, their knowledge of the discipline and their knowledge of pedagogy interact. But knowledge of the discipline structure does not in itself guide the teacher. For example, expert teachers are sensitive to those aspects of the discipline that are especially hard or easy for new students to master.
This means that new teachers must develop the ability to “understand in a pedagogically reflective way; they must not only know their own way around a discipline, but must know the ‘conceptual barriers’ likely to hinder others” (McDonald and Naso, 1986:8). These conceptual barriers differ from discipline to discipline.
An emphasis on interactions between disciplinary knowledge and pedagogical knowledge directly contradicts common misconceptions about what teachers need to know in order to design effective learning environments for their students. The misconceptions are that teaching consists only of a set of general methods, that a good teacher can teach any subject, or that content knowledge alone is sufficient.
Some teachers are able to teach in ways that involve a variety of disciplines. However, their ability to do so requires more than a set of general teaching skills. Consider the case of Barb Johnson, who has been a sixth-grade teacher for 12 years at Monroe Middle School. By conventional standards Monroe is a good school. Standardized test scores are about average, class size is small, the building facilities are well maintained, the administrator is a strong instructional leader, and there is little faculty and staff turnover. However, every year parents sending their fifth-grade students from the local elementary schools to Monroe jockey to get their children assigned to Barb Johnson’s classes. What happens in her classroom that gives it the reputation of being the best of the best?
During the first week of school Barb Johnson asks her sixth graders two questions: “What questions do you have about yourself?” and “What questions do you have about the world?” The students begin enumerating their questions, “Can they be about silly, little things?” asks one student. “If they’re your questions that you really want answered, they’re neither silly nor little,” replies the teacher. After the students list their individual questions, Barb organizes the students into small groups where they share lists and search for questions they have in common. After much discussion each group comes up with a priority list of questions, rank-ordering the questions about themselves and those about the world.
Back together in a whole group session, Barb Johnson solicits the groups’ priorities and works toward consensus for the class’s combined lists of questions. These questions become the basis for guiding the curriculum in Barb’s class. One question, “Will I live to be 100 years old?” spawned educational investigations into genetics, family and oral history, actuarial science, statistics and probability, heart disease, cancer, and hypertension. The students had the opportunity to seek out information from family members, friends, experts in various fields, on-line computer services, and books, as well as from the teacher. She describes what they had to do as becoming part of a “learning community.” According to Barb Johnson, “We decide what are the most compelling intellectual issues, devise ways to investigate those issues
and start off on a learning journey. Sometimes we fall short of our goal. Sometimes we reach our goal, but most times we exceed these goals—we learn more than we initially expected” (personal communication).
At the end of an investigation, Barb Johnson works with the students to help them see how their investigations relate to conventional subject-matter areas. They create a chart on which they tally experiences in language and literacy, mathematics, science, social studies and history, music, and art. Students often are surprised at how much and how varied their learning is. Says one student, “I just thought we were having fun. I didn’t realize we were learning, too!”
Barb Johnson’s teaching is extraordinary. It requires a wide range of disciplinary knowledge because she begins with students’ questions rather than with a fixed curriculum. Because of her extensive knowledge, she can map students’ questions onto important principles of relevant disciplines. It would not work to simply arm new teachers with general strategies that mirror how she teaches and encourage them to use this approach in their classrooms. Unless they have the relevant disciplinary knowledge, the teachers and the classes would quickly become lost. At the same time, disciplinary knowledge without knowledge about how students learn (i.e., principles consistent with developmental and learning psychology) and how to lead the processes of learning (i.e., pedagogical knowledge) would not yield the kind of learning seen in Barb Johnson’s classes (Anderson and Smith, 1987).
In the remainder of this chapter, we present illustrations and discussions of exemplary teaching in history, mathematics, and science. The three examples of history, mathematics, and science are designed to convey a sense of the pedagogical knowledge and content knowledge (Shulman, 1987) that underlie expert teaching. They should help to clarify why effective teaching requires much more than a set of “general teaching skills.”
HISTORY
Most people have had quite similar experiences with history courses: they learned the facts and dates that the teacher and the text deemed relevant. This view of history is radically different from the way that historians see their work. Students who think that history is about facts and dates miss exciting opportunities to understand how history is a discipline that is guided by particular rules of evidence and how particular analytical skills can be relevant for understanding events in their lives (see Ravitch and Finn, 1987). Unfortunately, many teachers do not present an exciting approach to history, perhaps because they, too, were taught in the dates-facts method.
Beyond Facts
In Chapter 2, we discussed a study of experts in the field of history and learned that they regard the available evidence as more than lists of facts (Wineburg, 1991). The study contrasted a group of gifted high school seniors with a group of working historians. Both groups were given a test of facts about the American Revolution taken from the chapter review section of a popular United States history textbook. The historians who had backgrounds in American history knew most of the items, while historians whose specialties lay elsewhere knew only a third of the test facts. Several students scored higher than some historians on the factual pretest. In addition to the test of facts, however, the historians and students were presented with a set of historical documents and asked to sort out competing claims and to formulate reasoned interpretations. The historians excelled at this task. Most students, on the other hand, were stymied. Despite the volume of historical information the students possessed, they had little sense of how to use it productively for forming interpretations of events or for reaching conclusions.
Different Views of History by Different Teachers
Different views of history affect how teachers teach history. For example, Wilson and Wineburg (1993) asked two teachers of American history to read a set of student essays on the causes of the American Revolution not as an unbiased or complete and definitive accounts of people and events, but to develop plans for the students’ “remediation or enrichment.” Teachers were provided with a set of essays on the question, “Evaluate the causes of the American Revolution,” written by eleventh-graders for a timed, 45-minute test. Consider the different types of feedback that Mr. Barnes and Ms. Kelsey gave a student paper; see Box 7.1.
Mr. Barnes’ comments on the actual content of the essays concentrated on the factual level. Ms. Kelsey’s comments addressed broader images of the nature of the domain, without neglecting important errors of fact. Overall, Mr. Barnes saw the papers as an indication of the bell-shaped distribution of abilities; Ms. Kelsey saw them as representing the misconception that history is about memorizing a mass of information and recounting a series of facts. These two teachers had very different ideas about the nature of learning history. Those ideas affected how they taught and what they wanted their students to achieve.
Studies of Outstanding History Teachers
For expert history teachers, their knowledge of the discipline and beliefs about its structure interact with their teaching strategies. Rather than simply introduce students to sets of facts to be learned, these teachers help people to understand the problematic nature of historical interpretation and analysis and to appreciate the relevance of history for their everyday lives.
One example of outstanding history teaching comes from the classroom of Bob Bain, a public school teacher in Beechwood, Ohio. Historians, he notes, are cursed with an abundance of data—the traces of the past threaten to overwhelm them unless they find some way of separating what is important from what is peripheral. The assumptions that historians hold about significance shape how they write their histories, the data they select, and the narrative they compose, as well as the larger schemes they bring to organize and periodize the past. Often these assumptions about historical significance remain unarticulated in the classroom. This contributes to students’ beliefs that their textbooks are the history rather than a history.
Bob Bain begins his ninth-grade high school class by having all the students create a time capsule of what they think are the most important artifacts from the past. The students’ task, then, is to put down on paper why they chose the items they did. In this way, the students explicitly articulate their underlying assumptions of what constitutes historical significance. Students’ responses are pooled, and he writes them on a large poster that he hangs on the classroom wall. This poster, which Bob Bain calls “Rules for Determining Historical Significance,” becomes a lightening rod for class discussions throughout the year, undergoing revisions and elaborations as students become better able to articulate their ideas.
At first, students apply the rules rigidly and algorithmically, with little understanding that just as they made the rules, they can also change them. But as students become more practiced in plying their judgments of significance, they come to see the rules as tools for assaying the arguments of different historians, which allows them to begin to understand why historians disagree. In this instance, the students’ growing ability to understand the interpretative nature of history is aided by their teacher’s deep understanding of a fundamental principle of the discipline.
Leinhardt and Greeno (1991, 1994) spent 2 years studying a highly accomplished teacher of advanced placement history in an urban high school in Pittsburgh. The teacher, Ms. Sterling, a veteran of over 20 years, began her school year by having her students ponder the meaning of the statement, “Every true history is contemporary history.” In the first week of the semester, Sterling thrust her students into the kinds of epistemological issues that one might find in a graduate seminar: “What is history?” “How do we know the past?” “What is the difference between someone who sits down to
|
BOX 7.1 Comments on Papers on the American Revoloution Student #7 When the French and Indian war ended, British expected Americans to help them pay back there war debts. That would be a reasonable request if the war was fought for the colonies, but it was fought for English imperialism so you can’t blame them for not wanting to pay. The taxes were just the start of the slow turn toward rebellion another factor was when parliament decided to forbid the colonial government to make any more money, Specie became scarcer than ever, and a lot of merchants were pushed into a “two way squeeze” and faced bankruptcy. If I had the choice between being loyal, or rebelling and having something to eat, I know what my choice would be. The colonist who were really loyal never did rebel, and 1/3 support the revolution. The main thing that turned most people was the amount of propaganda, speeches from people like Patrick Henry, and organizations like the “Association.” After the Boston Massacre and the issuing of the Intolerable acts, people were convinced there was a conspiracy in the royal government to extinguish America’s liberties. I think a lot of people also just were going with the flow, or were being pressured by the Sons of Liberty. Merchants who didn’t go along with boycotts often became the victims of mob violence. Overall though, people were sick of getting overtaxed and walked on and decided let’s do something about it. |
‘write history’ and the artifacts that are produced as part of ordinary experience?” The goal of this extended exercise is to help students understand history as an evidentiary form of knowledge, not as clusters of fixed names and dates.
One might wonder about the advisability of spending 5 days “defining history” in a curriculum with so much to cover. But it is precisely Sterling’s framework of subject-matter knowledge—her overarching understanding of the discipline as a whole—that permits students entry into the advanced world of historical sense-making. By the end of the course, students moved from being passive spectators of the past to enfranchised agents who could participate in the forms of thinking, reasoning, and engagement that are the hallmark of skilled historical cognition. For example, early in the school year, Ms. Sterling asked her students a question about the Constitutional Convention and “what were men able to do.” Paul took the question literally: “Uh, I think one of the biggest things that they did, that we talked about yesterday, was the establishment of the first settlements in the Northwest
|
Mr. Barnes’s Summary Comment —your topic sentence is weak —more factual detail would improve your essay —note spelling and grammar corrections C- Ms. Kelsey’s Summary Comment —The greatest strength of this essay is its outstanding effort to grapple thoughtfully with the question, why did the colonists rebel? Keep thinking personally, “What if I were here?” It is a great place to start. —To make the essay work, however, you need to refine your organization strategies significantly. Remember that your reader is basically ignorant, so you need to express your view as clearly as you can. Try to form your ideas from the beginning to a middle and then an end. In the beginning, tell what side you’re on: What made the colonists rebel— money, propaganda, conformity? In the middle, justify your view. What factors support your idea and will convince your reader? In the end, remind your reader again about your point of view. Go back and revise and hand this in again! SOURCE: Wilson and Wineburg (1993:Fig. 1). Reprinted by permission. |
area states.” But after 2 months of educating students into a way of thinking about history, Paul began to catch on. By January his responses to questions about the fall of the cotton-based economy in the South were linked to British trade policy and colonial ventures in Asia, as well as to the failure of Southern leaders to read public opinion accurately in Great Britain. Ms. Sterling’s own understanding of history allowed her to create a classroom in which students not only mastered concepts and facts, but also used them in authentic ways to craft historical explanations.
Debating the Evidence
Elizabeth Jensen prepares her group of eleventh graders to debate the following resolution:
Resolved: The British government possesses the legitimate authority to tax the American colonies.
As her students enter the classroom they arrange their desks into three groups—on the left of the room a group of “rebels,” on the right, a group of “loyalists,” and in the front, a group of “judges.” Off to the side with a spiral notebook on her lap sits Jensen, a short woman in her late 30s with a booming voice. But today that voice is silent as her students take up the question of the legitimacy of British taxation in the American colonies.
The rebels’ first speaker, a 16-year-old girl with a Grateful Dead T-shirt and one dangling earring, takes a paper from her notebook and begins:
England says she keeps troops here for our own protection. On face value, this seems reasonable enough, but there is really no substance to their claims. First of all, who do they think they are protecting us from? The French? Quoting from our friend Mr. Bailey on page 54, ‘By the settlement in Paris in 1763, French power was thrown completely off the continent of North America.’ Clearly not the French then. Maybe they need to protect us from the Spanish? Yet the same war also subdued the Spanish, so they are no real worry either. In fact, the only threat to our order is the Indians…but…we have a decent militia of our own…. So why are they putting troops here? The only possible reason is to keep us in line. With more and more troops coming over, soon every freedom we hold dear will be stripped away. The great irony is that Britain expects us to pay for these vicious troops, these British squelchers of colonial justice.
A loyalist responds:
We moved here, we are paying less taxes than we did for two generations in England, and you complain? Let’s look at why we are being taxed— the main reason is probably because England has a debt of £140,000,000. …This sounds a little greedy, I mean what right do they have to take our money simply because they have the power over us. But did you know that over one-half of their war debt was caused by defending us in the French and Indian War…. Taxation without representation isn’t fair. Indeed, it’s tyranny. Yet virtual representation makes this whining of yours an untruth. Every British citizen, whether he had a right to vote or not, is represented in Parliament. Why does this representation not extend to America?
A rebel questions the loyalist about this:
Rebel: What benefits do we get out of paying taxes to the crown?
Loyalist: We benefit from the protection.
Rebel: (cutting in) Is that the only benefit you claim, protection?
Loyalist: Yes—and all the rights of an Englishman.
Rebel: Okay, then what about the Intolerable Acts…denying us rights of British subjects. What about the rights we are denied?
Loyalist: The Sons of Liberty tarred and feather people, pillaged homes— they were definitely deserving of some sort of punishment.
Rebel: So should all the colonies be punished for the acts of a few colonies?
For a moment, the room is a cacophony of charges and countercharges. “It’s the same as in Birmingham,” shouts a loyalist. A rebel snorts disparagingly, “Virtual representation is bull.” Thirty-two students seem to be talking at once, while the presiding judge, a wiry student with horn-rimmed glasses, bangs his gavel to no avail. The teacher, still in the corner, still with spiral notebook in lap, issues her only command of the day. “Hold still!” she thunders. Order is restored and the loyalists continue their opening argument (from Wineburg and Wilson, 1991).
Another example of Elizabeth Jensen’s teaching involves her efforts to help her high school students understand the debates between Federalists and anti-Federalists. She knows that her 15- and 16-year-olds cannot begin to grasp the complexities of the debates without first understanding that these disagreements were rooted in fundamentally different conceptions of human nature—a point glossed over in two paragraphs in her history textbook. Rather than beginning the year with a unit on European discovery and exploration, as her text dictates, she begins with a conference on the nature of man. Students in her eleventh-grade history class read excerpts from the writings of philosophers (Hume, Locke, Plato, and Aristotle), leaders of state and revolutionaries (Jefferson, Lenin, Gandhi), and tyrants (Hitler, Mussolini), presenting and advocating these views before their classmates. Six weeks later, when it is time to study the ratification of the Constitution, these now-familiar figures—Plato, Aristotle, and others—are reconvened to be courted by impassioned groups of Federalists and anti-Federalists. It is Elizabeth Jensen’s understanding of what she wants to teach and what adolescents already know that allows her to craft an activity that helps students get a feel for the domain that awaits them: decisions about rebellion, the Constitution, federalism, slavery, and the nature of a government.
Conclusion
These examples provide glimpses of outstanding teaching in the discipline of history. The examples do not come from “gifted teachers” who know how to teach anything: they demonstrate, instead, that expert teachers have a deep understanding of the structure and epistemologies of their disciplines, combined with knowledge of the kinds of teaching activities that will help students come to understand the discipline for themselves. As we previously noted, this point sharply contradicts one of the popular—and dangerous—myths about teaching: teaching is a generic skill and a good teacher can teach any subject. Numerous studies demonstrate that any curriculum—including a textbook—is mediated by a teacher’s understanding of the subject domain (for history, see Wineburg and Wilson, 1988; for math, see Ball, 1993; for English, see Grossman et al., 1989). The uniqueness of the content knowledge and pedagogical knowledge necessary to teach his-
tory becomes clearer as one explores outstanding teaching in other disciplines.
MATHEMATICS
As is the case in history, most people believe that they know what mathematics is about—computation. Most people are familiar with only the computational aspects of mathematics and so are likely to argue for its place in the school curriculum and for traditional methods of instructing children in computation. In contrast, mathematicians see computation as merely a tool in the real stuff of mathematics, which includes problem solving, and characterizing and understanding structure and patterns. The current debate concerning what students should learn in mathematics seems to set proponents of teaching computational skills against the advocates of fostering conceptual understanding and reflects the wide range of beliefs about what aspects of mathematics are important to know. A growing body of research provides convincing evidence that what teachers know and believe about mathematics is closely linked to their instructional decisions and actions (Brown, 1985; National Council of Teachers of Mathematics, 1989; Wilson, 1990a, b; Brophy, 1990; Thompson, 1992).
Teachers’ ideas about mathematics, mathematics teaching, and mathematics learning directly influence their notions about what to teach and how to teach it—an interdependence of beliefs and knowledge about pedagogy and subject matter (e.g., Gamoran, 1994; Stein et al., 1990). It shows that teachers’ goals for instruction are, to a large extent, a reflection of what they think is important in mathematics and how they think students best learn it. Thus, as we examine mathematics instruction, we need to pay attention to the subject-matter knowledge of teachers, their pedagogical knowledge (general and content specific), and their knowledge of children as learners of mathematics. Paying attention to these domains of knowledge also leads us to examine teachers’ goals for instruction.
If students in mathematics classes are to learn mathematics with understanding—a goal that is accepted by almost everyone in the current debate over the role of computational skills in mathematics classrooms—then it is important to examine examples of teaching for understanding and to analyze the roles of the teacher and the knowledge that underlies the teacher’s enactments of those roles. In this section, we examine three cases of mathematics instruction that are viewed as being close to the current vision of exemplary instruction and discuss the knowledge base on which the teacher is drawing, as well as the beliefs and goals which guide his or her instructional decisions.
Multiplication with Meaning
For teaching multidigit multiplication, teacher-researcher Magdelene Lampert created a series of lessons in which she taught a heterogeneous group of 28 fourth-grade students. The students ranged in computational skill from beginning to learn the single-digit multiplication facts to being able to accurately solve n-digit by n-digit multiplications. The lessons were intended to give children experiences in which the important mathematical principles of additive and multiplicative composition, associativity, commutativity, and the distributive property of multiplication over addition were all evident in the steps of the procedures used to arrive at an answer (Lampert, 1986:316). It is clear from her description of her instruction that both her deep understanding of multiplicative structures and her knowledge of a wide range of representations and problem situations related to multiplication were brought to bear as she planned and taught these lessons. It is also clear that her goals for the lessons included not only those related to students’ understanding of mathematics, but also those related to students’ development as independent, thoughtful problem solvers. Lampert (1986:339) described her role as follows:
My role was to bring students’ ideas about how to solve or analyze problems into the public forum of the classroom, to referee arguments about whether those ideas were reasonable, and to sanction students’ intuitive use of mathematical principles as legitimate. I also taught new information in the form of symbolic structures and emphasized the connection between symbols and operations on quantities, but I made it a classroom requirement that students use their own ways of deciding whether something was mathematically reasonable in doing the work. If one conceives of the teacher’s role in this way, it is difficult to separate instruction in mathematics content from building a culture of sense-making in the classroom, wherein teacher and students have a view of themselves as responsible for ascertaining the legitimacy of procedures by reference to known mathematical principles. On the part of the teacher, the principles might be known as a more formal abstract system, whereas on the part of the learners, they are known in relation to familiar experiential contexts. But what seems most important is that teachers and students together are disposed toward a particular way of viewing and doing mathematics in the classroom.
Magdelene Lampert set out to connect what students already knew about multidigit multiplication with principled conceptual knowledge. She did so in three sets of lessons. The first set used coin problems, such as “Using only two kinds of coins, make $1.00 using 19 coins,” which encouraged children to draw on their familiarity with coins and mathematical principles that coin trading requires. Another set of lessons used simple stories and drawings to illustrate the ways in which large quantities could be grouped
for easier counting. Finally, the third set of lessons used only numbers and arithmetic symbols to represent problems. Throughout the lessons, students were challenged to explain their answers and to rely on their arguments, rather than to rely on the teacher or book for verification of correctness. An example serves to highlight this approach; see Box 7.2.
Lampert (1986:337) concludes:
…students used principled knowledge that was tied to the language of groups to explain what they were seeing. They were able to talk meaningfully about place value and order of operations to give legitimacy to procedures and to reason about their outcomes, even though they did not use technical terms to do so. I took their experimentations and arguments as evidence that they had come to see mathematics as more than a set of procedures for finding answers.
Clearly, her own deep understanding of mathematics comes into play as she teaches these lessons. It is worth noting that her goal of helping students see what is mathematically legitimate shapes the way in which she designs lessons to develop students’ understanding of two-digit multiplication.
Understanding Negative Numbers
Helping third-grade students extend their understanding of numbers from the natural numbers to the integers is a challenge undertaken by another teacher-researcher. Deborah Ball’s work provides another snapshot of teaching that draws on extensive subject content and pedagogical content knowledge. Her goals in instruction include “developing a practice that respects the integrity both of mathematics as a discipline and of children as mathematical thinkers” (Ball, 1993). That is, she not only takes into account what the important mathematical ideas are, but also how children think about the particular area of mathematics on which she is focusing. She draws on both her understanding of the integers as mathematical entities (subject-matter knowledge) and her extensive pedagogical content knowledge specifically about integers. Like Lampert, Ball’s goals go beyond the boundaries of what is typically considered mathematics and include developing a culture in which students conjecture, experiment, build arguments, and frame and solve problems—the work of mathematicians.
Deborah Ball’s description of work highlights the importance and difficulty of figuring out powerful and effective ways to represent key mathematical ideas to children (see Ball, 1993). A wealth of possible models for negative numbers exists and she reviewed a number of them—magic peanuts, money, game scoring, a frog on a number line, buildings with floors above and below ground. She decided to use the building model first and money later: she was acutely aware of the strengths and limitations of each
|
BOX 7.2 How Many Altogether? The teacher begins with a request for an example of a basic computation. Teacher: Can anyone give me a story that could go with this multiplication…12×4? Jessica: There were 12 jars, and each had 4 butterflies in it. Teacher: And if I did this multiplication and found the answer, what would I know about those Jessica: You’d know you had that many butterflies altogether. The teacher and students next illustrate Jessica’s story and construct a procedure for counting the butterflies. Teacher: Okay, here are the jars. The stars in them will stand for butterflies. Now, it will be easier for us to count how many butterflies there are altogether, if we think of the jars in groups. And as usual, the mathematician’s favorite number for thinking about groups is? [Draw a loop around 10 jars.] Sally: 10. The lesson progresses as the teacher and students construct a pictorial representation of grouping 10 sets of four butterflies and having 2 jars not in the group; they recognize that 12×4 can be thought of as 10×4 plus 2×4. Lampert then has the children explore other ways of grouping the jars, for example, into two groups of 6 jars. The students are obviously surprised that 6×4 plus 6×4 produces the same number as 10×4 plus 2×4. For Lampert, this is important information about the students’ understanding (formative assessment—see Chapter 6). It is a sign that she needs to do many more activities involving different groupings. In subsequent lessons, students are challenged with problems in which the two-digit number in the multiplication is much bigger and, ultimately, in which both numbers are quite large—28×65. Students continue to develop their understanding of the principles that govern multiplication and to invent computational procedures based on those principles. Students defend the reasonableness of their procedures by using drawings and stories. Eventually, students explore more traditional as well as alternative algorithms for two-digit multiplication, using only written symbols. |
model as a way for representing the key properties of numbers, particularly those of magnitude and direction. Reading Deborah Ball’s description of her deliberations, one is struck by the complexity of selecting appropriate models for particular mathematical ideas and processes. She hoped that the positional aspects of the building model would help children recognize that negative numbers were not equivalent to zero, a common misconception. She was aware that the building model would be difficult to use for modeling subtraction of negative numbers.
Deborah Ball begins her work with the students, using the building model by labeling its floors. Students readily labeled the underground floors and accepted them as “below zero.” They then explored what happened as little paper people entered an elevator at some floor and rode to another floor. This was used to introduce the conventions of writing addition and subtraction problems involving integers 4−6=−2 and −2+5=3. Students were presented with increasingly difficult problems. For example, “How many ways are there for a person to get to the second floor?” Working with the building model allowed students to generate a number of observations. For example, one student noticed that “any number below zero plus that same number above zero equals zero” (Ball, 1993:381). However, the model failed to allow for explorations for such problems 5+(−6) and Ball was concerned that students were not developing a sense that −5 was less than −2—it was lower, but not necessarily less. Ball then used a model of money as a second representational context for exploring negative numbers, noting that it, too, has limitations.
Clearly, Deborah Ball’s knowledge of the possible representations of integers (pedagogical content knowledge) and her understanding of the important mathematical properties of integers were foundational to her planning and her instruction. Again, her goals related to developing students’ mathematical authority, and a sense of community also came into play. Like Lampert, Ball wanted her students to accept the responsibility of deciding when a solution is reasonable and likely to be correct, rather than depending on text or teacher for confirmation of correctness.
Guided Discussion
The work of Lampert and Ball highlights the role of a teacher’s knowledge of content and pedagogical content knowledge in planning and teaching mathematics lessons. It also suggests the importance of the teacher’s understanding of children as learners. The concept of cognitively guided instruction helps illustrate another important characteristic of effective mathematics instruction: that teachers not only need knowledge of a particular topic within mathematics and knowledge of how learners think about the particular topic, but also need to develop knowledge about how the indi-
vidual children in their classrooms think about the topic (Carpenter and Fennema, 1992; Carpenter et al., 1996; Fennema et al., 1996). Teachers, it is claimed, will use their knowledge to make appropriate instructional decisions to assist students to construct their mathematical knowledge. In this approach, the idea of domains of knowledge for teaching (Shulman, 1986) is extended to include teachers’ knowledge of individual learners in their classrooms.
Cognitively guided instruction is used by Annie Keith, who teaches a combination first- and second-grade class in an elementary school in Madison Wisconsin (Hiebert et al., 1997). Her instructional practices are an example of what is possible when a teacher understands children’s thinking and uses that understanding to guide her teaching. A portrait of Ms. Keith’s classroom reveals also how her knowledge of mathematics and pedagogy influence her instructional decisions.
Word problems form the basis for almost all instruction in Annie Keith’s classroom. Students spend a great deal of time discussing alternative strategies with each other, in groups, and as a whole class. The teacher often participates in these discussions but almost never demonstrates the solution to problems. Important ideas in mathematics are developed as students explore solutions to problems, rather than being a focus of instruction per se. For example, place-value concepts are developed as students use base-10 materials, such as base-10 blocks and counting frames, to solve word problems involving multidigit numbers.
Mathematics instruction in Annie Keith’s class takes place in a number of different settings. Everyday first-grade and second-grade activities, such as sharing snacks, lunch count, and attendance, regularly serve as contexts for problem-solving tasks. Mathematics lessons frequently make use of math centers in which the students do a variety of activities. On any given day, children at one center may solve word problems presented by the teacher while at another center children write word problems to present to the class later or play a math game.
She continually challenges her students to think and to try to make sense of what they are doing in math. She uses the activities as opportunities for her to learn what individual students know and understand about mathematics. As students work in groups to solve problems, she observes the various solutions and mentally makes notes about which students should present their work: she wants a variety of solutions presented so that students will have an opportunity to learn from each other. Her knowledge of the important ideas in mathematics serves as one framework for the selection process, but her understanding of how children think about the mathematical ideas they are using also affects her decisions about who should present. She might select a solution that is actually incorrect to be presented so that she can initiate a discussion of a common misconception. Or she
may select a solution that is more sophisticated than most students have used in order to provide an opportunity for students to see the benefits of such a strategy. Both the presentations of solutions and the class discussions that follow provide her with information about what her students know and what problems she should use with them next.
Annie Keith’s strong belief that children need to construct their understanding of mathematical ideas by building on what they already know guides her instructional decisions. She forms hypotheses about what her students understand and selects instructional activities based on these hypotheses. She modifies her instruction as she gathers additional information about her students and compares it with the mathematics she wants them to learn. Her instructional decisions give her clear diagnoses of individual students’ current state of understanding. Her approach is not a free-for-all without teacher guidance: rather, it is instruction that builds on students’ understandings and is carefully orchestrated by the teacher, who is aware of what is mathematically important and also what is important to the learner’s progress.
Model-Based Reasoning
Some attempts to revitalize mathematics instruction have emphasized the importance of modeling phenomena. Work on modeling can be done from kindergarten through twelth grade (K–12). Modeling involves cycles of model construction, model evaluation, and model revision. It is central to professional practice in many disciplines, such as mathematics and science, but it is largely missing from school instruction. Modeling practices are ubiquitous and diverse, ranging from the construction of physical models, such as a planetarium or a model of the human vascular system, to the development of abstract symbol systems, exemplified by the mathematics of algebra, geometry, and calculus. The ubiquity and diversity of models in these disciplines suggest that modeling can help students develop understanding about a wide range of important ideas. Modeling practices can and should be fostered at every age and grade level (Clement, 1989; Hestenes, 1992; Lehrer and Romberg, 1996a, b; Schauble et al., 1995; see Box 7.3).
Taking a model-based approach to a problem entails inventing (or selecting) a model, exploring the qualities of the model, and then applying the model to answer a question of interest. For example, the geometry of triangles has an internal logic and also has predictive power for phenomena ranging from optics to wayfinding (as in navigational systems) to laying floor tile. Modeling emphasizes a need for forms of mathematics that are typically underrepresented in the standard curriculum, such as spatial visualization and geometry, data structure, measurement, and uncertainty. For example, the scientific study of animal behavior, like bird foraging, is se-
|
BOX 7.3 Physical Models Physical models, like models of solar systems or elbows, are microcosms of systems that draw heavily on children’s intuitions about resemblance to sustain the relationship between the world being modeled and the model itself. The photograph below displays a child’s model of the elbow. Note, for instance, the rubber bands that mimic the connective function of ligaments and the wooden dowels that are arranged so that their translation in the vertical plane cannot exceed 180 degrees. Though the search for function is supported by initial resemblance, what counts as resemblance typically changes as children revise their models. For example, attempts to make models exemplify elbow motion often lead to an interest in the way muscles might be arranged (from Lehrer and Schauble, 1996a, b).  Child’s Model of on Elbow |
verely limited unless one also has access to such mathematical concepts as variability and uncertainty. Hence, the practice of modeling introduces the further explorations of important “big ideas” in disciplines.
Conclusion
Increasingly, approaches to early mathematics teaching incorporate the premises that all learning involves extending understanding to new situations, that young children come to school with many ideas about mathematics, that knowledge relevant to a new setting is not always accessed spontaneously, and that learning can be enhanced by respecting and encouraging
children to try out the ideas and strategies that they bring to school-based learning in classrooms. Rather than beginning mathematics instruction by focusing solely on computational algorithms, such as addition and subtraction, students are encouraged to invent their own strategies for solving problems and to discuss why those strategies work. Teachers may also explicitly prompt students to think about aspects of their everyday life that are potentially relevant for further learning. For example, everyday experiences of walking and related ideas about position and direction can serve as a springboard for developing corresponding mathematics about the structure of large-scale space, position, and direction (Lehrer and Romberg, 1996b).
As research continues to provide good examples of instruction that help children learn important mathematics, there will be better understanding of the roles that teachers’ knowledge, beliefs, and goals play in their instructional thinking and actions. The examples we have provided here make it clear that the selection of tasks and the guidance of students’ thinking as they work through tasks is highly dependent on teachers’ knowledge of mathematics, pedagogical content knowledge, and knowledge of students in general.
SCIENCE
Two recent examples in physics illustrate how research findings can be used to design instructional strategies that promote the sort of problem-solving behavior observed in experts. Undergraduates who had finished an introductory physics course were asked to spend a total of 10 hours, spread over several weeks, solving physics problems using a computer-based tool that constrained them to perform a conceptual analysis of the problems based on a hierarchy of principles and procedures that could be applied to solve them (Dufresne et al., 1992). This approach was motivated by research on expertise (discussed in Chapter 2). The reader will recall that, when asked to state an approach to solving a problem, physicists generally discuss principles and procedures. Novices, in contrast, tend to discuss specific equations that could be used to manipulate variables given in the problem (Chi et al., 1981). When compared with a group of students who solved the same problems on their own, the students who used the computer to carry out the hierarchical analyses performed noticeably better in subsequent measures of expertise. For example, in problem solving, those who performed the hierarchical analyses outperformed those who did not, whether measured in terms of overall problem-solving performance, ability to arrive at the correct answer, or ability to apply appropriate principles to solve the problems; see Figure 7.1. Furthermore, similar differences emerged in problem categorization: students who performed the hierarchical analyses considered principles (as opposed to surface features) more often in
deciding whether or not two problems would be solved similarly; see Figure 7.2. (See Chapter 6 for an example of the type of item used in the categorization task of Figure 7.2.) It is also worth noting that both Figures 7.1 and 7.2 illustrate two other issues that we have discussed in this volume, namely that time on task is a major indicator for learning and that deliberate practice is an efficient way to promote expertise. In both cases, the control group made significant improvements simply as a result of practice (time on task), but the experimental group showed more improvements for the same amount of training time (deliberate practice).
Introductory physics courses have also been taught successfully with an approach for problem solving that begins with a qualitative hierarchical analysis of the problems (Leonard et al., 1996). Undergraduate engineering students were instructed to write qualitative strategies for solving problems before attempting to solve them (based on Chi et al., 1981). The strategies consisted of a coherent verbal description of how a problem could be solved and contained three components: the major principle to be applied; the justification for why the principle was applicable; and the procedures for applying the principle. That is, the what, why, and how of solving the problem were explicitly delineated; see Box 7.4. Compared with students who took a traditional course, students in the strategy-based course performed significantly better in their ability to categorize problems according to the relevant principles that could be applied to solve them; see Figure 7.3.
Hierarchical structures are useful strategies for helping novices both recall knowledge and solve problems. For example, physics novices who had completed and received good grades in an introductory college physics course were trained to generate a problem analysis called a theoretical problem description (Heller and Reif, 1984). The analysis consists of describing force problems in terms of concepts, principles, and heuristics. With such an approach, novices substantially improved in their ability to solve problems, even though the type of theoretical problem description used in the study was not a natural one for novices. Novices untrained in the theoretical descriptions were generally unable to generate appropriate descriptions on their own—even given fairly routine problems. Skills, such as the ability to describe a problem in detail before attempting a solution, the ability to determine what relevant information should enter the analysis of a problem, and the ability to decide which procedures can be used to generate problem descriptions and analyses, are tacitly used by experts but rarely taught explicitly in physics courses.
Another approach helps students organize knowledge by imposing a hierarchical organization on the performance of different tasks in physics (Eylon and Reif, 1984). Students who received a particular physics argument that was organized in hierarchical form performed various recall and problem-solving tasks better than subjects who received the same argument
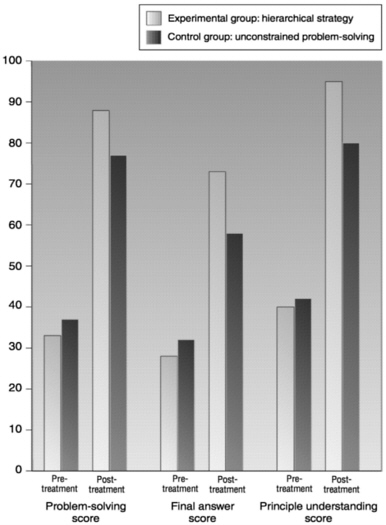
FIGURE 7.1 Effects of two methods of training on problem-solving, final answer, and principle understanding. SOURCE: Dufresne et al. (1992).
non-hierarchically. Similarly, students who received a hierarchical organization of problem-solving strategies performed much better than subjects who received the same strategies organized non-hierarchically. Thus, helping students to organize their knowledge is as important as the knowledge itself, since knowledge organization is likely to affect students’ intellectual performance.
These examples demonstrate the importance of deliberate practice and of having a “coach” who provides feedback for ways of optimizing performance (see Chapter 3). If students had simply been given problems to solve on their own (an instructional practice used in all the sciences), it is highly

FIGURE 7.2 Effects of two methods of training on considering principles for categorizing problems. SOURCE: Dufresne et al. (1992).
unlikely that they would have spent time efficiently. Students might get stuck for minutes, or even hours, in attempting a solution to a problem and either give up or waste lots of time. In Chapter 3, we discussed ways in which learners profit from errors and that making mistakes is not always time wasted. However, it is not efficient if a student spends most of the problem-solving time rehearsing procedures that are not optimal for promoting skilled performance, such as finding and manipulating equations to solve the problem, rather than identifying the underlying principle and procedures that apply to the problem and then constructing the specific equations needed. In deliberate practice, a student works under a tutor (human
|
BOX 7.4 Qualitative Strategies Written by Students Students enrolled in an introductory physics course were asked to write a strategy for an exam problem Exam Problem:
Strategy 1: Use the conservation of energy since the only nonconservative force in the system is the tension in the rope attached to the mass M and wound around the disk (assuming there is no friction between the axle and the disk, and the mass M and the air), and the work done by the tension to the disk and the mass cancel each other out. First, set up a coordinate system so the potential energy of the system at the start can be determined. There will be no kinetic energy at the start since it starts at rest. Therefore the potential energy is all the initial energy. Now set the initial energy equal to the final energy that is made up of the kinetic energy of the disk plus the mass M and any potential energy left in the system with respect to the chosen coordinate system. Strategy 2: I would use conservation of mechanical energy to solve this problem. The mass M has some potential energy while it is hanging there. When the block starts to accelerate downward the potential energy is transformed into rotational kinetic energy |
or computer based) to rehearse appropriate practices that enhance performance. Through deliberate practice, computer-based tutoring environments have been designed that reduce the time it takes individuals to reach real-world performance criteria from 4 years to 25 hours (see Chapter 9)!
Conceptual Change
Before students can really learn new scientific concepts, they often need to re-conceptualize deeply rooted misconceptions that interfere with the learning. As reviewed above (see Chapters 3 and 4), people spend considerable time and effort constructing a view of the physical world through
|
of the disk and kinetic energy of the falling mass. Equating the initial and final states and using the relationship between v and ω the speed of M can be found. Mechanical energy is conserved even with the nonconservative tension force because the tension force is internal to the system (pulley, mass, rope). Strategy 3: In trying to find the speed of the block I would try to find angular momentum kinetic energy, use gravity. I would also use rotational kinematics and moment of inertia around the center of mass for the disk. Strategy 4: There will be a torque about the center of mass due to the weight of the block, M. The force pulling downward is mg. The moment of inertia about the axle is 1/2 MR2. The moment of inertia multiplied by the angular acceleration. By plugging these values into a kinematic expression, the angular speed can be calculated. Then, the angular speed times the radius gives you the velocity of the block. The first two strategies display an excellent understanding of the principles, justification, and procedures that could be used to solve the problem (the what, why, and how for solving the problem). The last two strategies are largely a shopping list of physics terms or equations that were covered in the course, but the students are not able to articulate why or how they apply to the problem under consideration. Having students write strategies (after modeling strategy writing for them and providing suitable scaffolding to ensure progress) provides an excellent formative assessment tool for monitoring whether or not students are making the appropriate links between problem contexts, and the principles and procedures that could be applied to solve them (see Leonard et al., 1996). |
experiences and observations, and they may cling tenaciously to those views— however much they conflict with scientific concepts—because they help them explain phenomena and make predictions about the world (e.g., why a rock falls faster than a leaf).
One instructional strategy, termed “bridging,” has been successful in helping students overcome persistent misconceptions (Brown, 1992; Brown and Clement, 1989; Clement, 1993). The bridging strategy attempts to bridge from students’ correct beliefs (called anchoring conceptions) to their misconceptions through a series of intermediate analogous situations. Starting with the anchoring intuition that a spring exerts an upward force on the book resting on it, the student might be asked if a book resting on the
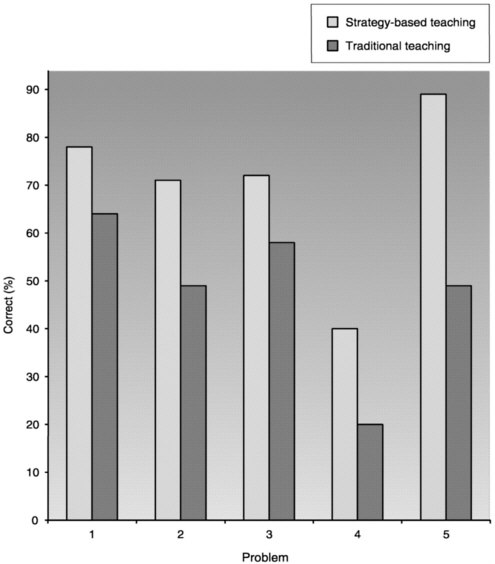
FIGURE 7.3 Percent correct choices under strategy-based and traditional teaching conditions by problem number in a categorization, multiple-choice task. SOURCE: Leonard et al. (1996).
middle of a long, “springy” board supported at its two ends experiences an upward force from the board. The fact that the bent board looks as if it is serving the same function as the spring helps many students agree that both the spring and the board exert upward forces on the book. For a student who may not agree that the bent board exerts an upward force on the book, the instructor may ask a student to place her hand on top of a vertical spring
and push down and to place her hand on the middle of the springy board and push down. She would then be asked if she experienced an upward force that resisted her push in both cases. Through this type of dynamic probing of students’ beliefs, and by helping them come up with ways to resolve conflicting views, students can be guided into constructing a coherent view that is applicable across a wide range of contexts.
Another effective strategy for helping students overcome persistent erroneous beliefs are interactive lecture demonstrations (Sokoloff and Thornton, 1997; Thornton and Sokoloff, 1997). This strategy, which has been used very effectively in large introductory college physics classes, begins with an introduction to a demonstration that the instructor is about to perform, such as a collision between two air carts on an air track, one a stationary light cart, the other a heavy cart moving toward the stationary cart. Each cart has an electronic “force probe” connected to it which displays on a large screen and in real-time the force acting on it during the collision. The teacher first asks the students to discuss the situation with their neighbors and then record a prediction as to whether one of the carts would exert a bigger force on the other during impact or whether the carts would exert equal forces.
The vast majority of students incorrectly predict that the heavier, moving cart exerts a larger force on the lighter, stationary cart. Again, this prediction seems quite reasonable based on experience—students know that a moving Mack truck colliding with a stationary Volkswagen beetle will result in much more damage done to the Volkswagen, and this is interpreted to mean that the Mack truck must have exerted a larger force on the Volkswagen. Yet, notwithstanding the major damage to the Volkswagen, Newton’s Third Law states that two interacting bodies exert equal and opposite forces on each other.
After the students make and record their predictions, the instructor performs the demonstration, and the students see on the screen that the force probes record forces of equal magnitude but oppositely directed during the collision. Several other situations are discussed in the same way: What if the two carts had been moving toward each other at the same speed? What if the situation is reversed so that the heavy cart is stationary and the light cart is moving toward it? Students make predictions and then see the actual forces between the carts displayed as they collide. In all cases, students see that the carts exert equal and opposite forces on each other, and with the help of a discussion moderated by the instructor, the students begin to build a consistent view of Newton’s Third Law that incorporates their observations and experiences.
Consistent with the research on providing feedback (see Chapter 3), there is other research that suggests that students’ witnessing the force displayed in real-time as the two carts collide helps them overcome their misconceptions; delays of as little as 20–30 minutes in displaying graphic data
of an event occurring in real-time significantly inhibits the learning of the underlying concept (Brasell, 1987).
Both bridging and the interactive demonstration strategies have been shown to be effective at helping students permanently overcome misconceptions. This finding is a major breakthrough in teaching science, since so much research indicates that students often can parrot back correct answers on a test that might be erroneously interpreted as displaying the eradication of a misconception, but the same misconception often resurfaces when students are probed weeks or months later (see Mestre, 1994, for a review).
Teaching as Coaching
One of the best examples of translating research into practice is Minstrell’s (1982, 1989, 1992) work with high school physics students. Minstrell uses many research-based instructional techniques (e.g., bridging, making students’ thinking visible, facilitating students’ ability to restructure their own knowledge) to teach physics for understanding. He does this through classroom discussions in which students construct understanding by making sense of physics concepts, with Minstrell playing a coaching role. The following quote exemplifies his innovative and effective instructional strategies (Minstrell, 1989:130–131):
Students’ initial ideas about mechanics are like strands of yarn, some unconnected, some loosely interwoven. The act of instruction can be viewed as helping the students unravel individual strands of belief, label them, and then weave them into a fabric of more complete understanding. An important point is that later understanding can be constructed, to a considerable extent, from earlier beliefs. Sometimes new strands of belief are introduced, but rarely is an earlier belief pulled out and replaced. Rather than denying the relevancy of a belief, teachers might do better by helping students differentiate their present ideas from and integrate them into conceptual beliefs more like those of scientists.
Describing a lesson on force, Minstrell (1989:130–131) begins by introducing the topic in general terms:
Today we are going to try to explain some rather ordinary events that you might see any day. You will find that you already have many good ideas that will help explain those events. We will find that some of our ideas are similar to those of the scientist, but in other cases our ideas might be different. When we are finished with this unit, I expect that we will have a much clearer idea of how scientists explain those events, and I know that you will feel more comfortable about your explanations…A key idea we are going to use is the idea of force. What does the idea of force mean to you?
Many views emerge from the ensuing classroom discussion, from the typical “push or pull” to descriptions that include sophisticated terms, such as en-
ergy and momentum. At some point Minstrell guides the discussion to a specific example: he drops a rock and asks students how the event can be explained using their ideas about force. He asks students to individually formulate their ideas and to draw a diagram showing the major forces on the rock as arrows, with labels to denote the cause of each force. A lengthy discussion follows in which students present their views, views that contain many irrelevant (e.g., nuclear forces) or fictitious forces (e.g., the spin of the earth, air). In his coaching, Minstrell asks students to justify their choices by asking questions, such as “How do you know?” “How did you decide?” “Why do you believe that?”
With this approach, Minstrell has been able to identify many erroneous beliefs of students that stand in the way of conceptual understanding. One example is the belief that only active agents (e.g., people) can exert forces, that passive agents (e.g., a table) cannot. Minstrell (1992) has developed a framework that helps both to make sense of students’ reasoning and to design instructional strategies. (For a related theoretical framework for classifying and explaining student reasoning, see the discussion of “phenomenological primitives” in DiSessa, 1988, 1993.) Minstrell describes identifiable pieces of students’ knowledge as “facets,” a facet being a convenient unit of thought, a piece of knowledge, or a strategy seemingly used by the student in addressing a particular situation. Facets may relate to conceptual knowledge (e.g., passive objects do not exert force), to strategic knowledge (e.g., average velocity can be determined by adding the initial and final velocities and dividing by two), or generic reasoning (e.g., the more the X, the more the Y). Identifying students’ facets, what cues them in different contexts, and how students use them in reasoning are all helpful in devising instructional strategies.
Interactive Instruction in Large Classes
One of the obstacles to instructional innovation in large introductory science courses at the college level is the sheer number of students who are taught at one time. How does an instructor provide an active learning experience, provide feedback, accommodate different learning styles, make students’ thinking visible, and provide scaffolding and tailored instruction to meet specific student needs when facing more than 100 students at a time? Classroom communication systems can help the instructor of a large class accomplish these objectives. One such system, called Classtalk, consists of both hardware and software that allows up to four students to share an input device (e.g., a fairly inexpensive graphing calculator) to “sign on” to a classroom communication network that permits the instructor to send questions for students to work on and permits students to enter answers through their input device. Answers can then be displayed anonymously in histogram
form to the class, and a permanent record of each student’s response is recorded to help evaluate progress as well as the effectiveness of instruction.
This technology has been used successfully at the University of Massachusetts-Amherst to teach physics to a range of students, from non-science majors to engineering and science majors (Dufresne et al., 1996; Wenk et al., 1997; Mestre et al., 1997). The technology creates an interactive learning environment in the lectures: students work collaboratively on conceptual questions, and the histogram of students’ answers is used as a visual springboard for classwide discussions when students defend the reasoning they used to arrive at their answers. This technology makes students’ thinking visible and promotes critical listening, evaluation, and argumentation in the class. The teacher is a coach, providing scaffolding where needed, tailoring “mini-lectures” to clear up points of confusion, or, if things are going well, simply moderating the discussion and allowing students to figure out things and reach consensus on their own. The technology is also a natural mechanism to support formative assessment during instruction, providing both the teacher and students with feedback on how well the class is grasping the concepts under study. The approach accommodates a wider variety of learning styles than is possible by lectures and helps to foster a community of learners focused on common objectives and goals.
Science for All Children
The examples above present some effective strategies for teaching and learning science for high school and college students. We drew some general principles of learning from these examples and stressed that the findings consistently point to the strong effect of knowledge structures on learning. These studies also emphasize the importance of class discussions for developing a language for talking about scientific ideas, for making students’ thinking explicit to the teacher and to the rest of the class, and for learning to develop a line of argumentation that uses what one has learned to solve problems and explain phenomena and observations.
The question that immediately occurs is how to teach science to younger children or to students who are considered to be educationally “at risk.” One approach that has been especially useful in science teaching was developed with language-minority grade-school children: Chèche Konnen, which in Haitian Creole means search for knowledge (Rosebery et al., 1992). The approach stresses how discourse is a primary means for the search for knowledge and scientific sense-making. It also illustrates how scientific ideas are constructed. In this way it mirrors science, in the words of Nobel Laureate Sir Peter Medawar (1982:111):
Like other exploratory processes, [the scientific method] can be resolved into a dialogue between fact and fancy, the actual and the possible; between what could be true and what is in fact the case. The purpose of scientific enquiry is not to compile an inventory of factual information, nor to build up a totalitarian world picture of Natural Laws in which every event that is not compulsory is forbidden. We should think of it rather as a logically articulated structure of justifiable beliefs about a Possible World— a story which we invent and criticize and modify as we go along, so that it ends by being, as nearly as we can make it, a story about real life.
The Chèche Konnen approach to teaching began by creating “communities of scientific practice” in language-minority classrooms in a few Boston and Cambridge, MA public schools. “Curriculum” emerges in these classrooms from the students’ questions and beliefs and is shaped in ongoing interactions that include both the teacher and students. Students explore their own questions, much as we described above in Barb Johnson’s class. In addition, students design studies, collect information, analyze data and construct evidence, and they then debate the conclusions that they derive from their evidence. In effect, the students build and argue about theories; see Box 7.5.
Students constructed scientific understandings through an iterative process of theory building, criticism, and refinement based on their own questions, hypotheses, and data analysis activities. Question posing, theorizing, and argumentation formed the structure of the students’ scientific activity. Within this structure, students explored the implications of the theories they held, examined underlying assumptions, formulated and tested hypotheses, developed evidence, negotiated conflicts in belief and evidence, argued alternative interpretations, provided warrants for conclusions, and so forth. The process as a whole provided a richer, more scientifically grounded experience than the conventional focus on textbooks or laboratory demonstrations.
The emphasis on establishing communities of scientific practice builds on the fact that robust knowledge and understandings are socially constructed through talk, activity, and interaction around meaningful problems and tools (Vygotsky, 1978). The teacher guides and supports students as they explore problems and define questions that are of interest to them. A community of practice also provides direct cognitive and social support for the efforts of the group’s individual members. Students share the responsibility for thinking and doing: they distribute their intellectual activity so that the burden of managing the whole process does not fall to any one individual. In addition, a community of practice can be a powerful context for constructing scientific meanings. In challenging one another’s thoughts and beliefs, students must be explicit about their meanings; they must negotiate conflicts in belief or evidence; and they must share and synthesize their knowledge to
|
BOX 7.5 Which Water Tastes Better? The seventh- and eighth-grade students in a Haitian Creole bilingual program wanted to find the “truth” of a belief held by most of their classmates: that drinking water from the fountain on the third floor, where the junior high was located, was superior to the water from the other fountains in their school. Challenged by their teacher, the students set out to determine whether they actually preferred the water from the third floor or only thought they did. As a first step, the students designed and took a blind taste test of the water from fountains on all three floors of the building. They found, to their surprise, that two-thirds of them chose the water from the first-floor fountain, even though they all said that they preferred drinking from the third-floor fountain. The students did not believe the data. They held firmly to their beliefs that the first-floor fountain was the worst because “all the little kids slobber in it.” (The first-floor fountain is located near the kindergarten and first grade classrooms.) Their teacher was also suspicious of the results because she had expected no differences among the three water fountains. These beliefs and suspicions motivated students to conduct a second taste test with a larger sample drawn from the rest of the junior high. The students decided where, when, and how to run their experiment. They discussed methodological issues: How to collect the water, how to hide the identity of the sources, and, crucially, how many fountains to include. They decided to include the same three fountains as before so that they could compare results. |
achieve understanding (Brown and Palincsar, 1989; Inagaki and Hatano, 1987).
What do students learn from participating in a scientific sense-making community? Individual interviews with students before and after the water taste test investigation (see Box 7.5), first in September and again the following June, showed how the students’ knowledge and reasoning changed. In the interviews (conducted in Haitian Creole), the students were asked to think aloud about two open-ended real-world problems—pollution in the Boston Harbor and a sudden illness in an elementary school. The researchers were interested in changes in students’ conceptual knowledge about aquatic ecosystems and in students’ uses of hypotheses, experiments, and explanations to organize their reasoning (for a complete discussion, see Rosebery et al., 1992).
|
They worried about bias in the voting process. What if some students voted more than once? Each student in the class volunteered to organize a piece of the experiment. About 40 students participated in the blind taste test. When they analyzed their data, they found support for their earlier results 88 percent of the junior high students thought they preferred water from the third-floor fountain, but 55 percent actually chose the water from the first floor (a result of 33 percent would be chance). Faced with this evidence, the students suspicions turned to curiosity. Why was the water from the first-floor fountain preferred? How can they determine the source of the preference? They decided to analyze the school’s water along several dimensions, among them acidity, salinity, temperature and bacteria. They found that all the fountains had unacceptably high levels of bacteria. In fact, the first-floor fountain (the one most preferred) had the highest bacterial count. They also found that the water from the first-floor fountain was 20 degrees (Fahrenheit) colder than the water from fountains on the other floors. Based on their findings, they concluded that temperature was probably a deciding factor in taste preference. They hypothesized that the water was naturally cooled as it sat in the city’s underground pipes during the winter months (the study was conducted in February) and warmed as it flowed from the basement to the third floor. SOURCE: Rosebery et al. (1992). |
Conceptual Knowledge
Not surprisingly, the students knew more about water pollution and aquatic ecosystems in June than they did in September. They were also able to use this knowledge generatively. One student explained how she would clean the water in Boston Harbor (Rosebery et al., 1992:86).
Like you look for the things, take the garbage out of the water, you put a screen to block all the paper and stuff, then you clean the water; you put chemical products in it to clean the water, and you’d take all the microscopic life out. Chlorine and alum, you put in the water. They’d gather the little stuff, the little stuff would stick to the chemical products, and they would clean the water.
Note that this explanation contains misconceptions. By confusing the cleaning of drinking water with the cleaning of sea water, the student suggests adding chemicals to take all microscopic life from the water (good for drinking water, but bad for the ecosystem of Boston Harbor). This example
illustrates the difficulties in transferring knowledge appropriately from one context to another (see Chapter 3). Despite these shortcomings, it is clear that this student is starting on the path to scientific thinking, leaving behind the more superficial “I’d take all the bad stuff out of the water” type of explanation. It is also clear that by making the student’s thinking visible, the teacher is in an excellent position to refine her (and perhaps the class’s) understanding.
Scientific Thinking
Striking changes appeared in students’ scientific reasoning. In September, there were three ways in which the students showed little familiarity with scientific forms of reasoning. First, the students did not understand the function of hypotheses or experiments in scientific inquiry. When asked for their ideas about what could be making the children sick, the students tended, with few exceptions, to respond with short, unelaborated, often untestable “hypotheses” that simply restated the phenomena described in the problem: “That’s a thing…. Ah, I could say a person, some person that gave them something…. Anything, like give poison to make his stomach hurt” (Rosebery et al., 1992:81).
Second, the students conceptualized evidence as information they already knew, either through personal experience or second-hand sources, rather than data produced through experimentation or observation. When asked to generate an experiment to justify an hypothesis—“How would you find out?” —they typically offered declarations: “Because the garbage is a poison for them…. The garbage made the fish die” (Rosebery et al., 1992:78).
Third, the students interpreted an elicitation for an experiment—“How would you be sure?” —as a text comprehension question for which there was a “right” answer. They frequently responded with an explanation or assertion of knowledge and consistently marked their responses as explanatory (“because”): “Because fish don’t eat garbage. They eat plants under the water” (page 78).
In the June interviews, the students showed that they had become familiar with the function of hypotheses and experiments and with reasoning within larger explanatory frameworks. Elinor had developed a model of an integrated water system in which an action or event in one part of the system had consequences for other parts (Rosebery et al., 1992:87):
You can’t leave [the bad stuff] on the ground. If you leave it on the ground, the water that, the earth has water underground, it will still spoil the water underground. Or when it rains it will just take it and, when it rains, the water runs, it will take it and leave it in the river, in where the water goes in. Those things, poison things, you aren’t supposed to leave it on the ground.
In June, the students no longer invoked anonymous agents, but put forward chains of hypotheses to explain phenomena, such as why children were getting sick (page 88):
Like, you could test what the kids ate and, like, test the water, too; it could be the water that isn’t good, that has microbes, that might have microscopic animals in it to make them sick.
The June interviews also showed that students had begun to develop a sense of the function and form of experimentation. They no longer depended on personal experience as evidence, but proposed experiments to test specific hypotheses. In response to a question about sick fish, Laure clearly understands how to find a scientific answer (page 91):
I’d put a fish in fresh water and one fish in a water full of garbage. I’d give the fresh water fish food to eat and the other one in the nasty water, I’d give it food to eat to see if the fresh water, if the one in the fresh water would die with the food I gave it, if the one in the dirty water would die with the food I gave it…. I would give them the same food to see if the things they eat in the water and the things I give them now, which will make them healthy and which wouldn’t make them healthy.
Conclusion
Teaching and learning in science have been influenced very directly by research studies on expertise (see Chapter 2). The examples discussed in this chapter focus on two areas of science teaching: physics and junior high school biology. Several of the teaching strategies illustrated ways to help students think about the general principles or “big” ideas in physics before jumping to formulas and equations. Others illustrate ways to help students engage in deliberate practice (see Chapter 3) and to monitor their progress.
Learning the strategies for scientific thinking have another objective: to develop thinking acumen needed to promote conceptual change. Often, the barrier to achieving insights to new solutions is rooted in a fundamental misconception about the subject matter. One strategy for helping students in physics begins with an “anchoring intuition” about a phenomenon and then gradually bridging it to related phenomena that are less intuitive to the student but involve the same physics principles. Another strategy involves the use of interactive lecture demonstrations to encourage students to make predictions, consider feedback, and then reconceptualize phenomena.
The example of Chèche Konnen demonstrates the power of a sense-making approach to science learning that builds on the knowledge that students bring with them to school from their home cultures, including their familiar discourse practices. Students learned to think, talk, and act scientifically, and their first and second languages mediated their learning in power-
ful ways. Using Haitian Creole, they designed their studies, interpreted data, and argued theories; using English, they collected data from their mainstream peers, read standards to interpret their scientific test results, reported their findings, and consulted with experts at the local water treatment facility.
CONCLUSION
Outstanding teaching requires teachers to have a deep understanding of the subject matter and its structure, as well as an equally thorough understanding of the kinds of teaching activities that help students understand the subject matter in order to be capable of asking probing questions.
Numerous studies demonstrate that the curriculum and its tools, including textbooks, need to be dissected and discussed in the larger contexts and framework of a discipline. In order to be able to provide such guidance, teachers themselves need a thorough understanding of the subject domain and the epistemology that guides the discipline (for history, see Wineburg and Wilson, 1988; for math and English, see Ball, 1993; Grossman et al., 1989; for science, see Rosebery et al., 1992).
The examples in this chapter illustrate the principles for the design of learning environments that were discussed in Chapter 6: they are learner, knowledge, assessment, and community centered. They are learner centered in the sense that teachers build on the knowledge students bring to the learning situation. They are knowledge centered in the sense that the teachers attempt to help students develop an organized understanding of important concepts in each discipline. They are assessment centered in the sense that the teachers attempt to make students’ thinking visible so that ideas can be discussed and clarified, such as having students (1) present their arguments in debates, (2) discuss their solutions to problems at a qualitative level, and (3) make predictions about various phenomena. They are community centered in the sense that the teachers establish classroom norms that learning with understanding is valued and students feel free to explore what they do not understand.
These examples illustrate the importance of pedagogical content knowledge to guide teachers. Expert teachers have a firm understanding of their respective disciplines, knowledge of the conceptual barriers that students face in learning about the discipline, and knowledge of effective strategies for working with students. Teachers’ knowledge of their disciplines provides a cognitive roadmap to guide their assignments to students, to gauge student progress, and to support the questions students ask. The teachers focus on understanding rather than memorization and routine procedures to follow, and they engage students in activities that help students reflect on their own learning and understanding.
The interplay between content knowledge and pedagogical knowledge illustrated in this chapter contradicts a commonly held misconception about teaching—that effective teaching consists of a set of general teaching strategies that apply to all content areas. This notion is erroneous, just as is the idea that expertise in a discipline is a general set of problem-solving skills that lack a content knowledge base to support them (see Chapter 2).
The outcomes of new approaches to teaching as reflected in the results of summative assessments are encouraging. Studies of students’ discussions in classrooms indicate that they learn to use the tools of systematic inquiry to think historically, mathematically, and scientifically. How these kinds of teaching strategies reveal themselves on typical standardized tests is another matter. In some cases there is evidence that teaching for understanding can increase scores on standardized measures (e.g., Resnick et al., 1991); in other cases, scores on standardized tests are unaffected, but the students show sizable advantages on assessments that are sensitive to their comprehension and understanding rather than reflecting sheer memorization (e.g., Carpenter et al., 1996; Secules et al., 1997).
It is noteworthy that none of the teachers discussed in this chapter felt that he or she was finished learning. Many discussed their work as involving a lifelong and continuing struggle to understand and improve. What opportunities do teachers have to improve their practice? The next chapter explores teachers’ chances to improve and advance their knowledge in order to function as effective professionals.